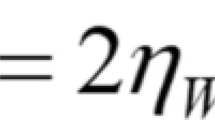Computations with viscoplastic and viscoelastoplastic fluids

Abstract

This numerical study focuses on regularised Bingham-type and viscoelastoplastic fluids, performing simulations for 4:1:4 contraction–expansion flow with a hybrid finite element–finite volume subcell scheme. The work explores the viscoplastic regime, via the Bingham–Papanastasiou model, and extends this into the viscoelastoplastic regime through the Papanastasiou–Oldroyd model. Our findings reveal the significant impact that elevation has in yield stress parameters, and in sharpening of the stress singularity from that of the Oldroyd/Newtonian models to the ideal Bingham form. Such aspects are covered in field response via vortex behaviour, pressure-drops, stress field structures and yielded–unyielded zones. With rising yield stress parameters, vortex trends reflect suppression in both upstream and downstream vortices. Viscoelastoplasticity, with its additional elasticity properties, tends to disturb upstream–downstream vortex symmetry balance, with knock-on effects according to solvent-fraction and level of elasticity. Yield fronts are traced with increasing yield stress influences, revealing locations where relatively unyielded material aggregates. Analysis of pressure drop data reveals significant increases in the viscoplastic Bingham–Papanastasiou case, O (12%) above the equivalent Newtonian fluid, that are reduced to 8% total contribution increase in the viscoelastoplastic Papanastasiou–Oldroyd case. This may be argued to be a consequence of strengthening in first normal stress effects.

Introduction and literature review

The concept of viscoplastic material was first introduced by Bingham (1922) (Bingham material) when describing several types of paints. Viscoplastic fluids rheology exhibit the so-called ‘yield stress, τ ₀ ’ that governs the transition from solid-like to liquid-like response¹. These fluids develop stagnation regions, where the material does not plastically deform due to elastic resistance from the microstructure. Hence, their velocity gradients vanish in these regions. The yielding process is depicted in the fluid viscometric response by a radical transformation in flow (or deformation) behaviour over a relatively narrow range of stress. Thus, under ideal Bingham, there is a finite stress level (yield stress) at vanishingly low shear rates. In areas of intense deformation, that is, above the yield stress limit, the material is observed to flow and behaves as a Newtonian fluid. These types of material are known as Bingham fluids (viscoplastic). It is the presence of these yielded and unyielded regions across the domain, which provides the intrinsic discontinuity within the model representation. From this theoretical basis, more complex viscoplastic models may be introduced, such as the Herschel–Bulkley model, with power-law viscous dependency, and the nonlinear Casson model. All such models are discontinuous, thus, it is necessary to develop robust numerical techniques which may discretise problems that manifest yielded and unyielded regions, and simultaneously their interface.

To handle such sharp discontinuity through numerical methods has posed something of a difficulty and various attempts have been made to introduce varying degrees of smooth approximations, cf. several modified versions of the discontinuous model proposed in (Burgos et al. 1999; Papanastasiou 1987). Of this type, Papanastasiou (1987) analysed steady two-dimensional flows of Bingham fluids based on a single modified constitutive relation, applicable to both yielded and unyielded regions. Such an approach proffers the advantage that it eliminates the need for explicit yield-surface tracking. Here, a continuation parameter is introduced to access numerical solutions, which in limiting terms may practically replicate ideal model results. This modified model has been benchmarked on several types of problems such as: one-dimensional channel flow, a two-dimensional boundary layer flow and a two-dimensional extrusion flow (Papanastasiou 1987). Later, Ellwood et al. (1990) introduced the same Papanastasiou equation to analyse the steady and transient behaviour of jets generated by circular and slit nozzles, to find that the yield stress suppresses the swelling of the jet. Abdali et al. (1992) studied entry and exit flows of Bingham fluids to observe unyielded regions, which as anticipated shrink with increasing shear rate. Nevertheless, applications of the Papanastasiou model have been somewhat limited to ‘Bingham-type’ materials, which manifest an apparent yield stress and Newtonian response under flow. Hence, to consider more complex rheological behaviour with a yield stress, one must look beyond such a model.

To allow a degree of deviation from viscous Newtonian behaviour, the power-law model was proposed. This model is widely employed to characterise shear-thinning/shear-thickening properties of fluids (inelastic). Further rheological development, incorporating either shear-thinning or thickening (power-law) and a yield stress (Bingham model), has been provided through the popular Herschel–Bulkley (HB) model. The behaviour of many materials such as colloidal suspensions, plastic propellant doughs (Carter and Warren 1987) and drilling fluids (Azouz et al. 1993) have all been analysed under HB-model assumptions, which has enabled a trace of microstructural changes during processing. In areas of intense deformation, where the local stress exceeds the yield stress, the microstructural dynamics lay give rise to non-uniform material properties (non-linear stress–strain relationship). As such, there is much debate in the literature as to whether power-law, Bingham or Herschel–Bulkley models are physically plausible models. For example, the shear-thinning power-law fluid predicts an infinite viscosity at zero strain rate. Moreover, some criticism (Balmforth and Craster 2001) has been raised with respect to the yield stress concept itself, as practically, in the zero shear-rate limit most materials weakly yield, or creep. From a mathematical perspective, the discontinuous surface defined by the yield condition, τ = τ ₀ in the HB-model, introduces several complications associated with the singularity at low shear-rates (as under Bingham). A principal aspect of this study will be to investigate the functional variation of the onset of yield stress and its influence on material system response (generalised HB). For example to achieve this, Mitsoulis et al. (1993) and Mitsoulis (2007) proposed a modified HB model by combining the original Herschel–Bulkley and Papanastasiou models to predict shear-thinning/thickening behaviour with a yield stress response. Such methodology is favoured in the present study also. Today, there is considerable interest industrially in the rheology of materials exhibiting yield behaviour and viscoelastic characteristics, such as in foods processing, paint, foam and bio-fluids. Saramito (2007) combines the Bingham viscoplastic and the Oldroyd viscoelastic models to develop a new constitutive viscoelastoplastic model, which theoretically satisfies the second law of thermodynamics. This model offers the distinct advantage of defining the viscoplastic–viscoelastoplastic transition via the stress variable (and not viscosity), and hence inherits frame invariance properties. Extensions to this model are attractive and represent a major step forward, exhibiting for example finite extensional properties and shear-thinning behaviour.

Our principal focus in this paper is to build upon the constructions introduced by Papanastasiou (1987) (and later by Mitsoulis et al. 1993 and Mitsoulis 2007) and apply this within the viscoplastic–viscoelastoplastic context, utilising the ‘classical’ Oldroyd-B model to introduce the viscoelastic dimension. The Papanastasiou modification to the Bingham-model generates the viscoplastic function with an exponential stress growth term, that smoothes the stress discontinuity and is valid at all rates of deformation. This functionality provides the viscous driving terms to replace the constant pure-Oldroyd shear viscosity function (as in White–Metzner constructions). Frigaard and Nouar (2005) presented a detailed analysis of the limitations of various regularisation models including the Papanastasiou model. The challenge posed to predictive simulation is to depict the ‘appropriate’ level of exponential growth for the deformation in question. Undoubtedly, the subject matter of viscoplasticity/viscoelastoplasticity remains a hotly debated and challenging topic, which has provoked more than a thousand papers prior to 2005 (see Barnes 1999 and Mitsoulis 2007). Moreover, there are many outstanding questions with regards to experimental measurement of yield stress that need to be considered. Barnes and Walters (1985) showed through experimental data, gathered from a constant stress rheometer, that in this context the yield stress concept was an idealisation, and that, given accurate measurement, no ‘actual’ yield stress existed. The argument was that discrepancy in viscometric plots should not be attributed to wall-slip/wall-depletion effects, once such disturbances have been removed, or corrected for. These authors stated that at low stress, material would flow slowly, introducing in turn the issue of time-scale and the concept ‘that everything flows’ (Barnes 1999). The non-existence of yield stress claimed by Barnes and Walters was challenged by Hartnett and Hu (1989), where a simple experiment using the falling ball viscometer was used to demonstrate unambiguously that an aqueous Carbopol solution exhibited a yield stress (an engineering reality). The basis of this work was that viscoplastic material, independently of stress level imposed, can be approximated uniformly as a liquid, which exhibits infinitely high viscosity in the limit of low shear rates, followed by a transition to a viscous liquid state. At that time and with the experimental means available, rheologists were faced with considerable difficulty in accurately measuring any sensible flow below the yield stress (Barnes 1999). To further complicate the situation, Møllera et al. (2006) related the uncertainty in the interpretation of some rheometrical measurement to material time dependency, i.e. thixotropic behaviour and time scale. In fact, no single method has been universally accepted as the standard for measuring yield stress and it is not unusual to find large variations in results obtained from different methods with the same material (Bonn 2009). This is often the case due to the difficulty of conducting precision measurements at vanishingly low shear rates. Hence, the debate continues on the meaning and usefulness of the yield stress concept—demanding respectable scientific definition and practical experimental determination.

Governing equations

The relevant equation system, given in non-dimensional terms, for isothermal, viscous, incompressible flow may be represented via conservation of mass and transport of momentum equations, as

$$ \nabla \,.\,u=0, $$

(1)

$$ {\rm Re}\frac{\partial u}{\partial t}=\nabla \cdot \left( {\tau +2\mu _{\rm s} d} \right)-{\rm Re}\,u\cdot \nabla u-\nabla p, $$

(2)

where field variables u, p and τ represent the fluid velocity, hydrodynamic pressure and extra-stress. The rate-of-deformation tensor is defined through the velocity gradient tensor, $d=\left( {\nabla u+\nabla u^\dag } \right)/2$. Here, the viscosity of the viscous fluid is μ _s. In addition, the dimensionless Reynolds number $\left( {{\rm Re}={\rho U\ell } \mathord{\left/ {\vphantom {{\rho U\ell } {\mu _0 }}} \right. \kern-\nulldelimiterspace} {\mu _0 }} \right)$ is introduced based on density ρ, characteristic velocity scale U (average velocity) and length scale $\ell$ (radius at contraction). From this, a time scale is derived ($\ell$/U), the inverse of which defines a characteristic deformation rate; together with the zero-shear rate viscosity (μ ₀), this leads to suitable scaling on stress, yield stress and pressure (see Aboubacar and Webster 2001). Here, creeping flow conditions are assumed (Re∼10^− 2).

Viscoplastic flow equations

For non-Newtonian fluids, the viscosity is considered as a nonlinear function of the second invariant (Π_d) of the rate-of-strain tensor (d _ij ). A Bingham material remains rigid when the shear-stress is below the yield stress τ ₀, (here, equivalent to the Bingham number, Bn, as in Mitsoulis 2007), but flows like a Newtonian fluid when the shear-stress exceeds τ ₀. Thus,

$$ \begin{array}{rll} \tau &=&\left( {\mu +\displaystyle\frac{\tau _0 }{2\left| {\mathrm{II}_\mathrm{d} } \right|^{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \right)\dot {\gamma }\,\quad\mathrm{for}\quad\,\left| {\mathrm{II}_\tau } \right|>\tau _0 ^2;\quad {\rm and} \\ \quad {\dot {\gamma }}&=& 0 \, \quad\mathrm{for}\quad\,\left| {\mathrm{II}_\tau } \right|\le \tau _0 ^2. \end{array} $$

(3)

Papanastasiou (1987) proposed a modified Bingham model, by introducing a regularisation stress growth exponent (m) to control the rate-of-rise in stress, in the form:

$$ \tau =\left( \mu +\tau _0 \frac{1-e^{-m | {\Pi _\mathrm{d}}|}} {2\left| {\rm{II}}_{\rm{d} } \right|^{\frac{1}{2}}} \right) {\dot { \rm \boldsymbol {\gamma }}}. $$

(4)

For consistency, in the present work, the Papanastasiou model is introduced by modifying the viscous part (in the momentum equation) of the extra-stress (4) through:

$$ \tau =2\,\phi \left( {\rm II_d } \right)\beta \;d, $$

(5)

Here, the zero shear viscosity is divided into polymeric (μ _p) and viscous (μ _s) contributions, so that μ ₀ = μ _p + μ _s with solvent-fraction β = μ _s / μ ₀ . The function $\phi \left( {\rm II_d } \right)$ is defined as:

$$ \phi \left( {\rm {II}}_{\rm {d}} \right)=\left[ {\rm{\eta}} _0 +\frac{\tau _0 \left( 1-{\rm e}^{\rm -m}\,|{\rm II}_{\rm d}|^{1/2} \right)}{2\left| {\rm {II}}_{\rm {d}} \right|^{1/2}}\right],\,{\rm and} $$

(6)

$$ \mathrm{II}_\mathrm{d} =\frac{1}{2}\;{\rm tr}\left( {d^{{\kern 1pt}\mathrm{2}}} \right) $$

(7)

Viscoelastoplastic flow and viscometric functions

From a viscoelastic modeling viewpoint, the governing Eqs. 1 and 2 should be supplemented by a constitutive equation for stress. For example, the system for an Oldroyd-B model may be expressed, viz

$$ {De}\frac{\partial \tau }{\partial t}=2\mu _p d-\tau -De\,\left( {u\cdot \nabla \tau -\tau \cdot \nabla u-\left( {\tau \cdot \nabla u} \right)^\dag } \right) $$

(8)

An additional dimensionless parameters is introduced in the form of the Deborah number $\left( {\mathrm{De}={\lambda _1 \,U} \mathord{\left/ {\vphantom {{\lambda _1 \,U} \ell }} \right. \kern-\nulldelimiterspace} \ell } \right)$ which is a function of material relaxation time, λ ₁, characteristic velocity scale U and length scale $\ell$.

For reasons of expediency under numerical discretisation, it is often convenient to introduce ‘stress splitting’ to extract a stress tensor with viscous τ ⁽¹⁾ and elastic parts τ ⁽²⁾, viz:

$$ \mathrm{\tau }=\mathrm{\tau }^{(1)}+\mathrm{\tau }^{(2)}, $$

(9)

$$ \mathrm{\tau }^{(1)}=2\,\beta \;{d},\,\,\,{\rm and} $$

(10)

$$ \mathrm{\tau }^{(2)}+De\mathop \tau \limits^{\nabla ^{(2)}} =2({1-{\rm {\beta}}}){\rm d}, $$

(11)

where, $\mathop \tau \limits^{\nabla^{(2)}}$ represents the upper-convected material derivative of τ defined by re-arranging (8) as:

$$ \mathop \tau \limits^{\nabla ^{(2)}}=\frac{\partial \tau }{\partial t}+u\cdot \nabla \tau -\left( {\nabla u} \right)^\dag \cdot \tau -\tau \cdot \left( {\nabla u} \right). $$

(12)

The set of Eqs. 9, 10 and 11 represent a respectable basis upon which to incorporate plastic (yield stress) behaviour that is through the viscoelastic (Oldroyd-B) model with the Papanastasiou function, utilising Eq. 5. Thus

$$ \tau =\tau ^{(1)}+\tau ^{(2)}, $$

(13)

$$ \tau ^{(1)}=2\,\phi \left( {\rm II_\mathrm{d} } \right)\beta \;d,\,{\rm and} $$

(14)

$$ \tau ^{\left( 2 \right)}+De\mathop {\tau ^{\left( 2 \right)}}\limits^\nabla =2\,{\rm{\phi}} \left( {\rm{II}}_{\rm{d} } \right)\left( 1-{\rm{\beta} } \right){\rm d}\mathrm{,} $$

(15)

In its own right, the Oldroyd-B model is often selected as a benchmark to develop numerical solutions in computational rheology. This popular nonlinear model manifests sufficient simplicity, being characterised as a constant shear-viscosity, strain-hardening non-linear model. Its drawback is that it also supports unbounded strain-hardening response. As such, the Papanastasiou–Oldroyd material functions are characterised as:

$$ {\rm{\eta}} = {\rm{\phi}} \left( {\rm {II}}_{\rm{d}} \right), $$

(16)

$$ \begin{array}{rll} {\rm{\eta}} _{\rm E} &=&3{\rm{\beta}} \,{\rm{\phi}} \left( {\rm {II}}_{\rm{d}} \right){\kern 1pt}{\kern 1pt}+3\left( 1-{\rm{\beta}} \right){\kern 1pt}\,{\rm{\phi}} \left( {\rm{II}}_{\rm{d}} \right){\kern 1pt}{\kern 1pt}{\kern 1pt} \\ &&\times\,\left[ {\frac{1}{1-{De}{\kern 1pt}\dot {\varepsilon }-2{De}^2{\kern 1pt}\dot {\varepsilon }^2}} \right],\,{\rm and} \end{array} $$

(17)

$$ N{ }_1=2{\kern 1pt}{\kern 1pt}{\rm{\phi}} \left( {\rm{II}}_{\rm{d}} \right)\left( {1-{\rm{\beta}}} \right)\mathrm{De}\,\dot {\gamma }^2. $$

(18)

From the expression of extensional viscosity as in Eq. 17, the extensional viscosity has a singularity at $\mathrm{De}\;\dot {\varepsilon }=0.5$, a contribution that arises due to the principal stress component. We observe with a more solvent-dominated fluid (approaching Newtonian state with β→1), the rise in extensional viscosity is delayed in $\mathrm{De}\,\dot {\varepsilon}$, and hence, is more steeply represented as it encounters the singularity than is the case for a more polymeric-based fluid (defined as that for which β→0).

Numerical method

The preferred discrete approximation to the steady incompressible solution of these viscoplastic–viscoelastoplastic contraction–expansion flow problems is to adopt a finite element approximation for the mass– momentum balance equations and a finite volume approximation for viscoelastic stress. Such a hybrid formulation has been thoroughly benchmarked on many different flow problems (steady/transient, confined/open/interfacial, incompressible/compressible, 2D/ 3D) and for many different constitutive models (phenomenological, kinetic, network, FENE, micellar, fibre-suspensions) (Aguayo et al. 2006; Baloch and Webster 1995; Tamaddon-Jahromi et al. 2010). The primary problem variables selected become those of velocity, pressure and stress. A transient formulation is adopted from the outset, so that time-stepping pervades the discrete description. The momentum-continuity balance is addressed through a pressure-correction splitting, so that the continuity equation is replaced by a Poisson equation governing pressure-temporal difference over a single time-step, an incremental pressure-correction procedure when 0 ≤ θ₁ ≤ 1. This introduces semi-discrete fractional-staged equations in time to a theoretical second-order of accuracy, when coupled to a two-step Lax-Wendroff scheme, which also draws upon an intermediate half-step stage. Spatial discretisation completes the approximation, whereupon the finite element method is utilised for velocity and pressure components of the system (elliptic–parabolic subsystem). Taken over triangular elements, this then resembles a fractional-staged Taylor–Galerkin pressure-correction (TGPC) scheme (Donea 1984; Zienkiewicz et al. 1985). The constitutive equation (hyperbolic subsystem) and stress variable is then solved by a sub-cell cell-vertex finite volume technique (see Matallah et al. 1998; Webster et al. 2005). For solenoidal conditions and with a forward time increment factor θ₂ = 0.5, this pressure-correction scheme attracts second-order temporal accuracy, with its incremental form (θ₁ > 0) proving superior in uniform temporal error bounds over its non-incremental counterpart (θ₁ = 0). The three-stage TGPC structure can be conveniently expressed (cf. Wapperom and Webster 1999; Webster et al. 2005) in semi-discrete representation on the single time step [t ⁿ; t ^n + 1], with starting values [u ⁿ; τ ⁿ, p ⁿ, p ^n − 1].

In short, Galerkin fe discretisation is applied to the embedded Stokesian system components; the momentum equation at Stage 1, the pressure-correction equation at Stage 2 and the incompressibility satisfaction constraint at Stage 3 (to ensure higher order precision). The fv tessellation is constructed from the fe grid by connecting the mid-side nodes. Stress variables are located at the vertices of fv sub-cells (cell-vertex method, equivalent to linear interpolation). In contrast, quadratic velocity interpolation is enforced on the parent fe cell, alongside linear pressure interpolation. This interpolation choice manifests piecewise continuity. Algebraic solvers for such systems are dealt with extensively elsewhere (Hawken et al. 1990). A direct solution method is employed at the fe pressure equation stage 2, whilst a space-efficient element-by-element Jacobi iteration is preferred over the remaining stages one and three, under the fe components. The element-by-element iteration avoids full system matrix construction, and normally, the mass–matrix iteration that results (m _itn) is performed only three to five times. Semi-implicitness is introduced at Stages 1a,b on pressure and diffusive terms to enhance stability in the strongly viscous regime. Note, pressure temporal increments invoke multi-step reference across three successive time levels [t ^n − 1, t ⁿ, t ^n + 1]. The stress equation under fv solution appears at stage one and the details of the discretisation and solution technique are provided below.

Finite volume cell-vertex scheme for stress

The cell-vertex oriented finite volume method is based around groupings of terms into flux, source and time derivative form. In the present context, this may be conveniently achieved by adopting a non-conservative representation and manipulating the constitutive equation, with dependency upon flux ($R=u.\nabla \tau ,)$ and absorbing remaining terms under the source (Q). Cell-vertex fv schemes are applied to this equation, whereupon upwinding is implemented through fluctuation distribution, which both distributes control volume residuals and provides nodal solution updates (Wapperom and Webster 1998). We consider each scalar stress component, τ, acting on an arbitrary volume $\Omega =\sum\limits_l {\Omega _l}$, whose variation is controlled through corresponding components of fluctuation of the flux (R) and the source term (Q).

For each finite volume triangle (Ω _l ), flux and source variations are evaluated and allocated to its three vertices by the chosen cell-vertex distribution scheme. Thus, by summing all contributions from its control volume Ω _l , the nodal update is obtained composed of all fv triangles surrounding node (l). The flux and source residuals may be evaluated over two separate control volumes associated with a given node (l) within the fv cell T. This generates a contribution governed over the fv triangle T, (R _T , Q _T ), and that subtended over the median-dual-cell zone, (R _mdc, Q _mdc). For reasons of temporal accuracy, this procedure demands appropriate area-weighting to maintain consistency, with extension to time-terms likewise. A generalised fv nodal update equation may be expressed per stress component in the form,

$$ \begin{array}{rll} {\kern-4pt} \left[ {\sum\limits_{\forall T_l } {\delta _T \alpha _l^T \Omega _T } +\sum\limits_{\forall {MDC}_l } {\left( {1-\delta _T } \right)\hat {\Omega }_l^T } } \right]\frac{\Delta \tau _l^{n+1} }{\Delta {\kern 1pt}t} \\ \quad =\sum\limits_{\forall T_l } {\delta _T \alpha _l^T b^T+} \sum\limits_{\forall {MDC}_l } {\left( {1-\delta _T } \right)b_l^{{MDC}} } \end{array} $$

(19)

where $b^T\!=\!\left( {-R_T \!+\!Q_T } \right),\,b_l^{\mathrm{MDC}} \!=\!\left( {-R_{\mathrm{MDC}} \!+\!Q_{\mathrm{MDC}} } \right)^l,$ Ω _T is the area of the fv triangle , and is the area of its median-dual-cell. The weighting parameter, 0 ≤ δ _T  ≤ 1, directs the balance taken between the contributions from the median-dual-cell and the fv triangle. The discrete stencil of Eq. 19 identifies fluctuation distribution and median dual cell contributions, area weighting and upwinding factors ($\alpha _l^T -\mathrm{scheme}\,\mathrm{dependent})$. For the interconnectivity of the fv triangular cells (T _i ) surrounding the sample node (l), the blue-shaded zone of mdc, the parent triangular fe cell, and the fluctuation distribution (fv upwinding) parameters $\left( {\alpha _i^T } \right)$, for i = l, j, k on each fv cell, see Webster et al. (2004) with additional details on the scheme.

Numerical results and discussion

Discussion is centred around themes of viscometric form, pressure drop analysis, vortex behaviour and stress field configurations.

Viscosity and stress—viscometric form

m Variation

Figure 1 illustrates the viscometric response in shear stress for the inelastic modified Bingham–Papanastasiou model, considering parametric variation through m at fixed τ ₀ of unity. This information sets out the initial context to allow clear segregation of purely viscous and elastic effects. The relatively elevated level of τ ₀  =  1.0 is preferred here to expand trend differences at limiting and low deformation rates. Variation is described in the range between extremes of Ideal Bingham for large m (∼10⁷) and Newtonian response for m  =  0. The two plots (Fig. 1a, b) convey log–log and linear data representations. From the logarithmic data one observes gradual stratification through increase in orders of m (exponent), with an order of magnitude shift in shear stress for each order change in m. The linear plot compacts the data (hence common preference for log–log view), so that only m  =  10 and m  =  10² plots can be distinguished from Ideal Bingham behaviour for shear rates of unity and below. Figure 1c contains equivalent data for ${\it \tau}_{0}= 10^{-2}$ to contrast with the proceeding viscoelastic data.

Fig. 1

Shear stress: modified Bingham-Papanastasiou fluids, m variation, τ ₀ = 1.0; a log–log plot, b linear plot, c log–log plot (τ ₀ = 0.01)

We next consider the position for the Papanastasiou-Oldroyd (B) model, providing counterpart data (log–log plots) for viscosity and stress with 10¹ ≤ m ≤ 10⁷ and τ $_{0 }= 10^{-2}$. Figure 2 conveys this information via shear stress (a), shear viscosity (b) and extensional viscosity (c). This is matched in Fig. 3 for N ₁ with m variation (a), with τ ₀-variation (b) and (principal) first normal stress difference in extension (c). At low shear-rate levels (∼10^− 4), the shear data reveals modest elevation in shear viscosity up to 6 U for m ≤ 10³, thereafter rising more rapidly to 40 at m = 10⁴ and 100 at m = 10⁷. There is no distinction apparent from the Oldroyd level (unity) with m = 10. Also with rising deformation rate, the trend shows unification with Oldroyd behaviour at rates ∼10^− 1. Figure 2a captures this position in shear stress and reflects the proximity in trends through m variation to the lower limit of linear Oldroyd behaviour (m = 0) and the upper limit of pure Bingham behaviour (large m, m∼10⁷). Note here, that the τ $_{0 }= 10^{-2}$ calibrates the yield stress level at vanishingly small shear rates, contrasting to that used in Fig. 2a for example. Data in Fig. 3a, b relates to trends in N ₁ in shear. This infers a strengthening of N ₁ for shear rates lower than 10^− 1, beyond the pure Oldroyd quadratic form. At the extremes of large m (m∼10⁷), which matched Bingham behaviour in shear stress, now an additional contribution from N ₁ appears. In effect, N ₁ behaviour reflects earlier and more prominent levels at lower shear rates than observed with Oldroyd response.

Fig. 2

a Shear stress, b shear viscosity, c extensional visocity: Papanastasiou Oldroyd-B, m variation, τ₀ = 0.01

Fig. 3

a First normal stress, m variation; b first normal difference, τ variation; c extensional stress: Papanastasiou Oldroyd-B, m variation, τ₀ = 0.01

The extensional data in Fig. 2c for extensional viscosity and Fig. 3c for extensional stress, are also new contributions specific to the viscoelastic setting. This describes elevation with rising m order in extensional viscosity at vanishing extension rates. The trend with rising deformation rate shows departure from Oldroyd behaviour at rates between 10^− 2 and 10^− 1. The limiting envelope is well captured in extensional stress between Oldroyd behaviour (m = 0) and the upper limit of Bingham-Oldroyd behaviour at large m (m∼10⁷). It is noticeable that there is a shift away from the Oldroyd-trend with non-zero m ≥ 10³ (similar form below this level for m = 10¹ and m = 10²), conveying a non-linear elevation thereafter with rise in m, up to the upper limit of Bingham-Oldroyd behaviour, m = 10⁷. Nevertheless, all Papanastasiou adjusted models ($m\ne 0$), unite and agree in extensional stress beyond rates ∼3 × 10^− 2. This is an important observation and rational for present parameter selection, as to the zone where matching occurs as seen in extensional viscosity, which itself adjusts into increasing rates with rise in τ ₀ value (cf. Fig. 4c). More precisely, for ${\tau}_{0 }= 10^{-2}$ and deformation rates between ∼10^− 1 and unity, there is correlation with Oldroyd response. As seen in Fig. 4c, with only a shift of one order in τ ₀, to $\tau_{0}= 10^{-1}$, matching with Oldroyd response is delayed to rates ∼1, which coincides with the complication of meeting the unbounded limit for the Oldroyd model.

Fig. 4

a Shear stress, b shear viscosity, c extensional viscosity: Papanastasiou Oldroyd-B, τ₀ variation, m = 10²

τ ₀ Variation

In contrast to the above, we next consider the viscometric response for these models through variation in τ ₀ (10^− 2 ≤ τ ₀ ≤ 10⁰) at fixed m value (m = 10²). Accordingly, Fig. 4 data demonstrates Papanastasiou–Oldroyd model response in shear stress, shear viscosity and extensional viscosity. Here, one is able to detect the consequence of larger τ ₀ influence (rising), in contrast to the data of Figs. 2 and 3 and (for τ ₀ = 0.01). So, for example with [τ $_{0 }= 1.0, m = 10^{2}$] in shear stress and at deformation rates ∼10^− 6, a limiting value is exposed of ∼5 × 10^− 5, which equates to that observed earlier with [for τ $_{0 }= 0.01, m = 10^{4}$]. The bounding envelope is established with the lower limit data and τ ₀ = 0.01 (practically that of Oldroyd, also equivalent to Newtonian response). In rate, the departure from the straight-line trend-plot (viewed in decreasing terms), now shifts by around two decades, from previously ∼10^− 1 for τ ₀ = 0.01 to ∼10^+ 1 for τ ₀ = 1. Once this departure has occurred, straight line trends are again resumed below rates of ∼10^− 2. Thus, at any particular rate below ∼10^− 2, there is a shift factor of around two orders in shear stress from data at τ ₀ = 0.01 to that at τ ₀ = 1.0. The shear viscosity plot complements this information for completeness, reflecting elevation in limiting zero-shear rate values through τ $_{0 }= (10^{-2}$, 0.1, 0.5, 1) of (1.5, 6, 25, 50). Similar information is conveyed through the extensional viscosity, denoting counterpart elevation in limiting zero-extension rate values through rising τ ₀ values of three times that in shear. Trends in N ₁ behaviour with τ ₀ variation are similar to those observed with m variation, with the noted difference of departure from Oldroyd response with upward shift in deformation rate by two orders (average rate here ∼10^− 1 from ∼10^− 3), accompanied by significant elevation in N ₁ order (from ∼10^− 5 at rate ∼10^− 3 with extreme m = 10⁷, to ∼10^− 1 at rate ∼10^− 1 with τ ₀ = 1.0).

Analysis of pressure drop results

Viscoplastic case

The viscoplastic (inelastic) data are reported in terms of the ‘excess pressure drop’ (epd) definition (used by Rothstein and McKinley 1999, 2001; Szabo et al. 1997), which gives comparison against the equivalent Newtonian fluid (m = 0) and corrects for the fully developed upstream and downstream pressure drop contributions. In this fashion, epd results are presented, as above, covering variation in both model parameters m and τ ₀. The comparison provides direct insight into the impact upon epd of viscous changes (i.e., from shear and extensional viscosity). For other related work on pressure drop and Bingham fluids see for example de Souza Mendes et al. (2007), who report on expansion–contraction flow and head loss (Δp), taking into account different geometry dimensions.

epd with m variation

Significantly in Fig. 5, relatively large increases in epd are observed, charateristically 24% above the unity Newtonian reference line, for τ ₀ = 0.1 at its maximum when m = 10³. This represents an increase from the increased level of epd around 2% for τ ₀ = 0.01 and m = 10³. Such increases may be attributed to the elevation observed in shear and extensional viscosity at low to moderate deformation rates, as here N ₁ = 0). Considering τ ₀ = 0.1 data, epd increases rapidly by some 12% up to m = 10² (see on to viscoelastoplastic case), doubling by m = 5 × 10², rising to its peak value (∼24%) at m = 10³, a level which is maintained to around m  = 2 × 10³. Thereafter with further increase in m, epd values tend to an asymptote with level of ∼1.22. This information provides the necessary insight to explain limiting trends with rising m at fixed τ ₀, to interpret more fully Fig. 6 below on epd with τ ₀ variation. With respect to numerical convergence, no limitation on m value is detected at low values of τ ₀ ≤ 10^− 2; whilst m _crit  = 3,500 for τ ₀ = 0.1. Upon analysing limiting m trends for τ $_{0 }= 10^{-2}$, a peak of 1.019 is detected around m = 2,000, with asymptote of 1.017 reached at m = 10⁴. This gives some credence to the generally held practical view that for many materials a reasonable choice is 10³ ≤ m ≤ 10⁴ (Walters 2009).

Fig. 5

Pressure drop (epd) vs. m, inelastic Bing-Pap, 4:1:4 axisymmetric

Fig. 6

Pressure drop (epd) vs. τ ₀, inelastic Bing-Pap model, 4:1:4 axisymmetric

epd with τ ₀ variation

Covering edp findings with τ ₀ variation, results are displayed in Fig. 6, for three different values of m = [10, 10², 10³] and a range for τ ₀ of 0 ≤ τ ₀ ≤ 0.5. As anticipated functionally and for any specific m value, the epd trend with rising τ ₀ is linear. The key point to note is the elevation in the rate of epd rise with m value (which is independent of τ ₀ setting). So that interpreted in relative terms to the Newtonian reference line, the percentage increase is 30% for m = 10 to 60% for m = 10² to 140% for m = 10³.

Viscoelastoplastic case

In the viscoelastoplastic instance for the Papanastasiou–Oldroyd model, whilst following the style above and theoretical discussion in Walters (2009), pressure drop data are now reported in dual terms of comparison, P ^∗ to the equivalent viscoplastic Bingham–Papanastasiou fluid (unity line in P ^∗ terms), and against the equivalent Newtonian fluid, via epd. The P ^∗ comparison lies as an extension to ‘excess pressure drop’ (epd) definition (Rothstein and McKinley 1999, 2001; Szabo et al. 1997); also used in Aboubacar and Webster (2001). Once more, these results are presented separately, covering variation in both m and τ ₀ parameters, noting that each parameter selection implies a different viscoplastic (inelastic) response. The P ^∗ comparison provides direct insight upon the additional viscoelastic influences upon ‘excess pressure drop’ (N ₁ effect) when read against the unity viscoplastic line. Furthermore, the epd comparison against the Newtonian reference yields the combination of viscoelastic and viscoplastic influences on ‘excess pressure drop’; thus, by difference and inference, viscoelastic additive and viscoplastic contributions may be quantified. In addition, there is the direct comparison available against Oldroyd (m = 0 or τ ₀ = 0) trends, devoid of yield stress inclusion.

m Variation

The normalised P ^∗ data with ${\it \tau}_{0}=10^{-2}$ is calibrated against Deborah number (De) with rising m parameter through values (0, 10², 10³), see Fig. 7. At this low level of τ ₀, these results demonstrate that there is no discernible difference in P ^∗ data for m ≤ 10², from that of the purely viscoelastic Oldroyd data (nb. P ^∗ trends for Oldroyd (m = 0 or τ ₀ = 0) default to epd). One may remind here that the trend with rising De, is one of initial decline in excess pressure drop to a minimum point (model/fluid dependent), prior to a monotonic rise thereafter (see Walters et al. 2009a, b) for fuller explanation). A decline in P ^∗ level is detectable once m exceeds 10³. For P ^∗ minimum around De = 2, this equates to adjusting a 3% Oldroyd drop to a 5% Papanastasiou–Oldroyd (m = 10³) drop. From earlier reasoning for purely viscoelastic models under constant shear viscosity setting (Walters et al. 2009c), reduction in N ₁ gave enhancement in excess pressure drop measures, whilst conversely increases in η _e gave enhancement in excess pressure drop. Adopting this line of argument, this decline in P ^∗ level may consistently be associated with increased N ₁ effects.

Fig. 7

Normalised pressure drop (P ^∗), Pap-OldB vs. inelastic equivalent, τ ₀ = 0.01, β = 0.9

τ ₀ Variation

With τ ₀ rise at fixed m = 10² in Fig. 8, P ^∗ data follow similar declining trends to that observed under m parameter variation. The upper limit for the viscoelastic Oldroyd model is meaningful, as this represents the relative τ ₀ = 0 position and the vanishing yield stress position. Quantifying outcomes for P ^∗ minimum around De = 2, this implies adjustment from 3% Oldroyd drop (τ ₀ = 0), to a 4% Papanastasiou–Oldroyd (τ ₀ = 0.1) drop, to a 6.5% Papanastasiou–Oldroyd (τ ₀ = 0.5) drop. Clearly, beyond τ ₀ = 0.1, the drop levels are becoming increasingly more significant. As above, the same rational of explanation holds true once more—where decline in P ^∗ level may consistently be associated with increased N ₁ effects.

Fig. 8

Normalised pressure drop (P ^∗), Pap-OldB vs. inelastic equivalent, m = 10², β = 0.9

In contrast, based on epd comparison for τ ₀ variation data (Fig. 9), one may consider the relative position for the Papanastasiou–Oldroyd (τ ₀ = 0.1) model against the Newtonian reference line for epd minimum around De = 2. This data reveals an 8% total contribution increase in epd. From this result one may infer a 12% pressure-drop increase due to viscoplastic contributions from shear and extensional viscosity (as for purely viscoplastic). This evidence is confirmed via direct cross-check with the Oldroyd data; the difference from the Papanastasiou–Oldroyd (τ ₀ = 0.1) value is 12% in epd minimum around De = 2. As anticipated, the increases in extensional viscosity (η _e ) would only be expected to provide enhancement in excess pressure drop; as likewise would the similar-form shear viscosity (η _s ) elevation above the base Newtonian reference line taken.

Fig. 9

Normalised pressure drop (epd), Pap-OldB vs. Newtonian equivalent, m = 10², β = 0.9

Vortex behaviour—upstream and downstream activity

Comparison may be made with rising De over three vortex measures, governing upstream and downstream activity—vortex intensity (ψ _int), vortex length on channel wall (X) and vortex length on contraction wall face (L), measurement procedure of tangent line to outer vortex line that is orthogonal to intercept with centre of vortex and projected sharp corner. Of this data, vortex intensity is perhaps the most revealing measure, as portrayed via stream function field data in Figs. 10, 11, 12, 13 and 14. Here, preference is given to parametric change in τ ₀ first, taking m parameter findings subsequently and in contrast, appealing to cross-reference across figures. In alternative vortex length measures at either fixed m or τ ₀, it noticeable that (X) does not adjust much with De rise; whilst there is slight rise seen in (L). Comparing upstream and downstream characteristics, these trends replicate in vortex length (X); this is also true, in vortex length (L) trends.

Fig. 10

Streamlines: Oldroyd-B, Pap-OldB (m = 10², 10³), β = 0.9

Fig. 11

Streamlines: Newtonian, inelastic Bing-Pap (m = 10², 10³), β = 0.9

Fig. 12

Streamlines: Newtonian, Oldroyd-B, inelastic and Pap-OldB (τ = 0.01, β = 0.9)

Fig. 13

Salient-corner vortex intensity: a upstream, b downstream, Pap-OldB, (m = 10², τ = 0.01, β = 0.9)

Fig. 14

Salient-corner cell-size: a horizontal, c vertical upstream; b horizontal, d vertical downstream, Pap-OldB (m = 10², τ = 0.01, β = 0.9)

τ₀ variation, τ₀ rise at fixed m = 10², 10³

Figure 10, provides field data for Papanastasiou–Oldroyd (De = 1, left column; De = 5, right column) with rising τ ₀ values (0, 0.01, 0.1). An additional Fig. 11, (De = 0), covers the Newtonian fluid (τ ₀ = 0) to inelastic Bingham–Papanastasiou solutions, through the same range of τ ₀ values. Considering downstream vortex intensity in the graph of Fig. 13b, at this level of heavy solvent fraction (β = 0.9) for the base-reference Oldroyd (τ ₀ = 0) fluid, there is initial decline from De = 0 (Newtonian) to the minimum point (De = 2, ψ _int = 0.36 × 10^− 3), prior to recovery and vortex growth with De rise up to (De = 5, ψ _int = 0.65 × 10^− 3). This finding lies in distinct contrast to the more common observation of downstream vortex reduction with De rise for highly polymeric Oldroyd fluids (β = 1/9, (Aguayo et al. 2008)) with De rise. The balance in symmetry between upstream and downstream vortices is maintained for viscous/viscoplastic (Newtonian/inelastic Bingham–Papanastasiou) fluids (also seen in X and L of Fig. 14). Introduction of elasticity disturbs this balance. The trend in downstream vortex behaviour with De rise, and as τ ₀ rises, is one of similar form to that of the purely viscoelastic fluid (initial decline, minimum at De = 2, recovery thereafter), but with ever increasing suppression as yield stress level rises (cf. Fig. 13). This is still apparent in the data at τ ₀ = 0.01, but must be zoomed to be observed at τ ₀ = 0.1 (insert). The relative starting values of ψ _int can be gathered at the De = 0 (Newtonian/viscoplastic) position. By τ ₀ = 0.1, the downstream vortex is extremely weak (in strength, two orders lower than Newtonian/Oldroyd) and has been almost completely suppressed (in size). In addition, according to Fig. 10, there is a clear statement to be made here through change in m level from m = 10² to m = 10³; notably the vortex intensity decreases as the parameter m rises, so that at τ ₀ = 0.01 and with m = 10³, there is little evidence of any vortex behaviour remaining. At the larger level τ ₀ = 0. 1 and m = 10³, there is no evidence of any vortex behaviour at all, whilst at the same level of τ ₀ = 0.1 and one of order of magnitude lower in m (m = 10²), there are still signs of vortex activity. For inelastic Bingham–Papanastasiou streamline patterns (Fig. 11), similar trends in vortex activity are observed when changing τ ₀ (from 0.01 to 0.1) and m (from 10² to 10³) parameters.

Turning next to consider trends of change in upstream vortex intensity, Fig. 13a, one may observe monotonic increase with De rise for the base-reference Oldroyd (τ ₀ = 0) fluid; ψ _int increases from 0.54 × 10^− 3 to 0.72 × 10^− 3. Then, with supplementary yield stress influence, once more gradual suppression of ψ _int increase is realised, to be practically flattened and removed by τ ₀ = 0.1 (see zoomed insert to detect actual rise, but at much lower magnitudes, two orders lower than Newtonian/Oldroyd).

In L measure at extremes (De = 5 of Fig. 15): L-upstream halves from 1.77 at τ ₀ = 0 to 0.86 at τ ₀ = 0.1; L downstream reduces by one third equivalently, see Fig. 14. In X measure there is similar adjustment: X upstream falls from 1.33 at τ ₀ = 0 to 0.63 at τ ₀ = 0.1; X downstream falls from 1.24 at τ ₀ = 0 to 0.53 at τ ₀ = 0.1.

Fig. 15

Velocity profiles at a z = 0 (contraction zone); b z = 10 (inlet zone), inelastic Bing-Pap, m = 10³, β = 0.9

m variation, m rise

In field solutions, Fig. 12 focuses, in one place for ease of reference, upon a selection of inelastic (left column) versus Papanastasiou–Oldroyd (De = 1, right column) results, at fixed τ ₀ = 0.01 with rising m values (0, 10², 10³). In Fig. 14, one is looking at the same data in m change or τ ₀ change for (τ ₀, m) pairings of (0, 0) and (0.01, 10²). Hence, trends in vortex response are found only to differ when comparing data at pairings (τ ₀ = 0.01, m = 10³) and (τ ₀ = 0.1, m = 10²). Downstream vortex intensities differ by one order of magnitude: for (τ ₀ = 0.01, m = 10³), initial, minimum and maximum are (0.48, 0.25, 0.60) × 10^− 4; whilst for (τ ₀ = 0.1, m = 10²), initial, minimum and maximum are (0.55, 0.27, 0.60) × 10^− 5. For upstream vortex intensities, the trend in one order of magnitude shift is similar, yet reflecting practically no change with De at each setting. This is noted in the shift from a characteristic initial value of 0.48 × 10^− 4 for (τ ₀ = 0.01, m = 10³) to 0.54 × 10^− 5 for (τ ₀ = 0.1, m = 10²).

Revisiting vortex length measures at extremes (De = 5 of Fig. 14) for m variation in contrast to τ ₀ variation: both L and X measures again reduce at upstream and downstream locations. Yet, this reduction is practically halved over results with τ ₀ variation reported above; for example, L upstream now falls from 1.77 at m = 0 (as for τ ₀ = 0) to 1.40 at m = 10³, τ ₀ = 0.01 (when compared to 0.86 at m = 10², τ ₀ = 0.1).

Velocity profiles are also included for reference (Fig. 16, m = 10³), sampled separately at the contraction centre plane (z = 0) and the inlet zone (z = −10). Variation is typified and represented for the viscoplastic Bingham–Papanastasiou fluid, over τ ₀ elevation through values (0, 0.01, 0.1). At the inlet zone, there is the core flow flattening of the flow profile, and the sharpening of the wall region, to approximate a plug flow. Maxima at core centre reduce by almost one half from U _z of 0.125 at τ ₀ = 0 to 0.093 at τ ₀ = 0.1; at the contraction zone, reduction levels in U _z are considerably lessened (∼5%).

Fig. 16

Second normal stress difference (N₂) field: Oldroyd-B, Pap-OldB, m = (10², 10³), β = 0.9

Stress fields—yielded and unyielded regions

Considering normal stress effects, first with τ ₀ changes and at m = 10², we can interrogate field structures in first and second normal stresses. N ₁ influence at De = 1, see Fig. 17, shows a drop in N ₁ with rising τ ₀, in both recess corners upstream and downstream, otherwise little differences apparent across the field. N ₁ maxima magnify some 20 times from De = 1 to De = 5 (at any τ ₀ level). From inference of cut-off zero-stress N ₁ contour-line (which ties in with N ₂ solutions), there is little change detectable in upstream vortex dynamics with De change (in contrast to τ ₀ change); whilst to the contrary, downstream dynamics are expanded in size. In terms of vortex capture, more can be gathered from N ₂ data directly, as in N ₂ influence at De = 1 of Fig. 16, where a clear decline in N ₂ is now seen with rising τ ₀, in both recess corners, upstream and downstream. N ₂ maximum levels magnify some 10 times to De = 5 from De = 1. From inference of cut-off zero-stress N ₂ contour line, there is significant reduction in upstream vortex size and dynamics with rise in τ ₀ (here, little effect due to De rise); likewise, there is prominent reduction in downstream vortex activity (again there is little effect due to De rise). Nevertheless, De rise does have a major influence on N ₂, as noted just beyond the contraction and close to the obstruction (maximum values); yet this viscoelastic feature appears unaffected by yield stress influences.

Fig. 17

First normal stress difference (N ₁) field: Oldroyd-B, Pap-OldB, m = (10², 10³), β = 0.9

Next with m change and observations between m = 10² and m = 10³, data in Fig. 16 for N ₂ begin to show some differences at higher elasticity levels (De ≈ 5); again, this is particularly noted in the corner recess zones (negative values of N ₂) and across the central constriction plane. On the contrary under N ₁ data of Fig. 17 and away from corner recesses, there are no significant differences detected in field solutions at the level of De ≈ 5 between the two values of m at τ ₀ = 0.1. This is consistent with above comments. The maximum and minimum values of N ₁ reflect this position, being in the same order for m = 10² and m = 10³ solutions.

Across models and settings, it is instructive to examine the divide between yielded and unyielded regions, as depicted in Fig. 18, where the cut-off criterion is based on the magnitude of stress (derived from its second invariant, see Mitsoulis 2007) exceeding the set level of τ ₀ in each instance. We consider first data for the inelastic Bingham–Papanastasiou model (m = 10³). Here we follow Mitsoulis (2007) in acknowledging that strictly speaking, vortex activity would not be expected within the unyielded regions, since these areas are denoted for their lack of deformation. Nevertheless, the vortex activity shown in the present work is a consequence of using the regularised Bingham model, according to the Papanastasiou modification, which renders the model valid in all flow zones and deformation rates, both yielded and unyielded, see also Dimakopoulos and Tsamopoulos (2003, 2007) for prediction of unyielded regions in the corners of a sudden contraction or expansion.

Fig. 18

Growth of the unyielded region (black) inelastic Bing-Pap, m = 10³

Consistent with Mitsoulis and Huilgol (2004) work on 2:1 expansion flow problem, the relatively yielded (red-white) region for τ ₀ = 0.01 occupies the zones close to the channel walls and that through the contraction–expansion. The unyielded regions (black) are then restricted to the core flow complement zones and the corner recess zones. Once τ ₀ has risen to 0.02, the core central unyielded zones have expanded out sufficiently towards the channel walls to link with the enlarged unyielded recess zones. With further rise in τ ₀ to 0.1, both core and recess unyielded regions have merged and swelled out to reach the walls. Now, only the enlarged doughnut-shaped contraction–expansion zone remains yielded (where gradients are high), swelling out before and after the contraction to cover a region over thrice its inner area. We take pains to emphasise that the last retained case in Fig. 18 with τ ₀ = 0.1 presents a solution well beyond the validity of the Papanastasiou model, from the data this being anticipated to be closer to τ ₀ = 0.02. Here, the entire domains of entry and exit pipe flow are interpreted as unyielded (relatively motionless, τ less than τ ₀), whereas in the constricted region the material is yielded and flows. This simply reveals the properties of the Papanastasiou model, which allows flow in regions where the second invariant of the rate of strain is non-zero, whilst simultaneously the second invariant of stress falls below the yield stress. These comments are moderated by a scaling on τ ₀ with the exponential multiplicative term (factor m = 10³), so that by construction, the model is always viscous (flowing to some time scale) tending to Ideal Bingham as m tends to infinity. Still further amplification of τ ₀ (not shown, due to model approximation limitations) shrinks the yielded contraction–expansion zone to occupy solely the space within the contraction itself. Results for the Papanastasiou–Oldroyd (De = 1) with τ ₀ rise do not differ in appearance from those for Bingham–Papanastasiou. Hence, for brevity, these are not shown. These findings concur with those of Mitsoulis and Huilgol (Mitsoulis and Huilgol (2004)) (downstream correspondence to the present contraction–expansion problem), who also noted the dead recess zones near the expansion corners, where the material remains relatively unyielded. As their Bingham number increased, the central core unyielded region became larger (more solid region), so that it began to impinge towards the expansion entrance itself. Finally, for very high Bingham number values, only the high-gradient areas near the entrance to the expansion remained unyielded.

Conclusions

The overall conclusions from this work point to the significant impact that yield stress inclusion has upon nonlinear flow behaviour, considered here in the context of contraction–expansion flow. Here, this has been explored through the viscoplastic regime (Bingham–Papanastasiou) and extended into the viscoelastoplastic regime (Papanastasiou–Oldroyd). Our findings reveal the significant impact that elevation has in yield stress parameters of (m,τ ₀), and in sharpening of stress singularity from that of the Oldroyd/Newtonian models to the ideal Bingham form. Such aspects are covered in field response via vortex behaviour (upstream–downstream, enhancement–suppression), pressure drops, stress field structures and yielded–unyielded zones. Vortex trends reflect suppression, with rising m or τ ₀, in both upstream and downstream vortices (more exaggerated in τ ₀ change than m change). Elasticity, via viscoelastoplasticity, disturbs upstream–downstream vortex symmetry balance. For such solvent dominated fluids considered: at low De = 1, upstream vortices dominate downstream vortices; at high De = 5, this position is reversed. With De rise and in vortex intensity, upstream growth trends are monotonic; downstream trends are non-monotonic, showing first a decline to a minimum (at De = 2), prior to growth thereafter.

With respect to the cut-off between yielded–unyielded flow zones (yield-front), rapid adjustment occurs for 0 ≤ τ ₀≤ 0.02, and once again between 0.02 ≤ τ ₀≤ 0.1. Unyielded regions begin by being restricted to the core flow complement zones and the corner recess zones. The core central unyielded zones have expanded out sufficiently towards the channel walls by τ ₀ = 0.02, to link with the enlarged unyielded recess zones. This eventually leads to merger of core and recess unyielded regions by τ ₀ = 0.1, reaching the walls, leaving only the enlarged doughnut-shaped contraction–expansion zone yielded.

Analysis of pressure drop data reveals increases in the viscoplastic case, through epd and m variation, of some (12%, 24%) above the unity Newtonian reference line, for τ ₀ = 0.1 when m = (10², 10³). In this inelastic context, N ₁ = 0, and such epd increases may be attributed to the elevation observed in shear and extensional viscosity at low to moderate deformation rates. In the viscoelastoplastic case, the P ^∗comparison provides direct insight upon the additional N ₁ viscoelastic influences upon ‘excess pressure drop’, when read against the unity viscoplastic line. Furthermore, the epd comparison against the Newtonian reference yields the combination of viscoelastic and viscoplastic influences. Characteristically, for the Papanastasiou–Oldroyd data (τ ₀ = 0.1, m = 10²), the 12% pressure drop increase due to viscoplastic contributions, is observed to reduce to 8% total contribution increase in epd (confirmed independently via cross-check against Oldroyd data). This may be argued to be a consequence of strengthening in N ₁ (above Oldroyd) at low deformation rates, as corresponding increases in extensional and shear viscosity only tend to promote enhancement in excess pressure drop. One may comment that for an additive viscoelastic component to pressure drop increase, the appropriate property to seek is the converse, weakening of N ₁.