Introduction

There have been a lot of theoretical studies on diffusiophoresis of particles of various types such as rigid spheres [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] (see in particular Ref. [6] for weakly charged spheres with arbitrary electrical double layer thickness, Ref. [14] for moderately charged spheres with arbitrary electrical double layer thickness, Ref. [4, 5, 12] for highly charged spheres, and Ref. [8, 11, 13] for spheres in a general electrolyte solution), rigid cylinders [16,17,18], particles in an electrolyte with finite ion size [19, 20], dielectric liquid drops [21,22,23], conducting drops or mercury drops [24,25,26], and soft particles (polymer-coated particles) [27,28,29,30,31,32,33]. The diffusioosmosis in fibrous porous media is closely related to the diffusiophoresis of cylindrical particles. Keh and his coworkers have developed the general theory of diffusioosmosis [34,35,36,37]. Keh and Wei [34] presented an analytic formula for the transverse diffusiophoretic mobility of a weakly charged cylindrical particle oriented perpendicular to the applied electrolyte concentration gradient field. This expression is correct to the second power of the zeta potential of the particle. In the present paper, we make corrections to the third powers of zeta potentials in their formula [34] and derive an analytic diffusiophoretic mobility expression for a cylinder in a symmetrical electrolyte solution applicable for low to moderate particle zeta potentials. We also calculate the diffusiophoretic mobility of a cylinder oriented at an arbitrary angle between its axis and the applied electrolyte concentration gradient field by combining the obtained transverse mobility expression with a previously obtained expression for the tangential diffusiophoretic mobility of a cylinder oriented parallel to the applied electrolyte concentration gradient field [18].

Theory

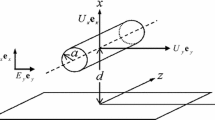
Consider an infinitely long cylinder of radius a and zeta potential ζ moving with a diffusiophoretic velocity U in an aqueous liquid of relative permittivity εr and viscosity η containing a symmetrical electrolyte of valence Z under an applied constant electrolyte concentration gradient. The ionic drag coefficient of electrolyte cations λ+ and that of electrolyte anions λ− may be different. We take a cylindrical coordinate system (r, θ, z) with its origin fixed at the center of the cylinder, where the z-axis coincides with the cylinder axis (Fig. 1). Let n+(r) be the concentration (number density) of cations at position r, n−(r) be that of anions, and n(r) be their concentrations beyond the electrical double layer around the cylinder, where n+(r) = n−(r) = n(r). Let the applied electrolyte concentration gradient be expressed in terms of n(r) as ∇n. We denote by n∞ the bulk concentration of electrolytes in the absence of ∇n. The following vector α proportional to ∇n is introduced:

$$\boldsymbol{\alpha }=\frac{kT}{Ze{n}^{\infty }}\nabla n$$
(1)

where k is the Boltzmann constant, T is the absolute temperature, and e is the elementary electric charge. We assume that the field α is weak so that U is linear in α and the Reynolds number of the liquid flow is low so that inertial terms in the Navier–Stokes equation can be neglected, and the liquid can be regarded as incompressible. We also assume that no electrolyte ions can penetrate the particle surface.

Fig. 1
figure 1

A cylindrical colloidal particle of radius a moving with a velocity U⊥ in a transverse electrolyte concentration gradient field ∇n or α

Full size image

We consider first the cylinder oriented perpendicularly to α and denote the diffusiophoretic velocity U by \({{\varvec{U}}}_{\perp }\). The z-axis, which coincides with the cylinder axis, is put perpendicular to α (Fig. 1).

It has previously been shown [12] that one can obtain the general expression for the diffusiophoretic velocity U of a colloidal particle in an electrolyte concentration gradient field α from the expression for its electrophoretic velocity UE in an applied electric field E by replacing E with α, since the governing electrokinetic equations take essentially the same form for U and UE [12]. The only difference is the far-field boundary condition for the deviations δμ±(r) of the electrochemical potentials of ions μ±(r) caused by α and E, where μ+(r) and μ−(r) are, respectively, the electrochemical potentials of cations and anions. The transverse diffusiophoretic velocity \({{\varvec{U}}}_{\perp }\) in a transverse field α can thus be derived from the corresponding expression for UE [38, 39], viz.,

$${{\varvec{U}}}_{\perp }=\frac{{a}^{2}}{8}{\int }_{a}^{\infty }\left[1-{\left(\frac{r}{a}\right)}^{2}\left\{1-2\;\mathrm{ln}\left(\frac{r}{a}\right)\right\}\right]G(r)dr\boldsymbol{\alpha }$$
(2)

with

$$G\left(r\right)=\;-\frac{Ze{n}^{\infty }}{\eta r}\frac{dy}{dr}\left({e}^{-y}{\phi }_{+}+{e}^{y}{\phi }_{-}\right)$$
(3)
$$\begin{aligned}{\phi }_{\pm }\left(r\right)=\;& \left(\mp 1+\beta \right)\left(r+\frac{{a}^{2}}{r}\right) \\ & - \frac{1}{2}\left(r+\frac{{a}^{2}}{r}\right) {\int }_{a}^{\infty }{g}_{\pm }\left(r\right)dr \\ &+\frac{1}{2}{\int }_{a}^{r}\left(r-\frac{{x}^{2}}{r}\right){g}_{\pm }\left(x\right)dx\end{aligned}$$
(4)
$${g}_{\pm }\left(r\right)=\pm \frac{dy}{dr}\left(\frac{d{\phi }_{\pm }}{dr}\mp \frac{{\lambda }_{\pm }}{Ze}\frac{h}{r}\right)$$
(5)

and

$$\begin{aligned}h\left(r\right)= & - \left(\frac{{r}^{3}}{16}- \frac{{a}^{2}r}{8}+\frac{{a}^{4}}{16r}\right){\int }_{a}^{\infty }G\left(r\right)dr \\ &-\left\{\frac{r}{8}-\frac{{a}^{2}}{8r}-\frac{r}{4}\mathrm{ln}\left(\frac{r}{a}\right)\right\}{\int }_{a}^{\infty }{r}^{3}G\left(r\right)dr \\ & +{\int }_{a}^{r}\left\{\frac{{r}^{3}}{16}-\frac{{x}^{4}}{16r}+\frac{r{x}^{2}}{4}\mathrm{ln}\left(\frac{x}{r}\right)\right\}G\left(x\right)dx\end{aligned}$$
(6)
$$\beta =\frac{{1/\lambda }_{+}-{1/\lambda }_{-}}{1/{\lambda }_{+}+1/{\lambda }_{-}}=-\frac{{\lambda }_{+}-{\lambda }_{-}}{{\lambda }_{+}+{\lambda }_{-}}=-\frac{{m}_{+}-{m}_{-}}{{m}_{+}+{m}_{-}}$$
(7)

where

$${m}_{\pm }=\frac{2{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}kT}{3\eta {Z}^{2}{e}^{2}}{\lambda }_{\pm }$$
(8)

are the scaled ionic drag coefficients of cations and anions. The equilibrium electric potential ψ(0)(r) is assumed to satisfy the cylindrical Poisson-Boltzmann equation, viz.,

$$\frac{{d}^{2}y\left(r\right)}{d{r}^{2}}+\frac{1}{r}\frac{dy\left(r\right)}{dr}={\kappa }^{2}\mathrm{sinh}y\left(r\right)$$
(9)

with

$$y(r)=\frac{Ze{\psi }^{(0)}(r)}{kT}$$
(10)
$$\kappa =\sqrt{\frac{2{Z}^{2}{e}^{2}{n}^{\infty }}{{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}kT}}$$
(11)

where y(r) is the scaled equilibrium electric potential, κ is the Debye-Hückel parameter, and εo is the permittivity of a vacuum. Equation (9) is subject to the following boundary conditions:

$${\psi }^{\left(0\right)}\left(r\right)\to 0 \ \mathrm{as} \ r \to \infty$$
(12)
$${\psi }^{\left(0\right)}\left(a\right)=\zeta$$
(13)

The liquid fluid velocity u(r) and the deviations δμ±(r) of the ionic electrochemical potentials μ±(r) due to α are related to h(r) and ϕ±(r), respectively, as

$${\varvec{u}}\left({\varvec{r}}\right)=\left(-\frac{1}{r}h\left(r\right)\mathrm{\alpha cos}\theta ,\frac{dh(r)}{dr}\alpha \mathrm{sin}\theta , 0\right)$$
(14)
$${\delta \mu }_{\pm }\left({\varvec{r}}\right)=\mp Ze\alpha {\phi }_{\pm }\left(r\right)\mathrm{cos}\theta$$
(15)

where α is |α|. Let us define the scaled diffusiophoretic mobility \({U}_{\perp }^{*}\) as

$${{\varvec{U}}}_{\perp }=\frac{2{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}kT}{3\eta Ze}{U}_{\perp }^{*}\boldsymbol{\alpha }$$
(16)

We expand y(r) in powers of ζ, which is the solution to Eq. (9) [39], viz.,

$$y\left(r\right)=\widetilde{\zeta }{y}_{1}\left(r\right)+{{\widetilde{\zeta }}^{3}y}_{3}\left(r\right)$$
(17)

with

$${y}_{1}\left(r\right)=\frac{{K}_{0}(\kappa r)}{{K}_{0}(\kappa a)}$$
(18)
$$\begin{aligned}{y}_{3}\left(r\right)= & \frac{1}{6{K}_{0}^{3}(\kappa a)}\left[{K}_{0}(\kappa r)\left\{\frac{{I}_{0}(\kappa a)}{{K}_{0}(\kappa a)}\right\} {\int }_{\kappa a}^{\infty }{K}_{0}^{4}(t)tdt \right. \\& \left. -{I}_{0}(\kappa r){\int }_{\kappa r}^{\infty }{K}_{0}^{4}(t)tdt\right.{-K}_{0}(\kappa r)\left.{\int }_{\kappa a}^{\kappa r}{I}_{0}(t){K}_{0}^{3}(t)tdt\right]\end{aligned}$$
(19)

where

$$\widetilde{\zeta }=\frac{Ze\zeta }{kT}$$
(20)

is the scaled zeta potential and In(κa) and Kn(κa) are, respectively, the nth order modified Bessel functions of the first and second kinds.

We first derive an expression for \({U}_{\perp }^{*}\) correct to the order of ζ2. It follows from Eqs. (3), (4), (6), and (17) that the following approximate form for G(r) correct to the order of ζ2, which involves only y1(r), can be obtained:

$$\begin{aligned}G\left(r\right)= & -\frac{2Ze{n}^{\infty }}{\eta }\frac{d\left({\widetilde{\zeta }y}_{1}\right)}{dr}\left(1+\frac{{a}^{2}}{{r}^{2}}\right) \\ & \left\{\beta +{\widetilde{\zeta }y}_{1}+\frac{1}{2}{\int }_{a}^{\infty }\frac{d\left({\widetilde{\zeta }y}_{1}\right)}{dr}\left(1-\frac{{a}^{2}}{{r}^{2}}\right)dr\right\} \\ & +\frac{Ze{n}^{\infty }}{\eta }\frac{d\left({\widetilde{\zeta }y}_{1}\right)}{dr}{\int }_{a}^{r}\frac{d\left({\widetilde{\zeta }y}_{1}\right)}{dx}\left(1-\frac{{x}^{2}}{{r}^{2}}\right)\left(1-\frac{{a}^{2}}{{x}^{2}}\right)dx\end{aligned}$$
(21)

By combining Eq. (2) with Eq. (21) for G(r) and Eq. (18) for y1(r), we obtain an approximate expression for U⊥* which is correct to the order of ζ2, viz.,

$${U}_{\perp }^{*}=\frac{3}{2}\beta \widetilde{\zeta }{f}_{1}\left(\kappa a\right)+\frac{3}{16}{\widetilde{\zeta }}^{2}{f}_{2}\left(\kappa a\right)$$
(22)

where

$${f}_{1}\left(\kappa a\right)=1-\frac{4(\kappa a{)}^{4}}{{K}_{0}(\kappa a)}{\int }_{\kappa a}^{\infty }\frac{{K}_{0}(t)}{{t}^{5}}dt+\frac{(\kappa a{)}^{2}}{{K}_{0}(\kappa a)}{\int }_{\kappa a}^{\infty }\frac{{K}_{0}(t)}{{t}^{3}}dt$$
(23)

and

$$\begin{aligned}{f}_{2}\left(\kappa a\right)= & -{\left(\kappa a\right)}^{2}{\int }_{a}^{\infty }\left[1-{\left(\frac{r}{a}\right)}^{2}\left\{1-2\;\mathrm{ln}\left(\frac{r}{a}\right)\right\}\right] \\ & \times \left[\frac{d{y}_{1}}{dr}\right.\left(1+\frac{{a}^{2}}{{r}^{2}}\right)\left\{{y}_{1}+\frac{1}{2}{\int }_{a}^{\infty }\frac{d{y}_{1}}{dr}\left(1-\frac{{a}^{2}}{{r}^{2}}\right)dr\right\} \\ & -\frac{1}{2}\frac{d{y}_{1}}{dr}{\int }_{a}^{\mathrm{r}}\frac{d{y}_{1}}{dx}\left(1-\frac{{x}^{2}}{{r}^{2}}\right)\left.\left(1-\frac{{a}^{2}}{{x}^{2}}\right)dx\right]dr\end{aligned}$$
(24)

Equation (22) agrees with the result of Keh and Wei [34]. Note that f1(κa) and f2(κa) are equivalent to Θ1(κa) and Θ2(κa), respectively, in their paper (Eqs. (35a) and (35b) in Ref. [34]). Equation (22) for U⊥* consists of two terms. The first term is the electrophoresis component and the second term is the chemiphoresis component. Note also that f1(κa) given by Eq. (23) corresponds to Henry’s function for the transverse electrophoretic mobility of a cylinder oriented perpendicular to an applied electric field [38, 39].

Next let us derive an expression for U⊥* correct to the order of ζ3. This term is related to the electrophoresis component, and thus, it is proportional to β. By using the same method employed to obtain the transverse electrophoretic mobility of a cylinder of radius a correct to the order of ζ3 [39], by using Eq. (17), we finally obtain the following expression for \({U}_{\perp }^{*}\) correct to the order of ζ3:

$$\begin{aligned}{U}_{\perp }^{*}=& \frac{3}{2}\beta \widetilde{\zeta }{f}_{1}\left(\kappa a\right)+\frac{3}{16}{\widetilde{\zeta }}^{2}{f}_{2}\left(\kappa a\right)-\frac{3}{2}\beta {\widetilde{\zeta }}^{3} \\ & \left\{{f}_{3}\left(\kappa a\right)+\left(\frac{{m}_{+}+{m}_{-}}{2}\right){f}_{4}\left(\kappa a\right)\right\}\end{aligned}$$
(25)

with

$$\begin{aligned}f_3\left(\kappa a\right)= & \frac{3(\kappa a)^2}{64}\int_a^\infty\left[1-\frac{r^2}{a^2}\left\{1-2\;\ln\left(\frac ra\right)\right\}\right]\frac{dy_1}{dr} \\ & \times\left\{\left(1+\frac{a^2}{r^2}\right)\int_a^\infty H_1(x)\frac{dy_1}{dx}dx \right. \\ & \left. -\int_a^r\left(1-\frac{x^2}{r^2}\right)H_1(x)\frac{dy_1}{dx}dx\right\}dr \\ & +\frac{(\kappa a)^2}{32}\int_a^\infty\left[1-\frac{r^2}{a^2}\left\{1-2\;\ln\left(\frac ra\right)\right\}\right]\frac{dy_1^2}{dr} \\ & \times\left\{\left(1+\frac{a^2}{r^2}\right)\int_a^\infty\left(1-\frac{a^2}{x^2}\right)\frac{dy_1}{dx}dx \right. \\ & \left. -\int_a^r\left(1-\frac{x^2}{r^2}\right)\left(1-\frac{a^2}{x^2}\right)\frac{dy_1}{dx}dx\right\}dr \\ & +\frac{(\kappa a)^2}8\int_a^\infty\left[1-\frac{r^2}{a^2}\left\{1-2\;\ln\left(\frac ra\right)\right\}\right] \\ & \left(1+\frac{a^2}{r^2}\right)\left(\frac{dy_3}{dr}+\frac16\frac{dy_1^3}{dr}\right)dr\end{aligned}$$
(26)

and

$$\begin{aligned}f_4\left(\kappa a\right)=&\frac{3(\kappa a)^2}{64}\int_a^\infty\left[1-\frac{r^2}{a^2}\left\{1-2\;\ln\left(\frac ra\right)\right\}\right]\frac{dy_1}{dr} \\ & \times\left\{\left(1+\frac{a^2}{r^2}\right)\int_a^\infty H_2(x)\frac{dy_1}{dx}dx \right. \\ & \left. -\int_a^r\left(1-\frac{x^2}{r^2}\right)H_2(x)\frac{dy_1}{dx}dx\right\}dr\end{aligned}$$
(27)

where

$$\begin{aligned}{H}_{1}(x)=& \frac{2}{3}\left(1-\frac{{a}^{2}}{{x}^{2}}\right){\int }_{a}^{\infty }\left(1-\frac{{a}^{2}}{{t}^{2}}\right)\frac{d{y}_{1}}{dt}dt \\ & -\frac{2}{3}{\int }_{a}^{x}\left(1+\frac{{t}^{2}}{{x}^{2}}\right)\left(1-\frac{{a}^{2}}{{t}^{2}}\right)\frac{d{y}_{1}}{dt}dt\end{aligned}$$
(28)

and

$$\begin{aligned}H_2(x)= & -\frac{\kappa^2}8\int_a^x\left\{x^2-\frac{t^4}{x^2}+4t^2\;\ln\left(\frac tx\right)\right\} \\ & \left(1+\frac{a^2}{t^2}\right)\frac{dy_1}{dt}dt+\frac{\kappa^2}8\int_a^\infty \left\{x^2 + \frac{a^4}{x^2} \right. \\ & \left. -2a^2+2\left(1-\frac{a^2}{x^2}\right)t^2-4t^2\;\ln\left(\frac xa\right)\right\} \\ & \left(1+\frac{a^2}{t^2}\right)\frac{dy_1}{dt}dt\end{aligned}$$
(29)

The first and second terms on the right-hand side of Eq. (25) are equivalent to Eq. (22), and the last term is the correction term of the order of ζ3 to Eq. (22). The above functions f1(κa), f2(κa), f3(κa), and f4(κka) defined by Eqs. (23), (24), (26), and (27) in the present paper, respectively, correspond to the functions f1(κa)–f4(κa) defined in the previous paper [39] but they differ from each other by a factor of 2/3 due to different definitions in the present paper and the previous paper [39].

In the large κa limit (κa → ∞), Eq. (25) becomes

$${U}_{\perp }^{*}=\frac{3}{2}\left(\beta \widetilde{\zeta }+\frac{1}{8}{\widetilde{\zeta }}^{2}\right)$$
(30)

which agrees with the result for a particle with a planar surface [1, 2]. In the small κa limit (κa → 0), on the other hand, Eq. (25) becomes

$${U}_{\perp }^{*}=\frac{3}{4}\beta \widetilde{\zeta }$$
(31)

It is thus seen that there are no contributions of f3(κa) and f4(κa) in the limits of κa → ∞ and κa → 0.

We next consider the tangential diffusiophoretic mobility \({U}_{\parallel }^{*}\) of a cylindrical particle oriented parallel to α. It can be shown [18] that \({U}_{\parallel }^{*}\) can be expressed as

$${U}_{\parallel }^{*}=\frac{3}{2}\left\{\beta \widetilde{\zeta }+\frac{1}{8}{\widetilde{\zeta }}^{2}f\left(\kappa a\right)\right\}$$
(32)

where

$$f\left(\kappa a\right)={\left(\kappa a\right)}^{2}\left[1+\frac{{K}_{2}(\kappa a)}{{K}_{0}(\kappa a)}-2{\left\{\frac{{K}_{1}(\kappa a)}{{K}_{0}(\kappa a)}\right\}}^{2}\right]$$
(33)

Note that Eq. (32) is already correct to the order of \({\widetilde{\zeta }}^{3}\), since the next-order correction term to Eq. (32) is of the order of \({\widetilde{\zeta }}^{4}\). It is to be noted that \({U}_{\parallel }^{*}\) depends on κa unlike the case of electrophoresis, where the tangential electrophoretic mobility of a cylinder does not depend on κa [38, 39].

In the limit of κa → ∞, f(κa) tends to 1 so that Eq. (32) tends to Eq. (30), viz.,

$${U}_{\parallel }^{*}=\frac{3}{2}\left(\beta \widetilde{\zeta }+\frac{1}{8}{\widetilde{\zeta }}^{2}\right)$$
(34)

In the opposite limit of κa → 0, f(κa) tends to 0 so that Eq. (32) tends to

$${U}_{\parallel }^{*}=\frac{3}{2}\beta \widetilde{\zeta }$$
(35)

It is thus seen that in the limit of κa → ∞, \({U}_{\perp }^{*}\) and \({U}_{\parallel }^{*}\) tend to the same limiting value (Eqs. (30) and (34)), while in the opposite limit of κa → 0, the limiting value of \({U}_{\parallel }^{*}\) (Eq. (35)) is twice that of \({U}_{\perp }^{*}\) (Eq. (31)).

For a cylindrical particle oriented at an arbitrary angle between its axis and the applied electrolyte concentration gradient field a, its diffusiophoretic mobility \({U}_{\mathrm{av}}^{*}\) averaged over a random distribution of orientation is given by [40]:

$${U}_{\mathrm{av}}^{*}=\frac{1}{3}{U}_{\parallel }^{*}+\frac{2}{3}{U}_{\perp }^{*}$$
(36)

Results and discussion

The main result of this paper is Eq. (25) for the transverse diffusiophoretic mobility \({U}_{\perp }^{*}\) of a cylinder oriented perpendicular to an applied electrolyte concentration gradient, which is correct to the order of ζ3. Equation (25) is an improvement of Eq. (22) correct to the order of ζ2.

Since Eqs. (23), (24), (26), (27), and (33) for f1(κa)–f4(κa) and f (κa) are not very convenient for the practical use, since they involve modified Bessel functions and numerical integrations, we derive simpler approximate formula for f1(ka), f3(ka), and f4(ka) without involving modified Bessel functions and numerical integrations on the basis of the same approximation method as used in the electrophoresis problem [38, 39]. As for f2(κa), Keh and Wei [34] derived an excellent approximate expression (Eq. (38)). Thus, we find that

$${f}_{1}\left(\kappa a\right)=\frac{1}{2}\left[1+\frac{1}{{\left\{1+\frac{2.55}{\kappa a(1+{e}^{-\kappa a})}\right\}}^{2}}\right]$$
(37)
$${f}_{2}\left(\kappa a\right)=1-\frac{1.15}{1+0.066{\left(\kappa a\right)}^{1.15}-0.02{\left(\kappa a\right)}^{0.2}}+\frac{0.15}{{\left[1+15{(\kappa a)}^{1.7}\right]}^{0.8}}$$
(38)
$${f}_{3}(ka)=\frac{\kappa a(\kappa a+0.162)}{3\{(\kappa a{)}^{3}+9.94(\kappa a{)}^{2}+18.7\kappa a+0.147\mathrm{ \ exp}(-9.41\kappa a)\}}$$
(39)
$${f}_{4}(ka)=\frac{3\kappa a\{\kappa a+0.361\mathrm{ \ exp}(-0.475\kappa a)+0.0878\}}{4\{(\kappa a{)}^{3}+10.8(\kappa a{)}^{2}+18.2\kappa a+0.0633\}}$$
(40)

Also, we find that f(κa) given by Eq. (33) can be approximated with negligible errors as

$$f\left(\kappa a\right)=\frac{\kappa a\left(\kappa a+2.5\right)}{(\kappa a{)}^{2}+3\kappa a+0.91\mathrm{ \ exp}\left(-0.59\kappa a\right))}+\frac{2\mathrm{ \ exp}\left(-5.7\kappa a\right)}{1.62-\mathrm{ln}(\kappa a)}$$
(41)

By using the above equations, Eq. (25) becomes

$$\begin{aligned}{U}_{\perp }^{*}= & \frac{3}{4}\beta \widetilde{\zeta }\left[1+\frac{1}{{\left\{1+\frac{2.55}{\kappa a(1+{e}^{-\kappa a})}\right\}}^{2}}\right] \\ & +\frac{3}{16}{\widetilde{\zeta }}^{2}\left\{1-\frac{1.15}{1+0.066{\left(\kappa a\right)}^{1.15}-0.02{\left(\kappa a\right)}^{0.2}} +\frac{0.15}{{\left[1+15{(\kappa a)}^{1.7}\right]}^{0.8}}\right\} \\ & -\beta {\widetilde{\zeta }}^{3}\frac{\kappa a(\kappa a+0.162)}{2\{(\kappa a{)}^{3}+9.94(\kappa a{)}^{2}+18.7\kappa a+0.147\mathrm{ \ exp} \ (-9.41\kappa a)\}} \\ & -\beta {\widetilde{\zeta }}^{3}\left(\frac{{m}_{+}+{m}_{-}}{2}\right)\frac{9\kappa a\{\kappa a+0.361\mathrm{ \ exp} \ (-0.475\kappa a)+0.0878\}}{8\{(\kappa a{)}^{3}+10.8(\kappa a{)}^{2}+18.2\kappa a+0.0633\}}\end{aligned}$$
(42)

and Eq. (32) becomes

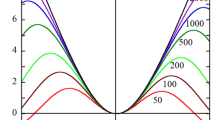
$$\begin{aligned}{U}_{\parallel }^{*}= & \frac{3}{2}\beta \widetilde{\zeta }+\frac{3}{16}{\widetilde{\zeta }}^{2}\left\{\frac{\kappa a\left(\kappa a+2.5\right)}{(\kappa a{)}^{2}+3\kappa a+0.91\mathrm{ \ exp}\left(-0.59\kappa a\right))} \right. \\ & \left. +\frac{2\mathrm{ \ exp}\left(-5.7\kappa a\right)}{1.62-\mathrm{ln}(\kappa a)}\right\}\end{aligned}$$
(43)

Figure 2a, b shows some results of \({U}_{\perp }^{*}\) calculated via Eq. (25) (or Eq. (42) with negligible errors) for a cylinder of radius a in an aqueous KCl solution (m+  = 0.176, m−  = 0.169, β =  − 0.02) (Fig. 2a) and NaCl solution (m+  = 0.258, m−  = 0.169, β =  − 0.2) (Fig. 2b) at 25 °C (solid curves) in comparison with those obtained via Eq. (22) (dotted curves, Keh and Wei [34]). The contribution of the correction term of order ζ3 is related to the electrophoresis component of diffusiophoresis and becomes more significant as β becomes larger. Indeed, it is seen from Fig. 2a, b that this correction contribution is larger for NaCl (β =  − 0.2) than for KCl (β =  − 0.02). We also see that this contribution is large for moderate values of κa (0.1 < κa < 100) and becomes small for large κa (> 100) or small κa (< 0.1), vanishing in the limit of κa → ∞ (thin double layer limit) or κa → 0 (thick double layer limit). Note that in these two limiting cases the solid and dotted curves coincide with each other.

Fig. 2
figure 2

Scaled diffusiophoretic mobility \({U}_{\perp }^{*}\) of a cylindrical colloidal particle of radius a in an aqueous electrolyte solution at 25 °C as a function of the scaled zeta potential \(\widetilde{\zeta }\) at several values of κa. Calculated via Eq. (25) (or Eq. (42) with negligible errors) (solid curves) in comparison with the results for \({U}_{\perp }^{*}\) correct to the order of ζ.2 obtained from Eq. (22) (Keh and Wei [8]) (dotted curves). Results for KCl (m+  = 0.176, m−  = 0.169, β =  − 0.02) (a) and NaCl (m+  = 0.258, m−  = 0.169, β =  − 0. 2) (b)

Full size image

In Fig. 3a, b, we plot the scaled average electrophoretic mobility given by Eq. (36) of a cylinder of radius a and zeta potential ζ as a function of scaled zeta potential \(\widetilde{\zeta }\) (solid curves) in comparison with the scaled diffusiophoretic mobility \({U}_{\mathrm{sp}}^{*}\) of a sphere of the same radius a and zeta potential ζ as the cylinder, which is correct to the order of ζ3 (dotted curves) [14]. It is seen that the curve for Usp* lies between those for \({U}_{\parallel }^{*}\) and \({U}_{\perp }^{*}\) and is close to that of \({U}_{\mathrm{av}}^{*}\).

Fig. 3
figure 3

Scaled average diffusiophoretic mobility Uav* of a cylindrical colloidal particle of radius a in an aqueous electrolyte solution at 25 °C as a function of the scaled zeta potential \(\widetilde{\zeta }\) at κa = 10. Calculated via Eqs. (25) and (32) (or Eqs. (42) and (43) with negligible errors) (solid curves) in comparison with the results for the diffusiophoretic mobility Usp* for a spherical particle [14] (dotted curves). Results for KCl (m+  = 0.176, m−  = 0.169, β =  −0.02) (a) and NaCl (m+  = 0.258, m−  = 0.169, β =  −0. 2) (b)

Full size image

It has been shown [1, 2] that in the case of diffusiophoresis of a sphere, the chemiphoresis component causes the particle to move toward higher electrolyte concentrations, while the electrophoresis component moves the particle toward higher or lower electrolyte concentrations depending on the sign of the particle zeta potential, which may cause a sign reversal of the diffusiophoretic mobility in some cases. Figures 2 and 3 demonstrate that a cylinder exhibits the same diffusiophoretic behavior as a sphere. That is, for electrolytes with almost equal ion mobilities such as KCl (β =  −0.02, Figs. 2a and 3a), the electrophoretic contribution becomes negligible relative to chemiphoresis and almost only chemiphoresis component moves the cylinder toward higher electrolyte concentrations (positive diffusiophoretic mobility). In the case of a cylinder with large κa in NaCl (β =  −0. 2, Figs. 2b and 3b), however, a particle of low to moderate positive zeta potential migrates toward lower electrolyte concentrations, while a particle of high positive zeta potential can migrate toward higher electrolyte concentrations.

Evel and others [41] measured the diffusiophoretic mobility of spherical latex particles. As for cylindrical particles, McMullen and others [42] recently performed diffusiophoresis measurement of DNA cylinders. The present theory is thus expected to apply for such systems.

Concluding remarks

Keh and Wei [34] derived an analytic expression for the transverse diffusiophoretic mobility of a cylinder in a symmetrical electrolyte solution correct to the order of ζ2. In the present paper, we have provided the next-order correction terms to the mobility expression by Keh and Wei [34] and derived Eq. (25) as well as its simpler approximate expression (Eq. (42)). These equations, which are correct to the order of ζ3, are applicable for any values of κa at low to moderate values of ζ. The contribution of the correction terms becomes larger as the magnitude of β becomes larger and becomes zero in the limits of κa → ∞ and κa → 0. We also present an approximate expression (Eq. (43)) for the tangential diffusiophoretic mobility and calculate the average diffusiophoretic mobility of a cylinder oriented at an arbitrary angle between its axis and the applied electrolyte concentration gradient field using Eq. (36).