Introduction

Electrokinetic phenomena in a suspension of mercury drops are quite different from those of rigid particles [1]. In particular, the electrophoretic mobility of a mercury drop of radius a surrounded by a thin electrical double layer in an electrolyte solution is considerably larger than that of a rigid particle of the same radius a and zeta potential by the order of κa (1/κ being the double layer thickness). The large mobility of mercury drops arises from their finite viscosity, which gives rise to a tangential frictional force acting on the surface smaller than that for rigid particles. The tangential component of the liquid flow velocity must be zero on the surface of a rigid particle but does not vanish on the drop surface. The tangential flow component decays from the electrophoretic velocity value U (just outside the double layer) to zero (at the drop surface) over the double-layer thickness 1/κ. The tangential frictional force on the surface is then of order of ηU/κ−1. For a mercury drop, on the other hand, the tangential flow component becomes zero at a certain point inside the drop, which is located at a distance of the order of a from the drop surface, i.e., decays over distances of order a. The tangential frictional force on the drop surface is then of order ηdU/a and hence the order of the ratio of the mobility of a mercury drop to that of a rigid particle becomes O(ηκa/ηd) ≈ O(κa). It should also be noticed that mercury drops are different from dielectric liquid drops in that mercury drops behave like an ideally polarizable conductor and the drop surface is always equipotential during electrophoresis. The tangential component of the Maxwell stress tensor is thus zero on the mercury drop surface.

For the case of diffusiophoresis, which is the motion of a particle in an applied electrolyte concentration gradient (for example, see Refs. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] for rigid particles, Refs. [11,12,13,14,15,16,17,18,19,20,21] for liquid drops, and Refs. [22,23,24,25,26,27] for soft particles), the same phenomenon due to the relaxation effect should be observed. In a previous paper [21], we derived an approximate analytic expression for the diffusiophoretic mobility of a mercury drop and indeed it exceeds that of a rigid particle by the order of κa. The expression derived in previous paper [21], however, can be applied for weakly charged mercury drops, since it neglects the relaxation effect, which becomes appreciable for higher zeta potential values. In the present paper, we treat mercury drops with thin electrical double layers (i.e., large κa) and zeta potential of arbitrary values, taking into account the relaxation effect and derive an approximate analytic mobility expression.

Theory

Consider a spherical mercury drop of radius a, viscosity ηd, and zeta potential ζ, moving with a diffusiophoretic velocity U in an aqueous liquid of viscosity η and relative permittivity εr containing a symmetrical electrolyte under a constant applied gradient of electrolyte concentration ∇n. The electrolyte is of the z:z symmetrical type with valence z but may have different ionic drag coefficients λ+ and λ- for cations and anions, respectively. Let n∞ be the bulk concentration of electrolytes in the absence of the applied electrolyte concentration gradient. We introduce a constant vector α proportional to ∇n, viz.,

$$\boldsymbol{\alpha }=\frac{kT}{ze{n}^{\infty }}\nabla n$$
(1)

where k is the Boltzmann constant, T is the absolute temperature, and e is the elementary electric charge. The symbol “e” refers to the elementary electric charge in Eqs. (1), (8), (10), (14), and (15). In other places “e” is the exponential constant.

The origin of the spherical polar coordinate system (r, θ, φ) is held fixed at the center of the mercury drop and the polar axis (θ = 0) is put parallel to α. For a spherical particle, U is parallel to α. The concentration gradient field α is assumed to be weak so that U is linear in α. The main assumptions are as follows. (i) The Reynolds number of the liquid flow is small enough to ignore inertial terms in the Navier–Stokes equation and the liquid can be regarded as incompressible. (ii) The equilibrium electric potential in the absence of the field α satisfies the Poisson-Boltzmann equation. (iii) No electrolyte ions can penetrate the drop surface. (iv) The drop surface remains spherical during diffusiophoresis. (v) The mercury drop behaves like an ideally polarizable conductor and the drop surface is always equipotential during diffusiophoresis.

We have previously shown that the general expression for the diffusiophoretic velocity U of a colloidal particle in an electrolyte concentration gradient field α is obtained from the expression for its electrophoretic velocity UE in an applied electric field E by replacing E with α. Indeed, the fundamental equations take the same form for these two velocities [15, 16, 21]. The only difference is the far-field boundary condition for the deviations δμ±(r) of the ionic electrochemical potentials μ±(r) caused by α, where μ+(r) and μ-(r) are, respectively, the electrochemical potentials of cations and anions. The diffusiophoretic velocity U of a mercury drop can thus be derived from the corresponding expression for the electrophoretic mobility [1, 21] with the result that:

$${\varvec{U}}=\frac{{a}^{2}}{9}{\int }_{a}^{\infty }\left\{\frac{3{\eta }_{\mathrm{d}}}{3{\eta }_{\mathrm{d}}+2\eta }-\frac{{3r}^{2}}{{a}^{2}}+\frac{6\left({\eta }_{\mathrm{d}}+\eta \right){r}^{3}}{\left(3{\eta }_{\mathrm{d}}+2\eta \right){a}^{3}}\right\}G\left(r\right)dr\boldsymbol{\alpha }$$
(2)

with

$$G\left(r\right)=-\frac{ze{n}^{\infty }}{\eta r}\frac{dy}{dr}\left\{{e}^{-y}{\phi }_{+}(r)+{e}^{y}{\phi }_{-}(r)\right\}$$
(3)
$${\phi }_{\pm }\left(r\right)=\left(\mp 1+\beta \right)\left(r+\frac{{a}^{3}}{2{r}^{2}}\right)-\frac{1}{3}\left(r+\frac{{a}^{3}}{2{r}^{2}}\right){\int }_{a}^{\infty }{g}_{\pm }\left(r\right)dr+\frac{1}{3}{\int }_{a}^{r}\left(r-\frac{{x}^{3}}{{r}^{2}}\right){g}_{\pm }\left(x\right)dx$$
(4)
$${g}_{\pm }\left(r\right)=\pm \frac{dy}{dr}\left(\frac{d{\phi }_{\pm }}{dr}\mp \frac{2{\lambda }_{\pm }}{ze}\frac{h}{r}\right)$$
(5)
$$h\left(r\right)=-\left\{\frac{{r}^{3}}{30}-\left(\frac{{\eta }_{\mathrm{d}}}{3{\eta }_{\mathrm{d}}+2\eta }\right)\frac{{a}^{2}r}{6}+\left(\frac{{\eta }_{\mathrm{d}}-\eta }{3{\eta }_{\mathrm{d}}+2\eta }\right)\frac{{a}^{5}}{15{r}^{2}}\right\}{\int }_{a}^{\infty }G\left(x\right)dx$$
$$+\left\{\left(\frac{{\eta }_{\mathrm{d}}+\eta }{3{\eta }_{\mathrm{d}}+2\eta }\right)\frac{r}{3a}-\frac{1}{6}+\left(\frac{{\eta }_{\mathrm{d}}}{3{\eta }_{\mathrm{d}}+2\eta }\right)\frac{{a}^{2}}{6{r}^{2}}\right\}{\int }_{a}^{\infty }{x}^{3}G\left(x\right)dx$$
$$-{\int }_{a}^{r}\left(-\frac{{r}^{3}}{30}+\frac{r{x}^{2}}{6}-\frac{{x}^{3}}{6}+\frac{{x}^{5}}{30{r}^{2}}\right)G\left(x\right)dx$$
(6)
$$\beta =\frac{{1/\lambda }_{+}-{1/\lambda }_{-}}{1/{\lambda }_{+}+1/{\lambda }_{-}}=-\frac{{\lambda }_{+}-{\lambda }_{-}}{{\lambda }_{+}+{\lambda }_{-}}=-\frac{{m}_{+}-{m}_{-}}{{m}_{+}+{m}_{-}}$$
(7)
$${m}_{\pm }=\frac{2{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}kT}{3\eta {z}^{2}{e}^{2}}{\lambda }_{\pm }$$
(8)
$$y(r)=\frac{ze}{kT}{\psi }^{(0)}(r)$$
(9)

where r =|r| is the radial distance from the drop center, m+ and m- are, respectively, the scaled ionic drag coefficients of cations and anions, ψ(0)(r) is the equilibrium electric potential at position r outside the mercury drop in the absence of the field α, y(r) is its scaled quantity, and εo is the permittivity of a vacuum. The functions h(r) and ϕ±(r) are, respectively, related to the liquid fluid velocity u(r) outside the drop (r > a) and the deviations δμ±(r) of the ionic electrochemical potentials μ±(r) due to α as

$${\varvec{u}}\left({\varvec{r}}\right)=\left(-\frac{2}{r}h\left(r\right)\mathrm{\alpha cos}\theta , \frac{1}{r}\frac{d}{dr}\left[rh(r)\right]\mathrm{\alpha sin}\theta , 0\right)$$
(10)

and

$${\delta \mu }_{\pm }\left({\varvec{r}}\right)=\mp ze\alpha {\phi }_{\pm }\left(r\right)\mathrm{cos}\theta$$
(11)

where α =|α|. We now introduce the diffusiophoretic mobility U* defined by

$${\varvec{U}}=\frac{2{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}kT}{3\eta ze}{U}^{*}\boldsymbol{\alpha }$$
(12)

On the basis of the same approximation method as used for deriving the electrophoretic mobility of a mercury drop [1], we finally obtain the following expression for U*, which is correct to the order O((1/κa)0) and thus applicable for large κa (κa ≥ 30):

$${U}^{*}=\frac{\kappa a}{\frac{{\eta }_{\mathrm{d}}}{\eta }+\frac{2}{3}+D}\left\{{2\mathrm{sinh}}^{2}\left(\frac{\stackrel{\sim }{\zeta }}{4}\right)+\beta \mathrm{sinh}\left(\frac{\stackrel{\sim }{\zeta }}{2}\right)\right\}$$
$$+\frac{3\left(1+\beta \right)}{\frac{{\eta }_{\mathrm{d}}}{\eta }+\frac{2}{3}+D}\left\{\frac{{\eta }_{\mathrm{d}}}{\eta }+\frac{2}{3}+{m}_{+}{\left({1-e}^{-\stackrel{\sim }{\zeta }/2}\right)}^{2}\right\}\mathrm{ln}\left(\frac{1+{e}^{\stackrel{\sim }{\zeta }/2}}{2}\right)$$
$$+\frac{3\left(1-\beta \right)}{\frac{{\eta }_{\mathrm{d}}}{\eta }+\frac{2}{3}+D}\left\{\frac{{\eta }_{\mathrm{d}}}{\eta }+\frac{2}{3}+{m}_{-}{\left({1-e}^{\stackrel{\sim }{\zeta }/2}\right)}^{2}\right\}\mathrm{ln}\left(\frac{1+{e}^{-\stackrel{\sim }{\zeta }/2}}{2}\right)$$
(13)

with

$$\stackrel{\sim }{\zeta }=\frac{ze\boldsymbol{ }\zeta \boldsymbol{ }}{kT}$$
(14)
$$\kappa ={\left(\frac{2{z}^{2}{e}^{2}{n}^{\infty }\boldsymbol{ }\boldsymbol{ }}{{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}kT}\right)}^{1/2}$$
(15)
$$D={m}_{+}{\left({1-e}^{-\stackrel{\sim }{\zeta }/2}\right)}^{2}+{m}_{-}{\left({1-e}^{\stackrel{\sim }{\zeta }/2}\right)}^{2}$$
(16)

where \(\stackrel{\sim }{\zeta }\) is the scaled zeta potential, κ is the Debye-Hückel parameter and D is Dukhin’s number for liquid drops [1].

Results and discussion

Equation (13) is the required large κa approximate expression for the diffusiophoretic mobility U* of a spherical mercury drop of radius a in an electrolyte concentration gradient field α. Equation (14), which is applicable for arbitrary zeta potentials, takes into account the relaxation effect though Dukhin’s parameter D defined by Eq. (16),

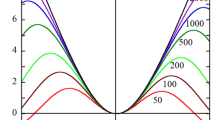
Figure 1 shows some examples of the results of the calculation via Eq. (13) for U* of a mercury drop in an aqueous KCl solution at 25 ℃ \({m_+=0.176,m_-=0.169,\beta=-0.02,\eta=0.89\;\mathrm{mPa {\cdot}s}}\). In Fig. 1, U* is plotted as a function of \(\widetilde\zeta\) for various values of κa, showing how strongly U* depends on κa. It is seen that U* exhibits two maxima due to the relaxation effect as in the case of electrophoresis [1]. The values of \(\widetilde\zeta\) at which U* exhibit maxima are \(\widetilde\zeta\) \(\approx\) \(\pm3.5,\mathrm i.\mathrm e.,\zeta\approx\pm88\) mV, which are easily experimentally accessible.

Fig. 1
figure 1

Scaled diffusiophoretic mobility U* of a spherical mercury drop of radius a, viscosity ηd = 1.525mPa·s, and zeta potential z in an aqueous KCl solution at 25℃ (m+  = 0.176, m- = 0.169,  β= -0.02, η = 0.89mPa·s) as a function of the scaled zeta potential at several values of κa in comparison with that for a rigid sphere (ηd  \(\rightarrow\infty\)) of radius a. Calculated via Eq. (13)  for a mercury drop (solid lines) and via Eqs. (17) and (18)  for a rigid sphere (dashed lines). Dotted lines represent results calculated via the low zeta potential approximation Eq. (24)

Full size image

Figure 1 compares the results of U* for a mercury drop and those or a rigid sphere, showing a remarkable difference between mercury drops (solid lines) and rigid particles (dashed lines) in that the diffusiophoretic mobility of mercury drops much exceeds that of rigid particles for large κa as in the case of electrophoresis [1]. The large κa approximate expression for a rigid sphere is given by [15, 16]

$${U}^{*}=\frac{6}{{m}_{+}+{m}_{-}}\left\{{m}_{+}\mathrm{ln}\left(\frac{1+{e}^{-\stackrel{\sim }{\zeta }/2}}{2}\right)+\frac{{m}_{-}}{1+F}\mathrm{ln}\left(\frac{1+{e}^{\stackrel{\sim }{\zeta }/2}}{2}\right)\right\} \mathrm{ if} \stackrel{\sim }{\zeta } >0$$
(17)
$${U}^{*}=\frac{6}{{m}_{+}+{m}_{-}}\left\{\frac{{m}_{+}}{1+F}\mathrm{ln}\left(\frac{1+{e}^{-\stackrel{\sim }{\zeta }/2}}{2}\right)+{m}_{-}\mathrm{ln}\left(\frac{1+{e}^{\stackrel{\sim }{\zeta }/2}}{2}\right)\right\}\mathrm{ if} \stackrel{\sim }{\zeta } <0$$
(18)

with

$$F=\frac{2}{\kappa a}\left(1+3{m}_{-}\right)\left({e}^{\stackrel{\sim }{\zeta }/2}-1\right) \mathrm{for}\stackrel{\sim }{\zeta }>0$$
(19)
$$F=\frac{2}{\kappa a}\left(1+3{m}_{+}\right)\left({e}^{-\stackrel{\sim }{\zeta }/2}-1\right) \mathrm{ for}\stackrel{\sim }{\zeta }<0$$
(20)

where F is Dukhin’s number for rigid particles. By comparing Eq. (13), (17) and (18), we find that

$$\frac{{U}^{*}(\mathrm{mercury})}{{U}^{*}(\mathrm{rigid})}=O(\kappa a)$$
(21)

That is, the diffusiophoretic mobility of a mercury drop is considerably larger than that of a rigid sphere for large κa, as is seen in Fig. 1.

As is also seen in Fig. 1 , in the limit of very high ζ, Eq. (13) for U* of a liquid drop (solid lines in Fig. 1) and Eqs. (17) and (18) for a rigid sphere (dashed lines in Fig. 1) tend to the same limiting value given by

$${U}^{*}\to -\frac{6{m}_{+}}{{m}_{+}+{m}_{-}}\mathrm{ln}2\;\mathrm{as} \stackrel{\sim }{\zeta }\to +\infty$$
(22)
$${U}^{*}\to -\frac{6{m}_{-}}{{m}_{+}+{m}_{-}}\mathrm{ln}2\;\mathrm{ as} \stackrel{\sim }{\zeta }\to -\infty$$
(23)

Namely, in the limit of very high zeta potential ζ, a liquid drop behaves like a rigid particle. This solidification effect at high ζ occurs generally for electrokinetic phenomena including electrophoresis of mercury drops [1].

Finally, we compare the present result Eq. (13) and a low-zeta-potential mobility expression correct to the order of ζ2 [21], which is given by

$${U}^{*}=\frac{3}{2}\beta \stackrel{\sim }{\zeta }{f}_{1}\left(\kappa a\right)+\frac{3}{16}{\stackrel{\sim }{\zeta }}^{2}{f}_{2}\left(\kappa a\right)$$
(24)

with

$${f}_{1}\left(\kappa a\right)=\frac{\eta }{3{\eta }_{\mathrm{d}}+2\eta }\kappa a+\frac{3{\eta }_{\mathrm{d}}+\eta }{3{\eta }_{\mathrm{d}}+2\eta }+2{e}^{\kappa a}{E}_{5}\left(\kappa a\right)-\frac{15{\eta }_{\mathrm{d}}}{3{\eta }_{\mathrm{d}}+2\eta }{e}^{\kappa a}{E}_{7}(\kappa a)$$
(25)

and

$${f}_{2}\left(\kappa a\right)=\frac{2\eta }{3{\eta }_{\mathrm{d}}+2\eta }\kappa a+\frac{3{\eta }_{\mathrm{d}}}{3{\eta }_{\mathrm{d}}+2\eta }-\frac{8}{3}{e}^{\kappa a}{E}_{3}\left(\kappa a\right)+8{e}^{\kappa a}{E}_{4}\left(\kappa a\right)$$
$$+\frac{8{\eta }_{\mathrm{d}}}{3{\eta }_{\mathrm{d}}+2\eta }{e}^{\kappa a}{E}_{5}\left(\kappa a\right)-8{f}_{1}\left(\kappa a\right){e}^{\kappa a}{E}_{5}\left(\kappa a\right)-\frac{40{\eta }_{\mathrm{d}}}{3{\eta }_{\mathrm{d}}+2\eta }{e}^{\kappa a}{E}_{6}\left(\kappa a\right)$$
$$+\frac{10}{3}{e}^{2\kappa a}{E}_{6}\left(2\kappa a\right)+\frac{7{\eta }_{\mathrm{d}}}{3{\eta }_{\mathrm{d}}+2\eta }{e}^{2\kappa a}{E}_{8}\left(2\kappa a\right)$$
(26)

where En(ka) is the n th order exponential integral of order n defined by

$${E}_{n}\left(\kappa a\right)={(\kappa a)}^{n-1}{\int }_{\kappa a}^{\infty }\frac{{e}^{-t}}{{t}^{n}}dt$$
(27)

In the limit of large κa, Eq. (24) tends to

$${U}^{*}=\frac{3\eta \kappa a}{2(3{\eta }_{\mathrm{d}}+2\eta )}\left(\beta \stackrel{\sim }{\zeta }+\frac{{\stackrel{\sim }{\zeta }}^{2}}{4}\right)$$
(28)

which agrees with the low zeta potential limiting form of Eq. (13). As is seen in Fig. 1 , the results obtained by Eq. (24) (dotted lines) agrees quite well with the results by Eq. (13) (solid lines) for |\(\stackrel{\sim }{\zeta }\)|≤ 2, implying that Eq. (24) is a good approximation for |\(\stackrel{\sim }{\zeta }\)|≤ 2 with negligible errors.

Concluding remarks

We have derived a simple approximate analytic expression, Eq. (13), for the diffusiophoretic mobility U* of a mercury drop applicable for arbitrary zeta potential values and large κa. Equation (13) takes into account the relaxation effect through Dukhin’s number D. It is shown that the diffusiophoretic mobility U* plotted as a function of the drop zeta potential exhibits maxima due to the relaxation effect. It is also shown that in the limit of very high zeta potential, the diffusiophoretic mobility of a mercury drop tends to a non-zero limiting value given by Eqs. (22) and (23). This limiting mobility value is found to be the same as that for a rigid sphere as in the case of electrophoresis (solidification effect).