Paired-domination number of claw-free odd-regular graphs

Abstract

A paired-dominating set of a graph G is a dominating set of vertices whose induced subgraph has a perfect matching, while the paired-domination number is the minimum cardinality of a paired-dominating set in the graph, denoted by $\gamma _{pr}(G)$. Let G be a connected $\{K_{1,3}, K_{4}-e\}$-free cubic graph of order n. We show that $\gamma _{pr}(G)\le \frac{10n+6}{27}$ if G is $C_{4}$-free and that $\gamma _{pr}(G)\le \frac{n}{3}+\frac{n+6}{9(\lceil \frac{3}{4}(g_o+1)\rceil +1)}$ if G is $\{C_{4}, C_{6}, C_{10}, \ldots , C_{2g_o}\}$-free for an odd integer $g_o\ge 3$; the extremal graphs are characterized; we also show that if G is a 2 -connected, $\gamma _{pr}(G) = \frac{n}{3}$. Furthermore, if G is a connected $(2k+1)$-regular $\{K_{1,3}, K_4-e\}$-free graph of order n, then $\gamma _{pr}(G)\le \frac{n}{k+1}$, with equality if and only if $G=L(F)$, where $F\cong K_{1, 2k+2}$, or k is even and $F\cong K_{k+1,k+2}$.

1 Introduction

All graphs considered in this paper are finite and simple. For a graph $G=(V,E)$, |V| and |E| are called the order and the size of G, respectively. As usual, $\delta (G)$ and $\Delta (G)$ denote the minimum degree and the maximum degree of G, respectively. The odd girth of a graph G, denoted by $g_o(G)$, is the minimum length of an odd cycle in G.

A matching in a graph G is a set of pairwise nonadjacent edges. If M is a matching, the two ends of each edge of M are said to be matched under M, and each vertex incident with an edge of M is said to be covered by M. A perfect matching is one which covers every vertex of the graph, a maximum matching one which covers as many vertices as possible. The number of edges in a maximum matching of a graph G, denoted $\alpha '(G)$, is called the matching number of G.

For a graph G, a set $S\subseteq V(G)$ is called a dominating set of G if each vertex $v\in V(G)\setminus S$ has a neighbor in S. Furthermore, S is called a paired-dominating set of G if the subgraph G[S] induced by S contains a perfect matching. Every graph without isolated vertices has a paired domination set, since the end-vertices of any maximal matching form such a set. The paired-domination number of G, denoted $\gamma _{pr}(G)$, is the minimum cardinality of a paired domination set. Paired-domination was introduced by Haynes and Slater (1995), Haynes and Slater (1998) as a model for assigning backups to guards for security purposes, and studied in Cheng et al. (2007), Dorbec et al. (2007), Favaron and Henning (2004), Fitzpatrick and Hartnell (1998), Goddard and Henning (2009), Henning (2007), Huang et al. (2013). We refer to an excellent survey Desormeaux and Henning (2014) for known results and unsolved research problems on paired domination of graphs.

Let $G=(V(G), E(G))$ be a graph. The line graph of G, denoted by L(G), is the graph whose vertex set is E(G), in which two vertices are adjacent if and only if they are adjacent in G as the edges of G. Let ${\mathcal {H}}$ be a family of graphs. As usual, $K_n$ and $C_n$ denotes the complete graph and the cycle of order n. The complete bipartite graph with parts of sizes m and n is denoted by $K_{m,n}$. A graph G is called ${\mathcal {H}}$-free if no induced subgraph of G is isomorphic to any $H\in {\mathcal {H}}$. In particular, we simply write H-free instead of $\{H\}$-free if ${\mathcal {H}}=\{H\}$. A graph G is claw-free if it is $K_{1,3}$-free. It is well-known that every line graph is a claw-free graph. In 2004, Favaron and Henning (2004) proved the following theorem for claw-free cubic graphs.

Theorem 1.1

(Favaron and Henning 2004) Let G be connected cubic graph G of order n. Then

• (1) if G is $\{K_{1,3}, K_{4}-e\}$-free and is 2-connected, then $\gamma _{pr}(G) \le \frac{n}{3}$;

• (2) if $\{K_{1,3}, K_{4}-e , C_{4}\}$-free and $n\ge 6$, then $\gamma _{pr}(G)\le \frac{3}{8}n$;

• (3) if G is $\{K_{1,3}, K_{4}-e\}$-free and $n\ge 6$, then $\gamma _{pr}(G) \le \frac{2}{5}n$;

• (4) if G is claw-free, then $\gamma _{pr}(G) \le \frac{n}{2}$.

The aim of this note is to improve the above results, and our main results are summarized as follows.

Theorem 1.2

Let G be connected cubic graph G of order n. Then

• (1) if G is $\{K_{1,3}, K_{4}-e\}$-free and is 2-connected, then $\gamma _{pr}(G)=\frac{n}{3}$;

• (2) if $\{K_{1,3}, K_{4}-e , C_{4}\}$-free and $n\ge 6$, then $\gamma _{pr}(G)\le \frac{10n+6}{27}$;

• (3) if $\{K_{1,3}$, $K_{4}-e, C_{4}\}$-free and is $C_{2i}$-free for each odd integer $3\le \ i\le g_o$, where $g_o$ is an odd integer at least 3, then

  $$\begin{aligned} \gamma _{pr}(G)\le \frac{n}{3}+\frac{n+6}{9\left( \lceil \frac{3}{4}(g_o+1)\rceil +1\right) }; \end{aligned}$$

  Moreover, all the graphs achieving the equality in (2), (3) are characterized.

Theorem 1.3

If G is a connected $(2k+1)$-regular $\{K_{1,3}, K_4-e\}$-free graph of order n, then $\gamma _{pr}(G)\le \frac{n}{k+1}$, with equality if and only if $G=L(F)$, where $F\cong K_{1, 2k+2}$, or k is even and $F\cong K_{k+1,k+2}$.

We remark that (2) of Theorem 1.2 was proven in Favaron and Henning (2008), although they impose the restriction that $n\ge 48$. Their proof is identical to their earlier proof in Favaron and Henning (2004), except that the proof Favaron and Henning (2008) in uses the matching property due to Biedl et al. (2004) that the matching number $\alpha '(G)$ of cubic graph G of order n is at least $\alpha '(G)\ge \frac{4n-1}{9}$. However, they do not provide a characterization of the extremal graphs.

The proofs of our results will be given separately in Sect. 3.

2 Preparations

Biedl et al. (2004) proved that for any connected cubic graph of order n, $\alpha '(G)\ge \frac{4n-1}{9}$. O and West (2010) characterized those graphs attaining the lower bound. Let $\mathcal {T}$ be the family of trees T such that every non-leaf vertex has degree 3 and all leaves have the same color in a proper 2-coloring of T. Let ${\mathcal {F}}_3$ be the family of cubic graphs which are obtained from trees in T by identifying each leaf of such a tree with the degree 2 vertex in a copy of B (the graph obtained from $K_4$ by subdividing an edge).

Theorem 2.1

(Biedl et al. 2004; O and West 2010) If G is a connected cubic graph of order n, then

$$\begin{aligned} \alpha '(G)\ge \frac{4n-1}{9}, \end{aligned}$$

with equality if and only if $G \in {\mathcal {F}}_3.$

Henning et al. (2012) extended the above result to a cubic graph of order n with an odd girth $g_o$ and characterized the extremal graphs.

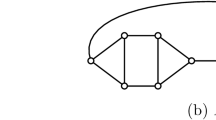
For every odd integer $g_o\ge 3$, we define a set of $\varphi (g_o)$ of graphs using the gadgets G(1), G(3), G(6) and G(4) in Fig. 1. Each of these gadgets is a graph plus two half edges.

Fig. 1

G(1), G(3), G(6), G(4)

If $g_o\equiv 1$ mod 4, then a graph G belongs to $\varphi (g_o)$ if it arises by arranging one copy of G(1) and $\frac{g_o-1}{4}$ copies of G(4) in a cyclic order and connecting for every pair ($G', G''$) of two cyclically consecutive gadgets $G'$ and $G''$, one half edge from $G'$ with one half edge from $G''$.

If $g_o=3$, then $\varphi (g_o)$ contains the graph that raises from G(3) by connecting its two half edges.

Finally, if $g_o\equiv -1$ mod 4 and $g_o\ge 7$, then a graph G belong to $\varphi (g_o)$ if it arises by arranging

• either one copy of G(1), one copy of G(6), and $\frac{g_o-7}{4}$ copies of G(4),

• or one copy of G(3) and $\frac{g_o-3}{4}$ copies of G(4) in a cyclic order and connecting for every pair $G', G''$ of two cyclically consecutive gadgets $G'$ and $G''$, one half edge from $G'$ with one half edge from $G''$. It is easy to check that every graph G in $\varphi (g_o)$ has exactly one vertex of degree 2, $n(G)-1$ vertices of degree 3.

Theorem 2.2

(Henning et al. 2012) If G is a connected cubic graph of order n and odd girth $g_o <\infty$, then

$$\begin{aligned} \alpha '(G)\ge \frac{n}{2}-\frac{n+2}{6(\lceil \frac{3}{4}(g_o-1)\rceil +1)}, \end{aligned}$$

with equality if and only if G arises from a tree T, where

• V(T) is the union of three independent sets X, R and S.

• there are no edges joining R to S.

• every vertex in X $\cup$ S has degree 3 in T, and

• every vertex in R has degree 1 in T, by adding |R| disjoint graphs $G_{u}$ from $\varphi (g_o)$ with u $\in$ R and identifying each vertex u in R with the unique vertex of degree 2 in $G_{u}$.

For the simplicity, for an odd integer $g_o\ge 3$, ${\mathcal {F}}_{g_o}$ denotes the set of extremal graphs defined the above theorem.

The following two theorems are well-known, see Hemminger and Beineke (1978) or Kang et al. (2014).

Theorem 2.3

Let G be graph. Then G is a line graph of a triangle-free graph if and only if G is $\{K_{1,3}, K_4-e\}$-free.

Theorem 2.4

If G is a connected $\{K_{1,3}, K_4-e\}$-free $(2k+1)$-regular graph on n vertices, then $G=L(F)$, where $F=F[X,Y]$ is a bipartite graph such that there exists an integer $l\in \{1, \ldots , k+1\}$, $d_F(x)=2k+3-l$ for all $x \in X$ and $d_F(y)=l$ for all $y \in Y$.

Let G be claw-free cubic graph. In what follows, the symbol $G^*$ denotes the graph obtained from G by contracting each triangle to a vertex; the subdivision graph $S_1(G)$ denotes the graph obtained from G by inserting a new vertex into each edge. Note that $G^*$ is also a cubic graph, but might have some parallel edges.

Corollary 2.5

For a cubic $\{K_{1,3}, K_4-e\}$-free graph G, $G\cong L(S_1(G^*))$.

Proof

It is obvious, and is left to the readers. $\square$

3 Cubic graphs

Favaron and Henning (2004) proved that if G is a 2-connected $\{K_{1,3}, K_4-e\}$-free cubic graph of order $n\ge 6$, then $\gamma _{pr}(G)\le \frac{n}{3}.$ Indeed, next we show that $\gamma _{pr}(G)=\frac{n}{3}$ under the same conditions.

Theorem 3.1

If G is a 2-connected $\{K_{1,3}, K_4-e\}$-free cubic graph of order $n\ge 6$, then $\gamma _{pr}(G)= \frac{n}{3}.$

Proof

By Corollary 2.5, $G=L(S_1(G^*))$, where $G^*$ is a cubic graph of order $n'=\frac{n}{3}$ and might have some parallel edges. Since G is 2-connected, $G^*$ is 2-connected. By the well-known Petersen’s theorem Petersen (1891), $G^*$ has a perfect matching $M'$. Let S be a paired dominating set of G constructed from $M'$ as follows: for each edge $u'v'\in M'$, we select an edge uv of G that joins a vertex u in the triangle corresponding to $u'$ and a vertex v in the triangle corresponding to $v'$, and we add the vertices u and v to S; Clearly S is a paired dominating set of G. So,

$$\begin{aligned} \gamma _{pr}(G) \le |S|=2\alpha '(G^*)=n'=\frac{n}{3}. \end{aligned}$$

On the other hand, let S be a minimum paired dominating set of G. Clearly, $2e(S)\ge |S|$. So,

$$\begin{aligned} 3|S|=2e(G[S])+e(S, \overline{S})\ge |S|+n-|S| = n, \end{aligned}$$

implying that $|S|\ge \frac{n}{3}$. $\square$

Theorem 3.2

If G is a connected $\{K_{1,3}, K_{4}-e, C_4\}$-free cubic graph of order $n\ge 6$, then

$$\begin{aligned} \gamma _{pr}(G)\le \frac{10n+6}{27}, \end{aligned}$$

with equality if and only if $G=L(S_1(G^*))$ with $G^*\in {\mathcal {F}}_3$.

Proof

Since G is a connected $\{K_{1,3}, K_{4}-e\}$-free cubic graph, by Corollary 2.5, $G=L(S_1(G^*))$, where $G^*$ is a cubic graph of order $n'=\frac{n}{3}$. Moreover, since G is $C_4$-free, $G^*$ is simple. Since each vertex of G belong to a unique triangle of G, we take a vertex from each triangle of G and denote by T the resulting subset. Trivially, $|T|=n'$. Let $T_0$ be such a set as constructed above, with an additional property that $e(G[T_0])$ is as large as possible. It is clear that $\alpha '(G^*)=e(G[T_0])$.

Now we construct a paired dominating set S of G: for each edge $uv\in E(G[T_0])$, we add the vertices u and v to S; for an isolated vertex w in $G[T_0]$, we put $w'$ and $w''$ into S, where $w, w',w''$ induces a triangle in G. Clearly, S is a paired dominating set of G.

By Theorem 2.1, $e(G[T_0])=\alpha '(G^*)\ge \frac{4n'-1}{9}$, and thus

$$\begin{aligned} |S|=2e(G[T_0])+2(|T_0|-2e(G[T_0]))=2(|T_0|-e(G[T_0])). \end{aligned}$$

Therefore,

$$\begin{aligned} \gamma _{pr}(G)\le |S|= 2(|T_0|-e(G[T_0]))\le 2\left( n'-\frac{4n'-1}{9}\right) =\frac{10n'+2}{9}=\frac{10n+6}{27}. \end{aligned}$$

If $\gamma _{pr}(G)=\frac{10n+6}{27}$, then we have the equality throughout this inequality chain, then $\alpha ' (G^*)= \frac{4n-1}{9}$. By Theorem 2.1, $G^*\in {\mathcal {F}}_3$.

Conversely, we assume that $G=L(S_{1}(G^*))$ for a graph $G^*\in {\mathcal {F}}_3$. We show that $\gamma _{pr}(G)\ge \frac{10n+6}{27}$. Let S be a minimum paired dominating set of G and let M is perfect matching of G[S]. Let $M'$ consists of those edges $e\in M$, which do not belong to a triangle in G. Let $S'$ be those vertices of S covered by an edge of $M'$ and $S''=S\setminus S'$. So,

$$\begin{aligned} |S|= & {} |S'|+|S''|= 2|M'|+2(n'-2|M'|)=2(n'-|M'|)\\\ge & {} 2(n'-\alpha '(G^*))\ge \frac{10n+6}{27}. \end{aligned}$$

So, the proof is completed. $\square$

Theorem 3.3

Let G be a connected $\{K_{1,3}$, $K_{4}-e, C_{4}\}$-free graph cubic graph of order $n\ge 6$. If $\{C_{6}, C_{10}, \ldots , C_{2g_o}$)-free for an odd integer $g_o\ge 3$, then

$$\begin{aligned} \gamma _{pr}(G)\le \frac{n}{3}+\frac{n+6}{9\left( \lceil \frac{3}{4}(g_o+1)\rceil +1\right) }, \end{aligned}$$

with equality if and only if $G=L(S_1(G^*))$, where $G^*\in {\mathcal {F}}_{g_o}$.

Proof

First we show the necessity. Since G is a connected $\{K_{1,3}, K_{4}-e, C_4\}$-free cubic graph, by Corollary 2.5, $G=L(S_1(G^*))$, where $G^*$ is a simple connected cubic graph of order $n'=\frac{n}{3}$. Furthermore, since G is $\{C_{6}, C_{10}, \cdots , C_{2g_o}\}$-free, $G^*$ is $\{C_{3}, C_{5}, \cdots , C_{g_o}\}$-free. Let $M'$ be a maximum matching of $G^*$. Let S be a paired dominating set as constructed in the proof of Theorem 3.2.

Since $|S|=2|M'|+2(n'-2|M'|)=2(n'-|M'|)=2(n'-\alpha ' (G^*))$,

$$\begin{aligned} \gamma _{pr}(G)\le & {} 2(n'-\alpha ' (G^*))\\\le & {} 2\left( n'-\frac{n'}{2}+\frac{n'+2}{6(\lceil \frac{3}{4}(g_o+1)\rceil +1)}\right) \\= & {} n'+\frac{n'+2}{3\left( \lceil \frac{3}{4}(g_o+1)\rceil +1\right) } \\= & {} \frac{n}{3}+\frac{n+6}{9\left( \lceil \frac{3}{4}(g_o+1)\rceil +1\right) }. \end{aligned}$$

If $\gamma _{pr}(G)= \frac{n}{3}+\frac{n+6}{9(\lceil \frac{3}{4}(g_o+1)\rceil +1)}$, then we have equality throughout this inequality chain, then $\alpha '(G^*)= \frac{n'}{2}-\frac{n'+2}{6(\lceil \frac{3}{4}(g_o+1)\rceil +1)}$. By Theorem 2.2, $G^*\in {\mathcal {F}}_{g_o}$.

Conversely, we assume that $G=L(S_1(G^*))$ for a graph $G^*\in {\mathcal {F}}_{g_o}$. To show that

$$\begin{aligned} \gamma _{pr}(G)=\frac{n}{3}+\frac{n+6}{9\left( \lceil \frac{3}{4}(g_o+1)\rceil +1\right) }, \end{aligned}$$

let S be a minimum paired dominating set of G and let M is a perfect matching of G[S]. $M'$ consists of those edges e of M, which do not belong to a triangle in G. Let $S'$ be those vertices of S covered by an edge of $M'$ and $S''=S\setminus S'$. So,

$$\begin{aligned} |S|= & {} |S'|+|S''|\\= & {} 2|M'|+2(n'-2|M'|) \\= & {} 2(n'-|M'|) \\\ge & {} 2(n'-\alpha '(G^*)) \\\ge & {} \frac{n}{3}+\frac{n+6}{9\left( \lceil \frac{3}{4}(g_o+1)\rceil +1\right) }.\\ \end{aligned}$$

So, the proof is completed. $\square$

4 Odd-regular graphs

Theorem 4.1

Let G be a connected $(2k+1)$-regular $\{K_{1,3}, K_4-e\}$-free graph of order n, then $\gamma _{pr}(G)\le \frac{n}{k+1}$, with equality if and only if $G=L(F)$, where $F\cong K_{1, 2k+2}$, or k is even and $F\cong K_{k+1,k+2}$.

Proof

Since G is a $(2k+1)$-regular $\{K_{1,3}, K_4-e\}$-free graph of order n, by Theorem 2.4, $G=L(F)$, where $F=F[X,Y]$ is a bipartite graph such that there exists an integer $l\in \{1, \ldots , k+1\}$, $d_F(x)=2k+3-l$ for all $x \in X$ and $d_F(y)=l$ for all $y \in Y$.

Clearly, $|Y|=\frac{2k+3-l}{l} |X|$. Let $X_{1}\subseteq X$ with $|X_1|$ as large as possible, subject to the following property: $|X_1|$ is even, $X_1$ can be partitioned into $\frac{|X_1|}{2}$ pairs of vertices such that each pair of vertices has a common neighbor in Y. Let $X_2=X\setminus X_1$. By the choice of $X_1$, no two distinct vertices of $X_2$ have a common neighbor in Y, thus $|X_2|\le \frac{|Y|}{2k+3-l}$. For each i ($1\le i\le \frac{|X_1|}{2}$), let $x_i$ and $x_i'$ be a pair of vertices in $X_1$ with a common neighbor $y_i$ in Y. Moreover, let $e_i=x_iy_i$ and $e_i'=x_i'y_i$. Let

$$\begin{aligned} E_1=\bigcup _{1\le i\le \frac{|X_1|}{2}}\{e_i, e_i'\}. \end{aligned}$$

For a vertex $x\in X_2$, let $e_x, e_x'$ be two edges incident with x in F. Let

$$\begin{aligned} E_2=\bigcup _{x\in S_2}\{e_x, e_x'\}. \end{aligned}$$

Note that $E_1\cup E_2$ is a paired dominating set of $G=L(F)$. Therefore

$$\begin{aligned} \gamma _{pr}(G)\le & {} |E_{1}|+|E_{2}|\\= & {} |X_1|+2|X_2|\\= & {} |X|+|X_2|\\\le & {} |X|+\frac{|Y|}{2k+3-l}\\= & {} |X|+\frac{\frac{2k+3-l}{l} |X|}{2k+3-l}\\= & {} \frac{(l+1)|X|}{l}\\= & {} \frac{(l+1)}{l}\frac{n}{2k+3-l}\\\le & {} \frac{n}{k+1}. \end{aligned}$$

Conversely, we assume that $\gamma _{pr}(G)=\frac{n}{k+1}$. By the above proof, $l\in \{1, k+1\}$ and $|X_2|(2k+3-l)=|Y|$. If $l=1$, then $G=L(K_{1,2k+2})=K_{2k+2}$. Next we consider the case when $l=k+1$.

Claim 1 $N(x_i)=N(x_i')$ for each $i\in \{1, \ldots , \frac{|X_1|}{2}\}$.

By contradiction, suppose that $N(x_i)\ne N(x_i')$. Let $v_i\in N(x_i)\setminus N(x_i')$ and $v_i'\in N(x_i')\setminus N(x_i)$. Since $|X_2|(2k+3-l)=|Y|$, there exist two distinct vertices $u_i, u_i'\in X_2$ such that $v_iu_i\in E(F)$ and $v_i'u_i'\in E(F)$. Let $X_1'=X_1\cup \{u_i, u_i'\}$. Note that $X_1'\subseteq X$ can be partitioned into $\frac{|X_1|}{2}+1$ pairs of vertices such that each pair of vertices has a common neighbor in Y ($x_i$ and $u_i$ are paired, and $x_i'$ and $u_i'$ are paired), contradicting the maximality of $X_1$.

Claim 2 $|N(N(x_i))\cap X_2|=1$ for each $i\in \{1, \ldots , \frac{|X_1|}{2}\}$.

By contradiction, suppose that $|N(N(x_i))\cap X_2|\ge 2$. Take two distinct vertices $u_i, u_i'$ from $N(N(x_i))\cap X_2$. Let $v_i\in N(x_i)$ and $v_i'\in N(x_i')$ such that $v_iu_i\in E(F)$ and $v_i'u_i'\in E(F)$. Let $X_1'=X_1\cup \{u_i, u_i'\}$. Note that $X_1'\subseteq X$ can be partitioned into $\frac{|X_1|}{2}+1$ pairs of vertices such that each pair of vertices has a common neighbor in Y ($x_i$ and $u_i$ are paired, and $x_i'$ and $u_i'$ are paired), contradicting the maximality of $X_1$.

For an integer $i\in \{1, \ldots , \frac{|X_1|}{2}\}$, Let $w_i$ be the unique vertex in $N(N(x_i))\cap X_2$. Let $v_i\in N(x_i)$. Since $d_F(v_i)=k+1$, $|N(v_i)\cap (X_1\setminus \{x_i,x_i'\})|=k-2$.

Claim 3 For any $x_j\in N(v_i)\cap (X_1\setminus \{x_i,x_i'\})$, $N(x_j)=N(x_i)$.

First we prove that $x_j'\in N(v_i)\cap (X_1\setminus \{x_i,x_i'\})$. Suppose this is not the case. Since $N(x_j)=N(x_j')$ by Claim 1, $v_ix_j'\in E(F)$, a contradiction.

Next we suppose that $N(x_j)\ne N(x_i)$. Take a vertex $v_j\in N(x_j)\setminus N(x_i)$. Let $X_1'=X_1\cup \{w_i, w_j\}$. Note that $X_1'\subseteq X$ can be partitioned into $\frac{|X_1|}{2}+1$ pairs of vertices such that each pair of vertices has a common neighbor in Y ($w_i$ and $x_j$ are paired, and $w_j$ and $x_j'$ are paired), contradicting the maximality of $X_1$.

So, we conclude that $F\cong K_{k+1, k+2}$. Since $|X_2|(2k+3-l)=|Y|$, $l=k+1$ and $|Y|=k+2$, we have $|X_2|=1$. Furthermore, Since $k+1=|X|=|X_1|+|X_2|$ and $|X_1|$ is even, it follows that k is even.

So, the proof of the theorem is completed. $\square$

5 For further research

It is an interesting problem to determine the sharp upper bound for the paired domination number of a connected r-regular claw-free graph of order n.