1 Introduction

Recently, micro/nano structures are increasingly applied because of their extraordinary electrical, thermal and mechanical properties [1,2,3,4,5,6,7]. Since micro/nano structures emerge as the next-generation technology, which are capable of making a significant difference in people’s lives and nanobeams are an important element of micro/nano structures, comprehensive studies such as these structures are necessary [8,9,10,11,12,13,14]. Some practical applications of micro/nano structures are: sensors, MEMS/NEMS devices, miniature robots, micro/nano tools, lens, and lasers [15, 16]. These devices have been applied in several industries such as aerospace, wireless networks, optical, biomedical, drug delivery systems and consumer products. Accordingly, accurate evaluation and detailed investigation of the mechanical behaviors of micro/nano structures including bending [17,18,19], buckling [10, 20], vibration [21,22,23,24,25] and wave propagation [26,27,28,29,30] are necessary to increase their reliability and obtain the proper design of small-scale systems. Due to the deficiency of classical continuum mechanics theories in analyzing the mechanical behaviors of micro/nano structures, modified elasticity theories such as couple stress (CS), strain gradient (SG), general nonlocal (GN) and Eringen’s nonlocal (EN) theories [4, 31,32,33,34,35,36] have been proposed to resolve these problems. Also, in the past 2 years, combined non-classical elasticity theories such as nonlocal strain gradient (NL-SG) theory have attracted the interests of researchers [37,38,39,40]. Ebrahimi et al. [41] investigated the wave propagation-thermal behaviors of graphene nanoplatelet-reinforced composite (GNPRC) porous cylindrical nanoshells on the basis of nonlocal strain gradient theory (NSGT) taking into account the calibrated values of nonlocal constant and material length scale parameter. Al-Furjan et al. [42] performed wave propagation simulations on multi-hybrid nanocomposite (MHC) reinforced doubly curved panels covered with piezoelectric actuators to reveal the effects of electrical load on the wave responses of smart panels. Zenkour and Sobhy [43] studied size-dependent wave propagation in functionally graded (FG) graphene platelet (GPL)-reinforced composite bi-layer nanobeams embedded in Pasternak elastic foundation.

Many researchers have considered the mechanical behaviors of micro/nano structures in recent years. The following literature review is allocated to the investigation of wave propagation behaviors of such small-scale elements. Kocaturk and Akbas [44] employed Bernoulli–Euler beam model and modified couple stress theory (MCST) to investigate the wave propagation behavior of nanobeams. Lim et al. [45] proposed a higher-order model capable of coupling nonlocal stresses and strain gradients to analyze wave propagation. They considered Timoshenko and Euler–Bernoulli nanobeams as examples and performed comprehensive tests. Li et al. [46] used Euler–Bernoulli beam model and nonlocal SG theory to study wave propagation in FG nanobeams. Ma et al. [47] illustrated wave propagation of smart nanobeam structures on the basis of nonlocal Timoshenko beam theory. Arefi and Zenkour [48] studied wave propagation in smart Timoshenko FG nanobeams via nonlocal elasticity theory. Barati and Zenkour [49] studied wave propagations in porous nanobeams establishing a general bi-Helmholtz NL-SG model. Narendar and Gopalakrishnan [50] investigated wave propagation performance in a rotating nanotube on the basis of EN theory. In another work, Sobhi and Zenkour [51] studied the bending of viscoelastic nanobeams laying on visco-Pasternak elastic foundations on the basis of a new shear and normal deformations beam theory. Zenkour et al. [52] showed that damping time and deflection were inversely proportional to thickness ratio, modes, thickness and aspect ratio of magnetostrictive layer to viscoelastic layer. In another work, Zenkour and El-Shahrany [53] investigated the vibration behaviors of magnetostrictive laminated beams resting on visco-Pasternak foundation.

Ebrahimi and Haghi [54] reported wave propagations in rotating FG nanoscale-beams by taking thermal effects into account on the basis of NL-SG theory. Moreover, they investigated the effect of fiber angle on the wave propagation behaviors of laminated cylindrical micro-shells. Zeighampour and Tadi Bani [55] preformed wave desperation in FG-CNTRC cylindrical micro-shells considering NL-SG and shear deformable shell theory. Ebrahimi and Dabbagh [56] studied wave propagation behaviors of piezoelectric nano-plates on elastic foundations. They employed NL-SG and Kirchhoff plate theories for model development. They also considered surface effects in extracting results. Shahsavari et al. [57] studied wave propagations in FG nano-plates on hybrid foundations considering thermal effects. They applied bi-Helmholtz NL-SG along with refined-higher order shear deformation plate theory for model establishing. Barati [58] studied wave propagation in bonded nanobeams with imperfections. He used general NL-SG model and refined shear deformation beam theory for the investigation of the effects of porosity and temperature on wave dispersion. Liu and Lv [59] investigated the effects of uncertain material properties on the wave propagations of smart nanobeams on the basis of nonlocal theory and Euler–Bernoulli beam model. Amiri et al. [60] employed NL-SG theory for the evaluation of wave propagation of smart piezoelectric nanotubes conveying viscous fluids. They took into account slip boundary conditions and surface stress effects. Ma et al. [61] reported wave dispersion behaviors of piezoelectric nano-plates on the basis of the NL theory and Kirchhoff and Mindlin nano-plate models considering thermo-electro-mechanical loads. Karami et al. [62] utilized NL-SG theory to evaluate hydrothermal wave propagation in viscoelastic graphene and nano-plate porous heterogeneous materials exposed to magnetic fields. She et al. [63] employed NL-SG theory to analyze the wave propagations of nano-tube wave propagations. More recently, She et al. [64] employed NL-SG theory and Reddy’s high order beam model to explore wave propagations in FG porous nanobeams. Zeighampour et al. [65] studied the wave propagation behaviors of viscoelastic nanotubes according to NL-SG and shell theories. Sobhy and Zenkour [51] applied normal and shear deformations beam theory to investigate the static and dynamic bendings of viscoelastic nanobeams resting on visco-Pasternak elastic foundations.

Recently, Ebrahimi and Dabbagh [66] performed detailed investigations on wave propagation in FG porous nano-m structures. They took into account coupling effects between Young’s moduli and density in porous materials. Masoumi et al. [67] explored the wave propagations of piezoelectric nanobeams using NL-SG theory and Reddy’s beam model to derive their governing equations and harmonic wave dispersion. Karami and Janghorban [68] reported transverse and longitudinal wave desperations of triclinic nanobeams for the first time on the basis of NL-SG and size-dependent shear deformation theories considering stretching effect. Wang and Liang [69] studied wave dispersion behaviors of nanobeams made of nano-porous metal foams using nonlocal elasticity theory and Timoshenko and Euler–Bernoulli beam models. Sobhy and Zenkour [70] utilized NL-SG theory to investigate wave propagations in bi-layer porous FG nano-plates in Winkler elastic medium. Also, Abouelregal and Zenkour [71] studied the vibrations of viscoelastic FG Euler–Bernoulli nanostructure beams using fractional-order calculus. Arani et al. [72] used NL theory considering surface and flexoelectric effects to illustrate wave propagations in FG nanobeams resting on elastic media. They extracted motion governing equations on the basis of Timoshenko beam model with residual surface stress. Ebrahimi et al. [41] used NL-SG theory for the analysis of wave propagation in graphene nano-platelet-reinforced composite porous cylindrical nano-shells considering thermal effects. Cao and Wang [73] employed NL-SG Rayleigh beam theory for the evaluation of wave propagations in viscoelastic lipid nanotubes conveying protein. Faroughi et al. [74] studied wave propagations in bi-directional FG rotating nanobeams based on GN theory and higher-order Reddy’s beam model. Recently, to more accurately capture size effects, some researchers have proposed the consolidation of non-classical theories for the analysis of micro/nano structures [75, 76]. Hence, in the current work, we have tried to present different possibilities of coupling effects of nonlocal elasticity and modified couple stress theories, so-called nonlocal modified couple stress theory (NL-MCST), for rotating nanobeams resting on visco-elastic foundations. We employed NL-MCST to capture the effect of the rotational degree of freedom of particles as well as nonlocal and long-range interactions between particles simultaneously. We propose to study the accuracy of our model in comparison to other models. Some other investigations have considered the coupling effects of modified couple stress and Eringen’s nonlocal theories simultaneously [77, 78]. Ebrahimi and Barati [79] performed vibration analyses on FG nanobeams using nonlocal elasticity and modified couple stress theories. They also applied Galerkin's method to obtain numerical results. Shariati et al. [80] presented the vibrational characteristics of FG nanobeams via the combination of nonlocal and couple stress theories considering surface effects. Ramezani and Mojra [81] conducted stability analyses on carbon nanotubes conveying nano-fluid under magnetic field. They used nonlocal elasticity and couple stress theories to construct a model and coupled Euler–Bernoulli beam theory with Navier–Stokes’s equation of magnetic-fluid flow to determine fluid–structure interactions. Attar et al. [82] investigated the vibrational behaviors of FG piezoelectric (FGP) plates considering simultaneous effects of nonlocal and couple stress based on Kirchhoff thin plate theory and Navier’s approach.

According to the above literature review, it was found that the existing reports on wave propagation in small-scale beams are mainly based on EN, SG, MCST and especially NL-SG theories. It is noteworthy that, unlike NL-SG theory, a clear gap in other studies is that the consolidation of Eringen’s nonlocal and modified couple stress theories has not been considered for wave propagation analysis yet. Hence, in this study, the combined effects of modified couple stress and nonlocal Eringen’s theories are employed to indicate the effect of local rotational DOF. Then, this effect is expressed in the framework of ENT which covers long-range and nonlocal interactions among particles. To capture both softening and hardening behaviors of materials, modified couple stress and nonlocal Eringen’s theories are combined. Actually, we illustrated that the waiver of couple stress effect decreases frequencies by decreasing nanobeam stiffness. Also, waiver the effect of nonlocal parameter makes nanobeams stiffer, which increases frequencies. Hence, the wave frequency predicted by NL-MCST theory is always between the values obtained from ENT and MCST theories. Furthermore, as a higher-order shear deformation theory, RBT is adopted to establish an accurate model and corresponding analytic solutions are obtained as numerical results. The results are illustrated for all torsional (TO), transverse (TA) and longitudinal (LA) wave propagations and are comprehensively discussed. In addition to this novel consideration, the current comprehensive study encompasses the interactions of rotation, thermal and viscoelastic effects of higher-order-shear deformation beam model.

2 Formulation

2.1 Description

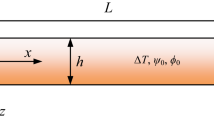
As shown in Fig. 1, a rotating viscoelastic nanobeam resting on a Winkler-Pasternak foundation is adopted to consider thermal effects. The nanobeam has length L, width b, rectangular cross-section a and thickness h.

Fig. 1
figure 1

Rotating viscoelastic nanobeam resting on a Winkler-Pasternak foundation

Full size image

2.2 Kinematics

Reddy’s beam theory, namely third-order shear deformation theory, is adopted to develop the kinematics model of viscoelastic nanobeams resting on Winkler-Pasternak foundations. Displacement fields are described as:

$${\varvec{u}}=\left({u}_{1},{u}_{2},{u}_{3}\right),$$
(1)
$${u}_{1}=u+z\varphi -{c}_{1}{z}^{3}\left(\varphi +\frac{\partial w}{\partial x}\right);\,{u}_{2}=0;\,{u}_{3}=w,$$
(2)

where \(w\) and \(u\) are transverse and longitudinal displacements, \(\varphi\) is the rotation of neutral axis cross-section and \({c}_{1}=4/(3{h}^{2})\).

The strains of Reddy beam model are expressed as:

$${\varepsilon }_{xx}=\frac{\partial {u}_{1}}{\partial x}=\frac{\partial u}{\partial x}+z\frac{\partial \varphi }{\partial x}-{c}_{1}{z}^{3}\left(\frac{\partial \varphi }{\partial x}+\frac{{\partial }^{2}w}{\partial {x}^{2}}\right),$$
(3a)
$$2{\varepsilon }_{xz}=\frac{\partial {u}_{1}}{\partial z}+\frac{\partial {u}_{3}}{\partial x}=\left(\varphi +\frac{\partial w}{\partial x}\right)-{c}_{2}{z}^{2}\left(\varphi +\frac{\partial w}{\partial x}\right),$$
(3b)

where rotation vector \({\varvec{\theta}}\) and symmetric curvature tensor \({\chi }_{ij}\) are given as:

$${\varvec{\theta}}=\frac{1}{2}\mathrm{curl}{\varvec{u}},$$
(4)
$${\chi }_{ij}=\frac{1}{2}\left({\theta }_{i,j}+{\theta }_{j,i}\right).$$
(5)

Substitution of Eq. (5) in Eq. (4) yields:

$$2{\chi }_{yx}=\frac{1}{2}\left(\frac{\partial \varphi }{\partial x}-\frac{{\partial }^{2}w}{\partial {x}^{2}}-{c}_{2}{z}^{2}(\frac{\partial \varphi }{\partial x}+\frac{{\partial }^{2}w}{\partial {x}^{2}})\right),$$
(6a)
$$2{\chi }_{yz}=-{c}_{2}z\left(\varphi +\frac{\partial w}{\partial x}\right),$$
(6b)

where \({c}_{2}=3{c}_{1}\).

3 Modified couple stress theory

According to modified couple stress theory [34], strain energy density \({\Pi }_{s}\) is given in terms of strain and curvature conjugated with stress and couple stress, respectively, as:

$${\Pi }_{s}={\int }_{0}^{L}{\int }_{A}({\varvec{\sigma}}:{\varvec{\varepsilon}}+{\varvec{m}}:{\varvec{\chi}})dAdx,$$
(7)

where \({\varvec{\sigma}},{\varvec{\varepsilon}},{\varvec{\chi}}\) are stress, strain and curvature tensors, respectively and, \({\varvec{m}}\) is the deviatoric part of couple stress tensor and can be expressed as:

$${m}_{ij}=2G{l}_{m}^{2}{\chi }_{ij},$$
(8)

where \(G\) and \({l}_{m}\) are shear modulus of rigidity and non-classical length scale parameter, respectively. By substituting Eqs. (3) and (6) into Eq. (7) and using some algebraic simplifications, strain energy density is obtained as:

$${\Pi }_{s}={\int }_{0}^{L}\left[\begin{array}{l}{M}_{xx}^{(0)}\frac{\partial u}{\partial x}+{M}_{xx}^{(1)}\frac{\partial \varphi }{\partial x}-{c}_{1}{M}_{xx}^{(3)}(\frac{\partial \varphi }{\partial x}+\frac{{\partial }^{2}w}{\partial {x}^{2}})+{Q}_{xz}^{(0)}(\varphi +\frac{\partial w}{\partial x})-{c}_{2}{Q}_{xz}^{(2)}(\varphi +\frac{\partial w}{\partial x})+\\ \frac{1}{2}{Y}_{yx}^{(0)}(\frac{\partial \varphi }{\partial x}-\frac{{\partial }^{2}w}{\partial {x}^{2}})-\frac{{c}_{2}}{2}{Y}_{yx}^{(2)}(\frac{\partial \varphi }{\partial x}+\frac{{\partial }^{2}w}{\partial {x}^{2}})-{c}_{2}{Y}_{yz}^{(1)}(\varphi +\frac{\partial w}{\partial x})\end{array}\right]dx,$$
(9)

where:

$${M}_{xx}^{(i)}={\int }_{A}{\sigma }_{xx}{z}^{i}dA;{Q}_{xz}^{(i)}={\int }_{A}{\sigma }_{xz}{z}^{i}dA;{Y}_{yx}^{(i)}={\int }_{A}{m}_{yx}{z}^{i}dA;{Y}_{yz}^{(i)}={\int }_{A}{m}_{yz}{z}^{i}dA.$$
(10)

4 Governing equations of motion

Based on Hamilton’s principle, motion equations can be defined as:

$$\delta H=\delta {\int }_{{t}_{1}}^{{t}_{2}}\left({\Pi }_{k}-({\Pi }_{s}+{\Pi }_{w})\right)dt=0,$$
(11)

where \({\Pi }_{k},{\Pi }_{s}\) and \({\Pi }_{w}\) indicate kinetic energy, strain energy and the work done by external forces, respectively.

Kinetic energy \({\Pi }_{k}\) is defined as:

$$\begin{aligned} {\Pi }_{k}& =\frac{1}{2}\rho {\int }_{0}^{L}{\int }_{A}\left((\frac{\partial {u}_{1}}{\partial t}{)}^{2}+(\frac{\partial {u}_{2}}{\partial t}{)}^{2}+(\frac{\partial {u}_{3}}{\partial t}{)}^{2}\right)dAdx \\ & =\frac{1}{2}{\int }_{0}^{L}\left[\begin{array}{c}{m}_{0}(\frac{\partial u}{\partial t}{)}^{2}+{m}_{2}(\frac{\partial \varphi }{\partial t}{)}^{2}+{c}_{1}^{2}{m}_{6}(\frac{\partial \varphi }{\partial t}+\frac{{\partial }^{2}w}{\partial x\partial t}{)}^{2}+2{m}_{1}(\frac{\partial u}{\partial t})(\frac{\partial \varphi }{\partial t})-\\ 2{c}_{1}{m}_{3}(\frac{\partial u}{\partial t})(\frac{\partial \varphi }{\partial t}+\frac{{\partial }^{2}w}{\partial x\partial t})-2{c}_{1}{m}_{4}(\frac{\partial \varphi }{\partial t})(\frac{\partial \varphi }{\partial t}+\frac{{\partial }^{2}w}{\partial x\partial t})+{m}_{0}(\frac{\partial w}{\partial t}{)}^{2}\end{array}\right]dx,\end{aligned}$$
(12)

where:

$${m}_{i}={\int }_{A}\rho {z}^{i}dA,$$
(13)
$${\bar{m}}_{i}={m}_{i}-{c}_{1}{m}_{i+2}=\rho {\bar{I}}_{i};\, {\widehat{m}}_{i}={\bar{m}}_{i}-{c}_{1}{\bar{m}}_{i+2}=\rho {\widehat{I}}_{i}.$$
(14)

Also, the first variations of \({\Pi }_{k},{\Pi }_{s}\) and \({\Pi }_{w}\) are defined as the following:

$$\delta {\Pi }_{k}={\int }_{0}^{L}\left[\begin{array}{c}\left(-{m}_{0}\frac{{\partial }^{2}u}{\partial {t}^{2}}-{\bar{m}}_{1}\frac{{\partial }^{2}\varphi }{\partial {t}^{2}}+{c}_{1}{m}_{3}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}\right)\delta u-\left({\bar{m}}_{1}\frac{{\partial }^{2}u}{\partial {t}^{2}}+{\widehat{m}}_{2}\frac{{\partial }^{2}\varphi }{\partial {t}^{2}}-{c}_{1}{\bar{m}}_{4}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}\right)\delta \varphi -\\ \left({m}_{0}\frac{{\partial }^{2}w}{\partial {t}^{2}}+{c}_{1}{m}_{3}\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}+{c}_{1}{\bar{m}}_{4}\frac{{\partial }^{3}\varphi }{\partial x\partial {t}^{2}}-{c}_{1}^{2}{m}_{6}\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}\right)\delta w\end{array}\right]dx,$$
(15)
$$\delta {\Pi }_{s}={\int }_{0}^{L}\left[\begin{array}{c}\left(-\frac{\partial {M}_{xx}^{(0)}}{\partial x}\right)\delta u-\left(\frac{\partial {\bar{M}}_{xx}^{(1)}}{\partial x}-{\bar{\bar{Q}}}_{xz}^{(0)}+\frac{\partial {\bar{\bar{Y}}}_{yx}^{(0)}}{\partial x}+{c}_{2}{Y}_{yz}^{(1)}\right)\delta \varphi -\\ \left({c}_{1}\frac{{\partial }^{2}{M}_{xx}^{(3)}}{\partial {x}^{2}}+\frac{\partial {\bar{\bar{Q}}}_{xz}^{(0)}}{\partial x}+\frac{{\partial }^{2}{\bar{Y}}_{yx}^{(0)}}{\partial {x}^{2}}-{c}_{2}\frac{\partial {Y}_{yz}^{(1)}}{\partial x}\right)\delta w\end{array}\right]dx,$$
(16)
$$\delta {\Pi }_{w}=-{\int }_{0}^{L}\left[\left(-\frac{\partial }{\partial x}\left({N}_{T}\frac{\partial w}{\partial x}\right)+q-{K}_{w}w-{K}_{d}\frac{\partial w}{\partial t}+{K}_{p}\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{\partial }{\partial x}\left(T\left(x\right)\frac{\partial w}{\partial x}\right)\right)\delta w+f\delta u\right]dx,$$
(17)

in which:

$${\bar{M}}_{xx}^{(1)}={M}_{xx}^{(1)}-{c}_{1}{M}_{xx}^{\left(3\right)};{\bar{\bar{Q}}}_{xz}^{\left(0\right)}={Q}_{xz}^{\left(0\right)}-{c}_{2}{Q}_{xz}^{\left(2\right)},$$
(18)
$${\bar{\bar{Y}}}_{yx}^{(0)}=\frac{1}{2}\left({Y}_{yx}^{(0)}-{c}_{2}{Y}_{yx}^{(2)}\right);{\bar{Y}}_{yx}^{(0)}=\frac{1}{2}\left({Y}_{yx}^{(0)}+{c}_{2}{Y}_{yx}^{(2)}\right),$$
(19)

\({N}_{T}={\int }_{A}(E\alpha \Delta T)dA\) is applied axial thermal force, and \(q\) and \(f\) are transverse and longitudinal distributed forces, respectively. Also, \({K}_{w},{K}_{d},{K}_{p}\) are Winkler, Pasternak and damping coefficients due to elastic foundation, respectively, and \(T(x)\) is the axial force due to centrifugal stiffening resulting from nanobeam rotation given as:

$$T\left(x\right)=b{\int }_{x}^{L}{\int }_{-\frac{h}{2}}^\frac{h}{2}\rho {\stackrel{\sim }{\omega }}^{2}xdzdx.$$
(20)

In which, \(\stackrel{\sim }{\omega }\) is the rotation speed of nanobeam. Motion equations can be derived by substituting Eqs. (15) to (17) into (11) based on MCST as follow:

$$\delta u:-{m}_{0}\frac{{\partial }^{2}u}{\partial {t}^{2}}-{\bar{m}}_{1}\frac{{\partial }^{2}\varphi }{\partial {t}^{2}}+{c}_{1}{m}_{3}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}+\frac{\partial {M}_{xx}^{\left(0\right)}}{\partial x}+f=0,$$
(21a)
$$\delta \varphi :-{\bar{m}}_{1}\frac{{\partial }^{2}u}{\partial {t}^{2}}-{\widehat{m}}_{2}\frac{{\partial }^{2}\varphi }{\partial {t}^{2}}+{c}_{1}{\bar{m}}_{4}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}+\frac{\partial {\bar{M}}_{xx}^{\left(1\right)}}{\partial x}-{\bar{\bar{Q}}}_{xz}^{\left(0\right)}+\frac{\partial {\bar{\bar{Y}}}_{yx}^{\left(0\right)}}{\partial x}+{c}_{2}{Y}_{yz}^{\left(1\right)}=0,$$
(21b)
$$\begin{aligned}\delta w:& -{m}_{0}\frac{{\partial }^{2}w}{\partial {t}^{2}}-{c}_{1}{m}_{3}\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}-{c}_{1}{\bar{m}}_{4}\frac{{\partial }^{3}\varphi }{\partial x\partial {t}^{2}}+{c}_{1}^{2}{m}_{6}\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}+{c}_{1}\frac{{\partial }^{2}{M}_{xx}^{(3)}}{\partial {x}^{2}}+\frac{\partial {\bar{\bar{Q}}}_{xz}^{(0)}}{\partial x}+\frac{{\partial }^{2}{\bar{Y}}_{yx}^{(0)}}{\partial {x}^{2}}\\ &-{c}_{2}\frac{\partial {Y}_{yz}^{\left(1\right)}}{\partial x}-\frac{\partial }{\partial x}({N}_{T}\frac{\partial w}{\partial x})+q-{k}_{w}w-{k}_{d}\frac{\partial w}{\partial t}+{k}_{p}\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{\partial }{\partial x}(T(x)\frac{\partial w}{\partial x})=0.\end{aligned}$$
(21c)

5 Nonlocal (Eringen) theory

According to Eringen [33], the stress field at any random point \({\varvec{x}}\) is a function of both strain field of that point (hyper-elastic case) and all other strain fields in the configuration. So, nonlocal stress tensor is denoted as:

$${\varvec{\sigma}}={\int }_{V}\kappa (\left|{{\varvec{x}}}^{^{\prime}}-{\varvec{x}}\right|,\eta ){\varvec{t}}\left({{\varvec{x}}}^{^{\prime}}\right)d{{\varvec{x}}}^{^{\prime}},$$
(22)

where \({\varvec{t}}\left(.\right)\) indicates local stress tensor at point (.) and \(\kappa (\left|{{\varvec{x}}}^{^{\prime}}-{\varvec{x}}\right|,\eta )\) referees to nonlocal modulus. Thus, the general from of nonlocal characteristic equation is represented as [33]:

$$\left[1-({e}_{0}a{)}^{2}{\nabla }^{2}\right]{t}_{ij}=\lambda {\varepsilon }_{rr}{\delta }_{ij}+G{\varepsilon }_{ij},$$
(23)

where \({t}_{ij}\) and \(\varepsilon\) illustrate nonlocal stress and strain tensor, respectively, \({\delta }_{ij}\) is Kronecker delta, \(\lambda\) and \(G\) are Lame’s constants and \(({e}_{0}a{)}^{2}\) denotes nonlocal parameter. Therefore, nonlocal constitutive relations can be expressed in the following forms [83]:

$${\sigma }_{xx}-({e}_{0}a{)}^{2}\frac{{\partial }^{2}{\sigma }_{xx}}{\partial {x}^{2}}=E{\varepsilon }_{xx},$$
(24a)
$${\sigma }_{xz}-({e}_{0}a{)}^{2}\frac{{\partial }^{2}{\sigma }_{xz}}{\partial {x}^{2}}=2G{\varepsilon }_{xz},$$
(24b)
$${m}_{yx}-({e}_{0}a{)}^{2}\frac{{\partial }^{2}{m}_{yx}}{\partial {x}^{2}}=2G{l}_{m}^{2}{\chi }_{yx},$$
(24c)
$${m}_{yz}-({e}_{0}a{)}^{2}\frac{{\partial }^{2}{m}_{yz}}{\partial {x}^{2}}=2G{l}_{m}^{2}{\chi }_{yz}.$$
(24d)

Using Eq. (10), nonlocal constitutive relations in Eqs. (24) can be developed as:

$${M}_{xx}^{(0)}-({e}_{0}a{)}^{2}\frac{{\partial }^{2}{M}_{xx}^{\left(0\right)}}{\partial {x}^{2}}=E{I}_{0}\frac{\partial u}{\partial x},$$
(25a)
$${\bar{M}}_{xx}^{(1)}-({e}_{0}a{)}^{2}\frac{{\partial }^{2}{\bar{M}}_{xx}^{\left(1\right)}}{\partial {x}^{2}}=E{\bar{I}}_{2}\frac{\partial \varphi }{\partial x}-{c}_{1}E{\bar{I}}_{4}\left(\frac{\partial \varphi }{\partial x}+\frac{{\partial }^{2}w}{\partial {x}^{2}}\right),$$
(25b)
$${M}_{xx}^{(3)}-({e}_{0}a{)}^{2}\frac{{\partial }^{2}{M}_{xx}^{\left(3\right)}}{\partial {x}^{2}}=E{I}_{4}\frac{\partial \varphi }{\partial x}-{c}_{1}E{I}_{6}\left(\frac{\partial \varphi }{\partial x}+\frac{{\partial }^{2}w}{\partial {x}^{2}}\right),$$
(25c)
$${\bar{\bar{Q}}}_{xz}^{(0)}-({e}_{0}a{)}^{2}\frac{{\partial }^{2}{\bar{\bar{Q}}}_{xz}^{\left(0\right)}}{\partial {x}^{2}}=G{\tilde{I }}_{0}\left(\varphi +\frac{\partial w}{\partial x}\right),$$
(25d)
$${\bar{\bar{Y}}}_{yx}^{(0)}-({e}_{0}a{)}^{2}\frac{{\partial }^{2}{\bar{\bar{Y}}}_{yx}^{\left(0\right)}}{\partial {x}^{2}}=\frac{1}{4}G{l}_{m}^{2}\left({I}_{0}^{*}\left(\frac{\partial \varphi }{\partial x}-\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)-{c}_{2}{I}_{2}^{*}\left(\frac{\partial \varphi }{\partial x}+\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)\right),$$
(25e)
$${\bar{Y}}_{yx}^{(0)}-({e}_{0}a{)}^{2}\frac{{\partial }^{2}{\bar{Y}}_{yx}^{\left(0\right)}}{\partial {x}^{2}}=\frac{1}{4}G{l}_{m}^{2}\left({\bar{\bar{I}}}_{0}\left(\frac{\partial \varphi }{\partial x}-\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)-{c}_{2}{\bar{\bar{I}}}_{2}\left(\frac{\partial \varphi }{\partial x}+\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)\right),$$
(25f)
$${Y}_{yz}^{(1)}-({e}_{0}a{)}^{2}\frac{{\partial }^{2}{Y}_{yz}^{\left(1\right)}}{\partial {x}^{2}}=-{c}_{2}G{l}_{m}^{2}{I}_{2}\left(\varphi +\frac{\partial w}{\partial x}\right),$$
(25g)

in which:

$${I}_{i}={\int }_{A}{z}^{i}dA,$$
(26)
$${\bar{I}}_{i}={I}_{i}-{c}_{1}{I}_{i+2};{\bar{\bar{I}}}_{i}={I}_{i}+{c}_{2}{I}_{i+2};{\tilde{I }}_{i}={\bar{I}}_{i}-{c}_{2}{\bar{I}}_{i+2};{I}_{i}^{*}={I}_{i}-{c}_{2}{I}_{i+2}.$$
(27)

Calculating \(\frac{{\partial }^{2}{M}_{xx}^{(0)}}{\partial {x}^{2}}\) from Eq. (21a) yields:

$$\frac{{\partial }^{2}{M}_{xx}^{(0)}}{\partial {x}^{2}}={m}_{0}\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}+{m}_{1}\frac{{\partial }^{3}\varphi }{\partial x\partial {t}^{2}}-{c}_{1}{m}_{3}\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}-\frac{\partial f}{\partial x}.$$
(28)

By substituting Eq. (28) into Eq. (25a) and applying Eq. (21a), it is found that:

$$\begin{aligned}-{m}_{0} & \left[\frac{{\partial }^{2}u}{\partial {t}^{2}}-({e}_{0}a{)}^{2}\frac{{\partial }^{4}u}{\partial {x}^{2}\partial {t}^{2}}\right]-{m}_{1}\left[\frac{{\partial }^{2}\varphi }{\partial {t}^{2}}-({e}_{0}a{)}^{2}\frac{{\partial }^{4}\varphi }{\partial {x}^{2}\partial {t}^{2}}\right] \\ &+{c}_{1}{m}_{3}\left[\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}-({e}_{0}a{)}^{2}\frac{{\partial }^{5}w}{\partial {x}^{3}\partial {t}^{2}}\right]+\left[f-({e}_{0}a{)}^{2}\frac{{\partial }^{2}f}{\partial {x}^{2}}\right]+E{I}_{0}\frac{{\partial }^{2}u}{\partial {x}^{2}}=0.\end{aligned}$$
(29)

Moreover, calculating \({\bar{\bar{Q}}}_{xz}^{(0)}\) and \(\frac{{\partial }^{2}{\bar{\bar{Q}}}_{xz}^{(0)}}{\partial {x}^{2}}\) from Eq. (21b) results in:

$${\bar{\bar{Q}}}_{xz}^{(0)}=-{\bar{m}}_{1}\frac{{\partial }^{2}u}{\partial {t}^{2}}-{\widehat{m}}_{2}\frac{{\partial }^{2}\varphi }{\partial {t}^{2}}+{c}_{1}{\bar{m}}_{4}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}+\frac{\partial {\bar{M}}_{xx}^{\left(1\right)}}{\partial x}+\frac{\partial {\bar{\bar{Y}}}_{yx}^{\left(0\right)}}{\partial x}+{c}_{2}{Y}_{yz}^{\left(1\right)},$$
(30)
$$\frac{{\partial }^{2}{\bar{\bar{Q}}}_{xz}^{(0)}}{\partial {x}^{2}}=-{\bar{m}}_{1}\frac{{\partial }^{4}u}{\partial {x}^{2}\partial {t}^{2}}-{\widehat{m}}_{2}\frac{{\partial }^{4}\varphi }{\partial {x}^{2}\partial {t}^{2}}+{c}_{1}{\bar{m}}_{4}\frac{{\partial }^{5}w}{\partial {x}^{3}\partial {t}^{2}}+\frac{{\partial }^{3}{\bar{M}}_{xx}^{\left(1\right)}}{\partial {x}^{3}}+\frac{{\partial }^{3}{\bar{\bar{Y}}}_{yx}^{\left(0\right)}}{\partial {x}^{3}}+{c}_{2}\frac{{\partial }^{2}{Y}_{yz}^{\left(1\right)}}{\partial {x}^{2}}.$$
(31)

Substituting Eqs. (30) and (31) into Eq. (25d) and applying Eqs. (25b), (25e) and (25g) lead to:

$$\begin{aligned}{\bar{m}}_{1}& \left[\frac{{\partial }^{2}u}{\partial {t}^{2}}-({e}_{0}a{)}^{2}\frac{{\partial }^{4}u}{\partial {x}^{2}\partial {t}^{2}}\right]+{\widehat{m}}_{2}\left[\frac{{\partial }^{2}\varphi }{\partial {t}^{2}}-({e}_{0}a{)}^{2}\frac{{\partial }^{4}\varphi }{\partial {x}^{2}\partial {t}^{2}}\right]-{c}_{1}{\bar{m}}_{4}\left[\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}-({e}_{0}a{)}^{2}\frac{{\partial }^{5}w}{\partial {x}^{3}\partial {t}^{2}}\right]\\ & \quad +\left[G{\tilde{I }}_{0}+{c}_{2}^{2}G{l}_{m}^{2}{I}_{2}\right]\varphi -\left[E{\widehat{I}}_{2}-\frac{1}{4}G{l}_{m}^{2}{I}_{0}^{^{\prime}}\right]\frac{{\partial }^{2}\varphi }{\partial {x}^{2}}+\left[G{\tilde{I }}_{0}+{c}_{2}^{2}G{l}_{m}^{2}{I}_{2}\right]\frac{\partial w}{\partial x}+\left[{c}_{1}E{\bar{I}}_{4}+\frac{1}{4}G{l}_{m}^{2}{\tilde{I }}_{0}\right]\frac{{\partial }^{3}w}{\partial {x}^{3}}=0.\end{aligned}$$
(32)

Also, \({\bar{\bar{Q}}}_{xz}^{(0)}\) can be obtained by calculating \(\frac{{\partial }^{2}{\bar{\bar{Q}}}_{xz}^{(0)}}{\partial {x}^{2}}\) from Eq. (21c) and substituting it into Eq. (25d) as:

$$\begin{gathered} \overline{\overline{Q}}_{xz}^{(0)} = (e_{0} a)^{2} \left[ \begin{gathered} m_{0} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} + c_{1} m_{3} \frac{{\partial^{4} u}}{{\partial x^{2} \partial t^{2} }} + c_{1} \overline{m}_{4} \frac{{\partial^{4} \varphi }}{{\partial x^{2} \partial t^{2} }} - c_{1}^{2} m_{6} \frac{{\partial^{5} w}}{{\partial x^{3} \partial t^{2} }} - c_{1} \frac{{\partial^{3} M_{xx}^{(3)} }}{{\partial x^{3} }} - \frac{{\partial^{2} \overline{Y}_{yx}^{(0)} }}{{\partial x^{2} }} + \hfill \\ c_{2} \frac{{\partial^{2} Y_{yz}^{(1)} }}{{\partial x^{2} }} - \frac{{\partial^{2} }}{{\partial x^{2} }}(N_{T} \frac{\partial w}{{\partial x}}) - \frac{\partial q}{{\partial x}} + K_{w} \frac{\partial w}{{\partial x}} + K_{d} \frac{{\partial^{2} w}}{\partial x\partial t} - K_{p} \frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{\partial^{2} }}{{\partial x^{2} }}(T(x)\frac{\partial w}{{\partial x}}) \hfill \\ \end{gathered} \right] + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,G\tilde{I}_{0} (\varphi + \frac{\partial w}{{\partial x}}). \hfill \\ \end{gathered}$$
(33)

Substitution of the first derivative of \({\bar{\bar{Q}}}_{xz}^{(0)}\) from Eq. (33) into Eq. (21c) and the application of Eqs. (25c), (25f) and (25g) results in:

$$\begin{aligned}& -{c}_{1}{m}_{3}\left[\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}-({e}_{0}a{)}^{2}\frac{{\partial }^{5}u}{\partial {x}^{3}\partial {t}^{2}}\right]-{c}_{1}{\bar{m}}_{4}\left[\frac{{\partial }^{3}\varphi }{\partial x\partial {t}^{2}}-({e}_{0}a{)}^{2}\frac{{\partial }^{5}\varphi }{\partial {x}^{3}\partial {t}^{2}}\right]\\ & \quad -\left[{m}_{0}\frac{{\partial }^{2}w}{\partial {t}^{2}}-({c}_{1}^{2}{m}_{6}+({e}_{0}a{)}^{2}{m}_{0})\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}+({e}_{0}a{)}^{2}{c}_{1}^{2}{m}_{6}\frac{{\partial }^{6}w}{\partial {x}^{4}\partial {t}^{2}}\right]-{K}_{d}\left[\frac{\partial w}{\partial t}-({e}_{0}a{)}^{2}\frac{{\partial }^{3}w}{\partial {x}^{2}\partial t}\right] \\ & \quad +\left[G{\tilde{I }}_{0}+{c}_{2}^{2}G{l}_{m}^{2}{I}_{2}\right]\frac{\partial \varphi }{\partial x}+\left[{c}_{1}E{\bar{I}}_{4}+\frac{1}{4}G{l}_{m}^{2}{\tilde{I }}_{0}\right]\frac{{\partial }^{3}\varphi }{\partial {x}^{3}}-{K}_{w}w+\left[\frac{\partial T}{\partial x}-({e}_{0}a{)}^{2}\frac{{\partial }^{3}T}{\partial {x}^{3}}\right]\frac{\partial w}{\partial x} \\ & \quad +\left[G{\tilde{I }}_{0}+{c}_{2}^{2}G{l}_{m}^{2}{I}_{2}+{K}_{p}+({e}_{0}a{)}^{2}{K}_{w}-{N}_{T}+T-3({e}_{0}a{)}^{2}\frac{{\partial }^{2}T}{\partial {x}^{2}}\right]\frac{{\partial }^{2}w}{\partial {x}^{2}}-\left[3({e}_{0}a{)}^{2}\frac{\partial T}{\partial x}\right]\frac{{\partial }^{3}w}{\partial {x}^{3}}\\ & \quad -\left[{c}_{1}^{2}E{I}_{6}+\frac{1}{4}G{l}_{m}^{2}{I}_{0}^{^{\prime\prime} }+({e}_{0}a{)}^{2}{K}_{p}+({e}_{0}a{)}^{2}T-({e}_{0}a{)}^{2}{N}_{T}\right]\frac{{\partial }^{4}w}{\partial {x}^{4}}+q-({e}_{0}a{)}^{2}\frac{{\partial }^{2}q}{\partial {x}^{2}}=0. \end{aligned}$$
(34)

where:

$$\begin{aligned}{I}_{i}^{{^{\prime}}} & ={I}_{i}^{*}-{c}_{2}{I}_{i+2}^{*};{I}_{i}^{^{\prime\prime} }={\bar{\bar{I}}}_{i}+{c}_{2}{\bar{\bar{I}}}_{i+2} \\ {\widehat{I}}_{i} & ={\bar{I}}_{i}-{c}_{1}{\bar{I}}_{i+2};{\tilde{I }}_{i}={I}_{i}^{*}+{c}_{2}{I}_{i+2}^{*}={\bar{\bar{I}}}_{i}-{c}_{2}{\bar{\bar{I}}}_{i+2}.\end{aligned}$$
(35)

Equations (29), (32) and (34) are motion equations in terms of generalized displacements. These equations are obtained by considering the effects of visco-elastic foundation, thermal forces and centrifugal stiffening due to the rotation of nanobeam.

To establish dimensionless motion equations, dimensionless parameters are achieved as the following:

$$\begin{gathered} \zeta = \frac{x}{L};\,\,\,\,\,U = \frac{u}{L};\,\,\,\,W = \frac{w}{L};\,\,\,\,\,\Phi = \varphi ;\,\,\,\,\,\mu = \frac{{e_{0} a}}{L};\,\,\,\,\,l_{0} = \frac{{l_{m} }}{h} \hfill \\ \overline{\tau } = \frac{T}{{T_{\max } }};\,\,\,\,\,\overline{q} = \frac{qL}{{EI_{0} }};\,\,\,\,\,\overline{f} = \frac{fL}{{EI_{0} }};\,\,\,\,\,\vartheta = \frac{{N_{T} }}{{EI_{0} }};\,\,\,\,\,\Omega_{w}^{2} = \frac{{m_{2} \,\omega^{2} }}{{EI_{0} }} \hfill \\ \overline{M}_{0} = \frac{{m_{0} \,L^{2} }}{{m_{2} }};\overline{M}_{1} = \frac{{\overline{m}_{1} \,L}}{{m_{2} }};\,\,\,\,\,\overline{M}_{2} = \frac{{\hat{m}_{2} }}{{m_{2} }};\overline{M}_{3} = \frac{{c_{1} m_{3} \,L}}{{m_{2} }};\,\,\,\,\,\overline{M}_{4} = \frac{{c_{1} \overline{m}_{4} }}{{m_{2} }};\,\,\,\,\,\overline{M}_{6} = \frac{{c_{1}^{2} m_{6} }}{{m_{2} }} \hfill \\ \alpha_{0} = \frac{{G\tilde{I}_{0} }}{{EI_{0} }};\,\,\,\,\,\alpha_{2} = \frac{{E\hat{I}_{2} }}{{EI_{0} L^{2} }};\,\,\,\,\,\alpha_{4} = \frac{{c_{1} E\overline{I}_{4} }}{{EI_{0} L^{2} }};\,\,\,\,\,\alpha_{6} = \frac{{c_{1}^{2} EI_{6} }}{{EI_{0} L^{2} }} \hfill \\ \beta^{\prime}_{0} = \frac{{Gl_{m}^{2} \,I^{\prime}_{0} }}{{4EI_{0} L^{2} }};\,\,\,\,\,\beta^{\prime\prime}_{0} = \frac{{Gl_{m}^{2} \,I^{\prime\prime}_{0} }}{{4EI_{0} L^{2} }};\,\,\,\,\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{\beta }_{0} = \frac{{Gl_{m}^{2} \,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{I}_{0} }}{{4EI_{0} L^{2} }};\,\,\,\,\,\beta_{2} = \frac{{c_{2}^{2} \,Gl_{m}^{2} \,I_{2} }}{{EI_{0} }} \hfill \\ k_{d} = \frac{{K_{d} \,L^{2} }}{{\sqrt {EI_{0} m_{2} } }};\,\,\,\,k_{w} = \frac{{K_{w} \,L^{2} }}{{EI_{0} }};\,\,\,\,\,k_{p} = \frac{{K_{p} }}{{EI_{0} }};\,\,\,\,\,\Im = \frac{{T_{\max } }}{{EI_{0} }} \hfill \\ \end{gathered}$$
(36)

where:

$$T_{\max } = \frac{1}{2}m_{0} L^{2} \tilde{\omega }^{2} .$$
(37)

Substituting Eq. (36) into Eqs. (29), (32) and (34) gives non-dimensional motion governing equations in terms of rotation and displacement as:

$$\begin{aligned} & \left[-{\bar{M}}_{0}\frac{{\partial }^{2}U}{\partial {t}^{2}}+{\mu }^{2}{\bar{M}}_{0}\frac{{\partial }^{4}U}{\partial {\zeta }^{2}\partial {t}^{2}}-{\bar{M}}_{1}\frac{{\partial }^{2}\Phi }{\partial {t}^{2}}+{\mu }^{2}{\bar{M}}_{1}\frac{{\partial }^{4}\Phi }{\partial {\zeta }^{2}\partial {t}^{2}}+{\bar{M}}_{3}\frac{{\partial }^{3}W}{\partial \zeta \partial {t}^{2}}-{\mu }^{2}{\bar{M}}_{3}\frac{{\partial }^{5}W}{\partial {\zeta }^{3}\partial {t}^{2}}\right]\\ & \quad +\frac{{\partial }^{2}U}{\partial {\zeta }^{2}}+\bar{f}-{\mu }^{2}\frac{{\partial }^{2}\bar{f}}{\partial {\zeta }^{2}}=0,\end{aligned}$$
(38a)
$$\begin{aligned} & \left[{\bar{M}}_{1}\frac{{\partial }^{2}U}{\partial {t}^{2}}-{\mu }^{2}{\bar{M}}_{1}\frac{{\partial }^{4}U}{\partial {\zeta }^{2}\partial {t}^{2}}+{\bar{M}}_{2}\frac{{\partial }^{2}\Phi }{\partial {t}^{2}}-{\mu }^{2}{\bar{M}}_{2}\frac{{\partial }^{4}\Phi }{\partial {\zeta }^{2}\partial {t}^{2}}-{\bar{M}}_{4}\frac{{\partial }^{3}W}{\partial \zeta \partial {t}^{2}}+{\mu }^{2}{\bar{M}}_{4}\frac{{\partial }^{5}W}{\partial {\zeta }^{3}\partial {t}^{2}}\right]\\ & \quad +\left[{\alpha }_{0}+{\beta }_{2}\right]\Phi -\left[{\alpha }_{2}+{\beta }_{0}^{^{\prime}}\right]\frac{{\partial }^{2}\Phi }{\partial {\zeta }^{2}}+\left[{\alpha }_{0}+{\beta }_{2}\right]\frac{\partial W}{\partial \zeta }+\left[{\alpha }_{4}+{\stackrel{\sim }{\beta }}_{0}\right]\frac{{\partial }^{3}W}{\partial {\zeta }^{3}}=0,\end{aligned}$$
(38b)
$$\begin{aligned} &\left[\begin{array}{c}-{\bar{M}}_{3}\frac{{\partial }^{2}U}{\partial \zeta \partial t}+{\mu }^{2}{\bar{M}}_{3}\frac{{\partial }^{5}U}{\partial {\zeta }^{3}\partial {t}^{2}}-{\bar{M}}_{4}\frac{{\partial }^{3}\Phi }{\partial \zeta \partial {t}^{2}}+{\mu }^{2}{\bar{M}}_{4}\frac{{\partial }^{5}\Phi }{\partial {\zeta }^{3}\partial {t}^{2}}-{\bar{M}}_{0}\frac{{\partial }^{2}W}{\partial {t}^{2}}\\ + ({\bar{M}}_{6}+{\mu }^{2}{\bar{M}}_{0})\frac{{\partial }^{4}W}{\partial {\zeta }^{2}\partial {t}^{2}}-{\mu }^{2}{\bar{M}}_{6}\frac{{\partial }^{6}W}{\partial {\zeta }^{4}\partial {t}^{2}}\end{array}\right]\\ & \quad +\left[-{k}_{d}\frac{\partial W}{\partial t}+{\mu }^{2}{k}_{d}\frac{{\partial }^{3}W}{\partial {\zeta }^{2}\partial t}\right]+\left[{\alpha }_{0}+{\beta }_{2}\right]\frac{\partial \Phi }{\partial \zeta }+\left[{\alpha }_{4}+{\stackrel{\sim }{\beta }}_{0}\right]\frac{{\partial }^{3}\Phi }{\partial {\zeta }^{3}} -{k}_{w}W\\ & \quad +\mathfrak{I}\left[\frac{\partial \bar{\tau }}{\partial \zeta }-{\mu }^{2}\frac{{\partial }^{3}\bar{\tau }}{\partial {\zeta }^{3}}\right]\frac{\partial W}{\partial \zeta }+\left[\mathfrak{I}\bar{\tau } -3{\mu }^{2}\mathfrak{I}\frac{{\partial }^{2}\bar{\tau }}{\partial {\zeta }^{2}}+{\alpha }_{0}+{\beta }_{2}+{k}_{p}+{\mu }^{2}{k}_{w}-\vartheta \right]\frac{{\partial }^{2}W}{\partial {\zeta }^{2}}\\ & \quad-\left[3{\mu }^{2}\mathfrak{I}\frac{\partial \bar{\tau }}{\partial \zeta }\right]\frac{{\partial }^{3}W}{\partial {\zeta }^{3}}-\left[-{\mu }^{2}\mathfrak{I}\bar{\tau }+{\alpha }_{6}+{\beta }_{0}^{^{\prime\prime} }+{\mu }^{2}{k}_{p}-{\mu }^{2}\vartheta \right]\frac{{\partial }^{4}W}{\partial {\zeta }^{4}}+\bar{q}-{\mu }^{2}\frac{{\partial }^{2}\bar{q}}{\partial {\zeta }^{2}}=0.\end{aligned}$$
(38c)

6 Solution procedure

In this section, the analytical solutions of wave propagation governing equations of rotating viscoelastic nanobeams resting on elastic foundations under thermal effects are described. Adopting harmonic method, wave propagation displacement fields are defined as [84]:

$$\left\{ {\begin{array}{*{20}c} {U(\zeta ,t)} \\ {W(\zeta ,t)} \\ {\Phi (\zeta ,t)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {U_{0} \exp [i(K\zeta - \Omega_{w} t)]} \\ {W_{0} \exp [i(K\zeta - \Omega_{w} t)]} \\ {\Phi_{0} \exp [i(K\zeta - \Omega_{w} t)]} \\ \end{array} } \right\},$$
(39)

where \({\Omega }_{w}\) and \(K\) are non-dimensional circular frequency and non-dimensional wave number, respectively, \({\varvec{X}}=({U}_{0},{W}_{0},{\Phi }_{0})\) is wave amplitude and \(i=\sqrt{-1}\). Since in this work wave propagation is considered in unbounded elastic domains, boundary conditions cannot be taken into account [85,86,87,88].

By substituting Eq. (39) and its derivatives into Eqs. (38), the characteristic equation is extracted as:

$$({\varvec{K}}+{\Omega }_{w}{\varvec{C}}+{\Omega }_{w}^{2}{\varvec{M}}){\varvec{X}}=0,$$
(40)

where M, K and C are mass, stiffness and damping matrices, respectively, and include complex terms:

$${\varvec{M}}=\left[\begin{array}{ccc}{m}_{{U}_{0}{U}_{0}}& {m}_{{U}_{0}{\Phi }_{0}}& {m}_{{U}_{0}{W}_{0}}\\ {m}_{{\Phi }_{0}{U}_{0}}& {m}_{{\Phi }_{0}{\Phi }_{0}}& {m}_{{\Phi }_{0}{W}_{0}}\\ {m}_{{W}_{0}{U}_{0}}& {m}_{{W}_{0}{\Phi }_{0}}& {m}_{{W}_{0}{W}_{0}}\end{array}\right];\quad {\varvec{K}}=\left[\begin{array}{ccc}{k}_{{U}_{0}{U}_{0}}& {k}_{{U}_{0}{\Phi }_{0}}& {k}_{{U}_{0}{W}_{0}}\\ {k}_{{\Phi }_{0}{U}_{0}}& {k}_{{\Phi }_{0}{\Phi }_{0}}& {k}_{{\Phi }_{0}{W}_{0}}\\ {k}_{{W}_{0}{U}_{0}}& {k}_{{W}_{0}{\Phi }_{0}}& {k}_{{W}_{0}{W}_{0}}\end{array}\right];\quad {\varvec{C}}=\left[\begin{array}{ccc}{c}_{{U}_{0}{U}_{0}}& {c}_{{U}_{0}{\Phi }_{0}}& {c}_{{U}_{0}{W}_{0}}\\ {c}_{{\Phi }_{0}{U}_{0}}& {c}_{{\Phi }_{0}{\Phi }_{0}}& {c}_{{\Phi }_{0}{W}_{0}}\\ {c}_{{W}_{0}{U}_{0}}& {c}_{{W}_{0}{\Phi }_{0}}& {c}_{{W}_{0}{W}_{0}}\end{array}\right].$$
(41)

In which:

$$\begin{aligned}{m}_{{U}_{0}{U}_{0}} &={\bar{M}}_{0}\left(1+{\mu }^{2}{K}^{2}\right); \quad { m}_{{U}_{0}{\Phi }_{0}}={\bar{M}}_{1}(1+{\mu }^{2}{K}^{2}); \quad{ m}_{{U}_{0}{W}_{0}}=-i{\bar{M}}_{3}K(1+{\mu }^{2}{K}^{2})\\{m}_{{\Phi }_{0}{U}_{0}}&=-{\bar{M}}_{1}\left(1+{\mu }^{2}{K}^{2}\right); \quad { m}_{{\Phi }_{0}{\Phi }_{0}}=-{\bar{M}}_{2}(1+{\mu }^{2}{K}^{2}); \quad{ m}_{{\Phi }_{0}{W}_{0}}=i{\bar{M}}_{4}K(1+{\mu }^{2}{K}^{2})\\{m}_{{W}_{0}{U}_{0}}& =i{\bar{M}}_{3}K\left(1+{\mu }^{2}{K}^{2}\right); \quad{ m}_{{W}_{0}{\Phi }_{0}}=i{\bar{M}}_{4}K\left(1+{\mu }^{2}{K}^{2}\right); \quad { m}_{{W}_{0}{W}_{0}}=({\bar{M}}_{0}+{K}^{2}{\bar{M}}_{6})(1+{\mu }^{2}{K}^{2})\\{k}_{{U}_{0}{U}_{0}} &=-{K}^{2}; \quad {k}_{{U}_{0}{\Phi }_{0}}={k}_{{\Phi }_{0}{U}_{0}}={k}_{{U}_{0}{W}_{0}}={k}_{{U}_{0}{W}_{0}}=0; \quad\\ {k}_{{\Phi }_{0}{\Phi }_{0}} & =\left({\alpha }_{0}+{\beta }_{2}\right)+\left({\alpha }_{0}+{\beta }_{0}^{^{\prime}}\right){K}^{2}; \quad {k}_{{\Phi }_{0}{W}_{0}}={k}_{{W}_{0}{\Phi }_{0}}=iK\left[({\alpha }_{0}+{\beta }_{2})-({\alpha }_{4}+{\stackrel{\sim }{\beta }}_{0}){K}^{2}\right]\\ {k}_{{W}_{0}{W}_{0}}& =-{k}_{w}+i\mathfrak{I}(\frac{\partial \bar{\tau }}{\partial \zeta }-{\mu }^{2}\frac{{\partial }^{3}\bar{\tau }}{\partial {\zeta }^{3}})K-(\mathfrak{I}\bar{\tau }-3{\mu }^{2}\mathfrak{I}\frac{{\partial }^{2}\bar{\tau }}{\partial {\zeta }^{2}}+{\alpha }_{0}+{\beta }_{2}+{k}_{p}+{\mu }^{2}{k}_{w}-\vartheta ){K}^{2}\\&\quad -i(3{\mu }^{2}\mathfrak{I}\frac{\partial \bar{\tau }}{\partial \zeta }){K}^{3}+({\alpha }_{6}+{\beta }_{0}^{^{\prime\prime} }+{\mu }^{2}{k}_{p}-{\mu }^{2}\vartheta -{\mu }^{2}\mathfrak{I}\bar{\tau }){K}^{4}\\ {c}_{{W}_{0}{W}_{0}}& =i{k}_{d}\left(1+{\mu }^{2}{K}^{2}\right); \quad {c}_{{U}_{0}{U}_{0}}={c}_{{U}_{0}{\Phi }_{0}}={c}_{{U}_{0}{W}_{0}}={c}_{{\Phi }_{0}{U}_{0}}={c}_{{\Phi }_{0}{\Phi }_{0}}={c}_{{\Phi }_{0}{W}_{0}}={c}_{{{W}_{0}U}_{0}}={c}_{{W}_{0}{\Phi }_{0}}=0.\end{aligned}$$
(42)

Also, it is obvious that: \({m}_{{U}_{0}{\Phi }_{0}}={ m}_{{U}_{0}{W}_{0}}={ m}_{{\Phi }_{0}{U}_{0}}={ m}_{{W}_{0}{U}_{0}}=0.\)

The standard form for eigenvalue problem solution in Eq. (40) is:

$$\left[\begin{array}{cc}-{{\varvec{M}}}^{-1}{\varvec{C}}& -{{\varvec{M}}}^{-1}{\varvec{K}}\\ {\varvec{I}}& 0\end{array}\right]\left\{\begin{array}{c}\dot{{\varvec{X}}}\\ {\varvec{X}}\end{array}\right\}={\Omega }_{w}\left\{\begin{array}{c}\dot{{\varvec{X}}}\\ {\varvec{X}}\end{array}\right\}.$$
(43)

Equation (43) is an eigenvalue problem in which, by setting the determinant of the above matrix to zero, TA, LA and TO wave frequencies can be easily estimated. In addition, phase velocities of waves can be simply calculated by \(c={\Omega }_{w}/K\).

7 Numerical results and discussions

In this section, numerical results are obtained and evaluated for the wave propagation of rotating viscoelastic nanobeams considering the variations of the six parameters of \(\frac{{e}_{0}a}{{l}_{m}},{k}_{w},{k}_{p},\Delta T,{\Omega }_{b}\) and \(\frac{L}{h}\). Also, the effects of the ratio of nonlocal to length scale \(\frac{{e}_{0}a}{{l}_{m}}\), non-dimensional Winkler and Pasternak coefficients \({k}_{w}\) and \({k}_{p}\), temperature gradient \(\Delta T\), non-dimensional beam rotating velocity \({\Omega }_{b}\) and slenderness ratio \(\frac{L}{h}\) are described. Therefore, we kept five out of six parameters constant in each step and changed the value of the remaining parameter to evaluate parameter effects and interactions. The thermo-mechanical characteristics of rotating viscoelastic nanobeams are given in Table 1.

Table 1 Material properties
Full size table

The results obtained for three TO, TA and LA wave propagation types in nano beams are illustrated and discussed in detail.

8 Model validation

For the validation of the developed model and accuracy verification of the findings, numerical results are obtained based on NL-MCST model with materials of Ref. [74] and compared with those reported in the mentioned reference. To this end, we reduced the presented NL-MCST into NL by considering \({l}_{m}=0\). Also, we used mechanical properties given in Ref. [74] considering \({n}_{x}={n}_{z}=\gamma =0\) to establish the results for comparison and model validation. The results are compared for two different slenderness ratios \((\frac{L}{h}=10\) and \(15)\) and three different values of nonlocal parameter \({e}_{0}a=1, 2\) and \(3 (\mathrm{nm})\). Comparison results are summarized in Table 2 for all TA, LA and TO wave propagation types. The comparison results given in Table 2 show good agreement between the results obtained by the developed method and those reported in Ref. [74] verifying the accuracy of our model.

Table 2 Model validation by comparison of frequencies for three types of wave propagation (THz) (\(\Delta T={k}_{w}={k}_{p}=0 \mathrm{and} {\Omega }_{b}=2 \mathrm{Grad}/s\))
Full size table

8.1 Effects of \({e}_{0}a\) and \({l}_{m}\)

Figure 2 illustrates the trends of TO, TA and LA wave propagation frequencies based on non-dimensional wave number. As can be seen, by the increase of non-dimensional wave number, LA wave propagation frequency is decreased but for TA and TO wave propagations, the values of non-dimensional frequencies are increased.

Fig. 2
figure 2

Wave propagation frequencies based on NL and NL-MCSTs. a Longitudinal (LA) waves. b Transverse (TA) wave. c Torsional (TO) wave. \((\Delta T={k}_{w}={k}_{p}={\Omega }_{b}=0)\)

Full size image

Also, Fig. 2 presents the comparison of wave propagation fundamental frequencies extracted by Eringen’s nonlocal (NL) and nonlocal modified couple stress (NL-MCST) theories. As is clear, for LA and TA wave propagations, the results obtained by NL-MCST were higher than those obtained by NL for all non-dimensional wave number. However, there was no difference between NL and NL-MSCT results for TO wave propagation. The results obtained for LA and TA wave propagations show that for the same value of \({e}_{0}a\) in NL and NL-MCST, the effect of length parameter \({l}_{m}\) on NL-MCST increases wave propagation frequency but has no effect on wave propagation. Also, it can be concluded that, for LA wave propagation, increase of non-dimensional wave number decreases the difference between NL and NL-MCST wave frequencies whereas for TA wave propagation, this is opposite.

The effects of different nonlocal parameter to length scale ratios \({e}_{0}a/{l}_{m}\) on non-dimensional fundamental wave propagation frequency for all wave propagation types are indicated in Fig. 3. The results shown here are obtained by three different slenderness ratios of \(L/h=\mathrm{5,10}\) and \(20\). As it is obvious from the figure and due to the decrease of stiffness, TO, TA and LA wave frequencies decrease with the increase of \({e}_{0}a/{l}_{m}\). Also, by increasing slenderness ratio, frequency difference for different \({e}_{0}a/{l}_{m}\) ratios decreases.

Fig. 3
figure 3

Wave propagation frequencies for different nonlocal parameter to length scale ratios. a Longitudinal (LA) wave. b Transverse (TA) wave. c Torsional (TO) wave. \((\Delta T={k}_{w}={k}_{p}={\Omega }_{b}=0)\)

Full size image

8.2 Effects of temperature

Figure 4 displays the effect of temperature variation on non-dimensional frequencies of LA, TA and TO wave propagations.

Fig. 4
figure 4

Wave propagation frequencies for different temperatures. a–d Transverse (TA) wave. e Torsional (TO) wave. f Longitudinal (LA) wave. \(({k}_{w}={k}_{p}={\Omega }_{b}=0)\)

Full size image

In this section, \({T}_{0}=2{0 }^{\circ }\mathrm{C}\) is considered as the reference temperature and temperature variation is considered at five different levels from \(\Delta T={0 }^{\circ }\mathrm{C}\) to \(\Delta T=+4{5 }^{\circ }\mathrm{C}\). According to Fig. 4, temperature gradient has no significant effects on TO and LA wave propagations. However, it strongly affects TA wave propagation. Figure 4a–c show TA wave frequencies for constant values of \({e}_{0}a/{l}_{m}=20\) and \({l}_{m}=1.5 \mathrm{h}\) and defferent slenderness ratio values of \(L/h=\mathrm{10,20}\) and \(50.\) Also, Fig. 4d shows the results obtained for local case with \({e}_{0}a={l}_{m}=0\) and \(L/h=20.\) Based on the results obtained for TA wave propagation, with the increase of temperature, the initiaton of TA wave propagation is delayed. Moreover, an increase in temperature reduces the value of TA wave frequencies. Also, with increasing slenderness ratio, wave propagation delay due to increasing temperature gradient increases.

8.3 Effects of Winkler-Pasternak coefficients

In this section, Winkler coefficient effect on non-dimensional wave frequency is considered. The effect of dimensionless Winkler coefficient \({k}_{w}\) on all types of wave propagation is presented in Fig. 5. The results are obtained for the constant values of \({e}_{0}a/{l}_{m}=15,{l}_{m}=0.5 \mathrm{h}\) and \(L/h=15\) but different values of \(0\le {k}_{w}\le 1\) in five steps. As it is clear, LA wave propagation is not affected by different values of \({k}_{w}\) and indicates the same behavior for all values of \({k}_{w}.\) However, the variation of \({k}_{w}\) has considerable effects on TO and TA wave propagations. In TA wave and for \({k}_{w}>0\), with the increase of non-dimensional wave number up to a certain value, frequency is not affected by \({k}_{w}\) but for higher non-dimensional wavenumbers, frequency trend is changed. It is obvious that the increase of \({k}_{w}\) increases the value of TA wave frequency. For TO wave type, by increasing \({k}_{w}\), the wave propagation initiates with high frequencies. Also, TO frequency remains constant up to certain value of non-dimensional wave number but for higher non-dimensional wavenumbers, frequency trend tracks similar paths to that of \({k}_{w}=0.\) In other words, the variation of \({k}_{w}\) above a certain value of non-dimensional wave number has no considerable influence on wave frequency.

Fig. 5
figure 5

Wave propagation frequencies for different non-dimensional Winkler coefficients. a Longitudinal (LA) waves. b Transverse (TA) wave. c Torsional (TO) wave. \((\Delta T={k}_{p}={\Omega }_{b}=0)\)

Full size image

Pasternak coefficient effect on the non-dimensional frequency of all wave propagation types is illustrated in Fig. 6. Similar to the effect of \({k}_{w}\) on LA wave, different values of \({k}_{p}\) has no effect on frequency. However, the effects of \({k}_{p}\) on TO and TA wave propagations is slightly different from that of \({k}_{w}\) which is clear in Fig. 6. It can be concluded that, with the increase of \({k}_{p}\) from 0 to 1, TA frequency increases. For \({k}_{p}>0\), frequency difference is affected by the value of non-dimensional wave number. In other words, for \({k}_{p}>0\) and higher non-dimensional wavenumbers (here \(K>1.3\)), all frequencies converge to the same trend as that of \({k}_{p}=1\) (Fig. 6b). For TO wave frequency and with increasing \({k}_{p}\), first, the frequency trend up to certain value of non-dimensional wave number follows the same trend of \({k}_{p}=0\). Then, for higher non-dimensional wave numbers, TO frequency increases with increasing \({k}_{p}\) (Fig. 2c).

Fig. 6
figure 6

Wave propagation frequencies for different non-dimensional Pasternak coefficients. a Longitudinal (LA) wave. b Transverse (TA) wave. c Torsional (TO) wave. \((\Delta T={k}_{w}={\Omega }_{b}=0)\)

Full size image

8.4 Effects of beam rotating velocity

In this section, the effects of dimensionless rotating velocities of viscoelastic nanobeams \({\Omega }_{b}\) on all types of wave propagations are considered. Dimensionless beam rotating velocity is defined as:

$${\Omega }_{b}=\stackrel{\sim }{\omega }{L}^{2}\sqrt{\frac{\rho A}{EI}},$$
(44)

where \(A,\stackrel{\sim }{\omega },L,I\) are cross-section area, beam rotating velocity, length, and second moment of cross-section area, respectively, \(E\) is Young’s modulus and \(\rho\) is the density of beam.

The effects of \({\Omega }_{b}\) on TO, TA and LA wave propagations are presented in Fig. 7. The results are obtained for constant values of \({e}_{0}a/{l}_{m}=15,{l}_{m}=1.5 \mathrm{h}\) and \(L/h=15\). Also, to perform a comperhensvie investigatin on the effect of dimensionless rotating velocity on wave propagation, rotating velocity \({\Omega }_{b}\) is applied in three different categories \(0\le {\Omega }_{b}\le 20\), \(20\le {\Omega }_{b}\le 50\) and \(50\le {\Omega }_{b}\le 150\). For LA wave propagations illustrated in graphs (a-1) to (a-3) of Fig. 7, the increase of \({\Omega }_{b}\) up to \({\Omega }_{b}=50\) has no effect on wave frequency and it shows descending trend for all \({\Omega }_{b}\le 50\). However, for \(50<{\Omega }_{b}\le 150\) and after a certain value of non-dimensional wave number, the descending trend is stopped and presents constant or ascending behaviors, as indicated in the Fig. 7a-3.

Fig. 7
figure 7

Wave propagation frequencies for different beam rotating velocity. a Longitudinal (LA) wave. b Torsional (TO) wave. c Transverse (TA) wave. \((\Delta T={k}_{w}={k}_{p}=0)\)

Full size image

Also, in TO wave propagations displayed in graphs (b-1) to (b-3) of Fig. 7, \({\Omega }_{b}\le 16\) has no effect on wave frequency. On the other hand, the increase of \({\Omega }_{b}\) has dual effects on wave frequency. For \(20\le {\Omega }_{b}\le 50\), wave frequency has a strictly ascending trend. However, for \({\Omega }_{b}>50\), the trend is ascending up to a certain value of non-dimensional wave number and then it descends and then tracks identical trend.

Graphs (c-1) to (c-3) of Fig. 7 indicate the effect of \({\Omega }_{b}\) on TA waves. It can be concluded that, only for \({\Omega }_{b}\le 20\), the frequency of TA wave propagation increases by the increase of \({\Omega }_{b}\). However, high values of \({\Omega }_{b}>20\) has no significant influence on TA wave frequency.

8.5 Effects of slenderness ratio

Figure 8 shows the effects of slenderness ratio on all types of wave propagation. The results are illustrated for constant values of \({e}_{0}a/{l}_{m}=20,{l}_{m}=1.5 \mathrm{h}\). To obtain the results, the value of slenderness ratio was varied from 2.5 to 50 in five steps. According to the obtained results for TA wave propagation, slenderness ratio has considerable effects at all non-dimensional wavenumbers. However, in LA and TO waves and for high non-dimensional wavenumbers, frequencies reach a constant value above which slenderness ratio has no significant effect. As shown, with the increase of slenderness ratio, the frequencies of TA and TO wave propagation types decrease but that of TA type increases. It is obvious that, by the increase of slenderness ratio, frequency gradient becomes smoother for all types of wave propagation. In other words, with the increase of slenderness ratio, the frequencies of LA and TA types of wave propagation reach to a constant value in higher non-dimensional wave numbers.

Fig. 8
figure 8

Wave propagation frequencies based on different slenderness ratio. a Longitudinal (LA) Waves. b Transverse (TA) Wave. c Torsional (TO) Wave. \((\Delta T={k}_{w}={k}_{p}={\Omega }_{b}=0)\)

Full size image

8.6 Effects of slenderness ratio

The effect of non-dimensional visco-damping coefficient \({k}_{d}\) on all types of wave propagation is illustrated in Fig. 9. The results are extracted based on different non-dimensional visco-damping coefficient values of \({k}_{d}=0, 1, 2, 4\) and \(8\) for, LA, TO and TA types of wave propagation. It can be concluded easily that, the variation of \({k}_{d}\) only affects the TA type of wave and has no effect on To and LA types of wave propagation. Also, it is clear from Fig. 9c–f that, wave propagation for TA type is postponed by the increment of the value of \({k}_{d}\). For example, in Fig. 9c, until non-dimensional wave number \(K\) reaches 5, the TA type of wave for \({k}_{d}=8\) has not propagated. However, the wave propagates for \({k}_{d}=0, 1, 2\) and \(4\) before \(K=5\).

Fig. 9
figure 9

Wave propagation frequencies based on different visco-damping coefficient. a Longitudinal (LA) Waves. b Torsional (TO) Wave. c–f Transverse (TA) Wave with different slenderness ratio. \((\Delta T={k}_{w}={k}_{p}={\Omega }_{b}=0)\)

Full size image

On the other hand, at the same value of non-dimensional wave number, wave frequency for TA type decreases with increasing the value of \({k}_{d}\). Finally, by increasing the value of L/h, the TA type of wave will propagate in small value of non-dimensional wave number. Also, with the increase of slenderness ratio, the increment of \({k}_{d}\) value loses its effect on the frequency of TA type of wave for higher non-dimensional wave numbers.

9 Conclusion

The aim of this research was to develop a comprehensive mathematical-mechanical model for the investigation of wave propagations in rotating viscoelastic nanobeams resting on Winkler-Pasternak foundations considering thermal effects. In this work, to capture both hardening and softening behaviors of materials in wave propagation, nonlocal Eringen’s and modified couple stress theories are incorporated to obtain governing equations of motion. In addition, higher order shear deformation beam model is applied to obtain motion equations and an analytic method is utilized to solve them. The results are illustrated for LA, TA and TO wave propagations and are discussed in detail. Moreover, the effects of nonlocal parameter to length scale ratios, thermal gradient, Winkler-Pasternak coefficients, rotating velocity of viscoelastic nanobeams and slenderness ratios are captured and are comprehensively discussed. The following major conclusions were drawn:

  • By increasing non-dimensional wave number, LA wave propagation frequency decreases but, for TA and TO wave propagation types, the value of non-dimensional frequency increases.

  • For LA and TA wave propagation types, the results obtained from NL-MCST are higher than those of NL for all non-dimensional wavenumbers. On the other hand, there is no difference between NL and NL-MSCT results for TO wave propagation.

  • LA, TA and TO types of wave frequencies decrease with the increase of \({e}_{0}a/{l}_{m}\).

  • Temperature gradient has no significant effects on LA and TO wave propagations. However, it strongly affects TA wave propagation.

  • With the increase of temperature, TA wave propagation is delayed. Also, increase of temperature reduces TA wave frequency.

  • LA wave propagation is not affected by different values of \({k}_{w}\) and \({k}_{p}\). However, the variation of \({k}_{w}\) and \({k}_{p}\) have considerable effects on TO and TA wave propagations.

  • The frequencies of TA wave propagations are affected only at \({\Omega }_{b}\le 20\).

  • The increase of \({\Omega }_{b}\) has dual effects on TA and TO wave frequencies.

  • With the increase of slenderness ratio, the frequencies of TA and TO wave propagations decrease but that of TA type increases.

  • The variation of non-dimensional visco-damping coefficient affects only the TA type of wave propagation.

  • For the same value of the non-dimensional wave number, the wave frequency of TA type decreases with increasing the value of non-dimensional visco-damping coefficient.

  • The wave propagation of TA type delays by increasing non-dimensional visco-damping coefficient.