Introduction

Dynamical analysis and engineering design of systems under moving loads have been challenging issues for researchers in recent years [1,2,3,4]. The research results in this field can be applied to a wide range of sciences, such as physics, mechanics, and civil engineering [5,6,7,8]. Scientific reports have revealed that systems subjected to traveling loads are prone to experiencing different dynamical phenomena, such as cancellation and resonance [9]. Also, their vibrational response is highly dependent on the occurrence of these dynamical phenomena. Therefore, researchers modeled various dynamical phenomena in engineering systems under moving loads for different operating conditions to predict structural performance. In this regard, Dimitrovova et al. [10] obtained the transient dynamical response of a beam embedded in a foundation with variable stiffness under the excitation of a moving load. They also analyzed the effects of abrupt local changes in foundation properties on the vibrational behavior of the system. The dynamical behavior analysis of uniform beams with simple support conditions under a single moving load was performed by Kumar et al. [11]. They examined the damping effect on the cancellation of the free response of the system and also proposed a novel formulation for the cancellation mechanism. Museros et al. [12] surveyed the cancellation and resonance phenomena in the free vibration of beams under moving loads. They discovered the influence of elastic supports on the cancellation and resonance conditions. Forced and free dynamical responses of laminated deep curved beams subjected to moving loads were analyzed by Sarparast and Ebrahimi-Mamaghani [13]. They reported the cancellation disappearance phenomenon in the system and showed that the resonance velocities for the symmetric and non-symmetric cross-ply layups are equal. Martinez-Rodrigo et al. [14] explored the resonance and cancellation mechanisms in the vibrational response of two-span beams under the action of traveling loads. They evaluated the effect of the velocity of moving loads on the maximum acceleration of the system. Forced and free vibrations of straight beams made of axially functionally graded (FG) materials subjected to a moving load are considered by Ebrahimi-Mamghani et al. [15]. They studied the effects of several factors, such as system geometry and axial gradation of materials, on the critical velocity of the moving load, dynamical amplification factor, and maximum free vibration amplitude of the system. Hu et al. [16] solved the dynamical problem of continuous multi-span beams subjected to moving masses with variable velocity. They clarified the impacts of damping and mass acceleration on the system vibration. Agrawal and Chakraborty [17] considered the vibrations of cantilevered beams with cracks under concentrated moving forces exploiting the discrete element method. They surveyed the impacts of crack properties and force speed on the system dynamics. Jiang et al. [18] computed the vibrational response of multi-layer beams resting on an elastic medium subjected to traveling forces. They evaluated the impressions of foundation features and material properties on the system behavior. Kheim et al. [19] addressed the dynamical characteristic of a cracked FG beam attached to a piezoelectric layer subjected to harmonic moving loads. They inspected the impacts of material factors, load velocity, and crack position on the vibration response of the beam.

Theoretical and experimental investigations have shown that applying classical theories to the dynamical analysis of small-scale structures does not provide reliable outcomes [20,21,22]. As a result, scientists have developed higher-order continuum theories by considering the size effects. One of the most well-known theories for the mathematical modeling of nanoscale structures is Eringen’s nonlocal elasticity theory. In this theory, the softening effects in nanosystems are justified by introducing the nonlocal parameter [23]. Accordingly, numerous reports have been devoted to explaining the vibrational behavior of nanostructures under moving load based on Eringen’s nonlocal elasticity theory. For instance, Hosseini et al. [24] obtained the axial and transverse dynamical responses of an FG nanobeam under a constant moving load. They inspected the impacts of structure parameters such as the aspect ratio, power index of FG material, and velocity of the moving load on the maximum axial and transverse displacements. According to the nonlocal Euler–Bernoulli beam theory, Simsek modeled the forced vibration of simply supported single-walled carbon nanotubes under the action of a traveling harmonic load [25]. His results exhibited that the dynamical deflection of the system is directly related to the nonlocal parameter. Pirmohammadi et al. [26] scrutinized the vibration control of a single-walled carbon nanoscale tube by considering the effects of a traveling harmonic load. They investigated the influences of scale parameter, slender ratio, velocity, and excitation frequency of the moving load on the dynamical deflection of the system. Gupta et al. [27] conducted a nonlocal stress analysis on an irregular FG porous system resting on a fiber-reinforced medium under the action of moving loads. They addressed the effects of the nonlocality, porosity, frictional coefficient, and material gradation parameters on the dynamical response of the system. Hosseini et al. [28] analyzed the forced and free vibrations of single-walled carbon nanotubes carrying a moving load utilizing the nonlocal elasticity theory. They also compared the effects of the scale parameter, geometrical characteristics of nanotubes, velocity, and frequency of the moving harmonic load on the system vibration obtained via the classical, Rayleigh, and Bishop theories. Wang et al. [29] characterized the forced and free lateral dynamical responses of a nanobeam subjected to a traveling load by considering the nonlocal and strain gradient effects. Their results proved that the material length scale and nonlocal parameters play essential roles in determining the transverse vibration amplitude of the system.

The literature review confirms that the performance of small-scale systems is substantially dependent on their environmental conditions [30]. For example, applying an external longitudinal magnetic field to a nanostructure enhances the effective stiffness of the system and improves its stability. On the other hand, hygro-thermal fields lead to strains and compressive stresses in the nanoscale structure that may reduce the system efficiency. Hence, an important engineering requirement is to evaluate the effects of environmental variations on the dynamical behavior of nanostructures under moving loads. In this field, Abouelregal et al. [31] acquired the vibrational response of a nanobeam excited by the temperature gradient and a moving load. Their results demonstrated the effects of the velocity of the moving load, temperature rise, and size-dependent parameters on the dynamical deflection and bending moment of the system. The vibrational response of an FG nanobeam subjected to a moving load in thermal fields was computed by Hosseini et al. [32]. Their results illustrated that ascending the temperature and nonlocal parameter amplifies the dynamical deflection of the system. Barati et al. [33] focused on the forced vibration of embedded nanoscale beams under concentrated moving loads in varying environments. They discussed the impacts of scale parameters, the velocity of the moving load, viscoelastic foundation, and hygro-thermal fields on the system dynamics. The thermo-mechanical behavior of bi-directional FG microscale beams subjected to a moving harmonic load was simulated by Liu et al. [34]. They analyzed the fundamental frequency variation and dynamical deflection of the system by considering the material gradation in the axial and transverse directions, different thermal loadings, and small-scale effects. According to Eringen’s nonlocal elasticity theory and the Kirchhoff–Love plate model, Ghadiri et al. [35] determined an analytical solution for the steady-state dynamical response of simply supported graphene sheets rested on a visco-Pasternak substrate subjected to magneto-thermo-mechanical fields and moving loads. They disclosed that, in contrast to the small-scale effects, the jump phenomenon is postponed by ascending the temperature, initial stress, and magnetic field strength. On the basis of the nonlocal strain gradient theory, the vibrational analysis of Timoshenko microscale beams exposed to a moving mass and magnetic fields was accomplished by Esen [36]. The results of his research proved that by applying a magnetic field, the dynamical deflection of the system is reduced.

Due to the high surface-to-volume ratio at the nanoscale, the free surface energy cannot be ignored compared to bulk energy. As a result, surface effects should be considered in the physical and mechanical properties of the system for mathematical modeling and design of nanoscale structures. Nevertheless, limited investigations are concentrated on the surface effects on the vibrational behavior of nanostructures subjected to moving loads. Within this context, according to surface elasticity theory, Ghadiri et al. [37] modeled an Euler–Bernoulli nanobeam located on a nonlinear viscoelastic medium with the moving load excitation in thermal fields. Their results showed that by ascending the nonlocality, temperature rise, as well as increment of the residual surface stress and the linear stiffness of the foundation, the possibility of a jump phenomenon in the dynamical behavior of the system is reduced. Exploiting the nonlocal strain gradient theory and considering the surface effects, the forced torsional vibrational analysis of a nanobeam subjected to a moving harmonic torque was carried out by Hamidi et al. [38]. They inspected the effects of velocity parameter and scale factors on the maximum dynamical torsion of the system. Hashemian et al. [39] solved the vibration problem of a Timoshenko nanoscale beam under the intermittent movement of nanoscale particles by considering the surface effects. They investigated the impacts of diverse parameters, such as the scale factor, Pasternak foundation coefficient, and nanoparticle inertia, on the dynamical instability of the system. Also, they declared that by considering the inertia of the moving nanoscale mass and size-dependent effects, the dynamical instability region of the system is displaced to lower frequencies. Based on the modified nonlocal elasticity theory, Rahmani et al. [40] analyzed the forced vibration of double-walled carbon nanoscale tubes under the excitation of a moving nanoscale particle by considering surface effects. They also compared the deduced results of Eringen’s nonlocal and modified nonlocal elasticity theories. Based on the Euler–Bernoulli beam model and nonlocal piezoelastic theory, a dynamical model for the axial and transverse vibrations of boron nitride nanotubes under the excitation of a moving nanoparticle was developed by Arani and Roudbari [41]. They explored the effects of geometry, small-scale parameters, residual surface stress, and visco-Pasternak foundation characteristics on vibrational behavior and dynamical deflection of the system. Rajabi et al. [42] studied the forced vibrational behavior of nanobeams under a point moving harmonic load by considering surface effects based on Euler–Bernoulli, Timoshenko, and modified Timoshenko beam models. They discovered the effects of the scale parameters, frequency and velocity of the moving harmonic load on the dynamical behavior of the system. Hosseini et al. [43] considered the surface effects on the forced vibration of a double-nanobeam system coupled with a viscoelastic layer under a traveling load. They found that surface effects greatly affect the system dynamics for short nanobeams.

A comprehensive literature review indicates that limited research has addressed the size-dependent dynamics of small-scale beams under moving loads in varying environmental conditions by considering surface effects. To the best of the authors’ knowledge, the effects of axial tensile force, rotational inertia factor, surface energy, hygro-thermo-magnetic environments, and different elastic foundations on the critical velocity of the traveling load, dynamical amplification factor, cancellation mechanisms, and maximum amplitude of free vibration for nanobeams under moving load have not been reported. The current work discusses the dynamical behavior and response of a nanoscale beam under a moving load by considering environmental effects and surface energy based on Eringen’s nonlocal elasticity theory and the Rayleigh beam model. In the following, the dynamical equation of the system is extracted based on the generalized Hamilton’s principle. The Galerkin discretization approach derives the reduced-order system equation. Then, by solving the eigenvalue problem, the vibrational frequencies of the system are acquired numerically. Forced and free vibrational responses of the system are obtained analytically. Comparison and parametric studies are presented, and finally, the effects of system parameters on the dynamical response are assessed and analyzed.

Mathematical Formulation

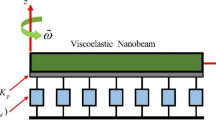
Figure 1 shows the schematic view of a hinged-hinged nanoscale beam with a surface layer under a moving point load. The nanobeam has a rectangular cross-section with a thickness of h and width of b. The length, perimeter, area, density, Young’s modulus, and moment of inertia of the nanobeam are indicated by L, S, A, ρ, E, and I, respectively. The moving load with a constant magnitude P and a constant velocity u moves along the axial direction of the system. The nanobeam is subjected to an axial tensile force F. Also, the system is under a magnetic field with the intensity B, temperature gradient ∆T, and moisture variation ∆H. The transverse displacement of the nanobeam is depicted by w.

Fig. 1
figure 1

Schematic view of a nanobeam with a surface layer subjected to a moving load

Full size image

By ignoring the nonlinear effects in the system, the axial strain of the nanobeam is expressed as follows [44, 45]:

$${\varepsilon }_{\mathrm{x}}=-z\frac{{\partial }^{2}w}{{\partial }^{2}x}$$
(1)

In practice, although the lateral movement is typically coupled with the longitudinal motion, the longitudinal displacement is small compared to the lateral displacement [46]. Consequently, lateral motion is only considered in the current research.

The following equation gives the strain energy of the system [44]:

$${E}_{\mathrm{e}}=\frac{1}{2}\underset{V}{\overset{}{\iiint }}{\sigma }_{\mathrm{x}}{\varepsilon }_{\mathrm{x}}\mathrm{d}V$$
(2)

where σx and V denote the axial stress and the volume of the system, respectively.

The stress–strain equations in the system are calculated from the following equations [47]:

$${\sigma }_{\mathrm{x}}=E{\varepsilon }_{\mathrm{x}}$$
(3)
$${\sigma }_{\mathrm{x}}^{\mathrm{s}}={\tau }_{0}^{\mathrm{s}}+{E}^{\mathrm{s}}{\varepsilon }_{\mathrm{x}}$$
(4)

in which \({\tau }_{0}^{\mathrm{s}}\) is the residual stress of the surface layer. The superscript “s” refers to the surface layer.

The resultant local bending moment due to normal stresses in the bulk and surface layer of the nanobeam is defined as follows [48]:

$${M}_{\mathrm{local}}={\int }_{A}z{\sigma }_{\mathrm{x}}\mathrm{d}x+{\int }_{S}z{\sigma }_{\mathrm{x}}^{\mathrm{s}}\mathrm{d}x=-{\left(\mathrm{EI}\right)}_{\mathrm{eff}}\frac{{\partial }^{2}w}{{\partial x}^{2}}$$
(5)

where (EI)eff is the equivalent flexural stiffness of the system and is introduced as follows [49]:

$${\left(\mathrm{EI}\right)}_{\mathrm{eff}}=\mathrm{EI}+{E}^{\mathrm{s}}\left({h}^{3}/6+b{h}^{2}/2\right)$$
(6)

By implementing Eqs. (1) and (2), the strain energy of the system can be rewritten as follows [50,51,52]:

$${E}_{\mathrm{e}}=-{\int }_{0}^{L}{M}_{\mathrm{local}}\frac{{\partial }^{2}w}{{\partial x}^{2}}\mathrm{d}x$$
(7)

The kinetic energy of the Rayleigh nanobeam due to the transverse displacement and the cross-section rotation can be computed by the following equation [15, 53]:

$$K=\frac{1}{2}\rho A{\int }_{0}^{L}{\left(\frac{\partial w}{\partial t}\right)}^{2}\mathrm{d}x+\frac{1}{2}\rho I{\int }_{0}^{L}{\left(\frac{{\partial }^{2}w}{\partial x\partial t}\right)}^{2}\mathrm{d}x$$
(8)

The first term is related to the lateral movement of the nanoscale beam. The second term is related to the cross-section rotation effect. The added rotary inertia effect enhances the kinetic energy and reduces the vibrational frequencies. The Rayleigh beam theory improves the Euler–Bernoulli beam theory by containing the cross-section rotation about the neutral axis. Consequently, it presents an appropriate approximation of the vibrational frequencies than the Euler–Bernoulli theory. It should be noted that compared with the Timoshenko beam model, the Rayleigh beam model does not consider the shear deformation effects.

The work done by external loads on the system (Wtot) is the sum of the work done by the elastic foundation (Wf), moving load (WP), as well as work done by the surface layer, axial tensile force, and environmental loads (We).

The work done by the variable elastic foundation is [54, 55]:

$${W}_{\mathrm{F}}={\int }_{0}^{L}{N}^{\mathrm{F}}w\mathrm{d}x$$
(9)

in which NF is the foundation force.

For linear, parabolic, and sinusoidal foundations, the foundation force can be calculated by Eqs. (10)–(12), respectively [56,57,58]:

$${N}_{\mathrm{L}}^{\mathrm{F}}={k}_{0}\left(1-{\sigma }_{\mathrm{L}}\frac{x}{L}\right)w , \quad 0\le {\sigma }_{\mathrm{L}}\le 1$$
(10)
$${N}_{\mathrm{P}}^{\mathrm{L}}={k}_{0}\left(1-{\sigma }_{\mathrm{P}}{\left(\frac{x}{L}\right)}^{2}\right)w , \quad 0\le {\sigma }_{\mathrm{P}}\le 1$$
(11)
$${N}_{\mathrm{S}}^{\mathrm{F}}={k}_{0}\left(1-{\sigma }_{\mathrm{S}}\mathrm{sin}\left(\frac{\uppi x}{2L}\right)\right)w ,\quad 0\le {\sigma }_{\mathrm{S}}\le 1$$
(12)

where k0 is the foundation modulus. Also, σL, σP, and σS are linear, parabolic, and sinusoidal variation parameters of the foundation, respectively.

It should be noted that by eliminating the foundation variation parameter, the considered foundation is reduced to the conventional Winkler foundation.

The work done by an external moving load is expressed as follows [59, 60]:

$${W}_{\mathrm{P}}=-{\int }_{0}^{L}P{\updelta }_{\mathrm{dir}}\left(x-ut\right)w\mathrm{d}x$$
(13)

in which δdir is the Dirac delta function.

The work done by hygro-thermo-magnetic environments, axial tensile force, and the transverse load due to the surface layer is given as follows [3, 61]:

$${W}_{\mathrm{e}}=-\frac{1}{2}{\int }_{0}^{L}\left({N}^{\mathrm{T}}+{N}^{\mathrm{H}}-{N}^{\mathrm{s}}-{N}^{\mathrm{M}}-F\right){\left(\frac{\partial w}{\partial x}\right)}^{2}\mathrm{d}x$$
(14)

where

$${N}^{\mathrm{T}}=EA\alpha \Delta T+2{E}^{\mathrm{s}}\left(b+h\right){\alpha }^{\mathrm{s}}\Delta T$$
(15)
$${N}^{\mathrm{H}}= EA\beta \Delta H+2{E}^{\mathrm{s}}\left(b+h\right){\beta }^{\mathrm{s}}\Delta H$$
(16)
$${N}^{\mathrm{M}}=\frac{A{B}^{2}}{\eta }+\frac{2{B}^{2}\left(b+h\right)}{{\eta }^{\mathrm{s}}}$$
(17)
$${N}^{\mathrm{s}}=2{\tau }_{0}^{\mathrm{s}}\left(b+h\right)$$
(18)

in which η is the permeability of the magnetic field. Also, α and β are the thermal and moisture expansion coefficients, respectively.

The generalized Hamilton’s principle is utilized according to the following equation to derive the dynamical equation of the system [62, 63]:

$$\updelta {\int }_{{t}_{1}}^{{t}_{2}}\left(K+{W}_{\mathrm{tot}}-{E}_{\mathrm{e}}\right)\mathrm{d}t=0$$
(19)

By utilizing Hamilton’s principle, the equilibrium equation of the system is obtained as follows:

$$\frac{{\partial }^{2}{M}_{\mathrm{local}}}{{\partial }^{2}x}=\rho A\frac{{\partial }^{2}w}{{\partial }^{2}t}-\rho I\frac{{\partial }^{4}w}{{\partial }^{2}x{\partial }^{2}t}+\left(EA\alpha \Delta T+2{E}^{\mathrm{s}}\left(b+h\right){\alpha }^{\mathrm{s}}\Delta T+ EA\beta \Delta H+2{E}^{\mathrm{s}}\left(b+h\right){\beta }^{\mathrm{s}}\Delta H-\frac{A{B}^{2}}{\eta }-\frac{2{B}^{2}\left(b+h\right)}{{\eta }^{\mathrm{s}}}-2{\tau }_{0}^{\mathrm{s}}\left(b+h\right)-F\right)\frac{{\partial }^{2}w}{{\partial }^{2}x}+{k}_{0}\left(1-{\sigma }_{\mathrm{L}}\frac{x}{L}-{\sigma }_{\mathrm{P}}{\left(\frac{x}{L}\right)}^{2}-{\sigma }_{\mathrm{S}}\mathrm{sin}\left(\frac{\uppi x}{2L}\right)\right)w-P{\updelta }_{\mathrm{dir}}\left(x-ut\right)$$
(20)

According to Eringen’s nonlocal elasticity theory [48, 64], the constitutive nonlocal relation for the bending moment in nanostructures is stated as follows:

$$M-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}M}{{\partial x}^{2}}={M}_{\mathrm{local}}$$
(21)

where e0a is the scale factor and reflects the small-scale effects in the system.

By inserting Eq. (21) into the equilibrium equation, the governing equation for the motion of the system is specified as follows:

$${\left(\mathrm{EI}\right)}_{\mathrm{eff}}{w}^{{\prime}{\prime}{\prime}{\prime}}+\left(1-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\right)\left[\rho A\ddot{w}-\rho I{\ddot{w}}^{{\prime}{\prime}}+\left(EA\alpha \Delta T+2{E}^{\mathrm{s}}\left(b+h\right){\alpha }^{\mathrm{s}}\Delta T+ EA\beta \Delta H+2{E}^{\mathrm{s}}\left(b+h\right){\beta }^{\mathrm{s}}\Delta H-\frac{A{B}^{2}}{\eta }-\frac{2{B}^{2}\left(b+h\right)}{{\eta }^{\mathrm{s}}}-2{\tau }_{0}^{\mathrm{s}}\left(b+h\right)-F\right){w}^{{\prime}{\prime}}+{k}_{0}\left(1-{\sigma }_{\mathrm{L}}\frac{x}{L}-{\sigma }_{\mathrm{P}}{\left(\frac{x}{L}\right)}^{2}-{\sigma }_{\mathrm{S}}\mathrm{sin}\left(\frac{\uppi x}{2L}\right)\right)w-P{\updelta }_{\mathrm{dir}}\left(x-ut\right)\right]=0$$
(22)

in which the dot and prime represent temporal and spatial derivatives, respectively. Also, ∇ = ∂/∂x.

To generalize the results of the current study, the following dimensionless parameters are introduced [65]:

$${x}^{*}=\frac{x}{L} ,\quad {w}^{*}=\frac{w}{L} ,\quad {\mathrm{EI}}_{\mathrm{eff}}^{*}=\frac{{\left(\mathrm{EI}\right)}_{\mathrm{eff}}}{\mathrm{EI}} ,\quad {t}^{*}=\frac{t}{{L}^{2}}\sqrt{\frac{\mathrm{EI}}{\rho A}} ,\quad \mu =\frac{{e}_{0}a}{L}$$
$${F}^{*}=\frac{F{L}^{2}}{\mathrm{EI}} ,\quad \lambda =\frac{I}{A{L}^{2}} ,\quad {P}^{*}=\frac{P{L}^{2}}{\mathrm{EI}} ,\quad {u}^{*}=uL\sqrt{\frac{\rho A}{\mathrm{EI}}} ,\quad {k}_{0}^{*}=\frac{{k}_{0}{L}^{4}}{\mathrm{EI}}$$
$${\delta }_{\mathrm{T}}=\frac{A\alpha\Delta T{L}^{2}}{I} ,\quad {\delta }_{\mathrm{H}}=\frac{A\beta {L}^{2}\Delta H}{I} ,\quad {\delta }_{\mathrm{M}}=\frac{A{B}^{2}{L}^{2}}{\eta \mathrm{EI}} ,\quad {\delta }_{\mathrm{s}}=\frac{2{\tau }_{0}^{\mathrm{s}}\left(b+h\right){L}^{2}}{\mathrm{EI}}$$
$${\delta }_{\mathrm{T}}^{\mathrm{s}}=\frac{2{E}^{\mathrm{s}}\left(b+h\right){\alpha }^{\mathrm{s}}\Delta T{L}^{2}}{\mathrm{EI}} ,\quad {\delta }_{\mathrm{H}}^{\mathrm{s}}=\frac{2{E}^{s}\left(b+h\right){\beta }^{\mathrm{s}}\Delta H{L}^{2}}{\mathrm{EI}} ,\quad {\delta }_{\mathrm{M}}^{s}=\frac{2{B}^{2}\left(b+h\right){L}^{2}}{{\eta }^{\mathrm{s}}\mathrm{EI}}$$
(23)

where μ is the nonlocal parameter, and λ is the rotational inertia factor.

By substituting the above-mentioned dimensionless parameters into Eq. (22) and omitting the star superscript, the dimensionless dynamical equation of the system is acquired as follows:

$${\left(\mathrm{EI}\right)}_{\mathrm{eff}}{w}^{{\prime}{\prime}{\prime}{\prime}}+\left(1-{\mu }^{2}{\nabla }^{2}\right)\left[\ddot{w}-\lambda {\ddot{w}}^{{\prime}{\prime}}+\left({\delta }_{\mathrm{T}}+{\delta }_{\mathrm{T}}^{\mathrm{s}}+ {\delta }_{\mathrm{H}}+{\delta }_{\mathrm{H}}^{\mathrm{s}}-{\delta }_{\mathrm{M}}-{\delta }_{\mathrm{M}}^{\mathrm{s}}-{\delta }_{\mathrm{s}}-F\right){w}^{{\prime}{\prime}}+{k}_{0}\left(1-{\sigma }_{\mathrm{L}}x-{\sigma }_{\mathrm{P}}{x}^{2}-{\sigma }_{\mathrm{S}}\mathrm{sin}\left(\frac{\uppi x}{2}\right)\right)w-P{\updelta }_{\mathrm{dir}}\left(x-ut\right)\right]=0$$
(24)

To separate the time and space domains, the Galerkin scheme is applied. According to this discretization method, the transverse displacement of the nanobeam is described as follows [12, 66, 67]:

$$w\left(x,t\right)=\sum_{j=1}^{n}{q}_{j}\left(t\right){\phi }_{j}\left(x\right)$$
(25)

in which ϕ is the vibration shape mode of the nanobeam. Furthermore, n is the number of vibrational modes, and q is the generalized coordinate.

The vibrational mode shape for the simply supported conditions is stated as follows [29, 68]:

$${\phi }_{j}\left(x\right)=\mathrm{sin}(j\uppi x)$$
(26)

The effect of the external moving load is ignored to extract the natural vibrational frequencies of the system. Equation (25) is substituted into the dynamical equation of the system, and the resultant is multiplied by the shape mode function. By integrating over the system length and using the orthogonality property of shape modes, the first-order differential equations of the system in the matrix form are obtained as follows:

$$\mathbf{M}\ddot{\mathbf{q}}\left(t\right)+\mathbf{K}\mathbf{q}\left(t\right)=0$$
(27)

where

$$\mathbf{q}={\left[{q}_{1}\left(t\right),{q}_{2}\left(t\right),\dots ,{q}_{n}\left(t\right)\right]}^{\mathrm{T}}$$
(28)
$${\left(\mathbf{M}\right)}_{sr}={\int }_{0}^{1}{\phi }_{s}\left(x\right)\left({\phi }_{r}\left(x\right)-{\mu }^{2}{\phi }_{r}^{{\prime}{\prime}}\left(x\right)\right)\mathrm{d}x-\lambda {\int }_{0}^{1}{\phi }_{s}\left(x\right)\left({\phi }_{r}^{{\prime}{\prime}}\left(x\right)-{\mu }^{2}{\phi }_{r}^{{\prime}{\prime}{\prime}{\prime}}\left(x\right)\right)\mathrm{d}x$$
(29)
$${\left(\mathbf{K}\right)}_{sr}={\left(\mathrm{EI}\right)}_{\mathrm{eff}}{\int }_{0}^{1}{\phi }_{s}\left(x\right){\phi }_{r}^{{\prime}{\prime}{\prime}{\prime}}\left(x\right)\mathrm{d}x+$$
$$\left({\delta }_{\mathrm{T}}+{\delta }_{\mathrm{T}}^{\mathrm{s}}+ {\delta }_{\mathrm{H}}+{\delta }_{\mathrm{H}}^{s}-{\delta }_{\mathrm{M}}-{\delta }_{\mathrm{T}}^{\mathrm{s}}-{\delta }_{\mathrm{s}}-F\right){\int }_{0}^{1}{\phi }_{s}\left(x\right)\left({\phi }_{r}^{{\prime}{\prime}}\left(x\right)-{\mu }^{2}{\phi }_{r}^{{\prime}{\prime}{\prime}{\prime}}\left(x\right)\right)\mathrm{d}x+$$
$${k}_{0}\left({\int }_{0}^{1}{\phi }_{s}\left(x\right)\left({\phi }_{r}\left(x\right)-{\mu }^{2}{\phi }_{r}^{{\prime}{\prime}}\left(x\right)\right)\mathrm{d}x\right)-{k}_{0}{\sigma }_{\mathrm{L}}\left({\int }_{0}^{1}{\phi }_{s}\left(x\right)\left(x{\phi }_{r}\left(x\right)-{\mu }^{2}\left(x{\phi }_{r}\left(x\right)\right){\prime}{\prime}\right)\mathrm{d}x\right)-{k}_{0}{\sigma }_{\mathrm{P}}\left({\int }_{0}^{1}{x}^{2}{\phi }_{s}\left(x\right)\left({\phi }_{r}\left(x\right)-{\mu }^{2}\left({x}^{2}{\phi }_{r}\left(x\right)\right)\right)\mathrm{d}x\right)-{k}_{0}{\sigma }_{\mathrm{S}}\left({\int }_{0}^{1}{\phi }_{s}\left(x\right)\left(\mathrm{sin}\left(\frac{\uppi x}{2}\right){\phi }_{r}\left(x\right)-{\mu }^{2}\left(\mathrm{sin}\left(\frac{\uppi x}{2}\right){\phi }_{r}\left(x\right)\right){\prime}{\prime}\right)\mathrm{d}x\right)$$
(30)

By solving the eigenvalue problem of Eq. (27), the complex eigenvalues are computed as a function of critical parameters. It should be noted that the imaginary parts of the system eigenvalues are the natural vibrational frequencies of the system (ω) [69,70,71].

The effects of external moving load are considered to obtain the dynamical response of the system. Under these conditions, the dynamical equation of the system for the n-th vibrational mode is rewritten as follows [72,73,74]:

$${\ddot{q}}_{n}\left(t\right)+{\omega }_{n}^{2}q\left(t\right)={P}_{n}\mathrm{sin}(n\uppi ut)$$
(31)

in which \({\omega }_{n}^{2}={\mathbf{K}}_{nn}/{\mathbf{M}}_{nn}\) and \({P}_{n}=\left(P\left(1+{\mu }^{2}{\left(n\uppi \right)}^{2}\right)\right)/{\mathbf{M}}_{nn}\)

It should be noted that to determine the coefficients of the reduced-order system equation, the derivative property of the Dirac delta function according to the following relation is used [24, 75]:

$${\int }_{{x}_{1}}^{{x}_{2}}f\left(x\right){\updelta }_{\mathrm{dir}}^{\left(n\right)}\left(x-\overline{x}\right)\mathrm{d}x=\left\{\begin{array}{cc}-{\left(-1\right)}^{n}{f}^{\left(n\right)}\left(\overline{x}\right)& {x}_{1}<\overline{x}<{x}_{2}\\ 0& \mathrm{otherwise}\end{array}\right.$$
(32)

When the nanobeam is under an external moving load (t < 1/u), the system experiences forced vibration. Also, the system undergoes free vibration when the moving load leaves the nanobeam (t > 1/u). The solution of Eq. (31), including homogeneous and particular solutions, is expressed as follows [11]:

$${q}_{n}^{\mathrm{force}}\left(t\right)=C\mathrm{sin}\left({\omega }_{n}t\right)+D\mathrm{cos}\left({\omega }_{n}t\right)+\frac{{P}_{n}}{{\omega }_{n}^{2}-{\left(n\uppi u\right)}^{2}}\mathrm{sin}\left(n\uppi ut\right)$$
(33)

in which C and D can be obtained from the initial displacement and velocity of the system.

By assuming zero initial conditions for the nanobeam, the dynamical response of the forced vibration of the system is given as follows:

$$\frac{{q}_{n}^{\mathrm{force}}\left(t\right)}{{P}_{n}/{\omega }_{n}^{2}}=\frac{{\omega }_{n}^{2}}{{\omega }_{n}^{2}-{\left(n\pi u\right)}^{2}}\mathrm{sin}\left(n\uppi ut\right)-\frac{n\uppi u{\omega }_{n}}{{\omega }_{n}^{2}-{\left(n\uppi u\right)}^{2}}\mathrm{sin}\left({\omega }_{n}t\right)$$
(34)

To characterize the forced vibrational behavior of systems under moving loads, the dynamical amplification factor (Dd), which is the ratio of the maximum amplitude of the forced vibration of the system to the static displacement, is defined as follows [76]:

$${D}_{\mathrm{d}}=\frac{\mathrm{max}\left({w}^{\mathrm{force}}\right)}{{w}_{\mathrm{st}}}=\frac{\sum_{n=1}^{\infty }{q}_{n}\left(t\right)\mathrm{sin}\left(\frac{n\pi }{2}\right)}{{w}_{\mathrm{st}}}$$
(35)

where wst is the static displacement of the system and can be calculated from the following relation [76]:

$${q}_{n,\mathrm{st}}=\frac{{w}_{\mathrm{st}}}{{n}^{4}}=\frac{{P}_{n}}{{\omega }_{n}^{2}}$$
(36)

When the moving load leaves the nanobeam, the free vibrational response can be determined depending on the final displacement and velocity of the nanobeam in the forced vibrational response. Generally, the free vibrational response of the nanobeam is expressed as follows [11]:

$${q}_{n}^{\mathrm{free}}\left(t\right)={q}_{n0}^{\mathrm{free}}\mathrm{cos}\left({\omega }_{n}t\right)+\frac{{\dot{q}}_{n0}^{\mathrm{free}}}{{\omega }_{n}}\mathrm{sin}\left({\omega }_{n}t\right)$$
(37)

in which \({q}_{n0}^{\mathrm{free}}\) and \({\dot{q}}_{n0}^{\mathrm{free}}\) are the initial displacement and velocity of the free vibration of the system for the n-th vibrational mode, respectively. The initial conditions of the free vibrational response can be obtained from the final conditions of the forced vibrational response of the system as follows:

$${q}_{n0}^{\mathrm{free}}={q}_{n}^{\mathrm{force}}\left(t=\frac{1}{u}\right)=\frac{n\uppi u{P}_{n}}{{\omega }_{n}\left({\left(n\uppi u\right)}^{2}-{\omega }_{n}^{2}\right)}\mathrm{sin}\left(\frac{{\omega }_{n}}{u}\right)$$
(38)
$${\dot{q}}_{n0}^{\mathrm{free}}={\dot{q}}_{n}^{\mathrm{force}}\left(t=\frac{1}{u}\right)=\frac{n\uppi u{P}_{n}}{{\omega }_{n}^{2}-{\left(n\uppi u\right)}^{2}}\left(\mathrm{cos}\left(n\uppi \right)-\mathrm{cos}\left(\frac{{\omega }_{n}}{u}\right)\right)$$
(39)

For convenience, the free vibrational response of the system (Eq. 37) is rewritten in the following simple form using trigonometric relations [76]:

$${q}_{n}^{\mathrm{free}}\left(t\right)={X}_{n}\mathrm{sin}\left({\omega }_{n}t-{\psi }_{n}\right)$$
(40)

where Xn and ψn are the magnitude and phase angle of the free vibration for the n-th vibrational mode of the system, respectively, and are derived from the following equations:

$${X}_{n}=\sqrt{{\left({q}_{n0}^{\mathrm{free}}\right)}^{2}+{\left(\frac{{\dot{q}}_{n0}^{\mathrm{free}}}{{\omega }_{n}}\right)}^{2}}=\frac{n\uppi u{P}_{n}\sqrt{2}}{{\omega }_{n}\left({\omega }_{n}^{2}-{\left(n\uppi u\right)}^{2}\right)}\sqrt{1-\mathrm{cos}\left(n\pi \right)\mathrm{ cos}\left(\frac{{\omega }_{n}}{u}\right)}$$
(41)
$$\mathrm{tan}\left({\psi }_{n}\right)=\frac{{\omega }_{n}{q}_{n0}^{\mathrm{free}}}{{\dot{q}}_{n0}^{\mathrm{free}}}=\frac{\mathrm{sin}\left(\frac{{\omega }_{n}}{u}\right)}{\mathrm{cos}\left(n\pi \right)-\mathrm{cos }\left(\frac{{\omega }_{n}}{u}\right)}$$
(42)

The normalized amplitude of free vibration is defined as follows to understand better the free vibrational behavior of the system [11]:

$${R}_{n}=\frac{{X}_{n}}{{w}_{\mathrm{st}}}=\frac{n\uppi u{\omega }_{n}\sqrt{2}}{{n}^{4}\left({\omega }_{n}^{2}-{\left(n\uppi u\right)}^{2}\right)}\times \sqrt{1-\mathrm{cos}\left(n\uppi \right)\mathrm{cos}\left(\frac{{\omega }_{n}}{u}\right)}$$
(43)

To identify the velocities of the moving load related to the maximum free vibration amplitude of the system, it can be written [11]:

$$\frac{\partial {X}_{n}}{\partial u}=0\Rightarrow \mathrm{tan}\left(\frac{{\omega }_{n}}{2{u}_{\mathrm{max}}^{n}}\right)=\frac{2{u}_{\mathrm{max}}^{n}\left({\omega }_{n}^{2}+{\left(n\uppi {u}_{\mathrm{max}}^{n}\right)}^{2}\right)}{{\omega }_{n}\left({\omega }_{n}^{2}-{\left(n\uppi {u}_{\mathrm{max}}^{n}\right)}^{2}\right)}$$
(44)

After the moving load passes through the nanobeam, the cancellation phenomenon occurs in the system when the amplitude of the free vibration of the system becomes zero. The velocity of the moving load related to the cancellation phenomenon is obtained as follows [11]:

$${X}_{n}=0\Rightarrow \mathrm{cos}\left(\frac{{\omega }_{n}}{{u}_{\mathrm{can}}^{n}}\right)\mathrm{cos}\left(n\pi \right)=1\Rightarrow {u}_{\mathrm{can}}^{n}=\frac{{\omega }_{n}}{{\mathrm{cos}}^{-1}\left(\frac{1}{\mathrm{cos}\left(n\uppi \right)}\right)}$$
(45)

According to Ref. [11], when the initial displacement and velocity of free vibration of the system are zero simultaneously, the system does not vibrate and undergoes the cancellation phenomenon. In this condition, for the initial conditions of free vibration of the system, it can be written as:

$${q}_{n0}^{\mathrm{free}}=0\Rightarrow {u}_{\mathrm{can}}^{n}=\frac{{\omega }_{n}}{j\uppi }$$
(46)
$${\dot{q}}_{n0}^{\mathrm{free}}=0\Rightarrow {u}_{\mathrm{can}}^{n}=\frac{{\omega }_{n}}{2\left(j-1\right)\uppi }$$
(47)

Based on Eqs. (46) and (47), it can be expressed that when the initial velocity of the free vibration is zero, the initial displacement is also zero, but not vice versa. Therefore, it can be inferred that the zero initial velocity of free vibration of the system is a sufficient condition for vibration cancellation in the system.

Results and Discussion

The results of the present investigation are compared and evaluated with those published in scientific reports under various working conditions to validate the proposed model and the solution method. In Fig. 2, the normalized amplitude of the free vibration of a beam in terms of the normalized velocity of the moving load (kn = nπu/ωn) is plotted for the first vibration mode. Moreover, the dynamical amplification factor of the system is displayed in this figure. As can be seen, the obtained results of the present investigation are in an acceptable correlation with those reported in Ref. [77]. As stated in Refs. [3, 13, 77], since the vibrational frequencies of the system are sufficiently separated, the effect of higher vibrational modes in comparison with the fundamental vibrational mode can be neglected.

Fig. 2
figure 2

Comparison of the normalized amplitude of free vibration and the dynamical amplification factor with Ref. [77] without considering foundations, environmental conditions, scale, and surface effects, for λ = μ = F = 0

Full size image

Figures 3 and 4 indicate the vibrational frequencies of the system by considering the axial tensile force and scale effects. According to these two figures, the current study results agree with those published in Ref. [78].

Fig. 3
figure 3

Comparison of natural vibrational frequencies of a nanobeam with Ref. [78] without considering foundations, surface effects, and environmental conditions for F = 5, λ = 0

Full size image
Fig. 4
figure 4

Comparison of natural vibrational frequencies of a nanobeam with Ref. [78] without considering foundations, surface effects, and environmental conditions for μ = 0.6, λ = 0

Full size image

The geometric and physical characteristics of the nanobeam are listed in Table 1 to obtain numerical examples and examine the effect of system parameters on the dynamical behavior of the system. It should be mentioned that the permeability of the magnetic field and the coefficients of thermal and moisture expansion for the bulk and surface layer are considered equal. Also, according to experimental observations, the coefficients of thermal expansion of small-scale systems at low (room) and high temperatures are different.

Table 1 Physical and geometrical properties of the considered system [3, 33, 61, 79]
Full size table

Figure 5 depicts the dynamical amplification factor variation regarding the velocity of the traveling load. The effect of different elastic substrates on the forced vibration of the system is also shown in this figure. According to this figure, as the velocity of the traveling load increases, the dynamical amplification factor ascends irregularly until it reaches its maximum value. The velocity of the traveling load related to the maximum amplitude of the forced vibration system is known as the critical velocity of the traveling load (ucr). The dynamical amplification factor is reduced smoothly by further increasing the velocity of the moving load. As can be seen, when the system is rested on an elastic foundation, the effective stiffness of the system improves, and the curve of the dynamical amplification factor displaces to higher velocities of the traveling load. In other words, the critical velocity of the moving load rises by considering an elastic foundation for the system. According to this figure, compared to the considered non-uniform foundations, the conventional Winkler substrate has a greater effect on the forced vibrational behavior of the system. Also, among the considered variable foundations, parabolic and sinusoidal foundations have the most and least impact on the dynamical amplification factor, respectively.

Fig. 5
figure 5

Dynamical amplification factor of the nanobeam as a function of the velocity of the moving load without considering surface effects and environmental conditions for λ = F = 0, μ = 0.2, k = 1000, σL = σS = σP = 0.9

Full size image

In Fig. 6, for different residual stresses and Young’s moduli of the surface layer, the dynamical amplification factor in terms of the velocity of the moving load is plotted. As is apparent, the increment in Young’s modulus and residual stress of the surface layer leads to a stiffer system, and the system experiences the maximum value of the dynamical amplification factor at higher velocities of the moving load. Consequently, it can be inferred that by considering the surface effects in small-scale systems, the effective stiffness of the system improves, and the critical velocity of the moving load is enhanced.

Fig. 6
figure 6

Effect of Young’s modulus and the residual stress of the surface layer on the dynamical amplification factor without considering foundations and environmental conditions for λ = F = 0, μ = 0.05

Full size image

The critical velocity of the moving load in terms of the nonlocal parameter is shown in Fig. 7 by considering different hygro-magnetic loads. Since the increment of nonlocality in the system leads to a softer system, the critical velocity of the moving load is reduced. It is also observed that as the magnetic field intensity is amplified, the critical velocity of the moving load ascends. This trend can be attributed to the hardening effects of the magnetic field. As indicated in the technical literature, the effective stiffness of the system is improved by the application of a magnetic field. Conversely, by absorbing water molecules in a moist environment, degradation conditions arise in the system. In this condition, the effective stiffness of the system is reduced, and as a result, the critical velocity of the moving load is diminished.

Fig. 7
figure 7

Critical velocity of the moving load as a function of the nonlocal parameter without considering foundations, temperature gradient, and surface effects for λ = F = 0

Full size image

In Fig. 8, the critical velocity of the traveling load in terms of the rotational inertia factor is demonstrated by considering the temperature gradient. According to the figure, the critical velocity of the moving load decreases as the rotational inertia factor increases. This trend can be justified by the fact that the rotational inertia factor has a mass-addition effect on the system. Thus, the vibrational frequencies of the system decrease with increasing the rotational inertia factor, and the system experiences greater deflection at lower velocities of the moving load. Also, the system has dual behavior in thermal environments. So, as the temperature rises at high-temperature conditions, the system undergoes compressive thermal stresses and deformation. Consequently, the effective stiffness and vibrational frequency of the system are diminished, and the critical velocity of the moving load is lessened. Conversely, because the sign of the coefficient of thermal expansion is different at room-temperature conditions, this trend is reversed in the low-temperature field. In this case, as the temperature rises, the critical velocity of the moving load improves.

Fig. 8
figure 8

Critical velocity of the moving load as a function of the rotational inertia factor without considering foundations, hygro-magnetic loads, and surface effects for F = μ = 0

Full size image

Figure 9 illustrates the critical velocity of the moving load in terms of the nanobeam thickness for different axial force values by considering the surface effects. As is clear, the ucr–h curves are overall descending with ascending the nanobeam thickness. This point can clarify this pattern such that as the nanobeam thickness increases, the role of surface energy relative to the bulk energy decreases. It can be observed that for small nanobeam thickness values, the critical velocity of the moving load decreases rapidly with increasing the nanobeam thickness. Conversely, for high nanobeam thickness values, the critical velocity of the moving load does not change significantly with the thickness variation. Furthermore, when the nanoscale beam is subjected to an axial compressive/tensile force, the effective stiffness of the system decreases/increases, and consequently, the critical velocity of the moving load decreases/increases. It should be noted that variations in axial force at high values of the nanobeam thickness are more evident.

Fig. 9
figure 9

Critical velocity of the moving load as a function of the nanobeam thickness without considering foundations and environmental conditions for λ = 0, μ = 0.05

Full size image

In Fig. 10a, b, the magnitude and phase angle of free vibration of the system are depicted in terms of the velocity of the moving load, respectively. According to these figures, the free vibration amplitude increases with a wavy trend as the velocity of the moving load enhances. It can be observed in Fig. 10a that the free vibration amplitude of the system is locally zero at cancellation velocities. Moreover, between two consecutive cancellation velocities, the free vibration amplitude of the system is locally maximized. At these velocities, the system experiences the maximum free vibration phenomenon, and the corresponding velocities are called the velocity of maximum free vibration. According to Fig. 10b, the phase angle of the free vibration of the system fluctuates around the zero value. Also, at cancellation velocities, it undergoes a sudden decrease with increasing the velocity of the moving load.

Fig. 10
figure 10

a Amplitude and b phase angle of free vibration of the embedded system in a parabolic foundation as a function of the velocity of the moving load without considering surface effects and environmental conditions for λ = μ = F = 0, k0 = 1000, σP = 0.5

Full size image

Initial conditions for free vibration of the system in terms of the velocity of the moving load are demonstrated in Fig. 11. It is observed that with the velocity variation of the moving load, the initial conditions of the free vibration behave similarly to the free vibration amplitude variations. So, with increasing the velocity of the moving load, the magnitudes of initial displacement and velocity of free vibration increase non-monotonously. By comparing Figs. 10 and 11, it can be deduced that the cancellation phenomenon occurs in the system when both the initial displacement and velocity of free vibration become zero. According to Fig. 11, one can infer that when the initial displacement of free vibration becomes zero, the initial velocity of free vibration also becomes zero.

Fig. 11
figure 11

Initial conditions of free vibration of the embedded system in a parabolic foundation as a function of the velocity of the moving load without considering surface effects and environmental conditions for λ = μ = F = 0, k0 = 1000, σP = 0.5

Full size image

Figure 12 indicates the effects of different foundations on the free vibration amplitude of the system. The embedded system has a higher effective stiffness than the case without a foundation. As a result, the nanobeam experiences cancellation and maximum free vibration phenomena at higher velocities of the moving load. In simple words, by considering a foundation for the system, the curve of the free vibration amplitude shifts to higher velocities of the moving load. Compared to the considered variable foundations, the uniform Winkler foundation has a greater effect on the free vibration amplitude of the system. Also, among the considered non-uniform foundations, sinusoidal and parabolic variations are the least and most effective foundations for the free vibration of the system, respectively.

Fig. 12
figure 12

Effect of different foundations on the free vibration amplitude of the system without considering surface effects and environmental conditions for λ = F = 0, μ = 0.1, k0 = 2000, σL = σS = σP = 0.9

Full size image

The first two cancellation velocities of the moving load in terms of the foundation modulus are displayed in Fig. 13. As expected, increasing the foundation modulus leads to a stiffer system, consequently enhancing the cancellation velocities. Also, cancellation velocities for the embedded system in non-uniform foundations have lower values than those for the system rested on a uniform Winkler foundation. In addition, among the considered variable foundations, the parabolic, linear, and sinusoidal foundations have higher cancellation velocities, respectively. It should be noted that by considering foundation effects, the second cancellation velocity has more significant changes.

Fig. 13
figure 13

Cancellation velocities of the moving load as a function of the foundation modulus without considering surface effects and environmental conditions for λ = F = 0, μ = 0.1, σL = σS = σP = 0.9

Full size image

Figure 14 demonstrates the first cancellation velocity in terms of the length-to-thickness ratio of the nanobeam for different rotational inertia factors by considering the surface effects. As can be seen, as the length-to-thickness ratio of the system increases, the cancellation velocity of the moving load also increases. Furthermore, due to the mass-addition effects of the rotational inertia factor, the cancellation velocity of the moving load decreases with increasing λ.

Fig. 14
figure 14

First cancellation velocity of the moving load as a function of the length-to-thickness ratio without considering foundations and environmental conditions for F = 0, μ = 0.05

Full size image

In Fig. 15, the first velocity of maximum free vibration in terms of the axial tensile force is drawn for different hygro-magnetic loads. According to this figure, when the axial tensile force is enhanced, the effective stiffness of the system improves. In such a condition, the nanobeam undergoes the maximum free vibration amplitude at higher velocities of the moving load. Moreover, due to the hardening effects of magnetic fields, the system experiences a higher velocity of maximum free vibration in the presence of a magnetic field. Conversely, in a moist field, the softening behavior of the system increases, and as a result, the velocity of maximum free vibration declines.

Fig. 15
figure 15

First velocity of maximum free vibration as a function of the axial tensile force without considering foundations, surface effects, and temperature gradient for λ = μ = 0

Full size image

The first velocity of maximum free vibration in terms of the nonlocal parameter in thermal environments is shown in Fig. 16. It can be observed that increasing the nonlocal parameter leads to the softening behavior of the system. As a result, the system experiences the maximum free vibration phenomenon at a lower velocity of the moving load by increasing nonlocal effects. Also, based on this figure, temperature variation in low- and high-temperature conditions have opposite impacts on the vibrational behavior of the system. So, in the room-temperature environment, the velocity of maximum free vibration improves by increasing the temperature. This trend is reversed in high-temperature conditions.

Fig. 16
figure 16

First velocity of maximum free vibration as a function of the nonlocal parameter without considering foundations, surface effects, and hygro-magnetic loads for λ = F = 0

Full size image

Finally, to better comprehend the vibrational behavior of the system under a traveling load, the time response of the system is investigated. In Fig. 17, the dynamical response of the nanobeam is plotted for u = 0.2. According to this figure, after passing the moving load, the system experiences free vibration with an amplitude of 0.17 without considering environmental conditions and surface effects. When the nanoscale beam is in a hygro-thermal environment, the forced vibration amplitude enhances, and the system undergoes the maximum free vibration phenomenon. Also, when surface effects are considered for the system, the forced vibration amplitude of the nanobeam is reduced, and the cancellation phenomenon occurs. In this case, the system no longer vibrates after the moving load passes over the nanobeam.

Fig. 17
figure 17

Time response of the system without considering foundations for λ = F = B = 0, μ = 0.1, u = 0.2

Full size image

Conclusion

In this work, the vibration of nanoscale beams embedded in variable elastic foundations under a transverse moving load and an axial tensile force is modeled based on the nonlocal Rayleigh beam theory by considering surface effects and environmental loadings. The dynamical equation of the system is derived and solved analytically. For validation purposes, comparison studies with published data are performed. The effects of various key parameters on the free and forced vibration mechanisms are examined. The key findings of the current research can be summarized below:

  • The critical velocity of the moving load reduces with increasing the rotational inertia factor and the axial compressive force.

  • By considering the foundation and surface effects, the maximum amplitude of the forced vibration of the nanobeam occurs at higher velocities of the moving load.

  • Cancellation velocities of the moving load increase/decrease in a magnetic field/moist environment.

  • The velocity of the traveling load related to the maximum free vibration decreases with increasing the nonlocal parameter and the temperature in a high-temperature environment.

  • Among the variable elastic foundations, the parabolic/sinusoidal medium has the most/least incremental effect on the cancellation and critical velocities of the moving load.

  • With the increase of foundation modulus, cancellation velocities of the moving load improve.

  • Contrary to the effects of the length-to-thickness ratio, the critical velocity of the moving load decreases by ascending the nanobeam thickness.

  • By fine-adjusting the environmental conditions and surface energy, unwanted vibration of the nanobeam can be eliminated.