1 Introduction

Due to high strength and stiffness of stiffened shells, these structures have widely utilized in aerospace components [1,2,3,4]. The major failure mode of stiffened shells is buckling capacity under axial compression loads [5,6,7]. Recently, increasing attentions on the hierarchical stiffened shell (HSS) are being paid due to its outstanding mechanical properties. In general, for robust design, the HSS is involved the multi-source dimensional uncertainties including skin, major and minor stiffeners. Wang et al. [8] first found that HSS has advantages for improving the load capacity and decreasing imperfection sensitivity. Wang et al. [9] extended HSS composed by orthogrid major and triangle minor stiffeners to improve the ability for buckling and imperfections. Advanced fabrication and failure testing investigations were carried out for the isogrid HSS and the orthogrid HSS by Li et al. [10] and Wu et al. [11]. For capturing the accurate post-buckling path, collapse point of HSS, the explicit dynamic FE framework can be used for the nonlinear buckling behavior as good choice due to robust analysis process with high-agreement by experimental results [12, 13]. The asymptotic homogenization method (AHM) was proposed efficient post-buckling analysis of HSSs, whose the analysis time is reduced in explicit dynamic analysis [9]. Tian et al. [14] established numerical-based smeared stiffener method (NSSM) based on AHM and Rayleigh–Ritz method, which achieves higher prediction accuracy for linear buckling load of HSSs than traditional smeared stiffener method (SSM). An adaptive strategy using NSSM was developed by Wang et al. [15] for HSSs to obtain the critical buckling mode. Tian et al. [16] proposed a fast analytical method for buckling load of shell structures using orthogonal decomposition basis eigenvalue buckling method. In the analytical approaches, the accurate result for buckling loads with fast computational time is the main changes in the robust design of HSS. Therefore, the hybrid design optimization can be used to enhance the computational burden using modelling approaches in optimization buckling capacity of HSS.

To robust design, the optimizations of HSSs are carried out for best conditions of dimensional sizes. The radial basis function (RBF) model was employed for optimizations of HSSs [15, 17, 18]. By decomposing a major (minor)-level as sub-optimization, Wang et al. [15] established a multilevel optimization method to search the global optimal solution. Tian et al. [14] proposed a competitive sampling basis surrogate model for optimizations of HSSs. the dative response surface method combined by harmony search was implemented to search the optimum conditions of stiffened panels [16]. By combining the Latinized partially stratified sampling and multi-fidelity methods, Tian et al. [19] developed enhanced variance reduction method for surrogate-based optimizations of HSSs. Recently, the variable-fidelity surrogate modelling approach for optimization HSSs was employed to improve accuracy of prediction-based surrogate model [20]. To provide the optimal results of stiffened panels, Keshtegar et al. [21] extended the adaptive harmony search combined by Kriging. Generally, the surrogate model can be combined with the optimization algorithms [22,23,24,25,26], for structural reliability analysis [27,28,29,30,31,32,33] and reliability-based design optimization [34,35,36]. The main effort of applied surrogate models is to provide the accurate results. However, the accurate results with efficient computation for analysis of the complex structures as HSS are the main challenge in the robust optimal design of thin-welded structures. The computation burden of HSS can be improved based on the hybrid intelligent optimization method as modelling techniques coupled by meta-heuristics optimization algorithms. However, the accurate optimal predictions using hybrid intelligent optimization method is main challenge for approximating buckling load and mass using Kriging model to provide the reliable optimal design condition for HSS.

A novel iterative active framework procedure is proposed as hybrid intelligent optimization to extract the accurate optimal results by Kriging model. The active data and adaptive data points are used to train the Kriging models. Using optimal results of GWO, the active data are given from initial sampled data points, while the adaptive data points are randomly simulated by dynamical radial samples. The accuracy of the active Kriging is compared with several models of SVR, Kriging and RSM. The results indicated that the proposed active procedure is strongly improved the accuracy predictions of optimal results, while the safe condition is provided for optimum load capacity of HSS.

2 Analytical buckling method

2.1 Studied example of HSS

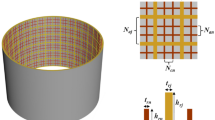
The configuration of studied HSS is displayed in Fig. 1 where diameter D = 3000 mm, and length L = 2000 mm with Young’s modulus (E) of 100,000 MPa and Poisson’s ratio (υ) of 0.3. The HSS has nine design variables involved with continues variables (i.e., ts = skin thickness, hrj = height of major stiffener, hrn = height of minor stiffener, trj = thickness of major stiffener and trn = thickness of minor stiffener) and discrete variables (i.e., Naj = number of major stiffeners at axial, Nan = number of axial minor stiffeners between axial major stiffeners, Ncn = number of circumferential minor stiffeners between circumferential major stiffeners, Ncj = number of circumferential major stiffeners). The boundary condition is clamped at lower end and fixed at upper end. On upper end of HSS, a uniform axial load is utilized.

Fig. 1
figure 1

Schematic diagram of hierarchical stiffened shell

Full size image

2.2 Analysis approach of HSS

In this paper, the explicit dynamic method is used as the analytical approach of HSS, which can capture the ultimate load-carrying capacity of HSS and yields a good agreement with the experiment [13]. The formulation of the explicit dynamic method is as follows:

$${\mathbf{Ma}}_{t} = {\mathbf{F}}_{t}^{{{\text{ext}}}} - {\mathbf{F}}_{t}^{{{\text{int}}}} - {\mathbf{CV}}_{t} - {\mathbf{KU}}_{t} ,$$
(1)

in which M stands mass matrix, a stands for the vector of nodal acceleration, stands for the vector of, \({\mathbf{F}}_{t}^{{{\text{ext}}}}\) and \({\mathbf{F}}_{t}^{{{\text{int}}}}\) denote applied external and internal force vector, respectively. C is damping matrix with nodal velocity vector V. K is stiffness matrix, U is nodal displacement vector, and t denotes time. Here, the central difference approach is employed to compute the explicit time integration for velocity and acceleration.

2.3 Initial database of HSS

The data points of load-carrying capacity and mass of HSS are computed based on FE method. This initial data is used for training process of the models as Kriging, SVR and RSM which are given using 400 data points. The input data for nine design variables of HSS is simulated using Latin hypercube sampling (LHS) to give the response of structures under buckling force. The input train data set and relative responses i.e., load capacity and mass of HSS which are computed by jointing nine design variables as input to a computer program. The statistical properties including maximum (Xmax), minimum (Xmin), average (Xmean), standard deviations (STD) and coefficient of variations (COV) of 400-total data for training models data are presented in Table 1. The COVs of the input variables are varied in the range from 0.2 to 0.4. As it can be seen, the load varies from 10,000 ot 35,000 kN with the mean of 18,427 kN, while mass for 200–610 kg with the mean of 351 kg. The bar diagram of the initial data points of load and mass computed by FE model is presented in Fig. 2.

Table 1 Statistical properties using 400 initial data points of design variables and FE results for load and mass
Full size table
Fig. 2
figure 2

Bar diagram of evaluated FE for load capacity and mass of HSS

Full size image

3 Optimization process

In hybrid intelligent model to find design point, optimization loop is one of major importance steps. In optimization framework, the buckling load (Pcr) as objective function should be maximized under the mass constraint (W) as subjective function for studied HSS. The optimization model for HSS problem is described by the following optimization model:

$$\begin{gathered} \max \,\,\,\,\,P_{cr} \hfill \\ {\text{s.t.}}\,W \le 369, \hfill \\ \end{gathered}$$
(2)

where \(P_{cr}\) and \(W\) are the two approximated functions that the Kriging model used to approximate these functions based on the initial data points-based active data set and the adaptive data set in the optimization process. The input data of this problem is used to calibrate the Kriging models based on nine design variables as Ncj, Naj, Ncn, Nan, ts, hrn, hrj, trj, and trn, in which four design variables, i.e., Naj, Ncj, Nan, and Ncn are the integer variables, while other are continues variables. The lower and upper bond of variables is, respectively, selected based on the Xmin and Xmax, as presented in Table 1. The allowable mass in this problem is given 369 kg that it used in subjective function. Using the optimization model of HSS, the penalty strategy can be used to define the unconstraint optimization model as below:

$$\max \,\,\,\,\,P_{cr} \,\, + \lambda \,\max \,(W - 369,\,\,0),$$
(3)

where \(\lambda\) is the penalty factor as \(\lambda = 10^{4}\) and \(\max \,(W - 369,\,0)\) represent the penalty function that it set to zero in the feasible domain on mass. The various optimization methods can be utilized to search optimal design of this problem [16, 22, 23, 35, 37,38,39,40]. The Grey wolf optimizer (GWO) is an swarm-inspired optimization method extracted from grey wolves in social hierarchy and hunting their behavior [41]. The GWO has advantages including solve-free mechanism, free parameters to control its convergence performance, simplicity to apply an optimization problem, and reducing the local optimum in optimization process. The presented results by [41] showed that GWO provided the highly performance to search the optimal results compared to well-known heuristics optimization algorithms. Consequently, the GWO can be used to find the optimal conditions of the complex engineering problem due to application of a random search in the optimizer processes. Recently, the GWO was implemented for optimization of different engineering problems [42, 43]. In the GWO, the random search process is obtained based on four categories of Wolf as delta (\(\delta\)), beta (β), and alpha (\(\alpha\)), while other wolves named as omega (ω). The delta (\(\delta\)), beta (β), and alpha (\(\alpha\)) are three best solutions which are used to adjust the new position of the ω wolves. Alpha (\(\alpha\)) Wolf has the responsibly of the optimal results among other wolves and the best solution is given based on alpha (\(\alpha\)) Wolf, while beta (β) provides the hunting (best solution) and to give decision-making for increasing the activities of alpha (\(\alpha\)) Wolf and reinforcing the decision of α to find best solution. Delta (\(\delta\)) has the three-rank in the wolves and they provide other design domain and try for producing the best position to find the best solution for \(\alpha\) and β wolves. The omega (\(\omega\)) have the lowest ranking wolves that they control the boundaries and territory of design domain and they guarantee to safe search for find the best solution in the optimization process. The positions of \(\delta\), β, and \(\alpha\) wolves are adjusted by the following random process using the below formulation:

$${\varvec{X}}(t + 1\user2{)} = {\varvec{X}}_{{\varvec{p}}} (t\user2{) - A|C}\user2{.X}_{{\varvec{p}}} (t\user2{) - X}(t\user2{)|,}$$
(4)

where the position vector of wolves \({\varvec{X}}\) is updated based on random parameter C and A at new position of t + 1. \({\varvec{X}}_{{\varvec{p}}}\) represents the wolves position of \(\alpha\), β, and δ. The type of alpha provides the best optimal results among other wolf’s positions. Based on the adjusting positions of the wolves, the iterative procedure to search the optimal results of HSS is given as follows:

Step 1: Define optimum model as \(f({\varvec{X}}) = \,\,P_{cr} \,\, + \lambda \,\max \,(W - 369,0)\).

Step 2: Set the upper bound (XU), lower bound (XL) of design variables, numbers of wolves (NW = 10), and maximum iterations (NI = 1000).

Step 3: Uniformly initialize variables as

$${\varvec{X}} = {\varvec{X}}_{{}}^{L} + {\text{rand}}()({\varvec{X}}_{{}}^{U} - {\varvec{X}}_{{}}^{L} ),$$
(5)

where \({\text{rand}}()\) is a random \({\text{rand}}()\) ∈ [0, 1] and X ∈ [ Naj, Nan, Ncn, Ncj, ts, hrn, hrj, trj, trn].

Step4: Check the boundaries of the each position for wolves as XL ≤ X ≤ XU.

Step 5: Compute f(Xi), i = 1, 2, …, NW for each agent.

Step 6: Determine \({\varvec{X}}_{\alpha } ,\,{\varvec{X}}_{\beta }\) and \({\varvec{X}}_{\delta }\) based on results obtained from step 5.

Step 7: Generate A and C as follows:

$$\begin{gathered} {\varvec{A}} = 2{\text{rand}}() \times \chi (t) - \chi (t) \hfill \\ {\varvec{C}} = 2{\text{rand}}(), \hfill \\ \end{gathered}$$
(6)

where rand() \(\in \left[0,1\right]\)and \(\chi (t)=2-2t\)/NI. A ∈ [− 2, 2] that it is given at a small value at the final iterations, i.e., A ~ 0 due to \(\chi (t)\) ~ 0.

Step 8: determine position of each agent as below:

$$\begin{gathered} {\varvec{X}}_{1} = {\varvec{X}}_{\alpha } \user2{ - A}_{1} \user2{|C}_{1} \user2{.X}_{\alpha } \user2{ - X|} \hfill \\ {\varvec{X}}_{2} = {\varvec{X}}_{\beta } \user2{ - A}_{2} \user2{|C}_{2} \user2{.X}_{\beta } \user2{ - X|,} \hfill \\ {\varvec{X}}_{3} = {\varvec{X}}_{\delta } \user2{ - A}_{3} \user2{|C}_{3} \user2{.X}_{\delta } \user2{ - X|} \hfill \\ \end{gathered}$$
(7)

where \({\varvec{X}}_{\alpha }\), \({\varvec{X}}_{\beta }\) and \({\varvec{X}}_{\delta }\), respectively, represent the position of alpha, beta and \({X}_{\delta }\) delta wolves.

Step 9: Update the position of \({\varvec{X}}\) \(X\) in the current solution as below:

$${\varvec{X}}(t + 1\user2{)} = \frac{{{\varvec{X}}_{1} + {\varvec{X}}_{2} + {\varvec{X}}_{3} }}{3}.$$
(8)

Step 10: Control convergence as t > NI.

In the optimization process, the optimization function is approximated using the Kinging model. Consequently, the accurate optimal condition is directly sensitive to predictions of Kriging model to evaluate the load and mass functions. In this current work, we enhanced the predictions of Kriging–based surrogate model using an active learning procedure.

4 Active learning Kriging

The Kriging model-based data-driven is enhanced for accurate prediction of the load-capacity and mass of HSS in the optimization process. The Kriging model is trained using two active data points. In the first selected data, the initial input data points are refined by selecting the active points. In the second stage, several adaptive points are simulated in active region of optimum condition.

4.1 Kriging model

The Kriging-based surrogate model was introduced for geostatistical problems by Krige and Danie in 1952 [44] Commonly, the Kriging model-based data-driven can be implemented for approximation of the nonlinear relations in engineering problems as hydrology [45] energy of solar [16], structural design optimization [46, 47], reliability analysis [34, 48,49,50,51], reliability-based design optimization [52, 53], and etc. The Kriging model is presented as follows:

$$P(X) = g(X)^{{\text{T}}} \beta + r(X)^{{\text{T}}} \gamma .$$
(9)

In Kriging model, the first term, i.e., \(g(X)^{{\text{T}}} \beta\) represents mathematical formulation, while the second term, i.e., \(r(X)^{{\text{T}}} \gamma\) represents the stochastic relation. g(X) and β, respectively, denote the basic function and unknown coefficient vectors. The stochastic term is given by Gaussian function with mean of zero and covariance vector as follows:

$${\text{cov}} () = \sigma^{2} R(\theta ,X_{p} ,X_{q} ),$$
(10)

where \(\sigma^{2}\) represents the variance, \(R(\theta ,X_{p} ,X_{q} )\) denotes the correlation function between input data points Xp and Xq (p, q = 1, 2, …, m, where m is number of train data). θ in \(R(\theta ,X_{p} ,X_{q} )\) denotes the correlation parameter. Generally, the correlation parameter θ is computed using the following maximizing function [29, 54]:

$$L(\theta ) = - m({\text{Ln}}(\sigma^{2} ) + {\text{Ln}}(\left| R \right|),$$
(11)

where Ln denotes the logarithmic operator. By determining θ, we can be given the β as below:

$$\beta = (g^{{\text{T}}} R^{ - 1} g)^{ - 1} g^{{\text{T}}} R^{ - 1} O,$$
(12)

and based on θ and β, we have

$$\gamma = R^{ - 1} (O - g^{{\text{T}}} \beta ),$$
(13)

where O is observed data in train phase, R is the correlation matrix and is determined as follows [27, 28]:

$$R = \left[ {\begin{array}{*{20}c} 1 & {} & {r(\mathop X\nolimits_{1} ,\mathop X\nolimits_{2} )} & \ldots \\ {r(\mathop X\nolimits_{2} ,\mathop X\nolimits_{1} )} & {} & 1 & {} \\ {} & \vdots & {} & \ddots \\ {r(\mathop X\nolimits_{m} ,\mathop X\nolimits_{1} )} & {} & {r(\mathop X\nolimits_{m} ,\mathop X\nolimits_{1} )} & \cdots \\ \end{array} \begin{array}{*{20}c} {r(\mathop X\nolimits_{1} ,\mathop X\nolimits_{m} )} \\ {r(\mathop X\nolimits_{2} ,\mathop X\nolimits_{m} )} \\ \vdots \\ 1 \\ \end{array} } \right],$$
(14)

in which r(Xp, Xq) is the covariance basis function which is computed using kernel basis Gaussian function as follows [31]:

$$r\left( {\mathop X\nolimits_{p} ,\mathop X\nolimits_{q} } \right) = \exp \left[ { - \sum\limits_{i = 1}^{k} {\theta^{i} (X_{p}^{i} - X_{q}^{i} )^{2} } } \right],$$
(15)

where \(\theta^{i}\), i = 1, 2, …, k represents the i-th correlation parameter for k input data. In Kriging model using the kernel function, \(r(X) = [R(\theta ,X_{1} ,X),\,R(\theta ,X_{2} ,X), \ldots ,R(\theta ,X_{n} ,X)]^{{\text{T}}}\). It can be conducted that the Kriging model is predicted data using covariance term which is provide using correlation matrix \(R\) by Gaussian kernel function. Consequently, the flexibility of the Kriging model for prediction the nonlinear relation may be increased compared to the polynomial regression. The Kriging is combined with global optimization method by satisfying feasible point based on sampling set for Kriging model [23, 55]. Recently, the Kriging model was applied to optimal design condition [28]. The design domain in the optimization process is approximated based on Kriging instead of space reduction methods by expensive point strategy [38].

4.2 Active learning procedure

There is tried to increase the effect of active region of optimal design space in calibrating process of Kriging model. Therefore, an iterative regression process using Kriging approach is introduced based on two major active samples. The first samples are given from initial data presented in Sect. 2.3 for HSS, while second active points are simulated using radial random samples, which are added into the input data set. Using the optimal design point (X*) given from optimization process, it is used to adjust the active and adaptive points. These data points are provided in modelling procedure as below.

4.2.1 First active data points

Using x* obtained by GWO, the active points are selected from initial data points using scalar criterion which is computed as below:

$${\text{SC}}_{i} = \left\| {Z_{i} - Z^{*} \,} \right\|\,\quad i = 1,2, \ldots ,{\text{NS,}}$$
(16)

where NV denotes the number of design variables. \(Z^{*}\) and \(Z_{i}\) are, respectively, the normalized design variables at optimum points (x*) and initial samples (x) computed as below:

$$Z_{i} = 2\frac{{x_{i} - X_{i}^{\min } }}{{X_{i}^{\max } - X_{i}^{\min } }} - 1\,\,\,\,\,\,\, - 1 \le Z_{i} \le 1\quad i = 1,2, \ldots ,{\text{NV,}}$$
(17)

in which \(X_{i}^{\max }\) \(X_{i}^{\min }\) are, respectively, the upper and lower bounds of \(i^{{{\text{th}}}}\) design variable which is given based on Table 1. The active points are selected in modelling process of Kriging when \({\text{SC}}_{i} \le \varepsilon_{a}\) where, \(\varepsilon_{a}\) is a factor.

4.2.2 Adaptive data points

In the proposed active model, several additive points are randomly simulated to increase the data set at the optimal region. Using optimal design point (\(Z^{*}\)), the normalized adaptive random points are generated as follows:

$$Z_{Ai} = R \times {\text{rand}}() \times \exp ( - k)\frac{{{\text{RD}}_{i} }}{{||{\text{RD}}_{i} ||}} + Z^{*} \quad i = 1,2, \ldots ,{\text{NA,}}$$
(18)

where \(R\) is the control factor, i.e., \(0.1 \le R \le 1\), k is iteration number to provide the additive points. rand() ∈ [0, 1]. \({\text{RD}}_{i}\) is the random input point. The adaptive points are generated using random radius of \(R \times {\text{rand}}() \times \exp ( - k)\frac{{{\text{RD}}_{i} }}{{||{\text{RD}}_{i} ||}}\). By increasing the iteration number to build the Kriging model in the optimization process, the random radius is decreased to provide. This means that, the additive data samples are located on the optimal design domain. Consequently, the predictions of Kinging model may be improved to evaluate the accurate results of optimal conditions for HSS. In this current work, we used \(R = 0.5\).

4.3 Framework of AK-GWO

Using additive and active points, the surrogate model is regressed then; calibrated model is implemented for approximating the optimum model of HSS in GWO framework presented in Fig. 3. In the first iteration, The Kriging model is trained using initial data. However, the Kriging model is adapted by the active process. The input dataset applied to train Kriging model are presented as below steps:

Step 1: Give the optimum point (x*), number of adaptive points (NA), R and the iterations for training the Kriging model (k).

Step 2: Normalize input data (\(Z_{i}\)).

Step 3: Select the active data as \(Z_{ai} \in \{ Z_{i} |{\text{SC}}_{i} \le \varepsilon_{a} \,\,\,i = 1,2, \ldots ,{\text{NS}}\}\).

Step 4: Generate RD = rand(NA, NV).

Step 5: Create the adaptive points using Eq. (18)

Step 6: Transfer active and adaptive data into original space as below:

$$x_{i} = \frac{{Z_{i} + 1}}{2}(X_{i}^{\max } - X_{i}^{\min } ) + X_{i}^{\min } \,.$$
(19)

Step 7: Compute the buckling loads and mass of HSS for adaptive points.

Fig. 3
figure 3

Framework of proposed intelligent optimization method for HSS

Full size image

The optimization result is affected on the active and adaptive points due to applying the optimal point. The framework of hybrid intelligent optimization method is proposed in the Fig. 3. The final optimal result is given as solution when the new optimum design point is followed on the previous optimum point. In this framework, the GWO is used to search the optimal conditions, while Kriging model is actively learned using adaptive and active points. The adaptive data is jointed to the FE model to give the buckling load and mass. The proposed hybrid modelling and nature-inspired optimization method involves two major loops as optimization operated by GWO and modelling loop operated using Kriging model trained by the active data sets.

5 Results and discussion

The abilities of proposed method for accurate optimum results are compared with Kriging without active learning process, response surface method and support vector regression. The parameter of the SVR are given as C = 9000, σ = 16.5 and ε = 0.25 in training phase buckling load and C = 5000, σ = 15 and ε = 0.15 in training process of mass. The factors to active learning Kriging model are set as \(\varepsilon_{a}\) = R = 0.5 and ||Z*(k) − Z*(k − 1)||< 10–2 is used for stopping criterion of the proposed hybrid intelligent model.

The results of the hybrid intelligent model as active Kriging combined by GWO are presented in Table 2. However, the relative buckling modes corresponding to each iterations 1–6 of active learning Kriging for studied HSS are presented in Fig. 4. By comparing results in Table 2 and Fig. 4, it can be conducted that the different predictions for loads are obtained in the first and second iterations. This means that the active data to increase the optimal domain in the optimization process may be improve the prediction of the buckling load. On the other hand at the final iterations, the buckling load predictions are followed to the same results as 23,330 kN.

Table 2 Iterative results of the proposed hybrid intelligent method for HSS structure
Full size table
Fig. 4
figure 4

Buckling mode at the optimum design point for different iterations of hybrid intelligent method for HSS

Full size image

Buckling modes for different iterations at optimum point of hybrid intelligent method for HSS are plotted in Fig. 4. It can be observed that, these buckling modes are all global buckling modes, which are considered as buckling modes with high load-carrying capacity for HSS [14].

The iterative procedure-based Step 1 to Step 6 of the active data points from initial simulation and adaptive data points from radial sampling for studied method are showed in Fig. 5 based on two principal dimensions which is computed based on principal component analysis (PCA) [56]. Note from Fig. 5 that the adaptive points are increased the chance to simulate the optimal design domain, while the active point is selected form initial database. By comparing the results, it can be conducted that the active data and adaptive data points of Step 5 are similar to Step 6.

Fig. 5
figure 5

Two-dimensional reduction of simulating input data using PCA for HSS

Full size image

Figure 6 illustrates the obtained results from the intelligent approach using AK and the FE model at the optimal design points for load and mass of HSS. It can be conducted that the accuracy prediction of Kriging for mass is more than the buckling load, while the approximated buckling loads by active learning Kriging model are followed to the FE results as well as the mass at the final iteration. This means that the proposed stagey can be provided the accurate results compared the Kriging combined by GWO.

Fig. 6
figure 6

Comparative results of load and mass using active learning Kriging and FE models

Full size image

The optimal design for different models as Kriging, AK-Kriging, SVR and RSM are presented in Table 3. As seen from the results of Table 3, the AK- Kriging is improved the accuracy of the Kriging model for load about 10% from 25,188.54 to 23,329.24 kN and for mass about 0.6% from 366.60 to 368.94 kg. By comparing the FE results for all models, the Kriging and AK-Kriging are satisfied the mass constraint of the optimum model for HSS as \(W \le 369\). Whereas, SVR and RSM models are provided optimal mass more than the 369 kg. Therefore, it can be conducted the RSM and SVR show the less relative error for prediction load capacity than the Kriging but the mass is not satisfied the optimum condition using the evaluating optimization model. However, AK-Kriging model is significantly improved the accuracy of predictions for load and mass compared to the RSM and SVR. The Kriging model is provided more accurate result for mass than RSM, while the stochastic term in Kriging model is not improved the accuracy of predicted load compared to the RSM.

Table 3 Comparative optimal results for different models in studied HSS
Full size table

Buckling modes at optimum design point for Kriging, AK-Kriging, SVR and RSM models for HSS are compared and displayed in Fig. 7. Similarly, it can be found that, these buckling modes are all global buckling modes

Fig. 7
figure 7

Comparing the buckling mode at optimum design point for different models for HSS

Full size image

6 Conclusions

In optimization complex engineering problems, the finding optimal design is time consuming process due to applying the finite element analyzer. The accurate optimum result for real engineering problems is vital issue to safe and reliable design conditions. A hybrid statistical and nature-inspired optimization method using active learning-based Kriging method combined by Grey Wolf optimizer (GWO) named AK-GWO is proposed to enhance the accuracy of optimal design condition for the hierarchical stiffened shells (HSS). To enhance the accuracy and efficiency of optimization for HSS for both load capacity as objective and mass as constraint, the active process can be implemented using Kriging model. An active learning process applied in Kriging is proposed using active and adaptive points. Using optimum determined by GWO, the active points are determined from initial simulated data, while the adaptive points are computed using convex procedure for training Kriging model. The accuracy of proposed AK-GWO are compared with several modelling methods as Kriging, support vector regression (SVR) and response surface method (RSM) which, are combined by GWO. The optimization results for maximum load-carrying capacity of HSS indicated that AK-GWO preformed superior accuracy compared to other models. The accuracy of optimum results using AK-GWO is improved about 10%, 6% and 7% for load and about 1%, 4% and 3% for mass compared to Kriging, SVR, and RSM, respectively. The mass constraint based results obtained by RSM and SVR are not satisfied, while the hybrid AK-GWO method is provided the accurate results with safe condition for HSS. The proposed optimization framework can be tested for searching the optimal condition of complex engineering problem, in future.