Inference for continuous-time long memory randomly sampled processes

Abstract

From a continuous-time long memory stochastic process, a discrete-time randomly sampled one is drawn using a renewal sampling process. We establish the existence of the spectral density of the sampled process, and we give its expression in terms of that of the initial process. We also investigate different aspects of the statistical inference on the sampled process. In particular, we obtain asymptotic results for the periodogram, the local Whittle estimator of the memory parameter and the long run variance of partial sums. We mainly focus on Gaussian continuous-time process. The challenge being that the randomly sampled process will no longer be jointly Gaussian.

1 Introduction

Irregularly observed time series occur in many fields such as astronomy, finance, environmental, and biomedical sciences. Discretization of a continuous time process can produce unevenly time series. For example, physiological signals such as electromyography (EMG), electrocardiogram (ECG), heartbeats [see e.g. Bardet and Bertrand (2010)], as well as market prices [see e.g. Dacorogna (2001)] are measured at non regularly spaced times. In these instances and many more, we do not control the way data are observed, as they are recorded at irregular time points. A common approach consists in fitting a continuous time process to discrete-time data [see for instance Jones (1985)].

Statistical tools available to handle unevenly time series are essentially developed for short range dependence [see e.g. Li (2014) and references therein]. We can also refer to numerous papers in astronomy, that focus on spectrum estimation [see e.g. Thiebaut and Roques (2005)].

To the best of our knowledge, few results are available when the continuous-time embedding process has a long memory. Actually, long memory statistical inference for continuous-time models is generally built upon a deterministically sampled process [see Tsai and Chan (2005a, 2005b); Chambers (1996); Comte (1996)]. However, as in the examples previously cited, in several applied contexts one has to deal with random sampling from a continuous process. In time-domain, Philippe et al. (2021) studied randomly-spaced observations, using a renewal process as a sampling tool. They showed that the intensity of the long memory is preserved when the distribution of sampling intervals has a finite moment, but there are also situations where a reduction of the long memory is observed. Consequently, the continuous time memory parameter cannot be estimated without a prior information on the sampling process. Bardet and Bertrand (2010) studied spectral density estimation of continuous-time Gaussian processes with stationary increments observed at random times.

Contrary to the paper mentioned above that focuses on the continuous process itself, we are interested in the resulting discrete-time-indexed randomly sampled process. More precisely, we study the spectral-domain properties and provide explicit expressions for the spectral density of the sampled process. We mention that Philippe and Viano (2010) addressed resampling from a discrete-time process and obtained the existence of the spectral density. However, their spectral density expression is less explicit since it is expressed as a non explicit limit of an integral and they do not address resampling from a continuous process and their techniques do not extend to our case.

Most of existing long memory inferential techniques assume that the process is a subordinated Gaussian/linear one. Philippe et al. (2021) established a rather surprising characteristic consisting in the loss of the joint-Gaussianity of the sampled process when the original process was Gaussian. Therefore we cannot apply such results to our sampled processes that are neither Gaussian nor linear. We study some aspects of the inference via spectral approaches. In particular, to establish the consistency of long memory parameter’s local Whittle estimator using Dalla et al. (2006)’s assumptions for nonlinear long memory processes.

We now describe our sampling model. We start with $X=(X_t)_{t\in \mathbb {R}^+}$, a continuous time process and a renewal process $(T_n)_{n\ge 0}$. We study the discrete-time indexed process $Y=(Y_n)_{n\ge 1}$ defined by

$$\begin{aligned} Y_n=X_{T_n}\quad n=1,2,\ldots . \end{aligned}$$

(1)

We want to emphasise that the sampling process $T_n$ is not observed. Throughout this paper, we will assume that, and refer to

$H_X$: :

X is second-order stationary continuous time process with auto-covariance function $\sigma _X$ and having a spectral density $f_X$: for all $t\in \mathbb {R}$

$$\begin{aligned} \sigma _X(t) = \int _{-\infty }^\infty e^{i\lambda t}f_X(\lambda )d\lambda .\end{aligned}$$

(2)

$H_T$: :

$(T_n)_{n\ge 0}$ independent of X and of i.i.d. increments $T_{j+1}-T_j=\Delta _j\ge 0$ non degenerate with cumulative distribution function S and we let $T_0=0$.

We impose this specific initialization $T_0=0$ only to simplify our notations since it implies that $\Delta _j = T_{j+1}-T_j$ for all $j\in \mathbb {N}$. However, all the results remain true if we take $T_0 = \Delta _0$ and $\Delta _j = T_{j}-T_{j-1}$, for $j\ge 1$.

The rest of the paper is organized as follows. Section 2 presents results on the existence of a spectral density for the process Y when the spectrum of X is absolutely continuous. We also provide an integral representation of such density. In Sect. 3, we establish the asymptotic distribution of the normalized periodogram of the sampled process. In Sect. 4, we show the consistency of Y-based local Whittle memory estimator. We also study the estimation of the so-called long-run variance.

2 Spectral density function of sampled process

Under the assumptions $H_X$ and $H_T$, Philippe et al. (2021) show that if X is stationary then so is Y. Moreover, its covariance function is of the following form

$$\begin{aligned} \sigma _Y(j)=\text {Cov}(Y_1,Y_{j+1})=\mathbb {E}(\sigma _X({T_j})). \end{aligned}$$

(3)

Note that the independence of X and the renewal process imposed in $H_T$, is required to get (3). In the next proposition, we prove that the existence of the spectral density is preserved by random sampling and we establish the link between the spectral densities of processes X and Y.

Proposition 1

Assume that the continuous-time process X satisfies $H_X$ and that $H_T$ holds. Then, the discrete-time process Y admits a spectral density and it is given by the following formula

$$\begin{aligned} f_Y(x)=\frac{1}{2\pi }\int _{-\infty }^\infty p(x,\Psi _S(\lambda ))f_X(\lambda )d\lambda , \end{aligned}$$

(4)

where $\Psi _S$ is the characteristic function of the cumulative distribution function S defined in $H_T$ and

$$\begin{aligned} p(x,z)=\frac{1-\vert z\vert ^2}{\vert 1-e^{-ix}z\vert ^2},\qquad \vert z\vert <1 \end{aligned}$$

is the well known Poisson kernel.

Proof

According to the stationarity property and (3) proved in Philippe et al. (2021) and the existence of the spectral density $f_X$ in (2), the covariance function of Y can be computed via Fubini’s theorem as follows:

$$\begin{aligned} \sigma _Y(j)= & {} \mathbb {E}(\sigma _X({T_j}))=\mathbb {E}\left( \int _{-\infty }^\infty e^{i\lambda T_j}f_X(\lambda )d\lambda \right) \nonumber \\= & {} \int _{-\infty }^\infty \left( \mathbb {E}\left( e^{i\lambda T_j}\right) \right) f_X(\lambda )d\lambda =\int _{-\infty }^\infty \left( \Psi _S(\lambda )\right) ^jf_X(\lambda )d\lambda . \end{aligned}$$

(5)

To prove (4), it will suffice to show that for every $j\ge 0$,

$$\begin{aligned} \sigma _Y(j)=\int _{-\pi }^\pi e^{ijx}f_Y(x)dx, \end{aligned}$$

(6)

as $f_Y$ defined by (4) is clearly an even function. For this, we will use the following Poisson integral formula for the disk: if u is an analytic function on the disk $\vert z\vert <1$ and continuous on $\vert z\vert =1$ then its real and imaginary parts are harmonic and therefore for $\vert z\vert <1$, we have

$$\begin{aligned} u(z)=\frac{1}{2\pi }\int _{-\pi }^\pi u(e^{ix})p(x,z)dx. \end{aligned}$$

Applying the above with $u(z)=z^j$, where j is a fixed nonnegative integer, we get

$$\begin{aligned} z^j=\frac{1}{2\pi }\int _{-\pi }^\pi e^{ijx}p(x,z)dx,\quad \text {for all }\vert z\vert <1, \end{aligned}$$

(7)

and since for Lebesgue a.e. $\lambda$, $\vert \Psi _S(\lambda )\vert <1$ (S being non degenerated), then for a.e. $\lambda$,

$$\begin{aligned} (\Psi _S(\lambda ))^j=\frac{1}{2\pi }\int _{-\pi }^\pi e^{ijx}p(x,\Psi _S(\lambda ))dx. \end{aligned}$$

(8)

Also taking $j=0$ in (7), we get

$$\begin{aligned} \frac{1}{2\pi }\int _{-\pi }^\pi p(x,z)dx=1\quad \text {for all }\vert z\vert <1. \end{aligned}$$

Hence, by Fubini’s theorem, we see that $f_Y$, as given in (4), is integrable on $[-\pi , \pi ]$. Applying Fubini’s theorem once again and substituting (8) in (5), we immediately get (6). $\square$

The following corollary gives a precise expression of the spectral density of Y in the most common case of Poisson renewal process.

Corollary 1

Assume that the continuous-time process X satisfies $H_X$ and that $(T_n)$ is a Poisson renewal process with rate 1, independent of X. If $\lambda ^2f_X(\lambda )$ is bounded and continuous on the real line then

$$\begin{aligned} f_Y(x)=\frac{u(\sin x,1-\cos x)}{2(1-\cos x)},\qquad \text {for a.e. }x\text { in the interval }(-\pi ,\pi ), \end{aligned}$$

(9)

where u(x, y) is the harmonic function on the upper half plane with boundary condition $u(x,0)=x^2f_X(x)$. In particular, both spectral densities are equivalent near zero, i.e., $f_Y(x)\sim f_X(x)$ as $x\rightarrow 0$.

Proof

The exponential distribution has characteristic function $(1-i\lambda )^{-1}$ and hence from Proposition 1, we can easily derive that

$$\begin{aligned} f_Y(x)= & {} \frac{1}{2\pi }\int _{-\infty }^\infty \left( \frac{\lambda ^2}{(\lambda -\sin x)^2+(1-\cos x)^2}\right) f_X(\lambda )d\lambda \end{aligned}$$

(10)

$$\begin{aligned}= & {} \frac{1}{2(1-\cos x)}\frac{1}{\pi }\int _{-\infty }^\infty \left( \frac{1-\cos x}{(\lambda -\sin x)^2+(1-\cos x)^2}\right) \lambda ^2f_X(\lambda )d\lambda . \end{aligned}$$

(11)

In the above we recognise the well known Poisson integral formula for the upper half plane for the function: $x\mapsto x^2f_X(x)$: if g is continuous and bounded on the real line then the function defined by

$$\begin{aligned} u(x,y):=\frac{1}{\pi }\int _{-\infty }^\infty \left( \frac{y}{(x-\lambda )^2+y^2}\right) g(\lambda )d\lambda \end{aligned}$$

(12)

is harmonic on the upper half plane and satisfies $u(x,0)=g(x)$ [see for example the result 7.3 on p. 147 of Axler et al. (2000)] and $\frac{u(x,y)}{g(x)} \rightarrow 1$ uniformly in x as $y\rightarrow 0$. Combining (11) and (12) we get the stated result. $\square$

The next proposition precises the behaviour of the spectral density of sampled process Y near zero, given in the previous corollary, under mild semi parametric conditions on the spectral density of the original process X.

Proposition 2

Assume that $T_n$ is a Poisson process independent of X with rate 1 and that X satisfies $H_X$ with spectral density of the form

$$\begin{aligned} f_X(\lambda )=\vert \lambda \vert ^{-2d}\phi (\lambda ), \end{aligned}$$

(13)

with $0<d<1/2$, $\phi (0)\ne 0$ and $\phi$ is continuous on $[-1,1]$ and differentiable on $(-1, 1 )$. Then

$$\begin{aligned} f_Y(x)=|x|^{-2d}f_Y^*(x) \end{aligned}$$

(14)

with $f_Y^*$ is positive continuous on $[-\pi ,\pi ]$ and

$$\begin{aligned} f_Y^*(x)=\phi (0)+\frac{\sigma _X(0)}{2\pi }|x|^{2d}+o(|x|^{2d}),\qquad \text {as }x\rightarrow 0. \end{aligned}$$

(15)

Proof

Since $f_Y$ is even, we will consider $x\in (0,\pi ]$. From (10), we have

$$\begin{aligned} f_Y(x)= & {} \frac{1}{2\pi }\int _0^\infty \frac{\lambda ^2}{(\lambda -\sin x)^2+(1-\cos x)^2}f_X(\lambda )d\lambda \nonumber \\{} & {} \quad +\frac{1}{2\pi }\int _0^\infty \frac{\lambda ^2}{(\lambda +\sin x)^2+(1-\cos x)^2}f_X(\lambda )d\lambda . \end{aligned}$$

(16)

We study both integrals in (16) near $x=0$.

$$\begin{aligned} \int _0^\infty \frac{\lambda ^2}{(\lambda +\sin x)^2+(1-\cos x)^2}f_X(\lambda )d\lambda \overset{x\rightarrow 0}{\rightarrow }\int _0^\infty f_X(\lambda )d\lambda =\frac{\sigma _X(0)}{2} \end{aligned}$$

(17)

since for fixed $\lambda$, as $x\rightarrow 0$, the integrand (in the left-hand side) clearly increases towards $f_X(\lambda )$. Let us deal with the first integral in (16).

$$\begin{aligned}{} & {} \int _0^\infty \frac{\lambda ^2}{(\lambda -\sin x)^2+(1-\cos x)^2}f_X(\lambda )d\lambda \nonumber \\{} & {} \quad =\int _0^{\sin x}\frac{\lambda ^2}{(\lambda -\sin x)^2+(1-\cos x)^2}f_X(\lambda )d\lambda \nonumber \\{} & {} \qquad +\int _{\sin x}^{2\sin x}\frac{\lambda ^2}{(\lambda -\sin x)^2+(1-\cos x)^2}f_X(\lambda )d\lambda \nonumber \\{} & {} \qquad +\int _{2\sin x}^\infty \frac{\lambda ^2}{(\lambda -\sin x)^2+(1-\cos x)^2}f_X(\lambda )d\lambda . \end{aligned}$$

(18)

Using the fact that $f_X(\lambda )=\lambda ^{-2d}\phi (\lambda )$ and $\sin ^2(x/2)=(1-\cos x)/2$ and putting $\lambda =t\sin x$, we obtain for the first integral in the right hand side above, with some $u(t)\in (0,1)$ and $v(t)\in (0,1)$,

$$\begin{aligned}{} & {} \int _0^{\sin x}\frac{\lambda ^2}{(\lambda -\sin x)^2+4(\sin (x/2))^4}f_X(\lambda )d\lambda \\{} & {} \quad =(\sin x)^{-2d}\int _0^1\frac{t^{2-2d}\sin x}{(1-t)^2+\tan ^2(x/2)}\phi (t\sin x)dt \\{} & {} \quad =(\sin x)^{-2d}\int _0^1\frac{(1-t)^{2-2d}\sin x}{t^2+\tan ^2(x/2)}\phi ((1-t)\sin x)dt \\{} & {} \quad =(\sin x)^{-2d}\int _0^1\big (1-(2-2d)(1-u(t))^{1-2d}t\big )\\{} & {} \quad \frac{\sin x}{t^2+\tan ^2(x/2)}(\phi (0)+\phi '(v(t))\sin x(1-t))dt\\{} & {} \quad =(\sin x)^{-2d}\Bigg [\int _0^1\frac{\phi (0)\sin x}{t^2+\tan ^2(x/2)}dt\\{} & {} \qquad +O\Bigg (\sin x\int _0^1\frac{t}{t^2+\tan ^2(x/2)}dt+\sin x\int _0^1\frac{\sin x}{t^2+\tan ^2(x/2)}dt\Bigg )\Bigg ]. \end{aligned}$$

Putting $t=u\tan (x/2)$ the right-hand-side of the last equation is equal to

$$\begin{aligned}{} & {} (\sin x)^{-2d}\Bigg [2\phi (0)\cos ^2(x/2)\int _0^{1/\tan (x/2)}\frac{1}{u^2+1}du \\{} & {} \quad \quad +O\left( \sin x\int _0^1\frac{t}{t^2+\tan ^2(x/2)}dt+\sin x\int _0^1\frac{\sin x}{t^2+\tan ^2(x/2)}dt\right) \Bigg ]\\{} & {} \quad =(\sin x)^{-2d}\Bigg [2\phi (0)\cos ^2(x/2)\arctan (1/\tan (x/2))\\{} & {} \qquad +O\Bigg (x(\log (1+x^2)-\log x)+2x\arctan (2/x)\Bigg )\Bigg ] \end{aligned}$$

Then

$$\begin{aligned}{} & {} \int _0^{\sin x}\frac{\lambda ^2}{(\lambda -\sin x)^2+4(\sin (x/2))^4}f_X(\lambda )d\lambda \nonumber \\{} & {} \qquad =x^{-2d}\left( \phi (0)\pi +O(x\log x)\right) ,\quad \text {as }x\rightarrow 0. \end{aligned}$$

(19)

Similarly, we have

$$\begin{aligned}{} & {} \int _{\sin x}^{2\sin x}\frac{\lambda ^2}{(\lambda -\sin x)^2+(\sin x/2))^4}f_X(\lambda )d\lambda \nonumber \\{} & {} \qquad =(\sin x)^{-2d}\int _1^2\frac{t^{2-2d}\sin x}{(1-t)^2+\tan ^2(x/2)}\phi (t\sin x)dt\nonumber \\{} & {} \qquad =(\sin x)^{-2d}\int _0^1\frac{(1+t)^{2-2d}\sin x}{t^2+\tan ^2(x/2)}\phi ((1+t)\sin x)dt\nonumber \\{} & {} \qquad =(\sin x)^{-2d}\int _0^1\big (1+(2-2d)(1+u(t))^{1-2d}t\big )\nonumber \\{} & {} \qquad \quad \frac{\sin x}{t^2+\tan ^2(x/2)}(\phi (0)+\phi '(v(t))\sin x(1+t))dt\nonumber \\{} & {} \qquad = x^{-2d}\left( \phi (0)\pi +O(x\log x)\right) . \end{aligned}$$

(20)

Then, we have as $x\rightarrow 0$

$$\begin{aligned} \int _{2\sin x}^\infty \frac{\lambda ^2}{(\lambda -\sin x)^2+\tan ^2(x/2)}f_X(\lambda )d\lambda \rightarrow \int _0^\infty f_X(\lambda )d\lambda =\frac{\sigma _X(0)}{2}, \end{aligned}$$

(21)

since the integrand is bounded uniformly in x by $4f_X(\lambda )$ and converges (as $x\rightarrow 0$) to $f_X(\lambda )$ and hence we can apply Lebesgue’s theorem. Combining (17) and (21) as well as (19) and (20), we obtain that

$$\begin{aligned} f_Y(x)=x^{-2d}f^*_Y(x),\qquad f^*_Y(x)=\phi (0)+\frac{\sigma _X(0)}{2\pi }x^{2d}+o\left( x^{2d}\right) \quad \text {as }x\rightarrow 0. \end{aligned}$$

Moreover, $f_Y^*$ is continuous and positive on $[-\pi ,,\pi ]$. Indeed, the continuity of $f_Y^*$ follows from the fact that the 2nd integrand in the right hand side of (16) is continuous and uniformly bounded in x by $4f_X(\lambda )$ which is integrable. As for the first integral in the right hand side of (16), after splitting it into three terms as in (18) and multiplying it by $x^{2d}$, we see that Lebesgue’s dominated convergence theorem still applies. This completes the proof of Proposition 2. $\square$

We now present a lemma that gives a quite precise expression of the covariance function of X from its spectral density. We will be imposing the following condition on $f_X$.

Condition $H_f$: $f_X(\lambda )=c\vert \lambda \vert ^{-2d}(1-h(\lambda ))$, $0<d<1/2$, where h is a nondecreasing function with $h(0)=0$ and $h(x)\rightarrow 1$ as $x\rightarrow \infty$ and h is differentiable at 0. We notice that condition $H_f$ is not one of the usual slowly varying type conditions for Tauberian and Abelian theorems in the context of long range dependence [see Leonenko and Olenko (2013)]. However, it guarantees a uniform control of the remainder g(x) in (22) rather than at infinity only.

Remark 1

If the spectral density $f_X$ satisfies $H_f$ instead of (13), then Proposition 2 still holds with $c:=c(d)$ instead of $\phi (0)$. The proof is essentially the same and is omitted.

Lemma 1

Assume that condition $H_f$ is satisfied. Then, there exist positive constants C(d) and c(d) such that for all $x>0$,

$$\begin{aligned} \sigma _X(x)=c(d)x^{2d-1}+g(x), \end{aligned}$$

(22)

with $\vert g(x)\vert \le \frac{C(d)}{\vert x\vert }.$

Proof

Let $x>0$ be fixed. Since $f_X$ is even we have,

$$\begin{aligned} \sigma _X(x)=2\int _0^\infty \cos (x\lambda )f_X(\lambda )d\lambda . \end{aligned}$$

Without loss of generality, we take $2c=1$ in $H_f$ and by the formula 3.761.9 of Gradshteyn and Ryzhik (2015)

$$\begin{aligned} \int _0^\infty \cos (x\lambda )\lambda ^{-2d}d\lambda =\Gamma (1-2d)\sin (\pi d) x^{2d-1}=:c(d)x^{2d-1}. \end{aligned}$$

Therefore, it remains to show that for some $C(d)>0$,

$$\begin{aligned} \left| \int _0^\infty \cos (\lambda x)\lambda ^{-2d}h(\lambda )d\lambda \right| \le C(d)x^{-1}. \end{aligned}$$

The rest of the proof relies on applying integration by parts for Stieltjes integrals.

Let $dU(\lambda )=\cos (\lambda x)\lambda ^{-2d}$. We have (by one integration by parts)

$$\begin{aligned} U(t)= & {} \int _0^t\cos (\lambda x)\lambda ^{-2d}d\lambda \\{} & {} =\frac{1}{x} \left[ \lambda ^{-2d}\sin (\lambda x)\right] _{\lambda =0}^{\lambda =t}+\frac{2d}{x}\int _0^t\lambda ^{-2d-1}\sin (\lambda x)d\lambda \\{} & {} =\frac{1}{x}\left( t^{-2d}\sin (tx)+2d\int _0^t\lambda ^{-2d-1}\sin (\lambda x)d\lambda \right) , \end{aligned}$$

clearly U is bounded and

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim }U(t)=\frac{2d}{x}\int _0^\infty \lambda ^{-2d-1}\sin (\lambda x)d\lambda . \end{aligned}$$

Using the fact that h is nondecreasing, $h(\lambda )\rightarrow 1$, as $\lambda \rightarrow \infty$, and $h(0)=0$, we obtain (via integration by parts at some steps in the calculation below

$$\begin{aligned} \int _a^b \cos (\lambda x)\lambda ^{-2d}h(\lambda )d\lambda =\int _a^ b h(\lambda )dU(\lambda )= \left[ U(\lambda )h(\lambda )\right] _a^b-\int _a^b U(\lambda )dh(\lambda ),\nonumber \\ \end{aligned}$$

(23)

with

$$\begin{aligned} \left[ U(\lambda )h(\lambda )\right] _a^b \xrightarrow [b\rightarrow \infty ]{a\rightarrow 0 }\frac{2d}{x}\int _0^\infty \lambda ^{-2d-1}\sin (\lambda x)d\lambda , \end{aligned}$$

$$\begin{aligned} -\int _a^b U(\lambda )dh(\lambda )= & {} - \frac{1}{x}\int _a^b\left( \lambda ^{-2d}\sin (\lambda x)+2d\int _0^\lambda u^{-2d-1}\sin (ux)du\right) dh(\lambda )\\= & {} - \frac{1}{x}\int _a^b\lambda ^{-2d}\sin (\lambda x)dh(\lambda )\nonumber \\{} & {} -\frac{2d}{x}\int _a^b\left( \int _0^\lambda u^{-2d-1}\sin (ux)du\right) dh(\lambda ),\\ \end{aligned}$$

also

$$\begin{aligned}{} & {} -\frac{2d}{x}\int _a^b\left( \int _0^\lambda u^{-2d-1}\sin (ux)du\right) dh(\lambda ) \\ {}{} & {} \quad = -\frac{2d}{x} h(b) \int _0^b \lambda ^{-2d-1}\sin (\lambda x)d\lambda \\ {}{} & {} \qquad +\frac{2d}{x} h(a) \int _0^a\lambda ^{-2d-1}\sin (\lambda x)d\lambda +\frac{2d}{x}\int _a^b \lambda ^{-2d-1}\sin (\lambda x)h(\lambda )d\lambda .\\ \end{aligned}$$

Since

$$\begin{aligned}{} & {} -\frac{2d}{x} h(b) \int _0^b \lambda ^{-2d-1}\sin (\lambda x)d\lambda \\{} & {} \quad +\frac{2d}{x} h(a) \int _0^a\lambda ^{-2d-1}\sin (\lambda x)d\lambda \xrightarrow [b\rightarrow \infty ]{a\rightarrow 0 } - \frac{2d}{x}\int _0^\infty \lambda ^{-2d-1}\sin (\lambda x)d\lambda , \end{aligned}$$

$\int _a^b U(\lambda )dh(\lambda )$ has the same limit as

$$\begin{aligned} - \frac{1}{x}\int _a^b\lambda ^{-2d}\sin (\lambda x)dh(\lambda ) + \frac{2d}{x}\int _a^b \lambda ^{-2d-1}\sin (\lambda x)h(\lambda )d\lambda , \end{aligned}$$

as $a\rightarrow 0$ and $b\rightarrow \infty$.

$$\begin{aligned}{} & {} \left| - \frac{1}{x}\int _a^b\lambda ^{-2d}\sin (\lambda x)dh(\lambda ) + \frac{2d}{x}\int _a^b \lambda ^{-2d-1}\sin (\lambda x)h(\lambda )d\lambda \right| \\{} & {} \le \frac{1}{x}\int _a^b \lambda ^{-2d}dh(\lambda )+\frac{2d}{x}\int _a^b\lambda ^{-2d-1}h(\lambda )d\lambda \\{} & {} \quad = \frac{1}{x} \left( h(b) b^{-2d} -h(a) a^{-2d}\right) + \frac{2d}{x}\int _a^b \lambda ^{-2d-1}h(\lambda )d\lambda +\frac{2d}{x}\int _a^b \lambda ^{-2d-1}h(\lambda )d\lambda \\{} & {} \quad =\frac{1}{x} \left( h(b) b^{-2d} -h(a) a^{-2d}\right) \\{} & {} \qquad + \frac{4d}{x}\int _a^b\lambda ^{-2d-1}h(\lambda )d\lambda \xrightarrow [b\rightarrow 0] {a\rightarrow 0} \frac{4d}{x}\int _0^\infty \lambda ^{-2d-1}h(\lambda )d\lambda :=\frac{C(d)}{x}. \end{aligned}$$

We note that the integral above is indeed finite since h is a bounded function, $h(0)=0$, and is differentiable at zero.

The proof of Lemma 1 is now complete. $\square$

Corollary 2

If $T_n$ is a Poisson process and $f_X$ satisfies condition $H_f$ then

$$\begin{aligned} \text {Var}\left( \sigma _X(T_r)\right) =O\left( r^{-\alpha }\right) ,\qquad \text {as }r\rightarrow \infty , \end{aligned}$$

where $\alpha =\min (2,3-4d)$.

Proof

We have from the previous lemma,

$$\begin{aligned}{} & {} \text {Var}\left( \sigma _X(T_r)\right) =\text {Var}\left( c(d)T_r^{2d-1}+g(T_r)\right) \\{} & {} \quad =c^2(d)\text {Var}\left( T_r^{2d-1}\right) +\text {Var}\left( g(T_r)\right) +2c(d)\text {Cov}\left( T_r^{2d-1},g(T_r)\right) \\{} & {} \quad \le c^2(d)\text {Var}\left( T_r^{2d-1}\right) +C^2(d)\mathbb {E}\left( T_r^{-2}\right) \\{} & {} \qquad +2c(d)C(d)\left[ \text {Var}\left( T_r^{2d-1}\right) \right] ^{1/2} \left[ \mathbb {E}\left( T_r^{-2}\right) \right] ^{1/2}. \end{aligned}$$

For $r\ge 3$, as $T_r$ has Gamma distribution with parameters (r, 1), we have

$$\begin{aligned} \mathbb {E}\left( T_r^{-2}\right) =\int _0^\infty \frac{x^{r-2-1}}{\Gamma (r)}e^{-x}dx=\frac{\Gamma (r-2)}{\Gamma (r)}=\frac{1}{(r-1)(r-2)}=O(r^{-2}). \end{aligned}$$

Also,

$$\begin{aligned} \text {Var}\left( T_r^{2d-1}\right)= & {} \mathbb {E}\left( T_r^{4d-2}\right) -\left( \mathbb {E}\left( T_r^{2d-1}\right) \right) ^2\\= & {} \frac{\Gamma (r-2+4d)}{\Gamma (r)}-\left( \frac{\Gamma (r-1+2d)}{\Gamma (r)}\right) ^2 \end{aligned}$$

We know that as $r\rightarrow \infty$,

$$\begin{aligned} \frac{\Gamma (r-a)}{\Gamma (r)}=r^{-a}\left( 1-\frac{a(-a+1)}{2r}+O\left( \frac{1}{r^2}\right) \right) , \end{aligned}$$

and therefore we obtain that

$$\begin{aligned} \text {Var}\left( T_r^{2d-1}\right) =(1-2d)^2r^{-2(1-2d)-1}+o\left( r^{-2(1-2d)-1}\right) =O\left( n^{-\alpha }\right) , \end{aligned}$$

which completes the proof of the corollary. $\square$

3 Asymptotic theory of the periodogram

We consider in this section a stationary long memory zero-mean Gaussian process $X=(X_t)_{ t\in \mathbb {R}^+}$ having a spectral density of the form (13). Let $Y = (X_{T_n})_{n\in \mathbb {N}}$, where $(T_n)_{n\in \mathbb {N}}$ is a Poisson process with rate equal 1 (actually any rate will do). As shown in Philippe et al. (2021) and in contrast with the original process X, while Y remains marginally normally distributed, it is no longer jointly Gaussian and, as a result, Y is not a linear process.

In this section, we extend some well-known facts about periodogram properties to the randomly sampled processes Y. In particular, our main result will be to establish that the normalized periodogram of Y will asymptotically converge to a weighted $\chi ^2$ distribution.

Theorem 1

Assume that X is a stationary Gaussian process satisfying $H_f$ and let $Y = (X_{T_n})_{n\in \mathbb {N}}$ where $(T_n)_{n\in \mathbb {N}}$ is a Poisson process with rate equal 1. Let

$$\begin{aligned} I_n(\lambda _j)=\frac{1}{2\pi n}\left| \sum _{k=1}^nY_ke^{ik\lambda _j}\right| ^2, \end{aligned}$$

be the periodogram of $Y_1,\ldots ,Y_n$ at Fourier frequency $\lambda _j=2\pi j/n$ for $j\in \lbrace 1,~\dots ~, \lfloor n/2\rfloor \rbrace$. Then, we have for any fixed number of Fourier frequencies $\nu \ge 1$, and any $j_1,\dots ,j_\nu \in \lbrace 1, \dots ,\lfloor n/2\rfloor \rbrace$ all distinct integers

$$\begin{aligned}{} & {} \left( \frac{I_n(\lambda _{j_1})}{f_Y(\lambda _{j_1})},\cdots ,\frac{I_n(\lambda _{j_\nu })}{f_Y(\lambda _{j_\nu })}\right) \nonumber \\{} & {} \qquad \overset{\mathcal {D}}{\rightarrow } \left( L_{j_1}(d)[Z^2_1(j_1)+Z^2_2(j_1)],\cdots ,L_{j_\nu }(d)[Z^2_1(j_\nu )+Z^2_2(j_\nu )]\right) , \end{aligned}$$

(24)

where $(Z_1(1),Z_2(1),\ldots ,Z_1([ n/2] ),Z_2([ n/2] )$ is a zero-mean Gaussian vector, with $Z_1(j),Z_2(k)$ are independent for all $j,k=1,\ldots , [n/2]$ and

$$\begin{aligned} \text {Var}(Z_1(j))=\frac{1}{2}-\frac{R_j(d)}{L_j(d)} \end{aligned}$$

(25)

and

$$\begin{aligned} \text {Var}(Z_2(j))=\frac{1}{2}+\frac{R_j(d)}{L_j(d)}, \end{aligned}$$

(26)

and for $j\ne k$,

$$\begin{aligned} \text {Cov}(Z_1(j),Z_1(k))= & {} \frac{L_{j,k}(d)-R_{j,k}(d)}{\sqrt{L_j(d)L_{k}(d)}} \end{aligned}$$

(27)

$$\begin{aligned} \text {Cov}(Z_2(j),Z_2(k))= & {} \frac{L_{j,k}(d)+R_{j,k}(d)}{\sqrt{L_j(d)L_{k}(d)}}, \end{aligned}$$

(28)

with

$$\begin{aligned} L_j(d)= & {} \frac{2}{\pi }\int _{-\infty }^\infty \frac{\sin ^2(\lambda /2)}{(2\pi j-\lambda )^2}\left| \frac{\lambda }{2\pi j}\right| ^{-2d}d\lambda , \end{aligned}$$

(29)

$$\begin{aligned} R_j(d)= & {} \frac{1}{\pi }\int _{-\infty }^\infty \frac{\sin ^2(\lambda /2)}{(2\pi j-\lambda )(2\pi j+\lambda )}\left| \frac{\lambda }{2\pi j}\right| ^{-2d}d\lambda , \end{aligned}$$

(30)

$$\begin{aligned} L_{j,k}(d)= & {} \frac{(jk)^d}{\pi }\int _{-\infty }^\infty \frac{\sin ^2(\lambda /2)}{(2\pi k-\lambda )(2\pi j-\lambda )}\left| \frac{\lambda }{2\pi }\right| ^{-2d}d\lambda , \end{aligned}$$

(31)

and

$$\begin{aligned} R_{j,k}(d)=\frac{(jk)^d}{\pi }\int _{-\infty }^\infty \frac{\sin ^2(\lambda /2)}{(2\pi k+\lambda )(2\pi j-\lambda )}\left| \frac{\lambda }{2\pi }\right| ^{-2d}d\lambda . \end{aligned}$$

(32)

Proof

We will prove the broader result

$$\begin{aligned} Z_n: =&\,\Bigg (\frac{1}{\sqrt{2\pi nf_Y(\lambda _{j_1})}}\sum _{r=1}^n\cos (r\lambda _{j_1})X_{T_r},\frac{1}{\sqrt{2\pi nf_Y(\lambda _{j_1})}}\sum _{r=1}^n \sin (r\lambda _{j_1})X_{T_r},\cdots , \nonumber \\&\frac{1}{\sqrt{2\pi nf_Y(\lambda _{j_\nu })}}\sum _{r=1}^n\cos (r\lambda _{j_\nu })X_{T_r},\frac{1}{\sqrt{2\pi nf_Y(\lambda _{j_\nu })}}\sum _{r=1}^n \sin (r\lambda _{j_\nu })X_{T_r}\Bigg ) \nonumber \\ {}&\xrightarrow []{\mathcal {D}}\left( \sqrt{L_{j_1}(d)}(Z_1(j_1),Z_2(j_1)),\cdots ,\sqrt{L_{j_\nu }(d)}(Z_1(j_\nu ),Z_2(j_\nu ))\right) . \end{aligned}$$

(33)

Conditionally on $T_1,\ldots ,T_n$, the vector $(X_{T_1},\ldots ,X_{T_n})$ is Gaussian, and hence so is $Z_n$. Its covariance matrix $\Sigma _T= \textrm{Var}(Z_n| T_1,\ldots ,T_n)$ has (i, k) entry of the form

$$\begin{aligned} \frac{1}{2\pi n\sqrt{f_Y(\lambda _{j_i})f_Y(\lambda _{j_k})}}\sum _{r=1}^n\sum _{s=1}^n\sigma _X(T_r-T_s)h_{i,k}(r,s) \end{aligned}$$

where

$$\begin{aligned} h_{i,k}(r,s)=\cos (r\lambda _{j_i})\cos (s\lambda _{j_k}),\text { or }\cos (r\lambda _{j_i})\sin (s\lambda _{j_k}),\text { or }\sin (r\lambda _{j_i})\sin (s\lambda _{j_k}). \end{aligned}$$

We prove (33) using the characteristic function: since X and T are independent, for $u\in \mathbb {R}^{2\nu }$, and with $u'$ being the transpose of u,

$$\begin{aligned} \mathbb {E}( e^{iu'Z_n})&= \mathbb {E} \left( \mathbb {E}\left( e^{iu'Z_n} \Big | T_1,\ldots ,T_n \right) \right) = \mathbb {E} \left( \exp \left( -\frac{1}{2}u'\Sigma _T u\right) \right) . \end{aligned}$$

As the characteristic function is bounded, it will suffice to show that

$$\begin{aligned} \Sigma _T\overset{P}{\rightarrow }\Sigma , \end{aligned}$$

(34)

where $\Sigma$ is the variance-covariance matrix of $(\sqrt{L_1(j_1)}(Z_1(j_1),Z_2(j_1)),\cdots ,\sqrt{L_\nu (j_\nu )}(Z_1(j_\nu ),Z_2(j_\nu )))$.

When i and k are fixed, the form of $h_{i,k}(r,s)$ is the same for all r and s and hence $\mathbb {E}\left( \Sigma _T\right)$ will have entries of the form

$$\begin{aligned}{} & {} \frac{1}{2\pi n\sqrt{f_Y(\lambda _{j_i})f_Y(\lambda _{j_k})}}\sum _{r=1}^n\sum _{s=1}^n\mathbb {E}(\sigma _X(T_r-T_s))h_{i,k}(r,s)\\{} & {} \quad = \frac{1}{2\pi n\sqrt{f_Y(\lambda _{j_i})f_Y(\lambda _{j_k})}}\sum _{r=1}^n\sum _{s=1}^n\sigma _Y(r-s)h_{i,k}(r,s) \end{aligned}$$

by (3), and therefore $\mathbb {E}(\Sigma _T)\rightarrow \Sigma$ by virtue of Theorem 5 of Hurvich and Beltrão (1993) (the only condition required is second order stationarity of the process $Y_i$ and the behaviour (14) of its spectral density). To complete the proof of (34), it will then suffice to show that

$$\begin{aligned} \text {Var}\left( \Sigma _T\right) \rightarrow 0, \end{aligned}$$

(35)

i.e. the variances of the entries of $\Sigma _T$ converge to zero. By Cauchy–Schwarz inequality, it will be enough to focus on the diagonals. We will treat those diagonals with cosine, as those with sine treat the same way. For some constant C (that may change from one expression to another), we obtain

$$\begin{aligned}&\textrm{Var}\left( \frac{1}{2\pi nf_Y(\lambda _j)}\sum _{r=1}^n\sum _{s=1}^n\sigma _X(T_r-T_s)\cos (r\lambda _j)\cos (s\lambda _j)\right) \nonumber \\&\quad \sim \frac{C}{n^{2+4d}}\sum _{r,s,r',s'=1}^n\textrm{Cov}\left( \sigma _X(T_r-T_s)\cos (r\lambda _j)\cos (s\lambda _j),\right. \nonumber \\&\quad \quad \left. \sigma _X(T_{r'}-T_{s'})\cos (r'\lambda _j)\cos (s'\lambda _j)\right) \nonumber \\&\quad \le \frac{C}{n^{2+4d}}\left( \sum _{r=1}^n\sum _{s=1}^n\sqrt{\textrm{Var}\left( \sigma _X(T_r-T_s)\right) }\right) ^2\nonumber \\&\quad \le \frac{C}{n^{4d}}\left( \sum _{h=1}^n \sqrt{\textrm{Var}\left( \sigma _X(T_h)\right) }\right) ^2\le C\frac{n^{2d}}{n^{4d}}\rightarrow 0, \end{aligned}$$

(36)

using Corollary 2. $\square$

4 Inference for the long-memory parameter

We still assume in this section that $X= (X_t)_{t\in \mathbb {R}^+}$ is a stationary long memory zero-mean Gaussian process having a spectral density satisfying $H_f$ condition. Periodogram-based approaches to estimate the long memory parameter d are very popular. Often one requires that the underlying process is linear or at least is built on martingale difference innovations. The reader is referred to Beran et al. (2013), Giraitis et al. (2012) for reviews of some recent works on this issue, as well as the book edited by Doukhan et al. (2003). The next lemma and its proof show that although it is not a linear process with i.i.d. innovations, the sampled process still satisfies important long memory 4th cumulant conditions. These 4th cumulant conditions will allow us to show both the convergence of an estimator of the memory parameter d and the estimation of the asymptotic variance, necessary for example in the inference about the mean of the original continuous time process X.

Lemma 2

Assume that X is a zero mean stationary Gaussian process satisfying $H_f$ and let $Y= (X_{T_n})_{n\in \mathbb {N}}$, where $(T_n)_{n\in \mathbb {N}}$ is a Poisson process. Then for all $d \in (0,1/2)$, we have

$$\begin{aligned} \sup _{h\in \mathbb {N}}\sum _{r,s=0}^n \vert \textrm{cum}(Y_0,Y_{h},Y_{r},Y_{s})\vert = O\big ( n^{2d}\big ). \end{aligned}$$

(37)

and

$$\begin{aligned} \sum _{h,r,s=0}^n \vert \textrm{cum}(Y_0,Y_{h},Y_{r},Y_{s})\vert = O\big (n^{4d}\log (n)\big ). \end{aligned}$$

(38)

Proof

The proof is postponed in Appendix. Note that the term $\log (n)$ in the right hand side of (38) is needed only in the particular case $d=1/4$, known to be borderline between weak long memory and strong long memory, as will be seen in the proof. $\square$

4.1 Consistency of local Whittle estimator

We consider local Whittle estimator of the memory parameter d defined by

$$\begin{aligned} \widehat{d}_n=\underset{\beta \in [-1/2,1/2]}{{\text {argmin}}}U_n(\beta ) \end{aligned}$$

where the contrast function $U_n$ is defined by

$$\begin{aligned} U_n(\beta )=\log \left( \frac{1}{m_n}\sum _{j=1}^{m_n}\lambda _j^{2\beta }I_n(\lambda _j)\right) -\frac{2\beta }{m_n}\sum _{j=1}^{m_n}\log \lambda _j, \end{aligned}$$

and the bandwidth parameter $m=m_n$ satisfies $m_n\rightarrow \infty$ and $m_n=o(n)$.

Theorem 2

Suppose X is a stationary Gaussian process satisfying condition $H_f$ and that $Y_n=X_{T_n}$, where $T_n$ is a Poisson process with rate 1. Then,

$$\begin{aligned} \widehat{d}_n\xrightarrow [n\rightarrow \infty ]{P}d. \end{aligned}$$

(39)

In addition, for $m_n=n^a$, $0<a<1$, we have

$$\begin{aligned} \widehat{d}_n-d=o_P\left( \frac{1}{\log n}\right) . \end{aligned}$$

(40)

Remark 2

Equation (40) provides a lower bound on the convergence rate of $\hat{d}$ uniformly in d. As can be seen from the proof, the non uniform rate (for each d) is much better. But this slow rate will be enough to plug $\hat{d}$ in the long run variance estimate below (see Proposition 3).

Proof

According to our result (15) and Dalla et al. (2006) (Corollary 1), we have

$$\begin{aligned} \hat{d}-d=O_P\left( m^{-1/2}\log m+\left( \frac{m}{n}\right) ^{2d}+r_n\right) , \end{aligned}$$

for some remainder $r_n$, which we will be controlling as in what follows, depending on the convergence rate of m/n to zero. To prove (39) it will suffice to show that $r_n\rightarrow 0$.

Case 1 $\sqrt{n}(\log n)^{4/(1-2d)}=O(m)$.   From part (iv) of Corollary 1 of Dalla et al. (2006), the remainder $r_n$ can be written as

$$\begin{aligned} r_n=\left( \frac{D_n^{**}}{n}\right) ^{1/2}\left( \frac{n}{m}\right) ^{1-2d}\log ^3 n\rightarrow 0, \end{aligned}$$

where

$$\begin{aligned} D_n^{**}=\sup _{h,r\in \mathbb {N}}\sum _{s=1}^n\vert \textrm{cum}(Y_0,Y_{h},Y_{r},Y_{s})\vert . \end{aligned}$$

We have

$$\begin{aligned} D_n^{**} \le \sup _{h\in \mathbb {N}}\sum _{r,s=0}^n \vert \textrm{cum}(Y_0,Y_{h},Y_{r},Y_{s})\vert , \end{aligned}$$

so that by (37) we get $D_n^{**}=O(n^{2d})$ and hence $r_n=O(1/\log n)$.

Case 2 $m=O(\sqrt{n}(\log n)^{4/(1-2d)})$. We use (iii) of Corollary 1 of Dalla et al. (2006),

$$\begin{aligned} r_n=\left( \frac{D_n^*}{n}\right) ^{1/2}\left( \frac{m}{n}\right) ^{2d}\log ^2 n\rightarrow 0, \end{aligned}$$

where

$$\begin{aligned} D_n^*=\sum _{h,r,s=0}^n \vert \textrm{cum}(Y_0,Y_{h},Y_{r},Y_{s})\vert . \end{aligned}$$

According to (38), $D_n^*=O(n^{4d}\log n)$, and therefore

$$\begin{aligned} r_n=O\left( n^{d-1/2}\left( \log n\right) ^{2(1+2d)/(1-2d)}\right) \rightarrow 0. \end{aligned}$$

This concludes proof of (39).

To prove (40), we show that $r_n=o(1/\log n)$. This is immediate in case (2) above. Since $m=n^a$, $0<a<1$, we will be in case (1) if $a>1/2$ and then

$$\begin{aligned} r_n=O\left( n^{1/2-d-a(1-2d)}\right) /\log n=o(1/\log n). \end{aligned}$$

$\square$

4.2 Long run variance

The 4th cumulant condition (37) is needed to estimate the long run variance of the sampled process. Such estimation plays a crucial role in many aspects of statistical inference. For example, when it comes to estimating the mean $\mu$ of the original process X, as we have from Philippe et al. (2021)

$$\begin{aligned} \left( \text {Var}\left( n^{1/2-d}\bar{Y}_n\right) \right) ^{-1/2}n^{1/2-d}(\bar{Y}_n-\mu )\overset{\mathcal {D}}{\rightarrow }\mathcal {N}(0,1) \end{aligned}$$

and hence, it is important to obtain a consistent estimator of the variance above. Also such estimator is important in testing for short memory versus long memory or for stationarity versus unit root as such tests involve V/S type statistics and require estimating the long run variance [see Giraitis et al. (2006) and references therein for details]. Let us write the spectral density of $Y_i$ under the form $f(\lambda )\sim c\vert \lambda \vert ^{-2d}$ as $\lambda \rightarrow 0$. Let

$$\begin{aligned} \hat{\sigma }(h)=\frac{1}{n}\sum _{j=1}^{n-h}\big (Y_j-\bar{Y}\big )\big (Y_{j+h}-\bar{Y}\big ) \end{aligned}$$

be the sample covariance function of $Y_i$. Let the asymptotic variance of the normalized sum be

$$\begin{aligned} S^2(d) =\underset{n\rightarrow \infty }{\lim }\left( \text {Var}\big (n^{1/2-d}\bar{Y}\big )\right) =4c\int _{-\infty }^\infty \left( \frac{\sin (\lambda /2)}{\lambda }\right) ^2\vert \lambda \vert ^{-2d}d\lambda . \end{aligned}$$

Let

$$\begin{aligned} \widehat{S}^2(d)=q^{-2d}\left( \hat{\sigma }(0)+2\sum _{h=1}^q\left( 1-\frac{h}{q}\right) \hat{\sigma }(h)\right) . \end{aligned}$$

Proposition 3

Let $\hat{d}$ be a consistent estimator for memory parameter d such that $\log (n)(\hat{d}-d)=o_P(1)$. Let $q\rightarrow \infty$ as $n\rightarrow \infty$ such that $q=O(\sqrt{n})$. Then we have

$$\begin{aligned} {\widehat{S}}^2(\hat{d})\overset{P}{\rightarrow }S^2(d). \end{aligned}$$

Proof

Referring to Theorem 2.2. of Abadir et al. (2009) we just need to verify the cumulant condition

$$\begin{aligned} \underset{h}{\sup }\sum _{r,s=1}^n\left| \text {Cum}(Y_0,Y_h,Y_r,Y_s)\right| \le \tilde{c}n^{2d}, \end{aligned}$$

for some positive constant $\tilde{c}$. This is the case according to Lemma 2. $\square$

Remark 3

A readily available candidate for $\hat{d}$ above is the Whittle estimator for which the $\log (n)$ consistency was established in Theorem 2.

5 Simulation and discussion

Recall that in the context of this work, a long memory continuous process is observed at random times $T_1,\ldots ,T_n$ according to a renewal process. Therefore the number of observations n is fixed in advance but time period length $T_n$ is random. In our simulation, we compare various strategies for sampling a continuous-time process to assess their impact on the inference regarding the mean and the long-memory parameter. It’s important to note that, in applications, the choice of sampling strategies is not deliberate but rather imposed.

The simulations are conducted in the following context. We consider a zero-mean Gaussian process $(X_t)$ with a covariance function

$$\begin{aligned} \sigma _X(x) = \frac{1}{1+x^{1-2d}}, \end{aligned}$$

where d is the memory parameter. This is actually a covariance function as it satisfies Theorem 1’s conditions in Pólya (1949). The sampling process can either be a Poisson process or deterministic. We contemplate two ways of constructing the Poisson process with rate $\lambda$: either by fixing n, the number of arrivals or by setting in advance T, the maximum duration for the observation period. The parameters of the three strategies given in Table 1 are chosen to ensure comparability of the simulation results. Indeed, on average, the time period length and the number of observations are the same for the three strategies.

Table 1 Parameters for the different sampling strategies

5.1 Description of the compared sampling strategies

The first corresponds to the sampling approach studied in this paper.

• 1. We fix n and we generate $T_1, T_2, \ldots , T_n$ as the first n arrivals of a Poisson process with rate $\lambda$. The interarrival times, denoted as $\Delta _i = T_{i+1} - T_{i}$, are independent Exponential($\lambda$) random variables. Then we generate a Gaussian vector $(X_{T_1},\ldots ,X_{T_n})$ with zero mean and covariance matrix $\Sigma _1$ with entries $\sigma _X(T_i-T_j)$.

• 2. We fix n and we consider deterministic values $t_1,\ldots ,t_n$ with increment $\lambda ^{-1}$ the mean value of interarrival time of the previous Poisson process. Then we generate a Gaussian vector $(X_{t_1},\ldots ,X_{t_n})$ with zero mean and covariance matrix $\Sigma _2$ with entries $\sigma _X(t_i-t_j)$.

• 3. We fix T, the maximum duration for the observation period, equal to the mean value of the last arrival time $T_n$ in the strategy 1, i.e. $T=\lambda ^{-1} n$. To simulate realisation of Poisson process on [0, T] with rate $\lambda$, we generate N the number of arrivals on [0, T] from the Poisson distribution with parameter $\lambda T$. We simulate $\tau _1,\ldots ,\tau _N$ as an ordered sample of the uniform distribution [0, T]. Then we generate a Gaussian vector $(X_{\tau _1},\ldots ,X_{\tau _N})$ with zero mean and covariance matrix $\Sigma _3$ with entries $\sigma _X(\tau _i-\tau _j)$.

5.2 Summary of the simulation study and future directions

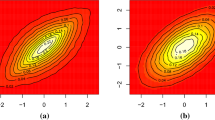
Numerical results are given in Table 2 and Figs. 1 and 2. We simulate from a Gaussian zero mean stationary process with memory parameter $d=.25$. We compare estimation results for the mean and the memory parameter for different rates of the renewal process $(\lambda =$ 1/2, 1 and 2).

Table 2 Bias and standard deviation of the sample mean and the Local Whittle estimate

Fig. 1

Estimation of the distribution of local Whittle estimate for $n=500$ and $\lambda = 1/2 \text { (left), } 1 \text { (middle) and } 2 \text { (right). }$ Estimation is based on 1000 independent replications of the Gaussian process with zero mean $\mu = 0$, long memory parameter $d=.25$ and $n=1000$

Fig. 2

Estimation of the distribution of sample mean for $n=500$ and $\lambda = 1/2 \text { (left), } 1 \text { (middle) and } 2 \text { (right). }$ Estimations are based on 1000 independent replications of the Gaussian process with zero mean $\mu = 0$, long memory parameter $d=.25$ and $n=1000$

We can see that as far as the mean is concerned, there is no noticeable difference between these three strategies with little changes when the rate $\lambda$ varies. For the memory parameter d, we also see that the bias and the standard deviations remain of the same orders across all three strategies. We retrieve the classical challenge of rightly choosing the bandwidth in local Whittle estimation. This is more acute in our context where the sampled process is neither Gaussian nor linear, despite the fact that the original process is Gaussian. It would be worth further investigating the third strategy of randomly sampling from a continuous time process at fixed period length T. One difficulty resides in the fact that interarrival times will be dependent.

Appendix: Proof of Lemma 2

Proof

The proof is essentially based on Corollary 2 and a well known cumulant formula.

Without loss of generality, we can assume that the Poisson rate is 1. The process Y is 4th order stationary as the conditional joint distribution of $(Y_k,Y_{k+h},Y_{k+r},Y_{k+s})$ given $(T_1,\dots ,T_{k+\max (h,r,s)})$ is a multivariate normal with variance-covariance matrix $M(T_k,T_{k+h},T_{k+r},T_{k+s})$ given by

$$\begin{aligned}{} & {} M(T_k,T_{k+h},T_{k+r},T_{k+s}) \nonumber \\{} & {} \quad :=\left( {\begin{matrix} \sigma _X(0)&{}\sigma _X(T_{k+h}-T_k)&{}\sigma _X(T_{k+r}-T_k)&{}\sigma _X(T_{k+s}-T_k)\\ \sigma _X(T_{k+h}-T_k)&{}\sigma _X(0)&{}\sigma _X(T_{k+r}-T_{k+h})&{}\sigma _X(T_{k+s}-T_{k+h})\\ \sigma _X(T_{k+r}-T_k)&{}\sigma _X(T_{k+r}-T_{k+h})&{}\sigma _X(0)&{}\sigma _X(T_{k+s}-T_{k+r})\\ \sigma _X(T_{k+s}-T_k)&{}\sigma _X(T_{k+s}-T_{k+h})&{}\sigma _X(T_{k+s}-T_{k+r})&{}\sigma _X(0) \end{matrix}}\right) \nonumber \\ \end{aligned}$$

(41)

which is k free. Hence it is enough to establish the lemma when $k=0$. We apply the total law of cumulance formula (Brillinger 1969), which for the sake of clarity, we remind here: for all random vectors $Z=(Z_1,\ldots ,Z_n)'$ and W, we have

$$\begin{aligned} \textrm{cum}(Z)=\sum _{\pi }\textrm{cum}\left[ \textrm{cum}(X_{\pi _1}\vert W),\ldots ,\textrm{cum}(X_{\pi _b}\vert W)\right] \end{aligned}$$

(42)

where $X_{\pi _j}=(X_i,i\in \pi _j)$, and $\pi _1,\ldots ,\pi _b$, ($b=1,\ldots ,n$) are the blocks of the permutation $\pi$, and the sum is over all permutations $\pi$ of the set $\{1,2,\ldots ,n\}$.

But condition on T, the process $Y_t$ is jointly zero-mean Gaussian and therefore $\mathbb {E}(Y_t\vert T)=0$ as well as $\textrm{cum}(Y_i,Y_j,Y_k,Y_\ell \vert T)=\textrm{cum}(Y_i,Y_j,Y_k\vert T)=0$ for all $i,j,k,\ell$. Hence applying (42) to $Y_t$ with $W=T$, only the two-by-two partitions of $\{0,h,r,s\}$ will survive. and since $\textrm{cum}(U,V)=\text {Cov}(U,V)$, we get from (41)

$$\begin{aligned} \textrm{cum}(Y_0,Y_{h},Y_{r},Y_{s})=\,&\textrm{Cov}(\sigma _X(T_h),\sigma _X(T_r-T_s))+\textrm{Cov}(\sigma _X(T_r),\sigma _X(T_h-T_s))\nonumber \\&+\textrm{Cov}(\sigma _X(T_s),\sigma _X(T_r-T_h)). \end{aligned}$$

(43)

Note that for $h< \min (r,s)$, $\textrm{Cov}(\sigma _X(T_h),\sigma _X(T_r-T_s))=0$. Moreover

$$\begin{aligned}&\sum _{1\le r \le h \le s \le n} |\textrm{Cov}(\sigma _X(T_h),\sigma _X(T_r-T_s)) |\\&\quad \le \sum _{1\le r \le h \le s \le n} \textrm{Var}(\sigma _X(T_h))^{1/2} \textrm{Var}( \sigma _X(T_s-T_r))^{1/2}\\&\quad \le \sum _{1\le r \le h \le s \le n} h^{-\alpha /2} (1 +s-r)^{-\alpha /2} \\&\quad \le h^{-\alpha /2} \sum _{1\le r \le h } \sum _{t=1}^n t ^{-\alpha /2} \\&\quad \le h^{1-\alpha /2} {\left\{ \begin{array}{ll} n^{1-\alpha /2} = n^{2d -1/2 }&{} \text {if d<1/4} \\ \log (n) &{} \text {if}\,\, d\ge 1/4 \\ \end{array}\right. }\\&\le {\left\{ \begin{array}{ll} n^{4d -1 }&{} \text {if} \,\, d<1/4 \\ \log (n) &{} \text {if}\,\, d\ge 1/4 \\ \end{array}\right. }\\&\le Cn^{2d} \; \text { for all } \; 0< d <1/2. \end{aligned}$$

The last configuration is

$$\begin{aligned} \sum _{r,s=1}^h | \textrm{Cov}(\sigma _X(T_h),\sigma _X(T_r-T_s))|&= \sum _{r,s=1}^h | \textrm{Var}(\sigma _X(T_h))^{1/2} \textrm{Var}( \sigma _X(T_s-T_r))^{1/2}\\&\le h^{-\alpha /2} \sum _{t=1}^h (h-t) t^{-\alpha /2} \\&\le h^{-\alpha /2 } {\left\{ \begin{array}{ll} C h^{1-\alpha /2} = Ch^{2d -1/2 }&{} \text {if} \,\,d<1/4 \\ \log (h) &{} \text {if}\,\, d\ge 1/4 \\ \end{array}\right. } \\&\le Cn^{2d} \; \text { for all } \; 0< d <1/2. \end{aligned}$$

Therefore uniformly in h we have

$$\begin{aligned} \sum _{r,s=1}^n | \textrm{Cov}(\sigma _X(T_h),\sigma _X(T_r-T_s))| \le Cn^{2d}. \end{aligned}$$

For the remaining two terms in the right hand side of (43) we have, for fixed h,

$$\begin{aligned} \sum _{r,s=1}^n | \textrm{Cov}(\sigma _X(T_r),\sigma _X(T_h-T_s))|&= \sum _{r,s=1}^n | \textrm{Cov}(\sigma _X(T_s),\sigma _X(T_h-T_r))| \\&\le \sum _{r,s=1}^n \textrm{Var}(\sigma _X(T_s))^{1/2} \textrm{Var}( \sigma _X(T_h-T_r))^{1/2}\\&\le \sum _{r,s=1}^n s^{-\alpha /2} (1+|h-r|)^{-\alpha /2} \\&\le C {\left\{ \begin{array}{ll} n^{2-\alpha } = n^{4d -1 }&{} \text {if}\,\, d<1/4 \\ \log (n)^2 &{} \text {if}\,\, d\ge 1/4 \\ \end{array}\right. } \\ {}&\le Cn^{2d} \; \text { for all } \; 0< d <1/2. \end{aligned}$$

This concludes the proof of (37).

Let us now prove (38). Note that

$$\begin{aligned} \sum _{h,r,s=0}^n \textrm{cum}(Y_0,Y_{h},Y_{r},Y_{s})&= 3 \sum _{h,r,s=1}^n \textrm{Cov}(\sigma _X(T_h),\sigma _X(T_r-T_s)) \nonumber \\&= 6 \sum _{h=1}^n\sum _{r<s=1}^n \textrm{Cov}(\sigma _X(T_h),\sigma _X(T_r-T_s)). \end{aligned}$$

(44)

Moreover, we have

$$\begin{aligned} \sum _{h,r,s=1}^n |\textrm{Cov}(\sigma _X(T_h),\sigma _X(T_r-T_s)) |&\le C \sum _{h,r,s=1}^n h^{-\alpha /2} (1+|r-s|)^{-\alpha /2} \\&\le C \sum _{h=1}^n h^{-\alpha /2} \sum _{t=1}^n (n-t) t^{-\alpha /2} \\&\le C {\left\{ \begin{array}{ll} n n^{2-\alpha } = n^{4d }&{} \text {if}\,\, d<1/4 \\ n \log (n)^2 &{} \text {if}\,\, d> 1/4 \\ \end{array}\right. } \\&\le Cn^{4d} \end{aligned}$$

In the particular case $d=1/4$ (where we still have $\alpha =2$), a supplementary term $\log (n)$ is needed in the bound. Indeed we split the sum in the right hand side of (44) into 3 configurations. when $1 \le h \le r< s \le n$ the covariance $\textrm{Cov}(\sigma _X(T_h),\sigma _X(T_r-T_s))$ is zero. When the sum is over $1 \le r< h \le s \le n$, we get

$$\begin{aligned} \sum _{1 \le r< h \le s \le n} |\textrm{Cov}(\sigma _X(T_h),\sigma _X(T_r-T_s)) |&\le C \sum _{s=1}^n \sum _{h=1}^s h^{-1 } \sum _{r=1}^{h-1} (s-h + h-r)^{-1} \\&\sim C \sum _{s=1}^n \sum _{h=1}^s h^{-1 } \left( \log (s) - \log (s-h) \right) \\&= -C \sum _{s=1}^n \sum _{h=1}^s (h/s)^{-1 } \log (1-h/s) (1/s) \\&\sim -C \sum _{s=1}^n\left( \int _{0}^1 \frac{ \log (1-x)}{x} \, dx\right) = C\frac{\pi ^2}{6} n. \end{aligned}$$

For the last sum over $1 \le r < s \le h \le n$ (where we will need the $\log$ term) we have

$$\begin{aligned} \sum _{1 \le r <s \le h \le n} |\textrm{Cov}(\sigma _X(T_h),\sigma _X(T_r-T_s)) |&\le C \sum _{h=1}^n h^{-1 } \sum _{s=1}^h \sum _{r=1}^{s-1} (s-r)^{-1} \\&= \sum _{h=1}^n h^{-1 } \sum _{t=1}^h (h-t) t^{-1} \\&= \sum _{h=1}^n \sum _{t=1}^h (1-t/h) t^{-1} \\&\sim C \sum _{h=1}^n ( \log (h) -1 ) \sim C n \log (n). \end{aligned}$$

This completes the proof of (38) in Lemma 2. $\square$