Measurement of density in axisymmetric jets using a novel background-oriented schlieren (BOS) technique

Abstract

A novel application of the adaptive Fourier–Hankel (AFH) Abel algorithm to reconstruct the radial density distribution of axisymmetric jets is presented. The fluid is imaged using the non-intrusive path-integrated background-oriented schlieren (BOS) technique. BOS images are cross-correlated to obtain background displacements that are proportional to the first derivative of the refractive index. The critical step is deconvolving the projected displacements. The AFH method is applied to simulated displacement data to validate the use of averaged turbulent fluctuations that approximate an axisymmetric field. The influence of experimental noise and variations in the flow on the accuracy of the method is discussed. The limitations of the system are demonstrated by applying it to low- and high-Reynolds (Re) number jets. The high-Re jets are produced from a high-pressure fuel injector operating at nozzle pressure ratios of 2, 3, and 4.

1 Introduction

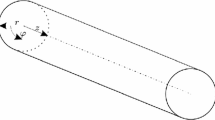
The background-oriented schlieren (BOS) technique is a non-intrusive optical line of sight flow visualisation tool that employs cross-correlation image analysis to investigate inhomogeneous fluids. BOS cross-correlates images to convert distortions in a distant background plane to path-integrated displacement values. The displacements are a result of density gradients between the observer and background, which deflect the light from its natural path, as shown in Fig. 1.

Fig. 1

Optical layout of BOS. Adapted from Raffel et al. (1998)

BOS was pioneered by Dalziel et al. (2000) and Raffel et al. (2000) who developed most of the early theory. The practical aspects were subsequently documented by Richard and Raffel (2001). These studies focussed on the large-scale applicability of BOS, but it has since been shown to excel in laboratory environments (Venkatakrishnan and Meier 2004; Atcheson et al. 2007; Reinholtz et al. 2010; Todoroff et al. 2014).

Goldhahn and Seume (2007) investigated the sensitivity, accuracy, and resolution of BOS. The sensitivity depends primarily on the experimental set-up, such as the focal length of the camera lens, the distance of the object from the camera and background, and the smallest detectable displacement in the background plane. Conversely, the accuracy and resolution are predominantly determined by the digital image processing algorithms.

Previous campaigns applied BOS to reconstruct the density from a single perspective. Elsinga et al. (2004) mapped the density of a two-dimensional Prandtl–Meyer expansion fan using calibrated colour schlieren (CCS) and BOS. The use of a two-dimensional geometry enabled the direct integration of the density gradients to obtain the local distribution. CCS and BOS agreed to within 2 and 3 % of Prandtl–Meyer expansion theory, respectively. Inaccuracies in BOS were due to insufficient resolution limiting the accuracy of the cross-correlation algorithm and the depth of field, which controls the focus of the density object. The dynamic range of BOS was reported to be five times greater than that of CCS. Hargather and Settles (2012) arrived at the same result by applying calibrated schlieren, colour schlieren, and BOS to a two-dimensional laminar free-convection boundary layer.

Higher dimensional problems require multi-camera arrangements to obtain a complete and accurate image. The local density field is calculated using tomographic algorithms like filtered back-projection tomography (FBPT). FBPT is based on the principle of Radon transforms, which relate an object’s projection to their cross section. Traditionally, FBPT has been used with BOS due to its popularity in computed tomography and its applicability to all flow geometries (Venkatakrishnan and Meier 2004; Sourgen et al. 2012; Goldhahn and Seume 2007).

A derivative of the Radon transform is the Abel transform, which is an alternative method that is restricted to axisymmetric flows. Subsequently, only a single camera system is required. Abel methods also have the similar noise-related issues as well as suffering from a singularity at the axis of symmetry. Fourier methods, such as the Fourier–Hankel (FH) method, account for the singularity and greatly reduce computation time (Ma et al. 2008). In general, the implementation of Abel algorithms is simpler and not as computationally expensive as FBPT.

The main criticism of Radon algorithms is that they are susceptible to noise. In the case of the FBPT, a filter is used to reduce the sensitivity to noise. Venkatakrishnan and Meier (2004) and Sourgen et al. (2012) implemented a Shepp–Logan filter, but the authors noted that this still led to a small amount of blurring. Ma et al. (2008) suggested the adaptive Fourier–Hankel (AFH) method as a way of accounting for noise and minimising truncation error without a separate filter function. Applications of tomographic algorithms to BOS have been successful; however, they usually lack a detailed error analysis.

Beginning with a description of the methodology, a novel application of the AFH method is proposed. An assessment of the uncertainty in the procedure is provided by examining a synthetic model that simulates typical projected displacements from a cylindrical flow. A low-Reynolds (Re) number helium jet was imaged to verify the method by isolating experimental errors from inversion errors. Mean density measurements across a turbulent helium jet were obtained. The density half-radius at nozzle pressure ratios (NPR) of 2, 3, and 4 was found to scale in agreement with Sautet and Stepowski (1994).

2 Principles of the BOS technique

2.1 Theory

The theory for BOS is well established (Raffel et al. 2000; Richard and Raffel 2001; Venkatakrishnan and Meier 2004; Goldhahn and Seume 2007) so only a brief summary follows.

A typical set-up consists of a light source, a background pattern, a camera, and an object of interest, as shown in Fig. 1. A reference image is taken of the background without any disturbances in the field of view, and the refracted image is obtained with the density object in place. Features in the background appear to move when light rays travelling through the medium are refracted. The displacements are proportional to density gradients in the medium (Eq. 3). The relationship between refractive index, n, and density, $\rho {}$, is given by the Gladstone–Dale equation

$$\begin{aligned} \frac{n-1}{\rho } = G \left( \lambda \right) \end{aligned}$$

(1)

where the Gladstone–Dale constant is

$$\begin{aligned} G \left( \lambda \right) = 2.2244 \times 10^{-4} \left( 1+ \left( \frac{6.7132\times 10^-8}{\lambda } \right) ^2 \, \right) \end{aligned}$$

Figure 2 outlines the procedure for measuring density from BOS data. The key steps are:

• 1. The reference and refracted images are cross-correlated (Raffel et al. 1998) to determine the background displacements, $\Delta$.

• 2. Deflections, $\epsilon$, are evaluated based on the geometric set-up (Eq. 2).

• 3. For two-dimensional flows, the refractive index field is calculated by solving the Poisson equation. The three-dimensional case requires the devolution of the projected deflections using tomography.

• 4. The absolute density is calculated using the Gladstone–Dale relation (Eq. 1).

Based on the geometry in Fig. 1, the deflections in the x and y directions have the same form. The deflection in the y direction, $\epsilon _{y}$, is approximated by

$$\begin{aligned} \epsilon _{y} \approx \frac{\Delta (y)}{Z_{\text {D}}} = M \left( \frac{\Delta _{\mathrm {image}}(y)}{Z_{\text {D}}} \right) \end{aligned}$$

(2)

The background displacements, $\Delta (y)$, are converted to the image displacements, $\Delta _{\mathrm {image}}(y)$, via a magnification factor, M. The deflections are a function of the variations in refractive index integrated over the width of the object plane, $\Delta {Z_{\text {D}}}$, such that

$$\begin{aligned} \epsilon _{y} = \frac{1}{n_0} \int \limits _{-\Delta {Z_{\text {D}}}/2}^{\Delta {Z_{\text {D}}}/2}{\frac{\partial {n}}{\partial {y}}}\;\text {d}{z} \end{aligned}$$

(3)

where $n_{0}$ is the refractive index in the ambient fluid. Combining Eqs. 2 and 3 reduces the problem to the Poisson equation, which is an elliptic partial differential equation given by

$$\begin{aligned} \frac{\partial ^2{n}}{\partial ^2{x}} + \frac{\partial ^2{n}}{\partial ^2{y}} = S(x,y) \end{aligned}$$

(4)

Equation 4 can be solved to yield the refractive index field and consequently the density (Eq. 1). This is typically done for two-dimensional flows where there is a priori knowledge of $\Delta {Z_{\text {D}}}$ (Elsinga et al. 2004; Vasudeva et al. 2005).

Fig. 2

Flow chart for calculating local density fields with BOS. Adapted from Jensen et al. (2005)

Quasi-two-dimensional flows with an axisymmetric geometry must be deconvolved using tomography. Only one viewing angle is needed since the same projection is seen from every perspective. The Abel inversion is suitable for extracting the density (Klinge et al. 2003), but can be very sensitive to noise. Subsequently, filtering algorithms such as FBPT have been employed to account for this (Venkatakrishnan and Meier 2004).

Multi-camera systems are required to reconstruct the complete three-dimensional density field (Atcheson et al. 2007; Ota et al. 2011; Todoroff et al. 2014; Hartmann et al. 2015), but this is beyond the scope of the paper. The current work seeks to extend the quantitative aspects of a single camera system.

2.2 Experimental design considerations

The background pattern requires sufficient contrast and detail so that cross-correlation algorithms can accurately track the displacements. Since the pattern is synthetically generated, there is significant control over its properties such that the background can be populated in a number of ways and to suit the experiment. Common approaches are to use natural backgrounds that utilise the surroundings, randomly distributed dots, and wavelet noise. However, natural backgrounds are suited to full-scale testing so will not be discussed further (Hargather and Settles 2010).

Randomly distributed dots that are optimised for a narrow band of system resolutions have commonly been used. The dot parameters are governed by the seeding parameters employed in particle image velocimetry (PIV) (Raffel et al. 1998). Atcheson et al. (2009) demonstrated the advantage of replacing the dots with multi-scale wavelet noise. High noise content is maintained over a range of spatial frequency, thus improving the reliability of the cross-correlation algorithms. Details on wavelet noise have been published by Cook and DeRose (2005).

The camera must be focussed on the background plane in order to resolve features in the pattern. Consequently, the density object will never be in sharp focus (Fig. 1). Moving the object closer to the background while keeping the camera fixed improves the resolution of the density gradients. However, for the same deflection, a smaller displacement is observed (Eq. 2), thereby reducing the system sensitivity (Goldhahn and Seume 2007).

One way to minimise object blur is to increase the f-stop, but greater background illumination is needed to maintain the same exposure time. An effective arrangement is to backlight the system. Other configurations, such as forward lighting, are generally reserved for confined environments (Reinholtz et al. 2010).

3 The AFH method

The Abel transform is a mathematical tool used for the tomographic analysis of spherically and cylindrically symmetric objects (Ramm and Katsevich 1996). The concept is illustrated in Fig. 3. The forward transform of the radially distributed refractive index difference, $\delta (r)$, gives the projected refractive index field, n(y). This is expressed as

$$\begin{aligned} n(y) = 2 \, \int \limits _{r}^{R_0}{\frac{\delta (r)\,r}{\sqrt{r^2-y^2}}}\;\text {d}{r} \end{aligned}$$

(5)

where

$$\begin{aligned} \delta (r)=\frac{n}{n_0}-1 \end{aligned}$$

(6)

It follows that the inverse is given by

$$\begin{aligned} \delta (r)&= -\frac{1}{\pi } \, \int \limits _{y}^{R_0}\frac{\left( \frac{\partial {n(y)}}{\partial {y}}\right) }{\sqrt{y^2-r^2}}\;\text {d}{y}\nonumber \\&\equiv -\frac{1}{\pi } \, \int \limits _{y}^{R_0}\frac{\epsilon (y)}{\sqrt{y^2-r^2}}\;\text {d}{y} \end{aligned}$$

(7)

and noting that there is no numerical differentiation of the data because $\partial {n(y)}/\partial {y}$ is proportional to the deflections, $\epsilon (y)$, via Eq. 3.

Fig. 3

A geometric interpretation of the Abel inversion illustrating the relationship between a the radial distribution $\delta (r)$, b the refractive index field n(y), and c the projected displacements $\Delta (y)$. Adapted from Sáinz et al. (2006)

Dasch (1992) discretised Eq. 7 such that $\delta (r)$ is given by a weighted sum of projections. Following the same notation for a data set with N samples and data spacing of $\Delta {y} = \Delta {r} = R_0/N$, Eq. 7 is reduced to

$$\begin{aligned} \delta (r_i) = \sum \limits _{j=0}^{N}{D_{ij} \epsilon _{j}} \end{aligned}$$

(8)

where $\delta (r_i)$ is the relative refractive index difference at every distance $r_i = i \, \Delta {r}$ and $\epsilon _j$ is the deflection angle at $y_j = j \, \Delta {y}$ with $i~\hbox{and}~j = 0, 1, \dots , N$. The coefficient matrix, $D_{ij}$, is based solely on the mesh so can be pre-computed.

The classic Fourier–Hankel method takes advantage of the Abel–Fourier–Hankel cycle of integral transforms (Ma et al. 2008; Chehouani and Fagrich 2013) to determine $D_{ij}$. The method takes the Fourier transform of the projected data before performing the inverse Hankel transform to evaluate the radial distribution. Denoting the Abel, Fourier, and Hankel operators as $\mathscr {A}$, $\mathscr {F}$, and $\mathscr {H}$, respectively, the inversion is

$$\begin{aligned} \delta (r) = \mathscr {H}^{-1} \left[ \mathscr {F} \left[ \mathscr {A}\left[ \epsilon (y) \right] \right] \right] \end{aligned}$$

(9)

Approximating the integral transforms, the coefficient matrix for the FH method is

$$\begin{aligned} D_{ij} = -{\frac{\alpha }{N}} \, {\sum \limits _{j=0}^{N}} \, {\sum \limits _{k=0}^{N}} \, {\sin {\left( \frac{\alpha \pi {j}{k}}{N}\right) }} \, {J_0{\left( \frac{\alpha \pi {k}{i}}{N}\right) }} \end{aligned}$$

(10)

where ${0}\le {i}\le {N}$ and $J_0$ is the zero-order Bessel function. Equation 10 is the FH method with a smoothing coefficient $\alpha {}$ that is given a value between 0 and 1. The method can suffer from large truncation errors since it drops the high-frequency components in the Fourier transform.

The modification proposed by Ma et al. (2008) reduces the truncation error by including the frequencies from $N+1$ to $N/\alpha$. Thus, extending the upper limit of the second summation, the coefficient matrix for the AFH method is

$$\begin{aligned} D_{ij} = -{\frac{\alpha }{N}} \, {\sum \limits _{j=0}^{N}} \, {\sum \limits _{k=0}^{\left[ N/\alpha \right] }} \, {\sin {\left( \frac{\alpha \pi {j}{k}}{N}\right) }} \, {J_0{\left( \frac{\alpha \pi {k}{i}}{N}\right) }} \end{aligned}$$

(11)

where $[{N/\alpha }]$ denotes the closest less than or equal to integer $N/\alpha$.

Semi-analytical interpolation schemes (Dasch 1992; Kolhe and Agrawal 2009) have traditionally been used to calculate the coefficients, but perform poorly near the singularity at the lower limit of the Abel inversion. Noise can also propagate through the inversion and introduce artificial structures in the final solution. The FH method accounts for the singularity, and the AFH improves on this by reducing the truncation errors.

4 Error analysis of the AFH method

Ma et al. (2008) explored the accuracy of the AFH method by demonstrating smaller inversion errors as a result of the insensitivity to noise. Chehouani and Fagrich (2013) used simulated Moire strips of a naturally convected flow to demonstrate the robustness of the AFH method. An optimal range of $\alpha$ was determined to range from 0.1 to 0.2, with the lower limit adopted for the present work.

The error analysis by Ma et al. (2008) and Chehouani and Fagrich (2013) assessed the performance when considering data sets contaminated with Gaussian noise. The approach taken in this paper was formulated in such a way as to model the expected characteristics of measurements from BOS experiments that accounts for small- and large-scale structures in the flow.

4.1 Modelling BOS data

Synthetic displacement profiles expected from the projection of a cylindrical object with a constant density distribution (Fig. 3c) are given by

$$\begin{aligned} \Delta (y) \thicksim \frac{\partial {n(y)}}{\partial {y}} = \frac{-y}{\theta {}^3 \sqrt{2\pi {}}}\text { exp} \left( \frac{-y^2}{2\theta {}^2} \right) \end{aligned}$$

(12)

where $\theta {}$ is a shape parameter that accounts for the refractive properties and variations of the flow geometry. The effects are shown in Fig. 4. Noting that $\Delta {} \thicksim \epsilon {}$, the analytical Abel inversion (Eq. 7) for $\delta (r)$ is

$$\begin{aligned} \delta (r)=\frac{1}{2\pi \theta {}^2} \text {exp}\left( \frac{-r^2}{2\theta ^2}\right) \end{aligned}$$

(13)

Inversion errors were calculated relative to Eq. 13. The test profiles are symmetric so were generated on an arbitrary half domain of 0 to 1 for $y/ {D}$ and $r/{D}$.

Global errors introduced by large-scale variations expected in the data, such as variations of the flow geometry, were emulated by varying $\theta {}$ within an upper ($\theta {}_2$) and lower ($\theta {}_1$) bound. Thus, we can define $\theta {}_\Delta {}$ as $\theta {}_2 - \theta {}_1$ as the range over which an unsteady flow may be expected to vary. Local errors, which include a combination of smaller scale variations and experimental noise, were applied by controlling the signal-to-noise ratio (SNR) of the individual signals. The parameters used to refer to the two types of error analysed are $\theta {}_\Delta {}$ and SNR.

Experimentally, an increase in $\theta {}_\Delta {}$ represents larger shot-to-shot variations due to turbulent fluctuations in the flow field of interest. Background noise contributing to the SNR is generally a result of small thermal variations that contaminates the data.

Figure 4a illustrates the upper ($\theta {}_2 = 15$) and lower ($\theta {}_1 = 5$) bounds imposed on the displacements such that $\theta {}_\Delta {} = 10$. These are represented by the solid lines with the remaining test profiles falling in between. The overline indicates the average of all profiles and is depicted by the dashed line. Noise is added to each curve so that there is an SNR of 35. The theoretical radial distributions are shown in Fig. 4b.

Fig. 4

Example of modelled BOS data with SNR = 35 and $\theta {}_\Delta {} = 10$

4.2 Equivalence of means and RMS

The averaged displacements of axisymmetric flows over a sufficient number of samples are assumed to approximate an axisymmetric field, thus enabling the application of the Abel inversion. To verify the validity of this assumption, 1000 noise-free signals (Eq. 12) were generated for $\theta {}_\Delta {} = 10$. A single mean radial distribution, $\overline{\delta (r)}$ and $\overline{\overline{\delta (r)}}$, was reconstructed in two ways:

• 1. $\overline{\delta (r)}$, the solution that is evaluated by finding the radial distribution of the mean displacements, $\overline{\Delta (y)}$, as shown in Fig. 4.

• 2. $\overline{\overline{\delta (r)}}$, the mean radial distribution obtained by averaging every $\delta (r)$ calculated from the corresponding $\Delta (y)$.

Fig. 5

Error of the mean radial distributions calculated using the AFH method with SNR = $\infty$ and $\theta {}_\Delta {} = 10$

The discrete AFH algorithm (Eq. 9) was used to calculate the radial distributions from the test profiles. No difference was found between $\overline{\delta (r)}$ and $\overline{\overline{\delta (r)}}$. The normalised root-mean-square (NRMS) error relative to the theoretical solution is negligible (Fig. 5). Only one case is shown since the means were found to be equivalent.

4.3 Statistical convergence of the error based on sample size

The number of samples required to minimise the NRMS error of $\delta (r)$ was examined for SNRs from 1 to 100. Error convergence was defined as the relative change in error that was less than 0.001 %. The error criterion was tested over 10 simulations at each test point. The effects of large-scale variations were considered for a single case with $\theta {}_\Delta {} = 15$.

The average sample size for the error to converge quickly drops as the SNR increases from 1 to 50, as shown in Fig. 6. Even though the NRMS error has converged for low SNRs, Fig. 6 does not give any indication of the absolute accuracy of the solution. The test only provides a guide to determine an appropriate number of samples based on an expected SNR.

Fig. 6

Number of samples required at SNRs of 1–100 for the relative NRMS error difference of $\delta (r)$ to reach a value less than 0.001 % with $\theta {}_\Delta {} = 15$

4.4 Effects of small- and large-scale noise

The influence of both small- and large-scale variations on the inversion error was examined to establish an uncertainty range for SNRs less than 100 and for $\theta {}_\Delta {}$ < 15. The sample size of the mean was varied from 200 to 2000 in steps of 50; however, the error distributions followed similar trends so only the test case for 1000 samples is shown (Fig. 7). The vertical variation was effectively constant at high SNR so the y-axis is reduced to 0 to 40.

The error peaks at low SNRs and large $\theta {}_\Delta {}$. This region is indicative of a turbulent flow with noisy data and is likely to have little to no physical relevance when the SNR approaches 0.

The simple error estimate here can be deceptive at low SNRs because it does not completely account for artificial structures created by the algorithm to satisfy the boundary conditions of the Abel inversion. Thus, the errors predicted in this section are only applicable when the cross-correlation algorithm is able to resolve the displaced background plane.

Fig. 7

Effect of the SNR and large-scale variations on the NRMS of the AFH method. Selected contours have been shown for clarity

4.5 Summary

The AFH method accurately calculated the radial distribution of noise-free test profiles. The simplified model demonstrated the equivalence of the two means, $\overline{\delta (r)}$ and $\overline{\overline{\delta (r)}}$, suggesting that the average can be performed before or after the inversion step. However, for experimental flows, and in particular turbulent ones, it is still necessary to calculate the average prior to the inversion because the algorithm relies on a precise definition for the axis of symmetry. Therefore, the first definition of the mean radial distribution ($\overline{\delta (r)}$) is used for the rest of the paper.

Two sources of error in the method have been identified. The accuracy of the algorithm was shown to improve when a higher number of samples were used to calculate the mean. The introduction of simulated flow variations ($\theta {}_\Delta {}$) and experimental noise (SNR) demonstrated that the resulting reconstruction contained larger errors. An 11 % error is returned for $\theta {}_\Delta {} < 10$.

Combining a simulated error model such as this with experimentally observed SNRs and standard deviations can provide an additional uncertainty bound on the measurements.

5 Experiments and methodology

The experiments were set up according to Fig. 1 with the parameters given in Table 1. The components were mounted on an optical table to ensure that they were aligned along the same optical axis. A wavelet noise background pattern was printed on a film transparency and backlit by a 28 by 36 array of $532\, \text {nm}$ LEDs with a pulse width of $100\,\upmu \mathrm {s}{}$ (Willert et al. 2012). A diffuser was used to uniformly distribute the light.

Images of a low-Re and turbulent jet were acquired using a high-resolution 16-bit PCO 4000 monochrome camera with a full CCD sensor size of 4008 by $2764\, \text {pixels}$ and a pixel size of $9\,\upmu \mathrm {m}{}$. A $200\, \text {mm}{}$ Nikon lens was used with an f-stop of 22 to maximise the depth of field. The camera was operated in single shutter mode with an exposure of $50\,\upmu \mathrm {s}{}$. A delay of $25\,\upmu \mathrm {s}{}$ accounted for any unexpected delays from the signal generator used to synchronise the camera and light source. Helium was used for all experiments due to its low density compared to air and was monitored via a flowmeter. Derived density values were compared with the centreline jet exit density measured with BOS for each experiment.

The PIVview 2C cross-correlation software was used to process the raw data and extract pixel displacements. The software has a reported sub-pixel accuracy of $0.05\, \text {pixels}{}$ (Willert 2015). A multi-grid cross-correlation algorithm (Soria 1998) with an initial interrogation window size of 128 by $128\, \text {pixels}{}$ and final size of 24 by $24\, \text {pixels}{}$ was used. A 75 % overlap was set to oversample the data and ensure that there were sufficient data points for the AFH method.

Preliminary tests imaged the nozzle and injector in two orthogonal orientations. The mean fields satisfied the axisymmetric approximation. Analysing the correlation planes of the reference and refracted images showed that the SNR ranged from 35 to 75. Thus, 1000 statistically independent images were acquired for each test (Fig. 6). The same analysis to obtain the SNR may be performed on images from different systems since the value depends only on the strength of the cross-correlation peak relative to the background noise. Large-scale variations were estimated by the RMS of the displacements. Distances and densities were normalised with the nozzle exit diameter, D, and the ambient density, $\rho _0$, respectively.

Table 1 Experiment parameters for the low-Re nozzle and HDEV 1.2 injector

5.1 Verification of the method

A low-Re jet issuing from a 16.8 contraction ratio nozzle (Grandchamp et al. 2012) was imaged up to 1.6D downstream to verify the method. Large-scale structures upstream of the nozzle were minimised ($\theta {}_\Delta {} \approx 0$) by inserting a wire mesh after a flow straightening honeycomb pattern with a cell length and edge-to-edge distance of 20 and $4\, \text {mm}{}$, respectively (Mehta and Bradshaw 1979). Experimental errors in the deconvolved flow were expected to be predominantly associated with experimental noise.

5.2 Fuel injector

The steady-state turbulent flow from a Bosch HDEV 1.2 high-pressure fuel injector was imaged to examine the scaling characteristics of the jet. The camera was triggered $200\, \text {ms}{}$ after the start of injection into atmospheric air at NPRs of 2, 3, and 4. The field of view extended to $40\text {D}$ downstream.

6 Results and discussion

6.1 Low-Re number jet

The mean transverse displacements, $\Delta /{D}$, at axial locations of $x/{D}= 0.1$, 0.5, and 1 are shown in Fig. 8a. Additional peaks observed at $x/{D}= \pm {0.5}$ were not included in the synthetic model (Eq. 12), but the Abel inversion was unaffected since the data remained symmetric. As shown in Fig. 8b, there is a top hat profile along the core near the nozzle exit, which evolves into a Gaussian farther away, as expected for small Re (Table 1). The entire deconvolved density field is shown in Fig. 8c. The absolute density is shown to demonstrate that the actual density is extracted using the proposed method.

Fig. 8

Processed BOS data of a low-Re jet. a Mean transverse displacements, b radial density profiles, c reconstructed density distribution, and d RMS of displacements

Fig. 9

Instantaneous absolute displacements of the low-Re jet

The greatest variations are seen in the shear layer at $x/{D}= \pm {0.5}$, and these continue to grow downstream (Fig. 8d). The overall RMS is relatively small. This is consistent with the instantaneous displacements shown in Fig. 9 where there is little variation until $y/{D}= 0.3$. The jet has buoyancy-driven instabilities in the shear layer (Cetegen 1997).

There is a difference of 4.3 % between the measured and the derived densities. The discrepancy is most likely due to background and experimental noise. Based on a maximum $\theta {}_\Delta {} = 4.2 \times 10^{-2}$, which is given by the largest RMS value (Fig. 8d), and an SNR of 58, the predicted NRMS error is 5.2 % (see Fig. 7). Therefore, the result is within the uncertainty bounds determined by the simulated error analysis.

6.2 Fuel injector

6.2.1 Near field

Figure 10 reveals the contrasting flow produced by the high-Re jet compared to the low-Re case (Fig. 8). The snapshots were taken $1000\,\upmu \mathrm {s}{}$ after injection.

Fig. 10

Instantaneous absolute displacement fields of a turbulent helium jet $1000\,\upmu \mathrm {s}{}$ after injection

Fig. 11

Mean steady-state density fields of a turbulent helium jet

Fig. 12

Centreline mean density variation

Normalised mean density fields of the turbulent jet are shown in Fig. 11. The data are non-dimensionalised by the difference between the jet centreline and the ambient value, $\overline{\rho _{\mathrm {cl}}}-\rho _{0}$. The relative difference between the measured and derived densities of helium was found to be 6.0, 7.3, and 9.0 % for the NPRs of 2, 3, and 4, respectively. The average SNR over all tests was 38.

In relation to the low-Re jet, there are larger errors when imaging the smaller diameter nozzle. There were approximately 120 sample points across the nozzle exit for the calibration, while there were only 11 for the injector resulting in a lower spatial resolution. Errors may have been exacerbated by the combination of a lower SNR and the increased number of larger scale structures due to turbulence, which has been shown to contribute to the experimental error (Sect. 4).

An increase in the NPR is associated with a reduced spreading rate of the plume (Fig. 11). A linear decay of the centreline density occurs farther downstream for the higher NPRs, as shown in Fig. 12, which suggests a longer potential core. Panda (2007) observed the same trend in centreline density variation of a heated jet at different Mach numbers.

6.2.2 Mean density scaling

Radial density profiles at $x/{D}= 0.5$, 5, 12, 20, and 30 for the three NPRs have a Gaussian shape (Fig. 13a). The density half-radius, $\delta _{\rho }$, scaled according to the linear relation given by Sautet and Stepowski (1994):

$$\begin{aligned} \frac{\delta _{\rho }(x)}{{D}} = \delta _{\rho }^{0} \left( \frac{x-x_{\rho }}{{D}} \right) \end{aligned}$$

(14)

where the slope corresponds to the growth rate, $\delta _{\rho }^{0}$. The half-radius was determined by interpolating the experimental data. Fitting the data to Eq. 14 results in an excellent collapse of the profiles, as shown in Fig. 13b.

Fig. 13

a Radial mean density profiles of a turbulent helium jet. b Similarity collapse of the data

Fig. 14

Scaling of the density half-radius at NPRs of 2, 3, and 4

The half-radius value increases linearly from $x/D\approx 8, 10$, and 12 for NPRs of 2, 3, and 4, respectively. These locations correspond to the end of potential core in Fig. 12 and where the flow is expected to become self-similar (Richards and Pitts 1993). The fits for all NPRs fall on the same curve with a growth rate of $\delta _{\rho }^{0} = 0.991$ as shown in Fig. 14, which agrees with the He/air gas jet measurements by So et al. (1990).

7 Conclusions

The BOS technique is a simple diagnostic tool capable of non-intrusively obtaining path-integrated density gradients. Local mean density measurements are evaluated by deconvolving the field with tomographic algorithms, such as the AFH method. The resolution is limited by the optical geometry and the accuracy of the cross-correlation algorithm. However, the simplicity of the experiment enables a wide range of applications for BOS, particularly when traditional methods are difficult to implement.

The robustness of the AFH method to deconvolve axisymmetric BOS measurements was investigated. Mean radial distributions were reconstructed from synthetic test profiles contaminated with local noise and large-scale variations to emulate real data. The equivalence of the means $\overline{\delta {}}$ and $\overline{\overline{\delta {}}}$ was shown. The recommended approach is to average the data prior to the inversion to ensure an axisymmetric input. An error analysis provided a simple uncertainty bound on the pairing of BOS with the AFH method.

The approach was verified by examining the flow from a nozzle designed to have a low Re such that experimental errors were isolated from inversion errors. The radial density profiles exhibited the characteristic top hat shape expected near the nozzle exit. The error between the derived and measured exit centreline densities was 4.3 %. Larger errors of 5.98, 7.3, and 9 % at NPRs of 2, 3, and 4, respectively, were calculated in the analysis of a turbulent jet from a fuel injector.

Increasing the NPR of the injector led to a decreased spread of the plume, while the end of the potential core extended farther downstream. The flow obeyed self-similarity laws and scaled beyond the potential core. The radial mean density profiles scaled linearly with the density half-radius, resulting in a growth rate of 0.099. The experimental data collapsed excellently for all test cases.