1 Introduction

1.1 Previous Work

Background Oriented Schlieren (BOS) is a relatively new technique, (Meier 1999), that has proven its effectiveness to determine changes in the local density of phenomena in transparent compressible flows like shock waves Venkatakrishnan (2004). Goldhahn and Seume (2007) made a tomographic reconstruction from BOS applied to two parallel supersonic jets on a sub-expanded regime. Clem et al. (2012) compared the results obtained with BOS to shadowgraphs of a supersonic flow in the range of \( 1 < M < 1.7 \) produced by a convergent divergent nozzle. He obtained the shock pattern and associated it with screech, identifying 8 states. Tipnis (2013) obtained a good correlation between his BOS results and his simulation of a supersonic jet.

1.2 Description of the Technique

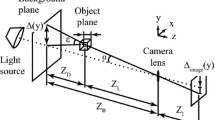
The BOS technique allows the quantification of local changes of density in a transparent medium. It consists in the digital comparison of two photographs of the same background, a dot matrix. The first image is obtained in the absence and the second in the presence of the flow. The apparent displacement of the background is produced by changes in the refractive index due to an axisymmetric supersonic jet, Fig. 1.

Fig. 1
figure 1

Apparent displacement of the background due to local changes in the density produced by the schlieren object

Full size image

Displacements are determined by a cross-correlation, with the same software used in PIV (Particle Image Velocimetry). The displacements can be related to the change in refractive index. Finally, the Gladstone Dale equation relates the refractive index with the density.

2 Theoretical Background

For a diatomic gas, with refractive index close to one, we can use the Gladstone-Dale equation, which relates the density of the medium with the refractive index:

$$ n - 1 = K_{G - D} \rho $$
(1)

where \( n \) is the refractive index of the medium of incidence, \( \rho \) is its density and \( K_{G - D} \) is the Gladstone-Dale coefficient which depends on the medium and the wavelength of the light.

When a beam of light passes through a matrix of dots (background), each of the dots will cast a shadow. If a different medium, called schlieren object, is placed between the matrix and the screen or camera, the light rays deviate an angle \( \upvarepsilon, \) and the shadows of the dots in the matrix have an apparent shift \( \varDelta y \) that can be written as (Raffel 2015)

$$ \Delta y = MZ_{D} \varepsilon_{i} $$
(2)

where \( M \) is the magnification of the optical arrangement, and \( Z_{D} \) is the distance from the schlieren object to the background and \( \varepsilon_{i} \) are the deflecting angles, where the i subindex refer to the angle direction. Under the assumption that deflection angles are small, and occur in the direction perpendicular to the optical axis (x and y), they can be expressed in terms of changes in the refractive index by the following equation (Raffel 2015; Venkatakrishnan 2004; Vinnichenko 2011):

$$ \varepsilon_{{x_{i} }} = \frac{1}{{n_{0} }}\int\limits_{{Z_{D} - z_{0} }}^{{Z_{D} + z_{0} }} {\frac{\partial n}{{\partial x_{i} }}dz} $$
(3)

where \( n_{0} \) is the refractive index of the surroundings, and the integration limits represent the boundaries along the optical axis of the schlieren object.

Under the assumption of small angles, Eq. (3) can be re written as (Vinnichenko 2011):

$$ \varepsilon_{i} = \frac{1}{{n_{0} }}\frac{\partial n}{{\partial x_{i} }}h $$
(4)

where \( h \) is the width of the schlieren object. Substituting Eq. (4) in (2), a differential equation for the refractive index in each direction is obtained:

$$ \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{\partial n}{\partial x} = \frac{{n_{0} \xi_{x} }}{{MZ_{D} h}}} \\ {} \\ \end{array} } \\ {\begin{array}{*{20}c} {\frac{\partial n}{\partial y} = \frac{{n_{0} \xi_{y} }}{{MZ_{D} h}}} \\ {} \\ \end{array} } \\ \end{array} } \right. $$
(5)

where \( \xi = (\xi_{x} ,\xi_{y} ) \) is the apparent displacement vector calculated for each point or set of points in the background. The usual way to integrate these equations, as shown by Vinnichenko (2011), Raffel (2015), Tipnis (2013) and Lee (2013), among others, is to derive both equations with respect to the corresponding variable and to add them. This results in a Poisson equation that is solved by a successive overrelaxation method:

$$ \frac{{\partial^{2} n}}{{\partial^{2} x}} + \frac{{\partial^{2} n}}{{\partial^{2} y}} = \frac{{n_{0} }}{{MZ_{D} h}}\left[ {\frac{{\partial \xi_{x} }}{\partial x} + \frac{{\partial \xi_{y} }}{\partial y}} \right] $$
(6)

Substituting the index of refraction by the density using the Gladstone-Dale equation, Poisson equation for the density is obtained:

$$ \frac{{\partial^{2} \rho }}{{\partial^{2} x}} + \frac{{\partial^{2} \rho }}{{\partial^{2} y}} = \frac{1}{{K_{G - D} }}\frac{{n_{0} }}{{MZ_{D} h}}\left[ {\frac{{\partial \xi_{x} }}{\partial x} + \frac{{\partial \xi_{y} }}{\partial y}} \right] $$
(7)

3 Supersonic Jet

As air flows through a straight nozzle, it can be accelerated to speeds (\( u \)) greater than the speed of sound (\( c) \). The dimensionless parameter used to characterize this phenomenon is the Mach number (M), defined as the ratio between the velocity of the object and the speed of sound.

Compressibility effects are significant from \( M \sim 0.7 \). A flow is considered supersonic when \( 1 \le M < 5. \) Supersonic flows are very complex, they are compressible and turbulent. An apparently stationary shock structure appears close to M = 1, with abrupt changes in density and pressure. They are usually represented as oblique lines.

The Mach number of a supersonic flow can be determined through Eq. 8 (Chapman 2000), that relates M with the complementary angle of the first shock wave with the nozzle as shown in Fig. 2.

Fig. 2
figure 2

Schematic of the angle used to determine the Mach number

Full size image
$$ M = \sqrt {1 + { \cot }^{2} \alpha } $$
(8)

4 Experimental Procedure

The experimental device used is shown in Fig. 3. The light source is a 100 Watts white LED (cree® Xlamp®cXa3050), which is collimated and sent to a first surface spherical mirror with a diameter of 15 cm. From the mirror parallel rays leave. The background matrix and the supersonic flow are placed in this region. The light is then captured by a focusing lens that directs the light into a fast camera (Phantom Miro M310) with another lens (Infinity CENTRIMAX K1). The system has a magnification of 0.6.

The supersonic flow is produced with a straight nozzle with a diameter of 4 mm. Experiments were performed at an altitude of 2290 m above sea level at a room temperature of 20 °C and relative humidity of 30 %.

Fig. 3
figure 3

Experimental setup

Full size image

The supersonic jet was recorded at 5435 fps with an exposure time of 80 ms and a resolution of 768 by 768 pixels.

5 Experimental Results

The three frames shown in Fig. 4 were chosen for analysis. The angle of the shock was measured from the frames using ImageJ software. Mach numbers 2.79, 1.89 and 1.79 were calculated with Eq. 8.

Fig. 4
figure 4

Background with supersonic jet. a Original image, b M = 2.78, c M = 1.89 and d M = 1.79

Full size image

Software was developed based on the work of Huang (1997). The technique was calibrated (Aguayo et al. 2014) for local changes in density. The apparent displacement was obtained using cross-correlation between the frames with a schlieren object and without it. The analysis was performed with interrogation areas of 64 by 64 pixels and 8 pixels refinement. The results are shown in Fig. 5.

Fig. 5
figure 5

Displacement field of the jet at three different Mach numbers. a M = 2.78, b M = 1.89, c 1.79 obtained from the images shown in Fig. 4

Full size image

Once the displacement vector field is determined, the results are used to obtain a Poisson equation for the index of refraction. To solve Eq. 6, inhomogeneous Dirichlet conditions were used in the eastern and western border, and Newmann boundary conditions in the northern and southern borders (Aguayo et al. 2014). The results are shown in Fig. 6.

Fig. 6
figure 6

Results obtained by solving the Poisson equation for the refractive index for each of the displacement fields. a M = 2.78, b M = 1.89, c M = 1.79

Full size image

With these results the density field is obtained through the Gladstone-Dale Eq. (1) for the supersonic flow. For air, the Gladstone-Dale constant is KG-D = 2.2649 × 10−4 m3/Kg. The results are shown in Fig. 7.

Fig. 7
figure 7

Results obtained by solving the Poisson equation and use Gladstone-Dale equation for the density for each of the displacement fields. a M = 2.78, b M = 1.89, c M = 1.79

Full size image

It may be noted in Fig. 6 that the greatest value of the refractive index corresponds to M = 2.78 and the smallest to M = 1.79. The same applies to the density. These results are consistent with shadowgraph images of the same supersonic flow. As could be expected from the linear relationship between the index of refraction and the density, their scalar fields are similar.

Figure 8 shows the density values along the centerline of the flow.

Fig. 8
figure 8

Plot of density versus position along the centerline of a supersonic jet with M = 2.79

Full size image

As can be observed in Fig. 8, the density at the exit is greater than that of the stagnant air, then decays below the atmospheric value and rises again to a maximum value. It keeps oscillating along the shock pattern.

An important result of this experiment is that density changes do not occur abruptly but through a certain thickness (3.4 mm). That is, shock waves have a finite width.

Figure 9 shows that the behavior of the three supersonic flows is similar. As the Mach number diminishes, the maximum value of the density is lower and it is reached at a shorter distance from the nozzle.

Fig. 9
figure 9

Plot of density versus position along the centerline for three flows with supersonic Mach numbers of 2.78, 1.89 and 1.79 respectively

Full size image

6 Conclusions

The experiment presented in this papers shows that BOS is a nonintrusive technique that can detect and quantify changes in the local densities, in flows where this measurement would be otherwise impossible. Thus, the apparent displacements, the refractive index and the density inside an axisymmetric supersonic jet were measured successfully. The results are consistent with the behavior found by Tipnis (2013). However, the geometry of the nozzle and the Mach numbers are different, so the numerical values cannot be compared. The technique has given new results that combined with other techniques used for the local velocity can give new insight of the behavior of supersonic flow, in particular close to the shock structure. In particular, the behavior of a fluid particle in this region is not understood.

Future work includes a more profound analysis of the boundary conditions used to solve the Poisson equation. The assumption that the bottom boundary condition is \( \frac{{\partial\uprho}}{{\partial {\text{x}}}} = 0 \) should be investigated more carefully.

Also, a refinement of the background matrix should be done, to reduce the uncertainty in the measurement of the displacements. The exposure times should be evaluated.

The great advantage of BOS over other techniques like PIV and LDA, is that it is completely non-intrusive.

Absolute values of the local densities instead of ratios could be determined, since the technique was calibrated in previous experiments.

We acknowledge support from UNAM through DGAPA PAPIIT IN117712 and the Graduate Program in Engineering.