Differential-Geometric-Control Formulation of Flapping Flight Multi-body Dynamics

Abstract

Flapping flight dynamics is quite an intricate problem that is typically represented by a multi-body, multi-scale, nonlinear, time-varying dynamical system. The unduly simple modeling and analysis of such dynamics in the literature has long obstructed the discovery of some of the fascinating mechanisms that these flapping-wing creatures possess. Neglecting the wing inertial effects and directly averaging the dynamics over the flapping cycle are two major simplifying assumptions that have been extensively used in the literature of flapping flight balance and stability analysis. By relaxing these assumptions and formulating the multi-body dynamics of flapping-wing micro-air-vehicles in a differential-geometric-control framework, we reveal a vibrational stabilization mechanism that greatly contributes to the body pitch stabilization. The discovered vibrational stabilization mechanism is induced by the interaction between the fast oscillatory aerodynamic loads on the wings and the relatively slow body motion. This stabilization mechanism provides an artificial stiffness (i.e., spring action) to the body rotation around its pitch axis. Such a spring action is similar to that of Kapitsa pendulum where the unstable inverted pendulum is stabilized through applying fast-enough periodic forcing. Such a phenomenon cannot be captured using the overly simplified modeling and analysis of flapping flight dynamics.

1 Introduction

Biological flyers represent a gold mine of scientifically rich problems and a wellspring of knowledge and inspiration for engineers and scientists. For example, some insects can thrust up to five times their weights (Ellington 1984a), while others have been observed to perform turning maneuvers of greater than 3000 deg/s, with less than a 30 ms delay (Deng et al. 2006), in situations that demand agility, such as chasing a potential mate. In normal everyday flight, birds may experience up to 14 g accelerations in super-maneuverable tasks (Rozhdestvensky and Ryzhov 2003), while the maneuverability of the most advanced fighter airplanes cannot exceed 8–9 g. Moreover, birds and insects outperform jet airplanes more than five times from a normalized power consumption perspective (Rozhdestvensky and Ryzhov 2003). This huge potential inspired engineers to design flapping-wing micro-air-vehicles (FWMAVs) (Wood 2008), mainly for reconnaissance and surveillance applications.

Indeed, flapping flight invokes and pushes the frontiers of mechanical and aerospace engineering disciplines. From an aerodynamic point of view, flapping flight creates an unsteady, nonlinear flow field exploiting unconventional mechanisms to generate lift. In fact, using classical aerodynamics, insect flight was deemed impossible for decades (e.g., Norberg 1975; Dudley and Ellington 1990; Ellington 1995; Willmott and Ellington 1997), as the required lift coefficients for balance are 2–3 times the maximum lift coefficients achieved by conventional aerodynamics. Later, biologists and engineers unraveled some of the unconventional lift mechanisms exploited by insect and bird flight. A stabilized leading edge vortex, first introduced by Ellington et al. (1996), forms the main unconventional lift mechanism that makes insect flight possible. Computational fluid dynamic simulations show that the leading edge vortex contributes $40\%$ of the total lift for insects (Liu et al. 1998).

As the aerodynamics of flapping flight became mature, the flight dynamic analysis followed promptly. To our knowledge, the first article on flapping flight dynamics is that of Thomas and Taylor (2001). Flapping flight dynamics represents a multi-body, nonlinear time-periodic (NLTP) dynamical system. Moreover, it is a multi-scale dynamical system because of the concomitant two timescales: the fast timescale of the flapping motion and the associated aerodynamic loads, and the relatively slow timescale of the body motion. All these challenges make flapping flight dynamics an intricate problem that necessitates a rigorous mathematical analysis.

Two major assumptions have been typically adopted in the flight dynamic analysis of FWMAVs (Taha et al. 2012): neglecting the wing inertial effects and directly averaging the dynamics over the flapping cycle. The first assumption might be justifiable because the mass of the wing is quite small when compared to that of the body (less than $5\%$ Wu et al. 2009). Moreover, adopting this assumption alleviates the problem’s complexity and yields flight dynamic equations similar to those of conventional aircraft. As such, most of the analyses in the literature of flapping flight dynamics and control have neglected the wing inertial effects (Thomas and Taylor 2001; Taylor and Thomas 2002, 2003; Taylor and Zbikowski 2005; Khan and Agrawal 2007; Sun and Xiong 2005; Xiong and Sun 2008; Dietl and Garcia 2008a; Oppenheimer et al. 2011; Hussein and Taha 2016; Tahmasian and Woolsey 2017). For more details about the effects of the wing’s inertia on the dynamics of flapping flight, the reader is referred to the review articles (Taha et al. 2012; Orlowski and Girard 2012), and the references therein.

The second major assumption (directly averaging the dynamics over the flapping cycle) has been refuted by Taha et al. (2014a, 2015) for hovering insects with a relatively small flapping frequency (e.g., hawkmoth and cranefly). They showed that despite the large ratio of the forcing flapping frequency to the natural frequency of the body motion (30 for the hawkmoth and 50 for the cranefly), there is a strong interaction between the system’s two timescales that considerably affects the flight balance and stability. Specifically, the intuition that an averaged lift due to flapping equal to the FWMAV’s weight ensures vertical balance at hover was interestingly refuted by showing that the aerodynamic–dynamic interaction results in a negative lifting mechanism. In addition, the interaction between the system’s two timescales results in a vibrational stabilization phenomenon that is quite similar to the well-known behavior of the Kapitsa pendulum (Kapitsa 1965): the unstable equilibrium of the inverted pendulum is stabilized through open-loop vertical oscillations of the pivot. These interactions are essentially neglected when direct averaging is used.

While pursuing the relaxation of those two assumptions, differential-geometric-control theory is naturally invoked as a rigorous analysis tool. It is particularly convenient for the analysis of multi-body, underactuated mechanical systems (Bullo and Lewis 2004). Moreover, when combined with chronological calculus (Agrachev and Gamkrelidze 1978), it provides constructive techniques for higher-order averaging of NLTP systems (Sarychev 2001a, b; Vela 2003) and dealing with multi-scale vibrational control systems (Bullo 2002). As such, the goal of this effort is to relax the aforementioned simplifying assumptions and hence: (1) derive the full (five degrees of freedom), multi-body, longitudinal flight dynamics of FWMAVs and cast it in a differential-geometric-control framework; (2) combine differential-geometric-control and averaging tools to rigorously and analytically investigate the balance and stability of flapping flight dynamics at hover; and (3) unravel the unconventional flight dynamic behavior of flapping flight (e.g., vibrational stabilization and negative lifting) and demonstrate the role of multi-body effects in such a behavior.

In this work, the full multi-body equations of motion governing the longitudinal flight dynamics of FWMAVs near hover are derived using the principle of virtual power (Greenwood 2003). A relatively simple, analytical aerodynamic model that accounts for the dominant contributions (e.g., leading edge vortex and rotational effects) is adopted. Combining these two models (aerodynamic and dynamic), a nonlinear, multi-body, time-varying, longitudinal flight dynamics model is developed, which captures aerodynamic–dynamic interactions. A three-degrees-of-freedom (DOF) model that resembles an experimental apparatus is then extracted from the full model as the simplest, yet rich enough, multi-body, flapping flight dynamics model for differential-geometric-control analysis. The geometric control–averaging tools are then applied to the three-DOF model to reveal the role of wing–body dynamical interaction in vibrational pitch stabilization for the insect/vehicle’s body. The vibrational pitch stabilization mechanism is induced by the interaction between the fast, periodic, aerodynamic wing forces and the relatively slow body motion (aerodynamic–dynamic interactions). Such a mechanism would have been entirely overlooked if direct averaging techniques are applied instead. Moreover, the obtained analytical results are verified through numerical periodic shooting and Floquet stability analysis. Finally, a comparison is made with the corresponding single-body model to provide insights into the multi-body effects.

2 Geometric-Control-Oriented Modeling

2.1 Wing Kinematics

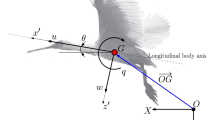
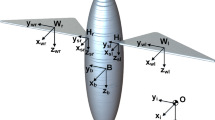
Figure 1 shows a schematic diagram of a FWMAV and its axis systems. Four reference frames are required to study the flight dynamics of a rigid-wing FWMAV: an inertial reference frame $\{x_{\mathrm{I}}, y_{\mathrm{I}}, z_{\mathrm{I}}\}$, a body-fixed reference frame $\{x_{\mathrm{b}}, y_{\mathrm{b}}, z_{\mathrm{b}}\}$, a stroke plane reference frame $\{x_{\mathrm{s}}, y_{\mathrm{s}}, z_{\mathrm{s}}\}$, and a wing-fixed reference frame $\{x_{\mathrm{w}}, y_{\mathrm{w}}, z_{\mathrm{w}}\}$ for each of the flight vehicle’s wings. Because only longitudinal flight is considered in this work, symmetric wing motions are assumed.

Fig. 1

A schematic diagram of a FWMAV hovering in a general orientation

By convention, the $x_{\mathrm{b}}$-axis points forward defining the vehicle’s longitudinal axis, the $y_{\mathrm{b}}$-axis points to starboard, and the $z_{\mathrm{b}}$-axis completes the right-handed frame. The conventional yaw–pitch–roll ($\psi$-$\theta$-$\phi$) Euler angle sequence, traditionally used with fixed-wing aircraft (Nelson 1989), is adopted here to describe the body’s inertial orientation. Because this effort is focused on longitudinal flight dynamics, only the body’s pitch angle $\theta$ is required.

The stroke plane is inclined to the horizontal plane with a stroke plane angle $\beta$. That is, the stroke plane reference frame is obtained from the inertial frame through a rotation by an angle $\beta$ about the $y_{\mathrm{I}}$-axis. The wing-fixed frame is defined such that it is aligned with the stroke plane frame at zero wing kinematic angles. The wing motion is typically described using three Euler angles: the flapping angle $\varphi$ (describing back and forth motion along the stroke plane), the plunging angle $\vartheta$ (describing out of stroke plane motion), and the pitching angle $\eta$ (describing rotation of the wing about a chord line). Consistent with observations of biological flyers (Weis-Fogh 1973; Ellington 1984a), the plunging motion is neglected ($\vartheta =0$).

2.2 Equations of Motion

Since the two wings move symmetrically, the equations of motion are defined in terms of five generalized coordinates: ${\varvec{q}}=[x \;,\; z \;,\; \theta \;,\; \varphi \;,\; \eta ]^*$, where * denotes transpose, and x and z are the inertial coordinates of the body center of mass along the $x_{\mathrm{I}}$ and $z_{\mathrm{I}}$ axes, respectively. We use the principle of virtual power (Greenwood 2003) to derive the equations of motion

$$\begin{aligned}&\sum _{i=\text{ b,w }} [m_i ( \dot{{\varvec{v}}}_i + {\ddot{{\varvec{\rho _c}}}}_i ) - {\varvec{f}}_i ] \cdot \frac{\partial {\varvec{v}}_i}{\partial \dot{q}_j} + [ \dot{{\varvec{h}}}_i + m_i{{\varvec{\rho _c}}}_i\times \dot{{\varvec{v}}}_i-{\varvec{M}}_i ] \cdot \frac{\partial {\varvec{\omega }}_i}{\partial \dot{q}_j} = 0, \nonumber \\&\quad j=\{1,\ldots ,5\}, \end{aligned}$$

(1)

where $m_i$ is the mass of the $i{\mathrm{th}}$ rigid body, ${\varvec{v}}_i$ is the inertial velocity vector of its reference point (the reference points of the body and wing frames are the body’s center of gravity and the wing’s hinge root, respectively), ${{\varvec{\rho _c}}}_i$ is the vector pointing from the reference point of the $i{\mathrm{th}}$ rigid body to its center of gravity, ${\varvec{\omega }}_i$ and ${\varvec{h}}_i$ are the angular velocity vector of the $i{\mathrm{th}}$ rigid body with respect to the inertial frame and the corresponding angular momentum vector, respectively, and ${\varvec{f}}_i$ and ${\varvec{M}}_i$ are the external force and moment vectors applied on the $i{\mathrm{th}}$ rigid body at its reference point. As such, the equations of motion can be written in an abstract form as

$$\begin{aligned} \begin{bmatrix} {\mathcal {M}}({\varvec{q}}) \end{bmatrix} \begin{pmatrix} {\dot{u}}\\ {\dot{w}}\\ \ddot{\theta }\\ \ddot{\varphi }\\ \ddot{\eta } \end{pmatrix} + \begin{pmatrix} {\mathcal {C}}({\varvec{q}},\dot{{\varvec{q}}}) \end{pmatrix}=\begin{bmatrix} R_{\mathrm{aero}} \end{bmatrix} \begin{pmatrix} F_x\\ F_z\\ M_x\\ M_y\\ M_z \end{pmatrix} + \begin{pmatrix} 0\\ 0\\ 0\\ 1\\ 0 \end{pmatrix} \tau _\varphi + \begin{pmatrix} 0\\ 0\\ \cos \varphi \\ 0\\ 1 \end{pmatrix} \tau _\eta , \end{aligned}$$

(2)

where $u={\dot{x}}$, $w={\dot{z}}$ are the body inertial velocity components, ${\mathcal {M}}({\varvec{q}})$ is the inertia matrix, ${\mathcal {C}}({\varvec{q}},\dot{{\varvec{q}}})$ represents Coriolis and centripetal effects, $R_{\mathrm{aero}}$ relates the aerodynamic loads ($F_x$, $F_z$, $M_x$, $M_y$, and $M_z$) in the wing frame to the generalized forces, and $\tau _\varphi$ and $\tau _\eta$ are the wing flapping and pitching control torques, respectively. The details of the derivation of Eq. (2) are given in “Appendix A.”

2.3 Aerodynamic Model

We extend the aerodynamic model, used in our earlier work (Taha et al. 2013a, 2014b) which is based on Refs. Taha et al. (2013b, 2014c), Berman and Wang (2007), to a more general setting that is convenient for aerodynamic–dynamic interactions. This model accounts for the dominant contributions (i.e., leading edge vortex (LEV) and rotational contributions) using a quasi-steady, strip theory formulation.

Dickinson et al. (1999) showed that for ultra-low Reynolds numbers, where insects operate ($\hbox {Re}=$200–4000), there is almost no stall; the lift has a smooth variation with the angle of attack. Berman and Wang (2007) showed that the steady lift coefficient due to a stabilized LEV can be simply written as

$$\begin{aligned} C_L= A \sin 2 \alpha , \end{aligned}$$

where $\alpha$ is the angle of attack. Taha et al. (2014c) provided a means to estimate the coefficient A in terms of the aspect ratio using the extended lifting line theory (Schlichting and Truckenbrodt 1979). Insects wings, similar to delta wings, experience LEVs, and hence, the flow separates at the leading edge losing the leading edge suction force (Polhamus 1966; Taha et al. 2014c). As such, the drag is given by $C_D=C_L \tan \alpha$ (Polhamus 1966; Taha et al. 2014c). Therefore, the resultant aerodynamic force is almost normal to the wing surface (i.e., $C_z=-2 A \sin \alpha$). That is, the shear contribution is minimal as shown in the experimental study of Dickinson et al. (1999) and the computational results of Wang (2000) and Ramamurti and Sandberg (2002). It should be noted that this crude (quasi-steady) modeling of the LEV might affect the overall stability characteristics of the combined flow-vehicle dynamics because of the interaction between the two dynamical systems: LEV dynamics and the associated flow on the one hand and the body–wing dynamics on the other hand. However, this simplistic modeling is adopted due the lack of richer dynamical models that capture LEV dynamic stability characteristics in a compact form that allows geometric nonlinear analysis of the interaction between the flow and the vehicle dynamics. For more insights into the insects LEV dynamic stability characteristics, the reader is referred to the following articles and the references therein (Ellington et al. 1996; Birch and Dickinson 2001; Birch et al. 2004).

As such, a two-dimensional airfoil undergoing a translational motion with velocity components $V_x$ and $V_z$ in the wing frame and a rotational pitching motion $\omega _y$, as shown in Fig. 2, is subjected to the following forces (Taha et al. 2013b, 2014c; Berman and Wang 2007; Hussein and Canfield 2017; Hussein et al. 2016)

$$\begin{aligned} \begin{array}{l} F_x'=\pi \rho c \Delta x V_z \omega _y \\ F_z'=-\frac{1}{2}\rho a_0 c V^2 \sin \alpha - \pi \rho c \Delta x V_x \omega _y \end{array}, \end{aligned}$$

(3)

where c is the chord length, $\Delta x$ is the distance between the pitching axis (hinge line) and the three-quarter chord point, $a_0$ is the two-dimensional lift curve slope that will be replaced by the three-dimensional lift curve slope when integrating over the whole wing, $V^2=V_x^2+V_z^2$, and the angle of attack is given by $\alpha =\tan ^{-1}\frac{V_z}{V_x}$. It should be noted that the added mass terms are neglected in Eq. (3) because their net effects on the flight dynamics were found to be minimal as shown in our previous effort (Taha et al. 2014b).

Fig. 2

A schematic diagram of an airfoil section undergoing translational and rotational motion

Fig. 3

A schematic diagram of the aerodynamic–dynamic interaction in a FWMAV

To account for aerodynamic–dynamic interaction, the body’s motion variables (u, w, and ${\dot{\theta }}$) and the aerodynamic inputs ($V_x$, $V_z$, and $\omega _y$) should be interconnected as shown in Fig. 3. As such, the velocity of a wing section that is at a distance r from the wing root is written as

$$\begin{aligned} {\varvec{V}}^{(\mathrm{w})}(r)=[{\varvec{R}}_{\mathrm{ws}}][{\varvec{R}}_\beta ] {\varvec{V}}_{\mathrm{w}}^{(\mathrm{I})} + {\varvec{\omega }}_{\mathrm{w}}^{(\mathrm{w})}\times r {\varvec{j}}_{\mathrm{w}}, \end{aligned}$$

(4)

where $[{\varvec{R}}_{\mathrm{ws}}]$ and $[{\varvec{R}}_\beta ]$ (given in “Appendix A”) are the rotation matrices from the stroke plane frame to the wing frame and from the inertial frame to the stroke plane frame, respectively. Also, ${\varvec{V}}_{\mathrm{w}}^{(\mathrm{I})}$ is the wing velocity vector in the inertial frame, and ${\varvec{\omega }}_{\mathrm{w}}^{(\mathrm{w})}$ is the wing angular velocity vector in the wing frame. Since the body motion (u, w, and ${\dot{\theta }}$) is evolving with a quite slower timescale than that of the wing, the term ($V^2 \sin \alpha$) in Eq. (3) could be approximated linearly with respect to the body states as follows

$$\begin{aligned} V^2 \sin \alpha = V^2 \frac{V_z}{\left| V \right| }=\left| V \right| V_z \simeq \left( \left| V \right| V_z \right) \bigg |_0+ \sum _{i=1}^{3} \frac{\partial (\left| V \right| V_z)}{\partial x_i}\bigg |_{x_i's=0} \Delta x_i, \end{aligned}$$

(5)

where $x_i's$ are the body states; u, w,  and ${\dot{\theta }}$. Hence, we obtain

$$\begin{aligned} V^2 \sin \alpha= & {} r^2 \sin {\eta }~ {\dot{\varphi }} \left| {\dot{\varphi }}\right| +u~ \biggl (2~ r \cos {\beta } \sin {\eta } \cos {\varphi } \left| {\dot{\varphi }}\right| +r \sin {\beta } \cos {\eta } \left| {\dot{\varphi }}\right| \biggr )+\nonumber \\&+\, w~ \biggl (r \cos {\beta } \cos {\eta } \left| {\dot{\varphi }}\right| -2~ r \sin {\beta } \sin {\eta } \cos {\varphi } \left| {\dot{\varphi }}\right| \biggr )+\nonumber \\&+\, r~ {\dot{\theta }} \left| {\dot{\varphi }}\right| \biggl (-r \cos {\eta } \sin {\varphi }+2~ x_{\mathrm{h}} \sin {\beta } \sin {\eta } \cos {\theta } \cos {\varphi }\nonumber \\&-\,2~ x_{\mathrm{h}} \cos {\beta } \sin {\eta } \sin {\theta } \cos {\varphi }+\nonumber \\&-\, x_{\mathrm{h}} \cos {\beta } \cos {\eta } \cos {\theta }-x_{\mathrm{h}} \sin {\beta } \cos {\eta } \sin {\theta }\biggr ), \end{aligned}$$

(6)

where $x_{\mathrm{h}}$ is the distance from the vehicle’s center of mass to the root of the wing hinge line (i.e., the intersection of the hinge line with the $x_{\mathrm{b}}$-axis), as shown in Fig. 1.

The time-varying aerodynamic loads (in the wing frame) can then be written as

$$\begin{aligned} \begin{array}{lll} \left( \begin{array}{c} F_x({\varvec{x}})\\ F_z({\varvec{x}})\\ M_x({\varvec{x}})\\ M_y({\varvec{x}})\\ M_z({\varvec{x}})\end{array} \right) = \left( \begin{array}{c} F_{x_0}\\ F_{z_0}\\ M_{x_0}\\ M_{y_0}\\ M_{z_0} \end{array} \right) + \left[ \begin{array}{ccc} F_{x_u} &{} F_{x_w} &{} F_{x_q}\\ F_{z_u} &{} F_{z_w} &{} F_{z_q}\\ M_{x_u} &{} M_{x_w} &{} M_{x_q} \\ M_{y_u} &{} M_{y_w} &{} M_{y_q} \\ M_{z_u} &{} M_{z_w} &{} M_{z_q} \end{array} \right] \left( \begin{array}{c} u \\ w \\ {{\dot{\theta }}} \end{array} \right) +\left( \begin{array}{c} F_{x_{nl}} \\ F_{z_{nl}} \\ M_{x_{nl}} \\ M_{y_{nl}} \\ M_{z_{nl}} \end{array} \right) , \end{array} \end{aligned}$$

(7)

where the terms (aerodynamic derivatives) in Eq. (7) are given in “Appendix B.” It should be noted that the aerodynamic derivatives here are not normalized by masses and inertias, in contrast to the conventional aerodynamic derivatives commonly used in flight dynamics literature (Nelson 1989; Etkin 1996).

As explained above, the aerodynamic loads generated by the wing oscillatory motion are represented as functions of the wing states ($\varphi$, $\eta$, ${\dot{\varphi }}$, and ${\dot{\eta }}$) as well as body states (u, w, $\theta$, and ${\dot{\theta }}$), in addition to the stroke plane angle $\beta$. As such, the interaction between the body motion and the generated aerodynamic loads by the wing can be accounted for, which is explained in Fig. 3. For given input torques and aerodynamic loads, the dynamic equations of motion (2), or equivalently (32–36), can be integrated to update the body motion variables (u, w, and $\theta$) and the wing flapping variables ($\eta$ and $\varphi$). Together, they dictate the motion of each airfoil section with respect to the surrounding quiescent air, represented by $V_x$, $V_z$, and $\omega _y$. These air speeds, in turn, completely determine the aerodynamic loads according to Eqs. (3) or (7). Accounting for such an interaction between the aerodynamic loads and the body motion allows for a more accurate and heuristic trim and stability analysis.

2.4 Three-DOF Flight Dynamic Model for Geometric Control Analysis

While the developed model (2, 7) is amenable to differential-geometric-control tools, we opt to demonstrate such tools on a simpler, yet rich enough, model, not to obscure the details of these tools with the complexity of the full model. In particular, we consider the minimal degrees of freedom required to demonstrate the vibrational pitch stabilization phenomenon. As such, we consider two DOF for the body: body’s vertical motion z and pitching angle $\theta$, and one DOF for the wing: the flapping angle $\varphi$. The body forward motion is restricted, and the wing pitching angle $\eta$ is assumed to have a piecewise constant variation, commonly used in flapping flight dynamics literature, e.g., Schenato et al. (2003), Doman et al. (2010), Oppenheimer et al. (2011), Taha et al. (2013c, 2013d)

$$\begin{aligned} \eta (t)= {\left\{ \begin{array}{ll} \alpha _m,&{} {\dot{\varphi }}>0\\ \pi -\alpha _m, &{} {\dot{\varphi }}<0 \end{array}\right. }, \end{aligned}$$

where $\alpha _m$ is the mean angle of attack over the up/down stroke. As such, we have $\sin {\eta }=\sin {\alpha _m}$ and $\cos {\eta }=\cos {\alpha _m}$ sign(${\dot{\varphi }}$). This multi-body, three-DOF model resembles (locally at the hovering equilibrium) a laboratory experiment apparatus (Taha et al. 2018) that has been developed to verify the results. In this laboratory experiment, however, the body vertical motion is transformed into pendulum rotation, as shown in Fig. 4.

Fig. 4

The experimental setup developed in Taha et al. (2018) to verify the vibrational pitch stabilization phenomenon

The three-DOF model can be written as

$$\begin{aligned} {\mathcal {M}}\left( {\varvec{q}};~\text {sign}({\dot{\varphi }})\right) ~\ddot{{\varvec{q}}}+{{\varvec{f}}}_c({\varvec{q}},\dot{{\varvec{q}}})={{\varvec{f}}}_{\mathrm{aero}}+{\varvec{g}}~\tau _{\phi }, \end{aligned}$$

(8)

where ${\mathcal {M}}$ is the inertia matrix, ${{\varvec{f}}}_c$ represents Coriolis and centripetal effects, ${{\varvec{f}}}_{\mathrm{aero}}$ represents the aerodynamic loads, ${\varvec{g}}$ is the input vector field, and $\tau _{\phi }$ is the input torque. To simplify the mathematical expressions and help achieve self-pitch trim at hover, now on, we set the parameter $x_{\mathrm{h}}=0$ (the distance from the vehicle’s center of mass to the root of the wing hinge line). As such, ${\mathcal {M}}$, ${{\varvec{f}}}_c$, ${{\varvec{f}}}_{\mathrm{aero}}$, and ${\varvec{g}}$ in system (8) are written as

$$\begin{aligned} {\mathcal {M}}= \begin{bmatrix} m_{\mathrm{v}}&\quad {\mathcal {M}}_{12}&\quad {\mathcal {M}}_{13} \\ {\mathcal {M}}_{21}&\quad {\mathcal {M}}_{22}&\quad {\mathcal {M}}_{23} \\ 0&\quad 0&\quad I_{y_{\mathrm{b}}} \end{bmatrix}, \end{aligned}$$

(9)

where

$$\begin{aligned}&\begin{array}{l} {\mathcal {M}}_{12}= -r_{\mathrm{cg}} \cos {\varphi } \sin {\theta }-{\bar{c}} {\hat{d}} \cos {\alpha _m}~ \text {sign}({\dot{\varphi }}) \sin {\varphi } \sin {\theta }\\ {\mathcal {M}}_{13}={\bar{c}} {\hat{d}} \cos {\alpha _m} \cos {\theta } \cos {\varphi }~ \text {sign}({\dot{\varphi }})-{\bar{c}} {\hat{d}} \sin {\alpha _m} \sin {\theta }-r_{\mathrm{cg}} \cos {\theta } \sin {\varphi }\\ {\mathcal {M}}_{21}=-m_{\mathrm{w}} r_{\mathrm{cg}} \cos {\varphi } \sin {\theta }-{\bar{c}} {\hat{d}}~ m_{\mathrm{w}} \cos {\alpha _m}~ \text {sign}({\dot{\varphi }}) \sin {\varphi } \sin {\theta }\\ {\mathcal {M}}_{22}=-\frac{1}{2} I_{x_{\mathrm{w}}} \cos ^2{\alpha _m}-\frac{1}{2} I_{z_{\mathrm{w}}} \sin ^2{\alpha _m}+\frac{I_F}{2}+\frac{I_{x_{\mathrm{w}}}+I_{z_{\mathrm{w}}}}{2}\\ {\mathcal {M}}_{23}=\frac{1}{2} I_{y_{\mathrm{w}}}~ \text {sign}({\dot{\varphi }}) \sin {2\alpha _m} \sin {\varphi } \end{array}, \nonumber \\ {{\varvec{f}}}_c= & {} \begin{bmatrix} -{\dot{\theta }}^2 \biggl ({\bar{c}} {\hat{d}}~ \sin {\alpha _m} \cos {\theta }+{\bar{c}} {\hat{d}}~ \cos {\alpha _m} \sin {\theta }~ \text {sign}({\dot{\varphi }}) \cos {\varphi }-r_{\mathrm{cg}} \sin {\theta } \sin {\varphi }\biggr )\\ -\,2 {\dot{\theta }} {\dot{\varphi }} \biggl ({\bar{c}} {\hat{d}} \cos {\alpha _m} \cos {\theta }~ \text {sign}({\dot{\varphi }}) \sin {\varphi }+r_{\mathrm{cg}} \cos {\theta } \cos {\varphi }\biggr )\\ +\,{\dot{\varphi }}^2 \biggl (r_{\mathrm{cg}} \sin {\theta } \sin {\varphi }-{\bar{c}} {\hat{d}} \cos {\alpha _m} \sin {\theta }~ \text {sign}({\dot{\varphi }}) \cos {\varphi }\biggr )-g m_{\mathrm{v}}\\ \\ -\,{\dot{\theta }} w \biggl ({\bar{c}} {\hat{d}}~ m_{\mathrm{w}} \cos {\alpha _m} \cos {\theta } ~\text {sign}({\dot{\varphi }}) \sin {\varphi }+m_{\mathrm{w}} r_{\mathrm{cg}} \cos {\theta } \cos {\varphi }\biggr )\\ +\,w {\dot{\varphi }} \biggl (m_{\mathrm{w}} r_{\mathrm{cg}} \sin {\theta } \sin {\varphi }-{\bar{c}} {\hat{d}}~ m_{\mathrm{w}} \cos {\alpha _m} \sin {\theta }~ \text {sign}({\dot{\varphi }}) \cos {\varphi }\biggr )\\ +\,{\dot{\theta }}^2 \biggl (\frac{1}{2} \cos ^2{\alpha _m} I_{y_{\mathrm{w}}} \sin {\varphi } \cos {\varphi }+\frac{1}{2} \sin ^2{\alpha _m} (I_{x_{\mathrm{w}}}-I_{z_{\mathrm{w}}}) \sin {\varphi } \cos {\varphi }\\ +\,\frac{1}{2} (-I_{x_{\mathrm{w}}}-I_{z_{\mathrm{w}}}) \sin {\varphi } \cos {\varphi }+\frac{1}{2} I_{y_{\mathrm{w}}} \sin {2 \varphi } \biggr )\\ \\ 0 \end{bmatrix}, \end{aligned}$$

(10)

$$\begin{aligned} {{\varvec{f}}}_{\mathrm{aero}}= & {} \begin{bmatrix} -F_x \left( \sin {\alpha _m} \cos {\theta }+\cos {\alpha _m} \sin {\theta }~ \text {sign}({\dot{\varphi }}) \cos {\varphi }\right) -F_z \left( \sin {\alpha _m} \sin {\theta } \cos {\varphi }-\cos {\alpha _m} \cos {\theta }~ \text {sign}({\dot{\varphi }})\right) \\ \sin {\alpha _m} M_x-\cos {\alpha _m} M_z~ \text {sign}({\dot{\varphi }})\\ -\cos {\alpha _m} M_x~ \text {sign}({\dot{\varphi }}) \sin {\varphi }+M_y \cos {\varphi }-\sin {\alpha _m} M_z \sin {\varphi } \end{bmatrix}, \nonumber \\ \end{aligned}$$

(11)

$$\begin{aligned} {\varvec{g}}= & {} \begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}, \end{aligned}$$

(12)

where $F_x$, $F_z$, $M_x$, $M_y$, and $M_z$ are the aerodynamic forces and moments represented in the wing frame, as shown in Eq. (7), $I_F$ is the flapping moment of inertia defined as $I_F=I_{x_{\mathrm{w}}}\sin ^2{\alpha _m}+I_{z_{\mathrm{w}}} \cos ^2{\alpha _m}$, ${\bar{c}}$ is the mean aerodynamic chord of the wing, and ${\hat{d}}$ and $r_{\mathrm{cg}}$ are the distances from the wing reference point (hinge point at the root section) to the wing center of mass along the negative $x_{\mathrm{w}}$-axis and the $y_{\mathrm{w}}$-axis respectively.

The three-DOF model (8) is then written in the standard nonlinear control-affine form

$$\begin{aligned} \dot{{\varvec{x}}}={\varvec{Z}}({\varvec{x}})+{\varvec{Y}}({\varvec{x}}) ~\tau _\varphi (t), \end{aligned}$$

(13)

where the state vector ${\varvec{x}}$ is $[{\varvec{q}} \quad \dot{{\varvec{q}}}]^*=[z \quad \varphi \quad \theta \quad w \quad {\dot{\varphi }} \quad {\dot{\theta }}]^*$, and the vector fields ${\varvec{Z}}({\varvec{x}})$ and ${\varvec{Y}}({\varvec{x}})$ are written as

$$\begin{aligned} {\varvec{Z}}({\varvec{x}})= \begin{bmatrix} \dot{{\varvec{q}}}\\ {\mathcal {M}}^{-1} ({{\varvec{f}}}_{\mathrm{aero}}-{{\varvec{f}}}_c) \end{bmatrix} , \quad \quad {\varvec{Y}}({\varvec{x}})= \begin{bmatrix} {\varvec{0}}\\ {\mathcal {M}}^{-1}{\varvec{g}} \end{bmatrix}. \end{aligned}$$

The geometric control and averaging tools are then combined to rigorously investigate the balance and stability of the NLTP system (13) and unravel the unconventional flight dynamic behavior of flapping flight (e.g., vibrational stabilization). The next section outlines the most important geometric control and averaging tools that will be used in this analysis.

3 Combined Geometric Control–Averaging Analysis Tools

Analysis of NLTP systems requires different set of tools than those used for nonlinear time-invariant (NLTI) systems. The essential difference between NLTP and NLTI systems emanates from the fact that an equilibrium state of NLTP systems is generally represented by a periodic orbit (PO), as opposed to a fixed point for NLTI systems. That is, at equilibrium, every state of the NLTP system takes a periodic sequence of values with some time period T. Figure 5 shows a simple illustration of difference between fixed point and periodic orbit equilibrium in a two-dimensional state space.

Fig. 5

An illustration of the difference between fixed point and periodic orbit

Stability analysis of NLTP flapping-wing dynamics could be performed on the original time-periodic system by numerically capturing a periodic orbit associated with a certain equilibrium condition and analyzing its linear stability through Floquet theorem (Dietl and Garcia 2008a; Wu and Sun 2012; Stanford et al. 2013). However, very little insights into stabilizing/destabilizing mechanisms could be obtained through this purely numerical approach. On the other hand, a time-invariant version of the NLTP flapping-wing dynamics could be obtained through averaging techniques (reviewed next). As such, the periodic orbit representing equilibrium is converted into a fixed point, around which the system could be linearized. Stability analysis is then easily performed for the linear time-invariant (LTI) system via eigenvalue analysis. Furthermore, utilizing the simple and tractable form of LTI systems, the stability of linearized, time-invariant, flapping-wing dynamics could be analytically scrutinized. Hence, insights into different stabilizing/destabilizing mechanisms (e.g., stiffness or damping) could be gained.

3.1 Averaging Theorem

The classical averaging theorem is a simple tool that could be used to convert a NLTP system into a NLTI one. However, it possesses several limitations, which will be discussed in the following subsections. Theorem 1 provides the formal statement of the standard averaging theorem.

Theorem 1

Consider the NLTP system

$$\begin{aligned} {\varvec{\dot{x}}}(t)=\epsilon {\varvec{X}}({\varvec{x}}(t),t), \end{aligned}$$

(14)

where $0 < \epsilon \ll 1$ is a small perturbation scale, e.g., $\epsilon$ could be seen as the reciprocal of the frequency when the system is subject to high-frequency forcing. Assuming that ${\varvec{X}}$ is a T-periodic vector field in t, the averaged dynamical system corresponding to (14) is written as

$$\begin{aligned} \dot{\overline{{\varvec{x}}}}(t)=\epsilon \overline{{\varvec{X}}}(\overline{{\varvec{x}}}(t)), \end{aligned}$$

(15)

where $\overline{{\varvec{X}}} (\overline{{\varvec{x}}}(t))=\frac{1}{T} \int _0^T {\varvec{X}}({\varvec{x}}(t),\tau )\,d\tau$. According to the averaging theorem (Guckenheimer and Holmes 2013; Sanders et al. 2007; Khalil 2002):

• If ${\varvec{x}}(0)-\overline{{\varvec{x}}}(0)=O(\epsilon )$, then there exist $b > 0$ and $\epsilon ^* > 0$ such that ${\varvec{x}}(t)-\overline{{\varvec{x}}}(t)=O(\epsilon )$$\forall t \in [0,b/\epsilon ]$ and $\forall \epsilon \in$ [0,$\epsilon ^*$].

• If ${\varvec{x}}^*$ is an exponentially stable equilibrium point of (15) and if $\left\| {\varvec{x}}(0)-{\varvec{x}}^* \right\| <\rho$ for some $\rho > 0$, then ${\varvec{x}}(t)-\overline{{\varvec{x}}}(t)=O(\epsilon )$$\forall t>0$ and $\forall \epsilon \in$ [0,$\epsilon ^*$]. Moreover, The system (14) has a unique, exponentially stable, T-periodic solution ${\varvec{x}}_T (t)$ with the property $\Vert {\varvec{x}}_T (t)-{\varvec{x}}^*\Vert \le k\epsilon$ for some k.

Thus, the averaging approach allows converting a non-autonomous system into an autonomous system. As such, if the equilibrium state of the NLTP system is represented by a periodic orbit ${\varvec{x}}_T (t)$, it reduces to a fixed point of the averaged dynamics. The problem of ensuring a specific periodic orbit corresponding to a desired equilibrium configuration is significantly simplified using the averaging approach, hence allowing for analytical results.

One caveat here is that the averaging theorem requires the vector field ${\varvec{X}}({\varvec{x}},t)$ to be smooth in ${\varvec{x}}$. Unfortunately, the NLTP system (13) is not smooth in the state ${\dot{\varphi }}$ because of the absolute value function $\left| {\dot{\varphi }} \right|$. In addition, the adopted approximation of the wing pitching angle $\eta$ results in the existence of the sign function $\text {sign}({\dot{\varphi }})$. We tackle both issues by writing $\left| {\dot{\varphi }} \right| ={\dot{\varphi }}~ \text {sign}({\dot{\varphi }})$ and introducing a smooth approximation for the sign function; $\text {sign}({\dot{\varphi }})\approx h({\dot{\varphi }})=(2/\pi )\tan ^{-1}(n~{\dot{\varphi }})$. We set an appropriate value of n such that, in 1% of the ${\dot{\varphi }}$ range around the origin, the approximate function $h({\dot{\varphi }})$ reaches 99% of the true value ($\pm \, 1$). Alternatively, a hyperbolic tangent sigmoid function could be used as a smooth approximation for the sign function instead of the inverse tangent one. For more details about the adopted smooth approximation, the reader is referred to an earlier work by Taha et al. (2016).

3.2 Nonlinear Variation of Constants Formula (VOC)

The considered system (13) is not amenable to the averaging theorem (Theorem 1), i.e., it is not written in the standard averaging form (14). The periodic forcing vector field ${\varvec{Y}}({\varvec{x}}) ~\tau _\varphi (t)$ is of higher magnitude and faster timescale (i.e., high frequency) than that of the dynamics (drift) vector field ${\varvec{Z}}({\varvec{x}})$. Therefore, averaging theorem cannot be directly applied to system (13). In fact, if direct averaging is applied to (13), the time-periodic, zero-mean forcing vector field ${\varvec{Y}}({\varvec{x}}) ~\tau _\varphi (t)$ would completely vanish. That is, the effects of the flapping-wing dynamics on the body would be completely ignored. In order to resolve this issue, we utilize the nonlinear variation of constants formula, which is a differential-geometric tool that is used to split the flow along two vector fields. As such, the averaged version of system (13) would be obtained through a multi-step process that is explained next.

Fig. 6

An illustration of the application of the VOC formula to system (16)

Consider a nonlinear system subjected to a high-frequency, high-amplitude, periodic forcing in the form

$$\begin{aligned} \dot{{\varvec{x}}}(t) = {\varvec{f}}({\varvec{x}}(t)) + \frac{1}{\epsilon }~{\varvec{g}}\left( {\varvec{x}}(t),\frac{t}{\epsilon }\right) , \quad {\varvec{x}}(0) = {\varvec{x}}_0, \end{aligned}$$

(16)

where $0 < \epsilon \ll 1$. The time-varying vector field $(1/\epsilon ){\varvec{g}}({\varvec{x}}(t),t/\epsilon )$ is assumed to be periodic in its second argument with period T. The system (16) is not amenable to direct averaging, i.e., is not in the form of (14), because ${\varvec{f}}$ and ${\varvec{g}}$ are not of the same order. The VOC resolves this issue by approximating the flow $\phi _{0,T}^{{\varvec{f}}+{\varvec{g}}}({\varvec{x}}_0)$ (i.e., flow along ${\varvec{f}}+{\varvec{g}}$ for a period T starting at initial point ${\varvec{x}}_0$) by a flow along the vector field ${\varvec{g}}$ staring at a different initial condition $\delta {\varvec{x}}_0$. That is, $\phi _{0,T}^{{\varvec{f}}+{\varvec{g}}}({\varvec{x}}_0)=\phi _{0,T}^{{\varvec{g}}}(\delta {\varvec{x}}_0)$, where the new initial point $\delta {\varvec{x}}_0$ is obtained through the flow along a new vector field ${{\varvec{F}}}$ that is introduced by the VOC formula. Figure 6 shows a simple explanatory sketch for the application of the VOC formula to the system (16). As such, the VOC formula allows separation of the system (16) into two companion systems as follows (Agrachev and Gamkrelidze 1978; Bullo and Lewis 2004)

$$\begin{aligned} \begin{array}{l} \dot{{\varvec{z}}}(t) = {{\varvec{F}}}({\varvec{z}}(t),t), \quad {\varvec{z}}(0) = {\varvec{x}}_0\\ \dot{{\varvec{x}}}(t) = {\varvec{g}}({\varvec{x}}(t),t), \quad {\varvec{x}}(0) =\delta {\varvec{x}}_0= {\varvec{z}}(t) \end{array}, \end{aligned}$$

(17)

where ${{\varvec{F}}}$ is the pullback of the vector field ${\varvec{f}}$ along the flow $\phi _t^{{\varvec{g}}}$ of the time-varying vector field ${\varvec{g}}$. Using the chronological calculus formulation of Agrachev and Gamkrelidze (1978), Bullo (2002) showed that, for a time-invariant ${\varvec{f}}$ and time-varying ${\varvec{g}}$, the pullback vector field ${{\varvec{F}}}({\varvec{x}}(t),t)$ can be written as

$$\begin{aligned} \begin{array}{l} {{\varvec{F}}}({\varvec{x}}(t),t)= {\varvec{f}}({\varvec{x}}(t))+ \sum \limits _{k=1}^{\infty } \int \limits _{0}^{t}...\int \limits _{0}^{s_{k-1}} \left( ad_{{\varvec{g}}({\varvec{x}}(t),~S_k)}...ad_{{\varvec{g}}({\varvec{x}}(t),~S_1)} {\varvec{f}}({\varvec{x}})\right) ds_k...ds_1, \end{array} \nonumber \\ \end{aligned}$$

(18)

where $ad_{{\varvec{g}}}{\varvec{f}}=[{\varvec{g}}, {\varvec{f}}]$ is the Lie bracket between the two vector fields ${\varvec{g}}$ and ${\varvec{f}}$ and is computed as $[{\varvec{g}}, {\varvec{f}}]=\frac{\partial {\varvec{f}}}{\partial {\varvec{x}}} {\varvec{g}} -\frac{\partial {\varvec{g}}}{\partial {\varvec{x}}} {\varvec{f}}$ (Nijmeijer and Van der Schaft 1990, PP. 23–72).

3.3 Averaging of of High-Amplitude Periodic Forcing

Since FWMAVs/insects experience high-amplitude, high-frequency periodic forcing (i.e., in the form (16)). Applying the VOC formula before averaging is necessary to obtain an averaged system that accounts for the multi-body and multi-timescale effects. The benefit of the VOC formula is that each of the systems in (17) is individually amenable to the averaging theorem. That is,

$$\begin{aligned} \begin{array}{l} \dot{\bar{{\varvec{z}}}}(t) = \frac{1}{T} \int _{0}^{T} {{\varvec{F}}}({\varvec{z}}(t),t)~\hbox {d}t, \quad \bar{{\varvec{z}}}(0) = {\varvec{x}}_0\\ \dot{\bar{{\varvec{x}}}}(t) = \frac{1}{T} \int _{0}^{T} {\varvec{g}}({\varvec{x}}(t),t)~\hbox {d}t, \quad \bar{{\varvec{x}}}(0) = \bar{{\varvec{z}}}(t) \end{array}. \end{aligned}$$

(19)

It should be noted that for the considered system (13), the time-periodic forcing vector field ${\varvec{Y}}({\varvec{x}}) ~\tau _\varphi (t)$ is of zero mean. Hence, averaging after applying the VOC implies

$$\begin{aligned} \bar{{\varvec{x}}}(t)=\bar{{\varvec{z}}}(t),~~ \dot{\bar{{\varvec{z}}}}=\bar{{{\varvec{F}}}}(\bar{{\varvec{z}}}). \end{aligned}$$

(20)

Therefore, the averaged dynamics of the original system (16), or alternatively (13) in our three-DOF FWMAV model, can be obtained just by averaging the pullback vector field ${{\varvec{F}}}({\varvec{x}}(t),t)$. Therefore, Theorem 1 is extended next to high-frequency, high-amplitude, periodically forced systems in the form of Eq. (16).

Theorem 2

Consider a NLTP system subject to a high-frequency, high-amplitude periodic forcing (16). Assuming that ${\varvec{g}}$ is a T-periodic in t, zero-mean vector field and both ${\varvec{f}}$ and ${\varvec{g}}$ are continuously differentiable, the averaged dynamical system corresponding to (16) is written as

$$\begin{aligned} \dot{\overline{{\varvec{x}}}}(t)=\epsilon \overline{{\varvec{F}}}(\overline{{\varvec{x}}}(t)), \end{aligned}$$

(21)

where $\overline{{\varvec{F}}} (\overline{{\varvec{x}}}(t))=\frac{1}{T} \int _0^T {\varvec{F}}({\varvec{x}}(t),\tau )\,d\tau$, and ${\varvec{F}}$ is the pullback of ${\varvec{f}}$ along the flow $\phi _t^{{\varvec{g}}}$ of the time-varying vector field ${\varvec{g}}$ as explained in Eq. (18). Moreover,

• If $\overline{{\varvec{x}}}(0)={\varvec{x}}(0)$, then there exist $b > 0$ and $\epsilon ^* > 0$ such that ${\varvec{x}}(t)-\overline{{\varvec{x}}}(t)=O(\epsilon )$$\forall t \in [0,b/\epsilon ]$ and $\forall \epsilon \in$ [0,$\epsilon ^*$].

• If ${\varvec{x}}^*$ is an exponentially stable equilibrium point of (21) and if $\left\| {\varvec{x}}(0)-{\varvec{x}}^* \right\| <\rho$ for some $\rho > 0$, then ${\varvec{x}}(t)-\overline{{\varvec{x}}}(t)=O(1)$$\forall t>0$ and $\forall \epsilon \in$ [0,$\epsilon ^*$]. Moreover, there exists an $\epsilon _1 > 0$ such that $\forall \epsilon \in$ [0,$\epsilon _1$], the system (16) has a unique, T-periodic, locally asymptotically stable trajectory that takes values in an open ball of radius O(1) centered at ${\varvec{x}}^*$.

The main difference between Theorem 1 (direct averaging) and Theorem 2 (VOC and averaging) is that the former guarantees a periodic orbit that is $O(\epsilon )$ from the corresponding fixed point of the averaged dynamics, while the latter allows for larger variations O(1) from the fixed point. This relatively large amplitude admitted by Theorem 2 is particularly useful in analyzing flapping flight while including wing dynamics where the flapping angle $\varphi$ becomes a state; the amplitude of the flapping angle is typically around 60 degrees. Therefore, the application of the VOC formula is essential in analyzing flapping flight, multi-body dynamics. We are emphasizing that Theorem 1 is not a viable option in this case as direct averaging would yield trivial results when applied to the three-DOF multi-body system (13); i.e., it would neglect the entire effects of the flapping input vector field ${\varvec{Y}}({\varvec{x}}) ~\tau _\varphi (t)$.

4 Geometric Control and Averaging Analysis of FWMAVs

In this section, we use the geometric control and averaging tools explained in the previous section to investigate the balance and stability of the three-DOF model derived in Sect. 2. As explained earlier, the direct application of the averaging theorem to the NLTP system (13), with zero-mean $\tau _\varphi$, yields trivial results (i.e., no effect of flapping on the dynamics). Therefore, we apply the VOC formula before averaging to obtain the pullback vector field (18), which accounts for the effects of the forcing vector field on the dynamics (drift) vector filed. That is, the averaged dynamics will be determined from Eq. (20). It should be noted that because of the mechanical structure of the system (13) and the non-conservative forces (aerodynamic loads) being quadratic in the generalized velocities, the integral series (18) of the pullback vector field is expected to terminate after two terms (Bullo 2002). However, the essentially high-order smooth approximation of the sign function hinders the termination after two terms in this case. The pullback series of the system (13) terminates after three terms and can be written as

$$\begin{aligned} {{\varvec{F}}}({\varvec{x}},t)= & {} {\varvec{Z}}({\varvec{x}})+\left[ {\varvec{Y}},~{\varvec{Z}}\right] \int \limits _{0}^{t} \tau _\varphi (s_1) ~d s_1 +ad_{{\varvec{Y}}}^2{\varvec{Z}} \int \limits _{0}^{t} \int \limits _{0}^{s_1} \tau _\varphi (s_2)~ \tau _\varphi (s_1)~ d s_2~ d s_1\nonumber \\&+\, ad_{{\varvec{Y}}}^3{\varvec{Z}} \int \limits _{0}^{t} \int \limits _{0}^{s_2} \int \limits _{0}^{s_1} \tau _\varphi (s_3) \tau _\varphi (s_2)~ \tau _\varphi (s_1)~d s_3~ d s_2~ d s_1, \end{aligned}$$

(22)

where $ad_{{\varvec{Y}}}^n{\varvec{Z}} \equiv [{\varvec{Y}},ad_{{\varvec{Y}}}^{n-1}{\varvec{Z}}]$.

4.1 Balance (Trim)

Unlike the simpler two-DOF model, which has been investigated in a previous effort by the authors Hassan and Taha (2016, 2017a), a simple harmonic waveform ($\tau _\varphi =U \cos {\omega t}$) for the the flapping torque cannot achieve balance for the three-DOF system (8), or equivalently (13), where the body pitching angle $\theta$ is a state. The reason is that a nonzero mean flapping angle may be required to adjust the center of pressure of the aerodynamic forces with respect to the body center of gravity to achieve pitch trim. Therefore, we suggest writing the input torque $\tau _\varphi (t)$ as

$$\begin{aligned} \tau _\varphi (t)=U_1\cos \omega t+U_2\sin \omega t, \end{aligned}$$

(23)

where the resultant amplitude of the two sinusoids will be denoted by $U_{\mathrm{R}}$ (i.e., $U_{\mathrm{R}}=\sqrt{U_1^2+U_2^2}$). Note that this same objective could be achieved by using only one harmonic with a phase shift. However, the adopted form (23) is easier to manipulate during the variation of constants and averaging processes.

Using the input waveform in Eq. (23), the averaged dynamics [i.e., the averaged pullback vector field (22)] is obtained as

$$\begin{aligned} \dot{\bar{{\varvec{x}}}}= & {} \bar{{{\varvec{F}}}}(\bar{{\varvec{x}}})={\varvec{Z}}(\bar{{\varvec{x}}})+\frac{U_2}{\omega }\left[ {\varvec{Y}},~{\varvec{Z}}\right] (\bar{{\varvec{x}}})+\biggl (\frac{U_1^2+3U_2^2}{4~\omega ^2}\biggr ) ad_{{\varvec{Y}}}^2{\varvec{Z}}(\bar{{\varvec{x}}})\nonumber \\&+\,\biggl (\frac{31 U_1^2 U_2+5 U_2^3}{12~\omega ^3}\biggr )ad_{{\varvec{Y}}}^3{\varvec{Z}}(\bar{{\varvec{x}}}). \end{aligned}$$

(24)

In order to achieve balance at hovering, we solve for the trim input torque amplitudes, $U_{1_{\mathrm{t}}}$ and $U_{2_{\mathrm{t}}}$, along with a fixed point $\bar{{\varvec{x}}}_0$ that ensure $\dot{\bar{{\varvec{x}}}}={\varvec{0}}$. Now on, we consider the hawkmoth insect for this analysis whose morphological parameters are given in “Appendix D.” As such, we obtain

$$\begin{aligned} \begin{array}{l} U_{1_{\mathrm{t}}}= 0.97~U^{\dagger }\\ U_{2_{\mathrm{t}}}= 0.24~U^{\dagger }\\ \bar{{\varvec{x}}}_0=[0 \quad 7.12^{\circ } \quad 0 \quad 0 \quad 0 \quad 0]^* \end{array}, \end{aligned}$$

(25)

where the subscript $\mathrm{t}$ denotes trim/balance condition at hover, $U^{\dagger }$ is the input torque amplitude needed to balance the two-DOF model (Hassan and Taha 2016, 2017a) at hover using a simple harmonic waveform, and is defined as

$$\begin{aligned} U^{\dagger }=\sqrt{\frac{2~g I_F^2 \omega ^2}{k_L}}, \end{aligned}$$

where $k_L$ is a constant that depends on the vehicle parameters

$$\begin{aligned} k_L=\frac{\rho ~C_{L_\alpha } I_{21} \sin {\alpha _m} \cos {\alpha _m}}{2~m_{\mathrm{v}}}. \end{aligned}$$

It should be noted that the resultant trim input torque amplitude ($U_{\mathrm{R}_{\mathrm{t}}}=\sqrt{U_{1_{\mathrm{t}}}^2+U_{2_{\mathrm{t}}}^2}$) is equal to $U^{\dagger }$. That is, the flapping torque amplitude required to maintain the hovering equilibrium for the considered three-DOF system (13) is the same as that of the previously analyzed two-DOF system (Hassan and Taha 2016, 2017a); only phase shift is required to achieve pitch trim as explained earlier.

4.2 Stability Analysis

Now, that balance/trim at the hovering equilibrium has been ensured for the averaged system (24), a linearized version of the averaged dynamics could be obtained at the hovering fixed point (25). Having an LTI version of the NLTP system (13) at hover would: (i) significantly simplify stability analysis: it can be analyzed by checking eigenvalues; and (ii) allow us to obtain analytical (or semi-analytical) results and gain insights into various stabilizing/destabilizing mechanisms.

To obtain an LTI representation of the NLTP dynamics (13), we evaluate the Jacobian matrix, ${\varvec{A}}$, of the averaged nonlinear dynamics (24) at the hovering trim point $(U_{1_{\mathrm{t}}}= 0.97~U^{\dagger },~U_{2_{\mathrm{t}}}= 0.24~U^{\dagger },~{\bar{z}}=0,~ {\bar{\varphi }}=7.12^{\circ },~ {\bar{\theta }}=0,~ {\bar{w}}=0,~\bar{{\dot{\varphi }}}=0 ,~\bar{{\dot{\theta }}}=0)$. As such, we obtain

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} \begin{pmatrix} {\bar{z}}\\ {\bar{\varphi }}\\ {\bar{\theta }}\\ {\bar{w}}\\ \bar{{\dot{\varphi }}}\\ \bar{{\dot{\theta }}} \end{pmatrix}= [{\varvec{A}}] (\bar{{\varvec{x}}})= \begin{bmatrix} 0&\quad 0&\quad 0&\quad 1&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 1&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 1\\ 0&\quad -\,0.19&\quad 4.7&\quad -\,4.05&\quad 0.0002&\quad 0.1\\ 0&\quad -\,19&\quad -\,621.98&\quad -\,0.85&\quad -\,9.55&\quad 0.005\\ 0&\quad 6093&\quad -\,72.96&\quad 269.22&\quad -\,5.42&\quad -\,1.54 \end{bmatrix} \begin{pmatrix} {\bar{z}}\\ {\bar{\varphi }}\\ {\bar{\theta }}\\ {\bar{w}}\\ \bar{{\dot{\varphi }}}\\ \bar{{\dot{\theta }}} \end{pmatrix}, \end{aligned}$$

(26)

where $[{\varvec{A}}]=\left[ \frac{\partial \bar{{{\varvec{F}}}}}{\partial \bar{{\varvec{x}}}}\right] \bigg |_{\bar{{\varvec{x}}}_0}$.

Investigating the eigenvalues of the linearized system (26), we find

$$\begin{aligned} \mathrm{eigenvalues} ({\varvec{A}})=-\,33.85 \pm 31.9~i,~ 28.31 \pm 30.8~i,~ -4.05,~0, \end{aligned}$$

which indicates an unstable averaged system due to the complex–conjugate pair ($28.31 \pm 30.8~i$) having positive real parts. This implies that a feedback control would be needed to stabilize this system at the hovering equilibrium. This result is consistent with many of the previous analyses in the literature (Sun and Xiong 2005; Xiong and Sun 2008; Taylor and Thomas 2002; Sun et al. 2007; Taha et al. 2014b; Cheng and Deng 2011) that concluded the hovering equilibrium of FWMAVs/insects to be open-loop unstable.

4.3 Stability Characterization

Thanks to the simultaneous analytical tractability and mathematical rigor of the geometric control–averaging tools, the stability of the NLTP system (13) could be investigated on a deeper level through scrutinizing the correspondent LTI system. The linearization of the averaged system (24) at the hovering fixed point $\bar{{\varvec{x}}}_0$ can be written abstractly as

(27)

where the analytical expressions of the elements of the matrix ${\varvec{A}}$ are shown in detail in “Appendix C.”

Since the open-loop instability at the hovering equilibrium of FWMAVs/insects has been mostly attributed to the lack of body pitch stiffness (Sun and Xiong 2005; Xiong and Sun 2008; Taylor and Thomas 2002; Sun et al. 2007; Taha et al. 2014b; Cheng and Deng 2011). It is of great interest to scrutinize the stability derivative $A_{63}$ which represents body pitch stiffness: it corresponds to a pitching moment resulting from a pitch angle disturbance. The stability derivative $A_{63}$ can be analytically written as

$$\begin{aligned} A_{63}=&\frac{1}{I_F^2 I_{y_b} m_{\mathrm{v}} \omega ^2}C_{L_\alpha } m_{\mathrm{w}} \rho \cos {\alpha _m} \\&\biggl (\cos {\alpha _m} \biggl ({\bar{c}} {\hat{d}} \biggl (I_{11} k \left( -5.23 I_F U_2 \omega +0.06 U_1^2+0.18 U_2^2\right) \\&+\, I_{12} \left( 3.9 I_F U_2 \omega -0.05 U_1^2-0.14 U_2^2\right) \biggr )+{\bar{c}} {\hat{d}}I_{21} \cos {\alpha _m} \left( U_2 (0.02 U_2\right. \\&\left. -\,2.4 I_F \omega )+0.01 U_1^2\right) +\\&+\,I_{21} r_{\mathrm{cg}} \left( U_2 (0.18 U_2-19.27 I_F \omega )+0.06 U_1^2\right) \biggr )\\&+\,r_{\mathrm{cg}} \biggl (I_{11} k \left( U_2 (1.48 U_2-41.88 I_F \omega )+0.49 U_1^2\right) +\\&+\,I_{12} \left( U_2 (31.4 I_F \omega -1.1 U_2)-0.37 U_1^2\right) \biggr )\biggr ). \end{aligned}$$

Considering the hawkmoth parameters, we find $A_{63}=-\,72.96$ as shown in Eq. (26). The negative sign indicates a restoring pitching moment under a pitch angle perturbation from the equilibrium, hence a stabilizing pitch stiffness. This result revises the community’s belief. That is, the natural (open-loop) longitudinal flight dynamics possesses a stabilizing body pitch stiffness mechanism.

To investigate the main contributors to this pitch stiffness mechanism, we write the averaged dynamics in terms of its two components: the dynamics vector field ${\varvec{Z}}$ and the Lie brackets between the dynamics and control vector fields (i.e., control effects), as shown in Eq. (24). As such, the Jacobian matrix ${\varvec{A}}$ can be considered as an addition of two matrices ${\varvec{A}}_{\mathrm{d}}$ and ${\varvec{A}}_{\mathrm{c}}$, where

$$\begin{aligned} \begin{array}{l} {\varvec{A}}_{\mathrm{d}}= \frac{\partial }{\partial \bar{{\varvec{x}}}}\bigg |_{\bar{{\varvec{x}}}_0} \biggl ({\varvec{Z}}\biggr )\\ {\varvec{A}}_{\mathrm{c}}= \frac{\partial }{\partial \bar{{\varvec{x}}}}\bigg |_{\bar{{\varvec{x}}}_0}\biggl (\frac{U_2}{\omega }\left[ {\varvec{Y}},~{\varvec{Z}}\right] +\biggl (\frac{U_1^2+3U_2^2}{4~\omega ^2}\biggr ) ad_{{\varvec{Y}}}^2{\varvec{Z}}+\biggl (\frac{31 U_1^2 U_2+5 U_2^3}{12~\omega ^3}\biggr )ad_{{\varvec{Y}}}^3{\varvec{Z}}\biggr ) \end{array}, \end{aligned}$$

(28)

where the subscripts $\mathrm{d}$ and $\mathrm{c}$ refer to dynamics and control, respectively. Hence, the effect emanating from each source can be shown separately. We find that, as maybe expected, $A_{\mathrm{d_{63}}}=0$. Hence, the pitch stiffness emanates solely from flapping actuation. This fact implies that the high-frequency periodic forcing applied on the wings induces a stabilizing effect on the slower body pitching motion. That is, this pitch stiffness mechanism relies essentially on the vibrational stabilization phenomenon.

It should be noted that the pitch stiffness term $A_{63}$ stems from a combined inertial–aerodynamic root; i.e.,

$$\begin{aligned} \lim _{m_{\mathrm{w}}\rightarrow 0} A_{63}=0~~ \text {and}~~ \lim _{C_{L_\alpha }\rightarrow 0} A_{63}=0. \end{aligned}$$

The pitch stiffness term $A_{63}$ can be abstractly written as

$$\begin{aligned} A_{63}= k_{63}~ m_{\mathrm{w}}\cos {\bar{\phi }}_0 M_{y_w}^{(I)}, \end{aligned}$$

where $k_{63}$ is a function of the vehicle parameters and the flapping torque amplitude and frequency, ${\bar{\phi }}_0$ is the average flapping angle at the trim condition (25), and $M_{y_w}^{(I)}$ is an aerodynamic derivative that represents a pitching moment in the inertial frame due to a disturbance in the vertical velocity w. For an intuitive explanation of this pitch stiffness mechanism and the role of wing inertia, consider a body pitch up disturbance $\Delta \theta$. This pitch disturbance causes a change of the lift force vector direction, which, in turn, results in a deficit in the lift force needed for balance. Hence, a downward vertical velocity disturbance $\Delta w$ would be generated. The vertical velocity disturbance $\Delta w$ can be written as an addition of two components: $\Delta w= \Delta {\bar{w}}+\Delta {\tilde{w}}$, where $\Delta {\bar{w}}$ is the cycle-average and $\Delta {\tilde{w}}$ is a zero-mean oscillatory component because of the fast timescale of the wing dynamics. Due to the aerodynamic derivative $M_{y_w}^{(I)}$, a pitching moment is generated as a consequence of $\Delta w$. The derivative $M_{y_w}^{(I)}$ can be decomposed similarly: $M_{y_w}^{(I)}={\bar{M}}_{y_w}+{\tilde{M}}_{y_w}$. As such, the resulting pitching moment $\Delta M_{y}^{(I)}=M_{y_w}^{(I)} \Delta w$ will have three contributions: (i) ${\bar{M}}_{y_w} \Delta {\bar{w}}$ which is captured by direct averaging; (ii) ${\bar{M}}_{y_w} \Delta {\tilde{w}}+{\tilde{M}}_{y_w} \Delta {\bar{w}}$ whose net effect cancel over the flapping cycle (zero mean); and (iii) ${\tilde{M}}_{y_w} \Delta {\tilde{w}}$ which is the multiplication of two zero-mean terms and will have a nonzero mean value if the variations of these two terms are synchronized. It should be noted that the last contribution is clearly due to the oscillation (vibration) of the system characteristics (i.e., the multi-timescale nature of the system); it is typically neglected by direct averaging. The wing inertial effects promote the last contribution, ${\tilde{M}}_{y_w} \Delta {\tilde{w}}$, through amplifying $\Delta {\tilde{w}}$ resulting from a pitch disturbance. This effect can be seen from the ${\dot{w}}$ equation in the three-DOF NLTP system, i.e., the fourth line in Eq. (13). The right-hand side of that line contains terms like the following: $m_{\mathrm{w}} r_{\mathrm{cg}} {\dot{\theta }} {\dot{\varphi }} \cos \theta \cos \varphi$; $m_{\mathrm{w}} r_{\mathrm{cg}} {\dot{\theta }}^2 \sin \theta \sin \varphi$; $m_{\mathrm{w}} {\bar{c}} {\hat{d}} \cos {\alpha _m} {\dot{\theta }} {\dot{\varphi }} \cos \theta \sin \varphi \text {sign}({\dot{\varphi }})$; and $m_{\mathrm{w}} {\bar{c}} {\hat{d}} \cos {\alpha _m} w {\dot{\theta }} \cos \theta \sin \varphi \text {sign}({\dot{\varphi }})$. This implies that these terms are producing body’s vertical velocity through an interaction between the wing inertial effects and the body pitch angle/rate. Therefore, any first-order analysis that neglects the wing inertial effects would yield a zero pitch stiffness for the body.

4.4 Averaging-Aided Shooting–Floquet Analysis

Although the adopted approach (applying the VOC formula first to the NLTP system and then averaging over the flapping cycle) captures a wide range of aerodynamic–dynamic interactions, it is still an approximation of the true time-periodic. Thus, there are some phenomena that are not very well captured in the averaged dynamics sense. One important aspect is the effect of the wing–body interactions on the generated lift over the cycle. That is, an averaged lift over the flapping cycle that is equal to the weight of the vehicle may not be enough for balance. This phenomenon has been referred to as a negative lifting mechanism in an earlier work by Taha et al. (2016). This phenomenon, in turn, affects stability since balance and stability are coupled in this problem. That is, if the flapping input torque amplitudes are not enough to ensure balance at hover, the vehicle will be deviating from its hovering periodic orbit (or fixed point in the averaged sense).

Therefore, in this subsection, a time-periodic analysis will be performed by using the averaging analysis results as an initial guess for an optimized periodic shooting method (Dednam and Botha 2015). This shooting method is used to determine the hovering periodic orbit of the three-DOF system (13) simultaneously with more accurate (i.e., accounts for the negative lifting mechanism) values of the trim input torque amplitudes ($U_{1_{\mathrm{t}}}$, $U_{2_{\mathrm{t}}}$). Such a procedure has been proposed and applied on a simpler model in our previous effort (Hassan and Taha 2017b, a). “Appendix E” presents details of the adopted optimized periodic shooting algorithm (Dednam and Botha 2015). The Floquet theorem (Nayfeh and Balachandran 1995) is then used to analyze stability of the captured hovering periodic orbit. In the Floquet stability analysis, the NLTP dynamics (13) is linearized about the numerically captured periodic orbit, yielding a linear, time-periodic (LTP) system. The stability of the obtained LTP system is then analyzed through investigating the monodromy matrix: the state transition matrix evaluated after one period T. The eigenvalues of the monodromy matrix (also called Floquet multipliers) have to be inside the unit disk (in the complex plane) for the periodic orbit to be stable. The Floquet multipliers could then be transformed into Floquet exponents, which represent eigenvalues of the corresponding continuous LTI system. That is, a positive real-part Floquet exponent implies instability. Therefore, the obtained Floquet exponents will be used to construct a comparison against the averaging stability results obtained in Sect. 4.2.

Feeding the trim input torque amplitudes ($U_{1_{\mathrm{t}}}$, $U_{2_{\mathrm{t}}}$) from Eq. (25) as an initial guess to the optimized periodic shooting, we obtain the following point on the hovering periodic orbit along with the associated trim input torque amplitudes

$$\begin{aligned} \varphi (0)= & {} -1.1~\hbox {rad},~~\theta (0) = 0.11~\hbox {rad},~~ w(0) = -0.01~\hbox {m/s}\nonumber \\ {\dot{\varphi }}(0)= & {} -0.74~\hbox {rad/s},~~{\dot{\theta }}(0) = 5.29~\hbox {rad/s}\nonumber \\ U_{1_{\mathrm{t_\mathrm{n}}}}= & {} 1.02~U^{\dagger },~~ U_{2_{\mathrm{t_\mathrm{n}}}}= 0.07~U^{\dagger }, \end{aligned}$$

(29)

where the subscript $\mathrm{n}$ in $U_{1_{\mathrm{t_\mathrm{n}}}}, U_{2_{\mathrm{t_\mathrm{n}}}}$, refers to the trim values obtained through the numerical optimized shooting method. Investigating the resultant trim amplitude, we find $U_{\mathrm{R}_{\mathrm{t}_{\mathrm{n}}}}=\sqrt{U_{1_{\mathrm{t_\mathrm{n}}}}^2+U_{2_{\mathrm{t_\mathrm{n}}}}^2}=1.0225~U^{\dagger }$. That is, the resultant trim amplitude from the optimized shooting is slightly higher than that of averaging. This result conforms with our previous findings for the two-DOF model (Hassan and Taha 2017a, b) that averaging may not very well capture the negative lifting phenomenon (i.e., averaging underestimates the required flapping torque to ensure hovering). Figure 7 shows the periodic orbit corresponding to the initial conditions and trim input torque amplitudes in (29).

Fig. 7

Numerical simulation of the captured hovering periodic orbit (29) for the NLTP system (13) under the input waveform (23) and using the hawkmoth parameters

To investigate stability, the NLTP dynamics (13) is linearized about the captured hovering periodic orbit (29). The Floquet multipliers for the obtained LTP system are found to be

$$\begin{aligned} 0.69 \pm 1.99i,~ 0.11 \pm 0.22i,~ 0.87,~0, \end{aligned}$$

which also indicates an unstable hovering periodic orbit due to the existence of the complex–conjugate pair ($0.69 \pm 1.99i$) outside the unit disk. Figure 8 shows the Floquet exponents corresponding to the above Floquet multipliers along with the eigenvalues from averaging for comparison. Both techniques yield similar stability characteristics: an unstable oscillatory mode, a stable oscillatory mode, a stable eigenvalue on the real line, and a neutral (zero) eigenvalue. Note that the zero eigenvalue corresponds to the ignorable coordinate z in both cases.

Fig. 8

Eigenvalues determining the stability of the NLTP system (13) for the hawkmoth case using averaging and Floquet theorem

4.5 Effects of High Flapping Frequency

It is well known that the vibrational pitch stabilization phenomenon is intimately tied to high-frequency periodic forcing (Bellman et al. 1985; Stephenson 1908; Kapitsa 1951, 1965). Therefore, the effect of flapping frequency on stability of the NLTP system (13) is investigated in this subsection.

Considering a flapping frequency that is ten times the documented value for the hawkmoth, the captured hovering periodic orbit is found to have the following trim input torque amplitudes

$$\begin{aligned} \begin{array}{l} U_{1_{\mathrm{t_\mathrm{n}}}}^{\mathrm{hf}}= 1.00~U^{\dagger }\\ U_{2_{\mathrm{t_\mathrm{n}}}}^{\mathrm{hf}}= 0.01~U^{\dagger } \end{array}, \end{aligned}$$

(30)

where the superscript $\mathrm{hf}$ denotes high frequency. It is noted that the resultant amplitude $U_{\mathrm{R}_{\mathrm{t}_{\mathrm{n}}}}^{\mathrm{hf}}= 1.00032~U^{\dagger }$, which is less than that of the original flapping frequency and closer to the averaging one. This implies that the negative lifting mechanism effects tends to diminish as the flapping frequency increases and hence the closeness to the averaging result. This, in fact, conforms with the averaging theorem statement that the averaging results are valid for high enough frequency. That is, the averaging results become more representative of the physical (time-periodic) system at higher frequencies.

The obtained Floquet multipliers for this high-frequency periodic orbit are

$$\begin{aligned} 1.1055 \pm 0.1297i,~0.8745 \pm 0.1074i,~0.9849,0, \end{aligned}$$

whose unstable pair ($1.1055 \pm 0.1297i$) shifts toward the stable region. This indicates that the higher flapping frequency amplifies the effect of the vibrational pitch stabilization mechanism. However, to achieve passive (open-loop) stability, a change in the vehicle parameters (e.g., wing mass, wing size, hinge location, etc.) maybe required.

4.6 Comparison with the Corresponding Single-Body Model

One legitimate question that needs to be addressed is: Can direct averaging (which is essentially less rigorous) capture such stabilizing effects? Realizing that direct averaging of the NLTP system (13) would yield trivial results (completely ignoring the flapping effects), the simplest non-trivial analysis, avoiding differential-geometric tools (e.g., VOC), would have to ignore the flapping dynamics and assume a waveform for the flapping angle $\varphi (t)$ as if the flapping wing is controlled by a fast servo mechanism. This analysis essentially neglects the multi-body nature of the problem (i.e., a single-body problem). Therefore, it is interesting to investigate the differences between the three-DOF model (13) and the single-body version of it. In the latter, the VOC formula would not be needed. After applying direct averaging to the single-body version of the system (13) and linearizing the resulting NLTI system, we obtain the following Jacobian matrix

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} \begin{pmatrix} \theta \\ w\\ {\dot{\theta }} \end{pmatrix} = [A_{sb}] ({\varvec{x}}_{sb})= \begin{bmatrix} 0&\quad 0&\quad 1\\ 0.01&\quad -\,0.15&\quad 0 \\ 0&\quad -\,0.03&\quad -\,0.88 \end{bmatrix} \begin{pmatrix} \theta \\ w\\ {\dot{\theta }} \end{pmatrix}, \end{aligned}$$

(31)

where the state vector is ${\varvec{x}}_{sb}=[\theta ~~w~~{\dot{\theta }}]^*$. It should be noted that the pitch stiffness, the element (3, 1), is zero, whereas in the multi-body averaged system (26), the pitch stiffness has a significant value ($-72.96$). This implies that the discovered pitch stiffness mechanism is essentially induced due to the mutual interactions between the body and wing dynamics. That is, such a mechanism is revealed only when the wing flapping dynamics is included and/or higher-order averaging is used.

5 Conclusion

The main finding of this paper is that the high-frequency periodic forcing on flapping-wing micro-air-vehicles induce vibrational stabilization mechanisms to their relatively slow body dynamics. These stabilizing mechanisms are mainly due to the interaction between the aero-inertial loads on the flapping wings due to the fast flapping motion and those due to the slow body motion: what we call aerodynamic–dynamic interaction. The main conclusion is that this interaction is instrumental for the open-loop stability analysis of such nonlinear time-periodic systems. Moreover, it cannot be captured by direct averaging or without accounting for the wing flapping dynamics. Therefore, the differential-geometric-control tools are essential to properly analyze the complex dynamics of these systems as they naturally account for the multi-body dynamics and hence capture the vibrational stabilization mechanisms due to aerodynamic–dynamic interactions. Finally, Fig. 9 summarizes the analysis performed in this paper.

Fig. 9

Summary of the analysis steps performed in Sect. 4

Appendices

Appendix

Derivation of the Five-DOF Equations of Motion

We use the principle of virtual power (Greenwood 2003), as explained in Sect. 2, to derive the five-DOF equations of motion (2) in detail. The various terms in Eq. (1) for the body and wing are given below.

1.1 Body

The linear velocity of the reference point of the body axis system (the body’s center of gravity) and the corresponding angular velocity are written as

$$\begin{aligned} {\varvec{v}}_{\mathrm{b}} = {\dot{x}} {\varvec{i}}_{\mathrm{I}} + {\dot{z}} {\varvec{k}}_{\mathrm{I}} \text{ and } {\varvec{\omega }}_{\mathrm{b}} = {{\dot{\theta }}} {\varvec{j}}_{\mathrm{b}} = {{\dot{\theta }}} {\varvec{j}}_{\mathrm{I}}, \end{aligned}$$

where ${\varvec{i}}$, ${\varvec{j}}$, and ${\varvec{k}}$ are unit vectors along the x, y, and z directions in the axis system indicated by the subscript. Thus, one obtains

$$\begin{aligned} \frac{\partial {\varvec{v}}_{\mathrm{b}}}{\partial {\dot{x}}}&= {\varvec{i}}_{\mathrm{I}} ~~ \frac{\partial {\varvec{v}}_{\mathrm{b}}}{\partial {\dot{z}}} = {\varvec{k}}_{\mathrm{I}} ~~ \frac{\partial {\varvec{v}}_{\mathrm{b}}}{\partial {{\dot{\theta }}}} = {\varvec{0}} ~~ \frac{\partial {\varvec{v}}_{\mathrm{b}}}{\partial {{\dot{\varphi }}}} = {\varvec{0}} ~~ \frac{\partial {\varvec{v}}_{\mathrm{b}}}{\partial {{\dot{\eta }}}} = {\varvec{0}} \\ \frac{\partial {\varvec{\omega }}_{\mathrm{b}}}{\partial {\dot{x}}}&= {\varvec{0}} ~~ \frac{\partial {\varvec{\omega }}_{\mathrm{b}}}{\partial {\dot{z}}} = {\varvec{0}} ~~ \frac{\partial {\varvec{\omega }}_{\mathrm{b}}}{\partial {{\dot{\theta }}}} = {\varvec{j}}_{\mathrm{I}} ~~ \frac{\partial {\varvec{\omega }}_{\mathrm{b}}}{\partial {{\dot{\varphi }}}} = {\varvec{0}} ~~ \frac{\partial {\varvec{\omega }}_{\mathrm{b}}}{\partial {{\dot{\eta }}}} = {\varvec{0}} , \end{aligned}$$

and

$$\begin{aligned} \dot{{\varvec{v}}}_{\mathrm{b}}=\ddot{x} {\varvec{i}}_{\mathrm{I}} + \ddot{z} {\varvec{k}}_{\mathrm{I}}. \end{aligned}$$

The angular momentum vector of the body about its center of gravity and its inertial derivative are given by

$$\begin{aligned} {\varvec{h}}_{\mathrm{b}}=I_{yb}{{\dot{\theta }}} {\varvec{j}}_{\mathrm{I}}, \quad \dot{{\varvec{h}}}_{\mathrm{b}}=I_{yb}\ddot{\theta }{\varvec{j}}_{\mathrm{I}}. \end{aligned}$$

The aerodynamic contribution of the body is neglected, and hence, the body exhibits gravitational forces only with no moments. Thus, the body force in the inertial frame is written as

$$\begin{aligned} {\varvec{f}}_{\mathrm{b}}^{(\mathrm{I})}= [0,\;\; 0,\;\; m_{\mathrm{b}} g]^*. \end{aligned}$$

1.2 Wing

The linear velocity of the reference point of the wing frame (the hinge root) and its angular velocity are written as

$$\begin{aligned} {\varvec{v}}_{\mathrm{w}} = ({\dot{x}}-x_{\mathrm{h}}{{\dot{\theta }}}\sin \theta ) {\varvec{i}}_{\mathrm{I}} + ({\dot{z}}-x_{\mathrm{h}} {{\dot{\theta }}}\cos \theta ) {\varvec{k}}_{\mathrm{I}}, {\varvec{\omega }}_{\mathrm{w}} = {{\dot{\theta }}} {\varvec{j}}_{\mathrm{b}}-{{\dot{\varphi }}} {\varvec{k}}_{\mathrm{s}}+{{\dot{\eta }}}{\varvec{j}}_{\mathrm{w}}. \end{aligned}$$

Thus, one obtains

$$\begin{aligned} \frac{\partial {\varvec{v}}_{\mathrm{w}}}{\partial {\dot{x}}}&= {\varvec{i}}_{\mathrm{I}} ~&\frac{\partial {\varvec{v}}_{\mathrm{w}}}{\partial {\dot{z}}}&= {\varvec{k}}_{\mathrm{I}} ~&\frac{\partial {\varvec{v}}_{\mathrm{w}}}{\partial {{\dot{\theta }}}}&= -x_{\mathrm{h}}(\sin \theta {\varvec{i}}_{\mathrm{I}}+\cos \theta {\varvec{k}}_{\mathrm{I}}) ~&\frac{\partial {\varvec{v}}_{\mathrm{w}}}{\partial {{\dot{\varphi }}}}&= {\varvec{0}} ~&\frac{\partial {\varvec{v}}_{\mathrm{w}}}{\partial {{\dot{\eta }}}}&= {\varvec{0}} ~ \nonumber \\ \frac{\partial {\varvec{\omega }}_{\mathrm{w}}}{\partial {\dot{x}}}&= {\varvec{0}} ~&\frac{\partial {\varvec{\omega }}_{\mathrm{w}}}{\partial {\dot{z}}}&= {\varvec{0}} ~&\frac{\partial {\varvec{\omega }}_{\mathrm{w}}}{\partial {{\dot{\theta }}}}&= {\varvec{j}}_{\mathrm{I}} ~&\frac{\partial {\varvec{\omega }}_{\mathrm{w}}}{\partial {{\dot{\varphi }}}}&= -{\varvec{k}}_{\mathrm{b}} ~&\frac{\partial {\varvec{\omega }}_{\mathrm{w}}}{\partial {{\dot{\eta }}}}&= -{\varvec{j}}_{\mathrm{w}} , \end{aligned}$$

and

$$\begin{aligned} \dot{{\varvec{v}}}_{\mathrm{w}}=[\ddot{x}-x_{\mathrm{h}}\ddot{\theta }\sin \theta -x_{\mathrm{h}}{{\dot{\theta }}}^2\cos \theta ] {\varvec{i}}_{\mathrm{I}} + [\ddot{z} -x_{\mathrm{h}}\ddot{\theta }\cos \theta +x_{\mathrm{h}}{{\dot{\theta }}}^2\sin \theta ] {\varvec{k}}_{\mathrm{I}}. \end{aligned}$$

The rotation matrix from the inertial frame to the stroke plane frame is given by

$$\begin{aligned} {\varvec{R}}_\beta = \left[ \begin{array}{ccc} \cos \beta &{}\quad 0 &{}\quad -\sin \beta \\ 0 &{}\quad 1&{}\quad 0 \\ \sin \beta &{}\quad 0 &{}\quad \cos \beta \end{array} \right] , \end{aligned}$$

and rotation matrices from the stroke plane frame to the wing frame are

$$\begin{aligned} {\varvec{R}}_\varphi = \left[ \begin{array}{ccc} \cos \varphi &{}\quad -\sin \varphi &{}\quad 0 \\ \sin \varphi &{}\quad \cos \varphi &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{array} \right] \;\;,\;\; {\varvec{R}}_\eta = \left[ \begin{array}{ccc} \cos \eta &{}\quad 0 &{}\quad -\sin \eta \\ 0 &{}\quad 1&{}\quad 0 \\ \sin \eta &{}\quad 0 &{}\quad \cos \eta \end{array} \right] , \end{aligned}$$

and

$$\begin{aligned} {\varvec{R}}_{\mathrm{ws}} = {\varvec{R}}_\eta {\varvec{R}}_\varphi . \end{aligned}$$

The wing angular velocity vector in the wing frame is

$$\begin{aligned} {\varvec{\omega }}_{\mathrm{w}}^{(\mathrm{w})} = \left( \begin{array}{c} \omega _1 \\ \omega _2 \\ \omega _3 \end{array} \right) = {\varvec{R}}_{\mathrm{ws}} \left( \begin{array}{c} 0 \\ {{\dot{\theta }}} \\ -{{\dot{\varphi }}} \end{array} \right) + \left( \begin{array}{c} 0 \\ {{\dot{\eta }}} \\ 0 \end{array} \right) = \left( \begin{array}{c} {{\dot{\varphi }}}\sin \eta - {{\dot{\theta }}}\cos \eta \sin \varphi \\ {{\dot{\theta }}}\cos \varphi +{{\dot{\eta }}} \\ -{{\dot{\varphi }}}\cos \eta -{{\dot{\theta }}}\sin \eta \sin \varphi \end{array} \right) . \end{aligned}$$

The position vector pointing from the hinge root to the wing center of gravity is ${{\varvec{\rho _c}}}_{\mathrm{w}}=-{\hat{d}}{\varvec{i}}_{\mathrm{w}} + r_{\mathrm{cg}} {\varvec{j}}_{\mathrm{w}}$ where ${\hat{d}}$ and $r_{\mathrm{cg}}$ are the distances between the wing root hinge point and the wing center of gravity along the negative $x_{\mathrm{w}}$-axis and the $y_{\mathrm{w}}$-axis, respectively. Thus, the inertial acceleration is obtained as

$$\begin{aligned} {\ddot{{\varvec{\rho _c}}}}_{\mathrm{w}}^{(\mathrm{w})}= \left( \begin{array}{c} \ddot{\rho }_1 \\ \ddot{\rho }_2 \\ \ddot{\rho }_3 \end{array} \right) = \left( \begin{array}{c} {\hat{d}}(\omega _2^2+\omega _3^2) - r_{\mathrm{cg}}({{\dot{\omega }}}_3-\omega _1\omega _2) \\ -{\hat{d}}({{\dot{\omega }}}_3+\omega _1\omega _2) - r_{\mathrm{cg}}(\omega _1^2+\omega _3^2) \\ {\hat{d}}({{\dot{\omega }}}_2-\omega _1\omega _3) + r_{\mathrm{cg}}({{\dot{\omega }}}_1+\omega _2\omega _3) \end{array} \right) . \end{aligned}$$

Assuming the wing reference frame is fixed in the wing principal axes, the inertial time derivative of the angular momentum vector represented in the wing frame is written as

$$\begin{aligned} \dot{{\varvec{h}}}_{\mathrm{w}}^{(\mathrm{w})}= \left( \begin{array}{c} \dot{h}_1 \\ \dot{h}_2 \\ \dot{h}_3 \end{array} \right) = \left( \begin{array}{c} I_x {{\dot{\omega }}}_1 +(I_z-I_y)\omega _2\omega _3\\ I_y {{\dot{\omega }}}_y +(I_x-I_z)\omega _1\omega _3 \\ I_z {{\dot{\omega }}}_3 +(I_y-I_x)\omega _1\omega _2 \end{array} \right) . \end{aligned}$$

The wing is subject to aerodynamic and gravitational forces. Noting that the $y_b$-components of the aerodynamic force on each wing are equal and opposite, the force vector applied on the wing is written as

$$\begin{aligned} {\varvec{f}}_{\mathrm{w}}=\left( \begin{array}{c} F_x \\ 0 \\ F_z \end{array} \right) ^{(\mathrm{w})} + \left( \begin{array}{c} 0 \\ 0 \\ m_{\mathrm{w}} g \end{array} \right) ^{(\mathrm{I})}, \end{aligned}$$

where $F_x$ and $F_z$ are the aerodynamic loads along the $x_{\mathrm{w}}$ and $z_{\mathrm{w}}$ directions, respectively. The moment vector comprises three contributions: aerodynamic, gravitational, and the control torque. The aerodynamic contribution ${\varvec{M}}_{\mathrm{a}_{\mathrm{w}}}$ is determined by integrating the radial distributions of the forces $F_x$ and $F_z$ over the wing. That is, ${\varvec{M}}_{\mathrm{a}_{\mathrm{w}}}=M_x {\varvec{i}}_{\mathrm{w}}+M_y {\varvec{j}}_{\mathrm{w}}+M_z {\varvec{k}}_{\mathrm{w}}$, where

$$\begin{aligned} M_x=2\int _0^R F_z'(r) r \hbox {d}r, \;\; M_y=2\int _0^R F_z'(r) d_{\mathrm{ac}}(r) \hbox {d}r, \;\; \text{ and } \;\; M_z=-2\int _0^R F_x'(r) r \hbox {d}r, \end{aligned}$$

where $F_x'(r)$ and $F_z'(r)$ are the two-dimensional aerodynamic loads on an airfoil that is at distance r from the wing root and $d_{\mathrm{ac}}(r)$ is the distance between the hinge line and the quarter chord line (aerodynamic center) at each airfoil section along $x_{\mathrm{w}}$ direction. The gravitational contribution is written as ${\varvec{M}}_{\mathrm{g}_{\mathrm{w}}}= (-{\hat{d}}{\varvec{i}}_{\mathrm{w}}+ r_{\mathrm{cg}}{\varvec{j}}_{\mathrm{w}}) \times m_{\mathrm{w}} g{\varvec{k_{\mathrm{I}}}}$. The last contribution (the control torque) is written as ${\varvec{M}}_{\mathrm{c}_{\mathrm{w}}}= -\tau _\varphi {\varvec{k}}_{\mathrm{s}}+\tau _\eta {\varvec{j}}_{\mathrm{w}}$, where $\tau _\varphi$ and $\tau _\eta$ are the actuating torque along the flapping and pitching directions, respectively.

Constructing all the required terms to apply the principle of virtual power (1), the five-DOF equations of motion are obtained as (with obvious correspondence to the abstract form (2))

$$\begin{aligned}&m_{\mathrm{w}} \biggl (\ddot{\rho _1} \left( \cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta }\right) +\ddot{\rho _3} \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) \nonumber \\&\qquad +\,\ddot{\rho _2} \cos {\beta } \sin {\varphi }- x_{\mathrm{h}} \ddot{\theta } \sin {\theta }-x_{\mathrm{h}} {\dot{\theta }}^2 \cos {\theta }\biggr ) + m_{\mathrm{v}} {\dot{u}} \nonumber \\&\quad =F_x \left( \cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta }\right) +F_z \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) \end{aligned}$$

(32)

$$\begin{aligned}&\qquad - m_{\mathrm{w}} \biggl (\ddot{\rho _1} \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) +\ddot{\rho _3}\left( \sin {\beta } \sin {\eta } \cos {\varphi }- \cos {\beta } \cos {\eta }\right) \nonumber \\&\qquad +\,\ddot{\rho _2} \sin {\beta } \sin {\varphi }+ x_{\mathrm{h}} \ddot{\theta } \cos {\theta }-x_{\mathrm{h}} {\dot{\theta }}^2 \sin {\theta }\biggr )+ m_{\mathrm{v}} ({\dot{w}}-g) \nonumber \\&\quad =-F_x \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) - F_z \left( \sin {\beta } \sin {\eta } \cos {\varphi }-\cos {\beta } \cos {\eta }\right) \nonumber \\ \end{aligned}$$

(33)

$$\begin{aligned}&m_{\mathrm{w}} \biggl [-x_{\mathrm{h}} \biggl (\ddot{\theta }~ {\hat{d}} \left( \cos {\beta } \cos {\eta } \cos {\theta } \cos {\varphi }+\sin {\beta } \cos {\eta } \sin {\theta } \cos {\varphi }-\sin {\beta } \sin {\eta } \cos {\theta } \right. \nonumber \\&\qquad \left. +\,\cos {\beta } \sin {\eta } \sin {\theta }\right) - \ddot{\theta }~ r_{\mathrm{cg}} \sin {\varphi }\cos (\beta -\theta )+ {\dot{\theta }}^2 \nonumber \\&\qquad \left( -r_{\mathrm{cg}} \sin {\varphi } \sin (\beta -\theta )+{\hat{d}} \cos {\eta } \cos {\varphi } \sin (\beta -\theta )+{\hat{d}} \sin {\eta } \cos (\beta -\theta )\right) \biggr )\nonumber \\&\qquad +\, {\dot{u}} \left( -\sin {\beta }~ r_{\mathrm{cg}} \sin {\varphi }+{\hat{d}} \sin {\beta } \cos {\eta } \cos {\varphi }+{\hat{d}} \cos {\beta } \sin {\eta }\right) \nonumber \\&\qquad +\, {\dot{w}} \left( -\cos {\beta }~ r_{\mathrm{cg}} \sin {\varphi }+{\hat{d}}\cos {\beta } \cos {\eta } \cos {\varphi }-{\hat{d}} \sin {\beta } \sin {\eta }\right) \biggr ]\nonumber \\&\qquad +\, I_{y_b} \ddot{\theta }+x_{\mathrm{h}} m_{\mathrm{w}} \biggl [\ddot{\rho _3} \sin {\beta } \sin {\eta } \cos {\theta } \cos {\varphi }+\ddot{\rho _1}\left( \cos {\eta } \cos {\varphi } \sin (\beta -\theta )\right. \nonumber \\&\qquad \left. +\,\sin {\eta } \cos (\beta -\theta )\right) - \ddot{\rho _3}\left( \cos {\beta } \sin {\eta } \sin {\theta } \cos {\varphi }\right. \nonumber \\&\qquad \left. -\, \cos {\beta } \cos {\eta } \cos {\theta }- \sin {\beta } \cos {\eta } \sin {\theta }\right) +\ddot{\rho _2} \sin {\varphi } \sin (\beta -\theta )+g \cos {\theta }\nonumber \\&\qquad +\, x_{\mathrm{h}} \ddot{\theta }-{\dot{u}} \sin {\theta } -{\dot{w}} \cos {\theta } \biggr ]-\dot{h_3} \sin {\eta } \sin {\varphi }-\dot{h_1} \cos {\eta } \sin {\varphi }+\dot{h_2} \cos {\varphi }\nonumber \\&\quad = \tau _{\eta } \cos {\varphi } - F_z~ x_{\mathrm{h}} \biggl (\sin {\beta } \left( \cos {\eta } \sin {\theta }-\sin {\eta } \cos {\theta } \cos {\varphi }\right) \nonumber \\&\qquad +\,\cos {\beta } (\sin {\eta } \sin {\theta } \cos {\varphi }+\cos {\eta } \cos {\theta })\biggr )\nonumber \\&\qquad +\, F_x x_{\mathrm{h}} (\cos {\eta } \cos {\varphi } \sin (\beta -\theta )+\sin {\eta } \cos (\beta -\theta )) \nonumber \\&\qquad -\,M_x \cos {\eta } \sin {\varphi }+M_y \cos {\varphi }-M_z \sin {\eta } \sin {\varphi } \end{aligned}$$

(34)

$$\begin{aligned}&r_{\mathrm{cg}}~ x_{\mathrm{h}}~ m_{\mathrm{w}} \cos {\varphi } \biggl (\ddot{\theta } \cos {\theta } \sin {\beta }- \ddot{\theta } \sin {\theta } \cos {\beta }-2 {\dot{\theta }}^2 \cos {\theta } \cos {\beta } -2~ {\dot{\theta }}^2 \sin {\theta } \sin {\beta }\biggr )\nonumber \\&\qquad +\, r_{\mathrm{cg}}~ m_{\mathrm{w}} \cos {\varphi } \biggl ({\dot{u}} \cos {\beta }+ u~ {\dot{\theta }} \sin {\beta }- {\dot{w}}~ \sin {\beta }+ w~ {\dot{\theta }} \cos {\beta } \biggr )\nonumber \\&\qquad +\, {\hat{d}}~x_{\mathrm{h}}~ m_{\mathrm{w}} \cos {\eta } \sin {\varphi } \biggl ( \ddot{\theta } \cos {\theta } \sin {\beta } - \ddot{\theta } \sin {\theta } \cos {\beta } -2~ {\dot{\theta }}^2 \cos {\theta } \cos {\beta } \nonumber \\&\qquad -\,2~ {\dot{\theta }}^2 \sin {\theta } \sin {\beta } \biggr ) + {\hat{d}}~m_{\mathrm{w}} \cos {\eta } \sin {\varphi } \biggl ( {\dot{u}} \cos {\beta } + u~ {\dot{\theta }} \sin {\beta } - {\dot{w}}~ \sin {\beta } \nonumber \\&\qquad +\, w~ {\dot{\theta }} \cos {\beta } \biggr ) +\dot{h_1} \sin {\eta }-\dot{h_3} \cos {\eta } = \tau _{\varphi } +M_x \sin {\eta }-M_z \cos {\eta } \end{aligned}$$

(35)

$$\begin{aligned}&{\hat{d}}~x_{\mathrm{h}}~ m_{\mathrm{w}} \biggl ( \ddot{\theta } \sin {\eta } \cos {\theta } \cos {\varphi } \sin {\beta }- \ddot{\theta } \sin {\eta } \sin {\theta } \cos {\varphi } \cos {\beta } - \ddot{\theta } \cos {\eta } \cos {\theta } \cos {\beta }\nonumber \\&\qquad -\, \ddot{\theta } \cos {\eta } \sin {\theta }\sin {\beta }- 2~ {\dot{\theta }}^2 \sin {\eta } \cos {\theta } \cos {\varphi } \cos {\beta }-2~ {\dot{\theta }}^2 \sin {\eta } \sin {\theta } \cos {\varphi } \sin {\beta } \nonumber \\&\qquad -\,2~ {\dot{\theta }}^2 \cos {\eta } \cos {\theta } \sin {\beta } +2~ {\dot{\theta }}^2 \cos {\eta } \sin {\theta } \cos {\beta }\biggr )\nonumber \\&\qquad +\, {\hat{d}}~m_{\mathrm{w}} \biggl ( {\dot{u}}~ \sin {\eta } \cos {\varphi } \cos {\beta } + {\dot{u}}~ \cos {\eta } \sin {\beta } + u~ {\dot{\theta }} \sin {\eta } \cos {\varphi }\sin {\beta }\nonumber \\&\qquad -\, u~{\dot{\theta }} \cos {\eta } \cos {\beta }- \sin {\eta } \cos {\varphi } \sin {\beta }~ {\dot{w}}\nonumber \\&\qquad +\, {\dot{w}} \cos {\eta } \cos {\beta }+w~ {\dot{\theta }} \sin {\eta } \cos {\varphi } \cos {\beta }+ w~ {\dot{\theta }} \cos {\eta } \sin {\beta }\biggr )+\dot{h_2}=\tau _{\eta }+M_y, \nonumber \\ \end{aligned}$$

(36)

where $m_{\mathrm{v}}=m_{\mathrm{b}}+m_{\mathrm{w}}$.

Aerodynamic Model

The aerodynamic derivatives in Eq. (7) are defined below

$$\begin{aligned} F_{x_0}= & {} \rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \sin {\eta }~ {\dot{\eta }} {\dot{\varphi }}\\ F_{z_0}= & {} -\frac{1}{2} \rho ~ C_{L_\alpha } I_{21} \sin {\eta }~ {\dot{\varphi }} \left| {\dot{\varphi }}\right| -\rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \cos {\eta }~ {\dot{\eta }} {\dot{\varphi }}\\ M_{x_0}= & {} -\frac{1}{2} \rho ~ C_{L_\alpha } I_{31} \sin {\eta }~ {\dot{\varphi }} \left| {\dot{\varphi }}\right| -\rho \pi \left( k I_{21}-\frac{1}{4} I_{22}\right) \cos {\eta }~{\dot{\eta }} {\dot{\varphi }} \\ M_{y_0}= & {} \frac{3}{4} \biggl (-\frac{1}{2} \rho ~ C_{L_\alpha } I_{22} \sin {\eta }~ {\dot{\varphi }} \left| {\dot{\varphi }}\right| -\rho \pi \left( k I_{12}-\frac{1}{4} I_{13}\right) \cos {\eta }~{\dot{\eta }} {\dot{\varphi }} \biggr )-k~F_{z_0}\\ M_{z_0}= & {} -\rho \pi \left( k I_{21}-\frac{1}{4} I_{22}\right) \sin {\eta }~ {\dot{\eta }} {\dot{\varphi }} \\ F_{x_u}= & {} \rho \pi \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) {\dot{\eta }}\\ F_{x_w}= & {} -\rho \pi \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \sin {\beta } \sin {\eta } \cos {\varphi }-\cos {\beta } \cos {\eta }\right) {\dot{\eta }}\\ F_{x_q}= & {} \rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \sin {\eta } \cos {\varphi }~ {\dot{\varphi }} -\rho \pi \biggl (x_{\mathrm{h}} \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \cos {\eta } \cos {(\beta -\theta )}\right. \\&\left. -\,\sin {\eta } \cos {\varphi } \sin {(\beta -\theta )}\right) + \cos {\eta } \sin {\varphi } \left( k I_{11}-\frac{1}{4}I_{12}\right) \biggr ) {\dot{\eta }} \\ F_{x_{nl}}= & {} \rho \pi \cos {\varphi }~ {\dot{\theta }} \left( k I_{01}-\frac{1}{4} I_{02}\right) \biggl ( u \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) \\&+\, w \left( \cos {\beta } \cos {\eta }-\sin {\beta } \sin {\eta } \cos {\varphi }\right) \biggr )\\&-\, \rho \pi \biggl (x_{\mathrm{h}} \cos {\varphi } \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \cos {\eta } \cos {(\beta -\theta )}-\sin {\eta } \cos {\varphi } \sin {(\beta -\theta )}\right) \\&+\,\cos {\eta } \sin {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) \biggr ) {\dot{\theta }}^2 \\ F_{z_u}= & {} -\frac{1}{2} \rho ~ C_{L_\alpha } I_{11} (2 \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }) \left| {\dot{\varphi }}\right| \\&-\,\rho \pi \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta }\right) ~{\dot{\eta }} \\ F_{z_w}= & {} \rho \pi \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) ~{\dot{\eta }} \\&-\,\frac{1}{2} \rho ~ C_{L_\alpha } I_{11} \left( \cos {\beta } \cos {\eta }-2 \sin {\beta } \sin {\eta } \cos {\varphi }\right) \left| {\dot{\varphi }}\right| \\ F_{z_q}= & {} \frac{1}{2} \rho ~ C_{L_\alpha } I_{21} \cos {\eta } \sin {\varphi }~\left| {\dot{\varphi }}\right| +\\&+\, \rho ~ C_{L_\alpha } I_{11} \left| {\dot{\varphi }}\right| \biggl (x_{\mathrm{h}} \sin {\beta } \sin {\eta } \cos {\theta } \cos {\varphi }+\frac{1}{2} \cos {\beta } \left( 2 x_{\mathrm{h}} \sin {\eta } \sin {\theta } \cos {\varphi }\right. \\&\left. +\,x_{\mathrm{h}} \cos {\eta } \cos {\theta }\right) + \frac{1}{2} x_{\mathrm{h}} \sin {\beta } \cos {\eta } \sin {\theta }\biggr ) \\&+\, \rho \pi ~ x_{\mathrm{h}} \cos {\eta } \cos {\varphi } \sin (\beta -\theta ) \left( \frac{1}{4} I_{02}-k I_{01}\right) {\dot{\eta }}\\&+\,\rho \pi ~ x_{\mathrm{h}} \sin {\eta } \cos (\beta -\theta ) \left( \frac{1}{4} I_{02}-k I_{01}\right) {\dot{\eta }} - \rho \pi \sin {\eta } \sin {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) {\dot{\eta }}\\&-\, \rho \pi \cos {\eta } \cos {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) {\dot{\varphi }} \\ F_{z_{nl}}= & {} -\rho \pi ~\cos {\varphi }~ {\dot{\theta }} \left( k I_{01}-\frac{1}{4} I_{02}\right) \biggl ( u~ (\cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta })\\&+\, w~ (\sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta })\biggr )\\&+\, {\dot{\theta }}^2 \biggl (2 \pi \rho x_{\mathrm{h}} \cos {\varphi } \left( \frac{1}{4} I_{02}-k I_{01}\right) \left( \cos {\eta } \cos {\varphi } \sin (\beta -\theta )+\sin {\eta } \cos (\beta -\theta )\right) \\&-\, 2 \pi \rho \sin {\eta } \sin {\varphi } \cos {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) \biggr ) \\ M_{x_u}= & {} -\frac{1}{2} \rho ~ C_{L_\alpha } I_{21} \left( 2 \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) \left| {\dot{\varphi }}\right| \\&-\,\rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) (\cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta }) ~{\dot{\eta }} \\ M_{x_w}= & {} \rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) ~{\dot{\eta }}\\&-\,\frac{1}{2} \rho ~ C_{L_\alpha } I_{21} (\cos {\beta } \cos {\eta }-2 \sin {\beta } \sin {\eta } \cos {\varphi }) \left| {\dot{\varphi }}\right| \\ \end{aligned}$$

$$\begin{aligned} M_{x_q}= & {} \frac{1}{2} \rho ~ C_{L_\alpha } I_{31} \cos {\eta } \sin {\varphi }~\left| {\dot{\varphi }}\right| +\rho ~ C_{L_\alpha } I_{21} \left| {\dot{\varphi }}\right| \biggl (x_{\mathrm{h}} \sin {\beta } \sin {\eta } \cos {\theta } \cos {\varphi }\\&+\, \frac{1}{2} \cos {\beta } (2 x_{\mathrm{h}} \sin {\eta } \sin {\theta } \cos {\varphi }+x_{\mathrm{h}} \cos {\eta } \cos {\theta })+\frac{1}{2} x_{\mathrm{h}} \sin {\beta } \cos {\eta } \sin {\theta }\biggr )\\&+\,\rho \pi x_{\mathrm{h}} \left( \frac{1}{4} I_{12}-k I_{11}\right) {\dot{\eta }}~ \biggl ( \cos {\eta } \cos {\varphi } \sin (\beta -\theta ) + \sin {\eta } \cos (\beta -\theta ) \biggr ) \\&-\, \rho \pi ~ \left( k I_{21}-\frac{1}{4} I_{22}\right) \biggl ( \sin {\eta } \sin {\varphi } ~{\dot{\eta }} - \cos {\eta } \cos {\varphi }~{\dot{\varphi }} \biggr ) \\ M_{x_{nl}}= & {} -\rho \pi ~ \cos {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta }\right) ~ {\dot{\theta }}~u\\&+\, \rho \pi ~ \cos {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) ~{\dot{\theta }}~w\\&+\, {\dot{\theta }}^2 \biggl (2 \rho \pi x_{\mathrm{h}} \cos {\varphi } \left( \frac{1}{4} I_{12}-k I_{11}\right) \left( \cos {\eta } \cos {\varphi } \sin (\beta -\theta )+\sin {\eta } \cos (\beta -\theta )\right) \\&-\, 2 \rho \pi \sin {\eta } \sin {\varphi } \cos {\varphi } \left( k I_{21}-\frac{1}{4} I_{22}\right) \biggr ) \\ M_{y_u}= & {} \frac{3}{4} \biggl (-\frac{1}{2} \rho ~ C_{L_\alpha } I_{12} (2 \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }) \left| {\dot{\varphi }}\right| \\&-\,\rho \pi \left( k I_{02}-\frac{1}{4} I_{03}\right) (\cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta })~{\dot{\eta }}\biggr )- k~F_{z_u} \\ M_{y_w}= & {} \frac{3}{4} \biggl (\rho \pi \left( k I_{02}-\frac{1}{4} I_{03}\right) \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) ~{\dot{\eta }} \\&-\,\frac{1}{2} \rho ~ C_{L_\alpha } I_{12} \left( \cos {\beta } \cos {\eta }-2 \sin {\beta } \sin {\eta } \cos {\varphi }\right) \left| {\dot{\varphi }}\right| \biggr )- k~F_{z_w} \\ \end{aligned}$$

$$\begin{aligned} M_{y_q}= & {} \frac{3}{4} \biggl (\frac{1}{2} \rho ~ C_{L_\alpha } I_{22} \cos {\eta } \sin {\varphi } \left| {\dot{\varphi }}\right| +\rho ~ C_{L_\alpha } I_{12} \left| {\dot{\varphi }}\right| \biggl [x_{\mathrm{h}} \sin {\beta } \sin {\eta } \cos {\theta } \cos {\varphi }\\&+\, \frac{1}{2} \cos {\beta } \left( 2 x_{\mathrm{h}} \sin {\eta } \sin {\theta } \cos {\varphi }+x_{\mathrm{h}} \cos {\eta } \cos {\theta }\right) +\frac{1}{2} x_{\mathrm{h}} \sin {\beta } \cos {\eta } \sin {\theta }\biggr ]\\&+\, \rho \pi x_{\mathrm{h}} \cos {\eta } \cos {\varphi } \sin (\beta -\theta ) \left( \frac{1}{4} I_{03}-k I_{02}\right) {\dot{\eta }}\\&+\,\rho \pi x_{\mathrm{h}} \sin {\eta } \cos (\beta -\theta ) \left( \frac{1}{4} I_{03}-k I_{02}\right) {\dot{\eta }}\\&-\, \rho \pi \sin {\eta } \sin {\varphi } \left( k I_{12}-\frac{1}{4} I_{13}\right) {\dot{\eta }}-\rho \pi \cos {\eta } \cos {\varphi } \left( k I_{12}-\frac{1}{4} I_{13}\right) {\dot{\varphi }} \biggr )-k~F_{z_q} \\ M_{y_{nl}}= & {} \frac{3}{4} \biggl (-\rho \pi \left( k I_{02}-\frac{1}{4} I_{03}\right) \cos {\varphi }~ {\dot{\theta }} \biggl [ u~ (\cos {\beta } \cos {\eta } \cos {\varphi }\\&\qquad -\,\sin {\beta } \sin {\eta })- w~ (\sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }) \biggr ]\\&+\, {\dot{\theta }}^2 \biggl [2 \rho \pi x_{\mathrm{h}} \left( \frac{1}{4} I_{03}-k I_{02}\right) \cos {\varphi }~ (\cos {\eta } \cos {\varphi } \sin (\beta -\theta )+\sin {\eta } \cos (\beta -\theta ))\\&-\, 2 \rho \pi \left( k I_{12}-\frac{1}{4} I_{13}\right) \sin {\eta } \sin {\varphi } \cos {\varphi }\biggr ]\biggr )-k~F_{z_{nl}} \\ M_{z_u}= & {} - \rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) {\dot{\eta }} \\ M_{z_w}= & {} \rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \sin {\beta } \sin {\eta } \cos {\varphi }-\cos {\beta } \cos {\eta }\right) {\dot{\eta }} \\ M_{z_q}= & {} \rho \pi \biggl (x_{\mathrm{h}} \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \cos {\eta } \cos {(\beta -\theta )}-\sin {\eta } \cos {\varphi } \sin {(\beta -\theta )}\right) \\&+\,\cos {\eta } \sin {\varphi } \left( k I_{21}-\frac{1}{4} I_{22}\right) \biggr )~ {\dot{\eta }} - \rho \pi \left( k I_{21}-\frac{1}{4}I_{22}\right) \sin {\eta } \cos {\varphi }~ {\dot{\varphi }} \\ M_{z_{nl}}= & {} -\rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \cos {\varphi }~{\dot{\theta }} \biggl ( u \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) \\&+\, w \left( \cos {\beta } \cos {\eta }-\sin {\beta } \sin {\eta } \cos {\varphi }\right) \biggr )\\&+\, \rho \pi ~ {\dot{\theta }}^2 \biggl (x_{\mathrm{h}} \cos {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \cos {\eta } \cos {(\beta -\theta )}\right. \\&\left. -\,\sin {\eta } \cos {\varphi } \sin {(\beta -\theta )}\right) +\cos {\eta } \sin {\varphi } \left( k I_{21}-\frac{1}{4} I_{22}\right) \biggr ), \\ \end{aligned}$$

where $k=c_r (1-x_{or})$, $c_r$ is the wing root chord, $x_{or}$ is the position of the hinge point along $x_w$ normalized by the root chord, and $x_{\mathrm{h}}$ is the distance from the vehicle center of mass to the root of the wing hinge line (i.e., the intersection of the hinge line with the $x_b$-axis). Also, $\rho$ is the air density, $C_{L_\alpha }$ is the three-dimensional lift curve slope of the wing, c(r) is the spanwise chord distribution, R is the wing radius, and $I_{mn}=2\int _0^R {r^m c^n(r) \,\hbox {d}r}$.

The Linearized Dynamics of the Averaged Three-DOF System

The linearized averaged version of the three-DOF system (8) at the trim condition can be written abstractly as

(37)

where the elements of the matrix ${\varvec{A}}$ can be written as (some elements have quite lengthy expressions, and hence, we only write their limits as the wing mass goes to zero):

$$\begin{aligned} \lim _{m_{\mathrm{w}}\rightarrow 0} A_{42}=\,&0 \\ \lim _{m_{\mathrm{w}}\rightarrow 0} A_{43}=\,&\frac{0.25 A I_{21} \rho U_1^2 \sin ^2{\alpha _m}+0.74 C_{L_\alpha } I_{21} \rho U_2^2 \sin ^2{\alpha _m}}{I_F^2 m_{\mathrm{v}} \omega ^2}\\&-\,\frac{98.86 C_{L_\alpha } I_{21} \rho U_2 \sin ^2{\alpha _m}}{I_F m_{\mathrm{v}} \omega }+\frac{3307 C_{L_\alpha } I_{21} \rho \sin ^2{\alpha _m}}{m_{\mathrm{v}}}\\ A_{44}=&\frac{1}{I_F I_{y_b} m_{\mathrm{v}} \omega } C_{L_\alpha } \rho \cos {\alpha _m} \biggl (\cos {\alpha _m} \biggl (I_{11} ({\bar{c}} {\hat{d}} k m_{\mathrm{w}} (0.98 U_2\\&-41.88 I_F \omega )+I_{y_b} (0.5 U_2-78.37 I_F \omega ))\\&+\, m_{\mathrm{w}} \left( {\bar{c}} {\hat{d}} I_{12} (31.4 I_F \omega -0.74 U_2)+I_{21} r_{\mathrm{cg}} (2.4 I_F \omega -0.02 U_2)\right) \\&+\, {\bar{c}} {\hat{d}} I_{21} m_{\mathrm{w}} \cos {\alpha _m} (0.12 U_2-19.27 I_F \omega )\biggr )\\&+\, m_{\mathrm{w}} r_{\mathrm{cg}} \left( 5.23 I_{11} I_F k \omega -0.12 I_{11} k U_2-3.92 I_{12} I_F \omega +0.09 I_{12} U_2\right) \biggr )\\ \lim _{m_{\mathrm{w}}\rightarrow 0}A_{45}=&\frac{C_{L_\alpha } I_{21} \rho U_2 \sin {\alpha _m} \cos {\alpha _m}}{I_F m_{\mathrm{v}} \omega }-\frac{42.5 C_{L_\alpha } I_{21} \rho \sin {\alpha _m} \cos {\alpha _m}}{m_{\mathrm{v}}}\\ \lim _{m_{\mathrm{w}}\rightarrow 0} A_{46}=&\frac{1}{I_F m_{\mathrm{v}} \omega } \biggl ( I_{11} k \rho (1.56 U_2-66.29 I_F \omega )+I_{12} \rho (16.57 I_F \omega -0.39 U_2)\biggr )\\ A_{52}=&\frac{1}{I_F^3 I_{y_b} \omega ^2} C_{L_\alpha } I_{y_{\mathrm{w}}} \rho \sin {\alpha _m} \sin {2 \alpha _m} \biggl (I_{21} k \left( -3230 I_F^2 \omega ^2\right. \\&\left. +\,96.6 I_F U_2 \omega -0.24 U_1^2-0.73 U_2^2\right) \\&+\, I_{22} \left( 2422 I_F^2 \omega ^2-72.43 I_F U_2 \omega +0.18 U_1^2+0.55 U_2^2\right) \\&+\, I_{31} \cos {\alpha _m} \left( -222 I_F^2 \omega ^2+10.5 I_F U_2 \omega -0.06 U_1^2-0.18 U_2^2\right) \biggr )\\ \lim _{m_{\mathrm{w}}\rightarrow 0} A_{53}=&0\\ A_{54}=&\frac{1}{I_F^2 I_{y_b} \omega } C_{L_\alpha } \rho \cos {\alpha _m} \biggl (I_{y_{\mathrm{w}}} \sin {2 \alpha _m} \biggl (-2.6 I_{11} I_F k \omega +\,0.06 I_{11} k U_2+1.96 I_{12} I_F \omega \\&{-}\,0.05 I_{12} U_2{+}\, I_{21} \cos {\alpha _m} (0.01 U_2-1.2 I_F \omega )\biggr ){+}I_{21} I_{y_b} \sin {\alpha _m} (U_2-42.5 I_F \omega )\biggr )\\ \end{aligned}$$

$$\begin{aligned} A_{55}=&\frac{1}{I_F^2 I_{y_b} \omega } C_{L_\alpha } \rho \sin {\alpha _m} \biggl (I_{y_{\mathrm{w}}} \sin {2 \alpha _m} \biggl (-12.25 I_{21} I_F k \omega \\&+\,0.12 I_{21} k U_2+9.19 I_{22} I_F \omega -0.09 I_{22} U_2\\&+\, I_{31} \cos {\alpha _m} (0.02 U_2-0.65 I_F \omega )\biggr )-I_{21} I_F I_{y_b} \omega \sin {\alpha _m}\biggr )\\ A_{56}=&\frac{1}{I_F^2 I_{y_b} \omega } \rho \sin {\alpha _m} \cos {\alpha _m} \biggl (C_{L_\alpha } I_{y_{\mathrm{w}}} \cos {\alpha _m} \left( 0.65 I_{21} I_F k \omega \right. \\&\left. -\,0.02 I_{21} k U_2-0.49 I_{22} I_F \omega +0.01 I_{22} U_2\right) \\&+\, C_{L_\alpha } I_{31} \left( 5.27 I_F I_{y_b} \omega +0.15 I_F I_{y_{\mathrm{w}}} \omega -0.12 I_{y_b} U_2-0.001 I_{y_{\mathrm{w}}} U_2\right) \\&+\, C_{L_\alpha } I_{31} I_{y_{\mathrm{w}}} \cos { 2 \alpha _m} (0.15 I_F \omega -0.001 U_2)\\&+\, I_{y_{\mathrm{w}}} \sin {\alpha _m} \biggl (k (-30 I_{11} I_F k \omega +0.19 I_{11} k U_2\\&+\, 30 I_{12} I_F \omega -0.19 I_{12} U_2)+I_{13} (0.04 U_2-5.6 I_F \omega )\biggr )\\&+\, I_{y_{\mathrm{w}}} (-2 I_{21} I_F k \omega +0.05 I_{21} k U_2+0.5 I_{22} I_F \omega -0.01 I_{22} U_2)\biggr )\\ A_{62}=&\frac{1}{I_F^2 I_{y_b} \omega ^2}C_{L_\alpha } \rho \sin {\alpha _m} \biggl (I_{21} k \left( -826 I_F^2 \omega ^2+24.7 I_F U_2 \omega -0.06 U_1^2-0.19 U_2^2\right) \\&+\,I_{22} \left( 619.6 I_F^2 \omega ^2-18.5 I_F U_2 \omega +0.05 U_1^2+0.14 U_2^2\right) \\&+\, I_{31} \cos {\alpha _m} \left( 1795 I_F^2 \omega ^2-84.4 I_F U_2 \omega +0.5 U_1^2+1.49 U_2^2\right) \biggr )\\ A_{63}=&\frac{1}{I_F^2 I_{y_b} m_{\mathrm{v}} \omega ^2}C_{L_\alpha } m_{\mathrm{w}} \rho \cos {\alpha _m} \biggl (\cos {\alpha _m} \biggl ({\bar{c}} {\hat{d}} \biggl (I_{11} k \left( -5.23 I_F U_2 \omega \right. \\&\left. +\,0.06 U_1^2+0.18 U_2^2\right) +\, I_{12} \left( 3.9 I_F U_2 \omega -0.05 U_1^2-0.14 U_2^2\right) \biggr )\\&+\,{\bar{c}} {\hat{d}}I_{21} \cos {\alpha _m} \left( U_2 (0.02 U_2-2.4 I_F \omega )+0.01 U_1^2\right) \\&+\,I_{21} r_{\mathrm{cg}} \left( U_2 (0.18 U_2-19.27 I_F \omega )+0.06 U_1^2\right) \biggr )\\&+\,r_{\mathrm{cg}} \biggl (I_{11} k \left( U_2 (1.48 U_2-41.88 I_F \omega )+0.49 U_1^2\right) \\&+\,I_{12} \left( U_2 (31.4 I_F \omega -1.1 U_2)-0.37 U_1^2\right) \biggr )\biggr )\\ \end{aligned}$$

$$\begin{aligned} A_{64}=&\frac{1}{I_F I_{y_b} \omega }C_{L_\alpha } \rho \cos {\alpha _m} \biggl (42.2 I_{11} I_F k \omega - I_{11} k U_2-31.7 I_{12} I_F \omega \\&+\,0.74 I_{12} U_2+I_{21} \cos {\alpha _m} (19.4 I_F \omega -0.12 U_2)\biggr )\\ A_{65}=&\frac{1}{I_F I_{y_b} \omega }C_{L_\alpha } \rho \sin {\alpha _m} \biggl (198 I_{21} I_F k \omega -2 I_{21} k U_2-148 I_{22} I_F \omega \\&+\,1.5 I_{22} U_2+I_{31} \cos {\alpha _m} (10.5 I_F \omega -0.25 U_2)\biggr ) \\ A_{66}=&\frac{\rho }{I_F I_{y_b} \omega } \biggl (C_{L_\alpha } \cos {\alpha _m} \left( -5.23 I_{21} I_F k \omega +0.12 I_{21} k U_2+3.9 I_{22} I_F \omega -0.09 I_{22} U_2\right) \\&+\, C_{L_\alpha } I_{31} \cos { 2 \alpha _m} (0.01 U_2-1.2 I_F \omega )-1.2 C_{L_\alpha } I_{31} I_F \omega +0.01 C_{L_\alpha } I_{31} U_2\\&+\, \sin {\alpha _m} \biggl (k (242 I_{11} I_F k \omega -1.5 I_{11} k U_2-242 I_{12} I_F \omega \\&+\,1.5 I_{12} U_2)+I_{13} (45.5 I_F \omega -0.29 U_2)\biggr )\\&+\, 16.43 I_{21} I_F k \omega -0.39 I_{21} k U_2-4.1 I_{22} I_F \omega +0.1 I_{22} U_2\biggr ). \end{aligned}$$

Hawkmoth Morphological Parameters

The morphological parameters and the wing planform for the hawkmoth, as given in Sun et al. (2007) and Ellington (1984b), are

$$\begin{aligned} R= & {} 51.9\, \mathrm {mm}, \; S=947.8\, \mathrm {mm}^2,\; {\overline{c}}=18.3\,\mathrm {mm},\\ {\hat{r}}_1= & {} 0.44,\; {\hat{r}}_2=0.525,\; f=26.3\, {\mathrm{Hz}}, \; \Phi =60.5^\circ ,\\ \alpha _m= & {} 30^\circ ,\; m_b=1.648\,\mathrm {gm},\; \text{ and }\; I_{yb}=2080\,\mathrm {mg\,cm}^2, \end{aligned}$$

where R is the semi-span of the wing, S is the area of one wing, ${\overline{c}}$ is the mean chord, f is the flapping frequency, $\Phi$ is the flapping angle amplitude, $m_b$ is the mass of the body, and $I_{yb}$ is the body moment of inertia around the body y-axis. The moments of the wing chord distribution ${\hat{r}}_1$ and ${\hat{r}}_2$ are defined as

$$\begin{aligned} I_{k1}=2\int _0^R {r^k c(r) \,\hbox {d}r}=2SR^k{\hat{r}}_k^k. \end{aligned}$$

As for the wing planform, the method of moments used by Ellington Ellington (1984b) is adopted here to obtain a chord distribution for the insect that matches the documented first two moments ${\hat{r}}_1$ and ${\hat{r}}_2$; that is,

$$\begin{aligned} c(r)=\frac{{\overline{c}}}{\beta } \left( \frac{r}{R}\right) ^{\lambda -1} \left( 1-\frac{r}{R}\right) ^{\gamma -1}, \end{aligned}$$

where

$$\begin{aligned}&\lambda ={\hat{r}}_1\left[ \frac{{\hat{r}}_1(1-{\hat{r}}_1)}{{\hat{r}}_2^2-{\hat{r}}_1^2}-1\right] \;,\; \gamma =(1-{\hat{r}}_1)\left[ \frac{{\hat{r}}_1(1-{\hat{r}}_1)}{{\hat{r}}_2^2-{\hat{r}}_1^2}-1\right] ,\\&\quad \text{ and }\;\; \beta =\int _0^1 {{\hat{r}}^{\lambda -1} (1-{\hat{r}})^{\gamma -1} \,d{\hat{r}}}. \end{aligned}$$

The mass of one wing is taken as 5.7% of the body mass according to Wu et al. (2009) and is assumed uniform with an areal mass distribution $m'$ The inertial properties of the wing are then estimated as

$$\begin{aligned}&I_x=2\int _0^R {m' r^2 c(r) \,\hbox {d}r} \;,\; I_y=2\int _0^R {m' {\hat{d}}^2 c^3(r) \,\hbox {d}r}\\&,I_z=I_x+I_y,~\text{ and }~ r_{\mathrm{cg}}=\frac{2\int _0^R {m' r c(r) \,\hbox {d}r}}{m_{\mathrm{w}}}=\frac{I_{11}}{2S}, \end{aligned}$$

where ${\hat{d}}$ is the chord-normalized distance from the wing hinge line to the center of gravity line.

Optimized Shooting Method

Periodic shooting methods have been used in the literature of FWMAVs/insects to capture the periodic orbits associated with different equilibrium configurations (e.g., hovering) (Dietl and Garcia 2008b; Wu and Sun 2012; Stanford et al. 2013; Hussein et al. 2018). The stability of these orbits are then analyzed using the Floquet theorem (Nayfeh and Balachandran 1995). Dednam and Botha (2015) provided an optimized shooting approach to capture a periodic solution of a nonlinear system. This optimized shooting approach adopts the Levenberg–Marquardt optimization algorithm to minimize the residual. This algorithm is based on two methods: the gradient descent method and the Gauss–Newton method. According to Gavin (2011), when the parameters are far from the optimal values, the Levenberg–Marquardt algorithm operates in a way similar to gradient descent. However, it operates similar to the Gauss–Newton method when approaching the optimal point.

Consider the following system of equations

$$\begin{aligned} \dot{{\varvec{x}}}(t)={\varvec{f}}({\varvec{x}}(t),{\varvec{\alpha }},t), \end{aligned}$$

(38)

where ${\varvec{x}}$$\in$$\mathbb {\mathbb {R}}^{n}$ and ${\varvec{f}}$: $\mathbb {\mathbb {R}}^{n} \times \mathbb {\mathbb {R}}^{k} \times \mathbb {\mathbb {R}}_{\ge 0}$$\rightarrow$$\mathbb {\mathbb {R}}^{n}$, and ${\varvec{\alpha }}$ are the system parameters. This system corresponds to a non-autonomous vector field. Thus, a solution ${\varvec{x}}(t)$ to the system (38) is periodic if there exists a constant $T>0$ such that

$$\begin{aligned} {\varvec{x}}(t)={\varvec{x}}(t+T). \end{aligned}$$

(39)

The optimized shooting method can be applied to any system that can be expressed in the form of (38), and, for convenience, a dimensionless time $\tau$ is introduced such that $t =\tau ~T$. Equation (38) is then written as

$$\begin{aligned} \frac{\hbox {d}{\varvec{x}}}{\hbox {d}\tau }=T{\varvec{f}}({{\varvec{x}}(\tau T),{\varvec{\alpha }},\tau T)}. \end{aligned}$$

(40)

Thus, this new variable $\tau$ allows the simplification of the boundary conditions in Eq. (39) so that $x(\tau = 0)= x(\tau = 1)$ and Eq. (40) can be integrated over one period (i.e., letting $\tau$ run from zero to one). Now, the residual can be written as

$$\begin{aligned} {\mathbf {R}}=T \int _{0}^{1} {\varvec{f}}({\varvec{x}}(\tau T), {\varvec{\alpha }},\tau T)~\hbox {d}\tau . \end{aligned}$$

(41)

According to Dednam and Botha (2015), the residual depends on the number of quantities to be optimized and can be expressed as

$$\begin{aligned} {\mathbf {R}}=\biggl ({\varvec{x}}(1)-{\varvec{x}}(0),~{\varvec{x}}(1+\varDelta \tau )-{\varvec{x}}(\varDelta \tau ),\ldots ,~{\varvec{x}}(1+(p-1)\varDelta \tau )-{\varvec{x}}((p-1)\varDelta \tau )\biggr ), \end{aligned}$$

(42)

where $\varDelta \tau$ is the integration step size and $p \in {\mathbb {N}}$. For solvability, the natural number p is chosen so that the number pn of components of the residual is greater than or equal to the number of unknowns (initial point on the periodic orbit and any unknown parameters such as the period in autonomous systems).