1 Introduction

Biological fliers have been a source of scientific inspiration for decades, thanks to their impressive performance. Due to a recent interest in flapping vehicles, there is a strong effort from the scientific community to unveil the biomechanics of animal flapping flight.

Control capabilities, in particular, are outstanding as demonstrated by accelerations of up to 14G, roll rates up to \(5000\frac{deg}{s}\) achieved by barn swallows (Hirundo rustica, Shyy et al. 1999), and the ability of mitigating environmental perturbations such as wind and gust. It is therefore critical to establish flight dynamic stability in order to investigate the mechanisms governing such behaviors. Over the years, a lot of work has been accomplished to assess flight dynamic stability at different scales.

The first attempt to assess the longitudinal stability in flapping flight was carried out by Taylor and Thomas (2002). They addressed the problem using a quasi-static and blade element approach in order to estimate aerodynamic loads. Subsequently, they analytically evaluated the static stability, by considering the variation of the pitching moment with respect to the angle of attack. They concluded that, in flapping flight, longitudinal stability drastically depends on where the quasi-static flight force acts with respect to the body center of mass. They suggested that particular wing motions, such as sweeping, have significant impact on the overall system stability.

However, static stability is only a necessary condition for dynamic stability. Early studies investigating dynamic stability leveraged on averaging the system dynamics over the flapping period. In particular, Taylor and Thomas (2003) and Xiong and Sun (2008) linearized the equations of motion from experimental measurements of the aerodynamic derivatives. The averaging approach however fails if the wingbeat frequency is close to the natural frequency of the body motion, such as for large birds in slow forward flight, or in transitions between two different flight regimes, such as from fast forward flight to hovering (Taylor and Thomas 2002; Iosilevskii 2014). Moreover, Taha et al. (2015) showed that direct averaging may also fail for larger time scales separation, requiring higher-order averaging methods.

Taylor and Żbikowski (2005) conducted the first study of stability in terms of periodic orbits, re-defining the stability of flapping flight as the asymptotic orbital stability in the phase space. For the first time, they introduced a limit cycle approach to study flapping flight dynamics.

Dietl and Garcia (2008) followed this approach by introducing forcing aerodynamic terms. They defined the trim condition as the limit cycle described by the state-space variables of the equations of motion with the same period as the flapping wingbeat, and used Floquet theory to determine its stability. They studied the longitudinal flight dynamics of an ornithopter treated as a rigid body, with imposed joint kinematic trajectories, and developed a limit cycle detection method based on a multiple-shooting algorithm to concomitantly identify the limit cycle, and assess its stability. Importantly, they restricted the kinematic analysis to two degrees of freedom only, namely the plunging angle, and the wing twist, defining the wingbeat amplitude and the angle of attack, respectively. This model did not capture important features of the wing, such as morphing and sweep angle.

This approach has also been found suitable to shed light on flapping flight dynamics at a level of insect scales (Hassan and Taha 2019; Wu and Sun 2012).

The estimation of the forces that a bird develops, coupled to the dynamical problem, comes from the aerodynamics of flapping wings, which has been a challenging research question for the last few decades. Early effort to model bioinspired aerodynamics were aimed to estimate power consumption of fliers. A pioneering work was carried out by Pennycuick (1968) who accounted for the effect of the induced velocity of a pigeon with a correction of the actuator disk theory. The first landmark of modeling the wake of a bird was proposed by Rayner (1979) with the ultimate goal to estimate the induced power. He proposed a new method where the wake was prescribed as a chain of elliptic vortex rings, whose dimensions were determined by the imposed bird kinematics and forward velocity. The wing was assumed to be aerodynamically loaded during the downstroke only, and the associated shed vortex rings were then interacting according to Biot–Savart law for determining the induced velocity field.

Subsequently, Phlips et al. (1981) applied for the first time the Prandtl lifting line theory. The wing was a single flapping element, oscillating about a hinge axis with one degree of freedom only. On the same wing model, Smith et al. (1996) implemented a panel method that gave the possibility to account for wing porosity and flexibility.

Thanks to the remarkable effort of describing the kinematics of bird wings (Tobalske and Dial 1996), an important leap forward has been possible in order to couple the aerodynamic models with a more realistic bird gait. A detailed wingbeat was proposed by Wu and Popović (2003) in the field of computer graphics, who for the first time modeled a bird wing with all of its joints and degrees of freedom, accounting for the feathers and tail. A similar wing model was employed by Parslew and Crowther (2010) which used high accuracy wing motion and a quasi-steady blade element theory to study the effect of the wing kinematics in terms of energy-saving and lift/drag production. Colognesi et al. (2021) proposed a model of morphing wing with an immersed lifting line aerodynamic model and the wake was modeled with a vortex-particle mesh method in order to capture its behavior over long distances.

Important effort of modeling aerodynamic loads of flapping wings has also been conducted at the insect scales. A CFD model of two degrees of freedom flapping wing was proposed by Wu and Sun (2012) in order to study the longitudinal dynamics of two hovering insects. Unsteady aerodynamics was also proposed by Mouy et al. (2017), Nogar et al. (2017), and Dickinson et al. (1999) to account for leading edge vortex phenomena and rotational effect, which are relevant features of lift production in small animal scales.

From a bird flight perspective, the wing kinematics also defines the flight regime. Indeed, birds can modulate different degrees of freedom in order to adapt their forward speed, gain or lose altitude, and perform maneuvers. To the best of our knowledge, an extensive analysis of the influence of such parameters on the stability properties of the flier, and on its performance, has not been conducted to date.

Based on the aforementioned definition of trimmed flight, this paper reports a method that relies on a multiple-shooting algorithm to identify limit cycles for large birds dynamics and evaluate their stability via Floquet theory. In particular, we couple an aerodynamics model that relies on a quasi-steady lifting line, and which is capable of dealing with poly-articulated morphing wings to the bird body moving in space. Finally, we identify a family of limit cycles corresponding to different flight regimes (climbing, descending, and level flight).

Furthermore, this analysis is successfully employed to investigate the sensitivity of flight stability to the reciprocal position between the wing root and the bird center of mass.

Two impacting results have been found. First, the wingbeat amplitude defines the flight regime (climbing, descending, or level) without significantly affecting its stability. Second, the wing insert position drastically impacts the system stability, suggesting that the attitude of the wing for developing nose-down moment is beneficial in terms of longitudinal stability.

The rest of the paper is structured as follows. Sect. 2 reports the dynamic model of the bird, and more particularly the coupling between the dynamical model of the animal and the aerodynamic loading. Sect. 3 presents the multiple-shooting algorithm and the numerical parameters employed in the simulations. Sect. 4 reports the results obtained in the numerical investigations. Finally, in Sect. 5, we discuss the influence the wingbeat amplitude and wing insert position have on the dynamic stability of the flier. The paper is finally concluded and some perspectives for controlling and achieving stable flight inspired by our model are outlined.

2 Dynamical Model of a Flying Bird

In this section, the equations of motion of a flying bird are developed. We build this model upon three main assumptions:

  1. 1.

    The flight is restricted to the longitudinal plane, so that the bird main body has only three degrees of freedom: two in translation and one in rotation. The system is symmetric with respect to this plane. As a consequence, lateral forces, rolling moments, and yawing moments are identically equal to zero at every time and therefore do not have to be considered in the equations of motion. Stability of these degrees of freedom is thus not discussed in the present paper.

  2. 2.

    The inertial effect of the wings on the main body can be neglected. The model therefore does not account of the effect of flapping on the motion of the center of gravity. This is guided by the fact that for large and fast migratory birds, the wing mass is much lower than the body mass, about 5% according to Berg and Rayner (1995). This assumption has been extensively used for both ornithopter and insect scale models (Taylor and Żbikowski 2005; Dietl and Garcia 2008; Dietl et al. 2011; Taha et al. 2014).

  3. 3.

    The aerodynamic effects due to the tail are not explicitly modeled. The proposed model compensates for the missing tail by sweeping of the wing around the body center of mass, thus providing the possibility to generate both nose-up and nose-down pitching moments.

The main morphological parameters used to model the main body and the wing kinematics are introduced in the following sections.

2.1 Equations of Longitudinal Motion

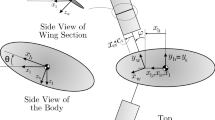
The considered bird is modeled as a rigid body of mass \(m_{b}\) located at the center of mass G, and moving in the longitudinal plane. Two reference frames are required in order to study the longitudinal flight dynamics, as shown in Fig. 1: a fixed inertial frame O(X, Y, Z), and a moving body frame \(G(x', y', z')\) with unit vectors \((\hat{\mathbf {e}}_{x'}, \hat{\mathbf {e}}_{y'}, \hat{\mathbf {e}}_{z'})\). Since only longitudinal motions are considered, the body state is captured by three degrees of freedom: the translations along the X and Z axes, and the relative angle between both frames, i.e., the so-called pitch angle \(\theta \) (Etkin and Reid 1959). The body frame is assumed to be centered in the center of mass of the bird, and oriented by taking the \(x'\)-axis aligned with the longitudinal axis of the flier and pointing forward, the \(z'\)-axis pointing downward, and \(y'\)-axis to define a right-handed frame (Fig. 1).

Fig. 1
figure 1

Reference frames describing flight dynamics in the longitudinal plane. The origin of the moving body frame is taken at the bird’s center of mass G. Image re-adapted from www.fotki.com

Full size image

Under the aforementioned hypotheses, the set of Newton–Euler equations governing the longitudinal dynamics is obtained following the conventional equations for fixed-wing aircraft, i.e., in the form of (Etkin and Reid 1959; Casarosa 2013)

$$\begin{aligned} {\dot{u}}= & {} -qw - g\sin \theta + \frac{1}{m_b}{F_{x'}({\mathbf {x}}(t), t)}\nonumber \\ {\dot{w}}= & {} qu + g\cos \theta +\frac{1}{m_b} F_{z'}({\mathbf {x}}(t), t)\nonumber \\ {\dot{q}}= & {} \frac{1}{I_{yy}}M_{y'}({\mathbf {x}}(t), t)\nonumber \\ {\dot{\theta }}= & {} q \end{aligned}$$
(1)

where u is the velocity component along local axis \(x'\), w is the velocity component along local axis \(z'\), \(\theta \) is the pitch angle describing the body inertial orientation, q is its derivative, i.e., the body angular velocity, positive according to the orientation given in Fig. 1 and t is the time. The parameter \(I_{yy}\) is the moment of inertia about the \(y'\)-axis.

Accordingly, the state vector describing the longitudinal motion is

$$\begin{aligned} {\mathbf {x}} = \left\{ u, w, q, \theta \right\} . \end{aligned}$$

The forcing terms in Eq. (1), namely \(F_{x'}\), \(F_{z'}\), and \(M_{y'}\), are the aerodynamic loads acting on the bird. Consequently, the bird model is actually a four-state non-autonomous system, where the aerodynamic terms at the generic time \(t>0\) depends not only on the instantaneous state vector, but also on the instantaneous configuration of the wing \(\varphi (t)\) in the flapping cycle. This is obviously the main difference with respect to an equivalent fixed-wing aircraft model.

Formally, the forcing terms depend on the whole past state history. Therefore, these forcing aerodynamic terms can be expressed in the form of Eq. (1) only if a quasi-steady-state approximation is used, which typically holds for large-scale birds (Taha et al. 2012).

2.2 Wing Kinematics

The wings are attached to the main body and feature kinematic degrees-of-freedom as pictured in Fig. 2. They both consist of three rigid bodies corresponding to the bird arm, forearm, and hand. Relative motions between these segments govern wing morphing. To these wing segments are attached “master-feather” bodies representing the plumage and capturing its movements.

Fig. 2
figure 2

Top view of the bird wing kinematic model. Each cylinder captures a rotational degree of freedom, i.e., three at the shoulder (between the body and arm), one at the elbow (between the arm and forearm), and two at the wrist (between the forearm and hand). Moreover, each master feather is attached to one of these bodies via two more degrees of freedom, except the most distal one which aligned with the last bone segment

Full size image

We do not solve the wing dynamics in the state-space equations of the flier, but we rather assume that their kinematics are imposed. Consequently, the internal torques in the wing joints do not have to be computed for solving the body equations of motion. The description of the right and the left wing kinematics are assumed to be mirror, since movements are symmetric. For the sake of simplicity, each joint angle i is considered to follow a harmonic trajectory \(q_i(t)\), with respective amplitude \(A_i\), offset \(q_{0,i}\) and phase \(\phi _{0,i}\):

$$\begin{aligned} q_i(t) = q_{0,i} + A_i \sin \left( \omega t + \phi _{0,i}\right) \end{aligned}$$
(2)

with \(\omega = 2\pi f\) and f is the flapping frequency, identical for each joint. For the six rotational joints of the model in Figure 2, this makes a total of 19 gait parameters (including the wingbeat frequency) prescribing a particular set of wing kinematics.

Feather movements are governed by a simplified version of the model developed in Colognesi et al. (2021), which is itself inspired from Wu and Popović (2003). Indeed, feathers are similarly attached to the wing bodies via two rotational degrees of freedom (allowing spreading and pitching in a bone-relative frame of reference) but the motion of these degrees of freedom follows here predefined trajectories, while they feature some dynamic compliance in Colognesi et al. (2021) and Wu and Popović (2003). More precisely, we constrained feather movements via kinematic relationships depending on the angles between the wing segments in order to make them spreading and folding smoothly with the wing. These kinematic relationships are reported in the online version of the code available at https://github.com/vortexlab-uclouvain/multiflap.

2.3 Aerodynamic Model

In this section, the model used to compute the aerodynamic forces acting on the wing is developed. The model assumes that all aerodynamic forces act on the wings, and none on the main body. We use a quasi-steady lifting line approach, where the wake is shed backward in the form of straight and infinitely long vortex filaments at each time step of the simulation. More details about this aerodynamic model are reported in Colognesi et al. (2021). We checked a posteriori the validity of these assumptions, reported in Appendix 2. The wing motion and its position are defined in a wing-bone frame \((x_{w}, y_{w}, z_{w})\) shown in Fig. 3. The respective unit vectors along these axes are \((\hat{\mathbf {e}}_{x'_{w}}, \hat{\mathbf {e}}_{y'_{w}}, \hat{\mathbf {e}}_{z'_{w}})\). This frame is taken to follow the orientation of the body frame, while the translation of its origin determines the position of the bird shoulder with respect to its center of mass. The projection of \(O_{w}\) on the \(x'\)-axis, identifies the \(O'_{w}\) point. From this wing position, the lifting line is then consequently extracted. It is defined as the line passing through the quarter of the chord, which is itself defined as the segment orthogonal to the lifting line, going from the leading to the trailing edge of the wing. From a given wing configuration, the leading and trailing edges are defined as follows. The former goes from the shoulder to the wrist in a straight line, then to the tip of the outermost feather. The latter connects the tip of each feather from the innermost to the outermost. The lifting line is then obtained through an iterative process guaranteeing that it is located at the quarter of the chord distance and that it is orthogonal to the chord at each points.

Fig. 3
figure 3

Aerodynamic forces acting on the wing are applied at the discretized points of the lifting line (red), over the wing span. Adapted from www.fotki.com

Full size image

In order to compute the aerodynamic forces, it is required to know the wing angle of attack. A generic wing cross section is shown in Fig. 4, where \(c(\mathbf {y})\) represents the aerodynamic chord length. Each wing element is identified by a plane containing the lifting line. The unit vector orthogonal to such a plane is denoted by \(\hat{\mathbf {e}}_n\), the unit vector tangent to the lifting line \(\hat{\mathbf {e}}_t\) and the binormal one \(\hat{\mathbf {e}}_b=\hat{\mathbf {e}}_t \times \hat{\mathbf {e}}_n\).

According to this notation, \(-w_{d}\hat{\mathbf {e}}_{n}\) is the induced velocity (downwash) and

$$\begin{aligned} \mathbf {U} = \mathbf {U}_{\infty } - \mathbf {U}_{kin} - \mathbf {v}_{q} \end{aligned}$$

is the relative velocity seen by a wing profile, which accounts for the flight speed \(\mathbf {U}_{\infty }\) and the wing motion \(\mathbf {U}_{kin}\) while its component along \(\hat{\mathbf {e}}_t\) is previously eliminated and \(\mathbf {v}_{q}\) is the contribution induced from the angular velocity of the body q computed as \({\mathbf {v}}_{q}({\mathbf {y}}) = q {{\hat{\mathbf{j}}}} \times ({\mathbf {P}}-{\mathbf {G}})\).

Hence, the effective angle of attack is given by

$$\begin{aligned} \alpha _{r} = \alpha - \alpha _{i}\simeq \alpha - \frac{w_{d}}{|\mathbf {U}|}. \end{aligned}$$
(3)
Fig. 4
figure 4

Left: Wing element between two wing profiles, and identifying a plane \(\Sigma \) containing the lifting line. Right: Cross section containing the chord point \(\mathbf {P}_i\) where the velocities are applied

Full size image

The wake is considered to be composed of semi-infinite vortex tubes aligned with the x-axis, as shown in Fig. 5. In theory, because the wing is not straight, the bound vortex (i.e., the circulation of the lifting line itself) also induces velocities on the line itself. However in the presented model, these induced velocities are neglected since their magnitude is much lower as compared to the flight velocity. Therefore, the only induced velocity accounted for is a vertical component due to the wake. This velocity at a point \(\mathbf {y}\equiv (y'_{w}, z'_{w}) \) along the wingspan and induced by a set of semi-infinite vortex tube of circulation \(d\Gamma _{i}\) is computed via Biot–Savart law (Buresti 2012), i.e.,

$$\begin{aligned} w_{d}(\mathbf {y}) = -\frac{1}{4\pi }\sum _{i}\Big (-d\Gamma _{i}\dfrac{(\mathbf {y}-\mathbf {y}_{i})\times \hat{\mathbf {e}}_{x'_{w}}}{\left| \mathbf {y}-\mathbf {y}_{i}\right| ^2}\Big ) \cdot \hat{\mathbf {e}}_{n} \end{aligned}$$
(4)

where i are the discretized elements of the lifting line.

Considering the theorem of Kutta–Joukowski, the local circulation \(\Gamma \) is computed as

$$\begin{aligned} \Gamma (\mathbf {y}) = \frac{1}{2}|\mathbf {U_{r}}(\mathbf {y})|c(\mathbf {y})C_{l\alpha }(\alpha - \alpha _{i}) \end{aligned}$$
(5)

where \(\mathbf {U_{r}}\) is the norm of the local relative velocity vector, c is the local chord, and \(C_{l\alpha }\) is equal to \(2 \pi \) as a result of thin airfoil theory. We now assume the downwash velocity to be sufficiently small to approximate \(|\mathbf {U_{r}}|(y)\simeq |\mathbf {U}|\). Considering Eq. (5) and injecting Eq. (4) in Eq. (3), we get the lifting line Equation:

$$\begin{aligned} \Gamma (\mathbf {y}) = \frac{1}{2}c(\mathbf {y})C_{l\alpha }\Big [|\mathbf {U}|\alpha (\mathbf {y}) - \frac{1}{4\pi }\sum _{i}\Big (-d\Gamma _{i}\dfrac{(\mathbf {y}-\mathbf {y}_{i})\times \hat{\mathbf {e}}_{x'_{w}}}{\left| \mathbf {y}-\mathbf {y}_{i}\right| ^2}\Big ) \cdot \hat{\mathbf {e}}_{n}\Big ]. \end{aligned}$$
(6)
Fig. 5
figure 5

The vortex wake of the bird is considered straight and infinite at each time step of the flapping period. The variations in the line circulation \(\Gamma \) induce vortex tubes of circulation \(d\Gamma _{i+1} = \Gamma _{i+1}-\Gamma _i\), which in turn induce velocities in the wake

Full size image

To satisfy the solenoidal property of the vorticity field, the circulation \(\Gamma \) must form closed loops. This means that the circulation of the vortex tubes can be computed from the variations of \(\Gamma \) along the lifting line. For a given vortex tube \(i+1\) between the points i and \(i+1\) of the lifting line, the circulation of a shed tube \(d\Gamma _{i+1}\) is equal to

$$\begin{aligned} d\Gamma _{i+1} = \Gamma _{i+1}-\Gamma _i \end{aligned}$$
(7)

where \(\Gamma _i\) is the local circulation at the \(i^\text {th}\) point of the lifting line.

The circulation of the lifting line is computed iteratively. Starting from an initial guess, the induced velocities are computed at each point of the lifting line, with the contribution of each vortex tube from Biot–Savart law. The angle of attack is then modified with the new local flow conditions and new values are obtained from Eq. (3). The circulation of the vortex tubes is then computed from Eq. (7), thus closing the loop.

Once all the circulations are computed at every time step, the aerodynamic force acting on each discretized point of the lifting line computed as

$$\begin{aligned} d\mathbf {F}_i= \rho \Gamma _{i}(\mathbf {U_{r}} \times \hat{\mathbf {e}}_t)dl_{i}. \end{aligned}$$
(8)

Finally, the global forces acting on the wing can be evaluated in order to close the system of Eq. (1), by summing each contribution and computing the corresponding pitching moment, i.e.,

$$\begin{aligned} \begin{aligned} F_{x'}&= \sum _{i=1}^{N} (d\mathbf {F}_i) \cdot \hat{\mathbf {e}}_{x'}\\ F_{z'}&= \sum _{i=1}^{N} (d\mathbf {F}_i) \cdot \hat{\mathbf {e}}_{z'}\\ M_{y'}&= \sum _{i=1}^{N} (\mathbf {GP_i})\times (d\mathbf {F}_i)\cdot \hat{\mathbf {e}}_{y'}. \end{aligned} \end{aligned}$$
(9)

3 Flight Dynamics Analysis

We can now address how to solve Eq. (1), with the aerodynamic terms that are computed according to Eq. (9). Since it has been previously established that the wings follow a periodic trajectory governed by harmonic functions, the solution of Eq. (1) must be a limit cycle, for some particular initial conditions. Therefore, studying the stability of these solutions requires a specific formalism, and we will use here Floquet stability analysis. This section investigates the key features of periodic orbits, presenting a numerical algorithm both for identifying limit cycles and quantifying their stability from the so-called corresponding Floquet multipliers.

3.1 Stability of Limit Cycles

The objective is to find a limit cycle corresponding to a trimmed configuration of the bird flight, i.e., the flight configuration corresponding to a periodic trajectory of all the state variables. Moreover, we are interested in assessing the stability of such a limit cycle. Considering a generic non-autonomous system of ordinary differential equations in the form

$$\begin{aligned} \dot{{\mathbf {x}}} = {\mathbf {v}}({\mathbf {x}}, t) \end{aligned}$$
(10)

the limit cycle is a particular solution such that \(\mathbf{x} ^*(t) = \mathbf{x} ^*(t+T)\) with T being the cycle period.

Limit cycles can be stable or unstable, depending on whether a perturbed initial value tends to be dynamically attracted or repelled by the periodic orbit.

Fig. 6
figure 6

Illustration of a periodic orbit (red) and a first integration over one period of the neighboring trajectory (blue)

Full size image

Their stability is assessed by Floquet theory (Floquet 1883), and governed by the eigenvalues \(\Lambda _{i}\) of the Jacobian matrix (or monodromy matrix) \( {\mathbb {J}}({\mathbf {x}}_0) \Big |_{t_0}^{t_0 + T}\) that quantifies how a small perturbation out of the limit cycle is deformed by the flow, after a period T (Cvitanović et al. 2016; Strogatz 2018; Seydel 2009). Calling \(\mathbf {x}_0\) the initial condition, this Jacobian matrix is thus the result of the integration of the following system up to time \(t=T\)

$$\begin{aligned} \begin{aligned} \frac{d{\mathbb {J}}}{dt}(\mathbf {x}_0) \Big |_{t_0}^{t}&= {\mathbb {A}}(\mathbf {x}, t) {\mathbb {J}}(\mathbf {x}_0) \Big |_{t_0}^{t}\\ {\mathbb {J}} (\mathbf {x}_0)\Big |_{t_0}^{t_0}&= {\mathbb {I}} \end{aligned} \end{aligned}$$
(11)

where the matrix

$$\begin{aligned} {\mathbb {A}}(\mathbf {x}, t) = \frac{\partial }{\partial x_j}v_{i(\mathbf {x}, t)} \Bigg | _{\mathbf {x}=\mathbf {x^{*}}} \end{aligned}$$
(12)

is called the Stability Matrix (Cvitanović et al. 2016) and is T-periodic on the limit cycle. These eigenvalues are also called Floquet Multipliers. In other words, the Jacobian Matrix maps infinitesimal perturbations embedded within a sphere around a specific point of the limit cycle at a given time \((\mathbf {x_0}, t_0)\), to a stretched ellipsoid after a time t (Cvitanović et al. 2016). This stretching ratio is governed by the Floquet Multipliers, and the stretching directions by its eigenvectors. Floquet multipliers have the property to be independent of the choice of \(\mathbf {x}_0\) on the limit cycle, while the Floquet matrix and its eigenvectors depend on it (Lust 2001).

If the system was autonomous, i.e., of the form \({{\dot{\mathbf{x}}}} = \mathbf {v}(\mathbf {x})\), one of the Floquet multipliers would systematically be equal to one and its eigenvector would be tangent to the limit cycle at \(\mathbf {x}_0\). In the literature, this eigenvalue is often called the trivial or marginal multiplier, and a periodic solution is said asymptotically stable if all Floquet multipliers except this one are strictly smaller than one in absolute value. For non-autonomous systems like the one considered here, all Floquet multipliers are non-trivial, and therefore stability requires that all Floquet multipliers to be smaller than one in absolute value (Taha et al. 2012).

3.2 Multiple-shooting Method

A multiple-shooting algorithm is employed in order to identify the periodic orbits corresponding to trimmed flight, and to simultaneously compute their stability through their Floquet multipliers.

We use a multiple-shooting scheme first proposed by Lust (2001), which was a modification of Keller (1968). This algorithm is adapted to our case with the advantage that the limit cycle period is known, since it must be equal to the flapping one (Dietl and Garcia 2008).

Fig. 7
figure 7

Generic computational scheme describing the multiple-shooting method of a phase-space \({\mathcal {M}} \in \mathrm IR^{3}\) (without loss of generalities). The black trajectory is traced out by integrating the equations from the guessed points (blue dots). The asymptotic limit cycle is represented in red, and the points belonging to it in green

Full size image

Considering a generic T-periodic non-autonomous system described by Eq. (10), this multiple-shooting method splits the limit cycle into several points and computes the time integration from one point to the following along the trajectory, as illustrated in Fig. 7.

Considering the operator

$$\begin{aligned} f(\mathbf {x}_{i}^{*}) \Big |_{t_i}^{t_{i}+\tau }= \int _{t_i}^{t_i+\tau } \mathbf {v}(\mathbf {x}, t) dt + \mathbf {x}_{i}^{*} \end{aligned}$$

the point \(\mathbf {x}^*_{i}\) is mapped to the point \(\mathbf {x}^*_{i+1}\) by

$$\begin{aligned} \mathbf {x}^*_{i+1} = f(\mathbf {x}^*_i) \big |_{t_{i}}^{t_{i}+\tau } = f(\mathbf {x}_i + \Delta \mathbf {x}_i) \big |_{t_{i}}^{t_{i}+\tau } \end{aligned}$$
(13)

Computing the Taylor first-order expansion of the right hand side of Eq. (13), the point \(\mathbf {x}^*_{i+1}\) can be expressed as function of the guessed points only

$$\begin{aligned} \mathbf {x}_{i+1} + \Delta \mathbf {x}_{i+1} =f(\mathbf {x}_i) \big |_{t_{i}}^{t_{i}+\tau } + {\mathbb {J}} (\mathbf {x}_i) \Big |_{t_{i}}^{t_{i}+\tau }\cdot \Delta \mathbf {x}_i \end{aligned}$$
(14)

where \({\mathbb {J}} \big |_{t_{i}}^{t_{i}+\tau }(\mathbf {x}_i)\) is the Jacobian matrix defined in Eq. (11). Re-arranging Eq. (14) as

$$\begin{aligned} {\mathbb {J}}(\mathbf {x}_i) \Big |_{t_{i}}^{t_{i}+\tau }\cdot \Delta \mathbf {x}_i -\Delta \mathbf {x}_{i+1} = \underbrace{-\big (f(\mathbf {x}_i)\big |_{t_{i}}^{t_{i}+\tau } - \mathbf {x}_{i+1}\big )}_{Error} \end{aligned}$$
(15)

the multiple-shooting scheme can be derived

$$\begin{aligned} \underbrace{ \begin{pmatrix} {\mathbb {J}} (\mathbf {x}_0) \Big |_{0}^{\tau } &{} - {\mathbb {I}}&{} 0&{} \dots &{} 0 \\ 0 &{} {\mathbb {J}} (\mathbf {x}_1)\Big |_{t_{1}}^{t_{1}+\tau }&{} - {\mathbb {I}} &{} \dots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} 0 &{}\dots &{} {\mathbb {J}}(\mathbf {x}_{m-1})\Big |_{t_{m-1}}^{T} &{} - {\mathbb {I}}\\ - {\mathbb {I}} &{} 0 &{}\dots &{} 0 &{} {\mathbb {I}}\\ \end{pmatrix}}_{\mathbf {M}\ [n \times M, n \times M]} \underbrace{ \begin{pmatrix} \Delta \mathbf {x}_{0}\\ \Delta \mathbf {x}_{1}\\ \vdots \\ \vdots \\ \vdots \\ \Delta \mathbf {x}_{m-1}\\ \Delta \mathbf {x}_{m} \end{pmatrix}}_{\Delta \mathbf {x}\ [n \times M]}= \underbrace{-\begin{pmatrix} f(\mathbf {x}_0) \big |_{0}^{\tau }- \mathbf {x}_1 \\ f(\mathbf {x}_1) \big |_{t_{1}}^{t_{1}+\tau }- \mathbf {x}_2 \\ \vdots \\ f(\mathbf {x}_{m-1}) \big |_{t_{m-1}}^{T} - \mathbf {x}_m\\ \mathbf {x}_{m}- \mathbf {x}_0\\ \end{pmatrix}}_{\mathbf {E}\ [n \times M]}. \nonumber \\ \end{aligned}$$
(16)

Calling n the number of states of the dynamical system and M the amount of points employed in the multiple-shooting, \(\mathbf {M}\) is the Multiple-shooting matrix of dimension \([n \times M, n \times M]\), \(\Delta \mathbf {x}\) the unknown vector of dimension \([n \times M]\) and \(\mathbf {E}\) the error vector of dimension \([n \times M]\).

By expressing Eq. (16), in a compact form

$$\begin{aligned} \mathbf {M}(\mathbf {x}_i) {\varvec{\Delta }}\mathbf {\mathbf {x}} = \mathbf {E}(\mathbf {x}_i). \end{aligned}$$
(17)

Finding the solution of Eq. (17) consists in finding \(\mathbf {x}_i^* \in \mathrm IR^{n}\) such that \(\mathbf {E}(\mathbf {x}_i^*) = \mathbf {0}\) and this can be solved with an iterative scheme. A Newton’s method can be derived to iterate on Eq. (17) until convergence to 0. However, the main drawback of this method, is the high sensitivity on the choice of the initial guess \(\mathbf {x}^{(0)}_i\). It can be mathematically proved that Newton’s method quadratically converges only if the choice of the initial conditions is sufficiently close to the solution (for a proof of this Theorem, please refer to Quarteroni et al. (2010), chap. 7).

Consequently, we implemented a modified Newton’s method, in order to improve the robustness of the scheme with respect to the initial value. The proposed method relies on the Levenberg–Marquardt algorithm (Marquardt 1963) (LMA). Such an implementation of LMA in a multi-shooting code was already adopted by Dednam and Botha Dednam and Botha (2015) and the code was validated with both autonomous and non-autonomous systems.

The estimation of a new unknown vector \(\delta \mathbf {x}\) that solves for Eq. 18, and used to update the state variables at the generic iteration step k, is computed as follows

$$\begin{aligned} \left[ \mathbf {M}^{T}\mathbf {M} + \lambda \text {diag}(\mathbf {M}^{T}\mathbf {M}) \right] \varvec{\delta } \mathbf {x} = \mathbf {M}^{T} \mathbf {E} \end{aligned}$$
(18)

where \(\lambda \) is a nonnegative, adaptive damping parameter, and a candidate algorithm is presented in Algorithm (1).

figure a

When the trajectory eventually converges to the limit cycle, the Jacobian matrix of the whole limit cycle obeys the semi-group property and can be expressed as the product of the submatrices of Equation (16), i.e.,

$$\begin{aligned} {\mathbb {J}} (\mathbf {x}_0) \Big |_{0}^{T} = {\mathbb {J}} (\mathbf {x}_{m-1}) \Big |_{t_{m-1}}^{T} \cdots {\mathbb {J}} (\mathbf {x}_1) \Big |_{t_{1}}^{t_{1}+\tau }\cdot {\mathbb {J}} (\mathbf {x}_0) \Big |_{0}^{\tau }. \end{aligned}$$
(19)

3.3 Computation of the Jacobian Matrix

Two concurrent approaches can be used to evaluate the Jacobian matrix and build the diagonal blocks of the multiple-shooting matrix \(\mathbf {M}\) in Eq. (16): the first one relies on a semi-analytical approach, while the second one relies on numerical computations only. Both methods are implemented in our code, and a comparison of the results is reported in Appendix 1. The semi-analytical approach is the one we used in the following simulations, and it is here described in details. The Jacobian matrix is obtained by solving the variational equation (11) and the state equation (10), i.e.,

$$\begin{aligned} \begin{pmatrix} \dot{\mathbf {x}}\\ \dot{{\mathbb {J}}} \end{pmatrix} = \begin{pmatrix} \mathbf {v}(\mathbf {x}, t)\\ {\mathbb {A}}(\mathbf {x}, t) \ {\mathbb {J}} \end{pmatrix} \end{aligned}$$
(20)

with the initial condition

$$\begin{aligned} \begin{pmatrix} {\mathbf {x}(t_0)}\\ {{\mathbb {J}}^{0}} \end{pmatrix} = \begin{pmatrix} \mathbf {x}_0 \\ {\mathbb {I}} \end{pmatrix}. \end{aligned}$$
(21)

This approach requires to simultaneously solve \((n+n^{2})\) ordinary differential equations (Seydel 2009). The solution of this system corresponds to the Jacobian matrix of a generic trajectory at time \(t_f\), obtained from an initial condition at time \(t_0\).

In our particular case, the matrix \({\mathbb {A}}(t)\) accordingly to Eq. (12) is

$$\begin{aligned} {\mathbb {A}}(\mathbf {x}(t), t) = \begin{pmatrix} \frac{1}{m}\frac{\partial {F_{x'}}}{\partial {u}} &{} \frac{1}{m}\frac{\partial {F_{x'}}}{\partial {w}} - q&{} - w + \frac{1}{m}\frac{\partial {F_{x'}}}{\partial {q}}&{} -g\cos {\theta } + \frac{1}{m}\frac{\partial {F_{x'}}}{\partial {\theta }}\\ q + \frac{1}{m}\frac{\partial {F_{z'}}}{\partial {u}} &{} \frac{1}{m}\frac{\partial {F_{z'}}}{\partial {w}}&{} u + \frac{1}{m}\frac{\partial {F_{z'}}}{\partial {q}} &{} g\sin {\theta } + \frac{1}{m}\frac{\partial {F_{z'}}}{\partial {\theta }}\\ \frac{1}{I_{yy}}\frac{\partial {M_{y'}}}{\partial {u}} &{} \frac{1}{I_{yy}}\frac{\partial {M_{y'}}}{\partial {w}}&{} \frac{1}{I_{yy}}\frac{\partial {M_{y'}}}{\partial {q}} &{} \frac{1}{I_{yy}}\frac{\partial {M_{y'}}}{\partial {\theta }}\\ 0 &{} 0 &{}1 &{} 0 \\ \end{pmatrix}. \end{aligned}$$
(22)

Given the complexity of our coupled system of Eq. (1), the main disadvantage of using this approach is the need of computing the derivatives of the aerodynamic forces. In other words, even by using such an analytical approach, a numerical differentiation is necessary to compute these derivatives in order to solve Eq. (20).

3.4 Numerical Parameters and Wingtip Trajectory

The aerodynamic model can be adapted to large-scale flapping fliers, and we implemented lengths of the bones and feathers to match those of the northern bald ibis (Geronticus eremita). This particular bird has been chosen because it has a high aspect ratio wing—which is well suited for the lifting line approach used—and uses non-stop flapping flight.

The parameters governing the wing kinematics described by Eq. (2) are constrained to follow the wing kinematics of real birds. No accurate data about the kinematics of ibises and other large birds are available in the literature. We thus re-scale the kinematics of a pigeon, reported in Tobalske and Dial (1996). The typical wingbeat frequency is retrieved from Berg and Rayner (1995) and we tuned the wingbeat amplitude accordingly, in order to keep the angle of attack in a realistic range.

Based on the aforementioned observations, all simulations reported in the rest of this paper have been computed with numerical parameters gathered in Table 1. The wingbeat frequency is taken equal to \(f=4Hz\). In this investigation, the frequency is kept fixed, for two main reasons: from a mathematical perspective the frequency does not alter the qualitative behavior of the forces and moments. From a biological point of view, birds tend to select a preferred frequency for a cruise flight, and even though for changing flight regimes they can change it, the available range for each species is limited (Pennycuick 1996).

Table 1 Numerical parameters used in the simulations
Full size table

The resulting wing kinematics are also pictured in Fig. 8, with a shoulder amplitude equal to \(A_{s,x}=42\deg \).

Fig. 8
figure 8

Snapshots of the wing kinematics within one flapping period, taken every T/4

Full size image

The reference position of the wing-bone frame is vertically aligned with the center of mass, and placed at a certain distance ahead of it. This default distance is 5 cm, although a dedicated sensitivity analysis on this parameter is conducted later on (see Sect. 4). Using the kinematic parameters of Table 1 in Eq. (2) for each joint, and considering the relative position between the wing-bone frame and the body frame, the resulting tip trajectory is shown in Fig. 9. Considering a counter-clockwise motion, the blue trajectory represents the region where the lifting line lies ahead of the center of mass G. Assuming a positive lift for the whole wingbeat period, this region provides a positive pitching moment due to the lift (nose-up). The tip positions corresponding to the orange segment of the trajectory correspond to the region where the lifting line lies behind the center of mass, generating a negative pitching moment due to the lift effect, under the aforementioned assumption. This is an important feature of our model since no additional lifting surface such as a tail is considered in the present study. Consequently, a necessary condition for the existence of a limit cycle is that the wing itself generates both positive and negative pitching moment, in order to achieve rotational equilibrium of the bird body over the cycle.

Fig. 9
figure 9

Tip path trajectory over a wingbeat cycle. Blue line: position of the lift ahead of the center of mass, contributing for a nose-up (positive) pitching moment; orange line: position of the lift ahead of the center of mass, contributing for a nose-down (negative) pitching moment. Scatter points represent the position of the wing profile every T/20

Full size image

The numerical parameters employed in multiple-shooting algorithm are reported in Table 2 and the numerical integration has been performed using a fourth-order Runge–Kutta scheme.

Table 2 Numerical parameters used in the multiple-shooting algorithm
Full size table

4 Results: Identification, Stability, and Sensitivity Analysis of Limit Cycles

This section reports three experiments that were conducted to validate the capacity of the developed framework to identify limit cycles, assess their stability, and quantify the sensitivity of flight regime and stability with respect to kinematic and morphological parameters

4.1 Experiment 1: Representative Limit Cycle and Stability Analysis

A representative limit cycle solution is reported here, as the result of a multiple-shooting computation. This solution corresponds to the reference case in which the kinematics is described by the governing parameters of Table 1, with \(A_{s,x}=42\deg \). The initial value at time \(t=0\) to start the multiple-shooting scheme was chosen to resemble a reasonable cruise flight condition of large birds

$$\begin{aligned} \mathbf {x}_0(t=0) = [16.5, 0.5, 0.5, 0] \end{aligned}$$

and the other \(M-1\) points were spread by straightforward numerical integration

$$\begin{aligned} \mathbf {x}_{n+1}(t_{n+1}) = f(\mathbf {x}_{n}(t_n)) \Big |_{t_n}^{t_{n}+\tau } \end{aligned}$$

in order to have a column of zeros in the RHS of Eq. (16), except for the last element. Convergence analysis and consequently stability results are shown in Fig. 10. In particular, rapid convergence is obtained, after seven iterations. The error is evaluated as the \(\max \{{|\mathbf {E}(\mathbf {x})|}\}\) of Eq. (17). Such configuration presents one expanding eigenvalue, which leads the system to be unstable. The numerical values of the Floquet multipliers, are also reported in Table 3

Fig. 10
figure 10

Convergence error (left) and Floquet multipliers (right) for the reference case with the imposed kinematics of Table 1

Full size image
Table 3 Floquet multipliers obtained for the reference case with the imposed kinematics of Table 1
Full size table

The expanding eigenvalue has an absolute value of \(\Lambda _{1}= 1.40\). The related eigenvector is \(e_{1} = [-0.69, 0.68, 0.12, 0.16]^{T} \) evaluated at the point \(\mathbf {x}(t_{0}=0)=[18.24, -1.93, -0.10, -0.115]^{T}\). This therefore excites the perturbation along each eigenbase directions with the same order of magnitude. Considering a flapping period of \(T=0.25s\), the expanding Floquet exponent is

$$\begin{aligned} \lambda _{1}=\frac{1}{T}\ln (\Lambda _{1})=1.34s^{-1} \end{aligned}$$

and therefore the time needed for the perturbation to double its value is approximately

$$\begin{aligned} t_\mathrm{doubling} = \frac{\ln (2)}{\lambda _{1}}\approx 0.51s. \end{aligned}$$

This corresponds to approximatively two flapping periods and is thus larger than the one reported in previous studies focusing on smaller-scale animals (Dietl and Garcia 2008; Taylor et al. 2006). The eigenvalue spectrum was found qualitatively similar to the one presented by Dietl and Garcia (2008), and interestingly a similar pattern was also observed for insect scales in previous research efforts (Taha et al. 2014; Xiong and Sun 2008; Gao et al. 2009). Figure 11 pictures the periodic solution of the state variables describing this limit cycle in the phase space. This solution is a trimmed state of the bird, for the prescribed kinematics and morphology. The states are plotted with respect to one cycle in the moving body frame. At time zero, the wing position corresponds to the middle of the downstroke.

On the right side of Fig. 11 is pictured the four-state limit cycle in the phase portrait. The periodicity in \(\theta \) is plotted as a color map on the trajectory described by the three others state-space variables.

Fig. 11
figure 11

Reference limit cycle solution. Trajectory of each state variable (left) and phase portrait (right)

Full size image

To better highlight what leads to trajectory separation, we ran another simulation with a perturbation of the limit cycle solution along the pure unstable direction \(e_{1}\) and let the system evolve over five flapping periods. The separation is driven from the pitch angle \(\theta \) which quickly tilts down, and is subsequently followed by an increase in the u-component of velocity, likely resulting from acceleration due to the larger action of the gravity along the local \(x'\)-axis as shown in Fig. 12.

Fig. 12
figure 12

Separation of the perturbed solution along the unstable eigenvector (black) over five flapping period, from the periodic orbit (red). Trajectory of each state variable (left) and phase portrait of the variables [u, w, q] (right)

Full size image

The aerodynamic forces and moment of the limit cycle solution are plotted in Fig. 13 and normalized with respect to \(m_{b}g\) (forces) and \(m_{b}g{\overline{c}}\) (moment). The global action of the forces and pitching moment over one period is zero, confirming the state of trimmed flight, and limit cycle condition (zero acceleration over one period).

The validity of this aerodynamic model was assessed by studying the resulting reduced frequency and angle of attack. Results of this verification are reported in dedicated Appendix 2.

Fig. 13
figure 13

Dimensionless forces and pitching moment developed by the flier, expressed in the fixed frame O(X, Z)

Full size image

Results from the simulation settle on values that are very compatible with biological observations for species of similar mass and aspect ratio (Sperger et al. 2017; Pennycuick et al. 2013; Pennycuick 1989). The corresponding Strouhal number for this flight condition is

$$\begin{aligned} St = \frac{f \Psi }{U_{\infty }} \approx 0.18 \end{aligned}$$

where f is the flapping frequency, \(\Psi \) the vertical length identified by the tip-to-tip excursion and \(U_{\infty }\) the forward flight velocity. It lies in the lower margin identified by Taylor et al. (2003) for maximizing power efficiency for birds in forward flight.

4.2 Experiment 2: Sensitivity Analysis of the Shoulder Amplitude

4.2.1 Methods

The multiple-shooting method has been applied to address the question of the gait sensitivity, since the framework can handle the analysis of several gait configurations. In particular, we exploited this to achieve a specific limit cycle solution corresponding to level flight. Indeed, the solution reported in Experiment 1 corresponds to trimmed flight, but not necessarily to level flight: trimmed flight might correspond to a flight regime with a nonzero averaged vertical velocity.

In order to achieve level flight, the mean vertical velocity with respect to the fixed frame has to be zero over the flapping period. Considering Fig. 1, the velocity components in the fixed frame are

$$\begin{aligned} \begin{aligned} U_{ff}&= {\dot{X}} = u\cos {\theta } + w\sin {\theta }\\ W_{ff}&= -{\dot{Z}} = u\sin {\theta } - w\cos {\theta }. \end{aligned} \end{aligned}$$
(23)

In particular, we report here a sensitivity analysis of the flapping gait as a function of one of the most important kinematic parameters, namely the wingbeat amplitude of the shoulder \(A_{s,x}\). Consequently, seeking for a level flight configuration reduces to a single parametric study consisting in finding the shoulder amplitude \(A^{*}_{s,x}\) that corresponds to a limit cycle whose mean vertical velocity is equal to zero, i.e.,

$$\begin{aligned} {\overline{W}}_{ff}(A^{*}_{s,x}) = 0. \end{aligned}$$
(24)

Since \({W}_{ff}\) is a nonlinear function of \(A_{s,x}\), we rely on a Newton–Raphson method to find its root. Finally, the climbing or descending ratio is identified by the trajectory angle, defined as

$$\begin{aligned} \beta = \tan ^{-1}{\frac{{\overline{W}}_{ff}}{{\overline{U}}_{ff}}}. \end{aligned}$$

4.2.2 Results

By applying the frame transformation of Eq. (23) and subsequently integrating the velocities, three different trajectories of the bird corresponding to three different flight conditions, are illustrated in Fig. 14. The relationships between the shoulder amplitude, and the corresponding flight velocities and trajectory angles have has also been investigated for an interval of \([40\deg< A_{s,x}<46\deg ]\), and results are plotted in Fig. 15. A quasi-linear relationship is found with high sensitivity response of the amplitude parameter to the flight condition.

Fig. 14
figure 14

Different flight trajectories over one flapping period. Red path: descending behavior with a shoulder amplitude of \(42\deg \); green path: level flight solution obtained with a shoulder amplitude of \(43.47\deg \); blue path: climbing behavior for a wingbeat amplitude of \(44\deg \)

Full size image

Descending trajectories are achieved for amplitudes smaller that \(43.47\deg \) corresponding to a negative vertical velocity, while climbing trajectories correspond to higher values of amplitudes. Also concerning the forward flight velocity, an increase in amplitude determines a linear increment of the flight speed, suggesting an active role of this parameter on the production of the thrust. Finally, we investigated the stability behavior for all the cases reported here. The Floquet multipliers are pictured in Fig. 16 and this shows that the four multipliers are marginally affected by changing the shoulder amplitude.

Fig. 15
figure 15

a Averaged horizontal velocity, b averaged vertical velocity, c averaged norm of the velocities, d trajectory angle

Full size image
Fig. 16
figure 16

Eigenvalues corresponding to several shoulder amplitudes and zoom on the unstable branch

Full size image

4.3 Experiment 3: Sensitivity Analysis on the Wing Insertion Point

4.3.1 Methods

We now conduct a sensitivity analysis of stability as a function of the relative position between the center of mass and the insertion point of the wing in the body frame. This wing insertion point coincides with the rotational shoulder joint. Since the wing is free to sweep around the body center of mass, we need to revisit the classical definition of stability margin from the literature in flight mechanics. Considering Fig. 3, we introduce a new morphological parameter that we call longitudinal margin LM, which defines the position of the center of mass with respect to the wing root projection along \(x'\), normalized by the mean aerodynamic chord, i.e.,

$$\begin{aligned} LM = \frac{(O'_{w}-G)}{{\overline{c}}}. \end{aligned}$$
(25)

When \(LM = 0\%\), the center of mass longitudinally coincides with the origin of the wing frame. The interval of variation of the longitudinal margin has been explored in the range \(17.5 \%< LM< 32\%\).

4.3.2 Results

Results are illustrated in Fig. 17 where the locus of the eigenvalues is reported for different longitudinal margins. It shows that the eigenvalues locus (and therefore stability) is governed by the wing position, relative to the center of mass, and thus from the generation of an adequate pitching moment. Looking at Fig. 17, the expanding eigenvalue is smaller as the wing tends to get closer to the center of mass. This means that the capability of the wing to generate negative (nose-down) moment is beneficial for the global stability behavior. In contrast, if the position of the wing is too much ahead of the center of mass, and consequently the capability of generating nose-down moment is reduced, the absolute value of the expanding eigenvalue, drastically increases, leading the system to be more and more unstable.

Fig. 17
figure 17

Sensitivity of the eigenvalues with respect to the reciprocal position between wing-bone frame and the body frame

Full size image

Thus, the characteristic doubling time is putatively modulated by the wing kinematics and position, and is not unique for a given species as suggested by Dietl and Garcia (2008).

Importantly, none of the tested configuration, corresponds to a stable solution. The distance between the wing insertion point and the center of mass could be made smaller to continue bringing the largest eigenvalue close to the unit circle, but there is a threshold above which the wing is not capable of generating enough pitching up moment, for guaranteeing the existence of a limit cycle solution. Indeed, zero average pitching moment over one period is a necessary condition of existence of a limit cycle. In sum, we did not manage to find such limit cycles for \(LM < 17.5\%\), and thus no stable limit cycle could be found.

5 Conclusions

Flapping flight stability is a central concept for understanding how complex a control scheme is or needs to be in animal fliers, such as birds, or ornithopters. Experimental, theoretical, and numerical studies on such “flapping systems” have provided valuable insights on their dynamic and stability (Taylor and Thomas 2002, 2003; Xiong and Sun 2008). With this contribution, we have made a step forward by using a new model which is more accurate than existing ones in a couple of ways: (1) our wing is morphing during the cycle and we have enriched the bird motion by introducing critical degrees of freedom of the wing, especially the shoulder sweep angle; and (2) we have considered the wake effect on aerodynamic force production via a quasi-steady lifting line approach.

Several trimmed trajectories have been retrieved by varying the gait parameters. In particular, the wingbeat amplitude relates quasi-linearly with the climbing angle and linear velocity in the explored range, thus determining whether the bird climbs, descends, or stays at constant altitude. It suggests that this degree of freedom could be a central control parameter for achieving level flight.

Results from the simulations agree with experimental observations of large bird species with a comparable mass and wingspan. In terms of forward flight velocity, the limit cycle converges to values that are effectively adopted by birds during migrations, i.e., within the range from 15 to 20\(ms^{-1}\), (Sperger et al. 2017; Pennycuick et al. 2013; Pennycuick 1989), and consequently the related Strouhal number lies in the lower range identified by Taylor et al. (2003) in order to maximize power efficiency.

Furthermore, Floquet theory combined with multiple-shooting algorithms is confirmed as an elegant and powerful framework for analyzing the solutions of such flapping gaits. It turns out that the relative position between the wing and bird center of mass clearly affects pitching moments and global stability. Since our wings are massless, this effect has been investigated by moving the relative position between the center of mass and shoulder joint, whereas in reality this can be obtained by sweeping movements. This choice was made in order to unveil the main physical relationship between the generation of pitching moment and stability. Note that a more extended and a dedicated parametric study of all kinematics degrees of freedom of the wing (in particular, regarding sweeping motion) is left for a future work. These future investigations will further focus on the performance of a bird flight, addressing the question of quantifying the cost of transport based on a prescribed kinematics, and searching for a trade-off between power consumption and flight stability. Although the expanding eigenvalue gets closer to the unit circle when the center of mass approaches the wing root, stable configurations have not been found. In sum, the wing cannot generate a fully stabilizing effect in pitch. If so, birds would need to continuously rely on sensory feedback to adapt their gait via active control. In sum, we clearly showed how the instability doubling time depends not only on the species, but also on the wing kinematics, its morphology, and how they relate with the pitching moment. Nevertheless, at least two important complementary aspects have not been investigated here. Stabilizing benefits could indeed arise either from wing compliance or from the aerodynamic contribution of the tail. These will be topic of our future investigations.

Other questions regarding inertial contributions of bird wings and head to dynamics also remain open. Comprehensive answers within this framework would require substantial modifications of the equations of motion adopted here.