Space-Efficient Algorithms for Longest Increasing Subsequence

Abstract

Given a sequence of integers, we want to find a longest increasing subsequence of the sequence. It is known that this problem can be solved in $O\left (n \log n\right )$ time and space. Our goal in this paper is to reduce the space consumption while keeping the time complexity small. For $\sqrt {n} \le s \le n$, we present algorithms that use $O\left (s \log n\right )$ bits and $O\left (\frac {1}{s} \cdot n^{2} \cdot \log n\right )$ time for computing the length of a longest increasing subsequence, and $O\left (\frac {1}{s} \cdot n^{2} \cdot \log ^{2} n\right )$ time for finding an actual subsequence. We also show that the time complexity of our algorithms is optimal up to polylogarithmic factors in the framework of sequential access algorithms with the prescribed amount of space.

1 Introduction

Given a sequence of integers (possibly with repetitions), the problem of finding a longest increasing subsequence (LIS, for short) is a classic problem in computer science which has many application areas including bioinfomatics and physics (see [38] and the references therein). It is known that LIS admits an O(n log n)-time algorithm that uses O(n log n) bits of working space [2, 17, 37], where n is the length of the sequence.

A wide-spread algorithm achieving these bounds is Patience Sorting, devised by Mallows [24,25,26]. Given a sequence of length n, Patience Sorting partitions the elements of the sequence into so-called piles. It can be shown that the number of piles coincides with the length of a longest increasing subsequence (see Section 3 for details). Combinatorial and statistical properties of the piles in Patience Sorting are well studied (see [2, 8, 33]).

However, with the dramatic increase of the typical data sizes in applications over the last decade, a main memory consumption in the order of Θ(n log n) bits is excessive in many algorithmic contexts, especially for basic subroutines such as LIS. We therefore investigate the existence of space-efficient algorithms for LIS.

Our Results

In this paper, we present the first space-efficient algorithms for LIS that are exact. We start by observing that when the input is restricted to permutations, an algorithm using O(n) bits can be obtained straightforwardly by modifying a previously known algorithm (see Section 3.3). Next, we observe that a Savitch type algorithm [36] for this problem uses O (log²n) bits and thus runs in quasipolynomial time. However, we are mainly interested in space-efficient algorithms that also behave well with regard to running time. To this end we develop an algorithm that determines the length of a longest increasing subsequence using $O\left (\sqrt {n} \log n\right )$ bits which runs in O (n^1.5 log n) time. Since the constants hidden in the O-notation are negligible, the algorithm, when executed in the main memory of a standard computer, may handle a peta-byte input on external storage.

More versatile, in fact, our space-efficient algorithm is memory-adjustable in the following sense. (See [3] for information on memory-adjustable algorithms). When a memory bound s with $\sqrt {n} \le s \le n$ is given to the algorithm, it computes with O (s log n) bits of working space in $O\left (\frac {1}{s} \cdot n^{2} \log n\right )$ time the length of a longest increasing subsequence. When s = n our algorithm is equivalent to the previously known algorithms mentioned above. When $s = \sqrt {n}$ it uses, as claimed above, $O\left (\sqrt {n} \log n\right )$ bits and runs in O (n^1.5 log n) time.

The algorithm only determines the length of a longest increasing subsequence. To actually find such a longest increasing subsequence, one can run the length-determining algorithm n times to successively construct the sought-after subsequence. This would give us a running time of $O\left (\frac {1}{s}\cdot n^{3} \log n\right )$. However, we show that one can do much better, achieving a running time of $O\left (\frac {1}{s} \cdot n^{2} \log ^{2} n\right )$ without any increase in space complexity, by recursively finding a near-mid element of a longest increasing subsequence.

To design the algorithms, we study the structure of the piles arising in Patience Sorting in depth and show that maintaining certain information regarding the piles suffices to simulate the algorithm. Roughly speaking, our algorithm divides the execution of Patience Sorting into O(n/s) phases, and in each phase it computes in O (n log n) time information on the next O(s) piles, while forgetting previous information.

Finally, we complement our algorithm with a lower bound in a restricted computational model. In the sequential access model, an algorithm can access the input only sequentially. We also consider further restricted algorithms in the multi-pass model, where an algorithm has to read the input sequentially from left to right and can repeat this multiple (not necessarily a constant number of) times. Our algorithm for the length works within the multi-pass model, while the one for finding a subsequence is a sequential access algorithm. Such algorithms are useful when large data is placed in an external storage that supports efficient sequential access. We show that the time complexity of our algorithms is optimal up to polylogarithmic factors in these models.

Related Work

The problem of finding a longest increasing subsequence (LIS) is among the most basic algorithmic problems on integer arrays and has been studied continuously since the early 1960’s. It is known that LIS can be solved in O(n log n) time and space [2, 17, 37], and that any comparison-based algorithm needs Ω(n log n) comparisons even for computing the length of a longest increasing subsequence [17, 32]. For the special case of LIS where the input is restricted to permutations, there are O(n loglog n)-time algorithms [6, 12, 20]. Patience Sorting, an efficient algorithm for LIS, has been a research topic in itself, especially in the context of Young tableaux [2, 8, 24,25,26, 33].

Recently, LIS has been studied intensively in the data-streaming model, where the input can be read only once (or a constant number of times) sequentially from left to right. This line of research was initiated by Liben-Nowell, Vee, and Zhu [22], who presented an exact one-pass algorithm and a lower bound for such algorithms. Their results were then improved and extended by many other groups [15, 18, 19, 28, 34, 35, 38]. These results give a deep understanding on streaming algorithms with a constant number of passes even under the settings with randomization and approximation. (For details on these models, see the recent paper by Saks and Seshadhri [35] and the references therein). On the other hand, multi-pass algorithms with a non-constant number of passes have not been studied for LIS.

While space-limited algorithms on both RAM and multi-pass models for basic problems have been studied since the early stage of algorithm theory, research in this field has recently intensified. Besides LIS, other frequently studied problems include sorting and selection [7, 16, 27, 30], graph searching [4, 9, 14, 31], geometric computation [1, 5, 10, 13], and k-SUM [23, 39].

2 Preliminaries

Let τ = 〈τ(1),τ(2),…,τ(n)〉 be a sequence of n integers, possibly with repetitions. For 1 ≤ i₁ < … < i_ℓ ≤ n, we denote by τ[i₁,…,i_ℓ] the subsequence 〈τ(i₁),…,τ(i_ℓ)〉 of τ. A subsequence τ[i₁,…,i_ℓ] is an increasing subsequence of τ if τ(i₁) < … < τ(i_ℓ). If τ(i₁) ≤… ≤ τ(i_ℓ), then the sequence τ is non-decreasing. We analogously define decreasing subsequences and non-increasing subsequences. By lis(τ), we denote the length of a longest increasing subsequence of τ.

For example, consider a sequence τ₁ = 〈2,8,4,9,5,1,7,6,3〉. It has an increasing subsequence τ₁[1,3,5,8] = 〈2,4,5,6〉. Since there is no increasing subsequence of τ₁ with length 5 or more, we have lis(τ₁) = 4.

In the computational model in this paper, we use the RAM model with the following restrictions that are standard in the context of sublinear space algorithms. The input is in a read-only memory and the output must be produced on a write-only memory. We can use an additional memory that is readable and writable. Our goal is to minimize the size of the additional memory while keeping the running time fast. We measure space consumption in the number of bits used (instead of words) within the additional memory.

3 Patience Sorting

Since our algorithms are based on the classic Patience Sorting, we start by describing it in detail and recalling some important properties regarding its internal configurations.

Internally, the algorithm maintains a collection of piles. A pile is a stack of integers. It is equipped with the procedures push and top: the push procedure appends a new element to become the new top of the pile; and the top procedure simply returns the element on top of the pile, which is always the one that was added last.

We describe how Patience Sorting computes lis(τ). See Algorithm 1. The algorithm scans the input τ from left to right (Line 2). It tries to push each newly read element τ(i) to a pile with a top element larger than or equal to τ(i). If on the one hand there is no such a pile, Patience Sorting creates a new pile to which it pushes τ(i) (Line 4). On the other hand, if at least one such pile exists, Patience Sorting pushes τ(i) to the oldest pile that satisfies the property (Line 6). After the scan, the number of piles is the output, which happens to be equal to lis(τ) (Line 8).

We return to the sequence τ₁ = 〈2, 8, 4, 9, 5, 1, 7, 6, 3〉 for an example. The following illustration shows the execution of Algorithm 1 on τ₁. In each step the bold number is the newly added element. The underlined elements in the final piles form a longest increasing subsequence τ₁[1, 3, 5, 8] = 〈2, 4, 5, 6〉, which can be extracted as described below.

$$\begin{array}{c} \textbf{2} \\ P_{1} \end{array} \begin{array}{cc} 2 & \textbf{8} \\ P_{1} & P_{2} \end{array} \begin{array}{cc} &\\ & \textbf{4} \\ 2 & 8 \\ P_{1} & P_{2} \end{array} \begin{array}{ccc} &&\\ & 4 & \\ 2 & 8 & \textbf{9} \\ P_{1} & P_{2} & P_{3} \end{array} \begin{array}{ccc} &&\\ & 4 & \textbf{5} \\ 2 & 8 & 9 \\ P_{1} & P_{2} & P_{3} \end{array} \begin{array}{ccc} &&\\ \textbf{1} & 4 & 5 \\ 2 & 8 & 9 \\ P_{1} & P_{2} & P_{3} \end{array} \begin{array}{cccc} &&&\\ 1 & 4 & 5 & \\ 2 & 8 & 9 & \textbf{7} \\ P_{1} & P_{2} & P_{3} & P_{4} \end{array} \hfill \begin{array}{cccc} &&&\\ 1 & 4 & 5 & \textbf{6} \\ 2 & 8 & 9 & 7 \\ P_{1} & P_{2} & P_{3} & P_{4} \end{array} \begin{array}{cccc} & \textbf{3} & & \\ 1 & {\underline{4}} & {\underline{5}} & {\underline{6}} \\ {\underline{2}} & 8 & 9 & 7 \\ P_{1} & P_{2} & P_{3} & P_{4} \end{array} $$

Proposition 3.1 ([2, 17, 37])

Given a sequenceτof lengthn,Patience Sortingcomputeslis(τ) inO(n log n) time usingO(n log n) bits of working space.

3.1 Correctness of Patience Sorting

It is observed in [8] that when the input is a permutation π, the elements of each pile form a decreasing subsequence of π. This observation easily generalizes as follows.

Observation 3.2

Given a sequence τ, the elements of each pile constructed by Patience Sorting form a non-increasing subsequence of τ.

Hence, any increasing subsequence of τ can contain at most one element in each pile. This implies that lis(τ) ≤ ℓ.

Now we show that lis(τ) ≥ ℓ. Using the piles, we can obtain an increasing subsequence of length ℓ, in reversed order, as follows [2]:

• 1. Pick an arbitrary element of P_ℓ;

• 2. For 1 ≤ i < ℓ, let τ(h) be the element picked from P_i+ 1. Pick the element τ(h^′) that was the top element of P_i when τ(h) was pushed to P_i+ 1.

Since h^′ < h and τ(h^′) < τ(h) in each iteration, the ℓ elements that are selected form an increasing subsequence of τ. This completes the correctness proof for Patience Sorting.

The proof above can be generalized to show the following characterization for the piles.

Proposition 3.3 ([8])

τ(i) ∈ P_jif and only if a longest increasing subsequence ofτending atτ(i) has lengthj.

3.2 Time and Space Complexity of Patience Sorting

Observe that at any point in time, the top elements of the piles are ordered increasingly from left to right. Namely, $\texttt {top}(P_{k}) < \texttt {top}(P_{k^{\prime }})$ if k < k^′. This is observed in [8] for inputs with no repeated elements. We can see that the statement holds also for inputs with repetitions.

Observation 3.4

At any point in time during the execution of Patience Sorting and for any k and k^′ with 1 ≤ k < k^′≤ ℓ, we have $\texttt {top}(P_{k}) < \texttt {top}(P_{k^{\prime }})$ if P_k and $P_{k^{\prime }}$ are nonempty.

Proof

We prove the statement by contradiction. Let i be the first index for which Patience Sorting pushes τ(i) to some pile P_j, so that the statement of the observation becomes false.

First assume that $\texttt {top}(P_{j}) \ge \texttt {top}(P_{j^{\prime }})$ for some j^′ > j. Let τ(i^′) be the element in P_j pushed to the pile right before τ(i). By the definition of Patience Sorting, it holds that

$$\tau(i^{\prime}) \ge \tau(i) = \texttt{top}(P_{j}) \ge \texttt{top}(P_{j^{\prime}}). $$

This contradicts the minimality of i because τ(i^′) was the top element of P_j before τ(i) was pushed to P_j.

Next assume that $\texttt {top}(P_{j^{\prime }}) \ge \texttt {top}(P_{j})$ for some j^′ < j. This case contradicts the definition of Patience Sorting since $\tau (i) = \texttt {top}(P_{j}) \le \texttt {top}(P_{j^{\prime }})$ and thus τ(i) actually has to be pushed to a pile with an index smaller or equal to j^′. □

The observation above implies that Line 6 of Algorithm 1 can be executed in O(log n) time by using binary search. Hence, Patience Sorting runs in O(n log n) time.

The total number of elements in the piles is O(n). By storing its position in the sequence, each element in the piles can be represented with O(log n) bits (instead of O(log |Σ|) bits, where Σ is the alphabet from which the input elements are taken). Thus Patience Sorting consumes O(n log n) bits in total. If it maintains all elements in the piles, it can compute an actual longest increasing subsequence in the same time and space complexity as described above. Note that to compute lis(τ), it suffices to remember the top elements of the piles. However, the algorithm still uses Ω(n log n) bits when lis(τ) ∈Ω(n).

3.3 A Simple O(n)-bits Algorithm for Permutations

Here we observe that, when the input is a permutation π of {1,…,n}, lis(π) can be computed in O(n²) time with O(n) bits of working space. The algorithm maintains a used/unused flag for each element of {1,…,n} assuming that each element appears exactly once in the sequence. Hence, this algorithm cannot be applied to general inputs where repetitions may happen and the alphabet size |Σ| can be much larger than the input length n.

Let τ be a sequence of integers without repetitions. A subsequence τ[i₁,…,i_ℓ] is the left-to-right minima subsequence if {i₁,…,i_ℓ} = {i : τ(i) = min{τ(j) : 1 ≤ j ≤ i}}. In other words, the left-to-right minima subsequence is made by scanning τ from left to right and greedily picking elements to construct a maximal decreasing subsequence.

Burstein and Lankham [8, Lemma 2.9] showed that the first pile P₁ is the left-to-right minima subsequence of π and that the i th pile P_i is the left-to-right minima subsequence of a sequence obtained from π by removing all elements in the previous piles P₁,…,P_i− 1.

Algorithm 2 below uses this characterization of piles. The correctness follows directly from the characterization. It uses a constant number of pointers of O(log n) bits and a Boolean table of length n for maintaining “used” and “unused” flags. Thus it uses n + O(log n) bits working space in total. The running time is O(n²): each for-loop takes O(n) time and the loop is repeated at most n times.

4 An Algorithm for Computing the Length

In this section, we present our main algorithm that computes lis(τ) with O(s log n) bits in $O\left (\frac {1}{s} \cdot n^{2} \log n\right )$ time for $\sqrt {n} \le s \le n$. Note that the algorithm here outputs the length lis(τ) only. The next section discusses efficient solutions to actually compute a longest sequence.

In the following, by P_i for some i we mean the i th pile obtained by (completely) executing Patience Sorting unless otherwise stated. (We sometimes refer to a pile at some specific point of the execution). Also, by P_i(j) for 1 ≤ j ≤|P_i| we denote the j th element added to P_i. That is, P_i(1) is the first element added to P_i and P_i(|P_i|) is the top element of P_i.

To avoid mixing up repeated elements, we assume that each element τ(j) of the piles is stored with its index j. In the following, we mean by “τ(j) is in P_i” that the j th element of τ is pushed to P_i. Also, by “τ(j) is P_i(r)” we mean that the j th element of τ is the r th element of P_i.

We start with an overview of our algorithm. It scans over the input O(n/s) times. In each pass, it assumes that a pile P_i with at most s elements is given, which has been computed in the previous pass. Using this pile P_i, it filters out the elements in the previous piles P₁,…,P_i− 1. It then basically simulates Patience Sorting but only in order to compute the next 2s piles. As a result of the pass, it computes a new pile P_j with at most s elements such that j ≥ i + s.

The following observation, that follows directly from the definition of Patience Sorting and Observation 3.4, will be useful for the purpose of filtering out elements in irrelevant piles.

Observation 4.1

Let τ(y) ∈ P_j with j≠i. If τ(x) was the top element of P_i when τ(y) was pushed to P_j, then j < i if τ(y) < τ(x), and j > i if τ(y) > τ(x).

Using Observation 4.1, we can obtain the following algorithmic lemma that plays an important role in the main algorithm.

Lemma 4.2

Having storedP_iexplicitly in the additional memory and given an indexj > i, the size |P_k| for alli + 1 ≤ k ≤ min{j,lis(τ)} can be computed inO(n log n) time withO((|P_i| + j − i)log n) bits. Iflis(τ) < j, then we can computelis(τ) in the same time and space complexity.

Proof

Recall that Patience Sorting scans the sequence τ from left to right and puts each element to the appropraiate pile. We process the input in the same way except that we filter out, and thereby ignore, the elements in the piles P_h for which h < i or h > j.

To this end, we use the following two filters whose correctness follows from Observation 4.1.

(FilteringP_hwithh < i). To filter out the elements that lie in P_h for some h < i, we maintain an index r that points to the element of P_i read most recently in the scan. Since P_i is given explicitly to the algorithm, we can maintain such a pointer r.

When we read a new element τ(x), we have three cases.

• If τ(x) is P_i(r + 1), then we increment the index r.

• Else if τ(x) < P_i(r), then τ(x) is ignored since it is in P_h for some h < i.

• Otherwise we have τ(x) > P_i(r). In this case τ(x) is in P_h for some h > i.

(FilteringP_hwithh > j). The elements in P_h for h > j can be filtered without maintaining additional information as follows. Let again τ(x) be the newly read element.

• If no part of P_j has been constructed yet, then τ(x) is in P_h for some h ≤ j.

• Otherwise, we compare τ(x) and the element τ(y) currently on the top of P_j.

  • If τ(x) > τ(y), then τ(x) is in P_h for some h > j, and thus ignored.

  • Otherwise τ(x) is in P_h for some h ≤ j.

We simulate Patience Sorting only for the elements that pass both filters above. While doing so, we only maintain the top elements of the piles and additionally store the size of each pile. This requires at most O((j − i)log n) space, as required by the statement of the lemma. For details see Algorithm 3.

The running time remains the same since we only need constant number of additional steps for each step in Patience Sorting to filter out irrelevant elements. If P_j is still empty after this process, we can conclude that lis(τ) is the index of the newest pile constructed. □

The proof of Lemma 4.2 can be easily adapted to also compute the pile P_j explicitly. For this, we simply additionally store all elements of P_j as they are added to the pile.

Lemma 4.3

GivenP_iand an indexj such thati < j ≤ lis(τ), we can computeP_jinO(n log n) time withO((|P_i| + |P_j| + j − i)log n) bits.

Assembling the lemmas of this section, we now present our first main result. The corresponding pseudocode of the algorithm can be found in Algorithm 4.

Theorem 4.4

There is an algorithm that, given an integers satisfying$\sqrt {n} \le s \le n$anda sequenceτof length n, computes lis(τ) in$O\left (\frac {1}{s} \cdot n^{2} \log n\right )$timewithO(s log n) bits of space.

Proof

To apply Lemmas 4.2 and 4.3 at the beginning, we start with a dummy pile P₀ with a single dummy entry P₀(1) = −∞. In the following, assume that for some i ≥ 0 we computed the pile P_i of size at most s explicitly. We repeat the following process until we find lis(τ).

In each iteration, we first compute the size |P_k| for i + 1 ≤ k ≤ i + 2s. During this process, we may find lis(τ) < i + 2s. In such a case we output lis(τ) and terminate. Otherwise, we find an index j such that i + s + 1 ≤ j ≤ i + 2s and |P_j|≤ n/s. Since $s \ge \sqrt {n}$, it holds that $|P_{j}| \le n/\sqrt {n} = \sqrt {n} \le s$. We then compute P_j itself to replace i with j and repeat.

By Lemmas 4.2 and 4.3, each pass can be executed in O(n log n) time with a working space of O(s log n) bits. There are at most lis(τ)/s iterations, since in each iteration the index i increases by at least s or lis(τ) is determined. Since lis(τ) ≤ n, the total running time is $O\left (\frac {1}{s} \cdot n^{2} \log n\right )$. □

In the case of the smallest memory consumption we conclude the following corollary.

Corollary 4.5

Given a sequenceτof lengthn,lis(τ) can be computed inO (n^1.5 log n) time with$O\left (\sqrt {n} \log n\right )$bitsof space.

5 An Algorithm for Finding a Longest Increasing Subsequence

It is easy to modify the algorithm in the previous section in such a way that it outputs an element of the final pile P_lis(τ), which is the last element of a longest increasing subsequence by Proposition 3.3. Thus we can repeat the modified algorithm n times (considering only the elements smaller than and appearing before the last output) and actually find a longest increasing subsequence.¹ The running time of this naïve approach is $O\left (\frac {1}{s} \cdot n^{3} \log n\right )$.

As we claimed before, we can do much better. In fact, we need only an additional multiplicative factor of O(log n) instead of O(n) in the running time, while keeping the space complexity as it is. In the rest of this section, we prove the following theorem.

Theorem 5.1

There is an algorithm that, given an integers satisfying$\sqrt {n} \le s \le n$anda sequenceτof length n, computes a longest increasing subsequence ofτin$O(\frac {1}{s} \cdot n^{2} \log ^{2} n)$timeusingO(s log n) bits of space.

Corollary 5.2

Given a sequenceτof lengthn, a longest increasing subsequence ofτcan be found inO (n^1.5 log²n) time with$O\left (\sqrt {n} \log n\right )$bitsof space.

We should point out that the algorithm in this section is not a multi-pass algorithm. However, we can easily transform it without any increase in the time and space complexity so that it works as a sequential access algorithm.

5.1 High-Level Idea

We first find an element that is in a longest increasing subsequence roughly in the middle. As we will argue, this can be done in $O\left (\frac {1}{s} \cdot n^{2} \log n\right )$ time with O(s log n) bits by running the algorithm from the previous section twice, once in the ordinary then once in the reversed way. We then divide the input into the left and right parts at a near-mid element and recurse.

The space complexity remains the same and the time complexity increases only by an O(log n) multiplicative factor. The depth of recursion is O(log n) and at each level of recursion the total running time is $O\left (\frac {1}{s} \cdot n^{2} \log n\right )$. To remember the path to the current recursion, we need some additional space, but it is bounded by O (log²n) bits.

5.2 A Subroutine for Short Longest Increasing Sequences

We first solve the base case in which lis(τ) ∈ O(n/s). In this case, we use the original Patience Sorting and repeat it O(n/s) times. We present the following general form first.

Lemma 5.3

Letτbe a sequences of lengthn andlis(τ) = k. Then a longest increasing subsequence ofτcan be found inO(k ⋅ n log k) time withO(k log n) bits.

Proof

Without changing the time and space complexity, we can modify the original Patience Sorting so that

• it maintains only the top elements of the piles;

• it ignores the elements larger than or equal to a given upper bound; and

• it outputs an element in the final pile.

We run the modified algorithm lis(τ) times. In the first run, we have no upper bound. In the succeeding runs, we set the upper bound to be the output of the previous run. In each run the input to the algorithm is the initial part of the sequence that ends right before the last output. The entire output forms a longest increasing sequence of τ.²

Since lis(τ) = k, modified Patience Sorting maintains only k piles. Thus each run takes O(n log k) time and uses O(k log n) bits. The lemma follows since this is repeated k times and each round only stores O(log n) bits of information from the previous round. □

The following special form of the lemma above holds since n/s ≤ s when $s \ge \sqrt {n}$.

Corollary 5.4

Letτbe a sequence of lengthn andlis(τ) ∈ O(n/s) for somes with$\sqrt {n} \le s \le n$. A longest increasing subsequence ofτcan be found in$O\left (\frac {1}{s} \cdot n^{2} \log n\right )$timewithO(s log n) bits.

5.3 A Key Lemma

As mentioned above, we use a reversed version of our algorithm. Reverse Patience Sorting is the reversed version of Patience Sorting: it reads the input from right to left and uses the reversed inequalities. (See Algorithm 5). Reverse Patience Sorting computes the length of a longest decreasing subsequence in the reversed sequence, which is a longest increasing subsequence in the original sequence. Since the difference between the two algorithms is small, we can easily modify our algorithm in Section 4 for the length so that it simulates Reverse Patience Sorting instead of Patience Sorting.

Let Q_i be the i th pile constructed by Reverse Patience Sorting as in Algorithm 5. Using Proposition 3.3, we can show that for each τ(i) in Q_j, the longest decreasing subsequence of the reversal of τ ending at τ(i) has length j. This is equivalent to the following observation.

Observation 5.5

τ(i) ∈ Q_j if and only if a longest increasing subsequence of τ starting at τ(i) has length j.

This observation immediately gives the key lemma below.

Lemma 5.6

P_k ∩ Q_{lis(τ)−k+ 1} ≠ ∅for allk with 1 ≤ k ≤lis(τ).

Proof

Let 〈τ(i₁),…,τ(i_ℓ)〉 be a longest increasing subsequence of τ. Proposition 3.3 implies that τ(i_k) ∈ P_k. The subsequence 〈τ(i_k),…,τ(i_ℓ)〉 is a longest increasing subsequence of τ starting at τ(i_k) since otherwise 〈τ(i₁),…,τ(i_ℓ)〉 is not longest. Since the length of 〈τ(i_k),…,τ(i_ℓ)〉 is i_ℓ − k + 1 = lis(τ) − k + 1, it holds that τ(k) ∈ Q_{lis(τ)−k+ 1}. □

Note that the elements of P_k and Q_{lis(τ)−k+ 1} are not the same in general. For example, by applying Reverse Patience Sorting to τ₁ = 〈2,8,4,9,5,1,7,6,3〉, we get Q₁ = 〈3,6,7,9〉, Q₂ = 〈1,5,8〉, Q₃ = 〈4〉, and Q₄ = 〈2〉 as below. (Recall that P₁ = 〈2,1〉, P₂ = 〈8,4,3〉, P₃ = 〈9,5〉, and P₄ = 〈7,6〉). The following diagram depicts the situation. The elements shared by P_k and Q_{lis(τ)−k+ 1} are underlined.

$$\begin{array}{c} \textbf{3} \\ Q_{1} \end{array} \begin{array}{c} \textbf{6} \\ 3 \\ Q_{1} \end{array} \begin{array}{c} \textbf{7} \\ 6 \\ 3 \\ Q_{1} \end{array} \hfill \begin{array}{cc} &\\ 7 \\ 6 \\ 3 & \textbf{1} \\ Q_{1} & Q_{2} \end{array} \begin{array}{cc} &\\ 7 \\ 6 & \textbf{5} \\ 3 & 1 \\ Q_{1} & Q_{2} \end{array} \begin{array}{cc} \textbf{9} \\ 7 \\ 6 & 5 \\ 3 & 1 \\ Q_{1} & Q_{2} \end{array} \begin{array}{ccc} 9 \\ 7 \\ 6 & 5 \\ 3 & 1 & \textbf{4} \\ Q_{1} & Q_{2} & Q_{3} \end{array} \begin{array}{ccc} 9 \\ 7 & \textbf{8} \\ 6 & 5 \\ 3 & 1 & 4 \\ Q_{1} & Q_{2} & Q_{3} \end{array} \begin{array}{cccc} 9 \\ {\underline{7}} & 8 \\ {\underline{6}} & {\underline{5}} \\ 3 & 1 & {\underline{4}} & {\textbf{\underline{2}}} \\ Q_{1} & Q_{2} & Q_{3} & Q_{4} \end{array} \begin{array}{cccc} &&&\\ & 3 & & \\ 1 & {\underline{4}} & {\underline{5}} & {\underline{6}} \\ {\underline{2}} & 8 & 9 & {\underline{7}} \\ P_{1} & P_{2} & P_{3} & P_{4} \end{array} $$

5.4 The Algorithm

We first explain the subroutine for finding a near-mid element in a longest increasing subsequence.

Lemma 5.7

Lets be an integer satisfying$\sqrt {n} \le s \le n$. Given a sequenceτof length n, thekth element of a longest increasing subsequence ofτfor somek withlis(τ)/2 ≤ k < lis(τ)/2 + n/scan be found in$O\left (\frac {1}{s} \cdot n^{2} \log n\right )$timeusingO(s log n) bits of space.

Proof

We slightly modify Algorithm 4 so that it finds an index k and outputs P_k such that |P_k|≤ s and lis(τ)/2 ≤ k ≤lis(τ)/2 + n/s. Such a k exists since the average of |P_i| for lis(τ)/2 ≤ i < lis(τ)/2 + n/s is at most s. The time and space complexity of this phase are as required by the lemma.

We now find an element in P_k ∩ Q_{lis(τ)−k+ 1}. Since the size |Q_{lis(τ)−k+ 1}| is not bounded by O(s) in general, we cannot store Q_{lis(τ)−k+ 1} itself. Instead use the reversed version of the algorithm in Section 4 to enumerate it. Each time we find an element in Q_{lis(τ)−k+ 1}, we check whether it is included in P_k. This can be done with no loss in the running time since P_k is sorted and the elements of Q_{lis(τ)−k+ 1} arrive in increasing order. □

The next technical but easy lemma allows us to split the input into two parts at an element of a longest increasing subsequence and to solve the smaller parts independently.

Lemma 5.8

Letτ(j) be thekth element of a longest increasing subsequence of asequenceτ. Letτ_Lbe the subsequence ofτ[1,…,j − 1] formed by the elements smaller thanτ(j). Similarly letτ_Rbe the subsequence ofτ[j + 1,…,|τ|] formed by the elements larger thanτ(j). Then, a longest increasing subsequence ofτcan be obtained by concatenating a longest increasing subsequence ofτ_L, τ(j), and a longest increasing subsequence ofτ_R, in this order.

Proof

Observe that the concatenated sequence is an increasing subsequence of τ. It suffices to show that lis(τ_L) + lis(τ_R) + 1 ≥lis(τ). Let τ[i₁,…,i_lis(τ)] be a longest increasing subsequence of τ such that i_k = j. From the definition, τ[i₁,…,i_k− 1] is a subsequence of τ_L, and τ[i_k+ 1,…,i_lis(τ)] is a subsequence of τ_R. Hence lis(τ_L) ≥ k − 1 and lis(τ_R) ≥lis(τ) − k, and thus lis(τ_L) + lis(τ_R) + 1 ≥lis(τ). □

As Lemma 5.8 suggests, after finding a near-mid element τ(k), we recurse into τ_L and τ_R. If the input τ^′ to a recursive call has small lis(τ^′), we directly compute a longest increasing subsequence. See Algorithm 6 for details of the whole algorithm. Correctness follows from Lemma 5.8 and correctness of the subroutines.

5.5 Time and Space Complexity

In Theorem 5.1, the claimed running time is $O\left (\frac {1}{s} \cdot n^{2} \log ^{2} n\right )$. To prove this, we first show that the depth of the recursion is O(log n). We then show that the total running time in each recursion level is $O\left (\frac {1}{s} \cdot n^{2} \log n\right )$. The claimed running time is guaranteed by these bounds.

Lemma 5.9

Given a sequenceτ, the depth of the recursions invoked byRecursiveLISof Algorithm 6 is atmost log_6/5lis(τ^′), whereτ^′is the subsequence ofτcomputed in Line3.

Proof

We proceed by induction on lis(τ^′). If lis(τ^′) ≤ 3|τ^′|/s, then no recursive call occurs, and hence the lemma holds. In the following, we assume that lis(τ^′) = ℓ > 3|τ^′|/s and that the statement of the lemma is true for any sequence τ^″ with lis(τ^″) < ℓ.

Since ℓ > 3|τ^′|/s, Algorithm 6 recurses into two branches on subsequences of τ^′. From the definition of k in Line 8 of Algorithm 6, the length of a longest increasing subsequence is less than ℓ/2 + |τ^′|/s in each branch. Since ℓ/2 + |τ^′|/s < ℓ/2 + ℓ/3 = 5ℓ/6, each branch invokes recursions of depth at most log6/5(5ℓ/6) = log6/5ℓ − 1. Therefore, the maximum depth of the recursions invoked by their parent is at most log6/5ℓ. □

Lemma 5.10

Given a sequenceτof lengthn, the total running time at each depth ofrecursion excluding further recursive calls in Algorithm 6 takes$O\left (\frac {1}{s} n^{2} \log n\right )$time.

Proof

In one recursion level, we have many calls of RecursiveLIS on pairwise non-overlapping subsequences of τ. For each subsequence τ^′, the algorithm spends time $O\left (\frac {1}{s} |\tau ^{\prime }|^{2} \log |\tau ^{\prime }|\right )$. Thus the total running time at a depth is $O\left ({\sum }_{\tau ^{\prime }} \frac {1}{s} |\tau ^{\prime }|^{2} \log |\tau ^{\prime }|\right )$, which is $O\left (\frac {1}{s} n^{2} \log n\right )$ since ${\sum }_{\tau ^{\prime }} |\tau ^{\prime }|^{2} \le |\tau |^{2} = n^{2}$. □

Finally we consider the space complexity of Algorithm 6.

Lemma 5.11

Algorithm 6 usesO(s log n) bits of working space on sequences of length n.

Proof

We have already shown that each subroutine uses O(s log n) bits. Moreover, this space of working memory can be discarded before another subroutine call occurs. Only a constant number of O(log n)-bit words are passed to the new subroutine call. We additionally need to remember the stack trace of the recursion. The size of this additional information is bounded by O(log²n) bits since each recursive call is specified by a constant number of O(log n)-bit words and the depth of recursion is O(log n) by Lemma 5.9. Since log²n ∈ O(s log n) for $s \ge \sqrt {n}$, the lemma holds. □

6 Lower Bound for Algorithms with Sequential Access

An algorithm is a sequential access algorithm if it can access elements in the input array only sequentially. In our situation this means that for a given sequence, accessing the i th element of the sequence directly after having accessed the j th element of the sequence costs time at least linear in |i − j|. As opposed to the RAM, any Turing machine in which the input is given on single read-only tape has this property. Note that any lower bound for sequential access algorithms in an asymptotic form is applicable to multi-pass algorithms as well since every multi-pass algorithm can be simulated by a sequential access algorithm with the same asymptotic behavior. Although some of our algorithms are not multi-pass algorithms, it is straightforward to transform them to sequential access algorithms with the same time and space complexity.

To show a lower bound on the running time of sequential access algorithms with limited working space, we need the concept of communication complexity (see [21] for more details). Let f be a function. Given $\alpha \in \mathcal {A}$ to the first player Alice and $\beta \in \mathcal {B}$ to the second player Bob, the players want to compute f(α,β) together by sending bits to each other (possibly multiple times). The communication complexity of f is the maximum number of bits transmitted between Alice and Bob over all inputs by the best protocol for f.

Consider the following variant of the LIS problem: Alice gets the first half of a permutation π of {1,…,2n} and Bob gets the second half. They compute lis(π) together. It is known that this problem has high communication complexity [19, 22, 38].

Proposition 6.1Proposition 6.1 ([19, 38])

Letπbe a permutation of {1,…,2n}. Given the first half ofπto Alice and the second half to Bob, they needΩ(n) bits of communication to compute lis(π) in the worst case (even with 2-sided error randomization).

Now we present our lower bound. Note that the lower bound even holds for the special case where input is restricted to permutations.

Theorem 6.2

Given a permutationπof {1,…,4n}, any sequential access (possibly randomized) algorithm computinglis(π) using b bits takes Ω(n²/b) time.

Proof

Given an arbitrary n > 1, let π^′ be a permutation of {1,…,2n}. We construct a permutation π of {1,…,4n} as follows. Let ${\pi }_{1}^{\prime } = \langle {\pi (1),\dots ,\pi (n)}\rangle$ be the first half of π^′, define ${\pi }_{2}^{\prime } = \langle {4n,4n-1,\dots , 2n + 2}\rangle$ and let ${\pi }_{3}^{\prime } =\langle {\pi (n + 1),\pi (n + 2),\ldots ,\pi (2n)}\rangle$ be the second half of π^′. Then we define π to be the concatenation of ${\pi }_{1}^{\prime }$, ${\pi }_{2}^{\prime }$, ${\pi }_{3}^{\prime }$ and the one element sequence ${\pi }_{4}^{\prime } =\langle {2n + 1}\rangle$, in that order.

It is not difficult to see that π is a permutation and that lis(π) = lis(π^′) + 1. To see the latter, observe that the concatenation of ${\pi }_{2}^{\prime }$ and ${\pi }_{4}^{\prime }$ is a decreasing subsequence of π. Hence any increasing subsequence of π can contain at most one element not in π^′. On the other hand, any increasing subsequence of π^′ of length ℓ can be extended with the element 2n + 1 of ${\pi }_{4}^{\prime }$ to an increasing subsequence of π of length ℓ + 1.

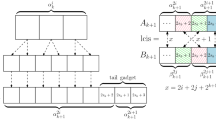
We say a sequential access algorithm traverses the middle if it accesses a position in ${\pi }_{1}^{\prime }$ and then accesses a position in ${\pi }_{3}^{\prime }$ or vice versa with possibly accessing elements in ${\pi }_{2}^{\prime }$ but only such elements in meantime. Since each traversal of the middle takes Ω(n) time, it suffices to show that the number of traversals of the middle is Ω(n/b).

Suppose we are given a sequential access algorithm M that computes lis(π) with t traversals of the middle. Using M, we construct a two-player communication protocol for computing lis(π^′) with at most tb bits of communication. (A similar technique is described for streaming algorithms in [38]).

Recall that the first player Alice gets the first half ${\pi }_{1}^{\prime }$ of π^′ and the second player Bob gets the second half ${\pi }_{3}^{\prime }$ of π^′. They compute lis(π^′) together as follows.

• Before starting computation, Alice computes π_A by concatenating ${\pi }_{1}^{\prime }$ and ${\pi }_{2}^{\prime }$ in that order, and Bob computes π_B by concatenating ${\pi }_{2}^{\prime }$, ${\pi }_{3}^{\prime }$, and ${\pi }_{4}^{\prime }$ in that order.

• They first compute lis(π) using M by repeating the following phases:

  • Alice starts the computation by M and continues while M stays in π[1,…,3n − 1] = π_A. When M tries to access π[3n,…,4n], and thus a traversal of the middle occurs, Alice stops and sends all b bits stored by M to Bob.

  • Bob restores the b bits received from Alice to the working memory of M and continues computation while M stays in π[n + 1,…,4n] = π_B. A traversal of the middle is occurred when M tries to access π[1,…,n]. Bob then stops and sends the b bits currently stored by M back to Alice.

• When M outputs lis(π) and terminates, the currently active player outputs lis(π) − 1 as lis(π^′) and terminates the protocol.

The two players correctly simulate M and, as a result, compute lis(π^′) together. Since the algorithm M invokes t traversals, the total number of bits sent is at most tb. Since tb ∈Ω(n) holds by Proposition 6.1, we have t ∈Ω(n/b) as required. □

Recall that our algorithms for the LIS problem use O(s log n) bits and run in $O(\frac {1}{s} n^{2} \log n)$ time for computing the length and in $O(\frac {1}{s} n^{2} \log ^{2} n)$ time for finding a subsequence, where $\sqrt {n} \le s \le n$. By Theorem 6.2, their time complexity is optimal for algorithms with sequential access up to polylogarithmic factors of log²n and log3n, respectively.

7 Concluding Remarks

Our results in this paper raise the following question:

Can we solve LIS with $o\left (\sqrt {n}\right )$-space in polynomial time?

Observe that an unconditional ‘no’ implies that SC ≠ P ∩PolyL, where SC (Steve’s Class) is the class of problems that can be solved by an algorithm that simultaneously runs in polynomial-time and polylogarithmic-space [11, 29]. As a conditional lower bound, we can use the (hypothetical) hardness of Longest Common Subsequence (LCS). Given two strings, LCS asks to find a longest sequence that is a subsequence of both strings. It is easy to see that a longest increasing subsequence of a sequence τ can be computed as a longest common subsequence of τ and the sequence obtained by sorting τ. The other direction is not that obvious, but there is a reduction from LCS on strings of length n to LIS on a string of length at most n² [20]. The reduction can be easily implemented in log-space. This implies that an O(f(n))-space polynomial-time algorithm for LIS can be used as an O(f(n²))-space polynomial-time algorithm for LCS. In particular, an $O(\sqrt {n}^{1-\epsilon })$-space polynomial-time algorithm for LIS gives an O(n^1−𝜖)-space polynomial-time algorithm for LCS for any 𝜖 > 0, and a log-space algorithm for LIS implies a log-space algorithm for LCS.

To make the presentation simple, we used the length n of τ to bound lis(τ) in the time complexity analyses of the algorithms. If we analyze the complexity in terms of lis(τ) instead of n when possible, we can obtain the following output-sensitive bounds.

Theorem 7.1

Lets be an integer satisfying$\sqrt {n} \le s \le n$, and letτbe a sequence of lengthn withlis(τ) = k. UsingO(s log n) bits of space,lis(τ) can be computed in$O\left (\frac {1}{s} \cdot k n \log k\right )$timeand a longest increasing subsequence ofτcan be found in$O\left (\frac {1}{s} \cdot k n \log ^{2} k\right )$time.