Exact Algorithms for the Bounded Repetition Longest Common Subsequence Problem

Abstract

In this paper, we study exact, exponential-time algorithms for a variant of the classic Longest Common Subsequence problem called the r-Repetition Longest Common Subsequence problem (or r-RLCS, for short): Given two sequences X and Y over an alphabet S, find a longest common subsequence of X and Y such that each symbol appears at most r times in the obtained subsequence. Without loss of generality, we will assume that $|X| \le |Y|$ from here on. The special case of 1-RLCS, also known as the Repetition-Free Longest Common Subsequence problem (RFLCS), has been studied previously; e.g., in [1], Adi et al. presented an (exponential-time) integer linear programming-based exact algorithm for 1-RLCS. However, they did not analyze its time complexity, and to the best of our knowledge, there are no previous results on the running times of any exact algorithms for this problem. In this paper, we first propose a simple algorithm for 1-RLCS based on the strategy used in [1] and show explicitly that its running time is bounded by $O(1.44225^{|X|}|X||Y|)$. Next, we provide a DP-based algorithm for r-RLCS and prove that its running time is $O((r+1)^{|X|/(r+1)}|X||Y|)$ for any $r \ge 1$. In particular, our new algorithm runs in $O(1.41422^{|X|}|X||Y|)$ time for 1-RLCS, which is faster than the previous one.

1 Introduction

An alphabet S is a finite set of symbols. Let X be a sequence over the alphabet S and |X| be the length of the sequence X. For example, $X = \langle x_1, x_2, \cdots , x_n\rangle$ is a sequence of length n, where $x_i \in S$ for $1\le i\le n$, i.e., $|X| = n$. For a sequence $X = \langle x_1, x_2, \cdots , x_n\rangle$, another sequence $Z = \langle z_1, z_2, \cdots , z_c\rangle$ is a subsequence of X if there exists a strictly increasing sequence $\langle i_1, i_2, \cdots , i_c\rangle$ of indices of X such that for all $j = 1, 2, \cdots , c$, we have $x_{i_j} = z_{j}$. Then, we say that a sequence Z is a common subsequence of X and Y if Z is a subsequence of both X and Y. Given two sequences X and Y as input, the goal of the Longest Common Subsequence problem (LCS) is to find a longest common subsequence of X and Y.

The problem LCS is clearly a fundamental problem and has a long history [4, 11, 14, 24]. The comparison of sequences via a longest common subsequence has been applied in several contexts where we want to find the maximum number of symbols that appear in the same order in two sequences. The problem LCS is considered as one of the important computational primitive, and thus has a variety of applications such as bioinformatics [3, 18, 20], data compression [23], spelling correction [19, 24], and file comparison [2].

The problem LCS of two sequences has been deeply investigated, and polynomial time algorithms are well-known [14, 15, 20, 21, 24]. It is possible to generalize LCS to a set of three or more sequences; the goal is to compute a longest common subsequence of all input sequences. This LCS of multiple sequences is NP-hard even on binary alphabet [17] and it is not approximable within factor $O(n^{1-\varepsilon })$ on arbitrary alphabet for sequences of length n and any constant $\varepsilon > 0$ [18]. Furthermore, some researchers introduced a constraint on the number of symbol occurrences in the solution. Bonizzoni, Della Vedova, Dondi, Fertin, Rizzi and Vialette considered the Exemplar Longest Common Subsequence problem (ELCS) [9, 22]. In ELCS, an alphabet S of symbols is divided into the mandatory alphabet $S_m$ and the optional alphabet $S_{o}$, and ELCS restricts the number of symbol occurrences in $S_{m}$ and $S_{o}$ in the obtained solution. The problem ELCS is APX-hard even for instances of two sequences [9]. In [10], Bonizzoni, Della Vedova, Dondi and Pirola proposed the following Doubly-Constrained Longest Common Subsequence problem (DCLCS): Let a sequence constraint C be a set of sequences over an alphabet S and let an occurrence constraint $C_{occ}$ be a function $C_{occ}: S\rightarrow \mathbb {N}$, assigning an upper bound on the number of occurrences of each symbol in S. Given two sequences X and Y over an alphabet S, a sequence constraint C and an occurrence constraint $C_{occ}$, the goal of DCLCS is to find a longest common subsequence Z of X and Y, so that each sequence in C is a subsequence of Z and Z contains at most $C_{occ}(s)$ occurrences of each symbol $s \in S$. Bonizzoni et al. showed that DCLCS is NP-hard over an alphabet of three symbols [10]. Adi, Braga, Fernandes, Ferreira, Martinez, Sagot, Stefanes, Tjandraatmadja, and Wakabayashi introduced the Repetition-Free Longest Common Subsequence problem (RFLCS) [1]: Given two sequences X and Y over an alphabet S, the goal of RFLCS is to find a longest common subsequence of X and Y, where each symbol appears at most once in the obtained subsequence. In [1], Adi et al. proved that RFLCS is APX-hard even if each symbol appears at most twice in each of the given sequences.

In this paper we study exact, exponential-time algorithms for RFLCS and its variant, called the r-Repetition Longest Common Subsequence problem (r-RLCS for short): Given two sequences X and Y over an alphabet S, the goal of r-RLCS is to find a longest common subsequence of X and Y, where each symbol appears at most r times in the obtained subsequence. Without loss of generality, we will assume that $|X| \le |Y|$ from here on. The special case 1-RLCS is identical to RFLCS. Also, it is easy to see that r-RLCS is a special case of DCLCS when a sequence constraint $C = \emptyset$ and an occurrence constraint $C_{occ}(s) = r$ for every $s\in S$. In [1], Adi et al. presented an (exponential-time) integer linear programming-based exact algorithm for 1-RLCS. However, they did not analyze its time complexity, and to the best of our knowledge, there are no previous results on the running times of any exact algorithms for this problem. In this paper, we first propose a simple algorithm for 1-RLCS based on the strategy used in [1] and show explicitly that its running time is bounded by $O(1.44225^{|X|}|X||Y|)$. Next, we provide a DP-based algorithm for r-RLCS and prove that its running time is $O((r+1)^{|X|/(r+1)}|X||Y|)$ for any $r \ge 1$. In particular, our new algorithm runs in $O(1.41422^{|X|}|X||Y|)$ time for 1-RLCS, which is faster than the previous one.

Related Work. Although this paper focuses on the exact exponential algorithms, we here make a brief survey on previous results for RFLCS, from the viewpoints of heuristic, approximation and parameterized algorithms. In [1], Adi et al. introduced first heuristic algorithms for RFLCS. After that, several metaheuristic algorithms for RFLCS were proposed in [6, 7, 12]. A detailed comparison of those metaheuristic algorithms was given in [8]. As for the approximability of RFLCS, Adi et al. showed [1] that RFLCS admits an $\texttt {occ}_{max}$-approximation algorithm, where $\texttt {occ}_{max}$ is the maximum number of occurrences of each symbol in one of the two input sequences. In [5], Blin, Bonizzoni, Dondi, and Sikora presented a randomized fixed-parameter algorithm for RFLCS parameterized by the size of the solution.

2 Warm-Up Algorithms

For a while, we focus on RFLCS, i.e., 1-RLCS. One can see that the following brute-force exact algorithm for RFLCS can work clearly in $O(2^{n}\cdot n\cdot m)$ time for two sequences X and Y where $|X| =n$, $|Y| = m$, and $|X| \le |Y|$: (i) We first create all the subsequences of X, say, $X_1$ through $X_{2^n}$¹. Then, (ii) we obtain a longest common subsequence of $X_i$ and Y for each i ($1\le i\le 2^n$) by using an $O(|X_i|\cdot m)$-time algorithm for LCS [20, 21, 24]. Finally, (iii) we find a repetition-free longest subsequence among those $2^n$ common subsequences obtained in (ii) and output it. The running time of the brute-force algorithm is $O(2^{n}\cdot n\cdot m)$.

In [1], Adi et al. presented the following quite simple algorithm for RFLCS: Let S be an alphabet of symbols. Suppose that each symbol in $S_{X}\subseteq S$ appears in X fewer times than Y, and $S_{X} = \{s_1, s_2, \cdots , s_{|S_X|}\}$. Also, let $S_{Y} = S\setminus S_{X}$ and $S_{Y} = \{s_{|S_X|+1}, s_{|S_X|+2}, \cdots , s_{|S|}\}$. (i) The algorithm creates all the subsequences, say, $X_1$ through $X_{N_{X}}$, from the input sequence X such that all the symbols in $S_{X}$ occur exactly once, but all the occurrences of symbols in $S_{Y}$ are kept in $X_i$ for every $1\le i\le N_{X}$. Also, the algorithm creates all the subsequences, say, $Y_1$ through $Y_{N_{Y}}$, from the input sequence Y such that all the symbols in $S_{Y}$ occur exactly once, but all the occurrences of symbols in $S_{X}$ are kept in $Y_j$ for every $1\le j\le N_{Y}$. Then, (ii) we obtain a longest common subsequence of $X_i$ and $Y_j$ for every pair of i and j ($1\le i\le N_{X}$ and $1\le j\le N_{Y}$) by using an $O(|X_i|\cdot |Y_j|)$-time algorithm for the original LCS. Finally, (iii) we find the longest subsequence among $N_{X}\cdot N_{Y}$ common subsequences obtained in (ii), which must be repetition-free, and output it. Clearly, the running time of this method is $O(N_{X}\cdot N_{Y}\cdot n\cdot m)$. In [1], Adi et al. only claimed that if the number of symbols which appear twice or more in X and Y is bounded above by some constant, say, c, then the running time is $O(m^c\cdot n\cdot m)$, i.e., RFLCS is solvable in polynomial time. However, no upper bound on $N_{X}\cdot N_{Y}$ was given in [1].

2.1 Repetition-Free LCS

In this section we consider an algorithm called ALG, based on the same strategy as one in [1] for RFLCS: (i) We first create all the subsequences, say, $X_1$ through $X_N$, from the input sequence X such that every symbol appears exactly once in $X_i$ for $1\le i\le N$. Then, (ii) we obtain a longest common subsequence of $X_i$ and Y for each i ($1\le i\le N$). Finally, (iii) we find a repetition-free longest subsequence among N common subsequences obtained in (ii) and output it. Therefore, the running time of ALG is $O(N\cdot n\cdot m)$. It is important to note that ALG is completely the same algorithm as one proposed in [1] if $S_{X} = S$ and thus $S_{Y} = \emptyset$.

A quite simple argument gives us the first upper bound on N:

Theorem 1

The running time of ALG is $O(1.44668^{n}\cdot n\cdot m)$ for RFLCS on two sequences X and Y where $|X| =n$, $|Y| = m$, and $|X| \le |Y|$.

Proof

Suppose that X has k symbols, $s_1$, $s_2$, $\cdots$, $s_k$, and $s_i$ occurs $\texttt {occ}_i$ times in X for each integer i, $1\le i\le k$. Since the number N of subsequences in X created in (i) of ALG is bounded by the number of combinations of k symbols, the following is satisfied:

$$\begin{aligned} N \le \prod ^{k}_{i=1} \texttt {occ}_i. \end{aligned}$$

From the inequality of arithmetic and geometric means, we have:

$$\begin{aligned} N \le \left( (\sum ^{k}_{i=1} \texttt {occ}_i)/k\right) ^{k} \le (n/k)^{k}. \end{aligned}$$

Here, by setting $p \overset{\mathrm {def}}{=} n/k \in \mathbb {R}^{+}$, we have:

$$\begin{aligned} N \le (p)^{n/p} = (p^{1/p})^n. \end{aligned}$$

Note that the value of $p^{1/p}$ becomes the maximum when $p = e$, where e denotes the Euler’s number. Therefore, N is bounded above by $e^{n/e} < 1.44668^{n}$. Therefore, the running time of ALG is $O(1.44668^{n}\cdot n\cdot m)$.    $\square$

By using more refined estimation, we can show a smaller upper bound on N:

Theorem 2

The running time of ALG is $O(1.44225^{n}\cdot n\cdot m)$ for RFLCS on two sequences X and Y where $|X| =n$, $|Y| = m$, and $|X| \le |Y|$.

Proof

Again suppose that X has k symbols, $s_1$, $s_2$, $\cdots$, $s_k$, and $s_i$ occurs $\texttt {occ}_i$ times in X for each integer i, $1\le i\le k$. Let $\max _{1\le i \le k}\left\{ \texttt {occ}_i\right\} = \texttt {occ}_{max}$. Now let $S_i = \{x_j | \texttt {occ}_j = i\}$ for $1\le i\le \texttt {occ}_{max}$. That is, $S_i$ is a set of symbols which appear exactly i times in X. Let $n_i = i\times |S_i|$. Since each symbol in $S_i$ appears i times in X, the following equality holds:

$$\begin{aligned} \sum ^{\texttt {occ}_{max}}_{i = 1} n_i = n. \end{aligned}$$

(1)

In the following, we show a smaller upper bound on N. From the fact that $n_i = i\times |S_i|$, one sees that the following equality holds:

$$\begin{aligned} N \le \prod ^{k}_{i=1} \texttt {occ}_i = \prod ^{\texttt {occ}_{max}}_{i=1} i^{n_i/i}. \end{aligned}$$

(2)

Here, from the inequality of arithmetic and geometric means, the following is obtained:

$$\begin{aligned} \left( \prod ^{\texttt {occ}_{max}}_{i=1} \left( i^{1/i}\right) ^{n_i} \right) ^{1/\sum ^{\texttt {occ}_{max}}_{i=1} n_i} \le \frac{\sum ^{\texttt {occ}_{max}}_{i=1}\left( i^{1/i}\right) \cdot n_i}{\sum ^{\texttt {occ}_{max}}_{i=1} n_i}. \end{aligned}$$

(3)

From the Eqs. (1), (2), and (3), we get:

$$\begin{aligned} N \le \left( \frac{\sum ^{\texttt {occ}_{max}}_{i=1} \left( i^{1/i}\right) \cdot n_i}{n}\right) ^{n}. \end{aligned}$$

(4)

Now, it is important to note that $i\in \mathbb {N}$, i.e., i is a positive integer while $p = n/k$ was a positive real in the proof of the previous theorem. Therefore, by a simple calculation, one can verify that the following is true:

$$\begin{aligned} \max _{i\in \mathbb {N}} \left\{ i^{1/i}\right\} = 3^{1/3}. \end{aligned}$$

Hence, we can bound the number N of all the possible repetition-free common subsequences as follows:

$$\begin{aligned} N \le \left( \frac{\sum ^{\texttt {occ}_{max}}_{i=1} 3^{1/3}\cdot n_i}{n}\right) ^{n} = \left( \frac{3^{1/3} \cdot \sum ^{\texttt {occ}_{max}}_{i=1} n_i}{n}\right) ^{n} = \left( 3^{1/3}\right) ^n < 1.44225^{n}. \end{aligned}$$

As a result, the running time of our algorithm is $O\left( 1.44225^n \cdot n\cdot m\right)$. This completes the proof.    $\square$

Corollary 1

There is an $O(\texttt {occ}^{n/\texttt {occ}}\cdot n\cdot m)$-time algorithm to solve RFLCS for two sequences X and Y where $|X| =n$, $|Y| = m$, and $|X| \le |Y|$ if all the occurrences of symbols in X are exactly occ.

Proof

By the assumption, $\texttt {occ}\times |S_{\texttt {occ}}| = n$ and thus $|S_{\texttt {occ}'}| = 0$ for $\texttt {occ}\ne \texttt {occ}'$. From the inequality (4), one can easily obtain the following:

$$\begin{aligned} N \le \left( \texttt {occ}^{1/\texttt {occ}}\right) ^{n}. \end{aligned}$$

   $\square$

For example, if each symbol appears exactly twice (five and six times, resp.) in the shorter sequence X, then the running time of ALG is $O\left( 1.41422^n\cdot n\cdot m\right)$ ($O\left( 1.37973^n\cdot n\cdot m\right)$ and $O\left( 1.34801^n\cdot n\cdot m\right)$, resp.).

2.2 r-Repetition LCS, $r\ge 2$

In this section we consider exact exponential algorithms for r-RLCS. First, by a straightforward extension of the algorithm for RFLCS, we can design the following algorithm, say, $\texttt {ALG}_{r}$ for r-RLCS: First, (i) we create all the subsequences, say, $X_1$ through $X_N$, from the input sequence X such that a symbol, say, s, appears exactly r times in $X_i$ for $1\le i\le N$ if X has more than k s’s; otherwise, all the occurrences of s in X are included in $X_i$. Then, (ii) we obtain a longest common subsequence of $X_i$ and Y for each i ($1\le i\le N$). Finally, (iii) we find a longest subsequence among N common subsequences obtained in (ii), which has at most r occurrences of every symbol, and output it.

Again, suppose that X has k symbols, $s_1$, $s_2$, $\cdots$, $s_k$, and $s_i$ occurs $\texttt {occ}_i$ times in X for each integer i, $1\le i\le k$, and $\max _{1\le i \le k}\left\{ \texttt {occ}_i\right\} = \texttt {occ}_{max}$. Let $S_i = \{s_j | \texttt {occ}_j = i\}$ for $1\le i\le \texttt {occ}_{max}$ and $n_i = i\times |S_i|$. Then, we estimate an upper bound on N for each r:

Theorem 3

For r-RLCS on two sequences X and Y where $|X| =n$, $|Y| = m$, and $|X| \le |Y|$, the running time of ALG$_r$ is as follows:

$$\begin{aligned} O\left( \left( \max _{i\in \mathbb {N}}\left\{ \left( \frac{i-\frac{r-1}{2}}{(r!)^{1/r}} \right) ^{r/i} \right\} \right) ^{n}\times n\cdot m\right) . \end{aligned}$$

Proof

First, the total number N of sequences created in (i) of $\texttt {ALG}_{r}$ can be obtained as follows:

$$\begin{aligned} N&= \prod ^{k}_{i=1} \left( \begin{array}{c} \texttt {occ}_{i} \\ r \end{array} \right) = \prod ^{\texttt {occ}_{max}}_{i=r+1} \left( \begin{array}{c} i \\ r \end{array} \right) ^{n_i/i}. \end{aligned}$$

From the inequality of arithmetic and geometric means, we can obtain the following inequality:

$$\begin{aligned} \left( i(i-1)(i-2)\cdots (i-r+1) \right) ^{1/r} \le \frac{(2i-r+1)r/2}{r} = i - \frac{r-1}{2}. \end{aligned}$$

Therefore, N is bounded:

$$\begin{aligned} \prod ^{\texttt {occ}_{max}}_{i=r+1} \left( \begin{array}{c} i \\ r \end{array} \right) ^{n_i/i}&\le \prod ^{\texttt {occ}_{max}}_{i=r+1} \left( \frac{(i - \frac{r-1}{2})^r}{r!} \right) ^{n_i/i} \\&= \prod ^{\texttt {occ}_{max}}_{i=r+1} \left( \left( \frac{i - \frac{r-1}{2}}{(r!)^{1/r}} \right) ^{r/i}\right) ^{n_i} \\&\le \left( \max _{i\in \mathbb {N}}\left\{ \left( \frac{i-\frac{r-1}{2}}{(r!)^{1/r}} \right) ^{r/i} \right\} \right) ^{n}. \end{aligned}$$

This completes the proof.    $\square$

We have obtained the specific values of $\max _{i\in \mathbb {N}}\left\{ \left( \frac{i-\frac{r-1}{2}}{(r!)^{1/r}} \right) ^{r/i} \right\}$, say, N(r), and i for r-RLCS by its empirical implementation. Table 1 shows N(r) and i for each $r = 2, 3, \cdots , 10$.

Table 1. N(r) and i for each r

3 DP-Based Algorithms

In this section we design a DP-based algorithm, say, $\texttt {DP}_1$, for RFLCS in Sect. 3.1 and then $\texttt {DP}_{r}$ for r-RLCS in Sect. 3.2.

First we briefly review a dynamic programming paradigm for the original LCS. For more details, e.g., see [13]. Given a sequence $X = \langle x_1, x_2, \cdots , x_n\rangle$, we define the ith prefix of X, for $i = 0, 1, \cdots , n$, as $X_{i} = \langle x_1, x_2, \cdots , x_i\rangle$. $X_{n} = X$ and $X_{0}$ is the empty sequence. Let $X = \langle x_1, x_2, \cdots , x_n\rangle$ and $Y = \langle y_1, y_2, \cdots , y_m \rangle$ be sequences and let $Z = \langle z_1, z_2, \cdots , z_h \rangle$ be any longest common subsequence of X and Y. It is well known that LCS has the following optimal-substructure property: (1) If $x_n = y_m$, then $z_h = x_n = y_n$ and $Z_{h-1}$ is a longest common subsequence of $X_{n-1}$ and $Y_{m-1}$. (2) If $x_n \ne y_m$, then (a) $z_h \ne x_n$ implies that Z is a longest common subsequence of $X_{n-1}$ and Y; (b) $z_h \ne y_m$, then Z is a longest common subsequence of X and $Y_{m-1}$.

We define L(i, j) to be the length of a longest common subsequence of $X_{i}$ and $Y_{j}$. Then, the above optimal substructure of LCS gives the following recursive formula:

$$\begin{aligned} L(i,j) = \left\{ \begin{array}{lcl} 0 &{}&{} \text{ if } i = 0\text { or }j = 0, \\ L(i-1, j-1) + 1 &{} &{} \text{ if } i,j> 0\text { and }x_i = y_j, \\ \max \left\{ L(i, j-1), L(i-1,j)\right\} &{} &{} \text{ if } i,j > 0 \text{ and } x_i \ne y_j. \end{array} \right. \end{aligned}$$

The DP algorithm for the original LCS computes each value of L(i, j) and stores it into a two-dimensional table L of size $n\times m$ in row-major order.

In the case of r-RLCS, we have to count the number of occurrences of every symbol in the prefix of Z. In the following we show a modified recursive formula and a DP-based algorithm for r -RLCS.

3.1 Repetition-Free LCS

Suppose that X has k symbols $s_1$, $s_2$, $\cdots$, $s_k$ and $s_i$ occurs $\texttt {occ}_{i}$ times in X for each integer i, $1\le i\le k$. A trivial implementation of a dynamic programming approach might be to use the DP-based algorithm for LCS for multiple sequences: We first generate all the permutations of k symbols, i.e., k! repetition-free sequences of k symbols, say, $X_1$ through $X_{k!}$ and then obtain a longest common subsequence of $X_i$, X, and Y for each i ($1\le i\le k!$) by using an $O(|X_i|\cdot n\cdot m)$-time DP-based algorithm solving LCS for multiple (three) sequences proposed in [16]. Therefore, the total running time is $O(k!\cdot k\cdot n\cdot m)$, which is polynomial if k is constant.

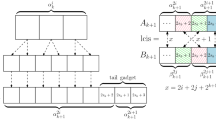
In the following we design a faster DP-based algorithm, named DP$_1$. Let $S_{\ge 2} = \{s_j \mid \texttt {occ}_{j} \ge 2\}$. Now suppose that $|S_{\ge 2}| = \ell$ and, without loss of generality, $S_{\ge 2} = \{s_1, s_2, \cdots , s_{\ell }\}$. Then, we prepare a 0-1 “constraint” vector of length $\ell$, say, $\varvec{v} = (v_1, v_2, \cdots , v_{\ell }) \in \{0, 1\}^{\ell }$, where the pth component $v_p$ corresponds to the pth symbol $s_p$ for $1\le p\le \ell$. Roughly speaking, $v_p = 1$ means that if $x_i = y_j = s_p$ and $s_p$ has not appeared yet in the temporally obtained common subsequence, then $s_p$ is allowed to be attended to the current solution; on the other hand, $v_p = 0$ means that $s_p$ is not allowed to be appended to the current solution even if $x_i = y_j = s_p$.

For the 0-1 constraint vector $\varvec{v} = (v_1, v_2, \cdots , v_{p}, \cdots , v_{\ell })$, we define a new vector $\varvec{v}|_{p=0} = (v'_1, v'_2, \cdots , v'_{p}, \cdots , v'_{\ell })$ where $v'_i = v_i$ for $i \ne p$ but $v'_p = 0$. Note that if $v_p = 0$ in $\varvec{v}$, then $\varvec{v}|_{p=0} = \varvec{v}$. Let $\varvec{0}$ ($\varvec{1}$, resp.) be a $\ell$-dimensional 0-vector (1-vector, resp.), i.e., the length of $\varvec{0}$ ($\varvec{1}$, resp.) is $\ell$ and all $\ell$ components are 0 (1, resp.).

Similarly to the above, we define $L(i, j, \varvec{v})$ to be the length of a repetition-free longest common subsequence of $X_{i}$ and $Y_{j}$, under the constraint vector $\varvec{v}$. Our algorithm for RFLCS computes each value of $L(i, j, \varvec{v})$ and stores it into a three-dimensional table L of size $n\times m \times 2^{\ell }$.

Theorem 4

(Optimal substructure of RFLCS). Let $X = \langle x_1, x_2, \cdots , x_n\rangle$ and $Y = \langle y_1, y_2, \cdots , y_m \rangle$ be sequences and let $Z = \langle z_1, z_2, \cdots , z_h \rangle$ be any longest common subsequence of X and Y. Let $S_{\ge 2} = \{s_1, s_2, \cdots , s_{\ell }\}$ be a set of $\ell$ symbols such that each $s_i$ occurs at least twice in X. The followings are satisfied:

• (1) If $x_n = y_m =s_q$ and $s_q\not \in S_{\ge 2}$, then $z_h = x_n = y_m$ and $Z_{h-1}$ is a repetition-free longest common subsequence of $X_{n-1}$ and $Y_{m-1}$.

• (2) If $x_n = y_m =s_q$, $s_q\in S_{\ge 2}$ and $v_q = 1$, then

  • (a) $z_h = x_{n} = y_{m}$ implies that $Z_{h-1}$ is a repetition-free longest common subsequence of $X_{n-1}$ and $Y_{m-1}$ such that $s_q$ does not appear in $Z_{h-1}$;

  • (b) $z_h \ne x_{n} = y_{m}$ implies that Z is a repetition-free longest common subsequence of $X_{n-1}$ and $Y_{m-1}$.

• (3) If $x_n = y_m =s_q$, $s_q\in S_{\ge 2}$ and $v_q = 0$, then $z_h \ne x_n = y_m$ and Z is a repetition-free longest common subsequence of $X_{n-1}$ and $Y_{m-1}$.

• (4) If $x_n \ne y_m$, then

  • (a) $z_h \ne x_n$ implies that Z is a repetition-free longest common subsequence of $X_{n-1}$ and Y;

  • (b) $z_h \ne y_m$ implies that Z is a repetition-free longest common subsequence of X and $Y_{m-1}$.

Proof

• (1) If $z_h \ne x_n$, then by appending $x_n = y_m = s_q$ to Z, we can obtain a repetition-free common subsequence of X and Y of length $h+1$ since Z does not have a symbol $s_q$ from the supposition $s_q\not \in S_{\ge 2}$. This contradicts the assumption that Z is a repetition-free longest common subsequence. Therefore, $z_h = x_n = y_m$ holds. What we have to do is to prove that the prefix $Z_{h-1}$ is a repetition-free common subsequence of $X_{n-1}$ and $Y_{m-1}$ with length $h-1$. Suppose for contradiction that there exists a repetition-free longest common subsequence $Z'$ of $X_{n-1}$ and $Y_{m-1}$ with length greater $h-1$. Then, by appending $x_{n} = y_{m} = s_{q}$, we obtain a repetition-free common subsequence of X and Y whose length is greater than h, which is a contradiction.

• (2) (a) If $z_h = x_{n} = y_{m}$, then $Z_{h-1}$ is a repetition-free common subsequence of $X_{n-1}$ and $Y_{m-1}$ such that $s_q$ does not appear in $Z_{h-1}$. If there is a repetition-free common subsequence $Z'$ of $X_{n-1}$ and $Y_{m-1}$ such that $s_q$ does not appear in $Z'$ with length greater than $h-1$, then by appending $x_{n} = y_{m} = s_{q}$ to $Z'$, we can obtain a repetition-free common subsequence of X and Y whose length is greater than h, which is a contradiction. (b) If $z_h \ne x_{n} = y_{m}$, then a repetition-free common subsequence of $X_{n-1}$ and $Y_{m-1}$ must include $s_{q}$ and be the longest one.

• (3)  If $v_q = 0$, then $s_p$ is not allowed to be included into Z. Thus, if $z_{h}\ne x_{n} = y_{m}$, then Z is a repetition-free common subsequence of $X_{n-1}$ and $Y_{m-1}$ and it must be the longest one.

• (4) (a) ((b), resp.) If $z_h\ne x_{n}$ ($z_h\ne y_{m}$, resp.), then Z is a repetition-free common subsequence of $X_{n-1}$ and Y (X and $Y_{m-1}$, resp.). If there is a repetition-free common subsequence $Z'$ of $X_{n-1}$ and Y (X and $Y_{m-1}$, resp.) with length greater than h, then $Z'$ would also be a repetition-free common subsequence of X and Y, contradicting the assumption that Z is a repetition-free longest common subsequence of X and Y.

   $\square$

Then, we can obtain the following recursive formula:

$$\begin{aligned}&L(i,j, \varvec{v}) \nonumber \\&= \left\{ \begin{array}{l} 0 \qquad \qquad \,\, \text{ if } i = 0,\, j = 0,\text { or }\varvec{v} = \varvec{0}, \\ L(i-1, j-1, \varvec{v}) + 1 \\ \qquad \qquad \,\, \text{ if } i,j> 0,\, x_i = y_j = s_q,\text { and }s_q \not \in S_{\ge 2} \\ \max \left\{ L(i-1,j-1, \varvec{v}|_{p=0})+1, L(i-1, j-1, \varvec{v})\right\} \\ \qquad \qquad \,\, \text{ if } i,j> 0,\, x_i = y_j = s_{p},\, s_p \in S_{\ge 2},\text { and }v_p = 1, \\ L(i-1,j-1,\varvec{v}) \\ \qquad \qquad \,\, \text{ if } i,j > 0,\, x_i = y_j = s_{p},\, s_p \in S_{\ge 2},\text { and }v_p = 0, \\ \max \left\{ L(i-1, j, \varvec{v}), L(i,j-1, \varvec{v})\right\} \\ \qquad \qquad \,\, \text{ otherwise. } \end{array} \right. \end{aligned}$$

Here is an outline of our algorithm DP$_1$, which computes each value of $L(i, j, \varvec{v})$ and stores it into a three-dimensional table L of size $n\times m\times 2^{\ell }$: Initially, we set $L(i, j, \varvec{v}) = 0$ and $pre(i, j, \varvec{v}) = \texttt {null}$ for every i, j, and $\varvec{v}$. Then, the algorithm DP$_1$ fills entries from $L(1, 1, \varvec{0})$ to $L(1, 1, \varvec{1})$, then from $L(1, 2, \varvec{0})$ to $L(1, 2, \varvec{1})$, next from $L(1, 3, \varvec{0})$ to $L(1, 3, \varvec{1})$, and so on. After filling all the entries in the first “two-dimensional plane” $L(1,j,\varvec{v})$, the algorithm fills all the entries in the second two-dimensional plane $L(2,j,\varvec{v})$, and so on. Finally, DP$_1$ fills all the entries in the nth plane. The algorithm DP$_1$ also maintains a three dimensional table pre of size $n\times m\times 2^{\ell }$ to help us construct an optimal repetition-free longest subsequence. The entry $pre(i, j, \varvec{v})$ points to the table entry corresponding to the optimal subproblem solution chosen when computing $L(i, j, \varvec{v})$. Further details could be appeared in the full version of this paper.

We bound the running time of DP$_1$:

Theorem 5

The running time of DP$_1$ is $O(2^{\ell }\cdot n\cdot m)$ for RFLCS on two sequences X and Y where $|X| =n$, $|Y| = m$, $|X| \le |Y|$, and $|S_{\ge 2}| = \ell$.

Proof

The algorithm DP$_1$ for RFLCS computes each value of $L(i, j, \varvec{v})$ and stores it into the three-dimensional table L of size $n\times m\times 2^{\ell }$. Clearly, each table entry takes O(1) time to compute. As a result, the running time of DP$_1$ is bounded above by $O(2^{\ell }\cdot n\cdot m)$.    $\square$

Corollary 2

The running time of DP$_1$ is $O(1.41422^{n}\cdot n\cdot m)$ for RFLCS on two sequences X and Y where $|X| =n$, $|Y| = m$, and $|X| \le |Y|$.

Proof

Recall that the number $|S_{\ge 2}|$ of symbols which appear at least twice in X is defined to be $\ell$. This implies that $\ell \le \frac{n}{2}$. Therefore, $2^{\ell } \le 2^{n/2} < 1.41422^{n}$ is satisfied.    $\square$

3.2 r-Repetition LCS, $r\ge 2$

The similar strategies of DP$_1$ can work well for r-RLCS; we can design a DP-based algorithm, named DP$_r$, for r-RLCS. The running time is as follows:

Theorem 6

The running time of DP$_r$ is $O((r+1)^{\ell }\cdot n\cdot m)$ for r-RLCS on two sequences X and Y where $|X| =n$, $|Y| = m$, $|X| \le |Y|$, and $|S_{\ge 2}| = \ell$.

Proof

It is enough to prepare a three-dimensional table L of size $n\times m\times (r+1)^{\ell }$ and each table entry takes O(1) time to compute.    $\square$

Corollary 3

The running time of DP$_r$ is $O((r+1)^{n/(r+1)}\cdot n\cdot m)$ for r-RLCS on two sequences X and Y where $|X| =n$, $|Y| = m$, and $|X| \le |Y|$.

Proof

Clearly $\ell \le \frac{n}{r+1}$, i.e., $(r+1)^{\ell }\le (r+1)^{n/(r+1)}$ holds.   $\square$

For example, by the above corollary, the running time of our algorithm is $O(1.44225^n\cdot n\cdot m)$ for 2-RLCS, $O(1.41422^n\cdot n\cdot m)$ for 3-RLCS, $O(1.37973^n\cdot n\cdot m)$ for 4-RLCS and so on.

4 Conclusion

We studied a new variant of the Longest Common Subsequence problem, called r-Repetition Longest Common Subsequence problem (r-RLCS). For $r = 1$, 1-RLCS is known as the Repetition-Free Longest Common Subsequence problem. We first showed that for 1-RLCS there is a simple exact algorithm whose running time is bounded above by $O(1.44225^{|X|}|X||Y|)$. Then, for r-RLCS ($r\ge 1$), we designed a DP-based exact algorithm whose running time is $O((r+1)^{|X|/(r+1)}|X||Y|)$. This implies that we can solve 1-RLCS in $O(1.41422^{|X|}|X||Y|)$ time. A promising direction for future research is to design faster exact (exponential-time) algorithms for r-RLCS. Also, it would be important to design approximation algorithms for r-RLCS.