Abstract
We study solution techniques for an evolution equation involving second order derivative in time and the spectral fractional powers, of order \(s \in (0,1)\), of symmetric, coercive, linear, elliptic, second-order operators in bounded domains \(\varOmega \). We realize fractional diffusion as the Dirichlet-to-Neumann map for a nonuniformly elliptic problem posed on the semi-infinite cylinder \(\mathcal {C}= \varOmega \times (0,\infty )\). We thus rewrite our evolution problem as a quasi-stationary elliptic problem with a dynamic boundary condition and derive space, time, and space–time regularity estimates for its solution. The latter problem exhibits an exponential decay in the extended dimension and thus suggests a truncation that is suitable for numerical approximation. We propose and analyze two fully discrete schemes. The discretization in time is based on finite difference discretization techniques: the trapezoidal and leapfrog schemes. The discretization in space relies on the tensorization of a first-degree FEM in \(\varOmega \) with a suitable hp-FEM in the extended variable. For both schemes we derive stability and error estimates. We consider a first-degree FEM in \(\varOmega \) with mesh refinement near corners and the aforementioned hp-FEM in the extended variable and extend the a priori error analysis of the trapezoidal scheme for open, bounded, polytopal but not necessarily convex domains \(\varOmega \subset {\mathbb {R}}^2\). We discuss implementation details and report several numerical examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We are interested in the numerical approximation of an initial boundary value problem for a space-fractional wave equation. Let \(\varOmega \) be an open and bounded domain in \(\mathbb {R}^n\) (\(n\ge 1\)) with boundary \(\partial \varOmega \). Given \(s \in (0,1)\), a forcing function f, and initial data g and h, we seek u such that
Here, \({\mathcal {L}}\) denotes the linear, elliptic, self-adjoint, second order, differential operator
supplemented with homogeneous Dirichlet boundary conditions. The coefficient \(A \in C^{0,1}({\bar{\varOmega }},{\text {\textsf {GL}}}(n,\mathbb {R}))\) is symmetric and uniformly positive definite and \(0 \le c \in L^\infty (\varOmega )\). By \(\mathcal {L}^s\), with \(s \in (0,1)\), we denote the spectral fractional powers of the operator \({{\mathcal {L}}}\).
One of the most common and studied physical processes is diffusion: the tendency of a substance to evenly spread into an available space. Classical models of diffusion lead to well-known models and even better studied equations. However, in recent times, it has become evident that many of the assumptions that lead to these models are not always satisfactory or even realistic: memory, heterogeneity, or a multiscale structure might violate them. In this setting, the assumption of locality does not hold and to describe diffusion one needs to resort to nonlocal operators. Different models of diffusion have been proposed, fractional diffusion being one of them. An incomplete list of problems where fractional diffusion appears includes finance [14, 40, 51], turbulent flow [15], quasi-geostrophic flows models [12, 36], models of anomalous thermoviscous behaviors [16], peridynamics [21, 56], and image science [28, 29].
The design of efficient solution techniques for problems involving fractional diffusion is intricate, mainly due to the nonlocal character of \(\mathcal {L}^s\) [8,9,10, 13]. Recently, and in order to overcome such a nonlocal feature, the Caffarelli-Silvestre extension has been proved useful in numerical analysis [5, 46, 47]. When \({\mathcal {L}} = -\varDelta \) and \(\varOmega = \mathbb {R}^n\), i.e., in the case of the Laplacian in the whole space, Caffarelli and Silvestre [10] showed that \({\mathcal {L}}^s\) can be realized as the Dirichlet-to-Neumann map for an extension problem to the upper half-space \(\mathbb {R}_{+}^{n+1}\); the extension corresponds to a nonuniformly elliptic PDE. This result was later extended in [9, 13, 57] to bounded domains \(\varOmega \) and more general operators, thereby obtaining an extension problem posed on the semi-infinite cylinder \(\mathcal {C}:= \varOmega \times (0,\infty )\). We shall thus rewrite problem (1.1) as the following quasi-stationary elliptic problem with a dynamic boundary condition [3, 18, 19, 60]:
with the initial conditions
where \(\partial _L \mathcal {C}= \partial \varOmega \times [0,\infty )\) corresponds to the lateral boundary of \(\mathcal {C}\), \(\alpha =1-2s \in (-1,1)\), \(d_s=2^{\alpha } \varGamma (1-s)/\varGamma (s)\), and the conormal exterior derivative of \(\mathscr {U}\) at \(\varOmega \times \{ 0 \}\) is
the limit must be understood in the sense of distributions [10, 13, 57]. We will call y the extended variable and the dimension \(n+1\) in \(\mathbb {R}_+^{n+1}\) the extended dimension of problem (1.2), (1.3). Finally, \({\mathbf {A}} = {\mathrm {diag}} \{A,1\} \in C^{0,1}(\mathcal {C},{\text {\textsf {GL}}}(n+1,\mathbb {R}))\). With the solution \(\mathscr {U}\) to the extension problem (1.2), (1.3) at hand, we can find the solution to (1.1) via [3, 9, 10, 13, 18, 19, 60]:
To the best of the authors knowledge this is the first work that provides a comprehensive treatment of efficient solution techniques for the space-fractional wave equation (1.1). In (1.1), \({\mathcal {L}}^s\) denotes the spectral fractional powers of the operator \({\mathcal {L}}\). Recently, problem (1.1) has been considered in [2] but with \({\mathcal {L}}^s = (-\varDelta )^s\) being the integral fractional Laplace operator [39]. The authors of this work propose a discrete scheme that is based on standard Galerkin finite elements for space discretization and the convolution quadrature approach for the discretization in time. We immediately comment that the spectral and integral definitions of the fractional Laplace operator do not coincide. In fact, as shown in [45] their difference is positive and positivity preserving. This, in particular, implies that the boundary behavior of the respective solutions is quite different [11, 32].
The outline of this paper is as follows. In Sect. 2 we introduce some terminology used throughout this work. We recall the definition of the fractional powers of elliptic operators via spectral theory in Sect. 2.1, and in Sect. 2.2 we briefly describe their localization via the Caffarelli–Silvestre extension and also introduce the functional framework that is suitable for studying problem (1.2), (1.3). In Sect. 3, we review existence and uniqueness results together with energy-estimates for problems (1.1) and (1.2), (1.3). In Sect. 4 we present space, time and space–time regularity results for the solution of problem (1.2), (1.3). The numerical analysis for problem (1.2), (1.3) begins in Sect. 5 where we introduce a truncated problem on the bounded cylinder 
and study some properties of its solution. In Sect. 6 we preset two fully discrete schemes for the truncated version of (1.2), (1.3) studied in Sect. 5. Both of them are based on the scheme of [5] for space discretization. For time discretization we consider an implicit finite difference discretization scheme and the so-called leapfrog scheme. We derive stability and a priori error estimates for the proposed schemes for all \(s \in (0,1)\). In Sect. 7, we extend the a priori error analysis of the trapezoidal scheme for open, bounded, polytopal but not necessarily convex domains \(\varOmega \subset {\mathbb {R}}^2\) on the basis of a continuous, piecewise linear, Lagrangian FEM in \(\varOmega \) with with mesh refinement near corners and a suitable hp-FEM in the extended variable. In Sect. 8 we comment on some implementation details pertinent to the problem at hand and present numerical experiments in one and two dimensional domains. An important conclusion is that due to the nonlocality of \((-\varDelta )^s\), the explicit nature of the leapfrog scheme seems to be lost.
2 Notation and preliminaries
Throughout this work, with the exception of Sect. 7, \(\varOmega \) is an open, bounded, and convex polytopal subset of \(\mathbb {R}^n\) (\(n\ge 1\)) with boundary \(\partial \varOmega \). In Sect. 7, instead, \(\varOmega \subset {\mathbb {R}}^2\) denotes an open and bounded, but not necessarily convex, polygon. We define the semi-infinite cylinder \(\mathcal {C}:= \ \varOmega \times (0,\infty )\) and its lateral boundary \(\partial _L \mathcal {C}:= \partial \varOmega \times [0,\infty )\). For 
, we define the truncated cylinder with base \(\varOmega \) and height 
as 
; its lateral boundary is denoted by 
. If \(x \in \mathbb {R}^{n+1}\), we write \( x = (x',y), \) with \(x' \in \mathbb {R}^n\) and \(y\in \mathbb {R}\).
For an open set \(D \subset \mathbb {R}^n\) (\(n \ge 1\)), if \(\omega \) is a weight and \(p \in (1,\infty )\), we denote the Lebesgue space of p-integrable functions with respect to the measure \(\omega \,\mathrm{d}x\) by \(L^p(\omega ,D)\) [33, 37, 59]. Similar notation will be used for weighted Sobolev spaces. If \(T >0\) and \(\phi : D \times (0,T) \rightarrow \mathbb {R}\), we consider \(\phi \) as a function of t with values in a Banach space X, \( \phi :(0,T) \ni t \mapsto \phi (t) \equiv \phi (\cdot ,t) \in X \). For \(1 \le p \le \infty \), \(L^p( 0,T; X)\) is the space of X-valued functions whose norm in X is in \(L^p(0,T)\). This is a Banach space for the norm
Whenever X is a normed space, \(X'\) denotes its dual and \(\Vert \cdot \Vert _{X}\) its norm. If, in addition, Y is a normed space, we write \(X \hookrightarrow Y\) to indicate continuous embedding. The relation \(a \lesssim b\) means \(a \le Cb\), with a constant C that neither depends on a or b. The value of C might change at each occurrence.
The next result, that follows from Young’s inequality for convolutions, will be instrumental in the analysis that we will perform.
Lemma 1
(continuity) If \(g \in L^2(0,T)\) and \(\phi \in L^1(0,T)\), then the operator
is continuous from \(L^2(0,T)\) into itself and \( \Vert \varPhi \Vert _{L^2(0,T)} \le \Vert \phi \Vert _{L^1(0,T)} \Vert g \Vert _{L^2(0,T)}. \)
Finally, since we assume \(\varOmega \) to be convex, in what follows we will make use, without explicit mention, of the following regularity result [31]:
2.1 Fractional powers of second order elliptic operators
We adopt the spectral definition for the fractional powers of the operator \({\mathcal {L}}\). To define \({\mathcal {L}}^s\), we begin by noticing that \({{\mathcal {L}}}\) induces the following inner product \(a_{\varOmega }(\cdot ,\cdot )\) on \(H^1_0(\varOmega )\)
and that \({{\mathcal {L}}}: H^1_0(\varOmega ) \ni u \mapsto a_{\varOmega }(u,\cdot ) \in H^{-1}(\varOmega )\) is an isomorphism. The eigenvalue problem:
has a countable collection of solutions \(\{ \lambda _{\ell }, \varphi _{\ell } \}_{\ell \in {{\mathbb {N}}}} \subset \mathbb {R}_+ \times H_0^1(\varOmega )\) with the real eigenvalues enumerated in increasing order, counting multiplicities, and such that, \(\{\varphi _{\ell } \}_{\ell =1}^{\infty }\) is an orthonormal basis of \(L^2(\varOmega )\) and an orthogonal basis of \((H_0^1(\varOmega ),a_{\varOmega }(\cdot ,\cdot ))\) [6, 35]. With these eigenpairs at hand, we introduce, for \(s \ge 0\), the fractional Sobolev space
where, for \(\ell \in {\mathbb {N}}\), \(w_\ell = (w,\varphi _\ell )_{L^2(\varOmega )}\). We denote by \(\mathbb {H}^{-s}(\varOmega )\) the dual space of \(\mathbb {H}^s(\varOmega )\). The duality pairing between the aforementioned spaces will be denoted by \(\langle \cdot , \cdot \rangle \). We notice that, if \(s \in (0,\tfrac{1}{2})\), \(\mathbb {H}^s(\varOmega )= H^s(\varOmega ) = H_0^s(\varOmega )\), while, for \(s \in (\tfrac{1}{2},1)\), \(\mathbb {H}^s(\varOmega )\) can be characterized by [41, 42, 58]
If \(s = \frac{1}{2}\), we have that \({\mathbb {H}}^{\frac{1}{2}}(\varOmega )\) is the so-called Lions–Magenes space \(H_{00}^{\frac{1}{2}}(\varOmega )\) [41, 58]. If \(s\in (1,2]\), owing to (2.1), we have that \(\mathbb {H}^s(\varOmega )= H^s(\varOmega )\cap H^1_0(\varOmega )\) [25].
The fractional powers of the operator \({{\mathcal {L}}}\) are thus defined by
2.2 Weighted Sobolev spaces
Both extensions, the one by Caffarelli and Silvestre [10] and the ones in [9, 13, 57] for bounded domains \(\varOmega \) and general elliptic operators, require us to deal with a local but nonuniformly elliptic problem. To provide an analysis for the latter it is thus suitable to define the weighted Sobolev space
Since \(\alpha \in (-1,1)\), \(|y|^{\alpha }\) belongs to the Muckenhoupt class \({A}_{2}\) [22, 43, 59]. The following important consequences thus follow immediately: \(H^1(y^{\alpha },\mathcal {C})\) is a Hilbert space and \(C^{\infty }(\varOmega ) \cap H^1(y^{\alpha },\mathcal {C})\) is dense in \(H^1(y^{\alpha },\mathcal {C})\) (cf. [59, Proposition 2.1.2, Corollary 2.1.6], [38] and [30, Theorem 1]). In addition, as [46, inequality (2.21)] shows, the following weighted Poincaré inequality holds:
Thus, \(\Vert \nabla w \Vert _{L^2(y^{\alpha },\mathcal {C})}\) is equivalent to the norm in 
.
We define the bilinear form 
by
which is continuous and, owing to (2.6), coercive on 
. Consequently, it induces an inner product on 
and the following energy norm:
For \(w \in H^1( y^{\alpha },\mathcal {C})\), \({{\,\mathrm{tr_\varOmega }\,}}w\) denotes its trace onto \(\varOmega \times \{ 0 \}\). We recall that, for \(\alpha = 1-2s\), [46, Proposition 2.5] yields
The seminal work of Caffarelli and Silvestre [10] and its extensions to bounded domains [9, 13, 57] showed that the operator \({\mathcal {L}}^s\) can be realized as the Dirichlet-to-Neumann map for a nonuniformly elliptic boundary value problem. Namely, if \({\mathfrak {U}}\) solves
where \(\alpha = 1-2s\), \(\partial _\nu ^{\alpha } {\mathfrak {U}} = -\lim _{y\downarrow 0} y^{\alpha } {\mathfrak {U}}_y\) and \(d_s = 2^{\alpha } \varGamma (1-s)/\varGamma (s)\) is a normalization constant, then \({\mathfrak {u}} = {{\,\mathrm{tr_\varOmega }\,}}{\mathfrak {U}} \in \mathbb {H}^s(\varOmega )\) solves
3 Well-posedness and energy estimates
In this section we briefly review the results of [49] regarding the existence and uniqueness of weak solutions for problems (1.1) and (1.2), (1.3). We also provide basic energy estimates.
3.1 The fractional wave equation
We assume that the data of problem (1.1) is such that \(f \in L^2(0,T;L^2(\varOmega ))\), \(g \in \mathbb {H}^s(\varOmega )\), and \(h \in L^2(\varOmega )\) and define
Definition 1
(weak solution for (1.1)) We call \(u \in L^2(0,T;\mathbb {H}^s(\varOmega ))\), with \(\partial _t u \in L^2(0,T;L^2(\varOmega ))\) and \(\partial _{t}^2 u \in L^2(0,T;\mathbb {H}^{-s}(\varOmega ))\), a weak solution of problem (1.1) if \(u(0) = g\), \(\partial _t u(0) = h\) and, a.e. \(t \in (0,T)\),
where \(\langle \cdot , \cdot \rangle \) denotes the duality pairing between \(\mathbb {H}^s(\varOmega )\) and \(\mathbb {H}^{-s}(\varOmega )\).
The following remark is in order.
Remark 1
(initial conditions) Since a weak solution u of (1.1) satisfies that \(u \in L^2(0,T;\mathbb {H}^s(\varOmega ))\), \(\partial _t u \in L^2(0,T;L^2(\varOmega ))\), and \(\partial _{t}^2 u \in L^2(0,T;\mathbb {H}^{-s}(\varOmega ))\), an application of [52, Lemma 7.3] reveals that \(u \in C([0,T]; L^2(\varOmega ))\) and \(\partial _t u \in C([0,T]; \mathbb {H}^{-s}(\varOmega ))\). The initial conditions involved in Definition 1 are thus appropriately defined.
Theorem 1
(well-posedness) Given \(s \in (0,1)\), \(f \in L^2(0,T;L^2(\varOmega ))\), \(g \in \mathbb {H}^s(\varOmega )\), and \(h \in L^2(\varOmega )\), problem (1.1) has a unique weak solution. In addition,
where the hidden constant is independent of the problem data.
Proof
The desired results can be obtained by slightly modifying the arguments, based on a Galerkin technique, of [24, 41, 52]. \(\square \)
3.2 The extended fractional wave equation
We consider the following notion of weak solution for problem (1.2), (1.3).
Definition 2
(extended weak solution) We call 
, with \({{\,\mathrm{tr_\varOmega }\,}}\partial _t \mathscr {U}\in L^{\infty }(0,T;L^2(\varOmega ))\) and \({{\,\mathrm{tr_\varOmega }\,}}\partial _{t}^{2} \mathscr {U}\in L^2(0,T;\mathbb {H}^{-s}(\varOmega ))\), a weak solution of problem (1.2), (1.3) if \({{\,\mathrm{tr_\varOmega }\,}}\mathscr {U}(0) = g\), \({{\,\mathrm{tr_\varOmega }\,}}\partial _t \mathscr {U}(0) = h\) and, for a.e. \(t \in (0,T)\),
where \(\langle \cdot , \cdot \rangle \) denotes the duality pairing between \(\mathbb {H}^s(\varOmega )\) and \(\mathbb {H}^{-s}(\varOmega )\) and the bilinear form a is defined as in (2.7).
Remark 2
(dynamic boundary condition) Problem (3.3) is an elliptic problem with the following dynamic boundary condition: \(\partial _{\nu }^{\alpha } \mathscr {U}= d_s(f - {{\,\mathrm{tr_\varOmega }\,}}\partial _t^{2} \mathscr {U})\) on \(\varOmega \times \{0\}\).
We present the following important localization result [3, 7, 9, 10, 13, 18, 19, 60].
Theorem 2
(Caffarelli–Silvestre extension property) Let \(s \in (0,1)\). If f, g, and h are as in Theorem 1, then the unique weak solution of problem (1.1), in the sense of Definition 1 satisfies that \(u = {{\,\mathrm{tr_\varOmega }\,}}\mathscr {U}\), where \(\mathscr {U}\) denotes the unique weak solution to problem (1.2), (1.3) in the sense of Definition 2.
We now present the well-posedness of problem (3.3) together with energy estimates for its solution.
Theorem 3
(well-posedness) Given \(s \in (0,1)\), \(f \in L^2(0,T;L^2(\varOmega ))\), \(g \in \mathbb {H}^s(\varOmega )\) and \(h \in L^2(\varOmega )\), then problem (1.2), (1.3) has a unique weak solution in the sense of Definition 2. In addition,
where the hidden constant is independent of the problem data and \(\varLambda (f,g,h)\) is defined as in (3.1).
Proof
See [49, Theorem 3.11]. \(\square \)
Remark 3
(initial data) The initial data g and h of problem (3.3) determine \(\mathscr {U}(0)\) and \(\partial _t\mathscr {U}(0)\) only on \(\varOmega \times \{ 0\}\) in a trace sense. However, in the analysis that follows it will be necessary to consider their extension to the whole cylinder \(\mathcal {C}\). We thus define \(\mathscr {U}(0) = {\mathcal {E}}_{\alpha }g\) and \(\mathscr {U}_t(0) = {\mathcal {E}}_{\alpha }h\), where the \(\alpha \)-harmonic extension operator
is defined as follows: If \(w \in \mathbb {H}^s(\varOmega )\), then 
solves
References [9, 13] provide, for \(w \in \mathbb {H}^s(\varOmega )\), the estimate \(\Vert \nabla {\mathcal {E}}_{\alpha } w \Vert _{L^2(y^{\alpha },\mathcal {C})} \lesssim \Vert w \Vert _{\mathbb {H}^s(\varOmega )}\).
3.3 Solution representation
In this section we present a solution representation formula for the solution to problem (3.3). To accomplish this task, we first notice that the solution to problem (1.1) can be written as \(u(x',t) = \sum _{k \in {\mathbb {N}}} u_k(t) \varphi _k(x')\), where, for \(k \in {\mathbb {N}}\), the coefficient \(u_k(t)\) solves
with \(g_k = (g,\varphi _k)_{L^2(\varOmega )}\), \(h_k = (h,\varphi _k)_{L^2(\varOmega )}\), and \(f_{k}(t) = (f(\cdot ,t),\varphi _k)_{L^2(\varOmega )}\). We recall that the sequence \(\{\lambda _k, \varphi _k \}_{k \in {\mathbb {N}}}\) corresponds to the eigenpairs of the operator \({{\mathcal {L}}}\) and are defined by (2.3). Basic computations reveal, for \(k \in {\mathbb {N}}\), that
With these ingredients at hand, we can write the solution \(\mathscr {U}\) of problem (3.3) as
where, for \(\alpha = 1-2s\), the functions \(\psi _k\) solve
If \(s = \tfrac{1}{2}\), we thus have \(\psi _k(y) = \exp (-\sqrt{\lambda _k}y)\) [9, Lemma 2.10]. If \(s \in (0,1) {\setminus } \{ \tfrac{1}{2}\}\), then [13, Proposition 2.1]
where \(c_s = 2^{1-s}/\varGamma (s)\) and \(K_s\) denotes the modified Bessel function of the second kind. We refer the reader to [1, Chapter 9.6] and [48, Chapter 7.8] for a comprehensive treatment of the Bessel function \(K_s\). We immediately state the following property of the function \(\psi _k\):
In addition, for \(a,b \in {\mathbb {R}}^{+}\), \(a < b\), we have [46, formula (2.33)]
[46, formula (2.32)]
and [46, formula (2.31)]
4 Regularity
In this section we review and derive space, time, and space–time regularity results for the solution \(\mathscr {U}\) of problem (3.3).
4.1 Space regularity
To present the space regularity properties of \(\mathscr {U}\), we introduce the weight
where \(\beta \in \mathbb {R}\) will be specified later. With this weight at hand, we define the norm
We now present the following pointwise, in time, bounds for \(\mathscr {U}\) [49, Theorem 4.2].
Proposition 1
(pointwise bounds) Let \(\mathscr {U}\) solve problem (1.2), (1.3) for \(s\in (0,1)\). Let \(0 \le \sigma < s\) and \(0 \le \nu < 1+s \). Then, there exists \(\kappa > 1\) such that the following estimates hold for all \(\ell \in {\mathbb {N}}_0\):
In all inequalities the hidden constants are independent of \(\mathscr {U}\), \(\ell \), and problem data.
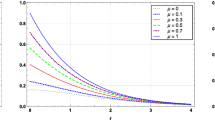
The result below shows the spatial analyticity of the solution \(\mathscr {U}\) with respect to the extended variable \(y \in (0,\infty )\): \(\mathscr {U}\) belongs to countably normed, power-exponentially weighted Bochner spaces of analytic functions with respect to y taking values in spaces \({\mathbb {H}}^r(\varOmega )\).
Proposition 2
(space regularity) Let \(\mathscr {U}\) solve (1.2), (1.3) for \(s\in (0,1)\). Let \(0 \le \sigma < s\) and \(0 \le \nu < 1+s \). Then, there exists \(\kappa > 1\) such that the following regularity estimates hold for all \(\ell \in {\mathbb {N}}_0\):
and
The hidden constants are independent of \(\mathscr {U}\), \(\ell \), and the problem data.
Proof
In view of (3.8) and the continuity estimate of Lemma 1, we conclude, for \(k \in {\mathbb {N}}\), that
The desired estimates (4.6)–(4.8) thus follow directly from (4.3)–(4.5). \(\square \)
4.2 Time regularity
We begin this section by defining, for \(\ell \in \{1,\dots ,4 \}\),
In addition, and to shorten notation, we define
We now derive regularity estimates in time for the solution \(\mathscr {U}\). These estimates will be needed in the analysis of the fully discrete schemes proposed in Sect. 6.
Theorem 4
(time-regularity) Let \(\mathscr {U}\) be the solution to problem (1.2), (1.3) for \(s\in (0,1)\). The following regularity estimates in time hold:
In all these inequalities the hidden constants do not depend either on \(\mathscr {U}\) or the problem data.
Proof
Since \(\{ \varphi _k \}_{k \in {\mathbb {N}}}\) is an orthonormal basis of \(L^2(\varOmega )\) and an orthogonal basis of \((H_0^1(\varOmega ),a_{\varOmega }(\cdot ,\cdot ))\), the definition of the energy norm \( \Vert {\cdot }\Vert _{\mathcal {C}}\), given in (2.8), and the properties (3.12) and (3.14) allow us to conclude, for \(\ell \in {\mathbb {N}}_0\), that
We have thus arrived at the estimate \( \Vert { \partial _t^{\ell } \nabla \mathscr {U}(\cdot ,t)}\Vert _{\mathcal {C}}^2 = \Vert \partial _t^{\ell } u(\cdot ,t) \Vert ^2_{\mathbb {H}^s(\varOmega )}\).
We now invoke the explicit representation of the coefficient \(u_k(t)\), with \(k \in {\mathbb {N}}\), which is provided in (3.8), to obtain
This, on the basis of the definition of the norm \( \Vert \cdot \Vert _{{\mathbb {H}}^r(\varOmega )}\), given in (2.4), and an application of Lemma 1, reveal that
which implies the desired estimate (4.11).
To derive (4.12) we invoke, again, the representation formula (3.8) and write
We thus use the definition of the norm \( \Vert \cdot \Vert _{{\mathbb {H}}^r(\varOmega )}\) to arrive at (4.12).
The estimates (4.13) and (4.14) follow similar arguments upon taking derivatives to the explicit representation of the coefficient \(u_k(t)\), with \(k \in {\mathbb {N}}\), provided in (3.8). This concludes the proof. \(\square \)
4.3 Space-time regularity
We present the following regularity result in space and time.
Theorem 5
(space–time regularity) Let \(\mathscr {U}\) solve (1.2), (1.3) for \(s\in (0,1)\). Let \(0 \le \sigma < s\) and \(0 \le \nu < 1+s \). Then, there exists \(\kappa > 1\) such that the following regularity estimates hold for all \(\ell \in {\mathbb {N}}_0\):
and
The hidden constants do not depend either on \(\mathscr {U}\) or the problem data.
Proof
Similar arguments to the ones used to derive (4.3) reveal that
To control the right-hand side of the previous inequality we invoke formula (4.15) and the definition of the \({\mathbb {H}}^r(\varOmega )\)-norm, given in (2.4). These arguments reveal the estimate
This yields (4.16). Similar arguments allow us to derive the regularity estimates (4.17) and (4.18). \(\square \)
As it will be used in the analysis that follows, we introduce
and notice that, if \(0 \le \sigma < s\), then
As a consequence of the estimate (4.19) and the previous definition, we can immediately arrive at the following regularity estimate.
Corollary 1
(space–time regularity) Let u solve (1.1) for \(s \in (0,1)\). Then
The hidden constant does not depend either on u or the problem data.
5 Truncation
A first step towards space-discretization is to truncate the semi-infinite cylinder \(\mathcal {C}\). In the next result we show that the solution \(\mathscr {U}\) to problem (1.2), (1.3) decays exponentially in the extended variable y for a.e. \(t \in (0,T)\). This suggests to truncate \(\mathcal {C}\) to 
, with a suitable truncation parameter 
, and seek solutions in this bounded domain.
Proposition 3
(exponential decay) Let \(s \in (0,1)\) and \(\mathscr {U}\) be the solution to (3.3). Then, for every 
, we have that
where \(\lambda _1\) denotes the first eigenvalue of \({{\mathcal {L}}}\) and \(\varLambda (f,g,h)\) is defined in (3.1).
Proof
We invoke (3.9) and the fact that \(\{ \varphi _k \}_{k \in {\mathbb {N}}}\) is an orthonormal basis of \(L^2(\varOmega )\) and an orthogonal basis of \((H_0^1(\varOmega ),a_{\varOmega }(\cdot ,\cdot ))\) to conclude that
We now apply formulas (3.12) and (3.13) to obtain that
The desired estimate (5.1) is thus a consequence of the energy estimate (3.2) for the solution u to problem (1.1). \(\square \)
To describe the truncated version of (3.3), we define the weighted Sobolev space
and the bilinear form 
as
where 
and 
.
On the basis of the results of Proposition 3, we thus consider the following truncated problem: Find 
with \({{\,\mathrm{tr_\varOmega }\,}}\partial _t \mathcal {U}\in L^{\infty }(0,T;L^2(\varOmega ))\) and \({{\,\mathrm{tr_\varOmega }\,}}\partial _{t}^{2} \mathcal {U}\in L^2(0,T;\mathbb {H}^{-s}(\varOmega ))\) such that \({{\,\mathrm{tr_\varOmega }\,}}\mathcal {U}(0) = g\), \({{\,\mathrm{tr_\varOmega }\,}}\partial _t \mathcal {U}(0) = h\), and, for a.e. \(t \in (0,T)\),
We define 
, the truncated \(\alpha \)-harmonic extension operator, as follows: if \(w \in \mathbb {H}^s(\varOmega )\), then \({{\mathcal {W}}}= {{\mathcal {H}}}_\alpha w\) solves
Remark 4
(initial data) As in Remark 3, we define \(\mathcal {U}(0) = {\mathcal {H}}_{\alpha }g\) and \(\mathcal {U}_t(0) = {\mathcal {H}}_{\alpha }h\), where \({\mathcal {H}}_{\alpha }\) is defined by (5.4). References [9, 13] provide the estimates \(\Vert \mathcal {U}(0) \Vert _{L^2(y^{\alpha },\mathcal {C})} \lesssim \Vert g \Vert _{\mathbb {H}^s(\varOmega )}\) and \(\Vert \partial _t \mathcal {U}(0) \Vert _{L^2(y^{\alpha },\mathcal {C})} \lesssim \Vert h \Vert _{\mathbb {H}^s(\varOmega )}\).
The following result shows that by considering (5.3) instead of (3.3) we only incur an exponentially small error
Lemma 2
(exponential error estimate) Let \(\mathscr {U}\) and \(\mathcal {U}\) be the solutions of problems (3.3) and (5.3), respectively. Then, for every \(s \in (0,1)\) and 
, we have
where \(\varSigma _1\) is defined by (4.9) and the hidden constant does not depend on either \(\mathscr {U}\), \(\mathcal {U}\), or the problem data.
Proof
We begin the proof by defining the cutoff function \(\rho \in W^{1,\infty }(0,\infty )\) as
Notice that by a trivial zero extension we realize that 
. We are thus allow to set \(\phi = \partial _t(\mathcal {U}-\rho \mathscr {U})\) in problems (3.3) and (5.3). With these choices of test functions, we subtract the ensuing equalities and obtain that
This expression yields
We thus integrate over time and use that \({{\,\mathrm{tr_\varOmega }\,}}\partial _t (\mathcal {U}-\mathscr {U})|_{t=0} = 0\) to arrive at
It thus remains to bound the right-hand side of (5.6). First, in view of the fact that \(\mathscr {U}(0) = {{\mathcal {E}}}_{\alpha } g\) and \(\mathcal {U}(0) = {{\mathcal {H}}}_{\alpha } g\), with \({{\mathcal {E}}}_{\alpha }\) and \({{\mathcal {H}}}_{\alpha }\) being defined as in (3.5) and (5.4), respectively, the results of [46, Lemma 3.3] allow us to conclude the estimate
To bound the term \({\mathrm {II}}\), we notice that if 
, \((\rho -1)\mathscr {U}\equiv 0\). If 
, then
Consequently,
A weighted Poincaré inequality, an application of (3.12) and (3.13), as in the proof of Proposition 3, and the use of the estimate (5.1) allow us to conclude the estimate
The regularity estimate (4.11) thus implies that
where C denotes a positive constant. Replacing the previous estimate for \(\text {II}\) and the one in (5.7) for \(\text {I}\) into (5.6) we obtain the desired exponential error estimate (5.5). \(\square \)
6 Space and time discretization
In this section we present two fully discrete schemes for approximating the solution to problem (1.1). In view of the localization results of Theorem 2 and the exponential error estimate (5.5) we shall thus discretize the truncated problem (5.3). We begin by setting notation on finite element spaces and introducing a finite element approximation in \(\varOmega \).
6.1 Finite element methods
We follow [5] and present a scheme based on the tensorization of a first-degree FEM in \(\varOmega \) with a suitable hp-FEM in the extended variable. The scheme achieves log-linear complexity with respect to the number of degrees of freedom in \(\varOmega \). To describe it, on the interval 
, we consider geometric meshes \({\mathcal {G}}^M_{\sigma } = \{ I_m \, | \,m =1,\dots M \}\) with M elements and grading factor \(\sigma \in (0,1)\):
Notice that the meshes \({\mathcal {G}}^M_{\sigma }\) are refined towards \(y=0\) in order to capture the singular behavior exhibited by the solution \(\mathscr {U}\) on the extended variable y as described in Propositions 1 and 2. On the aforementioned meshes, we consider a linear degree vector\({\varvec{r}}=(r_1,\dots ,r_M) \in {\mathbb {N}}^M\) with slope \(\mathfrak {s}\): \(r_m := 1 + \lceil \mathfrak {s}(m-1) \rceil \), where \(m=1,2,...,M\). With these ingredients at hand, we define the finite element space
and the subspace of 
containing functions that vanish at 
:
Let \(\mathscr {T}= \{ K\}\) be a conforming partition of \({\bar{\varOmega }}\) into simplices K. We denote by \(\mathbb {T}\) a collection of conforming and shape regular meshes that are refinements of an original mesh \(\mathscr {T}_0\). For \(\mathscr {T}\in \mathbb {T}\), we define \(h_{\mathscr {T}} = \max \{{{\,\mathrm{diam}\,}}(K) : K \in \mathscr {T}\}\) and \(N = \# \mathscr {T}\), the number of degrees of freedom of \(\mathscr {T}\). We introduce the finite element space:
With the meshes \({\mathcal {G}}_{\sigma }^M\) and \(\mathscr {T}\) at hand, we define 
and the finite-dimensional tensor product space
We write 
if the arguments are clear from the context.
Finally, we recall the standard \(L^2(\varOmega )\)-orthogonal projection operator \(\varPi _{x'} : L^2(\varOmega ) \rightarrow S^1_0(\varOmega ,\mathscr {T})\) which is such that
If \(\mathscr {T}\) is quasi-uniform, then [23, Lemma 1.131]
for all \(w \in H^1(\varOmega )\). If, in addition, \(w \in H^2(\varOmega )\), then [23, Proposition 1.134]
6.2 Weighted elliptic projector
We define the weighted elliptic projector
such that, for 
, it is given by
This operator is stable in 
[47, Proposition 26]:
In what follows we present approximation properties for 
.
Lemma 3
(error estimates for 
) Fix \(0< \sigma < 1\) and, for each \(\ell \), denote by \({\mathcal {G}}_{\sigma }^M\) the geometric mesh defined in (6.1) where 
with a sufficiently large constant. Assume that M is such that 
with absolute constants \(c_1\) and \(c_2\). Let \(w \in {\mathbb {H}}^{1+s}(\varOmega )\). If \({{\mathcal {W}}}\) denotes the truncated \(\alpha \)-harmonic extension of w, then there exists a minimal slope \(\mathfrak {s}_{min}\) such that for linear degree vectors \({\varvec{r}}\) with slope \(\mathfrak {s}\ge \mathfrak {s}_{min}\) there holds
In addition, if \(\mathscr {W}\) denotes the \(\alpha \)-harmonic extension of w, i.e., the solution to (3.6) with \(w \in {\mathbb {H}}^{1+s} (\Omega )\) as a datum, then
The hidden constants are independent of \({{\mathcal {W}}}\), \(\mathscr {W}\), w, and \(h_{\mathscr {T}}\).
Proof
Let 
and \(\varPi _{x'}\) be the univariate hp-interpolation operator of [5, Section 5.5.1] and the \(L^2(\varOmega )\)-projection operator defined in (6.4), respectively:
Set 
. Since 
, Galerkin orthogonality and definition (6.7) yield
It suffices to bound 
. The stability properties of \(\varPi _{x'}\), as described in (6.5), reveal that
The estimate (6.9) thus follows from the approximation properties of \(\varPi _{x'}\) as described in (6.6), the exponential interpolation error estimates of [5, Lemma 11], and the regularity properties of \({\mathcal {W}}\) [5, Theorem 1]. The estimate (6.10) follows similar arguments by using first the exponential decay of \(\mathscr {W}\) in the extended dimension [46, Proposition 3.1]:
This concludes the proof. \(\square \)
The following improved estimate for the weighted elliptic projection 
in the \(L^2(\varOmega )\)-norm can be obtained by invoking the estimates of Lemma 3 and the arguments elaborated in the proof of [47, Proposition 28].
Lemma 4
(\(L^2(\varOmega )\)-error estimates for 
) Let \({\mathcal {G}}_{\sigma }^M\) be the geometric mesh defined in (6.1) where 
with a sufficiently large constant. Let \(w \in {\mathbb {H}}^{1+s}(\varOmega )\). If \({{\mathcal {W}}}\) denotes the truncated \(\alpha \)-harmonic extension of w, then there exists a minimal slope \(\mathfrak {s}_{min}\) such that for linear degree vectors \({\varvec{r}}\) with slope \(\mathfrak {s}\ge \mathfrak {s}_{min}\) there holds
In addition, if \(\mathscr {W}\) denotes the \(\alpha \)-harmonic extension of w, i.e., the solution to (3.6) with \(w \in {\mathbb {H}}^{1+s}(\varOmega )\) as a datum, then
The hidden constants are independent of \({{\mathcal {W}}}\), \(\mathscr {W}\), w, and \(h_{\mathscr {T}}\).
6.3 Time discretization
Let \(K \in {\mathbb {N}}\) be the number of time steps. We define the uniform time step as \({\varDelta t}=T/K\), and we set \(t_k = k {\varDelta t}\), \(k=0,\dots , K\). If \(\mathcal {X}\) is a normed space with norm \(\Vert \cdot \Vert _{\mathcal {X}}\), then for \(w \in C([0,T];\mathcal {X})\) we denote \(w_k = w(t_k) \in \mathcal {X}\) and \(w_{{\varDelta t}} = \{ w_k \}_{k=0}^{K} \subset \mathcal {X}\). In addition, for \(w_{{\varDelta t}} \subset \mathcal {X}\) and \(p \in [1,\infty )\), we define
For a sequence of time-discrete functions \(w_{{\varDelta t}} \subset \mathcal {X}\), we define, for \(k=0,\dots ,K-1\),
We also define, for \(k = 1, \dots , K-1\),
and
6.4 Trapezoidal multistep method
Let us now describe our first fully discrete numerical scheme to solve problem (5.3). The space discretization is based on the finite element method on the truncated cylinder 
described in Sect. 6.1. The discretization in time is based on a trapezoidal multistep method.
The fully discrete scheme computes the sequence 
, an approximation of the solution to (5.3) at each time step. We initialize the scheme by setting
where \(\mathcal {H}_{\alpha }\) denotes the truncated \(\alpha \)-harmonic extension and \(\partial _t^2\mathcal {U}(0) = {{\mathcal {H}}}_\alpha w\) with \(w \in \mathbb {H}^s(\varOmega )\) satisfying
Note that, if \({{\,\mathrm{tr_\varOmega }\,}}\phi = 0\) the previous equation is satisfied for any w.
For \(k=1, \dots ,K-1\), let 
solve
for all 
, where \({\mathfrak {c}}V_k\) and \({\mathfrak {c}}f_k\) are defined in (6.16). To obtain an approximate solution to the fractional wave equation (1.1), we define the sequence
Remark 5
(locality) The main advantage of problem (6.18)–(6.20) is that it provides an approximated solution to the fractional wave equation (1.1) based on the resolution of the local elliptic problem with a dynamic boundary condition (5.3).
6.4.1 Stability
To present the stability of the scheme we introduce, for \(k=1,\dots ,K\), the unconditionally nonnegative discrete energy
Lemma 5
(energy conservation) If \(f \equiv 0\), then the fully discrete scheme (6.18)–(6.20) conserves energy, i.e., for all \(k \in \{1,\dots ,K\}\), we have that
If \(f \ne 0\), then, for \(\ell \in \{1,\dots ,K\}\), we have that
In particular, we have that \(E_{K}(V_{{\varDelta t}})^{\frac{1}{2}} \le E_{1}(V_{{\varDelta t}})^{\frac{1}{2}} + \tfrac{1}{\sqrt{2}}\Vert {\mathfrak {c}}f \Vert _{\ell ^1(L^2(\varOmega ))}\).
Proof
Set \(W=(2{\varDelta t})^{-1}(V_{k+1} - V_{k-1}) = 2^{-1}({{\mathfrak {d}}}V_{k+1} + {{\mathfrak {d}}}V_k) = ({\varDelta t})^{-1}(V_{k+1/2}-V_{k-1/2})\) in (6.20). Basic computations reveal that
If \(f \equiv 0\), the previous relation immediately yields (6.23). If \(f \ne 0\), an application of the Cauchy–Schwarz inequality allows us to conclude
which yields \( E_{k+1}(V_{{\varDelta t}})^{\frac{1}{2}} -E_k(V_{{\varDelta t}})^{\frac{1}{2}} \le \frac{{\varDelta t}}{\sqrt{2}} \Vert {\mathfrak {c}}f_k \Vert _{L^2(\varOmega )}. \) Adding over \(\ell \) we arrive at the desired estimate (6.24). This concludes the proof. \(\square \)
Let us now show the stability of the scheme.
Lemma 6
(stability) The fully discrete scheme (6.18)–(6.20) is stable, namely, for \(\ell \in \{1,\dots ,K\}\), we have that
where the hidden constant is independent of \(V_{{\varDelta t}}\) and \({\varDelta t}\).
Proof
The proof follows immediately from (6.24). \(\square \)
6.4.2 Error analysis
Let us now present an error analysis for the fully discrete scheme (6.18)–(6.20). To accomplish this task, we introduce the error \(e_{{\varDelta t}}:= V_{{\varDelta t}} - \mathcal {U}_{{\varDelta t}}\) and write, as usual,
The control of \(P_{{\varDelta t}}\) follows from (6.9) and (6.12): For \(\ell \in \{0,1,2\}\), we have the error estimates
and
where \({\mathfrak {A}}(f,g,h)\) is defined in (4.20). Notice that to obtain the estimates (6.27) and (6.28) the regularity estimates of Corollary 1 are essential.
In what follows we bound the sequence \(\varTheta _{{\varDelta t}}\).
Lemma 7
(error estimate for \(\varTheta _{{\varDelta t}}\)) Let \(\mathcal {U}\) be the solution to (5.3) and let \(V_{{\varDelta t}}\) be its fully discrete approximation defined as the solution to (6.18)–(6.20). If \({\mathfrak {A}}(f,g,h) < \infty \) and \(\varXi (f,g,h) < \infty \), then
where 
, \({\mathfrak {A}}(f,g,h)\) and \(\varXi (f,g,h)\) are defined in (4.20) and (4.10), respectively, and the hidden constant is independent of \(V_{{\varDelta t}}\), \(\mathcal {U}\), \({\varDelta t}\), and \(h_{\mathscr {T}}\).
Proof
We proceed in three steps.
Step 1. We invoke the continuous problem (5.3), the discrete equation (6.20), and the definition of 
, given by (6.7), to arrive at the problem that controls the error: For \(k = 1,\dots ,K-1\), 
solves
where \({\mathfrak {c}} \partial _t^2 \mathcal {U}(t_k)\) and 
are defined by (6.16) and (6.17), respectively. On the other hand, in view of Remark 4 and (6.18), we have that
and
Now, we write, for \(k \ge 1\), the difference 
as follows:
We thus apply the stability estimate (6.24) to (6.30) and obtain
where \(\delta _{{\varDelta t}} = \{ \delta _k \}_{k=1}^{K-1}\) and 
.
Step 2. We proceed to control the term \(\Vert \delta _{{\varDelta t}} \Vert _{\ell ^1(L^2(\varOmega ))}\). First, notice that
To control \(\Vert {{\,\mathrm{tr_\varOmega }\,}}{\mathrm {I}}_k \Vert _{L^2(\varOmega )}\) we employ a basic result based on Taylor’s Theorem. In fact, for \(k \ge 1\), we have
Now, notice that in view of (6.26) we have that \({\mathrm {II}}_k = -{{\mathfrak {d}}}^2 P(t_k)\). The same argument that yields (6.33) allow us to conclude the estimate
We invoke the trace estimate (2.9) and the stability estimate (6.8) of the weighted elliptic projection to conclude, for \(z \in (0,T)\), that \(\Vert {{\,\mathrm{tr_\varOmega }\,}}\partial _t^4 P(\cdot ,z) \Vert _{L^2(\varOmega )}\) is bounded by
Consequently, an application, again, of the trace estimate allows us to conclude an estimate for \({{\,\mathrm{tr_\varOmega }\,}}{\mathrm {II}}_k\):
where we have used (6.28) with \(\ell = 2\); \({\mathfrak {A}}(f,g,h)\) is defined in (4.20).
We finally bound \({\mathrm {III}}_k\). To accomplish this task, we invoke an argument based on Taylor’s Theorem. In fact, for \(k \ge 1\), we have
where \({\underline{z}}\) and \({\overline{z}}\) belong to \((t_{k-1},t_{k+1})\).
Replacing the estimates (6.33), (6.34), and (6.35) into (6.32) we arrive at
Step 3. We bound \(E_1(\varTheta _{{\varDelta t}})\). Since \(\varTheta _0 = 0\), we utilize (6.15) and write
In view of the trace estimate (2.9) and the stability property of 
, given in (6.8), we can thus conclude that
An application of Taylor’s Theorem reveals that
which immediately yields
The desired estimate follows from replacing (6.36) and (6.38) into (6.31) and using the time-regularity results of Theorem 4. \(\square \)
The exponential error estimate of Lemma 2 combined with the error estimate of Lemma 7 allow us to conclude the following error estimates.
Lemma 8
(error estimates for (6.18)–(6.20)) Let \(\mathscr {U}\) be the solution to (3.3) and let \(V_{{\varDelta t}}\) be the solution to the fully discrete problem (6.18)–(6.20). If \({\mathfrak {A}}(f,g,h) < \infty \) and \(\varXi (f,g,h) < \infty \) then, we have the following error estimates
and
where \({\mathfrak {A}}(f,g,h)\) and \(\varXi (f,g,h)\) are defined by (4.20) and (4.10), respectively, and the hidden constants are independent of \(V_{{\varDelta t}}\), \(\mathcal {U}\), \(\mathscr {U}\), \({\varDelta t}\), and \(h_{\mathscr {T}}\).
Proof
We proceed in several steps.
Step 1. We begin with the following trivial application of the triangle inequality:
To control the term \( \text {I}\) we invoke the exponential error estimate (5.5). The latter yields
The control of the term \(\text {II}\) is as follows:
where we recall that \(e_K = V_K - \mathcal {U}_K\). Replace the obtained estimates into (6.41). This yields
Step 2. The control of \(\text {II}_1 = \Vert {{\,\mathrm{tr_\varOmega }\,}}[ \partial _t \mathcal {U}(t_{K-1/2})- {{\mathfrak {d}}}\mathcal {U}_K] \Vert _{L^2(\varOmega )}\) follows from a simple application of Taylor’s Theorem. In fact, we have that
We now focus on the term \({\mathrm {II}}_2 = \Vert {{\,\mathrm{tr_\varOmega }\,}}{{\mathfrak {d}}}e_K \Vert _{L^2(\varOmega )}\). The triangle inequality yields
The result of Lemma 7 implies that
The control of \(\Vert {{\,\mathrm{tr_\varOmega }\,}}{{\mathfrak {d}}}P_K \Vert _{L^2(\varOmega )}\) follows the same arguments used to bound \(\text {II}_1:\)
The stability property (6.8) and the estimate (6.28) imply the estimates
The previous estimate combined with (6.43) allow us to control \({\mathrm {II}}_2\). Replacing the obtained estimates for \({\mathrm {II}}_1\) and \({\mathrm {II}}_2\) into (6.42) yield the desired estimate (6.39).
Step 3. To obtain (6.40) we invoke similar arguments upon using the estimate
This concludes the proof. \(\square \)
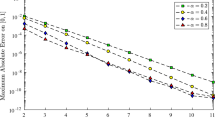
The following error estimates follow immediately from Lemma 8 and show how the fully discrete approximation \(U_{{\varDelta t}}\) approximates u.
Theorem 6
(error estimates for (6.21)) Let u be the solution to (1.1) and let \(U_{{\varDelta t}}\) be its fully discrete approximation defined by (6.21). If \({\mathfrak {A}}(f,g,h) < \infty \) and \(\varXi (f,g,h) < \infty \), then
and
where \({\mathfrak {A}}(f,g,h)\) and \(\varXi (f,g,h)\) are defined by (4.20) and (4.10), respectively, and the hidden constants are independent of \(U_{{\varDelta t}}\), u, \({\varDelta t}\), and \(h_{\mathscr {T}}\).
6.5 The leapfrog scheme
We now present a second fully discrete scheme to approximate the solution to (1.1). To advance in time we use the leapfrog time-stepping method while the discretization in space is based on the finite element method described in Sect. 6.1. The scheme computes a sequence 
, an approximation to the solution to (5.3) at each time step. To begin with the description of the scheme, we first initialize it by setting
where \(\partial _t^2\mathcal {U}(0) = {{\mathcal {H}}}_{\alpha }w\) and w solves (6.19). For \(k=1,\dots ,K -1\), 
solves
for all 
. As in the previous section, we define an approximated solution to problem (1.1) as
Note that in the k-th step we can assume to have \({{\,\mathrm{tr_\varOmega }\,}}V_k\) and \({{\,\mathrm{tr_\varOmega }\,}}V_{k-1}\) already computed. However, to be able to compute 
we need the discrete function \(V_k\) on the whole cylinder 
. The function \(V_k\) can be obtained by solving the following discrete problem: Find 
, an extension of \({{\,\mathrm{tr_\varOmega }\,}}V_k\), such that
Hence, the leapfrog scheme when applied to our problem requires the resolution of a linear system at each time step even when using mass-lumping. As a consequence of the nonlocality of \((-\varDelta )^s\), the explicit nature of the leapfrog scheme seems to be lost. Further details on the implementation of this scheme are given in Sect. 8.2.
In the analysis that follows, the following discrete inverse inequality will be instrumental.
Lemma 9
(discrete inverse inequality) Let \(\eta \in \mathbb {H}^{-s}(\varOmega )\) and let 
be the solution to
We thus have that \( \Vert { X }\Vert _{\mathcal {C}} \lesssim \Vert {{\,\mathrm{tr_\varOmega }\,}}X \Vert _{\mathbb {H}^s(\varOmega )}\) and that
for some constant \( C_{\mathrm{inv}} > 0\)
Proof
Define \(Z := {{\,\mathrm{tr_\varOmega }\,}}X \in S_0^1(\varOmega ,\mathscr {T})\). There exists 
such that \({{\,\mathrm{tr_\varOmega }\,}}\chi = Z\). In fact \(\chi = {{\mathcal {H}}}_{\alpha } Z\), where \({{\mathcal {H}}}_{\alpha }\) is defined in (5.4).
Let us introduce the operator \({\tilde{\varPi }} = \varPi _{x'} \otimes {\tilde{\varPi }}_{y}^ {{\varvec{r}}}\), where \({\tilde{\varPi }}_{y}^ {{\varvec{r}}}\) is a slight modification of the operator of [5, Section 5.5.1]: on the first interval \(I_1\), interpolation at the edge point 0 is used rather than in the middle point of \(I_1\). The operator \(\varPi _{x'}\) corresponds to the \(L^2(\varOmega )\)-orthogonal projection operator defined in (6.4). Define \({\tilde{X}} = {\tilde{\varPi }} \chi \) and notice that the stability properties of \({\tilde{\varPi }}\) and \( {\tilde{\varPi }}_{y}^ {{\varvec{r}}}\) yield
This, in view of the fact that \( \Vert {\chi }\Vert _{\mathcal {C}} \lesssim \Vert Z \Vert _{\mathbb {H}^s(\varOmega )}\), implies \( \Vert {{\tilde{X}}}\Vert _{\mathcal {C}} \lesssim \Vert Z \Vert _{\mathbb {H}^s(\varOmega )}\).
Now, since \(Z \in S_0^1(\varOmega ,\mathscr {T})\), we have that \({{\,\mathrm{tr_\varOmega }\,}}{\tilde{X}} = {{\,\mathrm{tr_\varOmega }\,}}\chi = Z = {{\,\mathrm{tr_\varOmega }\,}}X\) and then that \({{\,\mathrm{tr_\varOmega }\,}}(X-{\tilde{X}}) = 0\). Since 
, we can thus invoke problem (6.49) and conclude that
which yields
This immediately implies that \( \Vert {X}\Vert _{\mathcal {C}} \le \Vert {{\tilde{X}}}\Vert _{\mathcal {C}}, \) and thus, since \( \Vert {{\tilde{X}}}\Vert _{\mathcal {C}} \lesssim \Vert Z \Vert _{\mathbb {H}^s(\varOmega )}\), we can conclude that
Since \(Z = {{\,\mathrm{tr_\varOmega }\,}}X\), we have thus obtained the desired estimate \( \Vert {X}\Vert _{\mathcal {C}} \lesssim \Vert {{\,\mathrm{tr_\varOmega }\,}}X \Vert _{\mathbb {H}^s(\varOmega )}\). The estimate (6.50) thus follows, for instance, from the results of [17]. \(\square \)
6.5.1 Stability
To analyze the fully discrete scheme (6.46), (6.47), we define, for \(k= 1,\dots , K\), the discrete energy
where the bilinear form 
is defined in (5.2).
In the result that follows we show the nonnegativity of the discrete energy \( \mathscr {E}_k\) under the following CFL condition: \({\varDelta t}\) is chosen to be sufficiently small such that
The constant \(C_{\mathrm {inv}}\) is as in (6.50).
Lemma 10
(CFL condition and nonnegativity of \(\mathscr {E}_k\)) If (6.52) holds, then
for all \(k \in \{ 1,\cdots ,K\}\).
Proof
We invoke the inverse inequality (6.50) and the CFL condition (6.52) to arrive at
where, in the last step, we have used definition (6.15). Consequently,
which immediately yields (6.53). This concludes the proof. \(\square \)
Lemma 11
(energy conservation) If \(f \equiv 0\), then the fully discrete scheme (6.46), (6.47) conserves energy, i.e., for all \(k \in \{ 1, \dots , K\}\), we have that
If \(f \ne 0\), then, for \(\ell \in \{1,\dots ,K \}\), we have that
In particular, we have that \(\mathscr {E}_{K}(V_{{\varDelta t}})^{\frac{1}{2}} \le \mathscr {E}_{1}(V_{{\varDelta t}})^{\frac{1}{2}} + \tfrac{1}{\sqrt{2\theta }}\Vert f \Vert _{\ell ^1(L^2(\varOmega ))}\).
Proof
Set \(W=(2{\varDelta t})^{-1}(V_{k+1} - V_{k-1}) = 2^{-1}({{\mathfrak {d}}}V_{k+1} + {{\mathfrak {d}}}V_k)\) in (6.47). This yields
In the case that \(f \equiv 0\), (6.56) immediately yields (6.54). If \(f \ne 0\), a trivial application of the Cauchy–Schwarz inequality reveals that
Invoke the estimate (6.53) and conclude, for \(k \in \{1,\dots ,K-1\}\), that \(\mathscr {E}_{k}(V_{{\varDelta t}}) \ge (\theta /2) \Vert {{\,\mathrm{tr_\varOmega }\,}}{{\mathfrak {d}}}V_k\Vert ^2_{L^2(\varOmega )}\). Thus,
Consequently, we arrive at \(\mathscr {E}_{k+1}(V_{{\varDelta t}})^{\frac{1}{2}} - \mathscr {E}_{k}(V_{{\varDelta t}})^{\frac{1}{2}} \le ({\varDelta t}/\sqrt{2\theta }) \Vert f_k \Vert _{L^2(\varOmega )}\) which, by adding over \(\ell \), yields (6.55). This concludes the proof. \(\square \)
Lemma 12
(stability) The fully discrete scheme (6.46), (6.47) is stable: for \(\ell \in \{1,\dots ,K\}\), we have that
where the hidden constant is independent of \(V_{{\varDelta t}}\), \({\varDelta t}\) and \(h_{\mathscr {T}}\) but depends on the parameter \(\theta \).
Proof
We begin by noticing that (6.53) yields
Now, since
an application of the estimate (6.55) allows us to conclude that
The desired estimate (6.57) thus follows from replacing the previous estimate into (6.58). This concludes the proof. \(\square \)
6.5.2 Error analysis
We now present error estimates for the fully discrete approximation \(U_{{\varDelta t}}\) defined in (6.48) that is based on the solution \(V_{{\varDelta t}}\) to the fully discrete scheme (6.46), (6.47). The arguments are similar to the ones used to prove the results in Lemma 7, Lemma 8, and Theorem 6. For brevity we leave details to the reader.
Theorem 7
(error estimates for (6.48)) Let u be the solution to (1.1) and let \(U_{{\varDelta t}}\) be its fully discrete approximation defined by (6.48). If \({\mathfrak {A}}(f,g,h) < \infty \) and \(\varXi (f,g,h) < \infty \), then
and
where \({\mathfrak {A}}(f,g,h)\) and \(\varXi (f,g,h)\) are defined by (4.20) and (4.10), respectively, and the hidden constants are independent of \(U_{{\varDelta t}}\), u, \({\varDelta t}\), and \(h_{\mathscr {T}}\).
6.6 Computable data
In (6.18) we considered
as initial data for the fully discrete schemes of Sects. 6.4 and 6.5. Since the action of \({{\mathcal {H}}}_{\alpha }\) involves the resolution of a problem posed on an infinite dimensional space, we immediately conclude that the initial data \(V_0\) and \(V_1\)are not computable.
To overcome this deficiency, we introduce the discrete extension operator \({\mathcal {H}}_{\alpha }^{\mathscr {T}}\), which is defined as follows: if \(e \in S_0^1(\varOmega ,\mathscr {T})\), then 
is such that
With \({\mathcal {H}}_{\alpha }^{\mathscr {T}}\) at hand, we define the following computable initial data:
where \(Z \in S_0^1(\varOmega ,\mathscr {T})\) solves 
for all 
. Notice that Z corresponds to a finite element approximation of \({{\,\mathrm{tr_\varOmega }\,}}\partial _t^2 {\mathcal {U}}(0)\).
If we consider \({\widetilde{V}}_0\) and \({\widetilde{V}}_1\), instead of \(V_0\) and \(V_1\), as initial data for the schemes of Sects. 6.4 and 6.5, then, to provide an a priori error analysis, it is necessary to modify the first two elements of the sequence \(\varTheta _{{\varDelta t}}\), defined in (6.26), as follows:
In particular, it suffices to estimate
We present the following error estimates.
Lemma 13
(error estimates for \(\varTheta _0\) and \(\varTheta _1\)) If \((V_0,V_1)\) and \(({\widetilde{V}}_0, {\widetilde{V}}_1)\) are defined by (6.61) and (6.62), respectively, then
and
where \({\mathfrak {A}}(f,g,h)\) and \(\varXi (f,g,h)\) are defined by (4.20) and (4.10), respectively, and the hidden constants are independent of g, h, \((V_0,V_1)\), \(({\widetilde{V}}_0,{\widetilde{V}}_1)\), and \(h_{\mathscr {T}}\).
Proof
Since 
, we can invoke property (6.7) and conclude that
To bound \({\mathrm {I}}\), we notice that \({{\,\mathrm{tr_\varOmega }\,}}( {\widetilde{V}}_0 - {{\mathcal {H}}}_\alpha \varPi _{x'} g) =0\). On the other hand, \(V_0 - \widetilde{V}_0\) satisfies
and 
. Consequently, \( {\mathrm {I}} = 0. \) Now, since \({\mathcal {H}}_{\alpha }\) satisfies \( \Vert {{\mathcal {H}}_{\alpha } w}\Vert _{\mathcal {C}} \lesssim \Vert w \Vert _{\mathbb {H}^s(\varOmega )}\) for all \(w \in \mathbb {H}^s(\varOmega )\), we arrive at
Since \({\mathrm {I}} = 0\), the estimate for \({\mathrm {II}}\) yields (6.63).
We now control \( \Vert {\varTheta _1}\Vert _{\mathcal {C}}\). A basic application of the triangle inequality together with estimate (6.37) reveal that
It thus suffices to bound \( \Vert {{\widetilde{V}}_1 - V_1}\Vert _{\mathcal {C}}\). To accomplish this task, we first notice that a simple application of Taylor’s Theorem yields
with \({\overline{\zeta }} \in (0,t_1)\). Similar arguments allow us to conclude that
with \({\underline{\zeta }} \in (0,t_1)\). Consequently,
To estimate \({\mathrm {I}}\) we invoke the same arguments that lead to (6.63):
A bound for the term \({\mathrm {III}}\) follows from stability results. The collection of these estimates yield (6.64) \(\square \)
Lemma 14
(estimate for \(E_1(\varTheta _{{\varDelta t}})\)) If we consider \({\widetilde{V}}_0\) and \({\widetilde{V}}_1\) as initial data for the schemes of Sects. 6.4 and 6.5, we then have that
and
where \({\mathfrak {A}}(f,g,h)\) and \(\varXi (f,g,h)\) are defined by (4.20) and (4.10), respectively, and the hidden constants are independent of g, h, \((V_0,V_1)\), \(({\widetilde{V}}_0,{\widetilde{V}}_1)\), and \(h_{\mathscr {T}}\)
Proof
The proof of (6.68) follows directly from the estimates (6.63) and (6.64). In what follows we derive (6.67). To accomplish this task and simplify notation, we define
Now, notice that
The trace estimate (2.9), the stability property (6.8) and an application of Taylor’s Theorem reveal that
We now use the definitions of \({\widetilde{V}}_0\) and \({\widetilde{V}}_1\) to arrive at
To bound 
we proceed as follows:
where we have used (6.28) with \(\ell = 1\). Similar arguments allow us to control 
. This concludes the proof. \(\square \)
Remark 6
(influence of computable data in error estimates) If \(({\widetilde{V}}_0, {\widetilde{V}}_1)\) are used as initial data for the trapezoidal multistep method of Sect. 6.4 and the leapfrog scheme of Sect. 6.5, then the error estimates of Theorems 6 and 7 hold with no modifications.
7 Polygonal domains \(\varOmega \subset {\mathbb {R}}^2\)
In this section, we let \(\varOmega \subset {\mathbb {R}}^2\) be an open and bounded, but not necessarily convex, polygon and provide a priori error estimates for the trapezoidal multistep method (6.18)–(6.21). Notice that the error estimates that we have previously derived for this scheme, i.e., estimates (6.44) and (6.45), rely on the convexity of the domain \(\varOmega \). Given \(g \in H^{-1}(\varOmega )\), we consider the Dirichlet problem
It is immediate that problem (7.1) has a unique solution \(w\in H^1_0(\varOmega )\). However, in general the solution \(w \notin H^2(\varOmega )\), even if \(g \in C^{\infty }({\bar{\varOmega }})\) [31]. More precisely, for every \(\epsilon > 0\), there exists a polygon \(\varOmega _{\epsilon }\) and a smooth function \(g_{\epsilon }\) such that the corresponding solution \(w_{\epsilon }\) does not belong to \(H^{3/2+\epsilon }(\varOmega _{\epsilon })\) [53]. However, under additional regularity assumptions on A, c, and g, a regularity analysis can be carried out in weighted function spaces related to the geometry of \(\partial \varOmega \); see Proposition 4 below.
7.1 Regularity estimates in weighted spaces
Let \(\varOmega \subset {\mathbb {R}}^2\) be an open and bounded, but not necessarily convex, polygon with straight sides and corners \(\{{\varvec{c}}\}\) and \(\beta \ge 0\). We define the weight and the weighted Lebesgue space
We also define \(H^2_\beta (\varOmega )\) as the closure of \(H^2(\varOmega ) \cap H^1_0(\varOmega )\) with respect to the norm
With this setting at hand, we present the following regularity result for (7.1).
Proposition 4
(weighted regularity estimate) Let \(A \in W^{1,\infty }(\varOmega ,{\text {\textsf {GL}}}(\mathbb {R}^2))\) be uniformly positive definite and \(c\in W^{1,\infty }(\varOmega ,\mathbb {R})\) with \(c \ge 0\). Then, there exists \(\beta \in [0,1)\), depending only on \(\varOmega \), A, and c, such that for \(g\in L^2_\beta (\varOmega )\) the solution w of (7.1) belongs to \(H^2_\beta (\varOmega )\). In addition, the solution w satisfies the estimate
where the hidden constant is independent of g.
Proof
The result follows from [4, Theorem 1.1]. To observe this, it suffices to set, in the notation of that reference, \(m=1\), \(b_j=0\), and \(\beta = 1 - a\). \(\square \)
The following space regularity estimates follow from Propositions 2 and 4.
Theorem 8
(global regularity of \(\mathscr {U}\): weighted estimates in \(\varOmega \)) Let A and c satisfy the assumptions of Proposition 4. Let \(\mathscr {U}\) solve (1.2), (1.3) for \(s \in (0,1)\). Then, there exists \(\beta \in [0,1)\), depending only on \(\varOmega \), A, and c, such that the following regularity assertions hold:
-
(i)
For \(0 \le \nu ' < 1-s\), we have that
$$\begin{aligned}&\Vert \mathscr {U}\Vert ^2_{L^2(0,T;L^2(\omega _{\alpha -2\nu ',\theta },(0,\infty );H^2_\beta (\varOmega )))} \lesssim \Big ( \Vert g \Vert ^2_{{\mathbb {H}}^{1+\nu '+s}(\varOmega )} \nonumber \\&\quad + \Vert h \Vert ^2_{{\mathbb {H}}^{1+\nu '}(\varOmega )} + \Vert f \Vert _{L^2(0,T;{\mathbb {H}}^{1+ \nu '}(\varOmega ))}^2 \Big ). \end{aligned}$$(7.4) -
(ii)
For \(0 \le {\tilde{\nu }} < 1+s\), there exists \(\kappa >1\) such that
$$\begin{aligned}&\Vert \partial _y^{\ell +1}\mathscr {U}\Vert ^2_{L^2(0,T; L^2(\omega _{\alpha +2(\ell +1)-2{\tilde{\nu }} ,\theta },(0,\infty );H^2_\beta (\varOmega )))} \lesssim \kappa ^{2(\ell +1)}(\ell +1)!^2 \nonumber \\&\quad \cdot \left( \Vert g \Vert ^2_{{\mathbb {H}}^{1+{\tilde{\nu }}+s}(\varOmega )} + \Vert h \Vert ^2_{{\mathbb {H}}^{1+{\tilde{\nu }}}(\varOmega )} + \Vert f \Vert _{L^2(0,T;{\mathbb {H}}^{1+{\tilde{\nu }}}(\varOmega ))}^2 \right) , \end{aligned}$$(7.5)for all \(\ell \in {{{\mathbb {N}}}}_0\).
In both estimates the hidden constants are independent of \(\mathscr {U}\) and the problem data. In addition, in (7.5) the hidden constant is also independent of \(\ell \).
Proof
The proof of (7.5) follows from (4.8) and (7.3). In fact, for fixed \(y > 0\) and \(t>0\), set \(w = \partial _y^{\ell +1}\mathscr {U}(\cdot ,y,t)\) in (7.1) and hence \(g = \partial _y^{\ell +1}{\mathcal {L}}\mathscr {U}(\cdot ,y,t)\). Since \(\beta \ge 0\), we have that \(g \in L^2_{\beta }(\varOmega )\). We can thus apply the estimate (7.3) to arrive at
Square the previous estimate, multiply by the weight \(\omega _{\alpha +2(\ell +1)-2{\tilde{\nu }} ,\gamma }\) and integrate, first, with respect to y over \((0,\infty )\) and then with respect to t over (0, T). We thus utilize (4.8) to arrive at the desired estimate (7.5).
Similar arguments allow us to derive (7.4). For brevity, we skip details. \(\square \)
We conclude this section by mentioning that, on the basis of the estimate (4.18), the following space–time regularity estimate can be derived. Let \(0 \le \sigma < s\) and \(0 \le {\tilde{\nu }} < 1+s\). Then, there exists \(\kappa > 1\) such that the following estimate holds for all \(\ell \in {\mathbb {N}}_0\):
The hidden constant is independent of \(\mathscr {U}\), \(\ell \), and the problem data. Consequently,
where \({\mathfrak {A}}\) is defined in (4.20); compare with (4.21).
7.2 Meshes, finite element spaces, and quasi-interpolation operators
In the next section we will present error estimates for the trapezoidal scheme on the basis of a piecewise linear finite element discretization on properly refined meshes in \(\varOmega \). We stress that \(\varOmega \subset {\mathbb {R}}^2\) is an open and bounded, but not necessarily convex, polygon. The analysis requires meshes and approximation operators suitable for the approximation of functions with \(H^2_{\beta }(\varOmega )\) regularity. This is achieved with appropriate refinement toward the vertices of \(\varOmega \) [27].
In what follows, we will consider nested sequences \(\{ \mathscr {T}^\ell \}_{\ell \ge 0}\) of triangulations of \(\varOmega \) that are generated by bisection-tree refinement of a coarse, regular initial triangulation \(\mathscr {T}^0\) of \(\varOmega \). We denote by \(h_\ell =\max \{{{\,\mathrm{diam}\,}}(K) : K \in \mathscr {T}^\ell \}\) the meshwidth of \(\mathscr {T}^\ell \). On these meshes we will consider the finite element spaces \(S_0^1(\varOmega , \mathscr {T}^\ell )\) defined in (6.2).
We present the existence of a sequence of meshes \(\{ \mathscr {T}^\ell _{\beta } \}_{\ell \ge 0}\) and operators \(\varPi ^\ell _\beta \) that satisfy a series of properties on which our theory rests. In what follows, \(\beta \in (0,1]\).
Lemma 15
(meshes \(\{ \mathscr {T}^\ell _\beta \}_{\ell \ge 0}\) and operators \(\varPi ^\ell _\beta \)) There is a sequence \(\{\mathscr {T}^\ell _\beta \}_{\ell \ge 0}\) of nested, regular bisection-tree meshes with corresponding quasi-interpolation operators \(\varPi ^\ell _\beta :L^2(\varOmega ) \rightarrow S^1_0(\varOmega ,\mathscr {T}^\ell _\beta )\) such that the following properties hold:
-
(i)
\(N_\ell := {\text {dim}} S^1_0(\varOmega ,\mathscr {T}^\ell _\beta ) \lesssim h_\ell ^{-2}\).
-
(ii)
Simultaneous stability:
$$\begin{aligned} \Vert \varPi ^\ell _\beta v\Vert _{L^2(\varOmega )}&\lesssim \Vert v\Vert _{L^2(\varOmega )} \qquad \forall v \in L^2(\varOmega ), \\ \Vert \varPi ^\ell _\beta v\Vert _{H^1(\varOmega )}&\lesssim \Vert v\Vert _{H^1(\varOmega )} \qquad \forall v \in H^1_0(\varOmega ). \end{aligned}$$ -
(iii)
Projection property: \(\varPi ^\ell _\beta v = v\) for all \(v \in S^1_0(\varOmega ,\mathscr {T}^\ell _\beta )\).
-
(iv)
Optimal approximation rates for \(H^1_0(\varOmega )\) and \(H^2_\beta (\varOmega )\)-functions:
$$\begin{aligned}&N_\ell \Vert w - \varPi ^\ell _\beta w\Vert ^2_{L^2(\varOmega )} \lesssim \Vert w\Vert ^2_{H^1(\varOmega )} \end{aligned}$$(7.7)$$\begin{aligned}&N_\ell \Vert w - \varPi ^\ell _\beta w\Vert ^2_{L^2(\varOmega )} + \Vert \nabla _{x'} (w - \varPi ^\ell _\beta w)\Vert ^2_{L^2(\varOmega )} \lesssim N_\ell ^{-1} \Vert w\Vert ^2_{H^2_\beta (\varOmega )}, \end{aligned}$$(7.8)for all \(w \in H^1_0(\varOmega )\) and all \( w \in H^1_0(\varOmega ) \cap H^2_\beta (\varOmega )\), respectively.
In (ii) and (iv), constants hidden in \(\lesssim \) are independent of \(\ell \).
Proof
The meshes \(\{ \mathscr {T}^\ell _{\beta } \}_{\ell \ge 0}\) are constructed as described in [27]. By construction, property (i) follows. Approximation properties follow from [27] and [44, Section 5]:
where \(I_{\mathscr {T}}\) denotes the nodal interpolant. The operator \(\varPi ^\ell _\beta \) can be taken as the \(L^2(\varOmega )\)-orthogonal projection. The results of [26] thus guarantee the stability estimates stated in item (ii). The estimates (7.7) and (7.8) follow from the fact that \(\varPi ^\ell _\beta \) preserves the finite element space combined with (7.9). We refer the reader to the proof of [5, Lemma 8] for further details. \(\square \)
7.3 Approximation properties for the elliptic projector
We derive approximation properties for the elliptic projector 
, defined in (6.7), within the finite element framework described in Sect. 7.2.
Let \(\beta \in (0,1]\) be such that (7.3) holds. Let \((\mathscr {T}^\ell _\beta )_{\ell \ge 0}\) be a sequence of uniformly shape-regular meshes of meshwidth \(h_{\ell }\) such that the properties stated in Lemma 15 hold. Within this framework, the following error estimates can be derived; see also [5, Theorem 5].
Lemma 16
(error estimates) Fix \(0< \sigma < 1\) and, for each \(\ell \), denote by \({\mathcal {G}}_{\sigma }^M\) the geometric mesh on 
defined in (6.1), where 
with a sufficiently large constant. Assume that M is such that 
with absolute constants \(c_1\) and \(c_2\). Let \(w \in {\mathbb {H}}^{1+s}(\varOmega )\). If \({{\mathcal {W}}}= {{\mathcal {H}}}_{\alpha } w\) denotes the truncated \(\alpha \)-harmonic extension of w, then there exists a minimal slope \(\mathfrak {s}_{min}\) such that for linear degree vectors \({\varvec{r}}\) with slope \(\mathfrak {s}\ge \mathfrak {s}_{min}\) there holds
and
The hidden constants are independent of \({{\mathcal {W}}}\), w, and \(h_{\ell }\).
Proof
Replace, in the proof of Lemma 3, the operator \(\varPi _{x'}\) by \(\varPi ^\ell _\beta \). Invoke the stability and approximation properties of the latter, as described in Lemma 15, items (ii) and (iv), respectively, and utilize the weighted regularity estimate of [5, Theorem 2]. This concludes the proof. \(\square \)
7.4 Error estimates
In previous sections we have elaborated all the ingredients that can allow us to conclude the following error estimates for the trapezoidal scheme.
Theorem 9
(error estimates for (6.21)) Let u be the solution to (1.1) and let \(U_{{\varDelta t}}\) be its fully discrete approximation defined by (6.21). In the framework of Lemma 16, we have the following error estimates for the trapezoidal scheme
and
The hidden constants are independent of \(U_{{\varDelta t}}\), u, \({\varDelta t}\), and \(h_{\ell }\).
Proof
Invoke the arguments developed in the proof of Lemmas 7 and 8 upon utilizing the error estimates (7.10) and (7.11) for the weighted elliptic projector. \(\square \)
We conclude this section with the following remark.
Remark 7
(Leapfrog scheme) The extension of the error estimates (6.59) and (6.60) to the setting described in Sect. 7.2 would require a stability result as (6.57). This, in turns, requires a CFL condition that limits the choice of the size of the time step to be bounded by the minimal meshsize in the spatial finite element mesh. In view of the nature of the meshes \(\{ \mathscr {T}_{\beta }^{\ell } \}_{\ell \ge 0}\) this would lead to an impractical algorithm. Several techniques have been developed in order to remove such a critical restriction. These include local time-stepping [20, 34] and the incorporation of a subspace projection step inspired by numerical homogenisation [50].
8 Numerical results and implementation
Let \(\{ \phi _1, \dots , \phi _{\mathcal {M}} \}\) denote a basis of 
such that \(\phi _1(0) = 1\) and \(\phi _j(0) = 0\) for \(j > 1\). The corresponding mass and stiffness matrices are denoted by 
and 
:
We denote by \(B_{\varOmega }\) and \(A_{\varOmega }\) the standard mass and stiffness matrices corresponding to the finite element space \(S^1_0(\varOmega ,\mathscr {T})\). In what follows, we describe the implementation of a discrete Dirichlet-to-Neumann map. Once this operation is available the time-stepping methods that are proposed in this work can be implemented in a standard way; in the case of the implicit method some further steps may be needed in order to obtain an efficient algorithm.
8.1 Discrete Dirichlet-to-Neumann map
Given \(U \in S^1_0(\varOmega ,\mathscr {T})\), we consider the problem: Find 
and \(\eta \in S^1_0(\varOmega ,\mathscr {T})\) such that
Let us denote by \(\mathbf {U}\), \(\mathbf {V}\), and \(\varvec{\eta }\) the coefficient vectors associated with the discrete functions U, V, and \(\eta \), respectively. Note that the first N components of \(\mathbf {V}\) and \(\mathbf {U}\) are equal; we recall that \(N = \# \mathscr {T}\), the number of degrees of freedom of \(\mathscr {T}\). We denote the remaining components of \(\mathbf {V}\) by \({\widetilde{\mathbf {V}}} = (\mathbf {V})_i\), \(i = N+1,\dots , N\mathcal {M}\). With this notation at hand, the matrix system (8.1) takes the form
We denote by 
and 
the matrices that are obtained by removing the first row and first column from 
and 
, respectively. Let 
and 
denote the vectors containing the first components of the rows \(i \in \{ 2,\dots ,\mathcal {M}\}\) of the matrices 
and 
.
The vector \({\widetilde{\mathbf {V}}}\) is the solution to
Once this system is solved we can obtain \(\varvec{\eta }\) by solving
where 
and 
. We denote by \(L_h^s\) the matrix that describes the linear map \(u \mapsto \eta \):
The main computational cost when solving (8.1) is the resolution of (8.2). This can be done efficiently by diagonalizing the small matrices 
and 
. In fact, since both matrices are symmetric and positive definite, we can find a matrix of generalized eigenvectors X such that
where \(\mu _j > 0\) denote the eigenvalues of the generalized eigenvalue problem 
. The system (8.2) can thus be transformed to \(\mathcal {M}\) independent linear systems
where \({\hat{\mathbf {V}}}^T = ({\hat{\mathbf {V}}}^T_1,\dots , {\hat{\mathbf {V}}}^T_\mathcal {M})\),
and \(I \in {\mathbb {R}}^{N \times N}\) is the identity matrix.
8.2 Leapfrog time-stepping scheme
Using the previously defined operator \(L_h^s\), the leapfrog scheme can be now written in the familiar form
where \(\mathbf {f}_k\) is the coefficient vector containing the \(L^2\) projection of \(f(t_k)\) onto the space \(S^1_0(\varOmega ,\mathscr {T})\). The main cost is the application of \(L_h^s \mathbf {U}_k\) in each step followed by the inversion of the mass matrix \(B_\varOmega \); the latter being usually cheap.
8.3 Trapezoidal time-stepping scheme
The matrix system can be written, in a familiar form, involving only functions in \(S^1_0(\varOmega ,\mathscr {T})\):
The difficulty now is that at each step we need to solve the system
where \({\tilde{\mathbf {f}}}_k\) contains known terms. While we could solve this system iteratively, it is more efficient to unwrap again the operator \(L_h^s\) to see that \(\mathbf {U}_{k+1}\) satisfies the system
and
Denoting by \(E_1 = {\mathrm {diag}}(1,0,\dots ,0)\), we can write this as a single system
As the matrices 
and 
are again symmetric and positive definite a similar diagonalization procedure results in a decoupled system of linear systems that can be solved in parallel.
Remark 8
(comparison of the two schemes) When compared with the trapezoidal scheme the leapfrog scheme is easier to implement. However, it seems to lose one of the main advantages that it has for the resolution of the standard wave equation. As the diffusion operator is nonlocal, the explicit nature of the scheme is no longer an advantage; it requires the resolution of a linear system at each time step even when using mass-lumping. We would also like to mention that, in each time-step and for both schemes, the costliest operation is the solution of the decoupled linear systems. However, if the spatial mesh is graded, for instance, as in Sect. 7, the CFL condition for the leapfrog scheme requires a time-step that is much smaller. In conclusion, there seems to be little to recommend leapfrog over trapezoidal rule for the problem that we are considering.
8.4 Numerical results
8.4.1 A 1D example
Let us first perform a numerical example for \(n=1\). Let \(\varOmega = (0,1)\) and consider the space–fractional wave equation
with \(f(x',t) = (\pi ^{2s}-1)\sin (t) \sin (\pi x')\). The initial data are such that the exact solution is \(u(x',t) = \sin (t) \sin (\pi x')\). The initial values for both time-stepping schemes can be taken as \(U_0 = 0\) and \(U_1 = {\varDelta t}\varPi _{x'} \sin (\pi x')\). Note that the additional \(O({\varDelta t}^2)\) term that is needed in the definition of \(U_1\) is zero because \(u''(0) = 0\).
We set the final time as \(T = \pi /2\) and perform numerical experiments for the following choices of the parameter s: \(s = 1/4\) and \(s = 3/4\). For space discretization in \(\varOmega \), we consider a uniform mesh with meshwidth \(h_\mathscr {T}\). For the trapezoidal scheme, and to obtain linear convergence, we set \({\varDelta t}= (0.5 h_{\mathscr {T}})^{1/2}\). For the leapfrog scheme, in order to ensure the stability of the scheme, we choose \({\varDelta t}= (0.5 h_{\mathscr {T}})^{\max (1/2,s)}\). Notice that, the aforementioned choices of the parameter s would render the leapfrog scheme unstable as a solution technique for the standard wave equation.
In Fig. 1 we show the experimental rate of convergence for
We observe that, as expected, the error decays linearly with respect to \(h_{\mathscr {T}}\). We also notice that the errors for both discretization schemes are almost identical.
Experimental rates of convergence for the error (8.4) for a one dimensional example. The experiment for \(s = 1/4\) is shown on the left and the one for \(s = 3/4\) on the right
8.4.2 A 2D example
We let \(n= 2\), and consider the square domain \(\varOmega = (-1,1)^2 \subset {\mathbb {R}}^2\) and the space-fractional wave equation
The data of the problem is such that the exact solution is given by
We set \(T = 1.5\) and \({\varDelta t}= 0.5h_\mathscr {T}\). In this experiment we measure, in the \(L^2(\varOmega )\)-norm, the error committed in the approximation of the time-derivative:
The computations were done using the NGSolve/Netgen software package [54, 55].
The convergence properties of the leapfrog scheme are presented in Fig. 2. It can be observed that, for both values of the parameter s considered, the experimental rate of convergence for the \(\text {error}_{2D}\) decays quadratically with respect to \(h_{\mathscr {T}}\). We notice that the observed rates are better than the ones derived in Theorem 7, but are in agreement with approximation theory since, in this case, u is smooth. The improvement of the estimate (6.59) of Theorem 7 from \(h_{\mathscr {T}}^{1+s}\) to \(h_{\mathscr {T}}^2\) is an open problem.
Experimental rates of convergence for the error (8.5) when \(\varOmega = (-1,1)^2\) and for different values of s. Leapfrog time-discretization is used
References
Abramowitz, M., Stegun, I.A.: Handbook of Mathematical Functions with Formulas, Graphs, and Dover Publications, Inc., New York (1992)
Acosta, G., Bersetche, F., Borthagaray, J.P.: Finite element approximations for fractional evolution problems. arXiv:1705.09815v1 (2017)
Athanasopoulos, I., Caffarelli, L.A.: Continuity of the temperature in boundary heat control problems. Adv. Math. 224(1), 293–315 (2010)
Băcuţă, C., Li, H., Nistor, V.: Differential operators on domains with conical points: precise uniform regularity estimates. Rev. Roum. Math. Pures Appl. 62(3), 383–411 (2017)
Banjai, L., Melenk, J.M., Nochetto, R.H., Otárola, E., Salgado, A.J., Schwab, Ch.: Tensor FEM for spectral fractional diffusion. Found. Comput. Math. (2018). https://doi.org/10.1007/s10208-018-9402-3
Birman, M.Š., Solomjak, M.Z.: Spektralnaya teoriya samosopryazhennykh operatorov v gilbertovom prostranstve. Leningrad University, Leningrad (1980)
Bonforte, M., Sire, Y., Vázquez, J.L.: Existence, uniqueness and asymptotic behaviour for fractional porous medium equations on bounded domains. Discrete Contin. Dyn. Syst. 35(12), 5725–5767 (2015)
Cabré, X., Sire, Y.: Nonlinear equations for fractional Laplacians II: existence, uniqueness, and qualitative properties of solutions. Trans. Am. Math. Soc. 367(2), 911–941 (2015)
Cabré, X., Tan, J.: Positive solutions of nonlinear problems involving the square root of the Laplacian. Adv. Math. 224(5), 2052–2093 (2010)
Caffarelli, L., Silvestre, L.: An extension problem related to the fractional Laplacian. Commun. Part. Differ. Equ. 32(7–9), 1245–1260 (2007)
Caffarelli, L., Stinga, P.R.: Fractional elliptic equations, Caccioppoli estimates and regularity. Ann. Inst. H. Poincaré Anal. Non Linéaire 33(3), 767–807 (2016)
Caffarelli, L., Vasseur, A.: Drift diffusion equations with fractional diffusion and the quasi-geostrophic equation. Ann. Math. 171, 1903–1930 (2010)
Capella, A., Dávila, J., Dupaigne, L., Sire, Y.: Regularity of radial extremal solutions for some non-local semilinear equations. Commun. Part. Differ. Equ. 36(8), 1353–1384 (2011)
Carr, P., Geman, H., Madan, D.B., Yor, M.: The fine structure of asset returns: an empirical investigation. J. Bus. 75, 305–332 (2002)
Chen, W.: A speculative study of \(2/3\)-order fractional Laplacian modeling of turbulence: some thoughts and conjectures. Chaos 16(2), 1–11 (2006)
Chen, W., Holm, S.: Fractional laplacian time-space models for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency. J. Acoust. Soc. Am. 115(4), 1424–1430 (2004)
Dahmen, W., Faermann, B., Graham, I.G., Hackbusch, W., Sauter, S.A.: Inverse inequalities on non-quasi-uniform meshes and application to the mortar element method. Math. Comput. 73(247), 1107–1138 (2004)
de Pablo, A., Quirós, F., Rodríguez, A., Vázquez, J.L.: A fractional porous medium equation. Adv. Math. 226(2), 1378–1409 (2011)
de Pablo, A., Quirós, F., Rodríguez, A., Vázquez, J.L.: A general fractional porous medium equation. Commun. Pure Appl. Math. 65(9), 1242–1284 (2012)
Diaz, J., Grote, M.J.: Energy conserving explicit local time stepping for second-order wave equations. SIAM J. Sci. Comput. 31(3), 1985–2014 (2009)
Du, Q., Gunzburger, M., Lehoucq, R.B., Zhou, K.: Analysis and approximation of nonlocal diffusion problems with volume constraints. SIAM Rev. 54(4), 667–696 (2012)
Duoandikoetxea, J.: Fourier Analysis, Volume 29 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI (2001). Translated and revised from the 1995 Spanish original by David Cruz-Uribe
Ern, A., Guermond, J.-L.: Theory and Practice of Finite Elements. Springer, New York (2004)
Evans, L.C.: Partial Differential Equations, Volume 19 of Graduate Studies in Mathematics, 2nd edn. American Mathematical Society, Providence (2010)
Fujiwara, D.: Concrete characterization of the domains of fractional powers of some elliptic differential operators of the second order. Proc. Jpn. Acad. 43, 82–86 (1967)
Gaspoz, F.D., Heine, C.-J., Siebert, K.G.: Optimal grading of the newest vertex bisection and \(H^1\)-stability of the \(L_2\)-projection. IMA J. Numer. Anal. 36(3), 1217–1241 (2016)
Gaspoz, F.D., Morin, P.: Convergence rates for adaptive finite elements. IMA J. Numer. Anal. 29(4), 917–936 (2009)
Gatto, P., Hesthaven, J.S.: Numerical approximation of the fractional laplacian via \(hp\)-finite elements, with an application to image denoising. J. Sci. Comput. 65(1), 249–270 (2015)
Gilboa, G., Osher, S.: Nonlocal operators with applications to image processing. Multiscale Model. Simul. 7(3), 1005–1028 (2008)
Gol’dshtein, V., Ukhlov, A.: Weighted Sobolev spaces and embedding theorems. Trans. Am. Math. Soc. 361(7), 3829–3850 (2009)
Grisvard, P.: Elliptic Problems in Nonsmooth Domains, Volume 69 of Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA (2011). Reprint of the 1985 original [MR0775683], With a foreword by Susanne C, Brenner (2011)
Grubb, G.: Fractional Laplacians on domains, a development of Hörmander’s theory of \(\mu \)-transmission pseudodifferential operators. Adv. Math. 268, 478–528 (2015)
Heinonen, J., Kilpeläinen, T., Martio, O.: Nonlinear Potential Theory of Degenerate Elliptic Equations. Oxford Mathematical Monographs. Oxford University Press, New York (1993)
Hochbruck, M., Sturm, A.: Error analysis of a second-order locally implicit method for linear Maxwell’s equations. SIAM J. Numer. Anal. 54(5), 3167–3191 (2016)
Kato, T.: Perturbation Theory for Linear Operators. Classics in Mathematics. Springer, Berlin (1995). Reprint of the 1980 edition
Kiselev, A., Nazarov, F., Volberg, A.: Global well-posedness for the critical 2D dissipative quasi-geostrophic equation. Invent. Math. 167(3), 445–453 (2007)
Kufner, A.: Weighted Sobolev Spaces, Volume 31 of Teubner-Texte zur Mathematik [Teubner Texts in Mathematics]. BSB B. G. Teubner Verlagsgesellschaft, Leipzig (1980). With German, French and Russian summaries
Kufner, A., Opic, B.: How to define reasonably weighted Sobolev spaces. Comment. Math. Univ. Carol. 25(3), 537–554 (1984)
Landkof, N.S.: Foundations of Modern Potential Theory. Springer, New York (1972). Translated from the Russian by A. P. Doohovskoy, Die Grundlehren der mathematischen Wissenschaften, Band 180
Levendorskiĭ, S.Z.: Pricing of the American put under Lévy processes. Int. J. Theor. Appl. Finance 7(3), 303–335 (2004)
Lions, J.-L., Magenes, E.: Non-homogeneous Boundary Value Problems and Applications, vol. I. Springer, New York (1972). Translated from the French by P. Kenneth, Die Grundlehren der mathematischen Wissenschaften, Band 181
McLean, W.: Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press, Cambridge (2000)
Muckenhoupt, B.: Weighted norm inequalities for the Hardy maximal function. Trans. Am. Math. Soc. 165, 207–226 (1972)
Müller, F., Schötzau, D., Schwab, C.: Symmetric interior penalty discontinuous Galerkin methods for elliptic problems in polygons. SIAM J. Numer. Anal. 55(5), 2490–2521 (2017)
Musina, R., Nazarov, A.I.: On fractional Laplacians. Commun. Part. Differ. Equ. 39(9), 1780–1790 (2014)
Nochetto, R.H., Otárola, E., Salgado, A.J.: A PDE approach to fractional diffusion in general domains: a priori error analysis. Found. Comput. Math. 15(3), 733–791 (2015)
Nochetto, R.H., Otárola, E., Salgado, A.J.: A PDE approach to space-time fractional parabolic problems. SIAM J. Numer. Anal. 54(2), 848–873 (2016)
Olver, F.W.J.: Asymptotics and Special Functions. Computer Science and Applied Mathematics. Academic Press [A Subsidiary of Harcourt Brace Jovanovich, Publishers], New York (1974)
Otárola, E., Salgado, A.J.: Regularity of solutions to space-time fractional wave equations: a PDE approach. Fract. Calc. Appl. Anal. 21(5), 1262–1293 (2018)
Peterseim, D., Schedensack, M.: Relaxing the CFL condition for the wave equation on adaptive meshes. J. Sci. Comput. 72(3), 1196–1213 (2017)
Pham, H.: Optimal stopping, free boundary, and American option in a jump-diffusion model. Appl. Math. Optim. 35(2), 145–164 (1997)
Roubíček, T.: Nonlinear Partial Differential Equations with Applications, Volume 153 of International Series of Numerical Mathematics, 2nd edn. Birkhäuser, Basel (2013)
Savaré, G.: Regularity results for elliptic equations in Lipschitz domains. J. Funct. Anal. 152(1), 176–201 (1998)
Schöberl, J.: NETGEN an advancing front 2D/3D-mesh generator based on abstract rules. J. Comput. Vis. Sci. 1, 41–52 (1997)
Schöberl, J.: C++11 implementation of finite elements in NGSolve. Technical report (2014)
Silling, S.A.: Why peridynamics? In: Bobaru, F., Foster, J.T., Geubelle, P.H., Silling, S.A. (eds.) Handbook of Peridynamic Modeling, Advances in Applied Mathematics. CRC Press, Boca Raton (2017)
Stinga, P.R., Torrea, J.L.: Extension problem and Harnack’s inequality for some fractional operators. Commun. Part. Differ. Equ. 35(11), 2092–2122 (2010)
Tartar, L.: An Introduction to Sobolev Spaces and Interpolation Spaces, Volume 3 of Lecture Notes of the Unione Matematica Italiana. Springer, Berlin (2007)
Turesson, B.O.: Nonlinear Potential Theory and Weighted Sobolev Spaces, Volume 1736 of Lecture Notes in Mathematics. Springer, Berlin (2000)
Vázquez, J.L., Volzone, B.: Symmetrization for linear and nonlinear fractional parabolic equations of porous medium type. J. Math. Pures Appl. (9) 101(5), 553–582 (2014)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
EO is partially supported by CONICYT through FONDECYT Project 11180193.
Rights and permissions
About this article
Cite this article
Banjai, L., Otárola, E. A PDE approach to fractional diffusion: a space-fractional wave equation. Numer. Math. 143, 177–222 (2019). https://doi.org/10.1007/s00211-019-01055-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-019-01055-5