Abstract
The purpose of this work is to study solution techniques for problems involving fractional powers of symmetric coercive elliptic operators in a bounded domain with Dirichlet boundary conditions. These operators can be realized as the Dirichlet-to-Neumann map for a degenerate/singular elliptic problem posed on a semi-infinite cylinder, which we analyze in the framework of weighted Sobolev spaces. Motivated by the rapid decay of the solution to this problem, we propose a truncation that is suitable for numerical approximation. We discretize this truncation using first degree tensor product finite elements. We derive a priori error estimates in weighted Sobolev spaces. The estimates exhibit optimal regularity but suboptimal order for quasi-uniform meshes. For anisotropic meshes instead, they are quasi-optimal in both order and regularity. We present numerical experiments to illustrate the method’s performance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Singular integrals and nonlocal operators have been an active area of research in different branches of mathematics such as operator theory and harmonic analysis (see [59]). In addition, they have received significant attention because of their strong connection with real-world problems since they constitute a fundamental part of the modeling and simulation of complex phenomena that span vastly different length scales.
Nonlocal operators arise in a number of applications such as boundary control problems [33], finance [23], electromagnetic fluids [49], image processing [38], materials science [8], optimization [33], porous media flow [27], turbulence [5], peridynamics [58], nonlocal continuum field theories [34], and others. Therefore, the domain of definition \(\varOmega \) could be rather general.
To make matters precise, in this work we shall be interested in fractional powers of the Dirichlet Laplace operator \((-\varDelta )^s\), with \(s \in (0,1)\), which for convenience we will simply call the fractional Laplacian. In other words, we shall be concerned with the following problem. Let \(\varOmega \) be an open and bounded subset of \(\mathbb {R}^n\) (\(n\ge 1\)), with boundary \(\partial \varOmega \). Given \(s\in (0,1)\) and a smooth enough function \(f\), find \(u\) such that
Our approach, however, is by no means particular to the fractional Laplacian. In Sect. 7 we will discuss how, with little modification, our developments can be applied to a general second-order, symmetric, and uniformly elliptic operator.
The study of boundary value problems involving the fractional Laplacian is important in physical applications where long-range or anomalous diffusion is considered. For instance, in the flow in porous media, it is used when modeling the transport of particles that experience very large transitions arising from high heterogeneity and very long spatial autocorrelation (see [10]). In the theory of stochastic processes, the fractional Laplacian is the infinitesimal generator of a stable Lévy process (see [12]).
One of the main difficulties in the study of problem (1.1) is that the fractional Laplacian is a nonlocal operator (see [19, 21, 47]). To localize it, Caffarelli and Silvestre showed in [21] that any power of the fractional Laplacian in \(\mathbb {R}^n\) can be realized as an operator that maps a Dirichlet boundary condition to a Neumann-type condition via an extension problem on the upper half-space \(\mathbb {R}^{n+1}_+\). For a bounded domain \(\varOmega \), the result by Caffarelli and Silvestre was adapted in [16, 22, 60], yielding an extension problem that is now posed on the semi-infinite cylinder \(\mathcal {C}= \varOmega \times (0,\infty )\). This extension is the following mixed boundary value problem:
where \(\partial _L \mathcal {C}= \partial \varOmega \times [0,\infty )\) denotes the lateral boundary of \(\mathcal {C}\), and
is the the so-called conormal exterior derivative of \(\mathfrak {u}\), with \(\nu \) being the unit outer normal to \(\mathcal {C}\) at \(\varOmega \times \{ 0 \}\). The parameter \(\alpha \) is defined as
Finally, \(d_s\) is a positive normalization constant that depends only on \(s\); see [21] for details. We will call \(y\) the extended variable and the dimension \(n+1\) in \(\mathbb {R}_+^{n+1}\) the extended dimension of problem (1.2).
The limit in (1.3) must be understood in the distributional sense; see [16, 19, 21] or Sect. 2 for more details. As noted in [21, 22, 60], the fractional Laplacian and the Dirichlet-to-Neumann operator of problem (1.2) are related by
Using the aforementioned ideas, we propose the following strategy to find the solution to (1.1): given a sufficiently smooth function \(f\), we solve (1.2), thereby obtaining a function \(\mathfrak {u}: (x^{\prime },y) \in \mathcal {C}\mapsto \mathfrak {u}(x^{\prime },y) \in \mathbb {R}\). Setting \(u: x^{\prime } \in \varOmega \mapsto u(x^{\prime }) = \mathfrak {u}(x^{\prime },0) \in \mathbb {R}\), we obtain the solution to (1.1). The purpose of this work is then to make these ideas rigorous and to analyze a discretization scheme that consists of approximating the solution to (1.2) via first-degree tensor product finite elements. We will show suboptimal error estimates for quasi-uniform discretizations of (1.2) in suitable weighted Sobolev spaces and quasi-optimal error estimates using anisotropic elements.
The main advantage of the proposed algorithm is that we solve the local problem (1.2) instead of dealing with the nonlocal operator \((-\varDelta )^s\) of problem (1.1). However, this comes at the expense of incorporating one more dimension to the problem and raises questions about computational efficiency. The development of efficient computational techniques for the solution to problem (1.2) and issues such as multilevel methods, a posteriori error analysis, and adaptivity will be deferred to future reports. In this paper we carry out a complete a priori error analysis of the discretization scheme.
Before proceeding with the analysis of our method, it would be instructive to compare it with those advocated in the literature. First of all, for a general Lipschitz domain \(\varOmega \subset \mathbb {R}^n\) (\(n > 1\)), we may think of solving problem (1.1) via a spectral decomposition of the operator \(-\varDelta \). However, to have a sufficiently good approximation, this requires the solution to a large number of eigenvalue problems, which in general is very time consuming. In [42, 43] the authors studied computationally problem (1.1) in the one-dimensional case and with boundary conditions of the Dirichlet, Neumann, and Robin types and introduced the so-called matrix transference technique (MTT). Basically, MTT computes a spatial discretization of the fractional Laplacian by first finding a matrix approximation, \(A\), of the Laplace operator (via finite differences or finite elements) and then computing the \(s\)th power of this matrix. This requires diagonalization of \(A\), which, again, amounts to the solution to a large number of eigenvalue problems. For the case \(\varOmega = (0,1)^2\) and \(s\in (1/2,1)\), [62] applies the MTT technique and avoids diagonalization of \(A\) by writing a numerical scheme in terms of the product of a function of the matrix and a vector, \(f(A)b\), where \(b\) is a suitable vector. This product is then approximated by a preconditioned Lanczos method. Under the same setting, the work [18] makes a computational comparison of three techniques for the computation of \(f(A)b\): the contour integral method, extended Krylov subspace methods, and the preassigned poles and interpolation nodes method.
The outline of this paper is as follows. In §2 we introduce the functional framework that is suitable for the study of problems (1.1) and (1.2). We recall the definition of the fractional Laplacian on a bounded domain via spectral theory, and in addition, in §2.6, we study the regularity of the solution to (1.2). The numerical analysis of (1.1) begins in §3. Here we introduce a truncation of problem (1.2) and study some properties of its solution. Having understood the truncation we proceed, in §4, to study its finite element approximation. We prove interpolation estimates in weighted Sobolev spaces under mild shape regularity assumptions that allow us to consider anisotropic elements in the extended variable \(y\). Based on the regularity results of §2.6, we derive, in §5, a priori error estimates for quasi-uniform meshes that exhibit optimal regularity but suboptimal order. To restore optimal decay, we resort to the so-called principle of error equidistribution and construct graded meshes in the extended variable \(y\). They in turn capture the singular behavior of the solution to (1.2) and allow us to prove a quasi-optimal rate of convergence with respect to both regularity and degrees of freedom. In §6, to illustrate the method’s performance and theory, we provide several numerical experiments. Finally, in §7 we show that our developments apply to general second-order, symmetric, and uniformly elliptic operators.
2 Notation and Preliminaries
Throughout this work \(\varOmega \) is an open, bounded, and connected subset of \(\mathbb {R}^n\), \(n\ge 1\), with Lipschitz boundary \(\partial \varOmega \). We define the semi-infinite cylinder
and its lateral boundary
Given  , we define the truncated cylinder,
, we define the truncated cylinder,

The lateral boundary  is defined accordingly.
is defined accordingly.
Throughout our discussion we will be dealing with objects defined in \(\mathbb {R}^{n+1}\), and it will be convenient to distinguish the extended dimension because it plays a special role. A vector \(x\in \mathbb {R}^{n+1}\) will be denoted by
with \(x^i \in \mathbb {R}\) for \(i=1,\ldots ,{n+1}\), \(x^{\prime } \in \mathbb {R}^n\) and \(y\in \mathbb {R}\). The upper half-space in \(\mathbb {R}^{n+1}\) will be denoted by
Let \( \gamma = (\gamma ^1,\gamma ^2) \in \mathbb {R}^2\) and \(z \in \mathbb {R}^{n+1}\); the binary operation \( \odot : \mathbb {R}^2 \times \mathbb {R}^{n+1} \rightarrow \mathbb {R}^{n+1}\) is defined by
The relation \(a \lesssim b\) indicates that \(a \le Cb\), with a constant \(C\) that does not depend on either \(a\) or \(b\) but might depend on \(s\) and \(\varOmega \). The value of \(C\) might change at each occurrence. Given two objects \(X\) and \(Y\) in the same category, we write \(X \hookrightarrow Y\) to indicate the existence of a monomorphism between them. Generally, these will be objects in some subcategory of the topological vector spaces (metric, normed, Banach, Hilbert spaces), and in this case the monomorphism is simply continuous embedding. If \(X\) is a vector space, then we denote its dual by \(X^{\prime }\).
2.1 Fractional Sobolev Spaces
Let us recall some function spaces; for details the reader is referred to [28, 48, 50, 61]. For \(0<s<1\), we introduce the so-called Gagliardo–Slobodeckiĭ seminorm
The Sobolev space \(H^s(\varOmega )\) of order \(s\) is defined by
which, equipped with the norm
is a Hilbert space. An equivalent construction of \(H^s(\varOmega )\) is obtained by restricting functions in \(H^s(\mathbb {R}^n)\) to \(\varOmega \) (cf. [61, Chap. 34]). The space \(H_0^s(\varOmega )\) is defined as the closure of \(C_0^{\infty }(\varOmega )\) with respect to the norm \(\Vert \cdot \Vert _{H^s(\varOmega )}\), i.e.,
If the boundary of \(\varOmega \) is smooth, an equivalent approach to defining fractional Sobolev spaces is given by interpolation in [48, Chap. 1]. Set \(H^0(\varOmega ) = L^2(\varOmega )\); then Sobolev spaces with real index \(0 \le s \le 1\) can be defined as interpolation spaces of index \(\theta = 1 - s\) for the pair \([H^1(\varOmega ), L^2(\varOmega )]\), that is,
Analogously, for \(s \in [0,1]\setminus \{{\tfrac{1}{2}}\}\), the spaces \(H_0^s(\varOmega )\) are defined as interpolation spaces of index \(\theta = 1 - s\) for the pair \([H_0^1(\varOmega ), L^2(\varOmega )]\), in other words
The space \([H_0^1(\varOmega ), L^2(\varOmega )]_{{\tfrac{1}{2}}}\) is the so-called Lions–Magenes space,
which can be characterized as
(see [48, Theorem 11.7]). Moreover, we have the strict inclusion \( H_{00}^{1/2}(\varOmega ) \subsetneqq H_0^{1/2}(\varOmega )\) because \(1 \in H_0^{1/2}(\varOmega )\), but \(1 \notin H_{00}^{1/2}(\varOmega )\). If the boundary of \(\varOmega \) is Lipschitz, the characterization (2.9) is equivalent to the definition via interpolation, and definitions (2.7) and (2.8) are also equivalent to definitions (2.5) and (2.6), respectively. To see this, it suffices to notice that when \(\varOmega = \mathbb {R}^n\), these definitions yield identical spaces and equivalent norms (see [3, Chap. 7]). Consequently, using the well-known extension result of Stein [59] for Lipschitz domains, we obtain the asserted equivalence (see [3, Chap. 7] for details).
When the boundary of \(\varOmega \) is Lipschitz, the space \(C_0^{\infty }(\varOmega )\) is dense in \(H^s(\varOmega )\) if and only if \(s \le {\tfrac{1}{2}}\), i.e., \(H_0^s(\varOmega ) = H^s(\varOmega )\). If \(s>{\tfrac{1}{2}}\), we have that \(H_0^s(\varOmega )\) is strictly contained in \(H^s(\varOmega )\) (see [48, Theorem 11.1]). In particular, we have the inclusions \( H_{00}^{1/2}(\varOmega ) \subsetneqq H_0^{1/2}(\varOmega ) = H^{1/2}(\varOmega ) \).
2.2 Fractional Laplace Operator
It is important to mention that there is no unique way of defining a nonlocal operator related to the fractional Laplacian in a bounded domain. A first possibility is to suitably extend the functions to the whole space \(\mathbb {R}^n\) and use the Fourier transform
After extension, the following pointwise formula also serves as a definition of the fractional Laplacian:
where \(\mathrm p.v. \) stands for the Cauchy principal value and \(C_{n,s}\) is a positive normalization constant that depends only on \(n\) and \(s\) and is introduced to guarantee that the symbol of the resulting operator is \(|\xi ^{\prime }|^{2s}\). For details we refer the reader to [19, 28, 47] and, in particular, to [47, Sect. 1.1] or [28, Proposition 3.3] for a proof of the equivalence of these two definitions.
Even if we restrict ourselves to definitions that do not require extension, there is more than one possibility. For instance, the so-called regional fractional Laplacian ([14, 40]) is defined by restricting the Riesz integral to \(\varOmega \), leading to an operator related to a Neumann problem. A different operator is obtained by using the spectral decomposition of the Dirichlet Laplace operator \(-\varDelta \); see [16, 20, 22]. This approach is also different from the integral formula (2.10). Indeed, the spectral definition depends on the domain \(\varOmega \) considered, while the integral one at any point is independent of the domain in which the equation is set. For more details see the discussion in [57].
The definition that we shall adopt is as in [16, 20, 22] and is based on the spectral theory of the Dirichlet Laplacian ([35, 37]), as we summarize subsequently.
We define \(-\varDelta : L^2(\varOmega ) \rightarrow L^2(\varOmega )\), with the domain \({{\mathrm{Dom}}}(-\varDelta ) = \{v\in H^1_0(\varOmega ): \varDelta v \in L^2(\varOmega )\}\). This operator is positive, unbounded, and closed, and its inverse is compact. This implies that the spectrum of the operator \(-\varDelta \) is discrete and positive and accumulates at infinity. Moreover, there exist \(\{ \lambda _k,\varphi _k \}_{k\in \mathbb N} \subset \mathbb {R}_+\times H^1_0(\varOmega )\) such that \(\{\varphi _k \}_{k \in \mathbb N}\) is an orthonormal basis of \(L^2(\varOmega )\) and, for \(k\in \mathbb N\),
Consequently, \(\{\varphi _k \}_{k \in \mathbb N}\) is an orthogonal basis of \(H_0^1(\varOmega )\) and \(\Vert \nabla _{x^{\prime }} \varphi _k\Vert _{L^2(\varOmega )} = \sqrt{\lambda _k}\).
With this spectral decomposition at hand, the fractional powers of the Dirichlet Laplacian \((-\varDelta )^s\) can be defined for \(u \in C_0^{\infty }(\varOmega )\) by
where the coefficients \(u_k\) are defined by \( u_k = \int _{\varOmega } u \varphi _k \). Therefore, if \(f=\sum _{k=1}^{\infty }f_k \varphi _k\), and \((-\varDelta )^su = f\), then \(u_k = \lambda _k^{-s}f_k\) for all \(k \ge 1\).
By density, the operator \((-\varDelta )^s\) can be extended to the Hilbert space
The theory of Hilbert scales presented in [48, Chap. 1] shows that
where \(\theta = 1-s\). This implies the following characterization of the space \(\mathbb {H}^s(\varOmega )\),
We denote by \(\mathbb {H}^{-s}(\varOmega )\) the dual space of \(\mathbb {H}^s(\varOmega )\) for \(0 < s < 1\).
2.3 Weighted Sobolev Spaces
To exploit the Caffarelli–Silvestre extension [21] or its variants [16, 20, 22], we need to deal with a degenerate/singular elliptic equation on \(\mathbb {R}_+^{n+1}\). To this end, we consider weighted Sobolev spaces (e.g., [36, 41, 46]), with the specific weight \(|y|^{\alpha }\), with \(\alpha \in (-1,1)\).
Let \(\mathcal {D}\subset \mathbb {R}^{n+1}\) be an open set and \(\alpha \in (-1,1)\). We define \(L^2(\mathcal {D}, |y|^{\alpha })\) as the space of all measurable functions defined on \(\mathcal {D}\) such that
Similarly we define the weighted Sobolev space
where \(\nabla w\) is the distributional gradient of \(w\). We equip \(H^1(\mathcal {D},|y|^{\alpha })\) with the norm
Notice that taking \(\alpha = 0\) in the preceding definition, we obtain the classical \(H^1(\mathcal {D})\).
The properties of this weighted Sobolev space can be found in classical references like [41, 46]. It is remarkable that most of the properties of classical Sobolev spaces have a weighted counterpart, not because of the specific form of the weight but rather due to the fact that the weight \(|y|^\alpha \) belongs to the so-called Muckenhoupt class \(A_2(\mathbb {R}^{n+1})\); see [36, 39, 52]. We recall the definition of Muckenhoupt classes.
Definition 2.1
(Muckenhoupt class \(A_p\)). Let \(\omega \) be a positive and measurable function such that \(\omega \in L^1_{loc}(\mathbb {R}^{N})\) with \(N \ge 1\). We say \(\omega \in A_p(\mathbb {R}^N)\), \(1 < p < \infty \), if there exists a positive constant \(C_{p,\omega }\) such that
where the supremum is taken over all balls \(B\) in \(\mathbb {R}^N\) and \(|B|\) denotes the Lebesgue measure of \(B\).
Since \(\alpha \in (-1,1)\), it is immediate that \(|y|^{\alpha } \in A_2(\mathbb {R}^{n+1})\), which implies the following important result (see [39, Theorem 1]).
Proposition 2.2
(Properties of weighted Sobolev spaces). Let \(\mathcal {D}\subset \mathbb {R}^{n+1}\) be an open set and \(\alpha \in (-1,1)\). Then \(H^1(\mathcal {D},|y|^{\alpha })\), equipped with the norm (2.14), is a Hilbert space. Moreover, the set \(C^{\infty }(\mathcal {D}) \cap H^1(\mathcal {D},|y|^{\alpha })\) is dense in \(H^1(\mathcal {D},|y|^{\alpha })\).
Remark 2.3
(Weighted \(L^2\) vs. \(L^1\)). If \(\mathcal {D}\) is a bounded domain and \(\alpha \in (-1,1)\), then \(L^2(\mathcal {D},|y|^{\alpha }) \subset L^1(\mathcal {D})\). Indeed, since \(|y|^{-\alpha } \in L^1_{loc}(\mathbb {R}^{n+1})\),
The following result is given in [46, Theorem 6.3]. For completeness we present here a version of the proof on the truncated cylinder  , which will be important for the numerical approximation of problem (1.2).
, which will be important for the numerical approximation of problem (1.2).
Proposition 2.4
(Embeddings in weighted Sobolev spaces). Let \(\varOmega \) be a bounded domain in \(\mathbb {R}^n\) and  . Then
. Then

and

Proof
Let us prove (2.16), the proof of (2.17) being similar. Since \(\alpha >0\), we have  , whence
, whence  and
and  a.e. on
a.e. on  for all
for all  . This implies
. This implies  , which is (2.16). \(\square \)
, which is (2.16). \(\square \)
Define

This space can be equivalently defined as the set of measurable functions \(w: \mathcal {C}\rightarrow \mathbb {R}\) such that \(w \in H^1(\varOmega \times (s,t))\) for all \(0 < s < t < \infty \), \(w = 0\) on \(\partial _L \mathcal {C}\) and for which the following seminorm is finite:

see [22]. As a consequence of the usual Poincaré inequality, for any \(k \in \mathbb {Z}\) and any function \(w \in H^1(\varOmega \times (2^k,2^{k+1}))\), with \(w = 0\) on \(\partial \varOmega \times (2^k,2^{k+1})\), we have
where \(C_\varOmega \) denotes a positive constant that depends only on \(\varOmega \). Summing up over \(k \in \mathbb {Z}\), we obtain the following weighted Poincaré inequality:
Hence, the seminorm (2.19) is a norm on  , equivalent to (2.14).
, equivalent to (2.14).
For a function \(w \in H^1(\mathcal {C}, y^{\alpha })\), we shall denote by \({{\mathrm{tr_\varOmega }}}w\) its trace onto \(\varOmega \times \{ 0 \}\). It is well known that \({{\mathrm{tr_\varOmega }}}H^1(\mathcal {C}) = {H^{1/2}(\varOmega )}\); see [3, 61]. In the subsequent analysis we will need a characterization of the trace of functions in \(H^1(\mathcal {C}, y^{\alpha })\). For a smooth domain this was given in [20, Proposition 1.8] for \(s=1/2\) and in [22, Proposition 2.1] for any \(s \in (0,1)\setminus \ \left\{ {\tfrac{1}{2}}\right\} \). However, since the eigenvalue decomposition (2.12) of the Dirichlet Laplace operator holds true on a Lipschitz domain, we are able to extend this trace characterization to such domains. In summary, we have the following result.
Proposition 2.5
(Characterization of  ). Let \(\varOmega \subset \mathbb {R}^n\) be a bounded Lipschitz domain. The trace operator \({{\mathrm{tr_\varOmega }}}\) satisfies
). Let \(\varOmega \subset \mathbb {R}^n\) be a bounded Lipschitz domain. The trace operator \({{\mathrm{tr_\varOmega }}}\) satisfies  and
and

where the space \(\mathbb {H}^s(\varOmega )\) is defined in (2.13) and \(\alpha = 1 - 2s\).
2.4 Caffarelli–Silvestre Extension Problem
It was shown in [21] that any power of the fractional Laplacian in \(\mathbb {R}^n\) can be determined as an operator that maps a Dirichlet boundary condition to a Neumann-type condition via an extension problem posed on \(\mathbb {R}_+^{n+1}\). For a bounded domain, an analogous result was obtained in [20] for \(s={\tfrac{1}{2}}\) and in [16, 22, 60] for any \(s \in (0,1)\).
Let us briefly describe these results. Consider a function \(u\) defined on \(\varOmega \). We define the \(\alpha \)-harmonic extension of \(u\) to the cylinder \(\mathcal {C}\) as the function \(\mathfrak {u}\) that solves the boundary value problem
From Proposition 2.5 and the Lax–Milgram lemma we can conclude that this problem has a unique solution  whenever \(u\in \mathbb {H}^s(\varOmega )\). We define the Dirichlet-to-Neumann operator \(\varGamma _{\alpha ,\varOmega } : \mathbb {H}^s(\varOmega )\rightarrow \mathbb {H}^{-s}(\varOmega )\)
whenever \(u\in \mathbb {H}^s(\varOmega )\). We define the Dirichlet-to-Neumann operator \(\varGamma _{\alpha ,\varOmega } : \mathbb {H}^s(\varOmega )\rightarrow \mathbb {H}^{-s}(\varOmega )\)
where \(\mathfrak {u}\) solves (2.22) and \(\tfrac{\partial \mathfrak {u}}{\partial \nu ^{\alpha }}\) is given in (1.3). The space \(\mathbb {H}^{-s}(\varOmega )\) can be characterized as the space of distributions \(h = \sum _k h_k \varphi _k\) such that \(\sum _k |h_k|^2 \lambda _k^{-s} < \infty \). The fundamental result of [21], see also [22, Lemma 2.2], is stated in what follows.
Theorem 2.6
(Caffarelli–Silvestre extension). If \(s\in (0,1)\) and \(u \in \mathbb {H}^s(\varOmega )\), then
in the sense of distributions. Here, \(\alpha = 1-2s\), and \(d_s\) is given by
It seems remarkable that the constant \(d_s\) does not depend on the dimension. This was proved originally in [21], and its precise value appears in several references, for instance, [16, 19].
The relation between the fractional Laplacian and the extension problem is now clear. Given \(f \in \mathbb {H}^{-s}(\varOmega )\), a function \(u \in \mathbb {H}^s(\varOmega )\) solves (1.1) if and only if its \(\alpha \)-harmonic extension  solves (1.2).
solves (1.2).
If \(u=\sum _k u_k \varphi _k\), then, as shown in the proofs of [22, Proposition 2.1] and [16, Lemma 2.2], \(\mathfrak {u}\) can be expressed as
where the functions \(\psi _k\) solve
If \(s={\tfrac{1}{2}}\), then clearly \(\psi _k(y) = e^{-\sqrt{\lambda _k}y}\) (see [20, Lemma 2.10]). For \(s \in (0,1)\setminus \{{\tfrac{1}{2}}\}\) instead (cf. [22, Proposition 2.1])
where \(K_s\) denotes the modified Bessel function of the second kind (see [1, Chap. 9.6]). Using the condition \(\psi _k(0) = 1\) and formulas for small arguments of the function \(K_s\) (e.g., §2.5) we obtain
The function  is the unique solution to
is the unique solution to

where \(\langle \cdot , \cdot \rangle _{\mathbb {H}^{-s}(\varOmega )\times \mathbb {H}^s(\varOmega )}\) denotes the duality pairing between \(\mathbb {H}^s(\varOmega )\) and \(\mathbb {H}^{-s}(\varOmega )\), which, in light of Proposition 2.5, is well defined for all \(f \in \mathbb {H}^{-s}(\varOmega )\) and  . This implies the following equalities (see [22, Proposition 2.1] for \(s \in (0,1)\setminus \{{\tfrac{1}{2}}\}\) and [20, Proposition 2.1] for \(s = {\tfrac{1}{2}}\)):
. This implies the following equalities (see [22, Proposition 2.1] for \(s \in (0,1)\setminus \{{\tfrac{1}{2}}\}\) and [20, Proposition 2.1] for \(s = {\tfrac{1}{2}}\)):

Notice that for \(s = {\tfrac{1}{2}}\) or, equivalently, \(\alpha =0\), problem (2.26) reduces to the weak formulation of the Laplace operator with mixed boundary conditions, which is posed on the classical Sobolev space  . Therefore, the value \(s = {\tfrac{1}{2}}\) becomes a special case for problem (2.26). In addition, \(d_{1/2} = 1\), and
. Therefore, the value \(s = {\tfrac{1}{2}}\) becomes a special case for problem (2.26). In addition, \(d_{1/2} = 1\), and  .
.
At this point it is important to give a precise meaning to the Dirichlet boundary condition in (1.1). For \(s={\tfrac{1}{2}}\), the boundary condition is interpreted in the sense of the Lions–Magenes space. If \({\tfrac{1}{2}}< s \le 1\), then there is a trace operator from \(\mathbb {H}^s(\varOmega )\) into \(L^2(\partial \varOmega )\), and the boundary condition can be interpreted in this sense. For \(0 < s < 1/2\) this interpretation is no longer possible, and thus, for an arbitrary \(f \in \mathbb {H}^{-s}(\varOmega )\), the boundary condition does not have a clear meaning. For instance, for every \(s \in (0,{\tfrac{1}{2}})\), \(f = (-\varDelta )^s1\in \mathbb {H}^{-s}(\varOmega )\), and the solution to (1.1) for this right-hand side is \(u=1\). If \(f \in H^\zeta (\varOmega )\), with \(\zeta > {\tfrac{1}{2}}- 2s > -s\), using that \((-\varDelta )^s\) is a pseudodifferential operator of order \(2s\), then a shift-type result is valid, i.e., \(u \in H^{\varrho }(\varOmega )\) with \(\varrho = \zeta + 2s > 1/2\). In this case, the trace of \(u\) on \(\partial \varOmega \) is well defined and the boundary condition is meaningful. Finally, it was proved in [22, Lemma 2.10] that if \(f \in L^{\infty }(\varOmega )\), then the solution to (1.1) belongs to \(C^{0,\varkappa }(\overline{\varOmega })\) with \(\varkappa \in (0,\min \{2s,1\})\).
2.5 Asymptotic Estimates
It is important to understand the behavior of the solution \(\mathfrak {u}\) to problem (1.2), given by (2.24). Consequently, it becomes necessary to recall some of the main properties of the modified Bessel function of the second kind \(K_{\nu }(z)\), \(\nu \in \mathbb {R}\); see [1, Chap. 9.6] for (i)–(iv) and [51, Theorem 5] for (v):
-
(i)
For \(\nu >-1\), \(K_{\nu }(z)\) is real and positive.
-
(ii)
For \(\nu \in \mathbb {R}\), \(K_{\nu }(z) = K_{-\nu }(z)\).
-
(iii)
For \(\nu > 0\),
$$\begin{aligned} \lim _{z \downarrow 0} \frac{K_{\nu }(z)}{{\tfrac{1}{2}}\varGamma (\nu ) \left( {\tfrac{1}{2}}z \right) ^{-\nu } } = 1. \end{aligned}$$(2.28) -
(iv)
For \(k \in \mathbb {N}\),
$$\begin{aligned} \left( \frac{1}{z} \frac{\, \mathrm{d}}{\, \mathrm{d}z}\right) ^k \left( z^{\nu } K_{\nu }(z) \right) = (-1)^k z^{\nu -k}K_{\nu -k}(z). \end{aligned}$$In particular, for \(k=1\) and \(k=2\) we have, respectively,
$$\begin{aligned} \frac{\, \mathrm{d}}{\, \mathrm{d}z} \left( z^{\nu } K_{\nu }(z) \right) = -z^{\nu } K_{\nu -1}(z) = -z^{\nu } K_{1-\nu }(z) \end{aligned}$$(2.29)and
$$\begin{aligned} \frac{\, \mathrm{d}^2 }{\, \mathrm{d}z^2} \left( z^{\nu } K_{\nu }(z) \right) = z^{\nu } K_{2- \nu }(z) -z^{\nu -1} K_{1-\nu }(z). \end{aligned}$$(2.30) -
(v)
For \(z>0\), \(z^{\min \{\nu ,1/2\}}e^{z}K_{\nu }(z)\) is a decreasing function.
As an application we obtain the following important properties of the function \(\psi _k\), defined in (2.25). First, for \(s \in (0,1)\), properties (ii)–(iv) imply
Property (v) provides the following asymptotic estimate for \(s \in (0,1)\) and \(y \ge 1\):
Multiplying the differential equation of problem (2.25) by \(y^{\alpha }\psi _k(y)\) and integrating by parts yields
where \(a\) and \(b\) are real and positive constants.
Let us conclude this section with some remarks on the asymptotic behavior of the function \(\mathfrak {u}\) that solves (2.26). Using (2.24) we obtain
For \(s \in (0,1)\), using formula (2.31) together with (2.12), we arrive at
Notice that if \(s = {\tfrac{1}{2}}\), then \(\alpha =0\), \(d_{1/2}=1\), and thus (2.34) reduces to
For \(s \in (0,1) \setminus \left\{ {\tfrac{1}{2}}\right\} \) the asymptotic behavior of the second derivative \(\mathfrak {u}_{yy}\) as \(y \approx 0^+\) is a consequence of (2.30) applied to the function \(\psi _k(y)\). For \(s={\tfrac{1}{2}}\) the behavior follows from \(\psi _k(y) = e^{-\sqrt{\lambda _k}y}\). In conclusion, for \(y \approx 0^{+}\) we have
2.6 Regularity of Solution
Since we are interested in the approximation of the solution to problem (2.26), and this is closely related to its regularity, let us now study the behavior of its derivatives. According to (2.34), \(\mathfrak {u}_y \approx y^{-\alpha }\) for \(y \approx 0^+\). This clearly shows the necessity of introducing the weight because this behavior, together with the exponential decay given by (v) of §2.5, implies that \(\mathfrak {u}_y \in L^2(\mathcal {C},y^\alpha )\setminus L^2(\mathcal {C})\) for \(s \in (0,1/4]\).
However, the situation with second derivatives is much more delicate. To see this, let us first argue heuristically and compute how these derivatives scale with \(y\). From the asymptotic formula (2.35), we see that for \(0< \delta \ll 1 \) and \(s \in (0,1)\setminus \left\{ {\tfrac{1}{2}}\right\} \),
which, since \(\alpha \in (-1,1)\setminus \{0\}\), does not converge. However,
converges for \(\beta > 2\alpha + 1\), hinting at the fact that \(\mathfrak {u}\in H^2(\mathcal {C}, y^\beta ) \setminus H^2(\mathcal {C}, y^\alpha )\). The following result makes these considerations rigorous.
Theorem 2.7
(Global regularity of \(\alpha \)-harmonic extension). Let \(f \in \mathbb {H}^{1-s}(\varOmega )\), where \(\mathbb {H}^{1-s}(\varOmega )\) is defined in (2.13) for \(s\in (0,1)\). Let  solve (2.26), with \(f\) as datum. Then, for \(s \in (0,1) \setminus \left\{ {\tfrac{1}{2}}\right\} \), we have
solve (2.26), with \(f\) as datum. Then, for \(s \in (0,1) \setminus \left\{ {\tfrac{1}{2}}\right\} \), we have
and
with \(\beta >2\alpha +1\). For the special case \(s = {\tfrac{1}{2}}\), we obtain
Remark 2.8
(Compatibility of \(f\)). It is possible to interpret the result of Theorem 2.7 as follows. Consider \(s \in ({\tfrac{1}{2}},1)\) or, equivalently, \(\alpha \in (-1,0)\). Then the conormal exterior derivative condition for \(\mathfrak {u}\) gives us that \(\mathfrak {u}_y \approx -d_s y^{-\alpha }f\) as \(y \approx 0^+\) on \(\varOmega \times \{0\}\), which in turn implies that \(\mathfrak {u}_y \rightarrow 0\) as \(y \rightarrow 0^+\) on \(\varOmega \times \{0\}\). This is compatible with \(\mathfrak {u}= 0\) on \(\partial _L \mathcal {C}\) since it implies \(\mathfrak {u}_y = 0\) on \(\partial _L \mathcal {C}\). Consequently, we do not need any compatibility condition on the datum \(f \in H^{1-s}(\varOmega )\) to avoid a jump on the derivative \(\mathfrak {u}_y\). On the other hand, when \(\alpha \in (0,1)\), we have that, for a general \(f\), \(\mathfrak {u}_y \nrightarrow 0\) as \(y \rightarrow 0^+\) on \(\varOmega \times \{0\}\). To compensate this behavior we need the datum \(f\) to vanish at the boundary \(\partial \varOmega \) at a certain rate. This condition is expressed by the requirement \(f \in H_0^{1-s}(\varOmega )\).
Proof of Theorem 2.7
Let us first consider \(s={\tfrac{1}{2}}\). In this case (2.26) reduces to the Poisson problem with mixed boundary conditions. In general, the solution to a mixed boundary value problem is not smooth, even for \(C^\infty \) data. The singular behavior occurs near the points of intersection between the Dirichlet and Neumann boundaries. For instance, the solution \(w = \sqrt{r}\sin (\theta /2)\) of \(\varDelta w=0\) in \(\mathbb {R}^2_+\), with \(w_{x_2} = 0\) for \(\{ x_1 < 0, \ x_2 = 0\}\) and \(w = 0\) for \(\{ x_1 \ge 0, \ x_2 = 0\}\), does not belong to \(H^2(\mathbb {R}^2_+)\). To obtain more regular solutions, a compatibility condition between the data, the operator, and the boundary must be imposed (e.g., [55]). Since in our case we have the representation (2.24), we can explicitly compute the second derivatives, and, using that \(\{ \varphi _k\}_{k\in \mathbb N}\) is an orthonormal basis of \(L^2(\varOmega )\) and \(\{ \varphi _k/\sqrt{\lambda _k}\}_{k\in \mathbb N}\) of \(H_0^1(\varOmega )\), it is not difficult to show that \(f \in H_{00}^{1/2}(\varOmega )\) implies \(\mathfrak {u}\in H^2(\mathcal {C})\), and \(\Vert \mathfrak {u}\Vert _{H^2(\mathcal {C})} \lesssim \Vert f \Vert _{ H_{00}^{1/2}(\varOmega )}\).
In the general case, \(s \in (0,1) \setminus \left\{ {\tfrac{1}{2}}\right\} \), i.e., \(\alpha \in (-1,1)\setminus \{0\}\); using (2.33) as well as the asymptotic properties (2.31) and (2.32), we obtain
which is exactly the regularity estimate given in (2.37). To obtain the regularity estimate on \(\mathfrak {u}_{yy}\), we again use the exact representation (2.24) and properties of Bessel functions to conclude that any derivative with respect to the extended variable \(y\) is smooth away from the Neumann boundary \(\varOmega \times \{0\}\). By virtue of (2.25), we deduce that the following partial differential equation (PDE) holds in the strong sense:
Consider the sequences \(\{a_k = 1/\sqrt{\lambda _k}\}_{k\ge 1},\ \{b_k\}_{k\ge 1}\) and \(\{\delta _k\}_{k\ge 1}\) with \(0 < \delta _k \le a_k \le b_k\). Using (2.24) we have, for \(k\ge 1\),
Let us now estimate the first integral on the right-hand side of (2.39). Formulas (2.30) and (2.28) yield
where the integral converges because \(\beta > 2\alpha + 1\). Let us now look at the second integral. Using property (v) of the modified Bessel functions, we have
Substituting (2.40) and (2.41) into (2.39), and using that \(u_k = \lambda _k^{-s}f_k\), we deduce
because \(2-2s-\frac{\beta }{2}-\frac{1}{2} = \frac{1}{2}(1+2\alpha -\beta )< 0\). This concludes the proof. \(\square \)
For the design of graded meshes later in §5.2 we also need the following local regularity result in the extended variable.
Theorem 2.9
(Local regularity of \(\alpha \)-harmonic extension). Let \(\mathcal {C}(a,b) := \varOmega \times (a,b)\) for \(0 \le a < b\le 1\). The solution  to (2.26) satisfies for all \(a, b\)
to (2.26) satisfies for all \(a, b\)
and, with \(\delta := \beta -2\alpha -1 > 0\),
Proof
To derive (2.42), we proceed as in Theorem 2.7. Since \(0 \le a < b \le 1\), property (iii) of §2.5, together with (2.31), implies that
This, together with (2.33) and the property \(u_k=\lambda _k^{-s}f_k\), allows us to conclude
To prove (2.43), we observe that the same argument used in (2.40) gives
whence
because \(2-2s-\frac{\beta }{2}-\frac{1}{2} < 0\).
Remark 2.10
(Domain and data regularity). The results of Theorems 2.7 and 2.9 are meaningful only if \(f \in \mathbb {H}^{1-s}(\varOmega )\) and the domain \(\varOmega \) is such that
holds. In the analysis that follows we will, without explicit mention, make this assumption. Let us, however, remark that our method works even when these conditions are not satisfied. Refer to §6.3 for an illustration of that case.
3 Truncation
The solution \(\mathfrak {u}\) to problem (2.26) is defined on the infinite domain \(\mathcal {C}\), and consequently it cannot be directly approximated with finite element-like techniques. In this section we will show that \(\mathfrak {u}\) decays sufficiently fast – in fact exponentially – in the extended direction. This suggests truncating the cylinder \(\mathcal {C}\) to  for a suitably defined
for a suitably defined  . The exponential decay is the content of the next result.
. The exponential decay is the content of the next result.
Proposition 3.1
(Exponential decay). For every  , the solution \(\mathfrak {u}\) to (2.26) satisfies
, the solution \(\mathfrak {u}\) to (2.26) satisfies

Proof
Recall that if \(u \in \mathbb {H}^s(\varOmega )\) has the decomposition \(u = \sum _k u_k \varphi _k(x^{\prime })\), then the solution  to (2.26) has the representation \(\mathfrak {u}= \sum _k u_k \varphi (x^{\prime })\psi _k(y)\), where the functions \(\psi _k\) solve (2.25).
to (2.26) has the representation \(\mathfrak {u}= \sum _k u_k \varphi (x^{\prime })\psi _k(y)\), where the functions \(\psi _k\) solve (2.25).
Consider \(s={\tfrac{1}{2}}\). In this case, \(\psi _k(y) = e^{-\sqrt{\lambda _k}y}\). Using the fact that \(\{\varphi _k\}_{k=1}^\infty \) are eigenfunctions of the Dirichlet Laplacian on \(\varOmega \), orthonormal in \(L^2(\varOmega )\), and orthogonal in \(H_0^1(\varOmega )\), with \(\Vert \nabla _{x^{\prime }} \varphi _k\Vert _{L^2(\varOmega )}= \sqrt{\lambda _k}\), we get

Since \(\Vert u \Vert _{\mathbb {H}^{1/2}(\varOmega )} =\Vert f\Vert _{{\mathbb {H}^{-1/2}(\varOmega )}}\), this implies (3.1).
Consider now \(s\in (0,1)\setminus \{{\tfrac{1}{2}}\}\) and \(\psi _k(y) = c_s \left( \sqrt{\lambda _k}y\right) ^s K_s(\sqrt{\lambda _k} y)\). To be able to argue as previously, we need the estimates on \(K_s\) and its derivative for sufficiently large arguments discussed in §2.5. In fact, using (2.32) and (2.33), we obtain

Again, since \(\Vert u \Vert _{\mathbb {H}^s(\varOmega )} = \Vert f\Vert _{\mathbb {H}^{-s}(\varOmega )}\), we obtain (3.1).
Expression (3.1) motivates the approximation of \(\mathfrak {u}\) by a function \(v\) that solves

with  sufficiently large. Problem (3.2) is understood in the weak sense, i.e., we define the space
sufficiently large. Problem (3.2) is understood in the weak sense, i.e., we define the space

and search for  such that
such that

The existence and uniqueness of \(v\) follow from the Lax–Milgram lemma.
Remark 3.2
(Zero extension). For every  we have the embedding
we have the embedding

To see this, it suffices to consider the extension by zero for  .
.
The next result shows the approximation properties of \(v\), the solution to (3.3) in  .
.
Lemma 3.3
(Exponential convergence in  ). For any positive
). For any positive  we have
we have

Proof
Given  , denote by \(\phi _e\) its extension by zero to \(\mathcal {C}\). By Remark 3.2,
, denote by \(\phi _e\) its extension by zero to \(\mathcal {C}\). By Remark 3.2,  . Take \(\phi _e\) and \(\phi \) as test functions in (2.26) and (3.3), respectively. Subtract the resulting expressions to obtain
. Take \(\phi _e\) and \(\phi \) as test functions in (2.26) and (3.3), respectively. Subtract the resulting expressions to obtain

which implies that \(v\) is the best approximation of \(\mathfrak {u}\) in  , i.e.,
, i.e.,

Let us construct explicitly a function  to use in (3.6). Define
to use in (3.6). Define

Notice that \(\rho \in W^1_\infty (0,\infty )\), \(|\rho (y)| \le 1\), and  for all \(y > 0\). Set \(\phi _0(x^{\prime },y)= \mathfrak {u}(x^{\prime },y)\rho (y)\) for \(x^{\prime } \in \varOmega \) and \(y>0\). A straightforward computation shows
for all \(y > 0\). Set \(\phi _0(x^{\prime },y)= \mathfrak {u}(x^{\prime },y)\rho (y)\) for \(x^{\prime } \in \varOmega \) and \(y>0\). A straightforward computation shows

so that

To estimate the first term on the right-hand side of (3.8), we use the Poincaré inequality (2.20) over a dyadic partition that covers the interval  (see the derivation of (2.21) in §2.3) to obtain
(see the derivation of (2.21) in §2.3) to obtain

To bound the second integral in (3.8), we use (2.33) as in the proof of Proposition 3.1:

Inserting these estimates into (3.6) implies (3.5). \(\square \)
The following result is a direct consequence of Lemma 3.3.
Remark 3.4
(Stability). Let  ; then
; then

Indeed, by the triangle inequality,

The previous two results allow us to show a full approximation estimate.
Theorem 3.5
(Global exponential estimate). Let  ; then
; then

In particular, for every \(\epsilon >0\), let

where \(C\) depends only on \(s\) and \(\varOmega \). Then, for  , we have
, we have
Proof
Extending \(v\) by zero outside of  we obtain
we obtain

Hence, Lemma 3.3 and Proposition 3.1 imply

for all  . \(\square \)
. \(\square \)
4 Finite Element Discretization and Interpolation Estimates
In this section we prove error estimates for a piecewise \(\mathbb {Q}_1\) interpolation operator on anisotropic elements in the extended variable \(y\). We consider elements of the form \(T = K \times I\), where \(K \subset \mathbb {R}^n\) is an element isoparametrically equivalent to the unit cube \([0,1]^n\), via a \(\mathbb {Q}_1\) mapping, and \(I \subset \mathbb {R}\) is an interval. The anisotropic character of the mesh  will be given by the family of intervals \(I\).
will be given by the family of intervals \(I\).
The error estimates are derived in the weighted Sobolev spaces  and
and  , and they are valid under the condition that neighboring elements have comparable size in the extended \((n+1)\) dimension (see [30]). This is a mild assumption that includes general meshes that do not satisfy the so-called shape-regularity assumption, i.e., mesh refinements for which the quotient between the outer and inner diameter of the elements does not remain bounded (see [17, Chap. 4]).
, and they are valid under the condition that neighboring elements have comparable size in the extended \((n+1)\) dimension (see [30]). This is a mild assumption that includes general meshes that do not satisfy the so-called shape-regularity assumption, i.e., mesh refinements for which the quotient between the outer and inner diameter of the elements does not remain bounded (see [17, Chap. 4]).
Anisotropic or narrow elements are elements with disparate sizes in each direction. They arise naturally when approximating solutions to problems with a strong direction-dependent behavior since, using anisotropy, the local mesh size can be adapted to capture such features. Examples of this include boundary layers, shocks, and edge singularities (see [30, 31]). In our problem, anisotropic elements are essential to capture the singular/degenerate behavior of the solution \(\mathfrak {u}\) to problem (2.26) at \(y \approx 0^+\) given in (2.34). These elements will provide optimal error estimates, which cannot be obtained using shape-regular elements.
Error estimates for weighted Sobolev spaces were obtained in several works, for instance, [4, 9, 30]. The type of weight considered in [4, 9] is related to the distance to a point or an edge, and the type of quasi-interpolators are modifications of the well-known Clément [26] and Scott–Zhang [56] operators. These works are developed in three dimensions and two dimensions, respectively, and the analysis developed in [4] allows for anisotropy. Our approach follows the work of Durán and Lombardi [30] and is based on a piecewise \(\mathbb {Q}_1\) averaged interpolator on anisotropic elements. It allows us to obtain anisotropic interpolation estimates in the extended variable \(y\) and in weighted Sobolev spaces using only that \(|y|^{\alpha } \in A_2(\mathbb {R}^{n+1})\), the Muckenhoupt class \(A_2\) of Definition 2.1. We develop a general interpolation theory for weights of class \(A_p\), with \(1 < p < \infty \), in [54].
4.1 Finite Element Discretization
Let us now describe the discretization of problem (3.2). To avoid technical difficulties, we assume that the boundary of \(\varOmega \) is polygonal. The difficulties inherent in curved boundaries could be addressed, for instance, using the methods of [11] (see also [44, 45]). Let \(\fancyscript{T}_\varOmega = \{K\}\) be a mesh of \(\varOmega \) made of isoparametric quadrilaterals \(K\) in the sense of Ciarlet [24] and Ciarlet and Raviart [25]. In other words, given \(\hat{K} = [0,1]^n\) and a family of mappings \(\{ \mathcal {F}_K \in \mathbb {Q}_1(\hat{K})^n \}\), we have
and
The collection of triangulations is denoted by \(\mathbb {T}_\varOmega \).
The mesh \(\fancyscript{T}_{\varOmega }\) is assumed to be conforming or compatible, i.e., the intersection of any two isoparametric elements \(K\) and \(K^{\prime }\) in \(\fancyscript{T}_{\varOmega }\) is either empty or a common lower-dimensional isoparametric element.
In addition, we assume that \(\fancyscript{T}_\varOmega \) is shape-regular (cf. [24, Chap. 4.3]). This means that \(\mathcal {F}_K\) can be decomposed as \(\mathcal {F}_K = \mathcal {A}_K + \mathcal {B}_K\), where \(\mathcal {A}_K\) is affine and \(\mathcal {B}_K\) is a perturbation map, and if we define \(\tilde{K} = \mathcal {A}_K(\hat{K} )\), \(h_K = \mathrm diam (\tilde{K})\), \(\rho _K\) as the diameter of the largest sphere inscribed in \(\tilde{K}\) and the shape coefficient of \(K\) as the ratio \(\sigma _{K}=h_K/\rho _K\), then the following two conditions are satisfied:
-
(a)
There exists a constant \(\sigma _{\varOmega } > 1\) such that for all \(\fancyscript{T}_{\varOmega } \in \mathbb {T}_{\varOmega }\),
$$\begin{aligned} \max \left\{ \sigma _K : K \in \fancyscript{T}_\varOmega \right\} \le \sigma _\varOmega . \end{aligned}$$ -
(b)
For all \(K \in \fancyscript{T}_\varOmega \) the mapping \(\mathcal {B}_K\) is Fréchet differentiable and
$$\begin{aligned} \Vert D \mathcal {B}_K\Vert _{L^\infty (\hat{K} )} = \mathcal O(h_K^2) \end{aligned}$$for all \(K \in \fancyscript{T}_\varOmega \) and all \(\fancyscript{T}_\varOmega \in \mathbb {T}_\varOmega \).
As a consequence of these conditions, if \(h_K\) is small enough, then the mapping \(\mathcal {F}_K\) is one-to-one, its Jacobian \(J_{\mathcal {F}_K}\) does not vanish, and
The set \(\mathbb {T}_{\varOmega }\) is called quasi-uniform if for all \(\fancyscript{T}_{\varOmega } \in \mathbb {T}_{\varOmega }\)
In this case, we define \(h_{\fancyscript{T}_{\varOmega }}= \max _{K \in \fancyscript{T}}h_K\).
We define  as a triangulation of
as a triangulation of  into cells of the form \(T = K \times I\), where \(K \in \fancyscript{T}_\varOmega \), and \(I\) denotes an interval in the extended dimension. Notice that each discretization of the truncated cylinder
into cells of the form \(T = K \times I\), where \(K \in \fancyscript{T}_\varOmega \), and \(I\) denotes an interval in the extended dimension. Notice that each discretization of the truncated cylinder  depends on the truncation parameter
depends on the truncation parameter  . The set of all such triangulations is denoted by \(\mathbb {T}\). To obtain a global regularity assumption for \(\mathbb {T}\), we assume the aforementioned conditions on \(\mathbb {T}_\varOmega \), besides the following weak regularity condition:
. The set of all such triangulations is denoted by \(\mathbb {T}\). To obtain a global regularity assumption for \(\mathbb {T}\), we assume the aforementioned conditions on \(\mathbb {T}_\varOmega \), besides the following weak regularity condition:
-
(c)
There is a constant \(\sigma \) such that, for all
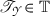 , if
, if  have nonempty intersection, then $$\begin{aligned} \frac{h_{I_1}}{h_{I_2}} \le \sigma , \end{aligned}$$
have nonempty intersection, then $$\begin{aligned} \frac{h_{I_1}}{h_{I_2}} \le \sigma , \end{aligned}$$where \(h_I = |I|\).
Notice that the assumptions imposed on \(\mathbb {T}\) are weaker than the standard shape-regularity assumptions since they allow for anisotropy in the extended variable (cf. [30]). It is also important to notice that, given the Cartesian product structure of the cells  , they are isoparametrically equivalent to \(\hat{T} = [0,1]^{n+1}\). We will denote the corresponding mappings by \(\mathcal {F}_T\). Then
, they are isoparametrically equivalent to \(\hat{T} = [0,1]^{n+1}\). We will denote the corresponding mappings by \(\mathcal {F}_T\). Then
where \(\mathcal {F}_K\) is the bilinear mapping defined in (4.1) for \(K\), and if \(I = (c,d)\), \(\mathcal {F}_I(y) = (y - c)/(d-c)\). From (4.2) we immediately conclude that
for all elements  , where \(h_T = \max \{h_K,h_I\}\).
, where \(h_T = \max \{h_K,h_I\}\).
Given  , we define the finite element space
, we define the finite element space  by
by

where  is called the Dirichlet boundary. The Galerkin approximation of (3.3) is given by the unique function
is called the Dirichlet boundary. The Galerkin approximation of (3.3) is given by the unique function  such that
such that

The existence and uniqueness of  follow from
follow from  and the Lax–Milgram lemma.
and the Lax–Milgram lemma.
We define the space  , which is simply a \(\mathbb {Q}_1\) finite element space over the mesh \(\fancyscript{T}_\varOmega \). The finite element approximation of \(u \in \mathbb {H}^s(\varOmega )\), the solution to (1.1), is then given by
, which is simply a \(\mathbb {Q}_1\) finite element space over the mesh \(\fancyscript{T}_\varOmega \). The finite element approximation of \(u \in \mathbb {H}^s(\varOmega )\), the solution to (1.1), is then given by

and we have the following result.
Theorem 4.1
(Energy error estimate). Let \(v\) solve (3.3), with  solves (4.4) and \(U_{\fancyscript{T}_{\varOmega }} \in \mathbb {U}(\fancyscript{T}_{\varOmega })\) is defined in (4.5), then we have
solves (4.4) and \(U_{\fancyscript{T}_{\varOmega }} \in \mathbb {U}(\fancyscript{T}_{\varOmega })\) is defined in (4.5), then we have

and

Proof
Estimate (4.6) is simply an application of the trace estimate of Proposition 2.5. Inequality (4.7) is obtained by the triangle inequality and (3.12). \(\square \)
By Galerkin orthogonality,

Theorem 4.1 and Galerkin orthogonality imply that the approximation estimate (4.7) depends on the regularity of \(\mathfrak {u}\). To see this, we introduce

where \(p\) is the unique cubic polynomial on  defined by the conditions
defined by the conditions  ,
,  ,
,  , and
, and  . Notice that
. Notice that  , \(|\rho (y)| \le 1\), \(|\rho ^{\prime }(y)| \lesssim 1\), and \(|\rho ^{\prime \prime }(y)| \lesssim 1\). Set \(\mathfrak {u}_0(x^{\prime },y) = \rho (y) \mathfrak {u}(x^{\prime },y)\) for \(x^{\prime } \in \varOmega \) and
, \(|\rho (y)| \le 1\), \(|\rho ^{\prime }(y)| \lesssim 1\), and \(|\rho ^{\prime \prime }(y)| \lesssim 1\). Set \(\mathfrak {u}_0(x^{\prime },y) = \rho (y) \mathfrak {u}(x^{\prime },y)\) for \(x^{\prime } \in \varOmega \) and  , and notice that
, and notice that  . With this construction at hand, repeating the arguments used in the proof of Lemma 3.3, we have that
. With this construction at hand, repeating the arguments used in the proof of Lemma 3.3, we have that

In addition, if we assume that there is an operator

that is stable, i.e.,  , for all
, for all  , then the following estimate holds:
, then the following estimate holds:

To see this, we use (4.7), together with Galerkin orthogonality and the stability of the operator  , to obtain
, to obtain

The second term on the right-hand side of the previous inequality is estimated as in Lemma 3.3. We leave the details to the reader.
Estimates for  on weighted Sobolev spaces are derived in §4.2. Clearly, these depend on the regularity of \(\mathfrak {u}_0\), which, in light of (4.9), depends on the regularity of \(\mathfrak {u}\). For this reason, and to lighten the notation, we shall in the sequel write \(\mathfrak {u}\) and obtain interpolation error estimates for it, even though \(\mathfrak {u}\) does not vanish at
on weighted Sobolev spaces are derived in §4.2. Clearly, these depend on the regularity of \(\mathfrak {u}_0\), which, in light of (4.9), depends on the regularity of \(\mathfrak {u}\). For this reason, and to lighten the notation, we shall in the sequel write \(\mathfrak {u}\) and obtain interpolation error estimates for it, even though \(\mathfrak {u}\) does not vanish at  .
.
4.2 Interpolation Estimates in Weighted Sobolev Spaces
Let us begin by introducing some notation and terminology. Given  , we call \(\mathcal {N}\) the set of its nodes and \(\mathcal {N}_{\, \mathrm in }\) the set of its interior and Neumann nodes. For each vertex \(\mathtt{v}\in \mathcal {N}\) we write \(\mathtt{v}= (\mathtt{v}^{\prime },\mathtt{v}^{\prime \prime })\), where \(\mathtt{v}^{\prime }\) corresponds to a node of \(\fancyscript{T}_\varOmega \), and \(\mathtt{v}^{\prime \prime }\) corresponds to a node of the discretization of the \((n+1)\) dimension. We define \(h_{\mathtt{v}^{\prime }}= \min \{h_K: \mathtt{v}^{\prime } \mathrm is a vertex of K\}\), and \(h_{\mathtt{v}^{\prime \prime }} = \min \{h_I: \mathtt{v}^{\prime \prime } \mathrm is a vertex of I\}\).
, we call \(\mathcal {N}\) the set of its nodes and \(\mathcal {N}_{\, \mathrm in }\) the set of its interior and Neumann nodes. For each vertex \(\mathtt{v}\in \mathcal {N}\) we write \(\mathtt{v}= (\mathtt{v}^{\prime },\mathtt{v}^{\prime \prime })\), where \(\mathtt{v}^{\prime }\) corresponds to a node of \(\fancyscript{T}_\varOmega \), and \(\mathtt{v}^{\prime \prime }\) corresponds to a node of the discretization of the \((n+1)\) dimension. We define \(h_{\mathtt{v}^{\prime }}= \min \{h_K: \mathtt{v}^{\prime } \mathrm is a vertex of K\}\), and \(h_{\mathtt{v}^{\prime \prime }} = \min \{h_I: \mathtt{v}^{\prime \prime } \mathrm is a vertex of I\}\).
Given \(\mathtt{v}\in \mathcal {N}\), the star or patch around \(\mathtt{v}\) is defined as
and for  we define its patch as
we define its patch as
Let \(\psi \in C^{\infty }(\mathbb {R}^{n+1})\) be such that \(\int \psi = 1\) and  , where \(B_r\) denotes the ball in \(\mathbb {R}^n\) of radius \(r\) and centered at zero, and
, where \(B_r\) denotes the ball in \(\mathbb {R}^n\) of radius \(r\) and centered at zero, and  and
and  . For \(\mathtt{v}\in \mathcal {N}_{\, \mathrm in }\), we rescale \(\psi \) as
. For \(\mathtt{v}\in \mathcal {N}_{\, \mathrm in }\), we rescale \(\psi \) as
and note that \({{\mathrm{supp\,}}}\psi _{\mathtt{v}} \subset \omega _{\mathtt{v}}\) and \(\int \limits _{\omega _{\mathtt{v}}} \psi _{\mathtt{v}} = 1\) for any interior and Neumann node \(\mathtt{v}\).
Remark 4.2
(Boundary conditions of Neumann type). For an interior node \(\mathtt{v}\), it would be natural to consider  as the support of the smooth function \(\psi \). However, for a Neumann node \(\mathtt{v}\), this choice would not provide the important properties \({{\mathrm{supp\,}}}\psi _{\mathtt{v}} \subset \omega _{\mathtt{v}}\) and \(\int \limits _{\omega _{\mathtt{v}}} \psi _{\mathtt{v}} = 1\). To treat both types of node indistinctly in the subsequent analysis, we have considered
as the support of the smooth function \(\psi \). However, for a Neumann node \(\mathtt{v}\), this choice would not provide the important properties \({{\mathrm{supp\,}}}\psi _{\mathtt{v}} \subset \omega _{\mathtt{v}}\) and \(\int \limits _{\omega _{\mathtt{v}}} \psi _{\mathtt{v}} = 1\). To treat both types of node indistinctly in the subsequent analysis, we have considered  .
.
Given a function  and a node \(\mathtt{v}\) in \(\mathcal {N}_{\,\mathrm in }\), we define, following Durán and Lombardi [30], the regularized Taylor polynomial of first degree of \(w\) about \(\mathtt{v}\) as
and a node \(\mathtt{v}\) in \(\mathcal {N}_{\,\mathrm in }\), we define, following Durán and Lombardi [30], the regularized Taylor polynomial of first degree of \(w\) about \(\mathtt{v}\) as
where \(P\) denotes the Taylor polynomial of degree 1 in the variable \(z\) of the function \(w\) about the point \(x\), i.e.,
As a consequence of Remark 2.3 and the fact that the averaged Taylor polynomial is defined for functions in  (cf. [17, Proposition 4.1.12]), we conclude that \(P\) is well defined for any function in
(cf. [17, Proposition 4.1.12]), we conclude that \(P\) is well defined for any function in  .
.
We define the averaged \(\mathbb {Q}_1\) interpolant  as the unique piecewise \(\mathbb {Q}_1\) function such that
as the unique piecewise \(\mathbb {Q}_1\) function such that  if \(\mathtt{v}\) lies on the Dirichlet boundary \(\varGamma _D\) and
if \(\mathtt{v}\) lies on the Dirichlet boundary \(\varGamma _D\) and  if \(\mathtt{v}\in \mathcal {N}_{~\mathrm in }\). If \(\lambda _{\mathtt{v}}\) denotes the Lagrange basis function associated with node \(\mathtt{v}\), then
if \(\mathtt{v}\in \mathcal {N}_{~\mathrm in }\). If \(\lambda _{\mathtt{v}}\) denotes the Lagrange basis function associated with node \(\mathtt{v}\), then

There are two principal reasons to consider averaged interpolation. First, we are interested in the approximation of singular functions, and thus Lagrange interpolation cannot be used since pointwise values become meaningless. In fact, this motivated the introduction of averaged interpolation (see [26, 56]). In addition, averaged interpolation has better approximation properties when narrow elements are used (see [2]).
Finally, for \(\mathtt{v}\in \mathcal {N}_{\, \mathrm in }\) we define the weighted regularized average of \(w\) as
4.2.1 Weighted Poincaré Inequality
To obtain interpolation error estimates in  and
and  , it is instrumental to have a weighted Poincaré-type inequality. Weighted Poincaré inequalities are particularly pertinent in the study of the nonlinear potential theory of degenerate elliptic equations; see [36, 41]. If the domain is a ball and the weight belongs to \(A_p\), with \(1 \le p < \infty \), this result can be found in [36, Theorems 1.3 and 1.5]. However, to the best of our knowledge, such a result is not available in the literature for more general domains. For our specific weight we present here a constructive proof, i.e., not based on a compactness argument. This allows us to study the dependence of the constant on the domain.
, it is instrumental to have a weighted Poincaré-type inequality. Weighted Poincaré inequalities are particularly pertinent in the study of the nonlinear potential theory of degenerate elliptic equations; see [36, 41]. If the domain is a ball and the weight belongs to \(A_p\), with \(1 \le p < \infty \), this result can be found in [36, Theorems 1.3 and 1.5]. However, to the best of our knowledge, such a result is not available in the literature for more general domains. For our specific weight we present here a constructive proof, i.e., not based on a compactness argument. This allows us to study the dependence of the constant on the domain.
Lemma 4.3
(Weighted Poincaré inequality I). Let \(\omega \subset \mathbb {R}^{n+1}\) be bounded, star-shaped with respect to a ball \(B\), and \({{\mathrm{diam}}}\omega \approx 1\). Let \(\chi \in C^0\left( \bar{\omega }\right) \), with \(\int \limits _{\omega } \chi = 1\), and \(\xi _{\alpha }(y) := \left| a|y| + b\right| ^{\alpha }\) for \(a,b\in \mathbb {R}\). If \(w \in H^1(\omega ,\xi _{\alpha }(y))\) is such that \(\int \limits _{\omega } \chi w = 0\), then
where the hidden constant depends only on \(\chi \), \(\alpha \), and the radius \(r\) of \(B\) but is independent of both \(a\) and \(b\).
Proof
The fact that \(\alpha \in (-1,1)\) implies \(\xi _{\alpha }\in A_2(\mathbb {R}^{n+1})\), with a Muckenhoupt constant \(C_{2,\xi _{\alpha }}\) in (2.15) uniform in both \(a\) and \(b\). Define
Clearly, \(\widetilde{w} \in L^1(\omega )\), and it has a vanishing mean value by construction.
Since \(\int \limits _{\omega } \chi w = 0\), we obtain
Consequently, given that \(\omega \) is star-shaped with respect to \(B\), and \(\xi _{\alpha }\in A_2(\mathbb {R}^{n+1})\), there exists \(F \in H_0^1(\omega ,\xi _{\alpha })^{n+1}\) such that \(- \mathrm div F = \widetilde{w}\), and
where the hidden constant in (4.16) depends on \(r\) and the constant \(C_{2,\xi _{\alpha }}\) from Definition 2.1 [32, Theorem 3.1].
Replacing \(\widetilde{w}\) with \(-\mathrm div F\) in (4.15), integrating by parts, and using (4.16), we obtain
To estimate \(\Vert \widetilde{w} \Vert _{L^2(\omega ,\xi _{\alpha }^{-1})}\), we use the Cauchy–Schwarz inequality and the constant \(C_{2,\xi _\alpha }\) from Definition 2.1 as follows:
Inserting the preceding inequality into (4.17), we obtain (4.14). \(\square \)
We need a slightly more general form of the Poincaré inequality for the applications that follow. We now relax the geometric assumption on the domain \(\omega \) and let the vanishing mean property hold just in a subdomain.
Corollary 4.4
(Weighted Poincaré inequality II). Let \(\omega =\cup _{i=1}^N\omega _i\subset \mathbb {R}^{n+1}\) be a connected domain and each \(\omega _i\) be a star-shaped domain with respect to a ball \(B_i\). Let \(\chi _i\in C^0(\bar{\omega }_i)\) and \(\xi _{\alpha }\) be as in Lemma 4.3. If \(w\in H^1(\omega ,\xi _{\alpha })\) and \(w_i:=\int \limits _{\omega _i} w\chi _i\), then
where the hidden constant depends on \(\{\chi _i\}_{i=1}^N\), \(\alpha \), the radius \(r_i\) of \(B_i\), and the amount of overlap between the subdomains \(\{\omega _i\}_{i=1}^N\) but is independent of both \(a\) and \(b\).
Proof
This is a consequence of Lemma 4.3 and [29, Theorem 7.1]. We sketch the proof here for completeness. It suffices to deal with two subdomains, \(\omega _1\) and \(\omega _2\), and the overlapping region \(B=\omega _1\cap \omega _2\). We observe that
together with \(\Vert w_1-w_2\Vert _{L^2(\omega _2,\xi _{\alpha })} = \left( \frac{\int \limits _{\omega _2}\xi _{\alpha }}{\int \limits _B\xi _{\alpha }} \right) ^{1/2} \Vert w_1-w_2\Vert _{L^2(B,\xi _{\alpha })}\) and
implies \(\Vert w-w_1\Vert _{L^2(\omega _2,\xi _{\alpha })} \lesssim \Vert \nabla w\Vert _{L^2({\omega _1 \cup \omega _2},\xi _{\alpha })}\). This, combined with (4.14), gives (4.18) for \(i=1\) with a stability constant depending on the ratio \(\frac{\int \limits _{\omega _2}\xi _{\alpha }}{\int \limits _B\xi _{\alpha }}\). \(\square \)
4.2.2 Weighted \(L^2\) Interpolation Estimates
Owing to the weighted Poincaré inequality of Corollary 4.4, we can adapt the proof of [30, Lemma 2.3] to obtain interpolation estimates in the weighted \(L^2\)-norm. These estimates allow a disparate mesh size on the extended direction, relative to the coordinate directions \(x_i\), \(i=1,\ldots ,n,\) which may in turn be graded. This is the principal difference with [30, Lemma 2.3], where the domain must be a cube.
Lemma 4.5
(Weighted \(L^2\)-based interpolation estimates). Let \(\mathtt{v}\in \mathcal {N}_{\, { in}}\). Then, for all \(w \in H^1(\omega _{\mathtt{v}},y^{\alpha })\), we have
and for all \(w \in H^2(\omega _{\mathtt{v}},y^{\alpha })\) and \(j=1,\ldots ,n+1\) we have
where, in both inequalities, the hidden constant depends only on \(\alpha \), \(\sigma _{\varOmega }\), \(\sigma \), and \(\psi \).
Proof
Define by \(\mathcal {F}_\mathtt{v}: (x^{\prime },y) \rightarrow (\bar{x}^{\prime },\bar{y}) \) the scaling map
along with \(\overline{\omega }_\mathtt{v}= \mathcal {F}_\mathtt{v}(\omega _\mathtt{v})\) and \(\bar{w}(\bar{x}) = w(x)\). Define also \( \bar{Q} \bar{w}= \int \bar{w} \psi , \) where \(\psi \) was introduced in Sect. 4.2. Since \({{\mathrm{supp\,}}}\psi \subset \overline{\omega }_{\mathtt{v}}\), integration takes place only over \(\overline{\omega }_\mathtt{v}\), and \(\int \limits _{\overline{\omega }_\mathtt{v}} \psi =1\). Then \(\bar{Q} \bar{w}\) satisfies \( \bar{Q} \bar{w} = \int \limits _{\overline{\omega }_{\mathtt{v}}}\bar{w} \psi = \int \limits _{\omega _{\mathtt{v}}} w \psi _{\mathtt{v}} = Q_{\mathtt{v}} w \) and
Simple scaling, using the definition of the mapping \(\mathcal {F}_{\mathtt{v}}\), yields
where \(\xi _{\alpha }(y) := | \mathtt{v}^{\prime \prime } + \bar{y}h_{\mathtt{v}^{\prime \prime }} |^{\alpha }\). By shape regularity, the mesh sizes \(h_{\mathtt{v}^{\prime }}, h_{\mathtt{v}^{\prime \prime }}\) satisfy \(1/{2\sigma } \le h_{\bar{\mathtt{v}}^{\prime \prime }} \le 2\sigma \) and \(1/2\sigma _{\varOmega } \le h_{\bar{\mathtt{v}}^{\prime }} \le 2\sigma _{\varOmega }\), respectively, and \({{\mathrm{diam}}}\overline{\omega }_{\mathtt{v}}\approx 1\). In view of (4.21), we can apply Lemma 4.3, with the weight \(\xi _{\alpha }\) and \(\chi = \psi \), to \(\omega = \overline{\omega }_{\mathtt{v}}\) to obtain
where the hidden constant depends only on \(\alpha \), \(\sigma _{\varOmega }\), \(\sigma \), and \(\psi \) but not on \(\mathtt{v}^{\prime \prime }\) and \(h_{\mathtt{v}^{\prime }}\). Applying this to (4.22), together with a change of variables with \(\mathcal {F}_{\mathtt{v}}^{-1}\), we obtain (4.19).
The proof of (4.20) is similar. Notice that
Since \(\partial _{\bar{z}_i} \bar{w}_0(\bar{z}) = \int \limits _{\overline{\omega }_{\mathtt{v}}} \partial _{\bar{x}_i} \bar{w}(\bar{x})\psi (\bar{x}) \, \mathrm{d}\bar{x}\) is constant, we have the vanishing mean value property
Applying Lemma 4.3 to \(\partial _{\bar{x}_i}\left( \bar{w}(\bar{x}) - \bar{w}_0(\bar{x}) \right) \) and scaling with \(\mathcal {F}_{\mathtt{v}}\), we obtain (4.20). \(\square \)
By shape regularity, for all \(\mathtt{v}\in \mathcal {N}_{\,\mathrm in }\) and \(T \subset \omega _\mathtt{v}\), the quantities \(h_{\mathtt{v}^{\prime }}\) and \(h_{\mathtt{v}^{\prime \prime }}\) are equivalent to \(h_K\) and \(h_I\), up to a constant that depends only on \(\sigma _{\varOmega }\) and \(\sigma \), respectively. This fact leads to the following result about interpolation estimates in the weighted \(L^2\)-norm on interior elements; see §4.2.4 for boundary elements.
Theorem 4.6
(Stability and local interpolation in weighted \(L^2\)-norm). For all  such that \(\partial T \cap \varGamma _D = \emptyset \) and \(w \in L^2(\omega _{T},y^{\alpha })\), we have
such that \(\partial T \cap \varGamma _D = \emptyset \) and \(w \in L^2(\omega _{T},y^{\alpha })\), we have

If, in addition, \(w \in H^1(\omega _{T},y^{\alpha })\), then

The hidden constants in both inequalities depend only on \(\sigma _{\varOmega }\), \(\sigma \), \(\psi \), and \(\alpha \).
Proof
Let  be an element such that \(\partial T \cap \varGamma _D = \emptyset \). Assume for the moment that
be an element such that \(\partial T \cap \varGamma _D = \emptyset \). Assume for the moment that  is uniformly bounded as a mapping from \(L^2(\omega _T,y^{\alpha })\) to \(L^2(T,y^{\alpha })\), i.e., (4.23).
is uniformly bounded as a mapping from \(L^2(\omega _T,y^{\alpha })\) to \(L^2(T,y^{\alpha })\), i.e., (4.23).
Choose a node \(\mathtt{v}\) of \(T\). Since \(Q_{\mathtt{v}}w\) is constant, we deduce  , whence
, whence

so that (4.24) follows from Corollary 4.4.
It remains to show the local boundedness (4.23) of  . By definition,
. By definition,

where \(\{ \mathtt{v}_{i} \}_{i=1}^{n_T}\) denotes the set of interior vertices of \(T\). By the triangle inequality,

so that we need to estimate \(\Vert w_{\mathtt{v}_i} \Vert _{L^{\infty }(T)}\). This follows from (4.11), along with
and, for \(\ell = 1,\ldots ,n+1\),
We obtain (4.27) upon integration by parts, and noticing that \(\psi _{\mathtt{v}_i} =0\) on \(\partial \omega _{\mathtt{v}_i}\), and \(|z_l - x_l| | \partial _{x_l} \psi _{\mathtt{v}_i} | \lesssim 1\) for \(1 \le l \le n+1\). Replacing (4.26) and (4.27) in (4.25), we get

where the last inequality is a consequence of \(\lambda _{\mathtt{v}_i}\) and \(\psi \) being bounded in \(L^{\infty }(\omega _T)\),
together with \(|y|^{\alpha } \in A_2(\mathbb {R}^{n+1})\); see (2.15). \(\square \)
4.2.3 Weighted \(H^1\) Interpolation Estimates on Interior Elements
Here we prove interpolation estimates on the first derivatives for interior elements. The rather technical proof is an adaptation of [30, Theorem 2.5] to our particular geometric setting. In contrast to [30, Theorem 2.5], we do not have the symmetries of a cube. However, exploiting the Cartesian product structure of the elements \(T = K \times I\), we are capable of handling the anisotropy in the extended variable \(y\) for general shape-regular graded meshes  . This is the content of the following result.
. This is the content of the following result.
Theorem 4.7
(Stability and local interpolation: interior elements). Let  be such that \(\partial T \cap \varGamma _D = \emptyset \). For all \(w \in H^1(\omega _{T},y^{\alpha })\) we have the stability bounds
be such that \(\partial T \cap \varGamma _D = \emptyset \). For all \(w \in H^1(\omega _{T},y^{\alpha })\) we have the stability bounds


and for all \(w \in H^2(\omega _{T},y^{\alpha })\) and \(j=1,\ldots ,n+1\) we have the error estimates

Proof
To exploit the particular structure of \(T\), we label its vertices in an appropriate way; see Fig. 1 for the three-dimensional case. In general, if \(T=K\times [a,b]\), we first assign a numbering \(\{\mathtt{v}_k\}_{k=1,\ldots ,2^{n}}\) to the nodes that belong to \(K\times \{a\}\). If \((\tilde{\mathtt{v}}^{\prime },b)\) is a vertex in \(K \times \{b\}\), then there is a \(\mathtt{v}_k \in K \times \{a\}\) such that \(\tilde{\mathtt{v}}^{\prime }=\mathtt{v}_k^{\prime }\), and we set \(\mathtt{v}_{k+2^n} = \tilde{\mathtt{v}}\). We proceed in three steps.
Derivative
\(\partial _y\)
in extended dimension. We wish to obtain a bound for the norm  . Since
. Since  and an estimate for the difference \(w - w_{\mathtt{v}_1}\) is given in Lemma 4.5, it suffices to consider
and an estimate for the difference \(w - w_{\mathtt{v}_1}\) is given in Lemma 4.5, it suffices to consider  . Thanks to the special labeling of the nodes and the tensor product structure of the elements, i.e., \(\partial _y \lambda _{\mathtt{v}_{i+2^n}} = -\partial _y\lambda _{\mathtt{v}_{i}}\), we obtain
. Thanks to the special labeling of the nodes and the tensor product structure of the elements, i.e., \(\partial _y \lambda _{\mathtt{v}_{i+2^n}} = -\partial _y\lambda _{\mathtt{v}_{i}}\), we obtain
so that
We now set \(i=1\) and proceed to estimate the difference \(| q(\mathtt{v}_1) - q(\mathtt{v}_{1+2^n}) |\). By the definitions of  and \(q\), we have
and \(q\), we have  , whence
, whence
and by the definition (4.11) of the averaged Taylor polynomial, we have
Recalling the operator \(\odot \), introduced in (2.4), we notice that for \(h_\mathtt{v}= (h_{\mathtt{v}^{\prime }},h_{\mathtt{v}^{\prime \prime }})\) and \(z\in \mathbb {R}^{n+1}\), the vector \(h_\mathtt{v}\odot z\) is uniformly equivalent to \((h_K z^{\prime }, h_I z^{\prime \prime })\) for all \(T = K \times I\) in the star \(\omega _{\mathtt{v}}\). Changing variables in (4.32) yields
To estimate this expression, define
and \(F_z(t) = P(\mathtt{v}_1 - h_{\mathtt{v}_1} \odot z + t\theta ,\mathtt{v}_{1+2^n})\). Using that \(\mathtt{v}_1^{\prime }=\mathtt{v}_{1+2^n}^{\prime }\) and \(h_{\mathtt{v}_1^{\prime }} = h_{\mathtt{v}_{1+2^n}^{\prime }}\), we easily obtain
Consequently,
and since \(\psi \) is bounded in \(L^{\infty }\) and \({{\mathrm{supp\,}}}\psi =D \subset B_1 \times (-1,1)\), we need to estimate the integral
Invoking the definitions of \(F_{z}\) and \(P(x,y)\), we deduce
and
Using these two expressions, we arrive at
Now, since \(|z^{\prime }|, |z^{\prime \prime }| \le 1\) and \(0 \le t \le 1\), we see that
Consequently,
Changing variables, via \(\tau = \mathtt{v}_1 - h_{\mathtt{v}_1} \odot z + t \theta \), we obtain
because the support \(D\) of \(\psi \) is contained in  and so is mapped into \(\omega _{\mathtt{v}_1}\subset \omega _T\). Notice also that \(h_{\mathtt{v}_1^{\prime \prime }} \lesssim (1-t)h_{\mathtt{v}_1^{\prime \prime }} + th_{\mathtt{v}_{1+2^n}^{\prime \prime }}\). This implies
and so is mapped into \(\omega _{\mathtt{v}_1}\subset \omega _T\). Notice also that \(h_{\mathtt{v}_1^{\prime \prime }} \lesssim (1-t)h_{\mathtt{v}_1^{\prime \prime }} + th_{\mathtt{v}_{1+2^n}^{\prime \prime }}\). This implies
which, together with (4.35), yields
Since \(|y|^\alpha \in A_2(\mathbb {R}^{n+1})\), we have
Substituting this into (4.37), we obtain
which, in this case, implies (4.30).
We now proceed to estimate the differences \(|q(\mathtt{v}_i) - q(\mathtt{v}_{i+2^n})|\) in (4.31) for \(i=2,\ldots ,2^n\). We employ the arguments presented in [30, Theorem 2.5], in conjunction with the techniques developed, to obtain the estimate (4.38). We start by writing
Term \(III\) is identical to (4.32). The novelty here is the presence of terms \(I\) and \(II\), which, in view of (4.11) and the fact that \(\mathtt{v}_i^{\prime } = \mathtt{v}_{i+2^n}^{\prime }\) for \(i=2,\ldots ,2^n\), can be rewritten as
To estimate this expression, we define \(\vartheta = (\mathtt{v}_1^{\prime } - \mathtt{v}_i^{\prime } - (h_{\mathtt{v}_1^{\prime }} - h_{\mathtt{v}_i^{\prime }})z\prime ,0)\) and the function \(G_z(t) = \partial _{y}w(\mathtt{v}_i - h_{\mathtt{v}_i} \odot z + t \vartheta )\). Then, using \(\mathtt{v}_1^{\prime \prime } = \mathtt{v}_{i}^{\prime \prime }\) and \(h_{\mathtt{v}_1^{\prime \prime }} = h_{\mathtt{v}_i^{\prime \prime }}\) for \(i=2,\ldots ,2^n\), we arrive at
Proceeding as in the case \(i=1\), we obtain
Collecting the preceding estimates for \(i=2,\ldots ,2^n\), we finally obtain
This, together with (4.38), implies the desired estimate (4.30) for \(j=n+1\).
Derivatives
\(\nabla _{x^{\prime }}\)
in domain
\(\varOmega \). To prove an estimate for  , we notice that, given a vertex \(\mathtt{v}\), the associated basis function \(\lambda _{\mathtt{v}}\) can be written as \(\lambda _{\mathtt{v}}(x) = \Lambda _{\mathtt{v}^{\prime }}(x\prime ) \mu _{\mathtt{v}^{\prime \prime }}(y)\), where \(\Lambda _{\mathtt{v}^{\prime }}\) is the canonical \(\mathbb {Q}_1\) basis function on the variable \(x^{\prime }\) associated to the node \(\mathtt{v}^{\prime }\) in the triangulation \(\fancyscript{T}_\varOmega \), and \(\mu _{\mathtt{v}^{\prime \prime }}\) corresponds to the piecewise \(\mathbb {P}_1\) basis function associated to the node \({\mathtt{v}^{\prime \prime }}\). Recall that, by construction, the basis \(\{ \Lambda _i \}_{i=1}^{2^n}\) possesses the so-called partition of unity property, i.e.,
, we notice that, given a vertex \(\mathtt{v}\), the associated basis function \(\lambda _{\mathtt{v}}\) can be written as \(\lambda _{\mathtt{v}}(x) = \Lambda _{\mathtt{v}^{\prime }}(x\prime ) \mu _{\mathtt{v}^{\prime \prime }}(y)\), where \(\Lambda _{\mathtt{v}^{\prime }}\) is the canonical \(\mathbb {Q}_1\) basis function on the variable \(x^{\prime }\) associated to the node \(\mathtt{v}^{\prime }\) in the triangulation \(\fancyscript{T}_\varOmega \), and \(\mu _{\mathtt{v}^{\prime \prime }}\) corresponds to the piecewise \(\mathbb {P}_1\) basis function associated to the node \({\mathtt{v}^{\prime \prime }}\). Recall that, by construction, the basis \(\{ \Lambda _i \}_{i=1}^{2^n}\) possesses the so-called partition of unity property, i.e.,
This implies that, for every \(q\in \mathbb {Q}_1(T)\),
whence, for \(j=1,\ldots ,n\),
This expression shows that the same techniques developed for the previous step lead to (4.30). In fact, we let  and estimate \(\delta q(\mathtt{v}_i):= q(\mathtt{v}_i) - q(\mathtt{v}_1)\) and \(\delta q(\mathtt{v}_{i+2^n}):= q(\mathtt{v}_{i+2^n}) - q(\mathtt{v}_{1+2^n})\) for \(i=2,\ldots ,2^n\) as follows; we deal with \(\delta q(\mathtt{v}_i)\) only because the same argument applies to \(\delta q (\mathtt{v}_{i+2^n})\). Using (4.11) and changing variables, we derive
and estimate \(\delta q(\mathtt{v}_i):= q(\mathtt{v}_i) - q(\mathtt{v}_1)\) and \(\delta q(\mathtt{v}_{i+2^n}):= q(\mathtt{v}_{i+2^n}) - q(\mathtt{v}_{1+2^n})\) for \(i=2,\ldots ,2^n\) as follows; we deal with \(\delta q(\mathtt{v}_i)\) only because the same argument applies to \(\delta q (\mathtt{v}_{i+2^n})\). Using (4.11) and changing variables, we derive
Defining the vector \(\varrho :=(\varrho _1, 0)=(\mathtt{v}_1^{\prime } - \mathtt{v}_i^{\prime } + (h_{\mathtt{v}_1}^{\prime } - h_{\mathtt{v}_i}^{\prime })z^{\prime },0)\) and \(H_z(t):= P(\mathtt{v}_i - h_{\mathtt{v}_i} \odot z + t \varrho ,\mathtt{v}_i)\) yields
Since \(\psi \) is bounded in \(L^{\infty }\) and \({{\mathrm{supp\,}}}\psi \subset D\), we next invoke the definitions of \(H_z\) and the polynomial \(P\) to deduce
Arguing as with the estimate (4.38) and using the scaling result
we infer that
Finally, collecting the preceding estimates we obtain (4.30) for \(\partial _{x_j}\) with \(j = 1,\ldots ,n\).
Stability. It remains to prove (4.28) and (4.29). By the triangle inequality,

so that it suffices to estimate the first term. Add and subtract \(w_{\mathtt{v}_1}\):

Let us estimate the first term. The definition of \(\psi _{\mathtt{v}_1}\), together with \(|y|^{\alpha } \in A_2(\mathbb {R}^{n+1})\), implies \(\Vert \psi _{\mathtt{v}_1}\Vert _{L^2(\omega _{\mathtt{v}_1},y^{-\alpha })} \Vert 1\Vert _{L^2(\omega _{\mathtt{v}_1},y^{\alpha })} \lesssim 1,\) whence invoking the definition (4.11) of the regularized Taylor polynomial \(w_{\mathtt{v}_1}\) yields
and
To estimate the second term of the right-hand side of (4.40), we repeat the steps used to obtain (4.30), starting from (4.32). We recall \(\delta q(\mathtt{v}_i) = q(\mathtt{v}_i) - q(\mathtt{v}_{i+2^n})\), and we proceed to estimate \(\delta q(\mathtt{v}_1)\). Integrating by parts and using that \(\psi _{\mathtt{v}_i} =0\) on \(\partial \omega _{\mathtt{v}_i}\), we obtain, for \(\ell = 1,\ldots ,n+1\),
whence
To estimate \(I_1\), we consider the same change of variables used to obtain (4.33). Define \(G_z(t) = (n+2) \cdot w(\mathtt{v}_1 - h_{\mathtt{v}_1}\odot z+ t\theta )\), with \(\theta \) as in (4.34), and observe that
Introducing the change of variables \(\tau = \mathtt{v}_1 - h_{\mathtt{v}_1} \odot z + t \theta \), we obtain
We now estimate \(I_2\). Changing variables,
where \(\vartheta = (\mathtt{v}^{\prime \prime }_{1+2^n} - \mathtt{v}^{\prime \prime }_{1})/{ h_{\mathtt{v}_1^{\prime \prime }}}\). Arguing as in the derivation of (4.43) we obtain
Inserting (4.43) and (4.44) into (4.42) we deduce
whence
because \(h_{\mathtt{v}^{\prime }_1}^{-n} \Vert \partial _y\lambda _{\mathtt{v}_1}\Vert _{L^2(\omega _T,y^\alpha )} \Vert 1\Vert _{L^2(\omega _T,y^{-\alpha })}\le C\). Replacing (4.45) in (4.31) we obtain

which, together with (4.40) and (4.41), implies the desired result (4.29) for \(i=1\). For \(i=2,\ldots ,2^n\), the estimates for \(\delta q(\mathtt{v}_i)\) follow the same steps as in . To prove the stability bound (4.28), we proceed as in to estimate the interpolation errors for the \(x^{\prime }\)-derivatives, but we skip the details. \(\square \)
4.2.4 Weighted Interpolation Estimates on Boundary Elements
Let us now extend the interpolation estimates of §4.2.2 and §4.2.3 to elements that intersect the Dirichlet boundary, where the functions to be approximated vanish. To do so, we start by adapting the results of [30, Theorem 3.1] to our particular case.
We consider, as in [30, Sect. 3], different cases according to the relative position of the element \(T\) in  . We define the three sets
. We define the three sets

The elements in \(\mathcal {C}_1\) are interior, so the corresponding interpolation estimate is given in Theorem 4.7. Interpolation estimates on elements in \(\mathcal {C}_3\) are a direct consequence of [30, Theorems 3.1] and 4.8 in what follows. This is due to the fact that, since  , the weight \(y^\alpha \) over \(\mathcal {C}_3\) is no longer singular nor degenerate. It remains only to provide interpolation estimates for elements in \(\mathcal {C}_2\).
, the weight \(y^\alpha \) over \(\mathcal {C}_3\) is no longer singular nor degenerate. It remains only to provide interpolation estimates for elements in \(\mathcal {C}_2\).
Theorem 4.8
(Weighted \(H^1\) interpolation estimates over elements in \(\mathcal {C}_2\)). Let \(T \in \mathcal {C}_{2}\) and \(w \in H^1(\omega _T,y^\alpha )\) vanish on  . Then we have the stability bounds
. Then we have the stability bounds

and

If in addition \(w \in H^2(\omega _T,y^\alpha )\), then, for \(j=1,\ldots ,n+1\),

Proof
For simplicity we present the proof in two dimensions. Let \(T = (0,a) \times (0,b) \in \mathcal {C}_2\), and let us label its vertices according to Fig. 1: \(\mathtt{v}_1 = (0,0)\), \(\mathtt{v}_2 = (a,0)\), \(\mathtt{v}_3 = (0,b)\), \(\mathtt{v}_4 = (a,b)\). Notice that this is the worst situation because over such an element the weight becomes degenerate or singular; estimates over other elements of \(\mathcal {C}_2\) are simpler. We proceed now to exploit the symmetry of \(T\). By the definition of  we have
we have

The proofs of (4.46) and (4.47) are similar to Step 3 of Theorem 4.7. To show (4.48), we write the local difference between a function and its interpolant as  . Proceeding as in the proof of Lemma 4.5, we can bound \(\partial _{x_j}(w - w_{\mathtt{v}_2})|_{T}\) for \(j=1,2\), in the \(L^2(T,y^\alpha )\)-norm, by the right-hand side of (4.48) because this is independent of the trace of \(w\). It remains then to derive a bound for
. Proceeding as in the proof of Lemma 4.5, we can bound \(\partial _{x_j}(w - w_{\mathtt{v}_2})|_{T}\) for \(j=1,2\), in the \(L^2(T,y^\alpha )\)-norm, by the right-hand side of (4.48) because this is independent of the trace of \(w\). It remains then to derive a bound for  , for which we consider two separate cases.
, for which we consider two separate cases.
Derivative in extended direction. We use \(w_{\mathtt{v}_2}\in \mathbb {Q}_1\), (4.49), and  to write
to write

Since \(w \equiv 0 \) on \(\{0\}\times (0,b)\), then \(\partial _y w \equiv 0\) on \(\{0\}\times (0,b)\). By the definition of the Taylor polynomial \(P\) given in (4.12), and the fact that \(\mathtt{v}_1^{\prime } = \mathtt{v}_3^{\prime }\), we obtain
Therefore,
Since, in view of the weak shape-regularity assumption on the mesh  , \(h_{\mathtt{v}_1^{\prime }}\approx h_{\mathtt{v}_2^{\prime }}\), \(h_{\mathtt{v}_1^{\prime \prime }}= h_{\mathtt{v}_2^{\prime \prime }}\), and \(y^{\alpha } \in A_2(\mathbb {R}_{+}^{n+1})\), we conclude that
, \(h_{\mathtt{v}_1^{\prime }}\approx h_{\mathtt{v}_2^{\prime }}\), \(h_{\mathtt{v}_1^{\prime \prime }}= h_{\mathtt{v}_2^{\prime \prime }}\), and \(y^{\alpha } \in A_2(\mathbb {R}_{+}^{n+1})\), we conclude that
Finally, to bound \(w_{\mathtt{v}_2}(\mathtt{v}_4) - w_{\mathtt{v}_4}(\mathtt{v}_4)\), we proceed as in Step 1 of the proof of Theorem 4.7, which is valid regardless of the trace of \(w\), and deduce
This, in conjunction with the previous estimate, yields (4.48) for the derivative in the extended direction.
Derivative in
\(x^{\prime }\)
direction. To estimate  , we proceed as in Theorem 4.7 and [30, Theorem 3.1], but we cannot exploit the symmetry of the tensor product structure now. For brevity, we shall only point out the main technical differences. Again, using that
, we proceed as in Theorem 4.7 and [30, Theorem 3.1], but we cannot exploit the symmetry of the tensor product structure now. For brevity, we shall only point out the main technical differences. Again, using that  ,
,

where
Define \(\theta =(0,\theta ^{\prime \prime })=(0,{ \mathtt{v}_4^{\prime \prime }-\mathtt{v}_2^{\prime \prime } - (h_{\mathtt{v}_4^{\prime \prime }}-h_{\mathtt{v}_2^{\prime \prime }})z^{\prime \prime } })\), and rewrite \(J(w_{\mathtt{v}_2},w_{\mathtt{v}_4})\) as follows:
where \(D\) \(=\) supp \(\psi \). Using the notation
and the change of variable \(z \mapsto \tau = \mathtt{v}_2 - h_{\mathtt{v}_2}\odot z + \theta t\) result in
whence \( \left| J(w_{\mathtt{v}_2},w_{\mathtt{v}_4})\right| \lesssim h_{\mathtt{v}_2^{\prime }}^{{\tfrac{1}{2}}} \Vert \partial _{x^{\prime }y} w \Vert _{L^2(\omega _T,y^{\alpha })} \left( \int \limits _{0}^{b}y^{-\alpha } \, \mathrm{d}y \right) ^{{\tfrac{1}{2}}} \). This implies
which follows from the fact that \(y^\alpha \in A_2(\mathbb {R}^+)\), and then (4.48) holds true.
The estimate of \(w_{\mathtt{v}_2}(\mathtt{v}_1)\partial _{x^{\prime }}\lambda _{\mathtt{v}_2}\) exploits the fact that the trace of \(w\) vanishes on  ; the same happens with \(w_{\mathtt{v}_4}(\mathtt{v}_3) \partial _{x^{\prime }}\lambda _{\mathtt{v}_4}\). In fact, we can write
; the same happens with \(w_{\mathtt{v}_4}(\mathtt{v}_3) \partial _{x^{\prime }}\lambda _{\mathtt{v}_4}\). In fact, we can write
To derive (4.48), we finally proceed as in the proofs of Theorem 4.7 and [30, Theorem 3.1]. We omit the details. \(\square \)
We now conclude with a result involving weighted \(L^2\) interpolation estimates on boundary elements. As in the weighted \(H^1\) case, the elements in \(\mathcal {C}_1\) are interior, and then the interpolation estimates are given by Theorem 4.6. It remains to analyze the interpolation estimates on the sets \(\mathcal {C}_2\) and \(\mathcal {C}_3\).
Theorem 4.9
(Weighted \(L^2\) interpolation estimates over elements in \(\mathcal {C}_2\) and \(\mathcal {C}_3\)). If \(T \in \mathcal {C}_{2} \cup \mathcal {C}_3\) and \(w \in H^1(\omega _T,y^\alpha )\) vanish on  and
and  , then
, then

Proof
We consider \(T \in \mathcal {C}_2\) and the same geometric setting as in the proof of Theorem 4.8; we skip the case \(T \in \mathcal {C}_3\) as in Theorem 4.8. We write the difference  . Applying Lemma 4.5, we can bound the term \((w - w_{\mathtt{v}_2})|_{T}\) in the \(L^2(T,y^{\alpha })\)-norm by the right-hand side of (4.50). Then it suffices to estimate
. Applying Lemma 4.5, we can bound the term \((w - w_{\mathtt{v}_2})|_{T}\) in the \(L^2(T,y^{\alpha })\)-norm by the right-hand side of (4.50). Then it suffices to estimate  . Writing
. Writing

and using the fact that the trace of \(w\) vanishes on  , we see that
, we see that
the same argument holds for \(w_{\mathtt{v}_2}(\mathtt{v}_3)\). On the other hand, we handle \(w_{\mathtt{v}_2}(\mathtt{v}_4)- w_{\mathtt{v}_4}(\mathtt{v}_4)\) with the same techniques as in the proof of Theorem 4.7. \(\square \)
5 Error Estimates
The estimates of §4.2.3 and §4.2.4 are obtained under the local assumption that \(w \in H^2(\omega _T,y^{\alpha })\). However, the solution \(\mathfrak {u}\) to (2.26) satisfies \(\mathfrak {u}_{yy} \in L^2(\mathcal {C},y^\beta )\) only when \(\beta > 2\alpha + 1\), according to Theorem 2.7. For this reason, in this section we derive error estimates for both quasi-uniform and graded meshes. The estimates of §5.1 for quasi-uniform meshes are quasi-optimal in terms of regularity but suboptimal in terms of order. The estimates of §5.2 for graded meshes are instead quasi-optimal in both regularity and order. Mesh anisotropy is able to capture the singular behavior of the solution and restore optimal decay rates.
5.1 Quasi-Uniform Meshes
We start with a simple one-dimensional case (\(n=1\)) and assume that we need to approximate over the interval  the function \(w(y) = y^{1-\alpha }\). Notice that \(w_y(y) \approx y^{-\alpha }\) as \(y \approx 0^+\) has the same behavior as the derivative in the extended direction of the \(\alpha \)-harmonic extension \(\mathfrak {u}\).
the function \(w(y) = y^{1-\alpha }\). Notice that \(w_y(y) \approx y^{-\alpha }\) as \(y \approx 0^+\) has the same behavior as the derivative in the extended direction of the \(\alpha \)-harmonic extension \(\mathfrak {u}\).
Given \(M \in \mathbb {N}\), we consider the uniform partition of the interval 

and the corresponding elements \(I_k =[y_k,y_{k+1}]\) of size  for \(k=0,\ldots ,M-1\).
for \(k=0,\ldots ,M-1\).
We can adapt the definition of  from §4.2 to this setting and bound the local interpolation errors
from §4.2 to this setting and bound the local interpolation errors  . For \(k=2,\ldots ,M-1\), since \(y \ge h\) and \(\alpha < 2\alpha + 1 < \beta \), (4.30) implies
. For \(k=2,\ldots ,M-1\), since \(y \ge h\) and \(\alpha < 2\alpha + 1 < \beta \), (4.30) implies
because \(\left( \frac{y}{h}\right) ^\alpha \le \left( \frac{y}{h}\right) ^\beta .\) The estimate for \(E_0^2+E_1^2\) follows from the stability of the operator  (4.29) and (4.47):
(4.29) and (4.47):
because \(w(y)\approx y^{-\alpha }\) as \(y\approx 0^+\). Using (5.2) and (5.3) in conjunction with \(2+\alpha -\beta <1-\alpha \), we obtain a global interpolation estimate

These ideas can be extended to prove an error estimate for \(\mathfrak {u}\) on uniform meshes.
Theorem 5.1
(Error estimate for quasi-uniform meshes). Let \(\mathfrak {u}\) solve (2.26), and let  be the solution to (4.4), constructed over a quasi-uniform mesh of size \(h\). If \(f \in \mathbb {H}^{1-s}(\varOmega )\) and
be the solution to (4.4), constructed over a quasi-uniform mesh of size \(h\). If \(f \in \mathbb {H}^{1-s}(\varOmega )\) and  , then for all \(\epsilon >0\)
, then for all \(\epsilon >0\)

where the hidden constant blows up if \(\varepsilon \) tends to \(0\).
Proof
Use first Theorems 3.5 and 4.1, combined with (4.10), to reduce the approximation error to the interpolation error of \(\mathfrak {u}\). Next, repeat the steps leading to (5.2)–(5.3), but combining the interpolation estimates of Theorems 4.7 and 4.8 with the regularity results of Theorem 2.7, which are valid because \(f \in \mathbb {H}^{1-s}(\varOmega )\). \(\square \)
Remark 5.2
(Sharpness of (5.5) for \(s\ne \frac{1}{2}\)). According to (2.34) and (2.37), \(\partial _y\mathfrak {u}\approx y^{-\alpha }\), and this formally implies \(\partial _y \mathfrak {u}\in H^{s-\varepsilon }(\mathcal {C},y^{\alpha })\) for all \(\varepsilon >0\) provided \(f\in \mathbb {H}^{1-s}(\varOmega )\). In this sense, (5.5) appears to be sharp with respect to regularity, even though it does not exhibit the optimal rate. We verify this argument via a simple numerical illustration for dimension \(n=1\). We let \(\varOmega = (0,1)\), \(s=0.2\), the right-hand side \(f = \pi ^{2s} \sin (\pi x)\), and note that \(u(x)=\sin (\pi x)\), and the solution \(\mathfrak {u}\) to (1.2) is
Figure 2 shows the rate of convergence for the  -seminorm. Estimate (5.5) predicts a rate of \(h^{-0.2-\varepsilon }\). We point out that for the \(\alpha \)-harmonic extension we are solving a two-dimensional problem and, since the mesh
-seminorm. Estimate (5.5) predicts a rate of \(h^{-0.2-\varepsilon }\). We point out that for the \(\alpha \)-harmonic extension we are solving a two-dimensional problem and, since the mesh  is quasi-uniform,
is quasi-uniform,  . In other words, the rate of convergence, when measured in terms of degrees of freedom, is
. In other words, the rate of convergence, when measured in terms of degrees of freedom, is  , which is what Fig. 2 displays.
, which is what Fig. 2 displays.
Remark 5.3
(Case \(s = {\tfrac{1}{2}}\)). Estimate (5.5) does not hold for \(s={\tfrac{1}{2}}\). In this case, there is no weight and the scaling issues in (5.2) are no longer present, so that \(E_k \lesssim h \Vert v \Vert _{H^2(I_k)}\). We thus obtain the optimal error estimate

5.2 Graded Meshes
The estimate (5.5) can be written equivalently

for quasi-uniform meshes in dimension \((n+1)\). We now show how to compensate the singular behavior in the extended variable \(y\) by anisotropic meshes and restore the optimal convergence rate \(-1/(n+1)\).
As in §5.1, we start the discussion in dimension \(n=1\) with the function \(w(y) = y^{1-\alpha }\) over  . We consider the graded partition
. We consider the graded partition  of the interval
of the interval  ,
,

where \(\gamma = \gamma (\alpha ) > 3/(1-\alpha )> 1\). If we denote by \(h_k\) the length of the interval

then

We again consider the operator  of §4.2 on the one-dimensional mesh
of §4.2 on the one-dimensional mesh  and wish to bound the local interpolation errors \(E_k\) of §5.1. We apply estimate (4.30) to interior elements to obtain that, for \(k=2,\ldots , M-1\),
and wish to bound the local interpolation errors \(E_k\) of §5.1. We apply estimate (4.30) to interior elements to obtain that, for \(k=2,\ldots , M-1\),

because  and \(w(y) = y^{1-\alpha }\) over
and \(w(y) = y^{1-\alpha }\) over  . Adding (5.7) over \(k = 2,\ldots ,M-1\) and using that \(\gamma (1-\alpha )>3\), we arrive at
. Adding (5.7) over \(k = 2,\ldots ,M-1\) and using that \(\gamma (1-\alpha )>3\), we arrive at

For the errors \(E_0^2,E_1^2\) we resort to the stability bounds (4.29) and (4.47) to write

where we have used (5.6). Finally, adding (5.8) and (5.9) gives

and shows that the interpolation error exhibits the optimal decay rate.
We now apply this idea to the numerical solution to problem (3.3). We assume \(\fancyscript{T}_\varOmega \) to be quasi-uniform in \(\mathbb {T}_\varOmega \), with \(\# \fancyscript{T}_\varOmega \approx M^n\), and construct  as the tensor product of \(\fancyscript{T}_\varOmega \) and the partition given in (5.6), with \(\gamma > 3/(1-\alpha )\). Consequently,
as the tensor product of \(\fancyscript{T}_\varOmega \) and the partition given in (5.6), with \(\gamma > 3/(1-\alpha )\). Consequently,  . Finally, we notice that since \(\fancyscript{T}_\varOmega \) is shape-regular and quasi-uniform, \(h_{\fancyscript{T}_{\varOmega }} \approx (\# \fancyscript{T}_{\varOmega })^{-1/n} \approx M^{-1}\).
. Finally, we notice that since \(\fancyscript{T}_\varOmega \) is shape-regular and quasi-uniform, \(h_{\fancyscript{T}_{\varOmega }} \approx (\# \fancyscript{T}_{\varOmega })^{-1/n} \approx M^{-1}\).
Theorem 5.4
(Error estimate for graded meshes). Let  solve (4.4), and let \(U_{\fancyscript{T}_{\varOmega }} \in \mathbb {U}(\fancyscript{T}_{\varOmega })\) be defined as in (4.5). If \(f \in \mathbb {H}^{1-s}(\varOmega )\), then
solve (4.4), and let \(U_{\fancyscript{T}_{\varOmega }} \in \mathbb {U}(\fancyscript{T}_{\varOmega })\) be defined as in (4.5). If \(f \in \mathbb {H}^{1-s}(\varOmega )\), then

Proof
In light of (4.10), with  , it suffices to bound the interpolation error
, it suffices to bound the interpolation error  on the mesh
on the mesh  . To do so, we first of all notice that if \(I_1\) and \(I_2\) are neighboring cells on the partition of
. To do so, we first of all notice that if \(I_1\) and \(I_2\) are neighboring cells on the partition of  , then there is a constant \(\sigma =\sigma (\gamma )\) such that \(h_{I_1}\le \sigma h_{I_2}\), whence the weak regularity condition \((c)\) holds. We can thus apply the polynomial interpolation theory of §4.2. We decompose the mesh
, then there is a constant \(\sigma =\sigma (\gamma )\) such that \(h_{I_1}\le \sigma h_{I_2}\), whence the weak regularity condition \((c)\) holds. We can thus apply the polynomial interpolation theory of §4.2. We decompose the mesh  into the sets
into the sets

We observe that for all \(T=K\times I_k\in \mathcal {T}_0\) we have \(k\ge 2\) and  . Applying Theorems 4.7 and 4.8 to elements in \(\mathcal {T}_0\) we obtain
. Applying Theorems 4.7 and 4.8 to elements in \(\mathcal {T}_0\) we obtain

We examine first the most problematic third term \(S_3\), which we rewrite as follows:

with  and
and  . We now invoke the local estimate (2.43), as well as the fact that
. We now invoke the local estimate (2.43), as well as the fact that  , to end up with
, to end up with

We now handle the middle term \(S_2\) with the help of (2.42), which is valid for \(b_k\le 1\). This imposes the restriction  , whereas for \(k>k_0\) we know that the estimate decays exponentially. We thus have
, whereas for \(k>k_0\) we know that the estimate decays exponentially. We thus have

The first term \(S_1\) is easy to estimate. Since \(h_K \lesssim M^{-1}\) for all \(K\in \fancyscript{T}_\varOmega \), we obtain

For elements in \(\mathcal {T}_1\), we rely on the stability estimates (4.28), (4.29), (4.46), and (4.47) of  and thus repeat the arguments used to derive (5.8) and (5.9). Adding the estimates for \(\mathcal {T}_0\) and \(\mathcal {T}_1\) we obtain the assertion. \(\square \)
and thus repeat the arguments used to derive (5.8) and (5.9). Adding the estimates for \(\mathcal {T}_0\) and \(\mathcal {T}_1\) we obtain the assertion. \(\square \)
Remark 5.5
(Choice of  ). A natural choice of
). A natural choice of  comes from equilibrating the two terms on the right-hand side of (5.10):
comes from equilibrating the two terms on the right-hand side of (5.10):

This implies the near-optimal estimate

Remark 5.6
(Estimate for \(u\)). In view of (4.6), we deduce the energy estimate

We can rewrite this estimate in terms of regularity \(u\in \mathbb {H}^{1+s}(\varOmega )\) and \(\#\fancyscript{T}_\varOmega \) as
and realize that the order is near-optimal given the regularity shift from left to right. However, our PDE approach does not allow for a larger rate \((\#\fancyscript{T}_\varOmega )^{(2-s)/n}\) that would still be compatible with piecewise bilinear polynomials but not with (5.11).
Remark 5.7
(Computational complexity). The cost of solving the discrete problem (4.4) is related to  , and not to \(\#\fancyscript{T}_\varOmega \), but the resulting system is sparse. The structure of (4.4) is such that fast multilevel solvers can be designed with complexity proportional to
, and not to \(\#\fancyscript{T}_\varOmega \), but the resulting system is sparse. The structure of (4.4) is such that fast multilevel solvers can be designed with complexity proportional to  . On the other hand, using an integral formulation requires sparsification of an otherwise dense matrix with associated cost \((\#\fancyscript{T}_\varOmega )^2\).
. On the other hand, using an integral formulation requires sparsification of an otherwise dense matrix with associated cost \((\#\fancyscript{T}_\varOmega )^2\).
Remark 5.8
(Fractional regularity). The function \(\mathfrak {u}\), solution of the \(\alpha \)-harmonic extension problem, may also have singularities in the direction of the \(x^{\prime }\)-variables and thus exhibit fractional regularity. This depends on \(\varOmega \) and the right-hand side \(f\) (Remark 2.8). The characterization of such singularities is as yet an open problem for us. The polynomial interpolation theory developed in §4.2, however, applies to shape-regular but graded mesh \(\fancyscript{T}_\varOmega \), which can resolve such singularities, provided we maintain the Cartesian structure of  . The corresponding a posteriori error analysis is an entirely different but important direction currently under investigation.
. The corresponding a posteriori error analysis is an entirely different but important direction currently under investigation.
Remark 5.9
(Simplicial elements). The approximation results presented in §4.2.2, the interpolation theory developed in §4.2.3 and §4.2.4, and, consequently, the error estimates of this section hinge solely on the fact that the mesh  has a tensor product structure, i.e., it is composed of cells of the form \(T = K \times I\). If we consider \(\fancyscript{T}_{\varOmega } = \{ K \}\) to be a mesh of \(\varOmega \subset \mathbb {R}^n\)
\((n \ge 1)\) made of simplicial elements, together with the finite element space,
has a tensor product structure, i.e., it is composed of cells of the form \(T = K \times I\). If we consider \(\fancyscript{T}_{\varOmega } = \{ K \}\) to be a mesh of \(\varOmega \subset \mathbb {R}^n\)
\((n \ge 1)\) made of simplicial elements, together with the finite element space,

we can adapt, without major modifications, all the approximation, interpolation, and convergence results of this work.
Remark 5.10
(Hanging nodes). It is important to note that the assumption that the mesh is conforming was never explicitly used in the results of Sect. 4 and that, actually, all that was required from the finite element space is the partition of unity property, i.e., (4.39). This observation allows us to generalize the results of Sect. 4 to meshes that possess hanging nodes, which is important if one desires to use mesh adaptation to resolve possible singularities in the solution.
6 Numerical Experiments for the Fractional Laplacian
To illustrate the proposed techniques, here we present a couple of numerical examples. The implementation was carried out with the help of the deal.II library (see [6, 7]), which, by design, is based on tensor product elements and thus is perfectly suited for our needs. The main concern while developing the code was correctness, and therefore integrals are evaluated numerically with Gaussian quadratures of sufficiently high order and linear systems are solved using CG with ILU preconditioner, with the exit criterion being that the \(\ell ^2\)-norm of the residual is less than \(10^{-12}\). More efficient techniques for quadrature and preconditioning are currently under investigation.
6.1 A Square Domain
Let \(\varOmega = (0,1)^2\). It is common knowledge that
If \(f(x_1,x_2) = ( 2\pi ^2)^{s} \sin (\pi x_1)\sin (\pi x_2)\), then, by (2.12), we have
and, by (2.24),
We construct a sequence of meshes  , where the triangulation of \(\varOmega \) is obtained by uniform refinement and the partition of
, where the triangulation of \(\varOmega \) is obtained by uniform refinement and the partition of  is as in §5.2, i.e.,
is as in §5.2, i.e.,  is divided with mesh points given by (5.6) with the election of the parameter \(\gamma > 3/(1-\alpha )\). On the basis of Theorem 3.5, for each mesh the truncation parameter
is divided with mesh points given by (5.6) with the election of the parameter \(\gamma > 3/(1-\alpha )\). On the basis of Theorem 3.5, for each mesh the truncation parameter  is chosen such that
is chosen such that  . This can be achieved, for instance, by setting
. This can be achieved, for instance, by setting

With this type of mesh,

which is near-optimal in \(\mathfrak {u}\) but suboptimal in \(u\), since we should expect (see [17])

Figure 3 shows the rates of convergence for \(s=0.2\) and \(s=0.8\). In both cases, we obtain the rate given by Theorem 5.4 and Remark 5.5.
6.2 A Circular Domain
Let \(\varOmega = \{ |x^{\prime }| \in \mathbb {R}^2 : |x^{\prime }|<1 \}\). Using polar coordinates it can be shown that
where \(J_m\) is the \(m\)th Bessel function of the first kind, \(j_{m,n}\) is the \(n\)th zero of \(J_m\), and \(A_{m,n}\) and \(B_{m,n}\) are real normalization constants that ensure \(\Vert \varphi _{m,n} \Vert _{L^2(\varOmega )}=1\) for all \(m,n \in \mathbb {N}\). It is also possible to show that \(\lambda _{m,n}=\left( j_{m,n} \right) ^2\).
If \(f = ( \lambda _{1,1})^{s} \varphi _{1,1}\), then (2.12) and (2.24) show that \(u = \varphi _{1,1}\) and
From [1, Chap. 9] we have that \(j_{1,1} \approx 3.8317\).
We construct a sequence of meshes  , where the triangulation of \(\varOmega \) is obtained by quasi-uniform refinement and the partition of
, where the triangulation of \(\varOmega \) is obtained by quasi-uniform refinement and the partition of  is as in §5.2. The parameter
is as in §5.2. The parameter  is chosen such that
is chosen such that  . With these meshes
. With these meshes

which is near optimal.
Figure 4 shows the errors of  for \(s = 0.3\) and \(s = 0.7\). The results, again, are in agreement with Theorem 5.4 and Remark 5.5.
for \(s = 0.3\) and \(s = 0.7\). The results, again, are in agreement with Theorem 5.4 and Remark 5.5.
6.3 Incompatible Data for \(s \in (0,1)\)
The computational results of the preceding sections always entail \(f \in \mathbb {H}^{1-s}(\varOmega )\) and illustrate the error estimates of Theorem 5.4. Let us now consider a datum \(f\) smooth but incompatible. Set \(\varOmega =(0,1)\) and \(f\equiv 1\). Notice that if \(s \le \frac{1}{2}\), then \(f \notin \mathbb {H}^{1-s}(\varOmega )\) due to the fact that the function does not vanish at the boundary. In fact, we have that
in other words, \(f \in \mathbb {H}^\sigma (\varOmega )\) if and only if \(\sigma <\frac{1}{2}\). Since the coefficients of the solution to (1.1) are given by \(u_k = \lambda _k^{-s} f_k\), we can only expect that
that is, \(u \in \mathbb {H}^\mu (\varOmega )\) for \(\mu < 2s + \tfrac{1}{2}\). In conclusion, full regularity is not possible, but, owing to the special character of the data, some shift can be expected; see Remark 2.8 and the discussion at the end of §2.4.
This heuristic argument is rather illuminating because it tells us that the best rate of convergence we can expect is
with \(r=\mu - s < s + \tfrac{1}{2}\). Since we are dealing with a one-dimensional problem, the extension has two dimensions, and consequently, we expect

Since \(\lambda _k = \pi ^2 k^2\) and \(\varphi _k = \sqrt{2} \sin (\sqrt{\lambda _k} x^{\prime })\), it is not difficult to show that \( f_k = \sqrt{2} (1 - (-1)^k )/\sqrt{\lambda _k}\), whence we can obtain an approximate solution \(u_N = \sum _{k=1}^N \lambda _k^{-s} f_k \varphi _k\) with \(N\) sufficiently large. Figure 5 shows the norm of the difference between  and the \(\alpha \)-harmonic extension of \(u_N\) for different values of \(s\). The experimental rates of convergence seem to agree with (6.3): they are suboptimal for \(s < \frac{1}{2}\).
and the \(\alpha \)-harmonic extension of \(u_N\) for different values of \(s\). The experimental rates of convergence seem to agree with (6.3): they are suboptimal for \(s < \frac{1}{2}\).
Computational rate of convergence for approximate solution of fractional Laplacian with incompatible datum \(f\equiv 1\). The domain \(\varOmega \) is the unit interval, and the mesh is graded in the extended dimension. We show the  norm of the difference between
norm of the difference between  and the harmonic extension of \(u_N\) with \(N=5 \cdot 10^4\). Left panel: rate for \(s=0.2\), \(0.4\); right panel: rate for \(s=0.6,\)
\(0.8\). As expected, the rate of convergence is optimal for values larger than \(\tfrac{1}{2}\). On the other hand, if \(s<\tfrac{1}{2}\), then we see a reduction in the rate of convergence, in accordance with (6.3)
and the harmonic extension of \(u_N\) with \(N=5 \cdot 10^4\). Left panel: rate for \(s=0.2\), \(0.4\); right panel: rate for \(s=0.6,\)
\(0.8\). As expected, the rate of convergence is optimal for values larger than \(\tfrac{1}{2}\). On the other hand, if \(s<\tfrac{1}{2}\), then we see a reduction in the rate of convergence, in accordance with (6.3)
To recover the optimal decay rate, we explore the a priori design of graded meshes in the \(x^{\prime }\)-direction, which is within our theory of §4 and §5 (Remark 5.8). Since \(u \in \mathbb {H}^\mu (\varOmega )\), with \(\mu < 2s + \frac{1}{2}\), we expect that \(u \approx r^{2s}\) as \(r\rightarrow 0\), where \(r\) denotes the distance to the boundary. This, at least heuristically, can be figured out as follows: if \( \partial _r^\mu r^{2s} \approx r^{2s-\mu }\), then
and \(r^{2s} \in \mathbb {H}^\mu (\varOmega )\) only for \(\mu < 2s+\tfrac{1}{2}\).
Having guessed the nature of the singularity, we can apply the principle of error equidistribution as in §5.2 to design an optimal graded mesh as \(x^{\prime }\) approaches either \(0\) or \(1\), with a grading parameter \(\gamma > \tfrac{3}{2(1+s)}\) [compare with (5.6)]. We proceed as follows: construct a quasi-uniform mesh of the interval \(\varOmega = (0,1)\) by bisection, and then transform the nodes \(\mathtt{v}\) by the rule \(\mathtt{v}\leftarrow \psi (\mathtt{v})\), where
We display in Fig. 6 convergence plots for \(s=0.2\) and \(s=0.4\) over graded meshes in \(\varOmega \) that restore the optimal decay rate. The construction requires a priori knowledge of the solution, which is not obvious in higher dimensions. Adaptivity might provide a way to recover an optimal rate without such knowledge (see Remark 5.10 regarding hanging nodes).
Computational rate of convergence for approximate solution of fractional Laplacian with incompatible datum \(f\equiv 1\) over meshes that are graded in both the \(x^{\prime }\)- and \(y\)-directions. The domain \(\varOmega \) is the unit interval. The grading in the extended dimension obeys (5.6), whereas the one in the \(x^{\prime }\)-direction is constructed using (6.4). We show the  norm of the difference between
norm of the difference between  and the harmonic extension of \(u_N\), with \(N=5 \cdot 10^4\). An optimal rate of convergence can be recovered irrespective of the fact that the solution does not possess full regularity
and the harmonic extension of \(u_N\), with \(N=5 \cdot 10^4\). An optimal rate of convergence can be recovered irrespective of the fact that the solution does not possess full regularity
7 Fractional Powers of General Second Order Elliptic Operators
Let us now discuss how the methodology developed in previous sections extends to a general second-order, symmetric, and uniformly elliptic operator. This is an important property of our PDE approach. Recall that in §2.4, we discussed how the fractional Laplace operator could be realized as a Dirichlet-to-Neumann map via an extension problem posed on the semi-infinite cylinder \(\mathcal {C}\). In the work of Stinga and Torrea [60], the same type of characterization is developed for the fractional powers of second-order elliptic operators.
Let \(\mathcal {L}\) be a second-order symmetric differential operator of the form
where \(c \in L^\infty (\varOmega )\), with \(c\ge 0\) almost everywhere, \(A \in \mathcal {C}^{0,1}(\varOmega ,{\mathsf{GL }}(n,\mathbb {R}))\) is symmetric and positive definite, and \(\varOmega \) is Lipschitz. Given \(f \in L^2(\varOmega )\), the Lax–Milgram lemma shows that there is a unique \(w \in H^1_0(\varOmega )\) that solves
The operator \(\mathcal {L}^{-1}: L^2(\varOmega )\rightarrow L^2(\varOmega )\) is positive, compact, and symmetric, which is why its spectrum is discrete and positive and accumulates at zero. Moreover, there exists \(\{ \lambda _k,\varphi _k \}_{k\in \mathbb N} \subset \mathbb {R}_+\times H^1_0(\varOmega )\) such that \(\{\varphi _k \}_{k\in \mathbb N}\) is an orthonormal basis of \(L^2(\varOmega )\), and for \(k\in \mathbb N\),
and \(\lambda _k\rightarrow \infty \) as \(k\rightarrow \infty \). For \(u \in C_0^{\infty }(\varOmega )\), we then define the fractional powers of \(\mathcal {L}\) as
where \(u_k = \int \limits _{\varOmega } u \varphi _k \). By density, the operator \(\mathcal {L}^s\) can be extended again to \(\mathbb {H}^s(\varOmega )\). This discussion shows that it is legitimate to study the following problem: given \(s\in (0,1)\) and \(f \in \mathbb {H}^{-s}(\varOmega )\), find \(u \in \mathbb {H}^s(\varOmega )\) such that
To realize the operator \(\mathcal {L}^s\) as the Dirichlet-to-Neumann map of an extension problem, we use the generalization of the result by Caffarelli and Silvestre presented in [60]. We seek a function \(\mathfrak {u}: \mathcal {C}\rightarrow \mathbb {R}\) that solves
where the constant \(d_s\) is as in (2.23). In complete analogy to §2.4, it is possible to show that
Notice that the differential operator in (7.5) is
where, for all \(x \in \mathcal {C}\), \(\mathbf {A}(x) = {{\mathrm{diag\,}}}\{A(x^{\prime }),1\} \in {\mathsf{GL }}(n+1,\mathbb {R})\).
It suffices now to notice that both \(y^\alpha c\) and \(y^\alpha \mathbf {A}\) are in \(A_2(\mathbb {R}^{n+1}_+)\), to conclude that, given \(f \in \mathbb {H}^{-s}(\varOmega )\), there is a unique  that solves (7.5) [36]. In addition, \(u = \mathfrak {u}(\cdot ,0) \in \mathbb {H}^s(\varOmega )\) solves (7.4), and we have the stability estimate
that solves (7.5) [36]. In addition, \(u = \mathfrak {u}(\cdot ,0) \in \mathbb {H}^s(\varOmega )\) solves (7.4), and we have the stability estimate
where the hidden constants depend on \(A\), \(c\), \(C_{2,y^\alpha }\), and \(\varOmega \).
The representation (2.24) of \(\mathfrak {u}\) in terms of the Bessel functions is still valid. Consequently, we can show \(\mathfrak {u}_{yy} \in L^2(\mathcal {C},y^{\beta })\). We can also repeat the arguments in the proof of Theorem 3.5 to conclude that

and introduce  – the solution of a truncated version of (7.5) – and show that
– the solution of a truncated version of (7.5) – and show that

Next, we define the finite element approximation of the solution to (7.5) as the unique function  that solves
that solves

We construct, as in §5.2, a shape-regular triangulation \(\fancyscript{T}_\varOmega \) of \(\varOmega \), which we extend to  , with the partition given in (5.6), with \(\gamma > 3/(1-\alpha )\). Following the proof of Theorem 5.4 we can also show the following error estimate.
, with the partition given in (5.6), with \(\gamma > 3/(1-\alpha )\). Following the proof of Theorem 5.4 we can also show the following error estimate.
Theorem 7.1
(Error estimate for general operators). Let  be the solution to (7.8), and let \(U_{\fancyscript{T}_{\varOmega }} \in \mathbb {U}(\fancyscript{T}_{\varOmega })\) be defined as in (4.5). If \(\mathfrak {u}\), the solution to (7.5), is such that \(\mathcal {L} \mathfrak {u},\ \partial _y \nabla \mathfrak {u}\in L^2(\mathcal {C},y^{\alpha })\), then we have
be the solution to (7.8), and let \(U_{\fancyscript{T}_{\varOmega }} \in \mathbb {U}(\fancyscript{T}_{\varOmega })\) be defined as in (4.5). If \(\mathfrak {u}\), the solution to (7.5), is such that \(\mathcal {L} \mathfrak {u},\ \partial _y \nabla \mathfrak {u}\in L^2(\mathcal {C},y^{\alpha })\), then we have

8 Conclusions
We develop PDE solution techniques for problems involving fractional powers \((-\varDelta )^s u = f\) of the Laplace operator in a bounded domain \(\varOmega \) with Dirichlet boundary conditions. To overcome the inherent difficulty of nonlocality, we exploit the cylindrical extension proposed and investigated by Cabré and Tan [20], which was in turn inspired by the breakthrough of Caffarelli and Silvestre [21]. This leads to the (local) elliptic PDE (1.2) in one higher dimension \(y\), with variable coefficient \(y^{\alpha }\), \(\alpha =1-2s\), which either degenerates \((s<1/2)\) or blows up \((s>1/2)\). Several remarks and comparisons with recent literature are now in order:
-
Regularity In §2.6 we derive global and local regularity estimates for the solution to problem (1.2) in weighted Sobolev spaces.
-
Truncation In §3 we propose the truncated problem (3.2) and show exponential convergence in the extended variable \(y\) to the solution to problem (1.2).
-
Tensor Product Meshes In §4.1 we study a finite element strategy to approximate problem (1.2), which allows anisotropic elements in the extended dimension \(y\).
-
Anisotropic Interpolation Theory In §4.2 we extend the anisotropic interpolation estimates of [30] to the weighted Sobolev space \(H^1(y^{\alpha })\). This hinges on \(y^{\alpha } \in A_2(\mathbb {R}^{n+1})\) and gives rise to a theory in Muckenhoupt weighted Sobolev spaces with a general weight in the class \(A_p\) \((1 < p < \infty )\), along with applications [54].
-
Error Analysis In §5.1 we derive a priori error estimates for quasi-uniform meshes that exhibit optimal regularity, according to §2.6, but suboptimal order. In §5.2 we restore the optimal decay rate upon constructing suitably graded meshes in the extended variable \(y\) and applying the interpolation theory of §4.2.
-
Assumptions on f and \(\varOmega \) We assume the regularity conditions of Remark 2.10 throughout solely for convenience. We could in fact compensate the lack of such regularity via graded but shape-regular meshes in \(\varOmega \), as illustrated in §6.3, which are within our theory.
-
General Operators In §7 we extend our finite element method and supporting theory to general linear second-order, symmetric, and uniformly elliptic operators.
-
Comparisons Inspired by our work, and while this paper was under review, Bonito and Pasciak developed in [15] an alternative approach, which is based on the integral formulation of fractional powers of self-adjoint operators [13, Chap. 10.4]. This yields a sequence of easily parallelizable uncoupled elliptic PDEs and leads to quasi-optimal error estimates in the \(L^2\)-norm instead of the energy norm, provided \(\varOmega \) is convex and \(f \in \mathbb {H}^{2-2s}(\varOmega )\). Note that we only require \(f\in \mathbb {H}^{1-s}(\varOmega )\).
-
Parabolic Problems In [53] we exploit the flexibility of the Caffarelli–Silvestre extension by applying it to the numerical treatment of linear parabolic equations with fractional diffusion and fractional time derivatives. In contrast, the extension of [15] to the heat equation with fractional diffusion is not completely evident.
References
M. Abramowitz and I.A. Stegun. Handbook of mathematical functions with formulas, graphs, and mathematical tables, volume 55 of National Bureau of Standards Applied Mathematics Series. For sale by the Superintendent of Documents, U.S. Government Printing Office, Washington, D.C., 1964.
G. Acosta. Lagrange and average interpolation over 3D anisotropic elements. J. Comput. Appl. Math., 135(1):91–109, 2001.
R.A. Adams. Sobolev spaces. Academic Press [A subsidiary of Harcourt Brace Jovanovich, Publishers], New York-London, 1975. Pure and Applied Mathematics, Vol. 65.
T. Apel. Interpolation of non-smooth functions on anisotropic finite element meshes. M2AN Math. Model. Numer. Anal., 33(6):1149–1185, 1999.
O.G. Bakunin. Turbulence and diffusion. Springer Series in Synergetics. Springer-Verlag, Berlin, 2008. Scaling versus equations.
W. Bangerth, R. Hartmann, and G. Kanschat. deal.II–differential equations analysis library. Technical Reference: http://dealii.org.
W. Bangerth, R. Hartmann, and G. Kanschat. deal.II–a general-purpose object-oriented finite element library. ACM Trans. Math. Software, 33(4):Art. 24, 27, 2007.
P.W. Bates. On some nonlocal evolution equations arising in materials science. In Nonlinear dynamics and evolution equations, volume 48 of Fields Inst. Commun., pages 13–52. Amer. Math. Soc., Providence, RI, 2006.
Z. Belhachmi, Ch. Bernardi, and S. Deparis. Weighted Clément operator and application to the finite element discretization of the axisymmetric Stokes problem. Numer. Math., 105(2):217–247, 2006.
D.A. Benson, S.W. Wheatcraft, and M.M. Meerschaert. Application of a fractional advection-dispersion equation. Water Resources Res., 36:91–109, 2000.
C. Bernardi. Optimal finite-element interpolation on curved domains. SIAM J. Numer. Anal., 26(5):1212–1240, 1989.
J. Bertoin. Lévy processes, volume 121 of Cambridge Tracts in Mathematics. Cambridge University Press, Cambridge, 1996.
M.Š. Birman and M.Z. Solomjak. Spektralnaya teoriya samosopryazhennykh operatorov v gilbertovom prostranstve. Leningrad. Univ., Leningrad, 1980.
K. Bogdan, K. Burdy, and Chen Z.Q. Censored stable processes. Probab. Theory Related Fields, 127(R-2):89–152, 2003.
A. Bonito and J.E. Pasciak. Numerical approximation of fractional powers of elliptic operators. Math. Comp. (to appear), 2014.
C. Brändle, E. Colorado, A. de Pablo, and U. Sánchez. A concave-convex elliptic problem involving the fractional Laplacian. Proc. Roy. Soc. Edinburgh Sect. A, 143(1):39–71, 2013.
S.C. Brenner and L.R. Scott. The mathematical theory of finite element methods, volume 15 of Texts in Applied Mathematics. Springer, New York, third edition, 2008.
Kevin Burrage, Nicholas Hale, and David Kay. An efficient implicit FEM scheme for fractional-in-space reaction-diffusion equations. SIAM J. Sci. Comput., 34(4):A2145–A2172, 2012.
X. Cabré and Y. Sire. Nonlinear equations for fractional Laplacians ii: Existence, uniqueness and qualitative properties of solutions. arXiv:1111.0796v1, 2011.
X. Cabré and J. Tan. Positive solutions of nonlinear problems involving the square root of the Laplacian. Adv. Math., 224(5):2052–2093, 2010.
L. Caffarelli and L. Silvestre. An extension problem related to the fractional Laplacian. Comm. Partial Differential Equations, 32(7–9):1245–1260, 2007.
A. Capella, J. Dávila, L. Dupaigne, and Y. Sire. Regularity of radial extremal solutions for some non-local semilinear equations. Comm. Partial Differential Equations, 36(8):1353–1384, 2011.
P. Carr, H. Geman, D.B. Madan, and M. Yor. The fine structure of asset returns: An empirical investigation. Journal of Business, 75:305–332, 2002.
P.G. Ciarlet. The finite element method for elliptic problems, volume 40 of Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2002. Reprint of the 1978 original [North-Holland, Amsterdam; MR0520174 (58 #25001)].
P.G. Ciarlet and P.-A. Raviart. Interpolation theory over curved elements, with applications to finite element methods. Comput. Methods Appl. Mech. Engrg., 1:217–249, 1972.
P. Clément. Approximation by finite element functions using local regularization. RAIRO Analyse Numérique, 9(2):77–84, 1975.
J. Cushman and T. Glinn. Nonlocal dispersion in media with continuously evolving scales of heterogeneity. Trans. Porous Media, 13:123–138, 1993.
E. Di Nezza, G. Palatucci, and E. Valdinoci. Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math., 136(5):521–573, 2012.
T. Dupont and R. Scott. Polynomial approximation of functions in sobolev spaces. Math. Comp., 34:441–463, 1980.
R.G. Durán and A.L. Lombardi. Error estimates on anisotropic \(Q_1\) elements for functions in weighted Sobolev spaces. Math. Comp., 74(252):1679–1706 (electronic), 2005.
R.G. Durán, A.L. Lombardi, and M.I. Prieto. Superconvergence for finite element approximation of a convection-diffusion equation using graded meshes. IMA Journal of Numerical Analysis, 32(2):511–533, 2012.
R.G. Durán and F. López García. Solutions of the divergence and Korn inequalities on domains with an external cusp. Ann. Acad. Sci. Fenn. Math., 35(2):421–438, 2010.
G. Duvaut and J.-L. Lions. Inequalities in mechanics and physics. Springer-Verlag, Berlin, 1976. Translated from the French by C. W. John, Grundlehren der Mathematischen Wissenschaften, 219.
A.C. Eringen. Nonlocal continuum field theories. Springer-Verlag, New York, 2002.
L.C. Evans. Partial differential equations, volume 19 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, second edition, 2010.
E. B. Fabes, C.E. Kenig, and R.P. Serapioni. The local regularity of solutions of degenerate elliptic equations. Comm. Partial Differential Equations, 7(1):77–116, 1982.
D. Gilbarg and N.S. Trudinger. Elliptic partial differential equations of second order. Classics in Mathematics. Springer-Verlag, Berlin, 2001. Reprint of the 1998 edition.
G. Gilboa and S. Osher. Nonlocal operators with applications to image processing. Multiscale Model. Simul., 7(3):1005–1028, 2008.
V. Gol’dshtein and A. Ukhlov. Weighted Sobolev spaces and embedding theorems. Trans. Amer. Math. Soc., 361(7):3829–3850, 2009.
Q.Y. Guan and Z.M. Ma. Reflected symmetric \(\alpha \)-stable processes and regional fractional laplacian. Probab. Theory Related Fields, 134(2):649–694, 2006.
J. Heinonen, T. Kilpeläinen, and O. Martio. Nonlinear potential theory of degenerate elliptic equations. Oxford Mathematical Monographs. The Clarendon Press Oxford University Press, New York, 1993. Oxford Science Publications.
M. Ilic, F. Liu, I. Turner, and V. Anh. Numerical approximation of a fractional-in-space diffusion equation. I. Fract. Calc. Appl. Anal., 8(3):323–341, 2005.
M. Ilic, F. Liu, I. Turner, and V. Anh. Numerical approximation of a fractional-in-space diffusion equation. II. With nonhomogeneous boundary conditions. Fract. Calc. Appl. Anal., 9(4):333–349, 2006.
V.G. Korneev. The construction of variational difference schemes of a high order of accuracy. Vestnik Leningrad. Univ., 25(19):28–40, 1970. (In Russian).
V.G. Korneev and S.E. Ponomarev. Application of curvilinear finite elements in schemes for solution of \(2n\)-order linear elliptic equations. I. Čisl. Metody Meh. Splošn. Sredy, 5(5):78–97, 1974. (In Russian).
A. Kufner. Weighted Sobolev spaces. A Wiley-Interscience Publication. John Wiley & Sons Inc., New York, 1985. Translated from the Czech.
N.S. Landkof. Foundations of modern potential theory. Springer-Verlag, New York, 1972. Translated from the Russian by A. P. Doohovskoy, Die Grundlehren der mathematischen Wissenschaften, Band 180.
J.-L. Lions and E. Magenes. Non-homogeneous boundary value problems and applications. Vol. I. Springer-Verlag, New York, 1972. Translated from the French by P. Kenneth, Die Grundlehren der mathematischen Wissenschaften, Band 181.
B.M. McCay and M.N.L. Narasimhan. Theory of nonlocal electromagnetic fluids. Arch. Mech. (Arch. Mech. Stos.) 33(3):365–384, 1981.
W. McLean. Strongly elliptic systems and boundary integral equations. Cambridge University Press, Cambridge, 2000.
K.S. Miller and S.G. Samko. Completely monotonic functions. Integral Transform. Spec. Funct., 12(4):389–402, 2001.
B. Muckenhoupt. Weighted norm inequalities for the Hardy maximal function. Trans. Amer. Math. Soc., 165:207–226, 1972.
R.H. Nochetto, E. Otárola, and A.J Salgado. A pde approach to space-time fractional diffusion. arXiv:1404.0068, 2014.
R.H. Nochetto, E. Otárola, and A.J. Salgado. Piecewise polynomial interpolation in Muckenhoupt weighted Sobolev spaces and appications. arXiv:1402.1916, 2014.
G. Savaré. Regularity and perturbation results for mixed second order elliptic problems. Comm. Partial Differential Equations, 22(5–6):869–899, 1997.
L.R. Scott and S. Zhang. Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Comp., 54(190):483–493, 1990.
R. Servadei and E. Valdinoci. On the spectrum of two different fractional operators. preprint, 2012.
S.A. Silling. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids, 48(1):175–209, 2000.
E.M. Stein. Singular integrals and differentiability properties of functions. Princeton Mathematical Series, No. 30. Princeton University Press, Princeton, N.J., 1970.
P.R. Stinga and J.L. Torrea. Extension problem and Harnack’s inequality for some fractional operators. Comm. Partial Differential Equations, 35(11):2092–2122, 2010.
L. Tartar. An introduction to Sobolev spaces and interpolation spaces, volume 3 of Lecture Notes of the Unione Matematica Italiana. Springer, Berlin, 2007.
Q. Yang, I. Turner, F. Liu, and M. Ilić. Novel numerical methods for solving the time-space fractional diffusion equation in two dimensions. SIAM J. Sci. Comput., 33(3):1159–1180, 2011.
Acknowledgments
This work is supported by NSF Grants DMS-1109325 and DMS-0807811. A.J.S. is also supported by NSF Grant DMS-1008058 and an AMS-Simons Grant. E.O. is supported by the Conicyt–Fulbright Fellowship Beca Igualdad de Oportunidades.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Albert Cohen.
Rights and permissions
About this article
Cite this article
Nochetto, R.H., Otárola, E. & Salgado, A.J. A PDE Approach to Fractional Diffusion in General Domains: A Priori Error Analysis. Found Comput Math 15, 733–791 (2015). https://doi.org/10.1007/s10208-014-9208-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10208-014-9208-x
Keywords
- Fractional diffusion
- Finite elements
- Nonlocal operators
- Degenerate and singular equations
- Second-order elliptic operators
- Anisotropic elements



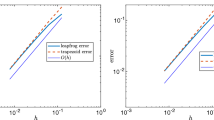
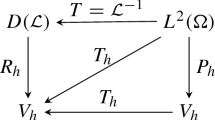
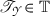 , if
, if  have nonempty intersection, then
have nonempty intersection, then 

 for quasi-uniform meshes
for quasi-uniform meshes  , with
, with 
 , in agreement with Theorem 5.4 and Remark 5.5
, in agreement with Theorem 5.4 and Remark 5.5
 , in agreement with Theorem 5.4 and Remark 5.5
, in agreement with Theorem 5.4 and Remark 5.5
