$L^p-L^q$ estimates for the circular maximal operator on Heisenberg radial functions

Abstract

$L^p$ boundedness of the circular maximal function ${\mathcal {M}}_{{\mathbb H}^1}$ on the Heisenberg group ${\mathbb H}^1$ has received considerable attentions. While the problem still remains open, $L^p$ boundedness of ${\mathcal {M}}_{{\mathbb H}^1}$ on Heisenberg radial functions was recently shown for $p>2$ by Beltran et al. (Ann Sc Norm Super Pisa Cl Sci. https://doi.org/10.2422/2036-2145.202001-006, 2021). In this paper we extend their result considering the local maximal operator $M_{{\mathbb H}^1}$ which is defined by taking supremum over $1<t<2$. We prove $L^p$–$L^q$ estimates for $M_{{\mathbb H}^1}$ on Heisenberg radial functions on the optimal range of p, q modulo the borderline cases. Our argument also provides a simpler proof of the aforementioned result due to Beltran et al.

1 introduction

For $d\ge 2$ the spherical maximal function is given by

$$\begin{aligned} {\mathcal {M}}_{{\mathbb R}^d} f(x)=\sup _{t>0}\left| \frac{1}{\sigma (\mathbb {S}^{d-1})} \int _{\mathbb {S}^{n-1}}f(x-ty)d\sigma (y)\right| , \end{aligned}$$

where $\mathbb {S}^{d-1}\subset {\mathbb {R}}^d$ is the $(d-1)$-dimensional sphere centered at the origin and $d\sigma$ is the surface measure on ${\mathbb {S}}^{d-1}$. When $d\ge 3$, it was shown by Stein [21] that ${\mathcal {M}}_{{\mathbb R}^d} f$ is bounded on $L^p$ if and only if $p>\frac{d}{d-1}$. The case $d=2$ was later settled by Bourgain [5]. An alternative proof of Bourgain’s result was subsequently found by Mockenhaupt, Seeger, Sogge [11], who used a local smoothing estimate for the wave operator. We now consider the local maximal operator

$$\begin{aligned} M_{{\mathbb R}^d}f(x)=\sup _{1<t<2}\left| \int _{{\mathbb {S}}^{d-1}}f(x-ty)d\sigma (y)\right| . \end{aligned}$$

As is easy to see, the maximal operator ${\mathcal {M}}_{{\mathbb R}^d}$ can not be bounded from $L^p$ to $L^q$ unless $p=q$. However, $M_{{\mathbb R}^d}$ is bounded from $L^p$ to $L^q$ for some $p<q$ thanks to the supremum taken over the restricted range [1, 2]. This phenomenon is called $L^p$ improving. Almost complete characterization of $L^p$ improving property of $M_{{\mathbb R}^2}$ was obtained by Schlag [17] except for the endpoint cases. A different proof which is based on $L^p$–$L^q_\alpha$ smoothing estimate for the wave operator was also found by Schlag and Sogge [18]. They also proved $L^p$–$L^q$ boundedness of $M_{{\mathbb R}^d}$ for $d\ge 3$ which is optimal up to the borderline cases. Most of the left open endpoint cases were settled by the second author [8] but there are some endpoint cases where $L^p$–$L^q$ estimate remains unknown though restricted weak type bounds are available for such cases. There are results which extend the aforementioned results to variable coefficient settings, see [18, 19]. Also, see [1, 4, 14] and references therein for recent extensions of the earlier results.

The analogous spherical maximal operators on the Heisenberg group ${\mathbb H}^n$ also have attracted considerable interests. The Heisenberg group ${\mathbb H}^n$ can be identified with ${\mathbb R}^{2n}\times {\mathbb R}$ under the noncommutative multiplication law

$$\begin{aligned} (x,x_{2n+1})\cdot (y,y_{2n+1})=(x+y,x_{2n+1}+y_{2n+1}+x\cdot Ay), \end{aligned}$$

where $(x,x_{2n+1})\in {\mathbb {R}}^{2n}\times {\mathbb {R}}$ and A is the $2n\times 2n$ matrix given by

$$\begin{aligned}A=\begin{pmatrix} 0 &{} -I_n\\ I_n &{} 0 \end{pmatrix}. \end{aligned}$$

The natural dilation structure on ${\mathbb {H}}^n$ is $t(x,x_{2n+1})=(tx, t^2x_{2n+1})$. Abusing the notation, since there is no ambiguity, we denote by $d\sigma$ the usual surface measure of ${\mathbb {S}}^{2n-1}\times \lbrace 0\rbrace$. Then, the dilation $d\sigma _t$ of the measure $d\sigma$ is defined by $\langle f, d\sigma _t\rangle =\langle f(t\cdot ),d\sigma \rangle$. Thus, the average over the sphere is now given by

$$\begin{aligned} f*_{{\mathbb {H}}}d\sigma _t (x,x_{2n+1})=\int _{{\mathbb {S}}^{2n-1}}f(x-ty,x_{2n+1}-tx\cdot Ay) d\sigma (y). \end{aligned}$$

We consider the associated local spherical maximal operator

$$\begin{aligned} M_{{\mathbb H}^n}f(x,x_{2n+1})=\sup _{1<t<2}\left| f*_{{\mathbb {H}}}d\sigma _t (x,x_{2n+1}) \right| . \end{aligned}$$

Similarly, the global maximal operator ${\mathcal {M}}_{{\mathbb H}^n}$ is defined by taking supremum over $t>0$. As in the Euclidean case, $L^p$ boundedness of $M_{{\mathbb H}^n}$ is essentially equivalent to that of ${\mathcal {M}}_{{\mathbb H}^n}$ (for example, see [2] or Section 2.5). The spherical maximal operator on ${\mathbb H}^n$ was first studied by Nevo and Thangavelu [13]. It is easy to see that $M_{{\mathbb H}^n}$ is bounded on $L^p$ only if $p>\frac{2n}{2n-1}$ by using Stein’s example ([21]):

$$\begin{aligned} f(x,x_{2n+1})=\vert x\vert ^{1-2n} \log \frac{1}{\vert x\vert } \,\phi _0(x,x_{2n+1}), \end{aligned}$$

where $\phi _0$ is a cutoff function supported near the origin. For $n\ge 2$, $L^p$ boundedness of ${\mathcal {M}}_{{\mathbb H}^n}$ on the optimal range was independently proved by Müller and Seeger [10], and by Narayanan and Thangavelu [12]. Furthermore, for $n\ge 2$, Roos, Seeger and Srivastava[15] recently obtained the complete $L^p$–$L^q$ estimate for $M_{{\mathbb H}^n}$ except for some endpoint cases. Also see [7] for related results.

However, the problem still remains open when $n=1$.

Definition

We say a function $f: {\mathbb H}^1\rightarrow {\mathbb C}$ is Heisenberg radial if $f(x,x_3)=f(Rx,x_3)$ for all $R\in \mathrm{SO}(2)$.

Beltran, Guo, Hickman and Seeger [2] obtained $L^p$ boundedness of ${\mathcal {M}}_{{\mathbb H}^1}$ on the Heisenberg radial functions for $p>2$. In the perspective of the results concerning the local maximal operators [8, 15, 17, 18], it is natural to consider $L^p$–$L^q$ estimate for $M_{{\mathbb H}^1}$. The main result of this paper is the following which completely characterizes $L^p$ improving property of $M_{{\mathbb H}^1}$ on Heisenberg radial function except for some borderline cases.

Theorem 1.1

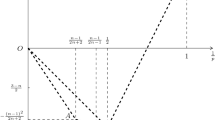
Let $P_0=(0,0), P_1=(1/2,1/2),$ and $P_2=(3/7,2/7)$, and let $\mathbf {T}$ be the closed region bounded by the triangle $\Delta P_0P_1P_2$. Suppose $(1/p,1/q)\in \lbrace P_0 \rbrace \cup (\mathbf {T}{\setminus } (\overline{P_1P_2}\cup \overline{P_0P_2}))$. Then, the estimate

$$\begin{aligned} \Vert M_{{\mathbb H}^1}f\Vert _q\lesssim \Vert f\Vert _{L^p} \end{aligned}$$

(1.1)

holds for all Heisenberg radial function f. Conversely, if $(1/p,1/q)\notin \mathbf {T}$, then the estimate fails.

Though the Heisenberg radial assumption significantly simplifies the structure of the averaging operator, the associated defining function of the averaging operator is still lacking of curvature properties. In fact, the defining function has vanishing rotational and cinematic curvatures at some points, see [2] for a detailed discussion. This increases the complexity of the problem. To overcome the issue of vanishing curvatures, Beltran et al. [2] used the oscillatory integral operators with two-sided fold singularities and the variable coefficient version of local smoothing estimate [3] combined with additional localization.

The approach in this paper is quite different from that in [2]. Capitalizing on the Heisenberg radial assumption, we make a change of variables so that the averaging operator on the Heisenberg radial function takes a form close to the circular average, see (2.1) below. While the defining function of the consequent operator still does not have nonvanishing rotational and cinematic curvatures, via a further change of variables we can apply the $L^p$–$L^q$ local smoothing estimate (see, Theorem 3.1 below) in a more straightforward manner by exploiting the apparent connection to the wave operator (see (2.2) and (2.3)). Consequently, our approach also provides a simplified proof of the recent result due to Beltran et al. [2]. See Sect. 2.5.

Even though we utilize the local smoothing estimate, we do not need to use the full strength of the local smoothing estimate in $d=2$ since we only need the sharp $L^p$–$L^q$ local smoothing estimates for (p, q) near (7/3, 7/2). Such estimates can also be obtained by interpolation and scaling argument if one uses the trilinear restriction estimates for the cone and the sharp local smoothing estimate for some large p (for example, see [9]).

The estimate (1.1) remains open when $(1/p,1/q)\in (\overline{P_1P_2}\cup \overline{P_0P_2}) {\setminus }\{ P_0, P_1\}$. However, we expect that those borderline cases should be true. Most of the corresponding endpoint estimates for the circular maximal function (in ${\mathbb {R}}^2$) are known to be true [8], but to implement the approach in [8] we need the local smoothing estimate without $\epsilon$-loss regularity, which we are not able to establish yet even under the Heisenberg radial assumption.

We close the introduction showing the necessity part of Theorem 1.1.

Optimality of p, q range. We show (1.1) implies $(1/p,1/q)\in \mathbf {T}$, that is to say,

$$\begin{aligned} \mathbf{(a)}\ p\le q , \ \ \ \mathbf{(b)} \ 1+1/{q}\ge {3}/{p} , \ \ \ \mathbf{(c)}\ {3}/{q}\ge {2}/{p}. \end{aligned}$$

To see $\mathbf{(a)}$, let $f_R$ be the characteristic function of a ball of radius $R\gg 1$, centered at 0. Then, $M_{{\mathbb H}^1}f_R$ is also supported in a ball B of radius $\sim R$ and $M_{{\mathbb H}^1}f_R\gtrsim 1$ on B. Thus, $\sup _{R>1}{\Vert M_{{\mathbb H}^1}f_R\Vert _q}/{\Vert f_R\Vert _p}$ is finite only if $p\le q$. For $\mathbf{(b)}$ let $g_r$ be the characteristic function of a ball of radius $r\ll 1$ centered at 0. Then, $\vert M_{{\mathbb H}^1}g_r(x,x_3) \vert \gtrsim r$ when $(x,x_3)$ is contained in a $c_0r-$neighborhood of $\lbrace (x,x_3):1<\vert x\vert <2, x_3=0 \rbrace$ for a small constant $c_0>0$. Thus, (1.1) implies $r^{1+{1}/{q}}\lesssim r^{{3}/{p}}$, which gives $1+{1}/{q}\ge {3}/{p}$ if we let $r\rightarrow 0$. Finally, to show $\mathbf{(c)}$ we consider $h_r$ which is the characteristic function of an $r-$neighborhood of $\lbrace (x,x_3):\vert x\vert =1, x_3=0 \rbrace$ with $r\ll 1$. Then, $\vert M_{{\mathbb H}^1}h_r(x,x_3)\vert \gtrsim c>0$ when $(x,x_3)$ is in an $r-$ball centered at 0. Thus, (1.1) gives $r^{3/{q}}\lesssim r^{2/{p}}$, which yields $3/{q}\ge 2/{p}$.

The maximal estimate (1.1) for general $L^p$ functions has a smaller range of p, q. Let $h_r$ be a characteristic function of the set $\lbrace (x,x_3) : |x_1-1|<r^2, |x_2|<r,|x_3|<r \rbrace$ for a sufficiently small $r>0$. Then $M_{{\mathbb H}^1}h_r (x,x_3)\sim r$ if $-1\le x_1\le 0, |x_2|< cr, |x_3|<cr$ for a small constant $c>0$ independent of r. Thus, (1.1) implies $r^{1+2/{q}}\lesssim r^{{4}/{p}}$. It seems to be plausible to conjecture that (1.1) holds for general f modulo some endpoint cases as long as $1+ {2}/{q}-4/{p}\ge 0$, $3/{q}\ge {2}/{p}$, and $1/{q}\le 1/{p}$. The range of p, q is properly contained in $\mathbf {T}$.

2 Proof of Theorem 1.1

In this section we prove Theorem 1.1 while assuming Proposition 2.1 and Proposition 2.2 (see below), which we show in the next section.

2.1 Heisenberg radial function

Since f is a Heisenberg radial function, we have $f(x,x_3)=f_0(|x|,x_3)$ for some $f_0$. Let us set

$$\begin{aligned} g(s,z)=f_0(\sqrt{2s}, z), \quad s\ge 0. \end{aligned}$$

Then, it follows $f(x ,x_3)=g(|x|^2/{2},x_3)$. Since $f*_{{\mathbb {H}}}d\sigma _t (r,0,x_3)=\int f(r-ty_1,-ty_2,x_3-try_2)d\sigma (y)=\int g(\frac{r^2+t^2}{2}-t ry_1,x_3-try_2)d\sigma (y)$, we have

$$\begin{aligned} f*_{{\mathbb {H}}}d\sigma _t (r,0,x_3) = g*d\sigma _{tr} \Big (\frac{r^2+t^2}{2},x_3\Big ). \end{aligned}$$

(2.1)

Let us define an operator ${\mathcal {A}}_t$ by

$$\begin{aligned} {\mathcal {A}}_t g(r,x_3)= \frac{1}{(2\pi )^2}\int _{{\mathbb {R}}^2} e^{i(\frac{r^2+t^2}{2}\xi _1+x_3\xi _2)} \widehat{d\sigma }(tr\xi ) \, \widehat{g}(\xi ) d\xi . \end{aligned}$$

(2.2)

Using Fourier inversion, we have

$$\begin{aligned} f*_{{\mathbb {H}}}d\sigma _t (r,0,x_3)={\mathcal {A}}_t g(r,x_3). \end{aligned}$$

(2.3)

Since $f*_{{\mathbb {H}}}d\sigma _t$ is also Heisenberg radial,¹$\Vert M_{{\mathbb H}^1}f\Vert _q^q = \int |M_{{\mathbb H}^1} f(r,0,x_3)|^q rdrdx_3.$ A computation shows $\Vert f\Vert _{L^p_{x, x_3}}=\Vert g\Vert _{L^p_{r,x_3}}$. Therefore, we see that the estimate (1.1) is equivalent to

$$\begin{aligned} \big \Vert r^\frac{1}{q} \sup _{1<t<2} |{\mathcal {A}}_t g | \big \Vert _{L^q_{r,x_3}}\le C \Vert g\Vert _p. \end{aligned}$$

(2.4)

In what follows we show (2.4) holds for p, q satisfying

$$\begin{aligned} p\le q, \ 3/p-1/q<1, \ 1/{p}+2/{q}> 1. \end{aligned}$$

(2.5)

Then, interpolation with the trivial $L^\infty$ estimate proves Theorem 1.1.

2.2 Decomposition

Let $\phi$ denote a positive smooth function on ${\mathbb R}$ supported in $[1-10^{-3}, 2 +10^{-3}]$ such that $\sum _{j=-\infty }^\infty \phi (s/2^j)=1$ for $s>0$. We set $\phi _j(s)=\phi (s/2^j)$. To show (2.4) we decompose ${\mathcal {A}}_t$ as follows:

$$\begin{aligned} {\mathcal {A}}_t g(r,x_3) = \sum _{k\in {\mathbb Z}} \phi _k(r) \mathcal A_t g(r,x_3). \end{aligned}$$

We break g via the Littlewood–Paley decomposition and try to obtain estimates for each decomposed pieces. For the purpose we denote $\phi _{<j}=\sum _{\ell <j }\phi _\ell$ and $\phi _{\,\ge j}=\sum _{\ell \ge j }\phi _\ell$ and define the projection operators

$$\begin{aligned} \widehat{{\mathcal {P}}_j g} (\xi ):=\phi _j(|\xi |) \widehat{g}(\xi ), \quad \widehat{{\mathcal {P}}_{<j} g} (\xi ):=\phi _{<j}(|\xi |) \widehat{g}(\xi ). \end{aligned}$$

Our proof of (2.4) mainly relies on the following two propositions, which we prove in Sect. 3.

Proposition 2.1

Let $|k|\ge 2$ and $j\ge -k$. Suppose

$$\begin{aligned} p\le q, \ 1/{p}+1/{q}\le 1, \ 1/{p}+3/{q}\ge 1. \end{aligned}$$

(2.6)

Then, for $\epsilon >0$ we have

$$\begin{aligned} \Big \Vert \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t \mathcal P_{\!j}g| \Big \Vert _{L^q_{r,x_3}} \lesssim {\left\{ \begin{array}{ll} 2^{(j+k)(\frac{3}{2p}-\frac{1}{2q}-\frac{1}{2}+\epsilon )+\frac{k}{q}-\frac{2k}{p}}\Vert g\Vert _{L^p}, &{}\quad \ \ \ k\ge 2, \\ 2^{(j+k)(\frac{3}{2p}-\frac{1}{2q}-\frac{1}{2}+\epsilon )+\frac{2k}{q}-\frac{2k}{p}}\Vert g\Vert _{L^p}, &{}\quad \ k< -2. \end{array}\right. } \end{aligned}$$

(2.7)

The estimate (2.7) continues to be valid for the case $k=-1,0,1$. However, the range of p, q for which (2.7) holds gets smaller.

Proposition 2.2

Let $j\ge -1$ and $k=-1,0,1$. Suppose $p\le q$, $1/{p}+1/{q}< 1$ and $1/{p}+2/{q}> 1$. Then, for $\epsilon >0$ we have

$$\begin{aligned} \Big \Vert \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t \mathcal P_{\!j}g| \Big \Vert _{L^q_{r,x_3}} \lesssim 2^{ \frac{j}{2}(\frac{3}{p}-\frac{1}{q}-1)+\epsilon j}\Vert g\Vert _{L^p}. \end{aligned}$$

We frequently use the following elementary lemma (for example, see [8]) which plays the role of the Sobolev imbedding.

Lemma 2.3

Let I be an interval and let F be a smooth function defined on $\mathbb {R}^n\times I$. Then, for $1\le p\le \infty$,

$$\begin{aligned} \Big \Vert \sup _{t\in I}\vert F(x,t)\vert \Big \Vert _{L^p(\mathbb {R}^n)}\lesssim {|I|^{-\frac{1}{p}}}\Vert F\Vert _{L^p(\mathbb {R}^n\times I)}+\Vert F\Vert _{L^p(\mathbb {R}^n\times I)}^{\frac{(p-1)}{p}}\Vert \partial _tF\Vert _{L^p(\mathbb {R}^n\times I)}^{\frac{1}{p}}. \end{aligned}$$

2.3 Proof of (2.4)

We prove (2.4) handling the three cases $k\le -2,$ $|k|\le 1,$ and $k\ge 2$, separately. We first consider a change of variables

$$\begin{aligned} (r,x_3,t)\rightarrow (y_1, y_2, \tau ):=\left( \frac{r^2+t^2}{2},x_3,rt \right) , \end{aligned}$$

(2.8)

which plays an important role in what follows. Note that

$$\begin{aligned} \det \frac{\partial (y_1, y_2, \tau )}{\partial (r,x_3,t)}= r^2-t^2. \end{aligned}$$

(2.9)

In order to show (2.4), we shall use the change of variables (2.8) to apply the local smoothing estimate to the averaging operator ${\mathcal {A}}_t$ (see Sect. 3.1). Since $1<t<2$, $|\det {\partial (y_1, y_2, \tau )} /{\partial (r,x_3,t)}|= |r^2-t^2|\sim \max (2^{2k}, 1)$ for $|k|\ge 2$. Thus, the cases $|k|\ge 2$ can be handled directly by using local smoothing estimates for the half wave propagator. However, the determinant of the Jacobian may vanish when $|k|\le 1$. This requires further decomposition away from the set $\{r=t\}$. See Sect. 3.3. This is why we need to consider the three cases separately.

Let us set $g_k={\mathcal {P}}_{<-k}\,g$ and $g^k= g- {\mathcal {P}}_{< -k}g$ so that $g=g_k+g^k$. Then, we break

$$\begin{aligned} \phi _k(r){\mathcal {A}}_t g= \phi _k(r){\mathcal {A}}_t g_k + \phi _k(r){\mathcal {A}}_t g^k. \end{aligned}$$

(2.10)

We use Propositions 2.1 and 2.2 to obtain the estimate for $\phi _k(r){\mathcal {A}}_t g^k$, whereas we show the estimate for $\phi _k(r){\mathcal {A}}_t g_k$ by elementary means using (2.2).

2.4 Case $k\le - 2$

We claim that

$$\begin{aligned} \Big \Vert r^{\frac{1}{q}} \sum _{k\le -2} \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t g| \Big \Vert _{L^q_{r,x_3}}\lesssim \Vert g\Vert _{L^p} \end{aligned}$$

(2.11)

holds provided that p, q satisfy $2/p<3/q$, $3/p-1/q<1$, and (2.6). Thus (2.11) holds for p, q satisfying (2.5).

We first consider $\phi _k(r){\mathcal {A}}_t g_k$. We shall show that

$$\begin{aligned} \Big \Vert r^{\frac{1}{q}} \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t g_k | \Big \Vert _{L^q_{r,x_3}} \lesssim 2^{\frac{3k}{q}-\frac{2k}{p}}\Vert g\Vert _{L^p} \end{aligned}$$

(2.12)

holds for $1\le p\le q\le \infty$. We recall (2.2) and note that $\partial _t(\widehat{d\sigma }(tr\xi ))$ is uniformly bounded because $|r\xi |\lesssim 1$. Since ${\text {supp}}\widehat{g_k }\subset \{\xi : |\xi |\le C2^{-k}\}$ and $\partial _t e^{\frac{r^2+t^2}{2}\xi _1}=t\xi _1 e^{\frac{r^2+t^2}{2}\xi _1}$, we have $\Vert \phi _k(r) \partial _t {\mathcal {A}}_t g_k\Vert _q\lesssim 2^{-k}\Vert \phi _k(r){\mathcal {A}}_t g_k\Vert _q$ by the Mikhlin multiplier theorem. Applying Lemma 2.3 to $\phi _k(r){\mathcal {A}}_t g_k$, we see that (2.12) follows if we show

$$\begin{aligned} \Vert \phi _k(r){\mathcal {A}}_t g_k \Vert _{L^q_{r,x_3,t}({\mathbb {R}}^2\times [1,2])}\lesssim 2^{\frac{3k}{q}-\frac{2k}{p}}\Vert g\Vert _{L^p}. \end{aligned}$$

(2.13)

We now make use of the change of variables (2.8). Since $k\le -2$ and $t\in [1,2]$, we have $|\det \frac{\partial (y_1, y_2, \tau )}{\partial (r,x_3,t)}|\sim 1$. Thus the left hand side of (2.13) is bounded by

$$\begin{aligned} C\Big \Vert \phi _k(r(y_1, y_2, \tau ))\int e^{iy\cdot \xi }\, \widehat{g}(\xi )\widehat{d\sigma }(\tau \xi )\phi _{<-k}(\xi )d\xi \Big \Vert _{L^q_{y,\tau }({\mathbb R}^2\times [2^{-1},2^2])}. \end{aligned}$$

Changing variables $\xi \rightarrow 2^{-k}\xi$ and $(y, \tau )\rightarrow (2^ky, 2^k\tau )$ gives

$$\begin{aligned} \Vert \phi _k(r){\mathcal {A}}_t g_k \Vert _{L^q_{r,x_3,t}({\mathbb {R}}^2\times [1,2])} \lesssim 2^{\frac{3k}{q}}\Big \Vert \int e^{i y\cdot \xi }\, \mathfrak m(\xi ) \widehat{g(2^k\cdot )} (\xi ) d\xi \Big \Vert _{L^q_{y,\tau }({\mathbb R}^2\times [2^{-1},2^2])}, \end{aligned}$$

where $\mathfrak m(\xi )= \widehat{d\sigma }( \tau \xi )\phi _{<0}(\xi )$. Since $\tau \sim 1$ and $\phi _{<0}(\xi )$ is a smooth function supported in the set $\lbrace \xi : |\xi |\lesssim 1 \rbrace$, $\mathfrak m(\xi )$ is a smooth multiplier whose derivatives are uniformly bounded. So, the multiplier operator given by $\mathfrak m$ is uniformly bounded from $L^p({\mathbb {R}}^2)$ to $L^q({\mathbb {R}}^2)$ for $\tau \in [2^{-1},2^2]$. Thus, via scaling we obtain (2.13) and, hence, (2.12).

Using the triangle inequality and (2.12), we have

$$\begin{aligned} \Bigg \Vert r^{\frac{1}{q}} \sup _{1<t<2} \sum _{k\le -2} | \phi _k(r){\mathcal {A}}_t g_k | \Bigg \Vert _{L^q_{r,x_3}} \lesssim \Bigg (\sum _{k\le - 2} 2^{\frac{3k}{q}-\frac{2k}{p}}\Bigg ) \Vert g\Vert _p \lesssim \Vert g\Vert _p \end{aligned}$$

because $2/p<3/q$. We now consider $\phi _k(r){\mathcal {A}}_t g^k$ for which we use Proposition 2.1. Since

$$\begin{aligned} \Bigg \Vert r^{\frac{1}{q}} \sup _{1<t<2} \sum _{k\le -2} | \phi _k(r){\mathcal {A}}_t g^k | \Bigg \Vert _{L^q_{r,x_3}} \le \sum _{k\le -2} \sum _{j\ge -k}\Bigg \Vert r^{\frac{1}{q}} \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t \mathcal P_{\!j}g | \Bigg \Vert _{L^q_{r,x_3}} \end{aligned}$$

and since p, q satisfy $3/p-1/q<1$, $2/p<3/q$, and (2.6), using the estimate (2.7), we get

$$\begin{aligned} \Bigg \Vert r^{\frac{1}{q}} \sup _{1<t<2} \sum _{k\le -2} | \phi _k(r){\mathcal {A}}_t g^k | \Bigg \Vert _{L^q_{r,x_3}} \lesssim \Bigg (\sum _{k\le - 2} 2^{\frac{3k}{q}-\frac{2k}{p}}\Bigg ) \Vert g\Vert _p \lesssim \Vert g\Vert _p. \end{aligned}$$

Combining this with the above estimate for $g\rightarrow \phi _k(r){\mathcal {A}}_t g^k$ gives (2.11) and this proves the claim.

2.5 Case $k\ge 2$

In this case we show

$$\begin{aligned} \Bigg \Vert r^{\frac{1}{q}} \sum _{k\ge 2} \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t g| \Bigg \Vert _{L^q_{r,x_3}}\lesssim \Vert g\Vert _{L^p} \end{aligned}$$

(2.14)

if $p\le q$, $3/p-1/q<1$, and (2.6) holds. So, we have (2.14) if (2.5) holds.

In order to prove (2.14) we first prove the following.

Lemma 2.4

Let $k\ge -1$. If $|t|\lesssim 1$ and $0\le s\lesssim 2^{2k}$, then

$$\begin{aligned} |{\mathcal {A}}_t {{\mathcal {P}}}_{<-k}g | (\sqrt{2s}, x_3)\lesssim {\mathcal {E}}^N_{k}*| g|(s, x_3), \end{aligned}$$

(2.15)

where ${\mathcal {E}}^N_\ell (y) =2^{-2\ell }(1+ 2^{-\ell }|y| )^{-N}.$

Proof

We note that

$$\begin{aligned} {\mathcal {A}}_t {{\mathcal {P}}}_{<-k}g(\sqrt{2s}, x_3)&= K*g \big (s+2^{-1}t^2, x_3 \big ), \end{aligned}$$

where

$$\begin{aligned} K(y)= \frac{1}{(2\pi )^2}\int e^{iy\cdot \xi }\phi _{<-k}(\xi )\widehat{d\sigma }(t\sqrt{2s}\xi ) d\xi . \end{aligned}$$

We note $\partial _{\xi }^\alpha [\phi _{<-k}(2^{-k}\xi )\widehat{d\sigma }(2^{-k} t\sqrt{2s}\xi ) ]=O(1)$ since $s\lesssim 2^{2k}$. Thus, changing variables $\xi \rightarrow 2^{-k}\xi$, by integration by parts we have $|K|\lesssim {\mathcal {E}}^N_{k}$ for any $N>0$. Since $|t|\lesssim 1$ and $k\ge -1$, we see ${\mathcal {E}}^N_{k} (y_1+2^{-1}t^2, y_2)\lesssim {\mathcal {E}}^N_{k} (y_1, y_2)$. Therefore, we get (2.15). $\square$

Proof of 2.14

We begin by observing a localization property of the operator ${\mathcal {A}}_t$. From (2.1) we note that

$$\begin{aligned} \frac{r^2+t^2}{2}-t ry_1 \subset I_k:= [2^{2k-1}( 1- 10^{-2}),2^{2k+1}( 1+10^{-2})] \end{aligned}$$

for $r\in {\text {supp}}\phi _k$ if k is large enough, i.e., $2^{-k}\le 10^{-3}$. Thus, from (2.1) and (2.3) we see that

$$\begin{aligned} \phi _k(r) {\mathcal {A}}_t g(r,x_3)= \phi _k(r){\mathcal {A}}_t ([g]_k)(r,x_3) \end{aligned}$$

(2.16)

where $[g]_k(r,x_3)=\chi _{I_k}(r) g(r,x_3)$. Clearly, the intervals ${I_k}$ are finitely overlapping and so are the supports of $\phi _k$. Since $p\le q$, by a standard localization argument it is sufficient for (2.14) to show

$$\begin{aligned} \Bigg \Vert r^{\frac{1}{q}} \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t g| \Bigg \Vert _{L^q_{r,x_3}}\lesssim \Vert g\Vert _{L^p} \end{aligned}$$

(2.17)

for $k\ge 2$.

Using the decomposition (2.10), we first consider $\phi _k(r){\mathcal {A}}_t g_k$. Changing variables $r\mapsto \sqrt{2s}$, we have

$$\begin{aligned} \Bigg \Vert r^\frac{1}{q} \sup _{1<t<2} |\phi _k(r){\mathcal {A}}_t g_k |\Bigg \Vert _{L^q_{r,x_3}}^q \lesssim \int \phi _k(\sqrt{2s}) \left( \sup _{1<t<2} |{\mathcal {A}}_t g_k(\sqrt{2s}, x_3) | \right) ^qdsdx_3. \end{aligned}$$

Since $1<t<2$, $k\ge 2$, and $g_k={\mathcal {P}}_{<-k} g$, by Lemma 2.4$|{\mathcal {A}}_t g_k(\sqrt{2s}, x_3) |\lesssim {\mathcal {E}}^N_{k}*| g|(s, x_3)$. Hence,

$$\begin{aligned} \Bigg \Vert r^\frac{1}{q} \sup _{1<t<2} |\phi _k(r){\mathcal {A}}_t g_k |\Bigg \Vert _{L^q_{r,x_3}} \lesssim \Vert {\mathcal {E}}^N_{k}*| g| \Vert _{L^q_{s,x_3}} \lesssim 2^{2k(1/q-1/p)} \Vert g\Vert _p \le \Vert g\Vert _p. \end{aligned}$$

The second inequality follows by Young’s convolution inequality and the third is clear because $k\ge 2$ and $p\le q$. We now handle $\phi _k(r){\mathcal {A}}_t g^k$. Since

$$\begin{aligned} \Big \Vert r^{\frac{1}{q}} \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t g^k | \Big \Vert _{L^q_{r,x_3}} \le \sum _{j\ge -k}\Big \Vert r^{\frac{1}{q}} \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t \mathcal P_{\!j}g | \Big \Vert _{L^q_{r,x_3}} \end{aligned}$$

(2.18)

and since $3/p-1/q<1$, $p\le q$, and (2.6) holds, using the estimate (2.7), we get

$$\begin{aligned} \Big \Vert r^{\frac{1}{q}} \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t g^k | \Big \Vert _{L^q_{r,x_3}} \lesssim 2^{\frac{2k}{q}-\frac{2k}{p}} \Vert g\Vert _p \lesssim \Vert g\Vert _p. \end{aligned}$$

Therefore, we get (2.17). $\square$

2.6 Case $|k|\le 1$

To complete the proof of (2.4), the matter is now reduced to obtaining

$$\begin{aligned} \Big \Vert r^\frac{1}{q} \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t g| \Big \Vert _{L^q_{r,x_3}}\lesssim \Vert g\Vert _{L^p}, \quad k=-1,0,1 \end{aligned}$$

if p, q satisfy (2.5). In order to show this we use Proposition 2.2. Using the decomposition (2.10), we first consider $\phi _k(r){\mathcal {A}}_t g_k$. Since $1<t<2$ and $|k|\le 1$, by Lemma 2.4 we have $\phi _k(r)|{\mathcal {A}}_t g_k|\lesssim {\mathcal {E}}^N_0*|g|$. Hence, it follows that

$$\begin{aligned} \Big \Vert r^{\frac{1}{q}} \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t g_k | \Big \Vert _{L^q_{r,x_3}} \lesssim \Vert g\Vert _p \end{aligned}$$

for $1\le p\le q\le \infty$.

We now consider $\phi _k(r){\mathcal {A}}_t g^k$. Note that (2.6) is satisfied if (2.5) holds. Since $3/p-1/q<1$, by (2.18) and Proposition 2.2 we see

$$\begin{aligned} \Big \Vert r^{\frac{1}{q}} \sup _{1<t<2} | \phi _k(r){\mathcal {A}}_t g^k | \Big \Vert _{L^q_{r,x_3}} \lesssim \sum _{j\ge -k} 2^{ \frac{j}{2}(\frac{3}{p}-\frac{1}{q}-1)+\epsilon j}\Vert g\Vert _{L^p} \lesssim \Vert g\Vert _p \end{aligned}$$

taking a small enough $\epsilon >0$. Therefore we get the desired estimate.

2.7 Global maximal estimate

Using the estimates in this section, one can provide a simpler proof of the result due to Beltran et al. [2], i.e.,

$$\begin{aligned} \Vert r^\frac{1}{p} \sup _{0<t<\infty } |{\mathcal {A}}_t g | \Vert _{L^p_{r,x_3}}\le C \Vert g\Vert _p \end{aligned}$$

(2.19)

for $2<p\le \infty$. In order to show this we use the following lemma which is a consequence of Propositions 2.1 and 2.2.

Lemma 2.5

Let $2\le p\le 4$. Then, for some $c>0$ we have

$$\begin{aligned} \big \Vert r^\frac{1}{p} \sup _{1<t<2} |{\mathcal {A}}_t \mathcal P_{\!j}g | \big \Vert _{L^p_{r,x_3}}\le C 2^{-cj} \Vert g\Vert _p\, . \end{aligned}$$

(2.20)

Proof

We briefly explain how one can show (2.20). In fact, similarly as before, we decompose

$$\begin{aligned} {\mathcal {A}}_t \mathcal P_{\!j}g= S_1+ S_3+ S_3+S_4, \end{aligned}$$

where

$$\begin{aligned} S_1:= \sum _{k<-j} \phi _k(r){\mathcal {A}}_t \mathcal P_{\!j}g, \quad S_2:= \sum _{-j\le k\le -2} \phi _k(r){\mathcal {A}}_t \mathcal P_{\!j}g, \quad S_3:= \sum _{-1\le k\le 1} \phi _k(r){\mathcal {A}}_t \mathcal P_{\!j}g, \end{aligned}$$

and $S_4= {\mathcal {A}}_t \mathcal P_{\!j}g - S_1- S_2- S_3.$ Then, the estimate (2.20) follows if we show $\Vert r^\frac{1}{p} \sup _{1<t<2} |S_\ell | \Vert _{L^p_{r,x_3}}\le C 2^{-cj} \Vert g\Vert _p$, $\ell =1,2,3, 4$ for some $c>0$. The estimate for $S_1$ follows from (2.12) and summation over $k<-j$. Using the estimate of the second case in (2.7), one can easily get the estimate for $S_2$. The estimate for $S_3$ is obvious from Proposition 2.2. By Proposition 2.1 combined with the localization property (2.16) we can obtain the estimate for $S_4$. However, due to the projection operator $\mathcal P_{\!j}$ we need to modify the previous argument slightly.

From (2.1) and (2.3) we see

$$\begin{aligned} {\mathcal {A}}_t \mathcal P_{\!j}g(r,x_3)=\iint g(z_1, z_2) K_j\Bigg (\frac{r^2+t^2}{2}-z_1- t ry_1,x_3-z_2-try_2\Bigg )d\sigma (y) d z, \end{aligned}$$

(2.21)

where $K_j={\mathcal {F}}^{-1}( \phi (2^{-j}|\cdot |)$. Note that $|K_j|\lesssim E_{-j}^N$ for any N and $k\ge 2$. If $r\in {\text {supp}}\phi _k$, $\sqrt{2z_1}\not \in I_k$, and k is large enough, then we have

$$\begin{aligned}&\Big | K_j\Big ( \frac{r^2+t^2}{2}-t ry_1 -z_1,x_3-try_2-z_2\Big )\Big |\\&\quad \lesssim 2^{-(2k+j)N} \Big (1+ 2^j|r^2-2z_1|+ 2^{-k}|x_3-z_2| \Big )^{-N} \end{aligned}$$

for any N since $|2^{-1}r^2-z_1|\gtrsim 2^{2k}$ and $|rty|\lesssim 2^k$. Hence it follows that

$$\begin{aligned} \Vert r^\frac{1}{p} \phi _k(r){\mathcal {A}}_t \mathcal P_{\!j}(1-\chi _{I_k})g\Vert _p\le C2^{-(k+j)N} \Vert g\Vert _p, \quad 1\le p\le \infty \end{aligned}$$

for any N. We break ${\mathcal {A}}_t \mathcal P_{\!j}g= {\mathcal {A}}_t \mathcal P_{\!j}\chi _{I_k}g+{\mathcal {A}}_t \mathcal P_{\!j}(1-\chi _{I_k})g$. Using the last inequality and then Proposition 2.1, we obtain

$$\begin{aligned} \Vert S_4\Vert _p\le \Bigg ( \sum _{k\ge 2 } \Vert r^\frac{1}{p} \phi _k(r){\mathcal {A}}_t \mathcal P_{\!j}\chi _{I_k}g\Vert _p^p\Bigg )^\frac{1}{p} + \sum _{k\ge 2 } 2^{-(k+j)N} \Vert g\Vert _p \lesssim 2^{-cj} \Vert g\Vert _p \end{aligned}$$

for some $c>0$ by taking an N large enough. $\square$

Once we have (2.20), using a standard argument which relies on the Littlewood–Paley decomposition and rescaling (for example, see [2, 5, 16] ) one can easily show (2.19). Indeed, we break the maximal function into high and lower frequency parts:

$$\begin{aligned} \sup _{0<t<\infty } |{\mathcal {A}}_t g| \le {\mathcal {A}}_{low\,} g + {\mathcal {A}}_{high\,} g, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {A}}_{low\,} g&= \sup _l \sup _{2^{l}\le t< 2^{l+1}} |{\mathcal {A}}_t {\mathcal {P}}_{<-2l} g|,\\ {\mathcal {A}}_{high\,} g&=\sum _{k\ge 0} \sup _l \sup _{2^{l}\le t < 2^{l+1}} |{\mathcal {A}}_t {\mathcal {P}}_{k-2l} g|. \end{aligned}$$

For ${\mathcal {A}}_{low\,} g$ we claim

$$\begin{aligned} \sup _{2^{l}\le t< 2^{l+1}} |{\mathcal {A}}_t {\mathcal {P}}_{<-2l} g(r, x_3)| \lesssim {\mathcal {M}}_{{\mathbb R}^2}g(2^{-1}r^2,x_3). \end{aligned}$$

(2.22)

This gives ${\mathcal {A}}_{low\,} g(r,x_3)\lesssim {\mathcal {M}}_{{\mathbb R}^2}g(2^{-1}r^2,x_3)$. Since ${\mathcal {M}}_{{\mathbb R}^2}$ is bounded on $L^p$ for $p>2$, for $2<p\le \infty$ we get

$$\begin{aligned} \Vert r^\frac{1}{p} {\mathcal {A}}_{low\,} g \Vert _{L^p_{r,x_3}}\le C \Vert g\Vert _p. \end{aligned}$$

We now proceed to prove (2.22). Note that $\sum _{j\le 2l} \phi (2^{-j}|\cdot |)=\phi _{<1}(2^{2l}|\cdot |)$ and $\phi _{<1}$ is a smooth function supported on $[-2^2,2^2]$. Thus, similarly as in (2.21) we note that ${\mathcal {A}}_t {\mathcal {P}}_{<-2l} g(r,x_3) = \iint g(z_1, z_2) \widetilde{K}_l *d\sigma _{tr} ( 2^{-1}(r^2+t^2)-z_1,x_3-z_2) d z$ where $\widetilde{K}_l={\mathcal {F}}^{-1}( \phi _{<1}(2^{2l}|\cdot |))$. Since $\widetilde{K}_l\lesssim {\mathcal {E}}_{2l}^N$ for any N, for $2^{l}\le t < 2^{l+1}$ we see

$$\begin{aligned} |{\mathcal {A}}_t {\mathcal {P}}_{<-2l} g(r,x_3)|\lesssim \int | g(z_1, z_2) | {\mathcal {E}}^{2N}_{2l} *d\sigma _{tr} \big (2^{-1}r^2- z_1,x_3-z_2\big ) d z \end{aligned}$$

(2.23)

because $2^{2l}t^2\lesssim 1$ and ${\mathcal {E}}^{2N}_{2l}=2^{-4l}(1+ 2^{-2l}|y| )^{-2N}.$ Hence, taking an N large enough, we note that

$$\begin{aligned} {\mathcal {E}}^{2N}_{2l} *d\sigma _{tr}(x) \lesssim {\left\{ \begin{array}{ll} (2^{2l} tr)^{-1} (1+ 2^{-2l} ||x|- tr|)^{-N}, &{} 2^{2l}\ll tr,\\ 2^{-4l} (1+ 2^{-2l} |x|)^{-N}, &{} 2^{2l} \gtrsim tr, \end{array}\right. } \end{aligned}$$

(2.24)

provided that $2^{l}\le t < 2^{l+1}$. Indeed, to show this we only have to consider the case $2^{2l}\ll tr$ since the other case is trivial. By scaling $x\rightarrow trx$ we may assume that $tr=1$. Thus, it is enough to show $\int L^{-2}(1+L^{-1}|x-y|)^{-2N}d\sigma (y)\lesssim L^{-1}(1+L^{-1}||x|-1|)^{-N}$ for $L\ll 1$ with an N large enough. However, this is easy to see since $|x-y|\ge ||x|-1|$ and $\int L^{-1}(1+L^{-1}|x-y|)^{-N}d\sigma (y)\lesssim 1$.

Therefore, combining (2.23) and (2.24), one can see

$$\begin{aligned} \sup _{2^{l}\le t< 2^{l+1}}|{\mathcal {A}}_t {\mathcal {P}}_{<-2l} g(r,x_3)| \lesssim {\mathcal {M}}_{{\mathbb R}^2}g(2^{-1}r^2,x_3) + \mathfrak M_2g(2^{-1}r^2,x_3). \end{aligned}$$

Here $\mathfrak M_2$ denotes the Hardy-Littlewood maximal function on ${\mathbb {R}}^2$. This proves the claim (2.22) since $\mathfrak M_2g\lesssim {\mathcal {M}}_{{\mathbb R}^2}g$.

So we are reduced to showing $\Vert r^\frac{1}{p} {\mathcal {A}}_{high\,} g \Vert _{L^p_{r,x_3}}\le C \Vert g\Vert _p$ for $p>2$. For the purpose it is sufficient to show

$$\begin{aligned} \Vert \sup _{2^{l}\le t < 2^{l+1}} |{\mathcal {A}}_t {\mathcal {P}}_{k-2l} g|\Vert _p \lesssim 2^{-ck} \Vert g\Vert _p \end{aligned}$$

(2.25)

because ${\mathcal {A}}_{high\,} g\le \sum _{k\ge 0} (\sum _l | \sup _{2^{l}\le t < 2^{l+1}} |{\mathcal {A}}_t {\mathcal {P}}_{k-2l} g|^p)^{1/p}$ and $(\sum _l \Vert {\mathcal {P}}_{k-2l} g\Vert _p^p)^{1/p}\lesssim \Vert g\Vert _p.$ By scaling, using (2.2), we can easily see the inequality (2.25) is equivalent to (2.20) while j replaced by k. So, we have (2.25) and this completes the proof of (2.19).

3 Proof of Propositions 2.1 and 2.2

In order to prove Propositions 2.1 and 2.2, we are led by (2.2) to consider $\widehat{d\sigma }(tr\xi )$ for which we use the following well known asymptotic expansion (see, for example, [20]):

$$\begin{aligned} \widehat{d\sigma }(\xi )= \sum _{j=0}^NC^\pm _j |\xi |^{-\frac{1}{2}-j} e^{ \pm i|\xi |}+ E_N( |\xi |), \quad |\xi |\gtrsim 1 \end{aligned}$$

(3.1)

where $E_N$ is a smooth function satisfying

$$\begin{aligned} | \frac{d^\ell }{dr^\ell } E_N(r)|\lesssim r^{-N} \end{aligned}$$

(3.2)

for $0\le \ell \le 4$ if $r\gtrsim 1$. The expansion (3.1) relates the operator ${\mathcal {A}}_t$ to the wave propagator. After changing variables, to prove Propositions 2.1 and 2.2 we can use the local smoothing estimate for the wave operator (see Proposition 3.1 below).

3.1 Local smoothing estimate

Let us denote

$$\begin{aligned} e^{it\sqrt{-\Delta }} f(x)=\frac{1}{(2\pi )^2}\int _{{\mathbb {R}}^2} e^{i(x\cdot \xi +t|\xi |)}\widehat{f}(\xi )d\xi . \end{aligned}$$

We make use of $L^p$–$L^q$ local smoothing estimate for the wave equation in ${\mathbb R}^2$.

Theorem 3.1

Let $j\ge 0$. Suppose (2.6) holds. Then, for $\epsilon >0$ we have

$$\begin{aligned} \left\| e^{it\sqrt{-\Delta }} \mathcal P_{\!j}f \right\| _{L^q_{x,t}({\mathbb R}^2\times [1,2])}\lesssim 2^{\frac{3}{2}\left( \frac{1}{p}-\frac{1}{q}\right) j+ \epsilon j}\Vert f\Vert _{L^p} \end{aligned}$$

(3.3)

This follows by interpolating the estimates (3.3) with $(p,q)=(2,2)$, $(1,\infty )$, and (4, 4). The estimate (3.3) with $(p,q)=(2,2)$ is a straightforward consequence of Plancherel’s theorem and (3.3) with $(p,q)=(1,\infty )$ can be shown by the stationary phase method (for example, see [8]). The case $(p,q)=(4,4)$ is due to Guth et al. [6].

From Theorem 3.1 we can deduce the following estimate via simple rescaling argument.

Corollary 3.2

Let $j\ge -\ell$. Suppose (2.6) holds. Then, for $\epsilon >0$ we have

$$\begin{aligned} \left\| e^{it\sqrt{-\Delta }} \mathcal P_{\!j}f \right\| _{L^q_{x,t}({\mathbb R}^2\times [2^\ell ,2^{\ell +1}])}\lesssim 2^{\frac{3}{2}\left( \frac{1}{p}-\frac{1}{q} \right) (\ell +j)+\left( \frac{3}{q}-\frac{2}{p}\right) \ell + \epsilon (\ell +j)}\Vert f\Vert _{L^p} . \end{aligned}$$

Proof

Changing variables $(x,t)\rightarrow 2^\ell (x,t)$, we see

$$\begin{aligned} \left\| e^{it\sqrt{-\Delta }} \mathcal P_{\!j}f \right\| _{L^q_{x,t}({\mathbb R}^2\times [2^\ell ,2^{\ell +1}])} = 2^{\frac{3\ell }{q}}\left\| e^{it\sqrt{-\Delta }} {\mathcal {P}}_{\ell +j} f(2^\ell \cdot ) \right\| _{L^q_{x,t}({\mathbb R}^2\times [1,2])}. \end{aligned}$$

Thus, using (3.3) we have

$$\begin{aligned} \left\| e^{it\sqrt{-\Delta }} \mathcal P_{\!j}f \right\| _{L^q_{x,t}({\mathbb R}^2\times [2^\ell ,2^{\ell +1}])} \lesssim 2^{\frac{3\ell }{q}+\frac{3}{2}\left( \frac{1}{p}-\frac{1}{q} \right) (\ell +j)+ \epsilon (\ell +j)}\Vert f(2^\ell \cdot )\Vert _{L^p}. \end{aligned}$$

So, rescaling gives the desired inequality. $\square$

3.2 Proof of Proposition 2.1

We now recall (2.2) and (3.1). To show Proposition 2.1 we first deal with the contribution from the error part $E_N$. Let us set

$$\begin{aligned} {\mathcal {E}}_t g (r,x_3) = \int e^{i(\frac{r^2+t^2}{2}\xi _1+x_3\xi _2)} E_N(tr|\xi |)\, \widehat{g}(\xi ) d\xi . \end{aligned}$$

Lemma 3.3

Let $j\ge -k$. Suppose (2.6) holds. Then, we have

$$\begin{aligned} \Big \Vert \sup _{1<t<2} | \phi _k(r){\mathcal {E}}_t \mathcal {P}_j g | \Big \Vert _{L^q_{r,x_3}} \lesssim {\left\{ \begin{array}{ll} 2^{-(N-3)(j+k)}2^{k(\frac{1}{q}-\frac{2}{p})}\Vert g\Vert _{L^p}, &{} \ k\ge -2, \\ 2^{-(N-3)(j+k)}2^{k(\frac{3}{q}-\frac{2}{p})} \Vert g\Vert _{L^p}, &{} \ k< -2. \end{array}\right. } \end{aligned}$$

(3.4)

Proof

We first consider the case $k\ge -2$. Using Lemma 2.3, we need to estimate $\phi _k(r){\mathcal {E}}_t \mathcal {P}_j g$ and $\phi _k(r)\partial _t {\mathcal {E}}_t \mathcal {P}_j g$ in $L^q_{r,x_3,t}({\mathbb {R}}^2\times [1,2])$. For simplicity we denote $L^q_{r,x_3,t}=L^q_{r,x_3,t}({\mathbb {R}}^2\times [1,2])$. We first consider $\phi _k(r){\mathcal {E}}_t \mathcal {P}_j g$. Changing variables $\frac{r^2}{2}\mapsto s$, we note that

$$\begin{aligned} \phi _k(\sqrt{2s}){\mathcal {E}}_t \mathcal {P}_j g(\sqrt{2s},x_3)=\phi _k(\sqrt{2s})\int \mathcal {K}\big ( s-y_1+ 2^{-1}{t^2},x_3-y_2 \big )g(y_1,y_2)dy, \end{aligned}$$

where

$$\begin{aligned} \mathcal {K}(s,u) = 2^{2j} \int e^{i2^j(s\xi _1+u\xi _2)}\phi _0(\xi )E_N(2^jt\sqrt{2s}|\xi |)d\xi . \end{aligned}$$

Since $s\sim 2^{2k}$, using (3.2), we have $|\mathcal {K}(s,u)|\lesssim 2^{2j}(1+2^j|(s,u)|)^{-M}2^{-N(j+k)}$ for $1\le M\le 4$ via integration by parts. Thus, we have $\Vert \phi _k(\sqrt{2s})\mathcal {K}(s+\frac{t^2}{2}, u) \Vert _{L^r_{s,u}}\le C 2^{-N(j+k)}2^{2j(1-\frac{1}{r})}$ for $1<t<2$ with a positive constant C. Young’s convolution inequality gives $\Vert \phi _k(\sqrt{2s}){\mathcal {E}}_t \mathcal {P}_j g(\sqrt{2s},x_3)\Vert _{L^q_{s,x_3,t}}\lesssim 2^{-N(j+k)}2^{2j(\frac{1}{p}-\frac{1}{q})}\Vert g\Vert _{L^p}$. Thus, reversing $s\rightarrow r^2/2$, after a simple manipulation we get

$$\begin{aligned} \Big \Vert \phi _k(r){\mathcal {E}}_t\mathcal {P}_j g \Big \Vert _{L^q_{r,x_3,t}}\lesssim 2^{-(N-2)(j+k)} 2^{k(\frac{1}{q}-\frac{2}{p})}\Vert g\Vert _{L^p} \end{aligned}$$

(3.5)

for $1\le p\le q\le \infty .$ Indeed, we need only note that $2j(\frac{1}{p}-\frac{1}{q})-\frac{k}{q}\le 2(j+k)+k( \frac{1}{q}-\frac{2}{p})$ because $j\ge -k$ and $\frac{1}{p}-\frac{1}{q}-1<0$.

We now consider $\phi _k(r)\partial _t {\mathcal {E}}_t \mathcal {P}_j g$. Note that

$$\begin{aligned} \partial _t {\mathcal {E}}_t g (r,x_3) = \int e^{i(\frac{r^2+t^2}{2}\xi _1+x_3\xi _2)}\big (t\xi _1 E_N(tr|\xi |)+ r|\xi |E_N'(tr|\xi |)\big ) \widehat{g}(\xi ) d\xi . \end{aligned}$$

(3.6)

Using (3.2), we can handle $\phi _k(r)\partial _t {\mathcal {E}}_t \mathcal {P}_j g$ similarly as before. In fact, since $|t\xi _1|\lesssim 2^j$ and $r|\xi |\sim 2^{k+j}$, we see

$$\begin{aligned} \Big \Vert \phi _k(r) \partial _t {\mathcal {E}}_t \mathcal {P}_j g \Big \Vert _{L^q_{r,x_3}} \lesssim 2^{-(N-2)(j+k)}2^{k(\frac{1}{q}-\frac{2}{p})}(2^{j+k}+2^j)\Vert g\Vert _{L^p}. \end{aligned}$$

Hence, combining this and (3.5) with Lemma 2.3, we get (3.4) for $k\ge -2$.

We now consider the case $k< -2$. We first claim that

$$\begin{aligned} \Vert \phi _k(r){\mathcal {E}}_t\mathcal {P}_j g\Vert _{L^q_{r,x_3,t}}\lesssim 2^{-(N-2)(j+k)}2^{k(\frac{2}{q}-\frac{2}{p})}\Vert g\Vert _{L^p}. \end{aligned}$$

(3.7)

We use the transformation (2.8). By (2.9) we have $|\frac{\partial (y_1,y_2,\tau )}{\partial (r,x_3,t)}|\sim 1$. Therefore,

$$\begin{aligned} \Vert \phi _k(r){\mathcal {E}}_t\mathcal {P}_j g\Vert _{L^q_{r,x_3,t}}\lesssim \Bigg ( \int \Big | \phi _k(r(y,\tau )) \widetilde{K}(\cdot ,\tau )*g(y) \Big |^qdy d\tau \Bigg )^{\frac{1}{q}}, \end{aligned}$$

where

$$\begin{aligned} \widetilde{K}(y,\tau )=\int e^{iy\cdot \xi }\phi _j(\xi )E_N(\tau |\xi |)d\xi . \end{aligned}$$

Note that $\tau \sim 2^k$. Changing $\tau \mapsto 2^k\tau$ and $\xi \mapsto 2^j\xi$, using (3.2) and integration by parts, we have $|\widetilde{K}(y,2^k\tau )|\le C 2^{2j}(1+2^j|y|)^{-M}2^{-N(j+k)}$ for $1\le M\le 4$ and $1<\tau <2$. Young’s convolution inequality gives

$$\begin{aligned} \Vert \phi _k(r){\mathcal {E}}_t\mathcal {P}_j g \Vert _{L^q_{r,x_3,t}}\lesssim 2^{-N(j+k)}2^{2j(\frac{1}{p}-\frac{1}{q})}\Vert g\Vert _{L^p}. \end{aligned}$$

Thus, we get (3.7). As for $\phi _k(r)\partial _t {\mathcal {E}}_t \mathcal {P}_j g$, we use (3.6) and repeat the same argument to see $\Vert \phi _k(r)\partial _t {\mathcal {E}}_t\mathcal {P}_j g \Vert _{L^q_{r,x_3,t}}\lesssim 2^{-N(j+k)} 2^j 2^{2j(\frac{1}{p}-\frac{1}{q})}\Vert g\Vert _{L^p}$ since $|t\xi _1|\lesssim 2^j$, $r|\xi |\sim 2^{k+j}$, and $k<-2$. Thus, we get

$$\begin{aligned} \Vert \phi _k(r)\partial _t {\mathcal {E}}_t\mathcal {P}_j g \Vert _{L^q_{r,x_3,t}} \lesssim 2^{-(N-2)(j+k)} 2^k 2^{k(\frac{2}{q}-\frac{2}{p})}\Vert g\Vert _{L^p}. \end{aligned}$$

Putting (3.7) and this together, by Lemma 2.3 we obtain (3.4) for $k<-2$. $\square$

By (3.1) and Lemma 3.3, to prove Propositions 2.1 and 2.2 we only have to consider contributions from the remaining $C^\pm _j |tr\xi |^{-\frac{1}{2}-j} e^{ \pm i|tr\xi |},$ $j=0,\ldots , N$. To this end, it is sufficient to consider the major term $C^\pm _0 |tr\xi |^{-\frac{1}{2}} e^{ \pm i|tr\xi |}$ since the other terms can be handled similarly. Furthermore, by reflection $t\rightarrow -t$ it is enough to deal with $|tr\xi |^{-\frac{1}{2}} e^{i|tr\xi |}$ since the estimate (3.3) clearly holds with the interval [1, 2] replaced by $[-2,-1]$.

Let us set

$$\begin{aligned} {\mathcal {U}}_t g(r,x_3) = \int e^{i(\frac{r^2+t^2}{2}\xi _1+x_3\xi _2+ tr|\xi |)} |r\xi |^{-\frac{1}{2}} \widehat{g}(\xi ) d\xi . \end{aligned}$$

(3.8)

To complete the proof of Proposition 2.1, we need to show

$$\begin{aligned} \Big \Vert \sup _{1<t<2} | \phi _k(r) {\mathcal {U}}_t \mathcal P_{\!j}g | \Big \Vert _{L^q_{r,x_3}} \lesssim {\left\{ \begin{array}{ll} 2^{(j+k)(\frac{3}{2p}-\frac{1}{2q}-\frac{1}{2}+\epsilon )+\frac{k}{q}-\frac{2k}{p}}\Vert g\Vert _{L^p}, &{} \ \ \ k\ge 2,\\ 2^{(j+k)(\frac{3}{2p}-\frac{1}{2q}-\frac{1}{2}+\epsilon )+\frac{2k}{q}-\frac{2k}{p}}\Vert g\Vert _{L^p}, &{} \ k\le -2. \end{array}\right. } \end{aligned}$$

(3.9)

Using Lemma 2.3, the matter is reduced to obtaining estimates for $\phi _k(r){\mathcal {U}}_t \mathcal P_{\!j}g$ and $\phi _k(r) \partial _t {\mathcal {U}}_t \mathcal P_{\!j}g$ in $L^q_{r,x_3,t}$. Note that

$$\begin{aligned} \partial _t{\mathcal {U}}_t \mathcal P_{\!j}g (r,x_3,t)=\int e^{i(\frac{r^2+t^2}{2}\xi _1+x_3\xi _2+ tr|\xi |)}\widehat{\mathcal P_{\!j}g}(\xi )\frac{t\xi _1+ r|\xi |}{|r\xi |^{1/2}} d\xi . \end{aligned}$$

(3.10)

By the Mikhlin multiplier theorem one can easily see

$$\begin{aligned} \Vert \phi _k(r) \partial _t{\mathcal {U}}_t \mathcal P_{\!j}g\Vert _{L^q_{r,x_3,t}} \lesssim {\left\{ \begin{array}{ll} 2^{j+k}\Vert \phi _k(r) {\mathcal {U}}_t \mathcal P_{\!j}g \Vert _{L^q_{r,x_3,t}}, \quad &{} k\ge 0, \\ 2^{j}\Vert \phi _k(r) {\mathcal {U}}_t \mathcal P_{\!j}g \Vert _{L^q_{r,x_3,t}}, \quad &{} k< 0, \end{array}\right. } \end{aligned}$$

where $L^q_{r,x_3,t}$ denotes $L^q_{r,x_3,t}({\mathbb {R}}^2\times [1,2])$. Therefore, by Lemma 2.3 it is sufficient for (3.9) to prove that

$$\begin{aligned} \Vert \phi _k(r) {\mathcal {U}}_t \mathcal P_{\!j}g \Vert _{L^q_{r,x_3,t}}\lesssim \ {\left\{ \begin{array}{ll} 2^{(j+k)(\frac{3}{2p}-\frac{3}{2q}-\frac{1}{2}+\epsilon )+\frac{k}{q}-\frac{2k}{p}}\Vert g\Vert _{L^p}, \quad &{} \ \ k\ge 2, \\ 2^{(j+k)(\frac{3}{2p}-\frac{3}{2q}-\frac{1}{2}+\epsilon )+\frac{3k}{q}-\frac{2k}{p}}\Vert g\Vert _{L^p} , \quad &{} k\le - 2. \end{array}\right. } \end{aligned}$$

We first consider the case $k\ge 2$. As before, we use the change of variables (2.8). Since $|\!\det \frac{\partial (y_1, y_2, \tau )}{\partial (r,x_3,t)}|\sim 2^{2k}$ from (2.9) and since $\tau =rt$ and $1<t<2$, we have

$$\begin{aligned} \big \Vert \phi _k(r) {\mathcal {U}}_t \mathcal P_{\!j}g\big \Vert _{L^q_{r,x_3,t}}\lesssim 2^{-\frac{2k}{q}-\frac{j+k}{2}}\big \Vert e^{i\tau \sqrt{-\Delta }} \mathcal {P}_jg \big \Vert _{{L^q_{y,\tau }({\mathbb R}^2\times [2^{k-1},2^{k+2}])}} \end{aligned}$$

since $|r\xi |\sim 2^{j+k}$. Thus, Corollary 3.2 gives the desired estimate (3.9) for $k\ge 2$. The case $k\le -2$ can be handled in the exactly same manner. The only difference is that $|\!\det \frac{\partial (y_1, y_2, \tau )}{\partial (r,x_3,t)}| \sim 1$. Thus, the desired estimate (3.9) immediately follows from Corollary 3.2.

3.3 Proof of Proposition 2.2

As mentioned already, the determinant of the Jacobian ${\partial (y_1, y_2, \tau )}/{\partial (r,x_3,t)}$ may vanish when $|k|\le 1$. So, we need additional decomposition depending on $|r-t|$. We also make decomposition in $\xi$ depending on $|\xi |^{-1}{\xi _1}+1$ to control the size of the multiplier $\left| t\xi _1+r|\xi | \right|$ in a more accurate manner (for example, see (3.22)).

For $m\ge 0$ let us set

$$\begin{aligned} \psi _m(\xi )&=\phi \big (2^m\big | |\xi |^{-1} \xi _1 +1\big |\big ),\\ \psi ^m(\xi )&=1-\sum _{0\le j <m}\psi _j(\xi ), \end{aligned}$$

so that $\sum _{0\le k <m}\psi _k+ \psi ^m=1$. We additionally define

$$\begin{aligned} {\mathcal {P}}_{\!j,m} g= ( \phi _j \psi _m \widehat{g})^\vee , \quad {\mathcal {P}}_{\!j}^{m} g= ( \phi _j \psi ^m\, \widehat{g})^\vee . \end{aligned}$$

So it follows that

$$\begin{aligned} \mathcal P_{\!j}=\sum _{0\le k <m} {\mathcal {P}}_{\!j,k}+ {\mathcal {P}}_{\!j}^{m}. \end{aligned}$$

(3.11)

Proposition 3.4

Let us set $\phi _{k,l}(r,t)= \phi _k(r)\phi (2^l|r-t|).$ Let $j\ge -1$ and $k=-1,0,1$. Suppose (2.6) holds. Then, for $\epsilon >0$ we have

$$\begin{aligned} \Vert \phi _{k,l} {\mathcal {U}}_t {\mathcal {P}}_{\!j,m}g\Vert _{L^q_{r,x_3,t}}\lesssim 2^{-\frac{j}{2}} 2^{\frac{l}{q}} 2^{(\frac{m}{2}-l)(\frac{1}{p}+\frac{3}{q}-1)+\frac{3j}{2}(\frac{1}{p}-\frac{1}{q})+\epsilon j}\Vert g\Vert _{L^p}. \end{aligned}$$

(3.12)

In order to prove Proposition 3.4, we make the change of variables (2.8). Since $|k|\le 1$, we need only to consider (r, t) contained in the set $[2^{-1} -10^{-2},2^2+10^2]\times [1,2]$. Set

$$\begin{aligned} S_l=\big \{( y_1, y_2, \tau ): 2^{-2l-1}\le |y_1-\tau |\le 2^{-2l+1}, \ y_1, \tau \in [2^{-3}, 2^3] \big \}. \end{aligned}$$

By (2.8) $y_1-\tau =(r-t)^2/2$. From (2.9) we note $|\!\det \frac{\partial (y_1, y_2, \tau )}{\partial (r,x_3,t)}|\sim 2^{-l}$ if $(y_1,\tau )\in S_l$. Thus, changing variables $(r,x_3,t)\rightarrow (y_1, y_2, \tau )$ we obtain

$$\begin{aligned} \Vert \phi _{k,l} {\mathcal {U}}_t \mathcal P_{\!j}h \Vert _{L^q_{r,x_3,t}}\lesssim 2^{-\frac{1}{2} j} 2^{\frac{l}{q}} \Vert e^{i\tau \sqrt{-\Delta }} \mathcal P_{\!j}h \Vert _{L^q_{y,\tau }(S_l)}. \end{aligned}$$

(3.13)

Therefore, for (3.12) it is sufficient to show

$$\begin{aligned} \Vert e^{i\tau \sqrt{-\Delta }} {\mathcal {P}}_{\!j,m}g\Vert _{L^q_{y,\tau }(S_l)}&\lesssim 2^{(\frac{m}{2}-l)(\frac{1}{p}+\frac{3}{q}-1)+\frac{3j}{2}(\frac{1}{p}-\frac{1}{q})+\epsilon j}\Vert g\Vert _{L^p} \end{aligned}$$

(3.14)

for p, q satisfying (2.6). For the purpose we need the following lemma, which gives an improved $L^2$ estimate thanks to restriction of the integral over $S_l$. Indeed, one can remove the localization $y_1,\tau \in [2^{-3},2^3]$.

Lemma 3.5

Let $D_l=\{(x_1,x_2,t): 2^{-2l}\le |x_1-t|\le 2^{-2l+1} \}$. Then, we have

$$\begin{aligned} \left\| \int e^{i(x\cdot \xi +t|\xi |)}\widehat{g}(\xi )\psi _m(\xi )d\xi \right\| _{L^2_{x,t}(D_l)}\lesssim 2^{\frac{m}{2}-l}\Vert g\Vert _{L^2}. \end{aligned}$$

(3.15)

Proof

We write $x\cdot \xi +t|\xi |=x_1(\xi _1+|\xi |)+ x_2\xi _2+(t-x_1)|\xi |.$ Then, changing variables $(x,t-x_1) \rightarrow (x, t)$ and $\xi \rightarrow \eta := \mathcal L(\xi )=(\xi _1+|\xi |,\xi _2),$ we see

$$\begin{aligned} \left\| \int e^{i(x\cdot \xi +t|\xi |)}\widehat{g}(\xi )\psi _m(\xi )d\xi \right\| _{L^2_{x,t}(D_l)} \le \Big \Vert \int e^{i(x\cdot \eta +t|\mathcal {L}^{-1}\eta |)}\frac{\widehat{h}(\mathcal {L}^{-1}\eta )}{|\!\det J\mathcal {L}(\eta )|} d\eta \Big \Vert _{L^2_{x,t}({\mathbb R}^2\times I_l)} \end{aligned}$$

where $\widehat{h}(\xi )=\widehat{g}(\xi )\psi _m(\xi )$ and $I_l=[-2^{-2l+1},-2^{-2l}]\cup [2^{-2l},2^{-2l+1}].$ By Plancherel’s theorem in the $x-$variable and integrating in t, we have

$$\begin{aligned} \left\| \int e^{i(x\cdot \xi +t|\xi |)}\widehat{g}(\xi )\psi _m(\xi )d\xi \right\| _{L^2_{x,t}(D_l)} \le C2^{-l}\Big \Vert \frac{\widehat{h}(\mathcal {L}^{-1}\cdot )}{|\!\det J\mathcal {L}|} \Big \Vert _{L^2_x}. \end{aligned}$$

A computation shows $\det J\mathcal {L}=1+|\xi |^{-1}{\xi _1}$, so $|\!\det J\mathcal {L}| \sim 2^{-m}$ on the support of $\widehat{h}$. Thus, by changing variables and Plancherel’s theorem we get (3.15). $\square$

We also use the following elementary lemma.

Lemma 3.6

For any $1\le p\le \infty$, j, and m, we have

$$\begin{aligned} \Vert ( \phi _j\psi _m \widehat{g}\,)^{\vee } \Vert _{L^p}\lesssim \Vert g \Vert _{L^p}, \quad \Vert ( \phi _j\psi ^m \widehat{g}\,)^{\vee }\Vert _{L^p}\lesssim \Vert g \Vert _{L^p}. \end{aligned}$$

Proof

Since $\psi ^m- \psi ^{m+1}=\psi _m$, it suffices to prove the second inequality only. By Young’s inequality we need only to show $\Vert (\phi _j\psi ^m)^{\vee }\Vert _{L^1}\lesssim 1.$ By scaling it is clear that $\Vert (\phi _j(\xi )\psi ^m(\xi ))^{\vee }\Vert _{L^1}=\Vert (\phi _0(\xi )\psi ^m(\xi ))^{\vee }\Vert _{L^1}.$ Note that $\mathfrak m(\xi ):=\phi _0(\xi )\psi ^m(\xi )$ is supported in a rectangular box with dimensions $2^{-m}\times 1$. So, $\mathfrak m(\xi _1, 2^{-m}\xi _2)$ is supported in a cube of side length $\sim 1$ and it is easy to see $\partial _\xi ^\alpha (\mathfrak m(\xi _1, 2^{-m}\xi _2))$ is uniformly bounded for any $\alpha$. This gives $\Vert (\mathfrak m(\cdot , 2^{-m}\cdot ))^\vee \Vert _1\lesssim 1$. Therefore, after scaling we get $\Vert (\phi _0(\xi )\psi ^m(\xi ))^{\vee }\Vert _{L^1}\lesssim 1.$ $\square$

Proof of 3.14

In view of interpolation the estimate (3.14) follows for p, q satisfying (2.6) if we show the next three estimates:

$$\begin{aligned}&\Vert e^{i\tau \sqrt{-\Delta }} {\mathcal {P}}_{\!j,m}g \Vert _{L^2_{y,\tau }(S_l)} \lesssim 2^{\frac{m}{2}-l}\Vert g\Vert _{L^2}, \end{aligned}$$

(3.16)

$$\begin{aligned}&\Vert e^{i\tau \sqrt{-\Delta }} {\mathcal {P}}_{\!j,m}g \Vert _{L^\infty _{y,\tau }(S_l)}\lesssim 2^{\frac{3j}{2}}\Vert g\Vert _{L^1},\\ \nonumber&\Vert e^{i\tau \sqrt{-\Delta }} {\mathcal {P}}_{\!j,m}g \Vert _{L^4_{y,\tau }(S_l)} \lesssim 2^{\epsilon j}\Vert g\Vert _{L^4}. \end{aligned}$$

(3.17)

The first estimate follows from Lemma 3.5. Corollary 3.2 and Lemma 3.6 give the other two estimates. $\square$

It is possible to improve the estimate (3.12) when $j>m$.

Proposition 3.7

Let $j\ge -1$ and $k=-1,0,1$. Suppose $1\le p\le q$, $1/{p}+1/{q}\le 1$, and $j>m$, then

$$\begin{aligned} \Vert \phi _{k,l} {\mathcal {U}}_t \mathcal {P}_{j,m}g\Vert _{L^q_{r,x_3,t}}\lesssim 2^{-\frac{j}{2}}2^{\frac{l}{q}}2^{\frac{2}{q}(\frac{m}{2}-l)+\frac{j-m}{2}(1-\frac{1}{p}-\frac{1}{q})+\frac{3j}{2}(\frac{1}{p}-\frac{1}{q})}\Vert g\Vert _{L^p}. \end{aligned}$$

Proof

By (3.13) it is sufficient to show

$$\begin{aligned} \Vert e^{i\tau \sqrt{-\Delta }} {\mathcal {P}}_{\!j,m}g\Vert _{{L^q_{y,\tau }(S_l)}}\lesssim 2^{\frac{2}{q}(\frac{m}{2}-l)+\frac{j-m}{2}(1-\frac{1}{p}-\frac{1}{q})+\frac{3j}{2}(\frac{1}{p}-\frac{1}{q})}\Vert g\Vert _{L^p} \end{aligned}$$

for p, q satisfying $1\le p\le q$, $1/{p}+1/{q}\le 1$. In fact, by interpolation with the estimates (3.16) and (3.17) we only have to show

$$\begin{aligned} \Vert e^{i\tau \sqrt{-\Delta }} {\mathcal {P}}_{\!j,m}g \Vert _{L^\infty _{y,\tau }(S_l)} \lesssim 2^{\frac{j-m}{2}}\Vert g\Vert _{L^\infty }. \end{aligned}$$

(3.18)

Let us set

$$\begin{aligned} K^{j,m}_t(x)= \frac{1}{(2\pi )^2}\int e^{i(x\cdot \xi +t|\xi |)}\phi _j(|\xi |)\psi _m(\xi )d\xi . \end{aligned}$$

Then $e^{i\tau \sqrt{-\Delta }} {\mathcal {P}}_{\!j,m}g = K^{j,m}_\tau *g .$ Therefore, (3.18) follows if we show

$$\begin{aligned} \Vert K^{j,m}_t \Vert _{L^1_x}\lesssim 2^{\frac{j-m}{2}} \end{aligned}$$

(3.19)

when $t\sim 1$. Note that $|\xi _2|/|\xi |=\sqrt{1-\xi _1/|\xi |}\sqrt{1+\xi _1/|\xi |}\lesssim 2^{-\frac{m}{2}}$ if $\xi \in {\text {supp}}\psi _m$. So, ${\text {supp}}\psi _m$ is contained in a conic sector with angle $\sim 2^{-\frac{m}{2}}$. Let $\mathcal {S}$ be a sector centered at the origin in ${\mathbb R}^2$ with angle $\sim 2^{-\frac{j}{2}}$ and $\phi _\mathcal {S}$ be a cut-off function adapted to $\mathcal {S}$. Then, by integration by parts it follows that

$$\begin{aligned} \Big \Vert \int e^{i(x\cdot \xi +t|\xi |)}\phi _j(|\xi |)\phi _\mathcal {S}(\xi )d\xi \Big \Vert _{L^1_x}\lesssim 1 \end{aligned}$$

if $t\sim 1$. (See, for example, [8]). Now (3.19) is clear since the support of $\psi _m$ can be decomposed into as many as $C2^{\frac{j-m}{2}}$ such sectors. $\square$

Finally, we prove Proposition 2.2 making use of Propositions 3.4 and 3.7. We recall (2.2) and (3.1). As mentioned before, by Lemma 3.3 we need only to consider ${\mathcal {U}}_t$ (see (3.8)) and it is sufficient to show

$$\begin{aligned} \big \Vert \sup _{1<t<2}| \phi _k(r) {\mathcal {U}}_t \mathcal P_{\!j}g| \big \Vert _{L^q_{r,x_3}}\lesssim 2^{ \frac{1}{2} (\frac{3}{p}-\frac{1}{q}-1)j +\epsilon j}\Vert g\Vert _{L^p} \end{aligned}$$

(3.20)

for p, q satisfying $p\le q$, $1/{p}+1/{q}< 1$ and $1/{p}+2/{q}> 1$.

Proof of 3.20

Let us set $\phi ^l(\cdot )=1-\sum _{j=0}^{l-1} \phi (2^j\cdot )$ and $\phi _k^l(r,t)=\phi _k(r)\phi ^l(|r-t|)$. Then, we decompose

$$\begin{aligned} \phi _k(r)=\sum _{0\le l\le j/2} \phi _{k,l}(r,t) + \sum _{j/2< l< j}^{} \phi _{k,l}(r,t) + \phi ^j_k(r,t). \end{aligned}$$

Combining this with (3.11) and using $\sum _{\frac{j}{2}<l< j} \phi _{k,l}+ \phi ^j_k\le \phi _{k}^{[j/2]-1}$, by the triangle inequality we have

$$\begin{aligned}&\big \Vert \sup _{1<t<2}| \phi _k(r) {\mathcal {U}}_t \mathcal P_{\!j}g| \big \Vert _{L^q} \le \sum _{i=1}^5 S_i, \end{aligned}$$

where

$$\begin{aligned} S_1&= \sum _{0\le l\le j/2}\, \sum _{0\le m\le l-1} \big \Vert \sup _{1<t<2} \phi _{k,l} |{\mathcal {U}}_t {\mathcal {P}}_{\!j,m}g |\big \Vert _{L^q}, \quad S_2=\sum _{0\le l\le j/2}\Vert \sup _{1<t<2}\phi _{k,l} |{\mathcal {U}}_t \mathcal {P}_j^l g| \Vert _{L^q}, \\ S_3&=\sum _{\frac{j}{2}<l< j}\,\sum _{0\le m\le j-1}\Vert \sup _{1<t<2} \phi _{k,l} |{\mathcal {U}}_t {\mathcal {P}}_{\!j,m}g |\Vert _{L^q} , \quad \ S_4= \sum _{0\le m\le j-1} \Vert \sup _{1<t<2} \phi _{k}^j |{\mathcal {U}}_t {\mathcal {P}}_{\!j,m}g | \Vert _{L^q}, \\&\qquad \qquad \qquad \qquad \qquad S_5=\Vert \sup _{1<t<2} \phi _{k}^{[j/2]-1} |{\mathcal {U}}_t \mathcal P_{\!j}^jg | \Vert _{L^q}. \end{aligned}$$

The proof of (3.20) is now reduced to showing

$$\begin{aligned} S_i \lesssim 2^{ \frac{1}{2} (\frac{3}{p}-\frac{1}{q}-1)j +\epsilon j}\Vert g\Vert _{L^p}, \quad 1\le i\le 5, \end{aligned}$$

(3.21)

for p, q satisfying $p\le q$, $1/{p}+1/{q}< 1$ and $1/{p}+2/{q}> 1$.

Before we start the proof of (3.21), we briefly comment on the decomposition $S_i$, $i=1,\ldots , 5$. As for $S_4$ and $S_5$, which are easier to handle, the sizes of $r-t$ and $|\xi |^{-1}\xi _1+1$ are sufficiently small on the supports of the associated multipliers, so we can remove the dependence of t by an elementary argument. For $S_1, S_2,$ and $S_3$, we use Lemma 2.3 combined with (3.10) to control the maximal operators. Different magnitudes of contribution come from $\partial _t\phi _{k,l}=O(2^l)$ and $|t\xi _1+r|\xi ||$, so we need to compare them. Writing $t\xi _1+r|\xi |= t\big ( |\xi |^{-1} \xi _1 +1\big )+(r-t)$, we note

$$\begin{aligned} | t\xi _1+r|\xi || \lesssim 2^j\max \{ 2^{-m}, 2^{-l}\}. \end{aligned}$$

(3.22)

The decompositions in $S_1, S_2,$ and $S_3$ are made according to comparative sizes of $\partial _t\phi _{k,l}=O(2^l)$ and $|t\xi _1+r|\xi ||$ in terms of l, m,  and j.

We first consider $S_1$. Using Lemma 2.3, we need to estimate $\phi _{k,l} {\mathcal {U}}_t {\mathcal {P}}_{\!j,m}g$ and $\partial _t (\phi _{k,l} {\mathcal {U}}_t {\mathcal {P}}_{\!j,m}g)$ in $L^q_{r,x_3,t}({\mathbb {R}}^2\times [1,2])$. Note that $\partial _t \phi _{k,l}=O(2^l)$ and $2^l\lesssim 2^{j-m}$. Thus, recalling (3.10), we apply Lemma 2.3 and the Mikhlin multiplier theorem to get

$$\begin{aligned} S_1\lesssim \sum _{0\le l\le j/2} \sum _{m=0}^{l-1} 2^{\frac{j-m}{q}} \big \Vert \phi _{k,l} {\mathcal {U}}_t {\mathcal {P}}_{\!j,m}g \big \Vert _{L^q}. \end{aligned}$$

Thus, by Proposition 3.4 it follows that

$$\begin{aligned} S_1&\lesssim 2^{-\frac{j}{2}+\frac{j}{q}+\frac{3j}{2}(\frac{1}{p}-\frac{1}{q})+\epsilon j} \sum _{0\le l\le j/2} 2^{l(1-\frac{1}{p}-\frac{2}{q})}\sum _{m=0}^{l-1}2^{\frac{m}{2}(\frac{1}{p}+\frac{1}{q}-1)}\Vert g\Vert _{L^p}. \end{aligned}$$

Since $1/{p}+1/{q}-1< 0$ and $1/p+2/q>1$, we obtain (3.21) with $i=1$.

We can show the estimate (3.21) with $i=2$ in the same manner. As before, since $\partial _t \phi _{k,l}=O(2^l)$ and $2^l\lesssim 2^{j-l}$, using (3.22), Lemma 2.3, and the Mikhlin multiplier theorem, we have

$$\begin{aligned} S_2\lesssim \sum _{0\le l\le j/2} 2^{\frac{j-l}{q}} \big \Vert \phi _{k,l} {\mathcal {U}}_t \mathcal P_{\!j}^l g \big \Vert _{L^q}. \end{aligned}$$

Thus, by (3.13) and Theorem 3.1, we have $S_2\lesssim \sum _{0\le l\le \frac{j}{2}} 2^{-\frac{j}{2}} 2^{\frac{j}{q}+\frac{3j}{2}(\frac{1}{p}-\frac{1}{q})+\frac{\epsilon }{2} j}\Vert g\Vert _{L^p},$ which gives (3.21) with $i=2$.

We now consider $S_3$, which we handle as before. Since $j<2l$, $2^j\max \lbrace 2^{-m},2^{-l}\}\le 2^l$ if $l+m\ge j$. Similarly, $2^{j-m}\ge 2^j\max \lbrace 2^{-m},2^{-l} \rbrace$ and $2^{j-m}\ge 2^l$ if $l+m< j$. Using (3.22) and (3.10), we see

$$\begin{aligned} S_3 \lesssim \sum _{\begin{array}{c} j/2<l< j \end{array}}\Bigg ( \sum _{ j-l\le m\le j-1} 2^{\frac{l}{q}}\Vert \phi _{k,l} {\mathcal {U}}_t {\mathcal {P}}_{\!j,m}g \Vert _{L^q}+\sum _{0\le m<j-l}2^{\frac{j-m}{q}} \Vert \phi _{k,l} {\mathcal {U}}_t {\mathcal {P}}_{\!j,m}g \Vert _{L^q} \Bigg ) \end{aligned}$$

Since $1/p+2/q>1$, using Proposition 3.7, we get (3.21) for $i=3$.

We handle $S_4$ and $S_5$ in an elementary way without relying on Lemma 2.3. Instead, we can control $S_4$ and $S_5$ more directly. Concerning $S_4$ we claim that

$$\begin{aligned} S_4\lesssim 2^{ \frac{1}{2} (\frac{3}{p}-\frac{1}{q}-1)j }\Vert g\Vert _{L^p} \end{aligned}$$

(3.23)

if ${5}/{q}> 1+{1}/{p}$ and $2\le p\le q\le \infty$. This clearly gives (3.21) with $i=4$ for p, q satisfying $p\le q$, $1/{p}+1/{q}< 1$ and $1/{p}+2/{q}> 1$. We note that

$$\begin{aligned} |\phi _{k}^j {\mathcal {U}}_t {\mathcal {P}}_{\!j,m}g (r,x_3)|\lesssim 2^{-\frac{1}{2} j}\Big |\phi _{k}^j \int e^{i2^j(r^2\xi _1+x_3\xi _2+ r^2|\xi |)} \mathfrak m(\xi )\phi _0(\xi )\psi _m(\xi )\widehat{g(2^{-j}\cdot )}(\xi )d\xi \Big |, \end{aligned}$$

where

$$\begin{aligned} \mathfrak m(\xi )= e^{i2^j(\frac{t^2-r^2}{2}\xi _1+ (t-r)r|\xi |)}|\xi |^{-\frac{1}{2}} \widetilde{\phi }_0(\xi ), \end{aligned}$$

and $\widetilde{\phi }_0$ is a smooth function supported in $[-\pi , \pi ]^2$ such that $\widetilde{\phi }_0\phi _0=1$. If $(r,t)\in {\text {supp}}\phi _{k}^j$, then $|t-r|\lesssim 2^{-j}$. Thus, $|\partial _\xi ^\alpha m(\xi )|\lesssim 1$ for any $\alpha$. We remove the dependence of t by using a bound on the coefficient of Fourier series, not the Sobolev embedding. Expanding $\mathfrak m$ into Fourier series on $[-\pi , \pi ]^2$ we have $\mathfrak m(\xi )= \sum _{k\in {\mathbb {Z}}^2} C_{\textbf{k}} (r,t) e^{i\textbf{k}\cdot \xi }$ while $|C_{\mathbf{k}} (r,t)|\lesssim (1+|\mathbf{k}|)^{-N}$. Since $1<t<2$, the estimate (3.23) follows after scaling $\xi \rightarrow 2^j\xi$ if we obtain

$$\begin{aligned} \Vert {\mathcal {R}} {\mathcal {P}}_{\!j,m}g\Vert _{L^q_{r,x_3}([2^{-2}, 2^3]\times {\mathbb {R}})} \lesssim 2^{ \frac{1}{2} (\frac{3}{p}-\frac{1}{q})j }\Vert g\Vert _{L^p}, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {R}} g(r,x_3)=\int e^{i(r^2\xi _1+x_3\xi _2+ r^2|\xi |)} \widehat{g}(\xi )d\xi . \end{aligned}$$

When $q=2$, changing variables $r^2\rightarrow r$ and following the argument in the proof of Lemma 3.5 we have $\Vert {\mathcal {R}} {\mathcal {P}}_{\!j,m}g\Vert _{L^2_{r,x_3}([2^{-2}, 2^3]\times {\mathbb {R}})} \lesssim 2^{{m}/{2}}\Vert g\Vert _{L^2}.$ On the other hand, (3.18) gives $\Vert {\mathcal {R}} {\mathcal {P}}_{\!j,m}g\Vert _{L^\infty _{r,x_3}([2^{-2}, 2^3]\times {\mathbb {R}})}\lesssim 2^{(j-m)/{2}}\Vert g\Vert _{L^\infty }.$ Interpolation between these two estimates gives

$$\begin{aligned} \Vert {\mathcal {R}}{\mathcal {P}}_{\!j,m}g\Vert _{L^q_{r,x_3}([2^{-2}, 2^3]\times {\mathbb {R}})} \lesssim 2^{\frac{m}{q}+\frac{j-m}{2}(1-\frac{2}{q})}\Vert g\Vert _{L^q} \end{aligned}$$

for $2\le q\le \infty$. Since the support $\widehat{{\mathcal {P}}_{\!j,m}g}(\xi )$ is contained in a rectangular region of dimensions $2^j\times 2^{j-\frac{m}{2}}$, by Bernstein’s inequality we have

$$\begin{aligned} \Vert {\mathcal {R}}_m^j g\Vert _{L^q_{r,x_3}([2^{-2}, 2^3]\times {\mathbb {R}})}\lesssim 2^{j(\frac{2}{p}-\frac{3}{q})+m(\frac{5}{2q}-\frac{1}{2}-\frac{1}{2p})}\Vert g\Vert _{L^p} \end{aligned}$$

for $2\le p\le q\le \infty$. Since ${5}/{q}> 1+{1}/{p}$, this proves the claimed estimate (3.23).

Finally, we show (3.21) with $i=5$. Changing variables $(\xi _1, \xi _2)\rightarrow (2^j\xi _1, \xi _2)$, we observe

$$\begin{aligned} \phi _{k}^{[j/2]-1} | {\mathcal {U}}_t \mathcal P_{\!j}^j g (r,x_3)|\lesssim 2^{\frac{j}{2}}\phi _{k}^{[j/2]-1} \Big |\int e^{i(\frac{(r-t)^2}{2} 2^j\xi _1+x_3\xi _2)} \mathfrak m(\xi )\widehat{{\mathcal {P}}_j^j g}(2^j\xi _1, \xi _2)d\xi \Big |, \end{aligned}$$

where

$$\begin{aligned} \widetilde{\mathfrak m}(\xi )= e^{i2^j rt( |(\xi _1, 2^{-j}\xi _2)|-\xi _1)}|(\xi _1, 2^{-j}\xi _2)|^{-\frac{1}{2}} \widetilde{\phi }_0(|(\xi _1, 2^{-j}\xi _2)|) \psi ^{j-1}(2^j\xi _1, \xi _2). \end{aligned}$$

Note that ${\text {supp}}\widetilde{\mathfrak m}\subset \{ \xi _1\in [2^{-1}, 2^2] , |\xi _2| \le 2^2 \}$. Since $|\partial _\xi ^\alpha m(\xi )|\lesssim 1$ for any $\alpha$, expanding $\widetilde{\mathfrak m}$ into Fourier series on $[-2\pi , 2\pi ]^2$ we have $\widetilde{\mathfrak m}(\xi )= \sum _{k\in {\mathbb {Z}}^2} C_{\textbf {k}} (r,t) e^{i 2^{-1}\textbf{k}\cdot \xi }$ while $|C_{\mathbf {k}} (r,t)|\lesssim (1+|\mathbf{k}|)^{-N}$. Hence, similarly as before, changing variables $(\xi _1, \xi _2)\rightarrow (2^{-j}\xi _1, \xi _2)$, to show (3.21) with $i=5$ it is sufficient to obtain

$$\begin{aligned} \Bigg \Vert \sup _{1<t<2} \mathcal {P}_j^j g\Big (\frac{(r-t)^2}{2},x_3\Big ) \Bigg \Vert _{L^q_{r,x_3}([2^{-2}, 2^3]\times {\mathbb {R}})} \lesssim 2^{ \frac{1}{2} (\frac{3}{p}-\frac{1}{q})j }\Vert g\Vert _{L^p} \end{aligned}$$

(3.24)

for $1\le p\le q\le \infty$. Clearly, the left hand side is bounded by $\Vert \mathcal {P}_j^j g(x_1,x_3)\Vert _{L^q_{x_3}(L^\infty _{x_1})}$. The Fourier transform of $\mathcal {P}_j^j g$ is supported on the rectangle $\{ \xi _1\in [2^{j-1}, 2^{j+2}] , |\xi _2| \le 2^{j+2} \}$. Thus, using Bernstein’s inequality in $x_1$, we get

$$\begin{aligned} \Bigg \Vert \sup _{1<t<2}\mathcal {P}_j^j g\Big (\frac{(r-t)^2}{2},x_3\Big ) \Bigg \Vert _{L^q_{r,x_3}([2^{-2}, 2^3]\times {\mathbb {R}})}&\lesssim 2^{-\frac{j}{2}+\frac{j}{q}}\Vert \mathcal {P}_j^j g\Vert _{L^q} \end{aligned}$$

for $1\le q\le \infty$. Another use of Bernstein’s inequality gives (3.24) for $1\le p\le q\le \infty$. This completes the proof of (3.20). $\square$