Compactness and existence results in weighted Sobolev spaces of radial functions. Part I: compactness

Abstract

Given two measurable functions $V(r )\ge 0$ and $K(r)> 0$, $r>0$, we define the weighted spaces

$$\begin{aligned} H_{V}^{1}=\left\{ u\in D^{1,2}(\mathbb {R}^{N}):\int _{\mathbb {R}^{N}}V( | x| ) u^{2}dx<\infty \right\} ,\quad L_{K}^{q}=L^{q}(\mathbb {R} ^{N},K( | x| ) dx) \end{aligned}$$

and study the compact embeddings of the radial subspace of $H_{V}^{1}$ into $L_{K}^{q_{1}}+L_{K}^{q_{2}}$, and thus into $L_{K}^{q}$ ($=L_{K}^{q}+L_{K}^{q}$) as a particular case. Both super- and sub-quadratic exponents $q_{1}$, $q_{2}$ and $q$ are considered. Our results do not require any compatibility between how the potentials $V$ and $K$ behave at the origin and at infinity, and essentially rely on power type estimates of their relative growth, not of the potentials separately. Applications to existence results for nonlinear elliptic problems like $-\triangle u+V( | x| ) u=f( | x|,u)$ in $\mathbb {R}^{N}$, $u\in H_{V}^{1}$, will be given in a forthcoming paper.

1 Introduction

Consider the nonlinear elliptic radial equation

$$\begin{aligned} -\triangle u+V( | x| ) u=K( | x|) f( u) \quad \mathrm{in }\,\,\mathbb {R}^{N}, \end{aligned}$$

(1)

where $N\ge 3$, $f:\mathbb {R}\rightarrow \mathbb {R}$ is a continuous nonlinearity satisfying $f( 0) =0$ and $V\ge 0,K>0$ are given potentials. The motivation of this paper is concerned with the problem of the existence of non-zero non-negative solutions to Eq. (1) in the following weak sense: we say that $u\in H_{V}^{1}$ is a weak solution to (1) if

$$\begin{aligned} \int _{\mathbb {R}^{N}}\nabla u\cdot \nabla h\,dx+\int _{\mathbb {R}^{N}}V( | x| ) uh\,dx=\int _{\mathbb {R}^{N}}K( | x| ) f( u) h\,dx\quad \mathrm{for\,\, all }\,\,h\in H_{V}^{1}, \end{aligned}$$

(2)

where

$$\begin{aligned} H_{V}^{1}:=H_{V}^{1}\left( \mathbb {R}^{N}\right) :=\left\{ u\in D^{1,2}\left( \mathbb {R}^{N}\right) :\int _{\mathbb {R}^{N}}V( | x| ) u^{2}dx<\infty \right\} \end{aligned}$$

(3)

is the energy space associated to the linear part of the equation, which is a Hilbert space with respect to the following inner product and related norm:

$$\begin{aligned} ( u\mid v) :=\int _{\mathbb {R}^{N}}( \nabla u\cdot \nabla v+V( | x| ) uv) dx,\ \ \Vert u\Vert ^2:=\int _{\mathbb {R}^{N}}\left( | \nabla u| ^{2} +V( | x| ) u^{2}\right) dx. \end{aligned}$$

By well known arguments, such solutions lead to special solutions (solitary waves and solitons) for several nonlinear field theories, such as Schrödinger and Klein–Gordon equations (see e.g. [4, 13, 29]). In this respect, since the early studies of [17, 20, 24, 25], Eq. (1) has been massively addressed in the mathematical literature, recently focusing on the case of $V$ possibly vanishing at infinity, i.e., $\liminf _{|x| \rightarrow \infty }V( | x| ) =0$ (some first results on such a case can be found in [2, 10, 15, 16]; for more recent references, see e.g. the bibliography of [1, 12, 26]).

The natural approach in studying Eq. (1) is variational, since its weak solutions are (at least formally) critical points of the Euler functional

$$\begin{aligned} I( u) :=\frac{1}{2}\Vert u\Vert ^{2}-\int _{\mathbb {R} ^{N}}K( | x| ) F( u) dx, \end{aligned}$$

(4)

where $F( t) :=\int _{0}^{t}f( s) ds$. Then the problem of existence is easily solved if $V$ does not vanish at infinity and $K$ is bounded. Indeed, in this case, introducing the weighted Lebesgue space

$$\begin{aligned} L_{K}^{q}:=L_{K}^{q}\left( \mathbb {R}^{N}\right) :=L^{q}\left( \mathbb {R} ^{N},K( | x| ) dx\right) , \end{aligned}$$

(5)

one easily sees that the embeddings $H_{V}^{1}\hookrightarrow H^{1}(\mathbb {R} ^{N})$ and $L^{q}(\mathbb {R}^{N})\hookrightarrow L_{K}^{q}$ are continuous, so that, by the well known theory of $H^{1}(\mathbb {R}^{N})$, the embedding

$$\begin{aligned} H_{V}^{1}\left( \mathbb {R}^{N}\right) \hookrightarrow L_{K}^{q}\left( \mathbb {R} ^{N}\right) ,\qquad 2<q<2^{*}:=\frac{2N}{N-2}, \end{aligned}$$

is continuous and becomes compact if restricted to the radial subspace of $H_{V}^{1}$, namely

$$\begin{aligned} H_{V,\mathrm {r}}^{1}:=H_{V,\mathrm {r}}^{1}\left( \mathbb {R}^{N}\right) := \left\{ u\in H_{V}^{1}\left( \mathbb {R}^{N}\right) : u( x) =u( | x| ) \right\} . \end{aligned}$$

(6)

Therefore, assuming that $f$ grows as a super-linear and subcritical power, the functional $I$ is of class $C^{1}$ on $H_{V}^{1}$ (because its non-quadratic part is of class $C^{1}$ on $L_{K}^{q}$) and, under some additional conditions on the nonlinearity, by-now almost standard in the literature, the restriction of $I$ to $H_{V,\mathrm {r}}^{1}$ has a mountain-pass geometry and satisfies the Palais–Smale condition, so that it has a non-zero critical point by the Mountain-Pass Theorem [3]. Such a critical point is actually a critical point of $I$, i.e., a weak solution of (1) in the sense of (2), thanks to the Palais’ Principle of Symmetric Criticality [23], which applies since $I$ is rotationally invariant and of class $C^{1}$ on $H_{V}^{1}$.

If $V$ vanishes at infinity, the space $H_{V}^{1}$ is no more necessarily contained in $L^{2}(\mathbb {R}^{N})$ and thus the embedding properties of $H^{1}(\mathbb {R}^{N})$ become useless, so that the above scheme fails in essentially two points: the compactness properties of the radial subspace of $H^{1}(\mathbb {R}^{N})$ are no more available and a growth condition of the form $| F( u) | \le ( \mathrm {const.}) | u| ^{q}$, $q\ne 2^{*}$, does not ensure the differentiability, not even the finiteness, of $I$ on $H_{V}^{1}$. A possible way of saving the scheme, then, is to face and solve the following problems:

• i. find a compact embedding of $H_{V,\mathrm {r}}^{1}$ into a space $X$ where the non-quadratic part of $I$ is of class $C^{1}$;

• ii. prove a symmetric criticality type result, ensuring that the critical points of $I_{\mid H_{V,\mathrm {r}}^{1}}$ are weak solutions of Eq. (1) in the sense of definition (2).

Problem (i) has been largely investigated in the literature for $X=L_{K}^{q}$ and, as far as we know, the more general results in this direction are the ones recently obtained by Su et al. [28], Su and Tian [26], and Bonheure and Mercuri [18] (for older results, see the references in [26, 28]; for related results without symmetry assumptions, see [1, 19] and the references therein). In particular, [26, 28] and [18] respectively concern the cases $q\ge 2$, $1<q<2$ and $q>2$. We also observe that [26, 28] actually deal with the more general case of Banach energy spaces $W_{V,\mathrm {r}}^{1,p}$, $1<p<N$, which we do not study here. The spirit of the results of [26, 28] (for $p=2$) is essentially the following: assuming that $V,K$ are continuous and satisfy power type estimates of the form:

$$\begin{aligned} \liminf _{r\rightarrow 0^{+}}\frac{V( r) }{r^{a_{0}}}>0,\ \liminf _{r\rightarrow +\infty }\frac{V( r) }{r^{a}}>0,\ \limsup _{r\rightarrow 0^{+}}\frac{K( r) }{r^{b_{0}}}<\infty ,\ \limsup _{r\rightarrow +\infty }\frac{K( r) }{r^{b}}<\infty , \end{aligned}$$

(7)

the authors find two limit exponents $\underline{q}=\underline{q}( a,b)$ and $\overline{q}=\overline{q}( a_{0},b_{0})$ such that the embedding $H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}$ is compact if $\underline{q}<q<\overline{q}$. The exponent $\underline{q}$ is always defined, while $\overline{q}$ exists provided that suitable compatibility conditions between $a_{0}$ and $b_{0}$ occur. Moreover, the condition $\underline{q}<q<\overline{q}$ also asks for $\underline{q}< \overline{q}$, which is a further assumption: a compatibility is also required between the behaviours of the potentials at zero and at infinity. These results are extended in [18] by replacing (7) with estimates on $V$ and $K$ in terms of a much wider class of comparison functions than the powers of $r$ (the so-called Hardy–Dieudonné comparison class). A price to pay for such a generality is that the compact embedding $H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}$ is no more ensured for a range of exponents $q$, but under assumptions which join $q$ and the comparison functions together.

Motivated by a wide recent use of the sum of weighted Lebesgue spaces in dealing with nonlinear problems (see the references in [9]), the case $X=L_{K}^{q_{1}}+L_{K}^{q_{2}}$ has been considered in [9], generalizing a result of [14] and studying the compactness of the embedding of $H_{V,\mathrm {r}}^{1}$ (and of $W_{V,\mathrm {r}}^{1,p}$, $1<p<N$) into $L_{K}^{q_{1}}+L_{K}^{q_{2}}$ for $V=0$ and $K$ satisfying power type estimates from above at zero and infinity (see Example 2 below).

Here we investigate problem (i) for $X=L_{K}^{q_{1}}+L_{K}^{q_{2}}$ with $q_{1}$ and $q_{2}$ not necessarily different, and thus for $X=L_{K}^{q}$ ($=L_{K}^{q}+L_{K}^{q}$) as a particular case. Some properties of the $L_{K}^{q_{1}}+L_{K}^{q_{2}}$ spaces will be recalled in Sect. 4. We consider $q_{1},q_{2}\in ( 1,+\infty )$, so that both super- and sub-quadratic cases are covered. Our embedding results are given by the combination of Theorem 1 with Theorems 2, 3, 4 and 5, which give sufficient conditions in order to apply Theorem 1. The spirit of the results is essentially the following: assuming that the relative growth of the potentials satisfies power type estimates of the form

we find two open intervals, say $\mathcal {I}_{1}=\mathcal {I}_{1}( \alpha _{0},\beta _{0})$ and $\mathcal {I}_{2}=\mathcal {I}_{2}( \alpha _{\infty },\beta _{\infty })$, the one depending on the behaviour of $V$ and $K$ at the origin, the other on their behaviour at infinity, such that the embedding of $H_{V,\mathrm {r}}^{1}$ into $L_{K}^{q_{1}}+L_{K}^{q_{2}}$ is compact for $q_{1}\in \mathcal {I}_{1}$ and $q_{2}\in \mathcal {I}_{2}$. These intervals are independent from one another and may not intersect; if they do, a compact embedding of $H_{V,\mathrm {r} }^{1}$ into $L_{K}^{q}$ ensues, by taking $q_{1}=q_{2}=q$.

The compactness results we present here generalize the ones of [9, 26, 28] (for $p=2$) and are complementary to the ones of [18]. The main novelties concern the decaying rates allowed for the potentials and the independence between their behaviours at the origin and at infinity.

As to the first issue, we do not require separate estimates on $V$ and $K$, but only on their relative growth, so that potentials which do not exhibit a power like behaviour, as prescribed in [26, 28], or cannot be estimated by Hardy–Dieudonné comparison functions, as prescribed in [18], are permitted (see Examples 3 and 4 below). Moreover, unlike in [18, 26, 28], we also allow that $V$ vanishes identically in a neighbourhood of zero, or of infinity, or both (see Remark 1(1) and Examples 2 and 4). On the other hand, many of the potentials considered in [18] do not fall into the class studied here, since they give rise to a ratio $K/V^{\beta }$ which behaves as a general Hardy–Dieudonné function and therefore cannot be estimated by a power of $r$. However, we think that our arguments can be extended in order to estimate $K/V^{\beta }$ by means of a wider class of functions than the powers of $r$, such as, indeed, the Hardy–Dieudonné comparison functions.

As far as the second issue is concerned, we avoid any compatibility requirement between how the potentials behave at the origin and at infinity, since the use of $L_{K}^{q_{1}}+L_{K}^{q_{2}}$ spaces, not simply of $L_{K}^{q}$, leads to the already mentioned independent intervals $\mathcal {I} _{1},\mathcal {I}_{2}$ for the exponents $q_{1},q_{2}$. This also provides new compact embeddings for potentials which belong to the classes considered in [18, 26, 28] but escape their results, for instance because $\underline{q}\ge \overline{q}$ (see Examples 1, 3 and 5).

Besides these general considerations, it is worth observing that we also improve the compact embeddings of [26] (for $p=2$), i.e., $H_{V, \mathrm {r}}^{1}\hookrightarrow L_{K}^{q}$ for $q$ sub-quadratic, in three further respects: for potentials satisfying the same assumptions of [26], we find that the embedding is compact for a wider interval of exponents than the range $\underline{q}<q<\overline{q}$ obtained in [26], as well as for cases in which $\underline{q}$ and $\overline{q}$ are not defined, or are such that $\underline{q}\ge \overline{q}$. This is thoroughly highlighted in Example 5, even though in a particular case.

A precise comparison with the compactness result of [9] (for $p=2$) will be given in Example 2.

As to problem (ii), it has been recently treated in [11] and [9] for particular potentials, respectively concerning nonlinearities satisfying a single-power and a double-power growth condition (see also [5] for a related cylindrical case). We will study the problem in the forthcoming paper [8], where we will prove a symmetric criticality type result that contains the ones of [9, 11] and, as announced in [6], it also completes the existence results of other papers (e.g. [26–28]), where a solution is found as a critical point of the restriction $I_{\mid H_{V, \mathrm {r}}^{1}}$ only.

The forthcoming paper [8] will be also (and mainly) devoted to applications of our embedding results to nonlinear elliptic problems like (1). Further applications will be given in [21], where the problem of existence without the Ambrosetti–Rabinowitz growth condition is faced.

This paper is organized as follows. In Sect. 2 we state our main results: a general result concerning the embedding properties of $H_{V, \mathrm {r}}^{1}$ into $L_{K}^{q_{1}}+L_{K}^{q_{2}}$ (Theorem 1) and some explicit conditions ensuring that the embedding is compact (Theorems 2, 3, 4 and 5). The general result is proved in Sect. 4, the explicit conditions in Sect. 5. In Sect. 3 we apply our results to some examples, with a view to both illustrate how to use them in concrete cases and to compare them with the literature mentioned above.

Notations. We end this introductory section by collecting some notations used in the paper.

• For every $R>0$, we set $B_{R}:=\{ x\in \mathbb {R} ^{N}:| x| <r\}$.

• For any subset $A\subseteq \mathbb {R}^{N}$, we denote $A^{c}:=\mathbb {R}^{N}\setminus A$. If $A$ is Lebesgue measurable, $| A|$ stands for its measure.

• By $\rightarrow$ and $\rightharpoonup$ we respectively mean strong and weak convergence.

• $\hookrightarrow$ denotes continuous embeddings.

• $C_{\mathrm {c}}^{\infty }(\Omega )$ is the space of the infinitely differentiable real functions with compact support in the open set $\Omega \subseteq \mathbb {R}^{d}$; $C_{\mathrm {c,rad}}^{\infty }(\mathbb {R} ^{N})$ is the radial subspace of $C_{\mathrm {c}}^{\infty }(\mathbb {R}^{N})$.

• If $1\le p\le \infty$ then $L^{p}(A)$ and $L_{ \mathrm {loc}}^{p}(A)$ are the usual real Lebesgue spaces (for any measurable set $A\subseteq \mathbb {R}^{d}$). If $\rho :A\rightarrow ( 0,+\infty )$ is a measurable function, then $L^{p}(A,\rho ( z) dz)$ is the real Lebesgue space with respect to the measure $\rho ( z) dz$ ($dz$ stands for the Lebesgue measure on $\mathbb {R}^{d}$).

• $p^{\prime }:=p/(p-1)$ is the Hölder-conjugate exponent of $p.$

• $D^{1,2}(\mathbb {R}^{N})=\{u\in L^{2^{*}}(\mathbb {R} ^{N}):\nabla u\in L^{2}(\mathbb {R}^{N})\}$, $N\ge 3$, is the usual Sobolev space, which identifies with the completion of $C_{\mathrm {c}}^{\infty }( \mathbb {R}^{N})$ with respect to the norm of the gradient; $D_{\mathrm {rad} }^{1,2}(\mathbb {R}^{N})$ is the radial subspace of $D^{1,2}(\mathbb {R}^{N})$; $D_{0}^{1,2}( B_{R})$ is closure of $C_{\mathrm {c}}^{\infty }( B_{R})$ in $D^{1,2}(\mathbb {R}^{N})$.

• $2^{*}:=2N/( N-2)$ is the critical exponent for the Sobolev embedding in dimension $N\ge 3$.

2 Main results

Assume $N\ge 3$ and recall the definitions (3), (6) and (5) of the spaces $H_{V}^{1}$, $H_{V,\mathrm {r}}^{1}$ and $L_{K}^{q}$. We will always require that the potentials $V$ and $K$ satisfy the following basic assumptions:

• $(\mathbf {V})$ $V:( 0,+\infty ) \rightarrow [ 0,+\infty ]$ is a measurable function such that $V\in L^{1}( ( r_{1},r_{2}) )$ for some $r_{2}>r_{1}>0;$

• $(\mathbf {K})$ $K:( 0,+\infty ) \rightarrow ( 0,+\infty )$ is measurable and such that $K\in L_{\mathrm {loc}}^{s}( ( 0,+\infty ) )$ for some $s>\frac{2N}{N+2}$.

Assumption $( \mathbf {V})$ implies that the spaces $H_{V}^{1}$ and $H_{V,\mathrm {r}}^{1}$ are nontrivial, while hypothesis $( \mathbf {K})$ ensures that $H_{V,\mathrm {r}}^{1}$ is compactly embedded into the weighted Lebesgue space $L_{K}^{q}(B_{R}\setminus B_{r})$ for every $1<q<\infty$ and $R>r>0$ (cf. Lemma 1 below). In what follows, the summability assumptions in $( \mathbf {V})$ and $( \mathbf {K})$ will not play any other role than this.

Given $V$ and $K$, we define the following functions of $R>0$ and $q>1$:

$$\begin{aligned} \mathcal {S}_{0}( q,R)&:= \sup _ {u\in H_{V,\mathrm {r}}^{1},\, \Vert u\Vert =1 } \int _{B_{R}}K( | x| ) | u| ^{q}dx, \end{aligned}$$

(8)

$$\begin{aligned} \mathcal {S}_{\infty }( q,R)&:= \sup _ {u\in H_{V,\mathrm {r}}^{1},\, \Vert u\Vert =1 } \int _{\mathbb {R} ^{N}\setminus B_{R}}K( | x| ) | u| ^{q}dx. \end{aligned}$$

(9)

Clearly $\mathcal {S}_{0}( q,\cdot )$ is nondecreasing, $\mathcal { S}_{\infty }( q,\cdot )$ is nonincreasing and both of them can be infinite at some $R$.

Our first result concerns the embedding properties of $H_{V,\mathrm {r}}^{1}$ into $L_{K}^{q_{1}}+L_{K}^{q_{2}}$ and relies on assumptions which are quite general, sometimes also sharp (see claim (iii)), but not so easy to check. More handy conditions ensuring these general assumptions will be provided by the next results. Some recallings on the space $L_{K}^{q_{1}}+L_{K}^{q_{2}}$ will be given in Sect. 4.

Theorem 1

Let $N\ge 3$, let $V$, $K$ be as in $( \mathbf {V} )$, $( \mathbf {K})$ and let $q_{1},q_{2}>1$.

• i. If

  

  then $H_{V,\mathrm {r}}^{1}(\mathbb {R}^{N})$ is continuously embedded into $L_{K}^{q_{1}}(\mathbb {R}^{N})+L_{K}^{q_{2}}(\mathbb {R}^{N})$.

• ii. If

  

  then $H_{V,\mathrm {r}}^{1}(\mathbb {R}^{N})$ is compactly embedded into $L_{K}^{q_{1}}(\mathbb {R}^{N})+L_{K}^{q_{2}}(\mathbb {R}^{N})$.

• iii. If $K( | \cdot | ) \in L^{1}(B_{1})$ and $q_{1}\le q_{2}$, then conditions $( \mathcal {S}_{q_{1},q_{2}}^{\prime })$ and $( \mathcal {S}_{q_{1},q_{2}}^{\prime \prime })$ are also necessary to the above embeddings.

Observe that, of course, $(\mathcal {S}_{q_{1},q_{2}}^{\prime \prime })$ implies $(\mathcal {S}_{q_{1},q_{2}}^{\prime })$. Moreover, these assumptions can hold with $q_{1}=q_{2}=q$ and therefore Theorem 1 also concerns the embedding properties of $H_{V,\mathrm {r}}^{1}$ into $L_{K}^{q}$ , $1<q<\infty$.

We now look for explicit conditions on $V$ and $K$ implying $(\mathcal {S} _{q_{1},q_{2}}^{\prime \prime })$ for some $q_{1}$ and $q_{2}$. More precisely, we will ensure $(\mathcal {S}_{q_{1},q_{2}}^{\prime \prime })$ through a more stringent condition involving the following functions of $R>0$ and $q>1$:

$$\begin{aligned} \mathcal {R}_{0}( q,R)&:= \sup _ { u\in H_{V,\mathrm {r}}^{1},\,h\in H_{V}^{1},\, \Vert u\Vert =\Vert h\Vert =1 } \,\int _{B_{R}}K( | x| )| u| ^{q-1}| h| dx, \end{aligned}$$

(10)

$$\begin{aligned} \mathcal {R}_{\infty }( q,R)&:= \sup _ { u\in H_{V,\mathrm {r}}^{1},\,h\in H_{V}^{1},\, \Vert u\Vert =\Vert h\Vert =1 } \,\int _{\mathbb {R}^{N}\setminus B_{R}}K( | x| ) | u| ^{q-1}| h| dx. \end{aligned}$$

(11)

Note that $\mathcal {R}_{0}( q,\cdot )$ is nondecreasing, $\mathcal {R}_{\infty }( q,\cdot )$ is nonincreasing and both can be infinite at some $R$. Moreover, for every $( q,R)$ one has $\mathcal {S}_{0}( q,R) \le \mathcal {R}_{0}( q,R)$ and $\mathcal {S}_{\infty }( q,R) \le \mathcal {R}_{\infty }( q,R)$, so that $(\mathcal {S}_{q_{1},q_{2}}^{\prime \prime })$ is a consequence of the following, stronger condition:

In Theorems 2 and 5 we will find some ranges of exponents $q_{1}$ such that $\lim _{R\rightarrow 0^{+}}\mathcal {R}_{0}(q_{1},R)$ $=0$, while in Theorems 3 and 4 we will do the same for exponents $q_{2}$ such that $\lim _{R\rightarrow +\infty }\mathcal {R}_{\infty }( q_{2},R) =0$. Condition $(\mathcal {R}_{q_{1},q_{2}}^{\prime \prime })$ then follows by joining Theorem 2 or 5 with Theorem 3 or 4.

The reason why we introduce the functions $\mathcal {R}_{0}$ and $\mathcal {R} _{\infty }$ is just a matter of future convenience: some of the results of [8] will need assumption $(\mathcal {R}_{q_{1},q_{2}}^{\prime \prime })$ and therefore we provide, already at this stage, sufficient conditions in order that $(\mathcal {R}_{q_{1},q_{2}}^{\prime \prime })$ holds. This does not affect our compactness results, since such sufficient conditions are exactly the same under which our arguments ensure $(\mathcal {S }_{q_{1},q_{2}}^{\prime \prime })$.

The fact that Theorem 1 allows the case of $V( r)=+\infty$ on a positive measure set is for future convenience as well, since it will be used in [8] to easily deduce existence results on bounded or exterior radial domains. Such a generality for $V$ is not so relevant in the next results, where we will thus assume that $V$ is finite almost everywhere.

For $\alpha \in \mathbb {R}$ and $\beta \in [ 0,1]$, we define two functions $\alpha ^{*}( \beta )$ and $q^{*}( \alpha ,\beta )$ by setting

$$\begin{aligned} \alpha ^{*}( \beta ) :=\max \left\{ 2\beta -1-\frac{N}{2},-( 1-\beta ) N\right\} =\left\{ \begin{array}{ll} 2\beta -1-\frac{N}{2} &{}\quad \mathrm {if }\,\,0\le \beta \le \frac{1}{2 } \\ -( 1-\beta ) N &{}\quad \mathrm {if }\,\,\frac{1}{2}\le \beta \le 1 \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} q^{*}( \alpha ,\beta ) :=2\frac{\alpha -2\beta +N}{N-2}. \end{aligned}$$

Note that $\alpha ^{*}( \beta ) \le 0$ and $\alpha ^{*}( \beta ) =0$ if and only if $\beta =1$.

The following Theorems 2 and 3 only rely on a power type estimate of the relative growth of the potentials and do not require any other separate assumption on $V$ and $K$ than $( \mathbf {V})$ and $( \mathbf {K})$, including the case $V( r) \equiv 0$ (see Remark 1(1)).

Theorem 2

Let $N\ge 3$ and let $V$, $K$ be as in $( \mathbf {V} )$, $( \mathbf {K})$. Assume that there exists $R_{1}>0$ such that $V( r) <+\infty$ almost everywhere on $(0,R_1)$ and

(12)

Then $\displaystyle \lim _{R\rightarrow 0^{+}}\mathcal {R}_{0}( q_{1},R) =0$ for every $q_{1}\in \mathbb {R}$ such that

$$\begin{aligned} \max \{ 1,2\beta _{0}\} <q_{1}<q^{*}( \alpha _{0},\beta _{0}). \end{aligned}$$

(13)

Theorem 3

Let $N\ge 3$ and let $V$, $K$ be as in $( \mathbf {V})$, $( \mathbf {K})$. Assume that there exists $R_{2}>0$ such that $V( r) <+\infty$ for almost every $r>R_2$ and

(14)

Then $\displaystyle \lim _{R\rightarrow +\infty }\mathcal {R}_{\infty }( q_{2},R) =0$ for every $q_{2}\in \mathbb {R}$ such that

$$\begin{aligned} q_{2}>\max \{ 1,2\beta _{\infty },q^{*}( \alpha _{\infty },\beta _{\infty }) \}. \end{aligned}$$

(15)

We observe explicitly that for every $( \alpha ,\beta ) \in \mathbb {R }\times [ 0,1]$ one has

$$\begin{aligned} \max \{ 1,2\beta ,q^{*}( \alpha ,\beta ) \} =\left\{ \begin{array}{ll} q^{*}( \alpha ,\beta ) &{} \quad \mathrm {if }\,\,\alpha \ge \alpha ^{*}( \beta ) \\ \max \{ 1,2\beta \} &{}\quad \mathrm {if }\,\,\alpha \le \alpha ^{*}( \beta ) \end{array} \right. . \end{aligned}$$

Remark 1

• 1. We mean $V( r) ^{0}=1$ for every $r$ (even if $V( r) =0$). In particular, if $V( r) =0$ for almost every $r>R_{2}$, then Theorem 3 can be applied with $\beta _{\infty }=0$ and assumption (14) means

  $$\begin{aligned} \mathop {\hbox {ess sup}}\limits _{r>R_{2}}\frac{K( r) }{r^{\alpha _{\infty }}} <+\infty \quad \mathrm {for\,\, some }\,\,\alpha _{\infty }\in \mathbb {R}. \end{aligned}$$

  Similarly for Theorem 2 and assumption (12), if $V( r) =0$ for almost every $r\in ( 0,R_{1})$.

• 2. The inequality $\max \{ 1,2\beta _{0}\} <q^{*}( \alpha _{0},\beta _{0})$ is equivalent to $\alpha _{0}>\alpha ^{*}( \beta _{0})$. Then, in (13), such inequality is automatically true and does not ask for further conditions on $\alpha _{0}$ and $\beta _{0}$.

• 3. The assumptions of Theorems 2 and 3 may hold for different pairs $( \alpha _{0},\beta _{0})$, $( \alpha _{\infty },\beta _{\infty })$. In this case, of course, one chooses them in order to get the ranges for $q_{1},q_{2}$ as large as possible. For instance, if $V$ is not singular at the origin, i.e., $V$ is essentially bounded in a neighbourhood of 0, and condition (12) holds true for a pair $( \alpha _{0},\beta _{0})$, then (12) also holds for all pairs $( \alpha _{0}^{\prime },\beta _{0}^{\prime })$ such that $\alpha _{0}^{\prime }<\alpha _{0}$ and $\beta _{0}^{\prime }<\beta _{0}$. Therefore, since $\max \{ 1,2\beta \}$ is increasing in $\beta$ and $q^{*}( \alpha ,\beta )$ is increasing in $\alpha$ and decreasing in $\beta$, it is convenient to choose $\beta _{0}=0$ and the best interval where one can take $q_{1}$ is $1<q_{1}<q^{*}( \overline{\alpha },0)$ with $\overline{\alpha }:=\sup \{ \alpha _{0}:\mathop {\hbox {ess sup}}\limits _{r\in ( 0,R_{1}) }\frac{K( r) }{r^{\alpha _{0}}}<+\infty \}$ (we mean $q^{*}( +\infty ,0) =+\infty$).

For any $\alpha \in \mathbb {R}$, $\beta \le 1$ and $\gamma \in \mathbb {R}$, define

$$\begin{aligned} q_{*}( \alpha ,\beta ,\gamma ) :=2\frac{\alpha -\gamma \beta +N}{ N-\gamma },\quad q_{**}( \alpha ,\beta ,\gamma ) :=2\frac{2\alpha +( 1-2\beta ) \gamma +2( N-1) }{ 2( N-1) -\gamma }. \end{aligned}$$

(16)

Of course $q_{*}$ and $q_{**}$ are undefined if $\gamma =N$ and $\gamma =2( N-1)$, respectively.

The next Theorems 4 and 5 improve the results of Theorems 2 and 3 by exploiting further informations on the growth of $V$ (see Remarks 2(2) and 3(3)).

Theorem 4

Let $N\ge 3$ and let $V$, $K$ be as in $( \mathbf {V} )$, $( \mathbf {K})$. Assume that there exists $R_{2}>0$ such that $V( r) <+\infty$ for almost every $r>R_2$ and

(17)

and

(18)

Then $\displaystyle \lim _{R\rightarrow +\infty }\mathcal {R}_{\infty }\left( q_{2},R\right) =0$ for every $q_{2}\in \mathbb {R}$ such that

$$\begin{aligned} q_{2}>\max \{ 1,2\beta _{\infty },q_{*},q_{**}\}, \end{aligned}$$

(19)

where $q_{*}=q_{*}\left( \alpha _{\infty },\beta _{\infty },\gamma _{\infty }\right)$ and $q_{**}=q_{**}\left( \alpha _{\infty },\beta _{\infty },\gamma _{\infty }\right) .$

For future convenience, we define three functions $\alpha _{1}:=\alpha _{1}\left( \beta ,\gamma \right)$, $\alpha _{2}:=\alpha _{2}\left( \beta \right)$ and $\alpha _{3}:=\alpha _{3}\left( \beta ,\gamma \right)$ by setting

$$\begin{aligned} \alpha _{1}:=-\left( 1-\beta \right) \gamma ,\quad \alpha _{2}:=-\left( 1-\beta \right) N,\quad \alpha _{3}:=-\frac{N+\left( 1-2\beta \right) \gamma }{2}. \end{aligned}$$

(20)

Then an explicit description of $\max \{ 1,2\beta ,q_{*},q_{**}\}$ is the following: for every $\left( \alpha ,\beta ,\gamma \right) \in \mathbb { R}\times \left( -\infty ,1\right] \times \left( -\infty ,2\right]$ we have

$$\begin{aligned} \max \{ 1,2\beta ,q_{*},q_{**}\} =\left\{ \begin{array}{ll} q_{**}\left( \alpha ,\beta ,\gamma \right) &{}\quad \mathrm {if }\,\,\alpha \ge \alpha _{1} \\ q_{*}\left( \alpha ,\beta ,\gamma \right) &{}\quad \mathrm {if }\,\,\max \left\{ \alpha _{2},\alpha _{3}\right\} \le \alpha \le \alpha _{1} \\ \max \left\{ 1,2\beta \right\} &{}\quad \mathrm {if }\,\,\alpha \le \max \left\{ \alpha _{2},\alpha _{3}\right\} \end{array} \right. , \end{aligned}$$

(21)

where $\max \{ \alpha _{2},\alpha _{3}\} <\alpha _{1}$ for every $\beta <1$ and $\max \{ \alpha _{2},\alpha _{3}\} =\alpha _{1}=0$ if $\beta =1$.

Remark 2

• 1. The proof of Theorem 4 does not require $\beta _{\infty }\ge 0$, but this condition is not a restriction of generality in stating the theorem. Indeed, under assumption (18), if (17) holds with $\beta _{\infty }<0$, then it also holds with $\alpha _{\infty }$ and $\beta _{\infty }$ replaced by $\alpha _{\infty }-\beta _{\infty }\gamma _{\infty }$ and $0$ respectively, and this does not change the thesis (19), because $q_{*}\left( \alpha _{\infty }-\beta _{\infty }\gamma _{\infty },0,\gamma _{\infty }\right) =q_{*}\left( \alpha _{\infty },\beta _{\infty },\gamma _{\infty }\right)$ and $q_{**}\left( \alpha _{\infty }-\beta _{\infty }\gamma _{\infty },0,\gamma _{\infty }\right) =q_{**}\left( \alpha _{\infty },\beta _{\infty },\gamma _{\infty }\right)$.

• 2. Denote $q^{*}=q^{*}\left( \alpha _{\infty },\beta _{\infty }\right)$ for brevity. If $\gamma _{\infty }<2$, then one has

  $$\begin{aligned}&\max \{ 1,2\beta _{\infty },q^{*}\}\\&=\left\{ \begin{array}{ll} \max \{ 1,2\beta _{\infty }\} =\max \{ 1,2\beta _{\infty },q_{*},q_{**}\} &{} \quad \mathrm {if }\,\,\alpha _{\infty }\le \alpha ^{*}( \beta _{\infty }) \\ q^{*}>\max \{ 1,2\beta _{\infty },q_{*},q_{**}\} &{}\quad \mathrm {if }\,\, \alpha _{\infty }>\alpha ^{*}( \beta _{\infty }) \end{array} \right. , \end{aligned}$$

  so that, under assumption (18), Theorem 4 improves Theorem 3. Otherwise, if $\gamma _{\infty }=2$, we have $q_{*}=q_{**}=q^{*}$ and Theorems 4 and 3 give the same result. This is not surprising, since, by Hardy inequality, the space $H_{V}^{1}$ coincides with $D^{1,2}(\mathbb {R}^{N})$ if $V\left( r\right) =r^{-2}$ and thus, for $\gamma _{\infty }=2$, we cannot expect a better result than the one of Theorem 3, which covers the case of $V\left( r\right) \equiv 0$, i.e., of $D^{1,2}(\mathbb {R}^{N})$.

• 3. Description (21) shows that $q_{*}$ and $q_{**}$ are relevant in inequality (19) only for $\alpha _{\infty }>\alpha _{2}\left( \beta _{\infty }\right)$. In this case, both $q_{*}$ and $q_{**}$ turn out to be increasing in $\gamma$ and hence it is convenient to apply Theorem 4 with the smallest $\gamma _{\infty }$ for which (18) holds. This is consistent with the fact that, if (18) holds with $\gamma _{\infty }$, then it also holds with every $\gamma _{\infty }^{\prime }$ such that $\gamma _{\infty }\le \gamma _{\infty }^{\prime }\le 2$.

In order to state our last result, we introduce, by the following definitions, an open region $\mathcal {A}_{\beta ,\gamma }$ of the $\alpha q$-plane, depending on $\beta \le 1$ and $\gamma \ge 2$. Recall the definitions (16) of the functions $q_{*}=q_{*}\left( \alpha ,\beta ,\gamma \right)$ and $q_{**}=q_{**}\left( \alpha ,\beta ,\gamma \right)$. We set

$$\begin{aligned} \begin{array}{l@{\quad }l} \mathcal {A}_{\beta ,\gamma }:=\left\{ \left( \alpha ,q\right) :\max \left\{ 1,2\beta \right\} <q<\min \left\{ q_{*},q_{**}\right\} \right\} \quad &{} \mathrm{if }\,\,2\le \gamma <N, \\ \mathcal {A}_{\beta ,\gamma }:=\left\{ \left( \alpha ,q\right) :\max \left\{ 1,2\beta \right\} <q<q_{**},\,\alpha >-\left( 1-\beta \right) N\right\} \quad &{} \mathrm{if }\,\,\gamma =N, \\ \mathcal {A}_{\beta ,\gamma }:=\left\{ \left( \alpha ,q\right) :\max \left\{ 1,2\beta ,q_{*}\right\} <q<q_{**}\right\} &{} \mathrm{if }\,\,N<\gamma <2N-2, \\ \mathcal {A}_{\beta ,\gamma }:=\left\{ \left( \alpha ,q\right) :\max \left\{ 1,2\beta ,q_{*}\right\} <q,\,\alpha >-\left( 1-\beta \right) \gamma \right\} &{} \mathrm{if }\,\,\gamma =2N-2, \\ \mathcal {A}_{\beta ,\gamma }:=\left\{ \left( \alpha ,q\right) :\max \left\{ 1,2\beta ,q_{*},q_{**}\right\} <q\right\} &{} \mathrm{if }\,\,\gamma >2N-2. \end{array} \end{aligned}$$

(22)

For more clarity, the set $\mathcal {A}_{\beta ,\gamma }$ is sketched in the five figures below, according to the five cases above. In viewing the pictures, recall the definitions (20) of the functions $\alpha _{1}=\alpha _{1}\left( \beta ,\gamma \right)$, $\alpha _{2}=\alpha _{2}\left( \beta \right)$ and $\alpha _{3}=\alpha _{3}\left( \beta ,\gamma \right)$.

Theorem 5

Let $N\ge 3$ and let $V$, $K$ be as in $\left( \mathbf {V} \right)$, $\left( \mathbf {K}\right)$. Assume that there exists $R_{1}>0$ such that $V\left( r\right) <+\infty$ almost everywhere on $(0,R_1)$ and

(23)

and

(24)

Then $\displaystyle \lim _{R\rightarrow 0^{+}}\mathcal {R}_{0}\left( q_{1},R\right) =0$ for every $q_{1}\in \mathbb {R}$ such that

$$\begin{aligned} \left( \alpha _{0},q_{1}\right) \in \mathcal {A}_{\beta _{0},\gamma _{0}}. \end{aligned}$$

(25)

Remark 3

• 1. Condition (25) also asks for a lower bound on $\alpha _{0}$, except for the case $\gamma _{0}>2N-2$, as it is clear from Figs. 1, 2, 3, 4 and 5.

• 2. The proof of Theorem 5 does not require $\beta _{0}\ge 0$, but this is not a restriction of generality in stating the theorem (cf. Remark 2(1)). Indeed, under assumption (24), if (23) holds with $\beta _{0}<0$, then it also holds with $\alpha _{0}$ and $\beta _{0}$ replaced by $\alpha _{0}-\beta _{0}\gamma _{0}$ and $0$ respectively, and one has that $\left( \alpha _{0},q_{1}\right) \in \mathcal {A}_{\beta _{0},\gamma _{0}}$ if and only if $\left( \alpha _{0}-\beta _{0}\gamma _{0},q_{1}\right) \in \mathcal {A }_{0,\gamma _{0}}$.

• 3. If (24) holds with $\gamma _{0}>2$, then Theorem 5 improves Theorem 2. Otherwise, if $\gamma _{0}=2$, then one has $\max \left\{ \alpha _{2},\alpha _{3}\right\} =\alpha ^{*}\left( \beta _{0}\right)$ and $\left( \alpha _{0},q_{1}\right) \in \mathcal {A}_{\beta _{0},\gamma _{0}}$ is equivalent to $\max \left\{ 1,2\beta _{0}\right\} <q_{1}<q^{*}\left( \alpha _{0},\beta _{0}\right)$, i.e., Theorems 5 and 2 give the same result, which is consistent with Hardy inequality (cf. Remark 2(2)).

• 4. Given $\beta \le 1$, one can check that $\mathcal {A}_{\beta ,\gamma _{1}}\subseteq \mathcal {A}_{\beta ,\gamma _{2}}$ for every $2\le \gamma _{1}<\gamma _{2}$, so that, in applying Theorem 5, it is convenient to choose the largest $\gamma _{0}$ for which (24) holds. This is consistent with the fact that, if (24) holds with $\gamma _{0}$, then it also holds with every $\gamma _{0}^{\prime }$ such that $2\le \gamma _{0}^{\prime }\le \gamma _{0}$.

Fig. 1

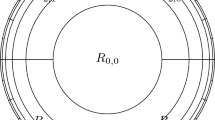
The set $\mathcal {A}_{\beta ,\gamma }$ for $\beta \le 1$ and $2\le \gamma <N$. If $\gamma =2$, the two straight lines above are the same. If $\beta <1$ we have $\max \left\{ \alpha _{2},\alpha _{3}\right\} <\alpha _{1}<0$; if $\beta =1$ we have $\max \left\{ \alpha _{2},\alpha _{3}\right\} =\alpha _{1}=0$ and $\mathcal {A}_{1,\gamma }$ reduces to the angle $2<q<q_{**}$

Fig. 2

The set $\mathcal {A}_{\beta ,\gamma }$ for $\beta \le 1$ and $\gamma =N$. If $\beta <1$ we have $\alpha _{1}=\alpha _{2}=\alpha _{3}<0$; if $\beta =1$ we have $\alpha _{1}=\alpha _{2}=\alpha _{3}=0$ and $\mathcal {A}_{1,\gamma }$ reduces to the angle $2<q<q_{**}$

Fig. 3

The set $\mathcal {A}_{\beta ,\gamma }$ for $\beta \le 1$ and $N<\gamma <2N-2$. If $\beta <1$ we have $\alpha _{1}<\min \left\{ \alpha _{2},\alpha _{3}\right\} <0$; if $\beta =1$ we have $\alpha _{1}=\min \left\{ \alpha _{2},\alpha _{3}\right\} =0$ and $\mathcal {A}_{1,\gamma }$ reduces to the angle $2<q<q_{**}$

Fig. 4

The set $\mathcal {A}_{\beta ,\gamma }$ for $\beta \le 1$ and $\gamma =2N-2$. If $\beta <1$ we have $\alpha _{1}<\min \left\{ \alpha _{2},\alpha _{3}\right\} <0$; if $\beta =1$ we have $\alpha _{1}=\min \left\{ \alpha _{2},\alpha _{3}\right\} =0$ and $\mathcal {A}_{1,\gamma }$ reduces to the angle $\alpha >0,\,q>2$

Fig. 5

The set $\mathcal {A}_{\beta ,\gamma }$ for $\beta \le 1$ and $\gamma >2N-2$. If $\beta <1$ we have $\alpha _{1}<\min \left\{ \alpha _{2},\alpha _{3}\right\} <0$; if $\beta =1$ we have $\alpha _{1}=\min \left\{ \alpha _{2},\alpha _{3}\right\} =0$ and $\mathcal {A}_{1,\gamma }$ reduces to the angle $q>\max \left\{ 2,q_{**}\right\}$

3 Examples

In this section we give some examples which might clarify how to use our results and compare them with the ones of [9, 18, 26, 28], cited in the Introduction. It will be always understood that $N\ge 3$.

Example 1

Consider the potentials

$$\begin{aligned} V\left( r\right) =\frac{1}{r^{a}},\quad K\left( r\right) =\frac{1}{r^{a-1}},\quad a\le 2. \end{aligned}$$

Since $V$ satisfies (18) with $\gamma _{\infty }=a$ (cf. Remark 2(3) for the best choice of $\gamma _{\infty }$), we apply Theorem 1 together with Theorems 2 and 4. Assumptions (12) and (17) hold if and only if $\alpha _{0}\le a\beta _{0}-a+1$ and $\alpha _{\infty }\ge a\beta _{\infty }-a+1$. According to (13) and (19), it is convenient to choose $\alpha _{0}$ as large as possible and $\alpha _{\infty }$ as small as possible, so we take

$$\begin{aligned} \alpha _{0}=a\beta _{0}-a+1,\quad \alpha _{\infty }=a\beta _{\infty }-a+1. \end{aligned}$$

Then $q^{*}=q^{*}\left( \alpha _{0},\beta _{0}\right)$, $q_{*}=q_{*}\left( \alpha _{\infty },\beta _{\infty },a\right)$ and $q_{**}=q_{**}\left( \alpha _{\infty },\beta _{\infty },a\right)$ are given by

$$\begin{aligned} q^{*}=2\frac{N-a+1-\left( 2-a\right) \beta _{0}}{N-2},\quad q_{*}=2\frac{ N-a+1}{N-a}\quad \mathrm{and}\quad q_{**}=2\frac{2N-a}{2N-a-2}, \end{aligned}$$

(26)

where $a\le 2$ implies $q_{*}\le q_{**}$. Note that $\alpha _{0}>\alpha ^{*}\left( \beta _{0}\right)$ for every $\beta _{0}$. Since $q^{*}$ is decreasing in $\beta _{0}$ and $q_{**}$ is independent of $\beta _{\infty }$, it is convenient to choose $\beta _{0}=\beta _{\infty }=0$, so that Theorems 2 and 4 yield to exponents $q_{1},q_{2}$ such that

$$\begin{aligned} 1<q_{1}<q^{*}=2\frac{N-a+1}{N-2},\quad q_{2}>q_{**}=2\frac{2N-a}{2N-a-2}. \end{aligned}$$

If $a<2$, then one has $q_{**}<q^{*}$ and therefore we get the compact embedding

$$\begin{aligned} H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}\qquad \mathrm{for}\quad 2\frac{ 2N-a}{2N-a-2}<q<2\frac{N-a+1}{N-2}. \end{aligned}$$

(27)

If $a=2$, then $q_{**}=q^{*}=2\left( N-1\right) /\left( N-2\right)$ and we have the compact embedding

$$\begin{aligned} H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q_{1}}+L_{K}^{q_{2}}\qquad \mathrm{for}\quad 1<q_{1}<2\frac{N-1}{N-2}<q_{2}. \end{aligned}$$

Since $V$ and $K$ are power potentials, one can also apply the results of [28] (or equivalently of [18], which are the same for power potentials), finding two limit exponents $\underline{q}$ and $\overline{q}$ such that the embedding $H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}$ is compact if $\underline{q}<q<\overline{q}$. These exponents $\underline{q}$ and $\overline{q}$ are exactly exponents $q_{**}$ and $q^{*}$ of (26) respectively, so that one obtains (27) again, provided that $a<2$ (which implies $\underline{q}<\overline{q}$). If $a=2$, instead, one gets $\underline{q}=\overline{q}$ and no result is available in [28] (nor in [18]). The results of [26] do not apply to $V$ and $K$, since the top and bottom exponents of [26] turn out to be equal to one another for every $a\le 2$.

Example 2

Taking $V\left( r\right) \equiv 0$, $K$ as in $\left( \mathbf { K}\right)$ and $\beta _{0}=\beta _{\infty }=0$, from Theorems 2, 3 and 1 (see also Remark 1(1)) we get the compact embedding $D_{\mathrm {rad}}^{1,2}(\mathbb {R} ^{N})\hookrightarrow L_{K}^{q_{1}}+L_{K}^{q_{2}}$ for

$$\begin{aligned} 1<q_{1}<2\frac{\alpha _{0}+N}{N-2}\quad \mathrm{and}\quad q_{2}>\max \left\{ 1,2\frac{\alpha _{\infty }+N}{N-2}\right\} , \end{aligned}$$

(28)

provided that $\exists R_{1},R_{2}>0$ such that

$$\begin{aligned} \mathop {\hbox {ess sup}}\limits _{r>R_{2}}\frac{K\left( r\right) }{r^{\alpha _{\infty }}} <+\infty \quad \mathrm{and}\quad \mathop {\hbox {ess sup}}\limits _{r\in \left( 0,R_{1}\right) } \frac{K\left( r\right) }{r^{\alpha _{0}}}<+\infty \quad \mathrm{with }\,\,\alpha _{0}>-\frac{N+2}{2}. \end{aligned}$$

(29)

This result has already been proved in [9, Theorem 4.1], assuming $K\in L_{\mathrm {loc}}^{\infty }(\left( 0,+\infty \right) )$. Of course, according to (28), in (29) it is convenient to choose $\alpha _{0}$ as large as possible and $\alpha _{\infty }$ as small as possible. For instance, if $K\left( r\right) =r^{d}$ with $d>-\left( N+2\right) /2$, we choose $\alpha _{0}=\alpha _{\infty }=d$ and obtain the compact embedding

$$\begin{aligned} D_{\mathrm {rad}}^{1,2}(\mathbb {R}^{N})\hookrightarrow L_{K}^{q_{1}}+L_{K}^{q_{2}}\qquad \mathrm{for}\quad 1<q_{1}<2\frac{d+N}{N-2} <q_{2}. \end{aligned}$$

Observe that $2(d+N)/(N-2)$ is the “critical exponent” found by Ni [22] for the Hénon equation. We also observe that, if (29) holds for some $\alpha _{0}>\alpha _{\infty }$, then we can take $q_{1}=q_{2}$ in (28) and we get the compact embedding

$$\begin{aligned} D_{\mathrm {rad}}^{1,2}(\mathbb {R}^{N})\hookrightarrow L_{K}^{q}\qquad \mathrm{for} \quad \max \left\{ 1,2\frac{\alpha _{\infty }+N}{N-2}\right\} <q<2\frac{ \alpha _{0}+N}{N-2} \end{aligned}$$

(cf. [9, Corollary 4.6]).

Example 3

Essentially the same result of Example 2 holds if $V$ is not singular at the origin and, roughly speaking, decays at infinity much faster than $K$ (or is compactly supported). The result becomes different (and better) if $K$ decays at infinity similarly to $V$, or much faster. For example, consider the potentials

$$\begin{aligned} V\left( r\right) =e^{-ar},\quad K_{1}\left( r\right) =r^{d},\quad K_{2}\left( r\right) =r^{d}e^{-br},\quad a,b>0,\quad d>-\frac{N+2}{2}. \end{aligned}$$

Since $V$ does not satisfy (24) or (18), we study the embedding properties of $H_{V,\mathrm {r}}^{1}$ by Theorems 2, 3 and 1. According to Remark 1(3), both for $K=K_{1}$ and $K=K_{2}$, Theorem 2 leads to take

$$\begin{aligned} 1<q_{1}<2\frac{d+N}{N-2}. \end{aligned}$$

If $K=K_{1}$, the ratio in (14) is bounded only if $\beta _{\infty }=0$ and the best $\alpha _{\infty }$ we can take is $\alpha _{\infty }=d$, which yields $q_{2}>2\frac{d+N}{N-2}$. Then we get the compact embedding

$$\begin{aligned} H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K_{1}}^{q_{1}}+L_{K_{1}}^{q_{2}}\qquad \mathrm{for}\quad 1<q_{1}<2\frac{d+N }{N-2}<q_{2}. \end{aligned}$$

If $K=K_{2}$, instead, assumption (14) holds with $\beta _{\infty }=0$ and $\alpha _{\infty }\in \mathbb {R}$ arbitrary, so that we can take $q_{2}>1$ arbitrary. Picking $q_{2}=q_{1}$, we get the compact embedding

$$\begin{aligned} H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K_{2}}^{q}\qquad \mathrm{for}\quad 1<q<2 \frac{d+N}{N-2}. \end{aligned}$$

A similar but weaker result follows from the theorems of [18], which yield the compact embedding

$$\begin{aligned} H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K_{2}}^{q}\qquad \mathrm{for}\quad 2<q<2 \frac{d+N}{N-2}. \end{aligned}$$

Note that this requires the restriction $d>-2$. Even though they belong to the Hardy–Dieudonné comparison class, no result is available in [18] for the potentials $V$ and $K_{1}$, due to a lack of compatibility between their behaviours at zero and at infinity.

Example 4

Consider the potentials

$$\begin{aligned} V\left( r\right) =e^{\frac{1}{r}},\quad K\left( r\right) =e^{\frac{b}{r} },\quad 0<b\le 1. \end{aligned}$$

Since $V$ satisfies (24), we apply Theorem 1 together with Theorems 3 and 5. Assumption (14) holds for $\alpha _{\infty }\ge 0$ and $0\le \beta _{\infty }\le 1$, so that the best choice for $\alpha _{\infty }$, which is $\alpha _{\infty }=0$, gives

$$\begin{aligned} \max \left\{ 1,2\beta _{\infty },q^{*}\left( 0,\beta _{\infty }\right) \right\} =2\frac{N-2\beta _{\infty }}{N-2}. \end{aligned}$$

Now we then take $\beta _{\infty }=1$, so that Theorem 3 gives $q_{2}>2$. Observe that the same result ensues by applying Theorem 4 with $\gamma _{\infty }=0$ in assumption (18). As to Theorem 5, hypothesis (24) holds with $\gamma _{0}\ge 2$ arbitrary and therefore the most convenient choice is to assume $\gamma _{0}>2N-2$ (see Remark 3(4)). On the other hand, we have

$$\begin{aligned} \frac{K\left( r\right) }{r^{\alpha _{0}}V\left( r\right) ^{\beta _{0}}}= \frac{e^{\frac{b-\beta _{0}}{r}}}{r^{\alpha _{0}}} \end{aligned}$$

and thus hypothesis (23) holds for some $\alpha _{0}\in \mathbb {R}$ if and only if $b\le \beta _{0}\le 1$. We now distinguish two cases. If $b<1$, we can take $\beta _{0}>b$ and thus (23) holds for every $\alpha _{0}\in \mathbb {R}$, so that Theorem 5 gives $q_{1}>\max \left\{ 1,2\beta _{0}\right\}$ (see Fig. 5), i.e., $q_{1}>\max \left\{ 1,2b\right\}$. If $b=1$, then we need to take $\beta _{0}=1$ and thus (23) holds for $\alpha _{0}\le 0$. Since $\gamma _{0}>2N-2$ implies

$$\begin{aligned} \mathcal {A}_{1,\gamma _{0}}&= \left\{ \left( \alpha ,q\right) \in \mathbb {R}^{2}:q>\max \left\{ 2,q_{**}\left( \alpha ,1,\gamma _{0}\right) \right\} \right\} \\&= \left\{ \left( \alpha ,q\right) \in \mathbb {R}^{2}:q>\max \left\{ 2,2-\frac{4\alpha }{\gamma _{0}-2\left( N-1\right) }\right\} \right\} , \end{aligned}$$

the best choice for $\alpha _{0}\le 0$ is $\alpha _{0}=0$ and we get that $\left( 0,q_{1}\right) \in \mathcal {A}_{1,\gamma _{0}}$ if and only if $q_{1}>2$. Hence Theorem 5 gives $q_{1}>\max \left\{ 1,2b\right\}$ again. As a conclusion, recalling the condition $q_{2}>2$ and observing that $0<b\le 1$ implies $\max \left\{ 1,2b\right\} \le 2$, we obtain the compact embedding

$$\begin{aligned} H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}\qquad \mathrm{for}\quad q>2. \end{aligned}$$

If we now modify $V$ by taking a compactly supported potential $V_{1}$ such that $V_{1}\left( r\right) \sim V\left( r\right)$ as $r\rightarrow 0^{+}$, everything works as above in applying Theorem 5, but we now need to take $\beta _{\infty }=0$ and $\alpha _{\infty }\ge 0$ in Theorem 3. This gives

$$\begin{aligned} \max \left\{ 1,2\beta _{\infty },q^{*}\left( \alpha _{\infty },\beta _{\infty }\right) \right\} =2\frac{\alpha _{\infty }+N}{N-2} \end{aligned}$$

and thus, choosing $\alpha _{\infty }=0$, we get the compact embedding

$$\begin{aligned} H_{V_{1},\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}\qquad \mathrm{for}\quad q>2^{*}. \end{aligned}$$

Similarly, if we modify $V$ by taking a potential $V_{2}$ such that $V_{2}\left( r\right) \sim V\left( r\right)$ as $r\rightarrow 0^{+}$ and $V_{2}\left( r\right) \sim r^{N}$ as $r\rightarrow +\infty$, Theorem 5 yields $q_{1}>\max \left\{ 1,2b\right\}$ as above and Theorem 3 gives $q_{2}>1$ (apply it for instance with $\alpha _{\infty }=-N/2$ and $\beta _{\infty }=1/2$), so that we get the compact embedding

$$\begin{aligned} H_{V_{2},\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}\qquad \mathrm{for}\quad q>\max \left\{ 1,2b\right\} . \end{aligned}$$

The compact embeddings $H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}$ and $H_{V_{2},\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}$ also follow from the results of [18], but for $q>2$ in both cases. No result is available in [18] for the embedding $H_{V_{1},\mathrm {r} }^{1}\hookrightarrow L_{K}^{q}$, since $V_{1}$ has compact support.

Example 5

Consider the potential

$$\begin{aligned} V\left( r\right) =r^{a},\quad -2\left( N-1\right) <a<-N, \end{aligned}$$

(30)

and let $K$ be as in $\left( \mathbf {K}\right)$ and such that

$$\begin{aligned} K\left( r\right) =O( r^{b_{0}}) _{r\rightarrow 0^{+}},\quad K\left( r\right) =O( r^{b}) _{r\rightarrow +\infty },\quad b_{0}>a,\quad b\in \mathbb {R}. \end{aligned}$$

(31)

Since $V$ satisfies (24) with $\gamma _{0}=-a$ (cf. Remark 3(4) for the best choice of $\gamma _{0}$), we apply Theorem 1 together with Theorems 3 and 5, where assumptions (14) and (23) hold for $\alpha _{\infty }\ge b-a\beta _{\infty }$ and $\alpha _{0}\le b_{0}-a\beta _{0}$ with $0\le \beta _{\infty }\le 1$ and $\beta _{0}\le 1$ arbitrary. Note that $N<\gamma _{0}<2N-2$. According to (15) and (25) (see in particular Fig. 3), it is convenient to choose $\alpha _{\infty }$ as small as possible and $\alpha _{0}$ as large as possible, so we take

$$\begin{aligned} \alpha _{\infty }=b-a\beta _{\infty },\quad \alpha _{0}=b_{0}-a\beta _{0}. \end{aligned}$$

(32)

Then $q^{*}=q^{*}\left( \alpha _{\infty },\beta _{\infty }\right)$, $q_{*}=q_{*}\left( \alpha _{0},\beta _{0},-a\right)$ and $q_{**}=q_{**}\left( \alpha _{0},\beta _{0},-a\right)$ are given by

$$\begin{aligned} q^{*}=2\frac{N+b-\left( a+2\right) \beta _{\infty }}{N-2},\quad q_{*}=2\frac{ N+b_{0}}{N+a}\quad \mathrm{and}\quad q_{**}=2\frac{2N-2+2b_{0}-a}{2N-2+a}. \end{aligned}$$

Since $a+2<2-N<0$, the exponent $q^{*}$ is increasing in $\beta _{\infty }$ and thus, according to (15) again, the best choice for $\beta _{\infty }$ is $\beta _{\infty }=0$. This yields

$$\begin{aligned} q_{2}>\max \left\{ 1,2\frac{N+b}{N-2}\right\} . \end{aligned}$$

(33)

As to Theorem 5, we observe that, thanks to the choice of $\alpha _{0}$, the exponents $q_{*}$ and $q_{**}$ are independent of $\beta _{0}$, so that we can choose $\beta _{0}=0$ in order to get the region $\mathcal {A} _{\beta _{0},-a}$ as large as possible (cf. Fig. 3 or the third definition in (22)). Then we get $\alpha _{0}=b_{0}>a=\alpha _{1}$ (recall (32) and the definition (20) of $\alpha _{1}$), so that $\left( \alpha _{0},q_{1}\right) \in \mathcal {A}_{0,-a}$ if and only if

$$\begin{aligned} \max \left\{ 1,2\frac{N+b_{0}}{N+a}\right\} <q_{1}<2\frac{2N-2+2b_{0}-a}{ 2N-2+a}. \end{aligned}$$

(34)

As a conclusion, we obtain the compact embedding

$$\begin{aligned} H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q_{1}}+L_{K}^{q_{2}}\qquad \mathrm{for\,\, every\,\, }\,\,q_{1},q_{2}\,\,\mathrm { satisfying\,\, (33)\,\, and\,\, (34).} \end{aligned}$$

If furthermore $a,b,b_{0}$ are such that

$$\begin{aligned} \frac{N+b}{N-2}<\frac{2N-2+2b_{0}-a}{2N-2+a}, \end{aligned}$$

(35)

then we can take $q_{1}=q_{2}$ and we get the compact embedding

$$\begin{aligned} H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}\qquad \mathrm{for}\quad \max \left\{ 1,2\frac{N+b_{0}}{N+a},2\frac{N+b}{N-2}\right\} <q<2\frac{ 2N-2+2b_{0}-a}{2N-2+a}. \end{aligned}$$

(36)

Observe that the potentials $V$ and $K$ behave as a power and thus they fall into the classes considered in [18, 26, 28]. In particular, the results of [28] and [18] (which are the same for $V,K$ as in (30), (31)) provide the compact embedding

$$\begin{aligned} H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}\qquad \mathrm{for}\quad \max \left\{ 2,2\frac{N+b}{N-2}\right\} =:\underline{q}<q<\overline{q}:=2\frac{ 2N-2+2b_{0}-a}{2N-2+a}. \end{aligned}$$

(37)

This requires condition (35), which amounts to $\underline{q} <\overline{q}$, and no compact embedding is found in [18, 28] if (35) fails. Moreover, our result improves ( 37) even if (35) holds. Indeed, $b_{0}>a$ and $N+a<0$ imply $\frac{N+b_{0}}{N+a}<1$ and thus one has

$$\begin{aligned} \underline{q}=\left\{ \begin{array}{ll} 2\frac{N+b}{N-2}=\max \left\{ 1,2\frac{N+b}{N-2},2\frac{N+b_{0}}{N+a} \right\} &{} \quad \mathrm{if }\,\,b\ge -2 \\ 2>\max \left\{ 1,2\frac{N+b}{N-2},2\frac{N+b_{0}}{N+a}\right\} &{}\quad \mathrm{if }\,\, b<-2 \end{array} \right. , \end{aligned}$$

so that (36) is exactly (37) if $b\ge -2$ and it is better if $b<-2$. This last case actually concerns sub-quadratic exponents, so it should be also compared with the results of [26], where, setting

$$\begin{aligned} b_{1}:=\frac{a-2-2N}{4},\qquad b_{2}:=\frac{a-2}{2},\qquad b_{3}:=-\frac{N+2 }{2} \end{aligned}$$

(notice that $-N<b_{1}<b_{2}<b_{3}<-2$ for $a$ as in (30)) and

$$\begin{aligned} \underline{q}^{\prime }:=\left\{ \begin{array}{ll} 2\frac{N+b}{N-2} &{} \quad \mathrm{if }\,\,b\in \left[ b_{3},-2\right) \\ 4\frac{N+b}{2N-2+a} &{}\quad \mathrm{if }\,\,b\in \left[ b_{1},b_{2}\right) \end{array} \right. ,\qquad \overline{q}^{\prime }:=\left\{ \begin{array}{ll} 2\frac{N+b_{0}}{N-2} &{} \quad \mathrm{if }\,\,b_{0}\in \left( b_{3},-2\right] \\ 4\frac{N+b_{0}}{2N-2+a} &{} \quad \mathrm{if }\,\,b_{0}\in \left( b_{1},b_{2}\right] \end{array} \right. , \end{aligned}$$

(38)

the authors find the compact embedding

$$\begin{aligned} H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q}\qquad \mathrm{for}\quad \underline{q}^{\prime }<q<\overline{q}^{\prime }. \end{aligned}$$

(39)

Our result (36)–(35) extends (39) in three directions. First, (39) requires that $\underline{q} ^{\prime }$ and $\overline{q}^{\prime }$ are defined, i.e., $b$ and $b_{0}$ lie in the intervals considered in (38), while (36) and (35) do not need such a restriction, also covering cases of $b\in \left( -\infty ,b_{1}\right) \cup \left[ b_{2},b_{3}\right)$ or $b_{0}\in \left( a,b_{1}\right] \cup \left( b_{2},b_{3}\right]$ (take for instance $b_{0}>a$ arbitrary and $b$ small enough to satisfy (35)). Moreover, (39) asks for the further condition $\underline{q}^{\prime }<\overline{q}^{\prime }$, which can be false even if $\underline{q}^{\prime }$ and $\overline{q}^{\prime }$ are defined (take for instance $b_{3}<b=b_{0}<-2$ or $b_{1}<b=b_{0}<b_{2}$, which give $\underline{ q}^{\prime }=\overline{q}^{\prime }$), while condition (35) does not. Indeed, as soon as $\underline{q}^{\prime }$ and $\overline{q} ^{\prime }$ are defined, one has $b<-2$ and $b_{0}>-N$, which imply

$$\begin{aligned} \frac{N+b}{N-2}-\frac{2N-2+2b_{0}-a}{2N-2+a}<1+\frac{2+a}{2N-2+a}=2\frac{N+a }{2N-2+a}<0. \end{aligned}$$

Finally, setting

$$\begin{aligned} \underline{q}^{\prime \prime }:=\max \left\{ 1,2\frac{N+b_{0}}{N+a},2\frac{ N+b}{N-2}\right\} \end{aligned}$$

for brevity, some computations (which we leave to the reader) show that, whenever $\underline{q}^{\prime }$ and $\overline{q}^{\prime }$ are defined, one has

$$\begin{aligned} \underline{q}^{\prime }=\left\{ \begin{array}{ll} 2\frac{N+b}{N-2}=\underline{q}^{\prime \prime } &{} \mathrm{if }\,\,b\in \left[ b_{3},-2\right) \\ 4\frac{N+b}{2N-2+a}=1=\underline{q}^{\prime \prime }~~ &{} \mathrm{if } \,\,b=b_{1} \\ 4\frac{N+b}{2N-2+a}>1=\underline{q}^{\prime \prime } &{} \mathrm{if }\,\,b\in \left( b_{1},b_{2}\right) \end{array} \right. \quad \mathrm{and}\quad \overline{q}^{\prime }<2\frac{2N-2+2b_{0}-a}{ 2N-2+a}. \end{aligned}$$

This shows that (36) always gives a wider range of exponents $q$ than (39).

4 Proof of Theorem 1

Assume $N\ge 3$ and let $V$ and $K$ be as in $\left( \mathbf {V}\right)$ and $\left( \mathbf {K}\right)$.

Recall the definitions (3) and (6) of the Hilbert spaces $H_{V}^{1}$ and $H_{V,\mathrm {r}}^{1}$ and fix two constants $S_{N}>0$ and $C_{N}>0$, only dependent on $N$, such that

$$\begin{aligned} \forall u\in H_{V}^{1}\left( \mathbb {R}^{N}\right) ,\quad \left\| u\right\| _{L^{2^{*}}\left( \mathbb {R}^{N}\right) }\le S_{N}\left\| u\right\| \end{aligned}$$

(40)

and

$$\begin{aligned} \forall u\in H_{V,\mathrm {r}}^{1}\left( \mathbb {R}^{N}\right) ,\quad \left| u\left( x\right) \right| \le C_{N}\left\| u\right\| \frac{1}{\left| x\right| ^{\frac{N-2}{2}}}\quad \mathrm {almost\,\, everywhere\,\, on }\,\,\mathbb {R}^{ N}. \end{aligned}$$

(41)

The first constant $S_{N}$ exists by Sobolev inequality and the continuous embedding $H_{V}^{1}\hookrightarrow D^{1,2}(\mathbb {R}^{N})$. The second constant $C_{N}$ does exist by Ni’s inequality [22] (see also [28, Lemma 1]) and the continuous embedding $H_{V,\mathrm {r} }^{1}\hookrightarrow D_{\mathrm {rad}}^{1,2}(\mathbb {R}^{N})$.

Recall from assumption $\left( \mathbf {K}\right)$ that $K\in L_{\mathrm {loc} }^{s}\left( \left( 0,+\infty \right) \right)$ for some $s>\frac{2N}{N+2}\ \left( = \frac{2^{*}}{2^{*}-1}\right)$.

Lemma 1

Let $R>r>0$ and $1<q<\infty$. Then there exists a constant $\tilde{C}=\tilde{C}\left( N,r,R,q,s\right) >0$ such that $\forall u\in H_{V,\mathrm {r }}^{1}$ and $\forall h\in H_{V}^{1}$ one has

$$\begin{aligned} \frac{\int _{B_{R}\setminus B_{r}}K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx}{\tilde{C}\left\| K\left( \left| \cdot \right| \right) \right\| _{L^{s}(B_{R}\setminus B_{r})}}\le \left\{ \begin{array}{l@{\quad }l} \left( \int _{B_{R}\setminus B_{r}}\left| u\right| ^{2}dx\right) ^{\frac{q-1}{ 2}}\left\| h\right\| &{} \mathrm{if }\,\,\hbox {q}\le {\tilde{q}} \\ \left( \int _{B_{R}\setminus B_{r}}\left| u\right| ^{2}dx\right) ^{\frac{ \tilde{q}-1}{2}}\left\| u\right\| ^{q-\tilde{q}}\left\| h\right\| \quad &{} \mathrm{if }\,\,\hbox {q}>{\tilde{q}} \end{array} \right. \end{aligned}$$

where $\tilde{q}:=2\left( 1+\frac{1}{N}-\frac{1}{s}\right)$ (note that $s> \frac{2N}{N+2}$ implies $\tilde{q}>1$).

Proof

For simplicity, we denote by $\sigma$ the Hölder-conjugate exponent of $2^{*}$, i.e., $\sigma :=2N/\left( N+2\right)$. By Hölder inequality (note that $\frac{s}{\sigma }>1$), we have

$$\begin{aligned}&\int _{B_{R}\setminus B_{r}}K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx \\&\quad \le \left( \int _{B_{R}\setminus B_{r}}K\left( \left| x\right| \right) ^{\sigma }\left| u\right| ^{\left( q-1\right) \sigma }dx\right) ^{\frac{1}{\sigma }}\left( \int _{B_{R}\setminus B_{r}}\left| h\right| ^{2^{*}}dx\right) ^{\frac{1}{2^{*}}} \\&\quad \le \left( \left( \int _{B_{R}\setminus B_{r}}K\left( \left| x\right| \right) ^{s}dx\right) ^{\frac{\sigma }{s}}\left( \int _{B_{R}\setminus B_{r}}\left| u\right| ^{\left( q-1\right) \sigma \left( \frac{s}{\sigma } \right) ^{\prime }}dx\right) ^{\frac{1}{\left( \frac{s}{\sigma }\right) ^{\prime }}}\right) ^{\frac{1}{\sigma }}S_{N}\left\| h\right\| \\&\quad \le S_{N}\left\| K\left( \left| \cdot \right| \right) \right\| _{L^{s}(B_{R}\setminus B_{r})}\left\| h\right\| \left( \int _{B_{R}\setminus B_{r}}\left| u\right| ^{2\frac{q-1}{\tilde{q}-1}}dx\right) ^{\frac{\tilde{q} -1}{2}}, \end{aligned}$$

where we computed $\sigma \left( \frac{s}{\sigma }\right) ^{\prime }=\frac{ 2Ns}{\left( N+2\right) s-2N}=\frac{2}{\tilde{q}-1}$. If $q\le \tilde{q}$, then we get

$$\begin{aligned}&\int _{B_{R}\setminus B_{r}}K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx \\&\quad \le S_{N}\left\| K\left( \left| \cdot \right| \right) \right\| _{L^{s}(B_{R}\setminus B_{r})}\left\| h\right\| \left( \left| B_{R}\setminus B_{r}\right| ^{1-\frac{q-1}{\tilde{q}-1}}\left( \int _{B_{R}\setminus B_{r}}\left| u\right| ^{2}dx\right) ^{\frac{q-1}{\tilde{ q}-1}}\right) ^{\frac{\tilde{q}-1}{2}} \\&\quad =S_{N}\left\| K\left( \left| \cdot \right| \right) \right\| _{L^{s}(B_{R}\setminus B_{r})}\left\| h\right\| \left| B_{R}\setminus B_{r}\right| ^{\frac{\tilde{q}-q}{2}}\left( \int _{B_{R}\setminus B_{r}}\left| u\right| ^{2}dx\right) ^{\frac{q-1}{2}}. \end{aligned}$$

Otherwise, if $q>\tilde{q}$, then by (41) we obtain

$$\begin{aligned}&\int _{B_{R}\setminus B_{r}}K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx \\&\quad \le S_{N}\left\| K\left( \left| \cdot \right| \right) \right\| _{L^{s}(B_{R}\setminus B_{r})}\left\| h\right\| \left( \int _{B_{R}\setminus B_{r}}\left| u\right| ^{2\frac{q-1}{\tilde{q}-1} -2}\left| u\right| ^{2}dx\right) ^{\frac{\tilde{q}-1}{2}} \\&\quad \le S_{N}\left\| K\left( \left| \cdot \right| \right) \right\| _{L^{s}(B_{R}\setminus B_{r})}\left\| h\right\| \left( \frac{C_{N}\left\| u\right\| }{r^{\frac{N-2}{2}}}\right) ^{q-\tilde{q}}\left( \int _{B_{R}\setminus B_{r}}\left| u\right| ^{2}dx\right) ^{\frac{\tilde{q}-1 }{2}}. \end{aligned}$$

This concludes the proof. $\square$

For future reference, we recall here some results from [9] concerning the sum space

$$\begin{aligned} L_{K}^{p_{1}}+L_{K}^{p_{2}}:=L_{K}^{p_{1}}( \mathbb {R}^{N}) +L_{K}^{p_{2}}( \mathbb {R}^{N}) :=\{ u_{1}+u_{2}: u_i\in L_K^{p_i}( \mathbb {R}^N),\quad i=1,2 \}, \end{aligned}$$

where we assume $1<p_{1}\le p_{2}<\infty$. Such a space can be characterized as the set of the measurable mappings $u:\mathbb {R} ^{N}\rightarrow \mathbb {R}$ for which there exists a measurable set $E\subseteq \mathbb {R}^{N}$ such that $u\in L_{K}^{p_{1}}\left( E\right) \cap L_{K}^{p_{2}}\left( E^{c}\right)$ (of course $L_{K}^{p_{1}}\left( E\right) :=L^{p_{1}}(E,K\left( \left| x\right| \right) dx)$, and so for $L_{K}^{p_{2}}\left( E^{c}\right)$). It is a Banach space with respect to the norm

$$\begin{aligned} \left\| u\right\| _{L_{K}^{p_{1}}+L_{K}^{p_{2}}}:=\inf _{u_{1}+u_{2}=u}\max \left\{ \left\| u_{1}\right\| _{L_{K}^{p_{1}}},\left\| u_{2}\right\| _{L_{K}^{p_{2}}}\right\} \end{aligned}$$

and the continuous embedding $L_{K}^{p}\hookrightarrow L_{K}^{p_{1}}+L_{K}^{p_{2}}$ holds for all $p\in \left[ p_{1},p_{2}\right]$.

Proposition 1

([9, Proposition 2.7]) Let $\left\{ u_{n}\right\} \subseteq L_{K}^{p_{1}}+L_{K}^{p_{2}}$ be a sequence such that $\forall \varepsilon >0$ there exist $n_{\varepsilon }>0$ and a sequence of measurable sets $E_{\varepsilon ,n}\subseteq \mathbb {R}^{N}$ satisfying

$$\begin{aligned} \forall n>n_{\varepsilon },\quad \int _{E_{\varepsilon ,n}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{p_{1}}dx+\int _{E_{\varepsilon ,n}^{c}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{p_{2}}dx<\varepsilon . \end{aligned}$$

(42)

Then $u_{n}\rightarrow 0$ in $L_{K}^{p_{1}}+L_{K}^{p_{2}}$.

Proposition 2

([9, Propositions 2.17 and 2.14, Corollary 2.19]) Let $E\subseteq \mathbb {R}^{N}$ be a measurable set.

• i. If $\int _{E}K\left( \left| x\right| \right) dx<\infty$, then $L_{K}^{p_{1}}+L_{K}^{p_{2}}$ is continuously embedded into $L_{K}^{p_{1}}\left( E\right)$.

• ii. Every $u\in (L_{K}^{p_{1}}+L_{K}^{p_{2}})\cap L^{\infty }\left( E\right)$ satisfies

  $$\begin{aligned} \left\| u\right\| _{L_{K}^{p_{2}}\left( E\right) }^{p_{2}/p_{1}}\le \left( \left\| u\right\| _{L^{\infty }\left( E\right) }^{p_{2}/p_{1}-1}+\left\| u\right\| _{L_{K}^{p_{2}}\left( E\right) }^{p_{2}/p_{1}-1}\right) \left\| u\right\| _{L_{K}^{p_{1}}+L_{K}^{p_{2}}}. \end{aligned}$$

  (43)

  If moreover $\left\| u\right\| _{L^{\infty }\left( E\right) }\le 1$, then

  $$\begin{aligned} \left\| u\right\| _{L_{K}^{p_{2}}\left( E\right) }\le 2\left\| u\right\| _{L_{K}^{p_{1}}+L_{K}^{p_{2}}}+1. \end{aligned}$$

  (44)

Recall the definitions (8)–(9) of the functions $\mathcal {S}_{0}$ and $\mathcal {S}_{\infty }$.

Proof of Theorem 1

We prove each part of the theorem separately.

• i. By the monotonicity of $\mathcal {S}_{0}$ and $\mathcal {S} _{\infty }$, it is not restrictive to assume $R_{1}<R_{2}$ in hypothesis $( \mathcal {S}_{q_{1},q_{2}}^{\prime })$. In order to prove the continuous embedding, let $u\in H_{V,\mathrm {r}}^{1}$, $u\ne 0$. Then we have

  $$\begin{aligned} \int _{B_{R_{1}}}K\left( \left| x\right| \right) \left| u\right| ^{q_{1}}dx=\left\| u\right\| ^{q_{1}}\int _{B_{R_{1}}}K\left( \left| x\right| \right) \frac{\left| u\right| ^{q_{1}}}{\left\| u\right\| ^{q_{1}}}dx\le \left\| u\right\| ^{q_{1}}\mathcal {S}_{0}\left( q_{1},R_{1}\right) \end{aligned}$$

  (45)

  and, similarly,

  $$\begin{aligned} \int _{B_{R_{2}}^{c}}K\left( \left| x\right| \right) \left| u\right| ^{q_{2}}dx\le \left\| u\right\| ^{q_{2}}\mathcal {S}_{\infty }\left( q_{2},R_{2}\right) . \end{aligned}$$

  (46)

  On the other hand, by Lemma 1 and the continuous embedding $D_{\mathrm {rad}}^{1,2}(\mathbb {R}^{N})\hookrightarrow L_{\mathrm {loc}}^{2}(\mathbb { R}^{N})$, we deduce that there exists a constant $C_{1}>0$, independent from $u$, such that

  $$\begin{aligned} \int _{B_{R_{2}}\setminus B_{R_{1}}}K\left( \left| x\right| \right) \left| u\right| ^{q_{1}}dx\le C_{1}\left\| u\right\| ^{q_{1}}. \end{aligned}$$

  (47)

  Hence $u\in L_{K}^{q_{1}}(B_{R_{2}})\cap L_{K}^{q_{2}}(B_{R_{2}}^{c})$ and thus $u\in L_{K}^{q_{1}}+L_{K}^{q_{2}}$. Moreover, if $u_{n}\rightarrow 0$ in $H_{V,\mathrm {r}}^{1}$, then, using (45), (46) and (47), we get

  $$\begin{aligned} \int _{B_{R_{2}}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{q_{1}}dx+\int _{B_{R_{2}}^{c}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{q_{2}}dx=o\left( 1\right) _{n\rightarrow \infty }, \end{aligned}$$

  which means $u_{n}\rightarrow 0$ in $L_{K}^{q_{1}}+L_{K}^{q_{2}}$ by Proposition 1.

• ii. Assume hypothesis $( \mathcal {S}_{q_{1},q_{2}}^{\prime \prime })$. Let $\varepsilon >0$ and let $u_{n}\rightharpoonup 0$ in $H_{V,\mathrm {r}}^{1}$. Then $\left\{ \left\| u_{n}\right\| \right\}$ is bounded and, arguing as for (45) and (46), we can take $r_{\varepsilon }>0$ and $R_{\varepsilon }>r_{\varepsilon }$ such that for all $n$ one has

  $$\begin{aligned} \int _{B_{r_{\varepsilon }}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{q_{1}}dx\le \left\| u_{n}\right\| ^{q_{1}}\mathcal {S} _{0}\left( q_{1},r_{\varepsilon }\right) \le \sup _{n}\left\| u_{n}\right\| ^{q_{1}}\mathcal {S}_{0}\left( q_{1},r_{\varepsilon }\right) <\frac{ \varepsilon }{3} \end{aligned}$$

  and

  $$\begin{aligned} \int _{B_{R_{\varepsilon }}^{c}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{q_{2}}dx\le \sup _{n}\left\| u_{n}\right\| ^{q_{2}}\mathcal {S} _{\infty }\left( q_{2},R_{\varepsilon }\right) <\frac{\varepsilon }{3}. \end{aligned}$$

  Using Lemma 1 and the boundedness of $\left\{ \left\| u_{n}\right\| \right\}$ again, we infer that there exist two constants $C_{2},l>0$, independent from $n$, such that

  $$\begin{aligned} \int _{B_{R_{\varepsilon }}\setminus B_{r_{\varepsilon }}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{q_{1}}dx\le C_{2}\left( \int _{B_{R_{\varepsilon }}\setminus B_{r_{\varepsilon }}}\left| u_{n}\right| ^{2}dx\right) ^{l}, \end{aligned}$$

  where

  $$\begin{aligned} \int _{B_{R_{\varepsilon }}\setminus B_{r_{\varepsilon }}}\left| u_{n}\right| ^{2}dx\rightarrow 0\quad \mathrm{as }\,\,n\rightarrow \infty \quad \mathrm {(} \varepsilon \,\, \mathrm {fixed)} \end{aligned}$$

  thanks to the compactness of the embedding $D_{\mathrm {rad}}^{1,2}(\mathbb {R} ^{N})\hookrightarrow L_{\mathrm {loc}}^{2}(\mathbb {R}^{N})$. Therefore we obtain

  $$\begin{aligned} \int _{B_{R_{\varepsilon }}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{q_{1}}dx+\int _{B_{R_{\varepsilon }}^{c}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{q_{2}}dx<\varepsilon \end{aligned}$$

  for all $n$ sufficiently large, which means $u_{n}\rightarrow 0$ in $L_{K}^{q_{1}}+L_{K}^{q_{2}}$ (Proposition 1). This concludes the proof of part (ii).

• iii. First we observe that $K\left( \left| \cdot \right| \right) \in L^{1}(B_{1})$ and assumption $\left( \mathbf {K}\right)$ imply $K\left( \left| \cdot \right| \right) \in L_{\mathrm {loc}}^{1}(\mathbb {R}^{N})$. Assume $H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q_{1}}+L_{K}^{q_{2}}$ with $q_{1}\le q_{2}$. Fix $R_{1}>0$. Then, by (i) of Proposition 2, there exist two constants $c_{1},c_{2}>0$ such that $\forall u\in H_{V, \mathrm {r}}^{1}$ we have

  $$\begin{aligned} \int _{B_{R_{1}}}K\left( \left| x\right| \right) \left| u\right| ^{q_{1}}dx\le c_{1}\left\| u\right\| _{L_{K}^{q_{1}}+L_{K}^{q_{2}}}^{q_{1}}\le c_{2}\left\| u\right\| ^{q_{1}}, \end{aligned}$$

  which implies $\mathcal {S}_{0}\left( q_{1},R_{1}\right) \le c_{2}$. By (41), fix $R_{2}>0$ such that every $u\in H_{V,\mathrm {r} }^{1}$ with $\left\| u\right\| =1$ satisfies $\left| u\left( x\right) \right| \le 1$ almost everywhere on $B_{R_{2}}^{c}$. Then, by (44), we have

  $$\begin{aligned} \int _{B_{R_{2}}^{c}}K\left( \left| x\right| \right) \left| u\right| ^{q_{2}}dx\le \left( 2\left\| u\right\| _{L_{K}^{q_{1}}+L_{K}^{q_{2}}}+1\right) ^{q_{2}}\le \left( c_{3}\left\| u\right\| +1\right) ^{q_{2}}=\left( c_{3}+1\right) ^{q_{2}} \end{aligned}$$

  for some constant $c_{3}>0$. This gives $\mathcal {S}_{\infty }\left( q_{2},R_{2}\right) <\infty$ and thus $( \mathcal {S}_{q_{1},q_{2}}^{ \prime })$ holds (with $R_{1}>0$ arbitrary and $R_{2}$ large enough). Now assume that the embedding $H_{V,\mathrm {r}}^{1}\hookrightarrow L_{K}^{q_{1}}+L_{K}^{q_{2}}$ is compact and, by contradiction, that $\lim _{R\rightarrow 0^{+}}\mathcal {S}_{0}\left( q_{1},R\right) >\varepsilon _{1}>0$ (the limit exists by monotonicity). Then for every $n\in \mathbb {N} \setminus \left\{ 0\right\}$ we have $\mathcal {S}_{0}\left( q_{1},1/n\right) >\varepsilon _{1}$ and thus there exists $u_{n}\in H_{V, \mathrm {r}}^{1}$ such that $\left\| u_{n}\right\| =1$ and

  $$\begin{aligned} \int _{B_{1/n}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{q_{1}}dx>\varepsilon _{1}. \end{aligned}$$

  Since $\left\{ u_{n}\right\}$ is bounded in $H_{V,\mathrm {r}}^{1}$, by the compactness assumption together with the continuous embedding $L_{K}^{q_{1}}+L_{K}^{q_{2}}\hookrightarrow L_{K}^{q_{1}}(B_{1})$ ((i) of Proposition 2), we get that there exists $u\in H_{V,\mathrm {r} }^{1}$ such that, up to a subsequence, $u_{n}\rightarrow u$ in $L_{K}^{q_{1}}(B_{1})$. This implies

  $$\begin{aligned} \int _{B_{1/n}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{q_{1}}dx\rightarrow 0\quad \mathrm{as }\,\,n\rightarrow \infty , \end{aligned}$$

  which is a contradiction. Similarly, if $\lim _{R\rightarrow +\infty } \mathcal {S}_{\infty }\left( q_{2},R\right) >\varepsilon _{2}>0$, then there exists a sequence $\left\{ u_{n}\right\} \subset H_{V,\mathrm {r}}^{1}$ such that $\left\| u_{n}\right\| =1$ and

  $$\begin{aligned} \int _{B_{n}^{c}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{q_{2}}dx>\varepsilon _{2}. \end{aligned}$$

  (48)

  Moreover, we can assume that $\exists u\in H_{V,\mathrm {r}}^{1}$ such that $u_{n}\rightharpoonup u$ in $H_{V,\mathrm {r}}^{1}$, $u_{n}\rightarrow u$ in $L_{K}^{q_{1}}+L_{K}^{q_{2}}$ and

  $$\begin{aligned} \left\| u_{n}-u\right\| \le \left\| u_{n}\right\| +\left\| u\right\| \le 1+\liminf _{n\rightarrow \infty }\left\| u_{n}\right\| =2. \end{aligned}$$

  (49)

  Now, by (49) and (41), fix $R_{2}>0$ such that $\left| u_{n}\left( x\right) -u\left( x\right) \right| \le 1$ almost everywhere on $B_{R_{2}}^{c}$. Then $\left\{ u_{n}-u\right\}$ is bounded in $L_{K}^{q_{2}}(B_{R_{2}}^{c})$ by (44) and therefore (43) gives

  $$\begin{aligned} \int _{B_{R_{2}}^{c}}K\left( \left| x\right| \right) \left| u_{n}-u\right| ^{q_{2}}dx\le c_{4}\left( \left\| u_{n}-u\right\| _{L_{K}^{q_{1}}+L_{K}^{q_{2}}}\right) ^{q_{1}}\rightarrow 0\quad \mathrm{as }\,\, n\rightarrow \infty \end{aligned}$$

  for some constant $c_{4}>0$. Since $u\in L_{K}^{q_{2}}(B_{R_{2}}^{c})$ by (41) and (43), this implies

  $$\begin{aligned} \int _{B_{n}^{c}}K\left( \left| x\right| \right) \left| u_{n}\right| ^{q_{2}}dx\rightarrow 0\quad \mathrm{as }\,\,n\rightarrow \infty , \end{aligned}$$

  which contradicts (48). We get $\lim _{R\rightarrow 0^{+}}\mathcal {S}_{0}\left( q_{1},R\right) =\lim _{R\rightarrow +\infty }\mathcal {S}_{\infty }\left( q_{2},R\right) =0$ and the proof is complete.

$\square$

5 Proof of Theorems 2–5

Assume $N\ge 3$ and let $V$ and $K$ be as in $\left( \mathbf {V}\right)$ and $\left( \mathbf {K}\right)$. As in the previous section, we fix a constant $S_{N}>0$ such that (40) holds.

Lemma 2

Let $\Omega \subseteq \mathbb {R}^{N}$ be a nonempty measurable set and assume that $V(r)<+\infty$ almost everywhere on $\Omega$ and

$$\begin{aligned} \Lambda :=\mathop {\hbox {ess sup}}\limits _{x\in \Omega }\frac{K\left( \left| x\right| \right) }{\left| x\right| ^{\alpha }V\left( \left| x\right| \right) ^{\beta } }<+\infty \quad { for\,\, some }\,\,0\le \beta \le 1\,\,{ ~and }\,\,\alpha \in \mathbb {R}. \end{aligned}$$

Let $u\in H_{V}^{1}$ and assume that there exist $\nu \in \mathbb {R}$ and $m>0$ such that

$$\begin{aligned} \left| u\left( x\right) \right| \le \frac{m}{\left| x\right| ^{\nu }}\quad { almost\,\, everywhere\,\, on }\,\,\Omega . \end{aligned}$$

Then $\forall h\in H_{V}^{1}$ and $\forall q>\max \left\{ 1,2\beta \right\}$ , one has

$\displaystyle \int _{\Omega }K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx$

$$\begin{aligned} \le \left\{ \begin{array}{ll} \Lambda m^{q-1}S_{N}^{1-2\beta }\left( \int _{\Omega }\left| x\right| ^{\frac{ \alpha -\nu \left( q-1\right) }{N+2\left( 1-2\beta \right) }2N}dx\right) ^{ \frac{N+2\left( 1-2\beta \right) }{2N}}\left\| h\right\| &{}\quad \mathrm {if }\,\,0\le \beta \le \frac{1}{2} \\ \Lambda m^{q-2\beta }\left( \int _{\Omega }\left| x\right| ^{\frac{\alpha -\nu \left( q-2\beta \right) }{1-\beta }}dx\right) ^{1-\beta }\left\| u\right\| ^{2\beta -1}\left\| h\right\| &{}\quad \mathrm {if }\,\,\frac{1}{2} <\beta <1 \\ \Lambda m^{q-2}\left( \int _{\Omega }\left| x\right| ^{2\alpha -2\nu \left( q-2\right) }V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{ \frac{1}{2}}\left\| h\right\| &{}\quad \mathrm {if }\,\,\beta =1. \end{array} \right. \end{aligned}$$

Proof

We distinguish several cases, where we will use Hölder inequality many times, without explicitly noting it.

Case $\beta =0$. We have

$$\begin{aligned} \frac{1}{\Lambda }\int _{\Omega }K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx&\le \int _{\Omega }\left| x\right| ^{\alpha }\left| u\right| ^{q-1}\left| h\right| dx \\&\le \left( \int _{\Omega }\left( \left| x\right| ^{\alpha }\left| u\right| ^{q-1}\right) ^{\frac{2N}{ N+2}}dx\right) ^{\frac{N+2}{2N}}\left( \int _{\Omega }\left| h\right| ^{2^{*}}dx\right) ^{\frac{1}{2^{*}}} \\&\le m^{q-1}S_{N}\left( \int _{\Omega }\left| x\right| ^{\frac{\alpha -\nu \left( q-1\right) }{N+2}2N}dx\right) ^{\frac{N+2}{2N}}\left\| h\right\| . \end{aligned}$$

Case $0<\beta <\frac{1}{2}$. One has $\frac{1}{\beta }>1$ and $\frac{1-\beta }{1-2\beta } 2^{*}>1$, with Hölder conjugate exponents $\left( \frac{1}{\beta } \right) ^{\prime }=\frac{1}{1-\beta }$ and $\left( \frac{1-\beta }{1-2\beta } 2^{*}\right) ^{\prime }=\frac{2N\left( 1-\beta \right) }{N+2\left( 1-2\beta \right) }$. Then we get

$$\begin{aligned}&\frac{1}{\Lambda }\int _{\Omega }K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx \le \int _{\Omega }\left| x\right| ^{\alpha }V\left( \left| x\right| \right) ^{\beta }\left| u\right| ^{q-1}\left| h\right| dx \\&\quad \le \left( \int _{\Omega }\left( \left| x\right| ^{\alpha }\left| u\right| ^{q-1}\left| h\right| ^{1-2\beta }\right) ^{\frac{1}{1-\beta }}dx\right) ^{1-\beta }\left( \int _{\Omega }V\left( \left| x\right| \right) \left| h\right| ^{2}dx\right) ^{\beta } \\&\quad \le \left( \int _{\Omega }\left( \left| x\right| ^{\frac{\alpha }{ 1-\beta }}\left| u\right| ^{\frac{q-1}{1-\beta }}\right) ^{\left( \frac{ 1-\beta }{1-2\beta }2^{*}\right) ^{\prime }}dx\right) ^{\frac{1-\beta }{\left( \frac{1-\beta }{1-2\beta }2^{*}\right) ^{\prime }}}\left( \int _{\Omega }\left| h\right| ^{2^{*}}dx\right) ^{\frac{(1-2\beta )(1-\beta )}{\left( 1-\beta \right) 2^{*}}} \left\| h\right\| ^{2\beta } \\&\quad \le m^{q-1} \left( \int _{\Omega }\left( \left| x\right| ^{\frac{ \alpha }{1-\beta }-\nu \frac{q-1}{1-\beta }}\right) ^{\left( \frac{1-\beta }{ 1-2\beta }2^{*}\right) ^{\prime }}dx\right) ^{\frac{1-2\beta }{\left( \frac{1-\beta }{1-2\beta }2^{*}\right) ^{\prime }}}S_{N}^{1-2\beta } \left\| h\right\| ^{1-2\beta } \left\| h\right\| ^{2\beta } \\&\quad = m^{q-1}\left( \int _{\Omega }\left| x\right| ^{\frac{\alpha -\nu \left( q-1\right) }{N+2\left( 1-2\beta \right) }2N}dx\right) ^{\frac{N+2\left( 1-2\beta \right) }{2N}}S_{N}^{1-2\beta }\left\| h\right\| . \end{aligned}$$

Case $\beta =\frac{1}{2}$. We have

$$\begin{aligned} \frac{1}{\Lambda }\int _{\Omega }K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx&\le \int _{\Omega }\left| x\right| ^{\alpha }\left| u\right| ^{q-1}V\left( \left| x\right| \right) ^{\frac{1}{2} }\left| h\right| dx \\&\le \left( \int _{\Omega }\left| x\right| ^{2\alpha }\left| u\right| ^{2\left( q-1\right) }dx\right) ^{\frac{1}{2}}\left( \int _{\Omega }V\left( \left| x\right| \right) \left| h\right| ^{2}dx\right) ^{\frac{1}{2}} \\&\le m^{q-1}\left( \int _{\Omega }\left| x\right| ^{2\alpha -2\nu \left( q-1\right) }dx\right) ^{\frac{1}{2}}\left\| h\right\| . \end{aligned}$$

Case $\frac{1}{2}<\beta <1$. One has $\frac{1}{2\beta -1}>1$, with conjugate exponent $\left( \frac{1}{2\beta -1}\right) ^{\prime }=\frac{1}{2\left( 1-\beta \right) }$. Then

$$\begin{aligned}&\frac{1}{\Lambda }\int _{\Omega }K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx \le \int _{\Omega }\left| x\right| ^{\alpha }V\left( \left| x\right| \right) ^{\beta }\left| u\right| ^{q-1}\left| h\right| dx\\&\quad \le \left( \int _{\Omega }\left| x\right| ^{2\alpha }V\left( \left| x\right| \right) ^{2\beta -1}\left| u\right| ^{2\left( q-1\right) }dx\right) ^{\frac{1}{2}}\left( \int _{\Omega }V\left( \left| x\right| \right) \left| h\right| ^{2}dx\right) ^{\frac{1}{2}} \\&\quad \le \left( \int _{\Omega }\left| x\right| ^{2\alpha }\left| u\right| ^{2\left( q-2\beta \right) }V\left( \left| x\right| \right) ^{2\beta -1}\left| u\right| ^{2\left( 2\beta -1\right) }dx\right) ^{\frac{1}{2} }\left\| h\right\| \\&\quad \le \left( \left( \int _{\Omega }\left| x\right| ^{\frac{\alpha }{1-\beta } }\left| u\right| ^{\frac{q-2\beta }{1-\beta }}dx\right) ^{2\left( 1-\beta \right) }\left( \int _{\Omega }V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{2\beta -1}\right) ^{\frac{1}{2}}\left\| h\right\| \\&\quad \le m^{q-2\beta }\left( \left( \int _{\Omega }\left| x\right| ^{\frac{ \alpha }{1-\beta }-\nu \frac{q-2\beta }{1-\beta }}dx\right) ^{2\left( 1-\beta \right) }\left( \int _{\Omega }V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{2\beta -1}\right) ^{\frac{1}{2}}\left\| h\right\| \\&\quad \le m^{q-2\beta }\left( \int _{\Omega }\left| x\right| ^{\frac{\alpha -\nu (q-2\beta )}{1-\beta }}dx\right) ^{1-\beta }\left\| u\right\| ^{2\beta -1}\left\| h\right\| . \end{aligned}$$

Case $\beta =1$. Assumption $q>\max \left\{ 1,2\beta \right\}$ means $q>2$ and thus we have

$$\begin{aligned}&\frac{1}{\Lambda }\int _{\Omega }K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx \le \int _{\Omega }\left| x\right| ^{\alpha }V\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx\\&\quad \le \left( \int _{\Omega }\left| x\right| ^{2\alpha }V\left( \left| x\right| \right) \left| u\right| ^{2\left( q-1\right) }dx\right) ^{\frac{1}{2 }}\left( \int _{\Omega }V\left( \left| x\right| \right) \left| h\right| ^{2}dx\right) ^{\frac{1}{2}} \\&\quad \le \left( \int _{\Omega }\left| x\right| ^{2\alpha }\left| u\right| ^{2\left( q-2\right) }V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{\frac{1}{2}}\left\| h\right\| \\&\quad \le m^{q-2}\left( \int _{\Omega }\left| x\right| ^{2\alpha -2\nu \left( q-2\right) }V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{ \frac{1}{2}}\left\| h\right\| . \end{aligned}$$

$\square$

As in the previous section, we fix a constant $C_{N}>0$ such that (41) holds. Recall the definitions (10)–(11) of the functions $\mathcal {R}_{0}$ and $\mathcal {R}_{\infty }$.

Proof of Theorem 2

Assume the hypotheses of the theorem and let $u\in H_{V,\mathrm {r}}^{1}$ and $h\in H_{V}^{1}$ be such that $\left\| u\right\| =\left\| h\right\| =1$. Let $0<R\le R_{1}$. We will denote by $C$ any positive constant which does not depend on $u$, $h$ and $R$. By (41) and the fact that

$$\begin{aligned} \mathop {\hbox {ess sup}}\limits _{x\in B_{R}}\frac{K\left( \left| x\right| \right) }{\left| x\right| ^{\alpha _{0}}V\left( \left| x\right| \right) ^{\beta _{0}}}\le \mathop {\hbox {ess sup}}\limits _{r\in \left( 0,R_{1}\right) }\frac{K\left( r\right) }{ r^{\alpha _{0}}V\left( r\right) ^{\beta _{0}}}<+\infty , \end{aligned}$$

we can apply Lemma 2 with $\Omega =B_{R}$, $\alpha =\alpha _{0}$, $\beta =\beta _{0}$, $m=C_{N}\left\| u\right\| =C_{N}$ and $\nu = \frac{N-2}{2}$. If $0\le \beta _{0}\le 1/2$ we get

$$\begin{aligned} \int _{B_{R}}K\left( \left| x\right| \right) \left| u\right| ^{q_{1}-1}\left| h\right| dx&\le C\left( \int _{B_{R}}\left| x\right| ^{\frac{\alpha _{0}- \frac{N-2}{2}\left( q_{1}-1\right) }{N+2\left( 1-2\beta _{0}\right) } 2N}dx\right) ^{\frac{N+2\left( 1-2\beta _{0}\right) }{2N}} \\&\le C\left( \int _{0}^{R}r^{\frac{2\alpha _{0}-\left( N-2\right) \left( q_{1}-1\right) }{N+2\left( 1-2\beta _{0}\right) }N+N-1}dr\right) ^{\frac{ N+2\left( 1-2\beta _{0}\right) }{2N}} \\&= C\left( R^{\frac{2\alpha _{0}-4\beta _{0}+2N-\left( N-2\right) q_{1}}{ N+2\left( 1-2\beta _{0}\right) }N}\right) ^{\frac{N+2\left( 1-2\beta _{0}\right) }{2N}}, \end{aligned}$$

since $2\alpha _{0}-4\beta _{0}+2N-\left( N-2\right) q_{1}=\left( N-2\right) \left( q^{*}\left( \alpha _{0},\beta _{0}\right) -q_{1}\right) >0.$ On the other hand, if $1/2<\beta _{0}<1$ we have

$$\begin{aligned} \int _{B_{R}}K\left( \left| x\right| \right) \left| u\right| ^{q_{1}-1}\left| h\right| dx&\le C\left( \int _{B_{R}}\left| x\right| ^{\frac{\alpha _{0}- \frac{N-2}{2}\left( q_{1}-2\beta _{0}\right) }{1-\beta _{0}}}dx\right) ^{1-\beta _{0}}\\&\le C\left( \int _{0}^{R}r^{\frac{\alpha _{0}-\frac{N-2}{2} \left( q_{1}-2\beta _{0}\right) }{1-\beta _{0}}+N-1}dr\right) ^{1-\beta _{0}}\\&= C\left( R^{\frac{2\alpha _{0}-\left( N-2\right) \left( q_{1}-2\beta _{0}\right) }{2\left( 1-\beta _{0}\right) }+N}\right) ^{1-\beta _{0}}, \end{aligned}$$

since

$$\begin{aligned} \frac{2\alpha _{0}-\left( N-2\right) \left( q_{1}-2\beta _{0}\right) }{ 2\left( 1-\beta _{0}\right) }+N=\frac{N-2}{2\left( 1-\beta _{0}\right) } \left( q^{*}\left( \alpha _{0},\beta _{0}\right) -q_{1}\right) >0. \end{aligned}$$

Finally, if $\beta _{0}=1$, we obtain

$$\begin{aligned} \int _{B_{R}}K\left( \left| x\right| \right) \left| u\right| ^{q_{1}-1}\left| h\right| dx&\le C\left( \int _{B_{R}}\left| x\right| ^{2\alpha _{0}-\left( N-2\right) \left( q_{1}-2\right) }V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{\frac{1}{2}} \\&\le C\left( R^{2\alpha _{0}-\left( N-2\right) \left( q_{1}-2\right) }\int _{B_{R}}V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{ \frac{1}{2}}\\&\le CR^{\frac{2\alpha _{0}-\left( N-2\right) \left( q_{1}-2\right) }{2}}, \end{aligned}$$

since $2\alpha _{0}-\left( N-2\right) \left( q_{1}-2\right) =\left( N-2\right) \left( q^{*}\left( \alpha _{0},1\right) -q_{1}\right) >0.$ So, in any case, we deduce $\mathcal {R}_{0}\left( q_{1},R\right) \le CR^{\delta }$ for some $\delta =\delta \left( N,\alpha _{0},\beta _{0},q_{1}\right) >0$ and this concludes the proof. $\square$

Proof of Theorem 3

Assume the hypotheses of the theorem and let $u\in H_{V,\mathrm {r}}^{1}$ and $h\in H_{V}^{1}$ be such that $\left\| u\right\| =\left\| h\right\| =1$. Let $R\ge R_{2}$. We will denote by $C$ any positive constant which does not depend on $u$, $h$ and $R$. By (41) and the fact that

$$\begin{aligned} \mathop {\hbox {ess sup}}\limits _{x\in B_{R}^{c}}\frac{K\left( \left| x\right| \right) }{ \left| x\right| ^{\alpha _{\infty }}V\left( \left| x\right| \right) ^{\beta _{\infty }}}\le \mathop {\hbox {ess sup}}\limits _{r>R_{2}}\frac{K\left( r\right) }{ r^{\alpha _{\infty }}V\left( r\right) ^{\beta _{\infty }}}<+\infty , \end{aligned}$$

we can apply Lemma 2 with $\Omega =B_{R}^{c}$, $\alpha =\alpha _{\infty }$, $\beta =\beta _{\infty }$, $m=C_{N}\left\| u\right\| =C_{N}$ and $\nu =\frac{N-2}{2}$. If $0\le \beta _{\infty }\le 1/2$ we get

$$\begin{aligned} \int _{B_{R}^{c}}K\left( \left| x\right| \right) \left| u\right| ^{q_{2}-1}\left| h\right| dx&\le C\left( \int _{B_{R}^{c}}\left| x\right| ^{\frac{\alpha _{\infty }-\frac{N-2}{2}\left( q_{2}-1\right) }{N+2\left( 1-2\beta _{\infty }\right) }2N}dx\right) ^{\frac{N+2\left( 1-2\beta _{\infty }\right) }{2N}} \\&\le C\left( \int _{R}^{+\infty }r^{\frac{2\alpha _{\infty }-\left( N-2\right) \left( q_{2}-1\right) }{N+2\left( 1-2\beta _{\infty }\right) } N+N-1}dr\right) ^{\frac{N+2\left( 1-2\beta _{\infty }\right) }{2N}} \\&= C\left( R^{\frac{2\alpha _{\infty }-4\beta _{\infty }+2N-\left( N-2\right) q_{2}}{N+2\left( 1-2\beta _{\infty }\right) }N}\right) ^{\frac{ N+2\left( 1-2\beta _{\infty }\right) }{2N}}, \end{aligned}$$

since $2\alpha _{\infty }-4\beta _{\infty }+2N-\left( N-2\right) q_{2}=\left( N-2\right) \left( q^{*}\left( \alpha _{\infty },\beta _{\infty }\right) -q_{2}\right) <0.$ On the other hand, if $1/2<\beta _{\infty }<1$ we have

$$\begin{aligned} \int _{B_{R}^{c}}K\left( \left| x\right| \right) \left| u\right| ^{q_{2}-1}\left| h\right| dx&\le C\left( \int _{B_{R}^{c}}\left| x\right| ^{\frac{\alpha _{\infty }-\frac{N-2}{2}\left( q_{2}-2\beta _{\infty }\right) }{1-\beta _{\infty }}}dx\right) ^{1-\beta _{\infty }} \\&\le C\left( \int _{R}^{+\infty }r^{\frac{\alpha _{\infty }-\frac{N-2}{2} \left( q_{2}-2\beta _{\infty }\right) }{1-\beta _{\infty }}+N-1}dr\right) ^{1-\beta _{\infty }} \\&= C\left( R^{\frac{2\alpha _{\infty }-\left( N-2\right) \left( q_{2}-2\beta _{\infty }\right) }{2\left( 1-\beta _{\infty }\right) }+N}\right) ^{1-\beta _{\infty }}, \end{aligned}$$

since

$$\begin{aligned} \frac{2\alpha _{\infty }-\left( N-2\right) \left( q_{2}-2\beta _{\infty }\right) }{2\left( 1-\beta _{\infty }\right) }+N=\frac{N-2}{2\left( 1-\beta _{_{\infty }}\right) }\left( q^{*}\left( \alpha _{_{\infty }},\beta _{_{\infty }}\right) -q_{2}\right) <0. \end{aligned}$$

Finally, if $\beta _{\infty }=1$, we obtain

$$\begin{aligned} \int _{B_{R}^{c}}K\left( \left| x\right| \right) \left| u\right| ^{q_{2}-1}\left| h\right| dx&\le C\left( \int _{B_{R}^{c}}\left| x\right| ^{2\alpha _{\infty }-\left( N-2\right) \left( q_{2}-2\right) }V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{\frac{1}{2}} \\&\le C\left( R^{2\alpha _{\infty }-\left( N-2\right) \left( q_{2}-2\right) }\int _{B_{R}^{c}}V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{\frac{1}{2}}\\&\le CR^{\frac{2\alpha _{\infty }-\left( N-2\right) \left( q_{2}-2\right) }{2}}, \end{aligned}$$

since $2\alpha _{\infty }-\left( N-2\right) \left( q_{2}-2\right) =\left( N-2\right) \left( q^{*}\left( \alpha _{\infty },1\right) -q_{2}\right) <0.$ This completes the proof, since in any case we get $\mathcal {R}_{\infty }\left( q_{2},R\right) \le CR^{\delta }$ for some $\delta =\delta \left( N,\alpha _{\infty },\beta _{\infty },q_{2}\right) <0$. $\square$

In proving Theorem 4, we will need the following lemma.

Lemma 3

Assume that there exists $R_{2}>0$ such that $V(r)<+\infty$ for almost every $r>R_2$ and

Then there exists a constant $c_{\infty }>0$, only dependent on $N$, such that $\forall u\in H_{V,\mathrm {r}}^{1}( \mathbb {R}^{N})$ one has

$$\begin{aligned} \left| u\left( x\right) \right| \le c_{\infty }\lambda _{\infty }^{-\frac{1}{4} }\left\| u\right\| \left| x\right| ^{-\frac{2(N-1)-\gamma _{\infty }}{4}} \quad \textit{almost}\,\, \textit{everywhere}\,\, \textit{in}\,\,B_{R_{2}}^{c}. \end{aligned}$$

(50)

Proof

The lemma is proved in [28, Lemma 4] under slightly different assumptions, but the result actually holds also in the form given here. See [8, Appendix] for a detailed proof. $\square$

Observe that $2(N-1)-\gamma _{\infty }>0$ in (50), since $\gamma _{\infty }\le 2$ and $N\ge 3$.

Proof of Theorem 4

Assume the hypotheses of the theorem and denote

$$\begin{aligned} \Lambda _{\infty }:=\mathop {\hbox {ess sup}}\limits _{r>R_{2}}\frac{K\left( r\right) }{ r^{\alpha _{\infty }}V\left( r\right) ^{\beta _{\infty }}}\quad \mathrm {and} \quad \lambda _{\infty }:=\mathop {\hbox {ess inf}}\limits _{r>R_{2}}r^{\gamma _{\infty }}V\left( r\right) . \end{aligned}$$

Let $u\in H_{V,\mathrm {r}}^{1}$ and $h\in H_{V}^{1}$ be such that $\left\| u\right\| =\left\| h\right\| =1$. Let $R\ge R_{2}$ and observe that $\forall \xi \ge 0$ one has

$$\begin{aligned} \mathop {\hbox {ess sup}}\limits _{r>R}\frac{K\left( r\right) }{r^{\alpha _{\infty }+\xi \gamma _{\infty }}V\left( r\right) ^{\beta _{\infty }+\xi }}\le \mathop {\hbox {ess sup}}\limits _{r>R_{2}}\frac{K\left( r\right) }{r^{\alpha _{\infty }}V\left( r\right) ^{\beta _{\infty }}\left( r^{\gamma _{\infty }}V\left( r\right) \right) ^{\xi }}\le \frac{\Lambda _{\infty }}{\lambda _{\infty }^{\xi }} <+\infty . \end{aligned}$$

(51)

We will denote by $C$ any positive constant which does not depend on $u$, $h$ or $R$ (such as $\Lambda _{\infty }/\lambda _{\infty }^{\xi }$ if $\xi$ does not depend on $u$, $h$ or $R$). Denoting $\alpha _{1}=\alpha _{1}\left( \beta _{\infty },\gamma _{\infty }\right)$, $\alpha _{2}=\alpha _{2}\left( \beta _{\infty }\right)$ and $\alpha _{3}=\alpha _{3}\left( \beta _{\infty },\gamma _{\infty }\right)$, as defined in (20), we will distinguish several cases, according to the description (21). In each of such cases, we will choose a suitable $\xi \ge 0$ and, thanks to (51) and ( 50), we will apply Lemma 2 with $\Omega =B_{R}^{c}$, $\alpha =\alpha _{\infty }+\xi \gamma _{\infty }$, $\beta =\beta _{\infty }+\xi$ (whence $\Lambda$ will be given by the left hand side of (51)), $m=c_{\infty }\lambda _{\infty }^{-1/4 }\left\| u\right\| =c_{\infty }\lambda _{\infty }^{-1/4 }$ and $\nu =\frac{2(N-1)-\gamma _{\infty }}{4}$. We will obtain that

$$\begin{aligned} \int _{B_{R}^{c}}K\left( \left| x\right| \right) \left| u\right| ^{q_{2}-1}\left| h\right| dx\le CR^{\delta } \end{aligned}$$

for some $\delta <0$, not dependent on $R$, so that the result follows.

Case $\alpha _{\infty }\ge \alpha _{1}$. We take $\xi =1-\beta _{\infty }$ and apply Lemma 2 with $\beta =\beta _{\infty }+\xi =1$ and $\alpha =\alpha _{\infty }+\xi \gamma _{\infty }=\alpha _{\infty }+\left( 1-\beta _{\infty }\right) \gamma _{\infty }$. We get

$$\begin{aligned} \int _{B_{R}^{c}}K\left( \left| x\right| \right) \left| u\right| ^{q_{2}-1}\left| h\right| dx&\le C\left( \int _{B_{R}^{c}}\left| x\right| ^{2\alpha -2\nu \left( q_{2}-2\right) }V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{\frac{1}{2}} \\&\le C\left( R^{2\alpha -2\nu \left( q_{2}-2\right) }\int _{B_{R}^{c}}V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{\frac{1}{2}}\\&\le CR^{\alpha -\nu \left( q_{2}-2\right) }, \end{aligned}$$

since

$$\begin{aligned} \alpha -\nu \left( q_{2}-2\right)&= \alpha _{\infty }+\left( 1-\beta _{\infty }\right) \gamma _{\infty }-\frac{2(N-1)-\gamma _{\infty }}{4}\left( q_{2}-2\right) \\&= \frac{2(N-1)-\gamma _{\infty }}{4}\left( q_{**}-q_{2}\right) <0. \end{aligned}$$

Case $\max \left\{ \alpha _{2},\alpha _{3}\right\} <\alpha _{\infty }<\alpha _{1}$. Take $\xi =\frac{\alpha _{\infty }+\left( 1-\beta _{\infty }\right) N}{N-\gamma _{\infty }}>0$ and apply Lemma 2 with $\beta =\beta _{\infty }+\xi$ and $\alpha =\alpha _{\infty }+\xi \gamma _{\infty }$. For doing this, observe that $\alpha _{3}<\alpha _{\infty }<\alpha _{1}$ implies

$$\begin{aligned} \beta =\beta _{\infty }+\xi =\frac{\alpha _{\infty }-\gamma _{\infty }\beta _{\infty }+N}{N-\gamma _{\infty }}\in \left( \frac{1}{2},1\right) . \end{aligned}$$

We get

$$\begin{aligned} \int _{B_{R}^{c}}K\left( \left| x\right| \right) \left| u\right| ^{q_{2}-1}\left| h\right| dx&\le C\left( \int _{B_{R}^{c}}\left| x\right| ^{\frac{\alpha -\nu \left( q_{2}-2\beta \right) }{1-\beta }}dx\right) ^{1-\beta }\\&\le C\left( R^{\frac{\alpha -\nu \left( q_{2}-2\beta \right) }{1-\beta }+N}\right) ^{1-\beta }, \end{aligned}$$

since

$$\begin{aligned} \frac{\alpha -\nu \left( q_{2}-2\beta \right) }{1-\beta }+N=\frac{\nu }{ 1-\beta }\left( 2\frac{\alpha _{\infty }-\beta _{\infty }\gamma _{\infty }+N }{N-\gamma _{\infty }}-q_{2}\right) =\frac{\nu }{1-\beta }\left( q_{*}-q_{2}\right) <0. \end{aligned}$$

Case $\beta _{\infty }=1$ and $\alpha _{\infty }\le 0=\alpha _{2}\,\left( =\max \left\{ \alpha _{2},\alpha _{3}\right\} \right)$. Take $\xi =0$ and apply Lemma 2 with $\beta =\beta _{\infty }+\xi =1$ and $\alpha =\alpha _{\infty }+\xi \gamma _{\infty }=\alpha _{\infty }$. We get

$$\begin{aligned} \int _{B_{R}^{c}}K\left( \left| x\right| \right) \left| u\right| ^{q_{2}-1}\left| h\right| dx&\le C\left( \int _{B_{R}^{c}}\left| x\right| ^{2\alpha _{\infty }-2\nu \left( q_{2}-2\right) }V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{\frac{1}{2}}\\&\le CR^{\alpha _{\infty }-\nu \left( q_{2}-2\right) }, \end{aligned}$$

since $\alpha _{\infty }-\nu \left( q_{2}-2\right) \le -\nu \left( q_{2}-2\right) <0.$

Case $\frac{1}{2}<\beta _{\infty }<1$ and $\alpha _{\infty }\le \alpha _{2}\,\left( =\max \left\{ \alpha _{2},\alpha _{3}\right\} \right)$. Take $\xi =0$ again and apply Lemma 2 with $\beta =\beta _{\infty }\in \left( \frac{1}{2},1\right)$ and $\alpha =\alpha _{\infty }$. We get

$$\begin{aligned} \int _{B_{R}^{c}}K\left( \left| x\right| \right) \left| u\right| ^{q_{2}-1}\left| h\right| dx&\le C\left( \int _{B_{R}^{c}}\left| x\right| ^{\frac{\alpha _{\infty }-\nu \left( q_{2}-2\beta _{\infty }\right) }{1-\beta _{\infty }}}dx\right) ^{1-\beta _{\infty }}\\&\le C\left( R^{\frac{\alpha _{\infty }-\nu \left( q_{2}-2\beta _{\infty }\right) }{1-\beta _{\infty }} +N}\right) ^{1-\beta _{\infty }}, \end{aligned}$$

since

$$\begin{aligned} \frac{\alpha _{\infty }-\nu \left( q_{2}-2\beta _{\infty }\right) }{1-\beta _{\infty }}+N=\frac{\alpha _{\infty }-\alpha _{2}-\nu \left( q_{2}-2\beta _{\infty }\right) }{1-\beta _{\infty }}<0 \end{aligned}$$

Case $\beta _{\infty }\le \frac{1}{2}$ and $\alpha _{\infty }\le \alpha _{3}\,\left( =\max \left\{ \alpha _{2},\alpha _{3}\right\} \right)$. Take $\xi =\frac{1-2\beta _{\infty }}{2}\ge 0$, we can apply Lemma 2 with $\beta =\beta _{\infty }+\xi =\frac{1}{2}$ and $\alpha =\alpha _{\infty }+\xi \gamma _{\infty }$. We get

$$\begin{aligned} \int _{B_{R}^{c}}K\left( \left| x\right| \right) \left| u\right| ^{q_{2}-1}\left| h\right| dx\le C\left( \int _{B_{R}^{c}}\left| x\right| ^{2\alpha -2\nu \left( q_{2}-1\right) }dx\right) ^{\frac{1}{2}}\le CR^{\alpha -\nu \left( q_{2}-1\right) +\frac{N}{2}}, \end{aligned}$$

since

$$\begin{aligned} \alpha -\nu \left( q_{2}-1\right) +\frac{N}{2}&= \alpha _{\infty }+\frac{ 1-2\beta _{\infty }}{2}\gamma _{\infty }+\frac{N}{2}-\nu \left( q_{2}-1\right) \\&= \alpha _{\infty }-\alpha _{3}-\nu \left( q_{2}-1\right) <0. \end{aligned}$$

$\square$

The proof of Theorem 5 will be achieved by a couple of lemmas.

Lemma 4

Assume that there exists $R>0$ such that $V(r)<+\infty$ almost everywhere on $(0,R)$ and

Then there exists a constant $c_{0}>0$, only dependent on $N$, such that $\forall u\in H_{V,\mathrm {r}}^{1}$ one has

$$\begin{aligned} \left| u\left( x\right) \right| \le c_{0}\left( \frac{1}{\sqrt{\lambda \left( R\right) }}+\frac{R^{\frac{\gamma _{0}-2}{2}}}{\lambda \left( R\right) }\right) ^{\frac{1}{2}}\left\| u\right\| \left| x\right| ^{-\frac{ 2N-2-\gamma _{0}}{4}}\ \ \textit{almost}\,\, \textit{everywhere}\,\, \textit{in}\,\,B_{R}. \end{aligned}$$

(52)

Proof

The lemma is proved in [28, Lemma 4] under a little different assumptions, but the result actually holds also in the form given here. See [8, Appendix] for a detailed proof. $\square$

Lemma 5

Assume that there exists $R>0$ such that $V(r)<+\infty$ almost everywhere on $(0,R)$ and

(53)

and

Assume also that there exists $q>2\beta$ such that

$$\begin{aligned} \left( 2N-2-\gamma _{0}\right) q<4\alpha +4N-2\left( \gamma _{0}+2\right) \beta . \end{aligned}$$

Then $\forall u\in H_{V,\mathrm {r}}^{1}$ and $\forall h\in H_{V}^{1}$ one has

$$\begin{aligned} \int _{B_{R}}K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx\le c_{0}^{q-2\beta }a\left( R\right) R^{\frac{4\alpha +4N-2\left( \gamma _{0}+2\right) \beta -\left( 2N-2-\gamma _{0}\right) q}{4} }\left\| u\right\| ^{q-1}\left\| h\right\| , \end{aligned}$$

where $a\left( R\right) :=\Lambda _{\alpha ,\beta }\left( R\right) \left( \frac{1}{\sqrt{ \lambda \left( R\right) }}+\frac{R^{\frac{\gamma _{0}-2}{2}}}{\lambda \left( R\right) }\right) ^{\frac{q-2\beta }{2}}$ and $c_{0}$ is the constant of Lemma 4.

Proof

Let $u\in H_{V,\mathrm {r}}^{1}\cap D_{0}^{1,2}\left( B_{R}\right)$ and $h\in H_{V}^{1}$. By assumption (53) and Lemma 4, we can apply Lemma 2 with $\Omega =B_{R}$, $\Lambda =\Lambda _{\alpha ,\beta }\left( R\right)$, $\nu =\frac{ 2N-2-\gamma _{0}}{4}$ and

$$\begin{aligned} m=c_{0}\left( \frac{1}{\sqrt{\lambda \left( R\right) }}+\frac{R^{\frac{ \gamma _{0}-2}{2}}}{\lambda \left( R\right) }\right) ^{\frac{1}{2}}\left\| u\right\| . \end{aligned}$$

If $\frac{1}{2}\le \beta <1$, we get

$$\begin{aligned}&\int _{B_{R}}K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx \\&\quad \le \Lambda m^{q-2\beta }\left( \int _{\Omega }\left| x\right| ^{\frac{\alpha -\nu \left( q-2\beta \right) }{1-\beta }}dx\right) ^{1-\beta }\left\| u\right\| ^{2\beta -1}\left\| h\right\| \\&\quad =c_{0}^{q-2\beta }a\left( R\right) \left( \int _{B_{R}}\left| x\right| ^{ \frac{4\alpha -\left( 2N-2-\gamma _{0}\right) \left( q-2\beta \right) }{ 4\left( 1-\beta \right) }}dx\right) ^{1-\beta }\left\| u\right\| ^{q-1}\left\| h\right\| \\&\quad \le c_{0}^{q-2\beta }a\left( R\right) \left( R^{\frac{4\alpha -\left( 2N-2-\gamma _{0}\right) \left( q-2\beta \right) }{4\left( 1-\beta \right) } +N}\right) ^{1-\beta }\left\| u\right\| ^{q-1}\left\| h\right\| , \end{aligned}$$

since

$$\begin{aligned} \frac{4\alpha -\left( 2N-2-\gamma _{0}\right) \left( q-2\beta \right) }{ 4\left( 1-\beta \right) }+N=\frac{4\alpha +4N-2\left( \gamma _{0}+2\right) \beta -\left( 2N-2-\gamma _{0}\right) q}{4\left( 1-\beta \right) } \end{aligned}$$

is positive. If instead we have $\beta =1$, we get

$$\begin{aligned}&\int _{B_{R}}K\left( \left| x\right| \right) \left| u\right| ^{q-1}\left| h\right| dx \\&\quad \le \Lambda m^{q-2}\left( \int _{\Omega }\left| x\right| ^{2\alpha -2\nu \left( q-2\right) }V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{\frac{1}{2}}\left\| h\right\| \\&\quad =c_{0}^{q-2}a\left( R\right) \left( \int _{B_{R}}\left| x\right| ^{\frac{ 4\alpha -\left( 2N-2-\gamma _{0}\right) \left( q-2\right) }{2}}V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{\frac{1}{2}}\left\| u\right\| ^{q-2}\left\| h\right\| \\&\quad \le c_{0}^{q-2}a\left( R\right) \left( R^{\frac{4\alpha -\left( 2N-2-\gamma _{0}\right) \left( q-2\right) }{2}}\int _{B_{R}}V\left( \left| x\right| \right) \left| u\right| ^{2}dx\right) ^{\frac{1}{2}}\left\| u\right\| ^{q-2}\left\| h\right\| \\&\quad \le c_{0}^{q-2}a\left( R\right) R^{\frac{4\alpha -\left( 2N-2-\gamma _{0}\right) \left( q-2\right) }{4}}\left\| u\right\| ^{q-1}\left\| h\right\| , \end{aligned}$$

since $4\alpha -\left( 2N-2-\gamma _{0}\right) \left( q-2\right) =4\alpha +4N-2\left( \gamma _{0}+2\right) -\left( 2N-2-\gamma _{0}\right) q>0.$ $\square$

Proof of Theorem 5

Assume the hypotheses of the theorem and denote

$$\begin{aligned} \Lambda _{0}:=\mathop {\hbox {ess sup}}\limits _{r\in \left( 0,R_{1}\right) }\frac{K\left( r\right) }{r^{\alpha _{0}}V\left( r\right) ^{\beta _{0}}}\quad \mathrm {and} \quad \lambda _{0}:=\mathop {\hbox {ess inf}}\limits _{r\in \left( 0,R_{1}\right) }r^{\gamma _{0}}V\left( r\right) . \end{aligned}$$

If $\gamma _{0}=2$ the thesis of the theorem is true by Theorem 2 (see Remark 3(3)), whence we can assume $\gamma _{0}>2$ without restriction. We claim that for every $0<R\le R_{1}$ there exists $b\left( R\right) >0$ such that $b\left( R\right) \rightarrow 0$ as $R\rightarrow 0^{+}$ and

$$\begin{aligned} \int _{B_{R}}K\left( \left| x\right| \right) \left| u\right| ^{q_{1}-1}\left| h\right| dx\le b\left( R\right) \left\| u\right\| ^{q_{1}-1}\left\| h\right\| , \quad \forall u\in H_{V,\mathrm {r}}^{1},\quad \forall h\in H_{V}^{1} \end{aligned}$$

(which clearly gives the result). In order to prove the claim, let $0<R\le R_{1}$. Then

$$\begin{aligned} \lambda \left( R\right) :=\mathop {\hbox {ess inf}}\limits _{r\in \left( 0,R\right) }r^{\gamma _{0}}V\left( r\right) \ge \lambda _{0}>0 \end{aligned}$$

(54)

and for every $\xi \ge 0$ we have

$$\begin{aligned} \Lambda _{\alpha _{0}+\xi \gamma _{0},\beta _{0}+\xi }(R)&:= \mathop {\hbox {ess sup}}\limits _{r\in (0,R) }\frac{K(r) }{r^{\alpha _{0}+\xi \gamma _{0}}V(r) ^{\beta _{0}+\xi }}\le \mathop {\hbox {ess sup}}\limits _{r\in (0,R_{1}) }\frac{K(r) }{r^{\alpha _{0}}V(r) ^{\beta _{0}}\left( r^{\gamma _{0}}V(r) \right) ^{\xi }}\nonumber \\&\le \frac{\Lambda _{0}}{\lambda _{0}^{\xi }}<+\infty . \end{aligned}$$

(55)

We now distinguish four cases. For the sake of brevity, we omit here some simple (but not so short) computations, which the interested reader can find, with full details, in the preprint version [7] of this paper.

Case $2<\gamma _{0}<N$. In this case, $\left( \alpha _{0},q_{1}\right) \in \mathcal {A}_{\beta _{0},\gamma _{0}}$ means

$$\begin{aligned} \displaystyle \alpha _{0}&> \max \left\{ -\left( 1-\beta \right) N , -\frac{N+\left( 1-2\beta \right) \gamma }{2} \right\} \quad \mathrm{and}\\ \max \left\{ 1,2\beta _{0}\right\}&< q_{1}<\displaystyle \min \left\{ 2\frac{\alpha _{0}-\beta _{0}\gamma _{0}+N}{N-\gamma _{0}},2\frac{2\alpha _{0}+\left( 1-2\beta _{0}\right) \gamma _{0}+2N-2}{2N-2-\gamma _{0}}\right\} \end{aligned}$$

and these conditions ensure that we can fix $\xi \ge 0$, independent of $R$ (and $u$ and $h$), in such a way that $\alpha =\alpha _{0}+\xi \gamma _{0}$ and $\beta =\beta _{0}+\xi$ satisfy

$$\begin{aligned} \frac{1}{2}\le \beta \le 1\quad \mathrm{and}\quad 2\beta <q_{1}<\frac{ 4\alpha +4N-2\left( \gamma _{0}+2\right) \beta }{2N-2-\gamma _{0}} \end{aligned}$$

(56)

(see [7, Appendix]). Hence, by (55) and (54), we can apply Lemma 5 (with $q=q_{1}$), so that $\forall u\in H_{V,\mathrm {r}}^{1}$ and $\forall h\in H_{V}^{1}$ we get

$$\begin{aligned} \int _{B_{R}}K\left( \left| x\right| \right) \left| u\right| ^{q_{1}-1}\left| h\right| dx\le c_{0}^{q_{1}-2\beta }a\left( R\right) R^{\frac{4\alpha +4N-2\left( \gamma _{0}+2\right) \beta -\left( 2N-2-\gamma _{0}\right) q_{1} }{4}}\left\| u\right\| ^{q_{1}-1}\left\| h\right\| . \end{aligned}$$

This proves the claim, since $R^{4\alpha +4N-2\left( \gamma _{0}+2\right) \beta -\left( 2N-2-\gamma _{0}\right) q_{1}}\rightarrow 0$ as $R\rightarrow 0^{+}$ and

$$\begin{aligned} a\left( R\right)&= \Lambda _{\alpha _{0}+\xi \gamma _{0},\beta _{0}+\xi }\left( R\right) \left( \frac{1}{\sqrt{\lambda \left( R\right) }}+\frac{R^{ \frac{\gamma _{0}-2}{2}}}{\lambda \left( R\right) }\right) ^{\frac{ q_{1}-2\beta }{2}}\\&\le \frac{\Lambda _{0}}{\lambda _{0}^{\xi }}\left( \frac{1 }{\sqrt{\lambda _{0}}}+\frac{R_{1}^{\frac{\gamma _{0}-2}{2}}}{\lambda _{0}} \right) ^{\frac{q_{1}-2\beta }{2}}. \end{aligned}$$

Case $N \le \gamma _{0}<2N-2$. In this case, as in the previous one, $\left( \alpha _{0},q_{1}\right) \in \mathcal {A}_{\beta _{0},\gamma _{0}}$ ensures that we can fix $\xi \ge 0$ in such a way that $\alpha =\alpha _{0}+\xi \gamma _{0}$ and $\beta =\beta _{0}+\xi$ satisfy (56) (see [7, Appendix]). The claim then ensues again by Lemma 5.

Case $\gamma _{0}=2N-2$. In this case, the condition $\left( \alpha _{0},q_{1}\right) \in \mathcal {A}_{\beta _{0},\gamma _{0}}$ ensures that we can fix $\xi \ge 0$ in such a way that $\alpha =\alpha _{0}+\xi \gamma _{0}$ and $\beta =\beta _{0}+\xi$ satisfy

$$\begin{aligned} \frac{1}{2}\le \beta \le 1,\quad q_{1}>2\beta \quad \mathrm {and}\quad 0<2\alpha +2N-\left( \gamma _{0}+2\right) \beta \end{aligned}$$

(see [7, Appendix]). The claim follows from Lemma 5, as before.

Case $\gamma _{0}>2N-2$. In this case, $\left( \alpha _{0},q_{1}\right) \in \mathcal {A}_{\beta _{0},\gamma _{0}}$ ensures that we can fix $\xi \ge 0$ in such a way that $\alpha =\alpha _{0}+\xi \gamma _{0}$ and $\beta =\beta _{0}+\xi$ satisfy

$$\begin{aligned} \frac{1}{2}\le \beta \le 1\quad \mathrm {and}\quad q_{1}>\max \left\{ 2\beta ,2\frac{2\alpha +2N-\left( \gamma _{0}+2\right) \beta }{2N-2-\gamma _{0}} \right\} \end{aligned}$$

(see [7, Appendix]). The claim still follows from Lemma 5. $\square$