1 Introduction

Fractional calculus (FC) generalizes the classical differential calculus and deals with integrals and derivatives of real, or even complex, order [1–7]. In the last decades, a vast number of applications emerged in the areas of physics and engineering, and active research is being pursued [8–19]. It was demonstrated that fractional models capture easily dynamic phenomena with long range memory behavior, in opposition with classical integer order models that reveal difficulties in capturing those effects. Nevertheless, many aspects of this mathematical tool are still to be explored and further research efforts are necessary for the development of practical models. Furthermore, fractional derivatives (FDs) are more elaborated than their integer counterparts and their calculation requires some type of approximation [20–26].

Evolutionary strategies [27, 28] were proposed during the last years for optimizing fractional algorithms [29–36]. Therefore, embedding the FC concepts and evolutionary optimization is a fruitful strategy for controller design.

Several studies focussed onto the application of complex-order derivatives (CDs) [37–44]. CDs yield complex valued results and, therefore, are of apparently limited interest. To overcome this difficulty, the use of conjugated-order differintegrals was proposed, that is, of pairs of derivatives whose orders are complex conjugates. These pairs allow the use of CDs while still producing real-valued responses and transfer functions. This article describes the adoption of CDs in control systems. Since CDs are a further step of generalization of FDs, we can foresee significant advantages in the resulting algorithms.

Bearing these ideas in mind, this paper addresses the optimal tuning of controllers using CDs and is organized as follows. Section 2 introduces FDs and their numerical approximation, and formulates the problem of optimization through genetic algorithms (GAs). Section 3 formulates the concepts underlying CDs and presents a set of experiments that demonstrate the effectiveness of the proposed optimization strategy. Finally, Sect. 4 outlines the main conclusions.

2 Fundamental Concepts

2.1 Fractional Calculus

There are several definitions of FDs of order α of the function f(t). The most commonly adopted are the Riemann–Liouville, Grünwald–Letnikov, and Caputo definitions:

(1)
(2)
(3)

where Γ(⋅) is Euler’s gamma function, [x] means the integer part of x, and h is the step time increment.

The Laplace transform leads to the expression:

$$ \mathcal{L} \bigl\{_{0}D_{t}^{\alpha}f (t ) \bigr\} =s^{\alpha }\mathcal{L} \bigl\{ f (t ) \bigr\} -\sum _{k=0}^{n-1}s^{k}{}_{0}D_{t}^{\alpha-k-1}f \bigl(0^{+} \bigr), $$
(4)

where s and \(\mathcal{L}\) represent the Laplace variable and operator, respectively.

The long standing discussion about the advantages of the different definitions is outside the scope of this paper, but, in short, while the Riemann–Liouville formulation involves an initialization of fractional order, the Caputo counterpart requires integer order initial conditions which are easier to apply. The Grünwald–Letnikov expression is often adopted in real-time control systems because it leads directly to a discrete-time algorithm based on the approximation of the time increment h through the sampling period T s . In fact, for converting expressions from continuous to discrete time, the Euler and Tustin formulae are often considered:

(5)
(6)

where z and T s represent the Z-transform variable and controller sampling period, respectively. Expression H 0 is simply the Grünwald–Letnikov definition of FD with the infinitesimal time increment h replaced by the sampling period T s . Weighting H 0 and H 1 by the factors p and 1−p leads to the arithmetic average:

$$ H_{av}^{\alpha} \bigl(z^{-1} \bigr)=pH_{0}^{\alpha} \bigl(z^{-1} \bigr)+ (1-p )H_{1}^{\alpha} \bigl(z^{-1} \bigr). $$
(7)

For obtaining rational expressions, the Taylor or Padé expansions of order r in the neighborhood of z=0 are usually adopted. In [45], several averages based on the generalized mean are evaluated, and in [46] the performances of series and fraction approximations for closed-loop discrete control systems are compared. In this paper, for simplicity, the Euler backward formula and the Taylor series expansion are considered. Therefore, for the real-valued fractional derivative and integral we have (α>0):

(8)
(9)

2.2 Genetic Algorithms

Genetic Algorithms (GAs) constitute a computational scheme for finding the solution of optimization problems. The GA computer simulation involves an evolving population with representatives of candidate solutions of the optimization problem accessed by means of the fitness function J. The GA starts by initializing the population randomly, and then evolves it towards better solutions through the iterative application of crossover, mutation, and selection operators. Therefore, in each generation, a part of the population is selected to breed an offspring. To avoid premature convergence towards sub-optimal solutions, and to guarantee diversity, some elements are modified randomly. The solutions are then evaluated through the fitness function, where fitter solutions are more likely to be selected to form a new population in the next iteration. The GA ends when a given termination criteria is accomplished, for example, when a maximum number of generations N is calculated, or a satisfactory fitness value is reached. The GA pseudo-code is:

  1. 1.

    Generate an initial population.

  2. 2.

    Evaluate the fitness of each element in the initial population.

  3. 3.

    Repeat.

    1. (a)

      Select the elements with best fitness for reproducing.

    2. (b)

      Generate new generation through crossover producing offspring and evaluate their fitness.

    3. (c)

      Mutate randomly some elements in the population and evaluate their fitness.

    4. (d)

      Replace the worst ranked part of population with the best elements of offspring.

  4. 4.

    Until termination criteria is reached.

For easing the GA convergence, a common scheme, denoted as elitism, consists in selecting the best elements of the population to be part of the next generation.

3 Complex-Order Controllers

3.1 Complex-Order Operators

The FC theory can be adopted in control systems and a typical case is the generalization of the classical Proportional-Integral-Differential (PID) controller. The fractional PID, or FrPID, consists of an algorithm with the integer I and D actions replaced by their fractional generalizations of orders 0<α≤1 and 0<β≤1, yielding the transfer function:

$$ G_{c} (s )=K_{p}+K_{i}s^{-\alpha}+K_{d}s^{\beta}, $$
(10)

where s denotes the Laplace variable, and K p , K i , and K d represent the proportional, integral, and derivative gains, respectively. Therefore, the classical PID is simply a particular case where α=1 and β=1.

For a sine function, at steady-state, the CD of order α±ıβ is given by:

(11)

where \(\imath=\sqrt{-1}\), t denotes time, and ω is the angular frequency.

Since we are interested in applications, for getting only real-valued results, we can group the conjugate order, into the operators:

(12)
(13)

Figure 1 shows the polar diagram of the frequency response of expressions (12)–(13) for \((\alpha,\beta )= \{ (-1,1 ), (1,1 ), (\frac{1}{2},-1 ), (-\frac{1}{2},-1 ) \}\).

Fig. 1
figure 1

Polar diagram of the frequency response of expressions (12)–(13) for \((\alpha,\beta )= \{ (-1,1 ), (1,1 ), (\frac{1}{2},-1 ), (-\frac {1}{2},-1 ) \}\)

Full size image

For real-time calculation, Taylor expansions of order r in the neighborhood of z=0 are adopted. Therefore, the pair of operators becomes:

(14)
(15)

where ψ 1(z −1) and ψ 2(z −1) are given by:

(16)
(17)

So, we can define the operators φ 1(z −1) and φ 2(z −1) such that

(18)
(19)

We verify that the pair of operators {φ 1(z −1),φ 2(z −1)} represents a weighted average of ψ 1 and ψ 2 by means of the terms cos[βln(T s )] and sin[βln(T s )]. These factors are due to the presence of \(\frac{1}{T_{s}^{\alpha\pm\imath\beta}}\) in (14)–(15). In the calculation of FDs of real order, the term \(\frac {1}{T_{s}^{\alpha}}\) is usually included in the control gain and only the z-series is considered. In this line of thought, the pair {ψ 1(z −1),ψ 2(z −1)} is also considered as another set of possible complex-order operators.

3.2 Application in Control Systems

We start by defining an appropriate optimization index in the perspective of system control. We consider the integral square error (ISE) and integral time square error (ITSE) defined as:

(20)
(21)

where e(t) represents the closed-loop control system error and T w is a time period sufficiently long for settling the response close to steady-state. Other optimization indexes, such as the IAE and ITAE, can also be adopted, leading to the same type of conclusions.

The set of controllers to be compared consists of four options:

  • PID,

  • FrPID,

  • proportional action and pair {ψ 1(z −1),ψ 2(z −1)},

  • proportional action and pair {φ 1(z −1),φ 2(z −1)}

given by

(22)
(23)
(24)
(25)

where k 0,k 1,k 2 are gains.

The system to be controlled may consist of three cases of increasing dynamical difficulty, namely:

  • S 1, a linear second order system with transfer function \(G_{p} (s )=\frac{1}{s (s+1 )}\),

  • S 2, a second order system \(G_{p} (s )=\frac{1}{s (s+1 )}\) followed by a static backlash [47, 48] with width Δ=1, and

  • S 3, a second order system with delay \(G_{p} (s )=\frac{1}{s (s+1 )}e^{-s}\).

For the experiments, the optimization of either J=ISE or J=ITSE is considered by means of a GA with a population of N=500 elements with I=200 iterations. Elitism is used and, during evolution, any unstable system is eliminated and substituted by a new randomly-generated element, so that the population number remains constant. The closed loop system is excited by a unit step input, the sampling period is T s =0.005, the truncation order of the Taylor series is r=10, the system is simulated using a Runge–Kutta algorithm of order four, and the time window for the calculation of the optimization indices is T w =15.

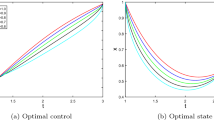
Figures 2, 3 and 4 show the closed-loop system time response for the ISE and ITSE indices under the action of the four controllers for the system S 1, S 2, and S 3, respectively.

Fig. 2
figure 2

Closed-loop system time response for the ISE and ITSE indices under the action of the four controllers for system S 1

Full size image
Fig. 3
figure 3

Closed-loop system time response for the ISE and ITSE indices under the action of the four controllers for system S 2

Full size image
Fig. 4
figure 4

Closed-loop system time response for the ISE and ITSE indices under the action of the four controllers for system S 3

Full size image

The results for the two optimization indices, four controllers, and three types of systems is summarized in Tables 1 and 2. We verify that the new complex-order controllers lead to better time responses in all cases. In what concerns the two proposed variants, we observe almost identical behavior, with G c3 slightly better than G c4.

Table 1 Controller optimal tuning for the ISE index
Full size table
Table 2 Controller optimal tuning for the ITSE index
Full size table

In conclusion, complex order algorithms reveal promising performances and may constitute the next step of development with non-integer controllers.

4 Conclusions

The advances in FC demonstrate the importance of this mathematical concept. During the last years, several control algorithms based on real-order FDs were proposed. This paper proposed a further step of generalization by adoption complex-order operators. For that purpose, several combinations of CDs were examined. Two alternative complex operators were proposed and their performance compared with classical integer-order and fractional order control actions. The tuning of the controller was accomplished by means of genetic algorithms and three systems were evaluated. The results reveal the superior performance and the adaptability of the complex-order operators.