Optimal fractional order adaptive controllers for AVR applications

Abstract

This work presents strategies for fractional order model reference adaptive control (FOMRAC) and fractional order proportional–integral–derivative control (FOPID) applied to an automatic voltage regulator (AVR). The paper focuses on tuning the gains and orders of the FOPID controller and the gains and orders adaptive laws of the FOMRAC controller, with the goal of minimizing non-linear and high dimensionality objective functions, using sequential quadratic programming (SQP), particle swarm optimization (PSO), and genetic algorithms (GA). Two models used for AVR have been studied and reported in the literature and are the bases of the three case studies reported in this paper. To analyze the advantages and disadvantages of the proposed MRAC, comparisons are made with the previous results, i.e. with the results obtained by a PID controller and an MRAC controller optimized by GA. We demonstrate through some performance criteria that fractional order controllers optimized by the PSO algorithm improve the behavior of the controlled system, specifically the robustness with respect to model uncertainties, and improvements with respect to the speed convergence of the signals.

1 Introduction

Power systems not only require devices that maintain and ensure their stability, but also require increasingly quick response times. The most important feature of a control scheme is that, it tunes its parameters in response to the uncertainties caused by changes in the operating conditions of the system. Model reference adaptive control (MRAC) is one of such techniques, which has the aim of finding a suitable control signal so that the output of the controlled system follows the output of the reference model, while at the same time, the stability of the closed loop system is preserved. Optimization algorithms, such as SQP, heuristic methods like GA, and algorithms based on groups like PSO, which optimize parameters minimizing an objective function (OF) considering several variables, are used to meet quick response times. The application of fractional calculus, which generalizes the classical differential calculus of integer order $\frac{\mathrm{d}x(t)}{\mathrm{d}t}$ to the calculus of fractional order $\frac{d^\alpha x(t)}{\mathrm{d}t^\alpha }$ is included in our study. This generalization is reflected by the extent of the search range which is used by algorithms to improve the minimization of cost functions.

Gaing [11], showed improvements on tuning PID controller parameters by minimizing an objective function optimized by PSO. Later, in [8], the authors used the same simplified linear model (SLM) of the generator that was used in [11], and introduced improvements in the optimization process based on a modification of PSO algorithm. Tang et al. [32], introduced chaotic characteristics (chaotic ant swarm) in the tuning process of the PID controller parameters, showing significant improvements over all previous methods, including GA. These authors considered variations of $\Delta V_r(t)= 1~\mathrm{(pu)}$ for comparing optimization strategies in terms of the minimum of a given cost function, where $\Delta V_r(t)$ denotes the variation of the reference voltage with respect to a nominal value. In [21], the previous SLM is used, but the authors use $\Delta V_r(t)= 0.01~\mathrm{(pu)}$, minimizing a cost function using the PSO method. Later, in [7] the same features as those in [21] are applied; however, another change to PSO was proposed, which showed improvements in minimizing the cost function.

Another control scheme introduced in the context of AVR systems with SLM, is fuzzy logic [30]. And, there have been proposals made of using the linear model (LM) of the generator proposed by Kundur [16], which also considers the mechanical characteristics of the synchronous machine. These features are used in optimization problems in [37], where the parameters of the PID controller are selected by the PSO algorithm. The latter introduces concepts of fractional calculus. In [1], the FOMRAC is proposed. It is considered as an optimization problem and solved by GA, under the same operating conditions that were reported in [37] and showed better results, in terms of robustness and the minimization of the cost function, than those reported in [37].

In our work, the FOMRAC technique is regarded as an optimization problem, in which gains and orders of adaptive laws defined by fractional-order differential equations are adjusted. These are based on objective functions subject to constraints provided by the LM and the SLM of the generator. They are detailed in the following paragraphs. This FOMRAC shows improvements in response characteristics and in robustness with respect to model uncertainties, reducing the value of the cost function up to $64\%$ and yielding improvements up to $69\%$ in terms of $t_s$ compared with those found in the literature. Three case studies are proposed and will be analyzed in this paper. To our knowledge, these three cases have not been previously reported and constitute the main aim of the paper together with the comparative analysis with numerous cases already studied in the technical literature.

The paper is organized as follows: Sect. 2 introduces general concepts of direct FOMRAC. It also introduces the concepts of optimization algorithms and models used in each case study. Section 3 establishes the conditions, the characteristics of the controller, and the objective functions. Section 4 presents experimental results, comparing the different control techniques and optimization strategies with results previously reported in the literature. Finally, Sect. 5 presents the conclusions.

2 General concepts

The main theoretical principles used in this work are presented in this section.

2.1 Fractional calculus

Fractional calculus is a generalization of the traditional calculus and is related to differential operators of type $D_t^{\alpha }$, where $\alpha$ is a real or complex number. According to Kilbas [15], the Riemann–Liouville (RL) fractional order integral is defined as

$$\begin{aligned} ^RD_0^{\alpha }f(t)=\frac{1}{\varGamma (n-\alpha )} \left( \frac{\mathrm{d}}{\mathrm{d}\tau }\right) ^n\int _0^t \frac{f(\tau )}{(t-\tau )^{\alpha -n+1}}\mathrm{d}\tau \end{aligned}$$

(1)

with $n=[\mathfrak {R}(\alpha )]+1; t> \alpha$, where $[\mathfrak {R}(\alpha )]$ is the integer part of $\mathfrak {R}(\alpha )$.

In most engineering applications, for $\alpha >0$, the Caputo derivative definition found in (2) is used since it incorporates initial conditions for $f(\cdot )$ i.e., initial conditions that are physically interpretable in the traditional way.

$$\begin{aligned} ^CD_0^{\alpha }f(t)= \frac{1}{\varGamma (n-\alpha )}\int _0^t \frac{f^{(n)}(\tau )}{(t-\tau )^{\alpha -n+1}}\mathrm{d}\tau \end{aligned}$$

(2)

with $n-1< \alpha < n$ and $n\in \mathbb {Z}^{+}$.

Oustaloup’s method [25] allows to make approximations of non-integer derivatives. It is one of the available frequency-domain methods that uses a recursive distribution of N poles and N zeros of the form

$$\begin{aligned} s^{\alpha }\approx k \prod _{n=1}^{N} \frac{1+(s/\omega _{z,n})}{1+(s/\omega _{p,n})} \end{aligned}$$

(3)

with $\alpha > 0$. Moreover, the frequencies of the poles and zeros ($\omega _{z,n}$ and $\omega _{p,n}$) are given by [37]. Zeros and poles are placed inside a frequency interval [$\omega _l; \omega _h$], and the gain k is adjusted so that the gain on both sides of (3) is 1 rad/s. The number of poles and zeros N is chosen in advance, and the desired performance of the approximation strongly depends on: low values cause simpler approximations, but may cause ripples in both gain and phase behaviors. Such ripples can be removed functionally by increasing the N, but the approximation will become heavier computationally. This approximation is available in the Ninteger toolbox for Matlab [34], and is the one used in the work reported in this paper.

2.2 Fractional order model reference adaptive control

Some pioneering works in the context of the FOMRAC are due to Vinagre et al. [35] and Ladaci et al. [17, 18]. For the classic direct MRAC, the controller parameters are adjusted using integer order differential equations (adaptive laws). However, this paper focuses on the direct FOMRAC, in which the parameters are adjusted adaptively using fractional-order differential equations (fractional adaptive law) keeping the same structure of direct MRAC [23]. Thus, this section begins by giving a brief introduction to classical MRAC. For real-life applications, some uncertainties are the result of the parameters being unknown. On the other hand, there are existing systems that can be only partially modeled due to external disturbances. In these cases, conventional control theory has not achieved satisfactory performance, while in the direct MRAC, the parameters of the controller are directly adjusted; that is to say, no identification of the plant parameters is attempted [23]. Given a known reference model $G_m(s)$, a reference signal r(t) is applied to obtain the measurable output $y_m(t)$. This output is compared with the AVR output voltage $y_p(t)$ to compute the control error defined as $e_1(t) = y_p(t) - y_m(t)$. In this paper, we will use $y_p(t)= \Delta V_T(t)$, $y_m(t)=\Delta V_M(t)$ and $u(t)=\Delta u(t)$ for Table 1 (see Fig. 1). Since the relative degree of the system to be analyzed here is $n * \ge 2$, the control scheme is shown in Fig. 1.

The details of the scheme of Fig. 1 can be found in [1]. However, when $n^*\ge 2$, there are some concepts that should be noted; an augmented error $\epsilon (t)$ is synthesized that permits stable adaptive laws to be implemented, and the auxiliary error signal $e_2(t)$ is generated. The most important details of this controller are shown in Table 1, in which n is the system order, so, $n-p=n^*$ and $q=n^*$, with q the model reference order. The size of the matrices ($\varLambda , l$), and the number of parameters to optimize will be defined in Sect. 3.

Table 1 General fractional order MRAC

Fig. 1

Block diagram for the implementation of the FOMRAC for the AVR [1]

2.3 Optimization algorithms

Basic concepts associated with optimization algorithms used in this work are presented in this section.

2.3.1 Particle swarm optimization

PSO is a heuristic global optimization technique which belongs to the category of evolutionary search algorithms [14]. It solves optimization problems based on the behaviour of existing virtual social groups in nature (flocks of birds, swarms, etc.) as reported by Ordóñez [24]. Furthermore, the method has shown improvements in minimizing cost functions, particularly when they have non-linear characteristics, multiple optimal values, and high dimensionality [37]. The individuals defined as potential solutions are particles that evolve iteratively according to different strategies to find the best possible global solution from a set of equations that update the velocity (4) and the position (5) of each particle in the search space [11].

$$\begin{aligned} v^{(t+1)}_{\mathrm{id}}= & {} w^{(t)}v^{(t)}_{\mathrm{id}}+c_{1}r_{1}^{(t)}(p_{\mathrm{id}}^{(t)} -x^{(t)}_{\mathrm{id}})+c_{2}r_{2}^{(t)}(p_{g}^{(t)}-x^{(t)}_{\mathrm{id}})\nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned} x^{(t+1)}_{\mathrm{id}}= & {} x^{(t)}_{\mathrm{id}}+v^{(t+1)}_{\mathrm{id}} \end{aligned}$$

(5)

where $w_{\mathrm{iter}}$ represents the inertia factor that is directly related to exploration ($w_{\mathrm{max}}$) and exploitation ($w_{\mathrm{min}}$) of the search space. This decreases as the iterations progress according to Eq. (6) [31].

$$\begin{aligned} w_{\mathrm{iter}}=w_{\mathrm{max}}-\dfrac{w_{\mathrm{max}}-w_{\mathrm{min}}}{\mathrm{iter}_{\mathrm{max}}}.\mathrm{iter} \end{aligned}$$

(6)

where $iter_{\mathrm{max}}$ represents the maximum number of iterations allowed by the search algorithm. $c_{1}$ and $c_{2}$ correspond to the cognitive and social constants for (4). These constants affect the rate of convergence of each particle. The variables $r_1,r_2$ with uniform distribution contribute to the stochastic environment, i.e. $r_1,r_2 \sim U[0,1]$. At the same time, these variables prevent particles from stagnating in a local optimum. For further details of the evolution of the PSO algorithm, see reference [37].

2.3.2 Genetic algorithms

GA is a method used to solve constrained or unconstrained optimization problems. These are based on natural selection processes which, in turn, are the basis of the biological evolution. The GA modifies a population of possible individual solutions iteratively. At each step, the genetic algorithm selects individuals at random from the current population. This population evolves over generations to produce better solutions to the problem. These algorithms can be applied to solve a variety of optimization problems that are not well suited for standard optimization algorithms, including problems in which the objective function is discontinuous, non-differentiable, stochastic, or highly non-linear. GA uses three main types of rules at each step to create the next generation of the population.

• Selection rules  Select the individuals, called parents, that contribute to the population at the next generation.

• Crossover rules  Combine two parents to form children for the next generation.

• Mutation rules  Apply random changes to individual parents to form children.

For more details about the specific steps taken by the algorithm, see reference [20].

2.3.3 Sequential quadratic programming

Recently, considerable progress in the development of general-purpose optimization techniques for SQP has been reported in the literature [4, 10]. These methods consider non-linear optimization, which is efficient and can be applied to large problems including linear and non-linear constraints. These methods require very few evaluations of the objective function and converge to a solution depending on the initial conditions of the problem. In general, the problem of optimizing a non-linear function subject to constraints can be written as:

$$\begin{aligned} \begin{array}{ll} \underset{x \in R^n}{\text{ minimize }} &{} \mathrm{OF}(x)\\ \text{ subject } \text{ to } &{} b_l \le \left\{ \begin{array}{l} Ax\\ c(x) \end{array} \right\} \;\le \; b_{u} \end{array} \end{aligned}$$

(7)

where c is a vector defining the non-linear constraints, A is a constant that defines the parameters of the linear constraints, and $b_l$ and $b_u$ are vectors defining the upper and lower bounds of each constraint, respectively. $\mathrm{OF}(x)$ is a generic objective function (OF) of certain vector variable x. In this study, two OFs are used and they are defined in Eqs. (12) and (13) denoted as $\mathrm{OF}_1$ and $\mathrm{OF}_2$, respectively.The basic idea of SQP is to solve the objective function from a given approximate solution $x^k$ through the formulation of a quadratic programming sub-problem. Then, it uses this sub-problem to build the best approximation of $x^{k+1}$. This process is iterated so that the expected solution converges to an optimal solution $x^*$ [5].

According to Boggs [5], the correct choice of the sub-problem reduces SQP to Newton’s method, with fast convergence. However, the presence of constraints causes both analyses to be significantly different. Two additional properties of this method are worth mentioning:

• SQP is not a feasible point method. The initial condition or some subsequent point generated by the algorithm will not necessarily be within the feasible solution space. A feasible point is one that satisfies all the constraints associated with the objective functions.

• The success of the SQP method depends on the existence of a fast and accurate algorithm for solving quadratic programs.

According to [19], Matlab uses the “fmincon” function which is configured to use this method.

Fig. 2

Block diagram of the first generator model

2.4 Automatic voltage regulators

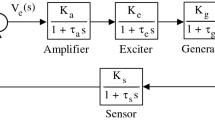
Generators often work at constant voltage through an AVR system which controls the terminal voltage through the excitation system. It makes the terminal voltage equal to the reference voltage [6]. Among the many events that cause voltage drop, reactive power transmitted through a line has a great impact on the voltage profile. It can also cause large voltage drops, and, therefore, should be avoided. Currently, there are alternatives to maintaining the generated voltage within a specified range [2]. However, our work focuses on the design of an AVR system, which is the most effective way to control the voltage in most power systems. The AVR system is composed of subsystems, which are the amplifier, exciter, generator, and sensor.

2.4.1 Generator models

Synchronous machines are the main source of power generation systems, and their stability depends mostly on maintaining synchronous operation [36]. Therefore, the understanding of the characteristics and the modeling of the dynamic behavior is of critical importance for the study of the stability of electric power systems. Thus, this paper presents two common dynamic models for the generator.

$\mathrm {Model_1}$ Figure 2 shows the block diagram of an LM associated with the generator model that considers whole mechanical and electrical phenomenology. This model considers the amplifier, exciter and sensor block diagrams (same as in $\mathrm {Model_2}$), but the transfer function of the generator from $\Delta V_E$ to $\Delta V_T$ considers the electrical and mechanical parameters and it is of third order (whereas in $\mathrm {Model_2}$ is of first order only). $K_1, K_2, \ldots ,K_6$ are electrical and mechanical machine parameters describing the generator [16]

This representation is far more general than the $\mathrm {Model_2}$ described below and it was taken from [16].

$\mathrm {Model_2}$  In this case, the transfer function considers a simplified relationship between the field voltage $\Delta V_E$ and generator terminal voltage $\Delta V_T$. This relationship can be expressed in terms of the gain $K_G$ and a time constant $\tau _G$, and is given by Gaing et al.[11], Mukherjee et al. [22] and Tang et al.[32]. Its transfer function is given by

$$\begin{aligned} G_g(s)=\frac{K_G}{1+\tau _G s}=\frac{\Delta V_T}{\Delta V_E}, \end{aligned}$$

(8)

while the block diagram for analyzing this case is presented in Fig. 3, whose values were taken from [7].

Fig. 3

Block diagram of the second generator model

2.4.2 Amplifier model

The amplifier model [11] is presented by the gain $K_A$ and a time constant $\tau _A$, whose transfer function is

$$\begin{aligned} G_a(s)=\frac{K_A}{1+\tau _A s}= \frac{\Delta V_A}{\Delta u}. \end{aligned}$$

(9)

2.4.3 Exciter model

The main function of the excitation system is to supply energy in the form of direct voltage and current to the generator field, creating a magnetic field. Its transfer function is given by

$$\begin{aligned} G_e(s)=\frac{K_E}{1+\tau _E s}=\frac{\Delta V_E}{\Delta V_A}, \end{aligned}$$

(10)

while the gain $K_E$ and time constant $\tau _E$ will be defined in Sect. 3.2

2.4.4 Measurement model

The voltage measurement block, including a rectifier and filter, is often modeled with a single time constant

$$\begin{aligned} G_s(s)=\frac{K_S}{1+\tau _S s}=\frac{\Delta V_S}{\Delta V_T}, \end{aligned}$$

(11)

while the gain $K_S$ and time constant $\tau _A$ will be defined in Sect. 3.2

3 AVR design using MRAC and optimization algorithms

This section introduces the values for the AVR parameters, and presents the design procedure of the FOMRAC and optimization algorithms.

3.1 Performance criteria

There are several performance criteria for designing controllers. This paper, however, includes only two objective functions, which have been used by other authors.

$\mathrm{OF}_1$  To achieve system performance according to control specifications, the first performance criterion used in the optimization process is defined according to [1, 37] as

$$\begin{aligned} \mathrm{OF}_1= & {} w_1O_s+w_2t_s+w_3E_{ss} \nonumber \\&+\, w_4\int _0^{t_f}|e_c(t)|\mathrm{d}t + w_5\int _0^{t}{u}^2(t)\mathrm{d}t \end{aligned}$$

(12)

When a FOMRAC strategy is used, Eq. (12) depends on vector $[\alpha ^T \ \gamma ^T] \in \mathfrak {R}^{22}$, a vector representing the derivative orders (vector $\alpha \in \mathfrak {R}^{11}$) and the adaptive gains (vector $\gamma \in \mathfrak {R}^{11}$) for the adaptive laws of the controller parameters. (See last row of Table 1). Thus, the optimization procedure for (12) is performed in a 22-dimensional space. To reduce the search space, each component of vectors $\alpha$ and $\gamma$ is constrained to $0< \alpha _i\le 2$, $0<\gamma _j\le 100$, and the final time is $t=100$. If the IOMRAC strategy is employed, function $\mathrm{OF}_1$ depends on 11 parameters only since the derivative order of the adaptive laws is fixed to 1 and only the adaptive gain can be varied.

This performance criterion includes the overshoot $O_s$, settling time $t_s$, steady-state error $E_{ss}$, integral of absolute error IAE with $e_c(t)=r(t)-\Delta V_T(t)$ as the control error, and $r(t)= \Delta V_r(t)$. The control signal generated by the FOMRAC is $\Delta u(t)$. Several trials were performed for the optimization process, using values for the weighting factors close to the values used in Aguila-Camacho et al. [1]. The smallest value of $\mathrm{OF}_1$ was obtained for $w_1=w_2=w_4=1,w_3=1000$ and $w_5=7$.

$\mathrm{OF}_2$: Chatterjee et al. [7] defined the objective function as Equation (13) [21, 22] which corresponds to minimum overshoot $O_s$, minimum settling time $t_s$, and $\mathrm{max}-\mathrm{d}v$ (Maximum point of the voltage signal derivative). The values for the weighting factors are $w_1=10000$, $w_2=1$ and $w_3=0.001$ from [7].

$$\begin{aligned} \mathrm{OF}_2= (w_1O_s)^2+w_2t_{s}^2+ \frac{w_3}{(\mathrm{max}-\mathrm{d}v)^2} \end{aligned}$$

(13)

Equation (13) contains to $[\alpha ^T \ \gamma ^T] \in \mathfrak {R}^{10}$ subject to $0< \alpha \le 2$ and $0<\gamma \le 9\times 10^8$.

According to Panda et al. [28], it should be noted that additional performance criteria are proposed for determining the efficiency of each control technique. These are the integral of the absolute error (IAE), the integral of the time-weighted absolute error (ITAE), the integral of the squared error (ISE), and the integral of the time-weighted squared error (ITSE).

3.2 Design of the MRAC

Two case studies, depending on the model of the generator used, were analyzed as described below.

3.2.1 Case 1

As mentioned in Sect. 2.4, the first model used in this case study corresponds to $\mathrm {Model_1}$ shown in Fig. 2 in which the parameters are $K_A=10$, $\tau _A=0.1~\mathrm{(s)}$, $K_E=1$, $\tau _E=0.5~\mathrm{(s)}$, $K_1=1.591$, $K_2=1.5$, $K_3=0.333$, $K_4=1.8$, $K_5=-0.12$, $K_6=0.3$, $\tau _3=1.91~\mathrm{(s)}$, $H=3$, $K_D=0$, $\omega _0=377~(\mathrm{rad}/\mathrm{s})$, $K_S=1$, and $\tau _S=0.06~\mathrm{(s)}$. These parameters were taken from [1, 16].

For fractional adaptive controller design purposes, the plant to be controlled has a sixth-order transfer function. However, since the dynamic of the sensor is very fast, its influence in the transfer function can be ignored. The plant transfer function $G_p(s)$ is then considered as one of the fifth order and with relative degree $n^*=3$. According to Narendra et al. [23], the reference model $G_{m1}(s)$ has to be chosen with a relative degree greater or equal to the plant relative degree, as is shown in (14) and as used in Aguila-Camacho et al. [1].

Parameters of the auxiliary signal and the reference model (14) for this Case 1 are $p=2$, $b_2=5.994$, $b_1=0$, $b_0=825.2$, $a_5=0.573$, $a_4=7.176$, $a_3=72.36$, $a_2=706.6$, $a_1=1302$, $a_0=260.8$, $\mathrm{Diag}(\varLambda )=[-1 \, -2 \, -3 \,-4]$, and $l=[-1 \, 1 \, 3 \, 4]^T$. This first application included the optimization of 11 parameters for the case of the IOMRAC (Integer Order MRAC) controller and 22 parameters for the FOMRAC controller.

$$\begin{aligned} G_{m1}=\dfrac{1.2}{s^{3}+ 5.2s^{2}+7s+1.2} \end{aligned}$$

(14)

It is interesting to note here that an FO model reference could also be chosen in the scheme, as long as some freedom on this choice is allowed in the controller design, and more importantly, the stability of the resulting overall adaptive system is preserved. This topic is currently being investigated [12].

To compare different control techniques and optimization strategies, MRAC controller parameters are adjusted, considering a unit step $\Delta V_r(t)=1~\mathrm{(pu)}$ as input.

3.2.2 Case 2

The model used in this case is shown in Fig. 3. According to Chatterjee et al. [7], the values of the constants are: $K_A=10$, $K_E=1$, $K_G=0.7$, $K_S=1$, $\tau _A=0.1$, $\tau _E=0.4$, $\tau _G=1$ and $\tau _S=0.01$. The open loop transfer function of the AVR system is a 4th order model, i.e., that the IOMRAC controller has nine parameters to adjust. As in Case 1, if the dynamic of the sensor can be ignored, then the system is a third-order model. However, the dynamic of the system can be considered as one of the 2nd order, because its step response is similar to the third-order system. Then, the controller will adjust just 5 parameters for the IOMRAC controller and 10 parameters for the FOMRAC controller. Beyond this, selection of the reference model is the responsibility of the control designer, and will be chosen according to the requirements to be met by the control scheme. In this case, given the characteristics of the power generation process, a smooth step response is desired. Also, a small overshoot and settling time, and minimal steady-state error. To satisfy these requirements, the reference model was selected as in (15) and the parameters of the auxiliary signals are $\mathrm{Diag}(\varLambda )=[-20]$, $l=[1]$ from Table 1.

$$\begin{aligned} G_{m2}=\dfrac{630}{21s^{3}+ 159.8s^{2}+524.8s+630} \end{aligned}$$

(15)

To compare with previous results, the parameters are adjusted taking as reference voltage $\Delta V_r(t)=0.01~\mathrm{(pu)}$. This is used in Chatterjee et al. [7].

3.3 Design of optimization algorithms

In this section, the parameters of the three optimization algorithms used in each proposed study case are defined.

3.3.1 Case 1

Limited by practical requirements, the lower bounds of the controller parameters ($\alpha$ and $\gamma$) are $\mathrm{LB}_{\gamma }= 0.1$ and $\mathrm{LB}_{\alpha }= 0.01$, respectively. The upper bounds are $\mathrm{UB}_{\gamma }= 100$ and $\mathrm{UB}_{\alpha }= 2$, respectively, which belong to the gains and orders of adaptive laws. For the FOMRAC controller, $\omega _l$ and $\omega _h$ in (3) are set to 0.001 and $1000 (\mathrm{rad}/\mathrm{s})$, respectively, and the order of approximation in (3) is set to $N=10$. For the PSO algorithm, the parameters used by [7] are defined as follows:

• The initial population cannot be chosen as in the literature, because this work is optimizing triple the number of parameters, and since the number of initial individuals is specific to each problem, 150 particles are defined.

• Inertia weight factor is set as (6), where $w_{\mathrm{max}}=1.9$ and $w_{\mathrm{min}}=0.4$.

• Acceleration constants $c_1=c_2=2$.

• Maximum iteration is set to $\mathrm{iter}_{\mathrm{max}}= 1000$.

• Time for the optimization is $t= 100~\mathrm{(s)}$.

The default parameters of the function ga of MatLab, and $t= 100~\mathrm{(s)}$ of (12) are used for the GA algorithm. For the SQP method, the default parameters of the function fmincon of MatLab are considered [19] and the initial conditions of the parameters are uniformly distributed in the search space.

Table 2 Gains and orders of adaptive laws, obtained by optimization algorithms Case Study 1

3.3.2 Case 2

In practical requirements, the lower bounds of the controller parameters are $\mathrm{LB}_{\gamma }= 0.1$ y $\mathrm{LB}_{\alpha }= 0.01$, also, and the upper bounds $\mathrm{UB}_{\gamma }= 9\times 10^8$ and $\mathrm{UB}_{\alpha }= 2$ which belong to the gains and orders of adaptive laws. For the FOMRAC controller, $\omega _l$ and $\omega _h$ in (3) are set to 0.001 and 1000 (rad/s), respectively, and the order of approximation in (3) is set to $N=10$. For the PSO algorithm, the parameters used by [7] are defined as follows:

• The initial population cannot be chosen as in the technical literature, because this work is optimizing triple the number of parameters, and since the number of initial individuals is specific to each problem, 150 particles are defined.

• Inertia weight factor is set as (6) where $w_{\mathrm{max}}=1.9$ and $w_{\mathrm{min}}=0.4$.

• Acceleration constants $c_1=2$, $c_2=2$.

• Maximum iteration is set to $iter_{\mathrm{max}}= 1000$.

• Time for the optimization is $t= 10~\mathrm{(s)}$.

With the GA method, the default parameters of the function $\mathrm{ga}$ of MatLab, and $t=10~\mathrm{(s)}$ in (13) are considered. For the SQP method, the default parameters of the function fmincon of MatLab are used [19], and the initial conditions for the parameters are uniformly distributed in the search space.

As shown above, the values for the optimization parameters for each case study are not equal. This is because of the different time response of each generator model used.

4 Simulation results

This section presents the results obtained for the AVR controlled by the FOMRAC designed in Sect. 3. These results are compared with previous investigations. The fractional adaptive laws were implemented using the Ninteger Toolbox for Matlab Version 8.1.0.604(R2013a) [33].

4.1 Case study 1

The results obtained at this stage with $\mathrm{OF}_1$ and the $\mathrm{Model}_1$ in Fig. 2 will be compared to Aguila-Camacho et al. [1] and Zamani et al. [37].

4.1.1 Behavior of the MRAC

Several trials were performed for the optimization process to find the best set of controller parameters based on minimizing $\mathrm{OF}_1$. The SQP and PSO algorithms obtained the best results. These are presented in Table 2, which will be compared with the results obtained by GA [1].

Figure 4 shows the step response of the controlled system, i.e., the voltage measured at the generator terminals. In this figure, two types of control are compared, which were taken from the literature. These are $\mathrm {IOPID_{GA}}$ and $\mathrm {IOMRAC_{GA}}$ versus $\mathrm { IOMRAC_{PSO,SQP}}$, proposed in this case study. Also, the IOMRAC controllers have $O_s=0$, while the $\mathrm {IOMRAC_{PSO}}$ controller makes the system have a shorter settling time, $t_s$, than the $\mathrm {IOMRAC_{SQP}}$ and $\mathrm {IOMRAC_{GA}}$. The characteristics of the responses can be seen in Table 3.

Fig. 4

Step responses of the AVR controlled by three IOMRACs, and IOPID

Fig. 5

Exciter control signals of the AVR controlled by the three IOMRAC’s, and IOPID

Figure 5 corresponds to the evolution of field voltage of the synchronous machine. This exciter control action is responsible for maintaining the voltage at the generator terminals during a predefined operation. $\mathrm {MRAC_{PSO}}$ has the lowest rise time $t_r$ in relation to those presented earlier. The exciter control effort is the associated cost and is shown in Fig. 5.

Table 3 Characteristics performance of step responses for Case Study 1

Table 3 shows the details of the performance criteria associated with each method of optimization. Performance criteria (IAE, ITAE, ISE, ITSE) analyze behaviour of the error within time intervals $[0\;100]s$.

In the case of fractional control (see Figs. 6 and 7), $\mathrm {FOMRAC_{PSO}}$ shows significant improvements in terms of $\mathrm{OF}_1$ and $t_s$ in relation to the integer order control or IOMRAC, which was shown above. At the same time, it is better than IOPID and FOPID presented by Aguila-Camacho et al. [1] and Zamani et al. [37], respectively. These are shown in Fig. 6 and their performance in Table 3.

Fig. 6

Step responses of the AVR controlled by three FOMRACs, and FOPID

Fig. 7

Exciter control signals of the AVR controlled by the three FOMRACs, and FOPID

Table 2 shows the values of the gains and the orders of adaptive laws for the MRAC controller. The lesser value, $\mathrm{OF}_1=112.3$, is obtained using the PSO algorithm for the FOMRAC controller rather than IOMRAC, IOPID, and FOPID controllers. As can be seen from Table 3, the settling time $t_s$ is shorter for the $\mathrm {FOMRAC_{PSO}}$, since it improves by 14.2 and $69.2\%$ compared with the $\mathrm {IOMRAC_{GA}}$ and the $\mathrm {FOMRAC_{GA}}$ controllers, respectively, reported in [1]. In terms of the sum of the performance indices, the J of $\mathrm {FOMRAC_{PSO}}$ is $34\%$ better than J of $\mathrm {IOMRAC_{GA}}$. Although a more demanding control signal is required as compared with the cases of FOPID and $\mathrm {FOMRAC_{GA}}$, it has the same control effort as the $\mathrm {IOMRAC_{PSO}}$. That is to say, the FOMRAC delivers a good balance between the transient response and the control signal behavior.

4.1.2 Robustness of the FOMRAC

The generator parameters may vary due to the wear of materials and changes in load. Therefore, the same robustness tests that were done in [1] will be performed here. Initially, the system is working in normal operation with the parameters set forth above; at $t=100~\mathrm{(s)}$, parameter $K_1=1.59$ changes to $K_1= 1$ due to changes in load conditions (Fig. 8).

Fig. 8

Step responses of the AVR controlled of integer and fractional controllers, under a parameter variation in the generator at $t=100~\mathrm{(s)}$

According to [1], the result obtained by controller $\mathrm {FOMRAC_{GA}}$ is better than FOPID in [37] regarding robustness tests. Figure 8 shows the best results obtained in this Case Study 1, which correspond to $\mathrm {FOMRAC_{PSO}}$. These will be compared with the results obtained by $\mathrm {MRAC_{GA}}$ [1], and PID [37] of integer and fractional orders, and with the $\mathrm {IOMRAC_{PSO}}$ controller of this work. Although the amplitude of the signal at the generator terminal voltage is the same in all four case MRAC controllers, the system controlled by $\mathrm { FOMRAC_{PSO}}$ has less settling time than $t_s$ of the system controlled by the $\mathrm { FOMRAC_{GA}}$ controller. These are 15.6 and $26.8\mathrm{(s)}$, respectively. Simply stated, the $\mathrm { FOMRAC_{PSO}}$ controller stabilizes the system $41\%$ faster than the $\mathrm { FOMRAC_{GA}}$ controller. Furthermore, the amplified control action or the exciter system voltage is very similar to that of $\mathrm {MRAC_{GA}}$ shown in Fig. 9.

Fig. 9

Field voltage of the AVR controlled by integer and fractional controllers, under a parameter variation in the generator at $t=100~\mathrm{(s)}$

In the second robustness test, another uncertainty in the exciter model was assumed, where the transfer function in (10) varies to $G_{E_1}=\frac{1}{0.5s+0.5}$ at $t=100~\mathrm{(s)}$. For comparison, this test was taken from [1]. Fig. 10 shows the step response of the controlled system under variations occurring in the load and the excitation system.

Fig. 10

Step responses of the AVR controlled of integer and fractional controllers, under variations in the parameters of the generator and the exciter transfer function at $t=100~\mathrm{(s)}$

It can be seen in Fig. 10 that the $\mathrm {FOMRAC_{PSO}}$ controller improved $57\%$ compared with the $t_s$ obtained with the $\mathrm { FOMRAC_{GA}}$ controller. As far as control action is concerned, the exciter control action of the controller $\mathrm {FOMRAC_{PSO}}$ does not have the associated cost shown in Fig. 11.

Fig. 11

Exciter control signals of the AVR controlled of integer and fractional controllers, under variations in the parameters of the generator and the exciter transfer function at $t=100~\mathrm{(s)}$

Fig. 12

Block diagrams of continuous-time ideal PID controller

Fig. 13

Block diagrams of continuous-time filtered PID controller

4.2 Case study 2

The results shown in this case study are obtained using the objective function $\mathrm{OF}_2$ written as in (13), associated with $\mathrm{Model}_2$. The simulation results will be compared with [7] and Mukherjee et al. [22] in which only an integer order PID controller is implemented for the AVR System. The gains for this control strategy were tuned by the PSO algorithm based on the objective function $\mathrm{OF}_2$. The results obtained and reported in this paper show improvement over previous investigations, and will be developed in this section.

Referring to the special case of the AVR system analyzed by Chatterjee et al. [7], the parameters obtained by the optimization algorithm are $K_p = 0.6658$, $K_i = 0.4821$ and $K_d = 0.1963$. The closed-loop transfer function of the system controlled by PID is shown in that paper with the block diagram of Fig. 12. Unfortunately, we are unable to reproduce the figures shown by Chatterjee et al. [7]. It is due to the derivative action in [7] is filtered (see Eq. (16)), where $N=100$ is the principal parameter for the filter. Therefore, the authors in [7] have not used an ideal PID controller like they highlight in their paper, but, a filtered PID controller shown in Fig. 13.

$$\begin{aligned} C(s)= K_p + \frac{K_i}{s} + K_d s \frac{N}{s+N} \end{aligned}$$

(16)

The ideal PID controller in the Laplace domain is $C(s)= K_p + \frac{K_i}{s} + K_d s$, which is an improper transfer function not supported by Simulink software because of the causality rule. Then MatLab adds a filter coefficient N to transfer function C(s) in a continuous-time parallel PID controller as written in (16),

Figure 14a shows the responses of the control features of the $\mathrm {PID_{FILTERED}}$ when $\Delta V_r(t)=0.01$ are $t_s= 0.7~\mathrm{(s)}$, $O_s= 0.3\%$ and $\mathrm{max}-\mathrm{d}v= 0.02$. Furthermore, $t_s= 3.9~\mathrm{(s)}$, $O_s= 11.4 \%$ and $\mathrm{max}-\mathrm{d}v= 0.02$ are the corresponding features of the $\mathrm {PID_{IDEAL}}$. This aspect is important to emphasize since comparisons are often made using the $\mathrm {PID_{IDEAL}}$ (Pan et al. [26, 27], Sahu et al. [29], Gozde et al. [13], dos Santos Coelho et al. [9] and the latest in Anwar et al. [3]).

Fig. 14

a Step responses of the AVR controlled by the Ideal PID controller and the Filtered PID controller. b Control signals of the AVR controlled by the Ideal PID controller and the Filtered PID controller

Comparisons in this paper will be made with the results in [7], where the system is controlled by a filtered PID controller, as shown in Fig. 13 (indicated by red dash lines).

4.2.1 Behavior of the MRAC

In the SLM in (8), the damping phenomena are neglected. According to Kundur et al. [16], this is a small-signal model. Table 4 shows the gains and orders of the adaptive laws of the MRAC controllers obtained by the proposed optimization algorithms. Figure 15 shows the terminal voltage of the generator when the system is controlled by the IOMRAC controllers and an IOPID controller (Table 5).

Table 4 Gains and orders of adaptive laws, obtained by optimization algorithms Case Study 2

The $t_s$ of the best result obtained in this case study for the integer-order controllers corresponds to those of $\mathrm {IOMRAC_{PSO}}$, which does not improve the results obtained by the researchers in [7] and shown in Fig. 15. However, comparisons can be made between the results obtained by optimization algorithms in terms of the objective function $\mathrm{OF}_2$. The IOMRAC controller optimized by the PSO improves $55.1\%$ over that obtained by the SQP algorithm and $96.4\%$ to that of the GA algorithm.

The generator terminal voltage is controlled through the voltage on the field of the rotor ($\Delta V_E(t)$ shown in Fig. 16). The best result found in previous investigations corresponds to $\mathrm {IOPID_{PSO}}$, where the cost associated is its exciter control signal, approximately $40\%$ higher than $\mathrm {IOMRAC_{PSO}}$. Practice shows that the fractional-order controller should provide better results considering the minimum performance criterion $\mathrm{OF}_2$. This is due to the expansions of the search space, i.e., the order of $\alpha = 1$ changes to $\alpha \in [0,2]$. Figure 17 presents the transient response of incremental change in terminal voltage for $1\%$ step in reference voltage or $\Delta V_r=0.01~\mathrm{(pu)}$.

Fig. 15

Transient response of terminal voltage for a $0.01 ~\mathrm{(pu)}$ step change in reference voltage, using integer-order controllers

Table 5 Performance criteria Case Study 2

Only the integer-order PID controller designed for AVR appears in previous investigations. To emphasize the advantages of fractional-order controllers, a FOPID controller was also designed using the same method depicted in Fig. 14a. The same evaluation function as in [32, 38] was used, in which the parameters obtained by the PSO algorithm are the gains $K_p = 1.5338\;K_i = 0.6523$, $K_d = 0.9722$, $\alpha = 0.9722$ is the fractional-order integral action, and $\beta = 1.2090$, is the fractional-order derivative action.

Figures 17 and 18 show three FOMRAC controllers optimized by SQP, GA and PSO, and a $\mathrm {FOPID_{PSO}}$ controller. Although the $\mathrm {FOPID_{PSO}}$ performance is better than FOMRAC in terms of $t_s$, it has a high cost for the voltage in the excitation system as shown in Fig. 18. Furthermore, the performance of $\mathrm {FOPID_{PSO}}$ proposed here is $85\%$ lower than the $\mathrm {IOPID_{PSO}}$ in terms of $\mathbf \mathrm{OF}_2$. The MRAC has higher robust stability than the IOPID, as is observed in the following simulations.

4.2.2 Robustness test

Robustness tests are performed to analyze the controlled system behavior under parametric variations. The PSO optimization algorithm associated with the FOPID controller obtained the best results for the evaluation function $\mathrm{OF}_2$. The robustness tests will show the real benefits of the controllers $\mathrm {IOMRAC_{PSO}}$ and $\mathrm {FOMRAC_{PSO}}$.

Tuned parameters for the PID controller are constant over time, but the parameters obtained by the MRAC vary with the tracking error. This is the main feature that stands out for the controllers presented in this paper.

Fig. 16

Exciter control signals of the AVR controlled by the $\mathrm {IOMRAC_{SQP}}$, $\mathrm {IOMRAC_{GA}}$, $\mathrm {IOMRAC_{PSO}}$ and PID controllers

Fig. 17

Transient response of incremental change in terminal voltage for a $0.01 ~\mathrm{(pu)}$ step change in reference voltage, using fractional-order controllers

Fig. 18

Exciter control signals of the AVR controlled by the $\mathrm {FOMRAC_{SQP}}$, $\mathrm {FOMRAC_{GA}}$, $\mathrm {FOMRAC_{PSO}}$ and FOPID controllers

The first robustness test conducted in this Case Study 2 corresponds to variations in the parameters of the generator. At $t = 10~\mathrm{(s)}$, $K_G=0.7$ and $\tau _G=1$ change to $K_G=0.87$ and $\tau _G=2.5$, respectively. Later, at $t=30~\mathrm{(s)}$, the parameters retake the parameters of the initial operating conditions. These are depicted in Fig. 19 to examine the robustness of the fractional controllers numerically. It can be seen that the $t_s$ of the $\mathrm {FOPID_{PSO}}$ controller is $11.1\%$ less rather than the $t_s$ of the $\mathrm {PID_{PSO}}$ controller. Furthermore, the evaluation function $\mathrm{OF}_2$ of the $\mathrm {FOMRAC_{PSO}}$ controller is $4.2\%$ less than the $\mathrm{OF}_2$ of the $\mathrm {PID_{PSO}}$ (Chatterjee et al. [7]).

Fig. 19

Step responses of the AVR controlled by the $\mathrm {MRAC_{PSO}}$ and $\mathrm {PID_{PSO}}$ of integer and fractional orders, under variations in the parameters of the generator at different times

Based on the additional performance index (J), it is shown that the best results in terms of error dynamics are those with the $\mathrm {FOPID_{PSO}}$ controller. It improves performance by $28\%$ compared to the $\mathrm {IOPID_{PSO}}$ controller reported in [7]. We can see that the adaptive strategies controls depicted in Fig. 20 are tripled compared with the exciter action control $\Delta V_E(t)$. However, this value is within the operating range of the excitation system.

Fig. 20

Exciter control signals of the AVR controlled by the $\mathrm {MRAC_{PSO}}$ and $\mathrm {PID_{PSO}}$ of integer and fractional orders, under variations in the parameters of the generator at different times

In the second robustness test, another uncertainty of the exciter model was assumed, in which the transfer function varies from $G_E(s)=\frac{1}{0.5s+1}$ to $G_{E1}=\frac{2}{5s+1}$ at $t=10~\mathrm{(s)}$. The behavior is shown in Fig. 21.

Fig. 21

Step responses of the AVR controlled by the $\mathrm {\mathrm{MRAC}_{\mathrm{PSO}}}$ and $\mathrm {\mathrm{PID}_{\mathrm{PSO}}}$ of integer and fractional orders, under variations in the parameters of the generator and the exciter transfer function

The analyses of the different control schemes show the advantages and disadvantages of fractional order control. The $\mathrm {IOPID_{PSO}}$ controller fails to stabilize the system within the defined time interval, compared to $\mathrm {FOPID_{PSO}}$, which stabilizes the system in $t_s=18~\mathrm{(s)}$. Then, the fractional-order controller demonstrates its robustness under parametric variations.

In this context, the $\mathrm {MRAC_{PSO}}$ controller proposed in this paper satisfies the aim of the control in $43.9~\mathrm{(s)}$ after the parameter variations. However, the $\mathrm {FOMRAC_{PSO}}$ controller offers an $8.2\%$ improvement in settling time compared with the $\mathrm {IOMRAC_{PSO}}$ controller. The performance criteria arithmetic sum offers a valuable tool for evaluating controlled systems. In this case, the J of the $\mathrm {FOMRAC_{PSO}}$ controller are $37.9\%$ less than the J of the $\mathrm {IOMRAC_{PSO}}$ controller.

Fig. 22

Exciter control signals of the AVR controlled by the $\mathrm {MRAC_{PSO}}$ and $\mathrm {PID_{PSO}}$ of integer and fractional orders, under variations in the parameters of the generator and the exciter transfer function at different times

Fig. 23

Terminal voltage signals of the AVR controlled by the MRACs, and PIDs

Fig. 24

Exciter control signals of the AVR controlled by the MRACs, and PIDs

Finally, the results obtained by the $\mathrm {FOPID_{PSO}}$ controller are more efficient than those of the $\mathrm {IOPID_{PSO}}$. The magnitude of the exciter control action is depicted in Fig. 22. However, the $\mathrm {FOMRAC_{PSO}}$ controller is still a good alternative for the AVR systems.

Table 6 Gains and orders of adaptive laws, obtained by optimization algorithms Case Study 3

4.3 Case study 3

This case is used to confirm the results obtained in the two previous cases. It will test the advantages of the fractional-order controllers in relation to the integer order ones. The results shown in this case study are performed using the objective function $\mathrm{OF}_2$ written as (13), associated with $\mathrm{Model}_2$. The difference with Case Study 2 is that the change of the reference voltage is chosen as $\Delta V_r=1~\mathrm{(pu)}$ and the gain of the generator $K_G=1$. As there is no standard cost function, we use $\mathrm{OF}_2$ in the simulations test. To start with, the parameters of the integer- and fractional-order PID controller are tuned, and then, the MRAC controllers are chosen using the PSO optimization technique. Finally, performance indices that assess the advantages and disadvantages of each type of control are assumed.

Before proceeding with the numerical analysis of these results, it is necessary to introduce the parameters obtained for the PID controller. These are $K_p = 0.54455$, $K_i =0.36898$, $K_d = 0.17382$ for the $\mathrm {IOPID_{PSO}}$, and $\alpha = 0.8448$, $\beta = 1.1123$, $K_p = 0.7697$, $K_i = 0.5171$, $K_d = 0.2302$ for the $\mathrm {FOPID_{PSO}}$.

4.3.1 Behaviour of the MRAC

The parameters obtained for the integer- and fractional-order $\mathrm {MRAC_{PSO}}$ controllers are shown in Table 6. Note that the PSO optimization algorithm is used because it shows significant advantages compared with the other optimization techniques for the AVR systems. The results are shown in Fig. 23.

According to Table 7, the settling time $t_s$ of the $\mathrm {FOMRAC_{PSO}}$, is $8.5\%$ less than $t_s$ of the $\mathrm {IOMRAC_{PSO}}$. On the other hand, the $t_s$ of the $\mathrm {FOPID_{PSO}}$ is $31.1\%$ less than $t_s$ of the $\mathrm {IOPID_{PSO}}$.

The integer- and fractional-order $\mathrm {PID_{PSO}}$ controllers use triple the exciting voltage compared with the adaptive strategies control $\mathrm {MRAC_{PSO}}$. The exciter voltage control $\Delta V_E(t)$ is shown in Fig. 24. The magnitude of the exciter control signal exceeds the operating ranges, which is due to $\Delta V_r$ changes of $100\%$ of the rated voltage of the AVR system.

Table 7 Performance criteria, obtained by the controllers with optimized parameters Case Study 3

4.3.2 Robustness test

At this stage, the benefits of each strategy of the fractional-order controller are emphasized. As in the previous case studies, changes can occur in the system parameters for different reasons. The parameters change from $K_G=1$, $\tau _G=1$ to 0.87 and 2.5, respectively. Another uncertainty in the exciter model was assumed in the robustness test, where the transfer function varies from $G_E(s)=\frac{1}{0.4s+1}$ to $G_E(s)=\frac{2}{6s+1}$ at $t=10~\mathrm{(s)}$. These changes represent the state of maximum stress of the AVR system.

Fig. 25

a  Step responses of the AVR controlled by the integer- and fractional-order $\mathrm {PID_{PSO}}$ controllers, under variations in the parameters of the generator and the exciter transfer function at $t=10~\mathrm{(s)}$. b  Exciter control signals of the AVR controlled by the integer- and fractional-order $\mathrm {PID_{PSO}}$ controllers under variations in the parameters of the generator and the exciter transfer function at $t=10~\mathrm{(s)}$

As can be seen in Fig. 25, the time interval starts at $t=10~\mathrm{(s)}$ and goes to $t=100~\mathrm{(s)}$, to emphasize the advantage of the $\mathrm {FOPID_{PSO}}$ controller in comparison with the $\mathrm {IOPID_{PSO}}$ controller. The $\mathrm {FOPID_{PSO}}$ controller does not have an associated cost, since $\Delta V_E$ is like the $\Delta V_E$ of the $\mathrm {IOPID_{PSO}}$ controller.

Fig. 26

a  Step responses of the AVR controlled by the integer and fractional order $\mathrm {MRAC_{PSO}}$ controllers, under variations in the parameters of the generator and the exciter transfer function at $t=10~\mathrm{(s)}$. b  Exciter control signals of the AVR controlled by the integer- and fractional-order $\mathrm {MRAC_{PSO}}$ controllers under variations in the parameters of the generator and the exciter transfer function at $t=10~\mathrm{(s)}$

For the MRAC controllers, the advantages of the $\mathrm {FOMRAC_{PSO}}$ controller in relation to the controller $\mathrm {IOMRAC_{PSO}}$ are noted one more time. The $\mathrm{OF}_2$ of the $\mathrm {FOMRAC_{PSO}}$ is $76.6\%$ less than the $\mathrm{OF}_2$ of the $\mathrm {IOMRAC_{PSO}}$, due to the value of $O_s$, and shown in Fig. 26a. Furthermore, the voltage of the excitation system shows that despite the improvement, there is not an associated cost, (it is even smaller as is shown in Fig. 26b). Another important feature is the $t_s$, since the $\mathrm {FOMRAC_{PSO}}$ controller exhibits a shorter settling time of about $42.3~\mathrm{(s)}$ compared to the $45.3~\mathrm{(s)}$ of the $\mathrm {IOMRAC_{PSO}}$ controller.

Defining $t=100~\mathrm{(s)}$ and the error like $e_c(t)=r(t)-y_p(t)$, the $\mathrm {IOPID_{PSO}}$ controller exhibits lesser J of about 340.1 compared to 76.9 for the $\mathrm {FOPID_{PSO}}$ controller, $90.7\%$ improvement . On the other hand, the controller $\mathrm {FOMRAC_{PSO}}$ exhibits lower J of about 3670.9 compared to 36867.7 for the $\mathrm {IOMRAC_{PSO}}$ controller, a $90\%$ improvement.

5 Conclusions

This paper presents the application of FOMRAC and FOPID to an AVR system. The gains and fractional orders are selected through optimization algorithms. Different optimization procedures in regard to the minimization of two evaluation functions associated with two models used for the AVR system are considered.

In Case Study 1, the $\mathrm {FOMRAC_{PSO}}$ controller improves the $t_s$ by $47.2\%$ over that reported in [1]. Furthermore, simulation studies show an improvement in characteristics of the response of the controlled system and in robustness with respect to model uncertainties when using the $\mathrm {FOMRAC_{PSO}}$ controller. The $\mathrm {FOMRAC_{PSO}}$ proposed in this paper improves the fitness function $\mathrm{OF}_1$ by $58.8\%$ compared with that reported for $\mathrm {FOPID_{PSO}}$ by Zamani et al. [37].

In Case Study 2, the simplification of the MRAC controller is done since the simplified linear model of an AVR system is used. The evaluation of each control structure is performed, finding an improvement in characteristics of the response of the controlled system and in robustness with respect to model uncertainties when using the fractional-order controller, since there is an improvement of $97.9\%$ with the $\mathrm {FOPID_{PSO}}$ compared to $\mathrm{OF}_2$ of the $\mathrm {IOPID_{PSO}}$ reported in [7]. Moreover, the controller $\mathrm {FOMMRAC_{PSO}}$ improves performance by $37.9\%$ compared to $\mathrm {IOMRAC_{PSO}}$ based on the sum performance indices (J) used to evaluate the behavior of the controllers.

To verify the advantages discussed, Case Study 3 is performed. The advantages of the fractional-order controllers in relation to the integer-order controllers is confirmed. This is based on the sum performance indices, when there are uncertainties in the plant.

For all optimization procedures, generalization to fractional-order controllers (FOPID and FOMRAC) present better results in terms of settling times. Also, $\mathrm{OF}_1$ and $\mathrm{OF}_2$ are improved at the minimum for each performance criterion evaluated in this work. Furthermore, it can be concluded from the above simulations that fractional order control is robust against variations in the internal parameters of the plant model. Many performance measures which assess the advantages and disadvantages of fractional control, were analyzed in this work, demonstrating the evident benefits of its application.