1 Introduction

Due to increased application of integration of wind power in power systems, a need for some specific technical requirement emerges, with grid codes the most important technical requirement. As low voltage cases emerge due to faults, grid codes must operate within certain limits [1]. For operation within certain limits of system, low voltage ride through (LVRT) capability methods is used in different studies in the literature.

Fig. 1
figure 1

DFIG circuit model

Full size image

To control rotor current and rotor voltage in rotor-side and grid-side converters of doubly fed induction generator (DFIG) during symmetrical voltage dip, hybrid current control models, feed-forward, vector control, and transient current control have been enhanced. Thanks to these models, inrush currents which occur in DFIG are removed [2–5]. For grid-rotor-side converter units of the DFIG, voltage control strategy is enhanced. Thanks to this voltage control, converter protection provides coordinated control during transient events, such as faults and wind speed increase–decrease [6, 7]. The finite-element method is used for the LVRT method in DFIG. Owing to the reduction of simple circuit components, the finite-element method provides active crowbar protection as well as torque control of DFIG [8]. Enhanced using the positive-sequence component, new LVRT capability improves voltage and phase angle during varios voltage sag problems with low-high-pass filters and reference current tracking used in wind farm based on DFIG [9, 10]. Electro-motive force voltages in DFIG based wind turbines provide the controls of not only rotor-side converter, but also stator-side converter during the transient cases, as well. With compensation of electro-motive force voltages, over-stator current and over-rotor current are reduced during transient cases. In [11, 12], passive and active LVRT compensators are used to improve the LVRT capability during symmetrical and asymmetrical faults in DFIG. The passive compensator and active compensator reduce power oscillations and time response of parameters during faults owing to new crowbar units. Besides, using virtual resistance, a different control strategy is proposed to reduce exceeding rotor-circuit currents in [13, 14], which can provide reactive power to compensate for the latest grid code requirement in transient conditions. To develop LVRT capability in DFIG, a different approach called crowbar trip activation time is used. Using bypass resistor in this control method, converter units prevent various faults cases [15]. As a new control strategy against transient cases in DFIG based on wind farm, DC-link voltage control techniques are used. With the modification of grid-side converter unit of DFIG, DC-link voltage control is carried out both by compensating active power of the system and by regulating voltage fluctuations for LVRT capability [16, 17]. Dynamic voltage resistor (DVR) devices are one of the most commonly used devices among control strategy of DFIG for LVRT capability. Besides, owing to the positive and sequence component in DFIG for LVRT, grid-side converter (GSC) and rotor-side converter (RSC) are provided for the control of DFIG during fault conditions [18, 19]. Power oscillation damping (POD) is important for regulating voltage dip or the exceed currents in the DFIG during grid faults, Besides, POD has provided to power control. Therefore, different LVRT methods with POD to protect of the DFIG are developed [20–22]. Besides all control strategies of DFIG based wind farm during transient conditions, capability, flexible AC transmission system (FACTS) devices are used to enhance LVRT capability. Especially, static synchronous compensator (STATCOM) has provided to reactive-power control and voltage controls as well as angle control [23, 24].

In this study, a new LVRT capability method in DFIG is enhanced. Not only stator, but also rotor circuits were modelled as electro-motive force instead of stator and rotor flux equations for LVRT in the DFIG, as well. Besides, for stability of the DFIG, the SDRU and RCC were developed. A comparison was made with and without the SDRU and RCC in conditions variations, such as three–two faults. It was shown that the SDRU–RCC LVRT capability control yielded efficient results in this study.

2 Doubly fed induction generators (DFIG)

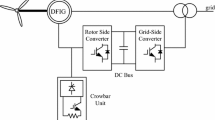
A crowbar unit, GSC and RSC are the components of DFIG based on wind turbine. The DFIG circuit model is given in Fig. 1.

It is essential that the grid-side converter regulates the DC-link voltage besides providing reactive power, while the rotor side is needed to regulate the real and reactive powers of the DFIG. A crowbar unit control regulates voltage-current limits. It is with d–q-axes equivalence circuits that voltage, current and flux calculations of the DFIG are facilitated [25–27]. Mathematical enhancement of DFIG is based on some assumptions. An arbitrary reference frame is used in determining DFIG equations, while calculations of the DFIG equations in power systems are facilitated with p.u. values. Voltage and linkage flux computations obtained in line with p.u. values in the DFIG are shown in Eqs. 1 and 4:

$$\begin{aligned} \left[ {{\begin{array}{l} {v_{ds} } \\ {v_{qs} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {R_s }&{} 0 \\ 0&{} {R_s } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] +w_s \left[ {{\begin{array}{ll} 0&{} {-1} \\ 1&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right] +\left[ {{\begin{array}{l} {\mathop {\lambda _{ds}}}\\ {\mathop {\lambda _{qs}}} \\ \end{array} }} \right] \nonumber \\\end{aligned}$$
(1)
$$\begin{aligned} \left[ {{\begin{array}{l} {v_{dr} } \\ {v_{qr} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {R_r }&{} 0 \\ 0&{} {R_r } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] +sw_s \left[ {{\begin{array}{ll} 0&{} {-1} \\ 1&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{dr} } \\ {\lambda _{qr} } \\ \end{array} }} \right] +\left[ {{\begin{array}{l} {\mathop {\lambda _{dr} }} \\ {\mathop {\lambda _{qr} }} \\ \end{array} }} \right] \nonumber \\\end{aligned}$$
(2)
$$\begin{aligned} \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {L_s +L_m }&{} 0 \\ 0&{} {L_s +L_m } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] +\left[ {{\begin{array}{ll} {L_m }&{} 0 \\ 0&{} {L_m } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] \nonumber \\\end{aligned}$$
(3)
$$\begin{aligned} \left[ {{\begin{array}{l} {\lambda _{dr} } \\ {\lambda _{qr} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {L_m }&{} 0 \\ 0&{} {L_m } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] +\left[ {{\begin{array}{ll} {L_r +L_m }&{} 0 \\ 0&{} {L_r +L_m } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$
(4)

where \({v}_{{ds}}\), \({v}_{{qs}}\), \({v}_{{dr}}\), \({v}_{{qr}}\): d- and q-axes are the stator and rotor voltages; \(\lambda _{{ds}},\,\lambda _{{qs}},\lambda _{{dr}},\,\lambda _{{qr}}\): d- and q-axes are the stator- and rotor-magnetizing fluxes; \({e}_{{d}}\), \({e}_{{q}}\): d- and q-axes are the stator source voltages; and \({w}_{{s}}\): synchronous speed, s: slip, \({r}_{{s}}\), \({r}_{{r}}\) are the stator and rotor resistances.

In creating the electro-motor force in the full-order model (FOM), Eq. 5 is obtained with the incorporation of Eq. 4 into Eq. 2:

$$\begin{aligned}&\left[ {{\begin{array}{l} {v_{dr}} \\ {v_{qr} } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {R_r }&{} 0 \\ 0&{} {R_r } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] \nonumber \\&\quad +\left[ {{\begin{array}{ll} 0&{} {-sw_s } \\ {sw_s }&{} 0 \\ \end{array} }} \right] \left\{ \left[ {{\begin{array}{ll} {L_r +L_m }&{} 0 \\ 0&{} {L_r +L_m } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] \right. \nonumber \\&\quad \left. +\left[ {{\begin{array}{ll} {L_m }&{} 0 \\ 0&{} {L_m } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] \right\} \nonumber \\&\quad +\left[ {{\begin{array}{ll} {L_r +L_m }&{} 0 \\ 0&{} {L_r +L_m } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\dot{i}}_{dr} \\ {\dot{i}}_{qr} \\ \end{array} }} \right] +\left[ {{\begin{array}{ll} {L_m }&{} 0 \\ 0&{} {L_m } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\dot{i}}_{ds} \\ {\dot{i}}_{qs} \\ \end{array} }} \right] .\nonumber \\ \end{aligned}$$
(5)

Equation 6 is obtained with the isolation of the stator d–q current in Eq. 3:

$$\begin{aligned} \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {\frac{1}{L_s +L_m }}&{} 0 \\ 0&{} {\frac{1}{L_s +L_m }} \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right] \nonumber \\&-\left[ {{\begin{array}{ll} {\frac{L_m }{L_s +L_m }}&{} 0 \\ 0&{} {\frac{L_m }{L_s +L_m }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] . \end{aligned}$$
(6)

d–q axes’ current obtained is given in Eq. 7:

$$\begin{aligned} \left[ {{\begin{array}{l} {\dot{i}}_{ds} \\ {\dot{i}}_{qs} \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {\frac{L_m }{L_m +L_s }}&{} 0 \\ 0&{} {\frac{L_m }{L_m +L_s }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} \dot{i}_{dr} \\ \dot{i}_{qr} \\ \end{array} }} \right] . \end{aligned}$$
(7)

Equation 8 is obtained with the incorporation of Eqs. 5 and 6 into Eq. 4:

$$\begin{aligned}&\left[ {{\begin{array}{l} {v_{dr} } \\ {v_{qr} } \\ \end{array} }} \right] =\left\{ \left[ {{\begin{array}{ll} {R_r }&{} 0 \\ 0&{} {R_r } \\ \end{array} }} \right] +\left[ {{\begin{array}{ll} {R_s }&{} 0 \\ 0&{} {R_s } \\ \end{array} }} \right] \right. \nonumber \\&\quad \times \left. \left[ {{\begin{array}{ll} {\frac{L_m ^{2}}{(L_m +L_s )^{2}}}&{} 0 \\ 0&{} {\frac{L_m ^{2}}{(L_m +L_s )^{2}}} \\ \end{array} }} \right] \right\} \left[ \begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} \right] +\left[ {{\begin{array}{ll} 0&{} {-sw_s } \\ {sw_s }&{} 0 \\ \end{array} }} \right] \nonumber \\&\quad \times \left\{ {\left[ {{\begin{array}{ll} {L_m +L_r }&{} 0 \\ 0&{} {L_m +L_r } \\ \end{array} }} \right] -\left[ {{\begin{array}{ll} {\frac{L_m ^{2}}{L_{ss} ^{2}}}&{} 0 \\ 0&{} {\frac{L_m }{L_{ss} }} \\ \end{array} }} \right] } \right\} \nonumber \\&\quad \times \left[ {{\begin{array}{l} i_{dr} \\ i_{qr} \\ \end{array} }} \right] +\left\{ \left[ {{\begin{array}{ll} {L_m +L_r }&{} 0 \\ 0&{} {L_m +L_r } \\ \end{array} }} \right] \right. \nonumber \\&\quad -\left[ {{\begin{array}{ll} {\frac{L_m ^{2}}{(L_m +L_s )^{2}}}&{} 0 \\ 0&{} {\frac{L_m ^{2}}{(L_m +L_s )^{2}}} \\ \end{array} }} \right] \left[ {{\begin{array}{l} \dot{i}_{dr} \\ \dot{i}_{qr} \\ \end{array} }} \right] \nonumber \\&\quad +\left[ {{\begin{array}{ll} {\frac{L_m }{L_m +L_s }}&{} 0 \\ 0&{} {\frac{L_m }{L_m +L_s }} \\ \end{array} }} \right] \left\{ \left[ {{\begin{array}{ll} {\frac{R_s }{L_m +L_s }}&{} 0 \\ 0&{} {\frac{R_s }{L_m +L_s }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right] \right. \nonumber \\&\quad \left. +\left[ {{\begin{array}{ll} 0&{} {w_s } \\ {-w_s }&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right] +\left[ {{\begin{array}{ll} 0&{} {-sw_s } \\ {sw_s }&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{dr} } \\ {\lambda _{qr} } \\ \end{array} }} \right] \right\} \end{aligned}$$
(8)

The rotor electro-motive-force in the FOM is given in Eq. 9.

$$\begin{aligned} \left[ {{\begin{array}{l} {E_d } \\ {E_q } \\ \end{array} }} \right]= & {} \frac{L_m }{L_s +L_m }\left\{ \left[ {{\begin{array}{l} {v_{dr} } \\ {v_{qr} } \\ \end{array} }} \right] +\left[ {{\begin{array}{ll} 0&{} {w_s } \\ {-w_s }&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right] \right. \nonumber \\&\left. +\left[ {{\begin{array}{ll} 0&{} {-sw_s } \\ {sw_s }&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right] \right\} \end{aligned}$$
(9)

In the DFIG reduced-order model (ROM), a electro-motive force and transient reactance are applied rather than stator flux derivations. Stator and rotor d–q voltages in the FOM in mathematical equation of the ROM are given in Eqs. 1 and 4. Simplified rotor d–q-axes currents are obtained in Eq. 10:

$$\begin{aligned} \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {\frac{1}{L_m +L_r }}&{} 0 \\ 0&{} {\frac{1}{L_m +L_r }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{dr} } \\ {\lambda _{qr} } \\ \end{array} }} \right] \nonumber \\&-\left[ {{\begin{array}{ll} {\frac{L_m }{L_m +L_r }}&{} 0 \\ 0&{} {\frac{L_m }{L_m +L_r }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] . \end{aligned}$$
(10)

With the incorporation of the rotor, d–q axes’ currents in Eq. 5 into Eqs. 3 and 11 are obtained:

$$\begin{aligned} \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {L_{ss} }&{} 0 \\ 0&{} {L_{ss} } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{ll} {L_m }&{} 0 \\ 0&{} {L_m } \\ \end{array} }} \right] \left\{ \left[ {{\begin{array}{ll} {\frac{1}{L_m +L_r }}&{} 0 \\ 0&{} {\frac{1}{L_m +L_r }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{dr} } \\ {\lambda _{qr} } \\ \end{array} }} \right] \right. \nonumber \\&\left. +\left[ {{\begin{array}{ll} {\frac{L_m }{L_m +L_r }}&{} 0 \\ 0&{} {\frac{L_m }{L_m +L_r }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] \right\} . \end{aligned}$$
(11)

Equation 12 is obtained with the re-designation of Eq. 11:

$$\begin{aligned} \left[ {{\begin{array}{lll} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {(L_m +L_s )-\frac{L_m^2 }{L_m +L_r }}&{} 0 \\ 0&{} {(L_m +L_s )-\frac{L_m^2 }{L_m +L_r }} \\ \end{array} }} \right] \nonumber \\&\times \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] +\left[ {{\begin{array}{ll} {\frac{L_m }{L_m +L_r }}&{} 0 \\ 0&{} {\frac{L_m }{L_m +L_r }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{dr} } \\ {\lambda _{qr} } \\ \end{array} }} \right] . \end{aligned}$$
(12)

While stator transient reactance is shown in Eq. 13, steady-state reactance is shown in 14:

$$\begin{aligned} X^{{\prime }}= & {} w_s \left( {(L_m +L_s )-\frac{L_m^2 }{L_m +L_r }} \right) \end{aligned}$$
(13)
$$\begin{aligned} X= & {} w_s (L_m +L_s ). \end{aligned}$$
(14)

Without considering the linkage flux derivation in Eq. 1, Eq. 15 is achieved according to the descriptions in Eqs. 7–10:

$$\begin{aligned} \left[ {{\begin{array}{l} {v_{ds} } \\ {v_{qs} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {R_s }&{} 0 \\ 0&{} {R_s } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] +\left[ {{\begin{array}{ll} 0&{} {-X^{{\prime }}} \\ {X^{{\prime }}}&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{ll} 0&{} 1 \\ {-1}&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {e_d } \\ {e_q } \\ \end{array} }} \right] \end{aligned}$$
(15)

With the incorporation of Eq. 10 into Eq. 2, the derivation of the electro-motive force shown as \({e}_{d}\) and \(e_q\) is given in Eq. 16 [28–30]:

$$\begin{aligned} \left[ {\begin{array}{l} \mathop {e_d }\limits ^{\bullet } \\ \mathop {e_q }\limits ^{\bullet } \\ \end{array}} \right]= & {} -\frac{1}{T_0 }\left\{ {\left[ {\begin{array}{l} e_d \\ e_q \\ \end{array}} \right] +\left[ {\begin{array}{l} 0\quad \quad \quad \quad \frac{L_m ^{2}}{L_m +L_r } \\ -\frac{L_m ^{2}}{L_m +L_r }\quad \quad \quad 0 \\ \end{array}} \right] \left[ {\begin{array}{l} i_{ds} \\ i_{qs} \\ \end{array}} \right] } \right\} \nonumber \\&+\;sw_s \left[ {\begin{array}{l} 0\quad \quad 1 \\ -1\quad \;\;0 \\ \end{array}} \right] \left[ {\begin{array}{l} e_d \\ e_q \\ \end{array}} \right] \nonumber \\&+\left[ {\begin{array}{l} 0\quad \quad \quad \quad -\frac{L_m }{L_m +L_r } \\ \frac{L_m }{L_m +L_r }\quad \quad \quad 0 \\ \end{array}} \right] \left[ {\begin{array}{l} v_{dr} \\ v_{qr} \\ \end{array}} \right] . \end{aligned}$$
(16)

The transient open-time constant of ROM in the DFIG is given in Eq. 17:

$$\begin{aligned} T_0 =\frac{L_r +L_m }{R_r }. \end{aligned}$$
(17)

The aim is to maintain dynamic control of GSC–RSC by creating an electro-motive force in the rotor axis apart from the electro-motive force created without considering stator flux derivations in the ROM [31]. The d–q axes stator voltage obtained without considering the stator axis linkage flux derivation in the ROM is given in Eq. 18:

$$\begin{aligned} \left[ {{\begin{array}{l} {v_{ds} } \\ {v_{qs} } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {R_s }&{} 0 \\ 0&{} {R_s } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] +w_s \left[ {{\begin{array}{ll} 0&{} {-1} \\ 1&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right] . \end{aligned}$$
(18)
Fig. 2
figure 2

DFIG modeling of SDRU

Full size image

With the incorporation of Eq. 4 demonstrated in the ROM into Eq. 2, Eq. 19 is achieved:

$$\begin{aligned} \left[ {{\begin{array}{l} {v_{dr} } \\ {v_{qr} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {R_r }&{} 0 \\ 0&{} {R_r } \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{ll} 0&{} {-sw_s } \\ {sw_s }&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {L_m +L_r }&{} 0 \\ 0&{} {L_m +L_r } \\ \end{array} }} \right] \left[ {{\begin{array}{l} i_{dr} \\ i_{qr} \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{ll} {L_m }&{} 0 \\ 0&{} {L_m } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{ll} {L_m +L_r }&{} 0 \\ 0&{} {L_m +L_r } \\ \end{array} }} \right] \left[ {{\begin{array}{l} \dot{i}_{dr} \\ \dot{i}_{qr} \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{ll} {L_m }&{} 0 \\ 0&{} {L_m } \\ \end{array} }} \right] \left[ {{\begin{array}{l} \dot{i}_{ds} \\ \dot{i}_{qs} \\ \end{array} }} \right] . \end{aligned}$$
(19)

Simplified d–q-axes stator currents in Eq. 3 are given in Eq. 20:

$$\begin{aligned} \left[ {{\begin{array}{l} {i_{ds} } \\ {i_{qs} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {\frac{1}{L_s +L_m }}&{} 0 \\ 0&{} {\frac{1}{L_s +L_m }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right] \nonumber \\&-\left[ {{\begin{array}{ll} {\frac{L_m }{L_s +L_m }}&{} 0 \\ 0&{} {\frac{L_m }{L_s +L_m }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] . \end{aligned}$$
(20)

The d–q-axes derivation of the stator flux is achieved in Eq. 21:

$$\begin{aligned} \left[ {{\begin{array}{l} \dot{i}_{ds} \\ \dot{i}_{qs} \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {\frac{L_m }{L_m +L_s }}&{} 0 \\ 0&{} {\frac{L_m }{L_m +L_s }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\mathop {i_{dr} }} \\ {\mathop {i_{qr} }} \\ \end{array} }} \right] . \end{aligned}$$
(21)

With the incorporation of Eqs. 20 and 21 into Eqs. 19, 22 is achieved:

$$\begin{aligned} \left[ {{\begin{array}{lll} {v_{dr} } \\ {v_{qr} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {R_r }&{} 0 \\ 0&{} {R_r } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] +\left[ {{\begin{array}{ll} 0&{} {-sw_s L_m } \\ {sw_s L_m }&{} 0 \\ \end{array} }} \right] \nonumber \\&\times \left[ {{\begin{array}{ll} {\frac{1}{L_s +L_m }}&{} 0 \\ 0&{} {\frac{1}{L_s +L_m }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right] \\&-\left[ {{\begin{array}{ll} {\frac{L_m }{L_s +L_m }}&{} 0 \\ 0&{} {\frac{L_m }{L_s +L_m }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{lll} 0&{} {-sw_s (L_r +L_m )} \\ {sw_s (L_r +L_m )}&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{ll} {\frac{L_m ^{2}}{L_s +L_m }}&{} 0 \\ 0&{} {\frac{L_m ^{2}}{L_s +L_m }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} \dot{i}_{dr} \\ \dot{i}_{qr} \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{lll} {L_r +L_m }&{} 0 \\ 0&{} {L_r +L_m } \\ \end{array} }} \right] \left[ {{\begin{array}{l} \dot{i}_{dr} \\ \dot{i}_{qr} \\ \end{array} }} \right] -\left[ {{\begin{array}{ll} {R_r }&{} 0 \\ 0&{} {R_r } \\ \end{array} }} \right] \nonumber \\&-\left[ {{\begin{array}{ll} 0&{} {\frac{-sw_s L_m }{L_s +L_m }} \\ {\frac{sw_s L_m }{L_s +L_m }}&{} 0 \\ \end{array} }} \right] \nonumber \\&\nonumber \\&+\left[ {{\begin{array}{ll} 0&{} {-sw_s (L_r +L_m )} \\ {sw_s (L_r +L_m )}&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{ll} {\frac{L_m ^{2}}{L_s +L_m }+L_r +L_m }&{} 0 \\ 0&{} {\frac{L_m ^{2}}{L_s +L_m }+L_r +L_m } \\ \end{array} }} \right] \nonumber \\&\times \left[ {{\begin{array}{l} {\mathop {i_{dr} }} \\ {\mathop {i_{qr} }} \\ \end{array} }} \right] +\left[ {{\begin{array}{ll} 0&{} {\frac{-sw_s L_m }{L_s +L_m }} \\ {\frac{sw_s L_m }{L_s +L_m }}&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \nonumber \\ \end{array} }} \right] . \end{aligned}$$
(22)

Equation 23 is achieved through the simplification of Eq. 22:

$$\begin{aligned} \left[ {{\begin{array}{lll} {v_{dr} } \\ {v_{qr} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {R_r }&{} 0 \\ 0&{} {R_r } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] +\left( -\frac{L_m }{L_s +L_m }+L_r +L_m \right) \nonumber \\&\times \left[ {{\begin{array}{ll} 0&{} {-sw_s } \\ {sw_s }&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_{dr} } \\ {i_{qr} } \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{ll} {\frac{L_m }{L_s +L_m }+L_r +L_m }&{} 0 \\ 0&{} {\frac{L_m }{L_s +L_m }+L_r +L_m } \\ \end{array} }} \right] \nonumber \\&\times \left[ {{\begin{array}{l} \dot{i}_{dr} \\ \dot{i}_{qr} \\ \end{array} }} \right] +\left[ {{\begin{array}{ll} 0&{} {-\frac{sw_s L_m }{L_s +L_m }} \\ {\frac{sw_s L_m }{L_s +L_m }}&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right] . \end{aligned}$$
(23)

The rotor electro-motive force of the ROM achieved without considering the stator resistance and d–q-axes stator voltage is given in Eq. 24:

$$\begin{aligned} \left[ {{\begin{array}{l} {E_d } \\ {E_q } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} 0&{} {-\frac{sw_s L_m }{L_s +L_m }} \\ {\frac{sw_s L_m }{L_s +L_m }}&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\lambda _{ds} } \\ {\lambda _{qs} } \\ \end{array} }} \right] . \end{aligned}$$
(24)

Whereas the angular speed based on stator flux is stable under normal operating conditions of DFIG, changes can be observed in angular speed in transient case. On the other hand, a drop in output voltage of DFIG does not change the flux drastically according to the basic flux rule. Accordingly, the stator flux ratio of the drop in three-phase’s voltage produces dc-component. This component is considered to be an oscillator during the transfer in synchronous reference frame, and it is applied as stator time constant at the same time. The stator flux change during the voltage drop is given in Eq. 25:

$$\begin{aligned} \lambda _{sdq0} = \left\{ \! {\begin{array}{l} \lambda _{sdq0} ^{+} \\ \lambda _{sdq2} ^{+} + \lambda _{sdq2} ^{-}e^{2w_s t} + (\lambda _{sdq0} ^{+}-\lambda _{sdq2} -^{+}\lambda _{sdq2} ^{-})e^{-\sigma t}e^{-w_s t} \\ \end{array}} \!\right\} \!. \end{aligned}$$
(25)

Considering Eq. (25) and without considering stator resistance and flux, equivalent rotor source voltage can be defined as in the following equation. The first line of Eq. 25 points to the pre-transient condition, while the second line points to the stator flux after transient conditions. The stator flux is demonstrated in two parts; before and after the voltage drop. The rotor d–q axes are used in controlling these two parts. In Eq. 26, \((L_m /L_{ss} )s\lambda _{sdq0} ^{+}\) points to the control as in the first part, when the sliding rate of Rotor \(E_{dq} \) voltage in transient conditions is comparatively low. In the second part, converter circuit in the rotor side is protected from the overcurrent and long-term unstable condition through rotor:

$$\begin{aligned} E_{sdq0} \!=\!\left\{ {\begin{array}{l} \frac{L_m }{L_{ss} }s\lambda _{sdq0} ^{+} \\ \frac{L_m }{L_{ss} }s\lambda _{sdq2} ^{+}\!-\! \frac{L_m }{L_{ss} }(1-s)(\lambda _{sdq0} ^{+}\!-\! \lambda _{sdq2} ^{+}\!-\!\lambda _{sdq2} ^{-})e^{-\sigma t}e^{-w_s t} \\ \end{array}} \right\} \end{aligned}$$
(26)

where \(\lambda _{sdqo} ^{+}\) is the positive-sequence steady stator flux linkage, while \(\lambda _{sdq2} ^{+}\) and \(\lambda _{sdq2} ^{-}\) are the positive and negative sequence transient stator flux linkages, respectively, t is the time, and \(\sigma \) is the stator-damping coefficient, as shown in Eq. (27):

$$\begin{aligned} \sigma =1-\frac{L_m }{L_s L_r }. \end{aligned}$$
(27)

3 Enhancement of SDRU and RCC in DFIG based wind farm

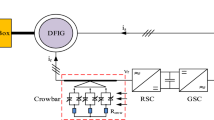
Three-phase resistors, r1, r2, and r3, directly connected to stator windings of DFIG based wind farm are shown in Fig. 2 [32, 33].

Fig. 3
figure 3

Positive and negative components’ control of rotor-side converter

Full size image
Fig. 4
figure 4

Simulated test system

Full size image
Table 1 Parameter values of the DFIG
Full size table

Equation 28 shows how the line voltages, ab and ca, of the stator and the grid voltages relate to each other:

$$\begin{aligned} \left[ {\begin{array}{l} v_{\mathrm{network}ab} \\ v_{\mathrm{network}ca} \\ \end{array}} \right] =\left[ {{\begin{array}{ll} {r_1 }&{} {-r_2 } \\ {-(r_1 +r_3 )}&{} {-r_3 } \\ \end{array} }} \right] \left[ {\begin{array}{l} i_{sa} \\ i_{sb} \\ \end{array}} \right] +\left[ {\begin{array}{l} v_{sab} \\ v_{sca} \\ \end{array}} \right] . \end{aligned}$$
(28)

Equation (28) is obtained on the assumption that a neutral current can find no way to flow out to ensure that zero sequence component of the stator current is zero. Accordingly, (\({i}_{{sa}} + {i}_{{sb}})\) replaces the phase c current \({i}_{{sc}}\). Following matrix multiplications, (28) is changed into the stationary reference frame through \(\alpha \beta \) axes, as follows:

$$\begin{aligned} \left[ {\begin{array}{l} v_{\mathrm{network}\alpha } \\ v_{\mathrm{network}\beta } \\ \end{array}} \right]= & {} \left[ {{\begin{array}{ll} {r_\alpha }&{} {r_{\alpha \beta } } \\ {r_{\alpha \beta } }&{} {r_\beta } \\ \end{array} }} \right] \left[ {\begin{array}{l} i_{s\alpha } \\ i_{s\beta } \\ \end{array}} \right] +\left[ {\begin{array}{l} v_{s\alpha } \\ v_{s\beta } \\ \end{array}} \right] \end{aligned}$$
(29)
$$\begin{aligned} \left[ {\begin{array}{l} v_{\mathrm{network}\alpha } \\ v_{\mathrm{network}\beta } \\ \end{array}} \right]= & {} \left[ {{\begin{array}{lll} {\frac{4r_1 +r_2 +r_3 }{6}}&{} {\frac{r_3 -r_2 }{2\sqrt{3}}} \\ {\frac{r_3 -r_2 }{2\sqrt{3}}}&{} {\frac{r_3 +r_2 }{2}} \\ \end{array} }} \right] \left[ {\begin{array}{l} i_{s\alpha } \\ i_{s\beta } \\ \end{array}} \right] +\left[ {\begin{array}{l} v_{s\alpha } \\ v_{s\beta } \\ \end{array}} \right] . \end{aligned}$$
(30)

The first line of (30) points to the grid voltage vector equation in stationary reference frame, demonstrated by

$$\begin{aligned} \left[ {\begin{array}{l} v_{\mathrm{network}\alpha } \\ v_{\mathrm{network}\beta } \\ \end{array}} \right] =\left[ {{\begin{array}{ll} {\frac{r_\alpha +r_\beta }{2}}&{} 0 \\ 0&{} {\frac{r_\alpha -r_\beta }{2}} \\ \end{array} }} \right] \left[ {\begin{array}{l} i^{*}_{s\alpha } \\ i^{*}_{s\beta } \\ \end{array}} \right] +\left[ {\begin{array}{l} v_{s\alpha } \\ v_{s\beta } \\ \end{array}} \right] . \end{aligned}$$
(31)

A dc term is obtained through the positive sequence component in the positive synchronous reference frame, d–q axes positive rotating at the angular speed. This can also be seen in the negative sequence component in the negative synchronous reference frame, d–q axes negative rotating at the angular speed. By replacing the positive into negative sequence components of the grid and d–q axes stator voltage shown in (31), Eq. (32) is obtained with some alterations as follows:

$$\begin{aligned} \left[ {\begin{array}{l} v_{\mathrm{network}d} \\ v_{\mathrm{network}q} \\ \end{array}} \right] =\left[ {{\begin{array}{ll} {\frac{r_\alpha +r_\beta }{2}}&{} 0 \\ 0&{} {\frac{r_\alpha -r_\beta }{2}} \\ \end{array} }} \right] \left[ {\begin{array}{l} i^{+}_{sdq} \\ i^{-}_{sq} \\ \end{array}} \right] +\left[ {\begin{array}{l} v^{+}_{sdq} \\ v^{-}_{dq} \\ \end{array}} \right] . \end{aligned}$$
(32)

The positive and negative sequence components of the grid voltage are described in Eqs. (31) and (32) as functions of d–q axes stator voltage.

Fig. 5
figure 5figure 5

a 34.5 kV bus voltage of test system, b output voltage of DFIG, c angular speed of DFIG, d electrical torque of DFIG, e d-axis stator current variations of DFIG, f q-axis stator current variations of DFIG, g d-axis rotor current variations of DFIG, h q-axis rotor current variations of DFIG

Full size image

Under normal conditions, the outer power control loops, also known as mainstream vector control, prove instrumental in achieving the d–q components of the rotor reference current. During fault conditions, the d–q components obtained in this way can be used to develop the LVRT capability. In this section, a solution is proposed to enhance the LVRT capability during unbalanced voltage dips with the application of the asymmetrical SDR and through a profound elaboration on how to choose the d–q components of the rotor reference current during the fault. In accordance with d–q axes stator flux equations, the stator positive/negative sequence current, in terms of stator flux and rotor current, is shown as

$$\begin{aligned} i^{+}_{sdq}= & {} \frac{\lambda ^{+}_{sdq} -L_m i^{+}_{rdq} }{L_s } \end{aligned}$$
(33)
$$\begin{aligned} i^{-}_{sdq}= & {} \frac{\lambda ^{-}_{sdq} }{L_s }. \end{aligned}$$
(34)

Transformation of (33) and (34) into (32) produces the negative sequence of the grid voltage in terms of rotor current, stator voltage, and flux:

$$\begin{aligned} v^{-}_{\mathrm{network}dq} =\frac{r_\alpha -r_\beta }{2}\times \frac{\lambda ^{+}_{sdq} -L_m i^{+}_{rdq} }{L_s }. \end{aligned}$$
(35)
Fig. 6
figure 6figure 6

a 34.5 kV bus voltage of test system, b output voltage of DFIG, c angular speed of DFIG, d electrical torque of DFIG, e d-axis stator current variations of DFIG, f q-axis stator current variations of DFIG, g d-axis rotor current variations of DFIG, h q-axis rotor current variations of DFIG

Full size image

In this way, the negative sequence components of the stator voltage and flux turn out to be zero, thereby eliminating unbalanced voltage fluctuation the stator voltage. It is important to note that \({v}_{sdq}\) and \(\lambda _{sdq} \) are inter-dependent during the unbalanced voltage dip. In the light of (35), it is plausible to select the positive and negative sequence components of the rotor reference current in the positive/negative synchronous reference frames as follows:

$$\begin{aligned} i^{+}_{{rdq-ref}}= & {} -\frac{L_s }{L_m }\times \frac{2}{r_\alpha -r_\beta }\times v^{-}_{\mathrm{network}dq} +\frac{1}{L_m }\lambda _{sdq}^+ \end{aligned}$$
(36)
$$\begin{aligned} i^{-}_{{rdq-ref}}= & {} 0. \end{aligned}$$
(37)

The assumption that rotor current control loop is fast enough gives rise to the possibility that the rotor current can be set to its reference value. Accordingly, with the rotor current during the unbalanced voltage dip chosen according to (34) and (35), it is possible to nullify the negative sequence component of the stator voltage and current, thereby balancing stator voltage. It must be emphasized that the positive components of rotor current are controlled in positive synchronous reference frame, while negative components of rotor current are controlled and in negative synchronous reference frame. Therefore, as given in Fig. 3, separate controllers must be used for positive and negative sequence components of the rotor current.

The positive d–q frame helps in controlling positive sequence rotor current with positive stator flux orientation, where the d positive axis is fixed to the positive stator flux with the rotation speed of \({w}_{b}\), with its phase angle with the \(\alpha \) axis measuring \(\theta _{\lambda s0} \). In d positive frame with positive stator flux orientation, the q positive axis rotor current is used for the real-power control as well as the reactive-power control, while in the d–q axes frame, used to control negative sequence rotor current, the angular speed of d negative axis rotation is \(-w_b\) with the phase angle \(-\theta _{\lambda s0} \) regarding the \(\alpha \) axis.

4 Simulation study

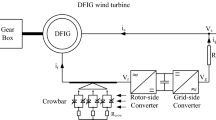
The transient behaviour of the wind turbine was investigated through the 2.3 MW wind power system, as given in Fig. 4.

The full-order DFIG based wind turbine model and the developed DFIG based wind turbine model with an SDRU and RCC are the two models that demonstrate the wind turbine generator, as can be seen in the previous section. A 2.6 MW, 0.69 kV Y/34.5 kV \(\Delta \) transformer was used in connecting the wind turbine to a 34.5 kV system [34]. The distance between the wind turbine and the 34.5 kV grid was 1 km. The transmission grid connection was made available through the 0.69 kV Y/34.5 kV \(\Delta \) transformers. 8 m/s was taken as the constant speed of wind. The saturation of the transformers was neglected. A 34.5 kV grid-side short-circuit power value was selected as 2500 MVA, while the X/R rate was selected as 7. As used in the DFIG-based wind farm, parameter values are given in Table 1.

5 Simulation results

A comparison was drawn for the effect of the SDRU and RCC upon the system parameters during transient cases. First, three fault was formed in the middle of the transmission line during a 0.55–0.6 s event. The observation for the DFIG with and without the SDRU and RCC was examined impacts on bus voltages and variation DFIG parameters. The comparisons drawn are shown from Fig. 5a–h.

Figure 4a, b shows that there was a increase in the peak values of the 34.5 kV bus voltage of test system and output voltage of DFIG, system stabilized within shorter time using the SDRU and RCC in LVRT. With and without SDRU and RCC use in LVRT, 34.5 kV bus voltage of test system was nearly 0.25 and 0.2 p.u., respectively. Moreover, there was a considerable decrease in oscillations in the angular speed, electrical torque, and d–q-axes stator currents with the use SDRU and RCC in LVRT. While DFIG, angular speed, electrical torque, and d–q-axes stator–rotor currents with SDRU and RCC were stabilized in nearly 1.5, 1.25, 3, and 3 s after three-phase fault, respectively, DFIG angular speed, electrical torque, and d–q-axes stator–rotor currents without SDRU and RCC were stabilized in nearly 7, 6.5, 6.5, and 6.5 s after three-phase fault in 34.5 kV bus, respectively.

Second, two faults were formed in the middle of the transmission line between 0.55 and 0.6 s. The observation for the DFIG with and without the SDRU and RCC was examined impacts on bus voltages and variation DFIG parameters, and comparisons are given from Fig. 6a–h.

When there was a two-phase fault, the bus voltage of 34.5 kV of test system values and the output voltage of DFIG were nearly 0.2 and 0.25 p.u. without and with an SDRU and RCC in the DFIG, respectively, with an increase in the latter. The SDRU and RCC use also reduced oscillations in some parameters, such as the DFIG angular speed, electrical torque, and d–q-axes stator current variations, as was the case in the three-phase fault. While DFIG, angular speed, electrical torque, and d–q-axes stator–rotor currents with SDRU and RCC were stabilized in nearly 1.5, 1.25, 1.25, and 1.25 s after three-phase fault, respectively, DFIG angular speed, electrical torque, and d–q-axes stator–rotor currents without SDRU and RCC were stabilized in nearly 3, 5, 5, and 5 s after three-phase fault in 34.5 kV bus, respectively.

6 Conclusions

This study throws light on the application of an SDRU and RCC for DFIG based wind turbine grid-connected. The comparison of the transient behaviors of the system with and without the SDRU and RCC in DFIG was based on voltage dip. A three-phase fault and two-phase fault were regarded as transient stability cases which are likely to lead to a low-voltage sag in the grid. Oscillation increased considerably in the three-phase fault DFIG parameters, but it was lower in the two-phase fault. The results showed that the output voltage of DFIG and 34.5 kV bus voltage of test system increased with the use of an SDRU and RCC in the both three and two faults. It was found in the analysis results that the observed oscillations after transient cases decreased within very short time using the SDRU and RCC in DFIG based wind turbine.