1 Introduction

The doubly fed induction generator (DFIG)-based wind farm has been widely used in recent years with integration to power systems. Today, the wind turbine innovatives have been provided by technologies used in both generators and power electronics. Modern wind farms have the different operation conditions and network connection by power electronic-based converters. Therefore, DFIG- based wind farms have a more widespread in the market national– international. DFIG has been utilized to crowbar units traditionally in order to protect power systems against variations voltage dip in the grid. However, these crowbar units may be insufficiently compensated for transient stability situations in balanced and unbalanced voltage dip. Therefore, variations in LVRT capability methods in DFIG-based wind farm are developed. In Ref. [1], the control method enhanced for LVRT provided optimum power flow during various faults in the grid. Besides, this control method control is used for constant voltage regulation in the DFIG, irrespective of surge of wind. In Ref. [2], maximum LVRT capability of DFIG-based wind farms is carried out for direct power control and vector control during fault cases. In a new approach to LVRT capability, active–reactive power control is examined during voltage dips. Due to active–reactive power control, the system can quickly respond to instability situations [3,4,5]. One of the most commonly used control strategy approaches in DFIG-based wind farm is the control of rotor-side converter and grid-side converter. Both rotor-side converter and grid -side converter are important to protect against exceed current in power system [6]. Enhanced with different current control modeling, these converter units are used widely against grid disturbances [7]. To provide LVRT capability in DFIG-based wind farm, the rotor current control is used in symmetrical voltage faults. As well as rotor current control, space vector control unit and new reference control have been also utilized for transient stability of system during symmetrical and unsymmetrical faults [8,9,10]. Used as new approaches to the LVRT capability, different operation units are also carried out in point common coupling (PCC) of DFIG [11,12,13], while current control protects against transient cases in the rotor-side converter unit of DFIG. Quadratic feedback centralized control model is another control technique used in the DFIG-based wind farm during instability cases [14]. New flux tracking method and rotor electromotor-force circuit model are developed to provide LVRT capability of DFIG during faults in the grid. Both new flux tracking method and rotor electromotor-force circuit model have overcome inrush current occurring in the DFIG [15, 16]. Magnetization and demagnetization control of the DFIG are important not only to improve LVRT capability but also to provide flux control of the rotor-side converter. Besides, the addition of magnetization and demagnetization to natural flux model has been compensated for power system during balanced voltage dips [17,18,19,20]. Power oscillation damping (POD) is important both to compensate voltage dip and to reduce inrush current in the DFIG-based wind farm during grid various faults and thus significantly increases the LVRT capability of the DFIG-based wind farm [21,22,23]. Moreover, flexible AC transmission system (FACTS) devices are used for LVRT capability in DFIG-based wind farm. While FACTS devices such as static synchronous compensator (STATCOM) and static VAR compensator (SVC) are provided to voltage and reactive power control of DFIG-based wind farm during instability conditions, they are also provided coordinate control of DFIG-based wind farm [24,25,26].

In this study, forcing demagnetization control (FDC) modeling is enhanced for LVRT capability of DFIG-based wind farm. Additionally, electromotor force (EMF) in both stator and rotor circuit for balanced faults is developed. A comparison was carried out between responds of the systems with and without stator-rotor EMF as well as FDC during three-phase fault and two-phase fault.

2 Enhancement of demagnetization control in DFIG-based wind farm

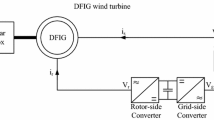
Doubly fed induction generator (DFIG) consists of back to back converter, as well as DC bus and crowbar unit. Circuit model of DFIG is given in Fig. 1.

Fig. 1
figure 1

Circuit model of DFIG

Full size image

Stator winding of DFIG is directly connected to network; on the other hand, rotor winding of DFIG is connected to converter unit back to back. Magnitude and angle control besides active and reactive power control of DFIG were provided through grid-side converter and rotor-side converter during steady state and voltage dip. Control equations rotor-side converter and grid-side converter are given between Eqs. 1 and  14.

$$\begin{aligned} \frac{\text {d}x_1}{\text {d}t}= & {} P_{ref} +P_s \end{aligned}$$
(1)
$$\begin{aligned} I_{qr\_{{ref}}}= & {} K_{p1} \left( P_{{{ref}}}+P_s\right) +K_{i1} x_1 \end{aligned}$$
(2)
$$\begin{aligned} \frac{\text {d}x_2}{\text {d}t}= & {} I_{qr\_{{ref}}} -I_{qr} =K_{p1} \left( P_{{{ref}}} +P_s\right) +K_{i1} x_1 -I_{qr}\end{aligned}$$
(3)
$$\begin{aligned} \frac{\text {d}x_3}{\text {d}t}= & {} v_{s\_{{ref}}} -v_s\end{aligned}$$
(4)
$$\begin{aligned} I_{dr\_{{ref}}}= & {} K_{p3} \left( v_{s\_{{ref}}}-v_s\right) +K_{i3} x_3\end{aligned}$$
(5)
$$\begin{aligned} \frac{\text {d}x_4}{\text {d}t}= & {} I_{dr\_{{ref}}} -I_{dr} =K_{p3} \left( v_{s\_{{ref}}} -v_s \right) +K_{i3} x_3 -I_{dr}\end{aligned}$$
(6)
$$\begin{aligned} v_{qr}= & {} K_{p2} \left( K_{p1} \Delta P+K_{i1} x_1 -I_{qr}\right) \nonumber \\&+\,{i2} x_2+sw_s L_m I_{ds} +sw_s L_{rr} I_{qr}\end{aligned}$$
(7)
$$\begin{aligned} v_{dr}= & {} K_{p2} \left( K_{p3} \Delta v+K_{i3} x_3 -I_{dr}\right) \nonumber \\&+\,{i2} x_4-sw_s L_m I_{qs} -sw_s L_{rr} I_{dr}\end{aligned}$$
(8)
$$\begin{aligned} \frac{\text {d}x_5}{\text {d}t}= & {} V_{dc\_{{ref}}} -V_{dc}\end{aligned}$$
(9)
$$\begin{aligned} I_{{{dgrid}}\_{{ref}}}= & {} -K_{{{pdgrid}}} \Delta v_{dc} +K_{1{{dgrid}}} x_5\end{aligned}$$
(10)
$$\begin{aligned} \frac{\text {d}x_6}{\text {d}t}= & {} I_{{{dgrid}}\_{{ref}}} -I_{{{dgrid}}}\nonumber \\= & {} -K_{{{pdgrid}}} \Delta v_{dc} +K_{1{{dgrid}}} x_5 -I_{{{dgrid}}}\end{aligned}$$
(11)
$$\begin{aligned} \frac{\text {d}x_7}{\text {d}t}= & {} I_{{{qgrid}}\_{{ref}}} -I_{{{qgrid}}}\end{aligned}$$
(12)
$$\begin{aligned} \Delta v_{{{dgrid}}}= & {} K_{{{pgrid}}} \frac{\text {d}x_6 }{\text {d}t}+K_{{{igrid}}} x_6\nonumber \\= & {} K_{{{pgrid}}} \left( -K_{{{pdgrid}}} \Delta v_{dc} +K_{1{{dgrid}}} x_5 -I_{{{dgrid}}}\right) \nonumber \\&+\,K_{1{{grid}}} x_6\end{aligned}$$
(13)
$$\begin{aligned} \Delta v_{{{qgrid}}}= & {} K_{{{pgrid}}} \frac{\text {d}x_7}{\text {d}t}+K_{{{igrid}}} x_7\nonumber \\= & {} K_{{{pgrid}}} \left( I_{{{qgrid}}\_{{ref}}} -I_{{{qgrid}}}\right) +K_{1{{grid}}} x_7 \end{aligned}$$
(14)

where \(K_{p1}\) and \(K_{i1}\) are the proportional and integrating gains of the power regulator, respectively; \(K_{p2}\) and \(K_{i2}\) are the proportional and integrating gains of the rotor-side converter current regulator, respectively; \(K_{p3}\) and \(K_{i3}\) are the proportional and integrating gains of the grid voltage regulator, respectively; \(I_{dr\_{{ref}}}\) and \(I_{qr\_{{ref}}}\) are the current control references for the d and q axis components of the generator side converter, respectively; \(v_{s\_{{ref}}}\) is the specified terminal voltage reference; and \(P_{{ref}}\) is the active power control reference, \(K_{{pdgrid}}\) and \(K_{{{idgrid}}}\) are the proportional and integrating gains of the DC bus voltage regulator, respectively; \(K_{{pgrid}}\) and \(K_{{igrid}}\) are the proportional and integrating gains of the grid-side converter current regulator, respectively; \(V_{dc\_{{ref}}}\) is the voltage control reference of the DC link; and \(I_{{{qgrid}}\_{{ref}}}\) is the control reference for the q axis component of the grid-side converter current [27].

Active and reactive power of DFIG that were obtained from d-q axis rotor current and grid voltage are given in Eqs. 15 and  16.

$$\begin{aligned} P_s= & {} V_{{{grid}}} \frac{L_m}{L_s}i_{{{dqr}}}\end{aligned}$$
(15)
$$\begin{aligned} Q_s= & {} V_{{{grid}}} \frac{L_m}{L_s}i_{{{dqr}}} -\frac{V_{{{grid}}}^{2}}{w_s L_s} \end{aligned}$$
(16)

Stator-rotor d-q axis voltage and electrical torque equations are shown in equations from 17 to 21.

$$\begin{aligned} v_{ds}= & {} R_s i_{ds} +w_s \lambda _{qs} +\frac{d}{\text {d}t}\lambda _{ds} \end{aligned}$$
(17)
$$\begin{aligned} v_{qs}= & {} R_s i_{qs} -w_s \lambda _{ds} +\frac{d}{\text {d}t}\lambda _{qs} \end{aligned}$$
(18)
$$\begin{aligned} v_{dr}= & {} R_r i_{dr} -sw_s \lambda _{qr} +\frac{d}{dt}\lambda _{dr} \end{aligned}$$
(19)
$$\begin{aligned} v_{qr}= & {} R_r i_{qr} +sw_s \lambda _{dr} +\frac{d}{\text {d}t}\lambda _{qr} \end{aligned}$$
(20)
$$\begin{aligned} M= & {} \lambda _{ds} i_{qs} -\lambda _{qs} i_{ds} \end{aligned}$$
(21)

d-q axis flux equations are given in equations from 22 to 25.

$$\begin{aligned} \lambda _{ds}= & {} \left( L_s +L_m\right) i_{ds} +L_m i_{dr} \end{aligned}$$
(22)
$$\begin{aligned} \lambda _{qs}= & {} \left( L_s +L_m\right) i_{qs} +L_m i_{qr} \end{aligned}$$
(23)
$$\begin{aligned} \lambda _{dr}= & {} \left( L_r +L_m\right) i_{dr} +L_m i_{ds} \end{aligned}$$
(24)
$$\begin{aligned} \lambda _{qr}= & {} \left( L_r +L_m\right) i_{qr} +L_m i_{qs} \end{aligned}$$
(25)

where \({v}_{{ds}}, {v}_{{dr}}, {v}_{{ qs}}, {v}_{{qr}}\) are the d and q axis voltages of the stator and rotor; \({i}_{{ds}}, {i}_{{dr}}, {i}_{{qs}}, {i}_{{qr}}\) are the d and q axis currents of the stator and rotor; \(\lambda _{{ds},} \lambda _{\mathrm{qs},} \lambda _{{dr},} \lambda _{{qr}}\) are the d and q axis fluxes of the stator and rotor; \(w_{s}\) is the angular speed of the stator; s is the slip; \({R}_{{s}}\) and \({R}_{{r}}\) are the stator and rotor resistance; \({L}_{{s}}\) and \({L}_{{r}}\) are the stator and rotor inductance; \({L}_{{m}}\) is the magnetic inductance; and M is the torque [28,29,30].

d-q axis rotor dynamic voltage equations are shown in Eq. 26 [31].

$$\begin{aligned} v_{{{dqr}}} =\frac{L_m }{L_s }\frac{d}{\text {d}t}\lambda _{{{dqs}}} w\lambda _{{{dqs}}} +\left( R_{r}+\sigma L_{r} \frac{d}{\text {d}t}i_{{{dqr}}}+\sigma L_{r} wi_{dqr}\right) \nonumber \\ \end{aligned}$$
(26)

where \(\sigma \) is the rotor damping coefficient. Rotor leakage coefficient is shown in Eq. 27.

$$\begin{aligned} \sigma =1-L_m^2 /(L_s L_r) \end{aligned}$$
(27)

Derivations of d-q axis stator flux have been neglected in reduced order model which are used for stator dynamic. D-q axis rotor voltage and EMF equations achieved in this situation are given in Eqs. 28 and  29.

$$\begin{aligned} v_{{{dqr}}}= & {} R_r i_{{{dqr}}} +\sigma L_r \frac{d}{\text {d}t}i_{{{dqr}}} \end{aligned}$$
(28)
$$\begin{aligned} e_{{{dqr}}}= & {} 0 \end{aligned}$$
(29)

It is in steady-state operation conditions that stator resistance is ignored for small values. According to the new condition, the steady-state stator flux is shown in Eq. 30.

$$\begin{aligned} \lambda _{{{dqs}}} =V_s e^{jw_s t}\big /jw_s \end{aligned}$$
(30)

Stator flux, as given in Eq. 30, is determined by grid voltage standing for the forced response of the system, and forced stator flux \(\lambda _{sf}\) is used to represent it. Therefore, \(\lambda _{sf}\) rotates synchronously, and its amplitude and the grid voltage are in proportion each other. Forced EMF of rotor with stator d-q axis flux is shown in Eq. 31.

$$\begin{aligned} e_{{{dqfr}}} =\frac{L_m}{L_s}sV_s e^{jw_s t}\big /jw_{s} \end{aligned}$$
(31)

The forced magnetizing current achieved by neglecting the leakage inductance is given in Eq. 32.

$$\begin{aligned} i_{fm} =\lambda _{fs} e^{jw_s t}\big /jw_s \end{aligned}$$
(32)

For the DFIG, EMF, described as the energy stored in the magnetic field, is a DC value in the steady state and it stands in proportion to the square of grid voltage. It is unlikely for the stator flux to change immediately in the initial time condition during symmetric grid voltage dip, which is possible to lead to an immediate change in the magnetic state of the machine, and it is hardly possible to come out in a practical point of view [31]. On the other hand, a gradual change may come out in the stator flux. The continuity of stator flux and magnetic energy is ensured through the generation of natural stator flux. The stator flux has been regulated as in Eqs. 33,  34,  35 and  36 by using reduced order model in stator side [17].

$$\begin{aligned} 0= & {} v_{ds} -R_s i_{ds} -w_s \lambda _{qs} \end{aligned}$$
(33)
$$\begin{aligned} 0= & {} v_{qs} -R_s i_{qs} +w_s \lambda _{ds} \end{aligned}$$
(34)
$$\begin{aligned} E_{ds}= & {} v_{ds} -R_s i_{ds} +X^{{\prime }}i_{ds} \end{aligned}$$
(35)
$$\begin{aligned} E_{qs}= & {} -v_{ds} +R_s i_{qs} -X^{{\prime }}i_{ds} \end{aligned}$$
(36)

A correct estimation of natural EMF is possible, rendering it to be fully compensated under reduced grid fault [32], leading the RSC to acting like an open circuit to the natural stator component. Subsequently, the natural stator current is used to induce the natural stator flux. Natural stator current and forcing stator current are shown in and Eqs. 37 and  38.

$$\begin{aligned} i_{{{dqsn}}}= & {} \lambda _{{{dqsn}}} \big /L_s \end{aligned}$$
(37)
$$\begin{aligned} i_{{{dqfs}}}= & {} \lambda _{{{dqfs}}} \big /L_s \end{aligned}$$
(38)

Considering \(i_{rn}=0\), changes in the natural and forced stator flux during grid fault are given in Eqs. 39 and  40.

$$\begin{aligned} \lambda _{{{dqns}}}= & {} PV_s e^{jw_s t_0 }e^{(t-t0)/L_s /R_s}\big /jw_s \end{aligned}$$
(39)
$$\begin{aligned} \lambda _{{{dqfs}}}= & {} (1-P)V_s e^{jw_s t}\big /jw_s \end{aligned}$$
(40)

It can be seen that the natural stator flux can be referred to as dc component and it is fixed to the stator winding. Therefore, it can also be called DC stator flux [31]. During the transient process, the DC stator flux changes as nonlinear with respect to the stator flux time constant. Likewise, natural and forcing stator flux generated during the grid fault is given in Eqs. 41 and  42.

$$\begin{aligned} \lambda _{{{dqns}}}= & {} PV_s e^{jw_s t_0 }e^{(t-t1)/L_s /R_s}\nonumber \\&\times \,^{t1-t0/L_s /R_s}-e^{jw_s t1-t0}\big /jw_s \end{aligned}$$
(41)
$$\begin{aligned} \lambda _{{{dqfs}}}= & {} V_s e^{jw_s t}\big /jw_s \end{aligned}$$
(42)

where t is the fault time; t0 is the before fault time; and t1 is the after fault time. The rotor EMF consists of two parts, one induced by the natural and the other one by forced rotor flux during the transient process in the grid fault. The natural and forced rotor flux equations are given in Eqs. 43 and  44.

$$\begin{aligned} e_{{{dqnr}}}= & {} \left( -\frac{R_s }{L_s }+jw\right) \times \frac{L_m }{L_s }e^{-(t-t0)/L_s /L_r \times e^{jw_s t}}\lambda _{{{dqns}}}\nonumber \\ \end{aligned}$$
(43)
$$\begin{aligned} e_{{{dqfr}}}= & {} s\frac{L_m }{L_s }(1-P)V_s e^{jw_s t} \end{aligned}$$
(44)

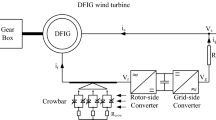
To reduce the effects of natural stator flux and enhance system LVRT capability under balanced grid fault, a forced demagnetization control is suggested as it does not require any system parameter information. Control modeling enhanced with FDC in DFIG-based wind farm is given in Fig. 2a, b.

Fig. 2
figure 2

a Demagnetization control without FDC in DFIG. b Demagnetization control with FDC in DFIG

Full size image
Fig. 3
figure 3

Test system

Full size image
Table 1 DFIG parameter values
Full size table

The active and reactive current may coexist by demagnetizing current during grid fault. The addition of reference d-q axis current and natural rotor flux may give rise to total rotor current. Given a balanced grid fault, demagnetizing rotor current, as opposed to the natural stator current, is integrated into the rotor circuit. The d-q axis reference current is shown in Eq. 45.

$$\begin{aligned} i^{*}_{{{dqrn}}}=K\times i_{{{dqns}}} +K\times i_{{{dqfs}}} \end{aligned}$$
(45)

where K is a positive demagnetization coefficient. In practice, a fixed value can be assigned to K, which can be dynamically manipulated in line with working conditions of the system. Limiting K somewhere between 1 and −1, a little lower than the critical point, is strongly suggested to ensure the system stability.

3 Simulation study

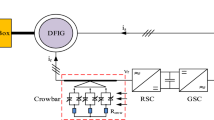
The 0.85 MW DFIG-based wind farm connected to power system is given in Fig. 3.

The connection of wind power plant to a 34.5 kV system was conducted through a 2.6 MW, 0.69 kV Y/34.5 kV \(\Delta \) transformers [33]. The distance between the plant and the 34.5 kV grid was one km. The transmission network connection was provided by a 0.69 kV Y/34.5 kV \(\Delta \) transformer. The wind speed was taken as a constant 8 m/s. The transformers saturation has been ignored. Network short-circuit power and the X/R rate were determined as 2500 MVA, and 7, respectively. Stator-rotor resistance stator-rotor inductance mutual inductance and inertia value are shown in Table 1.

4 Simulation results

The effect on the FDC of the system parameters was analyzed with three- phase fault and two-phase fault. As the first transient event, a three-phase fault was taken. The three-phase fault was generated in the middle of the transmission line in the time interval between 0.6 and 0.7 s. For the DFIG with and without the FDC, the 34.5 kV bus voltage, variations in terminal voltage of DFIG, angular speed of DFIG, electrical torque of DFIG and d-q axis stator current of DFIG were found. Figure 4a–f. shows the comparisons.

Fig. 4
figure 4

a 34.5 kV bus voltage in three-phase fault. b Terminal voltage of DFIG in three-phase fault. c Angular speed of DFIG in three-phase fault. d Electrical torque variations of DFIG in three-phase fault. e d axis stator current variations of DFIG in three-phase fault. f q axis stator current variations of DFIG in three-phase fault

Full size image

As shown in Fig. 4a, b, values of 34.5 kV bus voltage and terminal voltage of DFIG had lower values and the system was stabilized within a shorter time with the use of FDC. The 34.5 kV bus voltage was about 0.575 p.u. when DCC was used, while it turned to be 0.555 p.u. without the FDC. Furthermore, oscillations in angular speed, electrical torque and d-q axis stator currents showed significantly lower values when FDC was used, while DFIG, angular speed, electrical torque and d-q axes stator currents with FDC were stabilized in nearly 2.5, 3.5, 1.7, 1.7 s after three-phase fault, respectively.

Another two-phase fault was created as the second transient event. The fault was generated in the B 34.5 kV bus in the time intervals between 0.6 and 0.7 s. The 34.5 kV bus voltage, variations in terminal voltage of DFIG, angular speed of DFIG, electrical torque of DFIG and d-q axis stator current of DFIG were found with and without the FDC in the DFIG model. Figure 5a–f shows the comparisons.

Fig. 5
figure 5

a 34.5 kV bus voltage in two-phase fault. b Terminal voltage of DFIG in two-phase fault. c Angular speed of DFIG in two-phase fault. d Electrical torque variations of DFIG in two-phase fault. e d axis stator current variations of DFIG in two-phase fault. f q axis stator current variations of DFIG in two-phase fault

Full size image

In the two-phase fault event in middle line, while the voltage values of 34.5 kV bus turned out to be about 0.57 p.u. without the FDC in the DFIG, DFIG terminal voltage turned out to be about 0.2 p.u. without the FDC in the DFIG. However, there was increase in values reaching 0.575 0.22 p.u. when FDC was used in the DFIG, respectively. As was the case in the first three-phase fault, the FDC usage also contributed to damping oscillations that came out at the time in several parameters like the angular speed of DFIG, electrical torque of DFIG and d-q axis stator current of DFIG variations, while DFIG, angular speed, electrical torque and d-q axes stator currents with FDC were stabilized in nearly 2.5, 3.5, 1.7, 1.7 s after two-phase fault respectively,

5 Conclusion

In this study, both natural flux control and forcing flux control were applied for a network-connected DFIG-based wind farm. Stator electromotor force and rotor electromotor forces were examined in this study to show their effects on DFIG-based wind farm. The natural flux and forcing flux, besides the FDC, were developed in the DFIG. A comparison was drawn between the transient cases of the system with and without the FDC during three-phase and two- phase faults. It was seen as a result of three-phase fault and two-phase fault analysis that FDC modeling used in DFIG enables the system to be stable within a very short period of time. It was further found that oscillations decreased following the variation transient events such as three-phase fault and two-phase fault.