A Folk theorem for stochastic games with finite horizon

Abstract

This paper provides assumptions for a limit Folk theorem in stochastic games with finite horizon. In addition to the asymptotic assumptions à la Dutta (J Econ Theory 66:1–32, 1995) I present an additional assumption under which the Folk theorem holds in stochastic games when the horizon is long but finite. This assumption says that the limit set of SPE payoffs contains a state invariant payoff vector $w$ and, for each player $i$, another payoff vector that gives less than $w$ to $i$. I present two alternative assumptions, one on a finite truncation of the stochastic game and the other on stage games and on the transition function, that imply this assumption.

1 Introduction

The Folk theorem is a central result in repeated game theory according to which the set of equilibrium payoffs coincides with the set of payoffs that Pareto dominates the minimax point. There is not one Folk theorem but many: They vary along the class of games or the equilibrium notion taken into account. The aim of this paper is to provide conditions under which a Folk theorem holds in stochastic games with finite horizon.

Stochastic games model situations in which the one-period reward depends on the realization of a state. The distribution over states is determined by the realized state and the actions played at the previous period. Stochastic games are thus a generalization of nonstochastic games (here called repeated games) where players may not always face the same payoff matrix at each date. Public good games with gradual investments, or with an investment stock that depreciates over time, belong to the class of stochastic games. In this case the state variable is given by the amount of investments. Other economic situations such as duopoly games (Rosenthal 1982) or games of extracting resources (Levhari and Mirman 1980) can be modeled by stochastic games¹.

Stochastic games introduce an additional complication in comparison with repeated games: Not only may players want to deviate in order to improve their current gains but they may also want to influence the probability distribution over states. Under some conditions, Dutta (1995), for games with perfect observation, and then Hörner et al. (2011) and Fundenberg and Yamatoko (2011), for games with imperfect public monitoring, prove that any individually rational payoff vector can be approximated by a Subgame Perfect Equilibrium (SPE) if players are sufficiently patient and if the horizon is infinite.

Yet in many economic situations, agents are involved in relationships with a finite horizon. For instance, joint ventures generally have a limited shelf life. Also, the relationship between an employee and an employer is a finite time relationship since he will retire after a time. Yet, for significant classes of repeated games, the Folk theorem holds when the horizon is infinite but does not when it is finite. A typical example is the prisoner’s dilemma, in which cooperation is an equilibrium when the horizon is infinite, but is not with a finite, even very long, horizon.

Some authors (Friedman 1985; Benoit and Krishna 1985; Smith 1995; Gossner 1995; Hörner and Renault 2011) ² provided sufficient conditions for the Folk theorem to hold in finitely repeated games, but all these papers are about nonstochastic games. The reasoning of these papers is the following. Some outcomes can be supported as equilibria because the underlying strategy profile provides an appropriate and credible punishment in any case of deviation, if the number of remaining periods is sufficiently large—say if it is greater than some integer $R$. If the horizon is finite, there is a date at which the remaining time is not sufficient for these punishments to be credible or effective. In a game with horizon $F$, a deviation at $t\in \{F-R+1,\ldots ,F\}$ is called late deviation in contrast with an early deviation that occurs at $t<F-R$. An additional round of stage games, that will be called endgame in the rest of the paper, is played when the first $F$ periods are over. The strategy played in this endgame depends on whether or not a late deviation occurs and, in the latter case, on the identity of the deviator. When no deviation occurs then a reward SPE strategy profile is played. Otherwise a punishment SPE strategy profile is triggered. The difference between the reward payoffs and the punishment payoffs accumulated during the endgame is such that the late deviations are not profitable. The condition under which such equilibria can be constructed is due to Benoit and Krishna (1985) and has been generalized by Smith (1995). The one in Benoit and Krishna (1985) says that there are distinct Nash payoffs for each player in the stage game. To obtain the Folk theorem, it suffices to take $F$ large enough, so that the payoffs accumulated during the endgame can be made relatively small. Then it is possible to find an SPE strategy profile whose payoff vector approximates a target payoff profile.

To the best of my knowledge this paper is the first to study the Folk theorem in stochastic games with a finite horizon. In stochastic games, contrary to repeated games, repeatedly playing a static Nash equilibrium may not be SPE. The reason is that a player may want to lose money today in order to reach states in which payoffs are greater, even if he is punished. This fact has two consequences. First, constructing the reward and the punishment strategies in the endgame is more difficult. Second, players may have an incentive to deviate early on, in order to modify the state in which the endgame starts. Thus, preventing from late deviations may enter in conflict with deterring early deviations. In Sect. 2, I show via two examples that the Benoit and Krishna’s condition applied in each stage game is neither sufficient nor necessary for the Folk theorem to hold in stochastic games with finite horizon. In the first example, I construct a stochastic game in which each stage game is a prisoner’s dilemma. The cooperative outcome, which is not a Nash equilibrium in the static game, can be sustained as a SPE if the horizon is long enough. This means that the condition of Benoit and Krishna is not necessary. In the second example, I construct a game in which the condition of Benoit and Krishna (1985) is satisfied by the payoff matrix of each state. In other words, in all states, each player has at least two distinct Nash payoffs. This game also satisfies the Dutta assumptions. I show that the Folk theorem fails in this game. This fact suggests that the condition of Benoit and Krishna and the conditions of Dutta are not sufficient.

In this paper, I provide a condition that, in addition to Dutta’s assumptions, guarantees that any individually rational payoff vector of a stochastic game can be sustained as an SPE if the horizon is sufficiently long. It says that the set of the limit of SPE payoffs as horizon goes to infinity (called limit set of SPE in the rest of the paper) contains a vector payoff $w$ that is invariant to the initial state. It also contains for each player $i$ another payoff vector $w^{[i]}$ that gives smaller payoffs than $w$ to $i$. The richness part of assumption allows to construct reward and punishment strategy profiles that deter late deviations. The invariance assumption will permit to deter deviations aiming at modifying where the endgame starts.

If the set of states is a singleton, then this assumption is equivalent to the assumption of Smith (1995). The main drawback of this assumption is that it holds on the set of limit SPE payoffs in the dynamic game. Conditions on the stage games and the transition function would have been preferable. It is indeed difficult to accommodate the generality of stochastic games and the tractability of the conditions on the stage game. For this reason, I discuss two stronger alternative assumptions. The first one says that there is an integer $T$ such that the set of SPE payoffs of the $T$-period stochastic game is sufficiently rich. The second one holds on the stage games and on the transition. This one turns out to be sufficient in special class of games that contain games like those in which all stage games are prisoner’s dilemmas, and for public good games, for instance.

The rest of the paper is organized as follows. In Sect. 2, I present examples that illustrate some major differences between the Folk theorem in repeated games and in stochastic ones. Section 3 introduces the basic setting of the model. Assumptions and the main result are presented in Sect. 4. In Sect. 5, I discuss the richness assumption.

2 Examples

In this section two examples of stochastic games that satisfy the conditions of Dutta (1995) ³ are presented.

The first one shows that the condition of Benoit and Krishna (1985) applied in each state is not necessary. The second one shows that this condition is not sufficient, even if the conditions of Dutta (1995) are satisfied.

Example 1

Suppose that at each date $t=1,\ldots ,T$ players are either in state $s$, $s^{\prime }$ or $s^{\prime \prime }$ and must choose an action—$H$ or $B$ for player 1 and $G$ or $D$ for player 2. Players perfectly observe the actions played by their opponent and the current state. The transition function is:

• Players go from $s$ to $s^{\prime }$ with probability 1 if they play $(H,G)$.

• Players go from $s$ to $s^{\prime \prime }$ with probability 1 if they play $(B,G)$ or $(H,D)$.

• Players go from $s^{\prime }$ to $s$ with probability 1 if they play $(H,G)$.

• Players go from $s^{\prime \prime }$ to $s$ with probability 1 if they play $(H,G)$.

• Players go from $s^{\prime \prime }$ to $s^{\prime }$ with probability 1 if they play $(B,G)$, $(B,D)$ or $(H,D)$,.

• Otherwise players stay in the current state with probability 1.

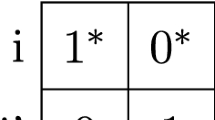
The following table gives the payoffs and the transition between states. The notation $s^{\prime }:1$ in the top left of the first matrix means that the game moves from $s$ to $s^{\prime }$ if players play $(H,G)$.

Note that the payoff matrix of each state is a prisoner’s dilemma. So the Benoit and Krishna condition does not hold in any state. If there were no possibility of transition between states, then the unique equilibrium payoff of a game of length $T$ would be the static Nash equilibrium of the initial state (which is $(B,D)$ in all states).

I show that the socially optimal payoff $(4,4)$ can be maintained as an SPE, if the horizon is sufficiently long. Let $F$ and $L$ be such that $T=F+L$. Suppose that $F>1$ and $L>2$. Consider the following strategy profile:

• Normal path (i.e. if there is no deviation):

  • At $t\in \{1,\ldots ,$ $F\}$ play $(H,G)$ in each state.

  • At $t=F+1$ play $(B,D)$ in $s$ and $(H,G)$ in $s^{\prime }$ and $s^{\prime \prime }$.

  • At $t\in \{F+2,\ldots ,T\}$ play $(B,D)$ in each state

• Punishment path (i.e. if a deviation occurs):

  • At $t\in \{1,\ldots ,T-1\}$: $(B,D)$ in $s^{\prime }$ and $s^{\prime \prime }$ and $(H,G)$ in $s$.

  • At $t=T$ play $(B,D)$ in each state.

Let me show that this strategy profile is an equilibrium.

No deviation from the punishment path for all $t\in \left\{ 1,\ldots ,T\right\}$.

If $t=T$ then players play a static Nash equilibrium. As it is the last period of the game, there is no profitable deviation. Now suppose that $t\le T-1$. If the current state is $s$, then the payoff generated on the punishment path is: $\frac{4+T-t}{T-t+1}$. If a player deviates, then the game goes to $s^{\prime \prime }$ and then to state $s^{\prime }$. Therefore the payoff is: $\frac{5-2+T-t-1}{T-t+1}$, which is smaller than $\frac{ 4+T-t}{T-t+1}$, for all $t\le T-1$. Now suppose that the state is $s^{\prime }$ or $s^{\prime \prime }$. If a player deviates then he loses 1 instantaneously. Also he does not improve his continuation payoff since a deviation does not modify the transition function.

No deviation from the normal path at $t\ge F+2$.

At $t=T$ there is no deviation since a Nash equilibrium is played. Observe that at $F+1$ the state is either $s$ or $s^{\prime }$ (Recall $F>2$). If it is $s$ then at $F+2$ the game stays in $s$ since $(B,D)$ is played at $F+1$. If it is $s^{\prime }$ then the game goes to $s$ since $(H,G)$ is played in $s^{\prime }$ at $F+1$. So the state at $t\ge F+2$ must be $s$. I need to check that there is no profitable deviation in $s$. No deviation gives $\frac{2(T-t+1)}{T-t+1}$, and a deviation gives $\frac{-2+T-t-1}{T-t+1}$, which is smaller.

No deviation from the normal path at $t=F+1$.

The state at $F+1$ must be either $s$ or $s^{\prime }$ on the normal path. Recall that $L=T-F$. I need to check that there is no profitable deviation in $s$ and $s^{\prime }$. If the state is $s$ then a deviation gives $\frac{ -2+L-2}{T-t+1}$, which is smaller than the payoff without deviation,$\frac{2L }{T-t+1}$ as $L>2$. If the state is $s^{\prime }$ then a deviation is not profitable since the deviator would have $\frac{5+L-1}{T-t+1}$ instead of $\frac{4+2(L-1)}{T-t+1}$.

No deviation from the normal path at $t\le F$.

Without deviation a player receives at least $\frac{4(F-t+1)+2L}{T-t+1}$. After a deviation, he receives at most $\frac{5+F-t+L}{T-t+1}$. The difference between the former and the later gives a nonnegative payoff. So there is no profitable deviation.

Conclusion

I have shown that the strategy profile described at the beginning of the example is an equilibrium after any history if $F>2$ and $L>2$. Also the associated payoff is $\frac{4F+2L}{T}$ and then converges to $4$ as $F$ increases once $L$ has been fixed.

Example 2

In the following example each stage game satisfies the Benoit and Krishna condition: Action profiles $(H,G)$ and $(M,K)$ are Nash equilibria in both stage games and give distinct payoffs to each player. This game also satisfies the Dutta conditions for obtaining the Folk Theorem when the horizon is infinite and players are patient enough. I show that the Folk theorem does not hold if the horizon is finite.

In the game repeated indefinitely many times the minimax payoff of player row is not greater than $3$ when the discount factor tends to one. The minimax payoff of player column is smaller than $1$ whatever the initial state and the horizon of the game. Then $(4,2.5)$ satisfies the definition of an individually rational payoff vector. In addition, it is feasible, since players can play $(B,D)$ at $t\ge 2$. In order to prove that the Folk theorem does not hold in this game, it suffices to show that this payoffs vector cannot be sustained as an equilibrium, even approximately.

Note that the stage game given by $s^{\prime }$ has two pure Nash equilibria: $(H,G)$ and $(M,K)$. $B$ and $D$ are dominated strategies and then must receive a 0 weight in any equilibrium. So there is only one strictly mixed Nash equilibrium. In this equilibrium player row puts a $0.6$ weight on $H$ and player column puts a $0.25$ weight on $G$. So the three Nash equilibrium payoff vectors are: $\{(3,2);(3,1.6);(4,2.5)\}$ where $(3,1.6)$ is the payoff vector generated by the mixed strategy profile.The stochastic game starting in $s^{\prime }$ and with an horizon $T=1$ has only three equilibrium payoff vectors.

Let $\Gamma _{T}(s^{\prime })$ denote the stochastic game starting in state $s^{\prime }$ and finishing at date $T>1$ and $P_{T}$ the associated set of SPE strategy profiles. In the following lines, I show by induction that the set of SPE in $\Gamma _{T}(s^{\prime })$ is $\left\{ (3,2);\left( \frac{(T-1)3+3}{T}, \frac{(T-1)2+1.6}{T}\right) ;\left( \frac{(T-1)3+4}{T},\right. \right. \left. \left. \frac{(T-1)2+2.5}{T}\right) \right\}$ for all $T$. Note that this is satisfied when $T=1$.

Suppose that the set of equilibrium payoffs of $\Gamma _{T-1}(s^{\prime })$ is

$$\begin{aligned} \left\{ (3,2);\left( \frac{(T-2)3+3}{T-1},\frac{(T-2)2+1.6}{T-1}\right) ;\left( \frac{(T-2)3+4}{T-1}, \frac{(T-2)2+2.5}{T-1}\right) \right\} (*) \end{aligned}$$

Let $\sigma$ be any strategy profile in $P_{T}$. Let me show that under $\sigma$ the action profile $(H,G)$ is played at the first date. I consider the case in which player column plays $G$. Player row receives at least $\frac{3+(T-2)3+3}{T}$ if he plays $H$ and at most $\frac{0+(T-2)3+4}{T}$ otherwise. So $H$ is the unique best reply against $G$. Suppose that player column plays $K$. Again, if player row plays $H$, he receives$\frac{3+(T-2)3+3 }{T}$ and at most $\frac{0+(T-2)3+4}{T}$ otherwise. So $H$ is the unique best reply against $K$. Suppose that player column plays $D$. Then, if player row plays $H$, then receives at least $\frac{6+(T-2)3+3}{T}$ and at most $\frac{4+(T-2)3+4}{T}$ otherwise. So $H$ is the unique best reply against $G,K$ and $D$. This proves that player row plays $H$ at the first period in all equilibria. Consequently, player column plays $G$ in the first period: Playing $G$ gives him at least $\frac{2+(T-2)2+1.6}{T}$, and not playing $G$ gives him at most $\frac{1+(T-2)2+2.5}{T}$. So at $t=1$ in all equilibrium, the action profile played in $s^{\prime }$ is $(H,G)$. So the equilibrium payoff $\Gamma _{T}(s^{\prime })$ is $\left\{ (3,2); \left( \frac{(T-1)3+3}{ T},\frac{(T-1)2+1.6}{T}\right) ; \left( \frac{(T-1)3+4}{T},\frac{(T-1)2+2.5}{T}\right) \right\}$.

The induction argument allows saying that the set of SPE is $(*)$ for all $T$. It follows that for all $T$, the individually rational payoff $(4,2.5)$ cannot be sustained as SPE in $\Gamma _{T}(s^{\prime })$.

3 Settings

A stochastic game is given by a finite set of players $I$, a finite set of states $S$, a finite set of actions $A^i$ for each player $i$,⁴ and a transition function $q:A\times S\rightarrow \Delta (S)$, where $\Delta (S)$ is the set of probability distributions over $S$ and $A=\prod _{i\in I}A^{i}$.

The one-period reward is $u^{i}:A\times S\rightarrow \mathbb {R}$.

Let $\Gamma _{T}$ be the stochastic game ending at date $T$. A $t$-history is a vector $h_{t}=(s_{1},a_{1},\ldots ,s_{t-1},a_{t-1},s_{t})$ where $a_{t}$ is the action profile played at $t$ and $s_{t}$ is the state realized at $t$ ($h_{1}$ is the initial state). Let $H_{t}$ be the set of all $t-$histories. A behavioral strategy in $\Gamma _{T}$ is given by $\sigma ^{i}_{T}=\{ \sigma _{(t)}^{i}\}_{t=1}^{T}$ where $\sigma _{(t)}^{i}:H_{t}\rightarrow \Delta (A^{i})$. Let $\sigma _{T}^i(a^i|h_{t})$ be the weight $i$ puts on $a^i\in A^i$ given $h_{T}$. Given a strategy profile $\sigma _{T}=\{ \sigma _{T}^i\}_{i\in I}$, let $\sigma _{T}^{-i\text { }}$ be the strategy profile played by player $i$’s opponents. For any initial state $s$ and strategy profile $\sigma$ in $\Gamma _{T},$ the undiscounted average payoff over $T$ periods (or $T-$period payoff) is:

$$\begin{aligned} U_{T}^{i}(\sigma ,s)=\frac{1}{T}E\left[ \sum _{t=1}^{T}u^{i}(a_{t},s_{t})|\sigma ,s\right] \end{aligned}$$

Let $U_{t\rightarrow T}^{i}(\sigma (h_{t}),s(h_{t}))$ be the continuation payoffs associated with $h_{t}$, where $\sigma (h_{t})$ is the continuation strategy and $s(h_{t})$ is the state at $t$ given by $h_{t}$. Formally:

$$\begin{aligned} U_{t\rightarrow T}^{i}(\sigma (h_{t}),s(h_{t}))=\frac{1}{T-t+1} E\left[ \sum _{t^{\prime }=t}^{T}u^{i}(a_{t^{\prime }},s_{t^{\prime }})|\sigma (h_{t}),s(h_{t})\right] \end{aligned}$$

A strategy profile is a SPE if for all $t\le T$, all $i\in I$, all $\hat{ \sigma }^{i}$, a strategy in $\Gamma _{T}$ and all $h_{t}\in H_{t}$:

$$\begin{aligned} U_{t\rightarrow T}^{i}(\sigma (h_{t}),s(h_{t}))\ge U_{t\rightarrow T}^{i}( \hat{\sigma }^{i}(h_{t}),\sigma ^{-i}(h_{t}),s(h_{t})) \end{aligned}$$

Let $P_{T}$ be the set of perfect equilibria of $\Gamma _{T}$.

A strategy profile “repeats” $\sigma _{T}$, a strategy in $\Gamma _{T}$, if it plays $\sigma _{T}$ over $T$ periods, then forget the past and play $\sigma _{T}$ over the next $T$ periods, and so on...

A stationary strategy profile $x$ is a strategy profile in which each decision depends only on the current state $s$. Let $x(s)$ be the action profile played in $s$. A set of states $R$ is recurrent given $x$ if for all $s,s^{\prime }\in R$ the probability of reaching $s$ from $s^{\prime }$ in finite time, without leaving $R$, is 1. The set of recurrent sets given $x$ is denoted by $\mathcal {R}_{x}$.

Like Dutta (1995), I assume that there exists a public randomization device.

In stochastic games, the set of feasible payoffs and the minimax may vary across states and game horizon. Let $F(s)$ be the set of feasible asymptotic average payoffs in the game starting in $s\in S$:

$$\begin{aligned} F(s)=\{v\in {\mathbb {R}}^{n}:\exists \{ \sigma _{T_{k} }\}_{k},\; T_{k+1}>T_{k} \text { s.t. }\lim _{k\rightarrow \infty }U_{T_{k}}^{i}(\sigma _{T_{k}} ,s)=v^{i},\forall i\in I\} \end{aligned}$$

The convex hull of $F(s)$ is denoted by $coF(s)$. As Dutta mentioned, this set can be understood as the set of payoffs that can be achieved when players use a public randomization device.⁵

The $T-$period minimax payoff is defined as: $m_{T}^{i}(s){=}\inf _{ \sigma ^{-i}_{T}}\sup _{\sigma ^{i}_{T}}U_{T}^{i}(\sigma ^{i}_{T},\sigma ^{-i}_{T},s)$. I assume that $m_{T}^{i}(s)$ is given by a pure strategy profile for all $T$. By Bewley and Kolhberg (1976), $\lim _{T\rightarrow \infty }\frac{m_{T}^i(s)}{T} =\lim _{\delta \rightarrow 1}m^i_{\delta }(s):=m^{i}(s)$ for all $s$ and $i$, where $m^{i}_{\delta }(s)$ is the value of the infinitely repeated stochastic game with $\delta$-discounted payoffs. Finally, the set of individually rational payoffs is: $F^{*}(s)=\{v\in coF(s):v^{i}>m^{i}(s), \forall i\in I\}$.

4 Main result

4.1 Assumptions

In this section I present the assumptions for the Folk theorem. The first three assumptions are borrowed from Dutta (1995). Hörner et al. (2011) use similar assumptions.⁶

Assumption 1

(A1) For all $s,s^{\prime }\in S,$ $coF(s)=coF(s^{\prime })=:coF$.

This first assumption says that the convex hull of asymptotic average payoffs is state invariant. Communicative games⁷ satisfy this assumption. The game in the second example is a communicative game since any action profile in $s$ leads to $s^{\prime }$ and $(H,M)$ in $s^{\prime }$ leads to $s$.

Assumption 2

(A2) For all $s,s^{\prime }\in S$ and $i\in I,m^{i}(s)=m^{i}(s^{\prime })=m^{i}.$

According to this assumption the asymptotic minimax does not depend on $s$. The game in the second example satisfies this assumption. The payoffs in $s$ are all dominated by those in $s^{\prime }$. Also for all action profiles played in $s$, the state $s^{\prime }$ is reached with probability one the next period. Thus, if a player is minimaxed, he prevents the game from reaching $s$. So $m^{i}(s)=m^{i}(s^{\prime })=1$. These first two assumptions imply that $F^*(s)=F^*(s^{\prime })$ for all $s$ and $s^{\prime }$.

Assumption 3

(A3) The set $coF$ has dimension $|I|$.

This assumption adapts the full dimensionality condition (Fudenberg and Maskin 1986) to stochastic games settings. Let me show that it is satisfied in the second example. Vectors $(6,0)$ and $(0,3)$ are linearly independent. Furthermore, they span a subset, say $V$, of $F(s^{\prime })$ and so of $F(s)$. So $\dim (F(s))\ge \dim (V)=2$. Also since $F(s)$ is a subset of $\mathbb {R}^2$, $\dim (F(s))=2$.

The stochastic game in the second example satisfies the assumptions under which Dutta (1995) proves the Folk theorem when the horizon is infinite and discounting is low.⁸ However, when the horizon is finite, the Folk Theorem does not hold in example 2. It fails because it is impossible to provide a punishment that deters player row from playing $H$ at $t<T$. A deviation from $(B,D)$ at the late stages is therefore unavoidable. A similar phenomenon arises in repeated games in the case in which the stage game is a prisoner’s dilemma. In order to obtain the Folk theorem in finitely repeated games, Benoit and Krishna (1985), Friedman (1985), Gossner (1995) and Smith (1995) construct an endgame in which the strategies that are played deter deviations in the last periods of the main game. Benoit and Krishna (1985) assume that each player has at least two distinct Nash payoffs in the stage game. The reward strategy profile in the endgame, namely the strategy profile played if there is no deviation in the last periods of the main game, consists in successively playing these static Nash equilibria of the game, for instance. The punishment strategy consists in repeatedly playing the Nash equilibrium that gives the worst payoff to the deviator.

As Example 2 shows, A1, A2 and A3 do not preclude late deviations. Such a system of rewards and punishments is thus needed. Two difficulties arise when one wants to construct an endgame in stochastic games. The first one is that for any $\sigma _{T}\in P_{T}$ and $\sigma _{T^{\prime }}\in P_{T^{\prime }}$, the strategy profile in the game of horizon $T+T^{\prime }$ that plays $\sigma _{T}$, and then forgets the past and plays $\sigma _{T^{\prime }}$ is not necessarily a SPE, contrary to repeated games (see Proposition 1 in Benoit and Krishna 1985). Then having distinct Nash equilibrium payoffs, as assumed in Benoit and Krishna (1985), does not prevent from deviations in the endgame. The second difficulty is that players may have incentives to deviate during the main game in order to modify the state in which the endgame starts. Since in stochastic games there is no stage game per se, a natural generalization of Benoit and Krishna (1985)’s condition to stochastic games, in line with Dutta (1995), may consist in making a richness assumption on the limit set of SPE payoffs. More precisely, consider the set of payoff vectors $w(s)$ such that there exists a sequence of SPE that converges toward $w(s)$:

$$\begin{aligned} \Pi (s)=\left\{ w(s)\in {\mathbb {R}} ^{|I|}:\exists \left\{ \sigma _{T}\right\} _{T\in \mathbb {N}}\; \text { s.t. }\sigma _{T}\in P_{T}\right. \\ \left. \text { and }\lim _{T\rightarrow \infty }U_{T}^{i}(\sigma _{T},s)=w^{i}(s),\forall i\in I\right\} \end{aligned}$$

Let $w^{[i],j}(s)$ be the $j^{th}$ element of $w^{[i]}(s)$.

Assumption 4

(A4) There exist $w(s), w^{[1]}(s),\ldots , w^{[|I|]}(s)\in \Pi (s)$ such that $(i)$ $w^{[i],i}(s)<w^{i}(s^{\prime })$ for all $i$ and $s,s^{\prime }$ and $(ii)$ $w(s)=w(s^{\prime })$ for all $s,s^{\prime }$.

A4 says that the limit set of SPE payoffs contains a state invariant vector payoff $w$. This condition allows deterring early deviations aiming at modifying where the endgame starts. Also, for all $i$, there is a limit payoff $w^{[i]}(s)$ that gives less to player $i$ than $w(s)$ for any $s$. A4 is the analog of Benoit and Krishna (1985)’s condition: it allows constructing punishments that deter late deviations. Let me show that A4 holds in example 1: $w(s)$ is generated by the strategy profile that plays $(B,D)$ in $s$ and $(H,G)$ in $s^{\prime }$ and $s^{\prime \prime }$ at $t=1$, and then plays $(B,D)$ in each state. Also $w^{[1]}$ and $w^{[2]}$ are generated by the strategy profile that plays $(B,D)$ in $s^{\prime }$ and $s^{\prime \prime }$ and $(H,G)$ in $s$ in all but the last date at which it plays $(B,D)$ in all states.

A drawback of this assumption is that it holds on the limit set of SPE payoffs. It may be difficult to check whether a stochastic game satisfies it or not. In Sect. 5, I present two alternative conditions to A4 that are less general but directly hold on the set of SPE of some $\bar{T}$ periods for the first one and on the stage games and the transition for the second one.

It is interesting to know how strong this assumption is if the set of states is a singleton. According to the next lemma, A4 is equivalent to the assumption of recursively distinct Nash payoffs in Smith (1995) in the case where there is only one state.

Lemma 1

Suppose that $|S|=1$ and that A3 holds. Then A4 is a necessary and sufficient condition for the Folk theorem.

Proof

In Sect. 5, I introduce a new assumption, A5, which is equivalent to A4 if the set of states is a singleton (Lemma 2). Then in Lemma 3 (Sect. 5) I show that A5 is necessary and sufficient for the Folk theorem, if A3 holds and $|S|=1$.$\square$

4.2 Folk theorem

Now, I present a Folk theorem for stochastic games with a finite horizon.

Theorem 1

Assume A1, A2, A3 and A4 hold. $\forall \epsilon >0$, $\forall v\in F^*$ there is a $T^{*}<\infty$ such that if $T\ge T^{*}$ then for all $s\in S$, there exists a Subgame Perfect Equilibrium $\bar{\sigma }$ in $\Gamma _{T}(s)$ whose payoff vector $U_{T}(\bar{\sigma },s)$ is within $\epsilon$ of $v$, that is $|U_{T}(\bar{\sigma },s)-v|<\epsilon$.

Proof

c.f. Appendix 6.3. $\square$

Let me give an idea of the proof. Let $F$ and $L$ be the length of the main game and the one of the endgame, respectively, so that the total length of the game is equal to $F+L=:T$. Given $\epsilon$ and $v$, I exhibit a candidate for the SPE strategy profile indexed by time. First, I show that this strategy is an SPE, if the horizon is long enough. Second, I check that the payoff vector generated by this strategy profile is close to $v$, if the horizon is long enough.

Let me describe the candidate strategy profile briefly. From date 0 to $F$, on the normal path, players play a strategy profile that generates payoffs close to $v$. From $F+1$ to $T$ they play $\sigma _{T-(F+1)}$ in the sequence of SPE $\{\sigma _{t}\}_{t}$ whose limit payoff is $w$. If a player deviates early, that is, before some date $F-R$, where $R$ is proportional to $\underline{x}(1+a)$ and $a,\underline{x}$ are yet to be determined, then the opponents trigger a punishment strategy. $R$ is interpreted as the minimal length of the punishment phase of the main game. In the main game the punishment is divided into two phases: In the first phase, the deviator is minimaxed, and in the second phase, players play a “personalized punishment” strategy profile that gives more to player $i$ if he is a punisher than if is punished. The second phase is about $a$ times larger than the first phase, where $a$ is yet to be determined. After date $F$ players play a SPE of a sequence with limit payoff $w$. If player $i$ deviates late, that is, at some date $t$ between $F-R+1$ and $F$, then players play $\sigma _{T-(F+1)}^{[i]}$ in the sequence of SPE $\{\sigma _{t}^{[i]}\}_{t}$ whose limit payoff is $w^{[i]}$. Clearly, there is no profitable deviation in the endgame because an SPE is played in any case. Then I choose the length of each punishment phase in order to deter deviations in the main game. I prove this point backward. First I show that there is no late deviation. Take $L$ equals to $m$ times $R$. Since $w$ gives more than $w^{[i]}$ to player $i$, it is possible to find a lower bound on $m$ independent of $R$, so that there is no profitable late deviation. Second I show there is no early deviation. I start to show that there is no profitable deviation that would modify the state where the endgame starts. To do so I assume that, whatever the number of remaining periods of the main game, a deviator loses at least a given amount $\mu >0$ on average. By increasing $L$, the benefit of deviating at $t$ in order to influence where the endgame starts vanishes (point (ii) of A4). But I have to be careful while increasing $L$: It makes the number of punishment periods of the main game relatively small and the average deviation loss may decrease at a higher rate than the benefit of modifying where the endgame starts. Using the fact that a deviator loses $\mu$ on average from $t$ to $F$ and because I set $L=mR$, I can fix a lower bound over $R$, independent of $a$, such that no deviation occurs in order to influence the state at which the endgame starts. Then I show that if a player deviates early, then loses at least $\mu$ on average from $t$ to $F$. In this step I use the fact that the personalized punishment phase is about $a$ times larger than the minimax phase. First I determine a lower bound over $\underline{x}$, independent of $a$ and then a $a$ such that a punisher loses payoffs if he deviates, for any value of $\underline{x}$ greater than the threshold I have just determined. Second I check that for such values a player has no profitable deviation from the normal path nor from his own punishment. The rest of the proof is standard: It suffices to take $F$ large in order to get a good approximation of the target payoff.

5 Discussion

In this section I present two alternative assumptions of A. The first one can be seen as an intermediary condition between A5 and the one in Benoit and Krishna (1985). It requires that in some finite truncation of the game, the set of SPE is rich enough. The second holds on the stage games and the transition.

5.1 An intermediary assumption

The following assumption says that there is a $\bar{T}$ such that the stochastic game admits a strategy profile $y$ in a particular subset of $P_{\bar{T}}$, which I define in the next paragraph, whose asymptotic payoff, $U^{i}(y,s)$, is state invariant. Also, for all $i$, there is another strategy profile $y^{\left[ i\right] }$ in this subset of $P_{\bar{T}}$ whose asymptotic payoff, denoted by $U^{i}(y^{\left[ i\right] },s)$, gives more than $U^{i}(y,s^{\prime })$ for all $s$ and $s^{\prime }$.

Let me first introduce some notations. I say that a strategy profile $\sigma _{T}^{\prime }$ “plays the same normal path as” $\sigma _{T}$ if $\sigma _{T}^{\prime }$ coincide with $\sigma _{T}$ after any history of the normal path, but not necessarily after a deviation. Let $\mathcal {P}_{T}$ be the set of strategy profiles $\sigma _{T}\in P_{T}$ such that, for all $n\in {\mathbb {N}}$, there is a $\sigma ^{\prime }\in P_{nT}$ that plays the same normal path as $\sigma _{nT}$, where $\sigma _{nT}$ is the strategy that repeats $\sigma _{T}$ $n$ times.

In nonstochastic games, $P_{T}$ and $\mathcal {P}_{T}$ coincide (Proposition 1 in Benoit and Krishna 1985). This may not be the case in stochastic games as example 2 suggests: Playing $(H,G)$ in $s$ and $(M,K)$ in $s^{\prime }$, which are both static Nash equilibrium, is not an SPE in games of horizon greater than $2$. Finally, given $\sigma$, a strategy profile in $\Gamma _{T}$ and $\sigma _{nT}$, a strategy profile that repeats $n$ times $\sigma$, let $U^{i}(\sigma ,s)$ denote the limit over $n$ of $U^{i}_{nT}(\sigma _{nT},s)$.⁹ The alternative assumption is the following:

Assumption 5

(A5) There exist an integer $\bar{T}$ and strategy profiles $y,y^{\left[ 1\right] },\ldots ,y^{\left[ |I|\right] }$ in $\mathcal {P}_{\bar{T}}$ such that $\forall i\in I,\forall s,s^{\prime }\in S$: (i) $U^{i}(y,s)>U^{i}(y^{[i]},s^{\prime })$, and (ii) $U^{i}(y,s)=U^{i}(y,s^{ \prime })$.

The next theorem says that A5 is stronger than A4 and is equivalent to A4, if the set of states is a singleton.

Lemma 2

A5 implies A4. If $|S|=1$ then the reverse is true: A4 implies A5.

Proof

I show that A5 implies A4. By A5 there exist $\bar{T}$ and $y, y^{[i]}\in \mathcal {P}_{\bar{T}}$ for all $i$ such that $U^i(y,s)=U^i(y,s^{ \prime })$ and $U^i(y,s)>U^{i}(y^{[i]}_{\bar{T}},s^{\prime })$, for all $s,s^{\prime }\in S$. I want to show that there exist sequences of SPE, $\{ \sigma _{T}^{*}\}_{T}$ and $\{ \sigma ^{*[i]}_{T}\}_{T,i}$, that converge toward $U(y,s)$ and $\{U(y^{[i]},s)\}_{i\in I}$, respectively, for all $s$. Fix $T>\bar{T}$ and let $\alpha \ge 1$ and $\beta <T$ be the integers such that $T=\alpha \bar{T}+\beta$. Let $\hat{\sigma }_{\alpha \bar{T}}$ be a SPE that plays the same normal path as $\sigma _{\alpha \bar{T}}$, where $\sigma _{\alpha \bar{T}}$ is a strategy profile that repeats $y$ $\alpha$ times. I know that such a strategy profile exists since $y\in \mathcal {P} _{\bar{T}}$. For all $s$, let $\hat{a}_{\beta }(s)\in A$ be a Nash equilibrium of the static game with payoffs $u^i(a,s)+(T-\beta )\sum _{s^{\prime }\in S}q(s^{\prime }|a,s)U^{i}_{T-\beta }(\sigma _{\alpha \bar{T}},s^{\prime })$, for all $i$ and $a$. I define $\hat{\sigma }_{T-\beta +1}$ as the strategy profile that plays $\hat{a}_{\beta }=:(\hat{a}_{\beta }(s))_{s\in S}$ at the first period, forgets everything and then plays $\sigma _{\alpha \bar{T}}$. For all $t<\beta$ and $s\in S$, let $\hat{a}_{t}(s)$ be a Nash equilibrium of the static game with payoffs $u^i(a,s)+(T-t)\sum _{s^{\prime }\in S}q(s^{\prime }|a,s)U^i_{T-t}(\hat{\sigma }_{T-t},s^{\prime })$ for all $i$ and $a$, where $\hat{\sigma }_{T-t}$ is the strategy profile that plays $\hat{a} _{t},\ldots ,\hat{a}_{\beta }$ and then $\sigma _{\alpha \bar{T}}$. Let the strategy profile $\sigma ^*_{T}$ be the one that plays $\hat{a}_{t}$ at $t\le \beta$ and then $\sigma _{\alpha \bar{T}}$. By construction, it is an SPE. Replicating this process for any $T>T^*$, I obtain a sequence of SPE that converges toward $U^i(y,s)$ for all $s$. By using the same reasoning I can construct for all $i$ a sequences of SPE $\{ \sigma ^{*[i]}_{T}\}_{T}$ that converge toward the desired payoffs.

Now suppose that $|S|=1$. By A4 there exist $T$, $\epsilon$, $y_{T}$ and $y_{T}^{[i]}$ for all $i$ in $P_{T}$ such that $U^i_{T}(y_{T},s)-U_{T}^i(y^{[i]}_{T},s)> \epsilon$. As $S$ is a singleton $P_{T}=\mathcal {P}_{T}$. Also $\lim _{n\rightarrow \infty }U^i_{nT}(y_{nT},s)=U^i_{T}(y_{T},s)=:U^i(y,s)$ and $\lim _{n\rightarrow \infty }U_{nT}^i(y^{[i]}_{nT},s)=U_{T}^i(y^{[i]}_{T},s)=:U^i(y^{[i]},s)$. So point $(i)$ in $A$ 5 is satisfied. Point $(ii)$ is satisfied since $S$ is a singleton.$\square$

A direct corollary of this lemma is that the Folk theorem holds under A5.

Corollary 1

Assume A1, A2, A3 and A5 hold. $\forall \epsilon >0$, $\forall v\in F^*$ there is a $T^{*}<\infty$ such that if $T\ge T^{*}$, then for all $s\in S$ there exists an SPE $\bar{\sigma }$ in $\Gamma _{T}(s)$ whose payoff vector $U_{T}(\bar{\sigma },s)$ is within $\epsilon$ of $v$, that is, $|U_{T}(\bar{\sigma },s)-v|<\epsilon$.

The next lemma implies that A5 is equivalent to the assumption of recursively distinct Nash payoffs in Smith (1995) if there is a unique state and if A3 holds. As A5 is equivalent to A4, this implies that A4 is equivalent to recursively distinct Nash payoff too.

Lemma 3

Suppose that $|S|=1$, for all $i\in I$ and that A3 holds. Then A 5 is necessary and sufficient.

Proof

According to the previous corollary it is sufficient. Let me show that it is necessary. Suppose that Theorem 1 holds. Let $\hat{w}, \{ \hat{w} ^{[i]}\}_{i\in I}$ be vectors of payoffs in $F^*$ such that $\hat{w}^i>\hat{w }^{i,[i]}$ for all $i$ (I omit the dependence to $s$ because $S$ is a singleton). By Theorem 1, for all $\epsilon$, there are $T(\epsilon )$ and SPE strategy profiles $\hat{y}_{T(\epsilon )},\; \{ \hat{y} ^{[i]}_{T(\epsilon )}\}_{i\in I}$ such that $|U_{T(\epsilon )}(\hat{y} _{T(\epsilon )},s)-\hat{w}|<\epsilon$ and $|U_{T(\epsilon )}(\hat{y} ^{[i]}_{T(\epsilon )},s)-\hat{w}^{[i]}|<\epsilon$. So there is an $\epsilon$ that is small enough so that $U^i_{T(\epsilon )}(\hat{y}_{T(\epsilon )},s)>U^i_{T( \epsilon )}(\hat{y}_{T(\epsilon )}^{[i]},s)$ for all $i$. As $P_{T}=\mathcal {P} _{T}$ for all $T$ and $\lim _{n\rightarrow \infty }U^i_{nT(\epsilon )}(\hat{y}_{nT(\epsilon )},s)=U^i_{T(\epsilon )}(\hat{y}_{T(\epsilon )},s)=:U^i(\hat{y}_{T(\epsilon )},s),\; \lim _{n\rightarrow \infty }U^i_{nT( \epsilon )}(\hat{y}_{nT(\epsilon )}^{[i]},s)=U^i_{T( \epsilon )}(\hat{y}_{T(\epsilon )}^{[i]},s)=:U^i(\hat{y}_{T(\epsilon )}^{[i]},s)$ point (i) in A5 holds. Point (ii) holds since $S$ is a singleton.$\square$

5.2 A sufficient and a necessary conditions on the stage games and the transition

What should I learn from Examples 1 and 2? Recall that in example 1, each stage game is a prisoner’s dilemma: There was a unique Nash equilibrium payoff vector in each payoff matrix. I have been able to construct punishments because each player’s Nash payoff was different from one state to the other. Actually it is a necessary condition: The Folk theorem does not hold if each stage game contains a same unique static Nash equilibrium.¹⁰ Furthermore, Example 2 shows that having distinct Nash payoffs does not guarantee that the Folk theorem holds. It suggests that the transition function plays an important role. The objective of this section is, first, to provide a necessary condition and then a sufficient condition for the Folk theorem that refers to the transition function and the stage games. To do so, I focus on a special class of games, that embeds some games with prisoner’s dilemmas in each stage game and public good games. Before formally presenting this class of games, let me give an informal description of it. I consider deterministic games¹¹ with a stationary strategy profile, denoted by $\check{x}$, that plays a pure Nash equilibrium in each state. (i) It gives the same static payoff in all states that belong to a recurrent set. (ii) The loss due to a deviation from $\check{x}$ cannot be compensated by improving the transition in the next $|S|+1$ periods. Under such conditions $\check{x}$ is in $\mathcal {P}_{1}$ (c.f. Lemma 5 in the proof of Proposition 1, Appendix 6.4 ). Moreover there is another pure stationary strategy profile such that (iii) the average one shot payoff is the same in any recurrent state and (iv) Pareto dominates that of $\check{x}$.

Let me explain the relationship between this class and public good games. Assume that players must choose to invest or not in a public good. The players’ utilities depend on a cost that is proportional to the investment effort and to the level of the public good determined by past and current investments. Investing alone is so costly in terms of opportunity cost that shirking is a static Nash equilibrium for any level of the public good. Let $\check{x}$ be the strategy profile in which everybody shirks. As no investment is made under $\check{x}$, the level of the public good depreciates and ends up reaching a lower bound $\check{u}$ (point (i)). If a player invests alone then the level of the public good increases, but not enough to offset the investment cost over the next $|S|+1$ periods if everybody continues to shirk (point (ii)). Now let me consider the case in which players invest. If a sufficient amount of investment is maintained over time, then of the public good value reaches a level $\hat{u}^{i}$ for each $i$ (point (iii)). Even if investing may not be a static Nash equilibrium, the payoffs Pareto dominate is the shirking payoffs if the level is high (point (iv)).¹²

Now I present this class of game formally. Let $V_{n}^{i}(a,s)\left[ x\right]$ be the $n$-period payoff that is generated by a strategy profile that plays $a$ in the first period and then follows the stationary strategy profile $x$. I consider the following class of deterministic games:

• There is a pure stationary strategy profile $\check{x}$ that plays a static Nash equilibrium in each state such that:

  • (i) $u^i(\check{x}(s),s)=u^i(\check{x}(s^{\prime } ),s^{\prime } )):=\check{u} ^{i},\; \forall s,s^{\prime }\in \mathcal {R}_{\check{x}},\; i\in I$.

  • (ii) For all $s\in S,\; i\in I,\; d\in A^i$, $V^i_{n}(\check{x}(s),s) \left[ \check{x}\right] \ge V^i_{n}(\check{x}^{-i}(s),d,s)\left[ \check{x} \right] ,\;$ $\forall n \le |S|+1$

• There is another pure stationary strategy profile $\hat{x}$ such that:

  • (iii) For all $R\in \mathcal {R}_{\hat{x}},\; i\in I$, $\frac{ \sum _{s\in R}u^i(\hat{x}(s),s)}{|R|}:=\hat{u}^{i}$.

  • (iv) $\min _{s^{\prime }\in R,R\in \mathcal {R}_{\hat{x}}}u^{i}(\hat{x} (s^{\prime }),s^{\prime })-u^{i}(\check{x}(s),s)\ge 0$ for all $s\in S$ and strict if $s\in \mathcal {R}_{\check{x}}$.

Now I present a necessary and a sufficient conditions for $\hat{u}$ to be an equilibrium payoff. More precisely, the first point of the next proposition gives a condition under which the anti-Folk theorem holds.¹³ According to it, there is a unique Nash equilibrium in each state ($\check{x}(s)$ for all $s$). Furthermore, for any other action profile, one player has profitable deviation in the static game that is not offset by a degradation of the transition in a near future. The second point says that the gain due to a deviation from $\hat{x}$ is offset the next period by a deterioration of the transition. This condition actually implies A4 ¹⁴. Let me rephrase these conditions in the public good game. The necessary condition says that, during any of the next $|S|+1$ periods, there is one player whose current deviation gain is greater than the deterioration of public good’s value. The sufficient condition says that if any player deviates from “everybody invests,” then the deterioration of the public good’s value is greater than the current deviation gain.

Proposition 1

Consider the class of games described above. Then:

• If $\check{x}$ is the unique Nash in all states and $\forall s\in S,\; 2\le n\le |S|+1, \;a\ne \check{x},\; \exists i\in I,\;d\in A^{i}$ such that $V_{n}^{i}(a,s) \left[ \check{x}\right] <V_{n}^{i}(a^{-i},d,s)\left[ \check{x}\right]$, then the anti-Folk theorem holds.

• If $\forall s,s'\in R$, $R\in \mathcal {R}_{\hat{x}}$, $\forall i$, $\forall a^{i}\in A^{i}$, $V_{2}^{i}(\hat{x}(s),s)\left[ \check{x}\right] \ge V_{2}^{i}(a^{i},\hat{x}(s')^{-i},s')\left[ \check{x}\right]$ then A 4 is satisfied.

Proof

See the Appendix 6.4.$\square$

Note that in the games in which $\check{x}(s)$ is the unique static Nash in all states $s$, the conditions of the anti-Folk theorem and the Folk theorem are related. The first one says: for any state $s$ and $2\le n\le |S|$, there is one player who has a profitable deviation from an action profile, which is different from $\check{x}$, in the next $n$ periods. The contrary would be: There are a state $s$, a $n$ and an action profile that is different from $\check{x}(s)$, so that no player can benefit from a deviation. The second condition says something similar, but not equivalent to the negation of the first condition: the action profile, the state and $n$ are not arbitrary.

6 Appendix

6.1 Note about the set of feasible payoffs

Consider a sequence $\{x_{t}\}$. Let $\lim \sup \{x_{t}\}=x^{+}$ and $\lim \inf \{x_{t}\}=x^{-}$. It is well known that $x^{+}$ is the greater cluster point of $\{x_{t}\}$. Also there is a subsequence of $\{x_{t}\}$ whose limit is the cluster point. So there is a subsequence whose limit is $x^{+}$. A similar reasoning holds for $x^{-}$. Let $\Lambda (\{x_{t}\})$ be a Banach limit of $\{x_{t}\}$. By definition there is a $\lambda \in [0,1]$ such that $\Lambda (\{x_{t}\})=\lambda x^{-}+(1-\lambda )x^{+}$. So there is a subsequence that converges to the Banach limit. As $coF(s)$ is a convex set all Banach limits are in this set.

6.2 Proof of footnote 14

Lemma 4

Let $\sigma$ be a strategy profile in $\Gamma _{T}$ and $U^{i}_{Tn}(\sigma ,s)$ be the $i$’s payoff generated by the strategy profile that repeats $\sigma$ $n$ times. Then $\lim _{n\rightarrow \infty }U^{i}_{Tn}(\sigma ,s)$ exists.

Proof

Let $\hat{\sigma }$ be the strategy profile that repeats $\sigma$ an infinite number of times. This means that under $\hat{\sigma }$ players play $\sigma$ over $T$ periods, forget everything at $T$ and then start again $\sigma$ over $T$ periods, then forget everything and so on...Let $a(h_{t})$ be the action profile that is played at $t-1$ according to $h_{t}$, where $h_{t}=s_{1},a_{1},\ldots ,a_{t-1},s_{t}$. Recall that $s(h_{t})$ is the state at $t$ under $h_{t}$ and let $a(h_{t})$, $\hat{s}(h_{t})$ be the action and state at $t-1$ under $h_{t}$. The strategy profile $\hat{\sigma }$ generates a Markov chain over the set the following set: $H_{2}\cup \cdots \cup H_{T}=:\mathcal {H}$. Let me explain the transition before presenting it formally. Given an history of length $t<T$, say $h_{t}$, players play an action profile at $t$, say $a$, with a probability weight $\sigma (a|h_{t})$. A new state, say $s$, is reached with probability $q(s|a,s(h_{t}))$. This gives a new history of length $t+1$ such that $s_{t+1}=s$, $a_{t}=a$, the $t-1$ first actions and the $t$ first states coincide with $h_{t}$. If the history $h_{t}$ has a length $T$ then I are in the special case in which players forget the past and resume playing $\sigma$. Note that, when players resume playing the strategy profile, then they only care about the current state. The latter is the $T^{th}$ state of the history $h_{T}$. Given this state, denoted by $s(h_{T})$, players choose an action profile, say $a$, and a new state is reached, say $s$. Then the new history is an element of $H_{2}$. Formally the transition is:

$$\begin{aligned} \hat{q}(h'_{t^{\prime }}|h_{t}) = \left\{ \begin{array}{ll} \sigma (a(h^{\prime }_{t'})|h_{t})\times q(s(h^{\prime }_{t'})|a(h^{\prime }_{t'}),s(h_{t})) &{} \text { if } t<T,\; t^{\prime }{=}t+1,\; h'_{t}{=}h_{t}\\ \sigma (a(h^{\prime }_{t'})|s(h_{t}))\times q(s(h^{\prime }_{t'})|a(h^{\prime }_{t'}),s(h_{t})) &{} \text { if } t{=}T,\; t^{\prime }{=}2,\; s(h_{t}){=}\hat{s}(h'_{t'}) \\ 0 &{} \text { otherwise} \end{array} \right. \end{aligned}$$

If $s$ is such that for all $(s,a',s')\in \mathcal {H}$ that occurs with a positive probability, $(s,a',s')$ is in a recurrent set $R$, then there exists a unique invariant distribution $\mu$ over $\mathcal {H}$. Let $\sum _{h\in \mathcal {H} }\mu (h)u(a(h),\hat{s}(h))=:U(\hat{\sigma },R)$. The weight $\mu (h)$ is interpreted as the asymptotic average frequency of stay in $h$. Let $\mu _{n}(h,s)$ be the average frequency of stay in $h$ from date 1 to $n$ given that $s$ is the initial state. Since the $\mathcal {H}$ is finite, $\mu _{n}(h,s)$ converges toward $\mu (h)$. Note that $U^{i}_{Tn}(\sigma ,s)=E\left[ \sum _{t=1}^{Tn}u^{i}(a_{t},s_{t})|\sigma _{nT} ,s\right] /Tn=\sum _{h\in \mathcal {H} }\mu _{Tn}(h,s)u(a(h),\hat{s}(h))$. Then $U^{i}_{Tn}(\sigma ,s)$ converges to $U(\hat{\sigma },R)$. Suppose that $s$ is such that for some $(s,a',s')$ that occurs with a positive probability, $(s,a',s')$ is not in a recurrent set. For any history $h$ in the infinitely repeated game, only one recurrent state is reached in finite time. Let $H(R)$ be the set of histories in which a recurrent set $R$ is reached. Then for any recurrent set $R$, $P(R\; \text {is reached in finite time}|\hat{\sigma },s)=\sum _{h\in H(R)} P(h|\hat{\sigma },s) =:\alpha _{R}\in [0,1]$. As a recurrent set is reached in finite time with probability one and since, once reached, the game stays in it forever, the limit $U(\hat{\sigma },s)$ exists and is equal to $\sum _{R\in \mathcal {R} }\alpha _{R}U(\hat{\sigma },R)$.$\square$

6.3 Proof of Theorem 1

Fix $\epsilon >0$ and $v\in \cup _{s}F^{*}(s)$. First I present some consequences of Dutta (1995) that will help us to prove the theorem. From Lemma 11 in Dutta, there exist $\hat{Z}$ and a family of publicly randomized pure strategy profiles in $\Gamma _{\hat{Z}}$, $\left\{ z^{\left[ i\right] }\right\} _{i\in I}$, that generates payoff vectors denoted by, with an abuse of notation, $U_{\hat{Z}}(z^{\left[ j \right] },s)$ for all $j\in I$ and $s\in S$. These payoffs are such that for all $i\ne j$ for all $s,s^{\prime };$ $U_{\hat{Z}}^{i}(z^{\left[ j\right] },s)>U_{\hat{Z}}^{i}(z^{\left[ i\right] },s^{\prime })$ and $U_{\hat{Z} }^{i}(z^{\left[ i\right] },s)=U_{\hat{Z}}^{i}(z^{\left[ i\right] },s^{\prime })$. Still by Dutta (1995), $U_{\hat{Z}}^{i}(z^{\left[ i\right] },s^{\prime })>m^{i}$ for all $s^{\prime }$ and $i$.

There is a $\eta ^{*}$ such that for all $\eta <\eta ^{*}$ there is $Z$, a multiple of $\hat{Z}$, such that all $Z^{\prime },Z^{\prime \prime }\ge Z$, $s,s^{\prime }\in S$, $i\ne j$:

$$\begin{aligned} \exists \; \sigma \text { s.t. }|U_{Z^{\prime }}^{i}(\sigma ,s)-v^{i}|&\le \epsilon /2,\quad \forall i\in I \\ \min \{ \min _{s\in S}U_{Z^{\prime }}^{i}(\sigma ,s),\min _{s\in S}U_{Z^{\prime }}^{i}(z^{\left[ j\right] },s)\}-U_{Z^{\prime \prime }}^{i}(z^{\left[ i \right] },s^{\prime })&\ge \eta \\ U_{Z^{\prime }}^{i}(z^{\left[ i\right] },s)-m_{Z^{\prime \prime }}^{i}(s^{\prime })&\ge \eta \end{aligned}$$

The first point is a consequence of Lemma 6 in Dutta. Fix such a $\eta$ and $Z$. Let the sequence of payoff vectors $\{w_{T}(s)\}_{T}$ be a sequence that converges toward $w$. Also let $\{w_{T}^{[i]}(s)\}_{T}$ be a sequence that converges toward $w^{[i]}(s)$. The strategy profile that generates $w_{T}$ is denoted by $y_{T}$, and the one that generates $w_{T}^{[i]}$ by $y_{T}^{[i]}$. There is a $N^*$ such that for all $N\ge N^*$, for all $i$, $\min _{s}w^i_{N}(s)>\max _{s} w^{[i],i}_{N}(s)$. Recall that $w(s)=w(s')$ for all $s,s'\in S$. So for all $i$ there are weights $\{\beta _{N}^{i}(s)\}_{s\in S, N\ge N^*}$, with $1\ge \beta _{N}^{i}(s)\ge 0$ and $\beta _{N}^{i}(s)\rightarrow 1$ as $N\rightarrow \infty$, such that $\beta _{N}^{i}(s)w_{N}^{i}(s)+(1-\beta _{N}^{i}(s))w_{N}^{[i],i}(s)=\beta _{N}^{i}(s^{\prime })w_{N}^{i}(s^{\prime })+(1-\beta _{N}^{i}(s^{\prime }))w_{N}^{[i],i}(s^{\prime })=:\tilde{w}_{N}^{[i],i}$ for all $s,s^{\prime }$.  Let $\tilde{y}_{N}^{[i]}$ be the publicly randomized strategy profile that generates $\tilde{w}_{N}^{[i]}$. More precisely it is the strategy profile that plays $y_{N}$ with probability $\beta _{N}^i(s)$ and $y^{[i],i}_{N}$, otherwise, if the state at which it is triggered is $s$. Note that $w_{N}^i(s)-\tilde{w}_{N}^{[i],i}(s^{\prime })$ and $\tilde{w}_{N}^{[j],i}(s)-\tilde{w}_{N}^{[i],i}(s^{\prime })$ converge toward 0 as $N\rightarrow \infty$, for all $s,s^{\prime }$. Also there exist $T^{*}$ and $\hat{\eta }>0$ such that for all $T,T^{\prime }\ge T^{*}$ and $i\in I$, $\min \{\min _{j\in I,s\in S} \tilde{w}_{T^{\prime }}^{[j],i}(s),\min _{s\in S}w^i_{T^{\prime }}(s)\}-\max _{s\in S}w_{T}^{[i],i}(s^{\prime })> \hat{\eta }$.

The rest of the proof consists in showing that for any horizon $T$ large enough, for all $s\in S$, there exists an SPE in $\Gamma _{T}(s)$ whose payoff vector is within $\epsilon$ of $v$. Let me first build the candidate strategy profile for the SPE in $\Gamma _{T}$. I partition the horizon of the game in the following way: $1,\ldots ,F-R,\ldots ,F,\ldots ,F+L=T$, where $R$ is to be determined. The game given by the first $F$ periods is called the main game and the one that is played during the $L$ last periods is called the endgame. Let me define a collection of strategy profiles (indexed by $\underline{x},a$ and $m$) as follows. Let $R=(1+a)\underline{ x}Z$, where $\underline{x},a\in \mathbb {N}^{*}$ and $L=mR$.

On the normal path, for all $t\in \{1,\ldots ,F\}$, $\sigma$ is played, and for all $t\in \{F+1,\ldots ,F+L\}$, the strategy profile $y_{L}$ is played. The punishment strategy proceeds as follows. Suppose that player $i$ is the last player who deviates at $t\le F-R$. Suppose also that this deviation occurs on the normal path. There are integers $n$ and $\tau <Z$ such that $F-t=nZ+\tau$. The integer $n$ can be rewritten as $x(1+a)+y$ where $y\le a$ and $a$ is to be determined. The punishment strategy of the main game is divided into two phases. In the first phase of the punishment, player $i$ will be minimaxed over $xZ+\tau$ periods. In a second phase players repeatedly play the $\hat{ Z}-$period strategy profile $z^{\left[ i\right] }$ over $(ax+y)Z$ periods. Then from $F+1$ to $F+L$ players play the strategy profile $\tilde{y}_{L}^{[i]}$. Suppose now that $i$ deviates during the first phase of his own punishment. In this case, players go on playing the punishment strategy until $F$ and, from $F+1$ to $F+L$, they play $\tilde{y} _{L}^{[i]}$. Let me call this type of early deviation “ type 1 deviation.” Any other early deviation is called “type 2 deviation.” If $i$ deviates during the second phase then players restart the punishment strategy immediately. From $F+1$ to $F+L$, the strategy profile $\tilde{y}_{L}^{[i]}$ is played. Suppose now that $j\ne i$ deviates from the punishment directed against $i$ at $t^{\prime }$ and $F-t^{\prime }\ge R$. In this case players start a new punishment directed against $j$. From $F+1$ to $F+L$ the strategy profile $\tilde{y} _{L}^{[j]}$ is played. If player $i$ is the first player to deviate at $t=F-R+1,\ldots ,F$, then players play the strategy profile $y_{T-t}^{[i]}$. If $j$ is the $n^{th}$ player to deviate, with $n\ge 2$, then players go on playing according to $y_{T-t}^{[i]}$. If a deviation occurs at $t>F$ players continue to play the strategy they used to play.

In the following lines, I check that there are $a,\underline{x}$ and $m$, such that the strategy profile defined above is an SPE in the game of length $T\ge R+L$, with $R=Z(1+a)\underline{x}$ and $L=mR$. I proceed backward. There is no profitable deviation at $t\ge F$ because an SPE is played. Now I show that there is no deviation if $t=F-R,\ldots ,F$. Clearly there is no deviation from the strategy profile $y_{T-t}^{[i]}$ (where $i$ is the first player to deviate late). Let me show that there is no other late deviation. On one hand, if $i$ does not deviate late, he receives at least $\min _{j\in I,s\in S}\tilde{w}_{L}^{[j],i}(s)$ if a deviation occurred during the main game and $\min _{s\in S}w^i_{L}(s)$, otherwise. On the other hand, if he deviates late, then he receives at most $\max _{s} w_{T-t}^{[i],i}(s)$. Recall that for $N$ and $N'$ large enough, $\min \{ \min _{j\in I,s\in S}\tilde{w}_{N^{\prime }}^{[j],i}(s),\min _{s\in S}w^i_{N^{\prime }}(s)\}-\max _{s\in S}w_{N}^{[i],i}(s)> \hat{\eta }$ for all $i\in I$. So if $L$ is large enough player $i$ gets at most $-\hat{\eta }$ during the last $L$ periods. Then an upper bound over the net gain of late deviation is: $\frac{R(b-w)-L\hat{ \eta }}{F+L-t+1}$. The nominator is negative if: $(b-w)-m\hat{\eta }<0$ since $L=mR.$ So for all $a$ and $\underline{x}$, there is a $m^{*}$ such that there is no profitable deviation at $t\in \{F-R,\ldots ,F+L\}$ for all $L=mR,\;m\ge m^{*}$.

In the following lines I show that no player has an interest to deviate at $t=1,\ldots ,F-R-1$. Suppose that $i$ deviates at $t=1,\ldots ,F-R-1$ and that he loses on average at least $\mu >0$ from $t$ to $F$. Recall that $\tilde{w}_{L}^{[i],i}(s)=\tilde{w}_{L}^{[i],i}(s')=\tilde{w}_{L}^{[i],i}$ for all $s,s'$. An upper bound over the net gain to deviate early is

$$\begin{aligned} \frac{{\overbrace{-\mu (F-t+1)}^{(1)}}+{\overbrace{L[\tilde{w}_{L}^{[i],i}-\min \{\min _{s\in S}w^i_{L}(s),\;\min _{j\in I,s\in S} \tilde{w}_{L}^{[j],i}(s)\}]}^{(2)}}}{F+L-t+1} \end{aligned}$$

• (1) upper bound over the gain from a deviation at $t<F-R$.

• (2) upper bound over net gain from a modification of the transition function

Since $L=mR$, it suffices to show that

$$\begin{aligned} -\mu +m\left[ \tilde{w}_{L}^{[i],i}-\min \{\min _{s\in S}w^i_{L}(s),\;\min _{j\in I,s\in S} \tilde{w}_{L}^{[j],i}(s)\}\right] <0. \end{aligned}$$

Recall that, $\tilde{w}_{L}^{[i],i}-\min \{\min _{s\in S}w^i_{L}(s),\;\min _{j\in I,s\in S} \tilde{w}_{L}^{[j],i}(s)\}\rightarrow 0$ when $L\rightarrow \infty$, for all $i$. Since $L=\underline{x}(1+a)Zm$, for all $\mu$, there is a $\underline{x}_{1}(\mu )$ such that for all $\underline{x}\ge \underline{x}_{1}(\mu )$ and $a\in {\mathbb {N}}^{*}$, the nominator is actually negative for all $i$.

In the following lines I show that any deviation of type 2 induces a loss of $\mu >0$ on average from the deviation date to $F$. Combined with the previous paragraph, I will conclude that there is no profitable deviation of type 2. Suppose that player $i$ deviates early at $t$ (type 2 deviation). Then the length of the first phase of player $i$’s punishment is $Zx+\tau$ and the one of the second phase is $(ax+y)Z$. Let $t^{\prime }<t$ so that $F-t^{\prime }\ge R$ and let me analyze the benefit for $j\ne i$ to deviate at $t^{\prime }$ when $i$ deviated at $t$. Without deviation, player $j$ would have from $t^{\prime }$ to $F$ at least:

$$\begin{aligned} \frac{{\overbrace{(xZ+\tau -(t^{\prime }-t))w}^{(1)}}+{\overbrace{(ax+y)Z\min _{s\in S}\inf _{T\ge Z}U_{T}^{j}(z^{\left[ i\right] },s)}^{(2)}}}{F-t^{\prime }+1} \end{aligned}$$

where:

• (1) lower bound over the $j^{\prime }$s payoff when he minimaxes $i$ over $xZ+\tau -(t^{\prime }-t)$ periods

• (2) lower bound over $j^{\prime }$s payoffs when he is rewarded for having punished $i$.

If player $j$ deviates at $t^{\prime }$ then $F-t^{\prime }$ is subdivided into a first phase of $\hat{x}Z+\hat{\tau }$ and a second phase $(\hat{x}a+ \hat{y})Z$ such that $(\hat{x}(1+a)+\hat{y})Z+\hat{\tau }=F-t^{\prime }$. In this case his payoff would be at most:

$$\begin{aligned} \frac{{\overbrace{(\hat{x}Z+\hat{\tau })b}^{(1)}}+\overbrace{{Z(\hat{x}a+\hat{y} )U_{T}^{j}(z^{\left[ j\right] })}}^{(2)}}{F-t^{\prime }+1} \end{aligned}$$

• (1) upper bound over the $j^{\prime }$s payoff when he does not minimax $i$ over $\hat{x}Z+\hat{\tau }$ periods

• (2) upper bound over $j^{\prime }$s payoffs during the second phase of a punishment directed against him.

Note that $\hat{x}\le x$. So $a\hat{x}+\hat{y}-(ax+y)\le a$. Then an upper bound over the net benefit to deviate is:

$$\begin{aligned}&\frac{Z(1+x+a)(b-w)+Za(x-1)(U_{Z}^{j}(z^{\left[ j\right] })-\min _{s\in S}\inf _{T\ge Z}U_{T}^{j}(z^{\left[ i\right] },s))}{F-t^{\prime }+1} \\&\le \frac{Z(1+x+2a)(b-w)-axZ\eta }{F-t^{\prime }+1}=\frac{ aZ(2(b-w)-\eta x)+Z(1+x)(b-w)}{F-t^{\prime }+1} \\&\le \frac{2(b-w)+a\left( \frac{2(b-w)}{x}-\eta \right) }{(a+1)+\frac{y}{x}+\frac{\tau -(t^{\prime }-t)}{Zx}} \end{aligned}$$

Let $\underline{x}_{2}$ be such that $\frac{2(b-w)}{\underline{x}_{2}}-\eta <0$. Then there is a $a^{*}$ large enough, such that the nominator is negative. Then if $\underline{x}\ge \underline{x}_{2}$, the net gain to deviate is lower than, for all $x\ge \underline{x}$:

$$\begin{aligned} \frac{2(b-w)+a^{*}\left( \frac{2(b-w)}{\underline{x}_{2}}-\eta \right) }{(a^{*}+1)+\frac{y}{x}+\frac{\tau -t^{\prime }+t}{Zx}}\le \frac{2(b-w)+a^{*}\left( \frac{2(b-w)}{\underline{x}_{2}}-\eta \right) }{2a^{*}+ 2}=:\quad \mu _{1}<0 \end{aligned}$$

Then player $j$ loses on average $\mu _{1}$ from $t$ to $F$ if he deviates.

Now I show that $i$ does not deviate early from the second phase of his punishment (a fortiori there is no profitable deviation from the normal path). Recall that the first punishment phase lasts $xZ+\tau$ periods and the second one lasts $Z(a^*x+y)$ periods. After a deviation player $i$ gets at most:

where:

• (1) is an upper bound on the current gain to deviate,

• (2) is an upper bound on the payoffs accumulated during the first phase,

• (3) is an upper bound on the payoffs accumulated during the second phase.

If he does not deviate then he gets at least:

$$\begin{aligned} \frac{{\overbrace{(\tau +1)w}^{(1)}}+{\overbrace{Z((1+a^{*})x+y)U_{Z}^{i}(z^{\left[ i\right] })}^{(2)}}}{F-t+1} \end{aligned}$$

where:

• (1) is a lower bound on the payoffs accumulated during a finishing cycle of $Z$ periods,

• (2) is a lower bound on the payoffs accumulated during the remaining periods of the second phase of the punishment.

An upper bound over the net gain of deviation is for all $x$:

$$\begin{aligned} \frac{Z(b-w)+xZ(\max _{s\in S}\sup _{T\ge Z}m_{T}^{i}(s)-U_{Z}^{i}(z^{\left[ i \right] }))}{F-t+1}\le \frac{\frac{2(b-w)}{\underline{x}_{2}}-\eta }{\frac{ F-t+1}{xZ}} \end{aligned}$$

Note that the nominator is negative. Then the net gain to deviate is lower than:

$$\begin{aligned} \frac{\frac{2(b-w)}{\underline{x}_{2}}-\eta }{2a^{*}+2}=\mu _{2}<0 \end{aligned}$$

Let $\mu ^{*}=\max \left\{ \mu _{1},\mu _{2}\right\}$. Note that $\mu ^{*}$ is a lower bound on the loss due to a deviation of type 2 before $F-R$ if $\underline{x}>\underline{x}_{2}$, which does not depend on the number of remaining periods. Then if $\underline{x}\ge \max \{ \underline{x}_{1}(\mu ^{*}),\underline{x}_{2}\}$ there is no type 2 deviation.

It is easy to check that there is no type 1 deviation. Actually since player $i$ is in best reply during the minimax phase, he cannot expect any payoff improvement during this phase. Also, he cannot influence the transition in a profitable way since the personalized punishment payoffs do not depend on the initial state as well as the payoffs he receives during the endgame. So I can conclude that there is no profitable deviation from $t=1$ to $t=F$. To sum up I have fixed $\underline{x}$, $a$ and $m$, such that the strategy profile indexed by $\underline{x}$, $a$ and $m$ described above is an SPE in any game of length greater than $R+L$, where $R=Z(1+a) \underline{x}$ and $L=mR$. I denote this strategy profile by $\bar{\sigma }$.

Now we exhibit a candidate for $T^{*}$, given $\epsilon$ and $v$. Notice that $R(=Z(1+a)\underline{x})$ and $L(=mZ(1+a)\underline{x})$ does not depend on $F$. By the choice of $Z$, for all $F\ge Z$, $|U_{F}^{i}(\sigma ,s)-v^{i}|\le \epsilon /2$. Also, as $R$ and $L$ are independent of $F$, there is $\hat{F}>R$ such that for all $F\ge \hat{F}$, $|U_{F+L}^{i}(\bar{\sigma },s)-U_{F}^{i}(\sigma ,s)|\le \epsilon /2$ $\forall i\in I$, where $\bar{\sigma }$ is the SPE strategy profile exhibited above. Let $T\ge \hat{F}+L=:T^{*}$. I check that it generates SPE payoffs in an $\epsilon -$neighborhood of $v$. Let for all $s\in S$:

$$\begin{aligned} |U_{T}^{i}(\bar{\sigma },s)-v^{i}|\le |U_{T}^{i}(\bar{\sigma } ,s)-U_{F}^{i}(\sigma ,s)|+|v^{i}-U_{F}^{i}(\sigma ,s)|\le \epsilon /2+\epsilon /2=\epsilon \end{aligned}$$

As $\bar{\sigma }$ is a SPE strategy profile the game of length $T$ I obtain the desired result.

6.4 Proof of Proposition 1

Lemma 5

The stationary strategy profile $\check{x}$ is a SPE for all horizon $T$ and the asymptotic payoff vector is $(\check{u}^{i})_{i}$.

Proof

At $t=T$ players play a Nash equilibrium. So there is no profitable deviation. Recall that for all $s\in R,$ $R\in \mathcal {R}_{\check{x}},$ $u^{i}(\check{x},s)=\check{u}^{i}$, for all $i$. Also, after $|S|$ periods the game must be in $\check{s}$, under $\check{x}$. The payoff without deviation is greater than:

$$\begin{aligned} \frac{{1\!\!1}_{T-t\le |S|+1}(T-t+1)V_{T-t}^{i}(\check{x},s)\left[ \check{ x}\right] +{1\!\!1}_{T-t> |S|+1}\{(|S|+1)V_{|S|+1}^{i}(\check{x},s)\left[ \check{x}\right] +(T-t-|S|)\check{u}^{i}\}}{T-t+1} \end{aligned}$$

Consider a deviation at $t<T$. Then the payoff is at most:

$$\begin{aligned} \frac{{1\!\!1}_{T-t\le |S|+1}(T-t+1)V_{T-t}^{i}(\check{x}^{-i},a^i,s) \left[ \check{x}\right] +{1\!\!1}_{T-t> |S|+1}\{(|S|+1)V_{|S|+1}^{i}( \check{x}^{-i},a^i,s)\left[ \check{x}\right] +(T-t-|S|) \check{u}^{i} \}}{T-t+1} \end{aligned}$$

Then the difference is:

$$\begin{aligned}&{1\!\!1}_{T-t\le |S|+1}\left\{ V_{T-t}^{i}(\check{x}^{-i},a^i,s)\left[ \check{x} \right] -V_{T-t}^{i}(\check{x},s)\left[ \check{x}\right] \right\} \\&\quad +{1\!\!1}_{T-t> |S|+1}\left\{ V_{|S|+1}^{i}(\check{x}^{-i},a^i,s)\left[ \check{x}\right] -V_{|S|+1}^{i}(\check{x},s)\left[ \check{x}\right] \right\} \frac{|S|+1}{T-t+1} \end{aligned}$$

By the third point of the description of the game, the difference is negative. So $\check{x}$ is an SPE in any game of length $T$. Note that it is true for all $T$ and then $\check{x}$ must be in $\mathcal {P}_{T}$ for all $T$. Also the asymptotic payoff vector is $(\check{u}^{i})_{i}=:\check{u}$ since $\check{x}$ is a stationary strategy and for all $s\in R,$ $R\in \mathcal {R}_{\check{x}},$ $u^{i}(\check{x},s)=\check{u}^{i}$, for all $i$.$\square$

6.4.1 Proof of the first point of Proposition 1

I show that $\check{x}$ is the unique strategy that is played at the equilibrium, whatever the horizon length $T$. At the last period players must be playing $\check{x}(s)$ since in all $s$, $\check{x}(s)$ is the unique Nash. Now suppose that there is only one continuation strategy profile, $\check{x}$, at $t$. Let me show that in all $s$, $\check{x}(s)$ must be played at the equilibrium. Suppose on the contrary that players play another action profile $a$. If there is no deviation then player $i$ gets at most:

$$\begin{aligned} \frac{{1\!\!1}_{T-t\le |S|+1}(T-t+1)V_{T-t}^{i}(a,s)\left[ \check{x} \right] +{1\!\!1}_{T-t> |S|+1}\{(|S|+1)V_{|S|+1}^{i}(a,s)\left[ \check{x} \right] +(T-t-|S|) \check{u}^{i}\}}{T-t+1} \end{aligned}$$

Playing $d\ne a^{i}$ gives at least:

$$\begin{aligned} \frac{{1\!\!1}_{T-t\le |S|+1}(T-t+1)V_{T-t}^{i}(a^{-i},d,s)\left[ \check{x }\right] +{1\!\!1}_{T-t> |S|+1}\{(|S|+1)V_{|S|+1}^{i}(a^{-i},d,s)\left[ \check{x}\right] +(T-t-|S|) \check{u}^{i}\}}{T-t+1} \end{aligned}$$

The difference is:

$$\begin{aligned}&{1\!\!1}_{T-t\le |S|+1}\left\{ V_{T-t}^{i}(a^{-i},d,s)\left[ \check{x}\right] -V_{T-t}^{i}(a,s)\left[ \check{x}\right] \right\} \\&\qquad +{1\!\!1}_{T-t> |S|+1}\left\{ V_{|S|+1}^{i}(a^{-i},d,s)\left[ \check{x}\right] -V_{|S|+1}^{i}(a,s)\left[ \check{x}\right] \right\} \frac{|S|+1}{T-t+1} \end{aligned}$$

According to the condition of the proposition, there is a $i$ and a $d$ such that the above line is strictly positive. So there is a profitable deviation and then a contradiction. By using an induction argument this shows that there is a unique SPE that plays $\check{x}$ for all $T$.

6.4.2 Proof of the second point of Proposition 1

According to lemma 5 the strategy profile $\check{x}$ is an equilibrium for all $T$ and $U(\check{x},s)=\check{u}$ for all $s$. I construct the SPE strategy profile $y$ that generates asymptotic payoff $\hat{u}>\check{u}$ for any initial state. This profile plays as follows:

• Normal path: if $t<T$ play $\hat{x}$ and if $t=T$ play $\check{x}$.

• Punishment path: play $\check{x}$ in all states.

I show that $y$ is an SPE if $T$ large enough. I know that there is no deviation on the punishment path. Let me check that there is no deviation on the normal path, for $T$ large enough. Clearly that there is no profitable deviation at $t=T$. Consider a date $t<T$. As $\min _{s^{\prime }\in R,R\in \mathcal {R}_{\hat{x}}}u^{i}(\hat{x},s^{\prime })> \check{u}^{i}$, there is a $T^{*}>|S|$ such that for all $T\ge T^{*}$, for all $s$ and all $i$:

$$\begin{aligned}&\frac{u^{i}(\hat{x},s)+|S|\min _{ s\in S}u^{i}(\hat{x},s)+(T-t-|S|-1) \min _{s^{\prime }\in R,R\in \mathcal {R}_{\hat{x}}}u^{i}(\hat{x},s^{\prime })+ \min _{s\in S}u^{i}(\check{x},s)}{T-t+1}>\\&\quad \frac{\max _{a^{i}}u^{i}(\hat{x}^{-i},a^{i},s)+|S|\max _{s\in S}u^{i}(\check{x} ,s)+(T-t-|S|)\check{u}^{i}}{T-t+1} \end{aligned}$$

The first line is a lower bound over the payoff generated by $y$ if it remains more than $|S|+2$ periods. Also the second line is an upper bound on a deviation from $y$. Suppose that the horizon is greater than $2T^{*}$. If $t\le T^{*}$ this means that there remains at least $T^{*}$ periods and then, according to the above inequality, there is no profitable deviation. If $t>T^{*}$ (and so $t>|S|$) then $s_{t}\in R,$ $R\in \mathcal {R}_{\hat{x}}$. The net gain to deviate is at most:

$$\begin{aligned} \frac{2\max _{\begin{array}{c} s,s'\in R \\ R\in \mathcal {R}_{\hat{x}} \end{array}}\{V_{2}(\hat{x }^{-i},a^{i},s)[\check{x}]-V_{2}(\hat{x},s')[\check{x}]\}+(T-t-1)(\max _{s\in S}u^{i}(\check{x},s)-\min _{s^{\prime }\in R,R\in \mathcal {R}_{\hat{x}}}u^{i}(\hat{x} (s^{\prime }),s^{\prime }))}{T-t+1} \end{aligned}$$

By assumption I have: $\max _{\begin{array}{c} s,s'\in R \\ R\in \mathcal {R}_{\hat{x} } \end{array}}\{V_{2}(\hat{x}^{-i},a^{i},s)[\check{x}]-V_{2}(\hat{x},s')[\check{x}]\}\le 0$ for all $i$ and $\max _{s\in S}u^{i}(\check{x},s)-\min _{s^{\prime }\in R,R\in \mathcal {R}_{\hat{x}}}u^{i}(\hat{x} (s^{\prime }),s^{\prime }))\le 0$ for all $i$. Then a deviation is not profitable. So $y$ is a SPE in $\Gamma ^{T}$ for all $T\ge 2T^{*}$.