Abstract
The “non-harmonicity” problem in residual terrain modelling (RTM) is a challenging issue, causing errors exceeding 200 mGal in the RTM gravity anomaly in rugged areas. Although various methods have been proposed to address this problem, including the condensation method, regularized downward continuation methods with Taylor series expansions (TS) and spherical harmonics (SH), complete harmonic correction (HC) method, closed-form complete HC method, and Kadlec's method, their performances in gravity field determination have not been directly validated. In this study, we reviewed and evaluated these methods, especially for their performance in regional geoid determination. We found that the HC's expression for the closed-form complete method is identical to that under the unlimited Bouguer plate approximation, and Kadlec’s method is equivalent to the condensation method with the same approximation for Bouguer masses. However, the HC associated with the complete HC method shows large differences compared to other methods. This is because the upward and downward continuations in the complete HC method consider an Earth with changing total mass. To address it, we propose a new three-step approach, proved to be equivalent to the HC using the TS method. Then the performance of various HC methods is evaluated in gravity anomaly synthesis and geoid determination over a select region in Colorado, USA. The best result is achieved when using the SH method to compute RTM gravity anomalies, resulting in a geoid accuracy of ~ 1.62 cm. Involving the HC for the height anomaly in the restore procedure slightly improves the accuracy to ~ 1.56 cm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Earth's gravity field, reflecting the Earth's mass distribution and changes in time, is a fundamental subject in geodetic and geophysical studies (Hofmann-Wellenhof and Moritz 2006). The residual terrain modelling (RTM) technique (Forsberg 1984), which relies exclusively on the density and geometric information of the Earth's topography, has been widely applied in the gravity field determination, e.g. for extending the contents of the global gravity field models (GGMs) with the accuracy at the mGal-level (Forsberg 1984; Hirt et al. 2013, 2019b; Rexer and Hirt 2015; Bucha et al. 2019a; Yang et al. 2018, 2020; Zingerle et al. 2020), or for the regional gravity field determination in the remove-compute-restore (RCR) framework (Forsberg and Tscherning 1997; Sjöberg 2005; Schwabe et al. 2012; Lin et al. 2014, 2019; Bucha et al. 2016; Willberg et al. 2019; Wu et al. 2019; Liu et al. 2020; Matsuo and Kuroishi 2020; Wang et al. 2021; Lin and Li 2022). Therefore, accurate calculation of RTM-related gravity signals is of great significance in gravity field determination.
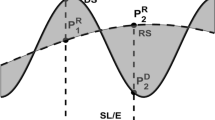
The “non-harmonicity” problem occurs in the RTM technique when a computation point, e.g. \(P_{2}^{D}\), is located below the reference topography (Forsberg and Tscherning 1981) (see Fig. 1), and some form of a harmonic correction (HC) is needed. Various studies have shown that the magnitude of HC would reach up to 200 mGal for the RTM gravitational attraction and several centimetres for the RTM height anomaly over rugged areas (Forsberg and Tscherning 1981; Hirt et al. 2019a; Yang 2020; Klees et al. 2022).
Principle of the RTM technique (Forsberg 1984; Bucha et al. 2019a; Yang et al. 2022). DS and RS denote the Earth’s surface represented by a detailed digital elevation model (DEM) and the smoothing reference topography, respectively. The computation points \(P_{1}^{D}\), \(P_{2}^{D}\) are located on the Earth’s surface and their respective points \(P_{1}^{R}\), \(P_{2}^{R}\) are on the reference topography
Numerous studies have been implemented to handle the “non-harmonicity” problem. The first method is the condensation method. It was first promoted by Forsberg and Tscherning (1981), and provided the HC expression for the RTM gravity anomaly. It has been widely applied for computing the HC of the RTM gravity field (Wu et al. 2019). However, it was proven to “underestimate the true value of the HC” by Hirt et al. (2019a), and the errors would reach up to more than 10 mGal over rugged areas. Hirt et al. (2019a) proposed that the approximation errors of unlimited Bouguer plate might be one of the reasons. Yang et al. (2022) developed the expressions of the HC for the RTM geoid height under various approximations, i.e. the unlimited Bouguer plate (UBP) approximation, the limited Bouguer plate (LBP) approximation that would reduce the mass inconsistency effect, the Bouguer shell (BS) approximation which reduces the effect of plate approximation and the limited Bouguer shell (LBS) approximation which could reduce both above-mentioned effects. In Yang et al. (2022), the expression under the BS approximation achieved the best results because of the remote mass effects. Up to the present, the effect of the unlimited Bouguer plate approximation on the evaluation of the HC for the RTM gravity anomaly has not yet been studied.
The regularized downward continuation method is another way to handle the “non-harmonicity” problem. Based on the provided equation for the RTM gravity anomaly by Forsberg and Tscherning (1981) and the regularized downward continuation method, Omang et al. (2012) gave the expression of the HC for the RTM geoid height. The regularized downward continuation method was also studied by Harrison and Dickinson (1989), Forsberg and Tscherning (1997), Elhabiby et al. (2009), and Bucha et al. (2016). These methods generally require numerical evaluation of higher-order derivatives at the computation point which would involve complex calculations, leading to the lower efficiency. Hirt et al. (2019a) developed an artificial method to compute the RTM gravity field, named as the RTM baseline solution. In this method, the gravity field generated by the topographic masses below the reference surface is calculated by spectral gravity forward modelling (SGM) (Bucha et al. 2019a; Hirt et al. 2019a, b; Yang 2020) which involves spherical harmonic analysis and synthesis of topographic masses. On the other hand, the gravity field generated by the detailed Earth's surface is obtained based on the global numerical integration which requires large numerical costs. This method has been successfully applied and validated in the RTM gravity anomaly/disturbance recovery (Hirt et al. 2019a, b). Bucha et al. (2016, 2019a) developed the cap-modified spectral gravity forward modelling method and applied it to the RTM technique (Bucha et al. 2019b) for harmonically downward continuing the gravity field implied by the reference masses. Klees et al. (2022) promoted the so-called complete method to compute the gravitational effects due to RTM masses and provided the expressions of the HC for RTM corrections to both gravity anomalies and height anomalies. Their numerical results suggested that the errors of the condensation method to the gravity anomaly would reach up to 100 mGal over rugged areas. In latest studies, Klees et al. (2023) provided exact and closed expressions of the complete RTM corrections for the disturbing potential, gravity disturbance, gravity anomaly and height anomaly. The closed-form complete RTM correction for the gravity disturbance achieves the same expression with the HC for the RTM gravity disturbance under the UBP approximation.
In addition, some studies (Kadlec 2011; Märdla et al. 2017) promote calculations of the RTM gravity field by dividing it into four constituents, the effect of a Bouguer layer having the thickness \(H\) that is derived from the detailed digital elevation model (DEM) and the corresponding terrain effect referring to the Earth’s surface, and the Bouguer effect of the thickness \(H_{{{\text{ref}}}}\) and the corresponding terrain effect referring to the reference surface (Kadlec 2011; Ďuríčková and Janák 2016). In this scenario, the computation point is always located outside the terrain masses. Furthermore, Kadlec (2011) provided the expressions of the Bouguer gravitational effects when computation points are located in the Bouguer masses.
Most of previous studies adopted the condensation method based on the UBP approximation to resolve the “non-harmonicity” problem in the RTM gravity field. The other methods, such as the condensation method based on the LBP, LBS and BS approximations, the downward continuation method, the complete method, and the Kadlec’s method as well as their performances in gravity field determination are not yet compared directly in a unified manner.
The main contributions of this study are as follows: (1) deriving the expressions of the HC for the RTM gravitational attraction under LBP, BS, and LBS approximations and investigating the error level in the classical condensation method, (2) evaluating the performance of various HC methods in gravity field synthesis, and (3) thoroughly investigating the HC effect on the regional geoid determination in the framework of RCR.
The remainder of this paper is organized as follows. Brief reviews and introductions of the five HC methods are given in Sect. 2. The unlimited Bouguer plate approximation errors including the mass inconsistency effect and the planar approximation effect are investigated in Sect. 3. The comparisons of various methods for the HC over Himalaya mountains are given in Sect. 4. Section 5 investigates the performances of various HC methods in gravity field synthesis and regional geoid determination over the Colorado area, USA. Finally, discussions and main conclusions are given in Sects. 6 and 7, respectively.
2 Methodology
In modern gravity field determination using the RTM technique, the real Earth’s topography is replaced by a smoother reference topography, and the data are reduced by the gravitational effects of the residual masses, which are defined as the mass deficit or difference between the two topographies. For the sake of convenience, we define here the RTM-reduced Earth as the Earth after the RTM reduction with the outer boundary being the reference topography, and call the gravitational effects implied by the residual masses as the RTM effects. In a more generalized way, the RTM correction plays the role of reducing the Earth gravity field functional to the corresponding functional of the RTM-reduced Earth by subtracting the RTM effect. The harmonicity of the reduced gravity field functional should be guaranteed in order to construct an accurate external gravity field with respect to the Earth topography. Since the reference topography represents the long-wavelength part of the real topography, its surface would be above or below the real topographic surface. This results in cases that the point on the Earth’s surface is located either above or below the reference surface. In the former case, because the point is in free air with respect to the reference topography, the corresponding RTM correction is harmonic, and so is the reduced gravitational field functional. In the latter case, since the point is buried inside the masses of the RTM-reduced Earth, the corresponding RTM correction for gravitational potential is not harmonic and the reduced gravity field functional represents a functional of the internal potential. This is the so called “non-harmonicity” problem that exists in the RTM technique. To solve it, HC is applied to transform the internal gravity field functional into a regularized harmonically downward continued gravity field functional.
Let \(\delta \tilde{g}_{{{\text{RTM}}}} \left( P \right)\) and \(\delta \tilde{V}_{{{\text{RTM}}}} \left( P \right)\) be, respectively, the harmonic corrected values of the RTM effect removed from the gravity \(g\left( P \right)\) and gravity potential \(W\left( P \right)\) measured at points \(P\) on or above the Earth’s surface. Here the gravity is the negative radial derivative of the potential. The gravity and potential after the RTM reduction are then defined as:
Both \(g_{{{\text{red}}}} \left( P \right)\) and \(W_{{{\text{red}}}} \left( P \right)\) refer to the RTM-reduced Earth which is mass-free outside the reference topography. For points \(P\) located in the RTM masses, they represent harmonically downward continued gravity field functionals. It is clear that the key issue is how the harmonic RTM correction can be obtained.
Since the original RTM correction is defined as the subtracted gravitational effect implied by the residual masses, its corrections to gravity and potential can also be described as:
In the above equations, \(\delta g_{{{\text{DEM}}}} \left( P \right)\) and \(\delta V_{{{\text{DEM}}}} \left( P \right)\) are the gravitational attraction and potential due to the real topography represented by a global high-resolution DEM, respectively, whilst \(\delta g_{{{\text{REF}}}} (P)\) and \(\delta V_{{{\text{REF}}}} (P)\) are the gravitational attraction and potential due to the terrain masses bounded by the reference topography. For the point \(P\) below the reference surface, formulas that also hold inside the RTM masses should be used for computing the corresponding potential and gravity.
Since the computation point \(P\) is either on or above the real topography, the corresponding gravitational effects due to the real topography (i.e. the first terms of the right-hand side of Eqs. (3) and (4)) are always harmonic. Therefore, the harmonicity of the RTM corrections computed by Eqs. (3) and (4) depends on the gravitational effects caused by the reference topography (i.e. the second terms of the right-hand side of Eqs. (3) and (4)). In the case that the computation point \(P\) is outside the reference topography, \(\delta g_{{{\text{REF}}}} \left( P \right)\) and \(\delta V_{{{\text{REF}}}} \left( P \right)\) are computed in space, where the gravitational potential is harmonic. Therefore, the directly computed RTM effects \(\delta g_{{{\text{RTM}}}} \left( P \right)\) and \(\delta V_{{{\text{RTM}}}} \left( P \right)\) are equivalent to \(\delta \tilde{g}_{{{\text{RTM}}}} \left( P \right)\) and \(\delta \tilde{V}_{{{\text{RTM}}}} \left( P \right)\), and can be used for Earth’s external gravity field modelling. When \(P\) is inside the reference topography, \(\delta g_{{{\text{REF}}}} \left( P \right)\) and \(\delta V_{{{\text{REF}}}} \left( P \right)\) are computed in the region, where the gravitational potential is no longer harmonic. To circumvent this problem, HC is necessary for the corresponding RTM corrections when they are used for Earth’s external gravity field modelling. Various methods were provided for such a correction. In the following, we only discuss the case that the computation point is located below the reference topography. For a better explanation, we further define \(\delta \tilde{g}_{{{\text{REF}}}}\) and \(\delta \tilde{V}_{{{\text{REF}}}}\) as the harmonic corrected version of \(\delta g_{{{\text{REF}}}}\) and \(\delta V_{{{\text{REF}}}}\), respectively.
2.1 HC of the condensation method
In the classical condensation method as proposed by Forsberg and Tscherning (1981), the RTM masses above the computation point are assumed to be an unlimited planar Bouguer plate. The masses above the computation point are first removed away, and then added back by compressing them into a mass layer with the surface density \(\rho \Delta h\) and moving down just below the computation point. Then the harmonic corrected gravitational attraction due to the reference topography follows:
with \(G\) denoting the universal Newton’s gravitational constant, \(\rho\) the density of topographic masses, and \(Q\) the respective point for \(P\) on the reference topography.
Then the harmonic RTM correction to gravity follows:
The HC for the RTM correction to gravity is denoted as:
The sign convention of using the HC in this paper follows that, the HC is added to the originally computed RTM effect to obtain its harmonic corrected value that is subtracted from the measured gravity and recovered potential (Klees et al. 2022). So, HC for the gravity disturbance is negative in nature. The expression for the harmonic RTM correction to gravity under the UBP approximation is finally given as:
Another perspective of explaining this approach by employing the concepts of upward and downward continuations can be found in Page 3 of 25 in Klees et al. (2022).
In order to reduce the approximation errors due to planar approximation and mass inconsistency effect, the masses between the computation point and the reference surface are approximated by a limited Bouguer plate (LBP, Kadlec 2011), a Bouguer shell (BS, Vaníček et al. 2002; Kadlec 2011), and a limited Bouguer shell (LBS, Kadlec 2011), and then compressed into their respective mass layers of infinitesimal thickness and moved down just below the computation point. The HC terms are then obtained as the differences between gravity fields induced by the RTM masses generally approximated by some regularly-shaped masses and their, respectively, compressed masses. This is consistent with the condensation method under UBP, LBP, BS, and LBS approximations in Yang et al. (2022). However, the HC expressions were only given for the RTM correction to geoid height in Yang et al. (2022). As a continuous work of Yang et al. (2022), the expressions of HC for the RTM correction to gravity under various approximations are derived in this study. For detailed derivations, please see Sects. S1-S3 of the Electronic Supplementary Material (ESM), also Heck and Seitz (2007). Only final expressions are given in the following.
The expressions of HC and the harmonic RTM correction to gravity under the LBP approximation follow:
where \(\eta\) indicates the radius of a limited Bouguer plate (vertical cylinder) (Fig. S1).
The expressions of HC and the harmonic RTM correction to gravity under the BS approximation follow:
where \(r_{1} = R + H\left( P \right)\) indicates the radius of the inner sphere and \(R\) is the mean Earth’s radius.
The expression of HC under the LBS approximation follows:
where \(V_{r}^{{{\text{LBS}}}}\) and \(V_{r}^{{{\text{LBSC}}}}\) denote the radial derivative of the gravitational potential generated by the LBS and its compressed mass layer, respectively. As a consequence, the expressions for the harmonic RTM correction to gravity under the LBS approximation are given as:
It depends on the opening angle \(\psi_{0}\) of the cone, which is depicted in Fig. S3 of ESM.
2.2 HC of the regularized downward continuation method of Taylor series expansions (TS method)
With assumption that the Taylor series of potential and its derivatives don’t diverge, for the point \(P\) located below the reference topographic surface, the corresponding gravity field signals generated by the masses between the geoid and the reference topographic surface are harmonically calculated based on the regularized downward continuation method of Taylor series expansion (Bucha et al. 2016, Eq. (10)). Here, the reference topographic surface is expanded to degree \(n_{\max } = 2159\) which equals the maximum degree of the global gravity field geopotential model EIGEN-6C4 (Förste et al. 2014) in the numerical experiments. In such a case, the reference topography is rather smooth. The Taylor series expansion can be truncated at \(k = 1\) for gravity and truncated at \(k = 2\) for potential (Bucha et al. 2016). This is reasonable considering the numerical test at Colorado mountain areas with the values of the second-order term at sub-mm level. Then the equations for gravitational attraction and potential follow:
Since the point \(Q\) is on the reference topographic surface, the computed gravitational effects of the reference topography at this point (i.e. \(\delta g_{{{\text{REF}}}} \left( Q \right)\) and \(\delta V_{{{\text{REF}}}} \left( Q \right)\)) are external gravitational field terms, and so are their downward continued functionals at \(P\).
Then we have:
Similarly,
Accordingly, the expressions of HC for RTM corrections to gravity and potential associated with the TS method are given as:
Need to mention that, the purpose of this study is to compute the RTM corrections to gravity and potential. Therefore, the harmonic RTM corrections to gravity and potential (\(\delta \tilde{g}_{{{\text{RTM}}}}\) and \(\delta \tilde{V}_{{{\text{RTM}}}}\)) are computed according to Eqs. (16) and (17), and the first line of Eqs. (18) and (19). Then the HC for RTM corrections are differences between \(\delta \tilde{g}_{{{\text{RTM}}}}\) and \(\delta g_{{{\text{RTM}}}}\), and \(\delta \tilde{V}_{{{\text{RTM}}}}\) and \(\delta V_{{{\text{RTM}}}}\). In Eqs. (16) and (17), the gravitational potential and attraction can be computed on the reference topography, while the high-order (\(\ge 2\)) radial derivatives are not defined on the reference surface due to the density discontinuity. As a remedy, Q can be moved upward with a constant value. In practical computations, the gradients can be obtained through a numerical differentiation of gravity, for instance, using gravity at points that are radially upward shifted by 100 and 200 m from \(Q\) as in Bucha et al. (2016). More rigorously, the radial gradient components of gravity and potential in this study are calculated using the TGF software (Yang et al. 2020). Besides, various truncations of the Taylor series expansion and different shifted distances of \(Q\) would also affect the final results, which are not further discussed in this study.
2.3 HC of the regularized downward continuation method of spherical harmonics (SH method)
In the baseline solution method (Hirt et al. 2019a), the full topography generated gravitational field \(\delta V_{{{\text{DEM}}}}\) and \(\delta g_{{{\text{DEM}}}}\) over the computation point \(P\) are computed by numerical integration using some spatial domain methods. The long-wavelength signals \(\delta \tilde{V}_{{{\text{REF}}}}\) and \(\delta \tilde{g}_{{{\text{REF}}}}\) are implied by the reference topography with spectral gravitational forward modelling (SGM) or cap-modified spectral technique (Bucha et al. 2019a). Thus, the RTM correction is simply obtained as their difference. In this case, the computation of \(\delta \tilde{V}_{{{\text{REF}}}}\) and \(\delta \tilde{g}_{{{\text{REF}}}}\) relies on the finite linear combination of external spherical harmonics with all Earth’s masses encompassed into the Brillouin sphere (Hotine 1969). Then the RTM corrections to gravity and potential are given as:
Then the expressions of HC using the downward continuation of spherical harmonics (SH) are:
Same to the method in Sect. 2.2, the \(\delta \tilde{g}_{{{\text{RTM}}}}\) and \(\delta \tilde{g}_{{{\text{RTM}}}}\) are firstly obtained with the first line of Eqs. (22) and (23). Then the HC for RTM corrections to gravitational attraction and potential could be obtained as differences between \(\delta \tilde{g}_{{{\text{RTM}}}}\) and \(\delta g_{{{\text{RTM}}}}\), and \(\delta \tilde{V}_{{{\text{RTM}}}}\) and \(\delta V_{{{\text{RTM}}}}\). The computation of \(\delta \tilde{V}_{{{\text{REF}}}}\) and \(\delta \tilde{g}_{{{\text{REF}}}}\) follows from Hirt et al. (2019a). The spherical harmonic coefficients \(H_{nm}\) of a detailed topography are firstly obtained through SH analysis. Then the heights of the reference topography \(H_{{{\text{REF}}}}\) are computed via SH synthesis with \(H_{nm}\) expanding to a maximum degree \(N\) which equals the maximum degree of the adopted global gravity field model. In this study, EIGEN-6C4 is applied and \(N\) equals 2159. Another SH analysis is implemented on the topographic height functions \(\left( {H_{{{\text{REF}}}} /R} \right)^{p}\) and expanded into related SH coefficients \(H_{nm}^{(P)}\). Here \(R\) is the mean Earth’s radius and \(p\) is the integer power. The SH coefficients of topographic potential are obtained via the transformation between SH coefficients of the topographic potential and the SH coefficients of the reference topography. The topographic potential coefficient of degree \(n\) and order \(m\) is given as Eq. (9) of Hirt et al. (2019a):
Here, \(M\) indicates the Earth’s mass and \(\rho\) is the mean Earth’s mass density.
Then \(\delta V_{{{\text{REF}}}}\) and \(\delta g_{{{\text{REF}}}}\) are computed via SH synthesis (Hirt et al. 2019a, Eqs. (9) and (10))
and
with \(r = R + H\left( P \right)\), and \(\left( {\varphi , \, \lambda } \right)\) indicating the latitude and longitude of the computation point. Equations (27) and (28) adapt to computing gravitational attraction and potential for points located above the Brillouin sphere because the SH series converges uniformly. For points on or below the Brillouin sphere, the SH series may diverge and produce gross errors in the results (Hirt and Kuhn 2017; Rexer 2017; Šprlák et al. 2020; Bucha and Kuhn 2023).
2.4 HC of the complete RTM correction method
The complete RTM correction method provides harmonically downward continued gravity field functionals referring to the RTM-reduced Earth bounded by the reference topographic surface (Klees et al. 2022). Ignoring the high-order error terms, the complete method gives the expressions of RTM corrections to gravity and potential from Eqs. (36) and (40) of Klees et al. (2022):
Here, the subscript “RTM” means the residual masses for integration. \(\delta g_{{{\text{RTM}}}}^{ + } \left( P \right)\) and \(\delta V_{{{\text{RTM}}}}^{ + } \left( P \right)\) indicate the gravitational attraction and potential at \(P\) due to the residual masses above the reference topographic surface; \(\delta g_{{{\text{RTM}}}}^{ - } \left( P \right)\), \(\delta g_{{{\text{RTM}}}}^{ - } \left( Q \right)\) and \(\delta V_{{{\text{RTM}}}}^{ - } \left( P \right)\), \(\delta V_{{{\text{RTM}}}}^{ - } \left( Q \right)\) indicate the gravitational attraction and potential at \(P\) and \(Q\) due to the residual masses below the reference topographic surface, respectively.
Then the expressions of HC for RTM corrections to gravity and potential are obtained as (Klees et al. 2022, Eqs. (37) and (41)):
2.5 HC of the Kadlec’s method
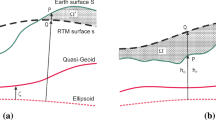
In the Kadlec’s method (Kadlec 2011), the RTM correction to gravity is split into four parts, the gravity field effect \(\delta g_{{{\text{BP}}}}\) of a Bouguer layer of thickness \(H\) and the corresponding terrain effect \(\delta g_{{{\text{TE}}}}\) referring to the Earth’s surface (see Fig. 2a, c), and the Bouguer effect \(\delta g_{{{\text{BP}}}}^{g}\) of thickness \(H_{{{\text{REF}}}}\) and the corresponding terrain effect \(\delta g_{{{\text{TE}}}}^{g}\) referring to the reference topographic surface (see Fig. 2b, d). With \(S\) indicating the area of the Bouguer layer, and \(l\) the distance between the integration point of height \(Z\) and the computation point of height \(Z^{\prime}\), then the detailed expression (Kadlec 2011, Eqs. 3.3–3.9) is given as follows:
with
In this procedure, the computation point \(P\) is located outside of two types of terrain masses, e.g. Fig. 2a, b for \(P\) above the reference topographic surface, and Fig. 2c, d for \(P\) below the reference topographic surface. In addition, \(P\) is located above the Bouguer masses of thickness \(H\) for \(\delta g_{{{\text{BP}}}} (P)\). Therefore, the harmonic correction is not required for terrain gravity effect \(\delta g_{{{\text{TE}}}} \left( P \right)\), \(\delta g_{{{\text{TE}}}}^{g} \left( P \right)\), and \(\delta g_{{{\text{BP}}}} \left( P \right)\). For computation of \(\delta g_{{{\text{BP}}}}^{g} \left( P \right)\), the point \(P\) is located inside the masses. The expressions of \(\delta g_{BP}^{g} (P)\) are given in Kadlec (2011) when the geometry of Bouguer masses is approximated by an unlimited Bouguer plate, limited Bouguer plate, Bouguer shell and limited Bouguer shell.
Considering
with
Then Eq. (33) becomes:
The expression of HC for the RTM correction to gravity associated with the Kadlec’s method is:
In the unlimited Bouguer plate approximation, \(\delta g_{{{\text{BP}}}}^{d} \left( P \right)\) is computed by assuming an infinite Bouguer plate. For \(P\) above the Earth’s surface and below the reference topographic surface, the expressions of \(\delta g_{{{\text{BP}}}}^{{}}\), \(\delta g_{{{\text{BP}}}}^{g}\), and \(\delta g_{{{\text{BP}}}}^{d}\) could be derived following Eqs. (2.78)–(2.80) of Kadlec (2011).
and
Then Eq. (38) becomes
Obviously, the above equation is the same as the classical condensation method. This means that the Kadlec's method achieves the same results with the classical condensation method. This conclusion adapts for the condensation method under various approximations.
3 The approximation errors of the classical condensation method
In our experiments, a detailed DEM model—MERIT2017 (Yamazaki et al. 2017; Hirt 2018) at 3″ resolution is used to represent the Earth's surface. It is developed based on the SRTM (Shuttle Radar Topography Mission) V2.1 DEM within ± 60° latitude, and AW3D DEM model above 60° N. Compared with many other SRTM DEMs, voids, outliers, radar errors, and tree canopy signals were better handled in this model. A spherical harmonic expansion of MERIT2017 provides a smoothing reference topographic surface for this study (Hirt et al. 2019b). It was obtained through SH analysis and synthesis from MERIT2017 (Hirt et al. 2019a). It is expanded up to degree of 2160 (MERIT2160) which shares the same order and degree with the widely used global gravity field model EGM2008 (Pavlis et al. 2012) and EIGEN-6C4 (Förste et al. 2014). About 50.75% of continental points reside in masses defined by the MERIT2160. The differences between MERIT2160 and MERIT2017 would reach up to 1350 m over points located in residual masses. Besides, the constant value of 2670 kg/m3 is adopted to approximate the density of residual masses, 6378.137 km for the Earth’s radius, and 6.6743 × 10–11 m3 kg−1 s−2 for the Newton’s gravitational constant.
Yang et al. (2022) studied the errors caused by the unlimited Bouguer plate approximation and its effect on the RTM geoid height. Similar to the experiment in Yang et al. (2022), planar approximation effect is studied here in terms of the gravitational attraction by comparisons between HC_UBP and HC_BS, and between HC_LBP and HC_LBS. From Eqs. (7) and (11), it is obvious that the magnitude differences between HC under UBP and HC under BS have positive correlation with the value of residual heights. This means that the planar approximation effect would be less than 0.07 mGal for the RTM correction to gravity when magnitude of residual height is less than 1350 m. This is negligible in many practical applications. However, this is different, in that the planar approximation would involve significant effect in HC for the RTM correction to geoid height (Yang et al. 2022). It is reasonable when considering different attenuation characters of the geoid height and gravitational attraction with distance increasing. The distant masses produce much more significant effect on the geoid height than its first-derivatives. Figure 3 displays the planar approximation on HC for the RTM correction to gravity (the left panel of Fig. 3). It is obvious that the planar approximation effect on HC increases with integration radius growth first and then tends to be sluggish. The errors due to planar approximation would be less than 0.06 mGal for \(\delta g^{{{\text{HC}}}}\), when the integration radius is extended up to 110 km from the computation point.
Errors due to planar approximation (left panel) and mass inconsistency (right panel). \(\delta g^{{{\text{HC}}}}\) indicates the HC for the RTM correction to gravity. \(\delta g^{{{\text{HC}}\_{\text{LBP}}}}\), \(\delta g^{{{\text{HC}}\_{\text{LBS}}}}\), \(\delta g^{{{\text{HC}}\_{\text{UBP}}}}\), and \(\delta g^{{{\text{HC}}\_{\text{BS}}}}\) denote the HC under the LBP, LBS, UBP, and BS approximation, respectively
The mass inconsistency effect is investigated through comparisons between HC_UBP and HC_LBP, and between HC_BS and HC_LBS. The results from comparison between HC_BS and HC_LBS show the same trend with results from comparison between HC_UBP and HC_LBP. Therefore, only results from comparison between HC_UBP and HC_LBP (the right panel of Fig. 3) rather than both comparisons are displayed in this study. It is obvious that the magnitudes of mass inconsistency effect decrease first with integration radius increasing and then tends to be sluggish around 0.9 mGal. The mass inconsistency would involve larger than 1 mGal effect in HC when the integration radius is less than 100 km.
4 Comparisons of various methods for HC over Himalaya mountains
The values of HC with four methods are computed and compared over the Himalaya mountains. It is the most rugged area on the Earth and is here bounded by latitudes of 27° N and 28° N, and longitudes of 87° E and 88° E. MERIT2017 and its respective reference topographic surface MERIT2160, and constant density assumption of 2670 kg/m3 are used to model the RTM masses. The computation points are arranged on a \(15^{\prime\prime} \times 15^{\prime\prime}\) grid on the Earth's surface defined by MERIT2017. Figure 4 gives the MERIT2017 topography (panel a) and respective RTM topography over this area (panel b). Then 50.70% of the computation points are located below the reference topographic surface defined by the MERIT2160. HCs over these points are calculated and compared.
Table 1 and Fig. 5 provide the statistical information of HCs with various methods and their comparison results. The magnitudes of HCs for RTM corrections to gravity would reach up to hundreds mGal over the study area. Therefore, HCs for the RTM corrections to gravity should be carefully considered. The values of HCs for RTM corrections to gravity are negative with the condensation method as shown in Fig. 5a, while there might be positive values using the other methods. This might be caused by the fact that the condensation method assumed that all masses indicated by the reference topography are all above the level of the computation point while other methods consider the reality that masses might located below the computation point. This has also been reported in Klees et al. (2022).
Values of HCs over the Himalaya and the comparison results depend on various methods. \(\delta g^{{{\text{HC}}\_{\text{UBP}}}}\), \(\delta g_{{}}^{{{\text{HC}}\_{\text{TS}}}}\), \(\delta g_{{}}^{{{\text{HC}}\_{\text{SH}}}}\), and \(\delta g_{{}}^{{{\text{HC}}\_{\text{complete}}}}\) indicate the HC for the RTM correction to gravity with the UBP approximation, with the regularized downward continuation method of TS, with the regularized downward continuation method of SH, and with the complete method, respectively
In the framework of the condensation method, the differences of HCs under various approximations, i.e. UBP, LBP, UBS, and LBS, are at sub-mGal-level. This is consistent with the results shown in Sect. 3. There are biases between UBP and LBP, UBP and LBS being larger than 0.1 mGal. Considering that a 0.1 mGal gravity bias might yield a geoid error in the order of 1 cm (Heiskanen and Moritz 1967; Märdla et al. 2017), the effects of these approximations in geoid determination should be carefully investigated.
In terms of comparison of HCs with various methods, the differences between HCs with UBP and HCs with continuation methods are within ~ 11.20 mGal for the TS method, and within ~ 10.87 mGal for the SH method. The STD of differences are ~ 0.94 mGal and ~ 1.30 mGal, respectively. The large differences, shown in Fig. 5b, c, are mainly located in very rugged areas. HC using the complete method shows the largest difference with the HC under the UBP approximation (see Fig. 5d). The corresponding STD values reach up to ~ 11.81 mGal.
From this experiment, it is easy to see that large differences are involved when using various HC methods for RTM corrections to gravity, especially over very rugged areas. This suggests a substantial discrepancy among current HCs based on various methods which will subsequently affect the accuracy of gravity field modelling. Therefore, related numerical experiments should be implemented to validate the performances of various HC methods in gravity field determination.
5 The effects of HC on gravity field modelling studies
The following experiments are implemented over the Colorado area. It is the study area of “the 1 cm geoid experiment” (Wang et al. 2021). Over this area, the RTM height (Fig. 6) ranges from ~ − 830 to ~ 1043 m. There are ~ 51.03% points with negative residual heights and locating below the reference topographic surface defined by MERIT2160. Besides, there are 58,913 terrestrial gravity measurements which would provide the numerical datasets for this study. And 222 GSVS17 (Geoid Slope Validation Survey 2017, van Westrum et al. 2021) GNSS/levelling measurements would provide geoid undulations with an accuracy of ~ 1.5 cm and height anomalies with accuracy of ~ 1.2 cm for evaluation purposes. All these make it a good place for studying the effect of HC on gravity field synthesis and on regional geoid determination. The details about the terrestrial measurements are given in Wang et al. (2021).
5.1 The effect of various HC methods on gravity field syntheses
RTM technique has been widely applied to augment the GGMs at high-frequency bands and to get an ultra-high-resolution global and regional gravity field models (Voigt and Denker 2007; Hirt et al. 2013; Ďuríčková and Janák 2016; Zingerle et al. 2020). Here, the high-frequency gravity anomalies from the RTM with various HC methods are combined with long-wavelength signals of EIGEN-6C4 expanded up to degree and order (d/o) 2159 to recover the gravity signals over the Colorado area. Based on this method, a synthesized gravity anomaly field is obtained. And it is compared with the terrestrial gravity measurements to evaluate the performance of various HC methods.
Over this area, the synthesized gravity anomalies are calculated over 58,913 points and HCs are considered for 34,493 points. Figure 7a shows the values of HCs for RTM corrections to gravity anomalies with the UBP method. The magnitudes of HCs range up to ~ 180.54 mGal, which should be carefully considered in gravity anomaly syntheses. This is obvious in Table 2, which gives the statistical information of gravity measurements and the residuals as differences between measured and synthesized gravity anomalies. The EIGEN-6C4 expanded up to d/o 2159 could recover ~ 63.71% of gravity signals; however, the combination of EGM2008 and the RTM without HC could only recover ~ 45.98% of gravity signals. This demonstrates the importance of including HCs in RTM corrections. The recovery capacity is greatly improved after involving HCs for RTM corrections to gravity anomalies. This is obvious from the decreased RMS of residual signals, e.g. ~ 9.10 mGal when involving HCs associated with the complete method, ~ 3.80 mGal when involving HCs associated with the UBP method, ~ 3.74 mGal when involving HCs associated with the TS method, and ~ 3.64 mGal when involving HCs associated with the SH method from ~ 20.74 mGal without HCs.
Performance comparisons of various HC methods in gravity field syntheses. a HC under the UBP approximation, b residual gravity anomaly when HC under the UBP approximation, c–e magnitude differences between residual gravity anomalies when involving HCs under the UBP approximation, with the TS method, with the complete method and residual gravity anomalies when involving HCs with the SH method
Although the involvement of HCs would improve the synthesized results, there are great differences between various methods. Here, the improvement rate is involved as an indicator of the performance of the synthesized gravity anomaly. With \(\Delta g_{{{\text{syn}}}}\) indicating the synthesized gravity anomaly and, \(\Delta g_{{{\text{obs}}}}\) the terrestrial measurements, then the improvement rate is defined as: \(\kappa = \left[ {{\text{RMS}}\left( {\Delta g_{{{\text{obs}}}} } \right) - {\text{RMS}}\left( {\Delta g_{{{\text{syn}}}} } \right)} \right]/{\text{RMS}}\left( {\Delta g_{{{\text{obs}}}} } \right)\). The improvement rates under various conditions are given in Table 2. The HC associated with the SH method achieves the best performance with the largest improvement rate of ~ 90.52%, then followed by the HC associated with the TS method and the HC associated with the UBP method with the improvement rates more than 90%. The HC with the complete method achieves the smallest improvement rate of ~ 76.30%. The condensation methods with various approximation achieve equivalent results. In addition to methodologies of various methods for HC, the methods adopted for numerical evaluation of Newton’s integration will also affect the performance of HCs. Here the spectral domain method is applied in SH for gravitational field calculation induced by reference topographic masses, while the spatial numerical evaluation method for the TS, UBP, and complete methods.
Figure 7b–e displays the residual gravity anomalies when HC associated with the UBP method (panel (b)) and the magnitude differences between residual gravity anomalies when involving HCs associated with the UBP method, TS method, complete method, and residual gravity anomalies when involving HC associated with the SH method. In panels (c)–(e), the red and yellow colours indicate the better performance of considering the HC with the SH method. As shown in Fig. 7b, c, most of the magnitude differences between gravity anomaly residuals when involving HCs with the UBP method, TS method, and gravity anomaly residuals when involving the HC with the SH method are within 10 mGal. HCs with the TS method show a slightly better performance over rugged area (Fig. 7d). The magnitude differences between gravity anomaly residuals when involving HCs with the TS method and gravity anomaly residuals when involving HCs with the SH method are mainly happened around rugged areas with values up to more than ~ 100 mGal.
5.2 The effect of various HC methods on local geoid determination
In the remove-compute-restore procedure, GGM and RTM corrections to gravity anomalies are first removed from gravity measurements. Then various methods, such as least-squares collocations (Moritz 1980; Tscherning and Rapp 1974) and radial basis functions (Klees and Wittwer 2007; Schmidt et al. 2007; Li 2018) can be applied to obtain the residual height anomalies. Here, we use the truncated Stokes’s kernel (Wong and Gore 1969) to obtain the residual height anomalies, considering that far zone contributions are negligible after removing GGM and RTM (Li and Wang 2011). Finally, the height anomalies derived from GGM and RTM are added to obtain the height anomalies. In the removal procedure, the HCs for RTM corrections to gravity anomalies are generally considered and corrected with the classical UBP method. However, the HCs for RTM corrections to height anomalies in the restore procedure are rarely studied.
The main purposes of the following experiments are to evaluate the performances of various HC methods in local geoid model determination and to investigate the effect of HCs for RTM corrections to height anomalies in the restore procedure. Therefore, 14 numerical experiments are implemented over the Colorado area. The definition of variables of 14 experiments is listed in Table 3.
In this study, height anomaly grid is the summation of long-wavelength signals indicated by EIGEN-6C4 on the Earth’s surface, short-wavelength signals of RTM on the Earth’s surface, and residual wavelength signals from the classical Stokes’s integration with truncated kernels (Wong and Gore 1969). The height anomaly is transformed into the geoid height (Fig. 8) as indicated in Wang et al. (2021). The GSVS17 GNSS/levelling data (222 benchmarks) provide the reference values for the validation of computed geoid models with various parameters (Wang et al. 2021). Each computed geoid grid is interpolated to the GNSS/levelling points to obtain the geoid heights that are then compared with the GNSS/levelling measurements. STD values of differences between GNSS/levelling data and interpolated geoid heights indicate the performance of computed geoid heights with various parameters. As suggested in studies, e.g. Wong and Gore (1969), kernels with low degree terms removed would improve the results. Here, the geoid heights with various truncation degrees are calculated and validated.
Figure 9 gives the STD values of differences between GNSS/levelling data and interpolated geoid heights with various variation of truncation degrees when using different HC methods. It is obvious that the STD values drop dramatically first and then tend to be stable with the truncation degree increasing. The case of the HC with the SH method achieves the best results with the smallest STD values, then is the condensation method and the TS method (Fig. 9). The case of the HC with the complete method achieves the largest STD values (Fig. 9). In the case of involving the HC with the SH method, the smallest STD value of ~ 2.04 cm is achieved when the truncation degree is chosen as 700. For various approximations based on the condensation method, the geoid height differences are at sub-mm level and could be ignored. The STD gets the smallest value of ~ 2.05 cm when the truncation degree is 700. When involving the HC with the TS method, the smallest STD value of ~ 2.10 cm is achieved at the truncation degree 700. When the truncation degree is larger than 1400, the HCs with the condensation method, with the TS method and with the SH method achieve almost the equivalent performance. When considering the HC with the complete method, the smallest STD value of ~ 2.29 cm is achieved at truncation degree 2500. This indicates the poor performance in long-wavelength correction of the complete method, which affects the accuracy of corrected gravity anomalies and then the accuracy of determined geoid heights.
STD values with the increasing of the truncation degree of Wong and Gore modified Stokes kernel. \(\Delta N_{{{\text{OBS}}}}^{{{\text{HC}}\_{\text{UBP}}}}\), \(\Delta N_{{{\text{OBS}}}}^{{{\text{HC}}\_{\text{complete}}}}\), \(\Delta N_{{{\text{OBS}}}}^{{{\text{HC}}\_{\text{SH}}}}\), and \(\Delta N_{{{\text{OBS}}}}^{{{\text{HC}}\_{\text{TS}}}}\) indicate the STD values of differences between estimated geoid heights and GNSS/levelling measurements when involving the HC using the UBP method, complete method, SH method, and TS method, respectively
In types 8–14, the HC for the RTM correction to the gravity anomaly in the removal procedure and the HC for the RTM correction to the height anomaly in the restore procedure are both considered. The consideration of the HC for the RTM correction to the height anomaly would slightly improve the results. The case using the HC with the BS method achieves the best result with the STD value of ~ 2.00 cm, then is the SH method with the STD value of 2.02 cm, the condensation method under UBP, LBP, and LBS approximations of 2.03 cm, the TS method of 2.08 cm and the complete method of 2.28 cm.
6 Discussions
6.1 The new expressions in the framework of the complete method
From the above numerical experiments, it is obvious that there is a large difference between HC with the complete method and HC with other methods. Klees et al. (2023) indicated that the adoption of “upper bounds based on the exterior gravity field of a homogeneous mean Earth sphere, and nth Taylor series for upward continuation” would involve large errors over deep valleys (Klees et al. 2023). This might be the underlying reason. In order to improve the method, Klees et al. (2023) adopted the superposition principle of gravitating masses, and derived the corrected and closed-form of expression for HC for the RTM correction to gravity disturbance (Klees et al. 2023, Eq. (36)) and disturbing potential (Klees et al. 2023, Eq. (26)). Considering the definition of HC in this study and HC in Klees et al. (2023) have opposite signs, the expressions of HC with closed-form complete method to gravitational attraction and potential are:
It is obvious that \(\delta g^{{{\text{HC\_complete\_closed}}}}\) equals \(\delta g^{{{\text{HC\_UBP}}}}\), while the \(\delta V^{{{\text{HC\_complete\_closed}}}}\) is double of \(\delta V^{{{\text{HC\_UBP}}}}\) (Yang et al. 2022). Therefore, the HC associated with the closed-form complete method and the HC associated with the UBP method will show almost the same results and achieve nearly equivalent performance in gravity synthesis. However, when considering the HC to the height anomaly in the restore procedure, the Klees et al. (2023) achieves almost equivalent results with the BS method, resulting in the STD value of ~ 2.00 cm.
Besides, it is worth to mention that, the expression of HC to the gravity anomaly is also provided by Klees et al. (2023):
It is obvious that, the difference between \(\Delta g^{{{\text{HC}}\_{\text{complete}}\_{\text{closed}}}}\) and \(\delta g^{{{\text{HC}}\_{\text{UBP}}}}\) is only the second term \(4\pi G\rho \frac{{\Delta h^{2} }}{r}\), which involves up to ~ 0.02 mGal differences over the Colorado study area. It is possible to be ignored and therefore is not further discussed in the manuscript.
In the following, we will discuss the complete method (Klees et al. 2023) with respect to Klees et al. (2022) from a new perspective.
Consider point \(P\) on the Earth's surface and its respective point \(Q\) on the reference surface, where point \(P\) is located below the reference surface (see Fig. 2c, d). As indicated in Klees et al. (2022), the HC is achieved by splitting the RTM masses into two parts, the exact masses above the reference topographic surface, and the filled masses below the reference topographic surface but above the Earth's surface. Ignoring the error term, the expressions of HC for RTM corrections to gravity and potential are Eqs. (31) and (32), respectively.
As the basic idea of the regularized downward continuation method of TS, the gravity field functional generated by reference topographic masses at point \(P\) is computed as the downward continuation of the gravity field functional at point. The expressions of HC for RTM corrections to gravity and potential are Eqs. (20) and (21), respectively.
It is obvious that Eqs. (20) and (31), and Eqs. (21) and (32) have similar form. The difference is that only the \(\Omega^{ - }\) masses are considered for Eqs. (31) and (32), while the reference topographic masses are considered for Eqs. (20) and (21). The four-step method in Klees et al. (2022) gives some insights about the underlying reasons. In the four-step method, the masses above the reference topographic surface are removed in the first step and the gravity continuation follows. Therefore, the gravity continuation is actually implemented in a space corresponding to the Earth with changed masses. This might be one of the main reasons why the HC computed by the complete method of Klees et al. (2022) differs much from those computed by the other methods as shown in Sects. 4 and 5. To deal with this, in the framework of the complete method, we derive a new three-step approach (TSA) implemented in the space of unchanged Earth’s masses. The detailed derivations can be found in Appendix D, and its equivalence to the TS method will be given as follows.
The expressions of HC with the TSA are given as (see Appendix D):
Considering
and
Equation (46) then becomes
which is the same as Eq. (20).
In a similar way, Eq. (47) can be rewritten as:
which is the same as Eq. (21).
In conclusion, the three-step complete method and the TS method should achieve equivalent results.
6.2 Computation of geoid heights at stations with the RCR method
As introduced in Sect. 5.2, the geoid grid at 1′ × 1′ resolution is computed first. Then the geoid heights at stations, such as GSVS17 GNSS/levelling benchmarks, are interpolated from such a geoid grid. This is the general method in regional/local geoid determination with limited computation capability. However, this would involve interpolation errors (Roman 1993, 1999; Smith 2022). At the present stage, super computers provide supercomputing capability. It allows us to compute the geoid heights at a large number of stations in the framework of RCR. Here, long-wavelength signals indicated by EIGEN-6C4, short-wavelength signals of RTM, and the residual wavelength signals from the classical Stokes’s integral with truncated kernels (Wong and Gore 1969; Li and Wang 2011) are directly calculated on the 222 GSVS17 GNSS/levelling benchmarks. The summation of these three parts is height anomalies at benchmarks which are then transformed into geoid heights. The geoid heights at benchmarks are compared with GNSS/levelling measurements.
Here, the SH method is used to make the HC for the RTM correction to the gravity anomaly in the removal procedure. This is made because that the gravity anomaly with the HC based on the SH method achieves the best performance in geoid height determination.
As shown in Fig. 10, the STD values fluctuate first and then tends to stabilize with increasing truncation degree. It is obvious that the geoid heights directly calculated in the RCR framework have a higher accuracy than that interpolated from a geoid grid. This is seen from the smaller STD values of \(\Delta N_{{{\text{OBS}}}}^{{{\text{HC}}\_{\text{SH}}\_{\text{station}}}}\) compared to STD values of \(\Delta N_{{{\text{OBS}}}}^{{{\text{HC}}\_{\text{SH}}}}\) with the truncation degree larger than 380. The geoid height directly calculated at the station achieves the best accuracy at truncation degree 630 with the STD value of ~ 1.62 cm when only considering the HC for the RTM correction to the gravity anomaly (Table 4). This value reduces to ~ 1.56 cm when additionally considering the HC for the RTM correction to the height anomaly. These values are much improved compared to results obtained from the interpolation of a geoid grid. Therefore, it is recommended to compute the geoid heights at GPS/levelling stations directly.
STD values with the increasing of the truncation degree of the Wong and Gore modified kernel. \(\Delta N_{{{\text{OBS}}}}^{{{\text{HC}}\_{\text{SH}}\_{\text{station}}}}\) indicates the STD value of differences between directly estimated geoid heights at stations and GNSS/levelling measurements, \(\Delta N_{{{\text{OBS}}}}^{{{\text{HC}}\_{\text{SH}}}}\) is the STD value of differences between interpolated geoid heights at stations and GNSS/levelling measurements. \(\Delta N_{{{\text{OBS}}}}^{{{\text{HC}}\_{\text{SH}}}}\) is the same as that as shown in Fig. 9
7 Conclusions
The harmonic correction is one of the main quantities that affects the accuracy of RTM technique in high-frequency gravity field recovery and subsequently affects the results of geoid determination. This study reviews and compares the expressions of HC for RTM corrections to gravity anomaly and height anomaly with various methods, i.e. the condensation method, the regularized downward continuation method of TS, the regularized downward continuation method of SH, the complete method, and the Kadlec’s method. In addition, the effects of HC on gravity field synthesis and on regional geoid determination in the RCR framework are firstly studied in this work.
In the framework of the condensation method, we have derived expressions of HC for the RTM correction to gravitational attraction using various approximations. In addition to the expression of HC with the UBP approximation (Forsberg 1984), we have derived the HC expressions under the LBP, BS, and LBS approximations firstly. These derivations provide a comprehensive understanding of errors in HC due to various approximations. The comparisons among HCs under various approximations indicate that errors due to the UBP approximation could be ignored in the mGal-level gravity field determination. This is confirmed in the extreme cases of the Himalaya area and in the gravity field determination of the Colorado area with approximation errors of 0.01 mGal in terms of RMS.
Numerical experiments were conducted to assess the performance of various HC methods, i.e. condensation method, TS method, SH method, and complete method, in the gravity field synthesis over the extreme rugged Himalaya mountain area. The results indicate that the HCs based on the TS method and the SH method are in the same order of magnitude with the HC based on the condensation method. The largest differences are within ~ 30 mGal for the HC based on the TS method and ~ 10 mGal for the HC based on the SH method in extreme cases. Large differences mainly occurred over very rugged areas. The HC based on the SH method shows the best performance in the gravity field synthesis. However, the HC based on the complete method shows a large difference with that based on the condensation method, TS method and SH method and achieve the worse results in the gravity field synthesis. The differences would be larger than 100 mGal over very rugged areas. In an effort to enhance the results obtained from the complete method, both Klees et al. (2023) and our study independently investigated the underlying reasons behind the large differences involved by the original complete method. Subsequently, new formulae were separately in each study to address these issues. In Klees et al. (2023), they focused on resolving the error associated with the boundary problem and derived a closed-form expression for HC that was found to be almost equivalent to the HC obtained using the UBP method. In our study, we introduce a new procedure to improve the original complete method. Our method involves a three-step approach within the framework of the complete method, as described in detail in S4 of ESM. A key improvement of our method is that it addresses the errors caused by changes in Earth's masses during the downward/upward continuation processes. Importantly, our method yields results that are consistent with those obtained using the TS method. The performance of UBP and TS methods in the gravity field synthesis confirms the effectiveness and reliability of these approaches.
In addition, the performances of HC with various methods in the RCR procedure for regional geoid determination are studied over the Colorado area. The geoid height grids at 14 cases are determined and validated through the comparison with GNSS/levelling measurements at 222 benchmarks. In the general case that the HC is made only for the RTM correction to gravity anomaly in the removal procedure, the HC with the SH method achieves the best performance, followed by the HC with the condensation method. The results could be slightly improved when the HC for the RTM correction to the height anomaly is included in the restore procedure. The accuracy of determined geoid heights is ~ 2 cm when using BS method. However, the geoid heights at specific points, e.g. geoid heights at GNSS/levelling points, are actually obtained from the geoid grids. This involves interpolation errors in the geoid heights at station points. With rapid development of computing power, it is possible to compute geoid heights directly at stations. This is tested and proved that computing geoid heights at stations improved the results. The accuracy is improved to ~ 1.56 cm. However, the validation results and conclusions are limited by the minority, non-homogeneously distribution, and accuracy of GPS/levelling datasets. Furthermore, the geoid height are computed from height anomaly with the quasigeoid-to-geoid method in Wang et al. (2020), which depends on the constant density assumption. This also affects the final results.
Based on the principles and numerical experiments of different methods, it is evident that the classical condensation method is not only the most efficient but also achieves moderate results. Furthermore, both Kadlec's method and the closed-form complete method yield the same equation as the classical condensation method but from different theoretical frameworks. This confirms the validity of the expression of HC obtained using the classical condensation method. Although the SH method for HC demonstrates the best performance in gravity field synthesis and regional geoid determination when the indirect effect is ignored, its implementation involves significant costs, and the improvement compared to the classical condensation method is minimal, e.g. sub-mGal improvement for gravity synthesis and sub-cm for geoid. Considering the indirect effect involved by HC in the restore procedure would slightly improve the results, and the BS method and the closed-form complete method yield the best results using a simple formula. They are much more efficient compared to the SH method. Consequently, the classical condensation method is still sufficient for computing the HC for gravitational attraction in most practical applications. However, it is advisable to consider the SH method when sub-mGal-level accuracy is required for gravity synthesis.
References
Bucha B, Janák J, Papčo J, Bezděk A (2016) High-resolution regional gravity field modelling in a mountainous area from terrestrial gravity data. Geophys J Int 207(2):949–966. https://doi.org/10.1093/gji/ggw311
Bucha B, Hirt C, Kuhn M (2019a) Cap integration in spectral gravity forward modelling: near-and far-zone gravity effects via Molodensky’s truncation coefficients. J Geodesy 93(1):65–83. https://doi.org/10.1007/s00190-018-1139-x
Bucha B, Hirt C, Yang M, Kuhn M, Rexer M (2019b) Residual terrain modelling (RTM) in terms of the cap-modified spectral technique: RTM from a new perspective. J Geodesy 93(10):2089–2108. https://doi.org/10.1007/s00190-019-01303-4
Bucha B., Kuhn M. (2023) Integration radius as a parameter separating convergent and divergent spherical harmonic series of topography-implied gravity. In: IUGG, the 28th General Assembly, 11–20 July, Berlin, presentation. https://doi.org/10.57757/IUGG23-0423
Ďuríčková Z, Janák J (2016) RTM-based omission error corrections for global geopotential models: case study in Central Europe. Stud Geophys Geod 60(4):622–643. https://doi.org/10.1007/s11200-015-0598-2
Elhabiby M, Sampietro D, Sanso F, Sideris M (2009) BVP, global models and residual terrain correction. In: Observing our changing earth. Springer, pp 211–217. https://doi.org/10.1007/978-3-540-85426-5_25
Forsberg R, Tscherning CC (1981) The use of height data in gravity field approximation by collocation. J Geophys Res 86(B9):7843–7854. https://doi.org/10.1029/JB086iB09p07843
Forsberg R, Tscherning CC (1997) Topographic effects in gravity field modelling for BVP. Springer, Berlin, pp 239–272. https://doi.org/10.1007/BFb0011707
Forsberg R (1984) A study of terrain reductions, density anomalies and geophysical inversion methods in gravity field modelling. OSU report 355, Ohio State University, Columbus, Department Of Geodetic Science and Surveying
Förste C, Bruinsma SL, Abrikosov O, Lemoine JM, Marty JC, Flechtner F, Balmino G, Barthelmes F, Biancale R (2014) EIGEN-6C4 the latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. GFZ Data Services. https://doi.org/10.5880/icgem.2015.1
Harrison J, Dickinson M (1989) Fourier transform methods in local gravity modeling. Bulletin Géodésique 63(2):149–166. https://doi.org/10.1007/BF02519148
Heck B, Seitz K (2007) A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. J Geodesy 81(2):121–136. https://doi.org/10.1007/s00190-006-0094-0
Heiskanen WA, Moritz H (1967) Physical geodesy. W. H. Freeman and Company, San Francisco
Hirt C (2018) Artefact detection in global digital elevation models (DEMs): the maximum slope approach and its application for complete screening of the SRTM v4. 1 and MERIT DEMs. Remote Sens Environ 207:27–41. https://doi.org/10.1016/j.rse.2017.12.037
Hirt C, Kuhn M (2017) Convergence and divergence in spherical harmonic series of the gravitational field generated by high-resolution planetary topography—a case study for the Moon. J Geophys Res 122:1727–1746. https://doi.org/10.1002/2017JE005298
Hirt C, Claessens S, Fecher T, Kuhn M, Pail R, Rexer M (2013) New ultra-high resolution picture of Earth’s gravity field. Geophys Res Lett 40(16):4279–4283. https://doi.org/10.1002/grl.50838
Hirt C, Bucha B, Yang M, Kuhn M (2019a) A numerical study of residual terrain modelling (RTM) techniques and the harmonic correction using ultra-high-degree spectral gravity modelling. J Geodesy 93:1469–1486. https://doi.org/10.1007/s00190-019-01261-x
Hirt C, Yang M, Kuhn M, Bucha B, Kurzmann A, Pail R (2019b) SRTM2gravity: an ultra-high resolution global model of gravimetric terrain corrections. Geophys Res Lett 46(9):4618–4627. https://doi.org/10.1029/2019GL082521
Hofmann-Wellenhof B, Moritz H (2006) Physical geodesy. Springer
Hotine M (1969) Mathematical geodesy. U.S. Department of Commerce, Washington
Kadlec M (2011) Refining gravity field parameters by residual terrain modeling. PhD thesis, University of West Bohemia, Pilsen, Czech Republic
Klees R, Wittwer T (2007) Local gravity field modelling with multipole wavelets. In: Tregoning P, Rizos C (eds) Dynamic planet monitoring and understanding a dynamic planet with geodetic and oceanographic tools. In: International association of geodesy symposia, vol 130, pp 303–308
Klees R, Seitz K, Slobbe D (2022) The RTM harmonic correction revisited. J Geodesy 96(6):39. https://doi.org/10.1007/s00190-022-01625-w
Klees R, Seitz K, Slobbe C (2023) Exact closed-form expressions for the complete RTM correction. J Geodesy 97(4):33. https://doi.org/10.1007/s00190-023-01721-5
Li X (2018) Using radial basis functions in airborne gravimetry for local geoid improvement. J Geodesy 92:471–485. https://doi.org/10.1007/s00190-017-1074-2
Li X, Wang Y (2011) Comparisons of geoid models over Alaska computed with different Stokes’ kernel modifications. J Geodetc Sci 1(2):136–142. https://doi.org/10.2478/v10156-010-0016-1
Lin M, Li X (2022) Impacts of using the rigorous topographic gravity modeling method and lateral density variation model on topographic reductions and geoid modeling: a case study in Colorado, USA. Surv Geophys 43:1497–1538. https://doi.org/10.1007/s10712-022-09708-1
Lin M, Denker H, Müller J (2014) Regional gravity field modeling using free-positioned point masses. Stud Geophys Geod 58:207–226. https://doi.org/10.1007/s11200-013-1145-7
Lin M, Denker H, Müller J (2019) A comparison of fixed- and free-positioned point mass methods for regional gravity field modeling. J Geodyn 125:32–47. https://doi.org/10.1016/j.jog.2019.01.001
Liu Q, Schmidt M, Sánchez L, Willberg M (2020) Regional gravity field refinement for (quasi-) geoid determination based on spherical radial basis functions in Colorado. J Geodesy 94(10):99. https://doi.org/10.1007/s00190-020-01431-2
Märdla S, Ågren J, Strykowski G, Oja T, Ellmann A, Forsberg R, Bilker-Koivula M, Omang O, Paršeliūnas E, Liepinš I, Kaminskis J (2017) From discrete gravity survey data to a high-resolution gravity field representation in the Nordic-Baltic region. Mar Geodesy 40(6):416–453. https://doi.org/10.1080/01490419.2017.1326428
Matsuo K, Kuroishi Y (2020) Refinement of a gravimetric geoid model for Japan using GOCE and an updated regional gravity field model. Earth Planets Space 72(1):33. https://doi.org/10.1186/s40623-020-01158-6
Moritz H (1980) Advanced physical geodesy. Herbert Wichmann Verlag, Karlsruhe
Omang OC, Tscherning CC, Forsberg R (2012) Generalizing the harmonic reduction procedure in residual topographic modeling. In: VII Hotine-Marussi symposium on mathematical geodesy, Springer, pp 233–238. https://doi.org/10.1007/978-3-642-22078-4_35
Pavlis NK, Holmes SA, Kenyon S, Factor JK (2012) The development and evaluation of the earth gravitational model 2008 (EGM2008). J Geophys Res 117(B4):B04406. https://doi.org/10.1029/2011JB008916
Rexer M, Hirt C (2015) Spectral analysis of the Earth’s topographic potential via 2D-DFT: a new data-based degree variance model to degree 90,000. J Geodesy 89(9):887–909. https://doi.org/10.1007/s00190-015-0822-4
Rexer M (2017) Spectral solutions to the topographic potential in the context of high-resolution global gravity field modelling. PhD thesis. Technische Universität München, München, Germany
Roman DR (1993) Gravity field approximations using the Hardy predictor with constraints. Ohio State University, Columbus
Roman DR (1999) An integrated geophysical investigation of Greenland’s tectonic history. Ohio State University, Columbus
Schmidt M, Fengler M, Mayer-Guerr T, Eicker A, Kusche J, Sanchez L, Han SC (2007) Regional gravity field modeling in terms of spherical base functions. J Geodesy 81(1):17–38. https://doi.org/10.1007/s00190-006-0101-5
Schwabe J, Scheinert M, Dietrich R, Ferraccioli F, Jordan T (2012) Regional geoid improvement over the Antarctic Peninsula utilizing airborne gravity data. In: Geodesy for planet earth, Springer, pp 457–464. https://doi.org/10.1007/978-3-642-20338-1_55
Sjöberg LE (2005) A discussion on the approximations made in the practical implementation of the remove-compute-restore technique in regional geoid modelling. J Geodesy 78(11):645–653. https://doi.org/10.1007/s00190-004-0430-1
Smith DA (2022) Interpolation from a grid of standard deviations, NOAA Technical Memorandum NOS NGS
Šprlák M, Han SC, Featherstone WE (2020) Spheroidal forward modelling of the gravitational fields of 1 Ceres and the Moon. Icarus 335:113412. https://doi.org/10.1016/j.icarus.2019.113412
Tscherning CC, Rapp RH (1974) Closed covariance expressions for gravity anomalies, geoid undulations, and deflections of the vertical implied by anomaly degree-variance models. Reports of the Department of Geodetic Science No. 208, The Ohio State University, Columbus
van Westrum D, Ahlgren K, Hirt C, Guillaume S (2021) A geoid slope validation survey (2017) in the rugged terrain of Colorado, USA. J Geodesy 95:9. https://doi.org/10.1007/s00190-020-01463-8
Vaníček P, Novák P, Martinec Z (2002) Geoid, topography, and the Bouguer plate or shell. J Geodesy 75:210–215. https://doi.org/10.1007/s001900100165
Voigt C, Denker H (2007) A study of high frequency terrain effects in gravity field modelling. In: Dergisi H (ed) 1st International symposium of the international gravity field service, “Gravity Field of the Earth”, Ankara, Turkey, vol 18, pp 342–347
Wang Y, Li X, Ahlgren K, Krcmaric J (2020) Colorado geoid modeling at the US National Geodetic Survey. J Geodesy 94:106. https://doi.org/10.1007/s00190-020-01429-w
Wang Y, Sánchez L, Ågren J, Huang J, Forsberg R, Abd-Elmotaal HA, Ahlgren K, Barzaghi R, Bašić T, Carrion D, Claessens S, Erol B, Erol S, Filmer M, Grigoriadis VN, Isik MS, Jiang T, Koç Ö, Krcmaric J, Li X, Liu Q, Matsuo K, Natsiopoulos DA, Novák P, Pail R, Pitoňák M, Schmidt M, Varga M, Vergos GS, Véronneau M, Willberg M, Zingerle P (2021) Colorado geoid computation experiment: overview and summary. J Geodesy 95(12):127. https://doi.org/10.1007/s00190-021-01567-9
Willberg M, Zingerle P, Pail R (2019) Residual least-squares collocation: use of covariance matrices from high-resolution global geopotential models. J Geodesy 93(9):1739–1757. https://doi.org/10.1007/s00190-019-01279-1
Wong L, Gore R (1969) Accuracy of geoid heights from modified Stokes kernels. Geophys J R Astr Soc 18:81–91. https://doi.org/10.1111/j.1365-246X.1969.tb00264.x
Wu Y, Abulaitijiang A, Featherstone W, McCubbine J, Andersen O (2019) Coastal gravity field refinement by combining airborne and ground-based data. J Geodesy 93(12):2569–2584. https://doi.org/10.1007/s00190-019-01320-3
Yamazaki D, Ikeshima D, Tawatari R, Yamaguchi T, O’Loughlin F, Neal JC, Sampson CC, Kanae S, Bates PD (2017) A high-accuracy map of global terrain elevations. Geophys Res Lett 44(11):5844–5853. https://doi.org/10.1002/2017GL072874
Yang M, Hirt C, Tenzer R, Pail R (2018) Experiences with the use of mass-density mapsin residual gravity forward modelling. Stud Geophys Geod 62(4):596–623. https://doi.org/10.1007/s11200-017-0656-z
Yang M, Hirt C, Pail R (2020) TGF: a new MATLAB-based software for terrain-related gravity field calculations. Remote Sens 12(7):1063. https://doi.org/10.3390/rs12071063
Yang M, Hirt C, Wu B, Deng X, Tsoulis D, Feng W, Wang C, Zhong M (2022) Residual terrain modelling: the harmonic correction for geoid heights. Surv Geophys 43:1201–1231. https://doi.org/10.1007/s10712-022-09694-4
Yang M (2020) Investigation of the residual terrain modelling (RTM) technique for high-frequency gravity calculations. PhD thesis, Technische Universität München, München, Germany
Zingerle P, Pail R, Gruber T, Oikonomidou X (2020) The combined global gravity field model XGM2019e. J Geodesy 94(7):66. https://doi.org/10.1007/s00190-020-01398-0
Acknowledgements
Meng Yang was supported by the National Natural Science Foundation of China (Grant No. 42104083), and the Natural Science Foundation of Guangdong Province, China (Grant No. 2021A1515011425). Miao Lin was supported by the National Natural Science Foundation of China (Grant No. 42004009). We are grateful for internal and constructive reviews by Prof. Roland Klees, Dr. Dennis Milbert and Dr. Blažej Bucha, and by the anonymous reviewers of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Yang, M., Li, X., Lin, M. et al. On the harmonic correction in the gravity field determination. J Geod 97, 106 (2023). https://doi.org/10.1007/s00190-023-01794-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00190-023-01794-2