Residual Terrain Modelling: The Harmonic Correction for Geoid Heights

Abstract

The harmonic correction (HC) is one of the key quantities when using residual terrain modelling (RTM) for high-frequency gravity field modelling. In the RTM technique, high-frequency topographic gravitational signals are obtained through removing gravitational effects of a long-wavelength reference surface, e.g., MERIT2160. There might be points located below the reference surface. In such cases, the RTM gravity field is calculated in the non-harmonic condition, HC is therefore required. Over past decades, though various methods have been proposed to handle the HC issue for the RTM technique, most of them were focused on the HC for RTM gravity anomaly rather than for other gravity functionals, such as RTM geoid height. In practice, the HC for RTM geoid height was generally assumed to be negligible, but a detailed quantification was missing for present-day RTM computations. This might cause large errors in the regional geoid determination over rugged areas. In this study, we derive HC expressions for the RTM geoid height in the framework of the classical condensation method. The HC terms are derived under four different assumptions separately: residual masses approximated by an unlimited Bouguer plate, residual masses approximated by a limited Bouguer plate which overcomes the mass inconsistency effect, residual masses approximated by a Bouguer shell which overcomes the effect of planar approximation, and residual masses approximated by a limited Bouguer shell which overcomes the errors induced by both planar approximation and mass-inconsistency. The errors due to various approximations in HC terms are investigated through comparison among various terms. Besides, HC terms are computed using an expansion up to degree and order 2159. Our results show that HC for RTM geoid height is less 1 mm and could be ignored over $\sim 99$% of continental areas, but be of great significance for regional geoid determination over mountain areas, e.g., more than 10 cm effect over very rugged areas. The validation through comparison with terrestrial measurements and a baseline solution of the RTM technique proves that the HC terms provided in this study can improve the accuracy of RTM geoid heights and are expected to be useful for applications of the RTM technique in regional and global gravity field modelling.

FormalPara Article Highlights

• Provide expressions of harmonic correction for the RTM geoid height under various approximations

• Investigate the errors due to the planar approximation and the mass-inconsistency effect in harmonic correction

• Evaluate the quantification of harmonic correction for the RTM geoid heights on the Earth’s surface

1 Introduction

Residual Terrain Modelling (RTM), as a key technique to retrieve the terrain-generated high-frequency gravity field signal, has been widely applied to a vast number of applications in physical geodesy and geophysics, such as to the smoothing of terrestrial and airborne gravity field observations prior to their continuation and interpolation in the framework of remove-compute-restore procedure (Forsberg and Tscherning 1981; Mainville et al. 1995; Forsberg and Tscherning 1997; Yildiz et al. 2012; Forsberg et al. 2014; Bucha et al. 2016; Wu et al. 2019; Willberg et al. 2019, 2020), to the augmentation of the global gravity field models (GGMs) by retrieving gravity functionals in high-frequency bands (Hirt et al. 2019), to ultra-high resolution gravity field determination of the Earth (Hirt et al. 2013; Zingerle et al. 2020) and of other planets (Hirt and Featherstone 2012; Hirt et al. 2012; Li et al. 2015), to the global height datum unification problem (Gruber et al. 2012; Grombein et al. 2017; Willberg et al. 2017; Vergos et al. 2018), to the determination of the combined GGMs as fill-in data, especially over remote countries where devoid of terrestrial measurements (Pavlis et al. 2007, 2012), or to the geophysical applications, such as gravity reduction for detection of near-surface mass-density anomalies (AllahTavakoli et al. 2015; Simav 2020; Tziavos et al. 2010).

Fig. 1

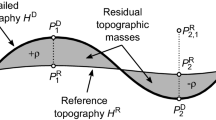
Principle of the Residual Terrain Modelling (RTM) technique (Forsberg 1984; Bucha et al. 2019; Yang 2020). DS, RS, and SL/E represent the detailed topographic surface (DS), reference surface (RS) and sea level/ellipsoid (SL/E), respectively. The $P^{\mathrm {D}}_1$ and $P^{\mathrm {D}}_2$ represent points on the Earth’s surface, and $P^{\mathrm {D}}_1$ is located above the reference surface while $P^{\mathrm {D}}_2$ below the reference surface. Points $P^{\mathrm {R}}_1$ and $P^{\mathrm {R}}_2$ are the respective points on the reference surface of $P^{\mathrm {D}}_1$ and $P^{\mathrm {D}}_2$

The basic idea of the RTM technique is presented in Fig. 1 (Forsberg 1984). A detailed representation of the Earth’s surface, e.g., through a high-resolution digital elevation model (DEM) (Merryman Boncori 2016; Fujisada et al. 2012; Jarvis et al. 2008; Tadono et al. 2014; Yamazaki et al. 2017; Wessel et al. 2018), is generally high-pass filtered by removing a long-wavelength reference surface often directly calculated from a detailed DEM through spherical harmonic analysis (Hirt et al. 2019a). With the assumption of spectral consistency between filtering in the gravitational and geometric domains, the RTM technique delivers the high-frequency spectral contents of the topography implied gravitational field signal (Rexer et al. 2018; Bucha et al. 2019). As is shown in Fig. 1, the computation point, e.g., $P^{\mathrm {D}}_2$, may be located below the reference surface. In such cases, the computation point is located in the masses, therefore, the directly calculated gravitational functionals from RTM cannot be used to describe the Earth’s external gravity field (Forsberg 1984, 1993; Bucha et al. 2019; Hirt et al. 2019a). Therefore, a harmonic correction (HC) is required to achieve harmonic condition which is almost exclusively required for the purpose of physical geodesy.

Over past decades, many efforts have been taken to reduce the effect of the “non-harmonicity” problem in the RTM technique when the computation points reside inside the reference topography (Forsberg and Tscherning 1981; Forsberg 1984; Harrison and Dickinson 1989; Elhabiby et al. 2009; Kadlec 2011; Omang et al. 2012; Bucha et al. 2016; Root et al. 2016; Duríčková and Janák 2016) (Bucha et al. 2019; Hirt et al. 2019a). These studies can be divided into three different categories:

• 1 the treatment of HC being avoided by involving some numerical methods. Here, the RTM gravity field is divided into two parts, the full-scale gravity signal implied by the detailed topography depending on global numerical integration in the spatial domain and its low-pass filtered version of the reference topography and related ultra-high frequency correction relying on spectral gravity forward modelling (SGM) (Bucha et al. 2019; Hirt et al. 2019a, 2019; Yang 2020). Because the computation points are located outside the detailed topography, the global numerical integration outside the Earth satisfies the harmonic condition. Besides, the SGM relies on the external spherical harmonic analysis and synthesis, the generated gravity field always represents the Earth’s external gravity field. Therefore, the “non-harmonicity problem” is well handled in such case. This method has been applied in the RTM gravity anomaly/disturbance recovering and improved the accuracy of RTM technique down to a sub-mGal level (Hirt et al. 2019a, 2019). However, it has not been used for RTM geoid height calculation up to the present. The treatment of HC can also be avoided by splitting the RTM gravity signal into four constituents, the effect of a Bouguer layer of thickness $H(P^{\mathrm {D}}_2)$ (from the detailed DEM) and corresponding terrain effect referring to the Earth’s surface, and the Bouguer effect of thickness $H(P^{\mathrm {R}}_2)$ and corresponding terrain effect referring to the reference surface (Kadlec 2011; Duríčková and Janák 2016). This method has been tested based on terrestrial measurements of geoid height, gravity anomaly and gravity gradient over Czech Republic (Kadlec 2011). Though the treatment of HC in these methods is avoided, the high numerical cost generally makes them challenging (Bucha et al. 2019; Hirt et al. 2019a, 2019).

• 2 the HC can be evaluated by means of the regularized analytical downward continuation (Forsberg and Tscherning 1997), e.g., via a Taylor series expansion (Harrison and Dickinson 1989; Elhabiby et al. 2009; Omang et al. 2012; Bucha et al. 2016). This method generally requires numerical integration of higher-order derivatives at computation points, for example, the third- or even higher-order derivatives for the evaluation of the HC for the second-order derivatives of the gravitational potential. Though it is possible to calculate the third-order derivatives of the gravitational potential of a tesseroid (Deng and Shen 2017, 2018a, b, 2019) and of a prism (Nagy et al. 2000; D’Urso 2017) directly, or from other gravitational functionals (Šprlák and Novák 2015), the calculation time of HC based on the analytical continuation increases with more computation points and detailed DEM models involved.

• 3 the classical condensation method (Forsberg and Tscherning 1981; Forsberg 1984). The residual masses between the computation point and the reference surface are approximated by an infinite Bouguer plate and then are compressed into an infinitesimal thick mass layer immediately below the computation point. The HC for RTM gravity anomaly is the difference between the gravity anomaly generated by this Bouguer plate and the gravity anomaly generated by its compressed infinitesimal thick mass layer. As a function of residual height at the computation point, the calculation of HC with the classical condensation method is much more efficient. Furthermore, the condensation method is capable of achieving mGal-level accuracy over the most rugged area of the Earth (Hirt et al. 2019a, 2019). Therefore, as one of the classical methods, the mass condensation method has been widely used for HC over the past decades (Forsberg and Tscherning 1997; Tziavos et al. 2010; Hirt et al. 2013; Yang et al. 2018, 2020). However, it suffers from two main problems:

  • (a) In terms of the classical mass condensation method, only the formula of HC for RTM gravity anomaly exists, which means that the HC terms for the other gravitational functionals (e.g., RTM geoid height) need to be defined. The HC for RTM geoid height was generally assumed to be negligible (Forsberg 1984), but quantification is not available. This brings great uncertainty in practical applications. Therefore, with regards to the condensation method, the formula of HC for geoid height is missing, and quantification is required when a reference topography with spherical harmonic coefficients (SHCs) is utilized to degree and order 2159 (Hirt et al. 2019a).

  • (b) In the classical condensation method for HC, the masses below the reference surface and above the Earth’s surface is approximated by an unlimited Bouguer plate. There are two main problems in this method that might affect the accuracy of HC and further affect the accuracy of the recovered gravitational field (Bucha et al. 2019; Hirt et al. 2019; Yang 2020): 1) only masses within a limited zone around the computation point are considered in the RTM technique, while infinite masses are involved by the infinite Bouguer plate model; 2) the planar assumption ignores the Earth’s curvature. Hirt et al. (2019a) promoted that the mass inconsistency and planar approximation would affect the accuracy of HC terms and should be evaluated. The task to study the errors due to mass inconsistency and the planar assumption is of great significance to the accurate evaluation of HC in the framework of the classical condensation method and gives insights into its applicability.

In terms of HC for RTM geoid height, Forsberg and Tscherning (1997) showed that HC for RTM geoid height is zero. This work was conducted through moving down the unlimited Bouguer plate and calculated differences between generated gravitational potentials before and after moving down. Theoretically, the infinite gravitational potentials are generated before and after moving down, therefore causing zero differences. However, it ignored the very smaller differences, therefore underestimating the value of HC for the RTM geoid height. This will be improved in this study. Kadlec (2011) put forward the problem of HC for RTM geoid height and also for the radial tensor component. They avoided HC by dividing RTM geoid height into four parts as introduced in the method 1. However, it endures a high numerical cost. Omang et al. (2012) gave the HC expression for RTM height anomalies as $\zeta _{\mathrm {HC}}=-4\pi G\rho \Delta h^2/\gamma$, where G denotes the gravitational constant, $\rho$ the mass density, $\Delta h$ the RTM height and $\gamma$ the normal gravity on the ellipsoid. This is obtained following from continuation theory and assumed the vertical gradient of potential is a constant $-4\pi G\rho \Delta h$. Actually, following the theory of Omang et al. (2012) deriving the above formula, the gradient of potential is a function of variable $\Delta h$ varying from reference surface to the Earth’s surface. More rigorously, it is $\partial V/\partial r$.

As the main contribution of this work, the formulas of HC for the RTM geoid height are derived relying on various approximations: (1) with the residual masses approximated by an unlimited Bouguer plate (HC-UBP) which is in the scope of the classical condensation method; (2) residual masses being approximated by a limited Bouguer plate (HC-LBP); (3) residual masses being approximated by a Bouguer shell (HC-BS); and (4) the method how to calculate HC under limited Bouguer shell approximation (HC-LBS) will be introduced. When the radius of the LBS equals the integration radius considered in the RTM technique, the mass inconsistency effect should be reduced and its magnitude would decrease with the integration radius increasing. The differences between HC-UBP and HC-LBP indicate the effect of mass inconsistency on HC in the classical condensation method. Similarly, the HC-BS terms are derived with residual mass approximated by a spherical shell and including the effect of the Earth’s curvature. Therefore, the effect of the planar assumption on HC terms could be ignored in the HC-BS terms. The differences between HC-UBP and HC-BS provide insights into the effect of planar approximation on HC terms in the classical condensation method.

The paper is organized as follows. The formulas of HC for the RTM geoid height are firstly derived with the residual masses approximated by an unlimited Bouguer plate (Sect. 2.1), residual masses are approximated by a limited Bouguer plate (Sect. 2.1). Sect. 2.2 describes the HC-BS method, where the residual masses are approximated by a Bouguer shell. Section 2.3 shows the calculation of HC based on the limited Bouguer shell approximation. The errors due to mass inconsistency (Sect. 3.1) and planar approximation (Sect. 3.2) are investigated. The quantification of HC with a reference surface computed for $N=2159$ on the Earth’s surface is provided in Sect. 3.3. The new formulas are validated in Sect. 4 through comparisons with an artificial solution of RTM geoid height which is devoid of the harmonic correction and with terrestrial measurements over New Zealand and in the Bavarian Alps in Germany. Finally, the main conclusions and outlooks on future studies are given in Sect. 5.

2 Methodology

2.1 HC Terms in the Unlimited Bouguer Plate Approximation and Limited Bouguer Plate Approximation

In this section, P denotes the computation point when it is located below the reference surface and the subscript $'+'$ indicates that the point adheres to or is just above the Earth’s surface. The magnitude of height difference between $P_+$ and its respective point $P^{\mathrm {R}}$ on the reference surface is h. In the scope of unlimited Bouguer plate approximation (left figure of Fig. 2), the masses between the surface defined by the computation point $P_+$ and the surface defined by $P^{\mathrm {R}}$ on the reference surface are approximated by an unlimited Bouguer plate of constant thickness h and constant density $\rho$. In order to solve the “non-harmonicity problem”, the masses represented by the unlimited Bouguer plate above the computation point are compressed into a single mass layer of density $\rho h$ and infinitesimal thickness, and moved just below the computation point $P_+$ as shown in Fig. 2. Thus, the computation point is located outside the masses defined by the single mass layer. Therefore, the single mass layer generated gravitational potential at computation point $P_+$ satisfies the harmonic condition. The HC-UBP terms are derived as the differences between gravitational functionals due to the unlimited Bouguer plate at point $P_+$ (left figure in Fig. 2) and the gravitational functionals due to the single mass layer at point $P_+$ (right figure in Fig. 2).

Fig. 2

Unlimited Bouguer plate after Kadlec (2011) and respective unlimited mass layer. Left figure: unlimited Bouguer plate with $P_+$ and $P^{\mathrm {R}}$ indicating the computation point on and above the bottom of the plate and its respective point on the top of the plate; Right figure: an unlimited mass layer of infinitesimal thickness with $P_+$ indicating the calculating points residing on and above this layer

In order to solve the infinite problem, one typically defines the limits into a bounded domain. Regarding the unlimited Bouguer plate, when the plate is truncated at radius R from the computation point, the limited Bouguer plate as a shape of a cylinder is obtained and shown in Fig. 3. In the right-handed Cartesian coordinate system, the origin lies on the top centre of the cylinder, the z axis is in the vertical direction and points outwards. The coordinates of any computation point P lying on the z axis are (0, 0, z). The position of infinitesimal mass-elements describing the integration is denoted as $(x',y',z')$ with $x'=r' \cos \varphi '$, $y'=r' \sin \varphi '$ and $(r',\varphi ')$ the polar coordinates of integration masses. The gravitational potential at P induced by this cylinder is (Hofmann-Wellenhof and Moritz 2006; Na et al. 2015):

$$\begin{aligned} V^{\mathrm {LBP}}(P)=G\rho \int \limits _{0}^{2\pi }\int \limits _{0}^{R}\int \limits _{-h}^{0}\frac{r'}{l}dz'dr'd\varphi ' \end{aligned}$$

(1)

where G is the gravitational constant. With l indicating the distance between computation point and integration mass-element, it is

$$\begin{aligned} l=\sqrt{r'^2+(z'-z)^2} \end{aligned}$$

(2)

In case the computation point is located above the bottom and below the top of the cylinder, $z<0$ and $z+h>0$. The solution of Eq. (1) becomes (Hofmann-Wellenhof and Moritz 2006; Kadlec 2011; Na et al. 2015)

$$\begin{aligned} V^{\mathrm {LBP}}(P)=\pi G\rho [R^2 \ln \frac{l_h+h+z}{l_0+z}-h^2+h(l_h-2z)-2z^2+z(l_h-l_0 )]; \end{aligned}$$

(3)

where $l_h=\sqrt{R^2+(z+h)^2}$ and $l_0=\sqrt{R^2+z^2}$.

For a computation point $P_+$, where $z+h\rightarrow 0^+$, the above expression becomes

$$\begin{aligned} V^{\mathrm {LBP}}(P_+)=\lim _{z+h\rightarrow 0^+}V^{\mathrm {LBP}}(P)=\pi G\rho (R^2 \ln \frac{R}{\sqrt{R^2+h^2}-h}-h^2+h\sqrt{R^2+h^2}); \end{aligned}$$

(4)

Fig. 3

Cylinder or limited Bouguer plate in right-handed Cartesian coordinate system xyz. The cylinder is of radius R and thickness h. $P_+$ and $P^{\mathrm {R}}$ indicate the computation point on and above the bottom of cylinder and its respective point on the top (Hofmann-Wellenhof and Moritz 2006; Kadlec 2011; Na et al. 2015)

In the framework of the condensation method under limited Bouguer plate approximation, the cylinder is compressed into a layer of the disc with a constant radius R, surface density $\rho h$, and infinitesimal thickness. This layer disc is moved down to just below the computation point. The general expression of the gravitational potential and its derivatives due to a disc and the related efficient methods for their calculation were investigated over the past decades (Singh 1977; Krogh et al. 1982; Tsoulis 1999; Hofmann-Wellenhof and Moritz 2006; Tatum 2007; Fukushima 2010).

In this case, the computation point $P_+$ has the coordinate of (0, 0, z), where $z\rightarrow 0_+$. The disc generated gravitational potential at $P_+$ is (Lass and Blitzer 1983; Tsoulis 1999; Hofmann-Wellenhof and Moritz 2006)

$$\begin{aligned} V^{\mathrm {DL}}(P_+)=2\pi G\rho h R \end{aligned}$$

(5)

The HC for RTM geoid height in the limited Bouguer plate approximation is defined as the difference between the disc produced gravitational potential ($V^{\mathrm {DL}}$) at point $P_+$ and the cylinder produced gravitational potential at point $P_+$ ($V^{\mathrm {LBP}}$).

$$\begin{aligned} V^{\text {HC-LBP}}(P_+)= & V^{\mathrm {DL}}(P_+)-V^{\mathrm {LBP}}(P_+) \nonumber \\= & \,2\pi G\rho hR-\pi G\rho \big [R^2\log \frac{R}{\sqrt{R^2+h^2}-h}-h^2+h\sqrt{R^2+h^2}\big ] \end{aligned}$$

(6)

Considering the relationship between the topographic generated geoid height and potential, the HC for RTM geoid height is

$$\begin{aligned} N^{\text {HC-LBP}}(P_+)=\frac{V^{\text {HC-LBP}}(P_+)}{\gamma } \end{aligned}$$

(7)

with $\gamma$ indicating the normal gravity value of respective point on the ellipsoid. When $R\rightarrow \infty$, the cylinder and corresponding disc become an unlimited Bouguer plate and an unlimited mass layer, respectively. Therefore, in the infinite Bouguer plate approximation, the HC for RTM geoid height is defined as the limiting values of Eq. (7) when $R\rightarrow \infty$. There is

$$\begin{aligned} \lim _{R\rightarrow \infty }\frac{h}{R}\rightarrow 0 \end{aligned}$$

(8)

Introducing this limit into Eqs. (6) and (7), we get

$$\begin{aligned} N^{\text {HC-UBP}}(P_+)=\lim _{R\rightarrow \infty }N^{\text {HC-LBP}}(P_+) =\frac{\pi G\rho h^2}{\gamma } \end{aligned}$$

(9)

For the detailed derivation process, please refer to Appendix A.

2.2 HC Terms in the Bouguer Shell Approximation

Fig. 4

Bouguer shell and Bouguer spherical layer (Kadlec 2011; Alex 2005). Left figure: the Bouguer shell is of inner radius $r_1$ and outer radius $r_2$ where $r_2=r_1+h$, and constant density $\rho$. $P_+$ and $P^{\mathrm {R}}$ indicate the computation point residing on and above the inner spherical surface and its respective point on the outer spherical surface. Right figure: a spherical layer of constant radius $r_1$, constant density $\rho (h+\frac{h^2}{r_1})$, and infinitesmal thickness. $P_+$ is the computation point on the spherical surface. $\psi$ is the angle distance between computation point and integration elements in both figures

The geometries of a Bouguer shell and a spherical layer are shown in Fig. 4. In the condensation method using a Bouguer shell approximation, the masses between the computation point $P_+(\varphi ,\lambda ,r)$ and its respective point $P^{\mathrm {R}}$ on the reference surface are approximated by a spherical shell with the inner radius $r_1$ and outer radius $r_2$. The subscript $'+'$ indicates that the computation point is located outside the sphere of radius $r_1$. The gravitational potential V due to this spherical shell is defined as (Alex 2005; Kadlec 2011),

$$\begin{aligned} V^{\mathrm {BS}}(P)=G\rho \int \limits _{0}^{2\pi }\int \limits _{0}^{\pi }\int \limits _{r_1}^{r_2}\frac{r'}{l}dr'd\varphi 'd\lambda ' \end{aligned}$$

(10)

with $l=\sqrt{r^2+r'^2-2rr'\cos \psi }$, and $\cos \psi =\sin \varphi \sin \varphi '+\cos \varphi \cos \varphi '\cos (\lambda '-\lambda )$ indicating the distance and angular distance between $P_+$ and the integration element $(\varphi ',\lambda ',r')$.

In case of $r_1<r<r_2$, the solution of the integral (Alex 2005; Kadlec 2011) follows,

$$\begin{aligned} V^{\mathrm {BS}}(P)= & {} \frac{\pi G\rho }{3r}[(r^2+r_2r-2r_2^2)(r_2-r)-(r^2+rr_1-2r_1^2)(r-r_1)-2r_1^3-3rr_1^2+2r_2^3+3rr_2^2]\nonumber \\= & {} \frac{2\pi G\rho }{3r}(3r_2^2r-r^3-2r_1^3) \end{aligned}$$

(11)

When the computation point is located on the spherical layer defined by radius $r_1$, i.e. for $r\rightarrow r_1$, the above equation array becomes

$$\begin{aligned} V^{\mathrm {BS}}(P_+)=2\pi G\rho (r_2^2-r_1^2) \end{aligned}$$

(12)

In the scope of the condensation method, the spherical shell of thickness h is compressed into a spherical layer (SL) of constant radius $r_1$, density $\rho (h+\frac{h^2}{r_1})$ and infinitesimal thickness. As shown in Fig. 4, the computation point $P_+$ is located outside the spherical layer. The gravitational potential due to this spherical layer at any exterior point is:

$$\begin{aligned} V^{\mathrm {SL}}(P)=G\rho (h+\frac{h^2}{r_1})\int \limits _{0}^{2\pi }\int \limits _{0}^{\pi }\frac{r'\sin \varphi '}{l}d\varphi 'd\lambda ' \end{aligned}$$

(13)

The general solution of Eq. (13) has been given in various studies, e.g., (Tsoulis 1999; Alex 2005; Roy 2008). At the computation point $P_+$, there is

$$\begin{aligned} V^{\mathrm {SL}}(P_+)=4\pi G \rho hr_1+4\pi G \rho h^2 \end{aligned}$$

(14)

The HC-BS at point $P_+$ is the difference between $V^{\mathrm {SL}}(P_+)$ and $V^{\mathrm {BS}}(P_+)$. And the HC-BS terms for RTM geoid height is

$$\begin{aligned} N^{\text {HC-BS}}(P_+)= & {} \frac{V^{\text {HC-BS}}(P_+)}{\gamma } \nonumber \\= & {} \frac{1}{\gamma }\left[ V^{\mathrm {SL}}(P_+)-V^{\mathrm {BS}}(P_+)\right] \nonumber \\= & {} \frac{1}{\gamma }\left[ 4\pi G \rho hr_1+4\pi G \rho h^2-2\pi G\rho (r_2^2-r_1^2)\right] \nonumber \\= & {} \frac{1}{\gamma }\left[ 4\pi G \rho hr_1+4\pi G \rho h^2-2\pi G\rho ((r_1+h)^2-r_1^2)\right] \nonumber \\= & {} \frac{2\pi G\rho h^2}{\gamma } \end{aligned}$$

(15)

2.3 HC Terms in the Limited Bouguer Shell Approximation

Fig. 5

Limited Bouguer shell (left figure) and the respective compressed layer (right figure). In the left figure, $r_1$ and $r_2$ indicate the lower and upper boundaries of the limited Bouguer shell, respectively. $P_+$ and $P^{\mathrm {R}}$ are the computation point residing on and above the lower boundary and its respective point on the upper boundary. $2\Delta \lambda$ and $2\Delta \varphi$ are the latitude differences and longitude differences of boundaries. The right figure is obtained by compressing the masses of the limited Bouguer shell into a surface of infinitesimal thickness

A Bouguer spherical cap with constant thick and constant density is generally used for representation of limited Bouguer shell. Its generated gravity field has been widely discussed in LaFehr (1991), Hensel (1992), Heck and Seitz (2007), and Tenzer et al. (2007). Instead of a spherical cap, a “limited Bouguer shell (LBS)” approximation is applied in this study. As shown in Fig. 5, the masses between the computation point $P_+(\varphi ,\lambda , r_1)$ and its respective point $P^{\mathrm {R}}$ on the reference surface are approximated by a “limited spherical shell” defined by three pairs of surfaces: a pair of concentric spheres ($r_1$, $r_2=r_1+h$), a pair of meridional planes ($\lambda _1=\lambda -\Delta \lambda$,$\lambda _2=\lambda +\Delta \lambda$), and a pair of parallels ($\varphi _1=\varphi -\Delta \varphi$, $\varphi _2=\varphi +\Delta \varphi$). The subscript $'+'$ indicates that the computation point is located outside the inner surface of radius $r_1$. This kind of geometry is a tesseroid horizontally symmetric around the computation point (Anderson 1976). Using the “limited Bouguer shell” rather than the general Bouguer spherical shell is because that this study is a continuous work of Yang (2020) and is expected to be added in the Terrain-related Gravity Field TGF software (Yang et al. 2020). In the TGF software, the integration masses around computation point are divided into four zones. The boundary of each zone is defined by a pair of meridional planes $\lambda \pm \Delta \lambda _{i}$ and a pair of parallels $\varphi \pm \Delta \varphi _{i}$, with $\Delta \lambda _{i}$ and $\Delta \varphi _{i}$ indicating the longitude difference and latitude difference between boundary of i-th zone to the computation point. The masses in various zones are approximated by four kinds of geometries, i.e. polyhedron, prism, tesseroid and point mass separately.

The gravitational potential generated by the tesseroid is (Anderson 1976):

$$\begin{aligned} V^{\mathrm {LBS}}(P_+)=G\rho \int _{\lambda -\Delta \lambda }^{\lambda +\Delta \lambda }\int _{\varphi -\Delta \varphi }^{\varphi {+}\Delta \varphi }\int _{r_1}^{r_2}\frac{r'^2\cos \varphi '}{l}dr'd\varphi 'd\lambda ' \end{aligned}$$

(16)

where $l=\sqrt{r_1^2+r'^2-2r_1r'\cos \psi }$ denotes the Euclidean distance between the computation point $P_+(\varphi ,\lambda {, r_1})$ and the integration point $Q(\varphi ',\lambda ', r')$. $\psi$ is the spherical distance between $P_+$ and Q.

In the scope of the condensation method, the limited spherical shell of thickness h is compressed into a “limited spherical layer” (LSL) of constant radius $r_1$, density $\rho (h+\frac{h^2}{r_1})$ and infinitesimal thickness. As shown in Fig. 4, the computation point $P_+$ is located outside the “limited spherical layer”. Its generated gravitational field is:

$$\begin{aligned} V^{\mathrm {LSL}}(P_+)=G\rho (h+\frac{h^2}{r_1})\int _{\lambda -\Delta \lambda }^{\lambda +\Delta \lambda }\int _{\varphi -\Delta \varphi }^{\varphi {+}\Delta \varphi }\frac{r_1^2\cos \varphi '}{l}d\varphi 'd\lambda ' \end{aligned}$$

(17)

The HC-LBS at point $P_+$ is the difference between $V^{\mathrm {LBS}}(P_+)$ and $V^{\text {HC-BS}}(P_+)$. And the HC-LBS for geoid height is

$$\begin{aligned} N^{\text {HC-LBS}}(P_+)= & {} \frac{V^{\text {HC-LBS}}(P_+)}{\gamma }\nonumber \\= & {} \frac{V^{\text {LSL}}(P_+)-V^{\mathrm {LBS}}(P_+)}{\gamma } \end{aligned}$$

(18)

Though various methods have been provided for the numerical solution of Eqs. (16) and (17) (Heck and Seitz 2007; Wild-Pfeiffer 2008; Grombein et al. 2013; Deng et al. 2016; Uieda et al. 2016; Deng and Shen 2018b; Fukushima 2018), Eq. (18) is the general solution of HC for RTM geoid height under limited Bouguer shell approximation. In the following experiments, the LBS is divided into a series (e.g., n) of finite elements and each approximated by a prism. The gravitational potential generated by the limited Bouguer shell is the comprehensive effect of all prisms (Wild-Pfeiffer 2008),

$$\begin{aligned} V^{\mathrm {LBS}}(P_+)= & {} \sum V^{\mathrm {Prism}}(P_+)=\sum G\rho \big [-(y-y')(z-z') \ln (x-x' +l)-(x-x') (y-y')\ln (z-z'+l) \nonumber \\&-\,(x-x')(z-z')\ln (y-y'+l)+\frac{(x-x')^2}{2}\arctan \frac{(y-y') (z-z')}{(x-x') l}\nonumber \\&+\,\frac{(y-y')^2}{2}\arctan \frac{(x-x') (z-z')}{(y-y') l}+\frac{(z-z')^2}{2}\arctan \frac{(y-y') (x-x')}{(z-z')l}\big ]|_{x_1,y_1,z_1}^{x_2,y_2,z_2} \end{aligned}$$

(19)

where $l=\sqrt{(x-x')^2+(y-y')^2+(z-z')^2}$ indicates the distance between the computation point $P_+(x,y,z)$ and integration point $Q(x',y',z')$.

Accordingly, the limited spherical layer is divided into a series (e.g., n) of mass layers sharing the same size as the top of the prism. The gravitational potential generated by the limited spherical layer is the comprehensive effect of mass layers (ML) (Wild-Pfeiffer 2008),

$$\begin{aligned} V^{\mathrm {LSL}}(P_+)= & {} \sum V^{\mathrm {ML}}(P_+)=\sum G\rho h\big [(x-x')\ln (y-y' +l)+(y-y') \ln (x-x' +l)\nonumber \\&-\,(z-z')\arctan \frac{(x-x') (y-y')}{(z-z') l}\big ]|_{x_1,y_1}^{x_2,y_2} \end{aligned}$$

(20)

where $z'=z_1$, $l=\sqrt{(x-x')^2+(y-y')^2+(z-z')^2}$.

In the general case, the limited Bouguer shell is represented by a Bouguer spherical cap. The expression of HC for geoid height in such cases is given in Appendix B.

3 Numerical Experiments

Currently, the most widely used global gravity field model EGM2008 and the upcoming EGM2020 are provided as spherical harmonic series expansions to degree and order (d/o) of 2159 (Pavlis et al. 2012; Barnes et al. 2020), which means that gravity details with a half-wavelength of $\sim 9$ km can be recovered reliably from GGMs. The details beyond the $\sim 9$ km threshold are linked to terrain fluctuations and to be obtained approximately via the RTM technique. All following experiments rely on this assumption. In terms of the main inputs, a detailed DEM model—MERIT2017 (Yamazaki et al. 2017) at a resolution of $3''$—is used to represent the Earth’s surface, and its directly derived spherical harmonic expansion to d/o 2159—MERIT2160 (Hirt et al. 2019a)—provides the smooth reference surface. RTM heights, differences between MERIT2017 heights and MERIT2160 heights, show that $\sim 50$% of the continental areas located below the reference surface over where HC is required.

3.1 The Effect of Planar Approximation on HC Terms in the Classical Condensation Method

The planar assumption is one of the main factors that affect the accuracy of derived HC terms in the classical condensation method. The comparisons between HC-UBP Eq. (9) and HC-BS Eq. (15), and between HC-LBP Eq. (7) and HC-LBS Eq. (18) provide measures for the planar approximation effect on HC terms. The HC for geoid height is $\pi G\rho h^2/\gamma$ in the unlimited Bouguer plate approximation, while it becomes $2\pi G\rho h^2/\gamma$ when using the spherical shell approximation. Therefore, the errors in $N^{\text {HC-UBP}}$ due to the planar approximation are $\pi G\rho h^2/\gamma$ which has a positive correlation with parameter $h^2$. When the magnitude of negative residual height has a value larger than 420 m, the errors due to planar approximation in $N^{\text {HC-UBP}}$ would be larger than 1 cm, and hence could not be ignored in the cm- and mm-level geoid determination.

Similarly, the difference between HC-LBP and HC-LBS provides insights on the errors in $N^{\text {HC-LBP}}$ due to planar approximation. Considering the character of Earth’s curvature, the errors due to planar approximation has a positive correlation with integration radius R. This is verified in Fig. 6. In this study, the Earth’s density of constant value $\rho =2670$ kg/m$^3$, and RTM height in extreme case $h=1350$ m are adopted for the calculation of $N^{\text {HC-LBP}}$ and $N^{\text {HC-LBS}}$. Besides, the integration masses around the computation point is divided into a grid at $15''\times 15''$ resolution and each grid element is then approximated by a prism for the calculation of $N^{\text {HC-LBS}}$. The integration radius changes from 1 km to 550 km with a step of 10 km both under LBS and under LBP. The results show that the magnitude of errors rises with the increased integration radius. With an integration radius of within 200 km, the errors due to planar approximation would be less than 0.5 cm.

Fig. 6

The effect of planar approximation. Here, $N^{\text {HC-LBS}}-N^{\text {HC-LBP}}$ indicates the differences between HC for geoid height under LBS approximation and under LBP approximation. Radius of limited Bouguer plate means that masses within the radius-defined zone are considered in the forward modelling

3.2 The Effect of Mass Inconsistency on HC Terms in the Classical Condensation Method

In this experiment, the effect of mass inconsistency on HC for RTM geoid height is studied through a comparison between HC-UBP and HC-LBP, and HC-BS and HC-LBS. From Eqs. (7), (9), (15), and (18), it is obvious that mass inconsistency effect is a function of parameter R and h.

In order to study the variation of errors due to mass inconsistency with increasing R, a constant residual height of $h=1350$ m was adopted. This is based on the positive correlation between error terms and the magnitude of the residual height. The maximum magnitude of negative residual height $h=1350$ m provides the extreme case in this study. The results are presented in Fig. 7a, c with R increasing from 0 km to 550 km. It is obvious that the effect of mass inconsistency on HC for geoid height shows the same trend in both spherical and planar approximations. The error magnitudes firstly decrease fast with increasing of integration radius R and then tend to be stable when R extends to enough distance. The difference between $N^{\text {HC-UBP}}$ and $N^{\text {HC-LBP}}$ tends to be less than 0.25 cm when $R>20$ km (Fig. 7a), which is a rather negligible value in present applications. However, the difference between $N^{\text {HC-BS}}$ and $N^{\text {HC-LBS}}$ is much larger than a magnitude of $\sim 10$ cm.

Fixing $R=110$ km, which is sometimes applied in RTM gravity field calculation (Yang et al. 2018), the variation of errors due to mass inconsistency with increasing h is shown in Fig. 7b, d. The results confirmed that the errors increase with increasing height h. The magnitude of errors in $N^{\text {HC-UBP}}$ is less than 0.07 cm with $h<1500$ m and $R>110$ km. When masses extending to an adequately distant area are considered in the RTM technique, such as for $R>110$ km, the effect due to mass inconsistency could be ignored in the cm-level gravity field determination. However, the mass inconsistency effect between $N^{\text {HC-BS}}$ and $N^{\text {HC-LBS}}$ would reach more than 10 cm and could not be ignored.

Fig. 7

The effect of mass inconsistency effect. a, c display the infinite approximation (mass inconsistency) effect on the HC for geoid height with varying integration radius; b, d display the infinite approximation (mass inconsistency) effect on the HC for geoid height with varying residual height

3.3 The Harmonic Correction on the Earth’s Surface

The HC on the Earth’s surface is calculated. This provides insight into the quantification of HC for RTM geoid height. The computation points are arranged in a grid of $15''\times 15''$ and are located on the Earth’s surface defined by MERIT2017. The residual heights are obtained by subtracting MERIT2160 from MERIT2017.

HC for RTM geoid height is calculated under various approximations. For the calculation of HC under LBS approximation, the integration masses within 110 km from the computation point are divided into a grid at $5''\times 5''$ resolution and each element is approximated by a prism. Figure 8 shows the residual height and the respective HC for geoid height under unlimited Bouguer plate approximation. With the negative radial heights varying between $-1350$ m and 0 m (Fig. 8a), the HC for RTM geoid height (Fig. 8b) varies from $\sim -10.49$ cm to $\sim 0$ cm with a mean of $-0.33$ cm and RMS of 0.11 cm for $N^{\text {HC-UBP}}$. When integration radius extends far than 110 km, the differences between $N^{\text {HC-UBP}}$, $N^{\text {HC-LBP}}$ and $N^{\text {HC-LBS}}$ are negligible. This could be clearly verified in the Sects. 3.1 and 3.2. Besides, the value of $N^{\text {HC-BS}}$ is double of $N^{\text {HC-UBP}}$. It is obvious that the HC for RTM geoid height is very small and could be ignored over most of the flat area on the Earth. However, over very rugged areas, such as Himalayas (Fig. 9), Tibetan Plateau, European Alps, American Rocky mountains, and Andes mountains, the HC for RTM geoid height reaches up to several cm.

Table 1 gives a detailed statistical description of the magnitude of HC for geoid height and its variation with changing of the magnitude of RTM height. Over areas with a magnitude of RTM height less than 93 m which occupies about $90.94\%$ continent, the HC for geoid height would be less than 1 mm. Over these areas, the HC for RTM geoid height could be ignored in the mm-level geoid height determination. Similarly, over 99.08% of continental areas, the HC for geoid height would be less than 1 cm and could be ignored in the cm-level geoid determination. However, over very rugged areas, which occupied about 0.92% of continental areas, the HC for RTM geoid height could be large than 1 cm and would reach $\sim 20$ cm in extreme cases. Therefore, HC should be carefully considered in these areas.

Table 1 The magnitude of HC on geoid height $N^{\text {HC-BS}}$ and $N^{\text {HC-UBP}}$, and their variations with changing of magnitude of RTM height $H_{\mathrm {RTM}}$

Fig. 8

Harmonic correction for RTM geoid heights on the Earth’s surface. a shows the residual height over places with $H_{\mathrm {RTM}}<0$. In order to display the correspondence between residual heights and HC, b shows the negative value of HC for RTM geoid height with reference surface of $N= 2159$

Fig. 9

Harmonic correction for RTM geoid heights over Himalaya areas. a shows the residual height at points with $H_{\mathrm {RTM}}<0$ over Himalaya areas; b displays the HC for RTM geoid height for reference surface of $N= 2159$ over Himalaya areas

4 Validation Results

4.1 Validation with Baseline Solution

In this experiment, we used an artificial method developed by Hirt et al. (2019a) for the RTM gravitational field calculation which avoids HC through dividing the RTM geoid height $N_{\text {RTM-baseline}}$ into two parts: (1) the full-scale gravity field signals implied by the detailed DEM depending on global numerical integration $N_{\mathrm {NI}}$, (2) long-wavelength gravity field $N_{\mathrm {SGM}}$ and ultra-high frequency correction $N_{\mathrm {HF}}$ relying on spectral forward modelling. Though the performance of this method in RTM geoid height calculation is not numerically investigated up to the present, it has been used in the calculation of RTM gravity disturbances globally and achieved great improvement in the accuracy of RTM technique to a sub-mGal level (Hirt et al. 2019a, 2019). This suggests the better performance of the artificial method than the classical method in the high-frequency gravity field recovering. Therefore, it is expected to yield better performance in RTM geoid height calculation and provide a reference for the validation of HC in RTM geoid height. In this validation experiment, the studied area is located in the most rugged area of the Earth, the Himalayas, bounded by latitudes of $27^{\circ }$ N and $28^{\circ }$ N, and longitudes of $87^{\circ }$ E and $88^{\circ }$ E. This area covers the Himalaya Southern flanks and provides the extreme mountain topography which could serve as a worst-case example for RTM errors. Over this area, RTM geoid heights are calculated through the artificial method and RTM with various types of HC (i.e. HC-LBP, HC-UBP, HC-BS, HC-LBS) and without HC separately. Constant density assumption and same DEM models will be used in the artificial method, direct RTM technique, and HC.

RTM geoid heights are calculated with integration masses extending to 110 km from the calculation point. The directly calculated RTM geoid heights are corrected by adding HC under various approximations and are then compared with the RTM baseline solution $N_{\text {RTM-baseline}}$. The calculations of HC under LBP and LBS share the same integration radius with the calculation of RTM geoid heights. Table 2 gives statistical information of comparison results, while their distributions are shown in Fig. 10. Figure 11 displays the variation of residuals with changing of RTM heights. The values of RTM baseline solution vary from $-36.80$ to 32.08 cm (Fig. 10a), with a mean $-1.15$ and RMS 10.06 cm (Table 2). This indicates the significance of high-frequency signals for cm-level geoid determination. The residuals between directly calculated RTM geoid heights and RTM baseline solution vary between $\sim 2.13$ cm and $\sim 17.98$ cm with RMS $\sim 2.21$ cm. It is obvious that the large differences mainly occur when the computation points are located below the reference surface (Fig. 10b, c). The magnitudes of differences have a high correlation with the magnitude of RTM heights (Fig. 11a) for points located in masses. When the computation points are located outside masses, the differences vary around zero (Fig. 11a). The involvement of HC greatly improves results which could be seen from the minimized RMS values of $\Delta N_{\text {RTM-HC-UBP}}$ $\sim 1.23$ cm, $\Delta N_{\text {RTM-HC-LBP}}$ $\sim 1.23$ cm, $\Delta N_{\text {RTM-HC-LBS}}$ $\sim 1.21$ cm and $\Delta N_{\text {RTM-HC-BS}}$ $\sim 0.64$ cm (Table 2). The values of $\Delta N_{\text {RTM-HC-UBP}}$ (Fig. 10c) tend to be positive over points located in masses. This is in agreement with HC for RTM gravity anomaly results in Hirt et al. (2019a). When the integration masses are extended up to 110 km from the computation points, the mass inconsistency effect could be ignored (Table 2). The HC formulas under Bouguer spherical shell approximation achieve the best performance with the minimum magnitude (within 3 cm) and RMS of $\Delta N_{\text {RTM-HC-BS}}^\mathrm {baseline}$ of 0.64 cm. This is reasonable considering the global masses are included in the calculation of baseline solution and distant masses would come into effect.

Table 2 The statistical information of various types of RTM geoid height

Fig. 10

Residual geoid heights compared to RTM-baseline solution. a displays the RTM baseline solution for geoid height; b is the RTM heights; c shows residual geoid heights after removing the RTM geoid heights with HC under unlimited Bouguer plate approximation; d is the absolute difference between residual geoid heights using RTM geoid heights with HC under unlimited Bouguer plate approximation and under Bouguer shell approximation, the bluish indicates the better performance of HC under Bouguer shell approximation

Fig. 11

Residual geoid heights with changing of RTM height over Himalaya area. a is residual geoid heights after removing directly calculated RTM geoid heights without HC; b shows residual geoid heights after removing the RTM geoid heights with HC under unlimited Bouguer plate approximation

4.2 Validation with Terrestrial Measurements

One of the main applications of the RTM technique is the determination of an ultra-high-resolution gravity field through combining GGMs at long- and medium-wavelength bands and the RTM gravity field at short-wavelength bands. The accurate terrestrial geoid measurements are supposed to provide the full-scale gravity field signal on the Earth’s surface. Therefore, it is appropriate to use terrestrial measurements as reference values for evaluating the accuracy of the recovered gravity field model from GGM and RTM and investigating the performance of the RTM technique (Yang et al. 2018; Hirt et al. 2019). In this paper, terrestrial GPS/leveling over New Zealand and in the Bavarian Alps in Germany are used to validate the performance of RTM with various types of HC and without HC.

The validation experiment is implemented through comparison with 1272 first- to fourth-order GPS/leveling measurements over New Zealand. This means that the value of root mean squared error (RMSE) is less than 1 cm when the level line less than 1 km. Yang et al. (2018) and Yang (2020) have given detailed descriptions of this dataset. In this study, the synthesized geoid height model with EGM2008 $N_{\mathrm {EGM2008}}$, a combination of EGM2008 and direct RTM $N_{\mathrm {RTM}}$ without HC, a combination of EGM2008 and RTM with HC-LBP, a combination of EGM2008 and RTM with HC-UBP, a combination of EGM2008 and RTM with HC-BS and a combination of EGM2008 and RTM with HC-LBS are calculated separately. The 110 km integration radius is used for the calculations of RTM geoid heights, HC under limited Bouguer plate approximation, and limited Bouguer shell approximation. The residual geoid heights, being the differences between observed and synthesized geoid heights, indicate the representativity of synthesized geoid heights and therefore give insights into the performance of RTM with various types of HC and without HC. Considering the difference between the gravity potential of the global model and of vertical datum for the leveling work, a bias fit, e.g., the mean value of residuals, is applied to each of the comparisons.

Table 3 gives the statistical information of differences between geoid height measurements and synthesized geoid heights from EGM2008 and RTM without and with various HCs over New Zealand. Figure 12 shows the distribution of these differences. It is obvious from Table 3, EGM2008 is capable of recovering 99.4% of GPS/leveling measured geoid heights. This might be because that the GPS/leveling measurements in this study are mainly distributed in the relatively flat area where long-wavelength signals play a dominant role. The involvement of direct RTM determined geoid heights without HC achieved little improvement (Table 3, Fig. 12a, c). The involvement of HC reduces the values of RMS from 11.09 cm of $\Delta N_{\mathrm {RTM}}$ to less 11.08 cm of $\Delta N _{\text {RTM-HC-UBP}}$, $\Delta N_{\text {RTM-HC-LBP}}$, $\Delta N_{\text {RTM-HC-BS}}$ and $\Delta N_{\text {RTM-HC-LBS}}$ (Table 3). The improvement mainly takes place over valley points (Fig 12b, c). Besides, the application of RTM with HC under Bouguer shell approximation achieves the smallest value of RMS. The RMS of $\Delta N_{\text {RTM-HC-BS}}$ is reduced to $\sim 11.05$ cm (Table 3) and the improvement varies within $\sim 6$ cm.

Table 3 The statistical information of geoid height $N_{\mathrm {obs}}$ and differences with synthesized geoid height from EGM2008 and RTM without and with various HCs over New Zealand and Bavarian area

Fig. 12

Geoid height over New Zealand. a displays residual geoid heights after removing EGM2008 recovered geoid heights from terrestrial observations; b shows the RTM height; c shows residual geoid heights after removing the synthesized geoid height which uses RTM geoid heights with HC under unlimited Bouguer plate approximation; d is the absolute difference between residual geoid heights using RTM geoid heights with HC under Bouguer shell approximation and with HC under unlimited Bouguer plate approximation, the bluish indicates the better performance of HC under Bouguer shell approximation

A similar experiment is implemented over the Bavarian area in the south of Germany. 34 GPS/leveling measurements over this area (Hirt et al. 2010) are used to validate the performance of derived HC expressions. The accuracy of these measurements is $1-2$ cm. Table 3 gives the detailed descriptive statistics of comparisons. Adding the HC for geoid height reduces the values of RMS from $\sim 2.59$ cm to $\sim 2.53$ cm. With integration radius extending up to 110 km from the measurement points, the effect involved by mass inconsistency and planar approximation is neglectable. The expressions of HC under UBP, LBP, and LBS show equivalent performance. Like the results showed in New Zealand, the expression of HC under BS achieved the minimal RMS $\sim 2.49$ cm. Figure 13 shows the values of residuals after removing synthesized geoid heights from observed geoid heights. Over points located below the reference surface, the involvement of the HC for RTM geoid height reduces the magnitude of residuals (Fig. 13d).

Fig. 13

Geoid height over the Bavarian area. a displays residual geoid heights after removing EGM2008 recovered geoid heights from terrestrial observations; b shows the RTM heights; c shows residual geoid heights after removing the synthesized geoid height which uses RTM geoid heights with HC under unlimited Bouguer plate approximation; d is the absolute difference between residual geoid heights using RTM geoid heights with HC under Bouguer shell approximation and with HC under unlimited Bouguer plate approximation, the bluish indicates the better performance of HC under Bouguer shell approximation

The involvement of HC for RTM geoid height achieves improvements in the above two validation experiments. However, there are still significant residuals after involving HC for geoid height, e.g., the residuals varying within 60 cm over New Zealand and varying within $\sim 10$ cm over the Bavarian area (Fig. 12c, 13c), this may be caused by various reasons, such as the spectral filter problem encountered in the RTM technique (Rexer et al. 2018; Bucha et al. 2019), the accuracy of applied DEM and its spherical harmonic (SH) expansions, high-frequency signals due to density anomaly, ultra-high frequency signals exceeding the resolution of applied DEMs, the errors in HC, etc. Besides, the accuracy and distribution of terrestrial measurements would also affect the results. However, the reduced RMS of residuals after involving HC for RTM geoid height proves the feasibility of the derived formulas.

5 Discussion and Conclusions

RTM retrieved gravity functionals are the primary source of high-frequency gravity field signals and therefore are widely applied in the fine regional and global gravity field determination through combining gravity field-related measurements and GGMs. When using RTM gravity forward modelling, the computation point might reside in the masses defined by the reference surface. In such a case, the RTM directly recovered gravity field is not commensurate with values obtained in the harmonic condition and HC is required. The classical condensation method, as one of the most used techniques for HC, only provided the solution of HC for RTM gravity anomaly and its accuracy was compromised to infinite Bouguer plate approximation. In this study, the HC formulas for RTM geoid height are presented in the framework of the condensation method.

The present contribution provides the formulas of HC for RTM geoid height in four variants: (1) HC-UBP with the residual masses being approximated by an infinite Bouguer plate, (2) HC-LBP with the residual masses approximated by a limited Bouguer plate, (3) HC-BS with the residual masses approximated by a Bouguer shell, and (4) HC-LBS with the residual masses approximated by a limited Bouguer shell. As a continuous work of TGF (Yang et al. 2020), a tesseroid of integration radius in both latitude and longitude direction is applied for ”limited Bouguer shell” approximation instead of using a spherical cap. This will generate $\sim 0.04$ cm differences in HC for geoid height in the extreme case when integration mass extends up to 110 km and residual height to 1350 m (Appendix B). Therefore, the errors due to application tesseroid could be ignored to some extent. Compared to the classical condensation method with infinite Bouguer plate approximation, the limited Bouguer plate approximation would reduce the effect of inconsistency between masses involved in the RTM technique and masses involved in HC, the Bouguer shell approximation considers the effect of the Earth’s curvature, while the limited Bouguer shell approximation overcomes both mass inconsistency effect and planar approximation. Therefore, HC-LBP, HC-BS, and HC-LBS formulas are supposed to be more accurate than HC-UBP terms.

Secondly, based on four types of HC expressions (i.e. HC-UBP, HC-LBP, HC-BS, HC-LBS) for RTM geoid height, the effects of mass inconsistency and planar approximation on HC are studied. The results provide insights into the accuracy of generally applied HC-UBP when RTM is used for the augmentation of GGMs beyond d/o 2159. With integration masses extending up to a sufficient distance, the errors introduced by unlimited Bouguer plate approximation in HC terms can be considered negligible. For example, when integration masses extend up to 110 km for RTM geoid height, the infinite approximation effect is less than 0.1 cm. However, the errors introduced by planar approximation in HC for RTM geoid height are a function of $h^2$ and could reach a magnitude of $\sim 10$ cm over very rugged areas when the entire global masses are considered. Theoretically, this error would be largely reduced when the integration radius extends up to a limit distance in the RTM technique.

Thirdly, HC for RTM geoid height has been calculated when the reference surface is expanded to d/o 2159. Besides the highlighted HC for RTM gravity anomaly in previous studies, our study proved the significance of HC for geoid height. The HC for RTM geoid height may reach up to several cm over very rugged areas, such as Himalayas, Tibetan Plateau, European Alps, American Rocky mountains, and Andes mountains. These areas occupy $\sim 0.91$% of the continental areas. The HC for RTM geoid height should be carefully considered in the cm- and mm-level geoid determination over these areas. Over $\sim 99$% of continental areas with RTM height less than 93 m, HC for RTM geoid height would be less than 1 mm and could be ignored in the practical calculations.

The validation through comparison with terrestrial measurements and the RTM baseline solution confirmed that the HC terms provided in this study are suitable to deal with the “non-harmonicity problem” encountered in the RTM technique. It is expected to improve the RTM performance in geodetic applications, such as gravity continuation, interpolation, and regional gravity field determination in the framework of the remove-compute-restore technique, which will be studied in the future.

Appendices

Appendix A: Derivation of Harmonic Correction for the Geoid Height under Unlimited Bouguer Plate Approximation

As is introduced in Sect. 2.1, the HC-UBP with unlimited Bouguer plate approximation is value of HC-LBP with limited Bouguer plate approximation when $R\rightarrow \infty$,

$$\begin{aligned} N^{\text {HC-UBP}}(P_+)= & {} \frac{1}{\gamma }\lim _{R\rightarrow \infty }V^{\text {HC-LBP}}(P_+) \nonumber \\= & {} \frac{1}{\gamma }\lim _{R\rightarrow \infty }[2\pi G\rho hR-\pi G\rho (R^2\mathrm {\ln }\frac{R}{\sqrt{R^2+h^2}-h}-h^2+h\sqrt{R^2+h^2})]\nonumber \\= & {} \frac{\pi G\rho }{\gamma }\lim _{R\rightarrow \infty }[2hR-R^2\mathrm {\ln }\frac{R}{\sqrt{R^2+h^2}-h}+h^2-h\sqrt{R^2+h^2}]\nonumber \\= & {} \frac{\pi G\rho }{\gamma }\lim _{R\rightarrow \infty }[2hR-R^2\mathrm {\ln }\frac{R}{\sqrt{R^2+h^2}-h}-h\sqrt{R^2+h^2}]+\frac{\pi G\rho h^2 }{\gamma } \end{aligned}$$

(21)

Let $\kappa =\frac{1}{R}$, then

$$\begin{aligned}&\lim _{R \rightarrow \infty }[2hR-R^2\ln \frac{R}{\sqrt{R^2+h^2}-h}-h\sqrt{R^2+h^2}]\nonumber \\&\quad =\lim _{\kappa \rightarrow 0}[\frac{2h}{\kappa }+\frac{1}{\kappa ^2}\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)-\frac{h}{\kappa }\sqrt{1+\kappa ^2h^2}]\nonumber \\&\quad =\lim _{\kappa \rightarrow 0}\frac{2h+\frac{1}{\kappa }\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)-h\sqrt{1+\kappa ^2h^2}}{\kappa } \end{aligned}$$

(22)

It follows from L’Hospital’s rule (Taylor 1952) that

$$\begin{aligned}&\lim _{\kappa \rightarrow 0}\frac{2h+\frac{1}{\kappa }\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)-h\sqrt{1+\kappa ^2h^2}}{\kappa }\nonumber \\&\quad =\lim _{\kappa \rightarrow 0}\frac{d}{d\kappa }[2h+\frac{1}{\kappa }\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)-h\sqrt{1+\kappa ^2h^2}]\nonumber \\&\quad =\lim _{\kappa \rightarrow 0}[\frac{h^2-\kappa h^3(\sqrt{1+\kappa ^2h^2}-\kappa h)}{\sqrt{1+\kappa ^2h^2}(\sqrt{1+\kappa ^2h^2}-\kappa h)}-\frac{\frac{\kappa h}{\sqrt{1+\kappa ^2h^2}-\kappa h}+\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)}{\kappa ^2}] \end{aligned}$$

(23)

When $\kappa \rightarrow 0$, the first term above tends to $h^2$. The limit of the second term is concluded by applying L’Hospital’s rule again, that is

$$\begin{aligned}&\lim _{\kappa \rightarrow 0}\frac{\frac{\kappa h}{\sqrt{1+\kappa ^2h^2}-\kappa h}+\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)}{\kappa ^2} \nonumber \\&\quad =\lim _{\kappa \rightarrow 0}\frac{\frac{d}{d\kappa }[\frac{\kappa h}{\sqrt{1+\kappa ^2h^2}-\kappa h}+\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)]}{2\kappa } \end{aligned}$$

(24)

By direct computation of derivatives, we yield

$$\begin{aligned}&\frac{d}{d\kappa }[\frac{\kappa h}{\sqrt{1+\kappa ^2h^2}-\kappa h}]=\frac{h}{\sqrt{1+\kappa ^2h^2}-\kappa h}-\frac{\kappa ^2h^3}{(\sqrt{1+\kappa ^2h^2}-\kappa h)^2\sqrt{1+\kappa ^2h^2}}+\frac{\kappa h^2}{(\sqrt{1+\kappa ^2h^2}-\kappa h)^2}\end{aligned}$$

(25)

$$\begin{aligned}&\frac{d}{d\kappa }[\ln (\sqrt{1+\kappa ^2h^2}-\kappa h]=\frac{\kappa h^2}{(\sqrt{1+\kappa ^2h^2}-\kappa h)\sqrt{1+\kappa ^2h^2}}-\frac{h}{\sqrt{1+\kappa ^2h^2}-\kappa h} \end{aligned}$$

(26)

Therefore,

$$\begin{aligned}&\lim _{\kappa \rightarrow 0}\frac{\frac{d}{d\kappa }[\frac{\kappa h}{\sqrt{1+\kappa ^2h^2}-\kappa h}+\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)]}{2\kappa }\nonumber \\&\quad =\lim _{\kappa \rightarrow 0}\frac{1}{2}[\frac{h^2(2\sqrt{1+\kappa ^2h^2}-\kappa h)}{(\sqrt{1+\kappa ^2h^2}-\kappa h)^2\sqrt{1+\kappa ^2h^2}}-\frac{\kappa h^3}{(\sqrt{1+\kappa ^2h^2}-\kappa h)^2\sqrt{1+\kappa ^2h^2}}]\nonumber \\&\quad =h^2 \end{aligned}$$

(27)

Combing Eqs. (23), (24) and (27), we obtain

$$\begin{aligned} \lim _{\kappa \rightarrow 0}\frac{2h+\frac{1}{\kappa }\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)-h\sqrt{1+\kappa ^2h^2}}{\kappa }=0 \end{aligned}$$

(28)

Therefore,

$$\begin{aligned} N^{\text {HC-UBP}}(P_+)=\frac{\pi G\rho h^2}{\gamma } \end{aligned}$$

(29)

Appendix B: Derivation of Harmonic Correction for Geoid Height under Limited Bouguer Shell Approximation

Fig. 14

Geometry of limited Bouguer shell (spherical cap) and respective compressed mass layer. The left panel displays a limited Bouguer shell where the inner radius is denoted as $r_1$, the outer radius $r_2$, the thickness h, and the density $\rho$. The computation point $P_+$ locates above the inner boundary and its respective point on the outer boundary is $P^\mathrm {R}$. The right panel displays the respective compressed mass layer of the limited Bouguer shell. It shares the same masses with the spherical cap. $\psi _0$ is the half-angle subtended at the Earth’s centre

The geometry of the limited Bouguer shell is represented by a spherical cap at the left panel of Fig. 14. The inner radius of spherical cap is $r_1$, outer radius $r_2$, and density $\rho$. $\psi _0$ is the half-angle subtended at the Earth’s centre. $P_+ (0,0,r)$ denotes the computation point when it is located below the reference surface and the subscript $'+'$ indicates that the point adheres to or just above the Earth’s surface. The magnitude of height difference between $P_+$ and its respective point $P^{\mathrm {R}}$ on the reference surface is h. Its generated gravitational potential is (Tenzer et al. 2007; Kadlec 2011)

$$\begin{aligned} V=G\rho \int _{0}^{2\pi }\int _{0}^{\psi }\int _{r_1}^{r_2}\frac{1}{l}r'^2\sin \psi 'dr'd\psi 'd\alpha ' \end{aligned}$$

(30)

with $(\psi ',\alpha ',r')$ indicating the coordinates of integration point and

$$\begin{aligned} l=\sqrt{r^2+r'^2-2rr'\cos \psi '} \end{aligned}$$

(31)

Its analytical solution was widely discussed by LaFehr (1991), Hensel (1992), Heck and Seitz (2007), Tenzer et al. (2007), and Kadlec (2011). Here, the general solution in Kadlec (2011) was adopted. It adapts for various cases when computation points are located out or in the spherical cap.

$$\begin{aligned} V^{\mathrm {SC}}= & {} 2\pi G\rho \left[ \frac{(r_1-r)\vert r-r_1\vert (r+2r_1)+(r-r_2)\vert r-r_2\vert (r+2r_2)}{6r}\right. \nonumber \\&\quad +\,\frac{1}{2}r^2\sin ^2\psi \cos \psi \ln (\frac{r_2+l_2-r\cos \psi }{r_1+l_1-r\cos \psi })+\frac{l_2^3-l_1^3}{3r}\nonumber \\&\quad +\,\frac{1}{2}\cos \psi (l_2(r_2-r\cos \psi )-l_1(r_1-r\cos \psi )))\left. \right] \end{aligned}$$

(32)

where

$$\begin{aligned} l_1= & {} \sqrt{r^2+r_1^2-2rr_1\cos \psi }\nonumber \\ l_2= & {} \sqrt{r^2+r_2^2-2rr_2\cos \psi } \end{aligned}$$

(33)

In the framework of the condensation method under limited Bouguer shell approximation, the spherical cap is compressed into a mass layer with a constant radius $r_1$, infinitesimal thickness, and shares the same mass with the spherical cap. The spherical cap layer is moved down to just below the computation point $P_+$ (right panel at Fig. 14). Its generated gravitational potential could be derived following (Tenzer et al. 2007; Kadlec 2011)

$$\begin{aligned} V^{\mathrm {SCL}}=G\rho _c\int _{0}^{2\pi }\int _{0}^{\psi }\frac{1}{l}r_1^2\sin \psi 'd\psi ' \end{aligned}$$

(34)

with $\rho _c$ indicating the density of compressed masses, $(\psi ',\alpha ',r_1)$ the coordinates of integration point and

$$\begin{aligned} l=\sqrt{2r_1^2-2r_1^2\cos \psi '} \end{aligned}$$

(35)

After integration over $\alpha '$, we get

$$\begin{aligned} V^{\mathrm {SCL}}=2\pi G\rho _c\int _{0}^{\psi }\frac{1}{l}r_1^2\sin \psi 'd\psi 'd\alpha ' \end{aligned}$$

(36)

After integration over $\psi '$, we get

$$\begin{aligned} V^{\mathrm {SCL}}=\frac{2\pi G\rho _c r_1}{r}({\sqrt{r^2+r_1^2-2rr_1\cos \psi }-\sqrt{r^2+r_1^2-2rr_1}}) \end{aligned}$$

(37)

For computation point $P_+$, the HC for geoid height is

$$\begin{aligned} N^{\text {HC-LBS}}_{\mathrm {Spherical\, Cap}}(P_+)=\frac{V^{\mathrm {SCL}}(P_+)-V^{\mathrm {SC}}(P_+)}{\gamma (P_+)} \end{aligned}$$

(38)

Fig. 15

Differences of HC for geoid height based on various LBS, one using tesseroid for calculation, another uses spherical cap. $N^{\text {HC-LBS}}$ indicates HC for geoid height under LBS using tesseroid for calculation, $N^{\text {HC-LBS}}_{\text {Spherical Cap}}$ HC for geoid height under LBS using spherical cap for calculation

The comparison between two kinds of HC under LBS is implemented with an integration radius varying from 0 to 550 km. In this experiment, $N^{\text {HC-LBS}}$ is calculated following the method introduced in Sect. 2.3. The tesseroid is bounded by surfaces defined by $\lambda =-\psi$ and $\lambda =\psi$, $\varphi =-\psi$ and $\varphi =\psi$, and $r=r_1$ and $r=r_2$. The HC has calculated through diving the integration masses into a series of the prism at a resolution of $15^{\prime \prime }$. $N^{\text {HC-LBS}}_{\text {Spherical Cap}}$ is calculated with Eq.(38). The differences are shown in Fig. 15. It is obvious that the differences between $N^{\text {HC-LBS}}$ and $N^{\text {HC-LBS}}_{\text {Spherical Cap}}$ reduce with increasing integration radius. When the integration radius is larger than $\sim 20$ km, the differences would be less than 0.05 cm, which is able to be ignored in the most practical applications.