A numerical study of residual terrain modelling (RTM) techniques and the harmonic correction using ultra-high-degree spectral gravity modelling

Abstract

Residual terrain modelling (RTM) plays a key role for short-scale gravity modelling in physical geodesy, e.g. for interpolation of observed gravity and augmentation of global geopotential models (GGMs). However, approximation errors encountered in RTM computation schemes are little investigated. The goal of the present paper is to examine widely used classical RTM techniques in order to provide insights into RTM-specific approximation errors and the resulting RTM accuracy. This is achieved by introducing a new, independent RTM technique as baseline that relies on the combination of (1) a full-scale global numerical integration in the spatial domain and (2) ultra-high-degree spectral forward modelling. The global integration provides the full gravity signal of the complete (detailed) topography, and the spectral modelling that of the RTM reference topography. As a main benefit, the RTM baseline technique inherently solves the “non-harmonicity problem” encountered in classical RTM techniques for points inside the reference topography. The new technique is utilized in a closed-loop type testing regime for in-depth examination of four variants of classical RTM techniques used in the literature which are all affected by one or two types of RTM-specific approximation errors. These are errors due to the (1) harmonic correction (HC) needed for points located inside the reference topography, (2) mass simplification, (3) vertical computation point inconsistency, and (4) neglect of terrain correction (TC) of the reference topography. For the Himalaya Mountains and the European Alps, and a degree-2160 reference topography, RTM approximation errors are quantified. As key finding, approximation errors associated with the standard HC ($4\pi G\rho H_{\text{P}}^{\text{RTM}} )$ may reach amplitudes of ~ 10 mGal for points located deep inside the reference topography. We further show that the popular RTM approximation ($2\pi G\rho H_{\text{P}}^{\text{RTM}} - {\text{TC}}$) suffers from severe errors that may reach ~ 90 mGal amplitudes in rugged terrain. As a general conclusion, the RTM baseline technique allows inspecting present and future RTM techniques down to the sub-mGal level, thus improving our understanding of technique characteristics and errors. We expect the insights to be useful for future RTM applications, e.g. in geoid modelling using remove–compute–restore techniques, and in the development of new GGMs or high-resolution augmentations thereof.

1 Introduction

In physical geodesy, residual terrain modelling (RTM) is a key technique that is widely used to forward-model high-frequency gravity effects from topographic mass models (Forsberg and Tscherning 1981; Forsberg 1984). The RTM can be used to smooth gravity field observations for field interpolation (densification), e.g. in the context of remove–compute–restore gravity field computations (e.g. Denker 2013), mostly applied to determine high-resolution geoid models from gravimetric (Märdla et al. 2017) but also astrogeodetic data (Schack et al. 2018). Second, RTM gravity effects can be used to extend the spectral content of global geopotential models (GGMs) to the short-wavelength domain not resolved by the GGM (e.g. Hirt 2010; Bucha et al. 2016). This approach, also known as spectral enhancement method, has proven its value in the development of GGMs as fill-in method over areas with poor gravity coverage (Pavlis et al. 2007), enabled improved validation of GGMs (Hirt et al. 2011) and shown its utility in height system unification (Vergos et al. 2018). It has also facilitated the construction of ultra-high resolution maps of gravity field functionals (e.g. GGMplus, Hirt et al. 2013). RTM was also used in related applications, e.g. ice modelling (Schwabe et al. 2014), coastal zone modelling (Hirt et al. 2013), geophysics (AllahTavakoli et al. 2015) and combined with mass-density maps (Yang et al. 2018).

The main benefit of the RTM technique is its ability to directly deliver—in approximation—high-frequency gravity effects, solely based on the integration of gravity effects of elementary mass bodies (e.g. prism or tesseroids, e.g. Heck and Seitz (2007) or polyhedra, e.g. D’Urso (2014)) within some limited integration cap. Compared to other gravity forward modelling techniques that require more tedious global numerical integrations (e.g. Kuhn et al. 2009), residual gravity effects largely cancel out beyond some distance from the computation point, thus reducing the numerical costs (Forsberg and Tscherning 1981).

As disadvantage, RTM gravity computations can be subject to approximation errors. The most prominent example is the so-called harmonic correction (HC) that is needed when computation points reside inside the reference topography (Forsberg 1984; Omang et al. 2012; Denker 2013), but there are other RTM-specific approximations that are identified and investigated in this paper.

When the RTM is to be used for high-frequency GGM augmentation, spectral inconsistencies can act as error sources, e.g. when simplified methods, such as block-mean values or moving averages (Elhabiby et al. 2009; Forsberg 2010), are used to high-pass filter the digital elevation model (DEM) that represents the topographic masses. The spectral inconsistencies can be reduced by using a spherical harmonic (SH) reference surface (Hirt 2010) which is ideally derived from the DEM data itself via spherical harmonic analysis (Hirt et al. 2014). However, even when a rigorously consistent SH reference surface is used, the computed RTM gravity effects are subject to approximation errors, because filtering in the topography and gravity domains are not equivalent operations (“RTM filter problem”). On the one hand, high-frequency gravity signals as implied by the band-limited SH reference surface (e.g. Hirt and Kuhn 2014) are missing. On the other hand, unwanted low-frequency gravity signals may enter the RTM gravity effects. The RTM filter problem can be avoided by filtering gravity from a global numerical integration with a spectral topographic potential model (Grombein et al. 2017), or solved by applying filter corrections (Rexer et al. 2018).

While some of the RTM-specific approximation errors affecting the “classical” Forsberg (1984) RTM technique can be mitigated with the recent works, others, notably those associated with the harmonic correction, can still be present, but are little studied. With recent advances in ultra-high-resolution spectral gravity forward modelling (e.g. Balmino et al. 2012; Hirt et al. 2016; Rexer 2017), it has now become possible to close this knowledge gap and improve our understanding of RTM techniques, which is important considering the widespread use of RTM in physical geodesy.

The goal of the present paper is to validate widely used RTM techniques and to provide insights into RTM-specific approximation errors and the resulting RTM accuracy. This is achieved by introducing a new, independent RTM technique that serves as baseline. It relies on the combination of (1) a full-scale global numerical integration in the spatial domain with (2) an ultra-high-degree spectral topographic potential model that accurately delivers gravity implied by the reference topography. The RTM schemes are tested in a closed-loop type test environment using identical input data in order to avoid inconsistencies associated with the use of, e.g. different mass models or constants. Our testing allows comparisons between the “classical” RTM computation schemes (or variants thereof) with a baseline RTM solution that, while computationally demanding to obtain, is sufficiently accurate to provide meaningful feedback on the RTM approaches. This strategy is used here to constrain the approximation error associated with the harmonic correction, and to provide accuracy estimates for four classical RTM techniques used together with N = 2160 reference topographies over rugged terrain. To our knowledge, this is the first comprehensive attempt to study these errors, and our RTM validation experiment is the first of its kind that is reported in the literature.

We start with general aspects of the methodology (Sect. 2.1), give a short review of the classical RTM techniques (Sect. 2.2) and introduce the new RTM baseline technique based on ultra-high-degree spherical harmonics (Sect. 2.3). We then present a numerical experiment and its results (Sect. 3), which are discussed in Sect. 4 before conclusions are drawn in Sect. 5. The main focus of this paper is on the identification and numerical study of error sources specifically occurring in the RTM computation scheme, but not so much on the quantification of all possible error sources affecting forward computations, such as grid resolutions or choices for the mass model discretization (e.g. tesseroids vs. polyhedra) that are already discussed in the literature.

2 Methodology

2.1 General

RTM techniques can be considered as special cases of gravity forward modelling (GFM) techniques to compute the gravity field generated by some topographic mass distribution. Through global evaluation of Newton’s integral, GFM techniques deliver the (topography-implied) gravity field at all spatial scales. In contrast, RTM techniques yield the short-wavelength gravity field constituents only. This is commonly achieved by high-pass filtering of the topography prior to the forward modelling. In our study, a global digital elevation model (DEM) is used to approximate the upper bound of the topographic mass distribution, while the lower bound is represented by the geoid. We use the DEM in spherical approximation, i.e. with the heights $H$ referring to some Earth reference sphere with radius $R$ as an approximation of the geoid. The gravity signal $\delta g^{\text{H}}$ (first negative radial derivative of the potential) generated by the topographic mass model (defined through elevations $H$, mass density $\rho )$ is obtained via global evaluation of Newton’s integral [after Heck an Seitz (2007), Eq. 30 ibid]

$$ \begin{aligned} \delta g^{\text{H}} \left( {r,\varphi ,\lambda } \right) & = G\rho \mathop \int \limits_{{\lambda_{Q} = 0}}^{2\pi } \mathop \int \limits_{{\varphi_{Q} = - \pi /2}}^{\pi /2} \mathop \int \limits_{{r_{Q} = R}}^{R + H} \frac{{r_{Q}^{2} (r - r_{Q} \cos \psi )}}{{l^{3} }}{\text{d}}r_{Q} \cos \varphi_{Q} \,{\text{d}}\varphi_{Q} \,{\text{d}}\lambda_{Q} \\ & = G\rho \mathop \int \limits_{\psi = 0}^{{\psi_{0} = \pi }} \mathop \int \limits_{\alpha = 0}^{2\pi } \mathop \int \limits_{{r_{Q} = R}}^{R + H} \frac{{r_{Q}^{2} (r - r_{Q} \cos \psi )}}{{l^{3} }}{\text{d}}r_{Q} {\text{d}}\alpha \sin \psi {\text{d}}\psi \\ \end{aligned} $$

(1)

where $r,\varphi ,\lambda$ are the radius, latitude and longitude of the computation point $P$. Variables $r_{Q} ,\varphi_{Q} ,\lambda_{Q}$ are the radius and the geographical coordinates of the integration points $Q$ and $\psi$,$\alpha$ are the spherical distance and azimuth between $P$ and $Q$ which are separated by the Euclidian distance $l$. Variable $\psi_{0}$ denotes the radius of the integration cap, with $\psi_{0} = \pi$ required for global integrations.

For the practical evaluation of Newton’s integral, either numerical integration in the spatial domain (NI) or spectral gravity forward modelling (SGM) techniques can be used (e.g. Hirt and Kuhn 2014; Hirt et al. 2016). For NI, the topographic mass distribution is subdivided into elementary mass elements (e.g. prisms or tesseroids) for which the gravitational effect can be computed analytically or numerically. The composite gravity effect is then obtained through summation of all individual gravity contributions. Opposed to this, SGM does not require such a discretization. Instead, Newton’s integral is evaluated using spherical harmonics (Sect. 2.3).

For the high-pass filtering of the topography, we introduce a reference topography $H^{\text{REF}}$ that represents the long-wavelength part of $H$ up to spherical harmonic (SH) degree $N$

$$ H^{\text{REF}} \left( {\varphi ,\lambda } \right) = \mathop \sum \limits_{n = 0}^{N} \mathop \sum \limits_{m = - n}^{n} \bar{H}_{nm} \bar{Y}_{nm} \left( {\varphi ,\lambda } \right) $$

(2)

where $\bar{Y}_{nm} \left( {\varphi ,\lambda } \right)$ are the fully normalized surface SH functions of degree $n$ and order $m$ and $\bar{H}_{nm}$ are the fully normalized SH height coefficients obtained through spherical harmonic analysis (SHA) of $H$. The gravitational effect implied by $H^{\text{REF}}$ can be computed with

$$ \delta g^{{H_{\text{REF}} }} = G\rho \mathop \int \limits_{\psi = 0}^{{\psi_{0} = \pi }} \mathop \int \limits_{\alpha = 0}^{2\pi } \mathop \int \limits_{{r_{Q} = R}}^{{R + H_{\text{REF}} }} \frac{{r_{Q}^{2} (r - r_{Q} \cos \psi )}}{{l^{3} }}{\text{d}}r_{Q} {\text{d}}\alpha \sin \psi {\text{d}}\psi .$$

(3)

By subdividing the mass distribution into the two constituents $H$ and $H^{\text{REF}}$, residual gravity

$$ \delta g^{\text{RTM}} = \delta g^{\text{H}} - \delta g^{\text{HREF}} $$

(4)

is obtained that can be computed in two fundamentally different ways. The first way is the joint evaluation of both terms of Eq. (4) in one integration run (cf. Sect. 2.2.1 and Fig. 1). The second way is the separate evaluation of the terms $\delta g^{\text{H}}$ and $\delta g^{\text{HREF}}$ (Fig. 2) that can be done by two NIs (over $H$ and $H^{\text{REF}}$) in the spatial domain (Sect. 2.2.2), or alternatively, by a combination of global NI (over $H)$ with spectral forward modelling (over $H^{\text{REF}}$). The last case is suitable to provide a baseline solution that avoids some approximation errors of classical RTM techniques (Sect. 2.3).

Fig. 1

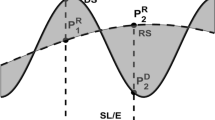
Basic principle of residual terrain modelling (technique RTM-A). The figure shows the two elevation models (high-resolution detailed DEM and long-wavelength reference DEM) relative to the height reference surface and residual topographic masses (in grey). Computation point always resides at the detailed DEM, so can be inside the reference DEM (see point P₂). In that case, some form of the HC is required when integration techniques are employed. Computation point P₁ is outside the reference DEM and no HC is required

Fig. 2

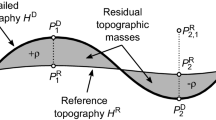
Residual terrain modelling via two components, a detailed topography, b reference topography. The computation of the gravity signal of the reference topography (b) using numerical integration is the difficult part. When computation points reside at the reference topography (this is the case in technique RTM-C), no HC is required at the expense of approximation errors associated with vertically different point locations for components a, b. The key contribution of this paper is the accurate evaluation of the gravity signal of the reference topography with spectral techniques at the orange points. Even for points of the detailed topography buried in the reference topography (P₂), no HC is required (b). This allows using identical computation points in a, b in the RTM baseline solution without additional approximation errors

2.2 The classical RTM techniques

2.2.1 RTM with harmonic correction (RTM-A and RTM-B)

In its basic form, the RTM is constructed as difference between the high-resolution topography $H$ and the reference topography $H^{\text{REF}}$ (Forsberg 1984), also see Fig. 1. The implied gravity signal $\delta g^{\text{RTM}}$ that follows from the RTM integral is evaluated with NI techniques (e.g. Heck and Seitz 2007). The RTM integral reads in spherical approximation

$$ \delta g^{\text{RTM}} \approx hc + G\rho \mathop \int \limits_{\psi = 0}^{{\psi_{0} }} \mathop \int \limits_{\alpha = 0}^{2\pi } \mathop \int \limits_{{r_{Q} = R + H_{\text{REF}} }}^{R + H} \frac{{r_{Q}^{2} (r - r_{Q} \cos \psi )}}{{l^{3} }}{\text{d}}r_{Q} {\text{d}}\alpha \sin \psi {\text{d}}\psi . $$

(5)

Because of the oscillating nature of the residual heights $H^{\text{RTM}} = H - H^{\text{REF}}$, the gravitational effects associated with the masses beyond radius $\psi_{0}$ cancel out to a large extent (Forsberg and Tscherning 1981; Forsberg 1984). The integration in Eq. (5) may therefore be restricted to a spherical cap of radius $\psi_{0}$ instead of a global integration (as in Eqs. 1 and 3), significantly reducing the computational costs. The associated truncation error can be kept reasonably small by choosing $\psi_{0}$ large enough (e.g. $\psi_{0} =$ 2° for gravity and $H^{\text{REF}}$ with $N = 2160$).

The fundamental difficulty of the RTM technique using NI methods (Eq. 5) comes into play when the computation points are located inside the reference topography (i.e. $H_{\text{P}} < H_{\text{P}}^{\text{REF}}$). In this case, the (RTM-delivered) gravitational potential is non-harmonic and cannot be used to describe the field external to the mass distribution which is almost exclusively needed for the purposes of physical geodesy. Conventionally, this problem is solved by removing the masses above and condensing them just below the computation point. This solution is known as the harmonic correction (HC)

$$ hc \approx 4\pi G\rho H_{\text{P}}^{\text{RTM}} , \quad H_{\text{P}}^{\text{RTM}} < 0 $$

(6)

(Forsberg and Tscherning 1981) that relies on a mass condensation based on a double Bouguer reduction with slab thickness $H_{\text{P}}^{\text{RTM}}$. It ensures that $\delta g^{\text{RTM}}$ values from NI become “compatible” with field representations such as (a) exterior spherical harmonics (e.g. GGMs), which are harmonic per definition, and (b) field observations, e.g. gravity measurements, carried out in harmonic space (above the Earth’s surface). For points with $H_{\text{P}}^{\text{RTM}} \geq 0$, $hc = 0$. Approximation errors associated with the HC from Eq. (6) have been acknowledged in the literature (e.g. Forsberg 2010; Omang et al. 2012), but not yet precisely characterized and quantified. In the literature, “the non-harmonicity [] below the reference height surface is considered today as a major theoretical problem with the RTM method” (Denker 2013).

In this study, we denote the formalism to compute RTM gravity values $\delta g^{\text{RTM}}$ with Eqs. (5) and (6) as RTM-A technique. In Eq. (5), the integration of mass-density effects in radial direction ($r_{Q} )$ is done between the limits $R + H^{\text{REF}}$ and $R + H.$ Alternative choices for the integration limits have been reported in the literature, e.g. using residual heights $H^{\text{RTM}}$ only (Hirt et al. 2010). In this case, denoted herein as RTM-B technique, the integration limits are $R$ and $R$ + $H^{\text{RTM}}$ in Eq. (5). The use of residual heights only gives rise to an approximation error in technique RTM-B, denoted the mass simplification error. In RTM-A, we use $r = R + H_{\text{P}}$ such that the computation points reside at the high-resolution DEM, i.e. at the surface just outside Earth’s masses, while $r = R + H_{\text{P}}^{\text{RTM}}$ in RTM-B.

2.2.2 RTM without harmonic correction (RTM-C and RTM-D)

Point locations inside the reference topography (RTM technique A, Fig. 1) can be circumvented—and the HC entirely avoided—by using two NIs (Fig. 2) where the computation points reside on the surface of the respective mass model. With this strategy (Forsberg 1984, p. 38), a first integration run with $r = R + H_{\text{P}}$ yields the gravity effect $\delta g^{\text{H}}$ implied by the detailed topography $H$ (Eq. 1), and a second integration run with $r = R + H_{\text{P}}^{\text{REF}}$ yields the gravity effect $\delta g^{\text{HREF}}$ implied by the reference topography (Eq. 3). RTM gravity $\delta g^{\text{RTM}}$ is obtained with Eq. (4) as difference $\delta g^{\text{H}} - \delta g^{\text{HREF}}$ (denoted here as technique RTM-C). The avoidance of the HC comes at the cost of another inconsistency because $\delta g^{\text{H}}$ and $\delta g^{\text{HREF}}$ are not computed at the same 3D location. The computation point heights differ by the residual topography $H^{\text{RTM}}$, so can reach ~ 1 to ~ 2 km or even more in steep terrain (denoted here as the computation point inconsistency error).

Following Forsberg (1984, p. 38) and Märdla et al. (2017), each term occurring on the right-hand side in Eq. (4) can be split into the Bouguer slab gravity effect ($2\pi G\rho H)$ and the terrain correction (tc). Equation (4) can thus be rewritten to

$$ \delta g^{\text{RTM}} = 2\pi G\rho H_{\text{P}} - {\text{tc}} \left| {{}_{{H_{\text{P}} }}^{H} } \right. - \left( {2\pi G\rho H_{\text{P}}^{\text{REF}} - {\text{tc}}\left| {{}_{{H_{\text{P}}^{\text{REF}} }}^{{H^{\text{REF}} }} } \right.} \right) $$

(7)

such that two TC computations are required instead of two full-scale NI runs. For $N = 180$ reference topographies, Forsberg (1984, p. 39) argued that the TC of the $H^{\text{REF}}$ component is generally small and can be neglected. Equation (7) was therefore rewritten in Forsberg (1984) to (technique RTM-D)

$$ \delta g^{\text{RTM}} \approx 2\pi G\rho \left( {H_{\text{P}} - H_{\text{P}}^{\text{REF}} } \right) - {\text{tc}}\left| {{}_{{H_{\text{P}} }}^{H} } \right. $$

(8)

such that the RTM gravity is obtained as effect of a Bouguer slab of thickness $H^{\text{RTM}}$ and TC. This expression, used, e.g. in Tziavos et al. (2010), Tocho et al. (2012) and Tziavos and Sideris (2013), is subject to (at least) two approximations: These are the neglect of TC associated with the reference topography (denoted reference topography TC error) and the previously discussed computation point inconsistency error because two different evaluation point heights are used in Eqs. (7) and (8). As advantage, Eq. (8) relies on the initial idea of using two integration runs to avoid the HC and associated approximation errors. Table 1 gives a summary of the four RTM variants (RTM-A to RTM-D) that will be examined in our numerical study.

Table 1 Brief characterization of RTM variants examined in this study

2.3 The baseline RTM technique (this work)

This section describes the new RTM baseline technique which mitigates the approximation errors of the classical RTM techniques. To obtain the RTM baseline solution, we evaluate Eq. (4) through a combination of gravity forward modelling techniques in the spatial domain (e.g. Heck and Seitz 2007; Kuhn et al. 2009) and in the spectral domain (e.g. Rummel et al. 1988; Chao and Rubincam 1989): A global NI in the spatial domain is used to compute term $\delta g^{\text{H}}$ (Sect. 2.3.1), while spectral-domain gravity forward modelling (SGM) to ultra-high degree delivers term $\delta g^{\text{HREF}}$ (Sect. 2.3.2), also see Fig. 3. The decisively crucial factor is the application of SGM instead of NI to obtain $\delta g^{\text{HREF}}$ even when points are inside $H^{\text{REF}} .$ Because SGM relies on exterior spherical harmonics—which are harmonic functions per definition anywhere outside the geocenter (cf., e.g. Remark 2.26 of Freeden and Gerhards 2013)—the problem of non-harmonicity (inside the reference topography, but outside the detailed topography, cf. Fig. 2) is not occurring.

Fig. 3

Test environment for RTM gravity computations—workflow, operations and comparisons. The figure shows how three forward modelling techniques are combined. Global NI and SGM give a reference solution (left and middle part) that is used to benchmark the performance of the RTM technique (right). The test environment allows examination of different RTM technique variants (A, B, C, D) as described in Sect. 2.2

2.3.1 Full-scale global NI

Newton’s integral (Eq. 1) is evaluated in the spatial domain with NI techniques (e.g. Kuhn et al. 2009; Kuhn and Hirt 2016). Global integration (that is, an integration domain of $\psi_{0} =$ 180°) yields the full-scale gravitational signal $\delta g^{\text{H}} = \delta g_{0 \ldots \infty }^{\text{NI}}$ implied by the detailed topographic mass model ($H,\rho )$ at computation points residing at the surface of the detailed topography $H.$ For the practical evaluation of Eq. (1), the high-resolution DEM is subdivided into elementary mass elements that are analytically evaluated (Sect. 3.3) before addition of all individual effects yields the total gravity signal $\delta g_{0 \ldots \infty }^{\text{NI}} .$ Because of attenuation of gravity signals with distance, the use of coarser grid resolutions to represent remote masses is permitted and common practice (e.g. Forsberg 1984; Smith 2002), without compromising the accuracy of the integration procedure.

2.3.2 Ultra-high-resolution SGM

Ultra-high-resolution SGM yields the gravity signal $\delta g^{\text{HREF}}$without employing NI. The SGM formalism and its practical aspects are well documented in the literature (e.g. Rummel et al. 1988; Balmino et al. 2012; Hirt and Kuhn 2014), so only a brief summary is given here. Input data for the SGM (cf. Fig. 3) are the SH coefficients $\bar{H}_{nm}$ of the detailed topography $H$ computed via a surface SH analysis. Heights of the reference topography $H^{\text{REF}}$ are computed via SH synthesis (Eq. 2) from $\bar{H}_{nm}$ to maximum harmonic degree $N$. A set of topographic height functions $\left( {H^{\text{REF}} /R} \right)^{p}$ of integer powers $p = 1 \ldots p_{\text{max} }$ is formed and expanded into SH coefficients $H_{nm}^{\left( p \right)}$ via surface SH analyses. Importantly, raising $H^{\text{REF}} /R$ to integer power $p$ gives rise to additional short-scale signals with spectral energy in band of degree $N + 1$ to $pN$ (cf. Freeden and Schneider 1998; Hirt and Kuhn 2014) which must be taken into account to model the gravitational field of $H^{\text{REF}}$ up to ultra-high degrees. In spherical approximation, the topographic potential coefficients $\bar V_{nm}$ implied by the reference topography $H^{\text{REF}}$ are obtained as function of the $H_{nm}^{\left( p \right)}$ (after Chao and Rubincam 1989)

$$ \bar V_{nm} = \frac{{4\pi R^{3} \rho }}{{\left( {2n + 1} \right)M}} \mathop \sum \limits_{p = 1}^{{p_{{\rm max} } }} \frac{{\mathop \prod \nolimits_{i = 1}^{p} \left( {n - i + 4} \right)}}{{p!\left( {n + 3} \right)}}H_{nm}^{\left( p \right)} $$

(9)

where $M$ is the planetary mass and $\bar V_{nm} = \left( {\bar{C}_{nm} ,\bar{S}_{nm} } \right)$ are the potential SHCs evaluated to $kN$ with $k \le p_{{\rm max} }$. Gravity values are computed via

$$ \delta g_{N1 \ldots N2}^{\text{SGM}} = \frac{GM}{{r^{2} }}\mathop \sum \limits_{n = N1}^{N2} \left( {n + 1} \right)\left( {\frac{R}{r}} \right)^{n} \mathop \sum \limits_{m = - n}^{n} \bar{V}_{nm} \bar{Y}_{nm} \left( {\varphi ,\lambda } \right) $$

(10)

in spectral band of degrees $N_{1}$ and $N_{2}$ at the location of the computation point $\left( {r = R + H_{\text{P}} , \varphi ,\lambda } \right)$. For efficient evaluation of Eq. (10) at densely spaced topography grids, 3D synthesis techniques based on Taylor series continuation (e.g. Balmino et al. 2012; Hirt 2012; Bucha and Janák 2014) can be used. The SGM delivers the gravity signal implied by the reference topography $\delta g^{\text{HREF}}$

$$ \begin{aligned} \delta g^{\text{HREF}} & = \delta g_{0 \ldots \infty }^{\text{SGM}} \\ & = \delta g_{0 \ldots N}^{\text{SGM}} + \delta g_{N + 1 \ldots kN}^{\text{SGM}} + \delta g_{kN + 1 \ldots \infty }^{\text{SGM}} \\ & \approx \delta g_{0 \ldots N}^{\text{SGM}} + \delta g_{N + 1 \ldots kN}^{\text{SGM}} \\ \end{aligned} $$

(11)

that we split into three components with different spectral content. The first is the gravity signal $\delta g_{0..N}^{\text{SGM}}$ that is implied by the reference topography $H^{\text{REF}}$ in spectral band of harmonic degrees 0 to $N$ and contains the bulk of the signal, while the other capture very short-scale gravity signals $\delta g_{N + 1..kN}^{\text{SGM}}$ and $\delta g_{kN + 1 \ldots \infty }^{\text{SGM}}$ implied by $H^{\text{REF}}$ beyond $N$ (cf. Hirt and Kuhn 2014). Because SGM can never be applied with infinite resolution, we choose the $k$ factor large enough such that the third term $\delta g_{kN + 1 \ldots \infty }^{\text{SGM}}$ becomes negligibly small. For a reference topography to $N = 2160$, reasonable choices are, e.g. $p_{\hbox{max} } = 30 \ldots 40$, $k = 5$ (cf. Hirt et al. 2016) to allow sub-mGal to $\mu$ Gal accurate modelling of the implied gravity signal to ultra-high degree $kN = 10,800$ over most areas of Earth.

3 Numerical study

3.1 Data set

We use the 3″ v1.0.1 MERIT (Multi-Error-Removed Improved-Terrain DEM) data set by Yamazaki et al. (2017). Opposed to many other SRTM products, the MERIT DEM has been stripped of the tree canopy signal and further radar error sources (see Yamazaki et al. 2017), so it represents—in good approximation—the bare ground. The MERIT DEM represents the surface of water bodies (oceans or lakes) where present and the surface of ice masses where present.

3.2 Generation of the SH reference surface

For testing of the various RTM techniques (Sect. 2.2) and computation of the RTM baseline solution (Sect. 2.3), a SH representation of the MERIT topography is required to degree 2160. It serves as high-pass filter in the construction of RTM data (Sect. 2.3.1) and is used as band-limited input topography in the SGM (Sect. 2.3.2). To derive an accurate SH expansion of the MERIT topography model, the 3″ MERIT global elevation grid was block averaged to 15″, 30″, 1′, 2′ and 5′ resolution using simple block means. Then, the down-sampled MERIT grids were harmonically analysed using the ultra-high-degree Gauss–Legendre SH analysis (GL-SHA) algorithm, as implemented in Rexer and Hirt (2015). In any case, a maximum SH expansion degree commensurate with the grid resolution (e.g. $N = 2160$ for 5′ grids, $N = 43,200$ for 15″ grids) was assigned to the GL-SHA algorithm, but the coefficients were used to $N = 2160$ only. Figure 4 shows the degree amplitudes (= square root of degree variances) of the SH coefficients as a function of the input grid resolution. The estimated SH spectrum strongly depends on the chosen input grid resolution used in the GL-SHA. When the block sizes are too large, the resulting SH spectrum is underpowered particularly at high harmonic degrees. We interpret the influence of the block size on the SH spectrum a result of down-sampling errors, including (1) aliasing, the effect of which lessens with smaller block sizes, (2) smoothing (block-mean averaging is a smoothing operation) and (3) to some degree also the influence of the interpolation to the GL grid nodes. To estimate the SH spectrum to $N = 2160$ widely free of down-sampling errors, very high-resolution grids must be used in the harmonic analysis. The coefficient differences between the $N = 2160$ SH spectra from 15″ and 5′ input grids reach maximum values of 670 m (14.8 m RMS) in the space domain. This is reduced to a maximum of 2.5 m (0.06 m RMS) for the differences between 15″ and 30″ grids. The associated error level will be at the sub-m level for 15″ resolution. These numbers exemplify the importance of using sufficiently small block sizes for accurate recovery of the SH coefficients of the global topography. If the coefficients of the SH topography were estimated from, e.g. 5′ blocks, down-sampling errors would reduce the quality of the RTM high-pass filtering, and thus of the RTM computations when seeking to spectrally augment GGMs at short spatial scales. Note that other studies thus far commonly used much lower spatial resolutions than 15″ to derive the $N$ = 2160 spectra.

Fig. 4

Degree amplitudes of SH coefficients obtained through GL-SHA with different input grid resolutions, ranging from 300″ (= 5 min) to 15″, and degree standard deviations of selected differences (dashed lines). The grey panel shows a zoom into the high-degree spectra. The figure shows the importance of using very high-resolution global grids for stable recovery of the SH spectrum to degree 2160

3.3 Test area and computations

As test area, we use the Himalaya Mountains bounded by 27°–28° geodetic latitude and 87°–88° longitude to cover extreme mountain topography providing a “worst-case” scenario. Results for a second test area (European Alps) are reported in “Appendix 1”. We use computation point grids with 15″ point separation in cell-centred registration (240 × 240 points per 1° tile), the high-resolution MERIT topography at 3″ resolution and the SH expansion of the 15″ block-averaged MERIT topography to $N = 2160$, a mass-density value $\rho = 2670$ kg m⁻³, a spherical reference radius $R = 6,378,137.0$ m and $G = 6.67384$ × 10⁻¹¹ m³ kg⁻¹ s⁻² to ensure consistency in all computations. Both in the full-scale global NI (Sect. 2.3.1) and in the RTM (Sect. 2.2), the MERIT topography is used at 3″ resolution to 0.5° radius around each computation point, and lower grid resolutions (between 15″ and 15′) beyond. While the 180° NI radius is needed to capture the full gravitational signal of the global MERIT topography, all our RTM computations (Sect. 2.2) rely on 200 km integration caps. For the discretization of the RTM integral (Eq. 5), a combination of polyhedra (in the near zone), tesseroids, prisms and point-masses was used as described in Yang et al. (2018). For the full-scale global NI, a combination of prisms (near-zone) and tesseroids (far-zone) was used, as implemented in the Curtin-inhouse Newtonian integrator that allows gravity forward modelling with a precision well below the mGal level (e.g. Hirt and Kuhn 2014).

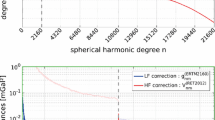
The SGM relies on the same SH topography as input model ($H^{\text{REF}}$) that is used in the RTM computations (Fig. 3). For accurate recovery of the high-frequency signals associated with topographic height functions of $p > 1$, all $\left( {H^{\text{REF}} /R} \right)^{p}$ values were computed in terms of 60″ grids, and the $H_{nm}^{\left( p \right)}$ coefficients were computed to $kN = 10,800$ with the ultra-high-degree GL-SHA extension by Rexer and Hirt (2015) that builds upon the SHTools package (Wieczorek and Meschede 2018). Figure 5 shows the first 40 contributions to the topographic potential implied by $H^{\text{REF}}$ (contributions with $p_{\text{max} } > 35$ are negligibly small) and the sum of all contributions $\bar V_{nm}$ (Eq. 9) in terms of degree variances of solid harmonic coefficients. For the synthesis of $\delta g_{0 \ldots 2160}^{\text{SGM}}$ values from $\bar V_{nm}$, 3D-SHS was applied with the isGrafLab software (Bucha and Janák 2014) with the computation points at the 3″ MERIT topography, a mean reference height of 3000 m and series expansions of 10th order. For the computation of the HF correction ($\delta g_{2161 \ldots 10,800}^{\text{SGM}}$), series expansions to 22nd order were used, which ensure sub-microGal precision (tested against 30th order).

Fig. 5

Degree variances of the topographic potential $\bar V_{nm}$ implied by the degree-2160 MERIT topography (black) and individual contributions to the topographic potential $\bar V_{nm}$ associated with the 40 topographic height functions (various colours). The figure also shows which part of the spectrum is required to compute the RTM high-frequency correction (band of degrees 2161–10,800)

3.4 Results

For our Himalaya test area, Fig. 6 illustrates the three gravity constituents $\delta g_{0 \ldots \infty }^{\text{NI}}$, $\delta g_{0 \ldots 2160}^{\text{SGM}}$ and $\delta g_{2161 \ldots 10,800}^{\text{SGM}}$. Term $\delta g_{0 \ldots 2160}^{\text{SGM}}$ captures the bulk of the gravity signal and has a similar range of values (about 800 mGal) as $\delta g_{0 \ldots \infty }^{\text{NI}}$. It delivers the large-scale features to ~ 10 km scales, but lacks—as expected—the fine structure of the field. The $\delta g_{2161 \ldots 10,800}^{\text{SGM}}$ term reaches ~ 28 mGal amplitude and ~ 5.7 mGal RMS (root-mean-square) signal strength (cf. Table 2), so is non-negligible for gravity validation experiments at the mGal level. Residual gravity obtained from the combination of $\delta g_{0 \ldots \infty }^{{{\text{RTM}} - {\text{Baseline}}}} = \delta g_{0 \ldots \infty }^{\text{NI}} - \delta g_{0 \ldots N}^{\text{SGM}} - \delta g_{N + 1 \ldots kN}^{\text{SGM}}$ represents the RTM baseline solution (Fig. 6d).

Fig. 6

Constituents and RTM baseline solution over the test area a full-scale NI, b SGM with N = 0–2160, c SGM with N = 2161–10,800, d RTM baseline solution = NI—SGM (0–2160)—SGM (2161–10,800). Unit in mGal

Table 2 Descriptive statistics of the constituents NI, SGM, HF, of the RTM (baseline solution and variants A, B, C, D) and their differences over the 1° × 1° test area “Himalaya Mountains”

Figure 7 shows the RTM gravity values from the four RTM variants A–D, see Table 1 for a summary of the most important conceptual differences. Variants A and B are similarly based on a single-run integration of residual masses, but differ in the mass geometry. Their differences—the mass simplification error—reach ~ 2 mGal RMS signal strength and amplitudes of ~ 13 mGal (panel e). Variants C and D equally decompose the mass model into two components (detailed and reference topography), but variant D neglects the TC associated with the reference topography. This error (panel f) is seen to reach very substantial RMS signal strengths of ~ 16 mGal and amplitudes of ~ 37 mGal (cf. Table 2).

Fig. 7

RTM gravity values from variants A–D and selected differences. a RTM-A (integration of RTM masses bounded by H and HREF), b RTM-B (integration of RTM masses bounded by H_RTM and 0), c RTM-C (RTM via two computations), d RTM-D (RTM via residual terrain correction). RTM-A and RTM-B rely on the harmonic correction, while RTM-C and RTM-D are free of the harmonic correction. e Differences RTM-A minus RTM-B, f differences RTM-C minus RTM-D, all units in mGal

The key results of this paper—the comparisons between the RTM baseline solution and the classical RTM variants (A–D)—are shown in Fig. 8. The original Forsberg (1984) technique (RTM-A) is in good agreement with the RTM baseline solution with ~ 1mGal RMS (Fig. 8a). However, larger differences at the ~ 10 mGal level are occasionally present; these differences likely reflect approximation errors of the “standard” $4\pi G\rho H_{\text{P}}^{\text{RTM}}$ HC (see discussion in Sect. 4). In variant RTM-B, the additional errors associated with a simplified mass geometry (use of residual heights only instead of two surfaces to bound the residual masses) previously seen in Fig. 7e come into effect, reducing the agreement with the reference solution to the ~ 2.5 mGal level (~ 15 mGal maximum differences), cf. Fig. 8b. The simplification of the mass geometry in RTM-B that has been used, e.g. for the GGMplus gravity maps (Hirt et al. 2013) as well as for Mars gravity maps (MGM 2011, Hirt et al. 2012), is not necessary and should be avoided in future computations. The RTM-C technique (two separate integration runs) avoids the previous error sources, but suffers from the problem of computation point inconsistency: the computation points reside at the surface of their respective mass model, so are vertically different. Figure 8c shows that this effect gives rise to approximation errors at the ~ 4.6 mGal RMS level (maximum differences of ~ 60 mGal). The HC issue of RTM-A is avoided in RTM-C at the expense of approximation errors much larger than those associated with the standard HC approach (Eq. 6) itself. The residuals between RTM-D and the RTM baseline solution, depicted in Fig. 8d, additionally reflect the effect of the neglected TC of the reference topography. The RTM-D technique (the $2\pi G\rho H_{\text{P}}^{\text{RTM}} - {\text{tc}}$ approximation) differs by ~ 16 mGal RMS and 95 mGal in the worst case from the reference solution. Further insight into the characteristics of the approximation errors affecting the four RTM techniques is given by Fig. 9 that shows the residuals $\delta g_{0 \ldots \infty }^{{{\text{RTM}} - {\text{Baseline}}}} - \delta g_{0 \ldots \infty }^{{{\text{RTM}}\, {\text{variants}}}}$ as function of the RTM height $H^{\text{RTM}}$. For RTM-A and RTM-C, a clear dependency of the residuals on $H^{\text{RTM}}$ is visible (Fig. 9a).

• For RTM-A, residuals are consistently at the sub-mGal level when $H^{\text{RTM}}> 0$, whereas its scatter width increases with $\left| {H^{\text{RTM}} } \right|$ when $H^{\text{RTM}} < 0$. In the latter case, the approximative $4\pi G\rho H_{\text{P}}^{\text{RTM}}$ HC was applied to all computation points, thus suggesting that the residuals reflect HC approximation errors. The residuals are constrained not to exceed a value of $\sim0.012\frac{\text{mGal}}{m} \cdot H^{\text{RTM}}$ (see light grey line in Fig. 9a). The mostly positive residuals suggest that the $4\pi G\rho H_{\text{P}}^{\text{RTM}}$ HC is often too small, so underestimates the true but unknown HC.

• For RTM-C, residuals are at the sub-mGal level only when the computation point inconsistency vanishes (i.e. $H^{\text{RTM}} \approx 0)$, but otherwise increase with $\left| {H^{\text{RTM}} } \right|$ both for positive and negative values of $H^{\text{RTM}} .$ The computation point inconsistency error can be constrained not to exceed a value of $\left| {\sim0.035\frac{\text{mGal}}{m}{\cdot} H^{\text{RTM}} } \right|$ (dark grey line in Fig. 9a).

• For RTM variants B and D (cf. Fig. 9b), the residuals are not so closely related to $H^{\text{RTM}}$, but there is a tendency that residuals are largest for RTM-B for large negative $H^{\text{RTM}}$ values (reflecting the harmonic correction issue). For RTM-D, residuals associated with the neglect of reference topography’s TC scatter within several 10s of mGal for a given $H^{\text{RTM}}$ value. The RTM-D technique, known as $2\pi G\rho H_{\text{P}}^{\text{RTM}} - {\text{tc}}$ RTM approximation, is therefore considered not suitable when high-degree reference topographies, e.g. to $N = 2160,$ are used.

For the classical technique RTM-A that is the least affected by approximation errors, a detailed analysis of residuals is presented in Fig. 10. The figure distinguishes between areas of negative (top row) and positive (bottom row) $H^{\text{RTM}}$ and shows the RTM topography (left) and residuals $\delta g_{0 \ldots \infty }^{{{\text{RTM}} - {\text{Baseline}}}} - \delta g_{0 \ldots \infty }^{{{\text{RTM}} - A}}$ (right). For areas with $H^{\text{RTM}} < 0$, the $4\pi G\rho H_{\text{P}}^{\text{RTM}}$ HC was applied. Over these areas, residuals often exceed 5 mGal amplitudes (Fig. 10b) and are generally largest where the computation points reside deep inside the RTM reference topography (Fig. 10a). However, there is no 1:1 relation recognizable between negative RTM heights and residuals which would have allowed a further error reduction through simple correction models. In the bottom row, the HC issue is absent because RTM heights are always positive (Fig. 10c). As a result, excellent agreement at the sub-mGal level (0.22 mGal RMS) is visible between residual gravity from RTM-A and our RTM baseline solution (Fig. 10d), also see Table 2. The remaining residuals reflect all remaining error sources affecting any of the modelling techniques involved to compute the terms $\delta g_{0 \ldots \infty }^{\text{NI}}$, $\delta g_{0 \ldots N}^{\text{SGM}}$ and $\delta g_{N + 1 \ldots kN}^{\text{SGM}}$ on the one hand and $\delta g_{0 \ldots \infty }^{{{\text{RTM}} - A}}$ on the other hand. Therefore, the chosen test set-up allows to control possible error sources well below the mGal level. These include (1) the discretization of the RTM and NI integrals, (2) truncation errors resulting from using limited integration radii in the RTM method, and errors in the SGM such as (3) remaining aliases, (4) truncation of the $\delta g_{N + 1 \ldots kN}^{\text{SGM}}$ term beyond $kN$ = 10,800 and (5) possible divergence of gravity series expansions (Eq. 10) inside the Brillouin sphere (sphere encompassing all field-generating masses). Note that in our case, the largest contributor to the ~ 0.2 mGal RMS level is the difference in the near-zone modelling (polyhedra in the RTM software vs. flat prisms in the global NI software); a further reduction is therefore possible.

Fig. 8

Gravity residuals between RTM baseline solution and RTM variants A to D shown in Fig. 7. Error patterns visible are in a harmonic correction, b as before, plus the simplified use of H_RTM heights, c different 3D point locations in both integration runs, d as before, plus the neglected terrain correction of the reference topography. The harmonic correction is only necessary for RTM-A and RTM-B, while no such correction is needed for RTM-C and RTM-D. The circle indicate locations where harmonic correction errors are largest in RTM-A, while errors are mostly smaller in RTM-C. Unit in mGals

Fig. 9

Gravity residuals for RTM variants A–D in mGal as function of the RTM height in m. a Residuals for techniques A and C, b residuals for techniques B and D. a Also shows the functions (in grey) constraining the maximum approximation errors as function of the RTM height (see text)

Fig. 10

Detailed analysis of gravity residuals of RTM variant A. a negative RTM heights, b residuals for computation points with negative RTM heights, c positive RTM heights, d residuals for computation points with positive RTM heights. Unit for heights in m (left column), unit for gravity residuals in mGal (right column)

4 Discussion

From a conceptual point of view, our work suggests two fundamentally different “mechanisms” that govern gravity evaluations inside the residual topographic masses.

• When NI techniques are employed for the computation of residual gravity—as in the classical RTM technique—the gravitational potential is non-harmonic for points inside the reference topography, requiring some form of the HC in the context of the RTM approach.

• In SGM, there is strong evidence that gravity values can be computed without the need to apply a harmonic correction when the computation points are located inside the field-generating reference topography. This is because with SGM, the needed harmonicity of the gravitational potential is implicitly ensured.

The key hypothesis of our paper is that spectral modelling techniques do not require a special treatment of the HC issue because they offer an inherent solution.

In agreement with the potential field theory, NI techniques deliver the gravitational potential that is harmonic outside the masses (that is, $H^{\text{RTM}} \ge 0)$, but non-harmonic inside the masses (that is, $H^{\text{RTM}} < 0)$. As such, there is nothing wrong with the NI, but it is the non-harmonicity inside the RTM masses that makes the RTM gravity values from Eq. (5) “incompatible” with, e.g. field functionals that can be observed outside the Earth’s surface where the gravitational potential is harmonic. To overcome the inconsistency for the purpose of external gravity field modelling, some solution is required:

• Use of the mass condensation scheme by Forsberg (1984), where the non-harmonicity of the gravitational potential obtained from NI inside the reference topography is corrected with the harmonic correction (Eq. 6), or

• Use of spectral techniques (SGM) which yield the gravitational potential via a finite linear combination of spherical harmonics, which are, by definition, harmonic also inside the masses. The gravitational potential from SGM can be thought of as a regularized downward continuation of the external harmonic potential inside the RTM reference topographic masses, but outside the detailed (Earth’s) topography.

Throughout our numerical study, no correction has been applied in the SGM for points inside the reference topography, while the standard $4\pi G\rho H_{\text{P}}^{\text{RTM}}$ HC was considered for those points in the RTM masses. The fact that the $4\pi G\rho H_{\text{P}}^{\text{RTM}}$ term is known to be approximative provides a plausible explanation for the (overall rather small) RMS residuals of ~ 1.5 mGal (cf. Table 2). It strongly suggests that a separate modelling of the HC is not required for the SGM. Importantly, however, for the SGM techniques to be applicable for computation of $\delta g^{\text{HREF}}$, the solid external spherical harmonic series (Eq. 10) must not suffer from the effect of series divergence (e.g. Moritz 1980; Hu and Jekeli 2015; Hirt and Kuhn 2017) that may seriously deteriorate (or even render useless) the results obtained from SGM based on external spherical harmonics. However, results by Hirt et al. (2016) suggest that gravity $\delta g_{0 \ldots N}^{\text{SGM}}$ from SGM and $N$ = 2160 reference topographies is not affected by series divergence, and the high-frequency signals $\delta g_{N + 1 \ldots kN}^{\text{SGM}}$ only little affected (say ~ 1–2 mGal at most) over very few locations around the globe when the computation points reside at the surface of the reference topography. Therefore, series divergence is not an obstacle for SGM-based gravity computations from $N$ = 2160 Earth reference topographies. However, we emphasize that we cannot rigorously prove our hypothesis and therefore cannot exclude a part of the differences shown in Fig. 10b to be associated with gravity syntheses inside the degree-2160 field-generating mass distribution. Then, our hypothesis would be not valid and some correction procedure required. In that case however, the corrections would be substantially smaller than those associated with the $4\pi G\rho H_{\text{P}}^{\text{RTM}}$ HC.

Compared to the strategy of assessing the RTM technique performances with ground-truth data (e.g. from gravity data bases) and GGMs (e.g. EGM2008, Pavlis et al. 2012 or EIGEN-6C4, Förste et al. 2015), the central benefit of the RTM test environment (Fig. 3) is its independence from any errors affecting real data (observation errors, biases, GGM commission errors), and from the effect of unknown mass-density anomalies. Our RTM testing scheme allowed scrutinizing classical RTM techniques (Sect. 2.2) down to the sub-mGal level (Table 2; Figs. 9, 10), so may provide insight into even subtle effects affecting the modelling quality in future studies.

We note that in Grombein et al. (2017), a related procedure has been presented. Similar to our work, Grombein et al. (2017) applied spatial and spectral techniques to high-pass filter gravity functionals implied by the topography. Different to our work, they obtained their spectral solution as a SH expansion of global geoid/potential values from numerical integration of a detailed 60″ topography. This aspect is conceptually similar to the $\delta g_{0 \ldots \infty }^{\text{NI}} - \delta g_{0 \ldots N}^{\text{SGM}}$ part of our RTM baseline solution. As the main difference to our work, Grombein et al. (2017) did not model the very high-frequency gravity signal term $\delta g_{N + 1 \ldots kN}^{\text{SGM}}$, because this was not required in their study. In our study, this term forms an important constituent of the RTM test environment required for a rigorous examination of the classical RTM techniques in Sect. 3. Note that the Rexer et al. (2018) HF correction is identical with our $\delta g_{N + 1 \ldots kN}^{\text{SGM}}$ term as a key component of the RTM test environment. We acknowledge that all RTM variants as well as the RTM baseline strategy conceptually suffer also from the RTM low-frequency (LF) error, as defined in Rexer et al. (2018). However, in the comparisons, this effect cancels out which is why a correction was not attempted in this study.

5 Conclusions

This study has assessed four selected RTM techniques using a new RTM baseline solution relying on a combination of ultra-high SGM with global NI. The RTM baseline technique has been used in a test environment to characterize and quantify four different types of approximation errors (1. harmonic correction, 2. mass model simplification, 3. computation point inconsistency, 4. neglect of terrain correction of reference topography) for $N = 2160$ reference topographies commonly used in physical geodesy over the last ten years. All tested RTM techniques were shown to be affected by one or two of the approximation errors (Table 3).

Table 3 Summary of RTM variants and technique-inherent approximation errors

RTM technique A that uses a single cap integration over residual masses and applies the $4\pi G\rho H_{\text{P}}^{\text{RTM}}$ harmonic correction for $H^{\text{RTM}} < 0$ has been shown to be in RMS agreement of ~ 1.1 mGal over our test area with the baseline solution, so is the best of the four tested classical RTM techniques. For the other variants, RMS approximation errors were shown to increase to ~ 2.4 mGal for RTM-B, ~ 4.6 mGal for RTM-C and ~ 16.8 mGal for RTM-D, the latter may be unacceptably large for most applications. In a relative sense, among the four identified RTM approximation errors, the $4\pi G\rho H_{\text{P}}^{\text{RTM}}$ HC approximation influences the quality of RTM gravity values the least. It should be noted that the empirical accuracy values depend on chosen test area, with the Himalaya Mountains likely providing a worst-case scenario. For numerical results from the European Alps area, see “Appendix 1”.

While technique A offers excellent sub-mGal agreement (~ 0.2 mGal) with the baseline solution where $H^{\text{RTM}} \ge 0$, approximation errors associated with the $4\pi G\rho H_{\text{P}}^{\text{RTM}}$ HC govern the error budget where $H^{\text{RTM}} < 0$. To further reduce these errors, higher-order series expansions of the harmonic correction should be explored in the future, as already pointed out in Forsberg (2010), Omang et al. (2012) and Bucha et al. (2016) and tested in Omang et al. (2012) to first order, or the improved HC solution based on multipole expansion of the terrain gravity field (Vermeer and Forsberg 1992).

The RTM baseline solution itself is not subjected to three of the four RTM approximation errors and most likely not affected by the harmonic correction problem. Therefore, it can be considered as superior to classical RTM techniques. One could consider using the RTM baseline instead of RTM-A in practical applications, thus mitigating the harmonic correction issue. However, for global-scale forward modelling application of 1″ or 3″ DEMs, the computational requirements for a full-scale global NI will be challenging, though with the increased availability of supercomputing resources becoming more feasible. An appealing alternative might be the combination of the new cap-integration SGM technique by Bucha et al. (2019) with classical spatial cap integration. This combination is considered promising because it could combine all conceptual benefits of the RTM baseline solution with the numerical efficiency of the classical RTM techniques.

The RTM test environment presented in this study should be suitable to validate other future short-scale gravity forward modelling techniques, to study effects such as ellipsoidal mass geometry at short scales and to clarify the role of non-harmonicity in evaluations inside the residual masses for other RTM functionals such as quasigeoid heights and vertical deflections. So far, the harmonic corrections for functionals other than RTM gravity are often assumed to be negligible, but a quantification is still missing for $N = 2160$ reference topographies. The insights into RTM approximation errors is expected to be useful for application of RTM approaches for gravity interpolation or prediction, e.g. in the context of remove–compute–restore geoid computations or the development of future GGMs such as EGM2020 (Barnes et al. 2015) where forward modelling might be used as fill-in, or to further reduce approximation errors in future global gravity maps.

Appendix 1

1.1 Results for the European Alps area

Table 4 reports the descriptive statistics of all gravity components and their differences over the European Alps. The RTM-A is in ~ 0.6 mGal RMS agreement with the baseline solution. For RTM-B, the agreement deteriorates to the level of ~ 1.8 mGal RMS (reflecting the mass simplification error) and RTM-C to the level of ~ 3.2 mGal RMS (computation point inconsistency error). For RTM-D, the RMS-differences w.r.t. the baseline solution are ~ 12.6 mGal and maximum errors exceed 50 mGal (cf. Table 4). Focussing on RTM-A and points with positive (negative) RTM elevations, the agreement with the baseline solution is 0.21 mGal (0.77 mGal). In the latter case, maximum errors may reach amplitudes of up to ~ 7.5 mGal, reflecting the approximative character of the harmonic correction. Overall, the error level associated with the various RTM approximations is somewhat lower over the European Alps (Table 4) than the Himalayas (Table 3) which is explained by the different ruggedness of the test areas.

Table 4 Descriptive statistics of the constituents NI, SGM, HF of the RTM (baseline solution and variants A, B, C, D) and their differences over the 2° × 2° test area “European Alps” (45°–47° latitude and 7°–9° longitude)