Satellite antenna phase center errors: magnified threat to multi-frequency PPP ambiguity resolution

Abstract

The dearth of frequency-specific satellite antenna phase centers (APCs), such as GPS Block IIF L5 phase center offsets (PCOs) and BeiDou System (BDS) phase variations (PVs), inconveniences multi-frequency precise point positioning (PPP). We find that the GNSS observation biases caused by incorrect frequency-specific APCs are both spatially incoherent and time variable. This spatiotemporal incoherency will be magnified by over a hundred times in the case of multi-frequency PPP wide-lane ambiguity resolution (PPP-WAR) and is likely to defer PPP convergences. We hence first impose deliberate errors on the Galileo frequency-specific APCs to mimic the common faulty operations of equating the GPS L5 with the L1/L2 ionosphere-free PCOs and ignoring the BDS PVs in typical high-precision GNSS. We then investigate how such APC errors can harm multi-frequency PPP using one month of E1/E5a/E5b data from 43 globally distributed stations. Although the APC errors tested in this study have minimal impact on dual-frequency PPP, a 5-mm horizontal PCO error does prolong multi-frequency PPP convergences by 15%; a 200-mm vertical PCO error or a PV error of up to 10 mm can even grow the convergence times by 60%. The vertical positioning precision of single-epoch PPP-WAR is deteriorated on average by 15 cm under a 200-mm vertical PCO error. Therefore, accurate frequency-specific GPS/BDS satellite APCs should be determined for multi-frequency PPP to maximize its convergence advantages over dual-frequency PPP.

1 Introduction

GNSS antenna phase center (APC) errors at either satellite or receiver end can compromise high-precision positioning and distort the scale of GNSS-based terrestrial reference frames (TRFs) (Ge et al. 2005; Zhu et al. 2003). The APC errors are usually split into the phase center offset and variations (PCO/PVs): the PCO can be taken as the mean phase center, while the PVs represent its further refinement to describe the instantaneous APC position with respect to elevations/nadirs and azimuths in the antenna’s local reference frame. Especially, Zhu et al. (2003) pointed out that a z-PCO (i.e., the radial direction towards the Earth’s center) error of 10 cm at the GPS satellites would result in a height bias of $-5$ mm at ground stations, or equivalently a scale bias of 0.78 parts-per-billion (ppb) for GPS-based TRFs.

Since GPS satellite APCs from the manufacturers were untrustworthy in high-precision positioning (e.g., Dilssner 2010; Dilssner et al. 2016; Mader and Czopek 2001), the International GNSS Service (IGS) chose to estimate GPS APCs by both fixing receiver APCs and aligning station coordinates with the ITRF (International Terrestrial Reference Frame) (Schmid et al. 2007, 2016). In particular, satellite PCOs were first estimated using the ionosphere-free combination observables where identical APCs on L1 and L2 were presumed. Next, nadir-dependent PVs without azimuthal variations were computed by fixing the pre-determined satellite PCOs (Schmid and Rothacher 2003). Schmid et al. (2007) demonstrated that the vertical or the z-PCOs were highly correlated with satellite clocks due to the limited GPS nadir span of 0–14$^\circ$ against ground stations; in contrast, the horizontal or the xy-PCOs were subject to the satellite attitude control and related to the Sun’s orbital elevations. As a result, satellite PCOs were likely to have large uncertainties when estimated along with satellite clocks and orbital elements. It was reported that the GPS/GLONASS satellite APCs disagreed among the IGS analysis centers to several centimeters for the xy-PCOs while a few decimeters for the z-PCOs (Schmid et al. 2016). Steigenberger et al. (2016) showed that the Galileo z-PCOs determined by GFZ (GeoForschungsZentrum) and DLR (Deutsches Zentrum für Luft- und Raumfahrt) deviated from each other by up to 20 cm. The discrepancy among the BDS-2 (BeiDou System) z-PCOs computed with disparate but professional software even reached 150 cm for IGSO (Inclined GeoSynchronous Orbit) satellites (Huang et al. 2018).

While the IGS efforts for satellite APCs were most intensified towards dual-frequency GNSS signals, the incompleteness of the third-frequency APCs in igs14.atx for either satellite or receiver end has been challenging high-precision multi-frequency GPS, BDS and Galileo applications. As a tentative remedy, it is often presumed that BDS-2 B1I/B2I, BDS-3 B1I/B1C/B2a and Galileo E1/E5a signals share the GPS receiver L1/L2 APCs, whereas the third-frequency GPS L5, BDS B3I and Galileo E5b/E6 replicate the GPS satellite/receiver L2 APCs, in spite of the unknown risks (e.g., Fan et al. 2019; Gong et al. 2020; Xiao et al. 2019). Fortunately, for the third IGS reprocessing campaign ([21]), a pilot ANTEX (Antenna Exchange Format) file igsR3_2077.atx is developed which contains multi-frequency GPS/BDS/Galileo/QZSS receiver APCs measured by the Geo++ robot for a good number of mainstream ground antennas (Schmitz et al. 2008; Villiger et al. 2020). Rebischung et al. (2019) have verified the consistency between the legacy GPS and the Galileo receiver APCs in estimating daily station coordinates. Regarding the satellite APCs, on the other hand, the European Global Navigation Satellite Systems Agency (GSA) and the Cabinet Office, Government of Japan (CAO) have released the manufacturers’ Galileo and QZSS (Quazi-Zenith Satellite System) APCs, respectively, for all frequency bands since 2017 (European GNSS Service Centre 2017; sps35 2017). Later, China Satellite Navigation Office (CSNO) published BDS-2/3 multi-frequency satellite antenna PCOs on December 30, 2019, though ignoring the PVs (China Satellite Navigation Office 2019). However, the GPS APCs announced by the satellite manufacturers are debated (Marquis and Reigh 2015), and we still rely on the IGS ionosphere-free APC estimates.

Therefore, of great concern to the GNSS community is the adverse impact of the ionosphere-free GPS APCs, the unknown GPS Block IIF L5 APCs and the missing BDS PVs on multi-frequency positioning. In this study, we aim at investigating whether and how multi-frequency GNSS precise point positioning (PPP) is compromised by equating the ionosphere-free APCs with real L1/L2 APCs, duplicating the L2 APCs to L5 as well as neglecting the BDS PVs. With regard to the receiver APCs, as a comparison, Xin et al. (2020) have found that Galileo dual-frequency PPP convergences were negligibly affected even though the GPS receiver APCs were thoughtlessly applied to Galileo; conversely, such reckless duplication prolonged the convergence times of triple-frequency PPP by 70% on average. Since the Galileo satellite and receiver APCs are quite complete in igsR3_2077.atx, we impose deliberate common APC errors on Galileo satellites to mimic the scenarios of incorrectly presumed GPS/BDS satellite frequency-specific APCs, and then demonstrate the adverse consequences. The article is thus organized as follows. Sections 2, 3 and 4 show how the APC errors are projected onto Galileo observations, and why they are magnified drastically in multi-frequency PPP; Sect. 5 shows the processing strategies for orbits, clocks and phase biases; Sects. 6 and 7 present the relevant results and discuss the remaining frequency-specific errors before Sect. 8 draws conclusions.

2 GNSS observation biases caused by satellite APC errors

The undifferenced triple-frequency Galileo observation equations between station i and satellite k in the unit of length can be briefly written as

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} P_{i,1}^{k}&{}=\rho _i^k+\dfrac{\gamma _i^k}{f_1^2}-d_{i,1}^k \\ P_{i,2}^{k}&{}=\rho _i^k+\dfrac{\gamma _i^k}{f_2^2}-d_{i,2}^k \\ P_{i,3}^{k}&{}=\rho _i^k+\dfrac{\gamma _i^k}{f_3^2}-d_{i,3}^k \\ L_{i,1}^{k}&{}=\rho _i^k-\dfrac{\gamma _i^k}{f_1^2}+\lambda _1 N_{i,1}^k-d_{i,1}^k \\ L_{i,2}^{k}&{}=\rho _i^k-\dfrac{\gamma _i^k}{f_2^2}+\lambda _2 N_{i,2}^k-d_{i,2}^k \\ L_{i,3}^{k}&{}=\rho _i^k-\dfrac{\gamma _i^k}{f_3^2}+\lambda _3 N_{i,3}^k-d_{i,3}^k \end{aligned} \end{array}\right. \end{aligned}$$

(1)

where $P_{i,1}^k$, $P_{i,2}^k$ and $P_{i,3}^k$ denote the pseudorange measurements on the E1, E5a and E5b signals, respectively; likewise, $L_{i,1}^k$, $L_{i,2}^k$ and $L_{i,3}^k$ denote the carrier-phase measurements; $\rho _i^k$ is the nominal station-satellite geometric distance which also contains clock errors, tropospheric delays and hardware delays; $f_1$, $f_2$ and $f_3$ are the frequencies of E1, E5a and E5b signals ($f_1$:$f_2$:$f_3$=154:115:118), respectively, and $\lambda _1=\dfrac{v}{f_1}$, $\lambda _2=\dfrac{v}{f_2}$ and $\lambda _3=\dfrac{v}{f_3}$ are their wavelengths where v is the speed of light in vacuum; $\dfrac{\gamma _i^k}{f_1^2}$, $\dfrac{\gamma _i^k}{f_2^2}$ and $\dfrac{\gamma _i^k}{f_3^2}$ nominally represent the first-order ionospheric delays on E1, E5a and E5b, respectively, where $\gamma _i^k$ is contaminated by pseudorange hardware delays (Geng et al. 2020); $N_{i,1}^k$, $N_{i,2}^k$ and $N_{i,3}^k$ are the nominal ambiguity terms containing non-integer hardware delays (Ge et al. 2008); of particular note, $d_{i,1}^k$, $d_{i,2}^k$ and $d_{i,3}^k$ denote the observation biases induced by satellite APC errors on the E1, E5a and E5b signals, respectively. We presume that the receiver APCs are precisely known while the satellite APCs are not, though both have been nominally corrected in Eq. 1. In addition, the terms for higher-order ionospheric delays and random noise are ignored in Eq. 1 for brevity.

Fig. 1

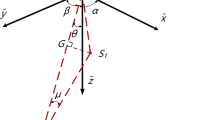
A diagram illustrating the projection of Galileo satellite antenna phase center (APC) errors onto the line-of-sight (LOS) directions. The ${\widetilde{z}}$ axis denotes the radial direction towards the Earth’s center, the ${\widetilde{y}}$ axis is along the solar panel axis and the ${\widetilde{x}}$ axis completes the right-handed satellite body frame. $O_0$ is the true APC and $O_1$ is the nominal APC which are both frequency dependent. G denotes the ground receiver APC. $\alpha$, $\beta$ and $\theta$ symbolize the angles between the axes ${\widetilde{x}}$, ${\widetilde{y}}$, ${\widetilde{z}}$ and the LOS direction $\overrightarrow{O_0G}$. T denotes the pedal point when $O_1$ is projected onto $\overrightarrow{O_0G}$. Note that the origin of the satellite body frame has been translated from the mass center to $O_0$

It is worth pointing out that the observation biases $d_{i,1}^k$, $d_{i,2}^k$ and $d_{i,3}^k$ are specific to not only frequencies, but also ground stations since their underlying APC errors have to be projected onto the line-of-sight (LOS) directions. Figure 1 depicts such an observation bias which equates $|\overrightarrow{O_0G}|-|\overrightarrow{O_1G}|$ where $O_0$ and $O_1$ are the true and nominal APCs, respectively, and G is the receiver APC in the satellite body frame. Hat “$\rightarrow$” denotes a vector and “$\mid \,\mid$” calculates its magnitude. Since G is more than 20,000 km away from the satellites and the APC errors usually do not exceed a few meters, we can approximate that $|\overrightarrow{O_0G}|-|\overrightarrow{O_1G}|\approx |\overrightarrow{O_0T}|$ where T is the pedal point of $O_1$ when projected onto $\overrightarrow{O_0G}$. Then, we have

$$\begin{aligned} |\overrightarrow{O_0T}|=\overrightarrow{O_0O_1}\cdot \widetilde{O_0G} \end{aligned}$$

(2)

where hat “$\widetilde{\;\;}$” denotes a unit vector. Suppose

$$\begin{aligned} \overrightarrow{O_0O_1}=a{\widetilde{x}}+b{\widetilde{y}}+c{\widetilde{z}} \end{aligned}$$

(3)

where ${\widetilde{x}}$, ${\widetilde{y}}$ and ${\widetilde{z}}$ denote the unit vectors for the three axes of the satellite body frame; a, b and c are the magnitudes of $\overrightarrow{O_0O_1}$ in the three orthogonal directions, or in other words, the x-PCO, y-PCO and z-PCO errors, respectively. As mentioned above, a and b can be up to a few centimeters, while c can reach several decimeters. Eq. 2 then becomes

$$\begin{aligned} \begin{aligned} |\overrightarrow{O_0T}|&=a{\widetilde{x}}\cdot \widetilde{O_0G}+b{\widetilde{y}}\cdot \widetilde{O_0G}+c{\widetilde{z}}\cdot \widetilde{O_0G} \\&=a\cos {\alpha }+b\cos {\beta }+c\cos {\theta } \end{aligned} \end{aligned}$$

(4)

where $\alpha$, $\beta$ and $\theta$ are the angles between the axes ${\widetilde{x}}$, ${\widetilde{y}}$, ${\widetilde{z}}$ and the LOS direction $\overrightarrow{O_0G}$. Roughly for Galileo satellites, the off-nadir angle $\theta \in [0^\circ ,\,12.5^\circ ]$, while both $\alpha$ and $\beta$ fall in $[77.5^\circ ,\,102.5^\circ ]$. Therefore, we have

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} \cos {\alpha }&{}\in [-0.22,\;0.22] \\ \cos {\beta }&{}\in [-0.22,\;0.22] \\ \cos {\theta }&{}\in [0.98,\;1.00] \end{aligned} \end{array}\right. \end{aligned}$$

(5)

where “$[\,]$” denotes an interval and “$\in$” means “fall in.” On account of the frequency-specific observation biases induced by APC errors in Eq. 1, we reformulate Eq. 4 as

$$\begin{aligned} d_{i,g}^k=a_g\cos {\alpha _i^k}+b_g\cos {\beta _i^k}+c_g\cos {\theta _i^k}+h_{i,g}^k \end{aligned}$$

(6)

where g denotes frequency E1, E5a or E5b; $h_{i,g}^k$ represents satellite PVs. We ignore the dependence of $\alpha$, $\beta$ and $\theta$ on frequency g, which holds in theory but presumed minimal since $|\overrightarrow{O_0G}|\gg |\overrightarrow{O_0O_1}|$.

Fig. 2

The GNSS observation biases (mm) caused by APC errors in the satellite body frame. The top-left panel shows the color-coded biases imputed to the z-PCO error of 10 mm (i.e., $c_g\cos {\theta _i^k}$ in Eq. 6), and the top-right panel shows those caused by both x-PCO and y-PCO errors of 10 mm (i.e., $\sqrt{a_g^2\cos ^2{\alpha _i^k}+b_g^2\cos ^2{\beta _i^k}}$ in Eq. 6). The concentric circles denote the off-nadir angle which is actually $\theta$ in Fig. 1. The most outer circle for the 12.5$^\circ$ nadir is graduated with azimuths. Note that the two color bars have different ranges. Similarly, the bottom two panels show the time-varying APC error-induced biases at station JFNG (Fig. 4) with respect to each visible Galileo satellite on day 133 of 2019. Each color represents a satellite. The bottom-left panel is for the 10-mm z-PCO error, while the bottom-right is for the horizontal PCO errors. Note that the bottom two panels have different vertical axis scales

Equation 5 shows that the z-PCO errors contribute much more to the observation biases than the horizontal PCO errors. However, it also reveals that the z-PCO error-induced observation biases change little with respect to nadirs and azimuths since its scaling factor $\cos {\theta }$ spans 0.98–1.00 only. In contrast, the observation biases caused by the horizontal PCO errors change more widely by a scaling factor ranging from $-0.22$ to 0.22. To be concrete, the top panels of Fig. 2 illustrate such bias variations with respect to nadirs and azimuths in the satellite body frame. Clearly, the z-PCO error-induced observation biases are nadir-dependent only where the peak bias corresponds to the zero nadir. For a 10-mm z-PCO error, the resulting biases change within about 9.8–10.0 mm for Galileo satellites. This fact implies that most (approx. 98%) z-PCO errors shared among ground stations can be absorbed by satellite clocks, echoing Schmid et al. (2007). In contrast, the xy-PCO error induced observation biases are strongly subject to both nadir and azimuth angles, or in other words spatially incoherent, which means that they cannot be totally assimilated into the satellite clocks. If both horizontal PCO components have a 10-mm error, the resulting biases can vary approximately within ± 3.0 mm. This result implies that the Galileo observations from widely distributed ground stations are biased diversely by the satellite antennas’ horizontal PCO errors, and such disparate observation biases among stations can hardly be fully absorbed by satellite clocks.

Fig. 3

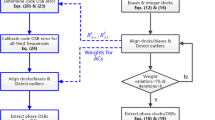
Processing scheme. Solid rectangles denote processes (e.g., orbit, clock and phase bias determination) at the server end and dashed rectangles denote those (e.g., PPP-F, PPP-WAR and PPP-AR) at the user end. Other shapes denote input/output data. Note that PPP-WAR requires both E1/E5a and E5a/E5b wide-lane phase biases while dual-frequency wide-lane AR needs only E1/E5a biases

On the other hand, in the bottom panels of Fig. 2, we present the satellite APC error-induced observation biases for station JFNG located in Wuhan, China, for day 133 of 2019. All visible Galileo satellites are color coded. When there is a 10-mm z-PCO error for a satellite, the resultant observation biases are mostly within 9.75–10.0 mm over the 24 h, except for E14 and E18 which suffer from elliptical orbits. Disregarding the satellite clock absorption above, this fact implies that the z-PCO error-induced carrier-phase biases for a particular satellite observed by a station over a continuous arc can mostly (approx. 98%) be absorbed into the ambiguities. However, we should also keep in mind that such favorable “absorption” may not suffice to mitigate the observation biases stemming from exceedingly large z-PCO errors. Moreover, in the bottom-right panel where a 10-mm error is imposed on both horizontal PCOs, the resultant observation biases for a satellite can range relatively widely within about 4 mm, accounting for 40% of the original PCO errors. We thus realize that the temporal variation of satellite APC error-induced observation biases is similar in magnitude to the spatial incoherency of such biases among ground stations, both of which thereby complete the spatiotemporal characteristics of those observation biases.

3 Absorption of satellite APC error-induced observation biases

In this study, we compute Galileo satellite clocks using the raw E1/E5a pseudorange and carrier-phase observables listed in Eq. 1 (Fig. 3). No explicit combination observables need to be formed. When such satellite clocks are applied to the E5b signals for multi-frequency PPP, a satellite-specific code bias has to be estimated on the E5b pseudorange at each station (Geng et al. 2020). The satellite clock estimates will absorb the hardware delays and most z-PCO error-induced biases on E1/E5a pseudorange (cf. Eq. 1).

Similarly, the ambiguities will absorb the hardware delays and most z-PCO error-induced biases on carrier-phase data, both of which contribute to the phase biases that destroy the integer property of PPP ambiguities. Ambiguity-fixed PPP is thus predicated on the correction of (extra-)wide-lane and narrow-lane phase biases to retrieve the integer ambiguities (Ge et al. 2008). In general, the phase bias estimation is to extract the fractional-cycle parts of PPP ambiguities which should be common among all stations observing the same Galileo satellites (Geng et al. 2019a). This is because the phase biases are initially defined to be associated with satellite-dependent quantities which affect all ground station observations unanimously. Again, we process the raw E1/E5a/E5b observables to gain the raw ambiguity estimates. The extra-wide-lane, wide-lane and narrow-lane ambiguities can then be computed as follows (Geng et al. 2020)

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} {\hat{N}}_{i,\mathrm {ew}}^k&{}={\hat{N}}_{i,3}^k-{\hat{N}}_{i,2}^k\\ {\hat{N}}_{i,\mathrm {w}}^k&{}={\hat{N}}_{i,1}^k-{\hat{N}}_{i,2}^k\\ {\hat{N}}_{i,1}^k&{}=\dfrac{f_1}{f_1-f_2}{\hat{N}}_{i,1}^k-\dfrac{f_2}{f_1-f_2}\biggl ({\hat{N}}_{i,2}^k+\breve{N}_{i,\mathrm {w}}^k\biggr ) \end{aligned} \end{array}\right. \end{aligned}$$

(7)

where hats “$\hat{\;\;}$” and “$\breve{\;\;}$” denote float and resolved ambiguities, respectively; ${\hat{N}}_{i,1}^k$ is now taken as the narrow-lane ambiguity as it has a wavelength of about 10.9 cm. Based on Eq. 7, we define a function

$$\begin{aligned} \psi _g^k=\digamma _{i=1}^m{\hat{N}}_{i,g}^k \end{aligned}$$

(8)

to compute the phase bias $\psi _g^k$ on frequency g for satellite k using the relevant ambiguities from m stations observing satellite k. One implementation of this $\digamma$ function is to separate the satellite phase bias from its receiver counterpart by differencing between satellites, and in turn the fractional-cycle part from its integer part by means of rounding operations (Ge et al. 2008; Geng et al. 2019a). It is $\psi _g^k$ that enables ambiguity-fixed PPP as they calibrate the phase bias contamination on integer ambiguities. To be specific, we correct the float ambiguities for satellite k with

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} {\hat{N}}_{i,\mathrm {ew}}^k-\psi _\mathrm {ew}^k&{}={\hat{N}}_{i,3}^k-{\hat{N}}_{i,2}^k-\psi _\mathrm {ew}^k\\ {\hat{N}}_{i,\mathrm {w}}^k-\psi _\mathrm {w}^k&{}={\hat{N}}_{i,1}^k-{\hat{N}}_{i,2}^k-\psi _\mathrm {w}^k\\ {\hat{N}}_{i,1}^k-\psi _1^k&{}=\dfrac{f_1}{f_1-f_2}{\hat{N}}_{i,1}^k-\dfrac{f_2}{f_1-f_2}\biggl ({\hat{N}}_{i,2}^k+\breve{N}_{i,\mathrm {w}}^k\biggr )-\psi _1^k \end{aligned} \end{array}\right. \nonumber \\ \end{aligned}$$

(9)

to achieve resolvable (extra-)wide-lane and narrow-lane ambiguities which can later be fixed to $\breve{N}_{i,\mathrm {ew}}^k$, $\breve{N}_{i,\mathrm {w}}^k$ and $\breve{N}_{i,1}^k$, respectively, through an integer least-squares estimator (Teunissen 1995).

In addition, since 98% of the z-PCO error-induced observation biases are absorbed by ambiguities, the phase bias estimation using the $\digamma$ function will be extra subject to such APC error-induced biases. However, what undermines the phase bias estimation is that the APC error-induced observation biases are in nature spatially incoherent and time variable (cf., Fig. 2), and thus cannot be thoroughly absorbed by satellite clocks or ambiguities. As a result, the spatiotemporal variability of those observation biases is likely to disturb the phase bias estimation from time to time and thus impair their temporal stability as preferred in ambiguity-fixed PPP. In this case, the spatially incoherent and time-variable parts of the biases imputed to the satellite APC errors should be cautiously addressed in high-precision GNSS. Based on Eqs. 5 and 6, we define

$$\begin{aligned} \varDelta d_{i,g}^k=0.44a_g+0.44b_g+0.02c_g+\varDelta h_{i,g}^k \end{aligned}$$

(10)

to denote the peak-to-peak variation of the APC error-induced observation biases over space and time. $\varDelta d_{i,g}^k$ is used in this study to quantify the nominal disturbances of satellite APC errors (i.e., PCOs $a_g$, $b_g$ and $c_g$ as well as PVs $h_{i,g}^k$) on the phase bias estimation and ambiguity-fixed PPP.

4 Satellite APC errors to defer PPP convergences

4.1 Dual-frequency PPP

We use the raw E1/E5a data to carry out dual-frequency PPP by estimating slant ionospheric delays without forming explicitly the ionosphere-free combination observables. If such slant ionospheric delays are computed as white-noise like parameters, our “uncombined” processing is essentially equivalent to standard PPP based on the ionosphere-free observables which are (Zhang et al. 2012; Zumberge et al. 1997)

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} P_{i,\mathrm {IF}}^{k}&{}=p_1P_{i,1}^k-p_2P_{i,2}^k\\ &{}=\rho _i^k-\biggl (p_1d_{i,1}^k-p_2d_{i,2}^k\biggr )\\ L_{i,\mathrm {IF}}^{k}&{}=p_1L_{i,1}^k-p_2L_{i,2}^k\\ &{}=\rho _i^k+\biggl (p_1\lambda _1 N_{i,1}^k-p_2\lambda _2 N_{i,2}^k\biggr )-\biggl (p_1d_{i,1}^k-p_2d_{i,2}^k\biggr )\\ &{}=\rho _i^k+\lambda _\mathrm {n}N_{i,1}^k+p_2\lambda _2\breve{N}_{i,\mathrm {w}}^k-\biggl (p_1d_{i,1}^k-p_2d_{i,2}^k\biggr ) \end{aligned} \end{array}\right. \nonumber \\ \end{aligned}$$

(11)

where $\lambda _\mathrm {n}$ is the narrow-lane wavelength; $\breve{N}_{i,\mathrm {w}}^k$ is the resolved wide-lane ambiguity; and

$$\begin{aligned} \left\{ \begin{array}{l} p_1=\dfrac{f_1^2}{f_1^2-f_2^2}\approx 2.26\\ p_2=\dfrac{f_2^2}{f_1^2-f_2^2}\approx 1.26 \end{array}\right. \end{aligned}$$

(12)

The narrow-lane ambiguity $N_{i,1}^k$ is derived only when the wide-lane ambiguity $N_{i,\mathrm {w}}^k$ is fixed to $\breve{N}_{i,\mathrm {w}}^k$. Substitute Eq. 6 into Eq. 11 and we have the APC error-induced bias on the ionosphere-free observables

$$\begin{aligned} \begin{aligned} d_{i,\mathrm {if}}^k=&p_1d_{i,1}^k-p_2d_{i,2}^k\\ =&\biggl (p_1a_1-p_2a_2\biggr )\cos {\alpha _i^k}+\biggl (p_1b_1-p_2b_2\biggr )\cos {\beta _i^k}\\&\quad +\biggl (p_1c_1-p_2c_2\biggr )\cos {\theta _i^k}\\&\quad +\biggl (p_1h_{i,1}^k-p_2h_{i,2}^k\biggr ) \end{aligned} \end{aligned}$$

(13)

According to Eqs. 12 and 13, we can derive that $d_{i,\mathrm {if}}^k=d_{i,1}^k=d_{i,2}^k$ if $a_1=a_2$, $b_1=b_2$, $c_1=c_2$ and $h_{i,1}^k=h_{i,2}^k$, but $d_{i,\mathrm {if}}^k$ can become larger if $d_{i,1}^k$ and $d_{i,2}^k$ differ. Similar to Eq. 10, we have

$$\begin{aligned} \begin{aligned} \varDelta d_{i,\mathrm {if}}^k=&0.44\biggl (p_1a_1-p_2a_2\biggr )+0.44\biggl (p_1b_1-p_2b_2\biggr )\\&\quad +0.02\biggl (p_1c_1-p_2c_2\biggr ) +\varDelta \biggl (p_1h_{i,1}^k-p_2h_{i,2}^k\biggr ) \end{aligned}\nonumber \\ \end{aligned}$$

(14)

The convergence efficiency of dual-frequency PPP is governed by pseudorange noise (Geng et al. 2011). Phase ambiguities, either the ionosphere-free ambiguities $\biggl (p_1\lambda _1 N_{i,1}^k-p_2\lambda _2 N_{i,2}^k\biggr )$ or their narrow-lane counterparts $N_{i,1}^k$ in Eq. 11, shall converge to precise estimates under the constraint of pseudorange. The lower the pseudorange errors, the faster convergence of PPP float (i.e., PPP-F) solutions can be achieved and the faster ambiguity-fixed PPP (i.e., PPP-AR to resolve $N_{i,1}^k$) can be ensured. Then revisiting Eq. 14, it can be seen that whether $d_{i,\mathrm {if}}^k$ will increase the error of the pseudorange $P_{i,\mathrm {IF}}^{k}$ depends generally on the relative APC error between the first two frequencies (i.e., $a_1-a_2$, $b_1-b_2$, $c_1-c_2$ and $h_{i,1}^k-h_{i,2}^k$).

4.2 Multi-frequency PPP

Multi-frequency PPP is also carried out using the raw observables in Eq. 1, and thus raw phase ambiguities on E1, E5a and E5b can be computed (Geng et al. 2020). It is worth pointing out that multi-frequency pseudorange can only minimally shorten PPP convergence times in contrast to dual-frequency pseudorange (Geng et al. 2020; Guo et al. 2016; Guo and Geng 2018). In fact, the advantage of multi-frequency signals in accelerating PPP convergences can be more manifested after resolving the (extra-)wide-lane ambiguities (Geng et al. 2020). We therefore compose the wide-lane ambiguities using the raw E1 ambiguity estimates minus their E5a counterparts, as well as the extra-wide-lane ambiguities using the E5b minus E5a ambiguity estimates (cf., Eq. 7). After phase bias corrections with both $\psi _\mathrm {ew}^k$ and $\psi _\mathrm {w}^k$, we then attempt to resolve both (extra-)wide-lane ambiguities (Fig. 3). Once they are fixed to integers successfully, we strictly superimpose the following two hard constraints for the raw ambiguity parameters on the normal equation of uncombined PPP

$$\begin{aligned} \left\{ \begin{array}{l} N_{i,1}^k-N_{i,2}^k=\breve{N}_{i,\mathrm {w}}^k\\ N_{i,3}^k-N_{i,2}^k=\breve{N}_{i,\mathrm {ew}}^k \end{array}\right. \end{aligned}$$

(15)

where $\breve{N}_{i,\mathrm {ew}}^k$ is the resolved extra-wide-lane ambiguity. In this case, we are essentially achieving the two ambiguity-fixed wide-lane combination observables

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} L_{i,\mathrm {W}}^k&{}=\dfrac{f_1}{f_1-f_2}L_{i,1}^k-\dfrac{f_2}{f_1-f_2}L_{i,2}^k \\ &{}=\rho _i^k+\dfrac{\gamma _i^k}{f_1f_2}+\lambda _\mathrm {w}\breve{N}_{i,\mathrm {w}}^k-\biggl (\dfrac{f_1}{f_1-f_2}d_{i,1}^k-\dfrac{f_2}{f_1-f_2}d_{i,2}^k\biggr )\\ L_{i,\mathrm {EW}}^k&{}=\dfrac{f_2}{f_2-f_3}L_{i,2}^k-\dfrac{f_3}{f_2-f_3}L_{i,3}^k \\ &{}=\rho _i^k+\dfrac{\gamma _i^k}{f_2f_3}+\lambda _\mathrm {ew}\breve{N}_{i,\mathrm {ew}}^k-\biggl (\dfrac{f_2}{f_2-f_3}d_{i,2}^k-\dfrac{f_3}{f_2-f_3}d_{i,3}^k\biggr ) \end{aligned} \end{array}\right. \nonumber \\ \end{aligned}$$

(16)

where $\lambda _{i,\mathrm {ew}}^k$ and $\lambda _{i,\mathrm {w}}^k$ are the (extra-)wide-lane wavelengths, respectively. These two observables can be taken as P1/P2-like pseudorange as shown in Eq. 1, since they are both unambiguous now. An ionosphere-free wide-lane observable can be essentially constituted using such two unambiguous carrier-phase combinations, that is

$$\begin{aligned} \begin{aligned} L_{i,\mathrm {IFW}}^k&=\dfrac{f_1}{f_1-f_3}\biggl (L_{i,\mathrm {W}}^k-\lambda _\mathrm {w}\breve{N}_{i,\mathrm {w}}^k\biggr )\\&\quad -\dfrac{f_3}{f_1-f_3}\biggl (L_{i,\mathrm {EW}}^k-\lambda _\mathrm {ew}\breve{N}_{i,\mathrm {ew}}^k\biggr ) \\&=\rho _i^k-\biggl (q_1d_{i,1}^k+q_2d_{i,2}^k-q_3d_{i,3}^k\biggr ) \end{aligned} \end{aligned}$$

(17)

where

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} q_1&{}=\dfrac{f_1^2}{(f_1-f_2)(f_1-f_3)}\approx 16.89\\ q_2&{}=\dfrac{f_2^2}{(f_1-f_2)(f_3-f_2)}\approx 113.03\\ q_3&{}=\dfrac{f_3^2}{(f_1-f_3)(f_3-f_2)}\approx 128.93 \end{aligned} \end{array}\right. \end{aligned}$$

(18)

We here reiterate that the combination observables in Eqs. 16 and 17 are not explicitly formed throughout our data processing, but implicitly or naturally enabled after the strict imposition of the hard constraints in Eq. 15. We present the (extra-)wide-lane and the ionosphere-free wide-lane combination observables in their explicit forms here to more clearly unravel how the satellite APC error induced observation biases are enlarged.

Equation 17 denotes an ionosphere-free ambiguity-fixed phase combination observable, which resembles the ionosphere-free pseudorange in Eq. 11 since they are both free from ambiguities. However, Eq. 17 is anticipated to have higher precision than the ionosphere-free pseudorange, despite its phase noise amplified by about 172 times (i.e., $\sqrt{q_1^2+q_2^2+q_3^2}$) compared to the raw carrier-phase (e.g., Geng and Bock 2013; Xiao et al. 2019; Xin et al. 2020). Such claim of “higher precision” is especially true for $L_{i,\mathrm {IFW}}^k$ of GPS and BDS-2 because the amplification factors therein decline to about 110, and even more to about 70 regarding Galileo E6 and BDS-3 signals (Geng et al. 2020). Geng et al. (2019b) have already shown that $L_{i,\mathrm {IFW}}^k$ alone can ensure decimeter-level positioning using a single epoch of data, which is called instantaneous PPP wide-lane ambiguity resolution (PPP-WAR). Therefore, $L_{i,\mathrm {IFW}}^k$ can be taken as a new pseudorange-like phase observable to replace the role of $P_{i,\mathrm {IF}}^k$ (Eq. 11) in speeding up the convergences of ionosphere-free and narrow-lane ambiguities to achieve PPP-AR eventually (Geng and Bock 2013).

Furthermore, in Eq. 17, the satellite APC error-induced observation bias and its peak-to-peak spatiotemporal variation can be expressed, respectively, as

$$\begin{aligned} \begin{aligned} d_{i,\mathrm {ifw}}^k&= q_1d_{i,1}^k+q_2d_{i,2}^k-q_3d_{i,3}^k\\&= \biggl (q_1a_1+q_2a_2-q_3a_3\biggr )\cos {\alpha _i^k}\\&\quad +\biggl (q_1b_1+q_2b_2-q_3b_3\biggr )\cos {\beta _i^k}\\&\quad +\biggl (q_1c_1+q_2c_2-q_3c_3\biggr )\cos {\theta _i^k}\\&\quad +\biggl (q_1h_{i,1}^k+q_2h_{i,2}^k-q_3h_{i,3}^k\biggr ) \end{aligned} \end{aligned}$$

(19)

and

$$\begin{aligned} \begin{aligned} \varDelta d_{i,\mathrm {ifw}}^k&=0.44\biggl (q_1a_1+q_2a_2-q_3a_3\biggr )\\&\quad +0.44\biggl (q_1b_1+q_2b_2-q_3b_3\biggr )\\&+0.02\biggl (q_1c_1+q_2c_2-q_3c_3\biggr )\\&\quad +\varDelta \biggl (q_1h_{i,1}^k+q_2h_{i,2}^k-q_3h_{i,3}^k\biggr ) \end{aligned} \end{aligned}$$

(20)

We can see that the PCO errors on the E5a and E5b signals are magnified by over 110 times (i.e., $q_2>110$ and $q_3>110$). This amplification with respect to multi-frequency data cannot be thoughtlessly ignored, since the resulting observation bias $d_{i,\mathrm {ifw}}^k$ is likely to bias dramatically the pseudorange-like phase observations $L_{i,\mathrm {IFW}}^k$. Even for the z-PCO errors which are presumably mitigated thanks to their near-thorough assimilation into the satellite clocks and ambiguities, the remaining spatially incoherent or time-variable errors (i.e., about 2% in proportion) can still reach several centimeters or even more under an amplification factor of more than 100 times (e.g., when $c_1=c_2=50$mm and $c_3=0$), not to mention the horizontal PCO errors. Therefore, regarding the problematic manufacturer’s GPS APCs and the missing BDS PVs, the APC error amplification becomes a real jeopardy now and has the potential to undermine the convergence efficiency of multi-frequency PPP-AR.

5 Data processing

The third IGS reprocessing employs a pilot ANTEX file igsR3_2077.atx to model satellite and receiver APCs (IGS AC Coordinator 2019). It contains the multi-frequency phase centers for all Galileo satellites and a good number of receiver antennas. In this study, we deliberately modified the E1/E5a/E5b APCs of all Galileo satellites to investigate the impact of satellite PCO/PV errors on multi-frequency PPP-AR. Note that whenever the E1/E5a APCs were modified, Galileo orbits and clocks had to be re-estimated using the E1/E5a data in the igs14 frame (Zhao et al. 2017). Satellite (extra-)wide-lane and narrow-lane phase biases were computed every 15 min in a simulated real-time manner and were re-estimated once satellite APCs on any Galileo frequency were changed. We used the solar radiation pressure model proposed by Montenbruck et al. (2015) for Galileo satellites as well as the satellite attitudes defined by GSA (European GNSS Service Centre 2017). In addition, the satellite clock estimation was also based on the E1/E5a signals with the pre-determined Galileo orbits fixed (Geng et al. 2020). Figure 3 summarizes the processing scheme of this study.

Fig. 4

Galileo station distribution. Eighty-five stations (green solid circles) are used for precise orbit determination and 131 stations (open circles) for satellite clock and phase bias computation. Another 43 stations (red solid circles) are used to test multi-frequency PPP. All stations have been corrected for multi-frequency receiver APCs using igsR3_2077.atx

Table 1 Models and strategies for Galileo PPP data processing

In total, Fig. 4 shows that 85 stations were used to compute Galileo orbits and 131 stations were used to estimate satellite clocks and phase biases for days 121–151 of 2019. We collected 30-s data from the IGS and the ARGN (Australian Regional GNSS Network). It is worth noting the multi-frequency Galileo data at all stations have been calibrated with the real Galileo receiver APCs, rather than those duplicated from GPS. The validity of these Galileo receiver APCs has been confirmed by Xin et al. (2020). At another 43 globally distributed stations, we carried out PPP where the correction models and processing strategies refer to Table 1. We started a simulated real-time kinematic PPP processing at the beginning of each integer hour and terminated it after 2 h. Then, we have nominally 23 solutions for each day at each station. However, we removed those solutions with less than six Galileo satellites at any epoch, and eventually there remained 9358 eligible solutions.

Fig. 5

The differences (mm) between the manufacturers’ and the estimated Galileo and BDS-2/3 satellite PCOs. Galileo, BDS-2/3 PCO estimates are based on E1/E5a, B1I/B2I and B1I/B3I ionosphere-free observables, respectively (Huang et al. 2018; Steigenberger et al. 2016; Yan et al. 2019). The estimated PCOs are subtracted from the manufacturers’ PCOs on the Galileo E1/E5a/E6, BDS-2 B1I/B2I/B3I and BDS-3 B1I/B2a/B3I signals, and then plotted in red, green and gold bars, respectively (cf., China Satellite Navigation Office 2019; European GNSS Service Centre 2017); within each panel, the PCO differences for the three frequencies of each satellite are sorted in ascending order and plotted in solid, dotted and hatched bars, respectively. Note that the three panels have different vertical scales and the bars beyond the vertical axis ranges are not plotted completely

At the 43 test stations, we first computed their kinematic PPP solutions based on the true Galileo satellite APCs to benchmark those based on the deliberately modified APCs. In total, we computed ambiguity-float solutions (i.e., PPP-F), the (extra-)wide-lane ambiguity-fixed solutions (i.e., PPP-WAR) and the narrow-lane ambiguity-fixed solutions (i.e., PPP-AR) (cf., Fig. 3) (Geng et al. 2019b, 2020). Equations 14 and 20 demonstrate that it is the relative error between all frequency-specific APCs of a satellite that matters in this study. Figure 5 thus shows the differences between the manufacturers’ and the estimated PCOs for each Galileo and BDS-2/3 satellite. The estimated PCOs are based on ionosphere-free observables, as is the case with GPS satellite PCOs. The solid, dotted and hatched bars denote different frequencies. We can see that BDS manufacturers’ horizontal PCOs can differ from the ionosphere-free PCOs by over 5 mm while all satellites’ vertical PCOs can differ by over 200 mm. Therefore, Table 2 presents three Galileo APC modification strategies in this study to mimic the GPS/BDS APC deficiencies. In particular, the satellites’ horizontal PCOs would be both increased by 2 or 5 mm, and the vertical PCOs be changed by ± 50, ± 100 or $\pm 200$ mm; GPS Block IIF and IIR-M PVs were added to the Galileo E5b PVs at all azimuths. With respect to such APC modifications, the following sections show how they affect multi-frequency PPP. Note that a “successful PPP convergence” in this study indicates achieving either successful PPP-AR (i.e., narrow-lane ambiguity resolution), or persistent positioning precision of better than 10 cm in the horizontal coordinates in the case of ambiguity-float or PPP-WAR solutions. Daily position estimates were used to benchmark the kinematic positions.

Table 2 Galileo satellite APC modification strategies to investigate GPS/BDS APC deficiencies

6 Results

6.1 Phase biases in the case of E1/E5a PCO errors

Section 3 claims that the APC error-induced observation biases, if not fully absorbed by satellite clocks or ambiguities, can deviate phase bias estimates from time to time. Figure 6 hence shows the phase biases every 15 min on day 133 impacted by the satellites’ E1/E5a 5-mm xy-PCO and 200-mm z-PCO errors (the middle and bottom panels), in contrast to those based on the true Galileo APCs (i.e., the benchmark phase biases in the top panels). All satellite phase biases have been color coded. The extra-wide-lane phase biases in the top-left panel are quite stable over time where the maximum and mean variations over the 24 h across all Galileo satellites are far smaller than 0.1 cycles. In contrast, the PCO errors make the mean temporal variations of extra-wide-lane phase biases 2–3 times larger. This outcome is ascribed to the fact that the PCO errors are imposed on the E1/E5a signals, but the extra-wide-lane phase biases are computed using E5a/E5b. Then, the PCO error-induced time-variable biases disturbing the E5a ambiguities will be completely translated into the E5b minus E5a (or extra-wide-lane) ambiguities, and in turn destabilize the extra-wide-lane phase biases. Fortunately, this disturbance is quite limited and extra-wide-lane ambiguity resolution will not be harmed.

Fig. 6

(Extra-)wide-lane and narrow-lane phase biases (cycle) every 15 min in the case of E1/E5a PCO errors on day 133 of 2019. The top panels show the phase biases based on the true Galileo PCOs, i.e., the benchmark phase biases. The middle and bottom panels show the phase biases based on the 5-mm xy-PCO errors and the 200-mm z-PCO errors, respectively. Each curve represents one Galileo satellite. “Max.” and “Mean” denote the maximum and the mean phase bias variations across all satellites in each panel

In contrast, the PCO errors do not grow the temporal instability of wide-lane phase biases, of which the maximum and the mean remain 0.15 cycles and 0.11 cycles, respectively, across all satellites over the 24 h in Fig. 6. We believe that the wide-lane phase biases’ stability seems immune to the PCO errors because the E1 and E5a signals suffer from identical PCO errors and their impacts mostly cancel in the computation of E1 minus E5a (or wide-lane) ambiguities. Similarly, despite the PCO errors, the narrow-lane phase biases’ maximum and mean variations are changed by less than 11% and 6%, respectively, against the benchmark phase biases. At this point, we realize that the wide-lane and narrow-lane phase biases’ temporal stabilities are minimally affected thanks to the same satellite PCO errors imposed on both E1 and E5a. However, we should not rule out the possibility that the temporal steadiness of phase biases can be compromised seriously in the case of other PCO errors.

Table 3 Mean convergence times (min) and kinematic positioning precision (m) of Galileo dual- and multi-frequency PPP at the 43 test stations in the case of different satellite E1/E5a PCO errors (mm)

Fig. 7

Distribution of PPP-WAR convergence times (min) in the case of different E1/E5a PCO errors. a, b The distribution of PPP-WAR and dual-frequency PPP-F convergence times, respectively, when the true Galileo PCOs are used. c, d The distributions of PPP-WAR convergence times in the case of 2-mm and 5-mm E1/E5a xy-PCO errors, respectively. Likewise, e–g are for the 50-mm, 100-mm and 200-mm z-PCO errors, and h–j are for the $-50$-mm, $-100$-mm and $-200$-mm z-PCO errors, respectively. The percentages of the kinematic PPP solutions that converge within 2 h in addition to those converging within 30 and 60 min are plotted at the top-right corner of each panel

6.2 PPP in the case of E1/E5a PCO errors

GPS satellite PCOs in the igs14.atx are not real frequency-specific quantities, but computed with ionosphere-free combination observables by presuming identical PCOs on the L1 and L2 signals. However, Fig. 5 shows that identical PCOs across frequencies are usually not true, especially for the vertical PCOs. For simplicity, we modified the satellite E1 and E5a PCOs equally as designed in Table 2. Table 3 summarizes the mean convergence times and kinematic positioning precisions for various dual- and multi-frequency PPP solutions. The “0” line indicates the benchmark Galileo solutions based on the true satellite APCs.

With regard to dual-frequency PPP, the convergence times of neither float nor fixed solutions are affected considerably by the E1/E5a PCO errors. They (i.e., ${\bar{t}}_\mathrm {dF}$ and ${\bar{t}}_\mathrm {dAR}$) remain around 30.3 min with slight deviations of less than 0.3 min, and 91–95% of all solutions converge successfully within 2 h irrespective of the PCO errors. The explanation for such immunization to PCO errors is twofold: first, neither wide-lane nor narrow-lane phase biases are impaired substantially by the PCO errors (cf., Fig. 6); second, Table 2 has shown that the peak-to-peak bias variation $\varDelta d_{i,\mathrm {if}}^k$ is less than 0.5 cm, which negligibly increases the pseudorange errors. However, the 5-mm xy-PCO errors slow down the PPP-WAR convergences (i.e., ${\bar{t}}_\mathrm {WAR}$) by 3.2 min on average, and as a result, the achievement of PPP-AR solutions (i.e., ${\bar{t}}_\mathrm {mAR}$) is delayed by 3.3 min compared to the benchmark solutions. The z-PCO errors can also cause such convergence degradation, though they must be at least 10 times larger. Figure 7 shows the distribution of convergence times for all 9358 PPP-WAR solutions. Without any PCO errors, 75.4% of benchmark PPP-WAR solutions can achieve convergences within 30 min (Fig. 7a). This percentage however drops to 69.9% and 64.1% in the case of the 5-mm xy-PCO (Fig. 7d) and the 200-mm z-PCO error (Fig. 7g) on E1/E5a, respectively. It is manifested that the horizontal PCO errors are able to prolong the convergences more markedly than their equal vertical counterparts. Owing to these PCO errors, a more nettlesome problem is that more and more multi-frequency solutions have even longer, rather than shorter, convergence times than those of dual-frequency solutions. In particular, the last two columns of Table 3 show that about 25% of benchmark solutions get worse in terms of longer convergence times when the E1/E5a-based PPP transitions to the E1/E5a/E5b-based PPP. This percentage rises to about 35% if the horizontal PCO errors reach 5 mm or the vertical PCO errors reach 200 mm.

Besides the exacerbated convergences, the vertical positioning precisions of the single-epoch PPP-WAR solutions (i.e., ${\bar{A}}_\mathrm {iWAR}$) are also deteriorated by up to 16 cm in the case of $-200$ mm z-PCO errors. However, whatever PCO errors are imposed on the satellite antennas, the kinematic positioning precisions are affected by less than 1 cm for both dual- and multi-frequency PPP-AR, as exposed in columns ${\bar{A}}_\mathrm {dAR}$ and ${\bar{A}}_\mathrm {mAR}$. The east, north and up components stay generally at the precision of 1, 1 and 3 cm, respectively. We believe that the positioning precision of PPP-AR is governed by narrow-lane ambiguity resolution where the PCO-induced observation bias variation is less than 0.5 cm (cf., Table 2).

Despite the adverse impacts of E1/E5a PCO errors above, an unusual case is the multi-frequency PPP solution impacted by the 50-mm z-PCO error. In Table 3, the convergence times of neither PPP-WAR nor multi-frequency PPP-AR are deferred by the 50-mm z-PCO error, but appear slightly shorter than the benchmark convergence times. This phenomenon can be more clearly illustrated by Fig. 7e where 77.8% of all solutions converge within 30 min, exceeding the 75.4% in Fig. 7a. Even if the z-PCO error rises to 100 mm (Fig. 7f), there are still as high as 75.9% of solutions achieving convergences using less than 30 min of data. The convergence deteriorations imputed to the $-50$, $-100$ and $-200$-mm z-PCO errors in Fig. 7h–j, respectively, are not reproduced by those in the case of the 50, 100 and 200-mm z-PCO errors in Fig. 7e–g, though these PCO errors have identical magnitudes but only opposite signs.

6.3 PPP in the case of E5b PCO errors

To inspect the impact of unknown GPS Block IIF L5 APCs, we modified the Galileo E5b APCs in either xy or z directions. Similar to Table 3, Table 4 exhibits the mean convergence times at the 43 test stations impacted by increasing E5b PCO errors. Since the E1/E5a APCs are not modified, $\varDelta d_{i,\mathrm {if}}^k$ in Table 2 remains zero and the mean convergence times (${\bar{t}}_\mathrm {dF}$ and ${\bar{t}}_\mathrm {dAR}$) stay at 30.4 and 30.2 min for float and fixed dual-frequency PPP, respectively, no matter how heavily the E5b PCOs are changed for all satellites. On the contrary, $\varDelta d_{i,\mathrm {ifw}}^k$ in Table 2 can reach several tens of centimeters, which defers multi-frequency PPP convergences, as shown by ${\bar{t}}_\mathrm {WAR}$ and ${\bar{t}}_\mathrm {mAR}$ in Table 4. Regarding the kinematic positioning precision, as expected, the single-epoch PPP-WAR solutions (${\bar{A}}_\mathrm {iWAR}$) suffer clearly in the vertical from the E5b PCO errors, while PPP-AR for both dual-frequency and multi-frequency solutions (${\bar{A}}_\mathrm {dAR}$ and ${\bar{A}}_\mathrm {mAR}$) are minimally impaired. Overall, the statistics in Table 4 deliver a similar pattern to that in Table 3, corroborating the more detrimental impact of the satellite PCO errors on multi-frequency PPP than dual-frequency PPP.

One interesting observation is that the multi-frequency PPP deterioration caused by the growing positive z-PCO error in Table 4 resembles that caused by the growing negative z-PCO error in Table 3, and vice versa. A plausible explanation is that $q_1+q_2-q_3=1$ as shown in Eq. 18, which means that the term $q_1c_1+q_2c_2$ (i.e., E1/E5a z-PCO errors) in Eq. 20 will be quite close to $q_3c_3$ (i.e., E5b z-PCO errors) if $c_1=c_2=c_3$ and $c_1$ is not huge (cf., Table 2).

Table 4 Mean convergence times (min) and kinematic positioning precision (m) of Galileo dual- and multi-frequency PPP at the 43 test stations in the case of different satellite E5b PCO errors (mm)

In addition, both Tables 3 and 4 show that the E1/E5a 50–100-mm and the E5b − (50–100)-mm z-PCO errors imposed on all Galileo satellites may improve, rather than degrade, the multi-frequency PPP convergences. Figure 8 thus exemplifies the PPP convergences in terms of the 3D positioning errors for station BRUX during the hour 18:00–19:00 on day 133. The top panels show the convergences when the 100-mm or $-100$-mm z-PCO error is imposed on E5b, while the bottom panels show those for the E1/E5a 100-mm or $-100$-mm z-PCO errors. In Fig. 8a, as expected, the z-PCO error slows down the PPP-WAR convergence (green curve) to the level of the PPP-F solution (black curve). However, in Fig. 8b, the $-100$-mm z-PCO error surprisingly makes the PPP-WAR convergence even rapider than that of the so-called benchmark solution (red curve). This seemingly abnormal result appears again in Fig. 8c, but is enabled by the positive 100-mm z-PCO error. Then, a question arises of whether the GSA Galileo z-PCOs need corrections or not, which will be discussed in section 7.

Fig. 8

PPP convergences at station BRUX over the hour 18:00–19:00 on day 133 in the case of 100-mm and $-100$-mm z-PCO errors. The ambiguity-float (PPP-F) dual-frequency solutions, the PPP-WAR solutions with and without PCO errors are plotted in black, green and red colors, respectively

Table 5 Mean convergence times (min) and kinematic positioning precision (m) of Galileo dual- and multi-frequency PPP at the 43 test stations in the case of different satellite PV errors

Fig. 9

Distribution of PPP-WAR convergence times (min) in the case of GPS Block IIF and IIR-M PV errors added to E5b PVs. The top two panels show the PVs of GPS Block IIF and IIR-M satellites expanded to all azimuths, and their resulting time distributions are shown in the bottom two panels whose illustrations refer to Fig. 7

6.4 PPP in the case of E5b PV errors

Besides the satellite PCOs, the PV errors are also a critical factor to degrade multi-frequency PPP. [8] shows that the Galileo PVs are normally as small as 1 mm across all nadirs and azimuths. However, [35] shows that the L1 and L2 PVs at some nadirs and azimuths for QZS-2 and QZS-4 can depart from each other by up to 7 mm. This suggests that BDS satellite PVs, which have to be presumed zero at the moment, may have errors of up to several millimeters. We therefore pick the PVs of GPS Block IIF and IIR-M satellites to simulate the possible BDS PV errors. We first duplicate the GPS nadir-dependent PVs to all azimuths, which produces the top panels of Fig. 9. Next, such PVs are added to the E5b PVs of all Galileo satellites. The top panels of Fig. 9 show that the IIF PVs at different nadirs and azimuths can differ by up to 10.5 mm, whereas the IIR-M PVs differ by up to 21.0 mm. According to Eq. 20, these two numerals will result in $-135.4$ cm and $-270.8$ cm for $\varDelta d_{i,\mathrm {ifw}}^k$ (Table 2). We can see that the absolute $\varDelta d_{i,\mathrm {ifw}}^k$ resulting from 10–20-mm PV errors easily exceed those caused by the 200-mm z-PCO errors. This can be understood by inspecting Eq. 20 where the PV errors add directly to $\varDelta d_{i,\mathrm {ifw}}^k$, while the z-PCO errors are first scaled by 0.02 before the addition. Therefore, appreciable satellite PV errors can more easily bias GNSS observations and do more harm to multi-frequency PPP.

Table 5 shows the mean PPP convergence times for the 43 test stations in the case of different E5b PV errors. It can be seen that the IIF and IIR-M PV errors prolong the PPP-WAR convergence times (${\bar{t}}_\mathrm {WAR}$) by 60–100%, and the PPP-AR convergence times (${\bar{t}}_\mathrm {mAR}$) by 45–95%. These percentages are more excessive than those imputed to the PCO errors shown in Tables 3 and 4. Correspondingly, Fig. 9 shows the distribution of the PPP-WAR convergence times with respect to the IIF and IIR-M PV errors. In detail, only 90% and 86% of all PPP-WAR solutions are able to converge successfully within 2 h, while 50% and 40% converge within 30 min under the two types of PV errors. Again, these percentages are clearly smaller than those corresponding to the PCO errors in Fig. 7. In addition, single-epoch PPP-WAR positioning precision (${\bar{A}}_\mathrm {iWAR}$) in Table 5 is also worsened by the PV errors, even in the horizontal components. Compared to Table 4, the vertical component shows doubled deteriorations.

Table 6 Mean RMS of the differences (mm) in the along-track, cross-track and radial directions between the Galileo orbits impacted by E1/E5a PCO errors and the benchmark orbits without PCO errors

7 Discussions

Section 3 has pointed out that the APC error-induced observation biases cannot be fully absorbed by satellite clocks or ambiguities because they are spatially incoherent and time variable. One remaining question is whether the satellite orbital parameters can assist in absorbing such observation biases since we re-estimate the orbits whenever the E1/E5a PCOs are modified. Table 6 thus shows the orbit comparison in terms of mean RMS differences in the along-track, cross-track and radial directions between the E1/E5a PCO error impacted orbits and the benchmark Galileo orbits based on the true PCOs. As exposed by the 2-mm and 5-mm xy-PCO errors, the horizontal PCO errors appear to have a 1-to-1 translation to the along-track and cross-track orbit components, though the satellite body frame does not always coincide with the orbital frame exactly. On the other hand, the vertical PCO errors have minor impact on orbits, but can still bias them by up to 15 mm if the z-PCO errors reach 200 mm. On account of the ${\bar{t}}_\mathrm {WAR}$ and ${\bar{t}}_\mathrm {mAR}$ statistics in Table 3, we realize that the E1/E5a PCO errors do change the Galileo orbits, but such orbit readjustments do not, or at least cannot sufficiently, absorb the APC error-induced spatially incoherent and time-variable observation biases.

Geng et al. (2020) have reported that 24.5% of multi-frequency PPP-WAR solutions converged more slowly, rather than rapidly, than the dual-frequency PPP-F solutions, when the GPS APCs were duplicated for BDS, Galileo and QZSS. Such solutions were designated as “ineffective PPP-WAR.” In the benchmark solution of this study (i.e., the “0” line of Table 3), we corrected for the true Galileo receiver and satellite APCs, but the percentage of ineffective PPP-WAR solutions still reaches 24.3% (cf., $t_\mathrm {dF}<t_\mathrm {WAR}$). This fact suggests that we cannot impute ineffective PPP-WAR to the APC errors only. There remain other frequency-specific errors which slow down multi-frequency PPP convergences, such as multipath effects, higher-order ionospheric delays and inter-frequency clock biases (Montenbruck et al. 2011). Such errors other than satellite APCs will also be amplified hugely through Eqs. 17 and 18.

Figure 8, Tables 3 and 4 reveal that the Galileo vertical PCOs announced by [8] might have an error of up to several centimeters after the satellites were deployed in space. This finding may echo the results by Rebischung et al. (2019) where the estimated Galileo z-PCOs using E1/E5a ionosphere-free data could differ from the GSA values by up to 7 cm and those by Bertiger et al. (2020) where their re-adjusted Galileo z-PCOs deviate from the GSA values by 13 cm on average. However, we should be cautious that this 7-cm or 13-cm difference could merely be a sort of PCO estimation errors, as agreed on by Bertiger et al. (2020). Another plausible cause for the seeming Galileo z-PCO errors is that the station coordinates in the igs14 frame were tightly constrained to compute Galileo satellite orbits/clocks where the satellite PCOs were fixed to the GSA values in this study. The incompatibility between the igs14 frame scale and the GSA Galileo vertical PCOs can be translated into a z-PCO error for the whole constellation. In either case, this unresolved problem warrants an approach of estimating satellite PCOs precisely for each frequency, especially when the GPS manufacturers’ APCs are untrustworthy and the official BDS APCs’ validity is pending.

In addition, it is worth indicating that the deliberate satellite APC errors tested in this study are rather limited, though they are selected according to our best knowledge on the possible GPS/BDS APC errors. We always impose identical APC errors on all satellites for either xy-PCO or z-PCO, which however is unrealistic and cannot represent all possible scenarios the GPS/BDS satellite APCs may suffer from. For example, we can impose identical PCO errors simultaneously on E1, E5a and E5b signals. Then, $\varDelta d_{i,\mathrm {ifw}}^k$ in Eq. 20 will not be magnified anymore because $q_1+q_2-q_3=1$.

8 Conclusions and suggestions

Since frequency-specific GPS satellite APCs are debated and the BDS satellite antenna PVs are missing from the spacecraft manufacturers, we study the impact of such APC deficiencies on multi-frequency PPP using Galileo E1/E5a/E5b signals whose true satellite APCs have been released by [8]. Theoretical analysis shows that the satellite APC errors cannot be fully absorbed by satellite orbits, clocks or ambiguities, and consequently, the horizontal PCO errors can result in 20 times larger spatially incoherent and time-variable observation biases on the pseudorange and carrier-phase than the vertical PCO errors can. We hence impose 2–5-mm errors on the Galileo satellite horizontal PCOs, while 50–200-mm errors on the vertical PCOs; the GPS Block IIF and IIR-M PVs in igs14.atx are added to the Galileo E5b PVs to mimic the scenarios when GPS and BDS APCs are untrustworthy. We then investigate how the convergences and positioning of multi-frequency PPP are harmed by such deliberate APC errors, and compare them against those of dual-frequency PPP.

With 31 days of Galileo data from globally distributed stations, we find that the convergence times of multi-frequency PPP-WAR solutions will be increased by 9–15% in the case of 5-mm horizontal PCO errors, and 30–60% in the case of 200-mm vertical PCO errors for all satellites, while those of dual-frequency PPP solutions remain almost the same no matter what PCO errors are imposed. Even worse, more and more (i.e., from 25% to 50%) multi-frequency PPP solutions converge even more slowly, rather than rapidly, than their dual-frequency counterparts if the vertical PCO errors rise to 200 mm. While the vertical positioning precision of single-epoch PPP-WAR can be worsened by up to 40% under various PCO errors, the positioning precisions of both dual- and multi-frequency PPP-AR are negligibly affected. We demonstrate that multi-frequency PPP is more deteriorated because the spatially incoherent and time-variable observation biases induced by APC errors can be magnified by a few hundred times, whereas those in dual-frequency PPP are amplified by at most a few times. This issue therefore warrants the frequency-specific satellite APC estimation to maximize the convergence advantages of multi-frequency PPP over its dual-frequency counterpart.