1 Introduction

GNSS precise point positioning (PPP) has been constantly plagued by its slow convergences or initializations to ambiguity-fixed solutions, which usually take tens of minutes of continuous observations (e.g., Bisnath and Gao 2009; Zumberge et al. 1997). Varieties of approaches have been proposed to resolve this problem. A well-known route is to provide external ionosphere corrections for each satellite, where the limitation is the unrealistic requirement for a dense reference network over wide areas if a significant improvement is desired (e.g., Banville et al. 2014; Geng et al. 2010; Wübbena et al. 2005). The advent of multi-GNSS poses new opportunities for rapid PPP initializations. It has been demonstrated that multi-GNSS data can be integrated to reach much faster PPP ambiguity resolution (PPP-AR). For example, Li et al. (2017) achieved ambiguity-fixed PPP solutions using 24.6 min of GPS/BeiDou data compared to 33.6 min for GPS-only data; Liu et al. (2017) experimented on a regional network and reported that 90% of GPS/GLONASS/BeiDou PPP solutions could be fixed within 10 min, whereas only 16% for GPS-only solutions; Nadarajah et al. (2018) showed that the convergence time in case of Australia-wide GPS/BeiDou/Galileo PPP-AR was reduced from 66 to 15 min. These achievements among other similar efforts can be understood in light of the enhanced satellite geometry and the improved partial ambiguity fixing when a good number of satellites contribute to PPP (e.g., Geng and Shi 2017).

While all efforts above are based exclusively on dual-frequency data, multi-frequency GNSS has also been highly expected to shorten the convergence time of PPP. It has been comprehensively demonstrated that multi-frequency data can speed up the convergence of medium to long baseline solutions (e.g., Vollath et al. 1999; Feng 2008, among others). In case of PPP, Geng and Bock (2013) used GPS L1, L2 and L5 signals to formulate an ionosphere-free wide-lane observable whose wavelength reaches 3.4 m. In spite of its huge noise of over 100 times larger than that of raw carrier-phase, the wide-lane ambiguity can still be resolved efficiently. The resultant ambiguity-fixed (or unambiguous) ionosphere-free wide-lane observable can be used instead of the raw pseudorange to constrain more tightly the position parameters and thus assist more strongly in speeding up PPP convergences. Simulated GPS data optimistically suggested that 78% of PPP-AR solutions could be accomplished within 2 min. Later on, Gu et al. (2015) experimented on real triple-frequency BeiDou IGSO/MEO (Inclined Geosynchronous Satellite Orbiter/Medium Earth Orbiter) data from within China and resolved the two wide-lane ambiguities on B1–B2 and B2–B3 with the aim of fixing B1 ambiguities more rapidly. Due largely to the poor BeiDou geometry, minutes of data were required to fix wide-lane ambiguities while hours of data to fix B1 ambiguities, which were both excessively longer than those anticipated by the GNSS community. With the great progress of BeiDou system over the years, however, Li et al. (2018) applied similar PPP-AR approaches to an even larger network spanning Southeast Asia and Australia and claimed that the mean convergence time to ambiguity-fixed solutions was reduced to 27.9 min with all B1/B2/B3 data from 31 min with only B1/B2 data. According to those multi-GNSS and multi-frequency studies, it is possible to expect an ultimate convergence efficiency for multi-frequency PPP-AR through the integration of GPS/BeiDou/Galileo/QZSS (Quazi-Zenith Satellite System) data.

In this study, therefore, we exploit real triple-frequency data from all GPS, BeiDou, Galileo and QZSS constellations to investigate how fast we can achieve ambiguity-fixed PPP solutions. We anticipate that multi-GNSS, despite the incomplete triple-frequency constellations at the moment, will ensure a stronger satellite geometry than BeiDou alone and hence benefit the rapid initialization of PPP. The remainder of the study is organized as follows. Section 2 describes the method we employ to fix triple-frequency PPP ambiguities; Sect. 3 presents the GNSS data and relevant processing strategies and correction models; Sects. 4 and 5 show the results on PPP (extra-)wide-lane ambiguity resolution and the initialization performance using triple-frequency data; conclusions are drawn in Sect. 6.

2 Methods

The raw triple-frequency GNSS observation equations in the unit of length from station \(i\) to satellite \(k\) take the form of

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} P_{i,1}^{k}&{}=\rho _i^k+c\left( t_i-t^k\right) +\gamma _i^k+d_{i,1}^\mathrm {s}-d_1^k\\ P_{i,2}^{k}&{}=\rho _i^k+c\left( t_i-t^k\right) +g_{\mathrm {s},2}^2\gamma _i^k+d_{i,2}^\mathrm {s}-d_2^k\\ P_{i,3}^{k}&{}=\rho _i^k+c\left( t_i-t^k\right) +g_{\mathrm {s},3}^2\gamma _i^k+d_{i,3}^\mathrm {s}-d_3^k\\ L_{i,1}^{k}&{}=\rho _i^k+c\left( t_i-t^k\right) -\gamma _i^k+\lambda _{\mathrm {s},1}\left( N_{i,1}^k+b_{i,1}^\mathrm {s}-b_1^k\right) \\ L_{i,2}^{k}&{}=\rho _i^k+c\left( t_i-t^k\right) -g_{\mathrm {s},2}^2\gamma _i^k+\lambda _{\mathrm {s},2}\left( N_{i,2}^k+b_{i,2}^\mathrm {s}-b_2^k\right) \\ L_{i,3}^{k}&{}=\rho _i^k+c\left( t_i-t^k\right) -g_{\mathrm {s},3}^2\gamma _i^k+\lambda _{\mathrm {s},3}\left( N_{i,3}^k+b_{i,3}^\mathrm {s}-b_3^k\right) \end{aligned} \end{array}\right. \end{aligned}$$
(1)

where \(P_{i,1}^{k}\), \(P_{i,2}^{k}\) and \(P_{i,3}^{k}\) are pseudorange and \(L_{i,1}^{k}\), \(L_{i,2}^{k}\) and \(L_{i,3}^{k}\) are carrier-phase on the three frequencies which are actually L1, L2 and L5 for GPS and QZSS, B1, B2 and B3 for BeiDou, and E1, E5a and E5b for Galileo; \(\rho _i^k\) denotes the sum of the station-satellite geometric distance and the slant troposphere delay; c is the speed of light in vacuum; \(t_i\) and \(t^k\) are the receiver and satellite clock errors, respectively; “s” symbolizes “G” for GPS, “C” for BeiDou, “E” for Galileo and “J” for QZSS; the wavelengths \(\lambda _{\mathrm {s},1}=\dfrac{c}{f_{\mathrm {s},1}}\), \(\lambda _{\mathrm {s},2}=\dfrac{c}{f_{\mathrm {s},2}}\) and \(\lambda _{\mathrm {s},3}=\dfrac{c}{f_{\mathrm {s},3}}\) where \(f_{\mathrm {s},1}\), \(f_{\mathrm {s},2}\) and \(f_{\mathrm {s},3}\) are the frequencies; \(\gamma _i^k\) is the first-order ionosphere delay on L1, B1 or E1 while \(g_{\mathrm {s},2}\) and \(g_{\mathrm {s},3}\) represent the scaling coefficients which equate \(\dfrac{f_{\mathrm {s},1}}{f_{\mathrm {s},2}}\) and \(\dfrac{f_{\mathrm {s},1}}{f_{\mathrm {s},3}}\), respectively; \(d_{i,1}^\mathrm {s}\), \(d_{i,2}^\mathrm {s}\) and \(d_{i,3}^\mathrm {s}\) denote pseudorange hardware biases at station i, whereas \(d_1^k\), \(d_2^k\) and \(d_3^k\) denote those at satellite k; similarly, \(b_{i,1}^\mathrm {s}\), \(b_{i,2}^\mathrm {s}\) and \(b_{i,3}^\mathrm {s}\) are the phase biases at station i and \(b_1^k\), \(b_2^k\) and \(b_3^k\) are those at satellite k, all in the unit of cycles; \(N_{i,1}^k\), \(N_{i,2}^k\) and \(N_{i,3}^k\) are integer ambiguities; we here ignore higher-order ionosphere delays, multipath effects, etc., for brevity. We note that Eq. 1 is rank deficient because of the linear dependency among hardware biases, clock errors and ionosphere delays. Hence, a reparameterization is necessary for our undifferenced multi-frequency GNSS functional model where the pseudorange and carrier-phase hardware biases are combined with clock errors and ionosphere delays (Odijk et al. 2016); this reparameterization is however subject to the time-varying properties of hardware biases.

In case of GPS, there exist pronounced inter-frequency clock biases (IFCBs) between its L5 and L1–L2 carrier-phase signals at the satellite end, which can reach tens of centimeters and are clearly time dependent (Montenbruck et al. 2011). Similar phenomena take place for BeiDou B3 against B1–B2 signals, though the magnitude of its IFCBs is only up to several centimeters. Therefore, we add a second satellite clock parameter dedicated to GPS L5 and BeiDou B3 signals to address the time-varying IFCBs (Guo and Geng 2018). Specifically, we have

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} P_{i,1}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_{{\widehat{12}}}^k\right) +\kappa _{i}^\mathrm {s}+{\bar{\gamma }}_i^k\\ P_{i,2}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_{{\widehat{12}}}^k\right) +\kappa _{i}^\mathrm {s}+g_{\mathrm {s},2}^2{\bar{\gamma }}_i^k\\ P_{i,3}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_3^k\right) +\kappa _{i}^\mathrm {s}+g_{\mathrm {s},3}^2{\bar{\gamma }}_i^k+h_i^\mathrm {s}\\ L_{i,1}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_{{\widehat{12}}}^k\right) +\kappa _{i}^\mathrm {s}-{\bar{\gamma }}_i^k+\lambda _{\mathrm {s},1}{\bar{N}}_{i,1}^k\\ L_{i,2}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_{{\widehat{12}}}^k\right) +\kappa _{i}^\mathrm {s}-g_{\mathrm {s},2}^2{\bar{\gamma }}_i^k+\lambda _{\mathrm {s},2}{\bar{N}}_{i,2}^k\\ L_{i,3}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_3^k\right) +\kappa _{i}^\mathrm {s}-g_{\mathrm {s},3}^2{\bar{\gamma }}_i^k+\lambda _{\mathrm {s},3}{\bar{N}}_{i,3}^k \end{aligned} \end{array}\right. \end{aligned}$$
(2)

where

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} t_i^\mathrm {G}&{}=t_i+\dfrac{1}{c}\left( \alpha ^\mathrm {G} d_{i,1}^\mathrm {G}-\beta ^\mathrm {G} d_{i,2}^\mathrm {G}\right) \\ t_{{\widehat{12}}}^k&{}=t^k+\dfrac{1}{c}\left( \alpha ^\mathrm {s} d_1^k-\beta ^\mathrm {s} d_2^k\right) \\ t_3^k&{}=t^k+\dfrac{1}{c}\left( g_{\mathrm {s},3}^2\beta ^\mathrm {s}(d_1^k-d_2^k)+d_3^k+\lambda _{\mathrm {s},3}\delta b_3^k\right) \\ \kappa _i^\mathrm {s}&{}=\alpha ^\mathrm {s} d_{i,1}^\mathrm {s}-\beta ^\mathrm {s} d_{i,2}^\mathrm {s}-\alpha ^\mathrm {G} d_{i,1}^\mathrm {G}+\beta ^\mathrm {G} d_{i,2}^\mathrm {G}\\ {\bar{\gamma }}_i^k&{}=\gamma _i^k-\beta ^\mathrm {s}(d_{i,1}^\mathrm {s}-d_{i,2}^\mathrm {s}-d_1^k+d_2^k)\\ h_i^\mathrm {s}&{}=g_{\mathrm {s},3}^2\beta ^\mathrm {s}(d_{i,1}^\mathrm {s}-d_{i,2}^\mathrm {s})-(\alpha ^\mathrm {s} d_{i,1}^\mathrm {s}-\beta ^\mathrm {s} d_{i,2}^\mathrm {s})+d_{i,3}^\mathrm {s}\\ {\bar{N}}_{i,1}^k&{}=N_{i,1}^k+b_{i,1}^\mathrm {s}-b_1^k-\dfrac{1}{\lambda _{\mathrm {s},1}}((\alpha ^\mathrm {s}+\beta ^\mathrm {s})d_{i,1}^\mathrm {s}-2\beta ^\mathrm {s} d_{i,2}^\mathrm {s} \\ &{}-(\alpha ^\mathrm {s}+\beta ^\mathrm {s})d_1^k+2\beta ^\mathrm {s} d_2^k)\\ {\bar{N}}_{i,2}^k&{}=N_{i,2}^k+b_{i,2}^\mathrm {s}-b_2^k-\dfrac{1}{\lambda _{\mathrm {s},2}}(2\beta ^\mathrm {s} d_{i,1}^\mathrm {s}-(\alpha ^\mathrm {s}+\beta ^\mathrm {s})d_{i,2}^\mathrm {s} \\ &{}-2\beta ^\mathrm {s} d_1^k+(\alpha ^\mathrm {s}+\beta ^\mathrm {s})d_2^k)\\ {\bar{N}}_{i,3}^k&{}=N_{i,3}^k+b_{i,3}^\mathrm {s}-\Delta b_3^k-\dfrac{1}{\lambda _{\mathrm {s},3}}(g_{\mathrm {s},3}^2\beta ^\mathrm {s}(d_{i,1}^\mathrm {s}-d_{i,2}^\mathrm {s}) \\ &{}+\alpha ^\mathrm {s} d_{i,1}^\mathrm {s}-\beta ^\mathrm {s} d_{i,2}^\mathrm {s}-2g_{\mathrm {s},3}^2\beta ^\mathrm {s}(d_1^k-d_2^k)-d_3^k)\\ \alpha ^\mathrm {s}&{}=\dfrac{g_{\mathrm {s},2}^2}{g_{\mathrm {s},2}^2-1}\\ \beta ^\mathrm {s}&{}=\dfrac{1}{g_{\mathrm {s},2}^2-1} \end{aligned} \end{array}\right. \end{aligned}$$
(3)

\(t_i^\mathrm {G}\) is the receiver clock parameter which has absorbed GPS receiver hardware biases; \(t_{{\widehat{12}}}^k\) is the legacy satellite clock parameter shared by L1/B1 and L2/B2, while \(t_3^k\) is the satellite clock monopolized by L5/B3; \(\delta b_3^k\) represents the time-variable IFCB; \(\kappa _i^\mathrm {s}\) denotes inter-system pseudorange bias of system “s” with respect to GPS where of particular note \(\kappa _i^\mathrm {G}=0\). \({\bar{\gamma }}_i^k\) is the new ionosphere parameter containing pseudorange biases; \(h_i^\mathrm {s}\) is a station-specific time-constant parameter intended to ingest the inter-frequency biases remaining between L1–L2/B1–B2 and L5/B3 pseudorange (Guo and Geng 2018); \({\bar{N}}_{i,1}^k\), \({\bar{N}}_{i,2}^k\) and \({\bar{N}}_{i,3}^k\) are the new ambiguity parameters contaminated by both pseudorange and phase biases; \(\Delta b_3^k\) is the time-constant portion of \(b_3^k\). For the satellite clock estimation, \(t_i^\mathrm {s}\), \(t_{{\widehat{12}}}^k\), \(t_3^k\), \(h_i^\mathrm {s}\) and \({\bar{\gamma }}_i^k\) in addition to all ambiguity and troposphere parameters are estimated by fixing station coordinates; for PPP, both \(t_{{\widehat{12}}}^k\) and \(t_3^k\) are fixed, while conversely, station coordinates are estimated.

In contrast, since negligible time-varying IFCBs are observed for the carrier-phase data from Galileo and QZSS (Montenbruck et al. 2011), we choose to apply identical satellite clock parameters across all three frequencies, while an inter-frequency bias parameter \(h_i^k\) was added on E5b/L5 for each satellite, that is (Li et al. 2018)

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} P_{i,1}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_{{\widehat{12}}}^k\right) +\kappa _{i}^\mathrm {s}+{\bar{\gamma }}_i^k\\ P_{i,2}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_{{\widehat{12}}}^k\right) +\kappa _{i}^\mathrm {s}+g_{\mathrm {s},2}^2{\bar{\gamma }}_i^k\\ P_{i,3}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_{{\widehat{12}}}^k\right) +\kappa _{i}^\mathrm {s}+g_{\mathrm {s},3}^2{\bar{\gamma }}_i^k+h_i^k\\ L_{i,1}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_{{\widehat{12}}}^k\right) +\kappa _{i}^\mathrm {s}-{\bar{\gamma }}_i^k+\lambda _{\mathrm {s},1}{\bar{N}}_{i,1}^k\\ L_{i,2}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_{{\widehat{12}}}^k\right) +\kappa _{i}^\mathrm {s}-g_{\mathrm {s},2}^2{\bar{\gamma }}_i^k+\lambda _{\mathrm {G},2}{\bar{N}}_{i,2}^k\\ L_{i,3}^{k}&{}=\rho _i^k+c\left( t_i^\mathrm {G}-t_{{\widehat{12}}}^k\right) +\kappa _{i}^\mathrm {s}-g_{\mathrm {s},3}^2{\bar{\gamma }}_i^k+\lambda _{\mathrm {G},3}{\bar{N}}_{i,3}^k \end{aligned} \end{array}\right. \end{aligned}$$
(4)

where

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} h_i^k&{}=g_{\mathrm {s},3}^2\beta ^\mathrm {s}(d_{i,1}^\mathrm {s}-d_{i,2}^\mathrm {s})-(\alpha ^\mathrm {s} d_{i,1}^\mathrm {s}-\beta ^\mathrm {s} d_{i,2}^\mathrm {s})+d_{i,3}^\mathrm {s}\\ &{}-g_{\mathrm {s},3}^2\beta ^\mathrm {s}(d_1^k-d_2^k)+\alpha ^\mathrm {s} d_1^k-\beta ^\mathrm {s} d_2^k-d_3^k\\ {\bar{N}}_{i,3}^k&{}=N_{i,3}^k+b_{i,3}^\mathrm {s}-b_3^k-\dfrac{1}{\lambda _{\mathrm {s},3}}(g_{\mathrm {s},3}^2\beta ^\mathrm {s}(d_{i,1}^\mathrm {s}-d_{i,2}^\mathrm {s})+\alpha ^\mathrm {s} d_{i,1}^\mathrm {s} \\ &{}-\beta ^\mathrm {s} d_{i,2}^\mathrm {s}-g_{\mathrm {s},3}^2\beta ^\mathrm {s}(d_1^k-d_2^k)-\alpha ^\mathrm {s} d_1^k+\beta ^\mathrm {s} d_2^k) \end{aligned} \end{array}\right. \end{aligned}$$

and \(h_i^k\) is a station-satellite-specific and time-constant parameter, which absorbs the inter-frequency pseudorange bias between E1–E5a/L1–L2 and E5b/L5; note that \({\bar{N}}_{i,3}^k\) differs from its counterpart in Eq. 3, whereas all others remain the same. Equation 4 exposes that the legacy E1–E5a/L1–L2 satellite clocks are imposed on the E5b/L5 signals for Galileo and QZSS, respectively. We note that this time \(t_i^\mathrm {s}\), \(t_{{\widehat{12}}}^k\), \(h_i^k\), \({\bar{\gamma }}_i^k\) as well as all ambiguity and troposphere parameters are estimated in the satellite clock determination. To overcome the rank defect caused by the linear dependency between satellite and receiver clocks in Eqs. 2 and 4, we apply zero-mean constraints on receiver-specific parameters such as \(\kappa _i^\mathrm {s}\), \(h_i^k\) and \(h_i^\mathrm {s}\) (Odijk et al. 2016).

Finally, under the assumption that all multi-frequency observables are independent of each other, we use a diagonal weight matrix to describe the stochastic model corresponding to Eqs. 2 and 4, where pseudorange or carrier-phase observables on different frequencies from differing GNSS are weighted equally.

2.1 Estimation of fractional cycle biases (FCBs)

The prerequisite of enabling PPP-AR is to compute the fractional cycle biases (FCBs) using a reference network. FCBs are the fractional part of uncalibrated phase delays (UPDs) coined by Ge et al. (2008), which are presumed to originate in hardware biases and will be assimilated into PPP ambiguities, as exposed in Eq. 3. Their integer portions become nominally part of the integer ambiguities while however the fractional portions (i.e., FCBs) destroy the integer nature of carrier-phase ambiguities. In this study, for triple-frequency PPP-AR, we shall estimate extra-wide-lane, wide-lane and narrow-lane FCB corrections commencing from Eqs. 2 and 4. At first, we compute the undifferenced estimates

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} \hat{{\bar{N}}}_{i,\mathrm {ew}}^k&{}=\hat{{\bar{N}}}_{i,2}^k-\hat{{\bar{N}}}_{i,3}^k\\ \hat{{\bar{N}}}_{i,\mathrm {w}}^k&{}=\hat{{\bar{N}}}_{i,1}^k-\hat{{\bar{N}}}_{i,2}^k\\ \hat{{\bar{N}}}_{i,\mathrm {if}}^k&{}=\dfrac{g_{\mathrm {s},2}^2}{g_{\mathrm {s},2}^2-1}\hat{{\bar{N}}}_{i,1}^k-\dfrac{g_{\mathrm {s},2}}{g_{\mathrm {s},2}^2-1}\hat{{\bar{N}}}_{i,2}^k \end{aligned} \end{array}\right. \end{aligned}$$
(5)

for the extra-wide-lane, wide-lane and ionosphere-free ambiguities, respectively. Note that the hat “\(\wedge \)” symbolizes a least-squares estimate from PPP processing. We stress that \(\hat{{\bar{N}}}_{i,\mathrm {ew}}^k\), \(\hat{{\bar{N}}}_{i,\mathrm {w}}^k\) and \(\hat{{\bar{N}}}_{i,\mathrm {if}}^k\) are not estimated with the linear extra-wide-lane, wide-lane and ionosphere-free combination observables, but obtained by combining the raw ambiguity estimates derived from Eq. 2 or 4. The third line of Eq. 5 can be further transformed into

$$\begin{aligned} \hat{{\bar{N}}}_{i,1}^k=\dfrac{g_{\mathrm {s},2}+1}{g_{\mathrm {s},2}} \hat{{\bar{N}}}_{i,\mathrm {if}}^k-\dfrac{1}{g_{\mathrm {s},2}-1} \hat{{\bar{N}}}_{i,\mathrm {w}}^k \end{aligned}$$
(6)

where \(\hat{{\bar{N}}}_{i,1}^k\) is taken as the narrow-lane ambiguity, though equates the raw L1/B1/E1 ambiguity in value.

Moreover, \(\hat{{\bar{N}}}_{i,\mathrm {ew}}^k\), \(\hat{{\bar{N}}}_{i,\mathrm {w}}^k\) and \(\hat{{\bar{N}}}_{i,1}^k\) can be identified as the sum of integer ambiguities and FCBs. Since station-specific FCBs cannot be separated from their satellite-specific counterparts, we choose to form single-difference ambiguities between satellites to eliminate station FCBs, that is

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} \hat{{\bar{N}}}_{i,\mathrm {ew}}^{kq}&{}=\breve{{\bar{N}}}_{i,\mathrm {ew}}^{kq}-{ \bar{b}}_\mathrm {ew}^{kq}\\ \hat{{\bar{N}}}_{i,\mathrm {w}}^{kq}&{}=\breve{{\bar{N}}}_{i,\mathrm {w}}^{kq}-{ \bar{b}}_\mathrm {w}^{kq}\\ \hat{{\bar{N}}}_{i,1}^{kq}&{}=\breve{{\bar{N}}}_{i,1}^{kq}-{\bar{b}}_\mathrm {n}^{kq} \end{aligned} \end{array}\right. \end{aligned}$$
(7)

where

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} \hat{{\bar{N}}}_{i,*}^{kq}&{}=\hat{{\bar{N}}}_{i,*}^k- \hat{{\bar{N}}}_{i,*}^q\\ \breve{{\bar{N}}}_{i,*}^{kq}&{}=\breve{{\bar{N}}}_{i,*}^k- \breve{{\bar{N}}}_{i,*}^q\\ {\bar{b}}_*^{kq}&{}={\bar{b}}_*^k-{\bar{b}}_*^q \end{aligned} \end{array}\right. \end{aligned}$$

and hat “\(\vee \)” denotes an integer or resolvable ambiguity quantity; “\(*\)” is a wildcard representing “ew”, “w”, “1” or “n”; satellite q belongs to the same GNSS as k; \(\breve{{\bar{N}}}_{i,\mathrm {ew}}^{kq}\), \(\breve{{\bar{N}}}_{i,\mathrm {w}}^{kq}\) and \(\breve{{\bar{N}}}_{i,1}^{kq}\) are the nominal integer (extra-)wide-lane and narrow-lane ambiguities, respectively; \({\bar{b}}_\mathrm {ew}^{kq}\), \({\bar{b}}_\mathrm {w}^{kq}\) and \({\bar{b}}_\mathrm {n}^{kq}\) are satellite-pair specific FCBs for the (extra-)wide-lane and narrow-lane ambiguities, respectively, which are the satellite phase bias products to be estimated for PPP-AR.

From Eq. 7, we can compute the satellite-pair (extra-)wide-lane FCB products through rounding operations. In particular,

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} \hat{{\bar{b}}}_\mathrm {ew}^{kq}&{}=frac\langle \hat{{\bar{N}}}_{ i,\mathrm {ew}}^{kq}\rangle =frac\langle \hat{{\bar{ N}}}_{i,2}^{kq}-\hat{{\bar{N}}}_{i,3}^{kq}\rangle \\ \hat{{\bar{b}}}_\mathrm {w}^{kq}&{}=frac\langle \hat{{\bar{N}}}_{i, \mathrm {w}}^{kq}\rangle =frac\langle \hat{{\bar{N}}}_{i,1}^{kq}-\hat{{\bar{N}}}_{i,2}^{kq}\rangle \\ \end{aligned} \end{array}\right. \end{aligned}$$
(8)

where \(frac\langle \Theta \rangle \) denotes an operation of extracting the fractional part of \(\Theta \). Though Eq. 8 seemingly shows that FCBs are computed using only station i, we must keep in mind that the FCB products in this study are estimated by averaging over a network of reference stations (Ge et al. 2008). Teunissen and Khodabandeh (2015) theoretically proved that the \(frac (\Theta )\) operator here is not rigorous in computing phase biases and the resulting positions would be biased. Geng et al. (2012, 2019) then suggested that the ultimate high-precision FCB products should be computed by resolving ambiguities of the network in advance.

Once wide-lane FCBs \(\hat{{\bar{b}}}_\mathrm {w}^{kq}\) are computed over a reference network, the resolved wide-lane ambiguity at station i can be recovered as

$$\begin{aligned} \hat{{\bar{N}}}_{i,\mathrm {w}}^{kq}=\breve{{\bar{N}}}_{i, \mathrm {w}}^{kq}-\hat{{\bar{b}}}_\mathrm {w}^{kq} \end{aligned}$$
(9)

and therefore Eq. 6 can be rewritten as

$$\begin{aligned} \hat{{\bar{N}}}_{i,1}^{kq}=\dfrac{g_{\mathrm {s},2}+1}{g_{\mathrm {s},2}} \hat{{\bar{N}}}_{i,\mathrm {if}}^{kq}-\dfrac{1}{g_{\mathrm {s},2}-1} \left( \breve{{\bar{N}}}_{i,\mathrm {w}}^{kq}-\hat{{\bar{b}}}_\mathrm {w}^{kq}\right) \end{aligned}$$
(10)

Then similar to Eq. 8, we can estimate the narrow-lane FCB using

$$\begin{aligned} \begin{aligned} \hat{{\bar{b}}}_\mathrm {n}^{kq}&=frac\langle \hat{{\bar{N}}}_{i,1}^{kq} \rangle =frac\langle \dfrac{g_{\mathrm {s},2}+1}{g_{\mathrm {s},2}} \hat{{\bar{N}}}_{i,\mathrm {if}}^{kq}-\dfrac{1}{g_{\mathrm {s},2}-1}( \breve{{\bar{N}}}_{i,\mathrm {w}}^{kq}-\hat{{\bar{b}}}_\mathrm {w}^{kq})\rangle \\ \end{aligned} \end{aligned}$$
(11)

According to the derivation from Eqs. 9 to 11, we note that the narrow-lane ambiguities \(\hat{{\bar{N}}}_{i,1}^k\) dedicated to the FCB estimation in Eq. 11 have to be obtained by first resolving \(\hat{{\bar{N}}}_{i,\mathrm {w}}^k\), as shown in Eq. 9.

2.2 Triple-frequency PPP-AR

The FCB products above will be disseminated to enable PPP-AR at a single station. In this section, we still begin with Eqs. 2 and 4 for undifferenced PPP solutions at station i. Before resolving PPP ambiguities at a particular epoch, we first map undifferenced raw ambiguities into their single-difference counterparts between satellites at the normal equation level. Then the single-difference ambiguities (i.e., \(\hat{{\bar{N}}}_{i,1}^{kq}\), \(\hat{{\bar{N}}}_{i,2}^{kq}\) and \(\hat{{\bar{N}}}_{i,3}^{kq}\)) are converted into the (extra-)wide-lane combinations (i.e., \(\breve{{\bar{N}}}_{i,\mathrm {ew}}^{kq}\) and \(\breve{{\bar{N}}}_{i,\mathrm {w}}^{kq}\)), which are subsequently corrected for FCBs to recover resolvable ambiguities, that is

$$\begin{aligned} \left( \begin{array}{l} \breve{{\bar{N}}}_{i,\mathrm {ew}}^{kq} \\ \breve{{\bar{N}}}_{i,\mathrm {w}}^{kq} \end{array}\right) = \left( \begin{array}{rrr} 0 &{} 1 &{} -1 \\ 1 &{} -1 &{} 0 \end{array}\right) \left( \begin{array}{l} \hat{{\bar{N}}}_{i,1}^{kq} \\ \hat{{\bar{N}}}_{i,2}^{kq} \\ \hat{{\bar{N}}}_{i,3}^{kq} \end{array} \right) + \left( \begin{array}{l} \hat{{\bar{b}}}_\mathrm {ew}^{kq} \\ \hat{{\bar{b}}}_\mathrm {w}^{kq} \end{array}\right) \end{aligned}$$
(12)

Note that the \(2\times 3\) mapping matrix in Eq. 12 is also used to convert the variance-covariance matrix for raw ambiguities into that for (extra-)wide-lane combinations (e.g., Dong and Bock 1989); this (extra-)wide-lane variance-covariance matrix along with \(\breve{{\bar{N}}}_{i,\mathrm {ew}}^{kq}\) and \(\breve{{\bar{N}}}_{i,\mathrm {w}}^{kq}\) will be injected into the LAMBDA (Least-squares AMBiguity Decorrelation Adjustment) function to search for integer ambiguity candidates (Teunissen 1995). Once ambiguities are resolved successfully, the positions, the troposphere delays and the raw ambiguities can be updated through the fixed-minus-float ambiguity increments, as well as the (extra-)wide-lane variance-covariance matrix (see Appendix B of Dong and Bock 1989).

Once wide-lane ambiguities are resolved, we can recover resolvable narrow-lane ambiguities similar to Eq. 10. Particularly, we have

$$\begin{aligned} \breve{{\bar{N}}}_{i,1}^{kq} = \left( \begin{array}{ll} \dfrac{g_{\mathrm {s},2}}{g_{\mathrm {s},2}-1}&\dfrac{-1}{g_{\mathrm {s},2}-1} \end{array}\right) \left( \begin{array}{l} \hat{{\bar{N}}}_{i,1}^{kq} \\ \hat{{\bar{N}}}_{i,2}^{kq} \end{array}\right) + \dfrac{\breve{{\bar{N}}}_{i,\mathrm {w}}^{kq}-\hat{{\bar{b}}}_ \mathrm {w}^{kq}}{1-g_{\mathrm {s},2}}+\hat{{\bar{b}}}_\mathrm {n}^{kq} \end{aligned}$$
(13)

Then again, we use the \(1\times 2\) mapping matrix in Eq. 13 to derive narrow-lane variance-covariance matrix for the LAMBDA function. The fixing of narrow-lane ambiguities and the resulting update of other parameters resemble the process of (extra-)wide-lane ambiguity resolution above.

It can be seen that we fix the (extra-)wide-lane ambiguities first and then the narrow-lane counterparts (e.g., Feng 2008; Tang et al. 2014). This cascading procedure seems to contradict the suggestion by Teunissen (1999) that the highest success rate of ambiguity resolution can be achieved in theory by resolving the full set of ambiguities simultaneously through the integer least-squares estimator, rather than by fixing the linear ambiguity combinations sequentially in an integer bootstrapping manner. However, we prefer this cascading procedure because the narrow-lane ambiguities to be resolved in this study are free from the first-order ionosphere contamination and thus can be more easily identified as integers. Though they take the form of “\({\bar{N}}_{i,1}^k\),” nominally the L1/B1/E1 ambiguity term, the narrow-lane ambiguities are actually derived after resolving their wide-lane antecedents according to Eq. 10. This wide-lane ambiguity fixing prescribed for narrow-lane conversion prevents us from fixing simultaneously the full set of ambiguities (i.e., extra-wide-lane, wide-lane and narrow-lane ambiguities, or alternatively raw uncombined ambiguities) in one integer least-squares estimator. In contrast, Gu et al. (2015) and Li et al. (2018) chose to resolve the raw L1/B1/E1 ambiguity \(\hat{{\bar{N}}}_{i,1}^k\) without decomposing ionosphere-free ambiguities and therefore were able to inject the full set of triple-frequency ambiguities into the LAMBDA function all at once. Section 5 will contrast their procedure with ours.

2.3 Further remarks on cascading PPP-AR

Geng and Bock (2013) developed an approach for triple-frequency PPP-AR which seemingly appears different from the method proposed in Sect. 2.2. In particular, Geng and Bock (2013) explicitly constituted (extra-)wide-lane combination observables with raw observables before initiating PPP. Once both ambiguities of (extra-)wide-lane observables were resolved (i.e., PPP (extra-)wide-lane ambiguity resolution or PPP-WAR hereafter), they used the resulting unambiguous observations to form an ionosphere-free wide-lane combination which usually had lower noise compared to raw pseudorange. It is therefore claimed that this combination was likely to improve the rapidity of subsequent narrow-lane ambiguity resolution. For clarity, we write down this ionosphere-free wide-lane combination observable as (Geng and Bock 2013)

$$\begin{aligned} L_{i,\mathrm {ifw}}^k= & {} \dfrac{g_{\mathrm {s},3}}{g_{\mathrm {s},3}-1}\underbrace{\left( \dfrac{g_{\mathrm {s},2}}{g_{\mathrm {s},2}-1}L_{i,1}^k-\dfrac{1}{g_{\mathrm {s},2}-1}L_{i,2}^k\right) }_\text {Wide-lane combination}-\nonumber \\&\dfrac{1}{g_{\mathrm {s},3}-1}\underbrace{\left( \dfrac{g_{\mathrm {s},3}}{g_{\mathrm {s},3}-g_{\mathrm {s},2}}L_{i,2}^k-\dfrac{g_{\mathrm {s},2}}{g_{\mathrm {s},3}-g_{\mathrm {s},2}}L_{i,3}^k\right) }_\text {Extra-wide-lane combination}\nonumber \\= & {} \dfrac{g_{\mathrm {s},2}g_{\mathrm {s},3}}{\left( g_{\mathrm {s},2}-1\right) \left( g_{\mathrm {s},3}-1\right) }L_{i,1}^k-\nonumber \\&\dfrac{g_{\mathrm {s},3}}{\left( g_{\mathrm {s},2}-1\right) \left( g_{\mathrm {s},3}-g_{\mathrm {s},2}\right) }L_{i,2}^k+\nonumber \\&\dfrac{g_{\mathrm {s},2}}{\left( g_{\mathrm {s},3}-1\right) \left( g_{\mathrm {s},3}-g_{\mathrm {s},2}\right) }L_{i,3}^k \end{aligned}$$
(14)

where the three scaling coefficients for carrier-phase \(L_{i,1}^k\), \(L_{i,2}^k\) and \(L_{i,3}^k\) are listed in Table 1 with respect to GPS/QZSS, BeiDou and Galileo signals.

Table 1 Combination coefficients of L1/B1/E1, L2/B2/E5a and L5/B3/E5b signals for the ionosphere-free wide-lane observable in Eq. 14
Full size table

This procedure for triple-frequency PPP-AR is well-known as the cascading ambiguity resolution, which means that longer-wavelength ambiguities are resolved first, and later contribute to improving the integer-cycle resolution of shorter-wavelength ambiguities. In this study, though we do not explicitly form the (extra-)wide-lane combination observables, nor do we formulate ionosphere-free observables to start PPP, we do later map the raw ambiguity estimates and their variance-covariance matrix into those of their (extra-)wide- and narrow-lane counterparts. In this sense, we are actually still carrying out cascading PPP-AR, despite the raw uncombined observations injected into PPP (e.g., Schaffrin and Bock 1988; Teunissen 1997b).

3 Data and models

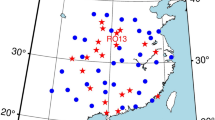
We processed 31 days (days 335–365 in 2017) of 30 s triple-frequency GPS/BeiDou/Galileo/QZSS data collected from IGS MGEX (International GNSS Service Multi-GNSS Experiment) and ARGN (Australian Regional GNSS Network). BeiDou GEOs (Geosynchronous Earth Orbiters) were all excluded and for GPS we only used the 12 BLOCK-IIF satellites that were able to emit L5 signals. The predicted orbits and Earth rotation parameters every 3 h by GFZ (German Research Centre for Geosciences) were fixed in all data processing of this study. We then picked 79 globally distributed stations (not shown here) to compute satellite clock products epoch by epoch in a real-time manner (Guo and Geng 2018). Of particular note, a second satellite clock was calculated with respect to L5/B3 signals for GPS and BeiDou satellites along with the legacy clock products devoted to L1–L2/B1–B2 signals; however, only legacy clocks were estimated and applied to all three frequencies for Galileo and QZSS satellites. We corrected for the differential code biases produced by CODE (Centre for Orbit Determination in Europe) to align legacy satellite clocks with P1–P2 pseudorange. Satellite clocks were then fixed together with orbits to estimate FCB products and further enable kinematic PPP. In particular, 35 stations within East Asia and Oceania were used to compute FCB products for GPS, BeiDou, Galileo and QZSS satellites (Fig. 1). On average, there were about four GPS, six BeiDou and five Galileo satellites in contrast to only one QZSS satellite usable during this period. Almost half of the stations in Fig. 1 which were equipped with Trimble receivers can track J01 only. Moreover, all FCBs were computed every 15 min as suggested by Ge et al. (2008). It is worth mentioning that satellite-pair FCBs were converted into satellite-specific quantities (pseudoabsolute values) by assigning zero value to a satellite FCB. At the user end, these FCBs were fixed in PPP to recover resolvable single-station ambiguities at all 76 stations consisting of 38 Trimble, 36 Septentrio and 2 Javad receivers (see Fig. 1). Note that we only resolved intra-system ambiguities, though Khodabandeh and Teunissen (2016) and Geng et al. (2018b) have demonstrated that the PPP convergence time could be shortened further by extra resolving inter-system ambiguities with pre-determined inter-system phase bias corrections. Positions were estimated at each epoch without any between-epoch constraints. We divided all data into hourly pieces which totaled 50,533 solutions for real-time kinematic PPP.

Fig. 1
figure 1

Distribution of multi-GNSS stations from days 335 to 365 in 2017. 35 stations denoted as red open circles are used to estimate FCB products for GPS, BeiDou, Galileo and QZSS satellites, while 41 stations denoted as green crosses contribute to GPS/BeiDou/Galileo/QZSS kinematic PPP. Three stations BDVL, BUR2 and STHG are especially denoted

Full size image

For all data processing above, we chose a cut-off angle of 10\(^\circ \) to eliminate low-elevation data. The a priori noise of pseudorange and carrier-phase were 0.2 m and 2 mm, respectively; an elevation-dependent weighting strategy was applied to scale the noise for observations below an elevation of 30\(^\circ \). Receiver clocks were computed epoch by epoch, and inter-system pseudorange biases with respect to GPS were estimated as constants over a day. Zenith troposphere delays (ZTDs) were first corrected with the Saastamoinen model (Saastamoinen 1973) by presuming standard meteorological conditions, which were then projected onto slant directions using the global mapping function (Boehm et al. 2006). Residual ZTDs were then estimated as hourly constants. On the contrary, ionosphere delays were computed without applying any mapping functions. Rather, we directly estimated their slant values for each satellite as random walk parameters with a process noise of 0.5 m/\(\sqrt{\mathrm {30~}s}\). Finally, we used the absolute antenna phase center offsets and variations (PCO/PCV) released by the IGS (Schmid et al. 2016). One problem was that GPS satellites did not have antenna corrections for their L5 signals, and we therefore used the L2 corrections to fill in this blank; even worse, a further barrier consisted in the lack of BeiDou, Galileo and QZSS PCO/PCV and the third-frequency PCO/PCV at receiver antennas, and we therefore chose to use GPS corrections for all GNSS while GPS L2 corrections for all third-frequency signals.

In addition, both dual- and triple-frequency PPP-AR were carried out for comparison in this study. The LAMBDA method was used to search for integer candidates of extra-wide-lane, wide-lane and narrow-lane ambiguities (Teunissen 1995). Note that extra-wide-lane and wide-lane ambiguities were fixed first, followed by narrow-lane. The ratio test with a threshold of 2.0, which contrasted the second minimum quadratic form of ambiguity residuals to the minimum (Euler and Schaffrin 1990), was applied to discriminate between candidate integer solutions. Moreover, if full ambiguity fixing failed, partial ambiguity fixing was then attempted to improve the success rates of PPP-AR (Teunissen et al. 1999). In particular, we required that at most four ambiguities could be excluded while at least four had to be reserved for partial ambiguity fixing. If partial ambiguity fixing still could not go through the ratio test at a given epoch, we kept the solutions float instead and moved on to the next epoch.

4 Results

4.1 Multi-GNSS FCBs

We estimated all FCBs every 15 min over all 31 days. Fig. 2 exemplifies the extra-wide-lane, wide-lane and narrow-lane FCB time series for all observed GPS, BeiDou, Galileo and QZSS satellites on day 335. As expected, extra-wide-lane FCBs for all satellites are quite stable over time with the maximum standard deviation below 0.01 cycles. A smaller standard deviation means a more stable FCB time series over time. Overall, the mean standard deviations of extra-wide-lane FCBs over all 31 days are smaller than 0.005 cycles for all GPS, BeiDou, Galileo and QZSS satellites (Table 2), which can be understood in terms of the super long wavelengths of extra-wide-lane ambiguities. In contrast, due to the much shorter wavelengths, wide-lane FCBs have slightly worse temporal stability than that of their extra-wide-lane counterparts, especially for the early portions of most FCB time series when PPP ambiguities have not yet converged to high precisions. For example, on day 335 the maximum standard deviations of wide-lane FCBs can reach around 0.05 cycles (Fig. 2); the mean standard deviations over the 31 days are roughly between 0.01 and 0.02 cycles for GPS, BeiDou, Galileo and QZSS (Table 2). Despite such pronounced time-varying signatures, wide-lane FCBs can still be precisely predicted over a relatively long period, such as hours, without compromising the efficiency of ambiguity resolution.

Fig. 2
figure 2

Extra-wide-lane, wide-lane and narrow-lane FCBs for all involved GPS, BeiDou, Galileo and QZSS satellites every 15 min on day 335. Extra-wide-lane FCBs are shown within the left panels, wide-lane FCBs within the central while narrow-lane FCBs within the right; all FCBs are uniformly color coded against satellites. Both maximum and minimum standard deviations (STD, cycle) of the FCBs among all satellites are plotted at the bottom of each panel. Note that the FCBs have been displaced vertically to avoid overlap of symbols; for each GNSS, the legend for satellite labels is divided into three parts and plotted separately within the three panels for (extra-)wide-lane and narrow-lane FCBs; QZSS FCBs are plotted in the top-right panel along with GPS FCBs

Full size image

However, narrow-lane FCBs reveal more significant temporal variations as depicted by the rightmost panels of Fig. 2. In particular, early narrow-lane FCB estimates present clearly large fluctuations of up to 0.1 cycles, which has been found by Geng et al. (2011). Such unfavorable fluctuations can even take place after narrow-lane FCBs have already converged to stable values, as evidenced by BeiDou C06 between hour 8 and 10 in the rightmost panel of the second row. This phenomenon is because of the loss of track of C06 by most stations, which results in a re-initialization of satellite clock estimates. Overall, the exemplary narrow-lane FCBs in Fig. 2 reach a maximum standard deviation of up to 0.1 cycles, while the mean over the 31 days all exceed 0.02 cycles for GPS, BeiDou, Galileo and QZSS (Table 2). In addition, it is worth mentioning that both Fig. 2 and Table 2 demonstrate that Galileo FCBs have better temporal stabilities compared to their GPS and BeiDou counterparts. In conclusion, (extra-)wide-lane FCBs can be predicted for real-time PPP over a long time span (e.g., hours to even days) with high precisions to ensure a high success rate of (extra-)wide-lane ambiguity resolution, while narrow-lane FCBs should be predicted with more cautions to reduce the risk of degraded PPP-AR efficiency.

4.2 PPP wide-lane ambiguity resolution (PPP-WAR)

Table 2 Mean standard deviations of extra-wide-lane, wide-lane and narrow-lane FCBs (cycle) for all GPS, BeiDou, Galileo and QZSS satellites on all days
Full size table
Fig. 3
figure 3

Positioning errors (m) for the east, north and up components at stations BDVL and BUR2 for PPP-WAR and ambiguity-float solutions. PPP-WAR indicates that both extra-wide-lane and wide-lane ambiguity fixing have been accomplished

Full size image

The fundamental idea behind rapid triple-frequency PPP-AR of this study is that, once both extra-wide-lane and wide-lane ambiguities are resolved (i.e., PPP-WAR achieved), an unambiguous ionosphere-free wide-lane carrier-phase can be obtained, no matter whether implicitly or not, which is expected to outweigh the raw pseudorange to speed up the convergences of narrow-lane ambiguities (Geng et al. 2018a). However, we should be cautious of such results, since it depends on whether such unambiguous wide-lane carrier-phase is indeed sufficiently less noisy than the raw pseudorange. From Table 1, we find that, compared to the raw carrier-phase, the noise of such wide-lane carrier-phase combination (Eq. 14) is amplified by over 100 times, which roughly reaches several decimeters according to the error propagation law. This noise level, unfortunately, has already closely approached the nominal precision of raw pseudorange in theory. To contrast the actual positioning performance between the unambiguous ionosphere-free wide-lane carrier-phase and the ionosphere-free pseudorange, Fig. 3 exemplifies two typical stations BDVL and BUR2; in particular, for PPP-WAR (red curves), we used triple-frequency data and resolved only (extra-)wide-lane ambiguities; for triple-frequency float PPP (blue curves), we also processed triple-frequency data but did not fix any ambiguities, whereas for dual-frequency float PPP (cyan curves) we employed only the legacy dual-frequency data. Moreover, we require that “convergence” is only achieved when, the horizontal and vertical components stay persistently at an accuracy of better than 10 cm and 20 cm for 20 min, respectively, as delimited by the horizontal dashed gray lines within the six panels of Fig. 3.

Fig. 4
figure 4

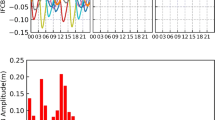
GPS, BeiDou and Galileo observation residuals (m) at station STHG on day 335, 2017. Three types of residuals are shown for ionosphere-free P1–P2 pseudorange from dual-frequency float PPP, ambiguity-fixed and ambiguity-float ionosphere-free wide-lane carrier-phase from triple-frequency PPP (see Eq. 14). All residuals are computed by fixing station coordinates, and color coded against satellites. The mean RMS of residuals (m) are plotted at the bottom right corner of each panel

Full size image

Station BDVL demonstrates the superiority of ambiguity-fixed wide-lane carrier-phase over raw pseudorange. When we only rely on the raw pseudorange to enable PPP, it takes about 28 min to achieve successful convergences for all three components. In contrast, this convergence time drops drastically to about 10 min after PPP-WAR is achieved at BDVL; the east and up components manifest the most significant improvement. This result verifies that the precision of ionosphere-free wide-lane carrier-phase (Eq. 14), though deteriorated by more than 100 times compared to the raw carrier-phase, still outperforms the ionosphere-free pseudorange precision. Nevertheless, despite this favorable achievement, station BUR2 shows that deterioration instead of improvement can still take place for position convergences. In particular, float PPP at BUR2 reaches successful convergences within about 10 min, while PPP-WAR costs almost 30 min even though the wide-lane ambiguities have been correctly resolved since the first epoch. We can see that the convergences of all three components slow down clearly after PPP-WAR. This outcome is even more discouraging when we find that 24.5% of hourly solutions suffer from such deteriorations.

In order to inspect how PPP-WAR contributes to PPP convergences, we compute all GPS, BeiDou and Galileo observation residuals for a representative station STHG on day 335 by fixing its coordinates to the truth benchmarks. Such residuals can be used to quantify the noise of GNSS observations. Figure 3 reveals that the third-frequency pseudorange has limited impact on float PPP solutions in terms of positioning errors and convergence times; this is because the addition of L5/B3/E5b signals does not improve the satellite geometry or the pseudorange precision, which are both critical to speeding up PPP convergence (see also Guo et al. 2016; Guo and Geng 2018). Thus, we show in the left panels of Fig. 4 only the pseudorange residuals of P1–P2 ionosphere-free combination. The remaining panels, in contrast, show the residuals of ionosphere-free wide-lane carrier-phase observations for all GPS, BeiDou and Galileo satellites. Note that we computed these residuals by combining the raw L1/B1/E1, L2/B2/E5a and L5/B3/E5b residuals with the coefficients listed in Table 1 according to Eq. 14. Of particular note, the central and right panels show the ambiguity-fixed and ambiguity-float residuals, respectively. As expected, these wide-lane residuals, though originally based on millimeter-level carrier-phase, reach decimeter-level magnitude after the amplification demonstrated in Table 1. Overall, the residuals from the left panels have clearly larger scatter than those from the central panels except for Galileo. The mean RMS for GPS and BeiDou pseudorange residuals double those of carrier-phase residuals. This result explains why we can accelerate PPP convergences through PPP-WAR compared to dual-frequency PPP; that is, the ionosphere-free wide-lane carrier-phase data become higher-precision pseudorange-like observations after PPP-WAR, and thus outweigh the raw pseudorange in speeding up PPP convergences. However, one exception is Galileo whose raw pseudorange achieves comparable precision to that of ionosphere-free wide-lane carrier-phase (the bottom row of panels of Fig. 4). This means that Galileo PPP-WAR may not be more constructive than the raw pseudorange in speeding up PPP convergences.

Then the remaining question is why we still have a considerable likelihood of slowing down PPP convergences even though we enable PPP-WAR. The rightmost three panels of Fig. 4 present the residuals of ionosphere-free wide-lane observations with float ambiguities. Once their wide-lane ambiguities are fixed, the mean RMS of residuals are increased appreciably by 10–20%, as shown in the central panels. A close look at these central panels reveals that a good number of residual time series are more distorted or deliver larger fluctuations over the periods of hours, compared to their counterparts in the right panels of Fig. 4. This result indicates that the errors absorbed originally by float wide-lane ambiguities are driven into the residuals after imposing PPP-WAR on coordinate-fixed solutions. We can thus postulate that, in kinematic PPP where coordinates are estimated, these errors are instead likely to contaminate position parameters since fixed ambiguities cannot accommodate them anymore. Therefore, we argue that the residual errors originally assimilated by wide-lane ambiguities are most likely to explain why PPP-WAR often deteriorates PPP positions as exemplified in Fig. 3.

Table 3 Mean convergence times (min.) and mean RMS of positioning errors (m) for multi-GNSS and BeiDou-only solutions in the east, north and up components with respect to the number of satellites
Full size table
Fig. 5
figure 5

Distribution of convergence times (minutes) of three types of solutions for all stations on all days. The solutions include dual- and triple-frequency float PPP and PPP-WAR. The percentages for those solutions converging successfully within 2, 5 and 10 min are plotted at the top-right corner of each panel

Full size image

Fortunately, the overall achievement of PPP-WAR for rapid convergences of positions is still satisfactory in this study. Table 3 exhibits for all stations on all days the mean convergence times and mean positioning errors with respect to the number of satellites for three types of solutions, i.e., dual- and triple-frequency float PPP and PPP-WAR. On the one hand, triple-frequency PPP converges on average faster than dual-frequency PPP by about 1 min, no matter how many multi-GNSS satellites are involved. PPP-WAR can further reduce this convergence time by 2 min on average, which again is irrespective of the number of contributing multi-GNSS satellites. BeiDou-only solutions show much worse performance (Gu et al. 2015; Li et al. 2018). We can also find that the more multi-GNSS satellites are employed, the shorter convergence times we can achieve; the mean convergence time declines almost twice when the satellite number rises from 10 to 20 in triple-frequency PPP. In addition, Fig. 5 shows the distribution of convergence times of all solutions. The percentage of successful convergences within 5 min is doubled in case of PPP-WAR compared to those float solutions, and almost half of them are accomplished within 2 min. On the other hand, while no significant positioning discrepancies are found between dual- and triple-frequency float PPP in Table 3, PPP-WAR however reduces dramatically the positioning errors on average from 0.23, 0.18 and 0.43 m to 0.12, 0.08 and 0.27 m for the east, north and up components, respectively, which roughly equate a 50% amelioration. More interestingly, the positioning errors in case of multi-GNSS PPP-WAR almost remain, no matter how many satellites are involved. This implies that growing the number of visible satellites benefits more the rapid PPP convergences than the positioning accuracy itself.

Fig. 6
figure 6

Positioning errors (m) for east, north and up components at stations BDVL and BUR2. Two solutions, i.e., dual- and triple-frequency PPP-AR, are presented. The vertical dashed red and cyan lines mark the epochs when successful PPP-AR is achieved. Note that triple-frequency PPP-AR is augmented by PPP-WAR discussed in Sect. 4.2

Full size image

4.3 Triple-frequency PPP-AR

In this section, triple-frequency PPP-AR implies that narrow-lane ambiguity fixing should be preceded by PPP-WAR discussed in Sect. 4.2; moreover, a successful initialization means that narrow-lane ambiguity fixing has been achieved. Since PPP-WAR is able to improve the positioning accuracy during the early stage of PPP convergences, we expect that narrow-lane ambiguities can be resolved more efficiently in contrast to those when only dual-frequency data are used. Figure 6 hence exhibits two typical stations BDVL and BUR2, which are already shown in Fig. 3. From the vertical dashed lines marking the epochs of successful initializations, we can see that narrow-lane ambiguity fixing at BDVL is accomplished within 5 min in triple-frequency PPP-AR, while more than 15 min are required for dual-frequency PPP-AR. Station BRU2 shows the opposite however; its PPP initialization is slowed down, rather than accelerated, by about 8 min when attempting triple-frequency instead of dual-frequency PPP-AR. This result is not surprising because Fig. 3 presents that PPP-WAR at BUR2 deteriorates its PPP convergence efficiency. We label this phenomenon afterward as “ineffective PPP-WAR”.

Table 4 Mean initialization times (minutes) for both dual- and triple-frequency PPP-AR in case of multi-GNSS and BeiDou-only solutions at all stations on all days with respect to the number of satellites
Full size table
Fig. 7
figure 7

Distribution of initialization times (minutes) for dual- and triple-frequency PPP-AR at all stations on all days. The percentages of the initialization times that are shorter than 2, 5 and 10 min are plotted at the top-right corner of each panel. Note that triple-frequency PPP-AR with N1 ambiguities fixed is shown in the rightmost panel

Full size image

Fortunately, this outcome is not predominant within our solutions. At all stations on all days, the initializations of about 12% of solutions get worse in case of triple-frequency PPP-AR, compared to dual-frequency PPP-AR. This percentage is only half of the percentage (i.e., 24.5%) for those PPP-WAR solutions where convergences are slowed down. This discrepancy implies that ineffective PPP-WAR solutions, though accounting for one fourth of all solutions, do not necessarily lead to decelerated narrow-lane ambiguity fixing. Moreover, Table 4 presents the mean initialization times of PPP-AR solutions at all stations on all days. It can be found that triple-frequency PPP-AR does have dramatically higher initialization efficiency than its dual-frequency counterpart. This advantage becomes more pronounced when more multi-GNSS satellites are involved; in particular, when over 20 satellites contribute to PPP-AR, the mean initialization time is reduced from 5.2 min in case of dual-frequency data to 2.7 min in case of triple-frequency data, showing a nearly 50% improvement. On average, 6.1 min of triple-frequency data are required to achieve PPP-AR, which in contrast takes 9.2 min for dual-frequency data. Furthermore, Fig. 7 displays the distribution of these initialization times. The percentage for the initializations achieved within 2 min is almost doubled when triple-frequency data are used instead of dual-frequency data (i.e., from 26.4 to 48.1%). In contrast, when counting the solutions initialized within 10 min, we find that the two percentages (i.e., 69.1% and 78.4%) do not depart widely from each other. This result indicates that PPP-WAR is more effective in speeding up initializations during the early stage of PPP convergences, echoing the results in Fig. 5.

5 Discussion on resolving narrow-lane ambiguities

In the triple-frequency BeiDou PPP-AR trials by Gu et al. (2015), it was the B1 ambiguities of about 20 cm wavelength that were fixed to integers in an integer least-squares estimator, rather than the narrow-lane ambiguities of about 10 cm wavelength. Particularly, the extra-wide-lane (B2–B3), wide-lane (B1–B2) and B1 ambiguities (Gu et al. 2015) were injected simultaneously into the LAMBDA function for Z-transformation and integer candidate search. No wide-lane ambiguity fixing is required before resolving B1 ambiguities, differing distinctively from the narrow-lane ambiguity fixing procedure in this study. We therefore attempted the strategy of Gu et al. (2015) to investigate whether we could achieve higher efficiency of resolving triple-frequency ambiguities. The same ambiguity search and validation strategies as those described in Sect. 3 were used. To be specific, Eq. 12 takes the new form of

$$\begin{aligned} \left( \begin{array}{l} \breve{{\bar{N}}}_{i,\mathrm {ew}}^{kq} \\ \breve{{\bar{N}}}_{i,\mathrm {w}}^{kq} \\ \breve{{\bar{N}}}_{i,1}^{kq} \end{array}\right) = \left( \begin{array}{rrr} 0 &{} 1 &{} -1 \\ 1 &{} -1 &{} 0 \\ 1 &{} 0 &{} 0 \end{array}\right) \left( \begin{array}{l} \hat{{\bar{N}}}_{i,1}^{kq} \\ \hat{{\bar{N}}}_{i,2}^{kq} \\ \hat{{\bar{N}}}_{i,3}^{kq} \end{array}\right) + \left( \begin{array}{l} \hat{{\bar{b}}}_\mathrm {ew}^{kq} \\ \hat{{\bar{b}}}_\mathrm {w}^{kq} \\ \hat{{\bar{b}}}_1^{kq} \end{array}\right) \end{aligned}$$
(15)

where we note that \(\hat{{\bar{b}}}_1^{kq}\) in Eq. 15 differs from \(\hat{{\bar{b}}}_\mathrm {n}^{kq}\) presented in Eq. 13. The transformation of variance-covariance matrix then is subject to the \(3\times 3\) matrix in Eq. 15, and the search for \(\breve{{\bar{N}}}_{i,\mathrm {ew}}^{kq}\), \(\breve{{\bar{N}}}_{i,\mathrm {w}}^{kq}\) and \(\breve{{\bar{N}}}_{i,1}^{kq}\) is carried out simultaneously in an integer least-squares estimator (Teunissen 1999). The results are shown in the last column of Table 4 and the rightmost panel of Fig. 7. We can find that the mean initialization time in case of fixing multi-GNSS N1 ambiguities are 77% longer than that of fixing narrow-lane ambiguities. No matter how many number of multi-GNSS satellites are involved, the initialization times are prolonged by 3–6 min after resolving N1 instead of narrow-lane ambiguities.

Considering the optimality of the integer least-squares estimator in achieving the highest success rate of ambiguity resolution, the N1 ambiguities in Eq. 15 should be fixed to integers more rapidly than their narrow-lane counterparts in Eq. 13. Indeed, we observed that this expectation was true, but N1 ambiguities were in practice more easily fixed to incorrect integers than narrow-lane ambiguities within a short period. If we take “fixing to correct integers” as the criterion for successful initializations, it can be understood why we found that narrow-lane ambiguity fixing were actually achieved more rapidly, rather than slowly, in our study. As indicated by Teunissen (1997a), the GNSS model in Eq. 15 relates in nature to an ionosphere-float model, resulting in highly correlated ambiguities and rather elongated search space, which can hardly ensure both fast and correct ambiguity fixing. Moreover, for this ionosphere-float model, ionosphere estimation are governed by noisy pseudorange data during the early stage of PPP convergences. Any ionosphere estimation errors will be translated into other parameter estimates (e.g., N1 ambiguities) due to their linear dependency within the functional model. As a result, N1 ambiguities are difficult to be identified as correct integers before ionosphere estimates converge to high-precision values (Li et al. 2014). On the contrary, narrow-lane ambiguity estimates are free from the first-order ionosphere delays, and thus less contaminated by atmospheric errors. These facts explains why we do not achieve shorter initialization times when resolving N1 instead of narrow-lane ambiguities.

6 Conclusions and outlook

We investigated the efficiency of PPP-AR using triple-frequency multi-GNSS data. Undifferenced raw observations are directly processed in PPP while raw ambiguities are mapped at the normal equation level into their extra-wide-lane, wide-lane and narrow-lane counterparts for integer-cycle resolution. Since the positioning accuracy can be improved significantly after triple-frequency PPP-WAR (i.e., (extra-)wide-lane ambiguity resolution) during the early stage of PPP convergences, narrow-lane ambiguity fixing which signifies a successful PPP initialization can thus be accomplished faster in case of triple-frequency data compared to dual-frequency data. This study can be taken as a demonstration for the PPP convergence efficiency in the prospect of future complete multi-frequency global constellations.

In total, 31 days of data from 76 stations in 2017 were used to investigate PPP-AR. We found that extra-wide-lane, wide-lane and narrow-lane FCBs every 15 min were quite stable over time with standard deviations of less than 0.005, 0.025 and 0.030 cycles, respectively. This favorable temporal property facilitated their precise predictions for real-time PPP-AR. (Extra-)wide-lane FCBs were used to enable PPP-WAR, where an ionosphere-free wide-lane carrier-phase observable was produced implicitly. This observable had noise of up to a few decimeters, which was about half of the ionosphere-free pseudorange noise for GPS and BeiDou satellites. In this case, such ionosphere-free wide-lane observations could outweigh the raw pseudorange to constrain position and ambiguity estimates for faster convergences. Overall, the positioning accuracy after triple-frequency PPP-WAR reached on average 0.12, 0.08 and 0.27 m for the east, north and up components, respectively, for the first 10 min of convergence periods, while those of float PPP solutions could only reach 0.23, 0.18 and 0.43 m. As a result, 14.5 min was required for PPP-WAR whereas 16.6 min for float PPP to achieve a horizontal positioning error of less than 10 cm and a vertical error of less than 20 cm. Due to the enhanced constraints on positions thanks to PPP-WAR, triple-frequency PPP-AR could be achieved within 2 min for 48.1% of all solutions, and overall the mean initialization time was 6.1 min. In contrast, dual-frequency PPP-AR asked for 9.2 min on average and only 26.4% of all solutions were accomplished within 2 min.

Finally, we also found that the mean initialization time of triple-frequency PPP-AR became clearly shorter when involving more satellites. It is therefore envisioned that ambiguity-fixed solutions at a single station can be more reliably achieved within a few (e.g., 1–3) minutes if all GPS, BeiDou, Galileo and QZSS constellations are complete in the near future. To reach the ultimate convergence time, more than three frequency signals should also be considered in the PPP-AR model; thus an extendable model for multi-GNSS multi-frequency PPP-AR should be the focus of future studies. Moreover, multi-frequency satellite clocks, differential code biases and phase biases need to be appropriately handled in the meantime.