Introduction

Global Navigation Satellite Systems (GNSSs) such as GPS, Galileo and BDS-3 are providing more than three signals for positioning, timing and navigation (Montenbruck et al. 2017). Precise Point Positioning (PPP), as one of the most popular multi-GNSS and multi-frequency data processing techniques, can provide millimeter-level services based on precise satellite orbit and clock products of International GNSS Service (IGS) (Malys and Jensen 1990; Zumberge 1997). Precise orbit products always use the satellite center of mass as the reference point. However, the electrical antenna phase center (APC), can be different for different emitted frequencies (Kouba 2009) and different nadir and azimuth angles (Rothacher 2001). For each frequency, it is then common to define a Phase Center Offset (PCO) with respect to the satellite center of mass, plus additional nadir and azimuth-dependent Phase Center Variations (PCVs) (Schmid and Rothacher 2003). The PCO is usually considered as the point which minimizes the PCVs, in the statistical sense (Schmid et al. 2007). The modelling and calibration of PCO and PCV are essential to high-precision data processing.

Satellite APC can be directly pre-calibrated with high accuracy on the ground before launching. European Union Agency for Space Program (EUSPA, formerly the GNSS Service Agency, GSA) and the Cabinet Office, Government of Japan (CAO), first released ground-based calibrated APC corrections for Galileo and QZSS, respectively (GSA 2016; CAO 2017). Similar products of BDS and GPS BLOCK III can be also found since 2020, provided by the China Satellite Navigation Office CSNO and the U.S. Coast Guard Navigation Center (NAVCEN), respectively (CSNO 2020; GPS 2021). IGS has collected all the calibration corrections into igs20.atx (Steigenberger and Montenbruck 2023). However, not all constellations have publicly available APC ground-based corrections such as GPS satellites of generations before the BLOCK III. The APC calibration of such satellites can be carried out during their orbit determination data processing.

In this processing, due to the strong correlation between PCO and PCV, PCOs and minimized PCVs are determined separately (Steigenberger et al.2016). Moreover, it is demonstrated that the estimated position of the PCO in the nadir direction (z-offset) is correlated with the terrestrial reference frame scale (Zhu et al. 2003), and is thus sensitive to errors in the radial direction, such as satellite clocks and phase biases. The first estimation of GPS BLOCK-specific APC corrections was proposed by Schmid et al. (2005). Steigenberger et al. (2016) used 20-month observations to model Galileo E1/E5a PCOs, while terrestrial frame scale was sufficiently constrained. These authors demonstrated that the Galileo IOV and FOC horizontal PCOs (e.g. x-offset and y-offset) could be estimated at a precision of several centimeters while the standard deviation of the z-offset estimates reached 15–20 cm. Huang et al. (2018) estimated BDS-2 B1I/B2I PCOs with a mean standard deviation of 2–5 cm for horizontal components and 7–20 cm for vertical component.

Since these APC determinations were based on dual-frequency ionosphere-free observations, they got dual-frequency APC corrections only. These values are reported for both L1 and L2 in the IGS file igs20.atx. By now, BLOCK IIF L5 APC corrections are not available yet, resulting in a rude strategy for multi-frequency GPS data processing, in which the APC corrections of the dual-frequency combination of L1/L2 are applied on L5 (Guo and Geng 2018). However, Geng et al. (2021) demonstrated that applying a correct model for the third-frequency APC could increase the PPP ambiguity resolution (PPP-AR) convergence time by more than 15%. To provide available L5 APC corrections, Xin et al. (2021) carried out the estimation of BLOCK IIF L5 based on triple-frequency L1/L2/L5 PPP model. They achieved a x-offset, y-offset and z-offset PCO precision of 4, 3 and 21 mm respectively. Zeng et al. (2021) estimated L5 PCO together with the satellite orbits and improved the accuracy to 2, 2 and 16 mm. In their researches, only L5 PCOs are estimated, while satellite orbit as well as L1/L2 APCs, satellite clock, tropospheric delay parameters are constrained by L1/L2 observational model. This can explain why these triple-frequency methods show huge improvement compared to previous dual-frequency methods. However, the researchers assumed that the L5 signal shared the same receiver antenna APC correction with the L2 signal, which is not precise enough to sufficiently constrain the terrestrial frame scale at the tracking station side. The PCO estimation can be affected as a consequence. At the same time, satellite L5 PCVs were not mentioned in the published studies.

In this study, we aim at implementing the estimation of GPS L5 PCO based on ground stations with calibrated ground-based antenna. At the same time, BLOCK IIF L5 PCVs are modeled to further improve the performance of GPS L5 data processing. The ground-based calibrated APC corrections of BLOCK III satellites are used to evaluate the precision of our computed APC products. This paper is organized as follows: we first derive the observation model for PCO/PCV estimation, as well as the ambiguity resolution method; then the details concerning to the data processing are presented; next, we validate the PCO and PCV products using dual-/triple-frequency PPP-AR; finally, we draw the conclusions based on the results.

Method

In the first subsection we illustrate the relationships between satellite APC errors and the line-of-sight projection errors. Then the triple-frequency PPP model based on IGS precise products are derived, after which the ambiguity resolution strategy is presented. Finally, the L5 satellite PCOs/PCVs are determined in a massive network, while the integer ambiguities are pre-eliminated using the candidates obtained from the former ambiguity resolution step.

Satellite APC errors

Satellite APC is the reference point of the pseudorange and carrier-phase observations on the satellite side, which can be depicted as \(S_{0}\) in Fig. 1 in a spacecraft-fixed reference system. \(\tilde{x},\;\tilde{y}\;{\text{and}}\;\tilde{z}\) are the axis vectors of the spacecraft-fixed reference system where \(\tilde{z}\) is always pointing at the center of earth. “\(\sim\)” marks a unit vector. \(R\) represents the APC of ground antenna which has been precisely calibrated. \(S_{1}\) represent the assumed signal transmitted point when inaccurate APC correction is applied. As a result, a bias “\(\left| {\overrightarrow {{S_{o} R}} } \right| - \left| {\overrightarrow {{S_{1} R}} } \right|\)” is introduced to the GNSS observation function. Considering that the distance from GNSS satellite to the ground is much larger than the APC errors \(\left| {\overrightarrow {{S_{o} S_{1} }} } \right|\), \(\mu\) is actually very small. We can have

(1)
Fig. 1
figure 1

Satellite APC errors in the spacecraft-fixed reference system

Full size image

Assuming the difference vector components between \(S_{0}\) and \(S_{1}\) in the spacecraft-fixed system are \(\left( {\begin{array}{*{20}c} a & b & c \\ \end{array} } \right)\), the observation bias caused by the APC errors can be derived as

(2)

From the above equations we know that the observation biases caused by APC errors are relative with both nadir and azimuth angle of the satellite. Normally the APC errors of x-offset and y-offset \(\left( {a\;{\text{and}}\;b} \right)\) are of the order of several millimeters while that of z-offset \(c\) can reach up to several hundreds of millimeters. Considering the range of GPS nadir angles \(\theta\) as 0°–14°, the projection errors on the radial direction will be \(\cos \theta \in [0.97,1]\) times of the z-offset APC error \(c\) (Geng et al. 2021).

Triple-frequency PPP model

In this study we estimate the L5 PCOs of GPS satellites in a global GNSS network, based on triple-frequency undifferenced and uncombined model. Owing to the heavy computing burden for resolving multi-frequency ambiguity parameters in a network, we first implement station-by-station triple-frequency PPP to obtain the integer ambiguities. These ambiguities are then utilized for directly eliminating the ambiguity parameters in the massive network data processing. The triple-frequency PPP model can be derived from the raw pseudorange and carrier-phase observation equations:

$$\left\{ \begin{gathered} P_{i,j}^{k} = \rho_{i,j}^{k} + t_{i} - t^{k} + m_{i}^{k} T_{i} + \gamma_{j}^{{}} \cdot I_{i}^{k} + d_{i,j}^{{}} - d_{j}^{k} + \varepsilon_{i,j}^{k} \hfill \\ L_{i,j}^{k} = \rho_{i,j}^{k} + t_{i} - t^{k} + m_{i}^{k} T_{i} - \gamma_{j}^{{}} \cdot I_{i}^{k} + \lambda_{j} (b_{i,j}^{{}} - b_{j}^{k} + N_{i,j}^{k} + \varphi_{i,j}^{k} ) \hfill \\ \end{gathered} \right.$$
(3)

where \(P_{i,j}^{k}\) and \(L_{i,j}^{k}\) denote the GPS pseudorange and carrier-phase raw observations with respect to satellite \(k\) and receiver \(i\). \(j = 1,2,5\) corresponds to the GPS L1, L2 and L5 signals respectively. \(\rho_{i,j}^{k}\) is the geometric distance between the antenna phase center of satellite and ground-tracking station, which can be precisely calculated using IGS satellite products and multi-frequency APC corrections. \(t_{i}\) and \(t^{k}\) denote the clock errors from the satellite and receiver end, respectively. \(T_{i}\) is the zenithal tropospheric delay with \(m_{i}^{k}\) the mapping function. \(I_{i}^{k}\) corresponds to the ionospheric delay for L1 signal with \(\gamma_{j}^{{}} = \left( {\frac{{f_{1}^{{}} }}{{f_{j} }}} \right)^{2}\) the frequency-dependent coefficient with respect to frequency \(f_{j}\). \(d_{i,j} \;{\text{and}}\;d_{j}^{k}\) are pseudorange hardware biases for the receiver and satellite, respectively. Similarly, \(b_{i,j}\) and \(b_{j}^{k}\) are the hardware biases of carrier-phase observations. \(N_{i,j}^{k}\) is the integer ambiguity in a wavelength of \(\lambda_{j}\). \(\varepsilon_{i,j}^{k} \;{\text{and}}\;\varphi_{i,j}^{k}\) represent unmodelled errors such as observation noise and multipath error.

Since the APC corrections of L5 signal for GPS BLOCK IIF satellites are missing, we apply the APC corrections of L2 signal to L5, remaining a biased geometry distance \(\rho_{i,5}^{\prime k}\) for L5 signal. APC errors, especially for those from the z-offset, are introduced into Eq. (3). In the last section, we have mentioned that about 97% to 100% of z-offset PCO errors are projected into the line-of-sight direction. These projection errors can be automatically coupled with the other radial parameters such as carrier-phase hardware biases and ambiguities, respectively. In this study we mark the polluted satellite pseudorange bias, carrier-phase bias, integer ambiguity of L5 signal as \(d_{5}^{\prime k} ,\;b_{5}^{\prime k} \;{\text{and}}\;N_{i,5}^{\prime k} ,\) respectively. Note that \(b_{5}^{\prime k}\) absorbs only the fractional-cycle of the PCO projection errors while those of integer parts can be lumped into ambiguities. Comparing to z-offset, APC errors from the x-offset and y-offset are normally several millimeters, whose effects on PPP can be ignored.

At the same time, Eq. (3) cannot be resolved yet, owing to the linear correlation between hardware biases and clock errors. To eliminate the rank deficiency, we introduce precise satellite clock products to correct the satellite clock errors \(t^{k}\), observation-specific bias (OSB) products to correct the pseudorange and carrier-phase satellite-end hardware biases (Geng et al. 2022). The dual-frequency undifferenced and uncombined PPP model are introduced to further address the receiver-end hardware biases, where the ionosphere-free combination of those for L1/L2 pseudorange are lumped into the receiver clock parameter. The ionosphere delay and ambiguity parameters can absorb the remain hardware bias terms (Zhang et al. 2012). Next, observational model for the L5 signal can be derived by sharing the same receiver clock and ionospheric delay parameters with the dual-frequency model, which can be derived as:

$$\left\{ \begin{gathered} P_{i,1}^{k} - \rho_{i,1}^{k} + t^{k} + d_{1}^{k} = \overline{t}_{i} + m_{i}^{k} T_{i} + \gamma_{1} \cdot \overline{I}_{i}^{k} + \varepsilon_{i,1}^{k} \\ P_{i,2}^{k} - \rho_{i,2}^{k} + t^{k} + d_{2}^{k} = \overline{t}_{i} + m_{i}^{k} T_{i} + \gamma_{2} \cdot \overline{I}_{i}^{k} + \varepsilon_{i,2}^{k} \\ P_{i,5}^{k} - \rho_{i,5}^{\prime k} + t^{k} + d_{5}^{\prime k} = \overline{t}_{i} + m_{i}^{k} T_{i} + \gamma_{5} \cdot \overline{I}_{i}^{k} + \varepsilon_{i,5}^{k} \\ L_{i,1}^{k} - \rho_{i,1}^{k} + t^{k} + b_{1}^{k} = \overline{t}_{i} + m_{i}^{k} T_{i} - \gamma_{1} \cdot \overline{I}_{i}^{k} + \lambda_{1} (\overline{N}_{i,1}^{k} + \varphi_{i,1}^{k} ) \\ L_{i,2}^{k} - \rho_{i,2}^{k} + t^{k} + b_{2}^{k} = \overline{t}_{i} + m_{i}^{k} T_{i} - \gamma_{2} \cdot \overline{I}_{i}^{k} + \lambda_{2} (\overline{N}_{i,2}^{k} + \varphi_{i,2}^{k} ) \\ L_{i,5}^{k} - \rho_{i,5}^{\prime k} + t^{k} + b_{5}^{\prime k} = \overline{t}_{i} + m_{i}^{k} T_{i} - \gamma_{5} \cdot \overline{I}_{i}^{k} + \lambda_{5} (\overline{N}_{i,5}^{\prime k} + \varphi_{i,5}^{k} ) \\ \end{gathered} \right.$$
(4)

where

$$\left\{ \begin{gathered} \overline{t}_{i} = t_{i} + (\alpha \cdot d_{i,1} - \beta \cdot d_{i,2} ) \hfill \\ \overline{I}_{i}^{k} = I_{i}^{k} - \beta (d_{i,1} - d_{i,2} ) \hfill \\ \overline{N}_{i,1}^{k} = N_{i,1}^{k} + b_{i,1}^{{}} - \frac{1}{{\lambda_{1} }}\left( {(\alpha + \beta )d_{i,1} - 2\beta \cdot d_{i,2} } \right) \hfill \\ \overline{N}_{i,2}^{k} = N_{i,2}^{k} + b_{i,2}^{{}} - \frac{1}{{\lambda_{2} }}\left( {2\alpha \cdot d_{i,1} - (\alpha + \beta )d_{i,2} } \right) \hfill \\ \overline{N}_{i,5}^{\prime k} = N_{i,5}^{\prime k} + b_{i,5} - \frac{1}{{\lambda_{5} }}\left( {\gamma_{5}^{{}} \cdot \beta (d_{i,1} - d_{i,2} ) + (\alpha \cdot d_{i,1} - \beta \cdot d_{i,2} )} \right) \hfill \\ \end{gathered} \right.$$
(5)

and

$$\left\{ \begin{gathered} \alpha = \frac{{\gamma_{2}^{{}} }}{{\gamma_{2}^{{}} - 1}} \hfill \\ \beta = \frac{1}{{\gamma_{2}^{{}} - 1}} \hfill \\ \end{gathered} \right.$$
(6)

\(\alpha \;{\text{and}}\;\beta\) are the coefficients of the ionosphere-free combination for GPS L1 and L2. The terms on the left side of the equations represent the errors which are pre-eliminated from the raw observations. \(\overline{t}_{i} \;{\text{and}}\;\overline{I}_{i}^{k}\) denote the reparametrized receiver clock and ionospheric delay parameters which absorb the combination of pseudorange hardware biases of the receiver end. \(\overline{N}_{i,1}^{k} ,\;\overline{N}_{i,2}^{k} \;{\text{and}}\;\overline{N}_{i,5}^{\prime k}\) are float ambiguities which absorb receiver-related hardware biases only. By resolving Eq. (4), we obtain all of these reparametrized parameters as well as the tropospheric delay.

Ambiguity resolution

Equation (4) shows that current IGS phase OSB products \(b_{5}^{\prime k}\) for L5 signal are coupled with z-offset APC errors due to the inappropriate APC correcting strategy. In this case, to determine L5 APC corrections, satellite phase bias products for L5 should be re-estimated in the observation model at the same time. To make the phase bias estimable, we need to resolve the integer ambiguities to address the linear correlation between ambiguity and phase bias parameters. After implementing station-by-station triple-frequency PPP, the integer ambiguities can be resolved commencing from the float ambiguity estimates. For clarity, the float ambiguities \(\overline{N}_{i,1}^{k}\), \(\overline{N}_{i,2}^{k}\) and \(\overline{N}_{i,5}^{\prime k}\) are rewritten as

$$\left\{ \begin{gathered} \overline{N}_{i,1}^{k} = N_{i,1}^{k} + \overline{b}_{i,1}^{{}} \hfill \\ \overline{N}_{i,2}^{k} = N_{i,2}^{k} + \overline{b}_{i,2}^{{}} \hfill \\ \overline{N}_{i,5}^{\prime k} = N_{i,5}^{\prime k} + \overline{b}_{i,5}^{{}} \hfill \\ \end{gathered} \right.$$
(7)

where \(\overline{b}_{i,j}^{{}} (j = 1,2,5)\) represent the hardware biases included in the float ambiguities. In this study, we assume that \(\overline{b}_{i,j}^{{}}\) denotes the fractional part of the hardware bias while the integer part is absorbed by integer ambiguity. For each epoch at each station, \(\overline{b}_{i,j}^{{}}\) can be calculated by averaging the fractional parts of the PPP float ambiguity estimates through the following equations:

$$\left\{ \begin{gathered} \hat{\overline{b}}_{i,1}^{{}} = \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\overline{N}_{i,1}^{k} - \left[ {\overline{N}_{i,1}^{k} } \right]} \right)} \hfill \\ \hat{\overline{b}}_{i,2}^{{}} = \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\overline{N}_{i,2}^{k} - \left[ {\overline{N}_{i,2}^{k} } \right]} \right)} \hfill \\ \hat{\overline{b}}_{i,5}^{{}} = \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {\overline{N}_{i,5}^{\prime k} - \left[ {\overline{N}_{i,5}^{\prime k} } \right]} \right)} \hfill \\ \end{gathered} \right.$$
(8)

where “\([\Theta ]\)” denotes the option to obtain the integer part of “\(\Theta\)”. \(n\) represents the number of available satellites. \(\hat{\overline{b}}_{i,j}^{{}}\) is the corresponding estimate for \(\overline{b}_{i,j}^{{}}\). Once the receiver-end biases \(\hat{\overline{b}}_{i,j}^{{}}\) are obtained, they are applied to recover the integer nature of the float ambiguities through

$$\left\{ \begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{i,1}^{k} = \overline{N}_{i,1}^{k} - \hat{\overline{b}}_{i,1}^{{}} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{i,2}^{k} = \overline{N}_{i,2}^{k} - \hat{\overline{b}}_{i,2}^{{}} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{i,5}^{k} = \overline{N}_{i,5}^{\prime k} - \hat{\overline{b}}_{i,5}^{{}} \hfill \\ \end{gathered} \right.$$
(9)

where \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{i,j}^{k}\) is the recovered ambiguity with integer nature. However, \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{i,j}^{k}\) is still an float owing to the observation errors and correlations between ambiguity parameters in the normal matrix. We further applied the Least-squares AMbiguity Decorrelation Adjustment (LAMBDA) to search for the optimal integer candidates \(N_{i,j}^{k} \;{\text{for}}\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{i,j}^{k}\), using the variance–covariance matrix of float ambiguities (Teunissen 1994).

APC estimation model

Using the integer ambiguities obtained from the previous step, we now derive the L5 APC estimation method commencing from an ambiguity-fixed observation model. Since the APC errors can be directly projected to the line-of-sight direction, the accurate geometric distance \(\rho_{i,5}^{k}\) can be defined as

$$\rho_{i,5}^{k} = \rho_{i,0}^{k} + \vec{v} \cdot \overrightarrow {PCO}_{5}^{k} + PCV_{5}^{k}$$
(10)

with

$$\left\{ \begin{gathered} \vec{v} \approx \left( {\begin{array}{*{20}c} {\frac{{X_{0}^{k} - X_{i,5}^{{}} }}{{\rho_{i,0}^{k} }}} & {\frac{{Y_{0}^{k} - Y_{i,5}^{{}} }}{{\rho_{i,0}^{k} }}} & {\frac{{Z_{0}^{k} - Z_{i,5}^{{}} }}{{\rho_{i,0}^{k} }}} \\ \end{array} } \right) \hfill \\ \overrightarrow {PCO}_{5}^{k} = \left( {\begin{array}{*{20}c} {PCOX_{5}^{k} } & {PCOY_{5}^{k} } & {PCOZ_{5}^{k} } \\ \end{array} } \right) \hfill \\ \end{gathered} \right.$$
(11)

where \(\rho_{i,0}^{k}\) is the geometric distance from satellite center of mass \(\left( {\begin{array}{*{20}c} {X_{0}^{k} } & {Y_{0}^{k} } & {Z_{0}^{k} } \\ \end{array} } \right)\) to the APC of receiver antenna \(\left( {\begin{array}{*{20}c} {X_{i,5}^{{}} } & {Y_{i,5}^{{}} } & {Z_{i,5}^{{}} } \\ \end{array} } \right)\) corresponding to the solution of the dual-frequency L1/L2 static PPP corrected for the L5 phase center corrections for this antenna. \(\vec{v}\) denotes the unit vector pointing from the receiver to the satellite. \(\overrightarrow {PCO}_{5}^{k}\) represents the satellite L5 PCO which can be transferred to the spacecraft-fixed reference system by multiplying with the corresponding mapping function. \(PCV_{5}^{k}\) denotes the nadir-dependent L5 PCV which are modelled by a 5th-order polynomial function:

$$PCV_{5}^{k} = \sum\limits_{n = 1}^{5} {a_{n}^{k} (e_{i}^{k} )^{n - 1} }$$
(12)

where \(a_{n}^{k}\) is the coefficient of the polynomial with respect to satellite nadir angle \(e_{i}^{k}\). In this study we applied a 5th-order polynomial to fit the satellite-specific PCVs. Referring to the carrier-phase observational model from Eq. (3), the ambiguity-fixed APC estimation model used in this study is written as

$$\left\{ \begin{gathered} L_{i,1}^{k} - \rho_{i,1}^{k} + t^{k} - \lambda_{1} N_{i,1}^{k} = t_{i} + m_{i}^{k} T_{i} - \gamma_{1} \cdot I_{i}^{k} + \lambda_{1} (b_{i,1} - b_{1}^{k} + \varphi_{i,1}^{k} ) \hfill \\ L_{i,2}^{k} - \rho_{i,2}^{k} + t^{k} - \lambda_{2} N_{i,2}^{k} = t_{i} + m_{i}^{k} T_{i} - \gamma_{2} \cdot I_{i}^{k} + \lambda_{2} (b_{i,2} - b_{2}^{k} + \varphi_{i,2}^{k} ) \hfill \\ L_{i,5}^{k} - \rho_{i,0}^{k} + t^{k} - \lambda_{5} N_{i,5}^{\prime k} = \vec{v} \cdot \overrightarrow {PCO}_{5}^{k} + PCV_{5}^{k} + t_{i} + m_{i}^{k} T_{i} - \gamma_{5} \cdot I_{i}^{k} + \lambda_{5} (b_{i,5} - b_{5}^{k} + \varphi_{i,5}^{k} ) \hfill \\ \end{gathered} \right.$$
(13)

where integer ambiguities, geometry distance and satellite clock error are pre-eliminated from the carrier-phase observations. \(b_{5}^{k}\) denotes the carrier-phase bias parameter for L5 signal. The phase bias resolved by Eq. (13) is different from the one in current IGS OSB products, since the former one is not coupled with any APC errors.

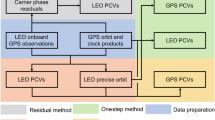
Even though both PCO and PCV are presented in Eq. (13), they are estimated sequentially during the data processing, owing to the correlations between nadir-dependent PCV and z-offset PCO (Schmid and Rothacher 2003), azimuth-dependent PCV and horizontal PCO (Schmid et al. 2005). L5 PCO is first estimated using L2 APC correction as the initial values. In the next step, L5 PCVs are determined while L5 PCO is constrained with the estimates in the first step. Phase bias \(b_{5}^{k}\) is estimated in both steps. Since nadir-dependent PCVs are linearly related to radial errors such as satellite phase biases, this study fixes the L5 PCV to the same value as L2 PCV on \(e_{i}^{k} = 0^{ \circ }\) to make PCVs estimable. This strategy may create a bias for PCV which will be absorbed by the phase bias of L5. Figure 2 gives the procedures to obtain PCO and PCV estimates according to Eqs. (4)–(13).

Fig. 2
figure 2

Flowchart of the L5 APC estimation method in this study

Full size image

Data processing strategies

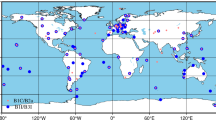
In this study we selected 118 globally distributed IGS stations for the PCO/PCV estimation (as shown in Fig. 3) while the other 37 stations are used for kinematic PPP validation. One-year of GPS L1/L2/L5 observations with a sampling rate of 30 s, ranging from day 213 of 2022 to day 212 of 2023 are used for the data processing. Precise satellite orbits, clocks, pseudoranges and carrier-phase OSB products released by Wuhan University are introduced to pre-eliminate satellite positions, clock errors and determine the integer ambiguities (Geng et al. 2022). Corresponding attitude quaternion products are also applied to keep the consistency of satellite gestures between the PCO estimation procedure in this study and the orbit products we used. Satellite and receiver antenna APCs are aligned using the corrections obtained from igs20.atx (Schmid et al. 2016). We then applied satellite L2 APC corrections as the initial values to estimate the L5 APCs. Based on a global network, satellite PCOs under spacecraft-fixed reference system are first estimated as constants over the day, after which satellite PCVs are modelled as 5th-order polynomial. The PCVs are ultimately expressed as nadir-dependent products with 1degree intervals. The one-year average of daily solutions of PCO and PCV estimates are released as the final products in this study. Carrier-phase OSBs are calculated together with APC corrections, tropospheric delay, ionospheric delay and receiver clock. The receiver positions are fixed to the daily solutions of L1/L2 PPP-AR implemented using the products from Wuhan University rather than fixed to the IGS weekly solutions. This permits to keep the ground receiver positions in the same achievement of terrestrial frame with those from Wuhan products. We modeled the tropospheric delays in the line-of-sight direction using the global mapping function proposed by Boehm et al. (2006). Saastamoinen model is applied to eliminate most of the troposphere delays while the residuals are estimated as random-walk parameters every 1 h with a noise of 10 mm (Saastamoinen 1973). The ionospheric delays are estimated every epoch using a random-walk noise of 10 m. The receiver clocks are estimated every 30 s as white-noise-like parameters with a priori noise of 900 m. The multi-frequency ambiguities are resolved using the LAMBDA method with a ratio test threshold of 3.0. If the ratio test fails, a partial ambiguity resolution is carried out until ambiguity candidates are less than 4. Table 1 gives more details about the data processing.

Fig. 3
figure 3

Distribution of GNSS ground-tracking stations used in this study. Green circles denote stations used for PCO/PCV estimation and red dots are those used for kinematic PPP validation

Full size image
Table 1 Details of the data processing strategies to estimate the third-frequency satellite APCs in this study
Full size table

Results

L5 PCO estimation

Now, we estimate the daily PCO of all BLOCK IIF and BLOCK III satellites based on 1-year GPS observations. The mean values of the daily estimates are used as the final PCO corrections. Figure 4 displays the PCO differences between the daily L5 APC estimates and released corrections of L2 in igs20.atx. For both BLOCK IIF and BLOCK III satellites, we determined the standard deviation (STD) on the daily solutions, and obtained for the horizontal PCOs a STD reaching 0.2 cm while the STD is 1.6 cm for the vertical PCO corrections. Figure 5 further gives the differences between final L5 PCO corrections and corresponding L2 PCO corrections. We obtained PCO differences of 4 mm in horizontal directions except for G26 for which the difference is 7 mm on x-offset. Compared to x-offset and y-offset, L5 z-offset PCO corrections can deviate by up to 50 mm from L2 PCOs. As seen from Fig. 5, the x-offset, y-offset and z-offset L5 PCOs are estimated with a STD of 0.23 cm, 0.21 cm and 19.50 cm respectively. To evaluate the absolute precision of the PCO estimates, ground-calibrated L5 PCOs of BLOCK III are introduced as benchmarks (red striped bars in Fig. 5). The x-offset L5 PCO estimates show a difference of 2 mm with benchmarks in average while the y-offset PCO estimates achieved a consistency better than 1 mm with the benchmarks. The z-offset estimates perform quite differently depending on the satellites. The z-offset estimated errors of G04, G11, G14 and G18 are within ± 1 cm while those of G23 and G28 are − 2.4 cm and 2.5 cm respectively. Table 2 lists the final L5 PCO corrections of all BLOCK IIF and BLOCK III satellites.

Fig. 4
figure 4

Differences between daily L5 PCO solutions and L2 PCO of G01 and G04 from igs20.atx. Horizontal gray dashed lines mark zero

Full size image
Fig. 5
figure 5

Differences between the L5 PCO estimates and L2 PCO provided in igs20.atx. The green bars are the differences; the red striped bar denote the differences in BLOCK III PCO for L5 between the estimates in this study and ground-based corrections in igs20.atx; the orange dashed lines display the standard deviations for 1-year L5 PCO estimates of each satellite

Full size image
Table 2 Mean L5 PCO estimates of both BLOCK IIF and BLOCK III
Full size table

L5 PCV estimation

After obtaining L5 PCO corrections, the daily PCVs of L5 signal are calculated by fixing L5 PCO. Figure 6 shows all daily PCV estimates for each BLOCK IIF satellite with respect to nadir angles from 0 to 14 degrees. PCVs at nadir larger than 14 degrees are not calculated since the maximum GPS satellite nadir angle observed by ground-based stations is about 14 degrees. The mean of 365 daily PCV solutions is used as the final PCV corrections (cyan lines in Fig. 6). Compared to L2 PCV corrections (yellow line), L5 PCVs have the similar trend with respect to the nadir angle, reaching the maximum around 9 degrees. Note that, at 0 degree, L5 PCV solutions of each panel are the same as the L2 PCV correction, since this study fixed 0-degree PCV. This is because that the PCV parameters are strongly correlated with satellite phase bias parameter that does not depend on the line-of-sight direction. As demonstrated in Schmid and Rothacher (2003), a constraint is required to prevent the normal equation system from becoming singular. In this case, we constrain the L5 PCV pattern at 0 degree using the value of L2 PCV pattern. The PCV STDs from 0 to 14 degrees have also been given in the figure (cyan error bars). For each satellite, the mean STDs are smaller than 1.2 mm, with a minimum mean STD of 0.6 mm for G27. For BLOCK IIF satellites, the dependence of L5 PCV with respect to the nadir angle is larger than the L2 PCV dependence. The differences between L5 PCV and L2 PCV corrections are significant at nadir angles between 4 and 12 degrees. For G30, this difference reaches 4 mm at 9 degrees. G32 shows the smallest L2-L5 PCV difference with a maximum of only 2 mm. In igs20.atx, the L5 PCVs of BLOCK III satellites are the same as L1 and L2 signals, which are estimated based on L1/L2 ionosphere-free combinations. We re-estimated L5 PCVs for BLOCK III by fixing the PCOs in igs20.atx. Figure 7 shows the BLOCK III PCV solutions. Similar to BLOCK IIF solutions, BLOCK III L5 PCVs show a good consistency with L1/L2 counterparts near nadir angles of 14 degrees, while differences reach up to 3 mm for nadir angles around 8 degrees. The L5 PCV of BLOCK III satellites are also larger than the L5 PCV of BLOCK IIF satellites, ranging from − 16 to + 12 mm, while for BLOCK IIF, the PCVs were limited between − 8 and + 6 mm. Table 3 lists the final L5 PCV corrections for both BLOCK IIF and BLOCK III satellites.

Fig. 6
figure 6

One-year daily L5 PCV estimates of BLOCK IIF satellites with respect to nadir angle. Yellow lines denote corresponding L2 PCV corrections. Cyan lines are the mean of one-year solutions while the error bars mark the STDs of the 1-year solutions obtained for each nadir angle

Full size image
Fig. 7
figure 7

One-year daily L5 PCV estimates of BLOCK III satellites with respect to the nadir angle. Yellow lines denote corresponding L5 PCV corrections in igs20.atx which are determined by the ionosphere-free combinations of L1 and L2. Cyan lines are the mean of one-year solutions while the error bars mark the STDs of the 1-year solutions obtained for each nadir angle

Full size image
Table 3 Mean L5 PCV estimates of BLOCK IIF and BLOCK III satellites with respect to the nadir angle
Full size table

Triple-frequency kinematic PPP-AR

Previous studies demonstrated that APC errors will lead to the slower convergence of multi-frequency PPP-AR (e.g. Geng et al. 2021). In this section we validate the L5 PCO/PCV estimates through L1/L2/L5 triple-frequency kinematic PPP-AR. Three APC correcting strategies are designed: (a) “L2PCO + L2PCV”: L5 signal applies L2 PCO/PCV corrections from IGS atx file; (b) “L5PCO + L2PCV”: L5 signal applies L5 PCO estimated in this study and L2 PCV from igs20.atx; (c) “L5PCO + L5PCV”: L5 signal applies L5 PCO/PCV estimates of this study. Figure 8 displays the distributions of the convergence time of these three experiments. Note that the triple-frequency PPP-AR procedure is reinitialized every 2 h to have more samples for the test of the convergence time. In this study, we consider a successful convergence time when the horizontal positioning errors converge into ± 10 cm and ± 20 cm for the vertical component. Dual-frequency static PPP-AR solutions are taken as the benchmarks to evaluate the positioning errors. Note that the positioning errors are evaluated after the successful convergence of the positions with the reference. 74.4% of L2PCO + L2PCV solutions converge successfully in 30 min. After applying L5 PCO/PCV corrections, this proportion increases to 80.4%. Compared to ambiguity-fixed solutions, ambiguity-float solutions based on the above three strategies show similar performance with only 40% of them achieving convergence in 30 min. This means that APC errors mainly deteriorate the convergence efficiency in triple-frequency PPP-AR which is not the case using float triple-frequency PPP. Table 4 shows the statistics of PPP-AR convergence times and positioning errors. The mean convergence time of PPP-AR with inaccurate L5 PCO and PCV is 26.3 min. It is shortened to 24.5 min after applying L5 PCO estimates of this study. When L5 PCV corrections are further applied, PPP-AR solutions can achieve convergence in 22.8 min, showing an improvement of 13%. There is however no significant improvement of the final kinematic positioning quality (i.e. after convergence) when using the L5 PCO/PCV instead of the L2 values provided in the igs20.atx.

Fig. 8
figure 8

Distribution of the convergence times of triple-frequency L1/L2/L5 PPP-AR when using a L2PCO + L2PCV, b L5PCO + L2PCV, c L5PCO + L5PCV. Red bars are those of L1/L2/L5 float PPP

Full size image
Table 4 Mean convergence time and positioning errors of triple-frequency L1/L2/L5 PPP-AR. “Float.” denotes the results of ambiguity-float PPP while “Fix.” denotes the results of ambiguity-fixed PPP. The positioning error is calculated based on the converged epochs of the 2-h period
Full size table

Dual-frequency static PPP-AR

L5 PCO/PCV corrections will also benefit to L1/L5 dual-frequency users. This section evaluates the effects of the L5 APC corrections on L1/L5 static PPP-AR. In this section, we carry out dual-frequency L1/L5 PPP-AR based on the same three PCO/PCV correcting strategies: “L2PCO + L2PCV”, “L5PCO + L2PCV” and “L5PCO + L5PCV” respectively. One-year GPS observations from 150 global-distributed stations are collected to calculate daily positioning solutions (all stations in Fig. 2). L1/L2 PPP-AR solutions are used as benchmarks. The differences with L1/L5 PPP-AR results are used to evaluate the positioning errors. Figure 9 displays the daily positioning errors of our solutions for each station, based on the three L1/L5 PPP-AR strategies. Figure 9a, b and c show that “L5PCO + L2PCV” PPP-AR has comparable positioning performance as “L2PCO + L2PCV”, achieving a Mean Root Mean Square (MRMS) of 6.2, 3.3 and 9.7 mm on the east, north and up components. This can be understood by the fact that more than 97% of z-offset PCO errors are absorbed by the phase OSBs. Figure 9d, e and f demonstrate that L1/L5 PPP-AR achieves the positioning precision of 6.2, 3.2 and 8.2 mm if further applying L5 PCV corrections. Compared to “L5PCO + L2PCV”, an improvement of 15% is observed on the up component. Figure 10 displays the station-dependent differences for the up-component positioning errors between “L2PCO + L2PCV” and “L5PCO + L2PCV”, and “L2PCO + L2PCV” and “L5PCO + L5PCV” respectively. Figure 10a shows that the positioning error differences among global stations are insignificant, as 97% of them fall into ± 1 mm. Conversely, Fig. 10b shows that “L5PCO + L5PCV” provides an obvious improvement of the positioning precision on the up component. Almost 70% of the stations achieve higher positioning precision on the up component after introducing L5 PCV and 7% of them show an improvement of more than 2 mm.

Fig. 9
figure 9

Positioning errors of daily L1/L5 PPP-AR for “L2PCO + L2PCV”, “L5PCO + L2PCV”, “L5PCO + L5PCV” when compared to L1/L2 static solutions. Each dot represents a daily solution of one station and 150 stations are plotted in each panel. The “L5PCO + L2PCV” and “L5PCO + L5PCV” are presented against the “L2PCO + L2PCV” in each panel for the east, north and up component. The gray dashed lines are diagonal for each panel. If a dot dwell under its corresponding gray line, the positioning accuracy derived based on the strategies labeling the vertical axes exceed those derived based on “L2PCO + L2PCV”. The mean RMS statistics over 150 stations for “L2PCO + L2PCV” are plotted along the horizontal axes while those for “L5PCO + L2PCV” and “L5PCO + L5PCV” are plotted along the vertical axes

Full size image
Fig. 10
figure 10

Differences of the positioning errors for the up component with respect to station locations. a Denotes the positioning error differences between “L2PCO + L2PCV” and “L5PCO + L2PCV”. b Denotes the positioning error differences between “L2PCO + L2PCV” and “L5PCO + L5PCV”

Full size image

Conclusions

This study introduces a method to estimate the GPS third-frequency satellite PCO and PCV based on undifferenced and uncombined pseudo-range and carrier-phase observations. Triple-frequency integer ambiguities are fixed to resolve APC parameters and satellite phase biases at the same time. Multi-frequency receiver APC corrections as well as satellite attitude quaternions products are applied to improve the reliability of the APC estimation.

One-year GPS triple-frequency observations collected from 118 globally distributed stations are used to estimate L5 PCO and PCV of BLOCK IIF and BLOCK III satellites. Triple-frequency PPP using precise orbit/clock/OSB products is first implemented to obtain the integer candidates of ambiguities. Daily PCOs of both BLOCK IIF and BLOCK III satellites are then resolved based on the global network, with mean STDs of 2.3, 2.1 and 19.5 mm respectively. Compared to the ground-based APC corrections in igs20.atx, the estimated L5 PCO corrections of BLOCK III are deviated by 1.8, 0.9 and 9.9 mm for the x-offset, y-offset and z-offset respectively.

The third-frequency PCVs are sequentially estimated after obtaining PCO products. A 5th-order polynomial is applied to model the L5 PCVs, which are then determined in a nadir-dependent form, from 0 to 14 degrees with intervals of 1 degree. PCV corrections are calculated with a STD better than 1.2 mm. For BLOCK IIF satellites, the dependence of L5 PCV with respect to the nadir angle we obtain is larger than the L2 PCV dependence. The maximum difference between L5 PCV estimates and L2 counterparts is observed at a nadir angle of 9 degrees, where it can reach 4 mm.

Triple-frequency kinematic PPP-AR is used to validate the L5 APC corrections. With the APC corrections of this study, L1/L2/L5 PPP-AR achieves a successful convergence in 22.8 min while 26.3 min are required for that based on using L2 APCs for L5. Dual-frequency static L1/L5 PPP-AR experiments show that L5 APC corrections contribute more on z-offset than horizontal offsets. An average improvement of 1.4 mm is observed on the up component after introducing L5 APC corrections to L1/L5 PPP-AR model.