1 Introduction

Ageing is considered as an important phenomena which has received great attention among researchers in the domain of reliability analysis. Because of its crucial influence on the lifetime of the components/devices under observation, Kupka and Loo (1989) put forward a new strategy called the vitality function, a measure of ageing process. Thereafter, for lifetime distributions Kotz and Shanbhag (1980) obtained several characterizations based on this concept. Further, this measure would be helpful in modelling lifetime data too.

In many practical situations, geometric mean is regarded as the suitable average compared to other averages. Mostly, it has been found useful in averaging ratios, rates and percentages as well. For instance, this serves better in finding relative performance of the system/components in the context of reliability. Apart from this, its influence on the stock market has been discussed in detail by Cover and Thomas (2006).

The fascinating applications of geometric mean paved the way for the establishment of a new measure called the Geometric Vitality Function (GVF) by Nair and Rajesh (2000). For a non-negative random variable (rv) Z having an absolutely continuous distribution function, F(z) with \(E[\log Z]<{+\infty }\), GVF is defined as

$$\begin{aligned} \log G(t) = E \left[ \log Z |Z>t \right] = \frac{1}{{{\bar{F}}(t)}}\int _{t}^{{+\infty }} \log z \, {f(z)}\,dz, \end{aligned}$$

where \({{\bar{F}}(t)}= P(Z > t)\) denotes the survival function. This measure represents the geometric mean of lifetimes of components which has survived up to time t. Although vitality function explains the life expectancy of a device it cannot be regarded as an appropriate tool for measuring the relative performance of the device/component under examination. Hence GVF overcomes this limitation and was also found to be applicable in the analysis of lifetime data as well. This measure has been studied in detail by many authors in the literature. Accordingly, Sunoj et al. (2009) proposed GVF for doubly-truncated random variables. Afterwards, Sathar et al. (2010) extended the notion of GVF to a bivariate set up and studied characterization properties of some bivariate models using the proposed measure. And finally, for the complete and censored samples, Rajesh et al. (2014) established non-parametric kernel estimators for GVF.

The foundation for the theory of information is the uncertainty measure introduced by Shannon (1948), which quantifies the amount of information in a rv Z assumed to be non-negative with the probability density function (pdf), f(z). Then Shannon entropy is given by

$$\begin{aligned} H(Z)= - \int _{0}^{{+\infty }} {f(z)} \log {f(z)}\,dz. \end{aligned}$$

According to information theory, it has come to light that under many experimental situations uncertainty has greater impact on past lifetime similar to the future. For instance, suppose a person has gone through a medical test at time t and the test results in positive. If Z represents the age at which the person was diseased, then the past lifetime or inactivity time refers to the time which has passed since the person had been infected by the disease. On the basis of this notion, Di Crescenzo and Longobardi (2002) proposed a new measure namely past entropy, which would be very effective in measuring information on the inactivity time of the device. Suppose f(z) be the pdf and F(z) be the cumulative distribution function (cdf) of the non-negative rv \({Z_{t}=\left( t-Z|Z \le t\right) }\), then past entropy is given as

$$\begin{aligned} {\bar{H}}(Z_{t})= -\int _{0}^{t} \dfrac{{f(z)}}{{F(t)}}\log \left( \dfrac{{f(z)}}{{F(t)}}\right) \,dz. \end{aligned}$$
(1)

This measure plays a vital role in forensic science as the lifetime distributions truncated above has greater significance. Further, several works were carried out in the literature based on the past lifetime, for instance one may refer to Di Crescenzo and Longobardi (2004), Kundu et al. (2010), Kumar et al. (2011) and Di Crescenzo and Toomaj (2015).

In the context of past lifetime, we define GVF as follows. For the rv \({Z_{t}=\left( t-Z|Z \le t\right) }\) having the pdf f(z) and cdf F(z) with \(E\left[ \log Z\right] < {+\infty }\), then past GVF (PGVF) is defined by

$$\begin{aligned} \log {\bar{G}}(t) = E \left[ \log Z |Z \le t \right] = \frac{1}{{F(t)}}\int _{0}^{t} \log z\, {f(z)}\, dz. \end{aligned}$$
(2)

Simplification of (2) gives

$$\begin{aligned} \log \left( \frac{{\bar{G}} (t)}{t}\right) =-\frac{1}{{F(t)}}\int _{0}^{t} \frac{{F(z)}}{z}\, dz. \end{aligned}$$
(3)

Although Shannon entropy leads a central role in the information theory, it is not suitable in certain circumstances for measuring the information. As a result of this, various measures were developed by different authors in this domain. One among them is the cumulative past entropy (CPE) introduced by Di Crescenzo and Longobardi (2009) and is defined for a non-negative rv Z with cdf F(z) as

$$\begin{aligned} \textit{CPE}(Z)= -\int _{0}^{{+\infty }} {F(z)} \log {F(z)} \, dz. \end{aligned}$$
(4)

In addition to this, Di Crescenzo and Longobardi (2009) also established dynamic cumulative past entropy (DCPE), which would be useful when the uncertainty relies on the inactivity time of the device. Consider \({Z_{t}=\left( t-Z|Z \le t\right) }\) be a non-negative rv with the cdf F(z), then the DCPE of Z is given by

$$\begin{aligned} \textit{DCPE}(Z_{t})= -\int _{0}^{t} \dfrac{{F(z)}}{{F(t)}} \log \left( \dfrac{{F(z)}}{{F(t)}}\right) \,dz. \end{aligned}$$
(5)

Table 1 represents the relative performance of PGVF with Past Entropy and DCPE for different life distributions.

Table 1 Comparison of PGVF and some reliability measures on specific lifetime distributions
Full size table

From Table 1, it can be observed that in some situations PGVF results in smaller values compared to the past entropy and DCPE measures. Hence one may conclude that PGVF holds more information than some of the existing reliability measures.

Let \(Z_{1},Z_{2},\ldots ,Z_{n}\) represents the random sample. Then the alignment of \(Z_{1},Z_{2},\ldots ,Z_{n}\) from the minimum to the maximum forms the order statistics of the sample. It has been of greater use in characterizing probability distributions, finding outliers, goodness-of-fit tests, reliability theory, statistical inference etc. For \(1 \le k\le n \), let \(Z_{k:n}\) denote the kth order statistic of the sample. According to reliability theory out of a sample of size n, the kth order statistic denotes the life length of an \((n-k+1)-out-of-n\)-system. In particular \(k=1\) and \(k=n\) denotes the lifetimes of series and parallel systems respectively.

The theoretical and practical aspects of order statistics has been discussed in detail by David and Nagaraja (2003). In the literature, Wong and Chen (1990), Park (1995) and Ebrahimi et al. (2004) contributed interesting results on entropy properties of order statistics. Further, Thapliyal and Taneja (2013) established the notion of past entropy on order statistics and under certain conditions characterization results are also discussed. Subsequently on past lifetime, Thapliyal et al. (2013) proposed cumulative and dynamic cumulative entropies for order statistics and has studied some of its properties as well. Recently, Goel et al. (2018) analysed past entropy for nth upper k-record value and provided certain characterization results for the proposed measure. Inspired by the role of past lifetime over many real life situations, here an attempt is made to study GVF on past lifetime in the context of order statistics. Throughout the article U(0, 1) denotes uniform distribution over the interval (0, 1).

In this article, a measure of GVF is proposed for the random variable which is truncated above the time point, t. The framework of the article is as follows. In Sect. 2, some of the monotone properties of the proposed measure on certain conditions are discussed. Further, the definition of PGVF in terms of probabilistic order along with some sufficient conditions for the order to hold are also studied in this section, whereas in Sect. 3 we have established those results in terms of ordered random variables particularly in order statistics. At the end of this section, we have established bounds for the proposed measure of order statistics. Characterizations of some lifetime distributions based on order statistics are discussed in Sect. 3.2. And finally, we have given the conclusion in Sect.  4.

2 Properties

In this section, we obtain several interesting properties for GVF based on the inactivity time. The immediate one describes the uniquely determine property of PGVF (2).

Based on (3), the relationship between PGVF and the reversed hazard rate is given by

$$\begin{aligned} \delta _{Z }(t) = \frac{-\frac{d}{dt}{\left( \log {\bar{G}}(t) \right) }}{{ \log \left( \frac{{\bar{G}}(t)}{t}\right) }}, \end{aligned}$$
(6)

where \(\delta _{Z }(t)=\frac{f(t)}{F(t)}\). Using (6), we can obtain the expression as follows

$$\begin{aligned} \frac{d}{dt} \log {\bar{G}}(t) + \delta _{Z }(t) \log {\bar{G}}(t)= \log t\, \delta _{Z }(t). \end{aligned}$$
(7)

Solving (7), we get

$$\begin{aligned} {\log {\bar{G}}(t) =\mathrm {e}^{-\int _{t_{0}}^{t} \delta _{Z }(z)dz} \left[ \int _{t_{0}}^{t} \log z\,\delta _{Z}(z) \, \mathrm {e}^{\int _{t_{0}}^{z} \delta _{Z }(w) dw } dz+ K\right] ,} \end{aligned}$$
(8)

where we can choose \(t_{0}=1\). The constant of integration K is obtained by letting \(t=1\) in (3). Hence (8) implies that the PGVF determines the corresponding distribution function uniquely.

The following definition might be helpful to prove the Theorem 2.1.

Definition 2.1

A rv Z is said to have a non-increasing (non-decreasing) PGVF denoted as DPGVF (IPGVF) if \(\log {\bar{G}}(t)\) is non-increasing (non-decreasing) in \(t\ge 0\).

The following theorem presents the expression for DPGVF (IPGVF) based on Definition 2.1.

Theorem 2.1

Let Z be a non-negative rv. Z has DPGVF (IPGVF) if and only if \( \log {\bar{G}}(t)\) \(\ge \left( \le \right) \log t \).

Proof

For a DPGVF, obviously \(\dfrac{d}{dt} \log {\bar{G}}(t) \le 0\). Using (7), we get \( \log {\bar{G}}(t) \ge \log t\). By retracing the steps given above we can easily obtain the converse part and is therefore omitted. Similarly, for an IPGVF we can obtain the result as \( \log {\bar{G}}(t) \le \log t\). Hence the theorem. \(\square \)

The application of Theorem 2.1 is illustrated through the following example.

Example 2.1

Assume the rv Z follows power distribution with cdf of the form \(F(z)=\left( \dfrac{z}{a}\right) ^{b}, 0\le z\le a;b>0\). Using (8), we obtain

$$\begin{aligned} \log {\bar{G}}(t) = K \, t^{-b} - \frac{1}{b}+ \log t. \end{aligned}$$

Letting \(t=1\), we have \(\log {\bar{G}}(1) = -\frac{1}{b} + K \). Also from (3), we get \(\log {\bar{G}}(1) = -\frac{1}{b}\). Thus \(K=0\) and the result follows immediately.

Let us look back on the definitions of two stochastic orderings from Shaked and Shanthikumar (2007), which might be helpful to prove the following theorem.

Definition 2.2

Let \({\bar{F}}\) and \({\bar{G}}\) denotes the survival functions, f and g denotes the pdf’s of two non-negative rv’s Z and X respectively, then Z is said to be smaller than X

  1. (1)

    in the likelihood ratio order, denoted by \( Z \le _{lr} X \), if \( \frac{f(z)}{g(z)} \) is decreasing in \( z \ge 0 \),

  2. (2)

    in the usual stochastic order, denoted by \( Z \le _{st} X \), if \( {\bar{F}}(z) \le {\bar{G}}(z) \) for all \( z \ge 0 \).

It is well known that \( Z \le _{lr} X \implies Z \le _{st} X \) and \(Z \le _{st} X \) if and only if \( E[\psi (Z)] \le E[\psi (X)]\) for all increasing functions \(\psi \).

The following theorem discusses the alternative condition under which PGVF (2) is non-decreasing in t.

Theorem 2.2

Let Z be a non-negative rv having the cdf F and pdf f. If \( \log {\left( F^{-1}(z)\right) }\) is increasing in \(z\ge 0\), then \( \log {\bar{G}}(t)\) is non-decreasing in \(t \ge 0\).

Proof

Suppose the rv \(W_{t}\) follows U(0, F(t)) with the pdf \(h_{t}(z)= \frac{1}{{F(t)}}\), \(0<z<{F(t)}\). Then (2) becomes,

$$\begin{aligned} \log {\bar{G}}(t) = \int _{0}^{{F(t)}} \log {\left( F^{-1}(w)\right) } h_{t}(w) dw= E\left[ \log {\left( F^{-1}\left( W_{t}\right) \right) }\right] . \end{aligned}$$

Assume \(0 \le t_{1} < t_{2}\). Then

$$\begin{aligned} \dfrac{h_{t_{1}}(z)}{h_{t_{2}}(z)}= {\left\{ \begin{array}{ll} {\frac{F\left( t_{2}\right) }{F\left( t_{1}\right) }} &{} if \, 0< z\le {F\left( t_{1}\right) } \\ 0 &{} if \, {F\left( t_{1}\right) }<z<{F\left( t_{2}\right) } \end{array}\right. }, \end{aligned}$$
(9)

where \({\frac{F\left( t_{2}\right) }{F\left( t_{1}\right) }}\) is a constant in \(0<z \le {F\left( t_{1}\right) }\). Thus \(\frac{h_{t_{1}}(z)}{h_{t_{2}}(z)}\) is decreasing in z on the interval \(\left( 0,{F\left( t_{2}\right) }\right) \). By Definition 2.2, we have \(W_{t_{1}} \le _{lr} W_{t_{2}}\) which implies \(W_{t_{1}} \le _{st} W_{t_{2}}\). Obviously

$$\begin{aligned} 0 \le E\left[ \log {\left( F^{-1}\left( W_{t_{1}}\right) \right) }\right] \le E\left[ \log {\left( F^{-1}\left( W_{t_{2}}\right) \right) }\right] \implies \log {\bar{G}}\left( t_{1}\right) \le \log {\bar{G}}\left( t_{2}\right) , \end{aligned}$$

since \(\log {\left( F^{-1}(z)\right) }\) is increasing in z. Hence the theorem. \(\square \)

The following example shows the application of Theorem 2.2.

Example 2.2

Let the rv Z be defined as in Example 2.1. Then \( \log \left( F^{-1}(z)\right) = \log a+ \frac{1}{b} \log z\), which satisfies the condition of Theorem 2.2. Hence the result follows.

Motivated by Di Crescenzo and Longobardi (2002), the order based on GVF for the past lifetime is given through the following definition.

Definition 2.3

Let Z and X be two non-negative rv’s representing the lifetimes of two components. Then \(Z{\mathop {\ge }\limits ^{\textit{PGVF}}} X\), if \(\log {\bar{G}}^{Z}(t)\ge \log {\bar{G}}^{X}(t)\).

Example 2.3

Suppose Z and X follow inverse exponential distribution with the parameters \( \lambda _{1}\) and \(\lambda _{2}\left( =\dfrac{\lambda _{1}}{3}\right) \) respectively. Then obviously they satisfy the Definition 2.3.

The expression for PGVF under scalar transformation is given in the following lemma which might be useful to prove the upcoming theorem.

Lemma 2.1

Define \({V}=\dfrac{Z}{a}\), where \(a>0\) is a constant and Z be any absolutely continuous rv. Then for \(t>0\),

$$\begin{aligned} \log {\bar{G}}^{{V}}(t)=\log {\bar{G}}^{Z}(at) - \log a, \end{aligned}$$

where F, G and f, g are the cdf and pdf of V and Z respectively.

Proof

Applying the transformation \({V}=\dfrac{Z}{a}\) in (2), the result is direct and is hence omitted. \(\square \)

In the following theorem we show that the PGVF is closed under increasing scalar transformation.

Theorem 2.3

Define \(U_{1}=\dfrac{Z}{a_{1}}\) and \(U_{2}=\dfrac{{X}}{a_{2}}\), where \(a_{1},a_{2}>0\) are constants and Z, X be any two absolutely continuous rv’s. Also, let (a) \(Z{\mathop {\ge }\limits ^{\textit{PGVF}}}{X}\) and (b) \(a_{1} \ge a_{2}\). Then \(U_{1}{\mathop {\ge }\limits ^{\textit{PGVF}}} U_{2}\), if either \(\log {\bar{G}}^{Z}(t)\) or \(\log {\bar{G}}^{{X}}(t)\) is non-decreasing in \(t>0\).

Proof

Suppose \(\log {\bar{G}}^{Z}(t)\) is non-decreasing in t. Since \(a_{1}t \ge a_{2}t\),

$$\begin{aligned} \log {\bar{G}}^{Z}(a_{1}t) \ge \log {\bar{G}}^{Z}(a_{2}t). \end{aligned}$$
(10)

Also, according to (a) we get

$$\begin{aligned} \log {\bar{G}}^{Z}(a_{2}t) \ge \log {\bar{G}}^{{X}}(a_{2}t). \end{aligned}$$
(11)

Combining (10) and (11), we have

$$\begin{aligned} \log {\bar{G}}^{Z}(a_{1}t) \ge \log {\bar{G}}^{{X}}(a_{2}t). \end{aligned}$$

Using Lemma 2.1 and Definition 2.3, we get

$$\begin{aligned} \log {\bar{G}}^{U_{1}}(t) \ge \log {\bar{G}}^{U_{2}}(t) \implies U_{1}{\mathop {\ge }\limits ^{\textit{PGVF}}} U_{2}. \end{aligned}$$

The same proof holds if \( \log {\bar{G}}^{{X}}(t)\) is non-decreasing and is therefore omitted. \(\square \)

The following example illustrates the application of Theorem 2.3.

Example 2.4

Suppose \(Z \sim F(z)= \dfrac{z}{2},\, 0 \le z \le 2\). Then \(\log {\bar{G}}^{Z}(t)= \log t-1, \, 0 \le t \le 2\) which is non-decreasing in t. Obviously, the condition for Theorem 2.3 is satisfied. Hence \(U_{1}{\mathop {\ge }\limits ^{\textit{PGVF}}} U_{2}\).

Taking \(a_{1}=a_{2}=a(>0)\) in Theorem 2.3 we have the following corollary.

Corollary 2.1

Define \(V_{1}=\dfrac{Z}{a}\), \(V_{2}=\dfrac{{X}}{a}\) and on the assumptions of Theorem 2.3, we have \(V_{1}{\mathop {\ge }\limits ^{\textit{PGVF}}} V_{2},\,\mathrm{if\,either}\,\log {\bar{G}}^{Z}(t)\,\mathrm{or}\,\log {\bar{G}}^{{X}}(t)\,\text {is non-decreasing in}\,t>0.\)

The following theorem discusses a more powerful result regardless of the condition that non-decreasing PGVF in Theorem 2.3.

Theorem 2.4

Define \(V_{1}=\dfrac{Z}{a}\) and \(V_{2}=\dfrac{{X}}{a}\), where \(a>0\) is a constant and Z, X be any two absolutely continuous rv’s. Then \(V_{1}{\mathop {\ge }\limits ^{\textit{PGVF}}} V_{2}\), if \(Z{\mathop {\ge }\limits ^{\textit{PGVF}}} {X}\).

Proof

Suppose \(Z {\mathop {\ge }\limits ^{\textit{PGVF}}} X\), then by using Definition 2.3 in view of scalar transformation we have

$$\begin{aligned} \begin{aligned} \log {\bar{G}}^{Z}(at) \ge \log {\bar{G}}^{X}(at). \end{aligned} \end{aligned}$$

Using Lemma 2.1 and Definition 2.3, we get

$$\begin{aligned} \log {\bar{G}}^{V_{1}}(t) \ge \log {\bar{G}}^{V_{2}}(t) \implies V_{1}{\mathop {\ge }\limits ^{\textit{PGVF}}} V_{2}. \end{aligned}$$

This completes the proof. \(\square \)

3 PGVF on order statistics

Let \({f_{k:n}(z)}\) and \({F_{k:n}(z)}\) denote the pdf and cdf of the kth order statistic, \(Z_{k:n}\). Then, for \(1 \le k \le n\),

$$\begin{aligned} {f_{k:n}(z)}= \frac{1}{B\left( k,n-k+1\right) } \left[ {F(z)}\right] ^{k-1}\left[ 1-{F(z)}\right] ^{n-k} {f(z)}, \end{aligned}$$

where \(B\left( m,n\right) = \int _{0}^{1}z^{m-1}\left( 1-z\right) ^{n-1}dz, \, m,n>0\) and

$$\begin{aligned} {F_{k:n}(z)} =\sum _{i=k} ^{n} \genfrac(){0.0pt}0{n}{i} \left[ {F(z)}\right] ^{i} \left[ 1-{F(z)}\right] ^{n-i}. \end{aligned}$$

The GVF associated with \(Z_{k:n}\) is given by

$$\begin{aligned} \log G_{k:n}(t)&=\frac{1}{{{\bar{F}}_{k:n}(t)}}\int _{t}^{{+\infty }} \log z \, {f_{k:n}(z)}\, dz \\&= \log t+ \frac{1}{{{\bar{F}}_{k:n}(t)}}\int _{t}^{{+\infty }} \frac{{{\bar{F}}_{k:n}(z)}}{z}\,dz, \end{aligned}$$

where \({{\bar{F}}_{k:n}(z)}= P\left( Z_{k:n}>z\right) \).

For the kth order statistic, we define the PGVF as

$$\begin{aligned} \log {\bar{G}}_{k:n}(t) =E \left[ \log Z_{k:n} |Z_{k:n} \le t \right] =\frac{1}{{F_{k:n}(t)}}\int _{0}^{t} \log z \, {f_{k:n}(z)}\, dz. \end{aligned}$$
(12)

Suppose that a \(\left( n-k+1\right) -out-of-n\) system is functioning at time t, then \(\log {\bar{G}}_{k:n}(t)\) represents the geometric mean of lifetimes of systems in the past period (0, t). Also, (12) can be rewritten as

$$\begin{aligned} \log \left( \frac{{\bar{G}}_{k:n} (t)}{t}\right) =-\frac{1}{{F_{k:n}(t)}}\int _{0}^{t} \frac{{F_{k:n}(z)}}{z}\,dz. \end{aligned}$$
(13)

Similar to (6), the relation between PGVF and the reversed hazard rate function based on order statistics is as follows

$$\begin{aligned} \delta _{k:n}(t) = \frac{-\frac{d}{dt}{\left( \log {\bar{G}}_{k:n}(t) \right) }}{{ \log \left( \frac{{\bar{G}}_{k:n} (t)}{t}\right) }}, \end{aligned}$$
(14)

where \(\delta _{k:n}(t)=\frac{f_{k:n} (t)}{F_{k:n} (t)}\).

3.1 Monotone properties

In this section we discuss the monotone properties of PGVF based on order statistics. The following example illustrates the nature of PGVF defined in (12) with respect to different time points.

Example 3.1

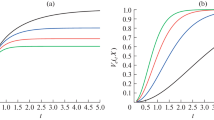
Let Z be a Weibull rv with the cdf \(F(z)\!=\! 1\!-\!\mathrm {e}^{-\left( \frac{{z}}{\beta }\right) ^{\alpha }},\, {z} \ge 0,\, \alpha ,\beta >0\). The cdf corresponding to the smallest and largest order statistics are given by \(F_{1:n}(z)\!=\! 1-\mathrm {e}^{-n \left( \frac{{z}}{\beta }\right) ^{\alpha }}\) and \(F_{n:n}(z)\!=\!\left[ 1-\mathrm {e}^{-\left( \frac{{z}}{\beta }\right) ^{\alpha }}\right] ^{n}\). Keeping \(\alpha =5\), \(\beta =8\) and \(n=3\) for different values of t we may obtain the following figures.

Figure 1a and 1b depicts the PGVF of smallest and largest order statistics drawn from Weibull distribution with respect to different choices of t and fixed values of \(\alpha \), \(\beta \) and n as mentioned above.

Fig. 1
figure 1

PGVF of order statistics arising from Weibull distribution

Full size image

From the figures, we can draw an outline that the PGVF of smallest as well as largest order statistics drawn from Weibull distribution shows a non-decreasing nature for different choices of t. Hence one may conclude that the result in Theorem 2.2 can also be extended to order statistics.

Based on order statistics, the following theorem discuss another interesting monotone property for the PGVF (12) with respect to different choices of n.

Theorem 3.1

If \( \log Z\) is increasing in z, then \(\log {\bar{G}}_{n:n} (t)\) is non-decreasing in \(n \ge 1\).

Proof

Putting \(k=n\) in (12), we get

$$\begin{aligned} \log {\bar{G}}_{n:n} (t)= \frac{1}{{F_{n:n}(t)}}\int _{0}^{t} \log z \ {f_{n:n}(z)}\, dz. \end{aligned}$$

Substituting the pdf and cdf of largest order statistic, the above expression becomes

$$\begin{aligned} \log {\bar{G}}_{n:n} (t)= \int _{0}^{t} \log z \, q_{n:n}^{t}(z)\,dz, \end{aligned}$$

where \(q_{n:n}^{t}(z)= \frac{n [{F(z)}]^{n-1} {f(z)}}{[{F(t)}]^{n} },\ z \le t \) represents the pdf of \([Z_{n:n}| Z_{n:n} \le t]\).

Therefore,

$$\begin{aligned} \log {\bar{G}}_{n:n} (t)=E[ \log Z_{n:n}| Z_{n:n} \le t]. \end{aligned}$$
(15)

Similarly, we get \(\log {\bar{G}}_{{n+1:n+1}} (t)=E[ \log Z_{{n+1:n+1}}| Z_{{n+1:n+1}} \le t]\).

Consider

$$\begin{aligned} {\frac{q_{n:n}^{t}(z)}{q_{n+1:n+1}^{t}(z)}=\frac{n}{n+1}\, \frac{F(t)}{F(z)} }\,\mathrm{is\,decreasing\,in}\,\left( 0,t \right] . \end{aligned}$$

Making use of Definition 2.2, we get the relation

$$\begin{aligned}{}[Z_{n:n}| Z_{n:n} \le t] \le _{lr} [Z_{{n+1:n+1}}| Z_{{n+1:n+1}} \le t] \end{aligned}$$

which implies \([Z_{n:n}| Z_{n:n} \le t] \le _{st} [Z_{{n+1:n+1}}| Z_{{n+1:n+1}} \le t]\). Since \( \log Z \) is increasing in z and using (15), we have \(\log {\bar{G}}_{n:n} (t) \le \log {\bar{G}}_{{n+1:n+1}} (t)\). Hence the theorem. \(\square \)

Next, the following counterexample analyse Theorem 3.1 in view of smallest order statistic of the PGVF.

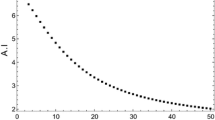
Counterexample 3.1

Continuing the assumptions on the rv Z as in Example 3.1, from (13) we have

$$\begin{aligned} \log {\bar{G}}_{1:n} (t) = \log t - \frac{1}{1-\mathrm {e}^{-n \left( \frac{t}{\beta }\right) ^{\alpha }}}\int _{0}^{t} \frac{1-\mathrm {e}^{-n \left( \frac{{z}}{\beta }\right) ^{\alpha }}}{{z}}\,{dz}. \end{aligned}$$

Fixing \(\alpha =2\), \(\beta =6\) and \(t=5\) for different values of n, we get

$$\begin{aligned} \log {\bar{G}}_{1:4} (5)= 0.747755<0.521095= \log {\bar{G}}_{1:7}(5), \end{aligned}$$

which implies \(\log {\bar{G}}_{1:n} (t)\) is not non-decreasing in \(n \ge 1\).

Remark 3.1

From the above counterexample it has been observed that even if \(\log Z\) is increasing in z, the PGVF on smallest order statistic does not satisfy Theorem 3.1 and hence the result in Theorem 3.1 could not be generalized to kth order statistic, \(Z_{k:n}\) respectively.

Here we discuss some order properties of PGVF in view of order statistics (12). The following example illustrates the stochastic ordering property of PGVF on order statistics.

Example 3.2

Suppose Z and X follows Inverse Rayleigh distribution with the parameters \( \beta _{1}\) and \(\beta _{2}\left( = \frac{\beta _{1}}{4}\right) \) respectively. Then for kth order statistic, we get the relation as \(\log {\bar{G}}_{k:n}^{Z}(t)\ge \log {\bar{G}}_{k:n}^{X}(t)\). Hence Z is greater than X in PGV order with respect to kth order statistic and is denoted by \(Z_{k:n}{\mathop {\ge }\limits ^{\textit{PGVF}}}X_{k:n}\). In general, one may conclude that the Definition 2.3 can be extended to order statistics also.

Lemma 3.1

Under the scalar transformation, the result in Lemma 2.1 holds also for the PGVF of order statistics (12).

The following example describes the closure of PGV order defined above under the increasing scalar transformation.

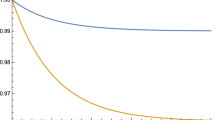
Example 3.3

Let the rv Z be defined as in Example 2.4. Keeping \(n=8\), we have \(\log {\bar{G}}_{n:n}^{Z}(t)= \log t- \dfrac{1}{n}\), \(0 \le t \le 2\) which is clearly non-decreasing in t. Similarly we obtain \(\log {\bar{G}}_{1:n}^{Z}(t)\) as a non-decreasing function in the same interval and is shown in Fig. 2. So, in general \(\log {\bar{G}}_{k:n}^{Z}(t)\) is non-decreasing in t. Hence \(U^{1}_{k:n}{\mathop {\ge }\limits ^{\textit{PGVF}}}U^{2}_{k:n}\) and it can be concluded that Theorem 2.3 extends this result to so called the order statistics.

Fig. 2
figure 2

Plot of \(\log {\bar{G}}_{1:n}(t)\) against \(t \in [0,2]\)

Full size image

As a direct consequence of Example 3.3 we get the result corresponding to Corollary 2.1. Subsequently, by dropping the condition of non-decreasing PGVF we can prove a stronger result similar to Theorem 2.4 and hence one may conclude that Theorem 2.4 holds also for order statistics.

In general it seems that the PGVF on order statistics does not have closed form expression. So by considering this fact here we obtain bounds for PGVF (13) through the following theorem.

Theorem 3.2

Let \(\log {\bar{G}}_{k:n}(t)\) denote the PGVF of \(Z_{k:n}\) arising from Z, which is supposed to be non-negative rv with an absolutely continuous distribution function F(z). If \({F_{k:n}(z)}\) is increasing in z, then

  1. (i)

    For \(0<t \le 1\), \( \log {\bar{G}}_{k:n}(t) \le \frac{Q_{k:n}(0)}{{F_{k:n}(t)}} \) and

  2. (ii)

    For \(t>1\), \( \log {\bar{G}}_{k:n}(t) > \frac{Q_{k:n}(0)}{{F_{k:n}(t)}} \),

where \(Q_{k:n}(0)=-\int _{0}^{+\infty } \frac{F_{k:n}(z)}{z}dz\).

Proof

(i) For \( 0<t \le 1\), we have \(\log t \le 0\). Hence (13) becomes

$$\begin{aligned} \log {\bar{G}}_{k:n}(t)&\le -\frac{1}{F_{k:n}(t)}\int _{0}^{t} \frac{F_{k:n}(z)}{z}dz \\&\le -\frac{1}{F_{k:n}(t)}\int _{0}^{+\infty } \frac{F_{k:n}(z)}{z}dz=\frac{Q_{k:n}(0)}{F_{k:n}(t)}. \end{aligned}$$

(ii) For \( t > 1\), we have \(\log t > 0\). Along the same lines as in (i), we obtain

$$\begin{aligned} \log {\bar{G}}_{k:n}(t) > \frac{Q_{k:n}(0)}{F_{k:n}(t)}. \end{aligned}$$

\(\square \)

3.2 Characterization results

This section presents characterizations of some lifetime distributions using PGVF in the context of order statistics. In the following theorem, we show that PGVF (13) with respect to maxima holds a constant value thereby it characterizes power distribution.

Theorem 3.3

Let Z be a non-negative rv having the support [0, a] with an absolutely continuous distribution function and let \( \log {\bar{G}}_{n:n}(t)\) represents the PGVF of the maxima \(({Z_{n:n}})\). Then the relation

$$\begin{aligned} \log \left( \dfrac{ {\bar{G}}_{n:n} (t) }{t} \right) = \frac{C}{n}, \end{aligned}$$
(16)

where \(C<0\) is a constant and \(n \ge 1\), holds for all \(t>0\) if and only if Z follows power distribution with the cdf \(F(z)=\left( \dfrac{z}{a}\right) ^{b}\), \(0 \le z \le a;\, b > 0\).

Proof

Letting \(k=n\) in (13) and using (16), we get

$$\begin{aligned} \int _{0}^{t} \frac{F_{n:n}\left( {z}\right) }{{z}}\, d{z}=-\left( \frac{C}{n}\right) F_{n:n}(t). \end{aligned}$$
(17)

Differentiating (17) with respect to t and making some rearrangements, we get

$$\begin{aligned} \delta _{n:n}(t)=\frac{f_{n:n}(t)}{F_{n:n}(t)}=\frac{n {b}}{t},\quad \text {where}\;{b}=-\frac{1}{C}<0. \end{aligned}$$
(18)

Using (18), we get \(F_{n:n}(z)= {\mathrm {e}^{- \int _{z}^{a} \delta _{n:n}\,(t) dt}=\left( \dfrac{z}{a}\right) ^{nb}}\), which is the cdf of power distribution. Hence the result is direct. The converse part is straightforward from (13) by considering \(k=n\). This completes the result. \(\square \)

The following theorem characterize certain distributions using the functional relationship between PGVF (13) and the first order reciprocal moment of Z with respect to maxima, \({\bar{S}}_{n:n}(t)\).

Theorem 3.4

Let Z be a non-negative rv having an absolutely continuous distribution with the support \(\left( 0,{+\infty }\right) \) and let \( \log {\bar{G}}_{n:n}(t)\) denotes the PGVF with respect to \({Z_{n:n}}\) of Z. Then the relation

$$\begin{aligned} \log \left( \frac{ {\bar{G}}_{n:n} (t) }{t} \right) = l+ m\, {\bar{S}}_{n:n}(t),\quad l>0, \end{aligned}$$
(19)

where \({\bar{S}}_{n:n}(t)= E[{Z^{-1}_{n:n}}|{Z_{n:n}} \le t],\) holds for all real \(t>0\) if and only if Z follows

  1. (i)

    Type 3 extreme value distribution with the cdf

    $$\begin{aligned} \qquad {F(t)}={\left\{ \begin{array}{ll} \mathrm {e}^{a(t-b)}, &{} t<b \\ 1, &{} t \ge b,\, a>0,\, b<{+\infty } \end{array}\right. }\;\mathrm{for}\;l=0. \end{aligned}$$
    (20)
  2. (ii)

    the Negative Pareto distribution with the cdf

    $$\begin{aligned} \begin{aligned} {F(t)}={\left\{ \begin{array}{ll} (1-t)^{-a}, &{}{} t<0 \\ 1, &{}{} t \ge 0,\ a>1 \end{array}\right. }\;\ \ \qquad \mathrm {for}\;l>0. \end{aligned} \end{aligned}$$
    (21)
  3. (iii)

    the Power distribution with the cdf

    $$\begin{aligned} \begin{aligned} {F(t)=\left( \dfrac{t}{a}\right) ^{b}, \quad 0 \le t \le a;\, b > 0} \;\ \quad \qquad \mathrm{for}\;l<0. \end{aligned} \end{aligned}$$
    (22)

Proof

Letting \(k=n\) in (13) and using (19), we get

$$\begin{aligned} {-}\int _{0}^{t} \frac{F_{n:n}\left( {z}\right) }{{z}}{dz}=l \, F_{n:n}(t)+ m \int _{0}^{t} \frac{f_{n:n}\left( {z}\right) }{{z}}\,{dz}. \end{aligned}$$
(23)

Differentiating (23) with respect to t and on simplification, we obtain

$$\begin{aligned} \delta _{n:n}(t)=- \frac{1}{lt+m}. \end{aligned}$$
(24)

But in accordance with the distributions mentioned in (20), (21) and (22), we get \( \delta _{n:n}(t)\) as

$$\begin{aligned} na,\ \dfrac{1}{\dfrac{1}{na}-\dfrac{t}{na}}\quad \mathrm{and}\quad \dfrac{1}{\dfrac{t}{{nb}}}. \end{aligned}$$
  1. (i)

    Comparing na with (24) we get \(l=0\), which characterizes the Type 3 extreme value distribution.

  2. (ii)

    On comparing

    $$\begin{aligned} \frac{1}{\dfrac{1}{na}-\dfrac{t}{na}}= - \frac{1}{lt+m} \end{aligned}$$

    we have obtained \(l>0\), thereby it characterizes the Negative Pareto distribution and

  3. (iii)

    We get \(l<0\) on comparing \(\dfrac{1}{\dfrac{t}{nb}}\) with (24), which characterizes the Power distribution.

The converse part of the theorem is obtained by direct computation of \(\log \left( \frac{ {\bar{G}}_{n:n} (t) }{t} \right) \). Then the expressions corresponding to the specified distributions are \(-(na)^{-1} {\bar{S}}_{n:n}(t)\), \((na)^{-1}-(na)^{-1} {\bar{S}}_{n:n}(t)\) and \(-(nb)^{-1}\), which are of the form as in (19). Hence the result follows. \(\square \)

The following theorem characterizes Gumbel Type II distribution using the functional relationship between PGVF (13) and the \( \alpha th\) order moment of Z with respect to maxima, \(T_{n:n}^{\alpha }(t)\).

Theorem 3.5

Suppose Z be a rv defined as in Theorem 3.4. Then the relation

$$\begin{aligned} \log \left( \frac{ {\bar{G}}_{n:n} (t) }{t} \right) = -\dfrac{ T_{n:n}^{\alpha }(t)}{n \alpha \beta }, \quad \alpha ,\beta >0, \end{aligned}$$
(25)

where \(T_{n:n}^{\alpha }(t)=E[{Z_{n:n}^{\alpha }}|{Z_{n:n}} \le t],\) holds for all \(t>0\) if and only if Z follows Gumbel Type II distribution with cdf of the form \(F\left( {z}\right) = \mathrm {e}^{-\beta {z}^{-\alpha }}\), \({z}>0,\, \alpha ,\beta >0\).

Proof

Letting \(k=n\) in (13) and using (25), we get

$$\begin{aligned} \int _{0}^{t} \frac{F_{n:n}(z)}{{z}}{dz}=\frac{1}{n\alpha \beta } \int _{0}^{t} {z}^{\alpha } f_{n:n}(z)\,{dz}. \end{aligned}$$
(26)

Differentiating (26) with respect to t and on simplification, we get

$$\begin{aligned} \delta _{n:n}(t)=n\alpha \beta \ t^{-\alpha -1}, \quad \alpha >0. \end{aligned}$$
(27)

Using (27), we get \(F_{n:n}(z)= \mathrm {e}^{- \int _{{z}}^{b} \delta _{n:n}(t)\, dt}= \mathrm {e}^{-n \beta {z}^{-\alpha }}\), which is the required result. Conversely, let us assume Z follows Gumbel Type II distribution, then the result immediately follows by integrating (27) with respect to z. Hence the theorem. \(\square \)

Remark 3.2

For \(\alpha =1\), Theorem 3.5 provides a characterization for inverse exponential distribution. Similarly it characterizes Inverse Rayleigh distribution when \(\alpha =2\).

Next, we look back on the definition of past entropy based on order statistics which would be useful to prove the following result. The past entropy function for the kth order statistic is given by

$$\begin{aligned} {\bar{H}}_{k:n}(t)&= -\int _{0}^{t} \frac{f_{k:n}({z})}{F_{k:n}(t)} \log \left( \dfrac{f_{k:n}({z})}{F_{k:n}(t)}\right) \,{dz} \nonumber \\&=1-\frac{1}{F_{k:n}(t)} \int _{0}^{t} f_{k:n}({z}) \log \delta _{k:n}\left( {z}\right) \,{dz}, \end{aligned}$$
(28)

where \(\delta _{k:n}(z)\) denotes the reversed hazard rate of \({Z_{k:n}}\).

In the following theorem we show that the difference between past entropy function (28) and PGVF (12) with respect to maxima holds a constant value thereby it characterizes power distribution.

Theorem 3.6

Let Z be a non-negative rv having an absolutely continuous distribution with the support \({\left[ 0,a\right] }\) and let \( \log {\bar{G}}_{n:n}(t)\) and \( {\bar{H}}_{n:n}(t)\) denote the PGVF and the past entropy function of \({Z_{n:n}}\). Then the relation

$$\begin{aligned} {\bar{H}}_{n:n}(t)- \log {\bar{G}}_{n:n}(t)= c, \end{aligned}$$
(29)

where c is a constant, holds for all real \(t>0\) if and only if Z follows power distribution with the cdf \({F(z)=\left( \dfrac{z}{a}\right) ^{b}, \, 0 \le z \le a;\, b > 0}\).

Proof

When (28) and (12) holds in view of (29), for \(k=n\) we get

$$\begin{aligned} -\int _{0}^{t} \log \delta _{n:n}(z) f_{n:n}(z)\, {dz} - \int _{0}^{t} \log {z}\, f_{n:n}(z)\,{dz} = \left( c-1\right) F_{n:n}(t). \end{aligned}$$

Differentiating the above expression with respect to t and on simplification, we obtain

$$\begin{aligned} \delta _{n:n}(t) =\frac{\beta }{t},\quad \beta =\mathrm {e}^{1-c} >0. \end{aligned}$$
(30)

From (30), we get \(\delta _{{Z}}(t) = \frac{\beta }{nt}\). Using the relation \({F(z)= \mathrm {e}^{- \int _{z}^{a} \delta _{Z}(t)\ dt}}\), we obtain

$$\begin{aligned} {F(z)=\left( \dfrac{z}{a}\right) ^{b},\quad \mathrm{where}\;b= \frac{n}{\beta }>0}, \end{aligned}$$

which is the required distribution. Conversely, let us assume Z follows power distribution, then we have obtained the difference of \({\bar{H}}_{n:n}(t)\) and \(\log {\bar{G}}_{n:n}(t)\) as \(c=1- \log n{b}\), which is a constant. Thus the result follows. \(\square \)

The theorem and lemma from Gupta and Kirmani (1998) and Gupta and Kirmani (2008) quoted below will be useful for proving the upcoming theorem.

Theorem 3.7

Gupta and Kirmani (1998). Let f be a continuous function defined in a domain \(D \subset R^{2} \) and let f satisfy Lipschitz condition (with respect to y) in D, that is \(|f\left( {z},y_{1}\right) -f\left( {z},y_{2}\right) | \le k|y_{1}-y_{2}|\), \(k>0\), for every point \(\left( {z},y_{1}\right) \) and \(\left( {z},y_{2}\right) \) in D. Then the function \(y= \phi (z)\) satisfying the IVP \(y^{'}=f\left( {z},y\right) \) and \(y\left( {z_{0}}\right) =y_{0},\ {z} \in I\) is unique.

Lemma 3.2

Gupta and Kirmani (2008) Suppose that the function f is continuous in a convex region \(D\subset R^{2} \), \( \frac{\partial f}{\partial y} \) exists and is continuous in D. Then f satisfies the Lipschitz condition in D.

In the following theorem, we show that the PGVF with respect to kth order statistic uniquely determines the parent distribution function.

Theorem 3.8

Let \(\log {\bar{G}}_{{Z}_{k:n}}(t)\) denote the PGVF of \({Z}_{k:n}\) arising from Z, which is assumed to be a non-negative rv with an absolutely continuous distribution function \(F\left( {z}\right) \). Then \(\log {\bar{G}}_{{Z}_{k:n}}(t)\) uniquely determines the distribution function.

Proof

Rearranging (14) and differentiating with respect to t, we get

$$\begin{aligned} \frac{d}{dt} \delta _{{Z}_{k:n}}(t) =\frac{{-}\frac{d^{2}}{dt^{2}}\log {\bar{G}}_{{Z}_{k:n}}(t) - \delta _{{Z}_{k:n}}(t)\left[ \frac{d}{dt} \log {\bar{G}}_{{Z}_{k:n}}(t) - \frac{1}{t}\right] }{\left[ \log {\bar{G}}_{{Z}_{k:n}}(t) - \log t \right] }. \end{aligned}$$
(31)

Suppose that \( \log {\bar{G}}_{{Z}_{k:n}}(t) = \log {\bar{G}}_{{X}_{k:n}}(t) = \gamma (t) \) for all \( t > 0 \) and \( n \ge k \). Then

$$\begin{aligned} \frac{d}{dt} \delta _{{Z}_{k:n}}(t) = \phi \left( t,\delta _{{Z}_{k:n}}(t) \right) \quad \text {and}\quad \frac{d}{dt} \delta _{{X}_{k:n}}(t) = \phi \left( t,\delta _{{X}_{k:n}}(t) \right) , \end{aligned}$$
(32)

where \(\phi (t,z)= \frac{{-}\gamma ^{''} (t)- z \left[ \gamma ^{'} (t)-\frac{1}{t}\right] }{\left[ \gamma (t)- \log t \right] }\). As a result of Theorem 3.7 and Lemma 3.2, we have \( \delta _{{Z}_{k:n}}(t) =\delta _{{X}_{k:n}}(t) \) for all \( t \ge 0 \) which in turn implies \( F_{k:n}(t) = G_{{k:n}}(t) \), where \( F_{{k:n}} (t)\) and \( G_{{k:n}} (t) \) are the cdf’s of \( {Z}_{{k:n}} \) and \( {X}_{{k:n}} \) respectively. Since we have \(F(t)= B^{-1}_{k,n-k+1}\left( F_{{k:n}} (t)\right) \) and \(G(t)= B^{-1}_{k,n-k+1}\left( G_{{k:n}} (t)\right) \) for all \(t \ge 0\), which implies \(F(t)=G(t)\). This completes the result. \(\square \)

4 Conclusion

In many practical situations it is often tedious to keep on monitoring the status of the system. Hence in such situation, one might be curious in collecting information regarding the history of the entire system for instance, the failure of the individual components are considered as an important data. Also, according to system designers it might be very important to have some knowledge about the average time elapsed since the failure has occurred. Bearing this in mind, in the present work we extend the concept proposed by Nair and Rajesh (2000) to the past lifetime of the random variable. Subsequently, under certain conditions we have established monotone properties as well as some ordering properties based on the proposed measure. Analogous results of the proposed measure of order statistics were also examined. As the PGVF generally cannot be obtained in closed form, we have established bounds for PGVF of order statistics. Some of the characterization results based on order statistics has been discussed for various distributions using the interrelationship among other uncertainty measure. The results obtained in this work has got much attention in both theoretical as well as practical view point.