1 Introduction

The study of ageing concepts, their properties, implications and applications is a major topic of research in reliability theory. Ageing represents the phenomenon, by which the residual life of a unit is affected by its age in some probability sense. The basic reliability concepts such as reliability function, hazard rate and mean residual life, etc. are employed to develop various ageing classes. A comprehensive review on this topic when lifetime is continuous is available in Lai and Xie [14] and Nair et al. [18].

There are many situations in which lifetime has to be treated as a discrete random variable. They occur naturally when measurements are made only at specified units of time or when lifetimes are treated in cycles where the number of cycles to failure is of interest. Sometimes it is more relevant to study the discrete case when measurements are available continuously. For example, when studying the lifetime of a photo copier (car tyre), the number of copies it produced (number of miles travelled) is more useful than the lifetimes measured in hours of operation. Moreover, unlike the continuous case, the discrete theory offers more than one approach for defining basic concepts like hazard rate, IHRA, NBU, etc., making the latter distinct in certain aspects. For some recent studies in the discrete case we refer to Sudheesh et al. [25], Nair and Sankaran [17], Cha and Finkelstein [7], Asha et al. [3], Szymkowiak and Iwińska [26], Déniz and Sarabia [9].

In many practical situations, one has to compare the reliabilities of more than one device or reliabilities of a device at different time points. For example, when devices for the same purpose are produced by several manufacturers, the choice has to be made with reference to ageing patterns of the competing devices. Relative ageing concepts specify which of two devices age faster by comparing the two on the basis of some criterion. Also, there are models, in which the nature of ageing depends on the parameter values, for example, the Weibull distribution. Then an analysis that reveals the relationship between the ageing property and the model parameters are required.

At present, it appears that there is no study concerning the relative ageing of two devices in the discrete time domain. The objective of the present study is to fill this gap by presenting some concepts and results that help the comparison of the intensity of ageing among competing devices, when the lifetime is discrete.

The above objective is accomplished in the following sections. Section 2 describes the basic concepts. In Sect. 3, we introduce stochastic ordering by ageing concepts when lifetime is treated as a discrete random variable. The concept of specific ageing factor is discussed in Sect. 4 and the relative ageing concepts are discussed in Sect. 5 where in characterizations of ageing concepts using these concepts are also presented. In Sect. 6, the ageing intensity function is studied in the context of discrete lifetime data analysis. In Sect. 7, we apply the relative ageing concepts to real data and interpret the results. The paper ends with a conclusion in Sect. 8.

2 Basic concepts

Let X be a non-negative integer valued random variable representing lifetime of a device with probability mass function f(x). Let \(S(x)=P[X\ge x]\) be the survival function of X. Then the hazard rate function of X is defined as,

$$\begin{aligned} h(x)=\dfrac{f(x)}{S(x)}. \end{aligned}$$
(2.1)

It is well known that \(0\le h(x)\le 1\) and the hazard rate function uniquely determines the distribution by the identity,

$$\begin{aligned} S(x)={\left\{ \begin{array}{ll} \prod _{u=0}^{x-1}\left( 1-h(u)\right) ;&{} x=1,2,\ldots \\ 1;&{} x=0. \end{array}\right. } \end{aligned}$$
(2.2)

An alternative definition for the discrete hazard rate, given by Cox and Oakes [8] is given by

$$\begin{aligned} h^*(x)=-\log \dfrac{S(x+1)}{S(x)}=-\log (1-h(x)) \end{aligned}$$
(2.3)

From (2.3), we can see that both h(x) and \(h^*(x)\) have the same monotonicity property. For a discussion of the alternative hazard rate \(h^*(x)\) and its relative merits over h(x),  see Xie et al. [27].

The mean of the residual life function of X is given by,

$$\begin{aligned} r(x)=E[X-x|X>x]. \end{aligned}$$
(2.4)

For various properties of h(x) and r(x),  one could refer to Lai and Xie [14], Salvia and Bollinger [22], Padgett and Spurrier [21] and Shaked et al. [24]. Apart from the above concepts, ageing criteria that are required in the sequel are defined as follows.

Definition 2.1

A discrete random variable X is said to be

  1. 1.

    Increasing (decreasing) hazard rate \(({\mathbf {IHR}}({\mathbf {DHR}}))\) property if \(h(x\!+\!1)\!\ge \! (\le )h(x)\text {for all}\,x=0,1,2,\ldots \)

  2. 2.

    Increasing (decreasing) hazard rate average (\({\mathbf {IHRA_1/DHRA_1}}\)) property, if \(\left[ S(x)\right] ^{\frac{1}{x}}\) is decreasing (increasing) in x.

  3. 3.

    Increasing (decreasing) hazard rate average (\({\mathbf {IHRA_2/DHRA_2}}\)) property, if the hazard rate average \(\frac{H(x)}{x}=\dfrac{1}{x}\sum _{t=0}^{x-1}h(t)\) is increasing (decreasing) in x.

  4. 4.

    New better (worse) than used (\({\mathbf {NBU_1/NWU_1}}\)) if \(S(x+t)\le (\ge )S(x)S(t)\) \(\,\text {for all } x,t=0,1,2,\ldots \)

  5. 5.

    New better (worse) than used (\({\mathbf {NBU_2/NWU_2}}\)) if \(\sum _{x=0}^{k-1}h(x)\le (\ge ) \sum _{x=j}^{j+k-1}h(x),\) \(j=0,1,2,\ldots ,k=1,2\ldots \)

  6. 6.

    New better (worse) than used in expectation \(({\mathbf {NBUE(NWUE)}})\) property if \(r(x)\le (\ge )E[X]\) for all \(x=1,2\ldots \)

  7. 7.

    Harmonically new better (worse) than used in expectation (\({\mathbf {HNBUE}}\) (HNWUE)) property if \(\sum _{x=0}^{n}r(x)^{-1}\ge (\le )\dfrac{n}{E[X]}.\)

  8. 8.

    \({\mathbf {NBU}}\)-\({\mathbf {y_0}}\) (\({\mathbf {NWU}}\)-\({\mathbf {y_0}}\)) if \(S(x+y_0)\le (\ge ) S(x)S(y_0)\,\text {for all}\, x=0,1,2,\ldots :y_0=1,2\ldots \)

  9. 9.

    \({\mathbf {NBU}}\)*\({\mathbf {y_0}}\) (\({\mathbf {NWU}}\)*\({\mathbf {y_0}}\)) property, if \(S(x+t)\le S(x)S(t),\,x=0,1,2\ldots :t= y_0,y_0+1\ldots \)

The NBU-\(y_0\) (NWU-\(y_0\)) requires that the lifetime after \(y_0\) is smaller (larger), compared to the original one in probability sense. Instead of keeping \(y_0\) fixed, we can think of the above behaviour beyond \(y_0,\) giving rise to the NBU*\(y_0\) (NWU*\(y_0\)). Thus we have, \(NBU_1\) \(\Rightarrow \) NBU*\(y_0\Rightarrow \) NBU-\(y_0.\)

3 Stochastic orders

To discuss relative ageing of two devices, let X and Y denote their lifetimes with hazard rates \(h_X(x)\) and \(h_Y(x)\) and alternative hazard rates \(h_X^*(x)\) and \(h_Y^*(x)\) respectively. A major difference in our discussion when compared to the continuous case is several new results in the discrete case, which has no parallel in the former case, exist owing to alternative ways in which same concepts are defined.

Definition 3.1

The random variable X is ageing faster than Y in hazard rate, written as \(X\le _{IHR}Y,\) if \(\frac{h_X(x)}{h_Y(x)}\) is increasing in x,  provided \(h_Y(x)\ne 0.\)

Definition 3.2

The random variable X is ageing faster than Y in alternative hazard rate, written as \(X\le _{IHR^*}Y,\) if \(\frac{h_{X}^*(x)}{h_{Y}^*(x)}\) is increasing in x.

When we look at the binary relation \(\le _{IHR}\) more closely, it says that the lifetime X is less than lifetime Y in the sense of the hazard rate if X is more IHR than Y. In other words, if the hazard rates of X and Y are such that \(\frac{h_X(x)}{h_Y(x)}\) is a constant (increasing/decreasing), then the device with lifetime X ages at the same rate (faster/ slower) than the device with lifetime Y.

Looking at the properties of the stochastic order, the different cases that can occur are: (a) \(h_X(x)\ge h_Y(x),\text { for all } x=0,1,2,\ldots \) (b) \(h_X(x)\) crosses \(h_Y(x)\) from below. Then, it is not essential that \(X\le _{IHR}Y\) should imply a corresponding ordering of \(h_X(x)\) and \(h_Y(x).\) This is illustrated in the following examples.

Example 3.1

Suppose that X has geometric distribution with \(p=\frac{3}{4}\) and Y has Waring distribution [19] with probability mass function

$$\begin{aligned} f(x)=\dfrac{(a-b)(b)_x}{(a)_{x+1}},\quad x=0,1,2,\ldots ;\,a>b, \end{aligned}$$

where, \((t)_x=t(t+1)\cdots (t+x-1).\) When \(a=3\) and \(b=1,\) the hazard rate is \(h_Y(x)=\frac{2}{3+x},\,x=0,1,2,\ldots \) Then \(X\le _{IHR}Y\) and \(h_X(x)\ge h_Y(x).\)

Example 3.2

When \(h_X(x)=\frac{1}{6-x},\) corresponding to the uniform distribution in [1, 5],  and \(h_Y(x)=\frac{2}{3+x}\) as in Example 3.1, we have \(h_X(x)\) and \(h_Y(x)\) crossing at \(x=3\) and \(X\le _{IHR}Y.\)

Theorem 3.1

\(X\le _{IHR}Y\) and \( X\le _{IHR^*}Y\) are not equivalent.

Proof

To prove the assertion, take

$$\begin{aligned} h_X(x)=1-\exp \{-2x-3\}\quad \text {and}\quad h_Y(x)=1-\exp \{-4x-5\}. \end{aligned}$$

Then \(X\le _{IHR}Y.\) But using (2.3),

$$\begin{aligned} \dfrac{h_X^*(x)}{h^*_Y(x)}=\dfrac{2x+3}{4x+5} \end{aligned}$$

is decreasing. So \(X\ge _{IHR^*}Y\). \(\square \)

Some properties of the order \(\le _{IHR}\) are given below.

  1. (a)

    From Definition 3.1, we have

    $$\begin{aligned} X\le _{IHR}Y\!\!\iff \!\! \dfrac{h_X(x+1)}{h_Y(x+1)}\ge \dfrac{h_X(x)}{h_Y(x)}\!\!\iff \!\! \dfrac{h_X(x+1)}{h_X(x)}\ge \dfrac{h_Y(x+1)}{h_Y(x)} \end{aligned}$$

    and so,

    $$\begin{aligned} X\le _{IHR}Y \quad \text {and}\quad Y\le _{IHR}Z\Rightarrow & {} \dfrac{h_X(x+1)}{h_X(x)}\ge \dfrac{h_Y(x+1)}{h_Y(x)}\ge \dfrac{h_Z(x+1)}{h_Z(x)}\\\Rightarrow & {} X\le _{IHR}Z. \end{aligned}$$

    Thus the ordering \(\le _{IHR}\) is defined as partial order among equivalence classes generated by the ratio \(\frac{h_Y(x)}{h_X(x)}.\)

  2. (b)

    Also, we obtain

    $$\begin{aligned} X\le _{IHR}Y\quad \text {and}\quad Y\le _{IHR}X\Rightarrow h_X(x)=c.h_Y(x) \end{aligned}$$

    for some constant \(c>0.\) Thus both \(X\le _{IHR}Y\) and \(Y\le _{IHR}X\) correspond to the equivalence class in which the proportional hazard rates model for discrete lifetimes hold.

  3. (c)

    The partial order \(\le _{IHR}\) can be used to define the IHR concept as X is IHR \(\iff \) \(X\le _{IHR}X_G,\) where \(X_G\) is the geometric random variable with probability mass function \(f(x)=q^xp;\,x=0,1,2\ldots \)

Remark 3.1

It can be seen that Definition 3.1 and the ordering with \(X_G,\) given above are analogous to Proposition 2.2(iii) and Proposition 2.1(iii), respectively in [23] in the continuous case. But the main difference is that neither Proposition 2.2(i),(ii) nor Definition 1 of [23] holds in the discrete case since \(-\log S(x)\) is not the cumulative hazard rate in the discrete case.

When the hazard rate is replaced by other reliability functions, we can have similar stochastic orders representing relative ageing. We consider only some important representations here.

Definition 3.3

We say that X is ageing faster than Y

  1. (a)

    in hazard rate average \(X\le _{IHRA_1}Y,\) if \(\frac{\log S_X(x)}{\log S_Y(x)}\) is increasing in \(x=1,2,\ldots \) and

  2. (b)

    in hazard rate average \(X\le _{IHRA_2}Y,\) if \(\frac{\sum _{0}^{x-1}h_X(t)}{\sum _{0}^{x-1}h_Y(t)}\) is increasing in \(x=0,1,2,\ldots \)

We interpret \(X\le _{IHRA_1}Y\left( X\le _{IHRA_2 }Y\right) \) by saying that a device with lifetime X has lesser life than the device with lifetime Y if X is more \(IHRA_1(IHRA_2)\) than Y. Since X has greater \(IHRA_1(IHRA_2),\) it ages more positively than Y. The stochastic orderings in Definition 3.3 satisfy the following properties.

  1. (i)

    X is \(IHRA_1\) \(\iff X\le _{IHRA_1} X_G\) and X is \(IHRA_2\) \(\iff X\le _{IHRA_2} X_G.\)

  2. (ii)

    \(X\le _{IHR}Y \Rightarrow X\le _{IHRA_2}Y.\)

  3. (iii)

    \(X\le _{IHR^*}Y \Rightarrow X\le _{IHRA_1}Y,\) since

    $$\begin{aligned} \dfrac{\log S_X(x)}{\log S_Y(x)}=\dfrac{\sum _{t=0}^{x-1}h_X^*(t)}{\sum _{t=0}^{x-1}h_Y^*(t)}. \end{aligned}$$
  4. (iv)

    \(X\le _{IHR} Y\nRightarrow X\le _{IHRA_{1}}Y.\)

    To prove this, let \(h_X(x)=1-\exp \{2x-3\}\) and \(h_Y(x)=1-\exp \{4x-5\}.\) Then, \(\frac{h_X(x)}{h_Y(x)}\) is increasing and so \(X\le _{IHR}Y.\) But \( \frac{\log S_X(x)}{\log S_Y(x)}=\frac{x+2}{2x+3}\) is decreasing.

Remark 3.2

Definition 3.3(a) is analogous to the definition in the continuous case in Sengupta and Deshpande [23], but Definition 3.3a and b are not equivalent because \(\sum _{0}^{x-1}h(t)\ne -\log S(x)\) in the discrete case.

Other stochastic orders like \(\le _{DMRL},\, \le _{NBU},\) etc. in Kochar and Wiens [13] and Kochar [12], may also be discussed in the discrete case on similar lines.

4 Specific ageing factor

Consider two devices or systems, whose lifetimes follow the same distribution with survival function S(x). One of the devices is new and the other is aged y units. Then, S(x) is the probability that the new device survives age x and \(\frac{S(x+y)}{S(y)}\) is the probability that the older device aged y survives the same duration x. Following Bryson and Siddiqui [6] in the continuous case, we define the specific ageing factor in discrete case as,

$$\begin{aligned} A(x,y)=\dfrac{S(x)S(y)}{S(x+y)},\quad x=0,1,2,\ldots \end{aligned}$$
(4.1)

which compares the survival probabilities of the two units. When \(A(x,y)\ge 1(\le 1), \) \(P[X>x+y|X>x]<(>)P[X>y],\) which means that a device of age x surviving for an additional lifetime y has lesser (greater) probability of surviving than a new unit to survive the same lifetime y. Thus A(x, y) provides a measure of relative ageing of an older unit in comparison with a new one. In other words it gives the impact of having survived x units of age, in the future life of the old unit. It seems that the potential of the specific ageing factor in determining ageing patterns and relative ageing have not been exploited in the continuous case. We give some properties of A(x, y).

Theorem 4.1

The random variable X has increasing (decreasing) hazard rate if and only if A(x, y) is increasing (decreasing) in y.

Proof

\(A(x,y)\text { is increasing in y} \)

$$\begin{aligned}&\iff A(x,y+1)-A(x,y)\ge 0.\\&\iff S(y+1)S(x+y)\ge S(y)S(x+y+1)\\&\iff \dfrac{S(y+1)}{S(y)}\ge \dfrac{S(x+y+1)}{S(x+y)}\\&\iff 1-h(y)\ge 1-h(x+y)\\&\iff X \text { is }IHR. \end{aligned}$$

The proof for DHR case is similar. \(\square \)

Theorem 4.2

  1. (i)

    X is \(NBU_1 (NWU_1)\) \(\iff A(x,y)\ge (\le )1\,\text {for all}\,x=0,1,2\ldots \)

  2. (ii)

    X is NBU-\(y_0\iff A(x,y_0)\ge (\le ) 1\,\text {for all}\,x=0,1,2,\ldots :y_0>0\)

  3. (iii)

    X is NBU*\(y_0\) (NWU*\(y_0)\!\!\iff \!\! A(x,y)\ge (\le )1\,\text {for all}\,x=0,1,2,\ldots :y= y_0,y_0+1,\ldots \)

The proof is a direct consequence of the Definitions 2.1(4), (8) and (9).

Remark 4.1

Since \(IHR\Rightarrow IHRA_1\Rightarrow IHRA_2,\) it follows that

$$\begin{aligned} A(x,y) \text { is increasing in }y \Rightarrow X \text { is } IHRA_1 \Rightarrow X \text { is }IHRA_2. \end{aligned}$$

Now since \(NBU_1\Rightarrow NBUE\Rightarrow HNBUE,\)

$$\begin{aligned} A(x,y)\text { is increasing }\Rightarrow X \text { is }NBU_1 \Rightarrow X\text { is }NBUE \Rightarrow X \text { is }HNBUE. \end{aligned}$$

We now establish the application of the measure A(x, y) to the data on the failure times of 50 devices in Aarset [1], by taking the first two observations as zeros. The quadratic hazard rate distribution with survival function,

$$\begin{aligned} S(x)=q^{ax+\frac{bx^2}{2}+\frac{cx^3}{3}},\quad q=e^{-1},\quad a>0,\quad c>0,\quad b\ge -(2ac)^{\frac{1}{2}} \end{aligned}$$
(4.2)

and hazard rate function

$$\begin{aligned} h(x)=1-e^{-a-b \left( x+\frac{1}{2}\right) -c \left( x^2+x+\frac{1}{3}\right) }, \end{aligned}$$
(4.3)

is a model that fits the data with parameter values, \(\hat{a}=0.0379894,\,\hat{b}=-0.00190263,\) \(\,\text {and }\hat{c}=0.0000274169.\) The parameters are estimated by minimizing the sum of squares of deviations between empirical survival function and S(x). The chi-square goodness of fit test gives a value of \(\chi ^2=0.468\) and p-value 0.79 when grouped into 6 classes. It can be seen in Table 1. The data yields a bathtub shaped hazard rate function and the change point is obtained as 34 by considering the minimum of h(x) with the estimated values. The values of A(x, y) for different x and y are shown in Table 2. From the table, we can see that when both x and y are less than 35, the values of A(x, y) are less than one implying that the older device is more reliable, agreeing with the bathtub hazard rate.

Table 1 Goodness of fit for Aarset data
Full size table
Table 2 Values of A(x, y) for different x and y
Full size table

5 Relative ageing factor

An alternate approach to quantify relative ageing of a new device and an old device with the same life distribution is to consider the identity,

$$\begin{aligned} P[X\ge g(x,y)+x|X\ge x]=P[X\ge y],\quad \text {for all }x,y=0,1,2,\ldots \end{aligned}$$
(5.1)

as in Abraham and Nair [2] in the continuous case. In (5.1), x is the current age of an old device and y is the proposed survival time of the old and new units. We can write (5.1) as,

$$\begin{aligned} S(x+g(x,y))=S(x)S(y) \end{aligned}$$

or

$$\begin{aligned} H^*(x+g(x,y))=H^*(x)+H^*(y), \end{aligned}$$
(5.2)

where \(H^*(.)\) is the alternative cumulative hazard rate [8] given by,

$$\begin{aligned} H^*(x)=-\log S(x). \end{aligned}$$
(5.3)

For example, when X is discrete Weibull with survival function \(S(x)=q^{x^\beta };\) \(\,x=0,1,2,\ldots , \,\beta >0,\)

$$\begin{aligned} g(x,y)=\left( x^\beta +y^\beta \right) ^{\frac{1}{\beta }}-x. \end{aligned}$$

It is assumed that the form of S(x) is determined from the data before calculating the ageing factor in a practical situation. We now write,

$$\begin{aligned} M(x,y)=\dfrac{g(x,y)}{y}, \end{aligned}$$
(5.4)

and interpret it as the rate at which an old unit is losing or gaining life in relation to a new unit with identical life distribution. Thus, M(x, y) provides a measure of the effect of ageing of a device. We call M(x, y) as the relative ageing factor. The expressions of M(x, y) of some discrete life distributions are presented in Table 3.

We now discuss the properties of M(x, y) and its role as a measure of relative ageing.

  1. (i)

    Since \(H^*(0)=0,\)

    $$\begin{aligned}&H^*(x+g(x,0))=H^*(x)+H^*(0)\\&H^*(g(0,y))=H^*(y)+H^*(0) \end{aligned}$$

    implies \(g(x,0)=x,\) \(g(0,y)=y\) and \(g(0,0)=0.\)

  2. (ii)

    When \(M(x,y)=1,\, g(x,y)=y\) so that (5.1) becomes the lack of memory property. Thus, \(M(x,y)=1\) represents the no-ageing property which characterizes the geometric law. Larger values of M(x, y) indicates more positive ageing.

  3. (iii)

    M(x, y) provides a measure of the extent of ageing of a device at different ages. For example, assume that X has discrete Weibull distribution in Table 3 with shape parameter \(\beta =2\) and that device with this distribution has survived a lifetime of 3 units. To compare the extent of ageing of this device with a new one with the same life distribution for a time period of 4 units, we have \(x=3\) and \(y=4\) to yield \(g(x,y)=2\) and \(M(x,y)=\frac{1}{2}.\) Thus the old unit has to work twice the time compared to the new one to produce the same output. The former is clearly wearing out and is therefore subject to positive ageing. In general \(g(x,y)\le (\ge ) x+y\) for any x and fixed y indicates the effect of spent life.

  4. (iv)

    There are some properties of M(x, y) that relate to the ageing concepts as shown below.

Theorem 5.1

The lifetime X is \(NBU_1 (NWU_1)\) if and only if \(M(x,y)\le (\ge ) 1.\)

Proof

Since \(H^*(x)\) is an increasing function,

$$\begin{aligned} g(x,y)+x\le x+y\Rightarrow H^*(g(x,y)+x)\le H^*(x+y) \end{aligned}$$

So form (5.2),

$$\begin{aligned} H^*(x)+H^*(y)\le H^*(x+y), \end{aligned}$$

which is a necessary and sufficient condition for X to be \(NBU_1.\) Also,

$$\begin{aligned} g(x,y)\le y\iff M(x,y)\le 1. \end{aligned}$$

The proof of \(NWU_1\) case is obtained by reversing the inequalities. \(\square \)

Remark 5.1

As in Theorem 4.2, we have

  1. (a)

    \(M(x,y_0)\le (\ge )1\!\!\iff \!\! X\) is NBU-\(y_0\)(NWU-\(y_0\)) \(\text {for all}\, x=0,1,2,\ldots :y_0=1,2\ldots \) and

  2. (b)

    \(M(x,y)\le (\ge ) 1\!\!\iff \!\! X\) is NBU*\(y_0\)(NWU*\(y_0\))\(\text { for all}\, x=0,1,2,\ldots :y= y_0,y_0+1\ldots \)

  1. (v)

    M(x, y) does not depend on the lifetime spent in the case of the geometric, discretized versions of the Lomax and re-scaled beta (see Table 3).

Since the specific ageing factor A(x, y) and relative ageing factor M(x, y) are similar in their purposes, it seems that a comparison of the two is in order. First we observe that,

$$\begin{aligned} \log A(x,y)= & {} -\log S(x+y)+\log S(x)+\log S(y)\\= & {} H^*(x+y)-H^*(x)-H^*(y), \end{aligned}$$

which is different from M(x, y). For instance, the discrete Weibull distribution has,

$$\begin{aligned} M(x,y)=\dfrac{\left( x^{\beta }+y^{\beta }\right) ^{\frac{1}{\beta }}-x}{y}, \end{aligned}$$
(5.5)

whereas,

$$\begin{aligned} A(x,y)=\dfrac{q^{\left( x^{\beta }+y^{\beta }\right) }}{q^{\left( x+y\right) ^{\beta }}}. \end{aligned}$$
(5.6)

Generally, the expressions for A(x, y) are algebraically more complex than that of M(x, y).

Theorem 5.2

M(x, y) is decreasing (increasing) in x

$$\begin{aligned}&\iff X\text { is }IHR (DHR).\\&\iff H^*(x)\text { is convex }(\text {concave}).\\&\iff A(x,y)\text { is increasing }(\text {decreasing})\text { in } x,\quad \text {for all}\, y=0,1,2,\ldots \end{aligned}$$

Proof

Define,

$$\begin{aligned} H_*^{-1}(t)=\inf \left\{ t:H^*(t)\ge t \right\} , \end{aligned}$$

and take the smallest integer contained in t as \(H_*^{-1}(t).\) Since \(H^*(x)\) is monotone, the inverse is unique. Also note that \(g(x,y)=H_*^{-1}\left( H^*(x)+H^*(y)\right) .\) M(x, y) is decreasing in x

$$\begin{aligned}&\iff g(x,y)\text { is decreasing}.\\&\iff H^{-1}_{*}(H^*(x)+H^*(y))-x\text { is decreasing}, \text {from } (5.2).\\&\iff H^{-1}_{*}(t+s)-H_*^{-1}(t)\text { is decreasing in } t \text { for all } s=H^*(y).\\&\iff H_*^{-1}(t) \text { is concave.}\\&\iff H^*(x)\text { is convex }\!\!\iff \!\! X \text { is }IHR. \end{aligned}$$

The rest of the implications follow from Theorem 4.1. \(\square \)

The M(x, y) function has applications in ordering life distributions on the basis of the \(NBU_1\) property.

Definition 5.1

The random variable X is less \(NBU_1\) than the random variable Y,  denoted by \(X\le _{M} Y\) if \(M_X(x,y)\le M_Y(x,y)\,\text {for all}\,x\) and a fixed y.

We now relate the order \(\le _M\) and super additive order in \(H_{X}^*(H^{-1}_{*,Y}(x)),\) where \(H_{X}^*(.)\) is the alternative cumulative hazard rate of X.

Theorem 5.3

$$\begin{aligned} X\le _{M}Y\iff H_{X}^*(H_{*,Y}^{-1}(x+y))\ge H_{X}^*(H_{*,Y}^{-1}(x))+H_{X}^*(H_{*,Y}^{-1}(y)) \end{aligned}$$
(5.7)

Proof

$$\begin{aligned} X\le _{M}Y\iff & {} M_X(x,y)\le M_Y(x,y)\\\iff & {} g_X(x,y)\le g_Y(x,y)\\\iff & {} H_{*,X}^{-1}(H_{X}^*(x)+H_{X}^*(y))\le H_{*,Y}^{-1}(H_{Y}^*(x)+H_{Y}^*(y))\\\iff & {} H_{X}^*(x)+H_{X}^*(y)\le H_{X}^*[H_{*,Y}^{-1}(H_{Y}^*(x)+H_{Y}^*(y))]\\\iff & {} H_{X}^*(H_{*,Y}^{-1}(t))+H_{X}^*(H_{Y}^*(s))\le H_{X}^*(H_{*,Y}^{-1}(t+s)) \end{aligned}$$

which proves the result. \(\square \)

Sengupta and Deshpande [23] says that a continuous random variable X is ageing faster than Y in the super additive sense, if the inequality of the right hand side of (5.7) is satisfied. Thus our function M(x, y) provides a stochastic order that is the discrete analogue of the ordering given in Sengupta and Deshpande [23].

Remark 5.2

If Y is \(NBU_1,\) \(X\le _{M}Y\Rightarrow X\) is \(NBU_1.\)

Finally, the relative ageing factor is useful in comparing life distributions by saying which is more positive ageing (negative ageing by reversing the inequality in (5.7), so that \(X\ge _{M}Y\) is equivalent to the sub additivity of \(H_{X}^*H^{-1}_{*,Y}(.),\) leading to \(NWU_1\) class, the dual of \(NBU_1.\) For example, the discrete Weibull distribution is less \(NBU_1\) than the discrete Lomax distribution, since,

$$\begin{aligned} x^{\beta }+y^{\beta }\le \left( x+y+\dfrac{xy}{\alpha }\right) ^{\beta }\quad \text {for } \beta >0 \end{aligned}$$

Thus the discrete Lomax distribution is more positive ageing than the discrete Weibull.

6 Ageing intensity function

In order to evaluate the ageing phenomenon quantitatively, Jiang et al. [11] proposed the ageing intensity function (AI) for continuous lifetime data. It is the ratio of the hazard rate to a baseline hazard rate, which was chosen by the authors as the average of h(x) in [0, x]. In the discrete case, we can define the ageing intensity function in two different ways, based on h(x) and \(h^*(x).\) We first define ageing intensity function as,

$$\begin{aligned} A^*(x)=\dfrac{h^*(x)}{H^*(x)/x}=\dfrac{xh^*(x)}{H^*(x)}, \end{aligned}$$
(6.1)

where \(h^*(x)\) is the alternative hazard rate mentioned above. The intensity function is unity when \(h^*(x)\) is a constant (geometric case), \(A^*(x)>1\) if X is IHR and \(A^*(x)<1\) when X is DHR. Thus large (small) values of \(A^*(x)\) indicate positive (negative) ageing. When h(x) is used to define the hazard rate, one can obtain a slightly different form

$$\begin{aligned} A(x)=\dfrac{xh(x)}{H(x)}, \end{aligned}$$
(6.2)

where \(H(x)=\sum _{u=0}^{x-1}h(u).\)

Writing \(A^*(x)\) in terms of h(x), 

$$\begin{aligned} A^*(x)=\dfrac{x\log (1-h(x))}{\sum _{0}^{x-1}\log (1-H(t)+H(t-1))} \end{aligned}$$
(6.3)

Reducing (6.1) recursively, after writing it as,

$$\begin{aligned} A^*(x)=x\left( \dfrac{\log S(x+1)}{\log S(x)}-1\right) , \end{aligned}$$

leads to

$$\begin{aligned} S(x)=S(1)^{(A^*(1)+1)(A^*(2)+1)\cdots (\frac{A^*(x-1)}{x-1}-1)}, \end{aligned}$$

S(1) being determined by using \(\sum _{x=0}^{\infty }f(x)=1.\) Thus the ageing intensity function determines the distribution uniquely. This enables comparison of distributions using their ageing intensity functions.

The monotonicity of the hazard rate function is not, in general, transferred to the monotonicity of AI function. Moreover, A(x) and \(A^*(x)\) need not be equal in general. In the following examples, we illustrate this using the AI function defined in (6.2)

Example 6.1

Let X have S distribution [5] with hazard rate

$$\begin{aligned} h(x)=p(1-\pi ^x),\quad 0<p<1,\,0\le \pi <1,\,x=1,2,\ldots \end{aligned}$$

Then,

$$\begin{aligned} H(x)=\sum \limits _{1}^{x}h(t)=px-\dfrac{p\pi }{1-\pi }(1-\pi ^x), \end{aligned}$$

so that,

$$\begin{aligned} A^*(x)=\frac{x \log \left( q+p\pi ^x\right) }{\log \prod _{i=1}^{x}(q+\pi ^i)} \end{aligned}$$

and

$$\begin{aligned} A(x)=\dfrac{(1-\pi )(1-\pi ^x)xp}{(1-\pi )xp-p\pi (1-\pi ^x)},\quad \text {where}, q=1-p. \end{aligned}$$

As seen from the above example, \(A^*(x)\) and A(x) are not equal in general. However, in the geometric case, \(A^*(x)=A(x)=1.\)

Fig. 1
figure 1

Graph of AI function

Full size image

Example 6.2

Let X follow negative binomial distribution with probability mass function

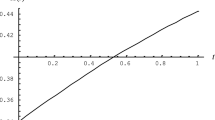
$$\begin{aligned} \dfrac{\Gamma (x+n)}{\Gamma (x+1) \Gamma (n)}p^n(1-p)^x,\quad x=0,1,2,\ldots ;\,0<p<1. \end{aligned}$$

Then X is IHR for \(n>1.\) In particular, for \(n=10\) and \(p=0.3,\) the AI function is decreasing as shown in Fig. 1.

We now demonstrate the utility of the ageing intensity function to assess relative ageing of two devices through the following definition.

Definition 6.1

A random variable X is ageing faster than Y in ageing intensity function, written as, \(X\le _{AIF}Y\) if, \(\dfrac{A_X(x)}{A_Y(x)}\) is increasing in x,  provided \(A_Y(x)\ne 0.\)

Example 6.3

Let

$$\begin{aligned} S_X(x)=e^{-4 x} (4 x+1),\quad x=0,1,2\ldots \end{aligned}$$
(6.4)

and

$$\begin{aligned} S_Y(x)=e^{-2 x} (2 x+1),\quad x=0,1,2\ldots . \end{aligned}$$
(6.5)

Then,

$$\begin{aligned} h_X(x)=1-\frac{e^{4 x-4 (x+1)} (4 (x+1)+1)}{4 x+1},\quad x=0,1,2\ldots \end{aligned}$$
(6.6)

and

$$\begin{aligned} h_Y(x)=1-\frac{e^{2 x-2 (x+1)} (2 (x+1)+1)}{2 x+1},\quad x=0,1,2\ldots \end{aligned}$$
(6.7)

It is seen that \( \dfrac{A_X(x)}{A_Y(x)} \) is increasing. Hence, \(X\le _{AIF}Y\) and X is ageing faster than Y.

The AIF concept and various ageing criteria do not have any natural implications although both are related to discrete ageing.

Theorem 6.1

  1. (i)

    \(X\le _{AIF}Y\) \(\nRightarrow \) \(X\le _{IHR}Y\) and \(X\le _{IHR}Y\) \(\nRightarrow X\le _{AIF}Y\)

  2. (ii)

    \(X\le _{AIF}Y\) \(\nRightarrow \) \(X\le _{IHRA_1}Y\)

  3. (iii)

    \(X\le _{AIF}Y\) \(\nRightarrow \) \(X\le _{IHRA_2}Y.\)

To prove the above assertions note that in Example 6.3, we have \(X\le _{AIF}Y.\) But, \( \frac{h_X(x)}{h_Y(x)},\) \( \frac{H_X(x)}{H_Y(x)} \) and \(\frac{\log S_X(x)}{\log S_Y(x)}\) are decreasing. Using the hazard functions of X and Y in the proof of Theorem 3.1,

$$\begin{aligned} \dfrac{h_X(x)}{h_Y(x)}=\frac{1-e^{-2 (x+1)-1}}{1-e^{-4(x+1)-1}} \end{aligned}$$
(6.8)

is increasing. Hence, \(X\le _{IHR}Y\) and also \(X\le _{IHRA_2}Y.\) Now the function,

$$\begin{aligned} \dfrac{A_X(x)}{A_Y(x)}=\frac{e^2 \left( e^{2 x+3}-1\right) \left( e^{4 x} \left( e \left( e^4-1\right) x-1\right) +1\right) }{\left( 1+e^2\right) \left( e^{4 x+5}-1\right) \left( e^{2 x} \left( e \left( e^2-1\right) x-1\right) +1\right) }, \end{aligned}$$
(6.9)

is decreasing. Hence \(X\nleq _{AIF}Y.\)

7 Application to real data

In this section, we consider the application of the methodology discussed in the earlier sections to the data on the 18 lifetimes of electronic devices reported in Jazi et al. [10]. They have fitted the observations to the discrete Weibull distribution

$$\begin{aligned} S_X(x)=q^{(x-1)^a},\quad x=1,2,\ldots ;\,a>0;\,0<q<1 \end{aligned}$$
(7.1)

and to the inverse Weibull model

$$\begin{aligned} S_Y(x)=1-q_{1}^{(x-1)^{-b}},\quad x=1,2,3,\ldots ;\,b>0;\,0<q_1<1 \end{aligned}$$
(7.2)

by finding the estimates of the parameters as \(\hat{a}=0.91,\,\hat{q_1}=0.99\) and \(\hat{q}=0.004,\,\hat{b}=0.4.\) The hazard rate according to the above estimates were evaluated by the formula

$$\begin{aligned} \hat{h}(x)=1-\dfrac{\hat{S}(x+1)}{\hat{S}(x)} \end{aligned}$$

and the results are tabulated in Table 4. Except at some terminal sample points, the general tendency of the hazard rates of both models is to decrease over time. Since X and Y represent different hazard conditions, we compare their relative ageing through \(X\le _{IHR}Y.\) It can be observed from the ratios \(\dfrac{h_Y(x)}{h_X(x)}\) at different points that it is decreasing except at the tail values. Accordingly, X is ageing faster than Y is a reasonable general conclusion. The discrepancy at the end values is due to the fact that \(S_X(420)=0.086,\) which is close to zero whereas \(S_Y(420)=0.3921,\) with substantial probability beyond the final entry 420, even though the fits are acceptable in both cases.

Table 3 Relative ageing factor for some life distributions
Full size table
Table 4 Hazard rates of electronic devices
Full size table

To analyse the data using other concepts, only one distribution is needed. Accordingly, the Weibull model (7.1) is chosen for the purpose. The ageing intensity function is estimated as

$$\begin{aligned} \hat{A^*}(x)=x\left[ \dfrac{\log \hat{S}(x+1)}{\log \hat{S}(x)}-1\right] =x\left[ \left( \dfrac{x}{x-1}\right) ^{0.91}-1\right] \end{aligned}$$

and is presented in Table 5. Since \(\hat{A}^*(x)\) assumes values less than unity, the lifetimes exhibit negative ageing property. However, as the age advances, the general tendency is to further improve the lifetime at a rather slow rate and then to become steady at the value 0.91.

Table 5 Ageing intensity function for electronic devices data
Full size table
Table 6 Estimated values of M(x, y)
Full size table

The relative ageing factor with respect to the Weibull model is estimated by using

$$\begin{aligned} \hat{g}(x,y)=\left[ (x-1)^{0.91}+(y-1)^{0.91}\right] ^{\frac{1}{0.91}}-(x-1) \end{aligned}$$

and \(\hat{M}(x,y)=y^{-1}\hat{g}(x,y).\) For a choice of \(y=10,\,50,\,100,\,150\) and 250 the estimates of M(x, y) are seen in Table 6. Except for the value \(x=4,\) the electronic devices improve their residual lives compared to new ones represented by M(.) values larger than unity. The efficiency of the older device is more than that of a new one. Like the other notions of relative ageing, the ageing factor M(x, y) also indicates negative ageing, but the intensities tend to decrease with larger values of y at all ages. Since the specific ageing factor has quite similar behaviour and it was illustrated for a real data previously, we have not included its discussion here. From the examples and illustrations, it is seen that the stochastic orders are meant for comparison of ageing in two life distributions and the rest of the notions enable quantification of the effect of ageing on the reliability of an old device in comparison to a new one. In this respect, among the various measures described, it seems that A(x, y) and M(x, y) are more informative than A(x) and \(A^*(x)\).

8 Conclusion

The role of relative ageing concepts is either to compare the ageing patterns of two devices at a fixed time or to investigate whether the same device is ageing more positively (negatively) at different points of time. In this paper, we have presented some concepts and results that lead to a quantitative assessment of which of two devices is ageing faster. Also, the impact of spent life of a device on its residual life can also be numerically evaluated. It was proved that the relative ageing concepts are related to the well known ageing classes such as \(IHR,\, NBU,\) etc.