Varentropy of Past Lifetimes

Abstract

In a variety of applicative fields the level of information in random quantities is commonly measured by means of the Shannon Entropy. In particular, in reliability theory and survival analysis, time-dependent generalizations of this measure of uncertainty have been considered to dynamically describe changes in the degree of information over time. The Residual Entropy and the Residual Varentropy, for example, have been considered in the specialized literature to measure the information and its variability in residual lifetimes. In a similar way, one can consider dynamic measures of information for past lifetimes, i.e., for random lifetimes of items when one assumes that their failures occur before a fixed inspection time. This paper provides a study of the Past Varentropy, defined as the dynamic measure of variability of information for past lifetimes. From this study emerges the interest on a particular family of lifetimes distributions, whose members satisfy the property to be the only ones having constant Past Varentropy.

1 INTRODUCTION

Let $X$ be an absolutely continuous non-negative random variable representing the lifetime of an item, or of an individual. If $f_{X}$ denotes its density, one can define the well-known Shannon information measure (or Entropy) as

$$H_{e}(X)=\mathbb{E}[IC(X)]=\mathbb{E}[-\log f_{X}(X)]=-\int\limits_{0}^{+\infty}f_{X}(x)\log f_{X}(x)\textrm{d}x,$$

(1.1)

where

$$IC(X)=-\log f_{X}(X)$$

denotes the Information Content of $X$, which can be understood as the self-information or ‘‘surprisal’’ associated with the possible outcomes of $X$ [34]. Actually, $H_{e}(X)$ measures the expected uncertainty contained in $f_{X}$ related to the predictability of an outcome of $X$. We refer [17, 35] two recent comprehensive monographs on information measures and their applications in a variety of fields (see also [29]). Note that, in statistics, one may think of the information content as the log likelihood function, that is of great interest in parameters estimation.

As already mentioned, it follows from (1.1) that the Shannon entropy represents the expectation of the (random) information content $IC(X)$. But for different purposes (see, e.g., [6]), one can also consider its variance, in order to evaluate the concentration of the information content around the entropy $H_{e}(X)$. Thus, one can also be interested in the Varentropy of $X$ (sometimes called Minimal Coding Variance of $X$, whenever $X$ is discrete), defined as

$$V_{e}(X)=\textrm{Var}[IC(X)]=\textrm{Var}[-\log f_{X}(X)]$$

$${}=\textrm{Var}[\log f_{X}(X)]=\mathbb{E}\left[(\log f_{X}(X))^{2}\right]-[H_{e}(X)]^{2}$$

$${}=\int\limits_{0}^{+\infty}f_{X}(x)[\log f_{X}(x)]^{2}\textrm{d}x-\left[\int\limits_{0}^{+\infty}f_{X}(x)\log f_{X}(x)\textrm{d}x\right]^{2}.$$

(1.2)

In recent literature several papers deal with the varentropy and its properties and applications, such as [26, 2] and references therein. For example, approximations of minimal rates for data compression in terms of entropy and varentropy are given in Kontoyiannis and Verdú (2014). Also, knowing the entropy and the varentropy one can define reference intervals for the information content $IC(X)$ of the form

$$\mathbb{E}[IC(X)]\pm k\sqrt{\textrm{Var}[IC(X)]}=H_{e}(X)\pm k\sqrt{V_{e}(X)}$$

(1.3)

for suitable choices of $k$. In the statistics field, this interval can be used to evaluate the uncertainty about likelihood estimates.

It must be pointed out that the Shannon entropy, as well as the varentropy, provides a measure of information for the random lifetime of an item which is new, whenever $X$ represents its lifetime. For such reason, different time dependent versions of this measure have been proposed in the context of reliability and survival analysis, where the behavior of residual lifetimes along time, or past lifetimes, are the main objects of the studies. The most well-known version of such dynamic ones is the Residual Entropy defined and studied in [28, 12], whose definition is recalled here. Given the absolutely continuous random lifetime $X$, having support $\mathcal{S}\subseteq\mathbb{R}^{+}$, survival function $\overline{F}_{X}$ and density $f_{X}$, let $X_{t}=(X-t|X>t)$ denote the corresponding Residual Lifetime at time $t\in\mathcal{S}$, i.e., the variable whose density is given by

$$f_{X_{t}}(x)=\frac{f_{X}(x+t)}{\overline{F}_{X}(t)},\quad x:x+t\in\mathcal{S}.$$

The Residual Entropy of $X$ is the function of time $t\in\mathcal{S}$ defined as

$$H_{e}(X_{t})=\mathbb{E}[IC(X_{t})]=\mathbb{E}[-\log f_{X_{t}}(X_{t})]=-\int\limits_{t}^{+\infty}\frac{f_{X}(x)}{\overline{F}_{X}(t)}\log\frac{f_{X}(x)}{\overline{F}_{X}(t)}\ \textrm{d}x.$$

It must be pointed out that the entropy (and the varentropy) of a random lifetime $Y$ is actually a functional of its density $f_{Y}$, depending only on the distribution of $Y$ and not on the value assumed by $Y$. But the residual entropy (such as the residual varentropy defined below) can be considered as a function of the inspection time $t$: to every time $t$ it corresponds a real value $H_{e}(X_{t})$ (defined as a functional of the density $f_{X_{t}}$), and this is the reason why we treat them here as if they were functions of $t$.

In a similar manner it can be defined a dynamic version of the varentropy, useful to evaluate the concentration of the information content in residual lifetimes when the time increases. This is the Residual Varentropy, studied in details in [11, 32] defined as

$$V_{e}(X_{t})=\textrm{Var}[IC(X_{t})]=\textrm{Var}[-\log f_{X_{t}}(X_{t})]$$

$${}=\textrm{Var}[\log f_{X_{t}}(X_{t})]=\mathbb{E}\left[(\log f_{X_{t}}(X_{t}))^{2}\right]-[H_{e}(X_{t})]^{2}$$

$${}=\int\limits_{t}^{+\infty}\frac{f_{X}(x)}{\overline{F}_{X}(t)}\left[\log\frac{f_{X}(x)}{\overline{F}_{X}(t)}\right]^{2}\textrm{d}x-\left[\int\limits_{t}^{+\infty}\frac{f_{X}(x)}{\overline{F}_{X}(t)}\log\frac{f_{X}(x)}{\overline{F}_{X}(t)}\textrm{d}x\right]^{2},\quad t\in\mathcal{S}.$$

A large number of studies in reliability theory deal with past lifetime, that is the random variable conditioned on the fact that the failure occurs before a specified inspection time $t$. We refer the reader [13, 29, and 20], and references therein, for results concerning past lifetime in reliability analysis (see also [13, 29, and 20], In many situations, uncertainty can refer to the past instead of the future. In fact, if we consider a system which is failed or down at time $t$, it could be of interest to study the uncertainty about the time in $(0,t)$ in which it has failed. Moreover, past lifetime plays a central role in the analysis of right-censored data (see, e.g., [1]). For past lifetimes, as well for residual lifetimes, it can be useful to provide dynamic versions of the entropy and the varentropy, whose definitions are similar to the ones described above. To this aim, recall that given the absolutely continuous random lifetime $X$, having support $\mathcal{S}\subseteq\mathbb{R}^{+}$, cumulative distribution $F_{X}$ and density $f_{X}$, its Past Lifetime at time $t\in\mathcal{S}$ is the variable ${}_{t}X=(X|X\leq t)$ whose density is

$$f_{{}_{t}X}(x)=\frac{f_{X}(x)}{F_{X}(t)}\quad x\in(0,t),$$

(1.4)

and whose mean, known as Mean Past Lifetime, is given by

$$\tilde{\mu}_{X}(t)=\int\limits_{0}^{t}\left(1-\frac{F_{X}(x)}{F_{X}(t)}\right)\textrm{d}x=t-\frac{1}{F_{X}(t)}\int\limits_{0}^{t}F_{X}(x)\textrm{d}x,\quad t\in\mathcal{S}.$$

(1.5)

The corresponding Past Entropy and Past Varentropy can be thus defined as

$$H_{e}(_{t}X)=\mathbb{E}[IC(_{t}X)]=\mathbb{E}[-\log f_{{}_{t}X}(_{t}X)]=-\int\limits_{0}^{t}\frac{f_{X}(x)}{F_{X}(t)}\log\frac{f_{X}(x)}{F_{X}(t)}\ \textrm{d}x$$

(1.6)

and

$$V_{e}(_{t}X)=\textrm{Var}[IC(_{t}X)]=\textrm{Var}[-\log f_{{}_{t}X}(_{t}X)]$$

$${}=\textrm{Var}[\log f_{{}_{t}X}(_{t}X)]=\mathbb{E}\left[(\log f_{{}_{t}X}(_{t}X))^{2}\right]-[H_{e}(_{t}X)]^{2}$$

$${}=\int\limits_{0}^{t}\frac{f(x)}{F(t)}\left[\log\frac{f_{X}(x)}{F_{X}(t)}\right]^{2}\textrm{d}x-\left[\int\limits_{0}^{t}\frac{f_{X}(x)}{F_{X}(t)}\log\frac{f_{X}(x)}{F_{X}(t)}\textrm{d}x\right]^{2}$$

(1.7)

for all $t\in\mathcal{S}$.

The past entropy $H_{e}(_{t}X)$ has been studied in details in [10], but there are no detailed studies describing specific properties of the past varentropy $V_{e}(_{t}X)$. The purpose of this paper is to fill this lack, providing a list of useful formulas, properties and examples for the past varentropy. As pointed out in the following sections, the past varentropy satisfies some properties which are similar to those satisfied by the residual varentropy (described in [11]), but one can also observe differences. For example, while there exist at least three families of lifetimes distributions with continuous densities for which the residual varentropy is constant, on the contrary there exists only one family for which such property is satisfied by the past varentropy.

2 MAIN RESULTS

First, we provide an alternative simple formula for the past varentropy of a random lifetime $X$. To this aim, recall that the reversed hazard rate function of $X$ is defined as

$$q_{X}(t)=\lim_{\Delta t\to 0^{+}}\frac{1}{\Delta t}\mathbb{P}(X\geq t-\Delta t|X\leq t)=\frac{f_{X}(t)}{F_{X}(t)}$$

(2.1)

for $t\in\mathcal{S}$. The reversed hazard rate function is the instantaneous failure rate occurring immediately before the time point $t$, i.e., that the failure occurs just before the time point $t$, given that the unit has not survived longer than time $t$ (see [5, 13] for more details about the reversed hazard rate function). We recall also the notion of inverse cumulative reversed hazard rate function, that is defined as

$$Q_{X}(t)=\int\limits_{t}^{+\infty}q_{X}(x)\textrm{d}x=-\log F_{X}(t),$$

(2.2)

(see for instance Li and Li, 2008). Also, note that the past entropy can be expressed as

$$H_{e}(_{t}X)=-Q_{X}(t)-\frac{1}{F_{X}(t)}\int\limits_{0}^{t}f_{X}(x)\log f_{X}(x)\textrm{d}x$$

$${}=1-\frac{1}{F_{X}(t)}\int\limits_{0}^{t}f_{X}(x)\log q_{X}(x)\textrm{d}x$$

(2.3)

as shown in Di Crescenzo and Longobardi (2002). Thus, through (1.7) and (2.3), one obtains

$$V_{e}(_{t}X)=\int\limits_{0}^{t}\frac{f(x)}{F(t)}\left[\log\frac{f_{X}(x)}{F_{X}(t)}\right]^{2}\textrm{d}x-[H_{e}(_{t}X)]^{2}$$

$${}=\frac{1}{F_{X}(t)}\int\limits_{0}^{t}f_{X}(x)(\log f_{X}(x))^{2}\textrm{d}x+\left(\log F_{X}(t)\right)^{2}-\frac{2\log F_{X}(t)}{F_{X}(t)}\int\limits_{0}^{t}f_{X}(x)\log f_{X}(x)\textrm{d}x$$

$${}-[H_{e}(_{t}X)]^{2}=\frac{1}{F_{X}(t)}\int\limits_{0}^{t}f_{X}(x)(\log f_{X}(x))^{2}\textrm{d}x+\left(Q_{X}(t)\right)^{2}+\frac{2Q_{X}(t)}{F_{X}(t)}\int\limits_{0}^{t}f_{X}(x)\log f_{X}(x)\textrm{d}x$$

$${}-[H_{e}(_{t}X)]^{2}=\frac{1}{F_{X}(t)}\int\limits_{0}^{t}f_{X}(x)(\log f_{X}(x))^{2}\textrm{d}x+\left(Q_{X}(t)\right)^{2}-2Q_{X}(t)\left[Q_{X}(t)+H_{e}(_{t}X)\right]-[H_{e}(_{t}X)]^{2}$$

$${}=\frac{1}{F_{X}(t)}\int\limits_{0}^{t}f_{X}(x)(\log f_{X}(x))^{2}\textrm{d}x-(Q_{X}(t)+H_{e}(_{t}X))^{2}$$

(2.4)

for $t\in\mathcal{S}$.

Remark 2.1. As well as, when $t$ tends to the supremum of the support $\mathcal{S}$, $u_{X}$, the past entropy tends to Shannon entropy, also the past varentropy reduces to the varentropy, i.e., $\lim_{t\to u_{X}}V_{e}(_{t}X)=V_{e}(X)$.

Now, consider the case in which $t$ tends to the infimum of the support, $l_{X}$. If the pdf $f_{X}$ of $X$ is differentiable and such that

$$\lim_{t\to l_{X}^{+}}f_{X}(t)\neq 0\quad\textrm{and}\quad\lim_{t\to l_{X}^{+}}f_{X}^{\prime}(t)\neq+\infty,$$

(2.5)

then $\lim_{t\to l_{X}^{+}}V_{e}(_{t}X)=0$. In fact, from (2.4) the past varentropy can be expressed as

$$V_{e}(_{t}X)=\frac{F_{X}(t)\int\limits_{l_{X}}^{t}f_{X}(x)\left(\log f_{X}(x)\right)^{2}\textrm{d}x-\left(\int\limits_{l_{X}}^{t}f_{X}(x)\log f_{X}(x)\textrm{d}x\right)^{2}}{F_{X}^{2}(t)},$$

and by using L’Hôpital’s rule twice, it readily follows

$$\lim_{t\to l_{X}^{+}}V_{e}(_{t}X)=\lim_{t\to l_{X}^{+}}\left(\frac{f^{\prime}_{X}(t)F_{X}(t)}{f_{X}^{2}(t)}\log f_{X}(t)-\frac{f_{X}^{\prime}(t)}{f_{X}^{2}(t)}\int\limits_{l_{X}}^{t}f_{X}(x)\log f_{X}(x)\textrm{d}x\right)$$

$${}=\lim_{t\to l_{X}^{+}}\frac{f_{X}^{\prime}(t)}{f_{X}^{2}(t)}\int\limits_{l_{X}}^{t}\frac{F_{X}(x)f^{\prime}_{X}(x)}{f_{X}(x)}\textrm{d}x=0,$$

where the last equality depends on the assumptions in (2.5).

By using (1.6) and (2.4) one can find the past entropy and past varentropy for some distributions of interest in reliability theory. Some examples are listed here.

• Let $X$ be a random variable with uniform distribution over $(0,b)$, i.e., $X\sim U(0,b)$, $b>0$. Hence, for $t\in(0,b)$ we have

  $$H_{e}(_{t}X)=\log t,$$
  $$V_{e}(_{t}X)=0.$$

• Let $X$ be a random variable with exponential distribution, i.e., $X\sim\mathrm{exp}(\lambda)$, for $\lambda>0$. Then, for $t>0$, we have

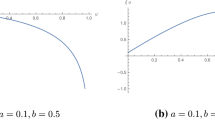
  $$H_{e}(_{t}X)=1+\log\left(\frac{1-\textrm{e}^{-\lambda t}}{\lambda}\right)-\frac{\lambda t\textrm{e}^{-\lambda t}}{1-\textrm{e}^{-\lambda t}},$$
  $$V_{e}(_{t}X)=1-\frac{\lambda^{2}t^{2}\textrm{e}^{-\lambda t}}{(1-\textrm{e}^{-\lambda t})^{2}}.$$

  The plots of past entropy and past varentropy are shown in Fig. 1 for different choices of $\lambda$. Observe that $\lim_{t\to 0^{+}}V_{e}(_{t}X)=0$ as expected since the exponential distribution satisfies the assumptions given in (2.5) for any value of the rate $\lambda$.

  Fig. 1

  

  Plots of past entropy and past varentropy of exponential distribution with parameter $\lambda=1,2,3,4$ (black, blue, red, and green, respectively).

• Let $X$ be a random variable such that $f_{X}(x)=2x$ and $F_{X}(x)=x^{2}$, $x\in(0,1)$. Hence, for $t\in(0,1)$, we have

  $$H_{e}(_{t}X)=\frac{1}{2}+\log\frac{t}{2},$$
  $$V_{e}(_{t}X)=\frac{1}{4}.$$

• Let $X$ be a random variable $Beta(2,2)$ distribution, i.e., such that $f_{X}(x)=6x(1-x)$ and $F_{X}(x)=3x^{2}-2x^{3}$, $x\in(0,1)$. Hence, for $t\in(0,1)$, we have

  $$H_{e}(_{t}X)=\frac{1}{t^{2}/2-t^{3}/3}\left[\left(\frac{t^{2}}{2}-\frac{t^{3}}{3}\right)\log\left(\frac{6(1-t)}{t(3-2t)}\right)+\frac{2}{9}t^{3}-\frac{1}{3}t^{2}-\frac{1}{6}t-\frac{1}{6}\log(1-t)\right]$$
  $$V_{e}(_{t}X)=\frac{1}{t^{2}/2-t^{3}/3}\left[\left(\frac{t^{2}}{2}-\frac{t^{3}}{3}\right)\log^{2}\left(\frac{6(1-t)}{t(3-2t)}\right)+\frac{1}{3}\left(\frac{4}{3}t^{3}-2t^{2}-t\right)\log\left(\frac{6(1-t)}{t(3-2t)}\right)\right.$$
  $${}+\left.\frac{1}{9}\left(-\frac{8}{3}t^{3}+4t^{2}+8t+5\log(1-t)\right)-\frac{1}{3}\log\left(\frac{1}{t^{2}/2-t^{3}/3}\right)\log(1-t)\right.$$
  $${}-\left.\frac{1}{6}\log^{2}(1-t)-\frac{\pi^{2}}{18}+\frac{1}{3}Li_{2}(1-t))\right]-[H_{e}(_{t}X)]^{2},$$

  where $Li_{2}$ is the Spence’s function or dilogarithm function (see, e.g., Morris, 1979). The plots of past entropy and past varentropy are shown in Fig. 2.

  Fig. 2

  

  Plots of past entropy and past varentropy of $X\sim\beta(2,2)$.

• Let $X$ be a random variable having cumulative distribution $F_{X}(x)=1-\big{(}\frac{b-x}{b}\big{)}^{\alpha}$, for $x\in(0,b)\subseteq\mathbb{R}^{+}$ and $\alpha>0$. Then, for $t\in(0,b)$:

  $$H_{e}(_{t}X)=\frac{b^{\alpha}}{b^{\alpha}-(b-t)^{\alpha}}\log\left(\frac{\alpha b^{(\alpha-1)}}{b^{\alpha}-(b-t)^{\alpha}}\right)-\frac{(b-t)^{\alpha}}{b^{\alpha}-(b-t)^{\alpha}}\log\left(\frac{\alpha(b-t)^{(\alpha-1)}}{b^{\alpha}-(b-t)^{\alpha}}\right)-\frac{\alpha-1}{\alpha},$$
  $$V_{e}(_{t}X)=\left(\frac{\alpha-1}{\alpha}\right)^{2}-\frac{b^{\alpha}(b-t)^{\alpha}}{[b^{\alpha}-(b-t)^{\alpha}]^{2}}\ \log^{2}\left[\left(\frac{b}{b-t}\right)^{\alpha-1}\right].$$

  The plots of this past entropy and of the corresponding past varentropy are shown in Fig. 3.

Fig. 3

Plots of past entropy and past varentropy of $X$ with cdf $F_{X}(x)=1-\big{(}\frac{b-x}{b}\big{)}^{\alpha}$ for $b=5$ and $\alpha=2,3,4,5$ (black, blue, red, and green, respectively).

It is interesting to observe that the past varentropy is constant in two of the cases described above, increasing in one case, and non-monotone in the other one. Thus, monotonicity of the varentropy is not always guaranteed. Let us remark that, if the reversed hazard rate is decreasing for all $t$, then the past entropy is increasing for all $t$ (see [10, Proposition 2.2]). However, monotonicity of the reversed hazard rate is not a sufficient condition for monotonicity of the varentropy. In fact, for the $\beta(2,2)$ distribution the reversed hazard rate $q_{X}(t)=6(1-t)/(3t-2t^{2})$ is decreasing, while the varentropy is not monotone. For this reason, conditions for the monotonicity of $V_{e}(_{t}X)$ and an implicit formula for the derivative of the past varentropy are now described.

Conditions for monotonicity of the past varentropy can be easily provided by using the results that appear in [32]. For it, we recall the definition of two stochastic comparisons between variables that are used in the proof. Given the random variables $X_{1}$ and $X_{2}$ having distributions $F_{1}$ and $F_{2}$, respectively, we say that $X_{1}$ is smaller than $X_{2}$ in the concave order, $X_{1}\leq_{c}X_{2}$ in notation, if $F_{2}^{-1}(F_{1}(x))$ is convex on the support of $F_{1}$. We say that $X_{1}$ is smaller than $X_{2}$ in the starshaped order, $X_{1}\leq_{\ast}X_{2}$ in notation, if $F_{2}^{-1}(F_{1}(x))/x$ is increasing on the support of $F_{1}$. Details and applications of these stochastic orders can be found in Shaked and Shanthikumar (2007).

Proposition 2.1. Let $X$ be a random lifetime with an absolutely continuous distribution $F_{X}$ and a strictly decreasing [increasing] density function $f_{X}$. If the ratio

$$\frac{f_{X}(F_{X}^{-1}(pF(s)))}{f_{X}(F_{X}^{-1}(pF(t)))}$$

(2.6)

is increasing in $p\in(0,1)$ for all $s\leq t$, then the corresponding past varentropy $V_{e}(_{t}X)$ is increasing [decreasing] in $t\in\mathcal{S}$.

Proof. Recall that, for any $t\in\mathcal{S}$, the past lifetime ${}_{t}X$ has density $f_{{}_{t}X}(x)=f_{X}(x)/F_{X}(t)$ and cumulative distribution $F_{{}_{t}X}(x)=F_{X}(x)/F_{X}(t)$, with $x\leq t$. Thus, the corresponding quantile function is $F_{{}_{t}X}^{-1}(p)=F_{X}^{-1}(pF_{X}(t))$, for $p\in(0,1)$. Also observe that, for $s\leq t$,

$$\frac{f_{{}_{s}X}(F_{{}_{s}X}^{-1}(p))}{f_{{}_{t}X}(F_{{}_{t}X}^{-1}(p))}=\frac{f_{X}(F_{X}^{-1}(pF_{X}(s)))}{F_{X}(s)}\cdot\frac{F_{X}(t)}{f_{X}(F_{X}^{-1}(pF_{X}(t)))}=\frac{f_{X}(F_{X}^{-1}(pF(s)))}{f_{X}(F_{X}^{-1}(pF(t)))}\cdot\frac{F_{X}(t)}{F_{X}(s)},$$

where the latter is increasing in $p$ by assumption (2.6). Then one has ${}_{s}X\leq_{c}\ {}_{t}X$ (see Remark 4.3 in [32], or Section 4.2 in [33]). Now observe that, since $f_{X}$ is decreasing [increasing] by assumption, then also $f_{{}_{s}X}$ and $f_{{}_{t}X}$ are decreasing [increasing]. Thus, by the equivalence pointed out in Remark 4.6 in Paolillo et al. (2021), one also has that $f_{{}_{s}X}(_{s}X)\leq_{\ast}f_{{}_{t}X}(_{t}X)$  [$f_{{}_{s}X}(_{s}X)\geq_{\ast}f_{{}_{t}X}(_{t}X)$], which, in turns, implies $V_{e}(_{s}X)\leq V_{e}(_{t}X)$ [$V_{e}(_{s}X)\geq V_{e}(_{t}X)$] by Theorem 5.2 in the same paper. $\Box$

It is easy to verify, for example, that exponential distributions satisfy the assumptions of Proposition 2.1 for any value of the rate $\lambda$.

The following result provides an implicit formula for the derivative of the past varentropy, useful to describe distributions having constant varentropy.

Proposition 2.2. For all $t\in\mathcal{S}$, the derivative of the past varentropy is

$$V_{e}^{\prime}(_{t}X)=-q_{X}(t)\left[V_{e}(_{t}X)-(H_{e}(_{t}X)+\log q_{X}(t))^{2}\right].$$

Proof. First observe that by differentiating both sides of (2.3) we get the following expression for the derivative of the past entropy:

$$H_{e}^{\prime}(_{t}X)=q_{X}(t)[1-H(_{t}X)-\log q_{X}(t)].$$

(2.7)

Consider now (2.4). By differentiating both sides we get

$$V_{e}^{\prime}(_{t}X)=\frac{q_{X}(t)}{F_{X}(t)}\int\limits_{0}^{t}f_{X}(x)(\log f_{X}(x))^{2}\textrm{d}x+q_{X}(t)(\log f_{X}(t))^{2}$$

$${}-2(Q_{X}(t)+H_{e}(_{t}X))(-q_{X}(t)+H_{e}^{\prime}(_{t}X)),$$

(2.8)

where $q_{X}(t)$ is defined in (2.1). Hence, recalling (2.7) and (2.4), from (2.8) we get

$$V_{e}^{\prime}(_{t}X)=-q_{X}(t)\left[V_{e}(_{t}X)+(Q_{X}(t)+H_{e}(_{t}X))^{2}-(\log f_{X}(t))^{2}\right.$$

$${}-\left.2(Q_{X}(t)+H_{e}(_{t}X))(H_{e}(_{t}X)+\log q_{X}(t))\right],$$

and, after straightforward calculations, one gets the statement. $\Box$

From (2.7) one can obtain conditions such that absolutely continuous distributions, having continuous densities, have a corresponding constant past varentropy. To this aim, consider first the case of random variables having support $\mathcal{S}=[0,1]$.

Proposition 2.3. Let $X$ have support $\mathcal{S}=[0,1]$. Then, its varentropy $V_{e}(_{t}X)$ is constant if, and only if, $X$ has cumulative distribution function

$$F_{X}(x)=x^{\alpha},\quad x\in[0,1],$$

(2.9)

for a parameter $\alpha>0$. In this case, one has $V_{e}(_{t}X)=(1-1/\alpha)^{2}$ for all $t\in[0,1]$.

Proof. First observe that, if $X$ has cumulative distribution defined as in (2.9), then the pdf is given by

$$f_{X}(x)=\alpha x^{\alpha-1},\quad x\in(0,1),$$

and, for $t\in(0,1)$, the past varentropy is defined as

$$V_{e}(_{t}X)=\int\limits_{0}^{t}\frac{\alpha x^{\alpha-1}}{t^{\alpha}}\left[\log\left(\frac{\alpha x^{\alpha-1}}{t^{\alpha}}\right)\right]^{2}\textrm{d}x-\left[\int\limits_{0}^{t}\frac{\alpha x^{\alpha-1}}{t^{\alpha}}\log\left(\frac{\alpha x^{\alpha-1}}{t^{\alpha}}\right)\textrm{d}x\right]^{2}.$$

By the change of variable $y=\left(\frac{x}{t}\right)^{\alpha}$, we get

$$V_{e}(_{t}X)=\int\limits_{0}^{1}\left[\log\left(\frac{\alpha y^{(\alpha-1)/\alpha}}{t}\right)\right]^{2}\textrm{d}y-\left[\int\limits_{0}^{1}\log\left(\frac{\alpha y^{(\alpha-1)/\alpha}}{t}\right)\textrm{d}y\right]^{2}$$

$${}=\log^{2}\left(\frac{\alpha}{t}\right)-\int\limits_{0}^{1}2\left(\frac{\alpha-1}{\alpha}\right)\log\left(\frac{\alpha y^{(\alpha-1)/\alpha}}{t}\right)\textrm{d}y-\left[\log\left(\frac{\alpha}{t}\right)-\frac{\alpha-1}{\alpha}\right]^{2}$$

$${}=\log^{2}\left(\frac{\alpha}{t}\right)-2\left(\frac{\alpha-1}{\alpha}\right)\log\left(\frac{\alpha}{t}\right)+2\left(\frac{\alpha-1}{\alpha}\right)^{2}-\left[\log\left(\frac{\alpha}{t}\right)-\frac{\alpha-1}{\alpha}\right]^{2}.$$

Thus $V_{e}(_{t}X)$ is constant and equal to $(1-1/\alpha)^{2}$. It follows now, from Proposition 2.2, that

$$(H_{e}(_{t}X)+\log q_{X}(t))^{2}=(1-1/\alpha)^{2}$$

and so

$$|H_{e}(_{t}X)+\log q_{X}(t)|=|1-1/\alpha|,\quad\forall t\in[0,1].$$

(2.10)

Since the density $f_{X}$ is continuous by assumption, then also $q_{X}$ and $H_{e}(X_{t})$ are continuous. Thus, $H_{e}(_{t}X)+\log q_{X}(t)$ is continuous in $t\in[0,1]$, so that equality (2.10) implies

$$H_{e}(_{t}X)+\log q_{X}(t)=c,\quad\forall t\in[0,1]$$

(2.11)

for some $c\in\mathbb{R}$.

As shown in [23, Theorem 2.1], Theorem 2.1, there exist only three families of distribution for which (2.11) is satisfied. Two of them have infinite support on the left, i.e., of the form $(-\infty,b]$, for $b\in\mathbb{R}$ (thus they cannot be distributions of random lifetimes), and the only one having support entirely contained in $\mathbb{R}^{+}$ (and in $[0,1]$ in particular) is the one defined in (2.9). Finally, since the family defined in (2.9) has constant past varentropy, the assertion follows. $\Box$

To generalize the above result to random lifetimes having different supports, we can use the following proposition, that deals with the past varentropy under linear transformations. We recall that if $Y=aX+b$ for $a>0$ and $b\geq 0$, then the past entropies of $X$ and $Y$ are related by

$$H_{e}(_{t}Y)=H_{e}\left({}_{\frac{t-b}{a}}X\right)+\log a\quad\forall t$$

(2.12)

(see Di Crescenzo and Longobardi, 2002).

Proposition 2.4. Let $Y=aX+b$, with $a>0$ and $b\geq 0$. Then, for their past varentropies, we have

$$V_{e}(_{t}Y)=V_{e}\left({}_{\frac{t-b}{a}}X\right),\quad\forall t.$$

(2.13)

Proof. From $Y=aX+b$ we know that $F_{Y}(x)=F_{X}\left(\frac{x-b}{a}\right)$ and $f_{Y}(x)=\frac{1}{a}f_{X}\left(\frac{x-b}{a}\right)$. Hence, from (1.7) and (2.12), we get

$$V_{e}(_{t}Y)=\int\limits_{0}^{\frac{t-b}{a}}\frac{f_{X}(x)}{F_{X}\left(\frac{t-b}{a}\right)}\left(\log\frac{\frac{1}{a}f_{X}\left(x\right)}{F_{X}\left(\frac{t-b}{a}\right)}\right)^{2}\textrm{d}x-\left(H\left({}_{\frac{t-b}{a}}X\right)+\log a\right)^{2}.$$

(2.14)

By writing

$$\log\frac{\frac{1}{a}f_{X}\left(x\right)}{F_{X}\left(\frac{t-b}{a}\right)}=\log\frac{f_{X}\left(x\right)}{F_{X}\left(\frac{t-b}{a}\right)}-\log a$$

and developing the two squares in (2.14), one easily obtains the statement. $\Box$

From Propositions 2.3 and 2.4 one immediately gets the following statement.

Corollary 2.1. Let $X$ be an absolutely continuous random lifetime with continuous density $f_{X}$ . Then, its varentropy $V_{e}(_{t}X)$ is constant if, and only if, $X$ has cumulative distribution function in the family

$$F_{X}(x)=\left(\frac{x-b}{a}\right)^{\alpha},\quad x\in[b,a+b],$$

(2.15)

for a parameter $\alpha$ such that $\alpha>0$.

Apart for the property stated in Corollary 2.1, the family defined in (2.15) is the only one of lifetimes distribution having continuous density that satisfies the property stated in the next proposition. Recall first that the Generalized Reversed Hazard Rate of a random lifetime is defined, for $\gamma\in\mathbb{R}$, as

$$q_{\gamma,X}(t)=\frac{f_{X}(t)}{[F_{X}(t)]^{1-\gamma}},\quad t\in\mathcal{S}$$

(2.16)

(see Buono et al. (2021), where their applications in the study of properties of aging intensity functions are described). We remark that, by choosing $\gamma=0$ in (2.16), we get $q_{0,X}(t)=q_{X}(t)$, i.e., $q_{0,X}$ is the usual reversed hazard rate function. Let us observe that for $\gamma=1$ the generalized reversed hazard rate function is equal to the density function. This is reasonable since the density function gives a first rough illustration of the aging tendency of the random variable by its monotonicity.

Proposition 2.5. Let $X$ be a random lifetime having continuous density, and let $\gamma\in\mathbb{R}$. Its generalized reversed hazard rate function $q_{\gamma,X}(t)$, with parameter $\gamma$, is constant if, and only if, $F_{X}$ is in the family defined in (2.15) and $\gamma=1/\alpha$. Moreover, in this case one has

$$q_{1/\alpha,X}(t)=\frac{f_{X}(t)}{[F_{X}(t)]^{1-1/\alpha}}=\textrm{e}^{1-1/\alpha-H_{e}(X)},\quad\forall t\in[b,a+b].$$

(2.17)

Proof. Let us suppose that there exists $c\in\mathbb{R}$ such that $q_{1-c,X}(t)=\textrm{e}^{c-H_{e}(X)}$ for all $t\in\mathcal{S}$, being $\mathcal{S}$ the support of $X$. From (2.1) and (2.3) we have

$$H_{e}(_{t}X)+\log q_{X}(t)=\log f_{X}(t)-\frac{1}{F_{X}(t)}\int\limits_{(0,t)\bigcap\mathcal{S}}f_{X}(x)\log f_{X}(x)\textrm{d}x$$

$${}=\log f_{X}(t)+\frac{1}{F_{X}(t)}\left[H_{e}(X)+\int\limits_{(t,+\infty)\bigcap\mathcal{S}}f_{X}(x)\log f_{X}(x)\textrm{d}x\right].$$

Moreover, from the hypothesis, we get

$$\int\limits_{(t,+\infty)\bigcap\mathcal{S}}f_{X}(x)\log f_{X}(x)\textrm{d}x=-H_{e}(X)\overline{F}_{X}(t)-cF_{X}(t)\log F_{X}(t)$$

and so

$$H_{e}(_{t}X)+\log q_{X}(t)=H_{e}(X)+\log\frac{f_{X}(t)}{[F_{X}(t)]^{c}}=c.$$

This last equality is satisfied only for distributions in the family described in (2.15), with $c=1-1/\alpha$. Conversely, if $X$ has distributions in the family described in (2.15), then, with a direct calculation, one can verify that (2.17) holds. $\Box$

A generalization of Proposition 2.1 will now be stated. For it, let $\phi$ be a differentiable and strictly monotonic function and let $Y=\phi(X)$ for a given $X$. It has been shown in Di Crescenzo and Longobardi (2002) that the past entropies of $X$ and $Y$ are related by the equations

$$H_{e}(_{t}Y)=\begin{cases}H_{e}\left({}_{\phi^{-1}(t)}X\right)+\mathbb{E}[\log\phi^{\prime}(X)|X<\phi^{-1}(t)],\quad\text{if}\quad\phi\text{ is strictly increasing}\\ H_{e}\left(X_{\phi^{-1}(t)}\right)+\mathbb{E}[\log(-\phi^{\prime}(X))|X>\phi^{-1}(t)],\quad\text{if}\quad\phi\text{ is strictly decreasing.}\end{cases}$$

(2.18)

Similar results can be proved for the past varentropy.

Proposition 2.6. Let $Y=\phi(X)$, where $\phi$ is a differentiable and strictly monotonic function. Then, if $\phi$ is strictly increasing, for the past varentropy of $Y$ we have

$$V_{e}(_{t}Y)=V_{e}\left({}_{\phi^{-1}(t)}X\right)-2\mathbb{E}\left[\left.\log\frac{f_{X}(X)}{F_{X}(\phi^{-1}(t))}\log\phi^{\prime}(X)\right|X<\phi^{-1}(t)\right]$$

$${}+\textrm{Var}[\log\phi^{\prime}(X)|X<\phi^{-1}(t)]-2H_{e}\left({}_{\phi^{-1}(t)}X\right)\mathbb{E}[\log\phi^{\prime}(X)|X<\phi^{-1}(t)],$$

(2.19)

whereas, if $\phi$ is strictly decreasing

$$V_{e}(_{t}Y)=V_{e}\left(X_{\phi^{-1}(t)}\right)-2\mathbb{E}\left[\left.\log\frac{f_{X}(X)}{\overline{F}_{X}(\phi^{-1}(t))}\log(-\phi^{\prime}(X))\right|X>\phi^{-1}(t)\right]$$

$${}+\textrm{Var}[\log(-\phi^{\prime}(X))|X>\phi^{-1}(t)]-2H\left(X_{\phi^{-1}(t)}\right)\mathbb{E}[\log(-\phi^{\prime}(X))|X>\phi^{-1}(t)].$$

(2.20)

Proof. Suppose first that $\phi$ is strictly increasing. From $Y=\phi(X)$ we know that $F_{Y}(x)=F_{X}\left(\phi^{-1}(x)\right)$ and $f_{Y}(x)=\frac{f_{X}(\phi^{-1}(x))}{\phi^{\prime}(\phi^{-1}(x))}$. Hence, from (1.7) and (2.18), we get

$$V_{e}(_{t}Y)=\int\limits_{0}^{\phi^{-1}(t)}\frac{f_{X}(x)}{F_{X}\left(\phi^{-1}(t)\right)}\left(\log\frac{f_{X}\left(x\right)}{F_{X}\left(\phi^{-1}(t)\right)}-\log\phi^{\prime}(x)\right)^{2}\textrm{d}x$$

$${}-\left[H_{e}\left({}_{\phi^{-1}(t)}X\right)+\mathbb{E}[\log\phi^{\prime}(X)|X<\phi^{-1}(t)]\right]^{2}.$$

Now, by developing the two squares in the previous equality, and observing that

$$\int\limits_{0}^{\phi^{-1}(t)}\frac{f_{X}(x)}{F_{X}\left(\phi^{-1}(t)\right)}\left(\log\phi^{\prime}(x)\right)^{2}\textrm{d}x-\mathbb{E}^{2}[\log\phi^{\prime}(X)|X<\phi^{-1}(t)]$$

$${}=\textrm{Var}[\log\phi^{\prime}(X)|X<\phi^{-1}(t)],$$

we obtain the result.

The proof is similar if $\phi$ is strictly decreasing. $\Box$

Example 2.1. The Inverted Exponential distribution (exp), introduced as a lifetime model in Lin et al. (1989), has been considered by many authors in reliability studies (see, e.g., [22, 31], and references therein). The past varentropy of an inverted exponential distribution can be actually obtained by using Proposition 2.6. To this aim, consider $X\sim\mathrm{exp}(\lambda)$ and $Y=\phi(X)=1/X$ so that $\phi$ is strictly decreasing and $Y\sim\mathrm{exp}(\lambda)$. We can use the result presented in (2.20) to evaluate the past varentropy of $Y$. In fact, we have

$$V_{e}(_{t}Y)=V_{e}\left(X_{1/t}\right)-2\mathbb{E}\left[\left.\log\frac{\lambda e^{-\lambda X}}{e^{-\lambda/t}}\log\left(\frac{1}{X^{2}}\right)\right|X>\frac{1}{t}\right]$$

$${}+\textrm{Var}\left[\left.\log\left(\frac{1}{X^{2}}\right)\right|X>\frac{1}{t}\right]-2H\left(X_{1/t}\right)\mathbb{E}\left[\left.\log\left(\frac{1}{X^{2}}\right)\right|X>\frac{1}{t}\right].$$

The residual entropy and the residual varentropy for the exponential distribution are given as

$$H_{e}(X_{t})=1-\log\lambda,\quad V_{e}(X_{t})=1,$$

and then the past varentropy of $Y$ is expressed as

$$V_{e}(_{t}Y)=1-2\mathbb{E}\left[\left.\log\frac{\lambda e^{-\lambda X}}{e^{-\lambda/t}}\log\left(\frac{1}{X^{2}}\right)\right|X>\frac{1}{t}\right]$$

$${}+\textrm{Var}\left[\left.\log\left(\frac{1}{X^{2}}\right)\right|X>\frac{1}{t}\right]-2(1-\log\lambda)\mathbb{E}\left[\left.\log\left(\frac{1}{X^{2}}\right)\right|X>\frac{1}{t}\right].$$

With several calculations, the above expression reduces to

$$V_{e}(_{t}Y)=-3+\frac{4\lambda}{t}\log\frac{1}{t^{2}}+\frac{8t}{\lambda}+\left(8-\frac{4\lambda}{t}\right)\frac{1}{e^{-\lambda/t}}Ei\left(-\frac{\lambda}{t}\right)-\frac{4}{e^{-2\lambda/t}}Ei^{2}\left(-\frac{\lambda}{t}\right)$$

$${}+\frac{4}{e^{-\lambda/t}}\log\frac{1}{t^{2}}Ei\left(-\frac{\lambda}{t}\right)-\frac{4}{\lambda e^{-\lambda/t}}\int\limits_{1/t}^{+\infty}\frac{\log x^{2}}{x^{2}}e^{-\lambda x}\textrm{d}x,$$

where $Ei(\cdot)$ is the exponential integral function (see, e.g., Gautschi and Gahill, 1972). The plot of this past varentropy is shown in Fig. 4 for different choices of $\lambda$.

Fig. 4

Plots of past varentropies of inverse exponential distributions with parameter $\lambda=1,2,3,4$ (black, blue, red, and green, respectively).

We conclude this section pointing out that there exists a strong relationship between the past varentropy and the residual varentropy of an absolutely continuous random lifetime $X$ whenever its support $\mathcal{S}$ is finite. Without loss of generality let $X$ assume values in $[0,u_{X}]$, and let $f_{X}$ be its density function. Then consider a random lifetime $\tilde{X}$ whose density is the symmetric of $f_{X}$ with respect to $u_{X}/2$, i.e., the lifetime having density $f_{\tilde{X}}(x)=f_{X}(u_{X}-x)$ for all $x\in[0,u_{X}]$. It is easy to observe that $X$ and $\tilde{X}$ have the same information content, i.e., that $IC(X)$ and $IC(\tilde{X})$ have the same distribution. Let now $t\in[0,u_{X}]$, and consider the conditioned lifetimes $(X|X>t)$ and $(\tilde{X}|\tilde{X}\leq u_{X}-t)$. Again, it is easy to verify that the corresponding densities are symmetric, i.e., that $f_{(\tilde{X}|\tilde{X}\leq u_{X}-t)}(x)=f_{(X|X>t)}(u_{X}-x)$, so that $IC(X|X>t)$ and $IC(\tilde{X}|\tilde{X}\leq u_{X}-t)$ have the same distribution. It obviously follows that, for all $t\in[0,u_{X}]$, it holds

$$H_{e}(\tilde{X}|\tilde{X}\leq u_{X}-t)=H_{e}(X|X>t)\quad\textrm{and}\quad V_{e}(\tilde{X}|\tilde{X}\leq u_{X}-t)=V_{e}(X|X>t).$$

Thus properties and explicit expressions of the past entropy and past varentropy of a random lifetime with finite support can be obtained from properties and explicit expressions of the corresponding residual entropy and residual varentropy, after an appropriate transformation of the density.

3 BOUNDS FOR THE PAST VARENTROPY

A very simple upper bound for the past varentropy can be provided for a large class of distributions, as stated in the next proposition.

Proposition 3.1. Let $X$ be a non-negative random variable with support $\mathcal{S}$ and log-concave pdf $f_{X}(x)$. Then

$$V_{e}(_{t}X)\leq 1\quad\text{for all}\quad t\in\mathcal{S}.$$

Proof. We observe that if $f_{X}(x)$ is log-concave, then also $f_{{}_{t}X}(x)=\frac{f_{X}(x)}{F_{X}(t)}$ is log-concave. From Theorem 2.3 of Fradelizi et al. (2016), we know that if $X$ has a log-concave pdf, then $V_{e}(X)\leq 1$ and the proof follows from this result. $\Box$

For example, the density $f_{X}(x)=6x(1-x)$, $x\in[0,1]$ of $X\sim\beta(2,2)$ is logconcave, so that the past varentropy of $X$ is always smaller than 1, as confirmed by its plot shown in Fig. 2.

However, by comparing this bound with the plot of $V_{e}(_{t}X)$, one can immediately observe that it is a really large bound. Better upper bounds can be provided, for any $X$, by using results available in the literature. For it recall that, for a random lifetime $X$, the corresponding Inactivity Time at $t$ is defined as $X_{(t)}=(t-X|X\leq t)=t-{{}_{t}X}$, i.e., the random time whose density is

$$f_{X_{(t)}}(x)=\frac{f_{X}(t-x)}{F_{X}(t)}.$$

The following upper bound for $\textrm{Var}[-\log f_{X_{(t)}}(X_{(t)})]$ has been proved in Goodarzi et al. (2016), Proposition 1, making use of an upper bound for variances proved in Cacoullos and Papathanasiou (1985):

$$\textrm{Var}[-\log f_{X_{(t)}}(X_{(t)})]\leq\mathbb{E}\left[\frac{\eta_{X}^{2}(t-X_{(t)})}{q_{X}(t-X_{(t)})}\left(m_{X}(t-X_{(t)})-m_{X}(t)+X_{(t)}\right)\right]$$

(3.1)

for all $t\in\mathcal{S}$, where $\eta_{X}(x)=-f^{\prime}_{X}(x)/f_{X}(x)$ is the eta function and $m_{X}(x)=\mathbb{E}[X_{(x)}]=x-\tilde{\mu}_{X}(x)$ is the mean inactivity time function, and where $\tilde{\mu}_{X}(x)$ is defined in (1.5). Now observe that

$$V_{e}(X_{(t)})=\textrm{Var}[-\log f_{X_{(t)}}(X_{(t)})]=\mathbb{E}[\log^{2}f_{X_{(t)}}(X_{(t)})]-\left[H_{e}(X_{(t)}))\right]^{2}$$

$${}=\int\limits_{0}^{t}\frac{f_{X}(t-x)}{F_{X}(t)}\log^{2}\left(\frac{f_{X}(t-x)}{F_{X}(t)}\right)\textrm{d}x-\left[\int\limits_{0}^{t}\frac{f_{X}(t-x)}{F_{X}(t)}\log\left(\frac{f_{X}(t-x)}{F_{X}(t)}\right)\textrm{d}x\right]^{2}$$

$${}=\int\limits_{0}^{t}\frac{f_{X}(x)}{F_{X}(t)}\log^{2}\left(\frac{f_{X}(x)}{F_{X}(t)}\right)\textrm{d}x-\left[\int\limits_{0}^{t}\frac{f_{X}(x)}{F_{X}(t)}\log\left(\frac{f_{X}(x)}{F_{X}(t)}\right)\textrm{d}x\right]^{2}$$

$${}=\textrm{Var}[-\log f_{{}_{t}X}(_{t}X)]=V_{e}(_{t}X).$$

Thus, recalling that $m_{X}(x)=x-\tilde{\mu}_{X}(x)$ and $X_{(t)}=t-{{}_{t}X}$, from (3.1) one gets the upper bound

$$V_{e}(_{t}X)\leq\mathbb{E}\left[\frac{\eta^{2}(_{t}X)}{q_{X}(_{t}X)}\left(\tilde{\mu}(t)-\tilde{\mu}(_{t}X)\right)\right]\quad\forall\ t\in\mathcal{S}.$$

A lower bound for the past varentropy can also be proved. For it, define first the variance past lifetime function $\tilde{\nu}^{2}_{X}$ as

$$\tilde{\nu}^{2}_{X}(t)=\textrm{Var}(_{t}X)=\textrm{Var}(X|X\leq t)=\frac{1}{F_{X}(t)}\int\limits_{0}^{t}x^{2}f_{X}(x)\textrm{d}x-(\tilde{\mu}_{X}(t))^{2},\quad t\in\mathcal{S}.$$

Note that, for every $t\in\mathcal{S}$ the variance past lifetime function $\tilde{\nu}^{2}_{X}(t)$ is the same as the variance of the inactivity time $X_{(t)}$ (see, e.g., [19] for details and properties of the variance of the inactivity time function).

Proposition 3.2. Let ${}_{t}X$ be the past lifetime of $X$ at time $t$, and let the mean past lifetime $\tilde{\mu}_{X}(t)$ and the variance past lifetime $\tilde{\nu}_{X}^{2}(t)$ be finite for all $t\in\mathcal{S}$. Then

$$V_{e}(_{t}X)\geq\tilde{\nu}_{X}^{2}(t)\left[\mathbb{E}(\omega_{t}^{\prime}(_{t}X))\right]^{2},$$

where the function $\omega_{t}(x)$ is defined by solving the equation

$$\tilde{\nu}_{X}^{2}(t)\omega_{t}(x)f_{{}_{t}X}(x)=\int\limits_{0}^{x}(\tilde{\mu}_{X}(z)-z)f_{{}_{t}X}(z)\textrm{d}z,\quad x\in\mathcal{S}.$$

(3.2)

Proof. Recall that if $X$ is a random variable with pdf $f_{X}$, mean $\mu_{X}$ and variance $\sigma_{X}^{2}$, then

$$\textrm{Var}[g(X)]\geq\sigma^{2}\left[\mathbb{E}(\omega(X)g^{\prime}(X))\right]^{2},$$

(3.3)

where $\omega(x)$ is defined by $\sigma^{2}\omega(x)f(x)=\int\limits_{0}^{x}(\mu-z)f(z)\textrm{d}z$ (see Cacoullos and Papathanasiou, 1989). Hence, in (3.3) choosing $g(x)=-\log f_{{}_{t}X}(x)$ and ${}_{t}X$ as $X$, one obtains

$$\textrm{Var}(-\log f_{{}_{t}X}(_{t}X))\geq\tilde{\nu}_{X}^{2}(t)\left[\mathbb{E}\left(\omega_{t}(_{t}X)\frac{f_{{}_{t}X}^{\prime}(_{t}X)}{f_{{}_{t}X}(_{t}X)}\right)\right]^{2}.$$

(3.4)

By differentiating both sides of (3.2), one has

$$\omega(x)\frac{f_{{}_{T}X}^{\prime}(x)}{f_{{}_{T}X}(x)}=\frac{\tilde{\mu}_{X}(x)-x}{\tilde{\nu}_{X}^{2}(t)}-\omega_{t}^{\prime}(x),$$

and then, from (3.4),

$$V(_{t}X)=\textrm{Var}(-\log f_{{}_{t}X}(_{t}X))\geq\tilde{\nu}_{X}^{2}(t)\left[\mathbb{E}\left(\frac{\tilde{\mu}_{X}(t)-{{}_{t}X}}{\tilde{\nu}_{X}^{2}(t)}-\omega^{\prime}(_{t}X)\right)\right]^{2}=\tilde{\nu}_{X}^{2}(t)\left[\mathbb{E}(\omega_{t}^{\prime}(_{t}X))\right]^{2}.$$

$\Box$

4 PAST VARENTROPY AND PARALLEL SYSTEMS

When the past varentropy $V_{e}(_{t}X)$ of a random lifetime $X$ is available, then in some cases it is possible to easily compute the past varentropy of another lifetime $Y$ whose distribution is a transformation of that one of $X$. An example is given by the scale model: the family of random variables $\{X^{(a)}:a>0\}$ follows a Scale model if there exists a non-negative random variable $X$ with cumulative distribution function $F$ and density $f$ such that $X^{(a)}$ has distribution $F^{(a)}(t)=F(at)$ for all $t$, where $a>0$ is the parameter of the model. Some examples are the exponential, Weibull (with a fixed shape parameter) and Pareto (with a fixed shape parameter) distributions. In these cases, from Proposition 2.4 one immediately obtains that

$$V_{e}(_{t}X^{(a)})=V_{e}\left({}_{at}X\right),\quad\forall t.$$

A more interesting case is when the family of random variables $\{X^{(a)}:a>0\}$ follows a Proportional Reversed Hazard Rate model, i.e., if there exists a non-negative random variable $X$ with cumulative distribution function $F_{X}$ and density $f_{X}$ such that

$$F^{(a)}(t)=\mathbb{P}(X^{(a)}\leq t)=[F_{X}(t)]^{a},\quad f^{(a)}(t)=a[F_{X}(t)]^{(a-1)}f_{X}(t),\quad t\in\mathcal{S},$$

(4.1)

being $F^{(a)}$ and $f^{(a)}$ the cumulative distribution function and the density of $X^{(a)}$, respectively (see Gupta and Gupta (2007) for more details). We remark that the model takes the name from the fact that the reversed hazard rate functions of the random variables in the family are proportional to the reversed hazard rate function of $X$; in fact, letting $q^{(a)}$ be the reversed hazard rate of $X^{(a)}$,

$$q^{(a)}(t)=\frac{f^{(a)}(t)}{F^{(a)}(t)}=a\ \frac{f_{X}(t)}{F_{X}(t)}=a\ q_{X}(t)\quad\forall t\in\mathcal{S}.$$

Moreover, we note that the inverse cumulative reversed hazard rate function is expressed as

$$Q_{X^{(a)}}(t)=-\log F^{(a)}(t)=aQ_{X}(t).$$

The proportional reversed hazard rate model finds applications, for example, in analysis of parallel systems. In fact, if we have a system composed by $n$ units in parallel and characterized by i.i.d. lifetimes $X_{1},\dots,X_{n}$ with distribution $F_{X}(t)$, then the lifetime of the system is given by $X^{(n)}=\max\{X_{1},\dots,X_{n}\}$. Then, we have $F_{X^{(n)}}(t)=[F_{X}(t)]^{n}$, i.e., the system satisfies the proportional reversed hazard rate model (4.1) with $a=n$. The purpose of the next examples is to highlight the behavior of the past varentropy when it refers to the lifetime of a parallel system with i.i.d. components.

To this aim, let us first evaluate the past entropy of $X^{(a)}$ and the past varentropy of $X^{(a)}$ for an arbitrary $a>0$. One has

$$H_{e}\left({}_{t}X^{(a)}\right)=-Q_{X^{(a)}}(t)-\frac{1}{[F_{X}(t)]^{a}}\int\limits_{0}^{t}f^{(a)}(x)\log f^{(a)}(x)\textrm{d}x$$

$${}=-aQ_{X}(t)-\frac{1}{[F_{X}(t)]^{a}}\int\limits_{0}^{[F_{X}(t)]^{a}}\gamma(y;a)\textrm{d}y,$$

with the change of variable $y=[F_{X}(x)]^{a}$, and where $\gamma(y;a)=\log\left[ay^{1-1/a}f_{X}(F_{X}^{-1}(y^{1/a}))\right]$. Hence, we obtain the past varentropy of $X^{(a)}$ as

$$V_{e}\left({}_{t}X^{(a)}\right)=\frac{1}{[F_{X}(t)]^{a}}\int\limits_{0}^{t}f^{(a)}(x)(\log f^{(a)}(x))^{2}\textrm{d}x-\left[\frac{1}{[F_{X}(t)]^{a}}\int\limits_{0}^{t}f^{(a)}(x)\log f^{(a)}(x)\textrm{d}x\right]^{2}$$

$${}=\frac{1}{[F_{X}(t)]^{a}}\int\limits_{0}^{[F_{X}(t)]^{a}}[\gamma(y;a)]^{2}\textrm{d}y-\left[\frac{1}{[F_{X}(t)]^{a}}\int\limits_{0}^{[F_{X}(t)]^{a}}\gamma(y;a)\textrm{d}y\right]^{2}.$$

Let us now consider, as an example, the case where $X$ has a modified Pareto distribution with $F_{X}(t)=t/(1+t)$ and density $f_{X}(t)=1/(1+t)^{2}$, for $t\geq 0$. In this case, $\gamma(y;a)=\log\left[ay^{1-1/a}(1-y^{1/a})^{2}\right]$, so that

$$H_{e}\left({}_{t}X^{(a)}\right)=a\log\left(\frac{t}{1+t}\right)-\frac{1}{[t/(1+t)]^{a}}\int\limits_{0}^{[t/(1+t)]^{a}}\gamma(y;a)\textrm{d}y,$$

$$V_{e}\left({}_{t}X^{(a)}\right)=\frac{1}{[t/(1+t)]^{a}}\int\limits_{0}^{[t/(1+t)]^{a}}[\gamma(y;a)]^{2}\textrm{d}y-\left[\frac{1}{[t/(1+t)]^{a}}\int\limits_{0}^{[t/(1+t)]^{a}}\gamma(y;a)\textrm{d}y\right]^{2}.$$

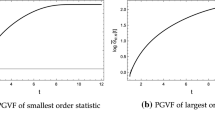
When $a$ is an integer, i.e., when $X^{(a)}$ represents the lifetime of a parallel system of a number $a$ of i.i.d. components, one obtains the past entropies and past varentropies shown in Fig. 5 (for different integer values of $a$). It is interesting to observe that both the past entropies and the past varentropies intersect each other for different values of $a$: for small values of the time $t$ one has the smaller past entropies and larger past varentropies when the number of components in parallel is large, and vice versa for large values of the time $t$. It means, for example, that in the long run (for large values of the inspection time $t$) the uncertainty of the information content of the past lifetime of a parallel system reduces as the number of components in the system increases (and vice versa for small $t$).

Fig. 5

Plots of past entropy and the past varentropy of modified Pareto PRHR model for $a=1$ (dashed line) and $a=2,3,4,5,6$ (blue, red, green, cyan, and black, respectively).

The same can be observed when $X$ has an exponential distribution with parameter $\lambda$. In this case, $\gamma(y;a)=\log\left[\lambda ay^{1-1/a}(1-y^{1/a})\right]$, so that

$$H_{e}\left({}_{t}X^{(a)}\right)=a\log\left(1-\textrm{e}^{-\lambda t}\right)-\frac{1}{[1-\textrm{e}^{-\lambda t}]^{a}}\int\limits_{0}^{[1-\textrm{e}^{-\lambda t}]^{a}}\gamma(y;a)\textrm{d}y,$$

$$V_{e}\left({}_{t}X^{(a)}\right)=\frac{1}{[1-\textrm{e}^{-\lambda t}]^{a}}\int\limits_{0}^{[1-\textrm{e}^{-\lambda t}]^{a}}[\gamma(y;a)]^{2}\textrm{d}y-\left[\frac{1}{[1-\textrm{e}^{-\lambda t}]^{a}}\int\limits_{0}^{[1-\textrm{e}^{-\lambda t}]^{a}}\gamma(y;a)\textrm{d}y\right]^{2}.$$

The plots of $H_{e}\left({}_{t}X^{(a)}\right)$ and $V_{e}\left({}_{t}X^{(a)}\right)$, for different integer values of $a$ and with $\lambda=2$, are shown in Fig. 6. As for the modified Pareto case, both the past entropies and the past varentropies intersect each other for different values of $a$, having a similar behavior.

Fig. 6

Plots of past entropy and the past varentropy of exponential PRHR model for $a=1$ (dashed line) and $a=2,3,4,5,6$ (blue, red, green, cyan, and black, respectively).

It must be observed that this behavior differs from what is shown in Example 4.1 in [11], where the residual varentropies for a proportional hazard model with an underlying generalized exponential distribution do not intersect for different values of the parameter $a$.

This behavior seems to be confirmed by other similar analysis we performed. But there exists a family for which the past varentropies do not intersect, which is the family discussed in Proposition 2.3, whose varentropies are constant. In fact, let $X_{\alpha}$ be a lifetime having support $\mathcal{S}=[0,1]$ and distribution $F_{\alpha}(x)=x^{\alpha}$, for $x\in\mathcal{S}$. Then, the corresponding parallel system with $n$ i.i.d. components has distribution $F_{n\alpha}(x)=x^{n\alpha}$ for $x\in\mathcal{S}$, which is still in the family of distribution having constant past varentropy. Thus, in particular, one has $V_{e}(_{t}X_{n\alpha})=(1-1/(n\alpha))^{2}$ for all $t\in\mathcal{S}$, and obviously these past varentropies do not intersect as $n$ varies in $\mathbb{N}^{+}$. This is another interesting property of such a family of distributions.

CONCLUSIONS

In this paper, we have introduced and studied the past varentropy. It is related to the past entropy, which is a measure of information about the past lifetimes. In particular, the past varentropy provides the variability of the information content of past lifetimes. We have given some examples of past varentropy and obtained conditions ensuring that it is monotone or constant. Moreover, its behavior under linear or monotonic transformations has been studied. A relationship between past varentropy and residual varentropy has been also provided, and upper and lower bounds for the past varentropy have been described. Finally, the behavior of the past varentropy under construction of parallel systems of i.i.d. components (and, more generally, under proportional reversed hazard rate models) has been discussed.