1 Introduction

Cutting vibration determines the stability of the machining system and affects the process level and workpiece quality. In order to alleviate the milling vibration and suppress the vibration in a robust way, these ways mainly include the changes in the spindle speed and tool parameters, which can interfere with the system delay and improve the process damping. The variable pitch tool, as a typical damping tool, has unequal tooth parameters, which affects the delay effect and the excitation force in the milling process, and plays a role in improving the cutting stability of the machining system. The concept of a tool with an irregular tooth angle was proposed for the first time by Slavicek in 1965 [1]. Opitz et al. [2, 3] analyzed the damping properties of the variable pitch tool, and a linear inhomogeneous differential dynamic model was developed to determine the chatter limit. Turner et al. [4, 5] discussed the damping mechanism of variable helical milling cutters; a cutting stability model was established. Jin et al. [6] presented a dynamic model of the milling system; process parameters were optimized to avoid chatter. The vibration mechanism of the variable pitch tool is analyzed to fully demonstrate that this type of cutter has superior vibration damping properties.

The cutting stability is a necessary problem for discussing the damping properties of the tool, the influencing factors of the vibration, and the optimization of system parameters, and then the solution method of the stability model affects the prediction accuracy. Altintas et al. [7,8,9,10] developed a prediction model of the regenerative chatter based on the frequency domain method to obtain the optimal pitch parameters, and a stability lobe diagram (SLD) of the variable pitch tool was obtained. Bari et al. [11] presented a new graphical-frequency method to determine the cutting stability of serrated tools with arbitrary geometry, and simulation time for the stability of the complex dynamic model with multiple delays was reduced. Insperger et al. [12,13,14] proposed the semi-discrete method (SDM) to solve the delay dynamics equation, and a higher-order discrete way was adopted to improve the prediction accuracy of the model. Sellmeier et al. [15] observed the generation mechanism of the stable island for the variable pitch tool under the condition of the low radial milling by combining the SDM. Based on the SDM, average time SDM, and finite element method (FEM), Sims et al. [16] verified a prediction model of the unequal tooth tool under different working conditions; the specific working conditions for different analysis methods were determined. Comak et al. [17] derived the optimal pitch parameters by the frequency domain method and the SDM. Guo et al. [18] adopted a semi-discretization method based on the improved Runge–Kutta to draw the stability lobe diagram of thin-walled parts. Ding et al. [19, 20] conducted a first- and second-order fully discrete methods (FDM) approached with a linear and Lagrangian interpolation. Insperger [21] compared the prediction accuracy of the two discrete methods followed by the theoretical delay differential equations of the FDM and the SDM under conditions of low-speed and high-speed cutting, respectively. Zhang et al. [22] studied the stability prediction taken into account for the consideration of the tool helix angle, the pitch angle, and the runout. Quo et al. [23] improved the FDM by taking a third-order Newtonian integral algorithm. The least squares method to approximate the system state term was more time-saving than the same-order integral method, and Ozoegwu et al. [24, 25] established the fourth-order FDM extended to a stability prediction model. Niu et al. [26, 27] presented the FDM with the Simpson and fourth-order Runge–Kutta algorithms, which were applied to the cutting stability prediction of the unequal tooth milling cutter considering the runout. Yan et al. [28] proposed a high-order FDM for analyzing the milling stability of the single-delay system and extended to the stability lobe diagrams of the multiple delays system. Totis et al. [29] devised a probabilistic method based on the Polynomial chaos and Kriging metamodels to increase the accuracy and the reliability of the chatter prediction. Wei et al. [30] investigated systematically the influence mechanism of multiple milling parameters on the milling stability, and three-dimensional SLDs under multiple milling parameters could be obtained. The prediction accuracy of the cutting stability model is mainly controlled by the solution method. At the same time, the convergence of the solution for the periodic differential equations is often accelerated by the analytical methods of differential equations. Liu et al. [31] studied the random vibration of structures with uncertain parameters and adopted the Gaussian integration method to calculate the response of the random structure, which effectively reduced the computational quantity. Srivastava et al. [32] proposed a Gaussian integration method to solve nonlinear equations, which leads to sixth-order convergence of the model solution. Liu et al. [33] proposed an efficient algorithm to calculate the dynamic response with first- and second-order derivatives based on the Gaussian integration method, and this method had a higher accuracy than the central difference method. A favorable analysis method can accurately and efficiently predict the cutting stability to present a theoretical basis for the stable cutting and high-quality machining.

The milling dynamic behavior affects the cutting stability of the system, and the mechanical property in the tool-workpiece contact is the major factor to affect the milling dynamic. The difference of cutting parameters under different cutting conditions leads to the size effect of the tool-workpiece contact, which affects the evolution of the mechanical behavior and the generation of the vibration excitation. The cutting force is the main source of the vibration excitation of the machining system during processing, and it affects the quality of the workpiece and the machining efficiency. The cutting force coefficient, as a major parameter of the cutting force model, is closely related to the machining size effect. For the identification of the cutting force coefficient, Ozturk et al. [34,35,36,37] proposed an algorithm for the calibration of milling force coefficients considering the lead angle, inclination angle, and helix angle for the free-form surface milled with the ball-end milling cutter. The immersion angle is considered; Larue et al. [38] discussed the prediction of the milling force of conical and ball nose end mills during the side milling. Wang et al. [39] presented a new calibration method of cutting force coefficients by the multiple linear regression of the average milling force. Campatelli et al. [40] conducted a cutting force model by analyzing the influence of different cutting parameters on the cutting force coefficient. Yao et al. [41] derived a bicubic polynomial function to describe the influence of the nonlinear cutting force coefficient and non-uniform chip size on the cutting force. Grossi et al. [42] investigated the cutting force coefficient under different spindle speeds followed by a genetic algorithm, and it was determined that the speed had a significant impact on the cutting force coefficient. Yu et al. [43] calibrated the linear cutting force coefficients based on the average cutting force model to acquire the corresponding stability lobe diagram.

The damping mechanism and the cutting stability of variable pitch tools have been gradually refined, but the multiple delays dynamic model with this type of tool still lacks consideration of the dynamic nonlinear problem of the machining system, and an in-depth study is required to solve the stability limit efficiently and accurately. This study discusses the regenerative dynamics of multiple delays, which is the main problem of the cutting stability with variable pitch tools, and the Gauss integral method is used to improve the full discrete method to obtain the state transition matrix of the multiple delays machining system. The cutting force coefficients are calibrated by the milling test of aluminum alloy milling with variable pitch tools, and a nonlinear expression of cutting force coefficients is developed. And then a method combining the improved FDM and nonlinear cutting force coefficients is used to predict the cutting stability; it has the effect of improving the prediction accuracy of machining system stability.

2 Mechanical model

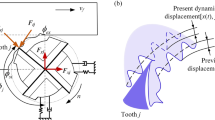
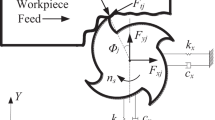
The variable pitch tools have different pitch parameters; the system delay and the thickness of each tooth are different. As the main excitation source in the machining process, the milling force resolves the vibration generation and the motion evolution of the system. The milling force is determined by the contact area between the tool and the workpiece. Figure 1 is a schematic diagram of mechanics with a variable pitch end mill (N = 4); the micro-element model of the milling force at the j-th tooth (Fig. 1(a)) is as follows:

$$dF_{j} = K_{c} h\left( {\phi_{j} \left( t \right)} \right)dz + K_{e} ds$$
(1)

where \(dF_{j} = \left[ {dF_{tj} ,dF_{rj} ,dF_{aj} } \right]\), dFtj, dFrj, and dFaj are the tangential, radial, and axial milling force elements, respectively; the stiffness of the machining system is high in the a-direction, dFaj is often ignored. \(K_{c} = \left[ {K_{tc} ,K_{rc} } \right]\), Ktc and Krc are the tangential and radial shear force coefficients. \(K_{e} = \left[ {K_{te} ,K_{re} } \right]\), Kte and Kre are the tangential and radial edge force coefficients. dz and ds are the depth of cut and the edge lengths. h(ϕj(t)) is the cutting thickness, ϕj(t) is the contact angle of the tool-workpiece, and the expression relationship is as follows:

$$\phi_{j} \left( t \right) = \left\{ \begin{gathered} wt - k_{\beta } z = \frac{n\pi t}{{30}} - k_{\beta } z \, j = 1 \hfill \\ wt - \sum\limits_{j = 2}^{N} {\varphi_{j} - k_{\beta } z \, j = 2,......N} \hfill \\ \end{gathered} \right. \,$$
(2)
Fig. 1
figure 1

Schematic diagram of down milling mechanics with a variable pitch end mill. a Micro-element distribution of the milling force. b Axial expansion of the cutting edge. c Dynamic cutting thickness. d Coordinate system of the milling force

Full size image

From Fig. 1(b), the progressive depth of cutting for the j-th helical edge \(z_{j} = \frac{R}{\tan \beta }\left( {\phi_{j} - \phi_{st} } \right)\), then the lag angle of the helical edge relative to the tool tip \(\theta = \frac{2z\tan \beta }{D} = k_{\beta } z\).

The cut-in and cut-out angles represent the effective cutting area (①②), which determine the participation of multiple teeth in the cutting; its expression in the down milling is as follows:

$$\begin{gathered} \varphi_{{{\text{st}}}} = {\text{arc}}\cos \left( {\frac{{a_{e} }}{R} - 1} \right) \hfill \\ \varphi_{{{\text{ex}}}} = \pi \hfill \\ \end{gathered}$$
(3)

Since the edge milling force is small, and it is not sensitive to the dynamic characteristics of the cutting process, the system rigidity is high in the axial; the edge milling force and the axial milling force are considered to be ignored in this study. So, the j-th tooth milling force is expressed as follows:

$$F_{j} \left( t \right) = \left\{ \begin{gathered} \int\limits_{{\phi_{j} \left( {t,0} \right)}}^{{\phi_{j} \left( {t,a_{p} } \right)}} {\frac{R}{\tan \beta }Kh_{j} \left( t \right)dz \, \phi_{{{\text{st}}}} < \phi_{j} < \phi_{{{\text{st}}}} + \theta } \hfill \\ \, Kh_{j} \left( t \right)a_{p} \, \phi_{{{\text{st}}}} + \theta < \phi_{j} < \phi_{{{\text{ex}}}} \hfill \\ \int\limits_{{\phi_{j} \left( {t,a_{p} } \right)}}^{{\phi_{j} \left( {t,0} \right)}} {\frac{R}{\tan \beta }Kh_{j} \left( t \right)dz \, \phi_{{{\text{ex}}}} < \phi_{j} < \phi_{{{\text{ex}}}} + \theta } \hfill \\ \end{gathered} \right.$$
(4)

where, \(K = K_{c}\) is coefficients matrix of the cutting force. \(h_{j} \left( t \right) = h\left( {\phi_{j} \left( t \right)} \right)\) is mainly composed of the static cutting thickness h0 determined by the feed per tooth and the dynamic cutting thickness Δh influenced by the vibration displacement (Fig. 1(c)), and the expression is the Eq. (5). The vibration mark on the workpiece surface is directly related to the regenerative effect of the machining system, as shown in Fig. 2; the phase between the vibration marks determines the dynamic cutting thickness, controls the occurrence of the regenerative chatter, and affects the evolution of the motion trajectory of the system.

$$h_{j} \left( t \right){ = }h_{0j} + \Delta h_{j} = f_{zj} \sin \left( {\phi_{j} \left( t \right)} \right) + \Delta x_{j} \sin \phi_{j} \left( t \right) + \Delta y_{j} \cos \phi_{j} \left( t \right) \,$$
(5)
Fig. 2
figure 2

Tool path. a Cutting thickness of the tool-workpiece contact. b Vibration ripple and phase

Full size image

According to the micro-element model of the milling force with the variable pitch tool, the coefficient matrix of the milling force K represents the milling force in the unit area of the edge line, and which is mainly affected by the material of the tool and the workpiece. As shown in Fig. 1(d), when \(a_{e} > R(1 - \cos \varphi )\), multi-tooth cutting of the helical edge occurs, then milling force model of the variable pitch tool in the x and y directions is as follows:

$$F\left( t \right) = \left[ \begin{gathered} F_{x} \left( t \right) \hfill \\ F_{y} \left( t \right) \hfill \\ \end{gathered} \right] = \sum\limits_{j = 1}^{N} {g\left( {\phi_{j} \left( t \right)} \right)\left[ \begin{gathered} \, \cos \phi_{j} \left( t \right) \, \sin \phi_{j} \left( t \right) \, \hfill \\ \, - {\text{sin}}\phi_{j} \left( t \right) \, \cos \phi_{j} \left( t \right) \hfill \\ \end{gathered} \right]} \left[ \begin{gathered} F_{tj} \left( t \right) \hfill \\ F_{rj} \left( t \right) \hfill \\ \end{gathered} \right]$$
(6)

where, \(g\left( {\phi_{j} \left( t \right)} \right)\) is the step response function, indicating whether the cutter tooth is involved in the cutting.

$$g\left( {\phi_{j} \left( z \right)} \right) = \left\{ \begin{gathered} 1 \, \varphi_{{{\text{st}}}} \le \phi \le \varphi_{{{\text{ex}}}} + \theta \hfill \\ 0{\text{ else}} \hfill \\ \end{gathered} \right.$$
(7)

Then the dynamic milling force model of the variable pitch tool is as follows:

$$F\left( t \right) = \sum\limits_{j = 1}^{N} {\frac{1}{2}a_{p} \left[ {K_{j} \left( t \right)} \right]} \left\{ {\Delta_{j} \left( t \right)} \right\}$$
(8)

where, \(\left\{ {\Delta_{j} \left( t \right)} \right\} = \left\{ \begin{gathered} \Delta x_{j} \left( t \right) \hfill \\ \Delta y_{j} \left( t \right) \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} x\left( t \right) - x\left( {t - \tau_{j} } \right) \hfill \\ y\left( t \right) - y\left( {t - \tau_{j} } \right) \hfill \\ \end{gathered} \right\}\), \(\tau_{j} = T\frac{{\varphi_{j} }}{2\pi }\) is the pitch delay, T is the milling period, a time-varying coefficient matrix of the cutting force \(\left[ {K_{j} \left( t \right)} \right] = \left[ \begin{gathered} a_{xx} \, a_{xy} \hfill \\ a_{yx} \, a_{yy} \hfill \\ \end{gathered} \right]\), \(\begin{gathered} a_{xx} = \left( {K_{t} - K_{t} \cos 2\phi_{j} + K_{r} \sin 2\phi_{j} } \right) \hfill \\ a_{xy} = \left( {K_{t} \sin 2\phi_{j} + K_{r} \cos 2\phi_{j} - K_{r} } \right) \hfill \\ a_{yx} = \left( { - K_{t} \sin 2\phi_{j} - K_{r} \cos 2\phi_{j} + K_{r} } \right) \hfill \\ a_{yy} = - \left( {K_{t} - K_{t} \cos 2\phi_{j} + K_{r} \sin 2\phi_{j} } \right) \hfill \\ \end{gathered}\).

Considering the relationship between the size effect and the cutting force coefficient, the milling force model with multiple delays of the variable pitch tool is developed by analyzing the relationship between regenerative effect and cutting thickness. The dynamic milling force is the main disturbance of the machining system, and the vibration system is represented by a dynamic model with multiple delays. The FDM is used to solve the regenerative dynamic model with multiple delays to deepen the regenerative chatter mechanism of the variable pitch tool.

The traditional dynamics model is mainly as follows:

$$M\ddot{u}\left( t \right) + C\dot{u}\left( t \right) + Ku\left( t \right) = \sum\limits_{j = 1}^{N} {F_{j} \left( t \right)}$$
(9)

where, M, C, and K are the effective mass, damping, and stiffness of the system, respectively, and u(t) is the motion response of the tool. When considering the multiple delays factor and the regenerative effect of the variable pitch tool, the mechanical model of a regenerative delay system is as follows:

$$M\ddot{u}\left( t \right) + C\dot{u}\left( t \right) + Ku\left( t \right) = \sum\limits_{j = 1}^{N} {\Delta F_{j} \left( t \right)} = \sum\limits_{j = 1}^{N} {B_{j} \left( t \right)\left[ {u\left( t \right) - u\left( {t - \tau_{j} } \right)} \right]}$$
(10)

where \(B_{j} \left( t \right) = \frac{1}{2}g\left( {\phi_{j} \left( t \right)} \right)a_{p} K_{t} \left[ {K_{j} \left( t \right)} \right]\), this model is a second-order multiple delays differential equation. When \(U\left( t \right) = \left[ {u\left( t \right) \, \dot{u}\left( t \right)} \right]^{T}\), the dynamic Eq. (10) is expressed as a first-order multiple delays state space by using the Cauchy transform.

$$\dot{U}\left( t \right) = AU\left( t \right) + \sum\limits_{j = 1}^{N} {B_{j} \left( t \right)\left[ {U\left( t \right) - U\left( {t - \tau_{j} } \right)} \right]}$$
(11)

where A is the time-invariant coefficient matrix of the system, \(B_{j} \left( t \right) = B_{j} \left( {t + T} \right)\), \(\tau_{j}\) is the delay of the system, \(\sum\limits_{j = 1}^{N} {\tau_{j} = T}\).

with

$$\begin{gathered} A\left( t \right) = \left[ \begin{gathered} \, 0 \, I \hfill \\ - M^{ - 1} K{ - }M^{ - 1} C \hfill \\ \end{gathered} \right] \hfill \\ B_{j} \left( t \right) = \left[ \begin{gathered} \, 0 \, 0 \, \hfill \\ - \sqrt {\frac{{M^{ - 1} }}{K}} B_{j} \left( t \right) \, 0 \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered}$$
(12)

The above dynamic differential equation is numerically solved, according to the multiple delays characteristics of the variable pitch tool; the time period T is equidistantly discretized into m time intervals \(\Delta t\) (\(T = m\Delta t\)), the delay \(\tau_{j} = k_{j} \Delta t\), \(m \approx \sum\limits_{j = 1}^{N} {k_{j} } = \sum\limits_{j = 1}^{N} {{\text{int}} \left( {\frac{{\tau_{j} + 0.5\Delta t}}{\Delta t}} \right)}\) (m and kj both are positive integers). For each time interval [ti, ti+1] = \(\left[ {i\Delta t, \, \left( {i + 1} \right)\Delta t} \right]\), taking \(U\left( {t_{i} } \right) = U_{i}\) as the initial condition, the dynamic response is expressed as follows:

$$U\left( t \right) = e^{{A\left( {t - t_{i} } \right)}} U\left( {t_{i} } \right) + \int_{{t_{i} }}^{t} {e^{{A\left( {t - \xi } \right)}} \sum\limits_{j = 1}^{N} {B_{j} \left( \xi \right)\left[ {U\left( \xi \right) - U\left( {\xi - \tau_{j} } \right)} \right]} } d\xi$$
(13)

The status item \(U\left( {t_{i + 1} } \right) = U_{i + 1}\) in the discrete point ti+1 is as follows:

$$U_{i + 1} = e^{A\Delta t} U_{i} + \int_{{t_{i} }}^{{t_{i + 1} }} {e^{{A\left( {t_{i + 1} - \xi } \right)}} } \sum\limits_{j = 1}^{N} {B_{j} \left( \xi \right)\left[ {U\left( \xi \right) - U\left( {\xi - \tau_{j} } \right)} \right]} d\xi$$
(14)

According to the Gauss–Legendre integral formula, the numerical approximation of the above equation is as follows:

$$U_{i + 1} = e^{A\Delta t} U_{i} + \sum\limits_{j = 1}^{N} {\frac{\Delta t}{2}\left\{ {e^{{A\left( {t_{i + 1} - t_{i}^{ * } } \right)}} B_{j} \left( {t_{i}^{ * } } \right)\left[ {U\left( {t_{i}^{ * } } \right) - U\left( {t_{i}^{ * } - \tau_{j} } \right)} \right] + e^{{A\left( {t_{i + 1} - t_{i + 1}^{ * } } \right)}} B_{j} \left( {t_{i + 1}^{ * } } \right)\left[ {U\left( {t_{i + 1}^{ * } } \right) - U\left( {t_{i + 1}^{ * } - \tau_{j} } \right)} \right]} \right\}}$$
(15)

where \(t_{i - 1}^{ * } = \frac{{t_{i} + t_{i + 1} }}{2} + \frac{\Delta t}{2}\left( { - \frac{1}{\sqrt 3 }} \right)\), \(t_{i}^{ * } = \frac{{t_{i} + t_{i + 1} }}{2} + \frac{\Delta t}{2}\left( {\frac{1}{\sqrt 3 }} \right)\).

The status item \(U\left( {t_{i}^{ * } } \right)\) and \(U\left( {t_{i + 1}^{ * } } \right)\) are linearly approximated

$$U\left( {t_{i}^{ * } } \right) = \left( {1 - \frac{{t_{i}^{ * } - t_{i} }}{\Delta t}} \right)U\left( {t_{i} } \right) + \frac{{t_{i}^{ * } - t_{i} }}{\Delta t}U\left( {t_{i + 1} } \right) = \frac{1}{2}\left( {1 + \frac{1}{\sqrt 3 }} \right)U\left( {t_{i} } \right) + \frac{1}{2}\left( {1 - \frac{1}{\sqrt 3 }} \right)U\left( {t_{i + 1} } \right)$$
(16)
$$U\left( {t_{i + 1}^{ * } } \right) = \left( {1 - \frac{{t_{i + 1}^{ * } - t_{i} }}{\Delta t}} \right)U\left( {t_{i} } \right) + \frac{{t_{i + 1}^{ * } - t_{i} }}{\Delta t}U\left( {t_{i + 1} } \right) = \frac{1}{2}\left( {1 - \frac{1}{\sqrt 3 }} \right)U\left( {t_{i} } \right) + \frac{1}{2}\left( {1 + \frac{1}{\sqrt 3 }} \right)U\left( {t_{i + 1} } \right)$$
(17)

The delay item \(U\left( {t_{i}^{ * } - \tau_{j} } \right)\) and \(U\left( {t_{i + 1}^{ * } - \tau_{j} } \right)\) are linearly approximated

$$U\left( {t_{i}^{ * } - \tau_{j} } \right) = \left( {1 - \frac{{t_{i}^{ * } - t_{i} }}{\Delta t}} \right)U\left( {t_{i} - \tau_{j} } \right) + \frac{{t_{i}^{ * } - t_{i} }}{\Delta t}U\left( {t_{i + 1} - \tau_{j} } \right) = \frac{1}{2}\left( {1 + \frac{1}{\sqrt 3 }} \right)U\left( {t_{i} - \tau_{j} } \right) + \frac{1}{2}\left( {1 - \frac{1}{\sqrt 3 }} \right)U\left( {t_{i + 1} - \tau_{j} } \right)$$
(18)
$$U\left( {t_{i + 1}^{ * } - \tau_{j} } \right) = \left( {1 - \frac{{t_{i + 1}^{ * } - t_{i} }}{\Delta t}} \right)U\left( {t_{i} - \tau_{j} } \right) + \frac{{t_{i + 1}^{ * } - t_{i} }}{\Delta t}U\left( {t_{i + 1} - \tau_{j} } \right) = \frac{1}{2}\left( {1 - \frac{1}{\sqrt 3 }} \right)U\left( {t_{i} - \tau_{j} } \right) + \frac{1}{2}\left( {1 + \frac{1}{\sqrt 3 }} \right)U\left( {t_{i + 1} - \tau_{j} } \right)$$
(19)

The above (16)–(19) are substituted (15)

$$U_{i + 1} = \left( {F_{0} + F_{i,1} } \right)U_{i} + F_{i,2} U_{i + 1} + \sum\limits_{j = 1}^{N} {F_{i,1} U_{{i - k_{j} }} } + \sum\limits_{j = 1}^{N} {F_{i,2} U_{{i + 1 - k_{j} }} }$$
(20)

with

$$F_{0} = e^{A\Delta t}$$
(21)
$$F_{i,1} = \frac{\Delta t}{2}\left( {E_{1} C_{1} B_{i} + E_{2} C_{2} B_{i + 1} } \right)$$
(22)
$$F_{i,2} = \frac{\Delta t}{2}\left( {E_{1} C_{2} B_{i} + E_{2} C_{1} B_{i + 1} } \right)$$
(23)

where, \(E_{1} = e^{{A\frac{\Delta t}{2}\left( {1 + \frac{1}{\sqrt 3 }} \right)}} {, }E_{2} = e^{{A\frac{\Delta t}{2}\left( {1 - \frac{1}{\sqrt 3 }} \right)}} {, }C_{1} = \frac{1}{2}\left( {1 + \frac{1}{\sqrt 3 }} \right){, }C_{2} = \frac{1}{2}\left( {1 - \frac{1}{\sqrt 3 }} \right){, }B_{i} = B\left( {t_{i}^{ * } } \right){, }B_{i + 1} = B\left( {t_{i + 1}^{ * } } \right)\).

If \(\left[ {I - F_{i,2} } \right]\) is the non-singular, the Eq. (23) is converted to a display expression

$$U_{i + 1} = \left[ {I - F_{i,2} } \right]^{ - 1} \left( {F_{0} + F_{i,1} } \right)U_{i} + \sum\limits_{j = 1}^{N} {\left[ {I - F_{i,2} } \right]^{ - 1} F_{i,1} U_{{i - k_{j} }} } + \sum\limits_{j = 1}^{N} {\left[ {I - F_{i,2} } \right]^{ - 1} F_{i,2} U_{{i + 1 - k_{j} }} }$$
(24)

If \(\left[ {I - F_{i,2} } \right]\) is the singular, then the generalized inverse of the matrix can be used instead of its inverse.

The processing system with the variable pitch tool constructs a discrete dynamic map on a single period in the case of multiple delays, and each discrete point is associated by mapping in the milling state space; the Eq. (24) is as follows:

$$V_{i + 1} = D_{i} V_{i}$$
(25)

where Vj is the state vector with

$$V_{i} = \left[ {U_{i} ,U_{i - 1} ,...U_{{i - k_{1} }} ,...U_{{i - k_{2} }} ,...U_{{i - k_{\max } }} } \right]$$
(26)

where kmax = max(kj), Zi is a discrete point, the conversion matrix between i and i + 1 is as follows:

$$\left[ {D_{i} } \right] = \left[ \begin{gathered} \left[ {I - F_{i,2} } \right]^{ - 1} \left( {F_{0} + F_{i,1} } \right){ 0 } \cdots { 0 0} \hfill \\ \, I{ 0 } \cdots { 0 0} \hfill \\ { 0 }I \, \cdots { 0 0} \hfill \\ \, \vdots \, \vdots \, \ddots \, \vdots \, \vdots \hfill \\ \, 0{ 0 } \cdots \, I{ 0} \hfill \\ \end{gathered} \right] + \sum\limits_{j = 1}^{N} {\left[ \begin{gathered} 0 \, \cdots \, \left[ {I - F_{i,2} } \right]^{ - 1} F_{i,1} \, \left[ {I - F_{i,2} } \right]^{ - 1} F_{i,2} \, \cdots { 0} \hfill \\ {0 } \cdots { 0 0 } \cdots { 0} \hfill \\ \, \vdots \, \vdots \, \ddots \, \vdots \, \vdots \, \vdots \hfill \\ {0 } \cdots { 0 0 } \cdots { 0} \hfill \\ {0 } \cdots { 0 0 } \cdots { 0} \hfill \\ \end{gathered} \right]}$$
(27)

where the positions of \(M_{j,i,a}\) and \(M_{j,i,b}\) are determined by the variable kj. According to Eqs. (26) and (27), if the solutions of k consecutive time intervals are coupled within a period T, then the state transition matrix Ω of the system in a single period is as follows:

$$V_{m} = D_{m - 1} D_{m - 2} \cdots D_{1} D_{0} V_{0} = \Omega V_{0}$$
(28)

The dynamic characteristics of the milling system are determined mainly by the eigenvalues of the state matrix Ω. If the modulus of all eigenvalues of the matrix Ω is less than 1 (\(\max \left( {\left| {eig\left( \Omega \right)} \right|} \right) < 1\)), the system tends to be asymptotically stable via Floquet theory.

3 Nonlinear cutting force coefficients

The mechanical model of the machine system with the variable pitch tool is solved by using the FDM; the state space of the system is mapped under multiple delays to obtain the boundary conditions for the stable cutting. According to the milling experiment, the model parameters are calibrated to verify the performance of the theoretical model. The cutting force coefficients are mainly determined by the materials and the tool-workpiece contact. The size effect of the tool-workpiece contact motivates the mechanical behavior of the milling, which makes the cutting process shows multiscale and nonlinear characteristics. The size effect of the tool-workpiece contact is mainly determined by the cutting parameters and the geometry angles of the tool. The nonlinear relationship between cutting force coefficients and cutting parameters is obtained by the coefficient calibration method.

Figure 3 shows the milling field experiment of Al7075-T651 materials with the variable pitch tool; experimental planning adopts a single factor methodology which refers to cutting parameters as in Table 1. The cutting force coefficients of the mechanical model are calibrated by analyzing the milling force under different cutting parameters; a model of the cutting force coefficients (Eq. (29)) is developed based on the nonlinear fitting. Figure 4 shows the comparison between the experimental data and the theoretical model under different cutting parameters, which reflects the effect of cutting parameters on the cutting force coefficients, and it verifies the accuracy of the theoretical model of the cutting force coefficients. At the same time, for the multi-factor variance analysis of the cutting force coefficients and cutting parameters, the variance analysis of the experimental results is carried out by using Matlab software. According to the results of variance analysis, the F ratio directly reflects the significant degree of the influence of the experimental factors on the experimental indexes, which are 2.37, 4.02, 4.86, and 2.21, respectively, that is, Ffr > Fap > Fae > Fn. Figure 5 is the comparison between the experimental data and the numerical simulation of cutting force coefficients and milling forces. It is determined that the prediction accuracy of the milling force model can reach more than 90%, indicating that the cutting force coefficient model has better precision.

$$\begin{gathered} K_{t} = 2.892a_{e}^{0.202} a_{p}^{0.301} f_{r}^{ - 0.318} n^{ - 0.261} \times 10^{3} \hfill \\ K_{r} = 2.934a_{e}^{0.214} a_{p}^{0.342} f_{r}^{0.383} n^{ - 0.232} \times 10^{3} \hfill \\ \end{gathered}$$
(29)
Fig. 3
figure 3

Field milling experiment with the variable pitch tool

Full size image
Table 1 Experimental cutting parameters
Full size table
Fig. 4
figure 4

Relationship between cutting force coefficients and cutting parameters. (a) Relationship curve between ae and K. (b) Relationship curve between ap and K. (c) Relationship curve between fr and K. (d) Relationship curve between n and K

Full size image
Fig. 5
figure 5

Comparison of experimental data and model simulation for the cutting force. a The cutting force in the x direction. b The cutting force in the y direction

Full size image

Figure 6 (a) shows the modal detection of the experiment system. The system response signal is obtained by giving a certain excitation to the tool, as shown in Fig. 6 (b). The modal parameters of the machining system are obtained by using the identification method of the modal parameter (Table 2)

Fig. 6
figure 6

Modal experiment of the machining system. a Experimental site. b Response signal

Full size image
Table 2 Modal parameters of the machining system
Full size table

4 Cutting stability

The multiple delays factor of variable pitch tools and the size effect under different cutting parameters have an important impact on the dynamics of the machining system. A cutting force coefficient model is proposed by taking into account for the consideration of the nonlinear mechanical behavior of the size effect in the tool-workpiece contact area. The mechanical model of the regenerative chatter determines the mapping relationship of the state space of the machining system with multiple delays, and the stability boundary is determined by using proposed method (Gauss FDM) which combined the FDM and the Gauss integration.

Considering the multiple delays and the size effect, the stability boundary of the machining system is calculated by using the Gauss FDM to obtain the limiting cutting depth of the variable pitch tool. In order to fully illustrate the effectiveness of the analysis method proposed in this study, the cutting parameters n = 5000 rpm and radial immersion aD = ae/D = 25% are selected to compare the eigenvalue convergence of the processing system under different discrete parameters (Fig. 7(a)). The result of the comparative analysis shows that the proposed method has better convergence by taking the linear FDM in the reference [19] as the convergence criterion of numerical analysis. Figure 7 (b) shows the comparison of the SLD under different discrete parameters; it is determined that the discrete parameters used in the numerical simulation of the SLD are 100 × 100 sized grid in this study.

Fig. 7
figure 7

Convergence of the eigenvalues. a Convergence rate of the critical eigenvalue for different discretization methods. b Stability boundary for different discrete parameters

Full size image

The boundary conditions for the stable cutting under different cutting parameters are obtained based on the above model dynamic parameters and simulation parameters. The direction matrix axx of the cutting force coefficient is evaluated in different radial immersions based on the nonlinear model of the cutting force coefficient (Fig. 8), and Fig. 9 shows the three-dimensional SLD (n-ap-aD). The process system is high intermittency with decreasing aD; the cutting stability region becomes larger. Considering the nonlinear relationship between model parameters and cutting parameters, the cutting depth has different changes in the corresponding speed region. When aD is decreased from 100 to 10%, the limiting cutting depth is approximately increased by 2–3 times within the spindle speed of 2000–10000 rpm.

Fig. 8
figure 8

Evaluation of the cutting force coefficient matrix

Full size image
Fig. 9
figure 9

Stability lobe diagram. a Three-dimensional SLD. b Two-dimensional SLD with different aD

Full size image

When aD = 25%, based on the milling experiments of the aluminum alloy (Fig. 10), the stability regions of the variable pitch tool with different types of cutting force coefficients are compared to verify the prediction accuracy of the theoretical model. As shown in Fig. 10(a), the nonlinear cutting force coefficient can improve the prediction accuracy of the cutting stability of the mechanical model. Based on the relationship between the eigenvalues of the system and cutting parameters in Fig. 10(b), it is obvious that the changing of eigenvalues of the system is more significant in the low-speed region (2000–4000 rpm). It also shows that the stable regions of different types of cutting force coefficients are more obviously in the low-speed region. Therefore, the dynamic characteristics of the machining system have a more sensitive dependence on the model parameters under low-speed cutting conditions.

Fig. 10
figure 10

Milling stability lobe diagram. a Comparison between SLD with constant, nonlinear, and linear [43] cutting force coefficients. b Distribution of system eigenvalues

Full size image

5 Conclusion

In this paper, combining the multiple delays and the regenerative effect, a dynamic cutting force and a dynamics mode of variable pitch tools are developed in the machining process. The state item is approximated by using the Gauss integral method, and linear interpolation is utilized to approximate the periodic and the delay terms. Then, the state transition matrix of the discrete system in the multiple delays period is obtained to analyze the milling chatter, and the cutting stability of the machining system is predicted based on the Floquet theory. According to the experimental data of the cutting force about aluminum alloy milling with the variable pitch tool, the influence law of cutting parameters on cutting force coefficients is conducted to acquire a nonlinear model of cutting force coefficients. The convergence speed of the proposed method is faster by comparing the convergence of the Gauss FDM and the traditional linear FDM on the eigenvalues of the state matrix of the dynamic model, which indicated that the proposed method has higher prediction efficiency than others. A three-dimensional SLD of the variable pitch tool is drawn to determine the boundary conditions of various cutting parameters for stable cutting, and the limiting cutting depth of the tool increases by 2–3 times when the radial invasion aD changes from 100 to 10%. The stability regions of three different types of cutting force coefficients are predicted by using Gauss FMD method. Combining with the milling experiment of the variable pitch tool, it is verified that the nonlinear cutting force coefficient can be better for improving the accuracy in the stability prediction than linear and constant cutting force coefficients. It was also found that the changing of dynamic model parameters is more sensitive on the low speed range of the spindle speed (2000–4000 rpm), and the vibration reduction performance of variable pitch tools is more significant under low speed cutting conditions.