1 Introduction

The tool in the milling process is continuously subjected to the excitation force, and the displacement under the forced vibration is relatively small. When the load frequency is close to the natural frequency of the system, the delay feedback of the vibration displacement causes the regenerative dynamic instability under the influence of state parameters in the internal mechanism of the system. The system can continuously obtain external energy, which will aggravate the vibration displacement in a short time and make the regenerative flutter stronger. The regenerative chatter leads to an unstable cutting of the tool and the occurrence of sticking or run-out of the tool, which reduces the service life of the tool and the machining accuracy of the workpiece, and seriously affects the performance of the tool.

For the chatter and stability problems in the machining, the chatter theory was proposed by Tobias et al. [1], and then Tlusty et al. [2] developed an analysis method for the stability of the self-excited vibration. The effects of tool-workpiece engagement and tool axis orientation are included in the dynamic cutting model [3, 4]. A method to avoid the vibration of milling flexible thin plates by the linear stability model was proposed in [5]. Considering the coupling effect of the spindle-tool system and workpiece system, Li et al. [6] developed the milling force based on the regeneration effect and constructed a 3D SLD along the toolpath. Ren et al. [7] proposed an adaptive Hankel low-rank decomposition technique for online milling chatter identification by considering the basic features of the chatter, which improves the efficiency and sensitivity of the chatter identification system. Since the process results in the machining are directly determined by the state parameters, these are also indirectly controlled by the process parameters. Therefore, the study of the chatter mechanism is important for determining the stability lobe diagram (SLD) by analyzing the regenerative chatter, where reasonable process parameters are selected for avoiding the chatter.

The chatter stability is analyzed for suppressing the vibration, which mainly discusses the mechanism of the unstable phase by interfering the regeneration. The cutting delay of changes is an effective way to interfere with the regeneration and suppress chatter, which mainly includes the changes in the spindle speed or tool structure. Liao et al. [8] proposed an online control method for suppressing the regenerative chatter by adjusting the spindle speed. Soliman et al. [9] designed a controller to modulate online the amplitude and frequency of the spindle speed for suppressing the milling chatter. Slavicek [10] proposed the concept of the irregular tooth pitch. The parameters of the tool structure are adjusted for suppressing the regeneration in a robust way, which is similar to the chatter frequency of changes in the spindle. Opitz et al. [11] and Olgac et al. [12] presented a nonhomogeneous linear differential equation model of the unequal pitch milling cutter for determining the chatter limit. Turner et al. [13] and Sims et al. [14] developed a cutting stability model of the variable helix milling cutter for predicting the chatter. Sellmeier et al. [15] explored the multiple delays of the variable pitch for analyzing the generation mechanism of stable islands in the low radial milling. Huang [16] and Jin [17] optimized the parameters of the milling process by analyzing the machining stability of variable pitch end mills. Wei et al. [18] systematically analyzed the influence mechanism of various cutting parameters on the milling stability and obtained the three-dimensional (3D) SLD under the multi-milling parameters. Shi et al. [19] proposed a method for calculating micro-milling SLD by considering the velocity effect to more accurately predict the chatter stability of the aerostatic spindle micro-milling,

The methods for predicting the chatter stability mainly include the frequency domain and time domain methods. Altintas et al. [20, 21] developed a prediction model of the regenerative chatter based on the frequency domain method. Turner et al. [22] analyzed the stability of different types of unequal tooth milling cutters by using the above method. Jin et al. [23] analyzed the stability of variable helix end mills by the frequency domain method and presented a stability prediction model. Otto et al. [24] considered the nonlinear milling force behavior of unequal tooth milling cutter and used the multi-frequency method to predict the cutting stability under low speed conditions. Song et al. [25] drew the cutting stability lobe diagram of end mills with equal teeth, variable helix, and variable pitch, respectively, and measured the vibration displacement of different tools to verify the vibration reduction effect of the tools. Huang et al. [26] used Fourier transform to analyze the frequency spectrum characteristics of the variable pitch end mills and showed that the amplitude of milling force in frequency domain is more dispersed and smaller due to the unequal pitch. Nie et al. [27] conducted frequency domain analysis on the milling force of three pitch distribution forms and optimized the pitch of the tool by minimizing the spectral amplitude. Insperger et al. [28, 29] analyzed dynamic delayed differential equations and developed a stability model by using the semi-discrete method. A high-order-discrete method is proposed by Insperger [30] to modify the dynamic stability model for further improving its prediction accuracy. Sims et al. [14] analyzed the prediction model of the chatter stability of unequal tooth milling cutters based on different methods and found that the corresponding analysis methods are suitable for specific cutting conditions. Ding et al. [31] proposed a full-discrete method for improving the prediction accuracy. Insperger [32] compared the characteristics of the full-discrete and the semi-discrete methods in cases of the low-speed and high-speed cutting. Niu et al. [33,34,35] presented the full-discretization method with the Simpson and fourth-order Runge–Kutta algorithms, which was applied to the cutting stability prediction of the unequal tooth milling cutter by considering the runout.

At present, the mechanism and the suppression and prediction methods of the milling chatter have been studied under different milling conditions. However, the relevant research only took the variable pitch end mills as the research object to reveal its damping mechanism and the cutting stability prediction, and does not specifically discuss the effect of the change in the pitch parameters on the cutting stability and the optimization of the pitch, among which the damping effect of different types of the pitch distribution is not involved. There is still lack of in-depth analysis on how end mills can make full use of the vibration reduction properties by adjusting the pitch parameters. In this paper, the effect of time delay variables on the cutting stability is analyzed, and the relationship between the pitch parameters and the limiting cutting depth is determined to optimize tool structure. Due to the unequal pitch of the milling cutter, the dynamic model of the system has multiple delays. The state parameters have impacts on the chatter mechanism and stability prediction. In this paper, a dynamic model of the variable pitch end mill is proposed, the influence of the multiple delay factors on the chatter stability is analyzed, and the pitch parameters are optimized so that the tool can give full play to the effect on the improvement of the chatter stability.

2 System dynamic model with multiple delays

The pitch periods of the variable pitch end mill are different, and the cutting thickness of each tooth involute changes continuously, which make the cutting load to fluctuate alternately. The dynamic system produces multiple delay factors, due to which the regeneration effect of the chatter is modulated, and the stability of the milling cutter is indirectly affected. Therefore, the dynamic behavior of multiple delays of variable pitch end mills is a vital factor for determining the chatter stability of the system.

2.1 Nonlinear milling behavior

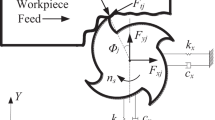
Due to the high stiffness of the machine tool along the z-axis, the milling forces are modeled mainly along the x and y directions (Fig. 1). Considering the regenerative chatter mechanism, the milling forces of the end mill are determined as follows [3].

$$F\left(t\right)=\begin{bmatrix}F_x\left(\text{t}\right)\\F_y\left(\text{t}\right)\end{bmatrix}=\sum_{j=1}^Ng\left(\phi_j\left(t\right)\right)\begin{bmatrix}\begin{array}{l}-sin\phi_j\left(t\right)-cos\phi_j\left(t\right)\\-cos\phi_j\left(t\right)\;sin\phi_j\left(t\right)\end{array}\\\end{bmatrix}\begin{bmatrix}F_{tj}\left(t\right)\\F_{rj}\left(t\right)\end{bmatrix}$$
(1)

where \({F}_{x}\left({\text{t}}\right)\) and \({F}_{y}\left({\text{t}}\right)\) are the milling forces in the x and y directions, respectively; \({\phi }_{st}\) is the cut-in angle; \({\phi }_{ex}\) is the cut-out angle; \({\phi }_{j}\left(t\right)\) is the contact angle of the j-th tooth; \(g\left({\phi }_{j}\left(t\right)\right)\) is the step response function that indicates whether the tooth is involved in the cutting; and \({F}_{tj}\left({\text{t}}\right)\) and \({F}_{rj}\left(t\right)\) are the tangential and radial milling forces of the j-th tooth, respectively.

Fig. 1
figure 1

Dynamic model of end mill with 2-DOF system. a Cutting force. b Dynamic displacement of regenerative chatter

Full size image

The expansion of the variable pitch end mill is shown in Fig. 2, where N (= 4) is the number of teeth in the end mill, R is the radius, β is the helix angle, φj (j = 1, 2, 3, 4) is the pitch angle, ap is the milling depth, ae is the milling width, vf is the milling feed, and n is the spindle speed, When \({a}_{e}>R(1-\mathrm{cos}\varphi )\), the end mill engages multiple teeth in the cutting, which mainly includes complete cutting and partial cutting of the cutting edge. When \({a}_{p}>\left({\phi }_{ex}-{\phi }_{st}\right)R\mathrm{arctan}\beta\) in Fig. 2b, ABCD occurs, otherwise AʹBʹCʹDʹ. By considering the effect of the helix angle of the variable pitch end mill, three situations can be obtained in the single-tooth cutting: partial cut-in, full cut-in, and partial cut-out. The contact angle of the helical edge determines the contact area between the edge line and the workpiece. The corresponding relationship is as follows.

$$F_j\left(t\right)=\left\{\begin{array}{c}\int\limits_{\phi_j\left(t,0\right)}^{\phi_j\left(t,a_p\right)}\frac R{\tan\beta}KH_j\left(t\right)dz\;\phi_{st}<\phi_j<\phi_{st}+\Delta\phi\\KH_j\left(t\right)a_p\;\phi_{st}+\Delta\phi<\phi_j<\phi_{ex}\\\int\limits_{\phi_j\left(t,a_p\right)}^{\phi_j\left(t,0\right)}\frac R{\tan\beta}KH_j\left(t\right)dz\;\phi_{ex}<\phi_j<\phi_{ex}+\Delta\phi\end{array}\right.$$
(2)

where \({F}_{j}\left(t\right)=\left[\begin{array}{c}{F}_{tj}\left(t\right)\\ {F}_{rj}\left(t\right)\end{array}\right]\) and \(K=\left[\begin{array}{c}{K}_{t}\\ {K}_{r}\end{array}\right]\) are the tangential and radial coefficients of cutting forces, respectively; \({H}_{j}\left(t\right)\) is the cutting thickness of the j-th tooth;\({H}_{j}\left(t\right)={h}_{j}\left(t\right)+\Delta {h}_{j}\left(t\right)={f}_{zj}\mathrm{sin}{\phi }_{j}+\Delta {h}_{j}\left(t\right)\); \({h}_{j}\left(t\right)\) is the static cutting thickness; and \(\Delta {h}_{j}\left(t\right)\) is the dynamic cutting thickness. z is the progressive depth of cutting, and \(\Delta \phi =\frac{{a}_{p}\mathrm{tan}\beta }{R}={k}_{\beta }z\) is the lag angle of the spiral edge relative to the tool tip. So the relationship between the step response and contact angle is

$$g\left(\phi_j\left(t\right)\right)=\left\{\begin{array}{l}1\;\phi_{st}<\phi_j<\phi_{ex}+\Delta\phi\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{else}\end{array}\right.$$
(3)
$$\phi_j\left(t,z\right)=\left\{\begin{array}{l}wt-k_\beta z\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,j=1\\wt-\sum\limits_{j=2}^N\varphi_j-k_\beta z\;j=2,...N\end{array}\right.$$
(4)

where w is the angular velocity of the milling cutter. Considering the nonlinear behavior of the exciting force, the system chatter is mainly caused by the dynamic cutting force, which is directly related to the dynamic cutting thickness. The relationship is as follows:

$$\Delta {h}_{j}\left(t\right)=\left[\Delta {x}_{j}\mathrm{sin}{\phi }_{j}\left(t\right)+\Delta {y}_{j}\mathrm{cos}{\phi }_{j}\left(t\right)\right]$$
(5)

where Δx and Δy are vibration displacements in the x and y directions, respectively. Therefore, the dynamic milling force model of the variable pitch end mill is

$$\left[\Delta F\left(t\right)\right]=\sum_{j=1}^{N}\frac{1}{2}g\left({\phi }_{j}\left(t\right)\right){a}_{p}{K}_{t}\left[{A}_{j}\left(t\right)\right]\left[\Delta {U}_{j}\left(t\right)\right]$$
(6)

where \(\left[\Delta {U}_{j}\left(t\right)\right]=\left[\begin{array}{c}\Delta {x}_{j}\left(t\right)\\ \Delta {y}_{j}\left(t\right)\end{array}\right]=\left[\begin{array}{c}x\left(t-{\tau }_{j}\right)-x\left(t\right)\\ y\left(t-{\tau }_{j}\right)-y\left(t\right)\end{array}\right]\), and \({\tau }_{j}={T}_{j}=\frac{{\varphi }_{pj}}{2\pi n}\) is the pitch delay of the j-th tooth. The time-varying coefficient matrix of the cutting force is \(\left[{A}_{j}\left(t\right)\right]=\left[\begin{array}{c}{a}_{xx}{a}_{xy}\\ {a}_{yx}{a}_{yy}\end{array}\right]\)where

Fig. 2
figure 2

Cutting process of variable pitch end mill. a Contact area of the tool-workpiece. b Schematic diagram of the spiral edge

Full size image
$$\begin{array}{c}{a}_{xx}=\left(1-\mathrm{cos}\left(2\phi \right)+{k}_{r}\mathrm{sin}\left(2\phi \right)\right)\\ {a}_{xy}=\left(\mathrm{sin}\left(2\phi \right)+{k}_{r}\mathrm{cos}\left(2\phi \right)-{k}_{r}\right)\\ {a}_{yx}=\left(-\mathrm{sin}\left(2\phi \right)-{k}_{r}\mathrm{cos}\left(2\phi \right)+{k}_{r}\right)\\ {a}_{yy}=-\left(1-\mathrm{cos}\left(2\phi \right)+{k}_{r}\mathrm{sin}\left(2\phi \right)\right)\end{array}$$

The period of motion of the variable pitch end mill is determined by the pitch angle and the spindle speed. The dynamic milling force is controlled by the dynamic parameters of the system.

2.2 Frequency domain method (FDM)

The coefficient matrix can be expanded as the Fourier series.

$$\begin{array}{c}\left[{A}_{j}\left(t\right)\right]=\sum\limits_{r=-\infty }^{+\infty }\left[{A}_{rj}\right]{e}^{irwt}\\ \left[{A}_{rj}\right]=\frac{1}{T}{\int }_{0}^{T}\left[{A}_{j}\left(t\right)\right]{e}^{-irwt}dt\end{array}$$
(7)

The harmonic order r affects the prediction accuracy and calculation efficiency of the model. When the radial invasion (ae/D) is large, the zero-order frequency domain method meets the basic prediction accuracy. When r = 0, the zero-order coefficient matrix A0 is

$$\left[{A}_{0}\right]=\frac{1}{2\pi }{\int }_{{\phi }_{st}}^{{\phi }_{ex}}\left[{A}_{j}\left(\phi \right)\right]d\phi =\frac{1}{2\pi }\left[\begin{array}{c}{\alpha }_{xx}{\alpha }_{xy}\\ {\alpha }_{yx}{\alpha }_{yy}\end{array}\right]$$
(8)

where

$$\begin{array}{c}{\alpha }_{xx}=\frac{1}{2}{\left(2\phi -\mathrm{sin}\left(2\phi \right)-{k}_{r}\mathrm{cos}\left(2\phi \right)\right)}_{{\phi }_{st}}^{{\phi }_{ex}}\\ {\alpha }_{xy}=\frac{1}{2}{\left(-\mathrm{cos}\left(2\phi \right)+{k}_{r}\mathrm{sin}\left(2\phi \right)-2{k}_{r}\phi \right)}_{{\phi }_{st}}^{{\phi }_{ex}}\\ {\alpha }_{yx}=\frac{1}{2}{\left(\mathrm{cos}\left(2\phi \right)-{k}_{r}\mathrm{sin}\left(2\phi \right)+2{k}_{r}\phi \right)}_{{\phi }_{st}}^{{\phi }_{ex}}\\ {\alpha }_{yy}=\frac{1}{2}{\left(-2\phi +\mathrm{sin}\left(2\phi \right)+{k}_{r}\mathrm{cos}\left(2\phi \right)\right)}_{{\phi }_{st}}^{{\phi }_{ex}}\end{array}$$

Finally, the dynamic model of the multiple delays for the variable pitch end mill is

$$\left[\Delta F\left(t\right)\right]=\frac{1}{2}{a}_{p}{K}_{t}\left[{A}_{0}\right]\sum_{j=1}^{N}\left[\Delta {U}_{j}\left(t\right)\right]$$
(9)

When the chatter occurs at the natural frequency wc, the vibration in the frequency domain can be obtained by using harmonic function as follows:

$$\begin{array}{c}\left[r\left(i{w}_{c}t\right)\right]=\left[G\left(i{w}_{c}\right)\right]\left[F\right]{e}^{i{w}_{c}t}\\ \left[r\left(i{w}_{c}\left(t-{\tau }_{j}\right)\right)\right]={e}^{-i{w}_{c}{T}_{j}}\left[r\left(t\right)\right]\end{array}$$
(10)

where \(r\left(i{w}_{c}t\right)\) and \(r\left(i{w}_{c}\left(t-{\tau }_{j}\right)\right)\) are the harmonic functions of the j-th and (j-1)-th teeth, respectively. The frequency response function of the system is

$$G\left(iw\right)=\left[\begin{array}{c}{G}_{xx}\left(iw\right){G}_{xy}\left(iw\right)\\ {G}_{yx}\left(iw\right){G}_{yy}\left(iw\right)\end{array}\right]$$
(11)

Then, the regenerative harmony on the occurrence of the chatter can be expressed as follows:

$$\begin{array}{c}\left[\Delta {U}_{j}\left(i{w}_{c}t\right)\right]=\left[U\left(i{w}_{c}t\right)-U\left(i{w}_{c}\left(t-{\tau }_{j}\right)\right)\right]\\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \text{=} \, \left(1-{e}^{-i{w}_{c}{\tau }_{j}}\right)\left[G\left(i{w}_{c}\right)\right]\left[F\right]{e}^{i{w}_{c}t}\end{array}$$
(12)

The regeneration of the chatter is substituted into the dynamic model given by Eq. (9).

$$\left[\Delta F\left(t\right)\right]{e}^{i{w}_{c}t}=\frac{1}{2}{k}_{r}{a}_{p}\sum_{j=1}^{N}\left[{A}_{0}\right]\left(1-{e}^{-i{w}_{c}{\tau }_{j}}\right)\left[G\left(i{w}_{c}\right)\right]\left[\Delta F\left(t\right)\right]{e}^{i{w}_{c}t}$$
(13)

The condition for solving Eq. (13) is that the determinant of the characteristic equation is zero, that is:

$$\mathrm{det}\left[\left[I\right]+\lambda \left[{G}_{0}\left(i{w}_{c}\right)\right]\right]=0$$
(14)

where \(\lambda\) is the eigenvalue and \({G}_{0}\left(i{w}_{c}\right)\) is the zeroth-order direction transfer matrix in the cutting process.

$${G}_{0}\left(i{w}_{c}\right)=\left[\begin{array}{c}{\alpha }_{xx}{G}_{xx}+{\alpha }_{xy}{G}_{yx}{\alpha }_{xx}{G}_{xy}+{\alpha }_{xy}{G}_{yy}\\ {\alpha }_{yx}{G}_{xx}+{\alpha }_{yy}{G}_{yx}{\alpha }_{yx}{G}_{xy}+{\alpha }_{yy}{G}_{yy}\end{array}\right]$$
(15)
$$\lambda =-\frac{1}{4\pi }{K}_{t}{a}_{p}\sum_{j=1}^{N}\left(1-{e}^{-i{w}_{c}{\tau }_{j}}\right)$$
(16)

where the regeneration is disturbed, which affects the system delay from the pitch angle and spindle speed. The limiting cutting depth is

$${a}_{p\mathrm{lim}}=-\frac{4\pi }{{K}_{t}}\frac{\lambda }{N-\sum\limits_{j=1}^{N}\left(\mathrm{cos}{w}_{c}{T}_{j}+i\mathrm{sin}{w}_{c}{T}_{j}\right)}$$
(17)

If aplim is the real value, then the imaginary part should be zero, that is:

$${a}_{p\mathrm{lim}}=-\frac{4\pi }{{K}_{t}}\frac{{\lambda }_{I}}{\sum\limits_{j=1}^{N}\mathrm{sin}\left({w}_{c}{T}_{j}\right)}=-\frac{4\pi }{{K}_{t}}\frac{{\lambda }_{I}}{S}$$
(18)

2.3 Semi-discretization method (SDM)

The spindle speed, delay, and lag angle in the cutting force model of the variable pitch end mill determine the contact of the cutter and workpiece, which directly interferes with the excitation input of the vibration. By discretizing the above three parameters in the model separately, the trend of the vibration evolution caused by the dynamical model in the discrete interval is determined. In the rotation period of the spindle, the delay between the teeth and cutting edge are discretized into m, k, and l parts, respectively (l < k < m). Then, the corresponding discrete size of the i-th interval [ti, ti + 1] becomes

$$\Delta t=\frac{T}{m}$$
(19)

Therefore, the discrete number of the multiple delays τj and the lag angle ∆ϕ is

$$\begin{array}{c}{k}_{j}=int(\frac{{\tau }_{j}}{\Delta t}+\frac{1}{2})\\ l=int(\frac{\Delta \phi }{\Delta t}+\frac{1}{2})\end{array}$$
(20)

The movement displacement on the tool is

$$U\left(t\right)=\sum_{j=1}^{N}{U}_{j}\left(t\right)=\sum_{j=1}^{N}\sum_{i=1}^{m}{U}_{j,i}\left(t\right)$$
(21)

The dynamic model of the traditional system can be given mainly as follows:

$$M\ddot{U}\left(t\right)+C\dot{U}\left(t\right)+KU\left(t\right)=\sum_{j=1}^{N}{F}_{j}\left(t\right)$$
(22)

where M, C, and K are the effective mass, damping, and stiffness of the system, respectively. Considering the multiple delays of the variable pitch end mills and the phase factor of the regenerative chatter, the dynamic model of the regenerative system with multiple delays can be expressed as follows:

$$M\ddot{U}\left(t\right)+C\dot{U}\left(t\right)+\left[K+\sum_{j=1}^{N}{P}_{j}\left(t\right)\right]U\left(t\right)=\sum_{j=1}^{N}\Delta {F}_{j}\left(t\right)=\sum_{j=1}^{N}\left[{P}_{j}\left(t\right)U\left(t-{\tau }_{j}\right)\right]$$
(23)

where \({P}_{j}\left(t\right)=\frac{1}{2}g\left({\phi }_{j}\left(t\right)\right){a}_{p}{K}_{t}\left[{A}_{j}\left(t\right)\right]\). It is a second-order differential equation with multiple delays. When \(Q\left(t\right)={\left[U\left(t\right)\dot{U}\left(t\right)\right]}^{T}\), the dynamic equation is expressed as a first-order multi-delay in the state space as follows:

$$\dot{Q}\left(t\right)=A\left(t\right)Q\left(t\right)+\sum_{j=1}^{N}\left[{B}_{j}\left(t\right)Q\left(t-{\tau }_{j}\right)\right]$$
(24)

where

\(A\left(t\right)=A\left(t+T\right)\), \({B}_{j}\left(t\right)={B}_{j}\left(t+T\right)\)with

$$\begin{array}{c}A\left(t\right)=\left[\begin{array}{c}0I\\ -{M}^{-1}\left[K+\sum\limits_{j=1}^{z}{P}_{j}\left(t\right)\right]{\text{ -M}}^{-1}C\end{array}\right]\\ {B}_{j}\left(t\right)=\left[\begin{array}{c}00\\ -{M}^{-1}{P}_{j}\left(t\right)0\end{array}\right]\end{array}$$
(25)

Then, the dynamic model in the interval [ti, ti + 1] becomes

$$\dot{Q}\left(t\right)={A}_{i}\left(t\right)Q\left(t\right)+\sum_{j=1}^{N}\left[{B}_{j,i}\left(t\right){Q}_{{\tau }_{j},i}\right]$$
(26)

where,

$$\begin{array}{c}{A}_{i}\left(t\right)=\frac{1}{\Delta t}{\int }_{{t}_{i}}^{{t}_{i}+1}A\left(t\right)dt\\ {B}_{j,i}\left(t\right)=\frac{1}{\Delta t}{\int }_{{t}_{i}}^{{t}_{i}+1}{B}_{j}\left(t\right)dt\\ {Q}_{{\tau }_{j},i}\left(t\right)=Q\left(t-{\tau }_{j}\right)\approx Q\left({t}_{i}+\frac{\Delta t}{2}-{\tau }_{j}\right)\approx {w}_{j,b}{Q}_{i-{k}_{j}}+{w}_{j,a}{Q}_{i-{k}_{j}+1}\\ {w}_{j,a}={k}_{j}+1/2-{\varphi }_{j}/\left(n\Delta t\right)\\ {w}_{j,b}=1-{w}_{j,a}\end{array}$$
(27)

where \({Q}_{i-{k}_{j}}\) means \(Q\left({t}_{i-{k}_{j}}\right)\) and \({w}_{j,a}\) and \({w}_{j,b}\) express the weight coefficients of \({Q}_{{\tau }_{j},i}\left(t\right)\) on the boundary poles of the discrete interval \(\left[{t}_{i-{k}_{j}},{t}_{i-{k}_{j}+1}\right]\).

When the initial value \(Q\left({t}_{i}\right)={Q}_{i}\), the general solution of the first-order state space Eq. (24) is

$$Q\left(t\right)={e}^{{A}_{i}\left(t-{t}_{i}\right)}\left[{Q}_{i}+\sum_{j=1}^{N}{{A}_{i}}^{-1}{B}_{j,i}{Q}_{{\tau }_{j},i}\right]-\sum_{j=1}^{N}{{A}_{i}}^{-1}{B}_{j,i}{Q}_{{\tau }_{j},i}$$
(28)

When t = ti + 1, substituting Eq. (27) into Eq. (28), the following is obtained:

$${Q}_{i+1}={R}_{i}{Q}_{i}+\sum_{j=1}^{N}\left({M}_{j,i,a}{Q}_{i-{m}_{j}+1}+{M}_{j,i,b}{Q}_{i-{m}_{j}}\right)$$
(29)

where,

$$\begin{array}{c}{R}_{i}={e}^{{A}_{i}\left(t-{t}_{i}\right)}\\ {M}_{j,i,a}=\left({e}^{{A}_{i}\left(t-{t}_{i}\right)}-I\right){{A}_{i}}^{-1}{B}_{j,i}{w}_{j,a}\\ {M}_{j,i,b}=\left({e}^{{A}_{i}\left(t-{t}_{i}\right)}-I\right){{A}_{i}}^{-1}{B}_{j,i}{w}_{j,b}\end{array}$$
(30)

The discrete points are mapped and associated in the milling state space. Then, the Eq. (29) takes the following form:

$${V}_{i+1}={Z}_{i}{V}_{i}$$
(31)

where Vj is the state vector with

$${V}_{i}=\left[{Q}_{i},{Q}_{i-1},...{Q}_{i-{k}_{1}},...{Q}_{i-{k}_{2}},...{Q}_{i-{k}_{\mathrm{max}}}\right]$$
(32)

where kmax = max(kj). Zi is the conversion matrix between discrete points i and i + 1, in the form

$$\begin{array}{c}{\left[{Z}_{i}\right]}_{4\left({k}_{\mathrm{max}}+1\right)}{}_{\times 4\left({k}_{\mathrm{max}}+1\right)}=\left[\begin{array}{c}{\left[{R}_{i}\right]}_{2\times 2} \, {0} \, \cdots \, {0} \, \, {0}\\ I \, \, \, \, \, \, {0} \, \cdots \, {0} \, \, {0}\\ \, \, {0} \, \, \, \, \, \, \, I\cdots \, {0} \, \, {0}\\ \vdots \vdots \ddots \vdots \vdots \\ 0 \, \, \, \, \, \, {0} \, \, \cdots I \, \, {0}\end{array}\right]+\sum\limits_{j=1}^{N}\left[\begin{array}{c}0\cdots {\left[{M}_{j,i,a}\right]}_{4\times 4}{\left[{M}_{j,i,b}\right]}_{4\times 4}\cdots \, {0}\\ {0} \, \cdots \, \, \, \, \, \, \, \, {0} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, {0} \, \, \, \, \, \, \cdots \, \, \, {0}\\ \vdots \vdots \ddots \vdots \vdots \vdots \\ {0} \, \cdots \, \, \, \, \, \, \, \, {0} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, {0} \, \, \, \, \, \, \cdots \, \, \, {0}\\ {0} \, \cdots \, \, \, \, \, \, \, \, {0} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, {0} \, \, \, \, \, \, \cdots \, \, \, {0}\end{array}\right]\\ \uparrow \uparrow \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, {4}\left({k}_{j}-1\right)\sim 4{k}_{j} \, \, {4}{k}_{j}+1\sim 4\left({k}_{j}+1\right)\end{array}$$
(33)

where positions \({M}_{j,i,a}\) and \({M}_{j,i,b}\) are determined by variable kj defined by the delay τj. Combining Eqs. (32) and (33), the solutions for k consecutive time intervals ∆t in a rotation period T are coupled, and the mapping relation for the corresponding period T is obtained as

$${V}_{m}={Z}_{m-1}{Z}_{m-2}\cdots {Z}_{1}{Z}_{0}{V}_{0}=\Omega {V}_{0}$$
(34)

The dynamic characteristics of the milling system are determined mainly by the eigenvalues of the state matrix Ω. According to Floquet theory [36], if the modulus of all the eigenvalues of matrix Ω is less than 1 (\(\mathrm{max}\left(\left|eig\left(\Omega \right)\right|\right)<1\)), then the system tends to be progressively stable.

3 Chatter stability of variable pitch end mill

3.1 Dynamic parameters of the model

The model parameters are determined for comparing the performance of the theoretical model with the actual milling test. The basic parameters of the tool and properties of the workpiece are shown in Fig. 3a, where the machining tool is a four-tooth variable pitch end mill with pitch angles of 85°, − 95°, − 85°, and − 95° and a helix angle of 40°. The workpiece is a typical aluminum alloy Al7075-T651, which is a common material for aeronautical structures. Figure 3b displays a detection test of the modality, where a frequency response function of the machining system is obtained by tapping the toolholder with an impact hammer and monitoring the output signal of the impact vibration. The modal parameters of the system are calculated as mx = 2.1 kg, my = 1.3 kg, wnx = 1116 Hz, wny = 982 Hz, ζx = 2.68%, ζy = 2.68%, kx = 2.89 × 107 N/m, and ky = 3.11 × 106 N/m. Figure 3c displays a conventional milling test for monitoring the milling force. In order to ensure that the cutting process is in a stable state, the cutting parameters of the tool are reasonably planned with reference to the control variable method. The cutting forces of the aluminum alloy workpiece processed by the variable pitch end mill under different cutting parameters are measured by a rotary dynamometer. Combining the theoretical model of the cutting force with the variable pitch end mills, the cutting forces under different cutting depths are calculated according to the coefficient calibration method. Finally, the average values are taken as the cutting force coefficients for the aluminum alloy (Kt = 860 MPa and Kr = 355 MPa). The prediction accuracy of the milling force model could reach more than 90% in comparison to the test data and theoretical simulation result.

Fig. 3
figure 3

Dynamic detection tests of the system. a Tool and workpiece parameters. b Modal parameters. c Cutting force coefficients

Full size image

3.2 Prediction of chatter stability

In order to further verify the prediction accuracy of stability, milling tests of the aluminum alloy under different speeds \(n\pm \Delta n\) and cutting depths \({a}_{p\mathrm{lim}}\pm \Delta a\) are planned based on the above relationship between n and aplim. The SLD by the time domain digital simulation (FDM and SDM) agrees very well with the results of milling tests (Fig. 4). When the radial ratio (ae/D) is 25%, the numerical simulations of the FDM and SDM methods show great agreement. But the running times for conducting MATLAB simulation by the FDM and SDM were 184 s and 651 s, respectively, making the FDM method faster.

Fig. 4
figure 4

Stability prediction of the variable pitch end mill (85°, − 95°, − 85°, − 95°). a System eigenvalue. b Stability lobe diagram. c Milling force, frequency spectrum and surface roughness

Full size image

The variations Δn and Δa in the spindle speed and the cutting depth are defined as 1000 rpm and 1 mm, respectively. A total of 16 groups of experimental parameters with different rotational speeds and cutting depths are planned, and the cutting force signals under the conditions of different cutting parameters are monitored and analyzed in the frequency domain, the quality of the machined surface for the corresponding workpiece is measured, and the vibration state of the machining system is comprehensively analyzed for different cutting parameters. The stability and chatter states of the system are compared to find the fundamental difference in the cutting vibration states. In this paper, two groups of process parameters with completely different cutting states are selected to compare the experimental results (Fig. 4c). In the first group, ap = 5 mm, n = 4000 rpm, the cutting system has stable cutting, no chatter, and milling force is stable. The signal of the cutting force in the y direction is relatively flat, and the spectrum analysis of the cutting force considers only the forced vibration. A surface finish of the workpiece with an average peak to valley of 4 um is considered, which meets the requirements of the machining technology. In the second group of process parameters, ap = 5 mm, n = 5000 rpm, the cutting system is unstable, chatter occurs, and the milling force changes drastically. There is a large chatter amplitude around the natural frequency, and a quite poor surface finish of 30 um with a measured average peak to valley. By comprehensively comparing the state of the cutting system under stable and chatter conditions, it is observed that the occurrence of the chatter could lead to sharp changes in the cutting force in the time domain, more natural frequency components in the frequency domain, and rapid reduction in the surface quality of the workpiece, which may lead to an unreachable requirement of critical component process. At the same time, the state results of multiple sets of parameters are also shown in Fig. 4b, where the experimental results indicate that the stability model has better prediction accuracy, and they provide a certain theoretical basis for further analysis of the chatter mechanism and optimization of stability related parameters.

4 Assessment of effect of multiple delays

The stability prediction of variable pitch end mills is verified by the aforementioned milling tests. However, the improvement of stability is more necessary than the prediction in the actual machining process. The stability model of variable pitch end mills belongs to the dynamic differential equation with multiple delays, and the chatter stability is improved mainly by increasing the limiting cutting depth. Since the pitch parameters determine the multiple delays of the system, they directly affect the chatter stability. The effect of multiple delays is assessed by using the stability dynamic model, and the pitch parameters are optimized by maximizing the limiting cutting depth for improving the chatter stability.

4.1 Factor of multiple delays

The pitch distribution is \({\varphi }_{1}\text{, }{\varphi }_{2},{\varphi }_{3}...\), and the pitch difference is \(\Delta {\varphi }_{j}={\varphi }_{j+1}-{\varphi }_{j}\). According to the changing trend of the pitch difference, distribution types of the pitch parameter are mainly alternating, linear, random, etc. In turn, the phase difference of the wave is modulated with the changing pitch period. In the milling process, the wavelength θj (spindle phase) within the pitch period Tj can be expressed as

$${\theta }_{j}={w}_{c}{T}_{j}=2{\eta }_{j}\pi +{\varepsilon }_{j}$$
(35)

where ηj is the number of vibrations within the pitch period and \({\varepsilon }_{j}\) is the initial phase. Therefore, the delay factor of the system is

$$S=\sum_{j=1}^{N}\mathrm{sin}{\theta }_{j}=\sum_{j=1}^{N}\mathrm{sin}{\varepsilon }_{j}$$
(36)

According to the limiting cutting depth model, the smaller the delay factor S, the greater is the limiting cutting depth aplim. Figure 5 shows the relationship among the tool path, phase and pitch difference angle of a four-tooth variable pitch end mill and indicates the effect of constant, decreasing and increasing pitch angles on the tool path, phase, and cutting thickness. The peak phase difference of the adjacent tooth trajectories is affected by the pitch difference angle and spindle speed. This peak difference of the adjacent tooth trajectories represents the cutting thickness of the tool, which is closely related to the feed and pitch angle. Therefore, it shows that the pitch angle of the tool determines the phase of the cutting trajectory, controls the cutting thickness of the tool and finally interferes with the cutting force and vibration. The relationship between the pitch difference Δφ and the phase difference Δθ is

Fig. 5
figure 5

Relationship between tool trajectory in the feed direction Xf, spindle phase θj and pitch difference ∆φ

Full size image
$$\Delta \theta =\frac{60{w}_{c}}{2\pi n}\Delta \varphi$$
(37)

Considering the alternating and linear pitch distribution, the pitch angles can be expressed as \({\varphi }_{0},{\varphi }_{0}+\Delta \varphi ,{\varphi }_{0},{\varphi }_{0}+\Delta \varphi ,...\) and \({\varphi }_{0},{\varphi }_{0}+\Delta \varphi ,{\varphi }_{0}+2\Delta \varphi ,{\varphi }_{0}+3\Delta \varphi ,...\), respectively. The delay factor is

$${S}_{A}=\left\{\begin{array}{c}\frac{N-1}{2}\left(\mathrm{sin}{\theta }_{1}+\mathrm{sin}{\theta }_{1}\mathrm{cos}\Delta \theta +\mathrm{cos}{\theta }_{1}\mathrm{sin}\Delta \theta \right)+sin{\theta }_{1} \, \, \, \, \, \, {\text{N}}\mathrm{=}{\text{o}}{\mathrm{d}}{\text{d}}\\ \frac{N}{2}\left(\mathrm{sin}{\theta }_{1}+\mathrm{sin}{\theta }_{1}\mathrm{cos}\Delta \theta +\mathrm{cos}{\theta }_{1}\mathrm{sin}\Delta \theta \right) \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, {\text{N}}\mathrm{=}{\text{e}}{\mathrm{v}}{\text{e}}{\mathrm{n}}\end{array}\right.\text{ Alternating}$$
(38)
$${S}_{L}=\mathrm{sin}{\theta }_{1}\left(1+\mathrm{cos}\Delta \theta +\mathrm{cos}2\Delta \theta +...\mathrm{cos}\left(N-1\right)\Delta \theta \right)+\mathrm{cos}{\theta }_{1}\left(\mathrm{sin}\Delta \theta +\mathrm{sin}2\Delta \theta +...\mathrm{sin}\left(N-1\right)\Delta \theta \right)\text{ Linear}$$
(39)

Figure 6 shows the relationship among the initial phase angle θ1, phase difference Δθ, and delay factor S for different number of teeth (N = 4, 5). In Fig. 6a, the influence of the pitch distribution on the system delay is consistent for different number of teeth, and the changing trend of the alternating type is more similar to that of the linear type. According to the Fig. 6, when the phase difference is at specific value, the initial phase value has little influence on the delay term, and the optimized results of phase difference are marked as white lines in Fig. 6b. As seen in Fig. 6b, when the delay factor is the smallest (\(\left|{S}_{A}\right|\)= min), the phase difference \(\Delta \theta \text{ = }\pi\) for the alternating distribution with N = 4, 5. For the linear distribution, the delay factor is the smallest \(\left(\left|{S}_{L}\right|=min\right)\) at \(\Delta \theta \text{ = }\frac{\pi }{2},\pi ,\frac{3\pi }{2}\) for N = 4. But the delay factor is the smallest (\(\left|{S}_{L}\right|\)= min) at \(\Delta \theta \text{ = }\frac{2\pi }{5},\frac{4\pi }{5},\frac{6\pi }{5},\frac{8\pi }{5}\) for N = 5. The minimum time delay distribution of the phase difference variation is more under the condition of odd-numbered teeth. The relationship diagrams among the initial phase, phase difference, and delay factor are symmetrical under the condition of different number of teeth and the types of the pitch angle.

Fig. 6
figure 6

Relationship between delay factor S, initial angle θ1, and phase difference ∆θ for different numbers of teeth N and distribution types

Full size image

Combining with the delay relationships (38) and (39), it is seen that the relationship between the phase and delay has periodicity, which can better provide a basis for the optimization of the pitch parameters. Therefore, the wave phase difference at the minimum delay factor is obtained as

$$\Delta \theta =\left\{\begin{array}{c}\eta \pi \, \, \, \, \, \, \, \, \, \, \, {\text{A}}{\mathrm{l}}{\text{t}}{\mathrm{e}}{\text{r}}{\mathrm{n}}{\text{a}}{\mathrm{t}}{\text{i}}{\mathrm{n}}{\text{g}}\\ \eta \frac{2\pi }{N} \, \, \, \, \, \, \, \, {\text{L}}{\mathrm{i}}{\text{n}}{\mathrm{e}}{\text{a}}{\mathrm{r}} \, \, \, \, \, \, \, \end{array}\right.\eta \text{ = }1,2...$$
(40)

As shown in Fig. 6c, the system delay factor of the five-tooth tool is more obviously affected by the initial phase angle than that of the four-tooth tool for the alternating distribution, and the even number of teeth is more effective in reducing delay factor S than the odd number of teeth for the alternating distribution. But for the linear distribution, the initial phase has little effect on the time delay under the condition of different number of teeth.

4.2 Optimization of pitch parameters

By analyzing the relationship between the wave phase and delay of the dynamic model, the relationship between the pitch angle and the limiting cutting depth is developed. According to Eq. (18), it is known that the time delay term and the limiting cutting depth are inversely proportional and the minimum time delay of the system corresponds to the maximum limiting cutting depth. Therefore, in combination with the value range of the minimum time delay term in Fig. 6, the optimal pitch angles are determined based on Eq. (40). Figure 7 shows the optimal pitch parameters at different number of teeth, spindle speeds, and pitch distributions. The pitch angles shows a linear relationship with the spindle speed, indicating that the optimization results of the pitch parameters corresponding to the adjacent speed intervals are similar. As the number of teeth increases, the average pitch angle of the tool decreases, while the optimal pitch angle of each tooth shows a regular downward trend. On the other hand, the linear distribution is smaller than the alternating distribution in case of both difference and initial value of the pitch angle. As per the design criteria of the tool, an excessively large pitch difference causes a large variation in the cutting thickness of each tooth. Due to the uneven force on the cutting edge, frequent impact and obvious oscillation may occur. Therefore, when the vibration reduction effect of tools is the same, a smaller pitch difference is preferred.

Fig. 7
figure 7

Optimal pitch angle at different numbers of teeth N, spindle speeds n and pitch distributions (FDM)

Full size image

4.3 Stability of optimized end mills

From the above analysis, it is observed that different spindle speeds and numbers of teeth lead to various optimization results of pitch parameters. In order to verify the improving effect on the chatter stability, the stability of the optimized end mills is discussed for different spindle speeds and pitch distributions at N = 4 and η = 1. Figure 8 displays the stability lobe diagram (aplim—n—∆φ), where the optimized ∆φ is determined by Eqs. (38)–(40) in the speed range of n = 3000–6000 rpm. Obviously, the stability region of optimized pitch difference ∆φ possesses a larger limiting cutting depth in the corresponding spindle speed range; the stability region of lobe diagram (n = 3000—6000 rpm) is relatively larger at the pitch angles of 82.5°, − 97.5°, − 82.5°, and − 97.5° (alternating distribution, Δφ = 15°, Δθ = π) and 78.75°, − 86.25°, − 93.75°, and − 101.25° (linear distribution, Δφ = 7.5°, Δθ = π/2) as shown in Figs. 8a and 8b, which indicates that the vibration reduction effect of this type of milling cutter covers a wider range of the spindle speed. However, the relationship between the pitch difference and the limiting cutting depth at n = 5000 rpm is compared for different pitch distributions by using the FDM method as shown in Fig. 8c. For the maximum limit cutting depth, it is found that the linear distribution has a higher value than the alternating distribution. Figure 9 shows the comparison of the stability lobe diagrams between the optimized result and the test too;, the limit cutting depth under n = 5000 rpm of the optimized tool (78.75°, − 86.25°, − 93.75°, − 101.25°) is 30% higher than that of the test tool (85°, − 95°, − 85°, − 95°). And by calculating the change area of the stability region of the optimized tool compared with the test tool in the spindle speed range of 3000–6000 rpm, the changes of the stability region are determined as follows: − 7.5%, + 5%, − 6.2%, + 16.5%, − 0.5%, and + 4.7%, finally, the stability region of the optimized tool is increased by about 12%.

Fig. 8
figure 8

Stability lobe diagrams (aplim-n-∆φ). a Alternating. b Linear. c Relationship between the pitch difference ∆φ and the limit cutting depth aplim at n = 5000 rpm for different distributions (FDM)

Full size image
Fig. 9
figure 9

Stability lobe diagrams of the optimized result and the test tool

Full size image

5 Conclusion

This paper presents an analytical method of improving chatter stability for variable pitch end mills. Considering that the characteristic equation of the system has a solution, boundary conditions for stable cutting in chatter-free are developed by using the frequency domain and semi-discretization methods. However, since the pitch parameters of the mill cutter are different, and the phase delay of the chatter between these consecutive rotations can evolve into multiple, multiple delays regeneration can be observed as a novel regeneration mechanism in the milling process. The developed analytical chatter stability prediction method takes above regeneration and effect of multiple delays into account to accurately predict the stability of the process. Actual milling tests were developed to verify the effectiveness of the proposed analytical chatter prediction approach by a time domain digital simulation. The higher prediction accuracy of the stability model could not only guide the optimization of the process parameters, but also analyze and optimize the parameters of the system state, which essentially enables elimination of the regenerative chatter. By assessing the relationship between the multiple delays of the system and the chatter stability, a method for optimal pitch parameters is presented to maximize the limiting cutting depth within the required speed range. Combining with the proposed prediction model of the chatter stability, it is verified that the optimized end mill (78.75°, − 86.25°, − 93.75°, − 101.25°) is 30% higher in the limiting cutting depth under n = 5000 rpm than the ordinary variable pitch end mill, and the chatter stability region is increased by about 12% in speed range of n = 3000–6000 rpm. Therefore, when the chatter is caused by the time-varying structural dynamics of the spindle or the part, the design of the variable pitch end mill could effectively eliminate vibration, which is of great significance to the development of high stability, high efficiency and high-quality machining.