1 Introduction

Milling operation is usually adopted in the machining process for many precision products. Regenerative chatter is a common phenomenon during milling operations. It is pointed out that the surface finish and machining efficiency of the products are still limited by chatter [1]. Moreover, chatter may accelerate tool wear and even shorten the lifetime of the machine tool. Therefore, the demand for stability prediction and chatter suppression has been increasing. Chatter-free parameters determined by using the SLD should be adopted to optimize the milling process.

The milling dynamics considering the regenerative mechanism can be mathematically modeled by time-periodic DDEs [2]. The stability lobe diagram (SLD), which illustrates the boundary of milling stability, can be obtained through the numerical solution of the DDE. According to the SLD, the parameter combinations in the stable region can be adopted for achieving high-efficiency and high-quality milling processes. Therefore, many efforts have been devoted to study chatter stability prediction methods. Altintas et al. [3] proposed a well-known zeroth-order approximation (ZOA) method. This method is commonly applicated to study milling stability. However, the effectiveness of the ZOA method is limited when the radial immersion ratio is small. Merdol et al. [4] proposed a multifrequency method to improve the limitation of the ZOA method. Bayly et al. [5] reported a temporal finite element analysis method; however, the reliability of this method is sensitive to the degree of freedom of the system. Then, the Chebyshev collocation method (CCM) [6], the zeroth-order semi-discretization method (SDM) [7], and the first-order SDM (1st SDM) [8] are developed. The CCM, SDM, and 1st SDM are applicable for the milling system with both one degree of freedom (1-DOF) and two degrees of freedom (2-DOF). Based on the idea of complete discretization, Li et al. [9] proposed a complete discretization scheme (CDS), and Xie et al. [10] improved the CDS to obtain the stability charts in milling. Combining the classical Runge-Kutta method and the CDS, Li et al. presented a Runge-Kutta-based complete discretization method [11]. To reduce computational time, Ding et al. presented the full-discretization method (FDM) [12] and second-order FDM (2nd FDM) [13]. Then, many other algorithms, such as the Hermite interpolation-based [14], the third-order FDM [15], the least squares approximation-based methods [16, 17], the orthogonal polynomials approximation-based methods [18], the second- and third-order updated FDM (2nd UFDM [19] and 3rd UFDM [20]), the second-order SDM [21], the improved precise integration method [22], the improved full-discretization method [23], the holistic-interpolation scheme-based method (HIM) [24], the precise integration-based third-order full-discretization method [25], and so on, have been reported inspired by the FDM and 2nd FDM. Some methods based on numerical integration scheme, such as the numerical integration method (NIM) [26], the updated NIM (UNIM) [27], the Simpson-based method [28], the Adams-Moulton-based method [29], the Runge-Kutta-based methods [30], and so on, are also proposed for milling stability analysis. Besides, the differential quadrature method [31], the wavelet-based method [32], and the numerical differentiation method [33] are also presented for obtaining the SLD in the milling process. Additionally, Balachandran [34], Zhao and Balachandran [35], and Long et al. [36, 37] considered the non-linear issues when calculating the SLD.

The above studies are focused on the milling stability analysis for the system with single-delay. That is, the uniform pitch cutters are employed in the milling process. As we know, variable pitch cutter (non-uniform pitch cutter) can be used to stabilize the milling process by disturbing the regeneration mechanism. Thus, the chatter vibration can be suppressed by using the variable pitch cutter during the milling process. The DDE with multi-delay can be used to describe the dynamics of milling with variable pitch cutter. Many efforts have been made to develop effective methods. Choudhury et al. [38] discussed the effect of the milling cutter with a non-uniform pitch on machine tool vibration. In this study, the phenomenon that the vibration is reduced by using the non-uniform cutter was observed. Altintas et al. [39] studied the stability in milling with variable pitch cutter analytically. In this work, the optimization process of the pitch angle was also demonstrated. Based on the analytical stability analysis model, Budak [40, 41] presented a method for designing the tools with variable pitch. In this work, the effectiveness of chatter suppression by using the non-uniform pitch cutters was illustrated. Song et al. [42] discussed how to design the structural geometry of variable pitch end mills with the consideration of chatter stability. Olgac and Sipahi [43] adopted the cluster treatment of characteristic roots to determine the SLD of the milling process using variable pitch cutter analytically. Sims et al. [44] proposed three alternative model formulations to detect the chatter in milling with different non-uniform tools under different immersion conditions. Huang et al. [45] studied chatter suppression in milling with variable pith tools by using robust active control. Many other methods, such as the unified method [46], the improved FDM [47], the Ackermann’s approach-based methods [48], the enhanced multistage homotopy perturbation method [49], the general spectral element approach [50], the extended SDM [51, 52], the extended differential quadrature method [53], the improved semi-discretization method [54], the extended 3rd FDM [55], the Laplace transform-based method [56], the extended Adams-Moulton-based method [57], the extended generalized Runge-Kutta method [58], the multifrequency solution-based method [59], and so on, have also been proposed to detect chatter milling with multi-delay.

As mentioned above, the 2nd UFDM and 3rd UFDM have a good performance on accuracy and efficiency. In these two methods, the state term and time-delay term are approximated by the same order interpolation polynomials, and the free vibration process is not considered in the derivation process. In this work, combined high-order interpolation polynomials, that is, interpolation polynomials with different orders, are respectively used to approximate the state term and time-delay term to improve the accuracy of the prediction method. As suggested in Ref. [60], the third-order and second-order interpolation polynomials are used to approximate the state term and time-delay term, respectively. Meanwhile, the free vibration process is taken into consideration in the derivation process. Then, the proposed method is extended to analyze the stability of milling with multi-delay.

This paper is organized as follows: Section 2 describes the dynamic model of the milling process with single-delay. Section 3 presents the derivation process of the CHFDM and validates the accuracy and efficiency of the presented method. Section 4 extends the CHFDM to obtain the SLD of the milling process with multi-delay. Section 5 summarizes the conclusions.

2 Dynamic model of milling process

In this section, the 1-DOF milling system with single-delay is employed to study the CHFDM. By taking the regeneration mechanism into consideration, the dynamic model of the milling process is given as follows:

$$ \ddot{x}(t)+2{\zeta \omega}_n\dot{x}(t)+{\omega}_n^2x(t)=-\frac{a_ph(t)}{m}\left(x(t)-x\left(t-\tau \right)\right) $$
(1)

where ζ, ωn, and m represent the damping ratio, angular natural frequency, and modal mass, respectively, ap represents the axial depth of cut, τ represents the time delay, and the specific cutting force coefficient h(t) is defined as

$$ h(t)=\sum \limits_{j=1}^Ng\left[{\varphi}_j(t)\right]\sin \left({\varphi}_j(t)\right)\left[{K}_{tc}\cos \left({\varphi}_j(t)\right)+{K}_{rc}\sin \left({\varphi}_j(t)\right)\right] $$
(2)

where Ktc and Krc are the tangential and the normal cutting force coefficients and N is the number of cutter teeth. The function g[φj(t)] is a step function which is used to judge whether the tooth is removing material. The angular position of the jth tooth φj(t) is expressed as

$$ {\varphi}_j(t)=\left(2\pi \Omega /60\right)t+\left(j-1\right)2\pi /N $$
(3)

where Ω is the spindle speed in rpm.

By introducing the vector \( \mathbf{x}(t)=\left[\begin{array}{c}x(t)\\ {}\dot{x}(t)\end{array}\right] \), the following equation is obtained after the state space transformation of the Eq. (1) is carried out:

$$ \overset{.}{\mathbf{x}}(t)=\mathbf{Ax}(t)+\mathbf{A}(t)\mathbf{x}(t)+\mathbf{B}(t)\mathbf{x}\left(t-\tau \right) $$
(4)

where \( \mathbf{A}=\left[\begin{array}{cc}0& 1\\ {}-{\omega}_n^2& -2{\zeta \omega}_n\end{array}\right] \), \( \mathbf{A}(t)=\left[\begin{array}{cc}0& 0\\ {}-\frac{a_ph(t)}{m}& 0\end{array}\right] \), and \( \mathbf{B}(t)=\left[\begin{array}{cc}0& 0\\ {}\frac{a_ph(t)}{m}& 0\end{array}\right] \).

Since the Eq. (4) cannot be solved analytically, the numerical method can be used to solve it. The relevant time period is equally discretized into n intervals. Then, Eq. (4) is solved on the interval [ti, ti + 1], resulting in

$$ \mathbf{x}(t)={e}^{\mathbf{A}\left(t-{t}_i\right)}\mathbf{x}\left({t}_i\right)+{\int}_{t_i}^t{e}^{\mathbf{A}\left(t-s\right)}\left[\mathbf{A}(s)\mathbf{x}(s)-\mathbf{A}(s)\mathbf{x}\left(s-\tau \right)\right] ds $$
(5)

Equation (5) can be equivalently written as

$$ \mathbf{x}\left({t}_{i+1}\right)={e}^{\mathbf{A}h}\mathbf{x}\left({t}_i\right)+{\int}_{t_i}^{t_{i+1}}{e}^{\mathbf{A}\left({t}_{i+1}-s\right)}\left[\left[\mathbf{A}(s)\mathbf{x}(s)-\mathbf{A}(s)\mathbf{x}\left(s-\tau \right)\right]\right] ds $$
(6)

3 Milling stability analysis using the CHFDM

3.1 The proposed method

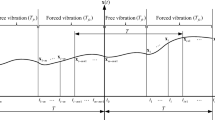
Generally, the state transition matrix of the milling system can be obtained by using the product that coupled a sequence of the discrete map or directly constructing the mapping relationship between the dynamic responses for current and previous periods. In this section, the state transition matrix is obtained directly. It is demonstrated in Ref. [26] that the milling system experiences free vibration when the cutter tooth leaves the part. Therefore, both the free vibration and forced vibration processes are considered in the CHFDM.

When the tool is not in cut, the milling system experiences free vibration process, and the matrixes A(t) and B(t) become to zero matrixes. Then, the solution of Eq. (5) can be given by

$$ \mathbf{x}(t)={e}^{\mathbf{A}\left(t-{t}_0\right)}\mathbf{x}\left({t}_0\right) $$
(7)

where t0 is the intimal time instant.

In the CHFDM, the forced vibration duration Tfo is divided into n equal small-time intervals; that is, Tfo = nh, h is the step length. Then, the time nodes are represented as follows:

$$ {t}_i={t}_0+{T}_{fr}+\left(i-1\right)h,\kern0.75em i=1,2,\cdots, n+1 $$
(8)

where Tfr is the free vibration duration. The time nodes t1 and tn − n + 1 have the following relation

$$ \mathbf{x}\left({t}_1\right)={e}^{\mathbf{A}{T}_{fr}}\mathbf{x}\left({t}_{n-n+1}\right) $$
(9)

To construct state transition matrix, the state term and time-delay term are interpolated by combined high-order polynomials. The nodal values x(ti − 2), x(ti − 1), x(ti), and x(ti + 1) denoted as xi − 2, xi − 1, xi, and xi + 1 are used to interpolate the state term, resulting in

$$ \mathbf{x}(s)=\frac{h^2s-{s}^3}{6{h}^3}{\mathbf{x}}_{i-2}+\frac{s^3+{hs}^2-2{h}^2s}{2{h}^3}{\mathbf{x}}_{i-1}+\frac{2{h}^3+{h}^2s-2{hs}^2-{s}^3}{2{h}^3}{\mathbf{x}}_i+\frac{s^3+3{hs}^2+2{h}^2s}{6{h}^3}{\mathbf{x}}_{i+1} $$
(10)

The time-delay term x(s-τ) and the matrix A(s) are interpolated by the following polynomials:

$$ \mathbf{x}\left(s-T\right)=\frac{2{h}^2-3 hs+{s}^2}{2{h}^2}{\mathbf{x}}_{i-n}+\frac{2 hs-{s}^2}{h^2}{\mathbf{x}}_{i-n+1}+\frac{s^2- hs}{2{h}^2}{\mathbf{x}}_{i-n+2} $$
(11)
$$ \mathrm{A}(s)=\left(1-\frac{s}{h}\right){\mathrm{A}}_i+\frac{s}{h}{\mathrm{A}}_{i+1} $$
(12)

Equations (10), (11), and (12) are substituted into Eq. (6), we can get

$$ \left[\begin{array}{c}\left({\mathbf{H}}_{15}{\mathbf{A}}_{i+1}+{\mathbf{H}}_{16}{\mathbf{A}}_i\right){\mathbf{x}}_{i+2-n}+\\ {}\left({\mathbf{H}}_{13}{\mathbf{A}}_{i+1}+{\mathbf{H}}_{14}{\mathbf{A}}_i\right){\mathbf{x}}_{i+1-n}+\\ {}\left({\mathbf{H}}_{11}{\mathbf{A}}_{i+1}+{\mathbf{H}}_{12}{\mathbf{A}}_i\right){\mathbf{x}}_{i-n}\end{array}\right]=\left[\begin{array}{c}\left({\mathbf{G}}_{17}{\mathbf{A}}_{\mathrm{i}+1}+{\mathbf{G}}_{18}{\mathbf{A}}_i-\mathbf{I}\right){\mathbf{x}}_{i+1}+\left({\mathbf{G}}_{15}{\mathbf{A}}_{i+1}+{\mathbf{G}}_{16}{\mathbf{A}}_i+{\mathbf{F}}_0\right){\mathbf{x}}_i+\\ {}\left({\mathbf{G}}_{13}{\mathbf{A}}_{i+1}+{\mathbf{G}}_{14}{\mathbf{A}}_i\right){\mathbf{x}}_{i-1}+\left({\mathbf{G}}_{11}{\mathbf{A}}_{i+1}+{\mathbf{G}}_{12}{\mathbf{A}}_i\right){\mathbf{x}}_{i-2}\end{array}\right] $$
(13)

where,

$$ {\displaystyle \begin{array}{l}{\mathbf{G}}_{11}=\frac{-{\mathbf{F}}_5}{6{h}^4}+\frac{{\mathbf{F}}_3}{6{h}^2},\kern0.75em {\mathbf{G}}_{12}=\frac{{\mathbf{F}}_5}{6{h}^4}-\frac{{\mathbf{F}}_4}{6{h}^3}-\frac{{\mathbf{F}}_3}{6{h}^2}+\frac{{\mathbf{F}}_2}{6h}\\ {}{\mathbf{G}}_{13}=\frac{{\mathbf{F}}_5}{2{h}^4}+\frac{{\mathbf{F}}_4}{2{h}^3}-\frac{{\mathbf{F}}_3}{h^2},\kern1em {\mathbf{G}}_{14}=\frac{-{\mathbf{F}}_5}{2{h}^4}+\frac{3{\mathbf{F}}_3}{2{h}^2}-\frac{{\mathbf{F}}_2}{h}\\ {}\begin{array}{l}{\mathbf{G}}_{15}=\frac{-{\mathbf{F}}_5}{2{h}^4}-\frac{{\mathbf{F}}_4}{h^3}+\frac{{\mathbf{F}}_3}{2{h}^2}+\frac{{\mathbf{F}}_2}{h},\kern0.75em {\mathbf{G}}_{16}=\frac{{\mathbf{F}}_5}{2{h}^4}+\frac{{\mathbf{F}}_4}{2{h}^3}-\frac{3{\mathbf{F}}_3}{2{h}^2}-\frac{{\mathbf{F}}_2}{2h}+{\mathbf{F}}_1\\ {}{\mathbf{G}}_{17}=\frac{{\mathbf{F}}_5}{6{h}^4}+\frac{{\mathbf{F}}_4}{2{h}^3}+\frac{{\mathbf{F}}_3}{3{h}^2},\kern1em {\mathbf{G}}_{18}=\frac{-{\mathbf{F}}_5}{6{h}^4}-\frac{{\mathbf{F}}_4}{3{h}^3}+\frac{{\mathbf{F}}_3}{6{h}^2}+\frac{{\mathbf{F}}^2}{3h}\end{array}\end{array}} $$
(14)
$$ {\displaystyle \begin{array}{c}{\mathbf{H}}_{11}=\frac{{\mathbf{F}}_2}{h}-\frac{3{\mathbf{F}}_3}{2{h}^2}+\frac{{\mathbf{F}}_4}{2{h}^3},\kern0.5em {\mathbf{H}}_{12}={\mathbf{F}}_1-\frac{5{\mathbf{F}}_2}{2h}+\frac{2{\mathbf{F}}_3}{h^2}-\frac{{\mathbf{F}}_4}{2{h}^3}\\ {}{\mathbf{H}}_{13}=\frac{2{\mathbf{F}}_3}{h^2}-\frac{{\mathbf{F}}_4}{h^3},\kern0.5em {\mathbf{H}}_{14}=\frac{2{\mathbf{F}}_2}{h}-\frac{3{\mathbf{F}}_3}{h^2}+\frac{{\mathbf{F}}_4}{h^3}\\ {}{\mathbf{H}}_{15}=-\frac{{\mathbf{F}}_3}{2{h}^2}+\frac{{\mathbf{F}}_4}{2{h}^3},\kern0.5em {\mathbf{H}}_{16}=-\frac{{\mathbf{F}}_2}{2h}+\frac{{\mathbf{F}}_3}{h^2}-\frac{{\mathbf{F}}_4}{2{h}^3}\end{array}} $$
(15)

where the identity matrix is denoted by I, the matrix F0 equals to eAh, and the “F” matrixes can be written as

$$ {\displaystyle \begin{array}{l}{\mathbf{F}}_1=\left({\mathbf{F}}_0-\mathbf{I}\right){\mathbf{A}}^{-1}\\ {}{\mathbf{F}}_2=\left({\mathbf{F}}_1-h\bullet \mathbf{I}\right){\mathbf{A}}^{-1}\\ {}\begin{array}{c}{\mathbf{F}}_3=\left(2{\mathbf{F}}_2-{h}^2\bullet \mathbf{I}\right){\mathbf{A}}^{-1}\\ {}{\mathbf{F}}_4=\left(3{\mathbf{F}}_3-{h}^3\bullet \mathbf{I}\right){\mathbf{A}}^{-1}\\ {}{\mathbf{F}}_5=\left(4{\mathbf{F}}_4-{h}^4\bullet \mathbf{I}\right){\mathbf{A}}^{-1}\end{array}\end{array}} $$
(16)

Combining Eqs. (9) and (13), the mapping relation of the dynamic displacements between two adjacent periods can be obtained as follows:

$$ {\boldsymbol{\Phi}}_1\left[\begin{array}{c}{\mathbf{x}}_1\\ {}{\mathbf{x}}_2\\ {}\vdots \\ {}\vdots \\ {}{\mathbf{x}}_n\\ {}{\mathbf{x}}_{n+1}\end{array}\right]={\boldsymbol{\Phi}}_2\left[\begin{array}{c}{\mathbf{x}}_{1-n}\\ {}{\mathbf{x}}_{2-n}\\ {}\vdots \\ {}\vdots \\ {}{\mathbf{x}}_{n-n}\\ {}{\mathbf{x}}_{n-n+1}\end{array}\right] $$
(17)

where,

$$ {\boldsymbol{\Phi}}_1=\left[\begin{array}{ccccccccccc}\mathbf{I}& 0& 0& 0& \cdots & 0& 0& 0& 0& 0& 0\\ {}{\mathbf{M}}_{1,0}+{\mathbf{F}}_0& {\mathbf{M}}_{2,1}-I& 0& 0& \cdots & 0& 0& 0& 0& 0& 0\\ {}{\mathbf{M}}_{2,-1}& {\mathbf{M}}_{2,0}+{\mathbf{F}}_0& {\mathbf{M}}_{2,1}-I& 0& \cdots & 0& 0& 0& 0& 0& 0\\ {}{\mathbf{M}}_{3,-2}& {\mathbf{M}}_{3,-1}& {\mathbf{M}}_{3,0}+{\mathbf{F}}_0& {\mathbf{M}}_{3,1}-I& \cdots & 0& 0& 0& 0& 0& 0\\ {}\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {}0& 0& 0& 0& \cdots & 0& 0& 0& 0& 0& 0\\ {}0& 0& 0& 0& \cdots & 0& {\mathbf{M}}_{n-1,-2}& {\mathbf{M}}_{n-1,-1}& {\mathbf{M}}_{n-1,0}+{\mathbf{F}}_0& {\mathbf{M}}_{n-1,1}-I& 0\\ {}0& -{\mathbf{M}}_{n,n-2}& 0& 0& \cdots & 0& 0& {\mathbf{M}}_{n,-2}& {\mathbf{M}}_{n,-1}& {\mathbf{M}}_{n,0}+{\mathbf{F}}_0& {\mathbf{M}}_{n,1}-I\end{array}\right] $$
(18)
$$ {\boldsymbol{\Phi}}_2=\left[\begin{array}{ccccccccccc}0& 0& 0& 0& 0& 0& \cdots & 0& 0& 0& {e}^{\boldsymbol{A}{T}_{tf}}\\ {}{\mathbf{M}}_{1,n}& {\mathbf{M}}_{1,n-1}& {\mathbf{M}}_{1,n-2}& 0& 0& 0& \cdots & 0& -{\mathrm{M}}_{1,-2}& -{\mathrm{M}}_{1,-1}& 0\\ {}0& {\mathbf{M}}_{2,n}& {\mathbf{M}}_{2,n-1}& {\mathbf{M}}_{2,n-2}& & 0& \cdots & 0& 0& -{\mathrm{M}}_{2,-2}& 0\\ {}0& 0& {\mathbf{M}}_{3,n}& {\mathbf{M}}_{3,n-1}& {\mathbf{M}}_{3,n-2}& 0& \cdots & 0& 0& 0& 0\\ {}\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots \\ {}0& 0& 0& 0& 0& 0& \cdots & {\mathbf{M}}_{n-2,n}& {\mathbf{M}}_{n-2,n-1}& {\mathbf{M}}_{n-2,n-2}& \\ {}0& 0& 0& 0& 0& 0& \cdots & 0& {\mathbf{M}}_{n-1,n}& {\mathbf{M}}_{n-1,n-1}& {\mathbf{M}}_{n-1,n-2}\\ {}0& 0& 0& 0& 0& 0& \cdots & 0& 0& {\mathbf{M}}_{n,n}& {\mathbf{M}}_{n,n-1}\end{array}\right] $$
(19)

where,

$$ {\displaystyle \begin{array}{c}{\mathbf{M}}_{i,-2}={\mathbf{G}}_{11}{\mathbf{A}}_{i+1}+{\mathbf{G}}_{12}{\mathbf{A}}_i,\kern0.5em {\mathbf{M}}_{i,-1}={\mathbf{G}}_{13}{\mathbf{A}}_{i+1}+{\mathbf{G}}_{14}{\mathbf{A}}_i\\ {}{\mathbf{M}}_{i,0}={\mathbf{G}}_{15}{\mathbf{A}}_{i+1}+{\mathbf{G}}_{16}{\mathbf{A}}_i,\kern0.5em {\mathbf{M}}_{i,1}={\mathbf{G}}_{17}{\mathbf{A}}_{i+1}+{\mathbf{G}}_{18}{\mathbf{A}}_i\\ {}{\mathbf{M}}_{i,n}={\mathbf{H}}_{11}{\mathbf{A}}_{i+1}+{\mathbf{H}}_{12}{\mathbf{A}}_i,\kern0.5em {\mathbf{M}}_{i,n-1}={\mathbf{H}}_{13}{\mathbf{A}}_{i+1}+{\mathbf{H}}_{14}{\mathbf{A}}_i\\ {}{\mathbf{M}}_{i,n-2}={\mathbf{H}}_{15}{\mathbf{A}}_{i+1}+{\mathbf{H}}_{16}{\mathbf{A}}_i\end{array}} $$
(20)

The state transition matrix ψ can be calculated through the matrixes Φ1 and Φ2 as follows:

$$ \boldsymbol{\uppsi} ={\left({\boldsymbol{\Phi}}_1\right)}^{-1}{\boldsymbol{\Phi}}_2 $$
(21)

Then, the SLD can be obtained by using the modules of the matrix ψ based on Floquet theory.

3.2 Rate of convergence

The rate of convergence reflects the local discretization errors between the approximated modules |μ(n)| and the ideal value |μ0|. Usually, the local discretization errors vary with the parameter n. In this study, the ideal value |μ0| is calculated by using the 1st SDM with n = 600. To estimate the rate of convergence of the CHFDM, the 2nd UFDM, the newly proposed UNIM and HIM are taken as the benchmark methods. The radial immersion ratio is ae/D = 1, and the parameter combinations of spindle speed Ω and axial depth of cut ap are as follows: Ω = 5000 rpm, and ap = 0.2, 0.5, 0.7, and 1.0 mm. The other main parameters are identical to those adopted in the literature [13]. The comparison of the rates of convergence for the CHFDM, 2nd UFDM, UNIM, and HIM is described in Fig. 1.

Fig. 1
figure 1

Rates of convergence of the 2nd UFDM, HIM, CHFDM, and UNIM. a ap = 0.2 mm, |μ0| = 0.819687; b ap = 0.5 mm, |μ0| = 1.073823; c ap = 0.7 mm, |μ0| = 1.221348; d ap = 1.0 mm, |μ0| = 1.406194

Full size image

As shown in Fig. 1, the 2nd UFDM and UNIM converge faster than the HIM and CHFDM when the variable ap is chosen as 0.2 mm. However, when the variable ap is equal to 0.5 mm, the CHFDM converges faster than the other methods. In general, the errors between |μ(n)| and |μ0| computed by the CHFDM are less than those computed by the other methods. It is also indicated from Fig. 1 that the rates of convergence of the 2nd UFDM, HIM, CHFDM, and UNIM are sensitive to the machining parameter combinations. Therefore, it is inadequate to estimate the accuracy of the prediction methods by using limited machining parameter combinations. In the following section, the SLDs generated by the 2nd UFDM, HIM, CHFDM, and UNIM are used to evaluate the accuracy further.

3.3 Stability lobe diagrams

In this section, the SLDs generated by the 2nd UFDM, HIM, CHFDM, and UNIM are presented. Meanwhile, the computational time of these methods is also studied. In the process of generating SLDs, the radial immersion ration is ae/D = 1, the value of the parameter Ω is between 5000 and 10,000 rpm with the step length of 25 rpm, and the value of the parameter ap is between 0 to 10 mm with the step length of 0.1 mm. The SLD obtained by the 1st SDM with n = 200 is taken as the reference. The SLDs calculated by the 2nd UFDM, HIM, CHFDM, and UNIM with n = 30 and 40 are presented in Table 1. Meanwhile, the computational time is also listed in Table 1.

Table 1 Stability charts obtained by the 2nd UFDM, HIM, CHFDM, and UNIM with ae/D = 1
Full size table

From Table 1, it can be found that the HIM consumes lest time to generate the SLDs. The CHFDM takes a little more time than the HIM but less time than the UNIM to generate SLDs. For the sake of fairness, all the methods are programmed under the same framework. In addition, Table 1 shows that the SLDs obtained by the CHFDM are much closer to the reference than those calculated by the other methods. Therefore, it is indicated that the CHFDM is more accurate than the other methods. Although there is an increment between the CHFDM and HIM in terms of computational time, the increment is very small. Consequently, CHFDM is available for obtaining the SLD of the milling process accurately and efficiently.

To further study the reliability of different methods, a small radial immersion ratio (ae/D = 0.05) is also used to generate SLDs. In the calculation process, the time period is divided into 20 and 30 parts. The SLDs obtained by the 2nd UFDM, HIM, CHFDM, and UNIM with ae/D = 0.05 are shown in Table 2.

Table 2 The SLDs obtained by the 2nd UFDM, HIM, CHFDM, and UNIM with ae/D = 0.05
Full size table

From Table 2, it shows that the SLDs generated by the HIM, CHFDM, and UNIM are closer to the reference than those generated by the 2nd UFDM. Since only the forced vibration part, rather than the whole tooth-passing period, is discretized in the HIM, CHFDM, and UNIM, the SLDs obtained by these three methods are more accurate than those calculated by the 2nd UFDM using the same value of parameters n. It is also found that the HIM, CHFDM, and 2nd UFDM consume much less time than the UNIM to obtain stability charts. The reliability of the proposed CHFDM is proved to be good.

4 Stability of milling with multi-delay using the CHFDM

In the milling process with multi-delay, the time period T equals to the spindle rotation period, that is, T = 60/Ω. It is not easy to directly construct the discrete mapping relation like that described in Eq. (17). Therefore, the state transition matrix is constructed by using the product that coupled a sequence of the discrete map in this section.

4.1 Mathematical model of milling with multi-delay

The mathematical model of the milling with multi-delay can be expressed by the multi-delay differential equation as

$$ \mathbf{M}\ddot{\mathbf{q}}(t)+\mathbf{C}\dot{\mathbf{q}}(t)+\mathbf{Kq}(t)=\sum \limits_{j=1}^N{\mathbf{H}}_j(t)\left[\mathbf{q}(t)-\mathbf{q}\left(t-{\tau}_j\right)\right] $$
(22)

where M, C, and K represent the modal mass, damping, and stiffness matrixes, respectively, and the vector q(t) represents the modal displacement matrix. These parameters are given as follows:

$$ {\displaystyle \begin{array}{c}\mathbf{M}=\left[\begin{array}{cc}{m}_x& 0\\ {}0& {m}_y\end{array}\right],\mathbf{C}=\left[\begin{array}{cc}2{m}_x{\zeta}_x{\omega}_{nx}& 0\\ {}0& 2{m}_y{\zeta}_y{\omega}_{ny}\end{array}\right]\\ {}\mathbf{K}=\left[\begin{array}{cc}{m}_x{\omega}_{nx}^2& 0\\ {}0& {m}_y{\omega}_{ny}^2\end{array}\right],\kern0.5em \mathbf{q}(t)=\left[\begin{array}{c}x(t)\\ {}y(t)\end{array}\right]\end{array}} $$
(23)

where mx, ζx, and ωnx are the modal parameters in the X direction, respectively, and my, ζy, and ωny are the modal parameters in the Y direction, respectively. The periodic coefficient matrix Hj(t) is defined as

$$ {\mathbf{H}}_j(t)=\left[\begin{array}{cc}-{h}_{j, xx}(t)& -{h}_{j, xy}(t)\\ {}-{h}_{j, yx}(t)& -{h}_{j, yy}(t)\end{array}\right] $$
(24)

where,

$$ {\displaystyle \begin{array}{c}{h}_{j, xx}(t)={\int}_0^{a_p}g\left({\varphi}_j\left(t,z\right)\right)\sin \left({\varphi}_j\left(t,z\right)\right)\left[{K}_{tc}\cos \left({\varphi}_j\left(t,z\right)\right)+{K}_{rc}\sin \left({\varphi}_j\left(t,z\right)\right)\right] dz\\ {}{h}_{j, xy}(t)={\int}_0^{a_p}g\left({\varphi}_j\left(t,z\right)\right)\cos \left({\varphi}_j\left(t,z\right)\right)\left[{K}_{tc}\cos \left({\varphi}_j\left(t,z\right)\right)+{K}_{rc}\sin \left({\varphi}_j\left(t,z\right)\right)\right] dz\\ {}{h}_{j, yx}(t)={\int}_0^{a_p}g\left({\varphi}_j\left(t,z\right)\right)\sin \left({\varphi}_j\left(t,z\right)\right)\left[-{K}_{tc}\sin \left({\varphi}_j\left(t,z\right)\right)+{K}_{rc}\cos \left({\varphi}_j\left(t,z\right)\right)\right] dz\\ {}{h}_{j, xx}(t)={\int}_0^{a_p}g\left({\varphi}_j\left(t,z\right)\right)\cos \left({\varphi}_j\left(t,z\right)\right)\left[-{K}_{tc}\sin \left({\varphi}_j\left(t,z\right)\right)+{K}_{rc}\cos \left({\varphi}_j\left(t,z\right)\right)\right] dz\end{array}} $$
(25)

where Ktc and Krc are also the cutting force coefficients, the angular position φj(t, z) varies with the cutter tooth z denotes the axial height, and the axial height, and it can be given by

$$ {\varphi}_j\left(t,z\right)=\left\{\begin{array}{c}\frac{2\pi \Omega}{60}t-\frac{z\tan \beta }{R},\kern2em if\kern0.5em j=1\\ {}\frac{2\pi \Omega}{60}t+\sum \limits_{j=2}^N{\psi}_j-\frac{z\tan \beta }{R},\kern1em if\kern0.62em 1<j<N\end{array}\right. $$
(26)

where R and β denote the radius and helix angle of the milling tool respectively, ψj denotes the pitch angle between the jth tooth and the (j-1)th tooth, z denotes the axial height, and Ω has been defined in Eq. (3).

Let \( \mathbf{x}(t)={\left[\mathbf{q}(t)\kern0.5em \dot{\mathbf{q}}(t)\right]}^T \), the following re-expression of Eq. (22) can be obtained

$$ \dot{\mathbf{x}}(t)=\mathbf{Ax}(t)+\mathbf{A}(t)\mathbf{x}(t)-\sum \limits_{j=1}^N\mathbf{B}(t)\mathbf{x}\left(t-{\tau}_j\right) $$
(27)

where,

$$ A=\left[\begin{array}{cccc}0& 0& 1& 0\\ {}0& 0& 0& 1\\ {}-{\omega}_{nx}^2& 0& -2{\zeta}_x{\omega}_{nx}& 0\\ {}0& -{\omega}_{ny}^2& 0& -2{\zeta}_y{\omega}_{ny}\end{array}\right],A(t)=\left[\begin{array}{cccc}0& 0& 0& 0\\ {}0& 0& 0& 0\\ {}-\frac{1}{m_x}\sum \limits_{j=1}^N{h}_{j, xx}& -\frac{1}{m_x}\sum \limits_{j=1}^N{h}_{j, xy}& 0& 0\\ {}-\frac{1}{m_y}\sum \limits_{j=1}^N{h}_{j, yx}& -\frac{1}{m_y}\sum \limits_{j=1}^N{h}_{j, yy}& 0& 0\end{array}\right] $$
$$ \mathbf{B}(t)=\left[\begin{array}{cccc}0& 0& 0& 0\\ {}0& 0& 0& 0\\ {}-\frac{1}{m_x}{h}_{j, xx}& -\frac{1}{m_x}{h}_{j, xy}& 0& 0\\ {}-\frac{1}{m_y}{h}_{j, yx}& -\frac{1}{m_y}{h}_{j, yy}& 0& 0\end{array}\right]. $$

Just like the Ref. [54], the spindle rotation period T is discretized into n small intervals. Equation (27) is solved on the interval [ti, ti + 1], resulting in

$$ \mathbf{x}(t)={e}^{\mathbf{A}\left(t-{t}_i\right)}\mathbf{x}\left({t}_i\right)+{\int}_{t_i}^t{e}^{\mathbf{A}\left(t-s\right)}\left[\mathbf{A}(s)\mathbf{x}(s)-\mathbf{B}(s)\mathbf{x}\left(s-{\tau}_j\right)\right] ds $$
(28)

Equation (28) can be equivalently written as

$$ \mathbf{x}\left({t}_{i+1}\right)={e}^{\mathbf{A}h}\mathbf{x}\left({t}_i\right)+{\int}_{t_i}^{t_{i+1}}{e}^{\mathbf{A}\left({t}_{i+1}-s\right)}\left[\mathbf{A}(s)\mathbf{x}(s)-\mathbf{B}(s)\mathbf{x}\left(s-{\tau}_j\right)\right] ds $$
(29)

Then, the CHFDM is extended to solve Eq. (29), so that the stability in milling with multi-delay can be analyzed.

4.2 Extend the CHFDM for stability analysis in milling with multi-delay

In this part, the CHFDM is extended to obtain the SLD of the milling system with multi-delay. The state term x(s) and time-delay term x(s − τj) are interpolated by third-order and second-order interpolation polynomials, respectively. In the calculation process, the state term still can be approximated by using Eq. (10). In the interpolation process for the time-delay term, the weight of the nodal value ωj is considered. Then, the time-delay term can be expressed as [54]

$$ {\displaystyle \begin{array}{c}\mathbf{x}\left(s-{\tau}_j\right)=\frac{\left({\omega}_jh-h+s\right)\left({\omega}_jh-2h+s\right)}{2{h}^2}{\mathbf{x}}_{i-{n}_j}-\frac{\left({\omega}_jh+s\right)\left({\omega}_jh-2h+s\right)}{h^2}{\mathbf{x}}_{i-{n}_j+1}+\\ {}\kern1.12em \frac{\left({\omega}_jh+s\right)\left({\omega}_jh-h+s\right)}{h^2}{\mathbf{x}}_{i-{n}_j+2}\end{array}} $$
(30)

where the weight ωj can be determined as

$$ {\omega}_j=\frac{n_jh-{\tau}_j}{h} $$
(31)

where nj is an integer that is determined by time delay τj and given as

$$ {n}_j= fix\left(\frac{\tau_j+0.5h}{h}\right) $$
(32)

The periodic coefficient matrix A(s) and B(s) are interpolated as

$$ {\displaystyle \begin{array}{l}\mathbf{A}(s)=\left(1-\frac{t}{h}\right){\mathbf{A}}_i+\frac{t}{h}{\mathbf{A}}_{i+1}\\ {}\mathbf{B}(s)=\left(1-\frac{t}{h}\right){\mathbf{B}}_i+\frac{t}{h}{\mathbf{B}}_{i+1}\end{array}} $$
(33)

Submitting Eqs. (10), (30), and (33) into Eq. (30) yields

$$ {\mathbf{x}}_{i+1}={\mathbf{P}}_i\left[\begin{array}{c}\left({\mathbf{G}}_{15}{\mathbf{A}}_{i+1}+{\mathbf{G}}_{16}{\mathbf{A}}_i+{\mathbf{F}}_0\right){\mathrm{x}}_i+\left({\mathbf{G}}_{13}{\mathbf{A}}_{i+1}+{\mathbf{G}}_{14}{\mathbf{A}}_i\right){\mathrm{x}}_{i-1}+\left({\mathbf{G}}_{11}{\mathbf{A}}_{i+1}+{\mathbf{G}}_{12}{\mathbf{A}}_i\right){\mathbf{x}}_{i-2}\\ {}+\sum \limits_{j=1}^N\left({\mathbf{W}}_{15}{\mathbf{B}}_{i+1}+{\mathbf{W}}_{16}{\mathbf{B}}_i\right){\mathbf{x}}_{i+2-{n}_j}+\sum \limits_{j=1}^N\left({\mathbf{W}}_{13}{\mathbf{B}}_{i+1}+{\mathbf{W}}_{14}{\mathbf{B}}_i\right){\mathbf{x}}_{i+1-{n}_j}+\sum \limits_{j=1}^N\left({\mathbf{W}}_{11}{\mathbf{B}}_{i+1}+{\mathbf{W}}_{12}{\mathbf{B}}_i\right){\mathbf{x}}_{i-{n}_j}\end{array}\right] $$
(34)

where,

$$ {\mathbf{P}}_i=\left(\mathbf{I}-{\mathbf{G}}_{17}{\mathbf{A}}_{\mathrm{i}+1}-{\mathbf{G}}_{18}{\mathbf{A}}_i\right) $$
(35)
$$ {\displaystyle \begin{array}{c}{\mathbf{W}}_{11}=\left(-\frac{1}{h}+\frac{3{\omega}_j}{2h}-\frac{\omega_j^2}{2h}\right){\mathbf{F}}_2+\left(\frac{3}{2{h}^2}-\frac{\omega_j}{h^2}\right){\mathbf{F}}_3-\frac{1}{2{h}^3}{\mathbf{F}}_4\\ {}{\mathbf{W}}_{12}=\left(-1+\frac{3}{2}{\omega}_j-\frac{1}{2}{\omega}_j^2\right){\mathbf{F}}_1+\left(\frac{5}{2h}-\frac{5{\omega}_j}{2h}+\frac{\omega_j^2}{2h}\right){\mathbf{F}}_2+\left(-\frac{2}{h^2}+\frac{\omega_j}{h^2}\right){\mathbf{F}}_3+\frac{1}{2{h}^3}{\mathbf{F}}_4\\ {}{\mathbf{W}}_{13}=\left(-\frac{2{\omega}_j}{h}+\frac{\omega_j^2}{h}\right){\mathbf{F}}_2+\left(-\frac{2}{h^2}+\frac{2{\omega}_j}{h^2}\right){\mathbf{F}}_3+\frac{1}{h^3}{\mathbf{F}}_4\\ {}{\mathbf{W}}_{14}=\left(-2{\omega}_j+{\omega}_j^2\right){\mathbf{F}}_1+\left(-\frac{2}{h}+\frac{4{\omega}_j}{h}-\frac{\omega_j^2}{h}\right){\mathbf{F}}_2+\left(\frac{3}{h^2}-\frac{2{\omega}_j}{h^2}\right){\mathbf{F}}_3-\frac{1}{h^3}{\mathbf{F}}_4\\ {}{\mathbf{W}}_{15}=\left(\frac{\omega_j}{2h}-\frac{\omega_j^2}{2h}\right){\mathbf{F}}_2+\left(\frac{1}{2{h}^2}-\frac{\omega_j}{h^2}\right){\mathbf{F}}_3-\frac{1}{2{h}^3}{\mathbf{F}}_4\\ {}{\mathbf{W}}_{16}=\left(\frac{1}{2}{\omega}_j-\frac{1}{2}{\omega}_j^2\right){\mathbf{F}}_1+\left(\frac{1}{2h}-\frac{3{\omega}_j}{2h}+\frac{\omega_j^2}{2h}\right){\mathbf{F}}_2+\left(-\frac{1}{h^2}+\frac{\omega_j}{h^2}\right){\mathbf{F}}_3+\frac{1}{2{h}^3}{\mathbf{F}}_4\end{array}} $$
(36)

The following mapping relation is obtained on the basis of Eq. (34)

$$ {\mathbf{y}}_{i+1}={\mathbf{D}}_i{\mathbf{y}}_i $$
(37)

where yi is expressed as follows:

$$ {\mathbf{y}}_i={\left[{\mathbf{x}}_i\kern0.5em {\mathbf{x}}_{i-1}\kern0.5em {\mathbf{x}}_{i-2}\kern0.5em \cdots \kern0.5em {\mathbf{x}}_{i-n+1}\kern0.5em {\mathbf{x}}_{i-n}\right]}^T $$
(38)

The state transition matrix of the milling process with multi-delay can be calculated by

$$ \boldsymbol{\uppsi} ={\mathbf{D}}_{n-1}{\mathbf{D}}_{n-2}\cdots {\mathbf{D}}_0 $$
(39)

where,

$$ {\displaystyle \begin{array}{c}{\mathbf{D}}_i=\left[\begin{array}{ccc}{\mathbf{D}}_{11}^i& {\mathbf{D}}_{12}^i& {\mathbf{D}}_{13}^i\kern0.5em \cdots \kern0.5em 0\kern0.5em 0\kern0.5em 0\\ {}\mathbf{I}& 0& \begin{array}{ccc}0& \cdots & \begin{array}{ccc}0& 0& 0\end{array}\end{array}\\ {}\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}\vdots \\ {}\begin{array}{c}0\\ {}0\end{array}\end{array}\end{array}& \begin{array}{c}\mathbf{I}\\ {}0\\ {}\begin{array}{c}\vdots \\ {}\begin{array}{c}0\\ {}0\end{array}\end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}0& \cdots & \begin{array}{ccc}0& 0& 0\end{array}\end{array}\\ {}\begin{array}{ccc}\mathbf{I}& \cdots & \begin{array}{ccc}0& 0& 0\end{array}\end{array}\\ {}\begin{array}{c}\begin{array}{ccc}0& \ddots & \begin{array}{ccc}\vdots & \vdots & \vdots \end{array}\end{array}\\ {}\begin{array}{ccc}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}\cdots \\ {}\cdots \end{array}& \begin{array}{ccc}\begin{array}{c}\mathbf{I}\\ {}0\end{array}& \begin{array}{c}0\\ {}\mathbf{I}\end{array}& \begin{array}{c}0\\ {}0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\\ {}+\sum \limits_{j=1}^N\left[\begin{array}{ccc}\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}\vdots \\ {}0\\ {}0\end{array}\end{array}\end{array}& \begin{array}{c}\cdots \\ {}\cdots \\ {}\begin{array}{c}\cdots \\ {}\cdots \\ {}\begin{array}{c}\vdots \\ {}\cdots \\ {}\cdots \end{array}\end{array}\end{array}& \begin{array}{ccc}\begin{array}{c}{\mathbf{D}}_{1,\left({n}_j-1\right)}^i\\ {}0\\ {}\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}\vdots \\ {}0\\ {}0\end{array}\end{array}\end{array}& \begin{array}{c}{\mathbf{D}}_{1,{n}_j}^i\\ {}0\\ {}\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}\vdots \\ {}0\\ {}0\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}{\mathbf{D}}_{1,\left({n}_j+1\right)}^i\\ {}0\\ {}\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}\vdots \\ {}0\\ {}0\end{array}\end{array}\end{array}& \begin{array}{c}\begin{array}{cc}\cdots & 0\end{array}\\ {}\begin{array}{cc}\cdots & 0\end{array}\\ {}\begin{array}{c}\begin{array}{cc}\cdots & 0\end{array}\\ {}\begin{array}{cc}\cdots & 0\end{array}\\ {}\begin{array}{c}\begin{array}{cc}\cdots & \vdots \end{array}\\ {}\begin{array}{cc}0& 0\end{array}\\ {}\begin{array}{cc}0& 0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\end{array}} $$
(40)

where,

$$ {\displaystyle \begin{array}{l}{\mathrm{D}}_{11}^i={\mathrm{P}}_i\left({\mathrm{F}}_0+{\mathrm{G}}_{15}{\mathrm{A}}_{i+1}+{\mathrm{G}}_{16}{\mathrm{A}}_i\right);\kern0.5em {\mathrm{D}}_{12}^i={\mathrm{P}}_i\left({\mathrm{G}}_{13}{\mathrm{A}}_{i+1}+{\mathrm{G}}_{14}{\mathrm{A}}_i\right)\\ {}{\mathrm{D}}_{13}^i={\mathrm{P}}_i\left({\mathrm{G}}_{11}{\mathrm{A}}_{i+1}+{\mathrm{G}}_{12}{\mathrm{A}}_i\right),\kern0.5em {\mathrm{D}}_{1,\left({n}_j-1\right)}^i={\mathrm{P}}_i\left({\mathrm{W}}_{15}{\mathrm{B}}_{i+1}+{\mathrm{W}}_{16}{\mathrm{B}}_i\right)\\ {}{\mathrm{D}}_{1,{n}_j}^i={\mathrm{P}}_i\left({\mathrm{W}}_{13}{\mathrm{B}}_{i+1}+{\mathrm{W}}_{14}{\mathrm{B}}_i\right);\kern0.75em {\mathrm{D}}_{1,\left({n}_j+1\right)}^i={\mathrm{P}}_i\left({\mathrm{W}}_{11}{\mathrm{B}}_{i+1}+{\mathrm{W}}_{12}{\mathrm{B}}_i\right)\end{array}} $$
(41)

The maximum value of nj determines the dimension of the matrix Di. In addition, the position of the matrixes \( {\mathbf{D}}_{1,\left({n}_j-1\right)}^i \), \( {\mathbf{D}}_{1,{n}_j}^i \), and \( {\mathbf{D}}_{1,\left({n}_j+1\right)}^i \) in the matrix Di depends on the value of parameter nj which is related to the time delay τj. For the 2-DOF milling systems, \( {\mathbf{D}}_{1,\left({n}_j-1\right)}^i \), \( {\mathbf{D}}_{1,{n}_j}^i \), and \( {\mathbf{D}}_{1,\left({n}_j+1\right)}^i \) are located in the columns from (4nj-7) to (4nj-4), from (4nj-3) to (4nj), and from (4nj+1) to (4nj+4) of the matrix Di, respectively.

The SLD of the milling process with multi-delay is obtained through Floquet theory.

4.3 Method verification

The 2-DOF milling dynamic system is considered to validate the effectiveness of the extended CHFDM for stability analysis in the milling system with multi-delay. The modal parameters and other main parameters employed in the literature [54] are also used in this study. The detail parameters are as follows: the milling tool has four flutes with the radius and the helix angle of 9.525 mm and 30°, respectively; the pitch angles between every two adjacent teeth are 70°, 110°, 70°, and 110°, respectively; the modal parameters are mx = 1.4986 kg, my = 1.199 kg, ζx = 0.0558, ζy = 0.025, ωnx = 3541.2 rad/s, and ωny = 3243.4 rad/s; and the cutting force coefficients are Ktc = 697 MPa and Krc=256 MPa, down-milling.

The extended SDM [51] and the method in Ref. [54] have been validated by experiments. Therefore, the comparisons between the SLDs obtained by the extended CHFDM and those obtained by the extended SDM [51] and the method in Ref. [54] are carried out. For obtaining SLDs, the spindle speed takes the value between 2000 and 15,000 rpm with the step length of 65 rpm, and the depth of cut takes the value between 0 and 25 mm with the step length of 0.1667 mm.

With the aim of validating the reliability of the extended CHFDM, both large (ae/D = 0.6 and ae/D = 1.0) and small (ae/D = 0.1 and ae/D = 0.3) radial immersion ratios are employed to obtain SLDs. The discrete number n is chosen as 80 to obtain stability charts. The SLDs obtained by the extended SDM [51], the method in Ref. [54], and the extended CHFDM under different conditions are shown in Table 3.

Table 3 The SLDs obtained by the extended SDM [51], the method in Ref. [54], and the extended CHFDM under different immersion conditions
Full size table

As shown in Table 3, the SLDs generated by the extended CHFDM are consistent with those obtained by the extended SDM [51] and the method in Ref. [54] under large immersion conditions (ae/D = 0.6 and 1.0), which means that the extended CHFDM is effective for stability analysis in milling with multi-delay. Regarding the small radial immersion ratios (ae/D = 0.1 and 0.3), the SLDs obtained by the extended CHFDM coincide well with those obtained by the extended SDM and the method in Ref. [54]. The results indicate that the extended CHFDM can be adopted to determine the stability boundaries of milling with multi-delay under different immersion conditions effectively and reliably.

5 Conclusions

In this paper, the CHFDM is presented to obtain the SLD of milling with single-delay. Then, the CHFDM is extended to calculate the stability boundaries of milling with multi-delay. The main conclusions are demonstrated as follows:

  1. (1)

    In general, the deviations between |μ(n)| and |μ0| calculated by the CHFDM are smaller than those obtained by the 2nd UFDM, HIM, and UNIM.

  2. (2)

    The SLDs obtained by the CHFDM is much closer to the reference than those obtained by the other benchmark methods under large immersion condition. Although there is an increment between the CHFDM and HIM in terms of computational time, the increment is very small.

  3. (3)

    The SLDs obtained by HIM, CHFDM, and UNIM are closer to the reference than those obtained by the 2nd UFDM under low immersion condition. Meanwhile, the HIM, CHFDM, and 2nd UFDM consume much less time than the UNIM to obtain stability charts.

  4. (4)

    The CHFDM can be extended to obtain the SLD of milling with multi-delay under different immersion conditions effectively and reliably.