1 Introduction

With the development of the world's oil and gas resources transferring to unconventionality, remote and harsh development environment and the development trend of oversized transmission have put forward higher requirements for pipeline construction. Longitudinally submerged arc welding (LSAW) pipes are made from high-steel wide plates, especially for long-distance oil and gas pipeline transportation and for laying pipes in deep-sea or cold areas. The straightness and roundness of formed welding pipe cannot meet the industrial standards due to the factors such as welding thermal stress, material properties and technical equipment [1,2,3]. The formed welding pipe needs to be straightened and rounded (the process of straightening and rounding is referred to as the calibration process in this paper). According to the American Petroleum Institute's industry standard ANSI/API Spec. 5L, the straightness and roundness of finished welding pipes have been strictly required. Namely the roundness does not exceed ± 0.75% of a nominal outer diameter, and the straightness is not greater than 0.2% of a total length [4].

At present, the roundness calibration process mainly includes the whole-diameter roundness calibration process [5, 6], the over-bending roundness calibration process [7,8,9] and the roll-type roundness calibration process [10, 11]. Common straightness calibration techniques include the pressure straightening [12,13,14] and the cross-roll straightening [15,16,17,18]. The existing roundness and straightness calibration processes are done separately. On the one hand, it leads to the growth of production process and the reduction of production efficiency, which is not easy to realize automatic and intelligent production; On the other hand, because the deformation process affects each other, the flattening problem of LSAW pipes cannot be solved [19]. It is difficult to adjust both the straightness and roundness to optimal levels, which also seriously affects on-site welding and pipeline safety [20]. In view of the application trend of LSAW pipes and the existing problem of calibration technology, a new three-roller continuous and synchronous calibration process of straightness and roundness was proposed [20,21,22,23]. The study of process deformation mechanism provides theoretical support for understanding the essence of the process and applying it to actual production.

Based on the combination of reference, theoretical analysis and numerical simulation, this paper further studies the deformation mechanism of the calibration process. It includes the axial reciprocating bending straightening process and the circumferential reciprocating bending rounding process. In addition, the distribution of equivalent stress, maximum and minimum principal stress of pipe in Section III is analyzed; the effects of axial stress, circumferential stress and radial stress on pipe deformation are discussed. The simulation and experimental results can support the theoretical analysis results.

2 Process introduction

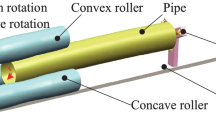
The three-roller continuous and synchronous calibration process of straightness and roundness for LSAW pipes is shown in Fig. 1. The process’ main working parts are three parallel rollers, including a convex roller (upper roller) and two concave rollers (lower rollers). Before experiment, each roller pushes the same radial reduction toward the pipe’s central axis. During the experiment, two concave rollers rotate simultaneously driven by servo motors. This makes the pipe and convex roller rotate under the action of friction. At the same time, the servo motor drives the push plate to make the pipe move along the slideway, thus finishing the calibration process.

Fig. 1
figure 1

Schematic diagram of the calibration process

Full size image

The schematic diagram of roller-shape is shown in Fig. 2. As shown in Fig. 2, both ends of the roller are loading section (Section I) and unloading section (Section V), both of which are truncated cone shape. The design enables the pipe to enter smoothly between the three rollers and ensures that the pipe can unload smoothly, so as to unify the curvature. Sections II and IV are roundness calibration sections, which are cylindrical in shape. The design can make the pipe undergo multiple reciprocating bending along the circumferential direction, resulting in elastic–plastic deformation. Thus, roundness calibration and complementary roundness calibration are realized. Section III is roundness and straightness calibration section. The upper roller part is convex, and the lower roller part is concave. The design ensures that the pipe can undergo multiple reciprocating bending along the circumferential and axial directions. Thereby, roundness and straightness calibration are realized.

Fig. 2
figure 2

Schematic diagram of roller-shape

Full size image

The curvature distribution of Section III is shown in Fig. 3. Section III is composed of n tangent arcs with changing curvature, whose curvature is gradually reduced from the middle to both ends. That is, \(K_{1}\) to \(K_{n}\) gradually increases in value, and \(K_{n}\) is the maximum curvature of Section III.

Fig. 3
figure 3

Curvature distribution of Section III–n-segment curvature

Full size image

Figure 4 is a schematic diagram of the loading parameter. Three rollers load the same radial reduction toward the pipe center, and the stroke of each roller is recorded as H.

$$H = R_{1} + R - H_{{\text{j}}}$$
(1)

where \(H\) is the radial reduction, \(R_{1}\) is the roller radius, \(R\) is the pipe radius, and \(H_{{\text{j}}}\) is the distance from the pipe’s center to the center of roller after loading.

Fig. 4
figure 4

Diagram of loading parameters

Full size image

3 Process deformation mechanism

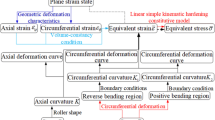
In this paper, the axial and circumferential reciprocating bending deformation are simplified to the pure bending problem of plane curved beam [24].

3.1 Reciprocating bending springback analysis of axial straightening

The straightening process of the calibration process is an axial reciprocating bending process. As shown in Fig. 3, the curvature distribution of Section III is constantly changing, with the curvature increasing from zero (\(K_{1}\)) to \(K_{n}\) and then reduced to zero. According to the geometric characteristics of LSAW pipe, a linear simple kinematic hardening (LSKH) constitutive model is adopted [15], as shown in Fig. 5.

Fig. 5
figure 5

LSKH constitutive model

Full size image

The expression is as follows:

$$\begin{gathered} \sigma { = }\left\{ \begin{gathered} D\varepsilon + \sigma_{0} \begin{array}{*{20}c} {} & {\varepsilon > 0} \\ \end{array} \hfill \\ D\varepsilon - \sigma_{0} \begin{array}{*{20}c} {} & {\varepsilon < 0} \\ \end{array} \hfill \\ \end{gathered} \right. \hfill \\ \begin{array}{*{20}c} {} & {\sigma_{0} } \\ \end{array} = \left( {1 - \frac{D}{E}} \right)\sigma_{{\text{s}}} \hfill \\ \end{gathered}$$
(2)

where \(\sigma_{s}\) is yield stress, \(D\) is plastic modulus, and \(E\) is elastic modulus.

The circular section of pipe is shown in Fig. 6. The coordinate system is established with the geometric center of the section as the coordinate origin. The bending moment M during loading can be simply described as

$$M = \int\limits_{A} {\sigma z{\text{dz = }}\left\{ \begin{gathered} DI\left( {K - K_{0} } \right) + M_{0} \begin{array}{*{20}c} {} & {K \ge K_{0} } \\ \end{array} \hfill \\ DI\left( {K - K_{0} } \right) - M_{0} \begin{array}{*{20}c} {} & {K < K_{0} } \\ \end{array} \hfill \\ \end{gathered} \right.}$$
(3)
Fig. 6
figure 6

Circular section of pipes

Full size image

where \(M_0=\frac{{4\sigma}_0}3(R_1^3-R_2^3)\), \(I=\frac\pi4(R_1^4-R_2^4)\), \(R_2\) is the inner diameter of pipe.

Since the deformation of each section is continuous, the current initial curvature can be used as the curvature after the last bending springback. According to Eq. (3), the recurrence equation of reciprocating bending can be expressed as

$$K_{{{\text{p}}n}} = \left\{ \begin{array}{l} \begin{array}{*{20}c} {K_{1} - \frac{{M_{1} (K_{1} ,K_{0} )}}{EI}} & {n = 1} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {K_{n} - \frac{{M_{n} (K_{n} ,K_{{{\text{p}}(n - 1)}} )}}{EI}} & {n \ge 2} \\ \end{array} \hfill \\ \end{array} \right.$$
(4)

where n is the times of reciprocating bending and \(K_{\mathrm pn}\) is the springback curvature after reciprocating bending n times.

Based on the springback theory of small curvature plane bending [25], the springback curvature of pipe micro-beam after reciprocating bending n times along the axis is deduced by mathematical induction. The reciprocating bending process is shown in Fig. 7.

Fig. 7
figure 7

Schematic diagram of reciprocating bending of micro-beam

Full size image

If the first bending is reverse bending, the unified equation of curvature after springback is

$$\begin{aligned} K_{pn} & = K_{n} - \frac{D}{E}(K_{n} - K_{n - 1} ) - \left( \frac{D}{E} \right)^{2} (K_{n - 1} - K_{n - 2} ) - \ldots \hfill \\ & - \left( \frac{D}{E} \right)^{n - 1} (K_{2} - K_{1} ) + ( - 1)^{n + 1} \left( {\frac{{16\sigma_{0} (R_{1}^{3} - R_{2}^{3} )}}{{3\pi (R_{1}^{4} - R_{2}^{4} )(E + D)}}} \right) \hfill \\ \end{aligned}$$
(5)

If the first bending is positive bending, the unified equation of curvature after springback is

$$\begin{aligned} K_{pn} & = K_{n} - \frac{D}{E}(K_{n} - K_{n - 1} ) - \left( \frac{D}{E} \right)^{2} (K_{n - 1} - K_{n - 2} ) - \ldots \hfill \\ & - \left( \frac{D}{E} \right)^{n - 1} (K_{2} - K_{1} ) + ( - 1)^{n} \left( {\frac{{16\sigma_{0} (R_{1}^{3} - R_{2}^{3} )}}{{3\pi (R_{1}^{4} - R_{2}^{4} )(E + D)}}} \right) \hfill \\ \end{aligned}$$
(6)

Equations (5) and (6) can be expressed uniformly as

$$\overline{K}_{pn} = f(D,E,\sigma_{0} ,R_{1} ,R_{2} ,K_{1} ,K_{2} , \ldots ,K_{n} )$$
(7)

Equation (7) proves that multiple reciprocating bending can eliminate the difference of initial curvature along the axial direction. This unifies the curvature to the same direction and value. \({\overline K}_{\mathrm pn}\) is related to material properties, inner and outer diameters of pipe and bending curvature. When the loading curvature \({K}_{n}\)  tends to zero, the springback curvature of the pipe along the axial direction after reciprocating bending is also close to zero, thus achieving straightening.

3.2 Reciprocating bending springback analysis of circumferential rounding

The rounding process of the calibration process is a circumferential reciprocating bending process. Similarly, a linear simple kinematic hardening (LSKH) constitutive model is adopted [15]. The relation between bending moment and curvature can be described as

$$M = \int\limits_{A} {\sigma z{\text{dz = }}\left\{ \begin{gathered} DI\left( {K - K_{0} } \right) + M_{0} \begin{array}{*{20}c} {} & {K \ge K_{0} } \\ \end{array} \hfill \\ DI\left( {K - K_{0} } \right) - M_{0} \begin{array}{*{20}c} {} & {K < K_{0} } \\ \end{array} \hfill \\ \end{gathered} \right.}$$
(8)

where \(M_{0} = \frac{{\sigma_{0} t^{2} }}{4}\).

Then, after reciprocating bending n times, the springback curvature of pipe micro-beam along the circumferential direction is deduced. The reciprocating bending process is shown in Fig. 7. The derivation process is the same as that of axial reciprocating bending.

If the first bending is reverse bending, the unified equation of curvature after springback is

$$\begin{aligned} K_{pn} & = K_{n} - \frac{D}{E}(K_{n} - K_{n - 1} ) - \left( \frac{D}{E} \right)^{2} (K_{n - 1} - K_{n - 2} ) - \ldots \hfill \\ & - \left( \frac{D}{E} \right)^{n - 1} (K_{2} - K_{1} ) + ( - 1)^{n + 1} \left( {\frac{{3\sigma_{0} }}{t(E + D)}} \right) \hfill \\ \end{aligned}$$
(9)

If the first bending is positive bending, the unified equation of curvature after springback is

$$\begin{aligned} K_{pn} & = K_{n} - \frac{D}{E}(K_{n} - K_{n - 1} ) - \left( \frac{D}{E} \right)^{2} (K_{n - 1} - K_{n - 2} ) - \ldots \hfill \\ & - \left( \frac{D}{E} \right)^{n - 1} (K_{2} - K_{1} ) + ( - 1)^{n} \left( {\frac{{3\sigma_{0} }}{t(E + D)}} \right) \hfill \\ \end{aligned}$$
(10)

Equations (9) and (10) can be expressed uniformly as

$$\overline{K}_{pn} = f(D,E,\sigma_{0} ,K_{1} ,K_{2} , \ldots ,K_{n} )$$
(11)

Equation (11) proves that multiple reciprocating bending can eliminate the difference of initial curvature along the circumferential direction. This unifies the curvature to the same direction and value. \(\overline{K}_{pn}\) is related to material properties, thickness of pipe wall and bending curvature. When the loading curvature \(\overline{K}_{n}\) tends to a certain value, the springback curvature of pipe along the circumferential direction after reciprocating bending tends to be consistent, thus achieving rounding.

4 Numerical simulation

Using the software ABAQUS, a finite element model of the LSAW pipe calibration process is established, as shown in Fig. 8. Regardless of the effect of pipe welds on the continuous calibration process, the mechanical properties and geometric dimensions of pipes are shown in Table 1 and the geometric dimensions of rollers are shown in Table 2. The pipe is set as a deformable body. The pipe wall is divided into 4 layers along the thickness, and the pipe is discretized by 8-node linear hexagonal nonconforming mode elements. Select the continuum distributing coupling method to couple the center point of the pipe cross section and the pipe cross-section boundary, and select all 6 degrees of freedom for the constrained area. The three rollers are set as discrete rigid bodies. The contact between the pipe and each roller is set to pure master–slave contact and motion contact conditions, and the coefficient of friction is 0.2.

Fig. 8
figure 8

Finite element model

Full size image
Table 1 Mechanical properties and geometric dimensions of pipes
Full size table
Table 2 Geometric dimension of rollers
Full size table

5 Results and discussion

During numerical simulation, the roller rotation speed is 150 mm/s and the pipe forward speed is 4 mm/s. The times of reciprocating bending of ST12 pipe from starting to contact the roller to completely separating from the roller is 67.

The equivalent stress distribution of one-half ST12 pipe in Section III is shown in Fig. 9. According to the symmetry, there are three positive bending regions and three reverse bending regions along the circumferential direction. They are evenly distributed in the whole pipe [21].

Fig. 9
figure 9

Equivalent stress distribution of one-half pipe

Full size image

The distribution of maximum and minimum principal stresses in Section III is shown in Fig. 10. The maximum and minimum principal stress values are shown in Table 3. In combination with Figs. 9 and 10, it can be seen that positions A and C are located in the reverse bending region. The maximum principal stress is generated in the inner layer of the pipe (nodes 97 and 427), and the minimum principal stress is generated in the outer layer of the pipe (nodes 67 and 454). Positions B and D are located in the positive bending region. The maximum principal stress is generated in the outer layer of the pipe (nodes 460 and 448), and the minimum principal stress is generated in the inner layer of the pipe (nodes 421 and 433). Based on the above analysis, the absolute values of the maximum principal stress and the minimum principal stress of the pipe any position are basically equal, which verifies the characteristics of pure bending deformation.

Fig. 10
figure 10

Distribution of maximum and minimum principal stresses

Full size image
Table 3 Maximum and minimum principal stresses
Full size table

The distribution of axial stress along the thickness and length directions in Section III is shown in Fig. 11. Plastic deformation occurs along the thickness and length directions due to axial stress. It is proved that the geometric dimension of the longitudinal section of the pipe has changed.

Fig. 11
figure 11

Distribution of axial stress

Full size image

Figure 11a shows the distribution of axial stress along the thickness direction. In the positive bending region, the pipe’s outer layer is stretched with a maximum stress of 249 MPa (node 5) and a minimum stress of 0 MPa (node 1); in the reverse bending region, the inner layer of the pipe is compressed with a maximum stress of 0 MPa (node 5) and a minimum stress of -278 MPa (node 1). The above indicates that one part of the pipe wall has reached yield strength, while the other part has produced only elastic deformation.

Figure 11b shows the distribution of axial stress along the length direction. The axial stress of the pipe’s outermost nodes increases gradually from both ends to the center along the length direction. And in the center of the roller curve, the axial stress reaches its maximum. That shows that the plastic deformation occurs in Section III along the length direction.

The distribution of tangential stress along the thickness and circumferential directions in Section III is shown in Fig. 12. As indicated in Fig. 12, plastic deformation occurs along the thickness and circumferential directions due to circumferential stress. It is proved that the geometric dimension of the circumferential section of the pipe has changed.

Fig. 12
figure 12

Distribution of tangential stress (I: positive bending region; II: reverse bending region)

Full size image

Figure 12a shows the distribution of circumferential stress along the thickness direction. In the positive bending region, the pipe’s outer layer is stretched with a maximum stress of 287 MPa (node 5); the inner layer is compressed with a minimum stress of -289 MPa (node 1). In the reverse bending region, the inner layer of the pipe is stretched, the maximum stress is 280 MPa (node 1); the outer layer is compressed, and the minimum stress is -276 MPa (node 5). From this, regardless of the positive bending region or the reverse bending region, the absolute value of the outer and inner circumferential stresses of the pipe is basically the same.

Figure 12b shows the distribution of circumferential stress along the circumferential direction. The circumferential stress values of the pipe’s outermost nodes are selected. As can be seen from Fig. 12b, the area of the positive bending region is larger than that of the reverse bending region. This is consistent with the equivalent stress distribution in Fig. 9. The absolute value of circumferential stress reaches the maximum at each region’s center and gradually decreases from the center to both ends.

The distribution of radial stress in Section III is shown in Fig. 13. It shows that the radial stress of the pipe is very small, about -2.0 MPa to 2.0 MPa, and only elastic deformation occurs.

Fig. 13
figure 13

Distribution of radial stress

Full size image

The effects of axial, circumferential and radial stresses on the pipe calibration process are discussed through numerical simulation. The results show that the pipe calibration process is realized by the synergy between axial stress and circumferential stress. As a result, the simulation results also support the theoretical analysis results.

The equivalent stress distribution of ST12 pipe after calibration is shown in Fig. 14. It can be observed in Fig. 14 that the distribution of equivalent stress tends to be uniform and the residual stress is small. The simulation results show that the residual roundness is within 0.14% and the residual straightness is within 0.17%. The results meet the standard requirements [4]. As a result, the feasibility of the process is initially verified.

Fig. 14
figure 14

Distribution of equivalent stress after calibration

Full size image

6 Experimental validation

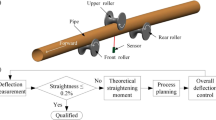
The experimental device for pipe calibration is shown in Fig. 15. The device can realize both continuous rounding and continuous straightening of LSAW pipes.

Fig. 15
figure 15

Experimental device for pipe calibration

Full size image

As shown in Fig. 15, the roller is connected with the slider fixed on the frame via bearing. The slider can slide vertically along the frame surface via a screw to adjust the radial reduction of the three rollers. The support assembly keeps the balance of the pipe during the experiment. The servo motor drives two lower rollers to rotate synchronously, which drives the pipe and the upper roller to start turning. At the same time, the push plate drives the pipe to move along the slideway. So far, the calibration process of simultaneous rotation and movement of the pipe is realized. The pipes and rollers selected for the experiment are the same as the pipes and rollers selected for the simulation.

The experimental results of ST12 pipes after calibration are shown in Table 4. From Table 4, it can be observed that the residual roundness is within 0.7% and the residual straightness is within 0.2%. Both meet industry standard requirements [4]. The experimental results further verify that the calibration process of pipes is achieved by axial and circumferential reciprocating bending. The forming effect of ST12 pipes is shown in Fig. 16.

Table 4 Experimental results after calibration
Full size table
Fig. 16
figure 16

Forming effect of ST12 pipes

Full size image

7 Conclusions

  1. 1.

    Theoretically, the reciprocating bending springback analysis of axial straightening and circumferential rounding are established, respectively. The deformation mechanism of the process is revealed. It is proved that the reciprocating bending can eliminate the difference of initial curvature, and unify the axial and circumferential curvature to the same direction and value. It provides theoretical support for the calibration process to be applied to actual production.

  2. 2.

    When the loading curvature tends to zero, the axial curvature after reciprocating bending is also close to zero. The straightness can be calibrated. When the loading curvature tends to a certain value, the circumferential curvature after reciprocating bending tends to be consistent. The roundness can be calibrated. The combination of axial reciprocating bending and circumferential reciprocating bending enables the calibration process of LSAW pipes.

  3. 3.

    The simulation results show that the distribution of the maximum and minimum principal stress accord with the characteristics of pure bending deformation; After unloading and springback, the residual stress is small and evenly distributed; the calibration process is mainly influenced by the synergy of axial stress and circumferential stress, which further supports the theoretical analysis results.