1 Introduction

Natural gas has become the main energy in the world. Large thin-walled pipes are widely used in oil and gas transportation in cold zones or deep water [1]. To ensure the strength and integrity of the design pipeline, Trifonov and Cherniy [2, 3] proposed a stress-strain analysis model of buried steel pipes subjected to active fault displacements. To expand the application range of spiral welded pipes in oil and gas transportation, Papadaki et al. [4] studied the structural properties of large diameter spiral welded steel pipes under pressure bending numerically. Draper et al. [5] combined beam bending model and prediction scour formula to simulate the pipeline lowering on a moving seabed. The model was also used to estimate the stability of the pipeline using the method of maximum design wave. Under the influence of external pressure, bending, and axial tension, the pipeline was prone to structural instability due to excessive oxidation, resulting in disastrous effects. Chatzopoulou et al. [6] used nonlinear finite element simulation tools to study the influence of UOE pipeline manufacturing process on the response and resistance of offshore pipeline structures. Subsea pipeline hydrodynamic stability is one of the most fundamental aspects of pipeline design. Robertson et al. [7] performed force balance calculations and complex dynamic finite element analysis, demonstrating that effective and accurate pipeline stability analysis was critical to avoid potentially high costs in complex stability solutions.

Due to the fluctuation of the material performance and some uncertain factors in the forming process, the roundness and straightness of pipes may not meet the industrial standards, and the over-standard pipes should be calibrated further [8]. The present roller calibrated methods, including straightness and roundness, are based on the unidirectional reciprocating bending [9], and the roundness calibration and straightness calibration are separate and independent in industrial practice. Huang et al. [10] carried out a numerical simulation and experimental study on three-roller continuous setting round process. Through the above two methods, the roundness can be corrected to less than 0.2%. It had a certain guiding significance for the overall rounding process of pipes. Despite this, there are limitations to the continuous rounding process of pipes. Wang et al. [11] proposed a three-roller continuous straightening method, and the straightness can be calibrated to within 0.2%. But this method can only calibrate the straightness of pipes, not the roundness. Since the axial and circumferential deformation of pipes are mutually restrictive, it fails to solve the flattening problem of large thin-walled pipes [12]. It is not easy to adjust the straightness and roundness to the optimum level. To address the coordinated regulation problem of roundness and straightness, the three-roller continuous and synchronous calibrating straightness and roundness process is developed [13]. In the paper, the mechanical model of axial and circumferential bidirectional deformation of large thin-walled pipes has been investigated in the process.

Most of the mechanical models proposed are based on a single direction. Karamitros et al. [14] derived the axial force on the pipeline using equations of equilibrium and compatibility of displacements, and calculated the developing bending moment in combination with the elastic beam foundation and elastic beam theory. Zhao et al. [15] presented a mechanical model of the static bending stage during the symmetrical three-roller setting round process. The model was analyzed for the circular cross-section of pipe. Moreover, the position of pipe stress concentration can be determined by the distribution of equivalent stress and equivalent strain [16]. It is of great significance to the actual production. Most of the proposed mechanical models only study the stress and strain in a single direction. Zhang [17] derived a unidirectional stress-strain model by using the large deformation kinematics for thin-walled shells. Taheri-Behrooz et al. [18] deduced the radial stress-strain distribution of composite pipes. Cheng et al. [19] built a mechanical analysis model. And only the equivalent stress distribution of the strain neutral layer was analyzed. Howbeit, the study of the mechanical model of bidirectional deformation has not yet emerged.

In this paper, a mechanical model of axial and circumferential bidirectional deformation is developed. This model provides a theoretical basis for the setting of process parameters and the optimization of roller shape. The plane strain state of the deformed element is identified based on the traditional assumptions in the present research. According to the geometric deformation characteristics, the axial and circumferential strain models in the deformation zone are established. Subsequently, the equivalent stress and equivalent strain equations are obtained by taking into account the volume-constancy condition and the linear simple kinematic hardening constitutive model [20]. Finally, the axial and circumferential deformation curves can be calculated based on the roller shape and boundary conditions. According to the curvature of axial and circumferential deformations, the equivalent stress and equivalent strain of the pipe’s any element in the deformation process can be obtained. Furthermore, this model is compared and verified by numerical simulation and physical experiments.

2 Process introduction

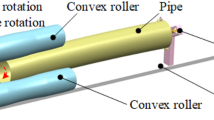
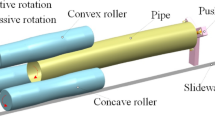
As shown in Fig. 1, the main working parts of the process are three parallel rollers, including a convex roller (upper roller) and two concave rollers (lower rollers). Two concave rollers are driven by servo motors to rotate simultaneously. This causes the pipe and convex roller to be driven to rotate under the effect of friction. At the same time, the pipe is fed continuously along the slideway by the push plate to realize the calibration process.

Fig. 1
figure 1

Schematic diagram of process

Full size image

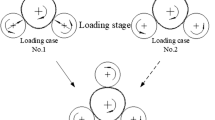
The schematic diagram of roller shape is shown in Fig. 2. Stage A is the loading stage, that is, the inlet end of the pipe. To make the pipe easy to enter the gap between three rollers and achieve radial reduction, it is designed to be of truncated cone shape. Stage D is the unloading stage, that is, the outlet end of the pipe. Its shape is also designed to be truncated cone to ensure that the pipe can be smoothly unloaded after calibration. Stage B1 and Stage B2 are the roundness calibration stages, where the shape is both cylindrical. Stage C is the synchronous calibrating straightness and roundness stage between Stage B1 and Stage B2. The upper roller part is convex, while the lower roller part is concave.

Fig. 2
figure 2

Schematic diagram of roller shape. Stage (A): loading stage. Stage (B) (B1 and B2): roundness calibration stage. Stage (C): roundness and straightness calibration stage. Stage (D): unloading stage

Full size image

As shown in Fig. 3, during this process, the three rollers move synchronously the same radial reduction toward the pipe center. The reduction of each roller is recorded as H.

$$ H={R}_1+R-{H}_{\mathrm{j}} $$
(1)

where H is the radial reduction, R1 is the radius of the roller, R is the radius of the pipe, and Hj is the distance from the pipe’s center to the center of roller after loading.

Fig. 3
figure 3

Diagram of loading parameters

Full size image

3 Mechanical model

The mechanical model is explained in this section. The flowchart of theoretical analysis is shown in Fig. 4.

Fig. 4
figure 4

Flowchart of theoretical analysis

Full size image

3.1 Basic assumptions

  1. (1)

    The pipe is continuous, homogeneous, and isotropic. The linear simple kinematic hardening (LSKH) constitutive model [20] is adopted, as shown in Fig. 5.

Fig. 5
figure 5

LSKH constitutive model

Full size image
$$ {\displaystyle \begin{array}{l}\overline{\sigma}=\left\{\begin{array}{l}D\overline{\varepsilon}+{\sigma}_0\kern0.5em \overline{\varepsilon}>0\\ {}D\overline{\varepsilon}-{\sigma}_0\kern0.5em \overline{\varepsilon}<0\end{array}\right.\\ {}\begin{array}{cc}& {\sigma}_0\end{array}=\left(1-\frac{D}{E}\right){\sigma}_{\mathrm{s}}\end{array}} $$
(2)

where σs is the yield stress, D is the plastic modulus, and E is the elastic modulus.

  1. (2)

    Any cross-section of the pipe is always perpendicular to the geometric central axis, and remains a plane during the deformation. There is no tilt or distortion between the two adjacent cross-sections [21]. So the shear stress and shear strain are negligible.

  2. (3)

    The deformation of pipe follows the principle of volume invariance.

  3. (4)

    According to the theory of thin-walled shells, the change of wall thickness is ignored, namely εr = 0.

  4. (5)

    Because the movement of neutral layer is small for thin-walled pipe in the deformation process, it can be considered that the strain neutral layer, stress neutral layer, and geometric central layer of the pipe are always coincided.

3.2 Plane strain state

According to the above assumptions, the deformation of pipe can be simplified to a plane strain problem, including the axial and circumferential deformation. An element is selected at any position of the pipe, and the meridian coordinate system is defined. The three-dimensional diagram of the initial state of the pipe is shown in Fig. 6. σφ and εφ are the stress and strain along the axial direction of pipe, respectively. σθ and εθ are the stress and strain along the tangent direction of pipe, respectively. σr and εr are the stress and strain along the radial direction of the pipe, respectively. The geometric relationships and variables are displayed in Fig. 7 and Fig. 8.

Fig. 6
figure 6

Three-dimensional diagram of the initial state of the pipe

Full size image
Fig. 7
figure 7

Meridian plane of pipe

Full size image
Fig. 8
figure 8

Cross-section of pipe

Full size image

3.2.1 Axial strain model

If the initial state of the element is in tension, it is compressed during the reverse axial bending process, as shown in Fig. 9. The initial length l01 of the element along the axial direction can be expressed as Eq. (3).

$$ {l}_{01}={R}_0\cdot d\varphi =\left({R}_{\rho }+r\sin \theta +\frac{rd\theta \cos \theta }{2}\right)\cdot d\varphi $$
(3)
$$ {R}_0=\left(\left({R}_{\rho }+r\sin \theta \right)+\left({R}_{\rho }+r\sin \left(\theta + d\theta \right)\right)\right)/2 $$
(4)

where r is the radius of the pipe, t is the wall thickness, Rρ is the initial curvature radius, θ is the angle of the element between the cross-section and the bending axis, and φ is the angle of the element between the meridian plane and the end of pipe.

Fig. 9
figure 9

Before and after the axial bending of the pipe. (a) Before bending. (b) After bending

Full size image

The length lBC(AD) of the element along the axial direction after the axial bending is obtained as Eq. (5).

$$ {l}_{\mathrm{BC}\left(\mathrm{AD}\right)}=\frac{1}{K}\cdot d{\varphi}_1 $$
(5)

where K is the curvature of the element after the axial bending, and dφ1 is the radian of the element after the axial bending. The axial strain εφ of the element after the axial bending can be expressed as follows:

$$ {\varepsilon}_{\varphi }=\ln \frac{l_{\mathrm{BC}\left(\mathrm{AD}\right)}}{l_{01}}=\ln \frac{2d{\varphi}_1}{\left(2{R}_{\rho }+2r\sin \theta + rd\theta \cos \theta \right)\cdot Kd\varphi} $$
(6)

Since the initial deflection of the pipe is small, the deformation of the pipe belongs to a small deformation problem [22]. It can be considered that the projection length of the element on the geometric central axis does not change before and after the axial deformation. So Eq. (7) can be obtained.

$$ {R}_{\rho}\cdot d\varphi =\frac{1}{K^{\prime }}\cdot d{\varphi}_1 $$
(7)

where K′ is the curvature at the pipe geometric central axis after the axial bending. Then, Eq. (7) is introduced into Eq. (6), the axial strain can be expressed as follows:

$$ {\varepsilon}_{\varphi }=\ln \frac{2{R}_{\rho }{K}^{\prime }}{\left(2{R}_{\rho }+2r\sin \theta + rd\theta \cos \theta \right)\cdot K} $$
(8)

Based on the geometric relationships as shown in Fig. 8 and Fig. 9, the distance between the element and the cross-section in which the pipe geometric central axis is located remains unchanged before and after the axial bending. So Eq. (9) can be obtained.

$$ \frac{1}{K}=\frac{1}{K^{\prime }}-\left(r\sin \theta +\frac{rd\theta \cos \theta }{2}\right) $$
(9)

Substituting Eq. (9) into Eq. (8), the axial strain of the element can be obtained, such as Eq. (10).

$$ {\varepsilon}_{\varphi }=\ln \frac{4{R}_{\rho }}{\left(2+2 rK\sin \theta + rKd\theta \cos \theta \right)\cdot \left(2{R}_{\rho }+2r\sin \theta + rd\theta \cos \theta \right)} $$
(10)

3.2.2 Circumferential strain model

The pipe before and after the circumferential bending is shown in Fig. 10. The cross-section, in which the element is located, is initially assumed circular. According to the stress state of the pipe, the compressed regions are defined as the reverse bending regions, and the regions between the two reverse bending regions are the positive bending regions. According to the loading condition and symmetry, there are three equal positive bending regions and three equal reverse bending regions evenly distributed across the entire pipe cross-section [10].

Fig. 10
figure 10

Before and after the circumferential bending of the pipe. (R) Reverse bending region. (P) Positive bending region

Full size image

The initial length l02 of the element along the circumferential direction is obtained as Eq. (11).

$$ {l}_{02}=r\cdot d\theta $$
(11)

The length lAB(DC) of the element along the circumferential direction after the circumferential bending can be expressed as Eq. (12).

$$ {l}_{\mathrm{AB}\left(\mathrm{DC}\right)}=\frac{1}{K_1}\cdot d{\theta}_1 $$
(12)

where K1 is the curvature of the element after the circumferential bending, and dθ1 is the radian of the element after the circumferential bending. The circumferential strain εθ of the element after the circumferential bending can be expressed as follows:

$$ {\varepsilon}_{\theta }=\ln \frac{l_{\mathrm{AB}\left(\mathrm{DC}\right)}}{l_{02}}=\ln \frac{d{\theta}_1}{rK_1 d\theta} $$
(13)

According to assumption (5), Eq. (14) can be obtained.

$$ \left(r-\frac{t}{2}\right)\cdot d\theta =\left(\frac{1}{K_1^{\prime }}-\frac{t}{2}\right)\cdot d{\theta}_1 $$
(14)

where \( {K}_1^{\prime } \) is the curvature of the neutral layer of pipe after the circumferential bending, and dθ1 is the radian at the neutral layer of pipe after the circumferential bending. Since the research object is a thin-walled pipe, the wall thickness is ignored. It can be considered that the curvature of the element after the circumferential bending is equal to that of the neutral layer of the element. So Eq. (15) can be obtained.

$$ {K}_1={K}_1^{\prime } $$
(15)

Equations (14) and (15) are introduced into Eq. (13); the circumferential strain εθ can be expressed as follows:

$$ {\varepsilon}_{\theta }=\ln \frac{2r-t}{\left(2-{tK}_1\right)\cdot r} $$
(16)

3.2.3 Equivalent strain \( \overline{\varepsilon} \) and equivalent stress \( \overline{\sigma} \)

According to assumption (3), it can be concluded as Eq. (17).

$$ {\varepsilon}_{\varphi }+{\varepsilon}_{\theta }+{\varepsilon}_r=0 $$
(17)

Because εr = 0,

$$ {\varepsilon}_{\varphi }=-{\varepsilon}_{\theta } $$
(18)

Based on reference [23], the equivalent strain can be obtained in Eq. (19).

$$ \overline{\varepsilon}=\frac{\sqrt{2}}{3}\sqrt{{\left({\varepsilon}_{\varphi }-{\varepsilon}_{\theta}\right)}^2+{\left({\varepsilon}_{\varphi }-{\varepsilon}_r\right)}^2+{\left({\varepsilon}_r-{\varepsilon}_{\theta}\right)}^2} $$
(19)

The equivalent strain \( \overline{\varepsilon} \) of the element after deformation can be described as follows:

$$ \overline{\varepsilon}=\frac{2\sqrt{3}}{3}\left|{\varepsilon}_{\varphi}\right|\kern0.5em \mathrm{or}\kern0.5em \overline{\varepsilon}=\frac{2\sqrt{3}}{3}\left|{\varepsilon}_{\theta}\right| $$
(20)

By substituting Eq. (20) into Eq. (2), the equivalent stress \( \overline{\sigma} \) of the element after deformation can be obtained as follows:

$$ \overline{\sigma}={\sigma}_s\left(1-\frac{D}{E}\right)+\frac{2\sqrt{3}\cdot D}{3}\left|{\varepsilon}_{\varphi}\right|\kern0.5em \mathrm{or}\kern0.5em \overline{\sigma}={\sigma}_s\left(1-\frac{D}{E}\right)+\frac{2\sqrt{3}\cdot D}{3}\left|{\varepsilon}_{\theta}\right| $$
(21)

3.3 Solution of mechanical model

According to the above analysis εφ =  − εθ, the equivalent strain of the element can be solved by analyzing the circumferential strain or axial strain. Each roller can be divided into five stages as shown in Fig. 2. The roundness and straightness calibration stage (Stage C) and roundness calibration stages (Stage B) are mainly analyzed during the deformation of the pipe, as shown in Fig. 11.

Fig. 11
figure 11

Diagram of the axial deformation of pipe

Full size image

3.3.1 Roundness and straightness calibration stage (Stage C)

Due to the constraints of the upper and lower rollers on the pipe, the outline of the pipe after deformation along the axial direction coincides with the shape curve of roller. The coordinates and curvature of the pipe are the same as those of the roller in the contact zone.

The roller shape curve of Stage C is assumed to be in the form of Eq. (22), as shown in Fig. 11.

$$ \frac{x^2}{m^2}-\frac{y^2}{n^2}=1 $$
(22)

where m and n are constants. The axial curvature of the element after deformation should meet the following condition:

$$ K=\frac{\left|{y}^{{\prime\prime}}\right|}{{\left(1+{y^{\prime}}^2\right)}^{3/2}}=\frac{mn^4}{{\left({y}^2\left({m}^2+{n}^2\right)+{n}^4\right)}^{3/2}} $$
(23)

where K is the axial curvature of the element after deformation. By substituting Eq. (23) into Eq. (10), the axial strain of the element can be obtained. The equivalent strain and equivalent stress of the element can be solved through Eqs. (20) and (21), such as Eqs. (24) and (25).

$$ \overline{\varepsilon}=\frac{2\sqrt{3}}{3}\left|\ln \frac{4{R}_{\rho }}{\left(2+2 rK\sin \theta + rKd\theta \cos \theta \right)\left(2{R}_{\rho }+2r\sin \theta + rd\theta \cos \theta \right)}\right| $$
(24)
$$ \overline{\sigma}={\sigma}_s\left(1-\frac{D}{E}\right)+\frac{2\sqrt{3}D}{3}\left|\ln \frac{4{R}_{\rho }}{\left(2+2 rK\sin \theta + rKd\theta \cos \theta \right)\left(2{R}_{\rho }+2r\sin \theta + rd\theta \cos \theta \right)}\right| $$
(25)

3.3.2 Roundness calibration stages (Stage B)

Because εφ = − εθ, it is convenient to solve the circumferential strain of pipe at Stage B, so as to solve the equivalent strain of pipe according to Eq. (19).

The circumferential deformation of pipe before and after loading is shown in Fig. 12. It can be observed that the curve PQ is in the reverse bending region, and the curvature decreases gradually from both ends to the center. The curve WT is in the positive bending region, and the curvature increases gradually from both ends to the center.

Fig. 12
figure 12

Circumferential deformation of pipe

Full size image

Reverse bending region

Based on the curvature variation law of the curve PQ, the curvature distribution of reverse bending region is described mathematically. The deformation curve of the reverse bending region is shown in Fig. 13.

Fig. 13
figure 13

Deformation curve of the reverse bending region

Full size image

As shown in Fig. 13, the curve PQ can be described in the form of Eq. (26).

$$ \frac{{x_1}^2}{{a_1}^2}+\frac{{y_1}^2}{{b_1}^2}=1\left({a}_1>{b}_1>0\right) $$
(26)

The curvature equation of the curve PQ can be expressed as follows:

$$ {K}_1=\frac{\left|{y}^{{\prime\prime}}\right|}{{\left(1+{y^{\prime}}^2\right)}^{3/2}}=\frac{{a_1}^4{b}_1}{{\left({a_1}^4+\left({b_1}^2-{a_1}^2\right){x_1}^2\right)}^{3/2}} $$
(27)

The coordinate of point Q under the coordinate system x1o1y1 is \( \left({m}_1,{y}_{m_1}\right) \). Since the curve PQ is symmetrical about the axis y1, the coordinate of point P can be represented as \( \left(-{m}_1,{y}_{m_1}\right) \).

Boundary conditions must be applied to obtain the constants in Eq. (26) and Eq. (27) [24]. As shown in Fig. 13, there is a boundary condition. That is, if x1 is 0, then y1 = r − H. By substituting it into Eq. (26), Eq. (28) can be obtained.

$$ {b}_1=r-H $$
(28)

Suppose the demarcation point of the positive and reverse bending regions is unchanged before and after the deformation, the following two boundary conditions can be obtained. The first is that if \( {x}_1=\pm {m}_1\left({m}_1>0\right) \), \( {y}_1={y}_{m_1} \), then \( {K}_1\left|{}_{x_1=\pm {m}_1}\right.=1/r \). The second is that if \( {x}_1=\pm {m}_1\left({m}_1>0\right) \), then \( {m_1}^2+{y_{m_1}}^2={r}^2 \).

The former is introduced into Eq. (27), and it is given as follows:

$$ \frac{{a_1}^4{b}_1}{{\left({a_1}^4+\left({b_1}^2-{a_1}^2\right){m_1}^2\right)}^{3/2}}=\frac{1}{r} $$
(29)

The latter is introduced into Eq. (27), and it is given as follows:

$$ \frac{{a_1}^4{b}_1}{{\left({a_1}^4+\left({b_1}^2-{a_1}^2\right)\frac{{a_1}^2\left({b_1}^2-{r}^2\right)}{{b_1}^2-{a_1}^2}\right)}^{3/2}}=\frac{1}{r} $$
(30)

In that case, the curve PQ can be solved by substituting Eqs. (28), (29), and (30) into Eq. (26) (see Appendix A for details) as follows:

$$ \left.\begin{array}{l}\frac{{x_1}^2}{\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\frac{a}{3}}+\frac{{y_1}^2}{{\left(r-H\right)}^2}=1\\ {}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}\kern1.00em \left(-{m}_1\le {x}_1\le {m}_1;{y}_{m_1}\le {y}_1\le r-H\right)\end{array}\right\} $$
(31)

where \( {m}_1=\sqrt{\frac{\left(\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\frac{a}{3}\right)\left({H}^2-2 rH\right)}{{\left(r-H\right)}^2-\left(\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\frac{a}{3}\right)}} \), \( {y}_{m_1}={\left({r}^2-{m_1}^2\right)}^{1/2} \).

The curvature equation of the curve PQ can be expressed as Eq. (32).

$$ {K}_1=\frac{{\left(\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\frac{a}{3}\right)}^2\left(r-H\right)}{{\left({\left(\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\frac{a}{3}\right)}^2+\left({\left(r-H\right)}^2-\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\frac{a}{3}\right){x_1}^2\right)}^{3/2}} $$
(32)

It is worth noting that the coordinates and circumferential curvature of any element of the pipe can be solved in the reverse bending region according to Eqs. (31) and (32). By substituting Eq. (32) into Eq. (16), the circumferential strain can be solved. And the equivalent strain and equivalent stress of the element can be further obtained through Eqs. (20) and (21) as follows:

$$ \overline{\varepsilon}=\frac{2\sqrt{3}}{3}\left|\ln \frac{2r-t}{\left(2-{tK}_1\right)r}\right| $$
(33)
$$ \overline{\sigma}={\sigma}_s\left(1-\frac{D}{E}\right)+\frac{2\sqrt{3}\cdotp D}{3}\left|\ln \frac{2r-t}{\left(2-{tK}_1\right)r}\right| $$
(34)

Positive bending region

Based on the curvature variation law of the curve WT, the curvature distribution of positive bending region is described mathematically. The deformation curve of the positive bending region is shown in Fig. 14.

Fig. 14
figure 14

Deformation curve of the positive bending region

Full size image

As shown in Fig. 14, the curve WT can be expressed as the form of Eq. (35).

$$ {x_2}^2-{y_2}^2={a_2}^2\left({a}_2\ne 0\right) $$
(35)

The curvature equation of the curve WT can be expressed as Eq. (36).

$$ {K}_2=\frac{\left|{y}^{{\prime\prime}}\right|}{{\left(1+{y^{\prime}}^2\right)}^{3/2}}=\frac{{a_2}^2}{{\left(2{y_2}^2+{a_2}^2\right)}^{3/2}} $$
(36)

The coordinate of point T under the coordinate system x2o2y2 is \( \left({x}_{m_2},{m}_2\right) \). Since the curve WT is symmetrical about the axis x2, the coordinate of point W is \( \left({x}_{m_2},-{m}_2\right) \).

As shown in Fig. 12, point Q and point W are coincident; the curvature of the two points is equal. Thus, a boundary condition can be obtained, namely if \( {x}_2={x}_{m_2} \), then \( {y}_2=-{m}_2\left({m}_2>0\right) \). According to this condition, the following equation can be given as follows:

$$ {K}_2\left|{}_{{\mathrm{y}}_2=-{m}_2}\right.=\frac{1}{r} $$
(37)

The curve WT is obtained as Eq. (38) (see Appendices B and C for details).

$$ \left.\begin{array}{l}{x_2}^2-{y_2}^2=\sqrt[3]{-\frac{q_1}{2}+\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}+\sqrt[3]{-\frac{q_1}{2}-\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}-\frac{e}{3}\\ {}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}\kern1.00em \left({a}_2\le {x}_2\le {x}_{m_2};-{m}_2\le {y}_2\le {m}_2\right)\end{array}\right\} $$
(38)

where \( {a}_2={\left(\sqrt[3]{-\frac{q_1}{2}+\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}+\sqrt[3]{-\frac{q_1}{2}-\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}-\frac{e}{3}\right)}^{1/2} \), \( {x}_{m_2}={\left({m_2}^2+{a_2}^2\right)}^{1/2} \), \( {m}_2=r\sin \frac{2\pi -6\arcsin \frac{m_1}{r}}{6} \).

The curvature equation of the curve WT can be expressed as Eq. (39).

$$ {K}_2=\frac{\sqrt[3]{-\frac{q_1}{2}+\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}+\sqrt[3]{-\frac{q_1}{2}-\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}-\frac{e}{3}}{{\left(2{y_2}^2+\sqrt[3]{-\frac{q_1}{2}+\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}+\sqrt[3]{-\frac{q_1}{2}-\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}-\frac{e}{3}\right)}^{3/2}} $$
(39)

It should be pointed out that, depending on Eqs. (38) and (39), the coordinates and circumferential curvature of any element of the pipe are solved in the positive bending region. By substituting Eq. (39) into Eq. (16), the circumferential strain can be solved. The equivalent strain and equivalent stress of the element can be further obtained by Eqs. (20) and (21) as follows:

$$ \overline{\varepsilon}=\frac{2\sqrt{3}}{3}\left|\ln \frac{2r-t}{\left(2-{tK}_2\right)r}\right| $$
(40)
$$ \overline{\sigma}={\sigma}_s\left(1-\frac{D}{E}\right)+\frac{2\sqrt{3}\cdot D}{3}\left|\ln \frac{2r-t}{\left(2-{tK}_2\right)r}\right| $$
(41)

The equivalent strain and equivalent stress of the element can be obtained as follows:

$$ \overline{\varepsilon}=\left\{\begin{array}{l}\frac{2\sqrt{3}}{3}\left|\ln \frac{4{R}_{\rho }}{\left(2+2 rK\sin \theta + rKd\theta \cos \theta \right)\left(2{R}_{\rho }+2r\sin \theta + rd\theta \cos \theta \right)}\right|\ \left(\mathrm{Stage}\ \mathrm{C}\right)\\ {}\left.\begin{array}{l}\frac{2\sqrt{3}}{3}\left|\ln \frac{2r-t}{\left(2-{tK}_1\right)r}\right|\ \left(\mathrm{Reverse}\ \mathrm{bending}\ \mathrm{region}\right)\\ {}\frac{2\sqrt{3}}{3}\left|\ln \frac{2r-t}{\left(2-{tK}_2\right)r}\right|\ \left(\mathrm{Positive}\ \mathrm{bending}\ \mathrm{region}\right)\end{array}\right\}\kern0.5em \left(\mathrm{Stage}\mathrm{s}\ \mathrm{B}\right)\end{array}\right.\kern0.5em $$
(42)
$$ \overline{\sigma}=\left\{\begin{array}{l}{\sigma}_s\left(1-\frac{D}{E}\right)+\frac{2\sqrt{3}D}{3}\left|\ln \frac{4{R}_{\rho }}{\left(2+2 rK\sin \theta + rKd\theta \cos \theta \right)\left(2{R}_{\rho }+2r\sin \theta + rd\theta \cos \theta \right)}\right|\left(\mathrm{Stage}\ \mathrm{C}\right)\\ {}\left.\begin{array}{l}{\sigma}_s\left(1-\frac{D}{E}\right)+\frac{2\sqrt{3}D}{3}\left|\ln \frac{2r-t}{\left(2-{tK}_1\right)r}\right|\ \left(\mathrm{Reverse}\ \mathrm{bending}\ \mathrm{region}\right)\\ {}{\sigma}_s\left(1-\frac{D}{E}\right)+\frac{2\sqrt{3}D}{3}\left|\ln \frac{2r-t}{\left(2-{tK}_2\right)r}\right|\ \left(\mathrm{Positive}\ \mathrm{bending}\ \mathrm{region}\right)\end{array}\right\}\left(\mathrm{Stage}\mathrm{s}\ \mathrm{B}\right)\end{array}\right. $$
(43)

where \( K=\frac{mn^4}{{\left({y}^2\left({m}^2+{n}^2\right)+{n}^4\right)}^{3/2}} \), b1 = r − H, a = 3b12 − 3r2, b = 3b14 − 7b12r2 + 3r4, c = b16 − 3b14r2 + 3b12r4 − r6, \( p=b-\frac{a^2}{3} \), \( q=\frac{2{a}^3}{27}+c-\frac{ab}{3} \), \( {K}_1=\frac{{\left(\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\frac{a}{3}\right)}^2\left(r-H\right)}{{\left({\left(\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\frac{a}{3}\right)}^2+\left({\left(r-H\right)}^2-\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\frac{a}{3}\right){x_1}^2\right)}^{3/2}} \), e = 6m22 − r2, f = 12m24, g = 8m26, \( {p}_1=f-\frac{e^2}{3} \), \( {q}_1=\frac{2{e}^3}{27}+g-\frac{ef}{3} \), \( {m}_2=r\sin \frac{2\pi -6\arcsin \frac{m_1}{r}}{6} \), \( {m}_1=\sqrt{\frac{\left(\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\frac{a}{3}\right)\left({H}^2-2 rH\right)}{{\left(r-H\right)}^2-\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}-\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\frac{a}{3}}} \), \( {K}_2=\frac{\sqrt[3]{-\frac{q_1}{2}+\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}+\sqrt[3]{-\frac{q_1}{2}-\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}-\frac{e}{3}}{{\left(2{y_2}^2+\sqrt[3]{-\frac{q_1}{2}+\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}+\sqrt[3]{-\frac{q_1}{2}-\sqrt{{\left(\frac{q_1}{2}\right)}^2+{\left(\frac{p_1}{3}\right)}^3}}-\frac{e}{3}\right)}^{3/2}} \).

4 Numerical simulation and experimental design

The Al6063 pipe is modeled in ABAQUS software, which aims to obtain the distribution of equivalent stress and equivalent strain and the coordinates of any element of the deformed pipe. Then, the results are compared with those of the mechanical model. Also, a three-roller bending device is designed in this section to obtain the deformation curves of the pipe in different directions. Then, the results are compared with the simulation results and theoretical result.

4.1 Numerical simulation

The geometric dimension and mechanical properties of the pipe are shown in Table 1 and Table 2. The geometric dimension of the roller is shown in Table 3. The deformation process is simulated. The finite element model is shown in Fig. 15. The pipe is set as a deformable body, and the upper roller and lower rollers are set as discrete rigid bodies. The pipe is discretized by 8-node linear hexagonal incompatible mode elements. The contact between the pipe and each roller is set as a pure master-slave and kinematic contact condition, and the frictional coefficient is 0.2.

Table 1 Geometric dimension of pipe
Full size table
Table 2 Mechanical properties of pipe
Full size table
Table 3 Geometric dimension of the rollers
Full size table
Fig. 15
figure 15

Finite element model

Full size image

4.2 Experimental design

A three-roller bending device is developed, as shown in Fig. 16. It is mainly composed of an upper roller, two lower rollers, three sliding blocks, and a rack. The three rollers are connected to the three sliding blocks fixed on the rack by corresponding bearings. The sliding blocks can slide vertically along the rack by rotating screws to adjust the radial reduction of three rollers. The geometric dimension of the three rollers is given in Table 3. The pipe selected for the experiment is the same as that for simulation.

Fig. 16
figure 16

Three-roller bending device

Full size image

The pipe is placed between three rollers. According to the pre-set process parameters, the radial reduction of the three rollers is adjusted. Then, the coordinates of the circumferential and axial outline of the loading pipe are measured by using the coordinate measuring machine with a measurement accuracy of 0.01mm.

5 Results and discussion

5.1 Distribution of equivalent stress and equivalent strain

The equivalent stress and equivalent strain at different stages and the equivalent stress and equivalent strain of different regions at the same stage are derived from the numerical simulation. The results are compared with the theoretical results. The distribution of equivalent stress and equivalent strain is shown in Fig. 17.

Fig. 17
figure 17

Distribution of equivalent stress and equivalent strain. (a) Equivalent stress. (b) Equivalent strain

Full size image

5.1.1 Roundness and straightness calibration stage (Stage C)

According to the symmetry of deformation, the one-third pipe is selected for analysis. The equivalent stress and equivalent strain of the section located at the center of Stage C are derived from the numerical simulation as shown in Fig. 17. The comparison between the theoretical results and simulation results is presented in Fig. 18. The maximum relative error ηmax between the simulation results and the theoretical results of equivalent stress and equivalent strain is 24.87% and 22.39%, respectively. The main reason for the error is that the constitutive models used in the simulation and theoretical analysis are different. In the simulation, the kinematic hardening constitutive model is adopted. However, to be solvable, the linear simple kinematic hardening constitutive model is adopted in the theoretical analysis, which is between the linear classical kinematic hardening constitutive model and the linear isotropic hardening constitutive model [20]. In this model, the parameters are few and constant, and the influence of deformation history on subsequent yield stress is ignored. During the process of reciprocating bending, the yield stress is always constant, which greatly facilitates the analysis of the reciprocating bending.

Fig. 18
figure 18

Comparison of theoretical results with simulation results at Stage C. (a) Equivalent stress. (b) Equivalent strain

Full size image

Further observed is that the maximum relative error occurs in the contact zone between the roller and the pipe. This is most likely due to a sharp increase in stress and strain caused by the constraints of the rollers on the pipe. Nevertheless, the stress-strain distribution solved by the mechanical model is generally consistent with the simulation results, thus verifying a good validity of the theoretical analysis of Stage C.

5.1.2 Roundness calibration stages (Stage B)

The curvature distribution in the positive and reverse bending regions at a radial reduction of 2.0 mm from theoretical results is shown in Fig. 19. It can be seen that the curvature gradually decreases from both ends to the center in the reverse bending region, while the curvature gradually increases from both ends to the center in the positive bending region.

Fig. 19
figure 19

Curvature distribution of Stage B from theoretical results

Full size image

Reverse bending region

The equivalent stress and equivalent strain of the reverse bending region of Stage B are derived from the numerical simulation as shown in Fig. 17. The comparison between the theoretical results and simulation results of the equivalent stress and equivalent strain in the reverse bending region is shown in Fig. 20.

Fig. 20
figure 20

Comparison of theoretical results with simulation results in the reverse bending region. (a) Equivalent stress. (b) Equivalent strain

Full size image

As can be found from Fig. 20, the maximum relative error ηmax between the simulation results and the theoretical results of the equivalent stress with a radial reduction of 1.0 mm is 12.36%, higher than the maximum relative error (3.78%) of 2 mm of the radial reduction. Similarly, the maximum relative error between the two results of the equivalent strain with a radial reduction of 1.0 mm is 18.57%, slightly larger than the value (12.11%) at a radial reduction of 2 mm. The above shows that radial reduction has played a role in the distribution of stress-strain of the pipe and the maximum relative error. In addition, the two results show a good match; the maximum relative error is not more than 20%, so that the theoretical analysis of the reverse bending region is proved to be available.

Positive bending region

The equivalent stress and equivalent strain of the positive bending region of Stage B are derived from the numerical simulation as shown in Fig. 17. The comparison between the theoretical results and simulation results of the equivalent stress and equivalent strain in the positive bending region is shown in Fig. 21. The maximum relative error ηmax between the two results of equivalent stress is not much different from the value of the equivalent strain, and varies in the range of 15 to 21%. From this, it can be found that the stress-strain distribution obtained by the mechanical model is consistent with the simulation results, thus confirming the feasibility of the theoretical analysis of the positive bending region.

Fig. 21
figure 21

Comparison of theoretical results with simulation results in the positive bending region. (a) Equivalent stress. (b) Equivalent strain

Full size image

In particular, it should be noted that the distribution of equivalent stress and equivalent strain, whether in the positive or reverse bending regions, is gradually steep with the increase of radial reduction. Consequently, the model provides a guide for the setting of process parameters.

5.2 Axial and circumferential deformation

To further verify the applicability of the mechanical model, the deformation curves of the circumferential and axial directions are compared with simulation results and experimental results.

5.2.1 Axial deformation

As mentioned in the previous analysis, the effect of the roller’s loading and unloading stages on the pipe is ignored, and Stage C and Stage B are mainly studied. The axial deformation of the pipe from numerical simulation is shown in Fig. 22. It is clear that the maximum equivalent stress along the axial direction of the pipe appears in Stage C, with a value of 295 MPa.

Fig. 22
figure 22

Axial deformation of the pipe from numerical simulation

Full size image

The axial deformation of the pipe from the experiment is shown in Fig. 23. The axial deformation curve is obtained by fitting the axial contour coordinates of the deformed pipe in the experiment.

Fig. 23
figure 23

Axial deformation of the pipe from experiment

Full size image

The comparison of the theoretical results, simulation results, and experimental results about the axial deformation curve is shown in Fig. 24. Comparing the axial deformation curve obtained by the mechanical model with the experimental results, a good match is obtained. However, compared with the above two results, the deformation curve obtained by simulation results has a difference of 1.15 mm, which is caused by the contact between rollers and pipes in numerical simulation.

Fig. 24
figure 24

Comparison of the axial deformation curves

Full size image

5.3 Circumferential deformation

The circumferential deformation of the pipe from numerical simulation is shown in Fig. 25. It can be seen that three reverse bending regions and three positive bending regions are uniformly distributed in the entire cross-section of the pipe at Stage B.

Fig. 25
figure 25

Circumferential deformation of the pipe from numerical simulation

Full size image

The circumferential deformation of the pipe from the experiment is shown in Fig. 26. The circumferential deformation curve is obtained by fitting the circumferential contour coordinates of the deformed pipe in the experiment.

Fig. 26
figure 26

Circumferential deformation of the pipe from the experiment

Full size image

The comparison of the circumferential deformation curves is shown in Fig. 27. As above, the circumferential deformation curve obtained by the mechanical model can be well matched with the experimental results. Yet the deformation curve obtained by the simulation results is different from the other two results, and there is still a difference of 2.78 mm. The cause of this result is consistent with that of the axial deformation.

Fig. 27
figure 27

Comparison of the circumferential deformation curves

Full size image

The axial and circumferential deformation curves obtained by the mechanical model fit well with the experimental and simulation results, and the maximum error is not greater than 3.0 mm. It is proved that the mathematical description of axial and circumferential deformation curves is basically accurate. Furthermore, the model can predict axial or circumferential deformation curves based on different roller shapes, thereby providing a shortcut to optimize the roller shape.

6 Conclusions

Mechanical models have been presented so far for calibrating roundness and straightness based on unidirectional reciprocating bending. Apart from these models’ errors concerning the practical reality, they cannot describe deformation curves in different directions. The deformation curve of the pipe in different directions can be depicted by the mechanical model developed in this paper. Roller shape and process parameters have been considered in this model. The stress-strain distribution of the pipe during the deformation process is obtained using the model. Specifically, Al6063 pipes are simulated and experimented. The results are compared with the theoretical results. The distribution of equivalent stress and equivalent strain obtained with the model is not much different from the simulation results. The maximum relative error is not more than 25%. The distribution of equivalent stress, equivalent strain, and maximum relative error is all related to the radial reduction, and the distribution tends to be gentle with the decrease of radial reduction, which provides guidance for the setting of process parameters. The pipe stress and strain concentration occurs at the center of the positive bending regions and the center of the reverse bending regions, that is, the contact zone between the pipe and the rollers. The axial and circumferential deformation curves calculated by the mechanical model are in good agreement with the simulation and experimental results, and the maximum error is not greater than 3.0 mm. Accordingly, the mechanical model developed in this paper is validated. This study can provide a theoretical basis for setting process parameters and optimizing roller shape.