1 Introduction

As we all know, precision machining is a kind of manufacturing technology targeted at high accuracy. It is not only given priority to develop by many countries but also becomes a standard to measure manufacturing level of a certain country [1]. The integrated volumetric error modeling is one of the effective ways to improve the machining accuracy. The integrated volumetric error modeling is one of the effective ways to improve the machining accuracy. It can be used with on-site measurement, error compensation technology [2,3,4,5], and process improvement method [6,7,8,9], which aims to establish the relationship between error components caused by assembled components and the resulting geometric errors, and to increase the accuracy of a precision machine tool [10]. The technology can describe the topological structure of MBS simply with matrix on the basis of Houston-proposed [11] multi-body system (MBS) and homogeneous transformation matrix (HTM) theory [12]. However, in terms of some error analysis, a parametric form of volumetric error modeling is included certainly if the technology is applied. Moreover, referring to crucial geometric errors identification [13,14,15,16], it is getting more and more important to reduce theoretical calculation errors and enhance modeling accuracy. In such cases, it is still required to establish a volume error model represented by multiple parameter variables.

Error modeling technology mainly involves two computational tasks. For one thing, pure mathematical 4 × 4 characteristic matrices are only adopted for the volumetric error modeling, where measurement values of the error components are directly substituted into elements of the error transfer matrices. Then, deviations for the tool relative to the workpiece are available from error components after the iterations. For another thing, as for error components represented by parametric variables, the iterations of 4 × 4 characteristic matrices are selected to establish a synthesis error model. According to the measurement standards [17,18,19], a synthesis error model with parameters, obtaining the total error effect in terms of individual error components, is established to identify critical geometric errors by various methods, such as decoupling geometric error [20, 21], representing sensitivity coefficient [22,23,24], separating the crucial geometric error [25,26,27], checking volumetric error compensation [28,29,30], and improving process [6,7,8,9, 21, 31,32,33,34] as well as selecting measurement scheme [35, 36]. For example, Zhou et al. [32] have studied the volumetric error theory and its compensation method regarding a large five-axis CNC gear grinding machine tool. Firstly, by using iterations of characteristics matrices where error components are represented by parameters, geometric errors of the tool relative to the workpiece gear were expressed as the position functions of motion errors in machine tool structures; then, geometric errors were decoupled and compensated to each axis through the Jacobian matrix of the machine tool; as a result, the machining accuracy of the precision CNC machine tool was totally improved. Besides, Chen et al. [37] put forward that a synthesis error model represented by parametric variables could be used for four-axis CNC machine tool to improve machining accuracy of a cycloid gear. During their research, some factors had an effect on volumetric error modeling, such as working conditions, processing measurements, and identification of crucial geometric errors. If those factors are considered, the volumetric error modeling inevitably involved the iterative solution of characteristic matrices with error components represented by parameters, so that the accuracy and machining performance of tool tip position could be enhanced by means of error compensation. Therefore, in case of error modeling technology applied into precision machine tools, it is very important to establish a volumetric error model represented by parameters before on-site measurement and error compensation experiments. Meanwhile, the veracity of modeling precision also plays a significant role in synthesis error modeling for a machine tool. In addition, Chen et al. [38], on the basis of MBS and HTM theory, established volumetric error model with the parametric variables for five-axis machine tool, and analyzed respectively the sensitivity of volumetric error regarding 37 error components. Consequently, their achievements are used for precision designing and manufacturing successfully. Moreover, according to MBS theory and error spatial morphology of S-shaped test piece, Wang et al. [39] adopted a novel causation analysis method and established tool axis surface parameterized error model of a five-axis machine tool, aiming at improving design accuracy. Finally, it can be seen that for MBS and HTM theory, analysis and solution of theoretical calculation error are essential works during iterations of the parametric transfer matrices.

However, it is shown in this study that with the increase of motion axes, the iterative computation and complexity are raised gradually after a lot of analogy analysis in the early stages of numerical simulations regarding volumetric error models, where error characteristic matrices are represented by parametric variables and error compensation experiments have been performed [21, 32, 37]. Moreover, if small error exists and higher-order terms are neglected, there are indeed certain amounts of theoretical calculation errors in the accuracy of the volumetric error modeling with parameters. For instance, given that real geometric value of errors caused by measuring instruments and process improvements as well as related working condition requirements is about 10−5, the modeling precision of volumetric error model expressed by parameters should be controlled to 10−6 at least to avoid theoretical calculation error brought by the decrease of modeling accuracy. It is presented that application of current solutions can only lead to an error modeling precision being equal to or even lower than the numerical deviations [21, 32, 37]. Moreover, if motion axes of precision CNC machine tool increase, the deviation for the error modeling precision will be larger, and even exceed real value of error components. That is to say, modeling accuracy is relatively reduced. As a result, the precision mentioned above would bring great uncertainty of theoretical calculation errors. Besides, there is a lack of theoretical verification method to judge if modeling accuracy is correct. Based on those analyses, it is seen that modeling accuracy plays an especially important role in error modeling technology used for precision machine tool. In consequence, the precision above would lead to great uncertainty in error modeling technology of precision machine tools and have certain influence on its machining accuracy and performance. Generally, elimination of current theoretical calculation error in design stage is the core to keep accuracy of error modeling and shall be paid attention to study deeply. But, at present, there is no practical way to realize it and researches on parametric modeling accuracy are in great short. What’s more, verification method to judge modeling precision is still in small number [2,3,4,5,6, 8, 10,11,12,13,14,15,16,17, 20, 21, 25,26,27,28,29,30, 32, 33, 35,36,37,38,39]. It is wished that the design methods and conclusions of this study can be an effective approach to optimize and verify the modeling accuracy during the process of theoretical design and verification. Meanwhile, if some researchers are interested in the technology, there is a hope that the methods and conclusions can serve their subsequent experiments better. Additionally, from the perspective of geometric error compensation, the increase of modeling precision and relative decrease of theoretical computation error have a great influence on improving performance of precision CNC machine tools and enhancing machining precision. With the development of our knowledge and demand for precision machining technology, it is witnessed that different times or technical phases have various definitions and standards. Among them, precision and ultra-precision are symbols of two standards. On one hand, they are related to specific indexes [40, 41], such as machining size, shape accuracy, and surface quality. On the other hand, it is generally considered that if the ratio of accuracy to machining size, namely accuracy ratio, reaches to 10−6, the machining is called as ultra-precision work [1]. But, for precision and ultra-precision machining targeted at high accuracy, it is always required to improve machining precision in complicated systems engineering for meeting technical needs in different times. Moreover, although experimenting is an effective way to proof theory, the basis of experiment is still theoretical design and calibration. Besides, experiment itself involves many objective factors, such as high cost, long period, and great uncertainty. Hence, in the field of cost-effective manufacturing, it is beneficial for technicians to learn about effects of the theoretical modeling accuracy on the precision machining in the early design stages, where error components are represented by parameters.

To sum up, the overall goal of this paper is to overcome certain theoretical calculation errors of volumetric error modeling represented by parametric variables and examine verification method for judging the accuracy of the modeling precision in the early design stages. From the viewpoint of mathematical theory, it is contributed to put forward an optimized algorithm and the verification methods. With the new mutual verification methods, it can realize the comparative analysis of different algorithms, such as numerical, iterative, and optimal as well as existing algorithm, which is not only able to reveal certain theoretical calculation errors caused by both the decrease of modeling precision and the lack of verification methods but also to demonstrate the effectiveness and accuracy of the proposed algorithm for a SKMC-3000/20 CNC form grinding machine tool. This has already become our research object and its error compensation experiments have been carried out [32]. As a result, the theoretical calculation errors can be identified respectively and eliminated largely by means of numerical simulations in the Matlab. Moreover, this research further explores a theoretical guidance in selecting appropriate treatment to achieve the modeling accuracy for iterations of the characteristic matrices expressed by parameters, with the consideration of working conditions. Finally, in case of error modeling technology, the machining accuracy and performance of precision machine tools can be significantly improved regarding theoretical modeling precision.

This study mainly includes five parts: Section 1-Introduction, Section 2-Factors affecting accuracy of the error modeling, Section 3-An optimized algorithm and the verification methods, Section 4-Illustrating example, and Section 5-Conclusions.

2 Factors affecting accuracy of the error modeling

To eliminate certain theoretical calculation errors, the factors influencing the accuracy of error modeling are firstly analyzed in the volumetric error modeling, where error components are represented by parameters. The details are listed as follows:

  1. 1.

    Under different working conditions, the solutions to the inverse matrix of the characteristic matrix would affect the modeling accuracy during iterations.

  2. 2.

    Regarding iterations of the characteristic matrices, different solutions have positive influence on modeling accuracy, such as effective removing of pseudo-inverse matrix and accurate avoiding of iterations containing denominator polynomial as well as precise judgment and elimination of higher-order term.

  3. 3.

    Based on the small error hypothesis theory and given that the contributions of high-order terms disappeared, it is known that with the increase of motion axes, the iterative computation and complexity of the volumetric error modeling would add relatively, which have certain impact on modeling accuracy.

Thus, in consideration of error modeling technology used in precision machines tools, there are three reasons in this study influencing modeling accuracy. However, the core is the elimination of current theoretical calculation errors to ensure the modeling accuracy and how to guarantee the accuracy is to be verified.

3 An optimized algorithm and the verification methods

3.1 An optimized algorithm

Based on the small error hypothesis theory and the ignoring of the high-order infinitesimal, a novel optimized algorithm is proposed to eliminate the theoretical calculation errors in geometric error modeling with parametric representation, with the above influencing factors being considered. What’s more, the algorithm has been applied for a patent. It includes the following four aspects. (1) Preprocess the inverse matrices involved in characteristic matrices under different conditions. If working conditions are ideal, the inverse matrices without the infinitesimal features are pretreated in ideal characteristic matrices of inter-body stillness and motion. However, under existing error conditions, the inverse matrices between ideal and error characteristic ones of inter-body motion would be performed with a pretreatment in a branch of topological structure. The reason is that during the iterations of the inverse matrix, some features are to be considered, such as the denominator polynomials, the infinitesimal features, and the high-order terms. The infinitesimal features refer to the parametric form of error components, such as angular errors (i.e., rotation angle errors), straightness errors, and squareness errors, as listed in Tables 2 and 3. (2) Removal of the denominator polynomials under different conditions. Specifically, under ideal conditions, the denominator polynomials are eliminated during iterations of the inverse matrices, which are involved in homogeneous coordinate transformation of ideal characteristic matrices of inter-body stillness and motion. Under existing error conditions, the same methodology can be used to remove the denominator polynomials of the inverse matrices, which are correlated with the transformation of error characteristic matrices of inter-body stillness and motion. (3) For each error term element in the error characteristic matrix, expression for additive form of multiple products is converted from mathematics to string. (4) The string representation, with contributions of high-order terms being ignored in volumetric error model, is obtained by judgment and removal of infinitesimal algorithms. Then, the above results are converted into a compile command in the Matlab and a simplified volumetric error model without higher-order terms approaches to a mathematical expression. Finally, the effect of the iterative solution precision on the theoretical calculation errors can be eliminated by application of the algorithm.

3.2 Verification methods

For the purpose of better understanding, it is necessary to define the following four algorithms: A-algorithm refers that the real value is obtained by iterations of 4 × 4 characteristic matrices, which merely consists of the numerical elements. B-algorithm shows that the iterative solutions of the six error term elements for error characteristic matrix, without ignoring high-order terms, are transformed from the characteristic matrices, where error components are represented by parameters. C-algorithm presents that the iterative solutions of the six error term elements for an error characteristic matrix represented by parameters, with ignoring the contributions of high-order terms, are severally deduced by current literature methods [21, 32]. D-algorithm is with the same neglecting as C-algorithm, but the iterative solutions are derived by the proposed algorithm. The design principle is that the only difference is lying on the solution methods. The random number groups are converted from the conventional units to SI units and substituted into parametric expression of each error term element in error characteristic matrix sequentially, so as to obtain the numerical solutions and to perform an analogy analysis of modeling accuracy.

In the field of cost-effective manufacturing, the checking mutual methods are proposed to judge and verify the modeling accuracy of the error term elements in two different ways. Meanwhile, the methods have already been applied for patents. The first verification method includes the following: firstly, the sampling method of one-dimensional distribution is adopted to select at least five groups of one-dimensional random, which correspond to the error components and are converted from their conventional units to SI units. Then, with fixed number of iterations, the simulation results are compared among the iterative solutions of A-, B-, C-, and D-algorithm. Finally, by adopting B-algorithm, the numerical deviations without neglecting higher-order terms are obtained based on A-algorithm. With the use of D- and C-algorithm, the numerical deviations with ignoring the contributions of high-order terms are obtained sequentially on the basis of A-algorithm. The second verification method is described as following: first of all, with sampling method of multi-dimensional distribution, the parametric forms of error components are taken as the dimensions. A set of one-dimension random arrays is selected, converted to its unit and matched with error components in turns. Secondly, due to the increase of computational density, the numerical solution and extreme value distributions are obtained by different algorithms in statistics, with total number of iterations being matched with computer memory. Once again, with the application of D- and C-algorithm, the numerical deviations are used to analyze the accuracy of error modeling and to be compared with the real values on the basis of A-algorithm. Finally, on one hand, based on A- and B-algorithm, means and standard deviations of the deviations from B- and A-algorithm are obtained successively. On the other hand, through adopting D- and C-algorithm, the variation laws of means and standard deviations are obtained respectively on the basis of A-algorithm. The purpose is to quantitatively separate the theoretical calculation errors of the treatment methods by using different algorithms. It’s worth noting that the numerical deviations above are applicable to each error term element of an error characteristic matrix.

4 Illustrating example

4.1 Topological structure and volumetric error modeling

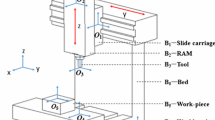
The SKMC-3000/20 in the form of vertical layout is a five-axis precision CNC machine tool with the configuration of TTTRR, as shown in Fig. 1. The order of a transmission chain of main kinematic pairs is simplified as workpiece gear (2), rotary table (1), bed (0), X-axis guide rail (3), Z-axis guide rail (4), grinding wheel deflection axis (5), Y-axis guide rail (6), and grinding wheel (7). According to the HTM theory and its topological structure, the characteristic matrices of the machine tool are divided into the two big categories for the volumetric error modeling, as shown in Table 1. Since there is no relative motion between grinding wheel and workpiece gear, the characteristic matrices of them are expressed in terms of the unit matrix.

Fig. 1
figure 1

The TTTRR-type five-axis gear profile grinding machine based on MBS and HTM theory: machine solid model and main kinematic chains. a Squareness errors, b rotation angle errors, c linear displacement errors, d HTM, e MBS

Full size image
Table 1 Schemes for error model in numerical calculation machine
Full size table

The error modeling mainly includes 38 error components (i.e., 33 geometric errors, 3 linear displacements, and 2 rotation angles), which are represented by parameters and used as independent variables. In order to establish a volumetric error model easily, relative principles and assumptions need to be built herein [37]. Then, according to MBS and HTM theory, homogeneous coordinate transformation of main motion pairs is obtained respectively under different conditions with the consideration of Tables 1, 2, and 3 as well as Fig. 1. Under ideal conditions (i.e., without error), the homogeneous coordinate transformation matrix T27 of grinding wheel coordinate system relative to workpiece gear coordinate system is:

$$ {\mathbf{T}}_{27}={\left({\mathbf{T}}_{01s}\right)}^{-1}\cdot {\mathbf{T}}_{03s}\cdot {\mathbf{T}}_{34s}\cdot {\mathbf{T}}_{45s}\cdot {\mathbf{T}}_{56s} $$
(1)
Table 2 The correspondence between error components and random arrays with five groups
Full size table
Table 3 Error components converted from the conventional units to the standardized units
Full size table

In the presence of errors, the homogeneous coordinate transformation matrix ΔT27 of grinding wheel coordinate system relative to workpiece gear coordinate system is shown as:

$$ {\boldsymbol{\Delta} \mathbf{T}}_{27}={\left({\mathbf{T}}_{01s}\cdot {\boldsymbol{\Delta} \mathbf{T}}_{01s}\right)}^{-1}\cdot \left({\mathbf{T}}_{03s}\cdot {\boldsymbol{\Delta} \mathbf{T}}_{03s}\right)\cdot \left({\boldsymbol{\Delta} \mathbf{T}}_{34p}\cdot {\mathbf{T}}_{34s}\cdot {\boldsymbol{\Delta} \mathbf{T}}_{34s}\right)\cdot \left({\mathbf{T}}_{45s}\cdot {\boldsymbol{\Delta} \mathbf{T}}_{45s}\right)\cdot \left({\boldsymbol{\Delta} \mathbf{T}}_{56p}\cdot {\mathbf{T}}_{56s}\cdot {\boldsymbol{\Delta} \mathbf{T}}_{56s}\right) $$
(2)

It can be seen that ΔT27 is equivalent to that of T27 superimposed to E27. Namely, both grinding wheel coordinate system and workpiece gear coordinate system contain error components based on HTM [32]:

$$ {\mathbf{E}}_{27}={\boldsymbol{\Delta} \mathbf{T}}_{27}\cdot {\left({\mathbf{T}}_{27}\right)}^{-1} $$
(3)

In Eq. (3), set the error characteristic matrix E27 to be:

$$ {\mathbf{E}}_{27}=\left[\begin{array}{cccc}1& -{\eta}_z& {\eta}_y& {P}_x\\ {}{\eta}_z& 1& -{\eta}_x& {P}_y\\ {}-{\eta}_y& {\eta}_x& 1& {P}_z\\ {}0& 0& 0& 1\end{array}\right] $$
(4)

where the adjoint matrix is often used to solve N−1 and R−1 [42]. Take the inverse matrix R−1 as an example (similarly hereinafter):

$$ {\mathbf{R}}^{-1}=\frac{1}{\left|\mathbf{R}\right|}\times {\mathbf{R}}^{\ast } $$
(6)

Meanwhile, the Cayley-Hamilton theorem is also adopted to solve N−1 and R−1. Given that R−1 is an n-order matrix in the number field of P, and then the characteristic polynomial of R−1 is solved as following [43]:

$$ f\left(\lambda \right)=\left|\lambda \mathbf{E}-\mathbf{R}\right|={\lambda}^n+{\mathrm{a}}_1{\lambda}^{n\hbox{-} 1}+\cdots +{\mathrm{a}}_n\lambda +{\mathrm{a}}_n $$
(7)

It is seen that the two methods above all involve the parametric form of iterations for |N|, |R|, and their denominators. So, it leads to larger iterative computation and great difficulty in neglecting of higher-order terms. In order to solve these problems, the detailed implementation process of the optimized algorithm is proposed and shown in Fig. 2, where the infinitesimal features refer to the parametric form of error components, including straightness errors δij, angular errors εij, and squareness errors Sii. In such cases, i represents linear motion axis, and j is the linear motion axis and rotation axis.

Fig. 2
figure 2

An optimized algorithm for a five-axis CNC form grinding machine tool

Full size image

4.1.1 Verification methods and their application

Here comes to the first verification method and its application. In order to avoid systematic errors in random arrays, the rand (5, 38) function is used to obtain one-dimensional random arrays of five groups. Each group consists of 38 data corresponding to 38 error components respectively (see Table 2). Then, those random arrays are converted sequentially from conventional units to SI units according to actual working conditions (see Table 3). The analogy analysis of numerical simulation is carried out through iterations of A-, B-, C- [32], and D-algorithm. As shown in Fig. 3, the numerical solutions of 6E27 are iterated by A- and B-algorithm and the numerical solutions of 6E′27 obtained by C- and D-algorithm, which are respectively represented as following: {A-ηx, B-ηx, C-ηx, D-ηx}, {A-ηy, B-ηy, C-ηy, D-ηy}, {A-ηz, B-ηz, C-ηz, D-ηz}, {A-Px, B-Px, C-Px, D-Px}, {A-Py, B-Py, C-Py, D-Py}, and {A-Pz, B-Pz, C-Pz, D-Pz}. The results show that there is on obvious deviation between the numerical solutions of 6E27 and those of 6E′27 by using D-algorithm. However, C-algorithm has a certain numerical deviation in comparison with A-, B-, and D-algorithm. It is suggested that some theoretical calculation errors do exist in the modeling accuracy.

Fig. 3
figure 3

Accuracy of error modeling by using the first verification method. a, b, c, d, e Respectively presenting the numerical computational results in five groups

Full size image

In order to check the modeling accuracy further, 6E27 is obtained by using B-algorithm and 6E′27 achieved respectively by adopting C- and D-algorithm. Then, the investigation is performed based on A-algorithm and sequentially includes the following: {B-ηx(A), B-ηy(A), B-ηz(A), B-Px(A), B-Py(A), B-Pz(A)}, {C-ηx(A), C-ηy(A), C-ηz(A), C-Px(A), C-Py(A), C-Pz(A)}, and {D-ηx(A), D-ηy(A), D-ηz(A), D-Px(A), D-Py(A), D-Pz(A)}, as shown in Figs. 4, 5, and 6. It is guaranteed that the numerical deviation of 6E27 is within 10−9 to 10−10 by adopting B-algorithm. Meanwhile, some error term elements have their numerical solutions iterated by B-algorithm been the same as those by A-algorithm (Fig. 4 without notes, similarly hereinafter). In particular, the forth random array has the identical numerical calculation result of 6E27, no matter by A-algorithm or B-algorithm. Namely, the numerical deviation between them is zero, so not shown in Fig. 4. Consequently, the theoretical calculation errors above can be ignored in error analysis. It is known in Fig. 5 that based on A-algorithm, the deviations for 6E′27 are obtained by C-algorithm. For rotation error term elements of the interrelated error components, the deviations are guaranteed to be 10−4–10−5; for displacement error term elements, they range from 10−5 to 10−7. Hence, numerical deviations of some error term elements are in the same order of magnitude, even a few numbers of them being larger than actually needed values. It is seen that under actual working conditions, the theoretical numerical deviations for error term elements of 6E′27 do have an influence on the accuracy of error modeling. As illustrated in Fig. 6, the numerical deviations for 6E′27 by D-algorithm are guaranteed from 10−9 to 10−10, even some numerical deviations of 6E27 reaching to zero. The fact is that iterations of D-algorithm and A-algorithm have micro-deviations caused by assumption of small error and the neglecting of higher-order term as well as the solution property of inverse matrix, leading to certain amount of numerical deviations. However, the deviations mentioned above are far smaller than those of the actually needed values so it can be ignored normally.

Fig. 4
figure 4

Deviations for B-algorithm obtained by the first verification method. a, b, c, d Random arrays with five groups sequentially

Full size image
Fig. 5
figure 5

Deviations for C-algorithm obtained by the first verification method. a, b, c, d, e Random arrays with five groups sequentially

Full size image
Fig. 6
figure 6

Deviations for D-algorithm obtained by the first verification method. a, b, c, d, e Random arrays with five groups sequentially

Full size image

In summary, according to the first verification method, the accuracy of 6E27 obtained by B-algorithm is verified and ensured to be within a certain order of magnitude. Therefore, the modeling accuracy of some error term elements for 6E′27 obtained by C-algorithm can be respectively guaranteed to be the same order of magnitude as the actual values, but there are indeed certain theoretical calculation errors during iterations. 6E′27 is also verified with the application of D-algorithm. It is seen that the certain theoretical calculation errors existing in 6E′27 are actually eliminated. Meanwhile, the requirements for modeling accuracy in a precision machine tool can be totally met.

Now, the second verification method and its application are introduced. Firstly, with the sampling method of multi-dimensional distribution, the 38 error components represented by parametric variables are taken as dimensions to enhance the calculation density. In order to comply with the univariate approach, production way of random array is the same as that of the first method. On the basis of the normrnd (38, 1) function, a set of one-dimensional random arrays is built. Meanwhile, it is converted from conventional units to SI units sequentially and stored with the zeros (1, 38) function. Finally, in order to perform the numerical simulation of the grid sampling strategy in high-dimensional spaces, the random array above is successively assigned to error components. It is noteworthy that the maximum number of loop iterations should be 3E17 for the frequently-used computer with an 8G memory. However, it is necessary to keep certain part of memory for processing image data subsequently by Matlab. Therefore, it is assumed that maximum loop iterations are all 3E16 in this study (i.e., 43046721, similarly hereinafter). As shown in Fig. 7, in terms of numerical calculation results as well as distribution of extreme values, 6E27 is obtained by A-algorithm and B-algorithm, and 6E′27 is obtained by D-algorithm. Although there are smaller deviations, numerical calculation results all approach to each other and extreme values are very close. However, 6E′27 got by C-algorithm, 6E′27 by D-algorithm, and 6E27 by A-algorithm and B-algorithm respectively have certain amount of numerical deviations in calculation results and extreme values. Take the error term element ηx of 6E27 and 6E′27 as an example. The numerical computational results achieved by C-algorithm do have certain deviations within the range of iterations in comparison with those by A-, B-, and D-algorithm, as shown in Fig. 7a. Moreover, other error term elements, including ηy, ηz, Px, Py, and Pz, have the same problem. And, their conclusions are identical to those got by the first method. Furthermore, the iterative results are comparatively analyzed as the following.

Fig. 7
figure 7

Accuracy of error modeling with the second verification method. a, b, c, d, e, f The numerical computational results for error term elements ηx, ηy, ηz, Px, Py, and Pz, respectively

Full size image

For one thing, it is known that there are numerical deviations from modeling accuracy between different algorithms. So, it is required to quantify the theoretical calculation errors. The first step is to obtain 6E27 by B-algorithm and 6E′27 by C- and D-algorithm respectively on the basis of A-algorithm. In this case, the marking way is the same as that of the first method. As shown in Fig. 8, the magnitude of deviation within the iterations is identical to the conclusion made by the first method in variation trend. Meanwhile, it suggests the accuracy of modeling precision built by D-algorithm. Then, in order to further analyze the changing rules of deviations from extreme values, numerical computational results above are separated and recorded as following: {Bm-ηx(A), Cm-ηx(A), Dm-ηx(A)}, {Bm-ηy(A), Cm-ηy(A), Dm-ηy(A)}, {Bm-ηz(A), Cm-ηz(A), Dm-ηz(A)}, {Bm-Px(A), Cm-Px(A), Dm-Px(A)}, {Bm-Py(A), Cm-Py(A), Dm-Py(A)}, and {Bm-Pz(A), Cm-Pz(A), Dm-Pz(A)}. It is noted that deviations from the extreme values of the error term elements, as shown in Fig. 9, are different from the magnitude of the deviation in the above analysis. With application of B-algorithm, the deviations of the maximum value for 6E27 are within 10−9 to 10−13 and the minimum deviations 10−9 to 10−10 on the basis of A-algorithm. Similarly, if it changes to C-algorithm, the maximum deviations of 6E′27 range from 10−4 to 10−5 and the minimum deviations 10−5 to 10−9 (these data are unstable). Referring to D-algorithm, the maximum deviations of 6E′27 are from 10−8 to 10−13 and the minimum deviations 10−8 to 10−9. When it comes to C- and D-algorithm, the final numerical computational results are obtained by using small error hypothesis theory, neglecting higher-order terms, removing the denominator polynomial in the form of 1/|N| and 1/|R|, and selecting the properties to solve the inverse matrices of characteristic matrices approximately. Because of this, the results above have some micro-deviations. Therefore, it can be concluded that the deviations for 6E27 by adopting B-algorithm and 6E′27 by using D-algorithm are at least one order of magnitude smaller than the actual values according to the definition and standard of precision machining [1]. Moreover, from the perspective of statistics, the deviations for D-algorithm are only one order of magnitude larger than those by using B-algorithm, with A-algorithm being considered. Meanwhile, for some error term elements, the deviations are guaranteed to be within the same level. It is suggested that the influence of the micro-deviations present in C- and D-algorithm on modeling accuracy can be ignored. What’s more, D-algorithm is proved to have high accuracy, which reaches to sub-micron and even nanometer level. Then, here comes a problem. If C-algorithm is used on the basis of A-algorithm, the numerical deviations of some error term elements in 6E′27 are actually in the same level as those of the actual values. But, several deviations order of magnitude are even larger than those of the actual values. In other words, the modeling accuracy is reduced in effect. Moreover, the deviations of numerical computational results obtained by adopting C-algorithm are at least two orders of magnitude greater or smaller than those of B-algorithm.

Fig. 8
figure 8

Deviations for B-, C-, and D-algorithm obtained by the second verification method. a, b, c, d, e, f Iterations for error term elements ηx, ηy, ηz, Px, Py, and Pz, respectively

Full size image
Fig. 9
figure 9

Deviations of extreme values from B-, C-, and D-algorithm obtained by the second verification method respectively

Full size image

For another thing, the study is proposed to obtain the means and standard deviations of numerical deviations quantitatively by using different algorithms. Firstly, if B-algorithm is used on the basis of A-algorithm and A-algorithm on B-algorithm, it can lead to those values of 6E27. They are recorded respectively as {B/A-ηx, B/A-ηy, B/A-ηz, B/A-Px, B/A-Py, B/A-Pz}. Now take ηx as an example. As shown in Fig. 10a, those of 6E27 are guaranteed to be within 10−10 to 10−16. So, it suggests that the iterations of a volumetric error model represented by parametric variables are correct without neglecting higher-order terms. Then, based on A- and B-algorithm, those of 6E′27 by adopting C- and D-algorithm are respectively described as {C-ηx, C-ηy, C-ηz, C-Px, C-Py, C-Pz} and {D-ηx, D-ηy, D-ηz, D-Px, D-Py, D-Pz}. Take ηx as an example to illustrate. As shown in Fig. 10b and c, when C-algorithm is applied upon A-algorithm, the mean and standard deviation of C-ηx are ensured to be 10−5 to 10−6. However, if D-algorithm is used, those of D-ηx are within 10−9 to 10−12. From the point of mathematical statistics, it not only suggests that this method is more stable and reliable than the first one but also verifies that D-algorithm can produce a feasible and higher modeling accuracy. What’s more, this method can improve the computation density, enhance the reliability of verification, check the correctness of the first method, and expand the verification scope of modeling accuracy. Nevertheless, it has a problem of heavy calculation.

Fig. 10
figure 10

Means and standard deviations of numerical deviations with the second verification method. a 6E27 by using B- and A-algorithm sequentially, b 6E′27 by using C-algorithm, and c 6E′27 by using D-algorithm

Full size image

The second verification method can be extended to other applications. With definition and standards of precision CNC machine tool being upgraded and improved constantly, it also can be used with the consideration of the changing rules of iterations, the causes of the theoretical calculation error, and the characteristics of the method. For example, through analogy analysis, the means and standard deviations of numerical deviations could be used to separate quantitatively theoretical calculation errors caused by various treatments. It can also be used as a theoretical guidance for choosing suitable treatment to meet the accuracy of an error model represented by parametric variables during iterations of the characteristic matrices. In addition, for some special applications, such as ultra-precision machining or measurement, it is required to consider micro-deviations in theoretical computation. In such cases, B-algorithm can be used on the basis of A-algorithm to obtain the numerical deviations quantitatively. Then, they can be used as micro-deviations in theoretical computation to make error compensation.

5 Conclusions

In consideration of HTM and MBS theory, it is very important to establish a volumetric error model represented by parameters before measurement and error compensation experiments. However, there are some theoretical calculation errors and modeling accuracy problems in early designing stages. Therefore, this study is intended to put forward a novel optimized algorithm and its verification methods for improving the accuracy of the parametric error modeling. Meanwhile, it is performed with a detailed research about the effects of the theoretical modeling accuracy in volumetric error model with parameters on the precision machining. Based on the results, conclusions have been drawn as following:

  1. 1.

    Referring to the error modeling technology used in precision machine tools, the study is presented with a novel optimized algorithm. It can not only meet the needs of a standard definition for precision machine tools but also can eliminate theoretical calculation errors. As a result, the numerical deviations can be at least one order of magnitude lower than the actual values. Meanwhile, the numerical deviations can be only one level higher than those of the iterative results without ignoring the contributions of high-order terms. As for parts of error term elements, the same order of magnitude can even be reached respectively. In other words, the modeling accuracy of this algorithm can reach to sub-micron and even higher.

  2. 2.

    The two mutual verification methods can be used to check the accuracy of the parametric modeling precision. On the one hand, although the first method has contingency caused by random data, its calculation work is relatively reduced. It can be applied to verify the accuracy of a volumetric error model with parameter variables in the related error modeling technology for precision machine tools. On the other hand, the second has higher calibration accuracy, but it has a large amount of computation. It can be extended to perform verification in the error modeling technology of both precision and ultra-precision machine tools. Moreover, the second method can isolate quantitatively the theoretical calculation errors and be used as a theoretical guidance for selecting an appropriate treatment to meet the accuracy of the error modeling during iterations of the characteristic matrices.

In a word, the optimized algorithm has relatively higher modeling precision and the two verification methods can check the veracity of parametric modeling precision in different ways. Meanwhile, it is important to learn about the influences of theoretical modeling accuracy with error components represented by parameters on the precision machining. In consideration of the theoretical modeling accuracy, the precision is improved and prediction veracity as well as uncertainty of the modeling precision can be evaluated. In addition, they can be also applied for the ultra-precision CNC machine tools with arbitrary multi-axis linkage. Finally, in the field of cost-effective manufacturing, the design methods and conclusions of this study can put forward an efficient way to optimize and verify the modeling accuracy in the early design stages. Meanwhile, some researchers interested in this technology can also use them to perform subsequent experiments better.