Geometric accuracy enhancement of five-axis machine tool based on error analysis

Abstract

The characteristics of geometric error affect both the positions and orientations of a five-axis machine tool, which are very important for precision manufacturing. It is necessary to conduct quantitative analysis for the above characteristics to improve the precision of the five-axis machine tool. In this paper, the synthetic volumetric error model of the five-axis machine tool with a turntable-tilting head has been established, which describes the effect of 43 geometric error terms on position and orientation error vector intuitively. The multidimensional output of geometric error vectors in the workspace of the machine tool is sufficiently taken into account, and global quantitative sensitivity analysis is introduced to determine the effect of each geometric error on the precision of the machine tool. The results showed that geometric errors of the rotary axes are dominant sensitivity factors, reaching 59.32 and 51.59% of sensitivity indices of the position and orientation error vector, respectively. Furthermore, geometric error terms that are noncritical and critical are extracted according to the result of mutual information analysis. Those geometric errors were removed from the geometric error compensation model, which are at the same time insensitivity errors and nonsignificant geometric errors. The geometric error compensation results show that the accuracy of the machined parts with complex curved surfaces was improved 56.22% after error compensation based on sensitivity and mutual information analysis. This research provides a feasible methodology for analyzing the effect of geometric errors and determining the compensation values of the machine tool.

1 Introduction

A five-axis machine can adjust both the tool tip optimal position and orientation relative to the workpiece simultaneously in the process of its machining, and it can realize machining complex shapes in a single setup, shortening the processing time by a big margin and improving the surface quality of the machining part when compared with the three-axis machine [1, 2]. Owing to their unique advantages, five-axis machine tools are extensively used in the field of automotive, shipbuilding, and aerospace [3]. One of the criteria on the performances of the five-axis machine tool is its quasi-static accuracy [4, 5]. Therefore, it has become one of the most important concerns, and the quasi-static errors (geometric errors and thermal errors) and dynamic errors (cutting force errors and dynamic errors) affect manufacturing accuracy together [6, 7]. Geometric errors account for 40–50% of the total machine errors [8,9,10], and it has characteristics of coupling effect and has nonlinear and high repeatability [4, 9]. Hence, it is important to establish a method for analyzing the characteristics of geometric error terms and applying the analysis results in error compensation to enhance the geometric accuracy of five-axis machine tools.

A five-axis machine tool with a turntable-tilting head has 30 position-dependent geometric errors (PDGEs) and 13 position-independent geometric errors (PIGEs) [11, 12]. PDGEs are mainly caused by manufacturing defects and wear of the machine tool itself, and PIGEs are mainly caused by assembling deviation between two motion axes [13,14,15].

The geometric error model is able to express the mapping relationship of the movement characteristics corresponding to two coordinate systems, the cutting tool position and orientation in the workpiece coordinate system can be determined based on the motion commands of each axis in a machine coordinate system, and therefore, geometric error modeling is the foundation of error identification, analysis, and compensation. The research works on geometric modeling are developed according to various methods, and these modeling approaches include the multibody system (MBS) theory [16,17,18], screw theory-based modeling method [19, 20], exponent product method [21], state space model [22], polynomials model [23, 24], stream of variation theory [25], and so on. Fan et al. [26] adopted truncated Fourier function to fit the distribution curve of geometric accuracy of the guideway and established the mapping model between the tolerance of the machine tool guideway and the geometric error. He et al. [27] proposed a hierarchical method for estimating motion errors of the linear axis and established mapping between the precision of the slideway and error motion of the work table. Based on rigid body kinematics and homogeneous transformation methods (HTMs), Mir et al. [28] established the general volumetric error model of a five-axis machine tool, and the Gauss–Newton method is used for calculating modified commands of geometric error compensation. Li et al. [24] established a PDGE model of linear axes based on moving least squares and Chebyshev polynomials method, and position accuracy of motion axis was improved by 90% after error compensation. Qiao et al. [29] proposed a PIGE calibration model of five-axis machine tools based on the product of exponentials (POE) formula, and the validity is validated by simulations and experiments. Yang et al. [30] presented the identification method for PIGEs of five-axis machine tools based on the screw theory, and the proposed correction model can be used for improving the precision of the table-tilting-type five-axis machine tool. Ibaraki et al. [31] established a geometric error model based on HTMs, they developed a scanning measurement method with laser displacement sensor, and they analyzed the influence of geometric error of rotary axes on the measurement accuracy of a five-axis machine tool. The mapping relation between tool posture error vectors and geometric error for a four-axis machine tool was proposed by Chen et al. [32] based on differential transformation theory, where the geometric error components were expressed as the differential movement relative to the ideal values. The screw theory-based modeling and HTM modeling based on MBS are efficient and common methods for geometric error modeling in the existing methods, and the former is used to describe a rigid body in a global coordinate system instead of establishing a local coordinate system on each motion axis. The latter is implemented for establishing homogeneous coordinate transformation matrix of the adjacent body, which includes geometric error components of motion axis, and the method can express the motion relationship among the components of five-axis machine tools simply and intuitively.

Five-axis machine tools can be classified into three types according to the positions of rotary and linear axes. The previously presented researches about geometric error modeling focus mainly on the machine type with a rotary and tilting table and a universal head, and the type with a tilting head and rotary table has received little attention. What needs to be stressed is that the number and nature of the geometric error has more remarkable differences in various types of five-axis machine tools; for example, a five-axis machine tool with tilting rotary table contains 11 PIGEs [4, 10], and a five-axis machine tool with tilting head and a turntable contains 13 PIGEs [10, 48], and thus, the existing geometric model cannot be directly used for describing the relationship between geometric error and the position and orientation of five-axis machine tools with tilting head and turntable [15, 33]; hence in this paper, the integrated model of geometric errors of five-axis machine tools with tilting head and turntable will be established.

PIGEs and PDGEs of motion axes of a five-axis machine tool are generally considered as independent in the identification process, which is not in accordance with the fact that some errors are correlative variables [14, 34]. Meanwhile, the difference of the effect of geometric error on precision of a machine tool was neglected. While many approaches for geometric error identification and compensation have been put forward, the investigation of the quantitative analysis of geometric error having influence on the precision of a five-axis machine tool is scarce. The coupling of geometric error on the machine accuracy exists in a five-axis machine tool [35], and geometric error distribution is characterized as nonlinear which brings obstructions to accuracy allocation and error compensation of the five-axis machine tool [9, 36]. Sensitivity analysis can be used for the quantitative evaluation of key factors and the coupling effects between geometric errors, and the sensitivity analysis can be categorized as global sensitivity analysis (GSA) and local sensitivity analysis (LSA) [37]. LSA focuses on the influence of certain parameters on the output of the model. On the contrary, the GSA method is used to analyze the influence of all parameters on the output of the model at the same time.

Much effort has been made by researchers to reveal the relative changes of machine tool accuracy which are caused by uncertainties of geometric error components from the perspective of qualitative analysis. Tsutsumi et al. [13] analyzed the influence of PIGEs of tilting rotary table-type five-axis machine tool on circular trajectory based on simulation and experiments. Based on the method of numerical simulation, Zargarbashi and Mayer [38] analyzed the influence of 12 PDGEs of trunnion axis on measure-trajectory with double ball bar (DBB), and this LSA method was evolved and applied for describing the influence of PIGEs and PDGEs [14, 34]. Cheng et al. [9, 39, 35] proposed the GSA method for determining crucial geometric error terms, and the stochastic and intercoupling characteristics of the geometric errors are considered as well, and the precision of the machine tool is improved after replacing the parts. Ibaraki et al. [40] conducted LSA based on numerical simulation to assess the contribution of position and orientation errors of motion axes of five-axis machine tool, and installation deviation that includes position and orientation errors of the workpiece is fully taken into account simultaneously. Lee and Lin [41] established a model of PIGEs which is caused by assembly deficiency and analyzed the sensitivities of indirect compensation geometric error terms based on the form-shaping function theory. The Spearman method is adopted by Chen et al. [42] to determine the key geometric error terms of a four-axis machine tool, and six geometric errors that have greater influence on the tool posture are determined. Lei et al. [43] measured dynamic errors of rotary axes by synchronous motion of linear and rotary axes, then mapping between rotational range and measurement sensitivity of the rotary axis was established, and error compensation is conducted to verify the feasibility of the modified identification values based on sensitivity analysis. Liu et al. [44] conducted research on the effect due to change of geometric error on the form error with different surfaces by numerical simulation method, and its effectiveness is verified through manufacturing and measuring a simple part that has a plane-spherical surface. Li et al. [45] defined new sensitivity indices for GSA and LSA through the projection of the error vectors and the effective cutting length of the cutting tool, and key factors are extracted from 41 geometric errors which include position and posture error of the cutting tool based on numerical simulation. Guo et al. [12] proposed an approach for determining the coupling effect of four adjustable PIGEs and compensation values of tilting head and a turntable-type five-axis machine tool. Error compensation was conducted by Zou et al. [46] based on the analysis of variance, and the influence of verticality error is eliminated by adjusting the assembly precision of the machine components. Du et al. [47] modeled position error and straightness geometric error based on Jacobian–Torsor, and the effect of manufacturing error on the comprehensive error of single-axis assembly and its cumulative effect is determined by the Monte Carlo simulation method.

Previous studies mainly focused on sensitivity analysis of the direct influence and coupling effect of geometric error for the three-axis and five-axis machine tools, and the same magnitude characteristics of geometric error numerical simulation parameters cannot reflect the unequal magnitude relationship of geometric error terms. In another respect, the position and posture accuracy of the machine tool are affected by some of the same geometric errors, while position and posture errors of the vector also interacted with each other. The influence of uncertainty of geometric error on the multidimensional output simultaneously has seldom been considered, although root mean square values of three error vectors are analyzed [11, 44, 46], and moreover, the result of sensitivity analysis is rarely directly applied in geometric error compensation except replacing parts of the machine tool and guiding the design. However, the geometric accuracy of machine tools will fluctuate due to the replaced parts, and sensitivity analysis is applied in the precision design of the machine tool only for error avoidance purposes, and it means that the abovementioned methods do not effectively and economically guarantee geometric accuracy of the CNC machine tool in operation and maintenance. The contributions of this paper are listed as follows: One is the volumetric error modeling of the five-axis machine tool with tilting head and rotary table by the MBS theory and HTM method, in which 43 error terms particular to the RTTTR-type five-axis machine tool are all involved. The other is that multivariate output characteristic of geometric error is taken into consideration, and then the identification of noncritical geometric error terms and error compensation based on sensitivity analysis for improving the geometric accuracy of the tilting head and a turntable-type five-axis machine tools is performed.

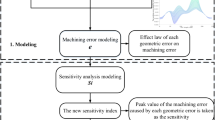
The structure of the paper is as follows: in Section 2, geometric error modeling of the five-axis machine tool with tilting head and turntable is presented with consideration given to position and orientation error vectors. In Section 3, the GSA model of geometric error for the five-axis machine tool is established and the identified results of sensitivity factors are described in detail and the relationship between geometric error and error vector is determined by mutual information analysis. In Section 4, experiments are carried out on the five-axis machine tool to validate the effectiveness of the analysis method. Some conclusions are drawn finally.

2 Geometric error model of the five-axis machine tool

2.1 Five-axis machine tool configuration

Five-axis machine tool with a tilting head and turntable is considered, as shown in Fig. 1, which consists of three linear axes (X-, Y-, and Z-axes) and two rotary axes (C- and A-axes). The direction of each local coordinate system is consistent with the reference coordinate system.

Fig. 1

Five-axis machine tool with tilting head and turntable

According to MBS, the five-axis machine tool with tilting head and turntable can be described abstractly as an adjacent body array in the form of a topological structure, in which components of the five-axis machine tool are abstracted into bodies, and the bodies are sorted in ascending order from machine bed to cutting tool and workpiece, respectively, which form two kinematic chains: tool kinematic chain and workpiece kinematic chain, as shown in Fig. 2.

Fig. 2

Schematic diagram of topology of the five-axis machine tool

2.2 Definition of PIGEs and PDGEs

Known from the nature of rigid body motion, each machine tool component has six degrees of freedom in the Cartesian coordinate system [49, 50]. PDGEs exist in moving components and each rotary axis has three positional errors (two runout errors and one axial shift error) and three angular errors. Each linear axis has three positional errors (one positioning error and two straightness errors) and three angular errors (yaw error, pitch error, and roll error). For the five-axis machine tool, there exist three squareness errors between three linear axes. The 43 geometric errors of the five-axis machine tool with a tilting head and rotary table should be considered [48, 11], which are listed in Table 1.

Table 1 Geometric error components of the five-axis machine tool

δ and ε represent translational errors and angle errors which belong to PDGEs of the linear and rotary axes, respectively, and the subscript is the error direction and the position coordinate is defined within the parenthesis. γ_xy, α_yz, and β_xz are squareness errors between each pair of axes, α_CY is the squareness error of the C-axis around the X-axis in the YOZ plane, β_CY is the squareness error of the C-axis around the Y-axis in the ZOX plane, δ_xCY is the position deviation of the C-axis in the X-direction, δ_yCY is the position deviation of the C-axis in the Y-direction, α_ZA is the angular deviation of initial of angular position of the A-axis in the ZOY plane, β_ZA is the squareness error of the A-axis center line around the Y-direction in the ZOX plane, γ_ZA is the squareness error of the A-axis center line around the Z-direction in the XOY plane, δ_yAS is the position deviations between the A-axis center line and spindle axis in the Y-direction in the XOY plane, δ_zAS is the position deviation between the ideal and actual of the spindle nose in the Z-direction in the ZOX plane, and β_AS is the squareness between the spindle axis center line and A-axis movement in the ZOX plane.

2.3 Modeling of geometric errors

According to the MBS theory, 4 × 4 matrices can be used for expressing the position relation and motion feature between classical lower bodies with respect to geometric errors of the five-axis machine tool. The characteristic matrices of geometric errors of the five-axis machine tool are listed in Table 2.

Table 2 The characteristic matrices of geometric error terms

${{}_j{}^iT}_{\mathrm{s}}$, $\kern0.1em {{}_j{}^iT}_{\mathrm{se}}$, ${{}_j{}^iT}_{\mathrm{m}}$, ${{}_j{}^iT}_{\mathrm{me}}$, ${{}_j{}^iR}_{\mathrm{m}}$, and $\kern0.1em {{}_j{}^iR}_{\mathrm{me}}\kern0.2em$ represent the position characteristic transformation matrix, position error characteristic transformation matrix, motion characteristic transformation matrix, motion error characteristic transformation matrix, angle transformation matrix, and angle error characteristic transformation matrix, respectively, which are from the j coordinate system to the i coordinate system. For the linear axes, the angle transformation matrices are equal to the unit matrix I_4 × 4.

The vector P_t represents the tool tip position in the tool coordinate system, and P_w represents the position of the workpiece-forming point in a workpiece coordinate system, which can be expressed as:

$$ {\boldsymbol{P}}_{\mathrm{t}}={\left({x}_{\mathrm{t}},{y}_{\mathrm{t}},{z}_{\mathrm{t}},1\right)}^T $$

(1)

$$ {\boldsymbol{P}}_{\mathrm{w}}={\left({x}_{\mathrm{w}},{y}_{\mathrm{w}},{z}_{\mathrm{w}},1\right)}^T $$

(2)

There is an overlap between the cutting point in the tool coordinate system and workpiece coordinate system, when there is no geometric error in the multibody system. The relationship of the cutting point between the reference frame and the workpiece coordinate system is shown below.

$$ \left({{}_1{}^0T}_{\mathrm{s}}{{}_1{}^0T}_{\mathrm{m}}{{}_2{}^1T}_{\mathrm{s}}{{}_2{}^1T}_{\mathrm{m}}{{}_3{}^2T}_{\mathrm{s}}{{}_3{}^2T}_{\mathrm{m}}{{}_4{}^3T}_{\mathrm{s}}{{}_4{}^3T}_{\mathrm{m}}\right){P}_{\mathrm{t}}=\left({{}_5{}^0T}_{\mathrm{s}}{{}_5{}^0T}_{\mathrm{m}}{{}_6{}^5T}_{\mathrm{s}}{{}_6{}^5T}_{\mathrm{m}}\right){P}_{\mathrm{w}} $$

(3)

The forming point of the tool will inevitably deviate from the ideal position under the influence of geometric errors in practice, and the volumetric position errors of the five-axis machine tool can be expressed as:

$$ {\displaystyle \begin{array}{l}{E}_{\mathrm{p}}={\left[{E}_{PX},{E}_{PY},{E}_{PZ},1\right]}^T\\ {}=\left({{}_1{}^0T}_{\mathrm{s}}{{}_1{}^0T}_{\mathrm{s}\mathrm{e}}{{}_1{}^0T}_{\mathrm{m}}{{}_1{}^0T}_{\mathrm{m}\mathrm{e}}{{}_2{}^1T}_{\mathrm{s}}{{}_2{}^1T}_{\mathrm{s}\mathrm{e}}{{}_2{}^1T}_{\mathrm{m}}{{}_2{}^1T}_{\mathrm{m}\mathrm{e}}{{}_3{}^2T}_{\mathrm{s}}{{}_3{}^2T}_{\mathrm{s}\mathrm{e}}{{}_3{}^2T}_{\mathrm{m}}{{}_3{}^2T}_{\mathrm{m}\mathrm{e}}{{}_4{}^3T}_{\mathrm{s}}{{}_4{}^3T}_{\mathrm{s}\mathrm{e}}{{}_4{}^3T}_{\mathrm{m}}{{}_4{}^3T}_{\mathrm{m}\mathrm{e}}\right){P}_{\mathrm{t}}-\left({{}_5{}^0T}_{\mathrm{s}}{{}_5{}^0T}_{\mathrm{s}\mathrm{e}}{{}_5{}^0T}_{\mathrm{m}}{{}_5{}^0T}_{\mathrm{m}\mathrm{e}}{{}_6{}^5T}_{\mathrm{s}}{{}_6{}^5T}_{\mathrm{s}\mathrm{e}}{{}_6{}^5T}_{\mathrm{m}}{{}_6{}^5T}_{\mathrm{m}\mathrm{e}}\right){P}_{\mathrm{w}}\end{array}} $$

(4)

Similarly, the projection of the ideal tool orientation in the tool coordinate system A_t and workpiece coordinate system A_w can be expressed as Eq. (5). Only angular errors and instruction values of motion axes will influence tool orientation, that is, different numbers of geometric errors will be considered for establishing volumetric positional error vector model and volumetric orientation error vector model.

$$ {\boldsymbol{A}}_{\mathrm{t}}={\left[{\boldsymbol{A}}_{\mathrm{t}\boldsymbol{x}},{\boldsymbol{A}}_{\mathrm{t}\boldsymbol{y}},{\boldsymbol{A}}_{\mathrm{t}\boldsymbol{z}},0\right]}^T $$

(5)

$$ {\boldsymbol{A}}_{\mathrm{w}}={\left[{\boldsymbol{A}}_{\mathrm{w}\boldsymbol{x}},{\boldsymbol{A}}_{\mathrm{w}\boldsymbol{y}},{\boldsymbol{A}}_{\mathrm{w}\boldsymbol{z}},0\right]}^T $$

(6)

Under ideal conditions, the relationship of A_w and A_t can be established with respect to the angle transformation matrix and angle error characteristic transformation matrix.

$$ \left({{}_3{}^2R}_{\mathrm{m}}\right){\mathbf{A}}_t=\left({{}_6{}^5R}_{\mathrm{m}}\right){\mathbf{A}}_w $$

(7)

Under the state of real operation of the machine tool, there are deviations between the actual orientation and ideal orientation of tool orientation. The volumetric orientation errors of the five-axis machine tool can be expressed as:

$$ {\displaystyle \begin{array}{l}{E}_A={\left[{E}_{AX},{E}_{AY},{E}_{AZ},1\right]}^T\\ {}=\left({{}_1{}^0R}_{\mathrm{s}}{{}_1{}^0R}_{\mathrm{s}\mathrm{e}}{{}_1{}^0R}_{\mathrm{m}}{{}_1{}^0R}_{\mathrm{m}\mathrm{e}}{{}_2{}^1R}_{\mathrm{s}}{{}_2{}^1R}_{\mathrm{s}\mathrm{e}}{{}_2{}^1R}_{\mathrm{m}}{{}_2{}^1R}_{\mathrm{m}\mathrm{e}}{{}_3{}^2R}_{\mathrm{s}}{{}_3{}^2R}_{\mathrm{s}\mathrm{e}}{{}_3{}^2R}_{\mathrm{m}}{{}_3{}^2R}_{\mathrm{m}\mathrm{e}}{{}_4{}^3R}_{\mathrm{s}}{{}_4{}^3R}_{\mathrm{s}\mathrm{e}}{{}_4{}^3R}_{\mathrm{m}}{{}_4{}^3R}_{\mathrm{m}\mathrm{e}}\right){A}_t-\left({{}_5{}^0R}_{\mathrm{s}}{{}_5{}^0R}_{\mathrm{s}\mathrm{e}}{{}_5{}^0R}_{\mathrm{m}}{{}_5{}^0R}_{\mathrm{m}\mathrm{e}}{{}_6{}^5R}_{\mathrm{s}}{{}_6{}^5R}_{\mathrm{s}\mathrm{e}}{{}_6{}^5R}_{\mathrm{m}}{{}_6{}^5R}_{\mathrm{m}\mathrm{e}}\right){A}_{\mathrm{w}}\end{array}} $$

(8)

The total volumetric positional error vector and the total volumetric orientation error vector including all the PIGEs and PDGEs of the five-axis machine tool with swiveling head can be used in error prediction, geometric error analysis, and compensation value determination.

2.4 Measurement and identification of geometric error

Effective measurement methods with special equipment have been recommended by ISO 230-1 and ISO 10791-6 for linear axes [48, 51], which include the multiline method and body diagonal measurement method based on the laser interference measurement system [52, 53]. For the measurement of rotation axes, circular test with DBB is the most popular indirect measurement method.

Based on the proposed method from a previous study in refs. [12, 54], 10 PIGEs of rotary axes are identified, and the DBB is adopted for measuring and identifying 12 PDGEs of rotation axes based on the method proposed in refs. [52, 55]. The 12-line method is applied to identify 21 geometric error terms for linear axes based on Renishaw XL-80 laser interferometer measuring system, as shown in Fig. 3.

Fig. 3

a, b Geometric error measurement and experiment setup

Multiple consecutive measurements are performed under the same conditions according to ISO 230-1 for the purpose of reducing the uncertainty of measurement. All the PIGEs and PDGEs can be identified by the corresponding identification algorithm [54, 55]. The identified values of PDGEs are shown in Fig. 4, and identification results of PIGEs are listed in Table 3.

Fig. 4

Identified values of geometric error of motion axes. a Identified values of position errors of the C-axis. b Identified values of angle errors of the C-axis. c Identified values of position errors of the A-axis. d Identified values of angle errors of the A-axis. e Identified values of position errors of the X-axis. f Identified values of angle errors of the X-axis. g Identified values of position errors of the Y-axis. h Identified values of angle errors of the Y-axis. i Identified values of position errors of the Z-axis. j Identified values of angle errors of the Z-axis

Table 3 The identification result of PIGEs

3 Geometric error analysis

3.1 Sensitivity analysis modeling of geometric error

The geometric errors of machine tools mainly originated from the defects in the assembling, adjustment, and manufacturing, and the geometric errors obey a normal distribution [39, 56]. Besides, coupling interaction exists among the geometric error terms [16, 54, 57], which will result in a total effect being not the simple algebraic stack of geometric errors. As an effective potential method, GSA plays a key role in revealing an interaction mechanism of PIGEs and PDGEs while quantitatively determining significant factors. The variance-based sensitivity analysis (multivariate output sensitivity analysis method) [58, 59] is selected in this paper.

The core idea of variance-based method is that a mathematic model will be decomposed into a combination of a single parameter and multiple parameters, and then sensitivity coefficients corresponding to the outputs of the model will be obtained, which reflect the effect of geometric error on the volumetric error vector.

Let Y_kv = g(X₁, X₂,….., X_n), (k = A, P; v = X, Y, Z) be the geometric error model of the five-axis machine tool, and these models are established in Section 2. The range of geometric errors can be determined according to the identified result after geometric error measurement; meanwhile, according to previous studies, the geometric error parameters are always normally distributed. The steps for conducting improved sensitivity method are as follows:

• 1. Firstly, geometric error model Y = g(X₁, X₂,….., X_n) is decomposed as

  $$ g(X)={g}_0+\sum \limits_{i=1}^n{g}_i\left({X}_i\right)+\sum \limits_{i_1=1}^n\sum \limits_{i_2={i}_1+1}^n{g}_{i_1{i}_2}\left({X}_{i1},{X}_{i2}\right)+\cdots +{g}_{1\cdots n}\left({X}_1,{X}_2,\cdots, {X}_n\right) $$

  (9)

Where (X₁, X₂,….., X_n) are the independent input variables, and g₀ is constant. g₀ represents the expected value of output Y, which can be expressed as

$$ {g}_0=\int g(X)\prod \limits_{i=1}^n\left[{f}_{x_i}\left({x}_i\right)d{x}_i\right] $$

(10)

Where f_xi(x_i) represents probability density function of input variables.

• 2. Secondly, defining Y₁ and Y₂ as the output parameters, i and j are complement subsets of (X₁, X₂,….., X_n), and Y₁ and Y₂ can be decomposed into several components.

  $$ {\displaystyle \begin{array}{l}{Y}_1={f}_0+{f}_u+{f}_v+{f}_{u,v}\\ {}{Y}_2={g}_0+{g}_u+{g}_v+{g}_{u,v}\end{array}} $$

  (11)

Based on the relation of the expected value of output f₀, g₀, and output parameters Y_i, the decomposition formulation of output response can be expressed as

$$ \left({Y}_1-{f}_0\right)\left({Y}_2-{g}_0\right)={f}_u{g}_u+{f}_v{g}_v+\left({f}_u{g}_v+{f}_v{g}_u+\cdots +{f}_{u,v}{g}_{u,v}\right) $$

(12)

Covariance decomposition relation of output response Y₁ and Y₂ can be obtained.

$$ C\left({Y}_1,{Y}_2\right)={C}_u+{C}_v+{C}_{u,v} $$

(13)

The above covariance decomposition can be expanded to k multidimensional output mode

$$ C\left({Y}_1,\cdots, {Y}_m\right)=\sum \limits_{i=1}^n{C}_i\left({Y}_1,\cdots, {Y}_m\right)+\sum \limits_{1\le i\le j\le n}^n{C}_{i,j}\left({Y}_1,\cdots, {Y}_m\right)+\cdots +{C}_{1,2\cdots, n}\left({Y}_1,\cdots, {Y}_m\right) $$

(14)

The covariance matrix of each output response can be decomposed into the following form

$$ C\left({Y}_1,\cdots, {Y}_m\right)=\left[\begin{array}{cccc}V\left({Y}_1\right)& C\left({Y}_2,{Y}_1\right)& \cdots & C\left({Y}_1,{Y}_m\right)\\ {}C\left({Y}_1,{Y}_2\right)& V\left({Y}_1\right)& \cdots & C\left({Y}_2,{Y}_m\right)\\ {}\cdots & \cdots & \cdots & \cdots \\ {}C\left({Y}_1,{Y}_m\right)& C\left({Y}_2,{Y}_m\right)& \cdots & V\left({Y}_m\right)\end{array}\right] $$

(15)

The decomposition form degrades to the variance analysis of single output as m equal to 1. The global sensitivity index can be defined as the ratio between the decomposition term of the covariance matrix and the covariance matrix, and the first-order sensitivity indices geometric error i can be expressed as

$$ {S}_i=\frac{C_i\left({Y}_1,\cdots, {Y}_m\right)}{C\left({Y}_1,\cdots, {Y}_m\right)} $$

(16)

• 3. Thirdly, converting matrix S_i into scalar quantity by calculating the trace of matrix of Eq. (17).

  $$ Tr\left[C\left({Y}_1,\cdots, {Y}_m\right)\right]=\sum \limits_{i=1}^n Tr\left[{C}_i\left({Y}_1,\cdots, {Y}_m\right)\right]+\sum \limits_{1\le i\le j\le n} Tr\left[{C}_{i,j}\left({Y}_1,\cdots, {Y}_m\right)\right]+\cdots + Tr\left[{C}_{1,2,\cdots, n}\left({Y}_1,\cdots, {Y}_m\right)\right] $$

  (17)

The modified first-order sensitivity indices geometric error i can be expressed as

$$ {S}_i=\left({Y}_1,\cdots, {Y}_m\right)=\frac{Tr\left[{C}_i\left({Y}_1,\cdots, {Y}_m\right)\right]}{Tr\left[C\left({Y}_1,\cdots, {Y}_m\right)\right]} $$

(18)

• 4. Fourthly, the covariance matrix and the decomposition term of the covariance matrix can be derived into the form of variance and conditional moments.

$$ {V}_i=V\left[E\left(Y|{X}_i\right)\right] $$

(19)

Then, Eq. (20) can be obtained according to Eq. (19).

$$ {V}_i=E\left[V(Y)-V\left(Y|{X}_i\right)\right] $$

(20)

Square calculation is introduced in order to avoid the problem of decreasing the importance of input random variables caused by the canceling effect of the positive and negative effects when deterring coefficients of the abovementioned global sensitivity.

$$ {V}_i^m=\sqrt{E{\left[V(Y)-V\left(Y|{X}_i\right)\right]}^2} $$

(21)

The global sensitivity coefficients can be modified and represented as

$$ {S}_i^m=\frac{\sqrt{E{\left[V(Y)-V\left(Y|{X}_i\right)\right]}^2}}{V(Y)} $$

(22)

Therefore, Eq. (23) can be obtained according to Eq. (22)

$$ {S}_i^m=\sqrt{\frac{S_i^2+\mathrm{V}\left[V\left(Y|{X}_i\right)\right]}{V^2(Y)}} $$

(23)

and therefore the generalized global sensitivity index in the form of conditional moments is represented as

$$ {S}_i^m\left({Y}_1,\cdots, {Y}_m\right)=\frac{\sum \limits_{j=1}^m\sqrt{{\mathrm{V}}^2\left[E\left({Y}_j|E\left({Y}_i\right)|{X}_i\right)\right]+\mathrm{V}\left[V\left(\left({Y}_j|E\left({Y}_j\right)\right)|{X}_i\right)\right]}}{\sum \limits_{j=1}^mV\left({Y}_j|E\left({Y}_j\right)\right)} $$

(24)

Define ${S}_i^m\left({Y}_{kv}\right)$, (k = A, P; v = X, Y, Z) as the multidimensional model of volumetric position errors vector E_p and volumetric posture errors vector E_a, which has been presented in Section 2. The sensitivity coefficient ${S}_i^m\left({Y}_{kv}\right)$ of geometric error elements represents the direct influence of the geometric error on the total variance of the multidimensional output.

3.2 GSA of geometric errors

Global sensitivity coefficient can be determined by conducting multivariate output sensitivity analysis based on the calculation procedure which was elaborated in detail in Section 3.1. The stroke of the X-, Y-, Z-, C-, and A-axis is 406 mm, 305 mm, 254 mm, 0° to 360°, and − 100° to + 10°, respectively. According to the varying range and probability distributions of PIGEs and PDGEs, 20,000 random values are taken for each geometric error based on the Latin hypercube sampling technique [9].

The calculated results of the sensitivity analysis about volumetric positional error vector E_p are shown in Fig. 5, and E_p is a multivariate output which is made up of three components of total positional error vector in three directions rather than the root mean square value of three components.

Fig. 5

Sensitivity analysis result of position error vector

As Fig. 5 illustrates, for the volumetric position error vector, the sensitivity coefficients of geometric error terms δ_x(x), δ_y(x), δ_z(x), δ_x(y), δ_x(z), δ_z(z), δ_x(a), δ_z(a), ε_x(a), ε_y(a), γ_xy, α_yz, α_CY, β_CY, δ_xCY, α_ZA, and γ_ZA are greater than 0.025. The sensitivity coefficients of geometric error terms ε_x(x), δ_y(y), δ_z(y), ε_x(y), ε_y(y), ε_x(z), ε_y(z), ε_z(z), δ_y(a), ε_z(a), δ_x(c), ε_x(c), ε_y(c), ε_z(c), γ_xy, β_ZA, δ_yAS, δ_yCY, and β_AS whose sensitivity coefficients are lower than 0.0125 are considered as the least important error terms. Geometric errors δ_x(x), δ_y(x), δ_z(x), δ_x(y), δ_x(z), δ_z(z), δ_x(a), δ_z(a), ε_x(a), ε_y(a), β_xz, α_yz, α_CY, β_CY, δ_xCY, and α_ZA are considered as the sensitive factors that impact the position precision of the machine tool. For the position error vector, the percentage of sensitivity indices of PIGEs and PDGEs of motion axes is 45.42 and 54.58%, respectively. The average sensitivity indices of PIGEs and PDGEs are 0.034 and 0.018, respectively.

For the volumetric orientation error vector, only 24 angular errors will have an effect on E_a. Similar to E_p, E_a is a multivariate output which is made up of three components of total orientation error vector in three directions rather than the root mean square value of three components. The analysis results of the global sensitivity analysis are shown in Fig. 6.

Fig. 6

Sensitivity analysis result of orientation error vector

The sensitivity coefficients of geometric error terms ε_x(x), ε_y(x), ε_z(x), ε_x(z), ε_y(z), ε_x(a), ε_y(a), ε_z(a), ε_y(c), β_xz, α_yz, α_CY, β_CY, β_ZA, and β_AS are greater than 0.025. The sensitivity coefficients of geometric error terms ε_x(y), ε_y(y), ε_z(y), ε_z(z), ε_z(c), γ_xy, α_ZA, and γ_ZA are lower than 0.015. So the geometric error terms ε_x(x), ε_y(x), ε_z(x), ε_x(z), ε_y(z), ε_x(a), ε_y(a), ε_z(a), ε_y(c), β_xz, α_yz, α_CY, β_CY, β_ZA, and β_AS are considered as sensitive factors that impact the orientation precision of the cutting tool. For the orientation error vector, the percentage of sensitivity indices of PIGEs and PDGEs of motion axes is 62.15 and 37.85%, respectively.

The sensitive geometric error terms for E_p and E_a can be obtained from Figs. 3 and 4, which are listed in Table 4. It can be concluded from Table 4 that the average sensitivity indices of PIGEs are larger than those of PDGEs of motion axes for position error vector. The average sensitivity indices of PIGEs have been shown to affect the volumetric position error more significantly than those of PDGEs of rotary axes and the latter are numerically superior.

Table 4 Sensitive geometric errors of E_p and E_a

For the volumetric orientation error vector, the average sensitivity indices of PDGEs and PIGEs of motion axes are 0.0368 and 0.0983, respectively. It can be concluded that PIGEs have a more sensitive function than PDGEs to volumetric orientation error. Furthermore, it should be noted that the percentage of sensitivity indices of the rotary axes and linear axes is 59.32 and 40.68%, respectively, for the position error vector. The percentage of sensitivity indices of the rotary axes and linear axes is 51.59 and 48.41%, respectively, for the orientation error vector. It shows that machine accuracy has more sensitivity in terms of the effect of the PIGEs and PDGEs on rotary axes.

3.3 Extraction of noncritical parameters

The identification of geometric error is usually based on the assumption that geometric errors are independent of each other; however, some errors are essentially related due to mutual coupling among the source of the errors and the unavoidable flaw in error modeling being factored in.

In order to further reveal the intrinsic relationship between geometric error and spatial error vector, the concept of mutual information is introduced [60]. This method can quantify the information of random variable that contains information of other factors. Let [G_min(j), G_min(j)] be the range of geometric error, and [E_min(i), E_min(j)] be the range of position and orientation error vector. The vector of position and posture and geometric error terms are divided into N and M equal intervals, separately.

The number of samples falling into each equal interval will be statistically measured, and the probability for P(E_i(j))(i = 1,2,…,n; j = 1,2,…, N) and P(D_k) (k = 1,2,…,M) will be calculated. According to the information theory, the mutual information between error vector and geometric error values of the machine tool motion axes can be expressed as

$$ I\left(E,{G}_i\right)=\sum \limits_{k=1}^M\sum \limits_{j=1}^NP\left({E}_k,{G}_i(j)\right)\times \lg \frac{P\left({E}_k,{G}_i(j)\right)}{P\left({G}_i(j),P\left({E}_k\right)\right)} $$

(25)

Where P(E_k,G_i(j)) is the probability distribution.

The analysis of key error sources is done to obtain the maximum information of error vector of position and orientation deviation of the five-axis machine tool by minimizing the number of geometric errors. The mutual information I(E, G_i) between the error vector and geometric error of each measuring point of motion axis is calculated, respectively.

The mutual information of geometric error and error vector is obtained, as shown in Table 5.

Table 5 Mutual information analysis result

Further analysis of Table 5 indicates that the mutual information between positioning errors, straightness errors, and volumetric error vectors is larger, and the geometric error term with smaller mutual information value contains smaller spatial error vector. The mutual information values between geometric errors and error vector are less than 1 simultaneously, which are as follows: δ_y(x), ε_x(x), ε_x(y), ε_y(y), ε_x(z), ε_z(z), ε_z(c), γ_xy, δ_yAS, δ_zAS, and δ_yCY, and this means that the correlations between the abovementioned geometric errors and error vectors are weak.

It can be seen from the above discussion that the effect of geometric error on the precision of the machine tool should be comprehensively analyzed. Geometric errors will be identified that are at the same time nonsignificant and insensitive. Insensitivity geometric error terms are determined based on the sensitivity analysis in Section 3, and the correlations between geometric error terms and error vectors are identified by the mutual information method. After implementing the proposed synthesis evaluation, the error terms would not be considered for geometric error compensation and error identification, which include ε_x(y), ε_y(y), ε_z(z), ε_z(c), γ_xy, δ_yAS, δ_zAS, and δ_yCY.

4 Experiments and results

Experiment was carried out to verify the feasibility of the above method of geometric accuracy enhancement through volumetric error model and error analysis. The machine tool used in the experiments was a HSC 75 five-axis CNC machine center with Heidenhain iTNC 530 control system. The X-, Y-, and Z-axis strokes are 406, 305, and 254 mm, respectively, and the rotation range of rotation axes C and A is − 100° to + 10° and 0° to 360°, respectively.

In our research, impellers were adopted as the test parts for measuring the performance of the five-axis machine tool. The machining process of test parts is mainly by the following order: rough machining of the impeller passage, semifinishing of the impeller passage, semifinishing and finishing of the blade of the impeller, and finishing of the impeller passage. Solid carbide cutting tools were selected for machining the impeller. The ball end cutter radius is 5 mm and the number of teeth of cutting is 2, which is used for rough machining. In the finishing stage, the conical ball end cutter radius is 3 mm, the number of teeth of cutting is 4, and the cutter taper is 3°. The maximum spindle speed was 6000 rpm during rough machining and semifinishing of the impeller passage, and feeding speed of the cutting tool is 400 mm/min. The maximum spindle speed was 8000 rpm during semifinishing and finishing of the blade of the impeller, and the maximum feeding speed of the cutting tool is 300 mm/min for machining of variable feedrate. The CAD/CAM software UG was used to design the test parts, as shown in Fig. 8. Toolpaths, feed, and withdraw of the blade are locally enlarged in Fig. 8a, in which part of the toolpath of the blade of the impeller is listed in Table 6 due to space constraints in this paper. All of the toolpath file is imported into the inverse kinematics model proposed in Section 2.3, and the motion command of each axis with ideal values and compensation values taken into account can be obtained.

Table 6 Parts of the toolpath of the blade

As described in Section 2, geometric error measurements were conducted for linear and rotary axes with a Renishaw laser interferometer and DBB. Based on the geometric error analysis results in Section 3, nonsignificant and insensitivity geometric errors were identified, including PDGEs ε_x(y), ε_y(y), ε_z(z), and ε_z(c) and PIGEs γ_xy, δ_yAS, δ_zAS, and δ_yCY. These geometric errors were removed from the geometric error compensation model according to Eqs. (4) and (8), geometric error compensation was conducted based on the generated new CNC codes, and the flowchart shows modeling, error analysis, and compensation for geometric accuracy enhancement, as shown in Fig. 7.

Fig. 7

The flowchart of geometric error compensation

Error vectors of position and attitude are determined with the kinematic model that was established in Section 2.3, and the actual values of error vectors Oa are quantitatively expressed based on recognition of noncritical geometric error terms, which can be used for determining the vector error Oe and compensation values of each motion axis.

The process for error compensation based on error analysis is carried out in following steps:

• Step 1. The machine tool is without geometric error in the ideal form, position and attitude vectors Oi = [E_PXi, E_PYi, E_PZi, E_AXi, E_AYi, E_AZi] can be generated with the UG software according to the 3D model, and the NC codes for motion axes of the five machine tool can be determined considering the constraints of acceleration and velocity.

• Step 2. The machine tool will be affected unavoidably by geometric error in actual state, the actual position and attitude vectors Oa = [E_PXa, E_PYa, E_PZa, E_AXa, E_AYa, E_AZa] can be determined with the identified values of geometric error and the kinematic model, and noncritical geometric error terms will not be involved in the progress of calculating Oa and NC codes.

• Step 3. The deviation Oe = [E_PXe, E_PYe, E_PZe, E_AXe, E_AYe, E_AZe] of actual position and attitude vectors Oa and ideal value Oi can be determined, which is expressed as:

$$ \mathbf{Oe}=\mathbf{Oi}-\mathbf{Oa} $$

(26)

When the deviation values Oe are greater than the tolerance of geometric accuracy of motion axes, the deviation value is superimposed on nominal trajectory Oi as error compensation values.

$$ \mathbf{Oc}=\mathbf{Oi}+\mathbf{Oe} $$

(27)

where Oc is the new position and attitude vector of the tool with error compensation, and the new NC codes of each motion axis with error compensation can be obtained by calculating the solution inverse with Oc. If residual error still exceeds the tolerance range after linear compensation, iterative operation is required.

The machined test parts before and after geometric error compensation are shown in Fig. 8.

Fig. 8

Experimental verification of geometric error compensation. a Three-dimension model of the impeller. b Impeller machining on a five-axis machine tool. c Machined impeller before and after compensation. d Accuracy measurement on CMM

After machining, the machined parts were measured on a coordinate measuring machine of Hexagon Global classic SR 575, as shown in Fig. 8 d. The measured results are listed in Table 7.

Table 7 Comparison of accuracy of the machined parts

The machined impeller 1 was milled with no compensation, and the impeller 2 was machined after geometric error compensation based on geometric error analysis. The blade thickness errors and profile deviations of the impeller were measured on the coordinate measuring machine. Table 7 shows that the blade thickness error changed significantly after geometric error compensation, which is reduced to 12.1 μm from 30.2 μm, and the profile deviation decreases to 6.6 μm from 13.9 μm after geometric error compensation is conducted. The deviation on each test term reduced by 59.93 and 52.51%, respectively.

5 Conclusions

With the rapidly increasing requirement of parts design and processing accuracy, the role of geometric accuracy of a five-axis machine tool has become increasingly prominent. The geometric error is quantitative characterization of geometric accuracy, and the influence of geometric error is not the simple algebraic stack of error terms due to coupling interaction among multiple geometric errors; however, the comprehensive effect of geometric error random variables on the error vector with multidimensional output has rarely been quantitatively analyzed, and existent methods cannot effectively overcome the shortfalls with canceling effect which is caused by algebraic stack of geometric error terms. Therefore, a new geometric accuracy enhancement method of the five-axis machine tool with tilting head and rotary table based on geometric error modeling, analysis, and compensation is proposed. The characteristics of this method are shown as follows:

• 1. A synthetic geometric error model for a five-axis machine tool with tilting head and turntable is established based on the multibody system theory and the method of homogeneous transformation, which includes position error vector and orientation error vector that consist of 30 PDGEs and 13 PIGEs, and the type and number of error terms are peculiar to the RTTTR-type five-axis machine tool. The analysis and compensation of geometric error for the five-axis machine tool can be achieved to improve accuracy with the error model.

• 2. The influence of uncertainty of geometric error on the multidimensional output simultaneously is quantitatively analyzed with the global sensitivity analysis method, and it prevents the loss of information of the quantitative objects with proper dimensionless indexes. The result of the sensitivity analysis shows that the effect of geometric error on position and attitude accuracy is quantified according to the type of error vector and property of geometric error, respectively. For the volumetric position error vector E_p, the average sensitivity indices of PDGEs and PIGEs of motion axes are 0.0428 and 0.0571, and for the volumetric attitude error vector E_a, the average sensitivity indices of PDGEs and PIGEs of motion axes are 0.0367 and 0.0981, respectively. Sensitivity coefficient of rotary axes accounted for 59.32 and 51.59% of the position and orientation error vector, respectively, whose effect is larger than that of the linear axis.

• 3. Insensitivity and nonsignificant geometric errors are determined by analyzing the correlation of error vector and geometric errors with mutual information and sensitivity analysis, which are removed in the geometric error compensation. The results show that the accuracy of machined parts has been significantly improved after geometric error compensation, which is conducted based on the geometric error analysis results and mutual information analysis. The enhancement methods of geometric accuracy are demonstrated on the five-axis machine tool, and the accuracy on blade thickness and profile of the machined part is advanced by 59.93 and 52.51% after geometric error compensation, respectively. The proposed research also established a reliable basis for the design and error compensation of other types of multi-axis machine tool.

In this paper, systematic approaches of geometric error modeling, analysis, and compensation are the main focus of the study. It should be pointed out that the geometric error modeling in this paper is based on the rigidity assumption and accuracy fluctuations caused by wear, and errors induced by thermal deformation and control accuracy are not considered. The abovementioned problems need to be researched for further improving machine precision.