Machining accuracy reliability analysis of multi-axis machine tool based on Monte Carlo simulation

Abstract

Although machine tool can meet the specifications while it is new, after a long period of cutting operations, the abrasion of contact surfaces and deformation of structures will degrade the accuracy of machine tool due to the increase of the geometric errors in six freedoms. Therefore, how to maintain its accuracy for quality control of products is of crucial importance to machine tool. In this paper, machining accuracy reliability is defined as the ability to perform its specified machining accuracy under the stated conditions for a given period of time, and a new method to analyze the sensitivity of geometric errors to the machining accuracy reliability is proposed. By applying Multi-body system theory, a comprehensive volumetric model explains how individual geometric errors affect the machining accuracy (the coupling relationship) was established. Based on Monte Carlo mathematic simulation method, the models of the machining accuracy reliability and sensitivity analysis of machine tools were developed. By taking the machining accuracy reliability as a measure of the ability of machine tool and reliability sensitivity as a reference of optimizing the basic parameters of machine tools, an illustrative example of a three-axis machine tool was selected to demonstrate the effectiveness of the proposed method.

Introduction

Machine tools used in manufacturing systems for production of goods and delivery of services constitute the vast majority of the capital in most industries nowadays (Zhang et al. 2013; Li et al. 2014). Multi-axis CNC machine tools are typical mechatronic equipment with high added value and wide applications, which are required to reach increasing high-performance machining (Mehrabi et al. 2002; Bohez 2002b; Deja and Siemiatkowski 2013). Machining accuracy is critical for the quality and performance of a mechanical product and is an important consideration for any manufacturer (Zeroudi and Fontaine 2015; El Ouafi et al. 2000). Chen et al. (2014) denoted that machining accuracy is influenced by machining errors belonging to several categories, e.g. geometric errors caused by mechanical-geometric imperfections, misalignments, wear of the linkages and elements of the machine tool structure, by the non-uniform thermal expansion of the machine structure, and static/dynamic load induced errors. How to improve the machining accuracy of NC machine tool has become a hot issue for domestic and foreign scholars (Ramesh et al. 2000). Wang and Guo (2013) concluded that among the several error sources, geometric error of machine tool components and structures is one of the biggest sources of inaccuracy, accounting for 40 % among all errors.

In the actual production, although the machining accuracy can meet the specifications while the machine tool is new, it is unable to guarantee that the accuracy still maintains at the acceptable tolerance range after a long-term operation (Fan et al. 2012). Because after a long period of cutting operations, obvious wear will occur on the contact surfaces of the slide and the guide-way. Such a wear will degrade the accuracy of machine tool due to the increase of Abbé errors (Fan et al. 2012). For example, positioning errors are dynamically related to the errors of the working stage, cutting forces induced errors, tool wear, slide-guide-way wear, ambient temperature, vibration, etc. Wear of the slide-guide-way will gradually increase during machining operations, which can increase the geometric errors in six freedoms, and decrease the machining accuracy (Stryczek 2014; Sarkar and Dey 2015).

Machine tool has to maintain its accuracy for quality control of products. Here, in this paper, the ability to perform its specified machining accuracy under the stated conditions for a given period of time is defined the machining accuracy reliability of machine tool. How to improve the machining accuracy reliability of machine tool is an important objective desired to be improved faced to manufacturers and users, and two tasks are involved to accomplish it. One is how to express and measure the machine accuracy reliability of machine tool; the other is how to identify the most critical geometric parameter errors that have biggest influence on the machining accuracy reliability from several ones.

Up to now, many researchers have put a good deal of efforts into the modeling and analysis of the machining accuracy of machine tool caused by geometric errors and so on. In order to improve the machining accuracy of CNC machine tools, error modeling is crucial to maximize the performance of machine tools (Ahn and Cho 2000; Çaydaş and Ekici 2012; Bohez et al. 1997). Error modeling technique can provide a systematic and suitable way to establish the error model. In recent years, much research work has been done on modeling of multi-axis machine tools to find out the resultant error of individual components in relation to tool and work-piece point deviation (Bohez 2002a). And, the modeling methods of the geometric errors from different perspectives have experienced several developing phases (Cheng et al. 2014). To describe the error of cutter location and tool orientation between the two kinematic chains, the error model is normally established using HTM (Liu et al. 2011; Eman et al. 1987; Lei and Hsu 2003), D-H (Jha and Kumar 2003), MD-H (Lin and Tzeng 2008), or Multi-body system (MBS) (Zhu et al. 2012; Zhang et al. 2003) theory. Among them, MBS, proposed by Houston (Liu 2000), has become the best method for geometric error modeling of machine tool to date because it can describe the topological structure of MBS simply and conveniently (Zhu et al. 2012).

However, there are many geometric errors in multi-axis machine tool. For example, there are 21 geometric errors in 3-axis machine tool. These geometric errors are inter-coupling (Habibi et al. 2011; Zhu et al. 2012) and how to determine the influence degree on the machining accuracy reliability is currently a difficult problem of machine tool design. Sensitivity analysis exactly is one approach to identify and quantify the relationships between input and output uncertainties (Xu and Gertner 2007). A number of sensitivity analysis methods exist in literature. Among them, Ditlevsen and Madsen (2007) presented an expression based on the first order reliability method (FORM) to evaluate reliability sensitivity for a structural system with linear limit-state and normal random variables. De-Lataliade et al. (2007) developed a method using Monte Carlo simulation (MCS) for reliability sensitivity estimations. Ghosh et al. (2001) proposed a method using the first order perturbation for stochastic sensitivity analysis.

Through sensitivity analysis of geometric errors, the most critical geometric errors can be identified and they can be strictly controlled, and thus the machining accuracy of machine tool can be significantly improved (Tsutsumi and Saito 2004; Stryczek 2014). Bohez (2002a) presented a new general approach on how to compensate for the systematic errors based on the closed loop volumetric error relations and analyzed the errors due to the 5-axis toolpath generation in current CAD/CAM and CNC in detail. Bohez et al. (2007) gave a new way to identify and compensate all the systematic angular errors separately and then used them further to identify the systematic translational error and proposed a new ways to measure the volumetric error directly. Hong et al. (2011) studied the influence of position-dependent geometric errors of rotary axes on cone frustum machining test in the five-axis machine tool. Lee and Lin (2012) studied the effect of each assembly error term on volumetric error of a five-axis machine tool according to form-shaping theory. Chen et al. (2013) studied the volumetric error modeling and its sensitivity analysis of a five-axis ultra-precision machine tool, and based on the local sensitivity analysis results, the key error components have small reduction, which decreases the difficulty to control the accuracy of the machine tool. Cheng et al. (2014) took the stochastic characteristic of geometric errors into consideration and used the Sobol’ global sensitivity analysis method to identify crucial geometric errors of machine tool, which is helpful to improve the machining accuracy of multi-axis machine tool.

Furthermore, sensitivity analysis could be used to provide information for the reliability-based design. Reliability sensitivity analysis can help the designer to select acceptable tolerances and parameters of product, and has been reported by many researchers, especially in structural reliability design, mechanical system reliability and tools reliability. Du et al. (2005) has summarized three useful ways to improve the reliability, including (1) change of the mean values of random variables, (2) change of the variances of random variables, and (3) truncation of the distributions of random variables. In reliability analysis and reliability-based design, sensitivity analysis can be used to identify the most significant uncertain variables that have the highest contribution to reliability (Guo and Du 2009). Song et al. (2009) have effectively decreased the computational cost in the random uncertainty analysis of flutter by use of the improved line sampling (LS) technique, and identified the important parameters and guided the structural optimization design by reliability sensitivity, which is defined by the partial derivative of the failure probability with respect to the distribution parameter of random variable. Xiao et al. (2011) considered both epistemic and aleatory uncertainties in reliability sensitivity analysis and propose a unified reliability sensitivity estimation method under both epistemic and aleatory uncertainties by integrating the principle of P-box, interval arithmetic, FORM, MCS, weighted regression. Guo and Du (2009) proposed a sensitivity analysis method for the mixture of random and interval variables, and defined six sensitivity indices for the sensitivity of the average reliability and reliability bounds with respect to the averages and widths of intervals. Tang (2001) proposed a new method based on graph theory and Boolean function for assessing reliability of mechanical systems. Avontuur and van der Werff (2002) studied a new method for systems reliability analysis of mechanical and hydraulic systems based on finite element equations, which describe motion and equilibrium between internal and external loads for structures and mechanisms. Lin (1998) investigated reliability and failure of face-milling tools when cutting stainless steel and the effect of cutting conditions (cutting speed, feed, depth of cut) on the tool life. Chen et al. (2011) studied the reliability estimation for cutting tools based on logistic regression model by using vibration signals. Lamond et al. (2014) discussed a tool management model for a flexible machine equipped with a tool magazine, variable cutting speed, and sensors to monitor tool wear, when tool life due to flank wear is stochastic. Benkedjouh et al. (2015) presented a method for tool condition assessment and life prediction based on nonlinear feature reduction and support vector regression. However no one has studied the machining accuracy reliability of the CNC machine tool.

The main problem that concerns the designer in reliability sensitivity is how to govern the fluctuations of the system parameters for safe operation. Parameter uncertainty is inherent in most engineering problems, and its effect on system reliability and reliability sensitivity should be assessed (Zhang et al. 2003). Monte Carlo method has been used in mechanical engineering fields. Mullany (2008) used the Monte Carlo method to analyze machine tool positional accuracy and repeatability standards. Andolfatto et al. (2011) implemented a multi-output Monte Carlo approach to evaluate the uncertainty on each identified error of five axis machine tool, and uncertainty sources in the measurement and identification chain—such as sensors output, machine drift and frame transformation uncertainties—can be included in the model and propagated to the identified errors. Ning et al. (2008) combined the MCS with cutting experiment to calculation the life reliability of cutting tools and proved that the reliability is primarily affected by the fracture toughness of the cutting tool material. Karandikar et al. (2014) used a Markov Chain Monte Carlo approach to predict the life of turning tool life. Fleischer et al. (2007) used the Monte-Carlo simulation for the flexible consideration of the entire system and the estimation of risk figures such as the Value-at-Risk. Wei-Liang and Qi-Xian (1989) established the stochastic models of the usual joints and analyzed the statistical characteristics and frequency histogram of the kinematic errors through MCS. So in this paper, in order to maintain stable machining quality and avoid iterative adjusting and repairing, a new method is proposed to establish the relationship model of stochastic geometric errors and machining accuracy reliability and identify the key geometric errors that have biggest influences on machining accuracy reliability by using Monte Carlo method.

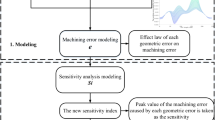
The rest of this study is organized as follows: Sect. “Volumetric Error Modeling by MBS theory” deals with the modeling of the volumetric machining accuracy with consideration of geometric error. The machining accuracy reliability analysis based on Monte Carlo mathematic simulation method is presented in Sect. “Machining accuracy reliability analysis”. The sensitivity analytical method based on Monte Carlo mathematic simulation method to identify the critical geometric errors is presented in Sect. “Reliability sensitivity analysis of machining accuracy based on Monte Carlo method”. In Sect. “Application and improvement”, a vertical machining center is selected as an example to verify the analytical method by experiment. The conclusions are presented in Sect. Conclusions”.

Volumetric error modeling by MBS theory

Machine structure diagram

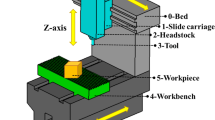
In this research, a three-axis CNC machine tool, whose 3-D structure model is shown in Fig. 1, was chosen as an example to describe the core idea of the methods presented here. It consists of a bed, workbench (X-axis), slide carriage (Y-axis), ram (Z-axis) and a tool. The dimensions of the members of the machine tool have been listed in Table 1. And the accuracy requirement of volumetric errors in X-, Y- and Z-directions have been listed in Table 2.

Fig. 1

Structure of precision vertical machining center

Table 1 Main parameters of the machine tool

Table 2 The Accuracy requirements of the volumetric errors in the X-, Y-, and Z-directions

Topological structure and lower body array

Based on MBS theory, various parts of the machine can be described just as an arbitrary classical body in terms of a geometric structure, and a machine tool can be abstracted into MBS (Kim and Kim 1991; Soons et al. 1992).

As shown in Fig. 2, the three-axis machine tool can be described as a double-stranded topology structure in which the first branch is composed of a bed, slide carriage, RAM and tool. The second branch is composed of bed, workbench, and work-piece. The bed is set as the inertial reference frame and expressed into the $\hbox {B}_{0 }$ body, and slide carriage is expressed into the $\hbox {B}_{1}$ body. According to the natural growth sequence, along the direction away from the body $\hbox {B}_{1}$ the bodies are sequentially numbered from one branch to another branch (Fu et al. 2014). Figure 2 illustrates the topology diagram for the machine tool. Table 3 is the lower body array of the selected precision vertical machining center, and Table 4 depicts the degrees of freedom between each unit to the constraints, where “0” means no degree of freedom and“1” means one degree of freedom.

Fig. 2

Topological graph of precision vertical machining center $\hbox {B}_{0}$-bed; $\hbox {B}_{1}$-slide carriage; $\hbox {B}_{2}$-RAM; $\hbox {B}_{3}$-tool; $\hbox {B}_{4}$-workbench; $\hbox {B}_{5}$-workpiece

Table 3 Lower body array of precision vertical machining center

Table 4 Adjacent body freedom of the precision vertical machining center

Geometric error parameter definition

The machining process of work-piece is the motion of tool forming point within the work-piece coordinate system. In ideal form, the cutting tool trace is in accordance with the ideal trace. But under actual conditions, because of the impact of various geometric errors, the cutting tool trace would deviate from the command trace, and this would lead to a decline in the machining accuracy (Rahman et al. 2000). Since, the selected machine tool has three prismatic joints; there are 18 position dependent systematic geometric errors. For the three joints, there are 3 position independent systematic geometric errors. Table 5 shows all the geometric errors and lists their physical significance.

Table 5 Geometric errors of precision vertical machining center

Generalized coordinate setting and characteristic matrix

In order to normalize and make the machine tool accuracy modeling more convenient, special agreements are needed for the coordinate system. The conventions used here are as follows: (1) Right-handed Cartesian coordinate systems were established for all the inertial components and the moving parts. These coordinates are generalized coordinates; the coordinate system on the inertial body is called as the reference coordinate system, and the coordinate system on other moving bodies are called the moving coordinate system. (2) Each coordinate system’s X-, Y-, Z-axis should be parallel (Shin et al. 1991).

In MBS theory, the relation between classical bodies of MBS can be expressed by $4\times 4$ matrices. The characteristic matrices of the selected machining center have been listed in Table 6.

Table 6 The characteristic matrices of precision vertical machining center

Suppose that the coordinate of the tool forming point in the coordinate system of tool is,

$$\begin{aligned} {\mathbf {P}}_t =\left[ {P_{tx} ,P_{ty} ,P_{tz} ,1} \right] ^{\mathrm{T}} \end{aligned}$$

(1)

And the coordinate of the work-piece forming point in the coordinate system of work-piece can be written as,

$$\begin{aligned} {\mathbf {P}}_w =\left[ {P_{wx} ,P_{wy} ,P_{wz} ,1} \right] ^{\mathrm{T}} \end{aligned}$$

(2)

In ideal form, the machine tool is without error; the tool forming point and the work-piece forming point will overlap together. As a result, the constraint equation for precision finishing under ideal conditions is given as,

(3)

By rearranging the terms, Eq. (3) can be rewritten as,

(4)

Machining accuracy is finally related to the relative displacement error between the tool forming points of machine and work-piece (Bohez et al. 2000, 2003). The constraint equation for precision finishing under actual conditions can be written as,

(5)

The comprehensive volumetric error caused by the gap between actual forming point and ideal forming point can be written as,

(6)

The comprehensive volumetric error mode of precision vertical machining center can be obtained from the characteristic matrices in Table 6 and Eq. (6). Similarly, the general volumetric error model for the machine tool can be established

$$\begin{aligned} {\mathbf {E}}={\mathbf {E}}\left( {{\mathbf {G}},{\mathbf {P}}_t ,{{\mathbf {H}}}} \right) \end{aligned}$$

(7)

In which, ${\mathbf {E}}=\left[ {E_x ,E_y ,E_z ,0} \right] ^{\mathrm{T}}$represents the volumetric error vector; ${\mathbf {G}}=\left[ {g_1 ,g_2 ,\ldots ,g_{21} } \right] ^{\mathrm{T}}$represents the vector consisting of 21 geometric errors, and $\Delta x_x$, $\Delta y_x$, $\Delta z_x$, $\Delta \alpha _x$, $\Delta \beta _x$, $\Delta \gamma _x$, $\Delta x_y$, $\Delta y_y$, $\Delta z_y$, $\Delta \alpha _y$, $\Delta \beta _y$, $\Delta \gamma _y$, $\Delta x_z$, $\Delta y_z$, $\Delta z_z$, $\Delta \alpha _z$, $\Delta \beta _z$, $\Delta \gamma _z$, $\Delta \gamma _{xy}$, $\Delta \beta _{xz}$, $\Delta \alpha _{yz} =g_1$, $g_2$, $g_3$, $g_4$, $g_5$, $g_6$, $g_7$, $g_8$, $g_9$, $g_{10}$, $g_{11}$, $g_{12}$, $g_{13}$, $g_{14}$, $g_{15}$, $g_{16}$, $g_{17}$, $g_{18}$, $g_{19}$, $g_{20}$, $g_{21}$; ${\mathbf {H}}=\left[ {x,y,z,0} \right] ^{\mathrm{T}}$ represents the position vector of motion axis for the machine center.

Machining accuracy reliability analysis

Definition of machining accuracy reliability

With the higher and higher requirement of machining accuracy, reliability is becoming a measurement index of machine tool. However, current research on reliability of machine tool mainly concentrates on strength and life, and it is seldom done on the machining accuracy of machine tool. Just as above said, after a long-term operation, the machining accuracy will degrade and cannot meet the specifications of the machine tool. Among the reasons for the degradation of machining accuracy, the increase of geometric errors along with the abrasion and deformation of contact surfaces and structures is a major cause.

Geometric error of the machine tool primarily comes from manufacturing or assembly defects misalignment of the machine’s axis and the position and straightness error of each axis. Because the errors of a drive or axis or the outcome of an assembly process are random at some level (Dorndorf et al. 1994); thus, the geometric errors vary at different locations instead of being constants and can be taken as a function of displacement (Khan 2010). In view of the fact of that the geometric errors are uncertain variables, the definition of machining accuracy reliability can be given as following.

Definition

Machining accuracy reliability is the ability to perform its specified machining accuracy under the stated conditions for a given period of time, which can reflect the machine accuracy retaining ability of machine tool. In general, the volumetric machining errors can be decomposed into X-, Y-, Z-axis, and if the machining accuracy is less than the specified requirement in X-, Y- and Z-direction respectively after a period of service time, it can be regarded as that the machining accuracy is in failure. Here, the machining accuracy is in a decline process and is not lost, and the machine tool usually can be in service and is not damaged. Therefore, machining accuracy reliability is different from the current reliability concept of machine tool, which is analyzed from the perspective of mechanics (such as strength, stress) (Tang (2001), Chen et al. (2011)), and if the machine tool (or functional unit, tool, etc.) is in failure condition, it means that it cannot work and needs repair or replacement.

Machining accuracy reliability analysis based on Monte Carlo simulation

The comprehensive volumetric error mode of the machine center can be expressed as follow

$$\begin{aligned} {\mathbf {E}}={\mathbf {E}}\left( {\mathbf {G}} \right) =\left[ {E_x \left( {\mathbf {G}} \right) ,E_y \left( {\mathbf {G}} \right) ,E_z \left( {\mathbf {G}} \right) ,0} \right] ^{\mathrm{T}} \end{aligned}$$

(8)

Assume that the maximum permissible volumetric error of the machine tool is ${\mathbf {A}}=\left( {a_x ,a_y ,a_z ,0} \right) ^{\mathrm{T}}$, in which $a_x ,a_y ,a_z$ indicates the maximum permissible volumetric error in X-, Y-, Z-direction respectively, the function matrix can be represented as follow:

$$\begin{aligned} {\mathbf {F}}= & {} \left[ {\mathbf {E}}-{\mathbf {A}} \right] =\left[ {E_x \left( {\mathbf {G}} \right) -a_x ,E_y \left( {\mathbf {G}} \right) -a_y ,E_z \left( {\mathbf {G}} \right) -a_z ,0} \right] ^{\mathrm{T}}\nonumber \\= & {} \left[ {{\begin{array}{c} {F_x \left( {\mathbf {G}} \right) } \\ {F_y \left( {\mathbf {G}} \right) } \\ {F_z \left( {\mathbf {G}} \right) } \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(9)

In general, the geometric errors of CNC machine tools are correlated normal variables. So the density function of the n-dimensional normal random variables vector ${\mathbf {G}}=\left( {g_1 ,g_2 ,g_3 \ldots g_n } \right) ^{\mathrm{T}}$ which is consisted of n geometric errors can be represented as follow:

$$\begin{aligned} D\left( {\mathbf {G}} \right)= & {} \left( {2\pi } \right) ^{-\frac{n}{2}}\left| {{\mathbf {C}}_{\mathbf {G}} } \right| ^{-\frac{1}{2}}\nonumber \\&\exp \left[ {-\frac{1}{2}\left( {{\mathbf {G}}-{\varvec{\mu }}_{\mathbf {G}} } \right) ^{\mathrm{T}}{\mathbf {C}}_{\mathbf {G}}^{-1} \left( {{\mathbf {G}}-{\varvec{\mu }}_{\mathbf {G}}} \right) } \right] \end{aligned}$$

(10)

In which,

$$\begin{aligned} {\mathbf {C}}_{\mathbf {G}}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\sigma _{g_1 }^2 }&{} {\rho _{g_1 g_2 } \sigma _{g_1 } \sigma _{g_2 } }&{} {{\begin{array}{cccc} {\rho _{g_1 g_3 } \sigma _{g_1 } \sigma _{g_3 } }&{} \cdots \\ \end{array} }}&{} {\rho _{g_1 g_n } \sigma _{g_1 } \sigma _{g_n } } \\ {\rho _{g_1 g_2 } \sigma _{g_1 } \sigma _{g_2 } }&{} {\sigma _{g_2 }^2 }&{} {{\begin{array}{cccc} {\rho _{g_2 g_3 } \sigma _{g_2 } \sigma _{g_3 } }&{} \cdots \\ \end{array} }}&{} {\rho _{g_2 g_n } \sigma _{g_2 } \sigma _{g_n } } \\ {\rho _{g_1 g_3 } \sigma _{g_1 } \sigma _{g_3 } }&{} {\rho _{g_2 g_3 } \sigma _{g_2 } \sigma _{g_3 } }&{} {{\begin{array}{cccc} {\sigma _{g_3 }^2 }&{} \\ \end{array} }}&{} {\rho _{g_3 g_n } \sigma _{g_2 } \sigma _{g_n } } \\ {{\begin{array}{cccc} \vdots \\ {\rho _{g_1 g_n } \sigma _{g_1 } \sigma _{g_n } } \\ \end{array} }}&{} {{\begin{array}{cccc} \vdots \\ {\rho _{g_2 g_n } \sigma _{g_2 } \sigma _{g_n } } \\ \end{array} }}&{} {{\begin{array}{cccc} {{\begin{array}{cccc} \vdots \\ {\rho _{g_3 g_n } \sigma _{g_2 } \sigma _{g_n } } \\ \end{array} }}&{} {{\begin{array}{cccc} \\ \cdots \\ \end{array} }} \\ \end{array} }}&{} {{\begin{array}{cccc} \vdots \\ {\sigma _{g_n }^2 } \\ \end{array} }} \\ \end{array} }} \right] \end{aligned}$$

(11)

${\mathbf {C}}_{\mathbf {G}}$ is the covariance matrix for G, ${\mathbf {C}}_{\mathbf {G}}^{-1}$ is the inverse matrix of ${\mathbf {C}}_{\mathbf {G}}$, and $\left| {{\mathbf {C}}_{\mathbf {G}} } \right|$ is the determinant of ${\mathbf {C}}_{\mathbf {G}}$.${\varvec{\mu }}_{\mathbf {G}} =\left( {\mu _{g_1 } ,\mu _{g_2 } ,\mu _{g_3 } ,\ldots ,\mu _{g_n } } \right) ^{\mathrm{T}}$ is a vector composed of the mean values of geometric errors, $\mu _{g_i }$ and $\sigma _{g_i }$ represents the mean value and variance of geometric error $g_i \left( {i=1,2,3,\ldots ,n} \right)$, and $\rho _{g_i g_j }$ represents the correlation coefficient of $g_i$and $g_j$.

Taking X-direction as an example, the function of machine tool in X-direction can be represented as:

$$\begin{aligned} F_x \left( {\mathbf {G}} \right) =F_x \left( {g_1 ,g_2 ,g_3 ,\ldots ,g_n } \right) \end{aligned}$$

(12)

And the limit state equation can be represented as:

$$\begin{aligned} F_x \left( {\mathbf {G}} \right) =F_x \left( {g_1 ,g_2 ,g_3 ,\ldots ,g_n } \right) =0 \end{aligned}$$

(13)

It can divide domain of geometric errors into failure region (when $F_x \left( {\mathbf {G}} \right) >0)$ and reliable region (when $F_x \left( {\mathbf {G}} \right) \le 0)$. So the failure probability of the volumetric machining accuracy in X-direction can be expressed as:

$$\begin{aligned} P_x =\int {\cdots \int {_{F_x ({\mathbf {G}})>0} } } D\left( {\mathbf {G}} \right) \hbox {d}g_1 \hbox {d}g_2 \cdots \hbox {d}g_n \end{aligned}$$

(14)

Indicator function of failure region is defined as:

$$\begin{aligned} I\left( {\mathbf {G}} \right) =\left\{ {{\begin{array}{cccc} {1\quad F_x \left( {\mathbf {G}} \right) >0} \\ {0\quad F_x \left( {\mathbf {G}} \right) \le 0} \\ \end{array} }} \right. \end{aligned}$$

(15)

And the failure probability can be further expressed as the mathematical expectation of indicator function as follow:

$$\begin{aligned} P_x= & {} \int {\cdots \int {_{\Omega ^{n}} } } I\left( {\mathbf {G}} \right) D\left( {\mathbf {G}} \right) \hbox {d}g_1 \hbox {d}g_2 \cdots \hbox {d}g_n\nonumber \\= & {} E\left[ {I\left( {\mathbf {G}} \right) } \right] \end{aligned}$$

(16)

In which, $\Omega ^{n}$ represents the n-dimensional variable space made up of n geometric errors, and $E\left[ {*} \right]$ denotes mathematical expectation operator.

According to the law of large numbers, the sample mean of the failure region indicator function can be used to approximate represent the mathematical expectation of the failure region indicator function.

According to the joint probability density function of geometric errors $D\left( {\mathbf {G}} \right)$, N associated normal sample points ${\mathbf {G}}_i \quad \left( {i=1,2,\ldots N} \right)$ can be extracted by using Latin Hypercube Sampling technique. Substituting these sample points into the function $F_x \left( {\mathbf {G}} \right)$, and the number of sample points falling into the failure region $\left\{ {{\mathbf {G}}\left| {F_x \left( {\mathbf {G}} \right) >0} \right. } \right\}$ is expressed as $N_F$.

The failure probability of volumetric machining accuracy in X-direction can be approximately expressed as:

$$\begin{aligned} \hat{{P}}_x =\frac{1}{N}\sum _{i=1}^N {I\left( {{\mathbf {G}}_i } \right) } =\frac{N_F }{N} \end{aligned}$$

(17)

And the reliability of machine tool in X-direction can be expressed as:

$$\begin{aligned} R\left( X \right) =1-\hat{{P}}_x \end{aligned}$$

(18)

Statistical analysis of geometric errors

Before using Monte Carlo method to analyze the machining accuracy reliability of the machine tool, the probability distribution of parameters should have been given. H date collection sites are selected from the machining tool’s workspace. As for each position dependent geometric error, it was measured 100 times at each point in the similar way. The six position dependent geometric errors of each prismatic joint were measured by dual-frequency laser interferometer (Homma and Saltelli 1996) and electronic level directly. The squareness errors were measured with dial indicator and flat ruler.

With statistical analysis of the gotten sample data, the probability distribution of geometric errors can be obtained. Taking the positioning error $\Delta x_x$ at $x= 200\,\hbox {mm}$, y=400mm, z=300mm as example, the $\Delta x_x$ geometric error approximately belongs to normal distribution. Actually the experiment results show that each position dependent geometric error belongs to normal distribution (Kim and Kim 1991). Table 7 gives the values of position independent errors. Table 8 gives the probability distributions of position dependent geometric errors at $x=200\,\hbox {mm}$, y=400mm, z=300mm, including the mean value (represented by M) and variance value (represented by V).

Table 7 The values of position independent errors

Table 8 The probability distributions of position dependent geometric errors

Calculation of machining accuracy reliability

By the proposed machining accuracy reliability model based on Monte Carlo method and the distribution characteristics of geometric errors at each point, the machining accuracy reliabilities of each test point can be obtained, which have been listed in Table 9. The design requirements of the machine tool about machining accuracy reliability has been listed in Table 10.

Table 9 Comparison of machining accuracy reliabilities at each test points

Table 10 Design requirements about machining accuracy reliability

The narrow bounds (Ditlevsen and Ditlevsen 1979) and advanced first order and second moment (AFOSM) (Kiureghian and Dakessian 1998) are the main methods used for the reliability and sensitivity analysis of a serial system (Cai et al. 2015; Karadeniz et al. 2009). In order to verify the effectiveness of the method introduced in this paper, the machining accuracy reliabilities of this machine tool based on the narrow bounds method and AFOSM were also calculated. The values of machining accuracy reliability were acquired and shown in Table 9.

From Table 9 we can notice that the approach addressed in this paper is verified because the values of machining accuracy reliability calculated by it are in the intervals obtained by the narrow bounds method and closed to the values based on AFOSM.

In contrast, the narrow bounds method fails to obtain the certain values of reliability and sensitivity, but the proposed method can obtain the certain values of reliability. When the AFOSM was used to analyze the machining accuracy reliability, the analysis accuracy of results depends on the nonlinearity of the function. When the degree of nonlinear is low, this method can get exact result. But when the degree of nonlinear is high, it may lead to that the iteration does not converge, and so the result is inexact. However, the method proposed in this paper can analyze the machining accuracy reliability through random simulation and statistical analysis. And it can be used to solve the reliability problem which has highly nonlinear function. In fact, as a highly complex machinery, CNC machine tool’s function is highly nonlinear. Therefore, the proposed method is more suitable for analyzing the machining accuracy of machine tool.

Reliability sensitivity analysis of machining accuracy based on Monte Carlo method

Machining accuracy reliability of machine tool is determined by the distribution types and distribution parameters of geometric errors. The sensitivities to machining accuracy reliability of different geometric errors are very different. The purpose of machining accuracy reliability sensitivity analysis is to determine how sensitive the distribution parameters of geometric errors to machining accuracy reliability.

The definitional equation which about the sensitivity of distribution parameters of geometric errors to machining accuracy reliability can be expressed as follows:

$$\begin{aligned} \frac{\partial P_x }{\partial \mu _{g_i } }= & {} \int {\cdots \int {_{F\left( {\mathbf {G}} \right) >0} } } \frac{\partial D\left( {\mathbf {G}} \right) }{\partial \mu { }_{g_i }}\hbox {d}{\mathbf {G}} \end{aligned}$$

(19)

$$\begin{aligned} \frac{\partial P_x }{\partial \sigma _{g_i } }= & {} \int {\cdots \int {_{F\left( {\mathbf {G}} \right) >0} } } \frac{\partial D\left( {\mathbf {G}} \right) }{\partial \sigma _{g_i }}\hbox {d}{\mathbf {G}} \end{aligned}$$

(20)

In which $\mu _{g_i }$ and $\sigma _{g_i }$ represents the mean value and variance of geometric error $g_i \left( {i=1,2,3,\ldots ,n} \right)$ respectively.

The machining accuracy reliability sensitivity can be obtained by using Monte Carlo digital simulation method. The definitional equation of machining accuracy reliability sensitivity can be transformed into mathematical expectation form and be shown in Eqs. (21) to (22).

$$\begin{aligned} \frac{\partial P_x }{\partial \mu _{g_i } }= & {} \int {\cdots \int \nolimits _{\Omega ^{n}} } \frac{\partial D\left( {\mathbf {G}} \right) }{\partial \mu { }_{g_i }}\frac{I\left( {\mathbf {G}} \right) }{\partial D\left( {\mathbf {G}} \right) }D\left( {\mathbf {G}} \right) \hbox {d}{\mathbf {G}}\nonumber \\= & {} E\left[ {\frac{\partial D\left( {\mathbf {G}} \right) }{\partial \mu _{g_i }}\frac{I\left( {\mathbf {G}} \right) }{\partial D\left( {\mathbf {G}} \right) }} \right] \end{aligned}$$

(21)

$$\begin{aligned} \frac{\partial P_x }{\partial \sigma _{g_i } }= & {} \int {\cdots \int \nolimits _{\Omega ^{n}} } \frac{\partial D\left( {\mathbf {G}} \right) }{\partial \sigma { }_{g_i }}\frac{I\left( {\mathbf {G}} \right) }{\partial D\left( {\mathbf {G}} \right) }D\left( {\mathbf {G}} \right) \hbox {d}{\mathbf {G}}\nonumber \\= & {} E\left[ {\frac{\partial D\left( {\mathbf {G}} \right) }{\partial \sigma { }_{g_i }}\frac{I\left( {\mathbf {G}} \right) }{\partial D\left( {\mathbf {G}} \right) }} \right] \end{aligned}$$

(22)

Further on, the sample mean can be used to estimate the machining accuracy reliability sensitivity in the mathematical expectation form. And the following estimating equations of machining accuracy reliability sensitivity can be obtained.

$$\begin{aligned} \mathop {S}\limits _h^x \left( {\mu _{g_i } } \right)= & {} \frac{\partial \hat{{P}}_x }{\partial \mu _{g_i } }=\frac{1}{N}\sum _{k=1}^N {I\left( {{\mathbf {G}}_k } \right) } \sum _{m=1}^n {\left( {{\mathbf {C}}_{\mathbf {G}}^{-1} } \right) _{mi} } \left( {g_{km} -\mu _{g_m } } \right) \end{aligned}$$

(23)

$$\begin{aligned} \mathop {S}\limits _h^x \left( {\sigma _{g_i } } \right)= & {} \frac{\partial \hat{{P}}_x }{\partial \sigma _{g_i }} =-\frac{1}{N}\sum _{k=1}^N {\frac{1}{2}I\left( {{\mathbf {G}}_k } \right) } \left[ {\left( {{\mathbf {G}}_k -{\varvec{\mu }}_{\mathbf {G}} } \right) ^{\mathrm{T}}\frac{\partial {\mathbf {C}}_{\mathbf {G}}^{-1} }{\partial \sigma _{g_i } }\left( {{\mathbf {G}}_k -{\varvec{\mu }}_{\mathbf {G}} } \right) +\frac{1}{\left| {{\mathbf {C}}_{\mathbf {G}} } \right| }\frac{\partial \left| {{\mathbf {C}}_{\mathbf {G}} } \right| }{\partial \sigma _{g_i } }} \right] \end{aligned}$$

(24)

In which, ${\mathbf {G}}_k \quad \left( {k=1,2,\ldots N} \right)$ represents the i-th associate normal sample vector extracted by using Latin Hypercube Sampling technique according to the joint probability density function of geometric errors $D\left( {\mathbf {G}} \right)$;

$\mathop S\limits _h^x \left( {\mu _{g_i } } \right)$ represents the machining accuracy reliability sensitivity about the mean value $\mu _{g_i }$ of the i-th geometric error to the failure probability of volumetric error in X-direction at the h-th test point;

$\mathop S\limits _h^x \left( {\sigma _{g_i } } \right)$ represents the machining accuracy reliability sensitivity about the variance $\sigma _{g_i }$ of the i-th geometric error to the failure probability of volumetric error in X-direction at the h-th test point;

$\left( {{\mathbf {C}}_{\mathbf {G}}^{-1} } \right) _{mi}$ represents the element of i-th line and m-th column of ${\mathbf {C}}_{\mathbf {G}}^{-1}$ which is the inverse matrix of the covariance matrix ${\mathbf {C}}_{\mathbf {G}}$;

$g_{km}$ represents the m-th element of the k-th sample vector ${\mathbf {G}}_k$.

Taking the point at (200, 400, 300) as an example, based on the above machining accuracy reliability sensitivity analysis method and the distributional characteristics of each geometric errors, the sensitivity coefficients of each geometric errors to machining accuracy reliability can be gotten and their absolute values have been listed in Tables 11 and 12. In order to analyze the data more directly, the results have been displayed in Figs. 3 and 4.

Table 11 Machine accuracy reliability sensitivity coefficients about mean values of each geometric errors at point (200, 400, 300)

Table 12 Machine accuracy reliability sensitivity coefficients about variances of each geometric errors at point (200, 400, 300)

Fig. 3

Machine accuracy reliability sensitivity coefficients about mean values of each geometric errors at point (200, 400, 300)

Fig. 4

Machine accuracy reliability sensitivity coefficients about variances of each geometric errors at point (200, 400, 300)

The result of machining accuracy reliability sensitivity analysis at every test point by method discussed above can be obtained. Then, using the weighted average method, the sensitivity analysis for whole working space can be calculated.

Defining the machining accuracy reliability sensitivity of the mean value $\mu _{g_i }$of geometric error $g_i$ in X-direction as $\mathop {S}\limits ^x \left( {\mu _{g_i } } \right)$, and the machining accuracy reliability sensitivity of the variance $\sigma _{g_i }$of geometric error $g_i$ in X-direction can be defined as $\mathop {S}\limits ^x \left( {\sigma _{g_i } } \right)$.

$$\begin{aligned} \mathop {S}\limits ^x \left( {\mu _{g_i } } \right)= & {} \frac{1}{H}\sum _{h=1}^H {\mathop {S}\limits _h^x \left( {\mu _{g_i } } \right) } \end{aligned}$$

(25)

$$\begin{aligned} \mathop {S}\limits ^x \left( {\sigma _{g_i } } \right)= & {} \frac{1}{H}\sum _{h=1}^H {\mathop {S}\limits _{h}^x \left( {\sigma _{g_i } } \right) } \end{aligned}$$

(26)

The calculated results of machine accuracy reliability sensitivity for the whole working space can be gotten and their absolute values have been listed in Tables 13 and 14. In order to analyze the data more directly, the results have been displayed in Figs. 5 and 6.

Table 13 Machine accuracy reliability sensitivity coefficients about mean values of each geometric errors for the whole workspace

Table 14 Machine accuracy reliability sensitivity coefficients about variances of each geometric errors for the whole workspace

Fig. 5

Machine accuracy reliability sensitivity coefficients about mean values of each geometric errors for the whole workspace

Fig. 6

Machine accuracy reliability sensitivity coefficients about variances of each geometric errors for the whole workspace

The aim of the machining accuracy sensitivity analysis is to identify the key geometric errors to machining accuracy reliability. According to the Figs. 3, 4 , 5 and  6, we can draw some conclusions about the machining accuracy reliability sensitivity analysis of the illustrated machine tool.

• 1) As shown in Fig. 3, the machining accuracy reliability sensitivity coefficients about mean values of $\Delta \beta _x$, $\Delta \gamma _x$, $\Delta \alpha _y$, $\Delta \beta _y$, $\Delta \gamma _y \quad \Delta \alpha _z$ and $\Delta \gamma _z$ are the largest, so the crucial parameters that affect machining accuracy reliability are mean values of $\Delta \beta _x$, $\Delta \gamma _x$, $\Delta \alpha _y$, $\Delta \beta _y$, $\Delta \gamma _y \quad \Delta \alpha _z$ and $\Delta \gamma _z$ at point (200, 400, 300). However, as shown in Fig. 5, for the whole work space, the crucial parameters that affect machining accuracy reliability are mean values of $\Delta \alpha _x$,$\Delta \alpha _z$, $\Delta \gamma _x$ and $\Delta \beta _z$.

• 2) As shown in Fig. 4, the machining accuracy reliability sensitivity coefficients about variances of $\Delta \alpha _x$, $\Delta \alpha _y$, $\Delta \gamma _y$ and $\Delta \beta _z$ are the largest, so the crucial parameters that affect machining accuracy reliability are variances of $\Delta \alpha _x$, $\Delta \alpha _{y}$, $\Delta {\gamma }_y$ and $\Delta \beta _z$ at point (200, 400, 300). However, as shown in Fig. 6, for the whole work space, the crucial parameters that affect machining accuracy reliability are variances of $\Delta x_x$ and $\Delta y_z$.

Application and improvement

The dimensions of studied machining center are listed in Table 1. In order to study the change law of the machining accuracy reliability of the selected machining center in the real processing environment, the machining center has been used to machine a specific part. The three dimensional graphics of the part has been shown in Fig. 7. And the picture of machining site has been shown in Fig. 8.

Fig. 7

The Three Dimensional Graphics of the part

Fig. 8

Picture of machining site

This experiment has been conducted about 9 mouths with around a 12-h run per working day. The total sliding distance accumulated to about 100km. For the machining center the wear is a function of total working hours, and the machining accuracy reliability changed with working hours. When the working time is 1000, 2000, and 3000 hours, the geometric errors are tested respectively. Figure 9 shows a picture of the test site for geometric errors by double frequency laser interferometer. The calculated result of machining accuracy reliability and the machine accuracy reliability sensitivity coefficients of each geometric errors for the whole workspace have been listed in Tables 15 and 16 respectively.

Fig. 9

Picture of the test site

Table 15 The calculated result of machining accuracy reliability

Table 16 The machine accuracy reliability sensitivity coefficients of crucial geometric errors for the whole workspace

According to the pervious tables, the machining accuracy reliability is reduced slightly during the manufacture process because the geometric errors are deteriorated by wear. And, we found that the geometric errors in X-axis are deteriorated more seriously than the ones in other two axes. This is consistent with the actual situation, which can demonstrate the validity of the proposed method. However, although the sensitivity values of the machining accuracy reliability to each geometric error fluctuate with the increasing of working time, the most crucial geometric errors which have greater effects on the machining accuracy reliability are invariant. These results are of great guiding significance to the adjustment and replacement in order to improve the machine accuracy retaining ability of machine tool.

Because the geometric errors in the machine tool are caused by the geometrical accuracy of the feeding components, there exist mapping relationships between the basic geometric errors and the accuracy parameters of feeding components. The corresponding relationships between the basic geometric errors and accuracy parameters of the components (Cheng et al. 2014) are listed in Table 17.

Table 17 The corresponding relationships between the basic geometric errors and accuracy parameters of the components

Combining with the results of machining accuracy reliability sensitivity analysis, it can be concluded that the crucial parameters that affect machining accuracy reliability are mean values of $\Delta \alpha _x$,$\Delta \alpha _z$, $\Delta \gamma _x$ and $\Delta \beta _z$, and variances of $\Delta x_x$ and $\Delta y_z$. So the following modification measures have been took:

• (1) Changing to a higher precision screw for X-guide-way;

• (2) Improve the straightness in horizontal plane of X, Z-guide-way;

• (3) Improve the parallelism of X-guide-way;

• (4) Improve the straightness in vertical plane of Z-guide-way.

The mean values and minimum values of machining accuracy reliability of the precision vertical machining center in X-, Y- and Z-direction after modification are analyzed and listed in Table 18. From the comparison, it can be concluded that the machine tool’s the mean values and minimum values of machining accuracy reliability of the precision vertical machining center in X-, Y- and Z-direction were greatly improved after modification. From this we can conclude that the proposed machining accuracy reliability sensitivity analysis method result is feasible and effective.

Table 18 The mean value and minimum value of machining accuracy reliability after modification

Conclusions

With the rapidly increasing requirement of machining accuracy, machine tools are demanded with not only satisfied machining accuracy, but also higher retaining ability of satisfied machining accuracy. How to evaluate and improve the retaining ability of machining accuracy of machine tool is an intractable problem. The present study proposed a sensitivity analysis approach of machining accuracy reliability to machine tools based on Monte Carlo mathematic simulation method, which aims to establish the relationship between model of stochastic geometric errors and machining accuracy reliability and identify the key geometric errors that have biggest influences on machining accuracy reliability. According to the analysis results, the crucial geometric errors can be modified purposefully and the machining accuracy reliability can be improved dramatically. In addition, the sensitivity analysis results also can offer a good reference for optimal design, accuracy control and error compensation of complex machine.

Despite the progress, it should be pointed out that the geometric errors analyzed in this paper are quasi-static in cold-start conditions, and the dynamical fluctuations caused by axis acceleration, dynamic load induced errors and thermal errors are not taken into consideration. Therefore, the geometric errors in working-conditions needs to be further addressed, which is of more practical significance.