1 Introduction

Graphene nanoplatelets (GNPs) have emerged as promising nanofillers for polymer-based materials due to their unique properties, such as high mechanical strength, excellent electrical conductivity, and remarkable thermal stability [1, 2]. Over the past few years, the incorporation of GNPs in various polymer matrices has resulted in the development of advanced composite materials with tailored properties for a wide range of applications [3]. The synergistic effect of GNPs and polymer matrices leads to enhanced mechanical, electrical, and thermal properties that significantly surpass those of the individual components [4, 5].

The diverse applications of GNP-polymer composites can be attributed to their tunable properties that cater to specific requirements in various industries. In the aerospace and automotive sectors, these composites are used for their exceptional strength-to-weight ratio, contributing to weight reduction and improved fuel efficiency without compromising structural integrity [6]. In the field of electronics, GNP-polymer composites exhibit excellent electrical conductivity, making them suitable for electromagnetic interference (EMI) shielding, flexible electronic devices, and printed circuit boards [7, 8]. Furthermore, GNP-polymer composites have demonstrated potential in energy storage applications such as batteries and supercapacitors, where their enhanced mechanical and electrical properties contribute to improved performance and longevity [9, 10]. These versatile materials also find applications in areas such as sensors, medical devices, and environmental remediation [11,12,13].

The incorporation of graphene nanoplatelets (GNPs) into polymer matrices has a significant impact on the mechanical properties of the resulting composites. GNPs, as two-dimensional nanofillers, possess extraordinary mechanical strength, with a tensile strength of around 130 GPa and Young’s modulus of approximately 1 TPa [14]. When uniformly dispersed within a polymer matrix, GNPs can improve the mechanical properties of the composite by effectively transferring stress between the polymer and the nanofillers [4].

One of the key factors influencing the mechanical enhancement of GNP-polymer composites is the aspect ratio of GNPs, which is the ratio of their lateral size to their thickness [15]. High aspect ratio GNPs create a large interfacial area between the polymer matrix and the nanofillers, facilitating efficient stress transfer and leading to improved mechanical properties such as tensile strength, Young’s modulus, and fracture toughness [12].

Another critical aspect is the uniform dispersion of GNPs within the polymer matrix, as agglomeration of GNPs can lead to stress concentration and reduced mechanical performance. Various methods, including in-situ polymerization, solution blending, and melt compounding, have been employed to achieve a uniform dispersion of GNPs in the polymer matrix [3]. On the other hand, researchers show that functionalized graphene enhances dispersion and adhesion in nanocomposites [16]. Therefore, functional groups can also be a key parameter in improving the properties of nanocomposites.

The orientation of graphene nanoplatelets (GNPs) in a polymer matrix can significantly influence the resulting properties of the composite. Two main types of orientation can be observed: isotropic and anisotropic.

In an isotropic orientation, GNPs are randomly dispersed within the polymer matrix, resulting in a composite with uniform properties in all directions. This uniformity can lead to enhanced mechanical properties, electrical conductivity, and thermal conductivity compared to the neat polymer [3, 4]. However, the improvements may be less significant compared to composites with anisotropic orientation due to the lack of directional reinforcement provided by the GNPs [17].

Anisotropic orientation, on the other hand, involves the alignment of GNPs in a specific direction within the polymer matrix. This alignment can be achieved through various methods, such as magnetic or electric field alignment, shear-induced alignment, or solvent evaporation-induced alignment [15, 18]. Anisotropic GNP-polymer composites exhibit direction-dependent properties. For example, mechanical strength, electrical conductivity, and thermal conductivity are significantly enhanced along the alignment direction compared to the perpendicular direction [19, 20]. This allows for the tailoring of composite properties for specific applications, such as high-strength materials, flexible electronics, or thermal management systems, where directional reinforcement and performance are crucial [21].

Nanocomposites with completely anisotropic particle distribution can be classified as a type of metamaterial with specific behaviours as examined by Barchiesi et al. [22] from both technological and theoretical perspectives. Computational techniques for analysing the parameters of metamaterial structures were proposed by Abali et al. [23] and Turco et al. [24] showed the nonlinear dynamics of origami metamaterials using a finite-dimensional Lagrangian system and numerical simulations. Generalized continuum models in the field of metamaterials can also be used to determine the parameters of these structural models. The enhanced continuum models were used to identify constitutive parameters for granular beam system, revealing exotic behaviours such as chirality through specific grain-pair interactions [25], or the identification of infill density effects used in additive manufacturing that differentiate the internal structural patterns to obtain metamaterials response [26]. De Angelo et al. [27] characterized pantographic structures and developed a second gradient orthotropic 2D solid model to identify nine constitutive parameters, which improved our comprehension of the mechanical behavior of these metamaterials under different loading conditions.

Numerous studies using analytical and numerical approaches show that the effective properties of fibers reinforced composites are influenced by the geometric shape of the reinforcements and their distribution within the matrix [28,29,30,31]. Pantographic micromechanisms leverage a specific arrangement of elements to achieve large, controlled deformations and unique mechanical properties, making them valuable in advanced material design and engineering applications. Some researchers use pantographic architecture to design metamaterial structures due to its ability to produce complex mechanical behaviors such as large elastic deformations [32,33,34,35] or damage [36, 37].

The use of polymer composites as substrates for microwave metamaterial absorbers, particularly in conformal applications, hinges significantly on the management of dispersion and bonding effects [38]. A judicious selection of filler materials, particularly in tandem with the chosen polymer matrix, is imperative to ensure the effective dispersion of fillers within the matrix. Dispersion issues and bonding typically arise when the density of the filler exceeds that of the matrix, or when the filler lacks appropriate functional groups, thereby predisposing it to filler particle aggregation or debonding within the polymer matrix. In the context of utilizing graphene nanoplatelets (GNPs) as fillers for metamaterial applications, the dispersion and bonding effects of GNPs become pivotal considerations [38].

By strategically enhancing the composite’s dielectric and mechanical properties through the incorporation of suitable fillers and fostering robust bonding mechanisms, the fabrication of metamaterial absorbers capable of operating across various frequency ranges can be feasibly achieved.

Multiscale modelling is a powerful computational approach used to study the behaviour and properties of different material such as GNP and CNT-polymer composites by considering the interactions and phenomena occurring at various lengths and time scales [39,40,41,42]. This method bridges the gap between atomic, micro, and macro scales, providing a comprehensive understanding of the structure–property relationships in GNP and CNT-polymer composites and facilitating the design and optimization of these materials for specific applications [34,35,36, 39, 43, 44].

In the context of GNP-polymer composites, multiscale modelling involves several hierarchical levels. At the atomic scale, quantum mechanical methods such as density functional theory (DFT) are employed to study the electronic structure, chemical interactions, and bonding between GNPs and the polymer matrix [45]. These interactions are crucial for understanding the interfacial properties and load transfer efficiency in the composites.

Molecular dynamics (MD) simulations and coarse-grained modelling are used to study the behaviour of GNP-polymer composites at the nanoscale [46]. These simulations can provide insights into the dispersion of GNPs within the polymer matrix, the influence of functionalization on the interfacial adhesion, and the impact of nanoplatelet orientation on composite properties. At the microscale, models like the finite element method (FEM) are employed to investigate the mechanical and thermal properties of GNP-polymer composites [47]. These methods consider the effects of GNP dispersion, orientation, and loading on the overall performance of the composite materials, such as stiffness, strength, and thermal conductivity. Finally, at the macroscale, continuum mechanics models are used to predict the overall behaviour and properties of GNP-polymer composites [48, 49]. These models incorporate the knowledge obtained from lower scales, including atomic and nanoscale simulations, to predict the performance of the composites in real-world applications.

Based on a hierarchical multi-scale modelling approach, Norouzi et al. [50] first calculated the properties of graphene by molecular dynamics methods and then calculated the effects of an anisotropic distribution of spiral graphene particles on the stress–strain curve by considering the interphase. It has been found that nanocomposites reinforced with graphene show higher stress in the direction perpendicular to the axis of the particles. An anisotropic behaviour of graphene/copper materials reinforced with aligned GNPs has been studied by Ke Chu et al. [51]. Moreover, this study shows that properties with in-plane tensile strength and elongation are significantly superior to those with through-plane tensile strength and elongation. According to the researchers, improving the interfacial bonding strength will be an important step towards optimizing the anisotropic mechanical properties of aligned graphene/metal composites. According to Hanzel et al. [52], the electrical conductivity of SiC/GNPs and SiC/GO composites increases significantly perpendicular to RHP pressing. Graphene-PMMA nanocomposites stereolithographically 3D printed with dynamic mechanical analysis (DMA) and Split-Hopkinson pressure bars were investigated for their viscoelastic properties. As a result of the alignment of graphene platelets along the printing axis within the polymer matrix, the anisotropic property of graphene nanocomposites was confirmed [53]. Results indicated that good interfacial bonding between GNPs and polymers was a key parameter. Compressive tests have demonstrated that graphene nanoplatelets reinforced aluminium composites possess orientation-dependent mechanical properties [54].

While numerous numerical and experimental studies have explored the anisotropic properties of nanocomposites, there remains a need for increased attention to how the distribution of nanoparticles influences damage behaviour within the bonding interface. This study employs a cohesive zone model to simulate the interface between the polymer (HDPE) and nanoparticles (GNPs). Drawing from our previous research involving molecular dynamics, we derive the parameters required for the cohesive zone model, using insights gained from our prior molecular dynamics analyses.

During validation of the multi-scale models based on RVE in this study, the stress–strain curves of uniaxial tensile responses of HDPE-GNP nanocomposite [55] were compared with numerical homogenization results by changing the aspect ratios of GNPs in weight fractions of 1% and 3%. Based on the stress amplification, the aspect ratio of GNPs was predicted. In the next part, we use RVEs with distributions ranging from isotropic to anisotropic to investigate the initiation and progression of debonding. Furthermore, we examine how these debonding behaviours influence the stress–strain response of the nanocomposite. Additionally, we explore whether the introduction of COOH functional groups enhances adhesion between GNPs and the matrix when subjected to both tensile and shear loads. This comprehensive investigation aims to shed light on the intricate relationship between nanoparticle distribution and debonding behaviour.

The transition from isotropic to anisotropic distribution of graphene nanoplatelets (GNPs) within polymer substrates has the potential to yield diverse properties. Examining the behaviour of composites reinforced with GNPs across a spectrum from fully isotropic to fully anisotropic distribution, with the aim of realizing anisotropic GNP polymer nanocomposites as metamaterials, holds promise for material design and optimization. Consequently, this research employs a multi-scale method to explore the impact of this distribution and the degree of nanoparticle bonding on mechanical properties, with the goal of advancing anisotropic GNP polymer nanocomposites as metamaterials.

2 Nanocomposite model

2.1 Multiscale finite element simulation

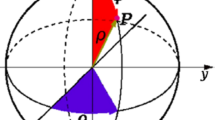
A three-dimensional (3D) representative volume element (RVE) was constructed for the graphene nanoplatelet (GNP)-polymer nanocomposite. A custom C\(++\) algorithm was developed to generate the RVE. Simulations were executed within a cubic unit cell possessing a side length of 0.04 mm. Three representative volume elements with volume fractions of 1.5% and aspect ratios of 40 were created. GNP distribution was considered in these three RVE, ranging from completely isotropic (Zenit angle \(=\)1 and azimuth angle \(=\)1) to completely anisotropic (Zenit angle \(=\)1000 and azimuth angle \(=\)1000, see Fig. 2) as shown in Fig. 1.

The geometry of each GNP was characterized by two parallel circular plates separated by the GNP’s thickness. Normal vectors, centre, and radii were used to uniquely identify each circular plate inside the RVE.

The Monte Carlo method was employed to randomly distribute the GNP centres within the matrix. Subsequently, random homogeneous functions were applied to generate the corresponding normal vector, resulting in the creation of randomly positioned points on the disc using Eq. 2.2.

$$\begin{aligned} \left\{ \begin{array}{ll} \theta =\textrm{2}\pi v\\ \varphi =\textrm{Arccos}(2u-1)\\ \end{array}\right. \end{aligned}$$
(2.2)

In the spherical coordinate the azimuth angle (\(\theta )\) is the angle measured in radians from the positive x-axis to the projection, in the x-y plane, of the line from the origin to P. The Zenith angle (\(\varphi )\) is the angle, measured in radians, from the positive z-axis to the line from the origin to P. In the mentioned equation, \(\theta \in [0,2\pi ]\) and \(\varphi \in [0,\pi ]\) represent spherical coordinates, as illustrated in Fig. 2. Additionally, u and v are random variables belonging to the interval \(\mathrm {[0,1]}\). The selected normal vectors ensure the GNPs are randomly and suitably oriented. The procedure of randomly choosing each GNP’s centre and normal direction was performed sequentially before generating the subsequent GNP in an identical manner. It is also important to note that the optimal size of the RVE was determined by increasing its volume until the homogenized stress–strain values exhibited negligible variation.

Fig. 1
figure 1

Three representative volume elements with volume fractions of 1.5% and aspect ratios of 40 ranging from completely isotropic to completely anisotropic

Full size image
Fig. 2
figure 2

An illustration of the spherical coordinates for a randomly selected point is provided in a three-dimensional space

Full size image

Analytical methods, considering nanoparticle-matrix debonding, were applied to analyse the mechanical properties of nanocomposites [56, 57]. Additionally, multi-scale models, using RVE, incorporated cohesive zone models with the Traction-Separation law to represent the interface between nanoparticles and the polymer [58]. These models enable the examination of various distributions with diverse geometric shapes of nanoparticles.

In order to model the GNP-matrix interface, the Cohesive Zone Model (CZM), governed by a bilinear traction/separation law, was applied to describe the interfacial behavior between the GNPs and the matrix material [59]. The study utilized the commercial finite element software ABAQUS 2021 to perform the simulations.

The choice between surface-based and element-based cohesive behaviour is available in this context, but due to the intricate geometry associated with GNPs, the surface-based method was deemed more suitable. This approach requires the definition of interaction properties for accurately representing the cohesive behaviour. Consequently, three key variables were considered to develop the cohesive law: stiffness, critical stress, and the critical value of displacement.

Precise characterization of interfacial or bonding materials is essential for the cohesive model. Nevertheless, determining the interaction between GNP and polymer experimentally in GNP/polymer nanocomposites presents a significant challenge. As a result, we used the findings from molecular Dynamics Simulations (MD) conducted on the interfacial interaction between graphene and polyethylene. The CZM consists of two crucial parameters: damage initiation and damage evolution. A standard traction-separation response, accompanied by a failure mechanism, is showed in Fig. 3.

The contact separations, which represent the distances between the master and slave node projection points in the contact normal and shear directions, undergo a transformation that relates to strain and displacement. When assessing cohesive behaviour at a surface, cohesive forces in the contact normal and shear directions are divided by the existing area at every contact point to assess stresses. The relationship between separation and traction stress is determined through Eq. 2.3 [60].

Fig. 3
figure 3

A Definition of the model for cohesive failure based on the traction-separation law. A schematic view is presented in B with the normal direction, perpendicular to the surface, and the first and second shear directions, and parallel to the surface along two in-plane axes

Full size image
$$\begin{aligned} T=\left\{ \begin{array}{*{20}c} t_{n}\\ t_{s}\\ t_{t}\\ \end{array}\right\} =\left( \begin{array}{*{20}c} k_{nn} & k_{ns} & k_{nt}\\ k_{ns} & k_{ss} & k_{st}\\ k_{nt} & k_{st} & k_{tt}\\ \end{array} \right) \left\{ \begin{array}{*{20}c} \delta _{n}\\ \delta _{s}\\ \delta _{t}\\ \end{array}\right\} =K\delta \end{aligned}$$
(2.3)

Within the specified equation, \(t_{n}\) refers to the normal direction traction stress, and \(t_{s}\textrm{,}t_{t}\) indicate traction stresses in the first and second shear directions, respectively. The nominal stiffness matrix is represented by K, while \(\delta _{n}\) corresponds to normal direction separation, and \(\delta _{s}\textrm{,}\delta _{t}\) designate separations in the first and second shear directions, respectively. By decoupling the normal and shear components, the equation can be simplified and presented as Eq. 2.4.

$$\begin{aligned} T=\left\{ \begin{array}{*{20}c} t_{n}\\ t_{s}\\ t_{t}\\ \end{array}\right\} =\left( \begin{array}{*{20}c} k_{nn} & \textrm{0} & \textrm{0}\\ \textrm{0} & k_{ss} & \textrm{0}\\ \textrm{0} & \textrm{0} & k_{tt}\\ \end{array}\right) \left\{ \begin{array}{*{20}c} \delta _{n}\\ \delta _{s}\\ \delta _{t}\\ \end{array}\right\} =K\delta \end{aligned}$$
(2.4)

After finalizing the linear elastic traction separation, the damage process begins. The initiation of damage is influenced by multiple factors. For this analysis, the maximum stress criteria were applied to evaluate the cohesive attributes predicted by the molecular dynamic’s simulation, as demonstrated in Eq. 2.5.

$$\begin{aligned} \textrm{MAX}\left\{ \frac{\left\langle t_{n} \right\rangle }{t_{n}^{\textrm{max}}},\frac{t_{s}}{t_{s}^{\textrm{max}}},\frac{t_{t}}{t_{t}^{\textrm{max}}} \right\} \mathrm {=1} \end{aligned}$$
(2.5)

These criteria indicate that the initiation of damage takes place when the maximum contact stress ratio attains a value of one. In the previously mentioned equation, the ramp function \(\left\langle t_{n} \right\rangle \mathrm {=0.5}\left( t_{n}\mathrm {+}\left| t_{n} \right| \right) \) represents the normal contact stress in the pure normal mode, while \(t_{s}\) and \(t_{t}\) are the shear contact stresses along the first and second shear directions, respectively.

The process of damage evolution starts when the appropriate initiation condition is met. As the damage evolution law dictates, the cohesive stiffness experiences degradation. Damage evolution may be categorized as separation-based or energy-based. In this research, the linear separation-based method (relying on displacement) was adopted. ABAQUS applies an evolution of the damage variable, D, for linear softening, which can be reduced to the expression recommended by Camanho and Davila [61] as presented in Eq. 2.6.

$$\begin{aligned} D=\frac{\delta _{m}^{f}\left( \delta _{m}^{\textrm{max}}\mathrm {-}\delta _{m}^{o} \right) }{\delta _{m}^{\textrm{max}}\left( \delta _{m}^{f}\mathrm {-}\delta _{m}^{o} \right) } \end{aligned}$$
(2.6)

In this equation, \(\delta _{m}^{f}\) stands for the effective displacement upon total failure, and \(\delta _{m}^{o}\) indicates the effective displacement at the onset of damage. Moreover, \(\delta _{m}^{\textrm{max}}\) represents the maximum effective displacement reached throughout the loading history.

The CSMAXSCRT parameter is employed to monitor damage initiation, with values ranging from 0 to 1. A value of 1 signifies the onset of damage, which will continue to progress as force increases until complete separation occurs. To study debonding, the CSDMG parameter, which varies between 0 and 1, is used; a value of 1 indicates complete separation. In this investigation, these two parameters are applied to identify damage initiation and debonding occurrence. In all instances, the applied strain at which the CSDMG parameter value reaches 1 is considered the fully debonding initiation strain at the contact point. The percentage of debonded surfaces is calculated using Eq. 2.7. DE represents the fraction of fully debonded nodes at the interfaces; N\(_{\textrm{d}}\) denotes the number of fully debonded nodes, and N\(_{\textrm{t}}\) denotes the total number of interfacial nodes [61].

$$\begin{aligned} DE=\frac{\mathrm {\sum }_{k\mathrm {=1}}^{N_{d}}N_{k}}{{\sum }_{k\mathrm {=1}}^{N_{t}}N_{k}} \end{aligned}$$
(2.7)

2.2 MD results calibration

In MD simulations, interfacial shear stress is one of the most important parameters that should be calculated using a pull-out test. The MD analysis assumes a nanocomposite structure that contains a nanoparticle in the centre and several polymer chains surrounding it. This research uses polyethylene as the polymer, and graphene or functionalized graphene as the nanoparticle. Figure 4 illustrates the results of the pull-out test for three functional groups and pure mode. In comparison to the other two functional groups, the COOH functional group creates the most adhesion between GNP and polymer. The research has continued with the calibration of MD results for COOH and pure functional groups in order to obtain cohesive zone parameters [61].

Figure 4 illustrates the calibrated Traction-Separation (T-S) curves (pertaining to shear) derived from MD simulation results for COOH functional group. As per the results from the MD analysis conducted by Karimi et al. [62] and Safaei et al. [63], the correlation between shear and normal stress can be approximated for different functional groups. In the case of COOH, the normal stress peak is 1.15 times higher than the shear stress. This correlation is employed in this study to estimate the normal stress data essential for finite element analysis. Cohesive zone parameters for pure and COOH functional groups are shown in Table 1.

Fig. 4
figure 4

A different types of functional groups (Pure, H, OH, COOH) at the end of the pull-out test and the number of polymer chains sticks to the graphene surface. B. left. The Force-displacement curves for the different functional groups B (Pure), C(H), D(OH), E(COOH)) [62, 63]. B-right. The calibrated T-S curve, derived from MD analysis for COOH functional groups

Full size image

2.3 Material modelling

In this study, it was assumed that GNPs exhibit isotropic, linear-elastic behaviour with a Poisson’s ratio of nu\(=\) 0.4 and a modulus of E \(=\) 1 TPa [65, 66]. A low strain rate elastic–plastic model was employed to simulate the high-density polyethylene (HDPE) [65]. The influence of strain rate on the polymer’s mechanical response was disregarded for HDPE, as it is only significant at high loading rates when adiabatic deformation occurs [67]. The required parameters for the elastic–plastic model included Young’s modulus, Poisson’s ratio, and a hardening curve (true tensile stress versus true tensile plastic strain). The von Mises yield criteria was applied under the assumption of isotropic work hardening. The equivalent stress, \(\sigma _{e}\), and the yield stress under tension, \(\sigma _{T}\), are related by the following equations:

$$\begin{aligned} & \sigma _{e}\,\mathrm {=}\,\sigma _{T}\end{aligned}$$
(2.8)
$$\begin{aligned} & \sigma _{e}\,\mathrm {=}\,\left\{ \frac{\textrm{1}}{\textrm{2}}\left[ \left( \sigma _{\textrm{1}}\mathrm {-}\sigma _{\textrm{2}} \right) ^{\textrm{2}}\mathrm {+}\left( \sigma _{\textrm{2}}\mathrm {-}\sigma _{\textrm{3}} \right) ^{\textrm{2}}\mathrm {+}\left( \sigma _{\textrm{3}}\mathrm {-}\sigma _{\textrm{1}} \right) ^{\textrm{2}} \right] \right\} ^{\mathrm {1/2}} \end{aligned}$$
(2.9)

The stress components \(\sigma _{\textrm{1}},\sigma _{\textrm{2}}\) and \(\sigma _{\textrm{3}}\), along with the tensile yield stress \(\sigma _{T}\), are the primary stress components. \(\sigma _{T}\) is a material property that represents the minimum value at which elastic behavior ends and plastic deformation starts, increasing with tensile plastic strain. The elastic properties of the linear isotropic polymer matrix were assumed to be E \(=\) 1100 MPa and \(\nu \) \(=\) 0.44, and the related von Mises stress for HDPE was obtained from [65, 68].

Table 1 The Cohesive parameters [64]
Full size table

To transfer the RVE, a Python script was developed based on the approach described for the ABAQUS commercial FE software. Six-node wedge elements (C3D6) and four-node linear tetrahedron elements (C3D4) were utilized for GNPs and RVE, respectively. The size of the tetrahedron elements varied from 0.6 µm near the GNPs to 1.5 µm in the bulk material. The quasi-static uniaxial displacement and shear loading were applied. This study considered the X and Y directions according to the anisotropy distribution of GNPs, as shown in Fig. 5A. For the fully anisotropic model, the loading in the X direction is orthogonal to the GNP axis, whereas the loading in the Y direction is parallel to the GNP axis. Figure 5B shows the boundary conditions for tensile and shear loading.

Fig. 5
figure 5

A Anisotropic distribution of GNPS with a volume ratio of 1.5 %. A GNPS axis lies parallel to the yaxis, while a GNPS axis lies perpendicular to the xaxis. B Applied boundary conditions for RVE in tensile and shear loads

Full size image

The study investigates anisotropic GNP distribution using three RVEs for each distribution. Tensile loading averages results in the X and Z directions, while Y-direction results are calculated separately. For shear loading, averages are computed in the XY and ZY planes, with ZX-plane results analysed individually. This approach helps assess the effects of anisotropic distribution under both shear and tensile loading.

Mass scaling was used to reduce processing time for the explicit FE simulation. The kinetic energy in all simulations was less than 1% of the total strain energy, indicating a quasi-static loading state.

In the Abaqus software, numerical stress and strain components were computed throughout the loading history using Python scripting and the homogenization approach [69].

$$\begin{aligned} {\bar{\sigma }}_{ij}\,\mathrm {=}\,\frac{\mathrm {\sum }_{k\mathrm {=1}}^{N_{ip}}\sigma _{ij\textrm{,}k}V_{k}}{\mathrm {\sum }_{k\mathrm {=1}}^{N_{ip}}V_{k}} \end{aligned}$$
(2.10)
$$\begin{aligned} {\bar{\epsilon }}_{ij}\,\mathrm {=}\,\frac{\mathrm {\sum }_{k\mathrm {=1}}^{N_{ip}}\epsilon _{ij\textrm{,}k}V_{k}}{\mathrm {\sum }_{k\mathrm {=1}}^{N_{ip}}V_{k}} \end{aligned}$$
(2.11)

The homogenized stress and strain components are \({\bar{\sigma }}_{ij}\) and \({\bar{\epsilon }}_{ij}\), respectively; \({\bar{\sigma }}_{ij\textrm{,}k}\) and \({\bar{\epsilon }}_{ij\textrm{,}k}\)are the stress and strain components at the integration point; N\(_{\textrm{ip}}\) is the total number of integration points; and V\(_{\textrm{k}}\) is the volume of element at the integration point.

3 Model validation and aspect ratio prediction

The stress–strain behavior of HDPE-GNP nanocomposites with varying weight fractions has been examined by Bourque et al. [55]. Using a micromechanical model and permeability analysis, they predicted the aspect ratio of nanoparticles under different weight fractions by incorporating stress amplification as a critical input parameter. We calculated the true stress–strain curve for HDPE-GNP nanocomposites with a variety of aspect ratios of GNPs using a finite element model based on the Representative Volume Element (RVE) approach that integrates cohesive parameters derived from molecular dynamics results. Subsequently, the calculated stress–strain curves were rigorously compared with experimental results. An inverse method was implemented to determine the aspect ratio of GNPs, where stress amplification values served as pivotal input data for predicting the aspect ratio.

Using the permeability results in conjunction with Gusev and Lusti’s equation for permeability reduction [55], it was also possible to predict the particle aspect ratio of the GNP particles in the composite material.

$$\begin{aligned} \frac{p}{p_{\textrm{0}}}\,\mathrm {=exp}\left( \mathrm {-}\left( \frac{A_{f}v_{f}}{x_{\textrm{0}}} \right) ^{\beta } \right) \quad \end{aligned}$$
(2.12)

\(p_{o}\) is the permeability of the neat materia \(v_{f}\) and \(A_{f} \)are the volume fraction and aspect ratio of the filler particles,and \(\beta \) and \(x_{o} are \)empirical constants. Particle aspect ratios predicted from permeability measurements are at least an order of magnitude greater than those predicted by micromechanical models. However, the trend toward decreasing aspect ratios with increasing GNP loading is consistentspsdo

The findings of this study demonstrated a commendable agreement between the calculated aspect ratios and those predicted by the permeability model, particularly for weight fractions of 1% and 3% [55, 69]. Table 2 compares the predicted aspect ratios of GNPs with different method in 1% and 3% weight fraction. Due to the stacking of GNPs, filler aggregates formed, leading to an overall reduction in the aspect ratio of dispersed particles and an elevation in their theoretical modulus. Stress–strain curves for weight fractions of 1% and 3%, featuring different aspect ratios, are visually represented in Fig. 5. These results exhibited strong concordance with experimental findings from [55], specifically for a weight fraction of 3% and an aspect ratio of 80.

Table 2 Comparison of predicted GNP aspect ratios in weight fractions of 1% and 3% with different method
Full size table

Figure 6 shows the stress–strain curve of experimental and numerical modeling in two weight fractions. As can be seen when cohesive parameters were employed in a functionalized mode (COOH), debonding occurred at higher strains, consequently amplifying stress. In Bourque et al.’s study [55], the absence of functional groups rendered the cohesive interface valid in a pure mode. Additionally, a comparison of results for the weight fraction of 1% demonstrated a noteworthy agreement between experimental and finite element stress amplification with AR=200 for GNPs. Furthermore, the permeability model predicted an aspect ratio of approximately 200 for this weight fractionspsdo

Fig. 6
figure 6

A Two generated RVEs, each with a weight fraction of 1 and 3%, and a GNP aspect ratio of 200 and 60, respectively. Examination and comparison of the true stress–strain curve between experimental findings [55] and numerical results derived from the Representative Volume Element (RVE) model for a weight fraction of B. 1% and C. 3%

Full size image

According to predictions, the aspect ratio exhibited a decreasing trend with an increase in weight fraction. The finite element analysis and inverse method employed in this study yielded predicted values that align well with those anticipated by the permeability model. Numerical analysis of the finite element model indicated improved accuracy in predicting mechanical properties using RVE with an increase in aspect ratio and weight fraction. This enhancement was observed when more GNPs with different orientations were strategically placed inside the RVE. The accurate prediction of mechanical properties at low weight fractions, particularly below 0.1%, was achieved by applying high aspect ratios (above 1000). The results of this study are consistent with those of the permeability model. However, it is important to note that the use of GNPs with aspect ratios exceeding 1000 in finite element models is constrained by computational limitations. Consequently, predicting mechanical property behavior in higher weight fractions based on the RVE model is expected to yield enhanced accuracyspsdo

4 Results and discussions

The purpose of this section is to present the results of our analysis of nanocomposites reinforced with GNPs under various loading conditions. After discussing the findings related to tensile loading, we will discuss the results obtained under shear loading. In addition to providing valuable insight into the mechanical behaviour of these nanocomposites and their response to different loading scenarios, these results also have implications for their practical applications and structural design.

4.1 GNP orientation and functionalization effect in tensile loading

4.1.1 Debonding initiation and propagation

Functional groups such as OH, H, and COOH increase the adhesion between GNPs and polymers. According to Sect.  3, the COOH functional group has the greatest impact on adhesion between GNPs and HDPE. The molecular dynamics results for this functional group were used to develop a cohesive zone model. The study examined three different distributions with varying zenith angles, ranging from a fully isotropic distribution to a fully anisotropic distribution. Representative Volume Elements (RVEs) with pure and COOH functional groups, which exhibit different cohesive properties between GNPs and matrix, were analysed for stress–strain curves and debonding behaviour.

We observed that debonding behaviour changes in various directions as an anisotropy level increases in our models. It is crucial to emphasize that these variations depend entirely on the adhesion between GNPs and the matrix. For the pure and COOH functional groups, Figs. 7, 8, 9 and 10 illustrate the extent of fully debonded surfaces in tensile loading models with different GNP distributions parallel and perpendicular to the GNP axis.

In an entirely anisotropic model, we observed significant differences in the debonding behaviour parallel and perpendicular to the GNP axis (Zenith angle \(=\) 1000). As shown in Fig. 7, debonding occurs at a greater strain when the loading is parallel to the GNP axis compared to when it is perpendicular. However, once debonding begins, the number of debonded surfaces increases relatively constantly, resulting in approximately 16% of GNP surfaces being fully debonded at a 20% strain. When the loading is perpendicular to the GNP’s axis, the debonding rate continues to increase at a relatively constant slope up to a strain of 4.7%. The rate at which GNPs completely debond from the matrix decreases after this point. Consequently, at a 20% applied strain, approximately 10.4% of GNPs are fully debonded.

Fig. 7
figure 7

A study of surface debonding versus applied tensile strain for a fully anisotropic distribution based on functional groups (COOH) and without functional groups parallel and perpendicular to the axis of GNPs

Full size image
Fig. 8
figure 8

Debonding growth (CSDMG Contour) in the anisotropic distribution with increasing tensile strain in the direction of the GNPS axis. Without functional group (Pure)

Full size image

In Figs. 9 and 10 debonded levels are illustrated for other distributions (Relatively anisotropic and fully isotropic). An anisotropic model with interface properties matching the COOH functional group showed no significant difference in debonding in two directions (parallel or perpendicular to the graphene axis). According to these findings, the extent of debonding in two directions, parallel and perpendicular to the GNP axis, remains relatively consistent under anisotropic distribution conditions. In all cases, using the COOH functional group substantially reduced the extent of debonded surfaces. This reduction was particularly pronounced, decreasing from 9.66% to less than 0.6% in an entirely isotropic distribution. Furthermore, the COOH functional group significantly delayed the onset of debonding. In an anisotropic distribution perpendicular to the GNP axis, debonding begins at approximately 0.13 strain, whereas debonding begins at approximately 0.035 strain in the pure state. Debonding behaviour is significantly influenced by distribution anisotropy and surface functionalization. The results of this study can provide valuable insights into designing and optimizing nanocomposites with tailored mechanical properties.

Fig. 9
figure 9

A study of surface debonding versus applied tensile strain for a relatively anisotropic distribution based on functional groups (COOH) and without functional groups parallel and perpendicular to the axis of GNPs

Full size image
Fig. 10
figure 10

The amount of debonded surface vs. applies tensile strain for fully isotropic distribution considering functional groups (COOH) and without functional group

Full size image

4.1.2 Averaged stress–strain curve

Figure 11 provides a comprehensive view of stress–strain curves for three distinct GNP distributions, ranging from completely isotropic to fully anisotropic, both with and without the presence of a COOH functional group. The behaviour of anisotropic distributions varies depending on whether they are aligned parallel or perpendicular to the GNP axis, as depicted in the figure. Notably, stress values are higher in loading directions perpendicular to the GNP axis compared to those parallel to it. These findings align with previous studies [50,51,52], which have also reported similar trends. Stress–strain curves for fully isotropic distributions fall between the curves for parallel and perpendicular loadings. The introduction of the COOH functional group into GNPs has a more significant impact on the mechanical behaviour in directions parallel and perpendicular to the GNP axis. Figure 6 illustrates that functional groups exert a more pronounced effect on anisotropic distributions than on isotropic ones, particularly in terms of the number of surfaces that undergo debonding.

When loaded parallel to the GNP axis, approximately 16% of the GNPs completely debond from the matrix at a strain of 20%. Figure 10 effectively shows how the initiation and progression of debonding affect the mechanical behaviour of nanocomposites. The effect of debonding initiation is evident in the stress–strain curve. As debonding progresses, the load transfer between GNP and matrix diminishes, leading to a noticeable drop in the stress–strain curve. In the case of the anisotropic model without functional groups, debonding initiation begins at approximately a strain of 0.021, and the stress–strain curves decline when this damage occurs in the interface area.

Comparing the stress–strain curves for the pure and COOH functional groups perpendicular to the GNP axis in Fig. 11 reveals that these two curves also diverge at around a strain of 0.021. This comparison can serve as a reference point to determine the strain at which debonding initiates for other distribution states. These findings underscore the critical role of distribution anisotropy and functionalization in influencing the mechanical behaviour of nanocomposites, particularly in the context of debonding initiation and progression.

Fig. 11
figure 11

A comparison of average stress–strain under tensile loading. Completely isotropic and completely anisotropic distributions when considering the COOH functional group in the interface area and without it. Parallel and perpendicular to the GNP axis

Full size image

4.2 GNP orientation and functionalization in shear loading

In pure shear loading, the rate of debonding behaviour in an anisotropic distribution differs between planes with the plane normal parallel to the GNP axis and planes with the plane normal perpendicular to the GNP axis. So, in parallel to the GNP axis, debonding begins at a lower strain, and debonding expands with increasing shear strain. The COOH functional group delays the initiation of debonding and reduces the debonded surface area to less than 1%. The COOH functional group has a significant effect, as seen in the shear stress–strain curve. In the plane perpendicular to the GNP axis, however, it can be observed that debonding occurs at higher strains, such that the percentage of debonded surfaces in the pure state is less than 0.7% at strain 0.15. Using a COOH functional group, debonding does not occur in this plane under shear loading up to a shear strain of.15. Figure 14 shows a comparison of the stress–strain curves for the pure and COOH states, indicates that these two states have the same stress–strain curves, indicating that debonding was unaffected. A value of the debonded surfaces and the stress–strain curve placed between these two results in an isotropic distribution. Consequently, in an isotropic distribution in the pure mode, approximately 6.5% of the surfaces are completely debonded, whereas in the COOH state, a completely isotropic distribution does not result in debonding.

If the shear loading is applied to a plane whose normal is in the direction of the GNP axis, the percentage of entirely debonded surfaces is approximately 10.5%. In other plans, the percentage is less than 1%. This shows that debonding initiation and propagation differ significantly in planes parallel and perpendicular to the GNP axis.

4.2.1 Debonding initiation and propagation

Figures 12 and 13 visually illustrate the CSDMG contour for both isotropic and anisotropic distributions. The shear stress–strain curve effectively reflects the initiation and progression of debonding in these scenarios.

Fig. 12
figure 12

CSDMG counter for fully anisotropic GNP distribution. With (COOH) or without (Pure) functional groups. Shear loading in XZ and XY planes

Full size image
Fig. 13
figure 13

debonding in shear loading for a fully anisotropic distribution of GNPs. Left pure. Right COOH. Under.15 shear strain, approximately 6.63% of the GNP surfaces are debonded in an isotropic distribution. No debonding is observed when using the COOH group

Full size image

Figure 14 clearly illustrates the stress–strain behavior when the loading is applied in two distinct directions: one in the plane perpendicular to the GNP axis (normal to the plane perpendicular to the GNP axis) and the other parallel to the GNP axis. In the case of loading in the plane perpendicular to the GNP axis, the stress–strain curves for both the PURE and COOH states perfectly coincide. This alignment extends to the amount of debonded surfaces and the applied strain at which debonding initiates. The mechanical response in this loading direction remains consistent between the two states.

Fig. 14
figure 14

A comparison of average stress–strain under shear loading. Completely isotropic and completely anisotropic distributions when considering the COOH functional group in the interface area and without it. Parallel and perpendicular to the GNP axis. The normal of the XZ plane is parallel to the GNP axis

Full size image

Conversely, when the loading occurs in the direction parallel to the GNPs axis, the stress–strain curves for these two states begin to diverge at a strain of approximately 0.024. This divergence indicates the onset and subsequent growth of debonding in this specific loading direction (In the figure, the XZ plane refers to the plane whose normal is parallel to the GNP axis).

5 Conclusions

This research employs a multi-scale methodology to investigate how the distribution and bonding of nanoparticles influence mechanical properties. The primary objective is to advance anisotropic High-Density Polyethylene-GNP nanocomposite as metamaterials. First the stress–strain curves of uniaxial tensile responses of a High-Density Polyethylene-GNP nanocomposite, derived from experimental results [55], were compared with the results generated through numerical homogenization. The validation process involved adjusting the aspect ratios of the GNPs at weight fractions of 1% and 3%. The stress amplification results were subsequently utilized as input parameters in a model that predicted the aspect ratio of GNPs. The permeability results and the predicted values for aspect ratio in this investigation are in excellent accord. Multi-scale models that incorporate RVEs with increased aspect ratios and weight fractions yield accurate results since they allow the addition of a greater number of different-oriented GNPs.

Considering the COOH functional group that increases adhesion between GNPs and polymer, this study examined the effect of an anisotropic distribution of GNPs on the initiation and growth of debonding. A cohesive zone model was used to study debonding. The parameters required for this model were derived from the authors’ molecular dynamics results. Graphene and the matrix adhere better when the COOH functional group is present. This has a significant impact on nanocomposites’ mechanical properties. Debonding and its effect on stress–strain were investigated for RVEs with completely isotropic to completely anisotropic distributions when subjected to tensile and shear loading. Graphene matrix bonding is a key parameter for optimizing nanocomposites’ anisotropic properties.

Models with an anisotropic distribution parallel and perpendicular to the GNPs axis exhibit different onsets and growth rates of debonding. It has been observed that debonding begins later in anisotropic models when loading parallel to the graphene axis, compared to loading perpendicular to the graphene axis. However, with increasing tensile loads, the rate of debonding in graphene’s parallel axis will increase. In this case, approximately 16% of the GNP surfaces are entirely debonded with the RVE at a volume fraction of 1.5% and without the functional group oriented parallel to the GNP axis. This value is approximately 10% when loading is perpendicular to the GNP axis and close to 10.4% in a completely isotropic distribution. The stress–strain curve clearly illustrates the effect of debonding on initiation and growth. In the presence of COOH functional groups, debonded surfaces decrease to less than 1%. Our exploration of debonding behavior in pure shear loading within anisotropic distributions has revealed intriguing patterns dependent on the orientation of planes relative to the GNP axis. Parallel orientations exhibit early and extensive debonding, which is significantly mitigated by the COOH functional group. In contrast, perpendicular orientations experience delayed and limited debonding, with the COOH group completely preventing it. In the plane parallel to the axis of GNPs, approximately 10.5% of the surfaces are debonded from the matrix when shear strain is 0.15. This value for a fully isotropic distribution is close to 6.5%.