1 Introduction

In this paper, structural elements having an origami-type microstructure and micro-kinematics are considered. The model used in order to get quantitative predictions about their nonlinear dynamical behaviour is finite dimensional: the origami microstructure configuration is characterized by means of the vertices positions of the constituent triangular discrete elements. All introduced triangular elements are suitably interconnected via holonomic constraints to constitute the considered metamaterial. A Lagrangian energy function is introduced to establish the evolution equations of the considered origami structures and the used time integration scheme allows us to explore the promising dynamical behaviour of an origami beam (for a survey of existing models for exploring the dynamical behaviour of metamaterial see [1]).

1.1 An ancient technique revived for modern technological applications

The Japanese word origami originally stands for the art of folding sheets of paper in order to produce three-dimensional shapes. The idea behind this art has been the source of several scientific proposals in the field of metamaterials [2, 3]. Specifically, during the 80’s, it has been the source of a proposal [4] on the design of periodic metamaterials whose unit cell can be folded, making use of typical origami techniques. Such a proposal has been then further developed in the papers [5,6,7].

Initially, the most promising application for such a kind of metamaterials was its use—in conjunction with solar panels—for space missions. More recently, several applications have been thought of for origami metamaterials in the biomedical field. Indeed, as an instance, they could be employed for building medical stents, see [8]. To this end, cylinders possessing the so-called Kresling pattern seem a very attractive solution [9], as they exhibit spontaneous buckling under torsional load. More generally, origami metamaterials can be used for building devices with programmable shape [10].

1.2 The possibilities opened by modern 3D-printing technology

Albeit the first papers dealing with origami metamaterials date back to the 80’s, owing to the lack of appropriate manufacturing technologies, the realization of these metamaterials has been long considered infeasible. Thanks to new developments in additive manufacturing like 3D-printing, which can reach extremely high precision and allows for creating complex assemblies without the need of performing an actual a posteriori assembling, origami-based materials are currently manufactured and studied. A wide scientific literature has been attempting at studying them from the purely geometric viewpoint. Indeed, folded sheets can only approximate surfaces, and moreover, passing from a flat to a curved surface is not always possible. It has to be remarked [11,12,13] that it has been possible to print 3D microstructures in which relative rotations and displacements of their different parts are made possible. This technological capacity clearly opened the path towards the construction of specimens of metamaterials, which, before, could be only conceived as a logical possibility.

1.3 Models for origami metamaterials

An increasingly wide literature is interested in describing the mechanical behaviour of origami metamaterials, aiming at characterizing their mechanical properties, mostly making use of (semi-)discrete and/or generalized continuum modelling [14,15,16], this last being required by the occurrence of (quasi-)zero-energy deformation modes [17], as well as local instabilities and size effects [18, 19].

It is worth to note that, addressing the so-called synthesis problem [20, 21], having the goal of developing a deployable metamaterial—namely a three-dimensional material that, exploiting mechanisms, can be compressed into surfaces or a two-dimensional material that can be compressed into curves—many solutions have been proposed in the literature, like pantographic metamaterials [22,23,24,25,26], which exploit a scissor-like mechanism.

It has to be also underlined that while the notion of convergence can be still used [27], the standard homogenization techniques used in the literature for finding continuum models cannot be extended easily to origami-based metamaterials. Actually, it seems to us that the class of generalized continua to be introduced as target models in the searched homogenization process must have a rather richer kinematics than those used systematically, up to now, in the literature. Therefore, we decided to focus our analysis on discrete Lagrangian models for origami beams, in order to describe their mechanical behaviour in a very thorough and detailed way, to get a logical basis for conjecturing the structure of a future effective continuum model to be used for their overall mechanical description.

1.4 A brief description of Miura-ori and Kresling origami microstructures

A plethora of geometries for origami metamaterials—essentially borrowed from classical origami tessellations—have been proposed in the literature and consist of the periodic repetition in a two-dimensional array of a foldable unit cell. The most studied geometries, as long as mechanical behaviours are concerned, are the ones based on the so-called Miura-ori cell and the egg box tessellation. The Miura-ori tessellation owes its name to the fact that it was first introduced in the scientific literature by Miura [4]. Indeed, as recalled above, Miura originally proposed this tessellation as an efficient geometry for packing and deploying solar panel sheets for space missions. It is however worth to mention that this kind of tessellation can be recognized in many biological systems, like leaves and embryonic intestine, which show geometric patterns that resemble the Miura-ori tessellation. Interestingly, such a tessellation also emerges in deformation patterns of surfaces subjected to biaxial compression, which somewhat points to its optimal properties.

To our knowledge, the study of the optimality of Miura-ori tessellation has not been fully explored yet: however, one can rather straightforwardly note that, if folding were allowed (only) in the most deformed regions, then the global stiffness would decrease, thus yielding an extremely compliant material that, once deformed, stores low deformation energy. It is in this regard relevant to mention that a pattern emerges when torsion tests are performed on thin-walled cylinders in paper or polypropylene: a thin sheet is wrapped around two coaxial mandrels, leaving a gap among the two of them and, when the mandrels are rotated about their axis, a folding pattern appears in the gap. Such a folding pattern is made up of inclined and stretched parallelograms, which are the mountain-folds, divided on their long diagonal by a valley-fold. This tessellation is known as the Kresling origami pattern [9] and it is seen that, for any given gap size between the mandrels, a left-hand or right-hand twist-buckling pattern appears. Still regarding folding patterns emerging from mechanical tests on thin sheets, it is also worth to mention that Kresling has demonstrated how a cone, when smashed, can fold itself into a structure that seems to mimic the spiral geometries of pinecones and mollusk shells [28].

1.5 Related geometric and synthesis problems in the theory of origami metamaterials

In Miura’s pioneering work, the original engineering problem, i.e. that of packing in a compact manner solar panels, was indeed overlying a fundamental mathematical—geometrical, specifically—problem which is at the very core of origami.

Such a problem reads as follows: given a surface, what are, if any, the transformations that are able to map rigidly, i.e. without stretch or compression, an intrinsically flat surface into a curved surface, i.e. a surface with intrinsic curvature? To better understand the previous problem statement it is worth to mention that by intrinsically flat surface we mean a surface that is completely flat and not a curved surface oscillating around a flat mid-plane.

This problem is strictly connected to the one of seeking to develop transformations mapping intrinsically flat surfaces into folded structures with apparent intrinsic curvature. This last problem can be regarded as analogous to the metamaterials’ synthesis one, although also mechanics would in that case be involved. Such a problem can be also regarded as an inverse one that, generally speaking, is very difficult to solve. Notwithstanding these difficulties, amplified by limitations due to inherent developability constraints, the rational design of the crease and cut patterns proved several times successful in enabling the shape-shifting of (nearly) inextensible sheets into geometries with apparent intrinsic curvature, i.e. the folded sheets. Note that by apparent intrinsic curvature we mean the curvature possessed by the mid-surface of the folded sheets.

1.6 Mechanics of the Miura-ori tessellation

In the case of the Miura-ori tessellation, a doubly corrugated surface, obtained via the repetition in a two-dimensional array of a unit cell as represented in Fig. 1, is considered [29, 30]. The fundamental cell is made up of four congruent parallelograms, each one characterized by the lengths of its two sides sharing one common vertex and an angle. The four parallelograms are arranged in such a way that the sum of the four angles which meet at one vertex is equal to \(2\pi \), which allows to have a developable surface [7]. As it can be seen in Fig. 1, the edges of the parallelograms form a re-entrant lattice. The geometry of the tessellation pattern can be described in terms of four parameters: the two lengths and the angle, specifying the parallelograms, and the angle between the flat plane and one of the parallelograms in the folded configuration. For Miura-ori tessellations, we can distinguish between in-plane and out-of-plane deformations, where the words “in-plane” and “out-of-plane” are referred to the plane passing through the valleys and mountains, i.e. resulting from the average of the mountain and valley array. As far as in-plane deformations are concerned, the behaviour of the Miura-ori tessellation is described by its in-plane Poisson’s ratio: one can immediately notice that the in-plane Poisson’s ratio is always negative [31], which can be easily deduced from the remark above: the edges of the parallelograms form a re-entrant lattice [32].

Fig. 1
figure 1

Standard Miura unit cell: before (left) and after (right) the folding

Full size image

When out-of-plane deformations are considered, it is extremely difficult to predict the behaviour of the Miura-ori tessellation without making use of simulations based on a mechanical model. Among the several models that have been developed in the course of the past years, it is here worth to mention the simple—yet extremely successful and powerful—mechanical model introduced by Schenk and Guest in [29, 33], which replaces the sheet with a system of bars interconnected via spherical pin-joints, and whose spirit is very close to the approach adopted in the present paper, as well as in relevant recent literature. Clearly, different descriptions are possible and, as an instance, the whole sheet could be modelled as a single thin shell or facets could be considered to move rigidly.

The presented description of the mechanical properties of the Miura-ori tessellation makes clear why it is so difficult to conceive a continuous model suitable to describe origami metamaterials based on the Miura-ori folding pattern at a macroscopic level: as an instance, macro-elongations are related mainly to relative micro-rotations and the macro-description of the system requires the possibility of accounting for these rotations. Moreover, the geometrical complexity of the Miura-ori tessellation makes very intricate the relationship between macro- and micro-kinematical descriptors, which mades the use of the micro–macro-kinematical identification rather difficult in homogenizing such a microstructure [34, 35].

1.7 Other origami microstructures can be useful in metamaterials design

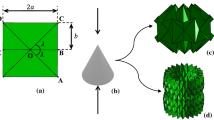
As mentioned above, a plethora of origami-based metamaterials can be obtained by exploiting different origami tessellations and, besides the Miura-ori pattern, the so-called egg box tessellation pattern (see Fig. 2) is one of the most studied ones. This pattern is obtained by alternating along a two-dimensional array pyramids with a quadrilateral base having opposite orientations. Unlike the Miura-ori, this pattern cannot be obtained by suitably folding a flat sheet, since the sum of the angles at each vertex is less than \(2\pi \). From the point of view of its mechanical properties, differently from the Miura-ori tessellation, this pattern presents a positive in-plane Poisson’s ratio. However, the previously mentioned models, and in particular the approach introduced by Schenk and Guest [36], can be applied also to the egg box pattern [33]. It is worth to remark that an approach has been recently developed in [30], which allows to find the surfaces that can be tessellated via an egg box pattern, in the limit for the characteristic length of every pyramid going to zero.

Fig. 2
figure 2

Pyramidal egg box unit cell (left) and pattern (right)

Full size image

1.8 Deformation energy for Miura-ori microstructures with non-rigid facets

The present paper attempts at studying computationally the nonlinear mechanical behaviour of origami metamaterials with non-rigid facets—facets are regions which the sheet is partitioned into, according to the crease pattern—making use of numerical tools, as well as of discrete spring model formulations, developed by the same authors in previous contributions to the literature on mechanical metamaterials [37,38,39]. The sheet is assumed to have zero thickness, which is equivalent to state that we assume no deformation to be undergone by the sheet in the thickness direction. Notwithstanding the generality of the approach, the formulation is specialized to the case of Miura-ori tessellations, where facets, which are parallelograms, are modelled as two adjacent triangular sheets having as common edge a diagonal of the parallelogram (see Fig. 1). In the present approach, triangles are allowed to undergo (only) affine deformations in the space. Therefore, the position of their vertices in the current configuration makes up a minimal set of global Lagrangian coordinates for the mechanical system. From a mechanical viewpoint, the current lengths of these triangles are sufficient to write the deformation energy of the system due to the in-plane stretch and shear experienced by the triangles. In particular, for a homogeneous, isotropic sheet, the elastic energy of a triangle (with zero thickness) undergoing (in-plane) affine deformations can be equivalently thought of as if its sides were extensional Hooke’s springs [40], which will be accordingly called in the sequel stretch springs. Torsional springs obeying Hooke’s law are placed in-between adjacent triangles, altogether called a panel, belonging to the same facet or to adjacent facets. The torsional springs placed in-between adjacent triangles belonging to the same facet are meant to model the bending behaviour of the facet, while those placed in-between adjacent triangles belonging to adjacent facets are meant to model the folding behaviour. In the sequel, according to such a distinction among torsional springs, we will refer to bending and folding springs, respectively.

For the sake of simplicity, the present contribution deals only with the nonlinear dynamical behaviour of origami metamaterials obtained as the periodic repetition of a Miura-ori unit cell along a single direction, i.e. with a one-dimensional array of Miura-ori unit cells. The present approach shares some features with the one presented recently by Liu and Paulino  [41], even if, unlike [41], the present contribution introduces also inertial forces and, accordingly, uses a specific time-integration strategy to recover the evolution of the system.

1.9 Outline of the present paper

Having in mind the aforementioned goals, after this section, Sect. 2 introduces the kinematics as a global maximal set of Lagrangian coordinates of the system—node, i.e. triangles’ vertices, positions—as well as the expression for the strain energy, consisting of contributions due to affine deformation of triangles in space, bending of facets, and folding of the sheet about creases, accounted for by stretch, bending, and folding springs, respectively. The expression of the kinetic energy is also introduced in Sect. 2. Expressions for strain and kinetic energies are discussed and motivated. Successively, in Sect. 3, what has been discussed in the previous section is used as a building block to formulate the time-stepping scheme, which is later used to perform numerical simulations presented and thoroughly discussed in Sect. 4. Concluding remarks and future challenges follow in Sect. 5. We finally note that the results obtained in the present paper suggest that the considered formulation can be fruitfully applied and developed further, aimed at exploring the class of behaviours that can be exhibited by origami metamaterials, possibly having tessellations different from the Miura-ori one and being obtained as the periodic repetition in two directions of unit cells that can be folded.

2 Specifying the model by means of its kinematics and associated energies

Aimed at exploring the mechanical behaviour of a generic origami metamaterial, a discrete model can be employed, having as fundamental brick a triangular element. Hence, strain and kinetic energies of the whole origami metamaterial can be computed by summing up over all the triangles, in which the origami geometry has been partitioned, these quantities.

In the discrete modelling that we adopt in this contribution, the reference configuration shall be completely defined by the vector \(\textbf{X}\) collecting the nodal coordinates, i.e. the coordinates of the vertices of all the triangles which form the origami, in the reference configuration. Since the nodes of an origami are, generally speaking, not lying all on the same plane, we cannot choose coordinate axes such that, a priori, the vector \(\textbf{X}\) has less than \(3 N_n\) entries, where \(N_n\) is the number of nodes. In the sequel, we will denote with \(N_t\) the number of triangles that the origami has been decomposed into.

The current configuration shall be completely defined by the vector \(\textbf{x}\) collecting the nodal coordinates in the current configuration. Reference and current configurations allow to compute the nodal displacement vector \(\textbf{u}=\textbf{x}-\textbf{X}\), having \(3 N_n\) entries, which are the Lagrangian coordinates used to describe the motion in our approach.

In such a framework, each triangle, in which the origami metamaterial geometry has been decomposed into, is mapped into a (different) triangle in the current configuration, i.e. each triangle deforms affinely. In order to completely define the mechanical model, besides the kinematics, we need to define for given Lagrangian coordinates and velocities, i.e. the rate—in time—of Lagrangian coordinates, the strain and kinetic energies of the assembly of triangles forming the origami. Concerning the strain energy, we can distinguish:

  1. 1.

    The energy stored in the triangles—regarded as elastic bodies—because of the change in their shapes;

  2. 2.

    The energy stored in torsional springs, which can be in turn subdivided into bending and folding contributions, storing energy for relative rotations of adjacent triangles of the same facet about their common side and for relative rotations of adjacent triangles of two different facets about their common side, respectively; mimicking Hencky’s idea for approximating through discrete modelling Euler’s beam, see [42], triangles can only deform in plane and bending of facets, as well as folding around creases, is modelled in a lumped-parameter fashion (for a distributed-parameter approach see [43]).

The two contributions to the energy mentioned above are analogous to—and are, actually, the natural extension to origami metamaterials of—those used to approximate the stretching and bending energies of an Euler–Bernoulli beam in two dimensions, see, e.g. [37]. In the present case, since the mechanical model describes two-dimensional structures moving in the three-dimensional space, it is necessary, even more than for the case of two-dimensional beams, to define the kinematics and the strain energy of the model as simply as possible.

2.1 Energy associated to in-plane deformation of triangular elements

Let us consider the e-th triangle of the origami and denote its vertices with the indices i, j, and k, all belonging to the set \([1; N_n]\). In the reference configuration, the coordinates of the vertices i, j, and k expressed in the global reference coordinate system are collected in the vectors \(\textbf{X}_i\), \(\textbf{X}_j\), and \(\textbf{X}_k\), respectively, see Fig. 3.

Fig. 3
figure 3

In-plane deformation of a triangular element

Full size image

The hypothesis that triangular elements deform affinely means that strain is uniform along each triangle. In order to define the strain energy of each triangle in the simplest way, an ingenious idea introduced by Argyris and co-workers, see [44], where the deformation state is characterized by imagining to place three strain gauges on the triangle sides, i.e. a rosette of strain gauges, shall be exploited.

As an instance, let us consider what will be henceforth called the k-side, i.e. the side opposite to node k. The direction and length of this side are encoded within the vector \(\textrm{d}\textbf{X}_k=\textbf{X}_j-\textbf{X}_i\) in the reference configuration and within the vector \(\textrm{d}\textbf{x}_k=\textbf{x}_j-\textbf{x}_i\) in the current one. The Green’s strain measure \(g_k\) of the k-side is defined as

$$\begin{aligned} g_k= \frac{\ell _k^2-L_k^2}{2 L_k^2} \, , \end{aligned}$$
(1)

where \(\ell _k^2=\textrm{d}\textbf{x}_k \cdot \textrm{d}\textbf{x}_k\) and \(L_k^2=\textrm{d}\textbf{X}_k \cdot \textrm{d}\textbf{X}_k\) are the squares of the current and the reference length of the k-side, respectively. Current positions of nodes i and j are \(\textbf{x}_i=\textbf{X}_i+\textbf{u}_i\) and \(\textbf{x}_j=\textbf{X}_j+\textbf{u}_j\), respectively.

We define the stretching energy associated to the k-side as

$$\begin{aligned} S_k = A_k L_k \dfrac{1}{2}E g_k^2 \, , \end{aligned}$$
(2)

where we have introduced the Young’s modulus E of the material the triangle is made of and the cross-sectional area \(A_k\) of a fictitious rod placed along the k-side. Essentially, Argyris’ idea consists of replacing the considered affinely-deforming triangle with an equivalent determinate truss whose elements are the sides of the triangle.

Clearly, the total stretching energy associated to the three sides of the considered triangle is given by the sum of the stretching energies associated to each side

$$\begin{aligned} S_e = S_i+S_j+S_k \, , \end{aligned}$$
(3)

A practicable way to identify the parameters \(A_i\), \(A_j\), and \(A_k\) consists of equating the strain energy \(E_t\) of the considered triangle with that associated to the three sides. Remind that, for the sake of simplicity, the triangles’ thickness s does not vary within each triangle and is the same for all triangles which the origami geometry has been partitioned into.

Concerning the Green’s strain measure associated to the considered triangle’s side, say the i-side, we can write

$$\begin{aligned} \ell _i^2-L_i^2=2 \textrm{d}\textbf{X}_i \cdot \textbf{G}\textrm{d}\textbf{X}_i \, , \end{aligned}$$
(4)

where \(\textbf{G}\) denotes the Green–Saint-Venant strain tensor associated to the considered triangle, which is obtained by assuming that no deformation occurs along the thickness of the triangles.

Let us now consider a local Cartesian reference system with origin in the barycentre of the considered triangle, and two axes lying in the triangle plane. Then, the previous relationship can be written as

$$\begin{aligned} \ell _i^2-L_i^2=2 \overline{\textrm{d}\textbf{X}}_i \cdot \overline{\textbf{G}} \overline{\textrm{d}\textbf{X}}_i \, , \end{aligned}$$
(5)

where the superimposed bars denote vectors and tensors in the local reference system. In such a reference system, only the strain measures \(\overline{G}_{11}\), \(\overline{G}_{22}\), and \(\overline{G}_{12}=\overline{G}_{21}\), associated to the two axes lying in the triangle plane, are non-vanishing and, hence, needed to compute component-wise the Green–Saint-Venant strain tensor associated to the considered triangle. Therefore, we can write the following system of equations

$$\begin{aligned} \begin{aligned} \ell _i^2-L_i^2&=2 \overline{\textrm{d}\textbf{X}}_i \cdot \overline{\textbf{G}} \overline{\textrm{d}\textbf{X}}_i \, , \\ \ell _j^2-L_j^2&=2 \overline{\textrm{d}\textbf{X}}_j \cdot \overline{\textbf{G}} \overline{\textrm{d}\textbf{X}}_j \, , \\ \ell _k^2-L_k^2&=2 \overline{\textrm{d}\textbf{X}}_k \cdot \overline{\textbf{G}} \overline{\textrm{d}\textbf{X}}_k \, , \end{aligned} \end{aligned}$$
(6)

to find \(\overline{G}_{11}\), \(\overline{G}_{22}\), and \(\overline{G}_{12}=\overline{G}_{21}\) starting from the knowledge of the i-, j-, and k-side stretch. By utilizing the vector \(\textbf{g}= [\overline{G}_{11} \; \overline{G}_{22} \; \overline{G}_{12}]^T\), the energy associated to in-plane deformation of the considered affinely-deforming triangular element can be written as

$$\begin{aligned} E_e = \dfrac{1}{2}s A_e \textbf{g}\cdot \textbf{C}\textbf{g}\, , \end{aligned}$$
(7)

where \(A_e\) and s denote the areaFootnote 1 and the thickness of the considered triangle, respectively. The matrix \(\textbf{C}\) represents in Voigt notation—in the local basis consisting of the two axes lying in the triangle plane—the elasticity tensor associated to the material the triangle is made up of, which is assumed to obey Hooke’s law, to be homogeneous and isotropic, and be the same for all triangles. Such a matrix encodes the constitutive law, i.e. the material behaviour, for the plane strain case and reads as

$$\begin{aligned} \textbf{C}= \frac{E}{(1+\nu )(1-2\nu )}\left[ \begin{array}{ccc}1-\nu &{}\quad \nu &{}\quad 0 \\ \nu &{}\quad 1-\nu &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \dfrac{1-2\nu }{2}\end{array}\right] \, , \end{aligned}$$
(8)

where the Poisson’s ratio \(\nu \) of the material has been introduced.

By equating the total stretching energy associated to the sides of the considered triangle, given by Eq. (3), and the energy associated to its in-plane deformation, see Eq. (7), we can identify the cross-sectional area of the fictitious rods making up the determinate truss system associated to the considered triangle so as to reach an exact energy equivalence between the two mechanical descriptions.

2.2 Bending and folding energies

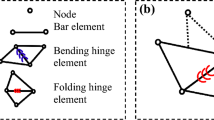
The strain energy associated to bending of a facet and that associated to folding of a crease can be chosen in an approximate, yet simple, way following the key idea proposed by Hencky in his celebrated doctoral thesis, see [42], aimed at estimating the buckling load of an Euler’s beam. A revival of Hencky’s idea can be found in a series of articles aiming at modelling pantographic structures [37], beams [45,46,47], and granular materials [39, 48, 49]. Roughly speaking, Hencky’s idea consists of stating the equivalence between the bending—and, in our case, folding—energy stored in a mechanical element by subdividing such an element in two adjacent elements hinged through cylindrical hinges in such a way that only relative rotations around the (considered) bending (or folding) axis is allowed. Resistance to such a relative rotation is added by placing a—Hooke’s in the classical approach, which we adopt also in the present contribution—torsional spring in-between the two elements, thus yielding a lumped-parameter model. In this paper, we adopt this very same concept to evaluate the energy stored in a panel, i.e. two triangles sharing a side, because of facet bending or origami folding about creases.

Figure 4 reports a generic panel of the considered origami in the current configurations, where m and n stand for the indices associated to the triangles in the panel.

Fig. 4
figure 4

Origami panel in the current configuration: nodes and normal unit vectors

Full size image

The vertices of the triangles in the considered panel, also called nodes, are labelled with the indices i, j, k, and h. Reference and current positions of each node are denoted by \(\textbf{X}\) and \(\textbf{x}\), respectively, and labelled with the associated index, i.e. i, j, k, or h. On each triangle we can consider three mutually orthogonal unit vectors, say \(\{ \textbf{d}_1, \textbf{d}_2, \textbf{d}_3 \}_{m}\) for the m-th triangle and \(\{ \textbf{d}_1, \textbf{d}_2, \textbf{d}_3 \}_{n}\) for the n-th triangle in the current configuration. The dihedral angle in-between the planes containing the triangles is denoted with the greek letter \(\delta \). An analogous figure can be traced for the reference configuration. In this case, we would use capital letter to indicate the mutually orthogonal unit vectors, i.e. \(\{ \textbf{D}_1, \textbf{D}_2, \textbf{D}_3 \}_{m}\) for the m-th triangle and \(\{ \textbf{D}_1, \textbf{D}_2, \textbf{D}_3 \}_{n}\) for the n-th triangle. The dihedral angle in the reference configuration is denoted with \(\delta _0\).

All the sets of unit vectors can be evaluated from node positions by using standard geometry formulas. As an instance, the three mutually orthogonal unit vectors related to the m-th triangle in the current configuration can be computed as

$$\begin{aligned} \begin{aligned} \textbf{d}_{1m}&= \frac{\textbf{x}_j-\textbf{x}_i}{\Vert \textbf{x}_j-\textbf{x}_i \Vert } \, , \\ \textbf{d}_{2m}&= \textbf{d}_3 \times \textbf{d}_1 \, , \\ \textbf{d}_{3m}&= \frac{(\textbf{x}_k-\textbf{x}_j) \times (\textbf{x}_j-\textbf{x}_i)}{\Vert (\textbf{x}_k-\textbf{x}_j) \times (\textbf{x}_j-\textbf{x}_i) \Vert } \, . \end{aligned} \end{aligned}$$
(9)

Both in the reference and current configurations of the m-th triangle, the unit vector in Eq. (9) having 1 as subscript is parallel to the k-side of the triangle, that with subscript 3 is orthogonal to the plane containing the considered triangle and, finally, that with subscript 2 is such that \(\textbf{d}_{2m} = \textbf{d}_{3m} \times \textbf{d}_{1m}\).

We now aim at defining a strain measure associated to bending of facets or folding of the origami around creases. The underlying idea is to measure, for each panel, the relative rotation of the two adjacent triangles making up a single panel. It is in this regard worth to be mentioned that, since the local bases \(\{\textbf{d}_{1m}, \textbf{d}_{2m}, \textbf{d}_{3m}\}\) and \(\{\textbf{d}_{1n}, \textbf{d}_{2n}, \textbf{d}_{3n}\}\) are built making use of one—remark, not the shared one—side of the stretched triangles m and n, respectively, the rotation leading from \(\{\textbf{d}_{1m}, \textbf{d}_{2m}, \textbf{d}_{3m}\}\) to \(\{\textbf{d}_{1n}, \textbf{d}_{2n}, \textbf{d}_{3n}\}\) is not occurring around the side shared by the triangles m and n, i.e. its eigenvector does not identify the direction of the shared side, thus not representing an ideal strain measure associated to bending of facets or folding of the origami around creases in the Hencky-type approach mentioned at the beginning of this subsection. To get a measure of the relative rotation of the two adjacent triangles making up a single panel that is fulfilling this desired property, we seek to write the rotation tensors associated to passing from \(\{\textbf{D}_{1m}, \textbf{D}_{2m}, \textbf{D}_{3m}\}\) and \(\{\textbf{D}_{1n}, \textbf{D}_{2n}, \textbf{D}_{3n}\}\) to \(\{\textbf{d}_{1m}, \textbf{d}_{2m}, \textbf{d}_{3m}\}\) and \(\{\textbf{d}_{1n}, \textbf{d}_{2n}, \textbf{d}_{3n}\}\), respectively, by filtering out the (spurious) rotations induced by the in-plane affine deformation of the triangles m and n, respectively. In order to do so, we make use of the right polar decomposition of the deformation gradient tensor \(\textbf{F}\) associated to the deformation in three space dimensions of the triangles m and n.

Referring to Fig. 4 the tensor \(\textbf{F}_m\) for the m-th triangle can be computed by making use of the following equations:

$$\begin{aligned} \begin{aligned} \textbf{F}_m (\textbf{X}_j-\textbf{X}_i)&= \textbf{x}_j-\textbf{x}_i \\ \textbf{F}_m (\textbf{X}_k-\textbf{X}_j)&= \textbf{x}_k-\textbf{x}_j \\ \textbf{F}_m \textbf{D}_{3m}&= \textbf{d}_{3m} \end{aligned} \end{aligned}$$
(10)

that represent a compatible linear system of nine scalar linearly independent algebraic equations in the nine independent components of \(\textbf{F}_m\), which are unknown. Such a system admits an elementary closed-form solution. The same holds for \(\textbf{F}_n\).

At this point, it is only necessary to recall the right polar decomposition formula

$$\begin{aligned} \textbf{F}= \textbf{R}\textbf{U}\, , \end{aligned}$$
(11)

where \(\textbf{R}\) is a proper orthogonal tensor representing the rotational part of the deformation gradient \(\textbf{F}\) and \(\textbf{U}\) is a positive definite symmetric tensor representing the stretch part of the deformation gradient \(\textbf{F}\).

Since

$$\begin{aligned} \textbf{F}^T \textbf{F}= \textbf{U}^T \textbf{R}^T \textbf{R}\textbf{U}= \textbf{U}^T \textbf{U}= \textbf{U}^2 \end{aligned}$$
(12)

then \(\textbf{U}=\sqrt{\textbf{F}^T \textbf{F}}\). Reminding that the square root of a tensor can be computed by means of its spectral decomposition, that is

$$\begin{aligned} \sqrt{\textbf{F}^T \textbf{F}} = \textbf{V}\sqrt{\mathbf {\Lambda }} \textbf{V}^T \, , \end{aligned}$$
(13)

being \(\textbf{V}\) and \(\mathbf {\Lambda }\) the orthogonal matrix collecting the eigenvectors of the symmetric tensor \(\textbf{F}^T \textbf{F}\) and the diagonal matrix whose elements are the eigenvalues of \(\textbf{F}^T \textbf{F}\) arranged in the same order as that of the corresponding eigenvectors in the matrix \(\textbf{V}\), respectively. Finally, when \(\textbf{U}\) is known, we can compute the pure rotation matrix \(\textbf{R}=\textbf{F}\textbf{U}^{-1}\).

Having hence defined the rotation matrices \(\textbf{R}_m\) and \(\textbf{R}_n\) for the m-th and n-th triangles in the p-th panel, the sought finite relative rotation tensor \(\Delta \textbf{R}\) can be defined as

$$\begin{aligned} \Delta \textbf{R}= \textbf{R}_m^T \textbf{R}_n \, . \end{aligned}$$
(14)

Rodrigues’ formula allows to rewrite in a more insightful way a rotation tensor \(\textbf{R}\) as

$$\begin{aligned} \textbf{R}= \cos \varphi \textbf{I}+ (1-\cos \varphi ) \textbf{e}\otimes \textbf{e}+ \sin \varphi \textbf{E}\end{aligned}$$
(15)

being \(\textbf{E}\) and \(\textbf{e}\) the tensor and its axial vector fulfilling the relationship \(\textbf{E}\textbf{v}= \textbf{e}\times \textbf{v}\) for any vector \(\textbf{v}\). From Eq. (15), simple computations give

$$\begin{aligned} 2 \cos \varphi = \text{ tr }(\textbf{R}) - 1 \, , \quad 2 \sin \varphi \, \textbf{e}= \textbf{R}_\times \, , \end{aligned}$$
(16)

where \(\text{ tr }(\cdot )\) is the trace operator and \(\textbf{R}_\times \) is the axial vector of the skew symmetric part of \(\textbf{R}\).

For computational purposes, it is convenient to introduce the rotation vector

$$\begin{aligned} \pmb {\vartheta }= 2 \tan \left( \frac{\varphi }{2} \right) \, \textbf{e}\, , \end{aligned}$$
(17)

which allows to rewrite the rotation tensor \(\textbf{R}\) as

$$\begin{aligned} \textbf{R}= \frac{1}{4+\vartheta ^2} \left( (4-\vartheta ^2) \, \textbf{I}+ 2 \, \pmb {\vartheta }\otimes \pmb {\vartheta }+ 4 \textbf{E}_{\pmb {\vartheta }} \right) \, , \end{aligned}$$
(18)

being \(\vartheta ^2=\pmb {\vartheta }\cdot \pmb {\vartheta }\) and \(\textbf{E}_{\pmb {\vartheta }} \textbf{v}= \pmb {\vartheta }\times \textbf{v}\). The version of the Rodrigues’ formula in Eq. (18) is equivalent to (15), but allows to avoid singularities that would otherwise arise when algebraic manipulations are performed, necessary to define quantities such as the strain energy and its first and second derivatives. In addition, the use of \(\textbf{R}\) defined by equation (18) makes the rotation vector vary in the same range, from \(-\infty \) to \(+\infty \), of the displacements vector and therefore, in principle, is beneficial for the well-conditioning of the equilibrium equations to be solved.

Since the relative finite relative rotation tensor \(\Delta \textbf{R}\) is orthogonal, by using (16) and the half-angle trigonometric formula, we can write the relative finite rotation vector

$$\begin{aligned} \Delta \pmb {\vartheta }= \frac{2 (\Delta \textbf{R})_\times }{1+\text{ tr }(\Delta \textbf{R})} \end{aligned}$$
(19)

and, finally, the folding strain energy for the p-th panel

$$\begin{aligned} B_{p} = \dfrac{1}{2}b \Vert \textbf{X}_k - \textbf{X}_j \Vert \Delta \pmb {\vartheta }\cdot \Delta \pmb {\vartheta }\, , \end{aligned}$$
(20)

being b the stiffness per unit length which controls the relative rotation in-between the two triangles in the considered panel. In principle, the quantity b can assume different values according to whether it is associated to bending or folding.

From the bending, folding, and stretching strain energies, we can compute the structural reaction vector \(\textbf{s}\) and the tangent stiffness matrix \(\textbf{K}\) of the system. Since these strain energies are additive quantities, we can define the total strain energy just for a single generic panel p, i.e. for two triangles, say m and n—see Fig. 4—sharing a side.

Let us denote with the symbol B the sum over the whole origami of the bending and folding strain energies associated to each panel and let us denote with the symbol S the sum over the whole origami of the sides’ stretching energy. We define the total strain energy associated to the origami as the sum \(B+S\). Collecting the displacements of the nodes i, j, k, and h in \(\textbf{u}_p\), we can write the structural reaction vector of the p-th panel as

$$\begin{aligned} \textbf{s}_p = \frac{\textrm{d}(B+S)}{\textrm{d}\textbf{u}_p} \, , \end{aligned}$$
(21)

while its tangent stiffness matrix reads accordingly as

$$\begin{aligned} \textbf{K}_p = \frac{\textrm{d}\textbf{s}_p}{\textrm{d}\textbf{u}_p} \, . \end{aligned}$$
(22)

Definitions (21) and (22) provide us with the tools to evaluate automatically the structural reaction vector and the tangent stiffness matrix associated to the total strain energy of the p-th panel. A simple assembly operation, following rules identical to those used in finite element codes, is necessary to build the structural reaction vector and the tangent stiffness matrix of the whole origami.

2.3 Kinetic energy

The kinetic energy associated to the e-th triangle of the origami can be written as

$$\begin{aligned} \mathcal {K}_e = \dfrac{1}{2}\int \limits _{V_e} \rho \, \dot{\textbf{u}} \cdot \dot{\textbf{u}} \, \textrm{d}V \, , \end{aligned}$$
(23)

where \(\rho \), \(V_e\), and \(\dot{\textbf{u}}\) are the mass density, the three-dimensional domain the triangle is associated to—namely the extruded triangle—and the velocity of the elementary volume \(\textrm{d}V\), respectively. We suppose the mass density and, as mentioned before, the thickness s of the triangle as uniform along the triangle. Let us choose a linear interpolant to approximate the velocity of the elementary volume \(\textrm{d}V\). Then the kinetic energy of the considered triangular element can be approximated as

$$\begin{aligned} \mathcal {K}_e \approx \dfrac{1}{2}\int \limits _{A_e} \rho \, s \, (\textbf{B}_e \dot{\textbf{u}}_e) \cdot (\textbf{B}_e \dot{\textbf{u}}_e) \, \textrm{d}A = \dfrac{1}{2}\rho s \dot{\textbf{u}}_e \cdot \left( \int \limits _{A_e} \textbf{B}_e^T \textbf{B}_e \textrm{d}A \right) \dot{\textbf{u}}_e \, , \end{aligned}$$
(24)

where \(A_e\) indicates the considered triangle. The shape function matrix \(\textbf{B}_e\) and the nodal velocity vector \(\dot{\textbf{u}}_e\) allow to compute the velocity vector in each point of the triangle, i.e. \(\dot{\textbf{u}}=\textbf{B}_e \dot{\textbf{u}}_e\). The shape function matrix \(\textbf{B}_e\) for a generic triangle can be defined in an indirect way by defining it just for a specific triangle, as it going to be done in Eq. (26), while the velocity vector reads as

$$\begin{aligned} \dot{\textbf{u}}_e = \left[ \begin{array}{c} \dot{\textbf{u}}_i \\ \dot{\textbf{u}}_j \\ \dot{\textbf{u}}_k \end{array}\right] \, . \end{aligned}$$
(25)

The computation of the mass matrix \(\textbf{M}_e\) of the considered triangular element, considering that the factor \(\rho s\) is uniform in space, requires the evaluation of the integral over the triangular element of the term \(\textbf{B}_e^T \textbf{B}_e\). Such an evaluation becomes straightforward if the integral is performed on the so-called reference triangle, i.e. the triangle having, in the Cartesian plane, as vertices the points with coordinates (0, 0), (1, 0) and (0, 1). For such a special triangle, the shape function matrix reads in formulas as

$$\begin{aligned} \widehat{\textbf{B}}_e = \left[ \begin{array}{ccccccccc} (1-\xi -\eta ) &{}\quad 0 &{}\quad 0 &{}\quad \xi &{}\quad 0 &{}\quad 0 &{}\quad \eta &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad (1-\xi -\eta ) &{}\quad 0 &{}\quad 0 &{}\quad \xi &{}\quad 0 &{}\quad 0 &{}\quad \eta &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad (1-\xi -\eta ) &{}\quad 0 &{}\quad 0 &{}\quad \xi &{}\quad 0 &{}\quad 0 &{}\quad \eta \end{array}\right] \end{aligned}$$
(26)

where \(0\le \xi \le 1\) and \(0\le \eta \le 1\).

Having introduced these tools, we are now able to write

$$\begin{aligned} \int \limits _{A_e} \textbf{B}_e^T \textbf{B}_e \textrm{d}A = 2 A_e \int \limits _{\widehat{A}_e} \widehat{\textbf{B}}_e^T \widehat{\textbf{B}}_e \textrm{d}\widehat{A} \, , \end{aligned}$$
(27)

where \(\hat{A}_e\) denotes the special triangle specified above and, with an abuse of notation, \(A_e\) denotes the area of the e-th triangle. More explicitly, the triangular element mass matrix reads as

$$\begin{aligned} \textbf{M}_e = \frac{\rho s A_e}{12} \left[ \begin{array}{ccc} 2 \, \textbf{I}_{3\times 3}&{}\quad \textbf{I}_{3\times 3}&{}\quad \textbf{I}_{3\times 3}\\ \textbf{I}_{3\times 3}&{}\quad 2 \, \textbf{I}_{3\times 3}&{}\quad \textbf{I}_{3\times 3}\\ \textbf{I}_{3\times 3}&{}\quad \textbf{I}_{3\times 3}&{}\quad 2 \, \textbf{I}_{3\times 3}\end{array}\right] \end{aligned}$$
(28)

where, aimed at keeping as short as possible the formula, the \(3 \times 3\) identity matrix, denoted with \(\textbf{I}_{3\times 3}\), has been utilized.

3 Stepwise approximate solution of the nonlinear equilibrium problem

By referring to the original work of Casciaro [50] or to the successive paper by Turco [51], where formulas are derived in a detailed way, commented, and light is shed on some otherwise unaddressed issues, we briefly recall here the main elements of the time integration scheme that we have utilized to solve in a stepwise fashion the nonlinear equilibrium problem deriving from the modelling presented in the previous sections and obtain the results that will be presented in the next one.

First of all, we shall specify that the integration scheme is based on subdividing in N time steps of equal length \(\Delta t\) the desired time horizon of the simulation. Starting from the knowledge of the initial conditions, i.e. the initial displacement vector \(\textbf{u}_0=\textbf{u}(t=0)\) and the initial velocity vector \(\dot{\textbf{u}}_0=\dot{\textbf{u}}(t=0)\), we want to reconstruct the solution at times \(t_{j+1}=t_j+\Delta t\) (\(j=0, 1, \dots , N\)). Since we are considering a recursive time integration scheme, and hence we can assume as known the solution for \(t_j\), i.e. we know the vectors \(\textbf{u}_j=\textbf{u}(t_j)\) and \(\dot{\textbf{u}}_j=\dot{\textbf{u}}(t_j)\), the scheme can be characterized by describing how to compute the solution \(\textbf{u}_{j+1}\) and \(\dot{\textbf{u}}_{j+1}\).

For each time step, since we are considering as unknowns the vectors \(\textbf{u}_{j+1}\) and \(\dot{\textbf{u}}_{j+1}\), two sets of equations are needed so as to equate the number of independent scalar equations and that of the scalar unknowns. Referring to Casciaro’s scheme, the following sets of equations are considered:

$$\begin{aligned} \textbf{u}_{j+1} = \textbf{u}_{j} + \left( \left( \dfrac{1}{2}-\beta \right) \dot{\textbf{u}}_{j} + \left( \dfrac{1}{2}+\beta \right) \dot{\textbf{u}}_{j+1} \right) \Delta t \, , \end{aligned}$$
(29)

and

$$\begin{aligned} \textbf{M}( \dot{\textbf{u}}_{j+1} - \dot{\textbf{u}}_{j} ) + \left( \left( \dfrac{1}{2}-\alpha \right) (\textbf{s}_{j}-\textbf{f}_{j}) + \left( \dfrac{1}{2}+\alpha \right) (\textbf{s}_{j+1}-\textbf{f}_{j+1}) \right) \Delta t = \textbf{0}\, . \end{aligned}$$
(30)

Equation (29) reflects the assumption that the unknown displacement vector \(\dot{\textbf{u}}_{j+1}\) depends, besides the displacement vector \(\textbf{u}_{j}\), upon the velocity vectors \( \dot{\textbf{u}}_{j}\) and \( \dot{\textbf{u}}_{j+1}\) weighted by two dimensionless factors that, in turn, are depending upon the parameter \(\beta \), which has to be chosen suitably. Readers who are familiar with B-splines can recognize that Eq. (29) is resembling that kind of interpolation. Indeed, in that equation, the displacement vector is extrapolated quadratically using its time derivative, i.e. the velocity, evaluated both at the beginning and at the end of the considered time step.Footnote 2

Equation (30) prescribes the equilibrium by means of the so-called momentum–impulse relationship. Indeed, the first term of Eq. (30) can be interpreted as a finite-difference approximation of the rate of momentum, while it can be recognized that the second term is the average net impulse. This last is weighted by two dimensionless factors depending upon the parameter \(\alpha \), which has to be selected suitably.

To summarize, Casciaro’s scheme makes use of a quadratic B-spline interpolation for the displacements and of the momentum–impulse relationship, introducing two dimensionless parameters \(\alpha \) and \(\beta \) that can be finely tuned to obtain the best performances from the integration scheme.

These two dimensionless parameters, following Casciaro’s spirit, have to be tuned according to the guess for the first, \(T_{1}\), and for the last, \(T_{N}\), natural periods of the considered system (with essential boundary conditions) and the chosen time-step length \(\Delta t\) that, generally speaking, must be in turn chosen on the basis of the considered problem (the first natural period, usually). Therefore, operationally speaking, an eigenvalue analysis limited to the first and the last natural periods computed in the reference configuration has to be performed. This preliminary analysis involves the mass matrix \(\textbf{M}\) and the stiffness matrix \(\textbf{K}\) computed in the reference configuration, i.e. \(\textbf{K}(\textbf{u}=\textbf{0})\).

In Casciaro’s paper [50], a rule for choosing in an optimal way the dimensionless parameters \(\alpha \) and \(\beta \) is presented. Such a rule is based on the analysis of a one-degree-of-freedom system in the linear regime. However, the work [50] illustrates only a few details concerning the derivation of this rule, while more extensive discussions are carried out in a series of reports published some years before, which cannot be easily found. This, along with the fact that the original formulas provided by Casciaro contained some typos, caused, most likely, that Casciaro’s idea was eventually forgotten.Footnote 3

The optimal values of the dimensionless parameters \(\alpha \) and \(\beta \) are

$$\begin{aligned} \begin{aligned} \beta = -\alpha&= \sqrt{-\frac{1}{4}+\frac{1}{\gamma ^{2}}-\frac{1+\sqrt{1+\tan ^{2} \gamma }}{2 \tan ^{2} \gamma }} \, , \qquad 0< \gamma< \frac{\pi }{2} \, ,\\ \beta = -\alpha&= \sqrt{-\frac{1}{4}+\frac{1}{\gamma ^{2}}-\frac{1-\sqrt{1+\tan ^{2} \gamma }}{2 \tan ^{2} \gamma }} \, , \qquad \frac{\pi }{2}< \gamma < \pi \, , \end{aligned} \end{aligned}$$
(31)

having introduced \(\gamma =2\pi \Delta t/T_{n}\). We remark that Eq. (31), when \(\Delta t \rightarrow 0\), leads to \(\beta =-\alpha =1/\sqrt{6}\). Instead, when \(\Delta t \rightarrow T_{n}/2\), \(\beta =-\alpha =1/\pi \) is obtained.

Conversely, when \(\Delta t > T_{n}/2\), the optimal values assume the form

$$\begin{aligned} \alpha = - \frac{T_{n}}{2 \pi \Delta t} + \frac{c^{3}}{1+2 c^{3}} \, , \quad \beta = \frac{T_{n}}{2 \pi \Delta t} + \frac{c^{3}}{1+2 c^{3}} \, , \quad c = \frac{2 \Delta t - T_{n}}{T_{1}-T_{n}} \, . \end{aligned}$$
(32)

Formulas (32) contain both the sum of two terms: the first one is a hyperbola branch, which links the optimal values of \(\alpha \) and \(\beta \) at the end of the interval \(\Delta t<T_n/2\); the second one is the ratio between two cubic polynomials, which tends—when \(\Delta t \rightarrow \infty \)—to the value 1/2. Hence, the values of \(\alpha \) and \(\beta \) corresponding to this case are able to reproduce a quasi-static solutions.Footnote 4

At this point, we shall sketch the solution strategy, which we have utilized, encoded in an algorithm, to solve—for each time step—the nonlinear equations prescribing the equilibrium, thus overcoming the difficulties due to the geometric nonlinearities included in structural reaction. The key ingredient of the solution strategy is the first order Taylor expansion of the structural reaction \(\textbf{s}_{j+1}=\textbf{s}(\textbf{u}_{j+1})\). In formulas, we have:

$$\begin{aligned} \textbf{s}_{j+1} \approx \textbf{s}_{j} + \textbf{K}_{j} (\textbf{u}_{j+1} -\textbf{u}_{j}) \, , \end{aligned}$$
(33)

where the stiffness matrix \(\textbf{K}_j\) is computed at the beginning of the considered time interval, i.e.:

$$\begin{aligned} \textbf{K}_j= \left. \frac{\textrm{d}\textbf{s}}{\textrm{d}\textbf{u}} \right| _{\textbf{u}_{j}} \, . \end{aligned}$$
(34)

Remark that the velocity variables collected in the vector \(\dot{\textbf{u}}_{j+1}\) can be eliminated by using Eq. (29) from the system formed by Eqs. (29) and (30). Therefore, Equations (29)-(30), along with the Taylor expansion (33), give the necessary tools to build a Newton-like algorithm for the considered problem. Starting from the formula expressing the reminder calculated at the i-th iteration

$$\begin{aligned} \textbf{r}_i = \textbf{M}(\dot{\textbf{u}}_{j+1,i} - \dot{\textbf{u}}_j) + \left( \dfrac{1}{2}-\alpha \right) (\textbf{s}_j - \textbf{f}_j) + \left( \dfrac{1}{2}+\alpha \right) (\textbf{s}_{j+1,i} - \textbf{f}_{j+1}) \, , \end{aligned}$$
(35)

an update estimate of the solution, using a Newton-like strategy, is given by the recursive relation

$$\begin{aligned} \textbf{u}_{j+1,i+1} = \textbf{u}_{j+1,i} - \textbf{H}_j^{-1} \textbf{r}_j \, , \end{aligned}$$
(36)

where the iteration matrix \(\textbf{H}_j\) is defined as

$$\begin{aligned} \textbf{H}_j = \nabla \textbf{r}\vert _j = \frac{1}{\dfrac{1}{2}+\beta } \textbf{M}+ \left( \dfrac{1}{2}+\alpha \right) \textbf{K}_{j,i} \, . \end{aligned}$$
(37)

For addressing the solution of problems involving origami metamaterials, modelled as explained in the previous sections, we used a slight modification of Casciaro’s scheme. Essentially, we used as primary variable the displacement vector instead of the velocity vector. This does not change significantly the properties of the scheme but, in practice, in view of addressing complex problems such as those involving origami metamaterials, it allows to get an algorithm that is significantly more stable.

At the end of this section, it is worth remarking that, for dynamic problems—even complex ones as those analysed in the present contribution—using the Newton method—as we do here to predict the behaviour of origami metamaterials—is not a major limitation. This could seem counter-intuitive since, as it is well known, when static problems are considered, Newton’s method is not able to get around limit points, i.e. configurations that make singular the stiffness matrix \(\textbf{K}\), because for such a method the iteration matrix coincides with the tangent stiffness matrix. Indeed, for this reason, its use for the static analysis of systems exhibiting limit points is not recommended. When dynamic analyses are concerned, since the iteration matrix also includes an additive contribution depending on the mass matrix (which does not vanish when the stiffness matrix is singular), see (37), the problem is instead regularized, thus making the Newton scheme usable to address complex systems exhibiting limit points, which is the case we are going to analyse in the next section.

4 Numerical simulation of origami beams

Using the model that has been sketched in the previous sections, we critically present in this section the results of some numerical simulations concerning straight and curved origami beams, in short o-beams, i.e. beams obtained as the repetition of a foldable unit cell in a mono-dimensional array, highlighting the peculiarities of such a kind of beams. Specifically, concerning the mechanical problems that we are going to study, we shall address the problem of a straight beam subjected to (1) a transverse shearing force, (2) an axial compression force, and (3) a torque at the free end, which are varying in time with an assigned law. Additionally, we analyse the case of a simply supported circular arch subjected to a time-varying shearing force applied in its mid-point.

Remark that, in this section, all the data and results, when not in non-dimensional form, are expressed in the MKS system of units.

4.1 Cantilever o-beam subjected to a shearing force at its free end

From now on, we study the straight origami beam sketched in Fig. 5 (where X-, Y-, and Z-view means view from the X, Y, and Z axis, respectively), obtained repeating 25 times along a straight unidimensional array the Miura-ori unit cell. In this subsection, let us focus on the so-called cantilever problem. The kinematic boundary conditions applied at the nodes of the clamped end prescribe vanishing nodal displacements. At the free end of the o-beam, which consists of the three nodes having vanishing X coordinate (see Fig. 5d), a shearing force acting in the plane having Y as normal, varying in time according to the law reported in Fig. 6, is applied on the mid-node.

Fig. 5
figure 5

Views of the o-beam unit cell—X- (a), Y- (b), Z- (c), and 3D-view (d)—and whole o-beam made up of 25 unit cells (e)

Full size image
Fig. 6
figure 6

Evolution law for the external loading

Full size image

As described in Sect. 3, the utilization of Casciaro’s scheme requires the choice of two parameters. In order to choose optimally these parameters, we evaluate the first and the last natural periods of the considered o-beam for the studied problem. For the problem studied in this subsection, with geometrical and material parameters chosen as those reported in Table 1, we obtain that the first natural period is \(T_1=1.76\), while the last one is \(T_n=1.90\times 10^{-4}\). In Fig. 7, we report the first nine natural modes.

Table 1 Utilized dataset of geometrical and material parameters in the MKS system of units
Full size table
Fig. 7
figure 7

First nine natural periods and modes for the o-beam subjected to cantilever boundary conditions. Gray and red colors indicate the reference configuration and the modes, respectively

Full size image

It is worth to remark that, among the first nine modes in Fig. 7, there are modes associated to bending of the o-beam in its plane of symmetry, having as normal vector the Y-axis, specifically the 1st, 3rd, 5th, and 7th mode. The 2nd, 4th, and 6th mode are instead associated to bending in the plane having as normal vector the Z-axis. The 8th and 9th mode are instead associated to extension and torsion, respectively.

The time evolution of the system, for the shearing load \(p_{\max }=5000\), \(t_i=1\), and \(t_d=0.25\), computed using a time integration step \(\Delta t=0.001\) is summarized in Fig. 8. The quantities u, v, and w in Fig. 8 are the displacement components along the axes X, Y, and Z, respectively, of the mid-node of the free end of the o-beam.

Fig. 8
figure 8

Origami cantilever beam subjected to a shearing force on the free end mid-point. Evolution in time of displacements (a) and velocities (b) along the X, Y, and Z directions of the mid-point at the free end of the o-beam. Stroboscopic pictures of the o-beam deforming in time observed from \(-Y\) (c) and \(-X\) (d)

Full size image

Henceforth, colours will be used in the stroboscopic pictures to indicate the time evolution. Specifically, ten different shots, equally spaced in time, will be taken to build the stroboscopic pictures. For each shot, the employed percentage of blue colour indicates the progression of time: grey corresponds to the reference configuration, light violet corresponds to the last shot.

It is worth to be remarked that the applied load causes an unexpected oscillation in the Y direction, as it can be clearly seen from the yellow line in Fig. 8a,d. This oscillation is triggered by the unavoidable presence of numerical errors. While the numerical scheme is unable to deal with this phenomenon, as no numerical viscous dissipation has been introduced to damp undesired oscillations, the observed oscillations in the Y direction hint to the high sensitivity of the o-beam to imperfections.

A videoclip showing the cantilever o-beam oscillations induced by the time-varying shearing load applied at the mid-point of its free end, considered in this subsection, can be found in the supplementary material, see the file c25bending.avi.

4.2 Cantilever o-beam subjected to compression forces at its free end

Using the same data of the previous test, we now study the problem of an o-beam with cantilever kinematic boundary conditions, subjected to a compression force along the X direction acting at its free end. Specifically, such a force is applied to all the nodes at the free end.

The maximum amplitude reached by the load, which is varying in time according to the law shown in Fig. 6, is equal to 8000. Using a time integration step \(\Delta t=0.001\), we obtain the plots shown in Fig. 9.

Fig. 9
figure 9

Origami cantilever beam subjected to compression forces on the free end nodes. Evolution in time of displacements (a) and velocities (b) along the X, Y, and Z directions of the mid-point at the free end of the o-beam. Stroboscopic pictures of the o-beam deforming in time observed from \(-Y\) (c) and \(-X\) (d)

Full size image

As for the previous test problem, also in this case the applied load produces an unexpected oscillation in the Y direction, due to numerical errors, as it can be clearly seen by looking at the yellow line in Fig. 9(a,d).

A videoclip showing the cantilever o-beam oscillations induced by the time-varying compression loads applied at the nodes of its free end, considered in this subsection, can be found in the supplementary material, see the file c25buckling.avi.

4.3 Cantilever o-beam subjected to a torque at its free end

In this subsection, we study the case of a cantilever origami beam subjected to a time-varying torque produced by two opposite and equal-in-magnitude time-varying forces acting in the Z direction, in the plane normal to the X-axis, acting on the opposite nodes of the free end. Such forces producing a torque are varying in time according to the law shown in Fig. 6 and reach, at their peak, a magnitude equal \(10^5\).

The time evolution of the system for the case analysed in this subsection, computed using a time integration step \(\Delta t=0.001\), is summarized in Fig. 10.

Fig. 10
figure 10

Origami beam subjected to a torque at its free end. Evolution in time of displacements (a) and velocities (b) along the X, Y, and Z directions of the first node of the free end of the o-beam. Stroboscopic picture of the o-beam deforming in time (c)

Full size image

In Fig. 10a, the time evolution of the displacement components u, v, and w along the axes X, Y, and Z, respectively, are shown for the first node of the free end, i.e. that having coordinates \(X=Y=Z=0\) (see Fig. 5). Figure 10b shows the evolution of the rate of the displacement components plotted in Fig. 10a, namely the evolution of the corresponding velocities, while Fig. 10c shows a stroboscopic picture of the o-beam deforming in time.

As it can be seen looking at the red line in Fig. 10a, the torque applied at the free end produces oscillations also in the X direction, which hints at the nonlinear coupling between torsional and extensional deformation modes in the o-beam.

A videoclip showing the o-beam oscillations observed from the X-axis for the case analysed in the present subsection can be found in the supplementary material, see the file c25twisting.avi.

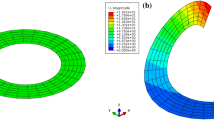
4.4 Simply-supported origami arch subjected to a shearing force at its mid-point

We now study the origami arch obtained by repeating along a curved line 25 unit cells, see Fig. 12. Specifically, the bottom-most nodes of the origami arch are placed along a circumference of radius 100. Material parameters considered in this subsection for the origami arch are the same reported in Table 1. Displacement of the mid-nodes of the two ends is completely prevented. For the remaining four nodes of the two ends, we prevent only displacement in the vertical direction, i.e. along the Z-axis. Since the geometry and kinematic boundary conditions have changed with respect to those analysed in the previous tests, we compute the first and the last natural periods to find the optimal parameters of the time-integration scheme. The eigenvalue analysis gives for the first and the last natural periods the values \(T_1=0.221\) and \(T_n=7.97 \times 10^{-5}\), respectively.

Fig. 11
figure 11

Origami arch with 25 unit cells

Full size image

Figure 12 reports the first nine natural modes and periods.

Fig. 12
figure 12

First nine natural periods and modes for the simply-supported origami arch. Gray and red colors indicate the reference configuration and the modes, respectively

Full size image

We remark that the first nine modes are all flexural modes. The odd modes correspond to deformations out of the plane which the origami is lying onto in the initial configuration, i.e. the \(X-Y\) plane, while the even modes lie in the initial origami plane.

The arch is loaded at its mid-point with a vertical force, directed towards the interior of the circumference, that is increasing in time with constant, unit velocity. Looking at Fig. 13, we observe an instability which resembles that experienced by the Von Mises arch when loaded quasi-statically. In the present case, the instability is much more complex, since occurs in dynamics and both in the plane normal to the Y-axis and in the plane normal to the Z-axis. It is worth to remark that the employed Newton scheme, which is used for a given time step to solve the nonlinear equilibrium equations, has proven successful in dealing with limit points since the iteration matrix also includes an additive contribution depending on the mass matrix.

Also for the case addressed in the present subsection a videoclip showing the deformation in time of the origami arch is included in the supplementary material, see the file arch25.avi.

Fig. 13
figure 13

Simply-supported origami arch subjected to a shearing force at its mid-point. Evolution in time of displacements (a) and velocities (b) along the X, Y, and Z directions of the mid-point of the origami arch. Stroboscopic pictures of the origami arch deforming in time observed from Y (c) and Z (d)

Full size image

5 Concluding remarks and future challenges

In this paper, we have presented a viable way to perform numerical simulations of origami metamaterials taking into account inertial effects and nonlinearities entering into play when large displacements are concerned. Employing a time integration algorithm inspired by a contribution by Casciaro, almost unrecognized in the literature, we were able to reconstruct the entire nonlinear equilibrium path. The key ingredients of the approach presented in this contribution are the definition of strain and kinetic energies of the fundamental brick of the origami metamaterial, i.e. what we have called the panel. For each triangle which the facets have been partitioned into, only affine transformations are considered. Therefore, the strain energy related to the in-plane deformation of triangles can be computed by making use of information concerning the stretch of their edges only, while that related to bending and folding, associated to a panel, i.e. two triangles sharing an edge, can be computed by knowing only the relative rotation of the two triangles around their common edge.

The general formulas reported in [41, 55, 56], which are making use of the change in the dihedral angle between two triangles in a panel, are simple and computationally efficient; these characteristics are essential for a code that should be able to deal with problems involving a large number of degrees of freedom. However, the approach presented in [41, 55, 56] is affected by some singularities that pose difficulties in computing the structural reaction and the stiffness matrix for some configurations using automatic symbolic computation. In this regard, it is worth to mention in this concluding section that, similarly to what has been done in [57], a tensorial definition of such a relative rotation has been introduced in this paper, which is not biased by in-plane affine deformation of triangles and can get around the singularities affecting the approach presented in [41, 55, 56].

Fig. 14
figure 14

Plate (a), vault (b), shell (c), and half-sphere (d) with standard Miura-ori folding pattern

Full size image

In other words, we have generalized some ideas developed to model beams and beam lattices in the so-called Hencky’s approach, presented in works devoted to formulate simple, yet effective and computationally efficient, mechanical models for metamaterials [37].

Fig. 15
figure 15

Depiction of the so-called Kresling tower

Full size image

We have shown that numerical simulations performed for origami beams folded according to the Miura-ori pattern reveal interesting features. The more relevant one is the sensitivity to imperfections, which causes unexpected vibrations, as it is possible to see by looking at the results presented in Sect. 4.

Concerning the outlooks of the present work, it is worth to mention the following future challenges that could be tackled:

  1. 1.

    This work has presented, in addition to the stepwise solution strategy, a quite general tool to compute the kinetic and elastic deformation energies of a triangle moving in space, as well as the bending and folding energies of a panel; summing up these contributions, it is straightforward to obtain the total energy associated to a unit cell and, consequently, that associated to the whole origami metamaterial; such a tool could be used in the future to analyse the vibrations of origami plates and shells (see Fig. 14) with an arbitrary folding pattern, as an instance the so-called Kresling pattern [58] (see Fig. 15, where we show a depiction of the so-called Kresling tower), which appears interesting for its wide application field. Regarding Kresling folding patterns, it is worth to mention that they show some analogies with the so-called duoskelion beam, introduced in previous works by the authors of the present contribution [59, 60]—exploiting chirality of the microstructure [61]—in that they have a very sensitive buckling behaviour, see [62]. In this regard, future works elaborating on top of the present contribution could deal with the exploration of the role of local Euler buckling in Kresling origami structures during pattern formation, induced by external loading [63].

  2. 2.

    The extremely simple form of bending and folding energies used in this wok does not ensure that relative rotations of two triangles in a panel making the triangles overlap are avoided, nor kinematic variables are constrained so to prevent such an occurrence; the way proposed by [41] to address this issue, by making use of an energy barrier, is interesting, but alternative routes could be explored in the future.

  3. 3.

    Despite the fact that the presented modelling approach has been here developed to perform dynamical analyses of origami metamaterials, the same approach, which is intrinsically discrete, could be exploited in the future to analyse numerically standard shells, taking advantage of its computational efficiency, see [64, 65]. We expect this to be particularly profitable when more complex material behaviours, as an instance damage and plasticity, are considered [64, 66, 67].

  4. 4.

    Finally, the authors believe that results reported in the recent paper [68] concerning the computation of some conservation laws along edges might improve the computational efficiency of the code built to analyse the nonlinear behaviour of origami-like structures.