1 Introduction

In the theory of meta materials one of the most interesting problems concerns the synthesis of microstructures which at macro level have a certain well specified behavior [1,2,3,4]. This behavior is made precise by the choice of an action functional and a dissipation functional [5,6,7,8]. In [9, 10], it is proven that an essential property of micro structures synthesizing second gradient continua consists in including elastic hinges and perfect pivots interconnecting bending fibres. Therefore, the technological problem of finding a 3D printing process producing perfect pivots and elastic hinges became relevant  [11,12,13,14]. This problem seems to have found some usefully solutions [15, 16]: however, a deeper theoretical insight is necessary in order to give the demanded support to such a complex technological demand. In the present paper, we start the modeling analysis necessary to fully understand the already available experimental evidences [9, 10, 12, 17,18,19,20,21]. This knowledge will be useful in pursuing the important further step aiming to improve elastic range of hinges introduced in pantographic structures [22].

Albeit one could believe that non-linear elastic phenomena occur in bias extension test of pantographic sheets, here we prove that also plasticity at micro level does justify observed experimental evidences. The here postulated assumption is that elastic hinges reach, in some of their parts, plastic regime and therefore that macroscopically observed non linearity finds its fundamental description in an elastoplastic model for the material constituting the hinges. This is consistent with the specific materials used, up to now, to build using 3D printing techniques pantographic sheets. Of course, non linear elastic effects may need to be included in the modeling when building specimens with other materials.

The major novelty in the present paper is that we demonstrate by a closed form analysis across micro and mesoscale that the change of concavity observed in bias extensional test of pantographic sheets is explained by elasto-plasticity in the hinges of such pantographic sheets.

Moreover, our analysis allows for the determination of the class of materials using which pantographic microstructures produce macro second gradient materials [23,24,25,26] with largest elastic regime: in the conclusions we present a comparison among different materials in this respect and we give a qualitative rational explanation of the high performances of the polyamid when compared to iron, aluminium and nickel.

2 Experimental evidences and constitutive meso modelling difficulties

Advancements in additive manufacturing and 3D printing techniques have enabled the production of pantographic metamaterials with exceptionally fine microstructures [9, 10, 27, 28]. For experimental evidence related to polyamide (PA) and metallic (ME) pantographic sheets subjected to bias extensional test, we refer to [29, 30].

These experimental results are used to calibrate a multi-scale model, introducing three distinct scales: macroscopic, mesoscopic, and microscopic.

On the macroscale, the pantographic sheet subjected to a bias extension test results in a macroscopic force-displacement relationship. In the particular case of a ME pantographic sheet [30], the length scale of the macroscopic scale is characterized by the dimensions of the specimen which is 21 cm long and 7 cm wide. The macroscopic force-displacement relationship is presented in Fig. 1. This curve shows a change in concavity that is not observed in PA samples [29].

Fig. 1
figure 1

\(u_{x}\mapsto R_{x}\) experimental curve of a metallic pantographic sample in bias elongation test, where \(u_{x}\) denotes the horizontal displacement and \(R_{x}\) the corresponding reaction force

Full size image

On the mesoscale, there are two main possible choices regarding the mesomodeling for describing the behavior of such a medium: continuous or discrete. If a continuous mesomodeling is chosen, a second-gradient continuum is typically used [31]. However, in this work, we will use a discrete meso-modeling approach. Specifically, we will employ the Hencky-type discrete model [12, 32,33,34]. Here, the pantographic material is modeled as an assembly of extensional springs interconnected by rotational springs. Extensional springs account for the elongation of pantographic fibers, while rotational springs account for both fiber bending (see Fig. 2b) and torsion of interconnecting hinges (see Fig. 2c). The length scale of the mesoscopic scale is related to the order of magnitude of the size of the structural elements from which the pantographic sheet is made of (namely the length and diameter of hinges and the dimensions of the cross section of the fibers which are approximately equal to 5 mm in the pantographic sheets presented in this paper).

Fig. 2
figure 2

Hencky-type model with: a axial extensional springs, b bending rotational springs and c torsional rotational springs

Full size image

On the mesoscale, the constitutive law describing the torsional behavior of the interconnecting hinges is the function \(\alpha \mapsto M(\alpha )\), where \(\alpha \) is the twist angle of each hinge and M is the torsional moment. The strain energy is expressed as the sum of stretching, bending, and shear contributions [12]. The axial, bending, and torsional specific energies, denoted as \(\ell \mapsto w_a(\ell )\), \(\beta \mapsto w_b(\beta )\), and \(\alpha \mapsto w_s(\alpha )\), respectively, can be defined by equations [22]:

$$\begin{aligned} w_{a}(\ell )&=\frac{1}{2}k_{a}\left( \ell -\ell _{0}\right) ^{2}\quad \quad w_{b}(\beta )=k_{b}\left( cos\beta +1\right) \quad \quad {w}_{s}(\alpha )=\frac{1}{2}{k}_{s}\alpha ^c \end{aligned}$$
(1)

where \(M(\alpha )=\partial w_{s}(\alpha )/\partial \alpha \). The geometrical significance of \(\beta \) and \(\gamma =\pi /2-\alpha \) is illustrated in Fig. 2b and c. Moreover, \(k_{a}\), \(k_{b}\), and \({k}_{s}\) represent the extensional, bending, and torsional stiffness, respectively. Symbols \(\ell _{0}=\left\| \overrightarrow{P_{i}P_{i+1}}\right\| \), \(\ell =\left\| \overrightarrow{p_{i}p_{i+1}}\right\| \) denote the lengths of the beams in the initial and actual configurations, \(\left\| \cdot \right\| \) represents the Euclidean norm. It has been observed in [30] that shear energy \(w_{s}\) in Eq. (1) is unsuitable for describing the pronounced change in the concavity of the force-elongation curve of metallic pantographic sheets during a bias elongation test (see Fig. 1). Moreover, the second derivative of the specific energy function \({w}_{s}\), defined in Eq.(1), tends to infinity for \(c<2\) and as \(\alpha \) approaches 0, leading to numerical difficulties. Numerical simulations reveal that altering the functions describing axial and bending energies, \(w_{a}\) and \(w_{b}\), has a negligible impact on the agreement between theoretical and experimental force-elongation curves obtained from a bias elongation test when a large change of concavity of the curve occurs. An alternative phenomenological two-parameter shear energy has been proposed in [30]. This new shear energy is defined by

$$\begin{aligned} {w}_s(\alpha )=k_s \left( \alpha \arctan \left( {a} \alpha \right) -\frac{\log \left( {a}^2 \alpha ^2+1\right) }{2{a}}\right) \, \end{aligned}$$
(2)

and leads to the simple constitutive law \(\alpha \mapsto M(\alpha )\) for the interconnecting hinges defined by

$$\begin{aligned} {M}(\alpha ) = \frac{\partial {w}_{s}(\alpha )}{\partial \alpha } = {k}_s\,\arctan \left( a \, \alpha \right) , \end{aligned}$$
(3)

in which \({k}_s\) and a are the two parameters of the constitutive law. This formulation provides a suitable representation for the force-elongation curve during a bias elongation test, accounting for high changes in concavity, with a single parameter a responsible for the concavity change. Using experimental results (see [30]), the following values of \(k_s\) and a have been identified:

  • Polyamide pantographic sheet: \(a=5\) and \(k_s = 1.66 \, \text {N~mm}\) (with hinge radius \(R=4.5 \,\text {mm}\)),

  • Metallic pantographic sheet: \(a=25\) and \(k_s =8.84 \, \text {N~mm}\) (with hinge radius \(R=5\, \text {mm}\)).

The associated graphs \(\alpha \mapsto M(\alpha )\) are presented in Fig. 3. Although this mesoscale model allows for the identification of the bias extension test of polyamide and metallic pantographic sheets, the issue of the microscopic origin of the mesoscale behavior leading to change of concavity on the macroscale remains an open problem. Coming back to Fig. 1, in which two successive loadings are applied, it is evident that a permanent displacement occurs after the first unloading, suggesting the occurrence of plasticity within the hinges. In this work, we aim to shift from the mesoscale to the microscale.

Fig. 3
figure 3

Graph of \(\alpha \mapsto M(\alpha )\) for a metallic and b polyamide pantographic sheets considering arctan laws obtained by assuming a \(a=25\) and \(k_{s}=8.84~\mathrm {N~mm}\) and b \(a=5\) and \(k_{s}=1.66~\mathrm {N~mm}\)

Full size image

As a 3D structure, the pantographic structure comprises an arrangement of 3D beams interconnected by 3D cylinders (hinges). It has already been observed in the literature that the macroscopic behavior of pantographic sheets depends mainly on their microstructure [35]. The length scale of the microscopic scale is about one hundredth of the smallest dimensions of hinges and beams, i.e. of the order of magnitude of 0.1 mm for the pantographic sheets considered in this paper. At this microscale, the constitutive law governing the 3D material behavior of the hinges will be represented in the present work as a 3D elastoplastic Cauchy medium. The mesoscale constitutive law \(\alpha \mapsto M(\alpha )\) will be derived as an analytical closed-form solution from the law \((\alpha ,r)\mapsto \tau (\alpha ,r)\) obtained by solving the 3D problem of a cylinder subjected to pure torsion made of an elastoplastic material.

3 Mesoscopic constitutive equations via micro-meso analysis

This section is devoted to deriving an analytical relationship between torque M and twist angle \(\alpha \) for a cylindrical hinge. To do so, we will model the hinge as a cylinder of radius R and height h, while considering the following boundary conditions expressed in cylindrical coordinates:

$$\begin{aligned} \left\{ \begin{aligned} \text {at } z=0 \;&:&\underline{\textrm{u}} \cdot \underline{\textrm{e}}_r&=0&\underline{\textrm{u}}\cdot \underline{\textrm{e}}_{\theta }&=0&(\underset{\sim }{\mathrm {\sigma }} \cdot \underline{\textrm{n}}) \cdot \underline{\textrm{z}}&=0 \\ \text {at } z=h \;&:&\underline{\textrm{u}} \cdot \underline{\textrm{e}}_r&=0&\underline{\textrm{u}}\cdot \underline{\textrm{e}}_{\theta }&=\alpha r&(\underset{\sim }{\mathrm {\sigma }} \cdot \underline{\textrm{n}}) \cdot \underline{\textrm{z}}&=0 \\ \text {at } r=R \;&:&\underset{\sim }{\mathrm {\sigma }} \cdot \underline{\textrm{n}}&=\underline{\textrm{0}} \end{aligned} \right. \end{aligned}$$
(4)

3.1 Elastic cylinder

The elasticity problem reads:

$$\begin{aligned} \left\{ \begin{aligned}&\underline{\mathrm {\textrm{div}}} \underset{\sim }{\mathrm {\sigma }} = \underline{\textrm{0}} \\&\text {boundary conditions (4)} \\&\underset{\sim }{\mathrm {\sigma }}= \lambda \, \textrm{tr} \underset{\sim }{\mathrm {\varepsilon }} + 2 \mu \;\underset{\sim }{\mathrm {\varepsilon }} \\&\underset{\sim }{\mathrm {\varepsilon }}(\underline{\textrm{u}})= \frac{1}{2} \left( \nabla \underline{\textrm{u}} + (\nabla \underline{\textrm{u}})^{T}\right) \end{aligned} \right. \end{aligned}$$
(5)

Let consider the kinematically admissible displacements field:

$$\begin{aligned} \underline{\textrm{u}}&=\frac{\alpha r z}{h} \underline{\textrm{e}}_{\theta }\, \end{aligned}$$
(6)

The associated strain field reads:

$$\begin{aligned} \underset{\sim }{\mathrm {\varepsilon }}&= \frac{\alpha r}{2 h}\underset{\sim }{\textrm{A}}&\underset{\sim }{\textrm{A}}&:=\underline{\textrm{e}}_{\theta }\otimes \underline{\textrm{e}}_{z}+\underline{\textrm{e}}_{z}\otimes \underline{\textrm{e}}_{\theta }\, \end{aligned}$$

Using the linear elastic constitutive law, the stress field reads:

$$\begin{aligned} \underset{\sim }{\mathrm {\sigma }}&= \frac{\mu \alpha r}{h} \underset{\sim }{\textrm{A}} \end{aligned}$$
(7)

This stress field is statically admissible so we deduce that Eqs. (6) and (7) give the solution of the elastic problem. The mesoscale constitutive law \(\alpha \mapsto M(\alpha )\) is obtained by:

$$\begin{aligned} M(\alpha ) =2 \pi \int _{0}^{R} \frac{\mu \alpha r}{h} r^{2}dr = \frac{\pi R^{4} \mu }{2 h} \; \alpha \end{aligned}$$
(8)

This solution is applicable in the pure elastic regime of the cylinder in torsion.

3.2 Elastoplasticity modeling at micro level

Elastoplasticity constitutive law considered in this paper will be part of generalized standard (isotropic) materials with Von Mises yield criterion and (isotropic or kinematic) hardening under the assumption of proportional monotonic loading [36].

In this specific context, the elastoplastic constitutive law can be integrated into the so-called Hencky Mises constitutive law:

$$\begin{aligned} \underset{\sim }{\mathrm {\varepsilon }}^{p}=\frac{3}{2}\frac{g(\sigma _{eq}-\sigma _Y)}{\sigma _{eq}}\underset{\sim }{\mathrm {\sigma }}^{D} \end{aligned}$$
(9)

in which \(\underset{\sim }{\mathrm {\sigma }}^{D}\) is the deviatoric part of stress, \(\underset{\sim }{\mathrm {\varepsilon }}^{p}\) is the plastic strain and

$$\begin{aligned} g(\sigma _{eq}-\sigma _Y)&=\varepsilon _{eq}^{p}&\sigma _{eq}-\sigma _Y&=\mathcal {R}(\varepsilon _{eq}^{p})&g \circ \mathcal {R} =Id \end{aligned}$$
(10)

with

$$\begin{aligned} \sigma _{eq}&=\sqrt{\frac{3}{2}\underset{\sim }{\mathrm {\sigma }}^{D}:\underset{\sim }{\mathrm {\sigma }}^{D}}&\varepsilon _{eq}^{p}&=\sqrt{\frac{2}{3}\underset{\sim }{\mathrm {\varepsilon }}^{p}:\underset{\sim }{\mathrm {\varepsilon }}^{p}} \end{aligned}$$

The choice of plasticity model is thus related to the choice of an hardening law \(\sigma _{eq}\mapsto g(\sigma _{eq}-\sigma _Y)\) or \(\varepsilon _{eq}^{p}\mapsto \mathcal {R}(\varepsilon _{eq}^{p})\).

3.3 Elastoplastic cylinder

The onset of plasticity is obtained for the angle \(\alpha _0\) and the couple \(M_0\) such that \(\sigma _{eq}=\sigma _Y\), which are equal to:

$$\begin{aligned} \alpha _0&:=\frac{1}{\sqrt{3}} \frac{h}{R} \frac{\sigma _Y}{\mu }&M_0&:=\frac{\pi }{2\sqrt{3}} R^{3} \sigma _Y \end{aligned}$$
(11)

Let now suppose that there exists an inner cylinder of radius \(R^{(e)}\) in the elastic regime, while the outer part of the cylinder (\(R^{(e)}\le r\le R\)) is in the elastoplastic regime. Let us assume that the solution is of the form:

$$\begin{aligned} \underline{\textrm{u}}&= u_{\theta }(r) \underline{\textrm{e}}_{\theta }&\underset{\sim }{\mathrm {\sigma }}&=\tau (r) \underset{\sim }{\textrm{A}} \end{aligned}$$
(12)

As \(\underset{\sim }{\textrm{A}}\cdot \underline{\textrm{e}}_{r}=0\), the solution in the inner part of the cylinder (\(0\le r\le R^{(e)}\)) is the same as in the purely elastic case, i.e.:

$$\begin{aligned}&0\le r\le R^{(e)} :&\underline{\textrm{u}}&=\frac{\alpha r z}{h} \underline{\textrm{e}}_{\theta }&\underset{\sim }{\mathrm {\sigma }}&= \frac{\mu \alpha r}{h} \underset{\sim }{\textrm{A}} \end{aligned}$$

The radius \(R^{(e)}\) is obtained assuming continuity of the equivalent stress \(\sigma _{eq}\) which is equal to \(\sigma _Y\) at the boundary between elastic and plastic parts of the cylinder, i.e.:

$$\begin{aligned} \sqrt{3} \frac{\mu \alpha R^{(e)}}{h}&= \sigma _{Y}&R^{(e)}&= \frac{\alpha _0}{\alpha }R \end{aligned}$$

Let us assume that the displacement solution in the inner part of the cylinder is valid in the entire cylinder:

$$\begin{aligned}&0\le r\le R :&\underline{\textrm{u}}&=\frac{\alpha r z}{h} \underline{\textrm{e}}_{\theta }&\underset{\sim }{\mathrm {\varepsilon }}&= \frac{\alpha r}{2 h}\underset{\sim }{\textrm{A}} \end{aligned}$$
(13)

The elastic part of the strain is obtained using the linear elastic constitutive law:

$$\begin{aligned} \underset{\sim }{\mathrm {\varepsilon }}^{e}=\frac{\tau }{2 \mu } \underset{\sim }{\textrm{A}} \end{aligned}$$
(14)

so that the plastic strain is given by:

$$\begin{aligned} \underset{\sim }{\mathrm {\varepsilon }}^{p}=\underset{\sim }{\mathrm {\varepsilon }}-\underset{\sim }{\mathrm {\varepsilon }}^{e}=\frac{1}{2}\left( \frac{\alpha r}{h}-\frac{\tau }{\mu } \right) \underset{\sim }{\textrm{A}} \end{aligned}$$
(15)

With \(\varepsilon ^{p}_{eq}=\frac{1}{\sqrt{3}}\left( \dfrac{\alpha r}{h}-\dfrac{\tau }{\mu } \right) \) and \(\sigma _{eq}=\sqrt{3} \tau \), Eq. (10) reads then

$$\begin{aligned} g(\sqrt{3} \tau - \sigma _Y)=\frac{1}{\sqrt{3}}\left( \frac{\alpha r}{h}-\frac{\tau }{\mu } \right) \end{aligned}$$
(16)

Using the property \(2 \pi \int _{0}^{R} \frac{\mu \alpha r}{h} r^{2}dr= \frac{M_0}{\alpha _0}\alpha \), the constitutive law at the mesoscale reads

$$\begin{aligned} M(\alpha )= \left\{ \begin{aligned}&\frac{M_0}{\alpha _0} \alpha & \text {for } \alpha \le \alpha _0\\&2 \pi \int _{0}^{\frac{\alpha _0}{\alpha }R} \frac{\mu \alpha r}{h} \; r^{2}dr + 2 \pi \int _{\frac{\alpha _0}{\alpha }R}^{R} \tau (\alpha ,r) \; r^{2}dr & \text {for } \alpha \ge \alpha _0 \end{aligned}\right. \end{aligned}$$
(17)

in which \(\tau \) is solution of (16):

$$\begin{aligned} \frac{\mu \alpha r}{h}- \tau =\sqrt{3} \mu \; g(\sqrt{3} \tau - \sigma _Y) \end{aligned}$$
(18)

.

4 Mesoscopic constitutive laws obtained by micro-meso analysis

On the microscale, classical hardening laws are:

  • Linear (non-saturating) hardening:

    $$\begin{aligned} R(\varepsilon _{eq}^{p})&=C \varepsilon _{eq}^{p}&g(\sigma _{eq}-\sigma _Y)&=\frac{\sigma _{eq}-\sigma _Y}{C} \end{aligned}$$
    (19)

  • Power law (non-saturating) hardening:

    $$\begin{aligned} R(\varepsilon _{eq}^{p})&=K \left( \varepsilon _{eq}^{p}\right) ^{\frac{1}{M}}&g(\sigma _{eq}-\sigma _Y)&=\left( \frac{\sigma _{eq}-\sigma _Y}{K}\right) ^{M} \end{aligned}$$
    (20)

  • Exponential (saturating) hardening:

    $$\begin{aligned} R(\varepsilon _{eq}^{p})&=R_{\infty }\left( 1 - \exp (-b \varepsilon _{eq}^{p})\right)&g(\sigma _{eq}-\sigma _Y)&=-\frac{1}{b}\log \left( 1-\frac{\sigma _{eq}-\sigma _Y}{R_{\infty }}\right) \end{aligned}$$
    (21)

In the case of Hencky Mises law, the plasticity model can also be defined by the direct choice of the function g, even though the inverse function is not analytically available, e.g.

$$\begin{aligned} g(\sigma _{eq}-\sigma _Y)= \left( \dfrac{\sigma _{eq}-\sigma _Y}{C}\right) + \left( \dfrac{\sigma _{eq}-\sigma _Y}{K}\right) ^{M} \end{aligned}$$
(22)

4.1 Linear hardening

Introducing \(\chi :=\frac{C}{3 \mu }\), the solution of Eq. (16), with the choice (19) reads

$$\begin{aligned} \tau =\frac{2}{\pi }\frac{M_{0}}{(1+\chi )R^{3}}\left( 1+\chi \,\frac{r}{R} \,\frac{\alpha }{\alpha _{0}}\right) \end{aligned}$$
(23)

so that we obtain:

$$\begin{aligned} M(\alpha )=\left\{ \begin{aligned}&\frac{M_0}{\alpha _0} \alpha & \text {for } \alpha \le \alpha _0\\&\frac{M_0}{1+ \chi }\left( \frac{4}{3}-\frac{1}{3}\left( \frac{\alpha _0}{\alpha }\right) ^{3}+ \chi \frac{\alpha }{\alpha _0}\right) & \text {for } \alpha \ge \alpha _0 \end{aligned}\right. \end{aligned}$$
(24)

The case of Elastic-perfectly plastic micro constitutive law is obtained by setting \(\chi =0\).

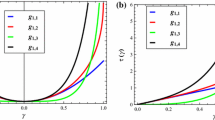
In Fig. 4 are presented the arctan laws (see Sect. 2) and the law \(\alpha \mapsto M(\alpha )\) of Eq. (24) with fitted parameters \(\alpha _0\), \(M_0\) and \(\chi \).

Fig. 4
figure 4

Graph of \(\alpha \mapsto M(\alpha )\) for a metallic and b polyamide pantographic sheets considering linear hardening (Eq. (24)-solid line) and arctan (Eq. (3)-dashed line) laws. The linear hardening laws are obtained by assuming a \(\alpha _{0}=0.1~\textrm{rad}\), \(M_{0}=18~\mathrm {N~mm}\), \(\chi =7.59\times 10^{-2}\), and b \(\alpha _{0}=0.25~\textrm{rad}\), \(M_{0}=2~\mathrm {N~mm}\), \(\chi =7.14\times 10^{-1}\). The arctan laws are obtained by assuming a \(a=25\) and \(k_{s}=8.84~\mathrm {N~mm}\) and b \(a=5\) and \(k_{s}=1.66~\mathrm {N~mm}\)

Full size image

4.2 Power law hardening

For the choices (20) or (22), (18) can only be solved analytically for \(M=2,3,4\) and Eq. (17) leads then to very cumbersome analytical solutions, so that it is preferable to use the following exponential hardening law instead.

Remark

For (20) or (22), the case \(M=1\) corresponds to linear hardening.

4.3 Exponential hardening

The solution of (16), with the choice (21), reads:

$$\begin{aligned} \tau =\frac{R_{\infty }+\sigma _Y}{\sqrt{3}}-\frac{\sqrt{3}\mu }{b} W\left[ \frac{b R_{\infty }}{3 \mu } \exp \left[ b\left( \frac{R_{\infty }+\sigma _Y}{3 \mu }-\frac{r \alpha }{\sqrt{3}h}\right) \right] \right] \end{aligned}$$
(25)

in which the function W(x) is the Lambert W function.

Introducing \(\xi :=\frac{b}{3 \mu }\) and \(\zeta :=\xi R_{\infty }\), the previous equation reads:

$$\begin{aligned} \tau =\frac{2 M_0}{\pi R^3}+ \frac{1}{\sqrt{3} \xi } \left( \zeta -W\left[ \zeta \exp \left[ \zeta +\frac{2 \sqrt{3}}{\pi } \frac{\xi M_0}{R^3} (1 -\frac{r}{R} \frac{\alpha }{\alpha _0}) \right] \right] \right) \end{aligned}$$
(26)

so that, introducing \(\omega \left[ \alpha \right] =\frac{2 \sqrt{3}}{\pi } \frac{M_{0} \xi }{R^3} \left( 1-\frac{\alpha }{\alpha _{0}}\right) \), we obtain for \(\alpha \ge \alpha _0\):

$$\begin{aligned} \begin{aligned} M(\alpha )&= M_{0}\left( \frac{\alpha _{0}}{\alpha }\right) ^3+ \frac{2}{9} (6 M_{0} \xi +\sqrt{3} \pi \zeta R^3) \left( 1-\left( \frac{\alpha _{0}}{\alpha }\right) ^3\right) \\&\quad - \frac{\pi ^2}{18} \frac{R^6 }{ M_{0}^3 \xi ^4} (6 M_{0}^2 \xi ^2+2 \sqrt{3} \pi M_{0} R^3 \xi +\pi ^2 R^6) \left( \frac{\alpha _0}{\alpha }\right) ^3 W\left[ \zeta \, e^{\zeta }\right] \\&\quad - \frac{\pi ^2}{144} \frac{R^6}{ M_{0}^3 \xi ^4} (24 M_{0}^2 \xi ^2+12 \sqrt{3} \pi M_{0} R^3 \xi +7 \pi ^2 R^6) \left( \frac{\alpha _0}{\alpha }\right) ^3 \left( W\left[ \zeta e^{\zeta } \right] \right) ^2\\&\quad - \frac{\pi ^3}{648} \frac{R^9 }{M_{0}^3 \xi ^4} (12 \sqrt{3} M_{0} \xi +11 \pi R^3) \left( \frac{\alpha _0}{\alpha }\right) ^3 \left( W\left[ \zeta \, e^{\zeta } \right] \right) ^3\\&\quad - \frac{\pi ^4}{432}\frac{ R^{12} }{M_{0}^3 \xi ^4} \left( \frac{\alpha _0}{\alpha }\right) ^3 \left( W\left[ \zeta \, e^{\zeta } \right] \right) ^4\\&\quad + \frac{\pi ^2}{18} \, \frac{ R^6 }{ M_{0}^3 \xi ^4} \left( 6 M_{0}^2 \xi ^2 \left( \frac{\alpha _0}{\alpha } \right) +2 \sqrt{3} \pi M_{0} R^3 \xi \left( \frac{\alpha _0}{\alpha } \right) ^2 +\pi ^2 R^6 \left( \frac{\alpha _0}{\alpha } \right) ^3 \right) W\left[ \zeta e^{\zeta +\omega [\alpha ]}\right] \\&\quad + \frac{ \pi ^2}{144} \, \frac{R^6}{M_{0}^3 \xi ^4} \left( 24 M_{0}^2 \xi ^2 \left( \frac{\alpha _0}{\alpha }\right) +12 \sqrt{3} \pi M_{0} R^3 \xi \left( \frac{\alpha _0}{\alpha } \right) ^2 +7 \pi ^2 R^6 \left( \frac{\alpha _0}{\alpha } \right) ^3 \right) \left( W\left[ \zeta e^{\zeta + \omega [\alpha ]}\right] \right) ^2\\&\quad + \frac{\pi ^3 }{648} \frac{R^9}{M_{0}^3 \xi ^4} \left( 12 \sqrt{3} M_{0} \xi \left( \frac{\alpha _0}{\alpha }\right) ^2+11 \pi R^3 \left( \frac{\alpha _0}{\alpha }\right) ^3\right) \left( W\left[ \zeta e^{\zeta +\omega [\alpha ]}\right] \right) ^3\\&\quad + \frac{\pi ^4}{432}\frac{R^{12} }{ M_{0}^3 \xi ^4} \left( \frac{\alpha _0}{\alpha }\right) ^3 \left( W\left[ \zeta e^{\zeta +\omega [\alpha ]}\right] \right) ^4 \end{aligned} \end{aligned}$$
(27)

In Fig. 5 are presented the arctan laws (see Sect. 2) and the law \(\alpha \mapsto M(\alpha )\) of Eq. (27) with fitted parameters \(\alpha _0\), \(M_0\), \(\xi \), \(\zeta \) and R.

Fig. 5
figure 5

Graph of \(\alpha \mapsto M(\alpha )\) for a metallic and b polyamid pantographic sheets considering exponential hardening (solid line) and arctan (Eq. (3)-dashed line) laws. The exponential hardening laws are obtained by assuming a \(\alpha _{0}=0.1~\textrm{rad}\), \(M_{0}=18~\mathrm {N~mm}\), \(\xi =4\times 10^{-3}\), \(\zeta =0.35\), \(R=0.5\, \textrm{mm}\) and b \(\alpha _{0}=0.25~\textrm{rad}\), \(M_{0}=2~\mathrm {N~mm}\), \(\xi =6\times 10^{-2}\), \(\zeta =1.92\), \(R=0.45~\textrm{mm}\). The arctan laws are obtained by assuming a \(a=25\) and \(k_{s}=8.84~\mathrm {N~mm}\) and b \(a=5\) and \(k_{s}=1.66~\mathrm {N~mm}\)

Full size image

5 Phenomenological meso constitutive model inspired by micro-meso modeling

As described in Sect. 2, it was postulated in [30] a 2 parameters heuristic meso modelling of the \(M(\alpha )\) constitutive law at meso scale:

$$\begin{aligned} M(\alpha )=K\arctan (a \alpha ) \end{aligned}$$
(28)

This law, not related to a micro-meso modeling via the elasto-plastic analytical study, did not introduce the definition of a boundary between elastic and plastic regimes. Moreover, for high initial slope, the arctan law is always quickly saturating.

In the previous section, we found, from a complete micro-meso analysis using exponential (or logarithmic) hardening, a precise meso constitutive law capable of reproducing the \(\arctan \) law and thus a bias test result. Nevertheless, this law is made of 5 parameters and might be too cumbersome for efficient use in an numerical optimization of pantographic structures, e.g. in inverse identification problem.

In this section we propose to introduce a new phenomenological meso-model constitutive law \(\alpha \mapsto M(\alpha )\) with a limited number of parameters capable of removing the drawbacks of the arctan law.

To this purpose, we look for a constitutive law \(\alpha \mapsto M(\alpha )\) which

  • should be made of two parts, one in a (linear) elastic regime, the second in a non-linear plastic regime,

  • can be saturated or not in the plastic regime,

  • has some consistency with an elastoplastic microscopic behavior,

  • derive from an explicit elastic potential,

  • is continuously differentiable.

Let introduce the following phenomenological mesoscopic constitutive law, with \(n>0\) and \(\chi >0\):

$$\begin{aligned} M(\alpha )=\left\{ \begin{aligned}&\frac{M_0}{\alpha _0} \alpha & \text {for } \alpha \le \alpha _0\\&\frac{M_0}{1+ \chi }\left( \frac{n+1}{n}-\frac{1}{n}\left( \frac{\alpha _0}{\alpha }\right) ^{n}+ \chi \frac{\alpha }{\alpha _0}\right) & \text {for } \alpha \ge \alpha _0 \end{aligned}\right. \end{aligned}$$
(29)

This law:

  • is saturating for \(\chi =0\), and non-saturating for \(\chi >0\),

  • is consistent with the meso constitutive law analytically obtained with linear hardening for \(n=3\),

  • derives from the potential

    $$\begin{aligned} n&\ne 1&w_s(\alpha )&= \left\{ \begin{aligned}&\frac{1}{2}\frac{M_0}{\alpha _0} \alpha ^{2} & \text {for } \alpha \le \alpha _0\\&\frac{M_0 \alpha }{1+\chi }\left( \frac{n+1}{n}+\frac{1}{n(n-1)}\left( \frac{\alpha _0}{\alpha }\right) ^n+\frac{\chi }{2}\frac{\alpha }{\alpha _0}\right) +C_0 & \text {for } \alpha \ge \alpha _0 \end{aligned}\right. \\ n&= 1&w_s(\alpha )&= \left\{ \begin{aligned}&\frac{1}{2}\frac{M_0}{\alpha _0} \alpha ^{2} & \text {for } \alpha \le \alpha _0\\&\frac{M_0}{1+\chi }\left( 2+\frac{\chi }{2}\frac{\alpha }{\alpha _0}-\frac{\alpha _0}{\alpha }\log (\alpha )\right) + C_1 & \text {for } \alpha \ge \alpha _0 \end{aligned}\right. \end{aligned}$$

    in which \(C_{0}=\dfrac{M_{0}\alpha _{0}}{2}\left( 1-\dfrac{2n+\chi (n-1)}{(1+\chi )(n-1)}\right) \) and \(C_{1}=\dfrac{M_{0}\alpha _{0}}{2}\left( 1-\dfrac{4+\chi -2\textrm{log}(\alpha _{0}))}{\alpha _0(1+\chi )}\right) \),

  • is continuously differentiable with

    $$\begin{aligned} M(\alpha _0)&=M_0&\left. \frac{\partial M}{\partial \alpha }\right| _{\alpha =\alpha _0}&=\frac{M_0}{\alpha _0} \end{aligned}$$

This law introduces 4 parameters with the following physical meaning:

  • \(M_0\) is the couple at the end of linear elastic regime,

  • \(\alpha _0\) is the angle at the end of linear elastic regime,

  • \(\frac{\chi }{1+\chi }\) is, for nonsaturating law, the ratio of slope of the asymptotic line in the plastic regime to elastic slope \(\frac{M_0}{\alpha _0}\),

  • \(\frac{n+1}{n}\) is, for saturating law, the ratio of maximal couple to \(M_0\).

In Fig. 6 are presented the arctan laws (see Sect. 2) and the law \(\alpha \mapsto M(\alpha )\) of Eq. (29) with fitted parameters \(\alpha _0\), \(M_0\), \(\chi \), n.

Fig. 6
figure 6

Graph of \(\alpha \mapsto M(\alpha )\) for a metallic and b polyamid pantographic sheets considering power n (Eq. (29))-solid line) and arctan ((3)-dashed line) laws. The power n laws are obtained by assuming (a) \(\alpha _{0}=0.1~\textrm{rad}\), \(M_{0}=18~\mathrm {N~mm}\), \(\chi =6\times 10^{-3}\), and \(\textrm{n}=0.9\), and b \(\alpha _{0}=0.25~\textrm{rad}\), \(M_{0}=2~\mathrm {N~mm}\), \(\chi =0.1\), and \(\textrm{n}=10^{-2}\). The arctan laws are obtained by assuming a \(a=25\) and \(k_{s}=8.84~\mathrm {N~mm}\) and b \(a=5\) and \(k_{s}=1.66~\mathrm {N~mm}\)

Full size image

6 Conclusions

Generalized continua are the mathematical models used for precisely describing the exotic mechanical behavior demanded to novel metamaterials [37, 38]. The standard continuum mechanics usually associated to the name of Cauchy, albeit very predictive of the behavior of many materials, cannot cover the whole range of possible mechanical behavior. One is obliged to use the the principle of virtual work when she needs to introduce continua models more general than Cauchy’s as the postulation scheme based on balance laws cannot be easily extended.

Once the desired generalized continuum model is chosen, then the problem of synthesizing a micro structure governed by chosen generalized continuum arises. In [9, 10], it is proven that in the synthesis problem pantographic microstructures play a very relevant role.

The motivation of the analysis presented in this paper was twofold: (1) Understanding and describing the mechanical phenomena occurring in the most important part of pantographic structure, e.g. deformable hinges  [39, 40]. (2) Giving theoretical indications for designing and constructing pantographic metamaterials showing the largest possible elastic regime  [25, 41,42,43].

Concerning point (1), we have obtained strong indications that the force displacement relationship observed in extension bias elongation test is determined not only by elastic phenomena but also by plasticity occurring in the hinge. We remark that we are aware of the limitations of the elastic plastic models at micro level we have introduced. Clearly more sophisticated description of plastic phenomena are possible and desirable. However we believe that at least for polyamide and metallic materials used, our description is satisfactory enough. We found at mesolevel a closed form constitutive equation for torsional moment in function of shear angle in the particular cases of linear or logarithmic hardening. For linear hardening, the mesoconstitutive equation is satisfactory at least qualitatively while for logarithmic hardening, a perfect match with the arctan law proves that the bias extension test can be identified with this particular elasto-plastic law on the micro level. Moreover, the available micro-meso identifications with linear hardening allowed us to conjecture a simple phenomenological relationship between couple and twist angle for pantographic hinges involving only 4 constitutive parameters which is suitable for deducing macro behavior, i.e. Force elongation curve in bias extension test and overall deformed shape of the pantographic structure.

Concerning point (2), we remark that it was a lucky choice to use polyamide in the first bias elongation test for pantographic structures while the choice the metals to be used in 3D printing was less happy: the onset of irreversible plastic deformation is \(\alpha _0=14^{\circ }\) for polyamide and \(\alpha _0=5^{\circ }\) for metallic pantographs. Moreover, the onset of irreversible plastic deformation occurring for the angle \(\alpha _0=\frac{1}{\sqrt{3}}\frac{h}{R}\frac{\sigma _Y}{\mu }\), better materials with respect to late occurrence of plasticity for a given geometrical configuration are those with greater ratio \(\frac{\sigma _Y}{\mu }\).

The performed analysis indicates that some new building strategies and solutions may be required for realizing perfect pivots and elastic hinges: the first proposed use of full cylinder being deformed in torsion seems not completely efficient, albeit it can be exploited for the already used micro materials   [22, 39, 44,45,46].

Finally, presented results will allow for the design of a novel experimental setup aimed at investigating the micro mechanical properties determining meso saturation effects of couple angle dependence, and change of concavity in macro force displacement dependence. In particular it seems very promising to use polymeric foam for building pantographic microstructures: their elongation and elastic performances could be outstanding.