Bias extension test for pantographic sheets: numerical simulations based on second gradient shear energies

Abstract

We consider a bi-dimensional sheet consisting of two orthogonal families of inextensible fibres. Using the representation due to Rivlin and Pipkin for admissible placements, i.e. placements preserving the lengths of the inextensible fibres, we numerically simulate a standard bias extension test on the sheet, solving a non-linear constrained optimization problem. Several first and second gradient deformation energy models are considered, depending on the shear angle between the fibres and on its gradient, and the results obtained are compared. The proposed numerical simulations will be helpful in designing a systematic experimental campaign aimed at characterizing the internal energy for physical realizations of the ideal pantographic structure presented in this paper.

1 Introduction

The objective of this work is the analysis of a rectangular sheet composed of two orthogonal families of inextensible fibres with low bending stiffness. The two families intersect the sides of the rectangle at an angle of $\pm 45^{\circ }$ in the initial configuration; we refer to this model as a 2D-continuum pantographic model. Mechanical systems of this kind are of great practical relevance in engineering applications. Indeed, the forming procedure of woven fabric represents the initial step in the production of many composite materials in both the aerospace and automotive industries. Hence, simulations dealing with the formation of woven fabrics (impregnated with polymer or dry) are very useful for pattern designing in the aforementioned context (e.g. [1–5]).

A bias extension test, in which a displacement at $45^{\circ }$ with the fibres is imposed, is widely used to characterize the mechanical behaviour of a woven fabric under large shear deformations, the curve force–displacement (along the bias direction) presenting the typical hardening effect due to geometric effects. Most commonly used fibres have a low (but non-zero) bending stiffness. In this work we analyse the bias extension test considering both first and second gradient deformation energy densities, continuing in the line of investigation introduced in [6–9] or, with the same topology but considering extensible beams instead of inextensible fibres, in [10, 11].

In this work, a new numerical scheme is implemented. Two main novelties characterize the present work. The first consists of a change in variables which reduces the order of differentiation of the problem formulation, making it a first gradient (rather than a second gradient) problem. Specifically, we adopt the rotations of the two fibres as degrees of freedom and assume for each rotation field a particular structure conforming with the Pipkin–Rivlin representation. The inextensibility constraint is therefore automatically satisfied. The displacement is successively evaluated by means of numerical integration of the two rotation fields. This new formulation of the problem leads clearly to an improved convergence as the computational cost is reduced with respect to a displacement-based formulation with Lagrangian multipliers accounting for the inextensibility constraint. The second novelty is the simulation of new energy models involving the shear angle and its gradient in the form $g_{2,1}$ (see subsequent section on numerical results).

The shape ratio of the specimen is 3:1, i.e. the short clamped side is one-third of the long side. The standard boundary conditions of the bias extension test are considered, i.e. the long sides of the rectangle are free, one of the short sides is fixed and on the other a prescribed displacement, parallel to the long sides, is imposed.

The paper is structured as follows. In the second section we give a brief description of the model, which is basically the one set in [6, 12], showing that by means of geometry and symmetry considerations, the kinematics of the system can be described in terms of one scalar field (representing the value of the shear deformation angle). In the third section a numerical formulation of the problem is developed, and a certain set of possible energies is given, with some heuristic considerations on our choices. In the fourth section the numerical results are presented and discussed.

1.1 Theoretical and technological contextualization of proposed line of investigation

The growing importance of the type of systems considered here arises both from their high strength-to-weight ratio and from their peculiarly safe behaviour under fracture. In fact, some theoretical and experimental results show that fracture can be forecast rather accurately, and it is also worth noting that from the start of the fracture to the complete split of the sample, the system is still able to store a considerable amount of deformation energy. Moreover, the development of 3D printing and other computer-aided manufacturing techniques allows for a physical realization of the most exotic geometries (see [13] for recent applications of advanced manufacturing). Therefore, a thorough understanding of the mechanical behaviour of the simple geometry proposed is a necessary first step towards the development of increasingly complex mechanical systems. The considered structure, because of its characteristics, can be indeed considered as a basic case of metamaterial, which can be enriched in different ways by generalizing its geometry, its mechanical properties or its kinematics (for a recent review on metamaterials, see [14]).

The theoretical framework in which it is natural, in the opinion of the authors, to study the behaviour of the considered system (and in general that of systems displaying complex microstructures) is the variational approach (see [15] for a general discussion), which of course is also the most suitable for the numerical formulation of the problem. The theoretical tools used for analysing the test are those set out in the works of Rivlin and Pipkin (see [16, 17] and [18–21]). On the basis of the principle of stationary action, some suitable forms of energy, depending only on shear deformations, have been postulated, considering both first and second gradient energy models. The problem lies in the field of non-linear constrained optimization in which the objective function is represented by the energy functional subjected to impenetrability and kinematical compatibility constraints. We formulate the problem directly considering Pipkin’s representation.

It is clear nowadays that a suitable homogenization (see [22–30] for some relevant examples) of such systems leads to models that can be properly contextualized in the field of micromorphic continua (see [31, 32]). A reader interested in the theory of micromorphic continua can see the classical references [33–36] and more recent ones [37–42], while for applications the following references are relevant: [43–51].

We propose in this paper some types of energy depending on the second gradient of displacement, embedding our model in the mathematical framework of generalized continua, and in particular of higher gradient continua theory, which by now relies on a solid theoretical and experimental background. For more on this topic, the interested reader may consult [52, 53] as standard references and [54–61] for more recent results in the field.

2 Theoretical model and set-up for bias extension test

In this section we consider a continuous model at every point of which two fibres (belonging to two orthogonal families) intersect. The fibres are assumed to be inextensible. It should be remarked that, in general, difficult theoretical and numerical problems can arise from constraints of this kind (for related problems, see for instance [62–64]). As we will see, indeed, the inextensibility condition is naturally expressed by means of integral terms, which are in general more difficult to handle than differential ones. The motion is described in a set of coordinates $\xi ^1,\xi ^2$ which have the same directions as fibres.

2.1 Rivlin–Pipkin decomposition theorem

Let ${\mathbf {D}}_1$ and ${\mathbf {D}}_2$ be the unit tangent vectors along the fibres in the reference configuration (Fig. 2a), and let

$$\begin{aligned} \mathbf{d }_1={\mathbf {R}}_1(\theta _1){\mathbf {D}}_1,\quad \mathbf{d }_2={\mathbf {R}}_2(\theta _2){\mathbf {D}}_2 \end{aligned}$$

(1)

be the in-plane rotated vectors by means of two independent rotation operators indicated by ${\mathbf {R}}_1(\theta _1)$ and ${\mathbf {R}}_2(\theta _2)$. Since we consider only plane motion, the axial vector of the rotation operators is simply characterized by the rotation angles $\theta _1,\theta _2$. Notice that the rotations $\theta _1,\theta _2$ are considered positive if the angle between the directions $\mathbf{D }_1, \mathbf{D }_2$ decreases. Because of the inextensibility constraints, the deformation tensor is then given by

$$\begin{aligned} {\mathbf {F}}=({\mathbf {R}}_1 {\mathbf {D}}_1)\otimes {\mathbf {D}}_1 + ({\mathbf {R}}_2 {\mathbf {D}}_2)\otimes {\mathbf {D}}_2. \end{aligned}$$

(2)

Rivlin (in [16]) proved that, in our assumptions, the placement splits into the sum of two vector functions as

$$\begin{aligned} \mathbf{r }'(\xi ^1,\xi ^2)=\mathbf{r }'_1(\xi ^1)+\mathbf{r }'_2(\xi ^2). \end{aligned}$$

(3)

Therefore, we have that $\theta _1=\theta _1(\xi ^1)$ and $\theta _2=\theta _2(\xi ^2)$.

The displacement field can be expressed in integral form observing that

$$\begin{aligned} \mathbf{d }_i = \mathbf{D }_i+\frac{\partial \mathbf{u }}{\partial \xi ^i} \end{aligned}$$

(4)

and, using Eqs. (1) and (3), we obtain by integration the relative displacement between two points P, Q of the specimen:

$$\begin{aligned} \begin{aligned} u_x^Q&= \left( \int _{\xi ^1_P}^{\xi ^1_Q}\left( \cos (\theta _1)-1\right) \mathrm{d}\xi ^1 + \int _{\xi ^2_P}^{\xi ^2_Q} \sin (\theta _2) \mathrm{d}\xi ^2\right) \mathbf{D }_1\cdot \mathbf{e }_x\\&\quad +\,\left( \int _{\xi ^1_P}^{\xi ^1_Q} \sin (\theta _1) \mathrm{d}\xi ^1 + \int _{\xi ^2_P}^{\xi ^2_Q} \left( \cos (\theta _2)-1\right) \mathrm{d}\xi ^2\right) \mathbf{D }_2\cdot \mathbf{e }_x + u_x^P,\\ u_y^Q&= \left( \int _{\xi ^1_P}^{\xi ^1_Q} \left( \cos (\theta _1)-1\right) \mathrm{d}\xi ^1 + \int _{\xi ^2_P}^{\xi ^2_Q} \sin (\theta _2) \mathrm{d}\xi ^2 \right) \mathbf{D }_1\cdot \mathbf{e }_y\\&\quad +\, \int _{\xi ^1_P}^{\xi ^1_Q}\left( \sin (\theta _1) \mathrm{d}\xi ^1 + \int _{\xi ^2_P}^{\xi ^2_Q})\cos (\theta _2)-1) \mathrm{d}\xi ^2\right) \mathbf{D }_2\cdot \mathbf{e }_y + u_y^P, \end{aligned} \end{aligned}$$

(5)

where $\mathbf{e }_x, \mathbf{e }_y$ are the unit vectors of the external reference frame.

2.2 Energy functional

We proceed now to the identification of a suitable energy functional for the considered structure.

Let $\gamma ={\mathbf {d}}_1\cdot {\mathbf {d}}_2={\mathrm {sin}} (\vartheta _1+\vartheta _2)$ be the shear between the fibre directions. In order for the transformation to be monodrome (single-valued), the shear must belong to the interval

$$\begin{aligned} \theta _1+\theta _2 \in \left( -\frac{\pi }{2},\frac{\pi }{2}\right) \Rightarrow \gamma \in (-1,1). \end{aligned}$$

(6)

The Cauchy deformation tensor is then

$$\begin{aligned} {\mathbf {C}}={\mathbf {D}}_1\otimes {\mathbf {D}}_1+ \gamma \left( {\mathbf {D}}_1\otimes {\mathbf {D}}_2 + {\mathbf {D}}_2\otimes {\mathbf {D}}_1\right) + {\mathbf {D}}_2\otimes {\mathbf {D}}_2. \end{aligned}$$

(7)

The Green’s strain tensor is

$$\begin{aligned} {\mathbf {E}}=\frac{\gamma }{2}\left( {\mathbf {D}}_1\otimes {\mathbf {D}}_2+{\mathbf {D}}_2\otimes {\mathbf {D}}_1\right) . \end{aligned}$$

(8)

Here we consider also the contribution of the second gradient of the displacements to the deformation. Since the basis vectors $\mathbf{D }_i$ are constant, the only non-zero terms of the gradient of the strain tensor $\mathbf{E }$ are

$$\begin{aligned} \nabla E_{121}=\nabla E_{211}= \frac{1}{2}\cos (\theta _1+\theta _2) \frac{\partial \theta _1}{\partial \xi ^1}, \quad \nabla E_{122}=\nabla E_{212}= \frac{1}{2}\cos (\theta _1+\theta _2) \frac{\partial \theta _2}{\partial \xi ^2}. \end{aligned}$$

(9)

The elements of the gradient of the strain tensor can be given a very useful interpretation. Indeed, it can be easily shown that $\frac{\partial \theta _i}{\partial \xi ^i}$ is the in-plane curvature of i-family fibres. The elements of $\nabla \mathbf{E }$ are the projection of these curvatures on the deformed directors and can be interpreted as

$$\begin{aligned} \nabla E_{121} = \mathbf{d }_1\times \mathbf{d }_2 \cdot \mathbf{e }_z \frac{\partial \theta _1}{\partial \xi ^1}, \end{aligned}$$

(10)

that is, the curvatures multiplied by the area of the deformed element, so that the second gradient deformation vanishes as the shear tends to 1, i.e. when the fibres tend to overlap. This interpretation will be useful for the choice of the second gradient energy.

Any isotropic first gradient energy functional must then be a function of $\gamma ^2$:

$$\begin{aligned} {\mathfrak {F}}_1= \int _{B} g_1\left( \gamma ^2\right) \mathrm{d}B. \end{aligned}$$

(11)

We also include in the energy functional a contribution of the strain gradient, given by the norm of $\nabla \mathbf{E }$,

$$\begin{aligned} \Vert \nabla \mathbf{E }\Vert ^2 = \frac{1}{2} \Vert \nabla \gamma \Vert ^2, \end{aligned}$$

(12)

so that, also accounting for the impenetrability constraints (6), the energy functional ${\mathfrak {F}}$ becomes

$$\begin{aligned} {\mathfrak {F}}= \int _{B} \left[ \left( \alpha g_1\left( \gamma ^2\right) +\beta g_2\left( \Vert \nabla \gamma \Vert ^2\right) \right) \right] \mathrm{d}B + U_K (\gamma ), \end{aligned}$$

(13)

in which we have introduced two constitutive parameters $\alpha$ and $\beta$, and $U_K$ is the indicator function of the set

$$\begin{aligned} K= \left\{ \left( \theta _1,\theta _2\right) : \gamma \left( \xi ^1,\xi ^2\right) \in (-1,1), \forall (\xi ^1,\xi ^2)\right\} ,\quad U_K ={\left\{ \begin{array}{ll} 0, &{}\quad \left( \theta _1,\theta _2\right) \in K, \\ + \infty , &{}\quad \text {otherwise.}\end{array}\right. } \end{aligned}$$

(14)

The latter condition implies a constraint on the optimization problem that can be included in various ways (e.g. penalty, Lagrangian multipliers).

2.3 First and second gradient energy models

For a first gradient deformation problem, a sufficient condition for the existence of a solution of the BVP (Boundary value problem) is that the energy functional is a convex function of the strain tensor. Therefore, only convex functionals ${\mathfrak {F}}_1$ are considered in this work. The following four forms of $g_1(\gamma )$ are used in the numerical analyses:

• First gradient shear energy model:

  $$\begin{aligned} g_{1,1}(\gamma ) = \frac{1}{2} \gamma ^2 = \frac{1}{2}\sin ^2(\theta _1+\theta _2); \end{aligned}$$

  (15)

• First gradient quadratic energy model:

  $$\begin{aligned} g_{1,2}(\gamma ) = \frac{1}{2} \arcsin ^2(\gamma ) = \frac{1}{2}(\theta _1+\theta _2)^2; \end{aligned}$$

  (16)

• First gradient quartic energy model:

  $$\begin{aligned} g_{1,3}(\gamma ) = \frac{1}{4} \arcsin ^4(\gamma ) = \frac{1}{4}(\theta _1+\theta _2)^4; \end{aligned}$$

  (17)

• First gradient quadratic and quartic energy model, [$\alpha =1$ in (13)]:

  $$\begin{aligned} g_{1,4}(\gamma ) = \alpha _1 \arcsin ^2(\gamma ) + \alpha _2 \arcsin ^4(\gamma ) = \alpha _1 (\theta _1+\theta _2)^2 + \alpha _2 (\theta _1+\theta _2)^4. \end{aligned}$$

  (18)

Figure 1a shows a sketch of the four energy models considered over the existence interval for the variable $\gamma$. Note that the functions $g_{1,2}$ and $g_{1,4}$ can be considered as series expansions of $g_{1,1}$, so that for small shears they coincide. However, the function $g_{1,3}$ is quite different, as is evidenced from the plot of the conjugated internal stress reproduced in Fig. 1b, showing that the stress remains very small for small values of the shear, then rapidly grows. This function can simulate the effect of the densification of the fibres as the shear grows.

Fig. 1

First gradient energy models: a first gradient energy functions, b conjugated shear stress

Two energy functionals accounting for the second gradient deformation are considered; the first, as stated, is the $L_2$ norm of the second gradient strain tensor, and the other is a truncated expansion of it:

• Second gradient shear energy model:

  $$\begin{aligned} g_{2,1}(\nabla \gamma ) = \Vert \nabla \gamma \Vert ^2 = \frac{1}{2}\cos ^2(\theta _1+\theta _2)\left[ \left( \frac{\partial \theta _1}{\partial \xi ^1}\right) ^2+ \left( \frac{\partial \theta _2}{\partial \xi ^2}\right) ^2\right] ; \end{aligned}$$

  (19)

• Second gradient quadratic energy model:

  $$\begin{aligned} g_{2,2}(\gamma ) = \frac{1}{2} \left[ \left( \frac{\partial \theta _1}{\partial \xi ^1}\right) ^2+ \left( \frac{\partial \theta _2}{\partial \xi ^2}\right) ^2\right] . \end{aligned}$$

  (20)

The existence and uniqueness of the minimum for the given energy functional is in general a non-trivial issue and is linked to the properties of the convexity, coercivity and lower semi-continuity of the functional. We conjecture that in our case there are no local minima in symmetric extensions, but this point, as well as a rigorous mathematical characterization of the proposed models, deserve future investigations in specific works.

The dual stresses, for the functional (13), are given by

$$\begin{aligned} \sigma ^1_j= & {} \alpha \,\partial _{\theta _1}( g_{1,j}),\quad \sigma ^2_j=\alpha \, \partial _{\theta _2}(g_{1,j}),\quad j=1,\ldots ,4,\nonumber \\ \tau ^1_i= & {} \beta \, \partial _{\theta _1}(g_{2,i}),\quad \tau ^2_i=\beta \, \partial _{\theta _2}(g_{2,i}),\quad i=1,2, \end{aligned}$$

(21)

where the definitions of the first gradient energies, $g_{1,j}$, are given in (15),  (16), (17) and (18), while the second gradient energies, $g_{2,i}$, are given in (19) and (20). In what follows, we limit ourselves to boundary conditions involving free normal derivatives of the kinematical descriptors and, therefore, null double forces.

2.4 Geometry of the problem

A quadrilateral specimen with a ratio of 1:3 of the sides subjected to a bias extension test is considered, as indicated in the introduction. Figure 2 shows the geometry of the sample and the intrinsic coordinate system considered. The x-axis coincides with the longitudinal direction of the specimen.

Under our assumptions the displacement field of the specimen can be divided into seven subregions, $\varDelta _{00}$, $\varDelta _{01}$, $\varDelta _{10}$, $\varDelta _{23}$, $\varDelta _{32}$, $\varDelta _{33}$ and $\varDelta =\varDelta _{11}\cup \varDelta _{12} \cup \varDelta _{21}\cup \varDelta _{22}$ (Figs. 2a and 3c), in each of which the displacement field obtained by integration of the strain field attains a specific functional form. In regions $\varDelta _{00}$ and $\varDelta _{33}$ the deformation vanishes. This is experimentally verified by the simple extension test on a 3D-printed polymeric specimen (Fig. 3).

A limit condition exists corresponding to the situation where, in the central region, the relative rotation between the fibres becomes $\pi /2$. No further deformation is allowed beyond this point since the fibres overlap and cannot stretch. The displacement that corresponds to this limit condition can be evaluated through the first equation, Eq. (5), setting $\theta _1=\theta _2 = \pi /4$, and is found to be $u_{lim} = 2 \sqrt{2}(\sqrt{2}-1) = 0.82 \sqrt{2}$.

Fig. 2

Set-up of bias extension test: a geometry and subregions, b mesh (for $n_e=6$)

2.5 Boundary conditions

Indicating by ${\varvec{u}}$ the imposed displacement along the free short side of the specimen, and by $u_x={\varvec{u}}\cdot \mathbf{e }'_x$ and $u_y={\varvec{u}}\cdot \mathbf{e }'_y$ its components, the bias extension test corresponds to the case $u_x=u, u_y=0$. Using the first of expressions (5) the boundary condition becomes (Fig. 2a)

$$\begin{aligned} \int ^3_1{\mathrm {cos}}(\theta _1(\xi _1))\mathrm{d}\xi _1+\int ^3_1{\mathrm {sin}} (\theta _2(\xi _2))\mathrm{d}\xi _2 -2=\frac{u}{\sqrt{2}},\quad \int ^3_1{\mathrm {cos}}(\theta _2(\xi _2))\mathrm{d}\xi _2+\int ^3_1{\mathrm {sin}} (\theta _1(\xi _1))\mathrm{d}\xi _1-2 =\frac{u}{\sqrt{2}}, \end{aligned}$$

(22)

which represents two line integrals along the line defined by the two points $\{1,1\}$ and $\{3,3\}$ (the internal vertexes of the two rigid triangles $\varDelta _{00}$ and $\varDelta _{33}$). Concerning higher-order boundary conditions, on the short side on which the displacement is imposed, no condition is imposed on the normal derivative of the field $\theta _1$ and $\theta _2$, and therefore, according to the weak formulation of the problem, the corresponding double forces (i.e. the dual quantities of the normal derivative in the energy) are zero. For the same reason, on the free sides of the specimen, both the force and double force are assumed to be zero.

3 Numerical formulation

In this work we approach the problem as a constrained minimization in which the objective functional is expressed in terms of two discretized rotation fields, $\vartheta _1(\xi _1)$ and $\vartheta _2(\xi _2)$, characterizing the unit tangent vectors to the fibres. A quadrilateral mesh consistent with the ratio 1:3 of the geometry of the specimen is introduced. We consider a piece-wise constant ($P_0$-)interpolation for the two rotation fields $\vartheta _1(\xi _1)$ and $\vartheta _2(\xi _2)$ on the uniform quadrilateral mesh. The discretized values of the rotations are denoted by $\vartheta _{1,ij}$ and $\vartheta _{2,ij}$, with $i=1,\ldots ,n_e-1$ and $j=1,\ldots ,3n_e-1$ and $n_e$ the number of elements along the short side of the specimen. According to Rivlin’s representation, all the elements having the same value $\xi ^1$ (resp. $\xi ^2$) of the centroid coordinate have the same value for $\vartheta _2$ (resp. $\vartheta _1$), as represented in Fig. 3, where the element with zero rotation according to the boundary conditions is also shown.

Fig. 3

Assumed piece-wise constant interpolations of rotation fields according to Rivlin–Pipkin constraint: a $\theta _{1,ij}$, b $\theta _{2,ij}$, c $\varTheta _{ij}=\theta _{1,ij}+\theta _{2,ij}$

3.1 Gradients of rotations

Since a piece-wise constant interpolation (or $P_0$-interpolation) has been used, the gradients of the rotations cannot be directly evaluated. They have therefore been collocated in the vertices of the mesh, and we evaluate for each node i, j the gradients of the two scalar rotation fields as

$$\begin{aligned}&\left( \partial _{S_1}\vartheta _1\right) _{i,j}= \frac{\vartheta _{1,i\,j+1}-\vartheta _{1,i+1\,j}}{\sqrt{2} h_e},\quad \left( \partial _{S_2}\vartheta _2\right) _{i,j}= \frac{\vartheta _{2,i+1\,j+1}-\vartheta _{2,ij}}{\sqrt{2} h_e}, \end{aligned}$$

(23)

with $h_e=L/n_e$ the element side length, while the second gradient deformation was calculated as

$$\begin{aligned} \nabla E_{121}= \cos \left( \vartheta ^m_{1,ij}+\vartheta ^m_{2,ij}\right) \left( \partial _{S_1}\vartheta _1\right) _{i,j}, \end{aligned}$$

(24)

in which $\vartheta ^m_{1,ij}$ and $\vartheta ^m_{2,ij}$ are mean values evaluated by averaging the rotations in the four elements connected at the selected node, and $S_1$ is the arclength corresponding to the parametric abscissa $\xi _1$.

3.2 Constrained minimization problem

The discrete problem reduces to a constrained optimization in which the energy functional, which depends only on the angle of rotation fields, represents the objective function, with inequality constraints on the angle fields (the incompressibility conditions) and equality constraints for the imposition of the displacement at the free edge in terms of the rotation:

$$\begin{aligned}&\underset{(\vartheta _1,\vartheta _2)}{{\mathrm {min}}}\quad {\mathfrak {F}}\left( \vartheta _1,\vartheta _2,\frac{\partial \vartheta _1}{\partial \xi _1},\frac{\partial \vartheta _2}{\partial \xi _2}\right) \\&\qquad \end{aligned}$$

$$\begin{aligned} \begin{aligned}&{\mathrm{subject}\,\,\, \mathrm{to}:}\left\{ \begin{array}{lll} -1<\vartheta _{1,ij}+\vartheta _{2,ij}<1,&{}\quad {\mathrm {(Inequality\; Constraint)}}\\ l_e \overset{d_e}{\underset{h=1}{\sum }}\left( \cos (\vartheta _{1h}) +\sin (\vartheta _{2h})\right) -2=u/\sqrt{2},&{}\quad {\mathrm {(Equality \;Constraint)}}\\ l_e \overset{d_e}{\underset{h=1}{\sum }}\left( \cos (\vartheta _{2h}) +\sin (\vartheta _{1h})\right) -2=u/\sqrt{2},&{}\quad {\mathrm {(Equality\; Constraint)}}\end{array}\right. \end{aligned} \end{aligned}$$

(25)

A Newton method with an interior point constraint was used to solve the constrained minimization problem. The objective function is given by one of the expressions (15), (16), (17), (18) for the first gradient energy models and (19) or (20) for the second gradient energy models previously considered.

4 Numerical results

In this section we present and compare the results obtained with the energy models considered. The distribution of the rotation angles as well as the deformation of the specimen will be analysed. The deformation of the specimen undergoing a bias extension test reproduces the regions indicated in Fig. 2a. In the central part of the specimen, the rotations show a continuous variation, either increasing or decreasing, going from the centre of the specimen towards its fixed part. It will be shown that this variation characterizes the influence of the second gradient deformation on the solution; therefore, an indicator parameter is introduced (Fig. 4).

With reference to Fig. 5, we measure the variation in the angle between the fibre directions at points $\mathbf{p }$ and $\mathbf{c }$ located at the vertex of the fixed region $\varDelta _{00}$ and at the centre of the specimen, $\varDelta \vartheta _p=\frac{\pi }{2}- \left( \vartheta _1(\mathbf{p })+ \vartheta _2(\mathbf{p })\right)$ and $\varDelta \vartheta _c=\frac{\pi }{2}- \left( \vartheta _1(\mathbf{c })+\vartheta _2(\mathbf{c })\right)$, and we define as the indicator parameter the difference $\varDelta \vartheta _{pc}{:=} \varDelta \vartheta _c-\varDelta \vartheta _p$. It will be shown that in the case of a first gradient energy model the angle $\varDelta \vartheta _{pc}$ turns out positive, that is the total rotation at the centre of the specimen is smaller than at the vertex, and the opposite occurs for second gradient dominated solutions.

Fig. 4

Photograph of 3D-printed pantographic specimen under bias extension test. The regions $\varDelta _{00}$, $\varDelta _{01}$, $\varDelta _{10}$, $\varDelta _{23}$, $\varDelta _{32}$ and $\varDelta _{33}$ are highlighted (see also Fig. 2a). It is clear that the regions $\varDelta _{00}$ and $\varDelta _{33}$ are undeformed

Fig. 5

Indicator angles of deformation located at vertex of fixed region and of centre of specimen

4.1 First gradient energy models

To verify the ability of the numerical model to correctly represent the solution of the problem, a convergence analysis for the relative energy error was performed (considering an overkill solution as an exact solution), and its results are presented in Fig. 6, which refers to a value of the displacement $u_1=u_2=0.6$ for three different energy cases specified in Sect. 2.3 (shear, quadratic and quartic energy). The square of the energy error is reported against the mesh size h in a log-log plot. In any case, the rate of convergence reaches the expected rate of 2, with the same accuracy for all considered cases.

Fig. 6

Convergence analysis: square of relative energy error versus mesh size, h, for a quadratric, b quartic and c shear energy first gradient models

4.1.1 Shear energy model

First we analyse the results obtained using the quadratic energy in $\gamma$ (15). Plots of the relative rotation between the fibres $\vartheta _1+\vartheta _2$ for three different values of the end displacement are shown in Fig. 7. For any value of the displacement the total rotation exhibits sharp jumps corresponding to the boundaries of the regions represented in Fig. 2. In the two triangles next to the ends of the specimens, the rotations are zero; then two sets of discontinuity lines are found. The two fields $\vartheta _1$ and $\vartheta _2$ and their sum are also represented as contour plots in Fig. 8, in which the same scale is used for the three values considered for the displacement, i.e. $u_1=u_2=0.6, \sqrt{3}-1$ and 0.8 respectively. As appears from the plots, the rotation is not constant in the central region, so that the parameter $\varDelta \vartheta _{pc}$ indicating the difference in the rotation between points $\mathbf{p }$ and $\mathbf{c }$ (Fig. 5) is non-zero. It is interesting to examine more closely the results for the relative rotation of the central region of the specimen (given by $\varDelta _{11} \cup \varDelta _{12}\cup \varDelta _{21}\cup \varDelta _{22}$; see Fig. 2a) shown in Fig. 7. From Fig. 7a shows that for small values of the imposed displacement ($u_y<u_c=\sqrt{3}-1$), the relative rotation at the centre of the specimen (point C; see Fig. 5) is lower than the relative rotation at the boundary (point P; see Fig. 5). The contour plot of the relative angles is shown in Fig. 8a.

However, there exists a critical value of the end displacement component, $u_1=u_2=u_c=\sqrt{3}-1$, for which both rotation fields become piece-wise constant. This value corresponds to a change in the sign of $\varDelta \vartheta _{pc}$ (Fig. 7). For this value of the end displacement we find $\varDelta \vartheta _{pc}=0$ (Fig. 7b).

For large values of the imposed displacement the relative rotation at the centre becomes greater than the rotation at the boundary of the central region of the specimen. The change in the sign of the difference of these relative rotations is a characteristic trend only for the first gradient shear energy model.

The relative rotations $\varDelta \vartheta _p$ at point $\mathbf{p }$, the angle $\varDelta \vartheta _c$ at point $\mathbf{c }$ and their difference $\varDelta \vartheta _{pc}$ are plotted in Fig. 9 as a function of the imposed end displacement. It can be observed that for values of the displacement $u < u_c$ one has $\varDelta \vartheta _{pc}>0$, while for $u>u_c$ the indicator $\varDelta \vartheta _{pc}$ becomes negative. At the critical displacement the angle at the centre is equal to the angle at the vertex, and then $\varDelta \vartheta _{pc}=0$. As observed in [12], the configuration corresponding to the critical displacement value remains stable, but note that, in general, stability issues concerning systems with a complex microstructure can be difficult. Useful tools for studying such problems can be found, for example, in [65].

Fig. 7

First gradient shear energy model – relative rotation $\vartheta _{1,ij}+\vartheta _{2,ij}$ for the specimen 1:3 and $\alpha =1$ for several imposed displacements: a $u_1 = u_2 = 0.65 < u_c$, b $u_1 = u_2 = u_c = \sqrt{3}-1$, c $u_1 = u_2 = 0.8 > u_c$

Fig. 8

First gradient shear energy model – contour plots of rotations $\vartheta _{1,ij}$, $\vartheta _{2,ij}$ and $\vartheta _{1,ij}+\vartheta _{2,ij}$ (yellow contours represent greater values than green contours), for the imposed displacements: a $u_1 = u_2 = 0.65 < u_c$, b $u_1 = u_2 = u_c = \sqrt{3}-1$, c $u_1 = u_2 = 0.8 > u_c$

Fig. 9

First gradient shear energy model: indicator angle $\varDelta \vartheta _{pc}$ and rotations $\varDelta \vartheta _p$, $\varDelta \vartheta _c$ for specimen 1:3 with $\alpha =1$

4.1.2 Quadratic energy model

Plots of the relative rotation $\vartheta _1+\vartheta _2$ between the fibres for the values of the end displacement 0.65, $\sqrt{3}-1$ and 0.8 are presented in Fig. 10. The plots must be compared with those of Fig. 7. The constitutive parameter $\alpha$ is set at 1. Also, in this case, the rotation is discontinuous along the diagonals of the specimen. Contrary to the first gradient shear energy model, in this case there is no change in the sign of the difference between the angles of the fibres at the centre and at the vertex of the rigid triangle of the specimen.

Indeed, the indicator angle $\varDelta \vartheta _{pc}$ (Fig. 11a) is always positive for every value of the imposed displacement $u\in [0,0.8]$. By differentiating the computed energy with respect to the imposed displacement, we obtain the resulting reaction on the loaded side (Fig. 11b). This curve is characterized by a hardening effect due to the alignment of the inextensible fibres. As the displacement approaches the limit value $2(\sqrt{2}-1)$, the end reaction tends to diverge.

Finally, in Fig. 12, the deformed configurations for the imposed displacements 0.65, 0.73 and 0.8 are shown. The central part of the specimen gets thinner and thinner, while its boundaries remain straight.

Fig. 10

First gradient quadratic energy model – relative rotation $\vartheta _{1,ij}+\vartheta _{2,ij}$ for specimen 1:3 with $\alpha =1$ for imposed displacements: a $u_1=u_2=0.65$, b $u_1=u_2=\sqrt{3}-1$, c $u_1=u_2=0.8$

Fig. 11

First gradient quadratic energy model: a indicator angle $\varDelta \vartheta$ and angles $\varDelta \vartheta _p$, $\varDelta \vartheta _c$, b force–displacement curve

Fig. 12

First gradient quadratic energy model – deformed configurations for imposed displacement: a $u_1 = u_2 = 0.65$, b $u_1 = u_2 = \sqrt{3}-1$, c $u_1 = u_2 = 0.8$

4.1.3 Quartic energy

The quartic energy density $g_{1,3}$ is considered next. As was observed at the end of Sect. 2.3, while the quadratic energy can be viewed as a truncated power series expansion of the energy quadratic on the shear, the quartic energy simulates a different network behaviour. Despite this, the results of the simulation are very similar to the those in the previous case, as shown by the plot of the relative rotations presented in Fig. 13.

The indicator angle $\varDelta \vartheta _{pc}$ also remains in this case always positive (Fig. 14a). Moreover, Fig. 15 proves that also for any combination of the quadratic and quartic energy modes, model $g_{1,3}$, the indicator angle $\varDelta \vartheta _{pc}$ does not change signs. The black line in the plot corresponds to the values $\alpha _1=1$ and $\alpha _2=1$.

Figure 14b summarizes the force–displacement curve obtained for the first gradient models examined. Again, the quartic energy model gives a different response than the other two.

Fig. 13

First gradient quartic energy model – relative rotation, $\vartheta _{1_ij}+\vartheta _{2,ij}$, for free end displacement $u_1 = u_2 = 0.8$

Fig. 14

First gradient quartic energy model: a indicator angle $\varDelta \vartheta _{pc}$ and angles $\varDelta \vartheta _p$, $\varDelta \vartheta _c$, b force–displacement curves

Fig. 15

Quartic and quadratic first gradient energy models – indicator angle $\varDelta \vartheta _{pc}$ for several $\{\alpha _1,\alpha _2\}$ constitutive parameters

In conclusion, for all the first gradient models considered, the distribution of the rotation is discontinuous. Only with the shear energy model is a change in the sign of $\varDelta \vartheta _{pc}$ in the deformation for a critical displacement $u_c$ observed.

4.2 Pure second gradient energy models

In this section we examine the results for the bias extension test in the case where the energy of the material is completely governed by the second gradient deformation. The model relates to the case where no energy is associated to the shear deformation between fibres, and the internal energy is completely due to the bending deformation that arises in them. The main effect would be to regularize the discontinuities found in the deformation of the sheet with the first order energy models.

The rate of convergence of the square of the energy error for the second gradient model is lower than for the first gradient model (Fig. 16), since a $P_0$-interpolation for the rotations was used, and the second gradient deformations were obtained using a collocation procedure. As a consequence, the accuracy level obtained in the present case is also smaller than in the previous first gradient case. As for the two different second gradient energies $g_{2,1}$ and $g_{2,2}$, the accuracy level is the same (Fig. 17).

Fig. 16

Convergence analysis: square of relative energy error versus mesh size, h, for a quadratric and b shear energy second gradient models

It is well known that in second gradient models a characteristic length determines the thickness of the boundary layer. In the presented numerical simulation, we selected a mesh size h fine enough to accurately describe this phenomenon, i.e. much smaller than the observed boundary layer. As is clear from a comparison between Fig. 18b and c, a coarse mesh is not able to reproduce the onset of boundary layers without significant jumps. For a detailed discussion of the theoretical prevision of the thickness of the boundary layer in this type of structure, see [66].

4.2.1 Second gradient shear energy (S-model)

The expression $g_{2,1}$ of the deformation energy is considered for this model. The plots of the relative rotations $\varDelta \vartheta _{ij}$ for free end displacements of 0.4, 0.6 and 0.8, presented in Fig. 18a–c respectively, show that in this case the solution does not present discontinuities in the distribution of the deformation (Fig. 19). The deformation of the long side is not straight, and smooth transition zones appear between the different regions. A neck clearly appears in the central part of the specimen. For values of the imposed displacement between 0.6 and 0.8, the relative rotation of the fibres in the neck reaches a limit value of $\pi /2$, so that the width of the specimen cannot be reduced any further. The phenomenon recalls the familiar necking in ductile plastic materials whose deformation is driven exclusively by shear.

The latter phenomenon can also be observed from the plot of Fig. 17a, where the results of the model $g_{2,1}$ are indicated by solid thick lines. It can be observed that the relative rotation at the centre of the specimen reaches its limit value for an end displacement around 0.7.

Fig. 17

Pure second gradient energy models (with $\beta =1$): a indicator angles $\varDelta \vartheta _p$, $\varDelta \vartheta _c$ and the difference $\varDelta \vartheta _{pc}$. (Thick line: second gradient shear model, thin line: second gradient quadratic model); b force–displacement curves

Fig. 18

Pure second gradient shear energy model (with $\beta =1$): relative rotations $\vartheta _{1,ij}+\vartheta _{2,ij}$ for several imposed displacements: a $u_1 = u_2 = 0.4$, b $u_1 = u_2 = 0.6$, c $u_1 = u_2 = 0.8$

Fig. 19

Pure second gradient shear energy model (with $\beta =1$) – reference and deformed configurations for several imposed displacements: a $u_1 = u_2 = 0.4$, b $u_1 = u_2 = 0.6$, c $u_1 = u_2 = 0.8$

4.2.2 Second gradient quadratic energy (Q-model)

The energy functional is given in this case by the expression $g_{2,2}$. Also, in this case, there are no discontinuities in the rotation field, but the transition is less smooth than in the previous case, as can be observed from Fig. 20, where the scalar field $\varDelta \vartheta _{ij}$ for three values of the free end displacement is shown. With respect to the model $g_{2,1}$, smaller deformations are obtained, as can be observed in Fig. 17a, where the relative angles at points $\mathbf{c }$ and $\mathbf{p }$ for the presented model are indicated by solid thin lines. However, even in this case, in the central part of the specimen, the limit relative rotation $\varDelta \theta =\pi /2$ is reached (Fig. 20c), although at a value of the end displacement greater than in the case of the energy based on the gradient of the shear.

The plot of the reaction vs. the end displacement is presented in Fig. 17b for both second gradient models. For comparison, the results obtained for the first order models are also reported. The second gradient solution is characterized by the same initial stiffness as the first gradient solution, but the stiffness of the specimen strongly increases for the highest values of the displacement, while in the first gradient solution there is a sharper transition to the asymptotic value.

Fig. 20

Pure second gradient quadratic energy model (with $\beta =1$) – relative rotation $\vartheta _{1,ij}+\vartheta _{2,ij}$ for several imposed displacements: a $u_1 = u_2 = 0.4$, b $u_1 = u_2 = 0.6$, c $u_1 = u_2 = 0.8$

4.3 First and second gradient energy models

In this subsection, combinations of the first and second gradient energy models are considered, with the aim of analysing the influence of the second gradient regularization on the solution of the bias extension test. The following four cases are examined:

• Model (SS): First gradient shear energy with second gradient shear energy:

  $$\begin{aligned} {\mathfrak {F}}_{SS}=\int _B (\alpha \, g_{1,1}+\beta \, g_{2,1}) \mathrm{d}B; \end{aligned}$$

• Model (QQ): First gradient quadratic energy with second gradient quadratic energy:

  $$\begin{aligned} {\mathfrak {F}}_{QQ}=\int _B (\alpha \, g_{1,2}+\beta \, g_{2,2}) \mathrm{d}B; \end{aligned}$$

• Model (SQ): First gradient shear energy with second gradient quadratic energy:

  $$\begin{aligned} {\mathfrak {F}}_{SQ}=\int _B (\alpha \, g_{1,1}+\beta \, g_{2,2}) \mathrm{d}B; \end{aligned}$$

• Model (QS): First gradient quadratic energy with second gradient shear energy:

  $$\begin{aligned} {\mathfrak {F}}_{QS}=\int _B (\alpha \, g_{1,2}+\beta \, g_{2,1}) \mathrm{d}B. \end{aligned}$$

The parameters $\alpha$ and $\beta$ are used as weights. Notice that changing the weights but leaving their ratio constant does not modify the deformation of the sheet for a given end displacement, only the reaction changes. Therefore, in what follows, only the deformation obtained with the four models is investigated, while the force–displacement relation is not reported.

The deformation of the specimen relative to the free end displacement $u_1=u_2=0.6$ for model SS are shown in Fig. 21. In each figure, six cases are considered, namely the first gradient energy model, the combinations $(\alpha =50, \beta =1), (\alpha =25, \beta =1), (\alpha =5, \beta =1), (\alpha =1, \beta =1)$, and the pure second gradient energy model. In the case of model QQ the deformed configurations are qualitatively the same but for the same values of the considered weights present a smaller necking effect with respect to model SS.

The transition from the second gradien–dominated deformation, with a smooth continuous variation of the rotations between the parts of the specimen characterized by different regimes, to the first gradient–dominated deformation, with sharp discontinuities along the borders of the different regions of the specimen, is apparent in both cases. It can be observed that the second gradient has a strong regularizing effect, the first order solution with sharp transitions being recovered only when the weight $\alpha$ is at least one order of magnitude greater than $\beta$.

In the following paragraphs, for the four cases considered, the rotation fields $\vartheta _{1,ij}+\vartheta _{2,ij}$ are reported. They are calculated for the end displacement $u_1=u_2=0.6$ and for three values of the weights. The differences among the energy models are better understood by examining the indicator angles $\varDelta \vartheta _c, \varDelta \vartheta _p$ and their differences, which relate to the deformation of the central section of the specimen, i.e. the one that presents greater differences in the numerical experiments performed.

Fig. 21

Reference and deformed configurations for SS model: transition from second to first gradient energy model for imposed displacement $u_1=u_2=0.6$ for several values of constitutive parameters $\alpha$ and $\beta$: a $\alpha =0$, $\beta =1$; b $\alpha =1$, $\beta =1$; c $\alpha =5$, $\beta =1$; d $\alpha =25$, $\beta =1$; e $\alpha =50$, $\beta =1$; f $\alpha =1$, $\beta =0$

4.3.1 First and second gradient quadratic energy: QQ-model

Figure 22 shows the relative angle of rotation for the cases $(\alpha =5, \beta =1)$ and $(\alpha =50, \beta =1)$, enlightening the existence of boundary layers among the regions of the specimen, whose width reduces as the weight of the first gradient energy increases.

It is interesting to examine the plots of the indicator angles, reported in Fig. 23 grouped in three ranges: the second gradient–dominated range, the transition range and the first gradient–dominated range. In the second gradient–dominated range, characterized by the weights $\beta \gg \alpha$, the second gradient energy predominates, so that smooth boundary layers are observed, and the angle $\varDelta \vartheta _p$ at the corner of the fixed zone of the specimen is always grater than the angle $\varDelta \vartheta _c$ at the centre of the specimen, that is, the centre of the specimen deforms more than the extremities, so that the difference $\varDelta \vartheta _{pc}$ is always negative (Fig. 23a). In the transition range, the weights have comparable values (actually $\alpha$ is one order of magnitude greater than $\beta$), $\varDelta \theta _{pc}\approx 0$, the two angles become comparable, and there is an inversion in the sign of $\varDelta \vartheta _{pc}$ (Fig. 23b). In the third first gradient–dominated range, $\alpha \gg \beta$, and the indicator angle $\varDelta \theta _{pc}$ becomes positive (Fig. 23c). In no case does the latter angle show a change of sign during the elongation.

Fig. 22

First gradient quadratic energy with second gradient quadratic energy (QQ model) – relative rotation $\vartheta _{1,ij}+\vartheta _{2,ij}$ for fixed displacement $u_1=u_2=0.6$ and $\beta =1$ for the two values of $\alpha$ parameter: a $\alpha =5$, b $\alpha =50$

Fig. 23

Indicator angles for QQ model: a second gradient–dominated range $\alpha =1, \beta =10^2$; b transition range $\alpha =50, \beta =1$; c first gradient–dominated range $\alpha =10^3, \beta =1$

4.3.2 First and second gradient shear energy: SS-model

Analogously to the previous case, Fig. 24 shows the rotation field $\varDelta \vartheta _{ij}$ for the same values of $\alpha$ and $\beta$ and for the same displacement previously considered. The solution in the proximity of the borders of the regions presents a more regular character with respect to the previous case. That is, the shear energy appears to have a greater regularizing effect with respect to the quadratic energy.

Fig. 24

First gradient shear energy with second gradient shear energy (SS model) – relative rotation $\vartheta _{1,ij} +\vartheta _{2,ij}$ for the fixed displacement $u_1=u_2=0.6$ and $\beta =1$ for the two values of the $\alpha$-parameter: a $\alpha =5$, b $\alpha =50$

The indicator angles are examined in Fig. 25 for the same combination of weights used in the case of model QQ. In this case for $\beta > \alpha$ not only is $\varDelta \vartheta _{pc}$ always negative (Fig. 25a), but in addition the angle at the centre of the specimen $\varDelta \vartheta _c$ becomes zero when the end displacement is between 0.6 and 0.7, indicating that the fibres at the centre are getting aligned. In the transition range $\varDelta \vartheta _c$ is still negative, even though the angle at the centre $\varDelta \vartheta _c$ does not become zero (Fig. 25b). In the first gradient–dominated range $\varDelta \vartheta _{pc}$ first changes its sign, and then the first order solution for which $\varDelta \vartheta _{pc}$ goes through the zero is recovered (Fig. 25c).

Fig. 25

Indicator angles for SS model: a second gradient–dominated range $\alpha =1, \beta =10^2$; b transition range $\alpha =50, \beta =1$; c first gradient–dominated range $\alpha =1, \beta =10^3$

4.3.3 Shear first gradient energy with quadratic second gradient energy: SQ model

The rotation fields are reported in Fig. 26. The indicator angles $\varDelta \vartheta _p$ and $\varDelta \vartheta _c$ and their difference are represented in Fig. 27a–c, analogously to what was done earlier. In this case, either in the second gradient–dominated range and in the transition range the angle at the centre $\varDelta \vartheta _c$ is always smaller than $\varDelta \vartheta _p$, but the difference is smaller than in the previous case (model SS). In the first gradient–dominated range, the two angles overlap, and the difference $\varDelta \vartheta _{pc}$ changes its sign during the evolution of the test, as was observed in model S with shear first gradient energy. In comparison with model SS it appears, then, that the quadratic second gradient energy has less of an ability to regularize the solution than the second gradient shear energy.

Fig. 26

First gradient shear energy and second gradient quadratic energy (SQ model) – relative rotation $\vartheta _{1,ij}+\vartheta _{2,ij}$ for fixed displacement $u_1=u_2=0.6$ and $\beta =1$ for two values of $\alpha$-parameter: a $\alpha =5$, b $\alpha =50$

Fig. 27

Indicator angles for SQ model: a second gradient–dominated range $\alpha =1, \beta =10^2$; b transition range $\alpha =50, \beta =1$; c first gradient–dominated range $\alpha =10^3, \beta =1$

4.4 Quadratic first gradient with shear second gradient energy: QS model

The situation is similar to that of the SS model, for the second gradient–dominated range (see Fig. 28 for the values of the rotations and Fig. 29a–c for the indicator angles). As for the second gradient shear energy model, the angle at the centre of the specimen reduces to zero for a value of $u_1=u_2$ between 0.6 and 0.7. In the transition range, $\varDelta \vartheta _{pc}$ is always negative and changes its sign only for the highest values of $\alpha$ but, contrary to the previous case, never becomes zero during the elongation.

Fig. 28

Quadratic first gradient energy and shear second gradient energy (QS model) – relative rotation $\vartheta _{1,ij} +\vartheta _{2,ij}$ for fixed displacement $u_1=u_2=0.6$ and $\beta =1$ for two values of $\alpha$-parameter: a $\alpha =5$, b $\alpha =50$

Fig. 29

Indicator angles for QS model: a second gradient–dominated range $\alpha =1, \beta =10^2$; b transition range $\alpha =50, \beta =1$; c first gradient–dominated range $\alpha =10^3, \beta =1$

Fig. 30

Comparison of distribution of $\vartheta {ij}= \vartheta 1_{ij}+\vartheta 2_{ij}$ for displacement $u_1=u_2=0.6$ and $\beta =1$ for several increasing values of $\alpha =5,25$ and $\alpha =50$ for the four first and second gradient energy models – QQ model: a $\alpha =5$, b $\alpha =25$, c $\alpha =50$; SS model: d $\alpha =5$, e $\alpha =25$, f $\alpha =50$; SQ model: g $\alpha =5$, h $\alpha =25$, i $\alpha =50$; QS model: j $\alpha =5$, k $\alpha =25$, l $\alpha =50$

5 Conclusions

The deformation of a sheet of woven fabrics composed of two sets of orthogonal inextensible fibres was numerically analysed. To intrinsically enforce the inextensibiity constraint, the rotations of the fibres were used as degrees of freedom of the model. An intrinsic reference frame was introduced, with the axes running in the directions of the two families of inextensible fibres. Using Pipkin’s result stating that the deformation field can be decomposed into the sum of two functions, each one depending only on one of the intrinsic coordinates, an expression for the boundary conditions in terms of the rotation fields was furnished. The problem was then formulated as a constrained minimization, with equality constraints enforcing the considered boundary conditions. A suitable piece-wise constant interpolation of the two independent rotation fields was used.

Three classes of cases were analysed, namely models with energy depending only on the first gradient deformation (which actually reduces to the shear between the fibres), models whose energy depends only on the second gradient deformation, and mixed models. It was shown that the results obtained with first gradient models reproduce the theoretical deformation field, which presents lines of discontinuity on the rotations. The energy based on a second gradient deformation has the effect of regularizing the solution, spreading the jump in the values of the rotations over a layer whose width depends on the model used. The regularization can be adjusted using mixed models.

The relative rotation $\varDelta \vartheta _{ij}=\vartheta _{1,ij}+\vartheta _{2,ij}$ obtained with the mixed models examined in Sect. 4.3 relative to the free end displacement $u_1=u_2=0.6$ and for three values of the weight $\alpha$ are compared in Fig. 30. Two observations can be made. The transition between the different zones of the specimen becomes increasingly sharper as the parameter $\alpha$ grows, that is, as the first gardient energy becomes dominant. For comparison, Fig. 26 relative to the first gradient shear energy should be examined.

The second observation is that the various models trested mainly differ in the deformation pattern obtained in the central zone of the specimen. As observed earlier, only in models where the first gradient shear energy dominates is there a change in the sign of $\varDelta \theta _{pc}$ in the plot of the rotations in the central region. This can be observed from Fig. 31, which collects the results for the indicator angles for most of the models examined.

These observations appear to be of great relevance for the experimental characterization of the internal energy of woven composites with a simple bias extension test. More complex cases, involving more general external actions, a richer geometry of the reference configuration or the generalization to 3D homogenized continua formed by inextensible fibres, will probably require suitably refined numerical tools, such as, for instance, isogeometric analysis or enriched finite-element analysis, such as those used in [67–71] and [67, 72, 73].

Fig. 31

Comparison of indicator angles for several energy models: a second gradient–dominated range, b transition range, c first gradient–dominated range

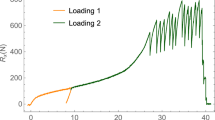
Finally, the systematic experimental study of the considered structures is of course crucial for further progress. Experimental studies on the subject are carried out in [74], and new comparisons of the obtained numerical results with experimental ones will be analysed in future works.