An efficient uncertainty quantification and propagation method through skewness and kurtosis fitting region

Abstract

Traditional methods for structural uncertainty problems with nonconventional distributions involve a significant computational burden, attributed to the nonlinear increase of structures incurred by the transformation of variables to conventional distributions. To solve the above problem, in this study, a derivative lambda probability density function (λ-PDF) is proposed for quantifying the uncertainties in a unified framework. Furthermore, an efficient uncertainty propagation approach for complex structures based upon the improved derivative λ-PDF and dimension reduction method (DRM) is developed. Firstly, the uncertainties of random variables with large skewness and kurtosis are quantified by the improved derivative λ-PDF. Secondly, the n-dimensional structural model is decomposed into a sum of several subsystems. Next, the first-four moments of structural responses are derived using the DRM and Gaussian-weighted integral. Finally, the probability density function and cumulative distribution function of structural responses are reconstructed to quantify their uncertainties by the improved derivative λ-PDF. Six demonstrative examples are engaged to illustrate the effectiveness and accuracy of the proposed method. Reference methods, such as Monte Carlo simulation, the maximum entropy method, the Edgeworth series expansion, and the shifted generalized lognormal distribution, are engaged as calibers to demonstrate the superiority of the proposed method.

1 Introduction

In practical engineering, uncertainties intrinsic in geometric dimensions, physical parameters, and material properties are inevitable in the processes of structural designing, manufacturing, and assembling (McKeand et al. 2021; Xu et al. 2020). With the ever-increasing structural complexity and accuracy in the modern industries, the uncertainties in structures are increasing exponentially, which should be addressed appropriately in the design process to warrant the robustness, reliability, and safety of complex structures (Jiang et al. 2020). In general, uncertainties can be classified into epistemic and aleatory uncertainties (Chen et al. 2021). Epistemic uncertainty is caused by the lack of information, which can be reduced by inferences to relevant knowledge or data. Aleatory uncertainty refers to the inherent uncertainties in the structure during the manufacturing and assembling processes due to nonperfectly accurate geometric or material parameters (Hu and Mahadevan 2017). To carry out uncertainty propagation analysis of complex structures, the most critical step is to quantify the uncertainties of structures. For this reason, a series of uncertainty models have been developed (Liu et al. 2018a).

The nonprobabilistic models have achieved significant advances recently due to their simplicity in modeling and independence from massive prior information (Wu et al. 2019), which mainly include evidence theory (Wang 2019), convex models (Jiang et al. 2019), fuzzy sets (Wang et al. 2019b), etc. The nonprobabilistic models require few samples to specify uncertainties, which are often used for the modeling of epistemic uncertainties (Long et al. 2019). However, the small sample size makes it impossible to derive accurate statistical data and function curve of structural response. The probabilistic models are the most commonly applied uncertainty quantification models due to their solid theoretical groundwork (Acar et al. 2021). In the probabilistic models, the uncertain parameters are characterized as random variables with different probability distributions, such as normal distribution, lognormal distribution, Weibull distribution, and extreme value distribution. The precise statistical data, such as probability density function (PDF), cumulative distribution function (CDF), and statistical moments, can be acquired via sufficient samples (Wang and Matthies 2020). A series of probability distribution models have been developed, which can reliably define the distribution of uncertainties and effectively approach the uncertainty propagation process, such as saddlepoint approximation (SPA) (Huang and Du 2006), maximum entropy method (MEM) (He et al. 2022, 2019), Edgeworth series expansion (EWE) (Kolassa and Kuffner 2020; Zhao and Zhang 2014), shifted generalized lognormal distribution (SGLD) (Xu and Dang 2019), and generalized lambda distribution (Acar et al. 2010).

Various methods have been developed for uncertainty propagation analysis of complex structures based on probabilistic models, which can be grouped into four categories. (1) The first category is the sampling-based methods, in which the typical methods are Monte Carlo simulation (MCS) (Alban et al. 2017), Latin hypercube sampling (Helton et al. 2005), and importance sampling (Zhang et al. 2020). In general, when the number of samples is large enough, the results obtained by this category of methods are approaching the theoretical results at infinity. However, large samples result in high computational costs and low efficiency, which limits its application in complex engineering problems. Consequently, the sampling-based methods are often used as caliber to demonstrate the effectiveness and accuracy of other uncertainty propagation analysis methods. (2) The second category is the most probable point (MPP)-based methods, which has been verified to be an efficient uncertainty propagation approach. The most representative methods are the first-order reliability method (FORM) (Li et al. 2018) and the second-order reliability method (SORM) (Park and Lee 2018). The limitation of MPP-based methods is that they involve multiple iterations to search MPPs of structural performance functions. And multiple MPPs may be targeted in one iteration process, which leads to intractable computational intensity frequently (Meng et al. 2018). (3) The third category is the surrogate model-based methods. This category of methods establishes an explicit surrogate model through design experiments to specify implicit or complex performance functions. The proficiency of this category method depends on the appropriate selection of the surrogate models and the associated parameters (Zhang et al. 2022). At present, the prevailing surrogate models mainly include the Kriging method (Xiao et al. 2020; Zhang et al. 2019), radial basis function network (Zhang et al. 2021a), response surface method (Huang et al. 2017), and polynomial chaos expansion (Wang et al. 2019a). (4) The last category of uncertainty propagation methods is moment-based methods. This category of methods recreates PDF through statistical moments of the system response, including integer-order and fractional-order moment-based methods (Liu et al. 2018b; Zhang et al. 2021b). Once the statistical moments of structural response are obtained by the moment propagation methods, the corresponding PDF of the performance function can be directly generated through the probability distribution evolution methods.

The application of moment-based methods can be divided into two steps including the derivation of the propagation of statistical moments and the reconstruction of structural response’s PDF. Among the prevailing moment propagation methods, the univariate dimension reduction method (UDRM) (Huang and Du 2006; Rahman and Xu 2004) is the most representative to display excellent efficiency and robustness when analyzing multivariate uncertainty problems (Zhou and Peng 2020). It decomposes an multi-dimensional system model into multiple one-dimensional subsystems and approximates the moments of the original multi-dimensional structure via the moments of each subsystem (Rahman and Xu 2004). On the other hand, UDRM may not be necessarily adequate for analyzing uncertainties in a highly nonlinear system. To improve the accuracy, Xu and Rahman (2004) proposed a generalized DRM to decompose the n-dimensional system into a sum of at most s-dimensional subsystems ($s \le n$). The accuracy of DRM with regard to moment estimation and uncertainty propagation was enhanced substantially by considering a high value of s. Nevertheless, the computational intensity increased significantly with the increasing input dimensions. Thus, it is critical to specify an appropriate s to ensure a balance between accuracy and efficiency. Huang and Du (2006) calculated the statistical moments of structural response via the bivariate dimension reduction method (BDRM) and Gaussian-weighted integrals (GWI), and improved simultaneously the accuracy and efficiency of uncertainty analysis. Xu and Zhou (2020) presented an adaptive trivariate dimension reduction method (TDRM) combining GWI for statistical moment estimations, and achieved the well trade-off balance between efficiency and accuracy of DRM. The second step recovers the PDF by probabilistic approximation methods, also known as probability distribution models, which construct unified functional forms with unknown parameters. The statistical moments of the structural response are used to determine these unknown parameters, and the derived specific function is considered as PDF of the original structural response. The typical methods are saddlepoint approximation (SPA), maximum entropy method (MEM), Edgeworth series expansion (EWE), shifted generalized lognormal distribution (SGLD), and generalized lambda distribution. Each of these methods has its merits and demerits (Zhou and Peng 2020). For example, SPA can obtain accurate probability estimation of calculated responses in the tail region, but singularity problems often occur during the numerical calculation (Huang and Du 2006). Zhang and Han (2020) evaluated the positional accuracy of robotic manipulators based on the DRM and SPA, and efficiently and accurately estimated the kinematics reliability of industrial robots. The MEM shows good performance in PDF modeling for the high and low reliability levels when the skewness is relatively high, but the inherent exponential form limits its application (Xi et al. 2012). Yun et al. (2019) proposed a novel approach to estimate the moment-independent global sensitivity combined with DRM and MEM, reducing the computational cost remarkably. EWE has the advantages of rapid convergence and reduced computational intensity to estimate PDFs of complex structures (Wang et al. 2020). Shi et al. (2018) proposed an effective method based upon the high-order moment standardization technique and EWE, improving the accuracy when analyzing uncertainties with high nonlinearity. SGLD is flexible in shape, reaches almost all the kurtosis–skewness regions achievable by the unimodal distributions, and provides high accuracy in the tail fitting. Xu and Dang (2019) presented a novel BDRM for moment evaluations and reconstructed PDF of the performance function using SGLD with sufficient accuracy and efficiency. The generalized lambda distribution is only applicable to the approximation of the single peak distribution with medium or low reliability levels (Acar et al. 2010). Liu et al. (2018b) presented a general frame combined with UDRM and derivative lambda probability density function (λ-PDF), which could represent arbitrary mono-peak PDF accurately when their kurtosis–skewness points are located in the fitting region.

However, most of the aforementioned methods are not straightforward to implement the structural uncertainty propagation analysis with large skewness and kurtosis. It is because the values of skewness and kurtosis may span large ranges due to the high complexities of parameters and the derived forms of λ-PDF. Various derivative forms result in different ranges of the derived thresholds. For instance, Liu et al. (2018b) adopted the derivative λ-PDF in the form of power functions to achieve a closed fitting region consisted of kurtosis–skewness points. However, it was complicated to precisely process the uncertain parameters beyond this closed fitting region. In view of that, an improved derivative λ-PDF is suggested in the form of coupled exponential and power functions in this study. Firstly, the improved derivative λ-PDF is utilized for constructing uncertainty models of the input random variables, whose kurtosis–skewness points locate in the fitting region. DRM is then used to decompose the n-dimensional structure model into a sum of several low-dimensional subsystems. GWI is applied to compute directly the multi-dimensional integrations to calculate the statistical moments of structure response. The improved derivative λ-PDF is subsequently employed to reconstruct PDF and CDF of structure response to realize the uncertainty propagation. The improved λ-PDF expands the fitting region, enhances the applicability of the derivative λ-PDF method and compensates the insufficiency of the aforementioned methods in analyzing the uncertainties of complex structures with large skewness and kurtosis.

The remainder of this paper proceeds as follows: Sect. 2 briefs the probabilistic tools and inadequacies in the currently prevailing uncertainty propagation methods, especially when considering large skewness and kurtosis. Section 3 reviews the relatable derivative λ-PDF methods to frame comprehension of the current study. Section 4 exposits the currently proposed uncertainty propagation analysis method in detail. Section 5 implements six examples to demonstrate the effectiveness and accuracy of the currently proposed method from various perspectives. Section 6 and Sect. 7 discuss and conclude this study.

2 Problem statement

Assuming that there is a structure with n-dimensional vectorized input random variables ${\mathbf{X}} = \left[ {X_{1} , \, X_{2} {, } \ldots { , }X_{n} } \right]^{{\text{T}}}$, where all the random variables X_i are statistically independent, the performance function of the structure can be expressed as (Liu et al. 2018b)

$$ Z = g\left( {\mathbf{X}} \right) = g\left( {X_{1} , \, X_{2} {, } \ldots { , }X_{n} } \right), $$

(1)

where $g\left( {\mathbf{X}} \right)$ represents the performance function of $X_{i}$ with respect to Z.

The probabilistic uncertainty propagation analysis is to estimate CDF, PDF, and statistical moments of Z with the given probability distributions of independent variables X. CDF of Z at z can be calculated through a multi-dimensional integral (Huang and Du 2006)

$$ F_{Z} \left( z \right) = P\left\{ {Z \le z} \right\} = \int_{{g\left( {\mathbf{X}} \right) \le z}} \cdots \int {f_{{\mathbf{X}}} } \left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}, $$

(2)

where $f_{{\mathbf{X}}} ({\mathbf{x}}) = f_{{X_{1} }} (x_{1} )f_{{X_{2} }} (x_{2} ) \cdots f_{{X_{n} }} (x_{n} )$ is the joint PDF of random variables X.

The moment-based methods reconstruct PDF and CDF of the structural response via finite-order statistical moments. The lth-order raw moment of the structural response can be estimated by (Liu et al. 2018b)

$$ M_{l} = \int_{ - \infty }^{ + \infty } {\left[ {g\left( {\mathbf{X}} \right)} \right]^{l} f_{{\mathbf{X}}} \left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}}. $$

(3)

The first-four center moments of the structural response can be obtained as (Liu et al. 2018b)

$$ \left\{ \begin{gathered} D_{1} = M_{1} \hfill \\ D_{2} = M_{2} - M_{1}^{2} \hfill \\ D_{3} = M_{3} - 3M_{2} M_{1} + 2M_{1}^{3} \hfill \\ {\kern 1pt} D_{4} = M_{4} - 4M_{3} M_{1} + 6M_{2} M_{1}^{2} - 3M_{1}^{4} \hfill \\ \end{gathered} .\right. $$

(4)

And then the mean, standard deviation, skewness, and kurtosis of the structural response can be written as (Liu et al. 2018b)

$$ \left\{ \begin{gathered} \mu = D_{1} \hfill \\ \sigma = \sqrt {D_{2} } \hfill \\ C_{s} = {{D_{3} } \mathord{\left/ {\vphantom {{D_{3} } {\left( \sigma \right)^{3} }}} \right. \kern-0pt} {\left( \sigma \right)^{3} }} \hfill \\ C_{k} = {{D_{4} } \mathord{\left/ {\vphantom {{D_{4} } {\left( \sigma \right)^{4} }}} \right. \kern-0pt} {\left( \sigma \right)^{4} }} \hfill \\ \end{gathered}. \right. $$

(5)

To prevent the intractable computational intensity incurred by the direct integration method to calculate the joint PDF of a highly nonlinear system with multi-dimensional variables, PDF approximation methods based upon the acquired statistical moments are developed. PDFs and CDFs of structural responses are reconstructed accurately and efficiently. In addition, the traditional PDF approximation methods usually ensue unsatisfactorily low accuracy for uncertainty propagation analysis in complex structures with large skewness and kurtosis. Therefore, a general probabilistic method for uncertainty quantification and propagation through improved skewness and kurtosis fitting region is proposed in this study.

3 Referenced derivative λ-PDF method

The PDF reconstruction is an integral step of the moment-based approach. As mentioned above, a series of PDF approximation methods have been developed. Among them, the maximum entropy method (MEM), the Edgeworth series expansion (EWE), the shifted generalized lognormal distribution (SGLD), and the referenced derivate λ-PDF method are adopted as calibers in this study to verify the effectiveness and accuracy of the currently proposed method for analyzing uncertainties in complex structures with high skewness and kurtosis. To facilitate the comprehension of the current study, the basic implementation procedures for the referenced derivate λ-PDF method are briefed in this section.

The λ-PDF represents a family of PDF, which can be expressed as follows (Liu et al. 2018b)

$$ f_{{\uplambda }} \left( z \right) = \left\{ {\begin{array}{ll} {\kappa \left( {1 - z^{2} } \right)^{{{\uplambda } - 0.5}} } & {\left| z \right| < 1} \\ 0 & {\left| z \right| \ge 1} \\ \end{array} } \right., $$

(6)

where z denotes random variable; λ is positive and controls the shape of $f_{{\uplambda }} \left( z \right)$.

The normalization factor κ can be expressed as follows

$$ \kappa = \frac{{\Gamma \left( {{\uplambda } + 1} \right)}}{{\Gamma \left( {0.5} \right)\Gamma \left( {{\uplambda } + 0.5} \right)}}, $$

(7)

wherein $\Gamma \left( \cdot \right)$ indicates gamma function.

The λ-PDF can be utilized to describe the distribution of z by selecting appropriate value of λ. However, the variables are restricted to the interval of [–1, 1] and are symmetric with respect to $z = 0$. As a result, the original method can only approximate a limited number of symmetric PDFs. To eliminate this limitation, a quadratic polynomial function can be applied

$$ v = h\left( z \right) = \delta_{0} + \delta_{1} z + \delta_{2} z^{2}, $$

(8)

where $h\left( z \right)$ is a function of variable z; $\delta_{i}$$\left( {i = {0, 1, 2}} \right)$ denote the coefficients of the polynomial. Thus, v can be extended to any interval and asymmetric probability distributions via determining appropriate coefficients. Besides, the curves do not exhibit a monotonic trend due to the nonlinear characteristics of quadratic polynomials. To guarantee the monotonicity of v, only two cases ($\delta_{2} > 0$, $\delta_{1} \ge 2\delta_{2}$ and $\delta_{2} < 0$, $\delta_{1} \le 2\delta_{2}$) are considered.

The quadratic PDFs with various ${\uplambda }$ in the two cases are shown in Fig. 1. Notably, the input parameter v is asymmetrical and spans a wide range of values. By selecting the appropriate $\delta_{i}$$\left( {i = 0, \, 1, \, 2} \right)$ and λ, any asymmetrical PDFs in any intervals can be fitted by the quadratic derivative λ-PDF. To demonstrate the high fitting ability of the quadratic derivative λ-PDF, a fitting region, which consists of the kurtosis–skewness points obtained by MCS with $10^{7}$ samples, is also given in Fig. 2.

Fig. 1

Derivative λ-PDF with different λ

Fig. 2

Fitting region of referenced derivative λ-PDF method

It can be illustrated in Fig. 2 that the kurtosis of the systems, whose PDF can be accurately recovered by the original quadratic derivative λ-PDF, basically goes between 1.5 and 3.2. When the kurtosis–skewness point falls out of the fitting region, an optimization algorithm is used to identify the closest point to the actual point in the fitting region, and its uncertainty model is applied for uncertainty propagation analysis. Obviously, the farther the distance between the two points is, the greater the discrepancy between the established uncertainty model and the actual uncertainty model, and the lower the accuracy of uncertainty propagation analysis. In addition, the quadratic polynomial is not monotonic, the range of random variables should be specified in advance. To overcome the ambiguity of the referenced λ-PDF method, an improved derivative λ-PDF is proposed in this study to expand the fitting region and enhance the applicability for the uncertainty propagation of complex structures with large skewness and kurtosis.

4 Currently proposed method

This section exposits the currently proposed method in detail. The layout of this section is that the uncertainty modeling method for the input variables is introduced in Section 4.1, in which the quadratic derivative λ-PDF is extended to a sum of power and log functions of arbitrary orders. The moment propagation analysis through the dimension reduction method (DRM) and Gaussian-weighted integrals (GWI) is presented in Section 4.2. The specific implementation procedure of the currently proposed method is subsequently outlined in Section 4.3.

4.1 Uncertainty modeling of input variables

The uncertain models of input variables are first constructed to quantify the uncertainties, which lays the groundwork for the moment propagation analysis.

4.1.1 Derivation of improved derivative λ - PDF

The original power function polynomial is improved, so that the fitting region is expanded to accommodate the original fitting region and lift the limitation to the second derivative. The improved polynomial can be expressed as

$$ v = h\left( z \right) = \delta_{{0}} \left( {z + \delta_{{1}} } \right)^{{\delta_{{2}} }} + \delta_{{3}}, $$

(9)

where $\delta_{i} \in \left( { - \infty , \, + \infty } \right)$ $\left( {i = {0, 1, 3}} \right)$ and $\delta_{{2}} \in \left( {{0}, \, + \infty } \right)$. When $\delta_{{2}}$ is an odd number, v is monotonic and unbounded. However, when $\delta_{{2}}$ is an even number, v is not monotonic but bounded. In particular, when $\delta_{{2}} = {2}$, Eq. (9) is in the second-order derivative form of Liu et al. (2018b).

The logarithmic function is monotonic and exhibits an infinite range of values (Gardini et al. 2021). In statistics, the logarithmic transformation is a monotonic transformation and the transformed variables retain the original statistical properties, such as mean and variance. The logarithmic function is then further improved

$$ v = h\left( z \right) = \delta_{{0}} \left( {z + \delta_{{1}} } \right)^{{\delta_{{2}} }} + \delta_{{3}} \ln \left( {z + {1}} \right) + \delta_{{4}}, $$

(10)

where $\delta_{i} \in \left( { - \infty , \, + \infty } \right)$ $\left( {i = {0, 1, 3, 4}} \right)$ and $\delta_{{2}} \in \left( {{0}, \, + \infty } \right)$.

Since it is not straightforward to determine the positive and negative terms in Eq. (10), the positive and negative terms of the polynomial are separated, so that

$$ v = h\left( z \right) = \delta_{0} \left( {z + \delta_{1} } \right)^{{\delta_{2} }} - \delta_{3} \left( { - z + \delta_{4} } \right)^{{\delta_{5} }} + \delta_{6} \ln \left( {z + 1} \right) - \delta_{7} \ln \left( { - z + 1} \right) + \delta_{8}, $$

(11)

where $\, \delta_{i} \ge {0}$$\left( {i = {0, 2, 3, 5, 6, 7}} \right)$; $\delta_{i} \ge {1}$$\left( {i = {1, 4}} \right)$; $\delta_{{8}} \in \left( { - \infty , + \infty } \right)$.

Equation (6) indicates that the λ-PDF method possesses probability density only when z falls in the range of [–1, 1]. To ensure the monotonicity of this function in the valid range of z, the ranges of the undetermined parameters $\delta_{i}$$(i = 0, \, 1, \ldots ,8)$ should also be specified. In view of that, $\delta_{1}$ and $\delta_{4}$ are assigned the nominal range of $\left( {1, + \infty } \right)$, $\delta_{8}$ is assigned the nominal range of $\left( { - \infty ,{ + }\infty } \right)$ and all the others are assigned the nominal range of $\left( {0, + \infty } \right)$.

Thus, $f_{\lambda } \left( v \right)$ can then be expressed as

$$ f_{\lambda } \left( v \right) = {{f_{\lambda } \left( z \right)} \mathord{\left/ {\vphantom {{f_{\lambda } \left( z \right)} {\left| {h^{\prime}\left( z \right)} \right|}}} \right. \kern-0pt} {\left| {h^{\prime}\left( z \right)} \right|}}, $$

(12)

where $f_{\lambda } \left( v \right)$ and $f_{\lambda } \left( z \right)$ are PDFs of v and z, respectively; and $h^{\prime}\left( z \right)$ expresses the derivative of $h\left( z \right)$. The lth-order raw moment $M_{l}$ can be derived as

$$ M_{l} = \int_{{v_{\min } }}^{{v_{\max } }} {v^{l} \cdot f_{\lambda } \left( v \right)} {\text{d}}v = \int_{ - 1}^{1} {h^{l} \left( z \right) \cdot \kappa \left( {1 - z^{2} } \right)}^{\lambda - 0.5} {\text{d}} z, $$

(13)

where $v_{\min }$ and $v_{\max }$ are the minimum and maximum values of the variable v, respectively. Because v increases monotonically with increasing z, when v reaches the minimum value, z takes the minimum value – 1; when v takes the maximum value, z takes the maximum value 1.$h(z)$ stands for a function of z with respect to v as shown in Eq. (11).

The parameters are optimized to derive the most appropriate values for approximation to PDF. Totally, ten parameters, such as λ and $\delta_{i}$$\left( {i = {0, 1, } \ldots { , 8}} \right)$, should be optimized, whose initial values are specified as (1, 2, 2, 0.5, 2, 2, 0.5, 2, 2, 1). The optimal solution of the parameters can be derived by searching the minimum sum of squared deviations of the approximate and exact first-four order moments. Combining Eqs. (4), (5), (11)–(13), the following optimization model can be established

$$ \left\{ \begin{gathered} {\text{find}} \lambda ,\delta_{i} \, \left( {i = 0,1, \ldots ,8} \right) \hfill \\ \min \, f = \left( {\mu - \mu_{0} } \right)^{2} + \left( {\sigma - \sigma_{0} } \right)^{2} + \left( {C_{s} - C_{s0} } \right)^{2} + \left( {C_{k} - C_{k0} } \right)^{2} \hfill \\ {\text{s.t.}}{\uplambda } \ge 0, \, \delta_{1} \ge 1{, }\delta_{4} \ge 1 \hfill \\ \delta_{i} > 0{, }i = 2,3,5,6,7 \hfill \\ \delta_{0} {, }\delta_{8} \in \left( { - \,\infty , + \,\infty } \right) \hfill \\ \end{gathered} \right., $$

(14)

where μ, σ, C_s, and C_k denote the first-four order statistical moments of the structure solved by substituting the unknown parameters of each iteration into the function of λ-PDF in the optimization process; μ₀, σ₀, C_s0, and C_k0 indicate the first-four order statistical moments of the parameters obtained from the statistical information of the input parameters or the first-four order statistical moments of the response calculated by the moment propagation method. The optimization strategy is solved by the quadratic sequential programming (SQP), and the calculation would stop when $f \le 10^{ - 6}$.

4.1.2 Standardization of random variables

To simplify the computational process and reduce the computational cost, the random variable $v$ is converted into a standard normal variable $u$.The relationship between $v$ and $u$ can be given as follows (Zhang and Han 2020)

$$ u = {{\left( {v - \mu_{v} } \right)} \mathord{\left/ {\vphantom {{\left( {v - \mu_{v} } \right)} {\sigma_{v} }}} \right. \kern-0pt} {\sigma_{v} }}. $$

(15)

In this way, calculation efficiency is improved when optimizing and determining parameters. The final calculation objects are PDF and CDF about $u$. The conversion relationship between $f\left( v \right)$ and $f\left( u \right)$ can be derived as

$$ f\left( v \right) = {{f\left( u \right)} \mathord{\left/ {\vphantom {{f\left( u \right)} {\sigma_{v} }}} \right. \kern-0pt} {\sigma_{v} }}. $$

(16)

Finally, combining Eqs. (6), (12), and (16), λ-PDF can be derived as

$$ f_{{\uplambda }} \left( z \right) = \left\{ {\begin{array}{*{20}c} {\frac{{\kappa \left( {1 - z^{2} } \right)^{{{\uplambda } - 0.5}} }}{{\sigma_{v} \left| {h^{\prime}\left( z \right)} \right|}}} & {\left| z \right| < 1} \\ 0 & {\left| z \right| \ge 1} \\ \end{array} }. \right. $$

(17)

The fitting region of the currently proposed method, which consists of the kurtosis–skewness points obtained by MCS with $10^{7}$ samples, is shown in Fig. 3. Compared with the fitting region of the referenced method in Fig. 2, the range of the fitting region of the currently proposed method is significantly increased, thus, the fitting ability is enhanced. Especially for the points located outside the reference fitting region but within the proposed fitting region, the fitting effect of the proposed method is remarkably better. To illustrate the fitting region of the proposed method more vividly, a comparison between the improved and referenced derivative λ-PDF method is presented in Section 4.1.3.

Fig. 3

Fitting region of currently proposed method

4.1.3 Comparison of fitting regions

To demonstrate the superiority of the currently proposed method, the improved and the original fitting regions are compared in Fig. 4, while MCS is implemented to obtain the kurtosis–skewness points.

Fig. 4

Improved vs. referenced fitting regions

From Fig. 4a, the improved region is much bigger than the original region. But the original fitting region is not accommodated in the improved fitting region completely. The potential reason may be that the uncovered area in the original region requires a minimum value of the parameter. Taking $\delta_{1}$ as an example, the kurtosis–skewness point of the structure can reach the uncovered area only when $\delta_{1} = 0.005$, which may not be captured properly by the diagram with a phenomenal parameter value range, such as [0, 4]. To prove that the improved region can cover the entire original region, a zoomed-in local comparison is conducted with a much-narrowed range of simulation parameters of [0, 0.5]. The comparison result is illustrated in Fig. 4b.

4.2 Moment propagation

After the uncertain models of the input variables are obtained, the statistical moments of structural response can be estimated through the moment propagation methods. In this study, DRM and GWI are adopted. DRM first decomposes the high-dimensional system into several low-dimensional subsystems, and the first-four statistical moments of the system response are then evaluated via GWI.

The lth original moment of Z can be written as (Huang and Du 2006)

$$ M_{l} = \int_{ - \infty }^{ + \infty } {\left[ {g\left( {\mathbf{X}} \right)} \right]^{l} f_{{\mathbf{X}}} \left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} = \int_{ - \infty }^{ + \infty } {Y\left( {\mathbf{X}} \right)f_{{\mathbf{X}}} \left( {\mathbf{x}} \right)} {\text{d}}{\mathbf{x}}. $$

(18)

For the DRM, the n-dimensional integral is estimated by the summation of multiple s-dimensional functions $\left( {s \le n} \right)$(Xu and Rahman 2004), and the UDRM is suitable for engineering applications with low accuracy requirements. Besides, the BDRM has lower computational efficiency, but it is more suitable for engineering problems with high accuracy requirements. In practical engineering, the UDRM or BDRM shall be selected in different cases according to specific accuracy and efficiency requirements. According to UDRM, the lth-order original moment can be expressed as (Xu and Rahman 2004)

$$ M_{l} = \int_{ - \infty }^{ + \infty } {\left[ {\sum\limits_{k = 1}^{n} {\hat{Y}_{k} \left( {{\mathbf{X}}_{k} } \right)} } \right]f_{{{\mathbf{X}}_{k} }} \left( {{\mathbf{x}}_{k} } \right)} {\text{d}} {\mathbf{x}}_{k} - \left( {n - 1} \right)Y_{0}, $$

(19)

where $\hat{Y}_{k} \left( {{\mathbf{X}}_{k} } \right) = Y\left( {\mu_{1} {, } \ldots {, }\mu_{k - 1} {, }X_{k} {, }\mu_{k + 1} {, } \ldots {, }\mu_{n} } \right)$ is the kth subsystem;$\mu_{k}$$\left( {k = {1, 2, } \ldots {,}n} \right)$ is the mean value of $X_{k}$; $Y_{0} = Y\left( {\mu_{1} {, }\mu_{2} {, } \ldots {, }\mu_{n} } \right)$.

According to BDRM, the lth-order original moment can be expressed as (Xu and Rahman 2004)

$$ M_{l} = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {Y_{2} f_{{X_{{k_{1} }} }} \left( {x_{{k_{1} }} } \right)f_{{X_{{k_{2} }} }} \left( {x_{{k_{2} }} } \right)} {\text{d}} x_{{k_{1} }} {\text{d}} x_{{k_{2} }} } - \left( {\begin{array}{*{20}c} {n - 2} \\ 1 \\ \end{array} } \right)\int_{ - \infty }^{ + \infty } {Y_{1} f_{{X_{k} }} \left( {x_{k} } \right)} {\text{d}} x_{k} + \left( {\begin{array}{*{20}c} {n - 1} \\ 2 \\ \end{array} } \right)Y_{0}, $$

(20)

where

$$ Y_{1} = \sum\limits_{k = 1}^{n} {Y\left( {\mu_{1} {, } \ldots {, }\mu_{k - 1} {, }X_{k} {, }\mu_{k + 1} {, } \ldots {, }\mu_{n} } \right)}. $$

(21)

$$ Y_{2} = \sum\limits_{{k_{1} < k_{2} }} {Y\left( {\mu_{1} {, } \ldots {, }X_{{k_{1} }} {, } \ldots {, }X_{{k_{2} }} {, } \ldots {, }\mu_{n} } \right)} {, }\left( {k_{1} {, }k_{2} = {1, 2, } \ldots {, }n} \right). $$

(22)

Equations (19) and (20) only involve one- and two-dimensional integrals, therefore, the computational cost of Eqs. (19) and (20) is lower than that of Eq. (18). However, the number of two-dimensional integrals is ${{n\left( {n - 1} \right)} \mathord{\left/ {\vphantom {{n\left( {n - 1} \right)} 2}} \right. \kern-0pt} 2}$, which implies that it still ensues high computational cost when dealing with high-dimensional problems. GWI is thus adopted to further reduce the computational cost because it approximates the integrals by summing up the weighted functions evaluated at Gauss points.

As to UDRM, $M_{l}$ can be transformed from Eq. (19) into (Rahman and Xu 2004)

$$ M_{l} \cong \sum\limits_{k = 1}^{n} {\sum\limits_{m = 1}^{r} {\omega_{m} Y\left( {\mu_{1} {, } \ldots {, }\mu_{k - 1} {, }X_{k}^{m} {, }\mu_{k + 1} {, } \ldots {, }\mu_{n} } \right)} } - \left( {n - 1} \right)Y\left( {\mu_{1} {, }\mu_{2} {, } \ldots {, }\mu_{n} } \right), $$

(23)

where $X_{k}^{m}$ is the mth Gauss point; $\omega_{m}$ denotes the corresponding Gauss weight; r stands for the number of the Gauss points (abscissa).

For the case of BDRM, $M_{l}$ can be converted from Eq. (20) to be

$$ \begin{gathered} M_{l} \cong \sum\limits_{{k_{1} < k_{2} }} {\sum\limits_{{m_{1} }}^{{r_{1} }} {\sum\limits_{{m_{2} }}^{{r_{2} }} {\omega_{{m_{1} }} \omega_{{m_{2} }} Y\left( {\mu_{1} {, } \ldots {, }X_{{k_{1} }}^{{m_{1} }} {, } \ldots {, }X_{{k_{2} }}^{{m_{2} }} {, } \ldots {, }\mu_{n} } \right)} } } \\ - \left( {\begin{array}{*{20}c} {n - 2} \\ 1 \\ \end{array} } \right)\sum\limits_{k = 1}^{n} {\sum\limits_{m = 1}^{r} {\omega_{m} Y\left( {\mu_{1} {, } \ldots {, }\mu_{k - 1} {, }X_{k}^{m} {, }\mu_{k + 1} {, } \ldots {, }\mu_{n} } \right)} } \\ + \left( {\begin{array}{*{20}c} {n - 1} \\ 2 \\ \end{array} } \right)Y\left( {\mu_{1} {, }\mu_{2} {, } \ldots {, }\mu_{n} } \right) \\ \end{gathered}, $$

(24)

where $X_{k}^{m}$ indicates the m_ith Gauss point to replace the k_ith variable in Y; $\omega_{{m_{1} }}$ and $\omega_{{m_{2} }}$ are the corresponding Gauss weights; $r_{1}$ and $r_{2}$ are the respective numbers of the Gauss points.

GWI requires the transformation of nonnormal distribution into a normal distribution, which increases the nonlinearity of the system. Therefore, it is advisable to choose the appropriate orthogonal polynomial models for the respective distributions of random variables. The orthogonal polynomials and the corresponding GWI functions for ordinary different probability distribution types are listed in Table 1 (Liu et al. 2018b). For simplicity, GWI formulas for one-dimensional integrals only, as examples, are given in Table 1. In consequence of the derivation of the statistic moments propagation, the improved derivative λ-PDF is further used to reconstruct the PDF and CDF of the system response following a similar procedure to the uncertainty modeling of the input variables in Section 4.1.

Table 1 GWI formulas for different distributions (Liu et al. 2018b)

Since the moment calculation is included in the two-dimensional and one-dimensional numerical integrals, the total number of function evaluations in BDRM is (Ding and Xu 2021)

$$ N = \frac{{n\left( {n - 1} \right)}}{2} \cdot \left( {d - 1} \right)^{2} + n \cdot \left( {d - 1} \right) + 1. $$

(25)

Similarly, the total number of function evaluations in UDRM can be obtained by (Zhang and Han 2020)

$$ N = n \cdot \left( {d - 1} \right) + 1, $$

(26)

where N is the number of function evaluations; n denotes the dimension of the uncertain system; d implies the number of GWI points.

4.3 Procedure of currently proposed method

The stepwise procedure of the proposed method for structural uncertainty propagation is shown in Fig. 5 and specified as follows:

Step 1:

Derive the probability data of input random variables. For variables with specific distributions, the probability data are calculated through the given parameters. On the other hand, for variables under arbitrary distributions, the probability data are approximated by the improved λ-PDF method when the kurtosis–skewness points locate in the improved fitting region. If the kurtosis–skewness points fall out of the improved fitting region, they are approximated by MEM.

Step 2:

Calculate the first-four statistical moments of structural response. DRM and GWI are adopted to implement the moment propagation analysis based on the probability data of input variables derived in Step 1. The calculated moments are regarded as the objective values in Eq. (14) to acquire the appropriate parameters.

Step 3:

Optimize the parameters λ and $\delta_{i}$ in Eq. (14). The initial parameters are substituted into Eq. (14) to start the optimization process. When the objective function is minimized, the first-four order statistical moments are identified as the data closest to the respective objective value. The final parameters are then determined.

Step 4:

The approximate PDF and CDF of structural response are obtained. The optimized parameters acquired in Step 3 are substituted into Eq. (17) to estimate the λ-PDF, which is regarded as PDF reconstructed by the currently proposed method. The corresponding CDF can finally be obtained by integration.

Fig. 5

Flowchart for implementation procedure of currently proposed method

5 Demonstrative examples

To illustrate the effectiveness and accuracy of the currently proposed method, six examples are engaged in this section. Considering the balance between accuracy and efficiency, different DRMs and GWI with 5 Gauss points are used in the examples when evaluating the statistical moments. MCS with 10⁷ samples is adopted as caliber. After derivation of the propagation of statistical moments, the methods for approximating PDF and CDF of the structural response are adopted. For comparison, the referenced λ-PDF method, MEM, EWE, and SGLD are also utilized to reconstruct PDF and CDF of the structural response. Besides, the currently proposed method and the reference λ-PDF method are referred to as PM and RM, respectively, in the figure legends for simplicity. To demonstrate the fitting capabilities of different methods, PDF and CDF are graphically illustrated for each example. To further reveal the tail accuracy of each method, logarithmic coordinates are used in the CDF figures.

5.1 Two-dimensional numerical example

To improve the accuracy of the currently proposed method when the kurtosis–skewness points fall out of the original region, a binary quadratic system (Acar et al. 2010) is considered

$$ Y = x_{1}^{2} + x_{2}^{2} - 1, $$

(27)

where $x_{i} \sim N\left( {0, 1} \right)$$\left( {i = {1, 2}} \right)$. To accomplish the uncertainty propagation of this binary quadratic system, the proposed method is realized through following steps:

• (1) Construct the uncertainty models of the input variables. The first-four order statistical moments of the two variables are derived from the respective distribution patterns and parameters.

• (2) Implement the moment propagation. The first-four order statistical moments of the structural response are calculated by the UDRM via Eq. (23), and the results are shown in Table 2. The statistical moments obtained in this step are regarded as the exact solutions, that is $\mu_{0}$, $\sigma_{0}$, $C_{s0}$ , and $C_{k0}$ in Eq. (14).

• (3) Determine the optimized λ-PDF. The unknown parameters λ and δ_i(i = 0, 1, …, 8) of initial values (1, 2, 2, 0.5, 2, 2, 0.5, 2, 2, 2, 1) are substituted into Eq. (17) to obtain the optimized λ-PDF.

• (4) Calculate the optimized first-four statistical moments. The optimized λ-PDF obtained in Step (3) is substituted into Eq. (18) to calculate the optimized moments in Eq. (14).

• (5) Compute the objective function $f = \left( {\mu - \mu_{0} } \right)^{2} + \left( {\sigma - \sigma_{0} } \right)^{2} + \left( {C_{s} - C_{s0} } \right)^{2} + \left( {C_{k} - C_{k0} } \right)^{2}$. The objective function f can be computed after calculating the exact moments and the optimized moments.

• (6) Determine if the convergence condition is satisfied. If the value of the objective function f is less than 10^–6, stop the iteration. On the contrary, update the parameter values and repeat Step (3) to Step (5) until the value of the objective function f is less than 10^–6. The iterations histories of objective function are shown in Fig. 6.

• (7) Output the optimized parameters. The final values of the optimized parameters λ and δ_i(i = 0, 1, …, 8) are (0.4426, 0.8470, 1.4003, 0.0186, 0.1671, 10.4037, 0.2256, 0.0037, 0.9425, − 0.8759).

• (8) Reconstruct the PDF and CDF of the system response. The final optimized λ-PDF can be obtained through substituting the final parameters into Eq. (17), and it is regarded as PDF of the system response. The CDF of the system response can be reconstructed through further derived. The reconstruction results are shown in Fig. 7.

Table 2 Statistical moments of system response in binary quadratic system

Fig. 6

Iterations histories of objective function

Fig. 7

PDFs and CDFs of system response in binary quadratic system

The moments of the system response acquired by MCS and UDRM are listed in Table 2. Obviously, the kurtosis of the system response indicates that the kurtosis–skewness point falls outside the original fitting region. According to Liu et al. (2018b), an approximate point within the original fitting region that is closest to the actual point of (2.0011, 9.0390) should be searched to fit the PDF and CDF. It is understood that, with this substantial gap between the two points, low accuracy will be ensued for the referenced λ-PDF method.

Figure 6 shows the optimization iteration process, from which it can be seen that the adopted optimization strategy satisfies the convergence condition after 25 iterations and completes the optimization model solution.

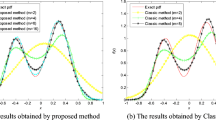
The recovered probability curves of the system response through the optimized parameters are shown in Fig. 7, where the PM and RM represent the proposed method and the referenced method, respectively. It can be known from Fig. 7, both the PDF and CDF approximated via the currently proposed method are in the closest agreements with those by MCS, while the referenced λ-PDF method yields the most deviation. When fitting the PDF and CDF of the system response, the result by the EWE is closer to MCS result than that by the MEM. On the other hand, when fitting the PDF of system response, the EWE shows large fluctuations when $x \ge {2}$, while the MEM is more stable on the whole. The fitting results demonstrate that the fitting region, i.e., the applicability of the derived λ-PDF, is expanded compared to that of the referenced method, while the accuracy is not compromised.

5.2 Three-dimensional numerical example

A nonlinear system with nonnormal distribution input variables is considered in this example, which can be expressed as

$$ Y = x_{1}^{2} x_{2}^{2} + 2x_{3}^{4}, $$

(28)

where $\ln x_{i} \sim N\left( {{1, 0}{\text{.1}}} \right)$$\left( {i = {1, 2}} \right)$, and $x_{3} \sim N\left( {{1, 0}{\text{.1}}} \right)$.

The statistical moments by MCS, UDRM, and BDRM are shown in Table 3. Notably, the results computed by the BDRM are more accurate than those by UDRM. Thus, the results computed by BDRM are used to approximate the PDF and CDF. PDF and CDF curves fitted by all four methods are presented in Fig. 8.

Table 3 Statistical moments of system response in three-dimensional example

Fig. 8

PDFs and CDFs of system response in three-dimensional example

From Fig. 8a, the PDF curve obtained by the currently proposed method is the closest to the curve obtained by MCS. The curve by the EWE method almost coincides with that by the currently proposed method except for some areas, where the curve by the EWE method is less accurate than that by the currently proposed method. Besides, the curve by the referenced λ-PDF method is better than that by the MEM in view of skewness and the overall trend, but not for kurtosis. From Fig. 8b, the curve by the currently proposed method is in closest agreement with that by MCS. The tail accuracy of the referenced λ-PDF method is followed by that of the currently proposed method, which is negated by overall fluctuation. The overall curve by the EWE method is smooth, but the tail accuracy is not high. The MEM displays the worst approximation to CDF. In brief, the currently proposed method yields the highest accuracy in approximating PDF and CDF for nonlinear systems.

5.3 High-dimensional numerical example

This example presents a high-dimensional system (Zhang et al. 2021a), where the number of variables can be changed without altering the level of failure probability. The function of the system is given by

$$ g\left( {x_{1} , \ldots ,x_{n} } \right) = \left( {n + 3\sigma \sqrt n } \right) - \sum\limits_{i = 1}^{n} {x_{i} }, $$

(29)

where n can be any value and n = 30 in this example;$\ln x_{i} \sim N\left( {{1, 0}{\text{.2}}} \right)$$\left( {i = {1, 2, } \ldots {, }n} \right)$.

Table 4 shows the statistical moments by MCS, UDRM, and BDRM. Notably, for the first-three order statistical moments, the results of UDRM show the same accuracy as those of BDRM, but UDRM is less accurate than BDRM in the calculation of C_k. Although the number of function calls for UDRM is less than that of BDRM, the computational results of BDRM are still selected for the system response PDF and CDF reconstruction in favor of its high computational accuracy. PDF and CDF curves approximated by the six methods are presented in Fig. 9. To further demonstrate the accuracy of the currently proposed method, the SGLD, which has proven to be an excellent method (Xu and Dang 2019), is incorporated as a comparison for recovering the probability curves of structural response in this example.

Table 4 Statistical moments of system response in high-dimensional example

Fig. 9

PDFs and CDFs of system response in 30-dimensional example

From Fig. 9, the accuracy of each fitting method is not significantly different from each other. Especially, for PDF approximation in Fig. 9a, only the curve obtained by the referenced method deviates slightly, and the other four curves acquired by other fitting methods exhibit high accuracy. As shown in Fig. 9b, the PM result is comparable in accuracy to the SGLD, MEM, and EWE results, all of which are significantly better than that of the RM method in the tail region. In short, the currently proposed method can also achieve high accuracy in approximating PDF and CDF for high-dimensional systems.

5.4 Plastic collapse mechanism

A plastic collapse mechanism of one-bay frame with linear performance function as shown in Fig. 10 is exemplified. The performance function can be given as follows (Xu and Dang 2019)

$$ Y = x_{1} + 2x_{2} + 2x_{3} + x_{4} - 5x_{5} - 5x_{6}. $$

(30)

Fig. 10

Plastic collapse mechanism

Table 5 shows the means and coefficient of variations (COV) of each variable. The statistical moments by MCS, UDRM, and BDRM are listed in Table 6. Accordingly, the kurtosis calculated by BDRM is more accurate than that by UDRM. Thus, the moments calculated by BDRM are used to reconstruct the PDF and CDF.

Table 5 Distribution information of random variables in plastic collapse mechanism

Table 6 Statistical moments of structural response in the plastic collapse mechanism

PDFs and CDFs reconstructed by the six approximation methods are presented in Fig. 11. It is observed that PDF by the currently proposed method is still in the closest agreement with that by MCS, while the curves acquired by the EWE and the SGLD almost coincide with that by the currently proposed method. PDF curves obtained by the MEM and the referenced λ-PDF method are close to each other as shown in Fig. 11a, while the PDF curve by the MEM exhibits a better fitting capability than that by the referenced λ-PDF method. From Fig. 11b, the currently proposed method displays the same high accuracy as the SGLD when approximating the CDF, especially in the tail area. The result calculated by MEM shows a higher accuracy than those by the EWE and the referenced λ-PDF method. On another negative note, the EWE and the referenced λ-PDF methods exhibit local fluctuations. And the referenced λ-PDF method yields the worst performance in fitting CDF in this example. In brief, the currently proposed method renders the highest accuracy when approximate both PDF and CDF for linear uncertainty propagation problems.

Fig. 11

PDFs and CDFs of structural response in plastic collapse mechanism

5.5 Annular column

A column with annular cross-section subject to axial compression load (Xu and Zhou 2020) is considered in this example, and the schematic is given in Fig. 12.

Fig. 12

Sketch for annular column

The nonlinear performance function is established with regard to the buckling failure. The performance function can be described as (Xu and Zhou 2020)

$$ Y = \frac{{\pi^{2} E}}{{L^{2} }} \cdot \frac{\pi }{64}\left[ {\left( {D + T} \right)^{4} - D^{4} } \right] - P, $$

(31)

where E denotes the elastic modulus of material; L is the height of column; D represents the internal diameter; T expresses the thickness; and P indicates the axial load.

The distribution data of random variables are given in Table 7. The first-four statistical moments by MCS and DRMs are listed in Table 8, where the results obtained by TDRM are quoted from Xu and Zhou (2020). Evidently, the results obtained by TDRM is the closest to that by MCS among the three DRMs. On the other hand, the computational efficiency of TDRM is the lowest. To obtain the most accurate result, the moments obtained by TDRM are applied in this example by using the data directly, and the low computational efficiency is not a concern.

Table 7 Distribution data of random variables in annular column

Table 8 Statistical moments of structural response in the annular column

Based on the moments obtained by TDRM, the PDFs and CDFs reconstructed with six methods: MCS, the currently proposed method, the referenced λ-PDF method, the MEM, the EWE, and the SGLD are shown in Fig. 13. Notably, the PDF curve acquired by the currently proposed method is the closest to that by MCS. From Fig. 13a, the curves acquired by the EWE and the SGLD successive to the currently proposed method are also in close agreement with those by MCS. The referenced λ-PDF method fits PDF well in the skewness, but not in the kurtosis. MEM exhibits a low accuracy in fitting PDF in this example. As shown in Fig. 13b, the SGLD exhibits the highest accuracy in the tail region, and the currently proposed method has inferior accuracy to the SGLD beyond the 10^–3 level, but is still superior to the other three methods. The result obtained by the referenced λ-PDF method presents higher accuracy than that of the EWE, and the MEM displays the lowest approximating capability herein. This example demonstrates again that the currently proposed method yields superior accuracy for the analysis of highly nonlinear uncertainty propagation problems.

Fig. 13

PDFs and CDFs of structural response in annular column

5.6 6-DoF industrial robot

To demonstrate further the accuracy of the currently proposed method in analyzing uncertainties in practical engineering structure, a 6-degree-of freedom (6-DoF) industrial robot (Kucuk and Bingul 2014) is analyzed in this example. Its mechanism diagram is sketched in Fig. 14.

Fig. 14

Diagram of 6-DoF industrial robot

The rotation angle of each joint is controlled to manipulate the movement of the end-effector in space. D–H parameters and uncertain variables of the industrial robot are shown in Tables 9 and 10, in which the determined parameters are $h_{{1}} { = 36}$, $d_{{2}} { = 24}$, $l_{{4}} { = 10}$, $d_{{6}} { = 10}$, $\theta_{{3}} { = 80}^{{\text{o}}}$ , and $\theta_{{4}} { = 49}^{{\text{o}}}$.

Table 9 D–H parameters of 6-DoF industrial robot

Table 10 Distribution data of random variables in 6-DoF industrial robot

The pose transformation matrices of the 6-DoF industrial robot can then be obtained sequentially as follows

$$ \begin{array}{*{20}c} {{}_{1}^{0} {\mathbf{T}} = \left[ {\begin{array}{*{20}c} {\cos \theta_{1} } & { - \sin \theta_{1} } & 0 & 0 \\ {\sin \theta_{1} } & {\cos \theta_{1} } & 0 & 0 \\ 0 & 0 & 1 & {h_{1} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],}{{}_{{2}}^{{1}} {\mathbf{T}} = \left[ {\begin{array}{*{20}c} {\cos \theta_{2} } & { - \sin \theta_{2} } & 0 & 0 \\ 0 & 0 & { - 1} & { - d_{2} } \\ {\sin \theta_{2} } & {\cos \theta_{2} } & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]} \\ {{}_{{3}}^{{2}} {\mathbf{T}} = \left[ {\begin{array}{*{20}c} {\cos \theta_{3} } & { - \sin \theta_{3} } & 0 & 0 \\ 0 & 0 & 1 & {l_{2} } \\ { - \sin \theta_{3} } & { - \cos \theta_{3} } & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],}{{}_{4}^{3} {\mathbf{T}} = \left[ {\begin{array}{*{20}c} {\cos \theta_{4} } & { - \sin \theta_{4} } & 0 & {l_{3} } \\ {\sin \theta_{4} } & {\cos \theta_{4} } & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]} \\ {{}_{{5}}^{{4}} {\mathbf{T}} = \left[ {\begin{array}{*{20}c} {\cos \theta_{5} } & { - \sin \theta_{5} } & 0 & {l_{4} } \\ 0 & 0 & 1 & 0 \\ { - \sin \theta_{5} } & { - \cos \theta_{5} } & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],}{{}_{{6}}^{{5}} {\mathbf{T}} = \left[ {\begin{array}{*{20}c} {\cos \theta_{6} } & { - \sin \theta_{6} } & 0 & 0 \\ 0 & 0 & { - 1} & { - d_{6} } \\ {\sin \theta_{6} } & {\cos \theta_{6} } & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]} \\ \end{array} $$

(32)

In this example, MCS, UDRM, and BDRM are used to calculate the first-four moments of the positioning accuracy of the end-effector. The computed results are shown in Table 11, in which the statistical moments of the three directions by BDRM exhibit the highest accuracy. Thus, these moments are used to approximate the PDF and CDF of the three directions of the industrial robot, as shown in Figs. 15, 16, and 17. It is seen from Table 11 that both the UDRM and BDRM yield high accuracies in μ and σ, while BDRM displays higher accuracy in the skewness and kurtosis, which are more preferential in approximating PDF and CDF for nonnormal distribution systems.

Table 11 Statistical moments of x, y, and z directions of 6-DoF industrial robot

Fig. 15

PDFs and CDFs of x direction of industrial robot

Fig. 16

PDFs and CDFs of y direction of industrial robot

Fig. 17

PDFs and CDFs of z direction of industrial robot

It can be found from Fig. 15a that the PDF curve of x direction of the industrial robot by the currently proposed method deviates slightly from that by MCS, especially in the tail area. Nevertheless, compared with the other four methods, the proposed method is still the closest method to MCS. The performance of the SGLD ranks second to that of the currently proposed method, followed by that of the EWE. The MEM yields the worst fitting among all the six methods. As shown in Fig. 15b, the CDF curve of the x direction obtained by the EWE is the closest to that by MCS, especially in the tail area. However, the overall curve fluctuates. Although the performance of the currently proposed method is inferior to that of the EWE in terms of tail accuracy, the overall curve is smooth and close to MCS result. The trend of the SGLD result is smooth and has a good overall accuracy, but the tail accuracy is lower than the currently proposed method. The overall MEM result is also fluctuating, and exhibits the worst accuracy in the tail area. The referenced λ-PDF method yields smooth trend but low tail accuracy.

As shown in Fig. 16a, the result achieved by the currently proposed method deviates locally from that by MCS, but accords well on a whole. Still, it exhibits the best performance compared with those by the other four methods. The result approximated by SGLD fits better in skewness than those by the referenced λ-PDF method, the EWE, and the MEM. The EWE shows better ability in fitting kurtosis than the referenced λ-PDF method. And MEM exhibits the worst performance in fitting the PDF of the y direction among all the five methods. It can be seen in Fig. 16b that the EWE yields high accuracy in the tail area, but fluctuating overall curve. The curves acquired by the currently proposed method and the SGLD are disadvantageous in the tail area, but are superior in terms of overall trend compared to the EWE. The tail accuracy of the SGLD is lower than the currently proposed method. Besides, the referenced λ-PDF method yields lower accuracy than the other three methods except for the MEM in the tail area. Thus, the MEM renders the lowest tail accuracy and fluctuates overall curve.

The currently proposed method yields the highest accuracy in approximating the PDF and CDF in the z direction of the industrial robot as shown in Fig. 17. The result obtained by the SGLD does not show much difference from that by the currently proposed method in Fig. 17a, and the EWE has the same accuracy except for the tail area, where the difference of the curves becomes obvious. The referenced λ-PDF method does not perform well in deriving kurtosis, whereas its results almost coincide with those by the proposed method in other derivations. The MEM still displays the worst fitting ability. As shown in Fig. 17b, it is noteworthy that the result achieved by the MEM method exhibits remarkable fluctuations in the tail region. The currently proposed method yields high overall accuracy, followed by the SGLD, while the referenced λ-PDF method does not fit well the CDF of the z direction, especially in the tail area. The result calculated by the EWE still exhibits overall fluctuation. In simple summary, the currently proposed method serves as an effective and accurate approach to the uncertainty propagation of the positioning accuracy of the industrial robot.

6 Discussion

In this paper, an enhanced derivative λ-PDF method for uncertainty quantification and analysis is proposed. Six examples are utilized to compare the performance of the currently proposed method with those of four existing methods. Some characteristics, advantages, and disadvantages of the different approaches have been presented through an adequate comparison.

The dimension reduction method (DRM) is used for statistical moments estimation, and the results of the MCS method are utilized as a benchmark. According to the calculation results of each example, the main difference between UDRM and BDRM calculation accuracy is reflected in the results of skewness and kurtosis. In Example 5.3, the high-dimensional numerical example, the relative error between the kurtosis values of UDRM and MCS even reaches 95.96%, while the relative error between the kurtosis values of BDRM and MCS in the same case is only 0.09%. In Example 5.6 (6-DoF industrial robot), the skewness and kurtosis values in the x, y, and z directions show that the accuracy of BDRM is higher than that of UDRM. In addition, the currently proposed method requires higher accuracy to calculate the skewness and kurtosis. Therefore, the results of BDRM are selected to recover the PDF and CDF of the structural response to ensure the accuracy of the proposed method.

In the case of PDF approximation methods, four methods are used to compare with the proposed method to adequately illustrate the accuracy of the proposed method, and MCS is still used as a benchmark. The proposed method exhibits excellent accuracy in both numerical and engineering examples, with an improvement compared to the referenced method, which is mainly due to the expanded fitting region. The accuracy of the referenced method is inferior in the examples because the kurtosis–skewness points of the responses of the six examples are outside the referenced fitting region, resulting in a lower accuracy of the reference method. The maximum entropy method (MEM), the Edgeworth series expansion method (EWE), and the shifted generalized lognormal distribution (SGLD) are all proven excellent methods, but their performances in all examples are not consistent. The accuracy of MEM is less accurate than that of the proposed method in most cases. The tail accuracy of the Edgeworth level expansion method for engineering examples is similar to that of the proposed method, but the overall trend fluctuates considerably. The proposed method can achieve equivalent accuracy compared with the SGLD method at the tail for numerical examples, however, for the engineering problem, the computational accuracy of the SGLD method in all three directions is inferior to the proposed method. Therefore, the proposed method can improve the computational accuracy for large skewness and kurtosis problems.

The comparisons of computational cost of the proposed method and other comparative methods in terms of CPU time are listed in Table 12. The computations are run in a laptop with Intel(R) Core(TM) i5-7300HQ CPU and 8 GB RAM. As shown in Table 12, the computational cost of the proposed method is much less than that of MCS, but slightly more than that of comparative methods. The reason for slightly high computational cost of the proposed method is to determine the unknown parameters in the optimization model Eq. (14). Although the computational cost is slightly higher, the total amount of CPU time is less than half a minute which is affordable for the most practical problems. The comparative methods without additional optimization models have high computational efficiency, but for problems with large skewness and kurtosis, most of them sacrifice the computational accuracy and even obtain incorrect results. Therefore, the proposed method can balance the computational accuracy and efficiency, which is superior to other methods for solving such problems with large skewness and kurtosis.

Table 12 Computational cost comparison among proposed method and other methods

7 Conclusions

In this paper, an efficient uncertainty analysis approach based on the currently proposed improved derivative λ-PDF and dimension reduction method is developed to perform uncertainty propagation of complex structures with large skewness and kurtosis. To implement uncertainty quantification in a uniform framework, an improved derivative λ-PDF is derived for uncertainty modeling of input random variables. The Gaussian-weighted integrals (GWI) and dimension reduction method (DRM) are used to decompose the n-dimensional system and compute the statistical moments of structural responses based on the statistical information of input variables. To reconstruct the PDF of structural responses, the improved derivative λ-PDF is applied to approximate PDF and CDF using an optimization method. The currently proposed method can effectively and accurately derive the uncertainty propagation analysis for complex systems with large skewness and kurtosis.

To demonstrate the effectiveness and accuracy of the currently proposed method, six examples are analyzed. Reference methods of Monte Carlo simulation, the maximum entropy method, the Edgeworth series expansion method, and the shifted generalized lognormal distribution are engaged as calibers. Different examples reflect the superiority of the proposed method in different aspects. Specifically, Example 1 illustrates that the improved fitting region with regard to the currently proposed method is significantly expanded compared to the original one. Example 2 is a numerical example, which demonstrates the high accuracy of the currently proposed method in processing nonlinear uncertainty problems. Example 3 presents a 30-dimensional system and proves the high accuracy of the currently proposed method in the uncertainty propagation of high-dimensional systems. Both linear and nonlinear performance functions in engineering structures of Example 4 and Example 5, respectively, demonstrate the applicability and accuracy of the currently proposed method in solving both linear and nonlinear engineering uncertainty propagation problems. Finally, the positioning accuracy of a 6-DoF industrial robot end-effector in three directions in Example 6 further corroborates the effectiveness and accuracy of the currently proposed method in processing high complex uncertainty propagation problems.

In summary, the currently proposed method exhibits significant improvement over the prevailing referenced methods. Further enhancements are desired in view of that when the kurtosis of the structural response is greater than 8, the bounds of the fitting region in the referenced λ-PDF method are not straightforward to be determined precisely. In addition, extending the fitting region by changing the derivative λ-PDF should also be attempted.