Concurrent shape optimization of a multiscale structure for controlling macrostructural stiffness

Abstract

We propose a novel shape optimization method for designing a multiscale structure with the desired stiffness. The shapes of the macro- and microstructures are concurrently optimized. The squared error norm between actual and target displacements of the macrostructure is minimized as an objective function. The design variables are the shape variation fields of the outer and interface shapes of the macrostructure and the shapes of holes in the microstructures. Subdomains with independent periodic microstructures are arbitrarily defined in the macrostructure in advance. Homogenized elastic tensors are calculated and applied to the correspondent subdomains. The shape gradient functions are theoretically derived with respect to each shape variation of the macro- and microstructures, and applied to the H¹ gradient method to determine the optimum shapes. The proposed method is applied to several numerical examples, including Poisson’s ratio design and deformation control designs of an L-shaped bracket and a both ends fixed beam with holes. The results of the design examples confirm that the desired stiff or compliant deformation can be achieved while obtaining clear and smooth boundaries. The influence on the final results of the initial shape of the unit cell, the connectivity of adjacent microstructures, and interface optimization is also discussed.

1 Introduction

Multiscale structures, examples of which are seen in plant skeletons and animal bones in nature, have the potential to provide greater performance while remaining lightweight, resilient, and multifunctional. Recent developments in 3D printing, or additive manufacturing, are accelerating research on multiscale optimization. In a multiscale structure as shown in Fig. 1, microstructures with small holes or lattices are distributed inside the overall macrostructure. Multiscale optimization optimizes the macro- and microstructures on both structural scales. In early research on multiscale structures, the macro- and microstructures were optimized separately and not concurrently due to the enormous amount of calculations involved.

Fig. 1

A multiscale structure consisting of five subdomains with various microstructures

Consequently, the homogenization method was established as a mathematical approach in the engineering field for evaluating the effective material properties of composite materials. It was later extended as a method for topology optimization or as a design method for multiscale structures (Hornung 1991; Yvonnet 2019). The early work of Bendsoe and Kikuchi (1988) and Suzuki and Kikuchi (1991) proposed the use of the homogenization method as a technique for topology optimization. In their studies, a periodic unit cell with a rectangular hole was defined in a macrostructure, and the size of the hole was optimized. Although it was a revolutionary method, there was a problem that it was difficult to fabricate fine structures with the manufacturing technology available at that time. The Solid Isotropic Material with Penalization (SIMP) method (or the density method) has been used for topology optimization instead of the homogenization method because of its convenience since the latter half of the 1990s (Wu et al. 2021).

In recent years, with the development of manufacturing technologies such as 3D printing, it has become possible to manufacture fine and complicated shapes that were previously considered difficult. The homogenization method has been investigated thoroughly in order to bridge the macro- and microstructures. Research on multiscale topology optimization using the homogenization method has attracted a great deal of attention anew. In 2002, Rodrigues et al. (2002) described hierarchical optimization of the macro- and microstructures using the SIMP method. Liu et al. (2008) proposed a concurrent multiscale optimization method using SIMP and the Porous Anisotropic Material with Penalization (PAMP) method for optimizing micro- and macrostructures of two-dimensional elastic bodies. Wang et al. (2016) presented an example of multiscale concurrent optimization of a two-dimensional elastic body using the level-set method. Sivapuram et al. (2016) presented concurrent topology optimization of macro- and microstructures using the level-set method for the purpose of rigidity design. Gao et al. (2019) presented a MATLAB code for concurrent multiscale optimization of 2D and 3D structures using a modified SIMP approach, in which mean compliance is minimized. Li et al. (2019) presented a concurrent multiscale optimization method for a two-dimensional elastic structure by varying the length–width ratio of the hole in the periodic cell. Although not concurrent multiscale optimization, the homogenization method has been applied for attractive metamaterial designs such as negative Poisson's ratio properties (Xu and Xie 2015; Jha and Dayyani 2021; Zhang and Khandelwal 2019; Ai and Gao 2017) and zero Poisson's ratio (Jha and Dayyani 2021).

In recent studies, researchers have been interested in connectivity (or compatibility) issues of microstructures in actual 3D printing. When optimized microstructures are actually distributed within the macrostructure, the walls of adjacent microstructures might not be properly connected due to mismatches (Wang et al. 2018, 2020). This leads to disconnection of the macrostructure or performance reduction. For the problem of microstructure connectivity in topology optimization, Du et al. (2018) introduced connectivity indicators that fill unconnected sections between adjacent microstructures. Zhang et al. (2019) proposed an optimization method based on the variable thickness sheet method (VTS) for two- or three-dimensional microstructures, in which kinematical connectors were introduced. Liu et al. (2020) proposed different microstructures for 2D and 3D structures, in which they defined the connection area between microstructures using concurrent multiscale topology optimization. Zhou et al. (2019) studied a two-dimensional inverse homogenization method for designing functionally graded materials consisting of graded microstructures, and applied connectivity constraints and an interpolation formulation for cell distribution to ensure connectivity while maintaining the gradient distribution. Garner et al. (2019) presented a method to find the optimal connectivity between topology-optimized microstructures for designing functionally graded materials using an inverse homogenization method and a linearly varied volume fraction constraint, in which the cells were optimized considering the assembly of adjacent cells. Furthermore, Radman et al. (2013) proposed stepwise topology optimization of microstructures for two- and three-dimensional structures to maintain microstructure connectivity. Zhou and Li (2008) proposed a method with kinematic constraints and pseudo-loads for ensuring connectivity in two-dimensional structures. Post-treatment methods have also been proposed for obtaining a continuous design from a multiscale design that separates the macrostructure and the microstructure (Pantz and Trabelsi 2008).

In almost all the concurrent multiscale structural optimization studies reported to date, topology optimization was conducted for optimizing macro- and microstructures. Many of the proposed methods are based on a gradient approach, but evolutionary methods are also used. For example, Xu and Xie (2015) presented a method using the bi-directional evolutionary structural optimization (BESO) method, in which two-dimensional structures were optimized with two types of distributed microstructures within the macrostructure. Huang et al. (2013) studied compliance minimization of a macrostructure by optimizing the microstructures using the BESO method. Yan et al. (2014) investigated compliance minimization using the BESO method for concurrent multiscale topology optimization of 2D and 3D structures. Zhao et al. (2018) utilized the method of moving asymptotes for addressing the optimization of compliance control issues in multiscale and multi-material problems, which have many more design variables than a single material. Evolutionary methods including the evolutionary structural optimization (ESO) method do not guarantee convergence to the solution, but have the advantage of not requiring sensitivity analysis and not causing the grayscale problem. Another feature of such methods is that multiple local solutions including the global optimum solution can be obtained by changing parameters like the element elimination ratio. However, the results obtained by evolutionary methods depend on the discretization scheme. Genetic algorithm (GA) and particle swarm optimization (PSO) also have the feature that multiple local solutions including the global optimum solutions can be obtained. However, they do not seem to be suitable for concurrent multiscale optimization that requires large-scale computation, and their use in this regard has not been reported so far as the authors know.

In concurrent multiscale topology optimization with the SIMP method or the ESO method, the results obtained have stepped or non-smooth boundaries along the finite elements the same as with general topology optimization. When the level-set method is used, the obtained boundaries are not stepped theoretically. However, since boundaries cross the elements, it is necessary to add or generate nodes on the boundaries. Actually, with every topology optimization method, a smoothing treatment such as isosurface processing is required for 3D printing, after topology optimization. This treatment causes both structural performance and volume errors compared with before the treatment.

There have been very few studies on multiscale shape optimization. Barbarosie (2003) studied shape optimization of 2D microstructures using the inverse homogenization method to obtain the desired material properties. The authors presented a shape optimization method of microstructures based on the H¹ gradient method for stiffness maximization of the macrostructure (Fujioka et al. 2021). As far as the authors know, no other paper has been published on shape optimization of concurrent multiscale structures.

Unlike topology optimization, the initial topology is kept in shape optimization until the final shape is obtained. In general, this may be a disadvantage in terms of the degrees of design freedom. However, due to functional and manufacturing requirements, designers may not want to change the topology of the micro- and macrostructures. For example, designers may want to create a closed cell microstructure or to avoid complicated microstructures for manufacturing, and do not want to make multi-connected structures or many holes to prevent strength reduction. In such cases, shape optimization may be suitable. In stiffness design with topology optimization, the obtained shapes of the unit cells are quite simple because of periodicity (Li et al. 2018; Xu et al. 2021). Accordingly, the application of shape optimization to the unit cell design is not necessarily inferior in terms of the degrees of design freedom.

In this study, we propose a shape optimization method for concurrent multiscale optimization of macro- and microstructures, which is based on the H¹ gradient method. The H¹ gradient method is a non-parametric shape optimization method proposed by Azegami (1994). The method has so far been applied to many design problems such as maximum stress and displacement minimization (Shimoda et al. 1997), robust optimization of frame, shell, and solid structures (Shimoda et al. 2019), and shape and topology optimization of laminated shell structures (Shimoda et al. 2021). The main features of this method are that it (1) obtains the clear and smooth optimal (free-form) shape, (2) does not need any parameterization of the design variables, (3) eliminates re-meshing in practical use, and (4) solves the large design problem efficiently by using a distributed-parameter optimization approach. A detailed description of the H¹ gradient method, including its other features, is given in Sect. 4.

In this study, we apply the H¹ gradient method to concurrent shape optimal design of multiscale structures for the first time, and propose a novel concurrent multiscale shape optimization method for stiffness control, i.e., displacement control of the target points. After arbitrarily sectioning a macrostructure into subdomains with independent microstructures, the shapes of the outer and the interface boundaries of the macrostructure are optimized concurrently with the shapes of the unit cells of the microstructures. The homogenization method is used to bridge the macrostructure and microstructures.

The novel aspects of the present paper from an academic standpoint are as follows: (1) Proposal of a newly researched concurrent multiscale shape optimization method, which allows large degrees of design freedom by freely moving the outer shape and the interfaces in addition to multiple microstructures. The zigzag shape problem (or numerical instability) caused by moving all the nodes is stabilized by using the H¹ gradient method. (2) The sensitivity functions including the adjoint equations for stiffness control with respect to the shape variations of the macro- and microstructures and the interfaces are theoretically derived. (3) The validity and superiority of the proposed concurrent method are demonstrated by comparing concurrent optimization with sequential optimization. (4) Considering the application of multiscale optimization to vibration and strength problems, topology optimization is shown to have some difficult problems to be solved such as accurate stress calculation on the boundaries and undesirable local vibration in void regions. Furthermore, topology optimization cannot currently be applied to out-of-plane shape design of plate and shell structures. The proposed method for shape optimization can solve these problems, and this paper provides the basis for its future expansion to such design issues.

The main useful points of the proposed method based on shape optimization are as follows: (1) One advantage of this method is that a detailed, clear, and smooth boundary shape can be obtained. This is advantageous for transferring the obtained finite element (FE) data to a 3D printer. Simple microstructures obtained with the proposed method are preferable considering periodicity and manufacturability. (2) As mentioned above, in standard topology optimization based on the level-set method, SIMP method, and ESO method, a proper post-treatment like isosurface processing is required to create smooth surfaces. This treatment causes both structural performance and volume errors compared with before the treatment. The proposed shape optimization method does not need any post-treatment and never induces errors. (5) Squared error with target displacement in an arbitrary region is used as the objective function. This is also useful in actual design work for a wider range of design application than the minimization of compliance. (6) Using the hole shape in a unit cell as the design boundary also offers the advantage that it is not necessary to worry about the connectivity of unit cells between subdomains. (7) The total area of microstructures is appropriately divided into the subdomains of a macrostructure depending on the magnitude of the sensitivity function. (8) Since a smooth and detailed shape is required, a stress evaluation that is essential in design can be performed. (9) It is also useful when the designer does not want to change the topology from the initial shape, which can be considered as a kind of manufacturing constraint. (10) Providing designers with an alternative method to topology optimization is important from the viewpoint of design diversity, selection, and adaptability according to the intended purpose.

This paper is organized as follows: Sect. 2 is dedicated to the formulation of a multiscale optimization problem. In Sect. 3, the Lagrange function is defined, and the shape gradient functions are derived using the material derivative method. Section 4 focuses on demonstrating the H¹ gradient method and its flow chart. In Sect. 5, numerical calculation results are presented to prove the effectiveness of the proposed method, and the conclusions of this study are summarized in the final part. The notations and the variables are summarized in the Appendix. The derivation of the shape gradient functions is also described in detail in the Appendix.

2 Formulation of multiscale optimization problem

Concurrent multiscale shape optimization is performed in this study using the H¹ gradient method, which is applied to both the macro- and microstructures to determine their detailed, clear, and smooth shapes explicitly.

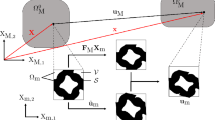
The design variables are the shape variation ${\varvec{V}}_{{}}^{M\left( I \right)}$ distributed on the outer boundary in subdomain I with an independent microstructure in the macrostructure, the shape variation ${\varvec{V}}_{{}}^{{B\left( {KL} \right)}}$ distributed on the interface boundary between subdomains K and L of the macrostructure (Haug et al. 1986; Pantz 2005; Shi and Shimoda 2015), and shape variation of the holes in the microstructures ${\varvec{V}}_{{}}^{\left( I \right)}$. $\left( {\cdot} \right)^{M}$ denotes a variable of the macrostructure. Figure 2 shows an example of a macrostructure with three independent microstructures.

Fig. 2

Design boundaries and subdomains of a multiscale structure with three independent microstructures

The objective function is to minimize the squared error $F_{M}^{(I)} (\varvec{u}^{M} - {\varvec{w}}^{M} ,\varvec{u}^{M} - {\varvec{w}}^{M} )$ between the actual displacement $\varvec{u}^{M}$ and the target displacement ${\varvec{w}}^{M}$ at the target point in subdomain I with an independent microstructure in the macrostructure, and the constraints are the state equation of the macrostructure (Eq. 3) and the homogenization equation of the microstructures (Eq. 6). This objective function can be applied to both stiff and compliant structural designs. Equations (4) and (5) are the conditions to be considered for the displacements and the Cauchy stress vector at the interfaces in the state equation of the macrostructure.

The macroscale domain is represented by $\Omega^{M}$, the displacement vector distributed within $\Omega^{M}$ of the boundary $\Gamma^{M}$ is denoted by ${\varvec{u}}^{M}$, and the target displacement distributed is ${\varvec{w}}^{M}$. $\Gamma^{D}$ is the boundary for defining the target displacement in the macrostructure. $\Gamma^{D}$ can be defined not only on a loaded boundary but also on an arbitrary boundary. ${\varvec{u}}^{M\left( I \right)}$ is the displacement vector of subdomain I $\Omega^{M\left( I \right)}$ in the macrostructure $\Omega^{M}$; it has the associated boundary denoted by $\Gamma^{M\left( I \right)}$, and each subdomain I has the elastic tensor of ${\varvec{E}}_{{}}^{M\left( I \right)}$. $\Gamma^{{M\left( {I,J} \right)}}$ is the interface boundary between subdomain I and adjacent subdomain J. $\Omega^{\left( I \right)}$ is the associated unit cell domain I.

In order to evaluate the homogenized characteristics of the microstructures in the macrostructure, the characteristic displacement ${{\varvec{\chi}}}^{\left( I \right)kl}$ of microstructure I for component kl is calculated for the associated unit initial strain field ${\varvec{I}}^{\left( I \right)kl}$ (See Fujioka et al. (2021) for the state of deformation of the unit cell upon application of the unit initial strain field). $\overline{{\left( {\, \cdot \,} \right)}}$ denotes the virtual displacement, N is the number of domain divisions, and $H_{0}^{1}$ denotes the Sobolev space of order 1.

$$find\quad {\varvec{V}}_{{}}^{M\left( I \right)} , \, {\varvec{V}}_{{}}^{{B\left( {KL} \right)}} , \, {\varvec{V}}_{{}}^{\left( I \right)} , \, \left( {I = 1,2, \ldots ,N} \right),\left( {K,L} \right) = \left( {1,2} \right),\left( {2,3} \right),\left( {3,1} \right), \ldots$$

(1)

$$that\,minimizes\quad \sum\limits_{I = 1}^{N} {F_{M(I)} (\varvec{u}^{M(I)} - {\varvec{w}}^{M(I)} ,\varvec{u}^{M(I)} - {\varvec{w}}^{M(I)} )}$$

(2)

$$subject\,to\quad \sum\limits_{I = 1}^{N} {a_{M\left( I \right)} (\varvec{u}^{M\left( I \right)} ,\overline{\varvec{u}}^{M\left( I \right)} )} - \sum\limits_{I = 1}^{N} {h_{M\left( I \right)} (\varvec{u}^{M\left( I \right)} ,\overline{\varvec{u}}^{M\left( I \right)} )} = \sum\limits_{I = 1}^{N} {l_{M\left( I \right)} (\overline{\varvec{u}}^{M\left( I \right)} )} ,{}^{\forall }\overline{\varvec{u}}^{M\left( I \right)} \in U^{M}$$

(3)

$${\varvec{u}}^{M\left( I \right)} = {\varvec{u}}^{M\left( J \right)} ,\left( {I = 1,2,3} \right),\,\left( {J = 1,2,3} \right),\left( {I \ne J} \right)\;{\text{on}}\;\Gamma^{M(I,J)} ,$$

(4)

$$E_{ijkl}^{M\left( I \right)} u_{k,l}^{M\left( I \right)} n_{j}^{M\left( I \right)} = - E_{ijkl}^{M\left( J \right)} u_{k,l}^{M\left( J \right)} n_{j}^{M\left( J \right)} ,\left( {I = 1,2,3} \right),\,\left( {J = 1,2,3} \right),\,\left( {I \ne J} \right)\,\;{\text{on}}\,\;\Gamma^{M(I,J)}$$

(5)

$$a_{\left( I \right)} ({{\varvec{\chi}}}^{\left( I \right)kl} - {\varvec{I}}^{\left( I \right)kl} ,{\overline{\varvec{\chi }}}^{\left( I \right)kl} ) = 0,\,\,{}^{\forall }{\overline{\varvec{\chi }}}^{\left( I \right)kl} \in U_{Y}^{\left( I \right)} ,\,\,\,\,\,\,\left( {k,l = 1,2} \right),\left( {I = 1,2, \cdots ,N} \right)$$

(6)

The virtual work due to the internal force of the microstructures and the macrostructure is given by Eqs. (7)–(9), the virtual work due to the external force of the macrostructure is given by Eq. (10), and the squared error between the target displacement and the actual displacement of the macrostructure. $F_{M(I)} ( \cdot , \cdot )$ in Eq. (2) is defined by Eq. (11), and $U_{Y}^{\left( I \right)}$ shows the Y-periodic allowable displacement field of microstructure I as shown in Eq. (12). $U^{M}$ in Eq. (3) denotes the kinetically admissible displacement field of the macrostructure.

$$a_{\left( K \right)} ({{\varvec{\chi}}}^{\left( K \right)kl} ,{\overline{\varvec{\chi }}}^{\left( K \right)kl} ) = \int_{{\Omega^{\left( K \right)} }} {E_{ijmn}^{{}} \chi_{m,n}^{\left( K \right)kl} \overline{\chi }_{i,j}^{\left( K \right)kl} } {\text{d}}\Omega^{\left( K \right)} ,\,\left( {K = 1,2, \cdots ,N} \right)$$

(7)

$$a_{M\left( K \right)} ({\varvec{u}}^{M\left( K \right)} ,{\overline{\varvec{u}}}^{M\left( K \right)} ) = \int_{{\Omega^{M\left( K \right)} }} {E_{ijkl}^{M\left( K \right)} u_{k,l}^{M\left( K \right)} \overline{u}_{i,j}^{M\left( K \right)} } {\text{d}}\Omega^{M\left( K \right)} ,\,\left( {K = 1,2, \cdots ,N} \right)$$

(8)

$$h_{M\left( K \right)} ({\varvec{u}}^{M\left( K \right)} ,{\overline{\varvec{u}}}^{M\left( K \right)} ) = \int_{{\Gamma^{{M\left( {K,L} \right)}} }} {E_{ijkl}^{M\left( K \right)} u_{k,l}^{M\left( K \right)} n_{j}^{M\left( K \right)} } \overline{u}_{i}^{M\left( K \right)} {\text{d}}\Gamma^{{M\left( {K,L} \right)}} ,\,\left( {K = 1,2, \cdots ,N} \right),\left( {L = 1,2, \cdots ,N} \right),\left( {K \ne L} \right)$$

(9)

$$l_{M\left( K \right)} ({\overline{\varvec{u}}}^{M\left( K \right)} ) = \int_{{\Gamma^{M\left( K \right)} }} {P_{i} \overline{u}_{i}^{M\left( K \right)} } {\text{d}}\Gamma^{M\left( K \right)} ,\,\left( {K = 1,2, \cdots ,N} \right)$$

(10)

$$F_{M(K)} (\varvec{u}^{M(K)} ,{\varvec{w}}^{M(K)} ) = \int_{{\Gamma^{D} }} {u_{i}^{M(K)} w_{i}^{M(K)} {\text{d}}\Gamma^{D} } ,\,\left( {K = 1,2, \cdots ,N} \right)$$

(11)

$$U_{Y}^{\left( K \right)} = \left\{ {{\overline{\varvec{\chi }}}^{\left( K \right)kl} \in H_{0}^{1} \left( {{\text{Y;}}{\mathbb{R}}^{2} } \right)\,\,\left| {\,\,{\overline{\varvec{\chi }}}^{\left( K \right)kl} \,{\text{is}}\,\,Y-{\text{periodic}}\,{\text{in}}\,{\text{subdomain}}\,K} \right.} \right\},\,\,\left( {k,l = 1,2} \right),\,\left( {K = 1,2, \cdots ,N} \right)$$

(12)

where ${\varvec{n}}_{{}}^{M\left( K \right)}$ is the outward unit normal vector on subdomain K, and ${\varvec{P}}$ is the surface force vector on the macrostructure. In order to bridge the macro- and microstructures, the elastic modulus of the macrostructure is obtained from the microstructures using the homogenization method. The homogenization elastic modulus is obtained with Eq. (13) using the characteristic displacement ${{\varvec{\chi}}}^{\left( I \right)kl}$ obtained with Eq. (6) and the unit cell area $\left| Y \right|$ (Suzuki and Kikuchi 1991; Bendsoe and Kikuchi 1988).

$$E_{ijkl}^{M\left( I \right)} = \frac{1}{\left| Y \right|}\int_{{\Omega^{\left( I \right)} }} {\left( {E_{ijkl}^{{}} - E_{ijmn}^{{}} \frac{{\partial \chi_{m}^{kl\left( I \right)} }}{{\partial y_{n} }}} \right)} {\text{d}}\Omega^{\left( I \right)} ,\left( {I = 1,2, \cdots ,N} \right)$$

(13)

3 Definition of Lagrange function and derivation of shape gradient functions

In this section, we define the Lagrange function based on the problem formulation above and derive shape sensitivity functions (called shape gradient functions) for the macro- and microstructures. The shape gradient functions for the outer boundary and the interface boundaries of the macrostructure and the boundaries of the unit cells are calculated by the Lagrange multiplier method, the adjoint variable method, and the material derivative formula (Choi and Kim 2005). The sensitivity calculation of the interface boundaries is based on methods presented in previous papers (Haug et al. 1986; Pantz 2005; Shi and Shimoda 2015). As will be mentioned in a later section, the optimal shape variations are determined by the derived shape gradient functions.

The Lagrange function for the case of three subdomains in the macrostructure (i.e., N = 3) takes the form:

$$\begin{gathered} L = \sum\limits_{{I = 1}}^{3} {F_{{M\left( I \right)}} \left( {\varvec{u}_{{}}^{{M\left( I \right)}} - {\varvec{w}}_{{}}^{{M\left( I \right)}} ,\varvec{u}_{{}}^{{M\left( I \right)}} - {\varvec{w}}_{{}}^{{M\left( I \right)}} } \right)} + \sum\limits_{{I = 1}}^{3} {\left\{ { - a_{{M\left( I \right)}} \left( {\varvec{u}^{{M\left( I \right)}} ,\varvec{\bar{u}}^{{M\left( I \right)}} } \right) + h_{{M\left( I \right)}} \left( {\varvec{u}^{{M\left( I \right)}} ,\varvec{\bar{u}}^{{M\left( I \right)}} } \right) + l_{{M\left( I \right)}} \left( {\varvec{\bar{u}}^{{M\left( I \right)}} } \right)} \right.} \hfill \\ \left. { - \int_{{\Omega ^{{M\left( I \right)}} }} {\sum\limits_{{k = 1}}^{2} {\sum\limits_{{l = 1}}^{2} {a_{{\left( I \right)}} \left( {{\varvec{\chi }}^{{\left( I \right)kl}} - {\varvec{I}}^{{\left( I \right)kl}} ,{\varvec{\bar{\chi }}}^{{\left( I \right)kl}} } \right)d\Omega ^{{M\left( I \right)}} } } } } \right\} \hfill \\ \end{gathered}$$

(14)

We assume that the derivatives of elastic modulus $E_{ijmn}^{\prime }$ and $I_{m,n}^{{kl^{\prime}}}$ of the microstructures are zero. The derivatives of surface force ${{\varvec{P}^{\prime}}} = 0$, the derivative of the elastic modulus of subdomain I is ${\varvec{E}}_{{}}^{M\left( I \right)\prime } = 0$, and the displacement prescribed boundary $\Gamma^{D}$ and the boundary on which the external force acts do not change shape.

The material derivative $\dot{L}$ of the Lagrange function with respect to the variations of the outer boundary and the interface boundary of the macrostructure, and the boundaries of the unit cells of the microstructures is shown in Eq. (15). $\left( {\, \cdot \,} \right)^{\prime }$ and $\mathop {\left( {\, \cdot \,} \right)}\limits$ denote the shape derivative and the material derivative, respectively (Haug et al. 1986; Choi and Kim 2005). Finally, the shape gradient density functions can be derived as Eqs. (16)–(18).

$$\begin{gathered} \dot{L} = \left\langle {\varvec{G},\varvec{V}} \right\rangle = \sum\limits_{I = 1}^{3} {\int_{{\Gamma^{M\left( I \right)} }} {G^{M\left( I \right)} {\varvec{V}}_{{}}^{M\left( I \right)} \cdot {\varvec{n}}^{{M(I)}} {\text{d}}\Gamma^{M\left( I \right)} } } + \int_{{\Gamma^{{M\left( {1,2} \right)}} }} {G^{{B\left( {12} \right)}} {\varvec{V}}_{{}}^{M\left( 1 \right)} \cdot {\varvec{n}}^{{M{(1)}}} {\text{d}}\Gamma^{{M\left( {1,2} \right)}} } \hfill \\ \, + \int_{{\Gamma^{{M\left( {2,3} \right)}} }} {G^{{B\left( {23} \right)}} {\varvec{V}}_{{}}^{M\left( 2 \right)} \cdot {\varvec{n}}^{{M{(2)}}} {\text{d}}\Gamma^{{M\left( {2,3} \right)}} } + \int_{{\Gamma^{{M\left( {3,1} \right)}} }} {G^{{B\left( {31} \right)}} {\varvec{V}}_{{}}^{M\left( 3 \right)} \cdot {\varvec{n}}^{{M{(3)}}} {\text{d}}\Gamma^{{M\left( {3,1} \right)}} } \hfill \\ \, + \sum\limits_{I = 1}^{3} {\int_{{\Omega^{M\left( I \right)} }} {\left( {\int_{{\Gamma^{\left( I \right)} }} {G_{\left( I \right)} {\varvec{V}}_{{}}^{\left( I \right)} \cdot {\varvec{n}}^{{{(}I{)}}} {\text{d}}\Gamma^{\left( I \right)} } } \right)} {\text{d}}\Omega^{M\left( I \right)} } \hfill \\ \end{gathered}$$

(15)

where

$$G^{M\left( I \right)} = - E_{ijkl}^{M\left( I \right)} u_{k,l}^{M\left( I \right)} \overline{u}_{i,j}^{M\left( I \right)} ,\,\,\,\,\left( {I = 1,2,3} \right),$$

(16)

$$\begin{gathered} G^{{B\left( {KL} \right)}} = - \left( {E_{ijkl}^{M\left( K \right)} u_{k,l}^{M\left( K \right)} \overline{u}_{i,j}^{M\left( K \right)} - E_{ijkl}^{M\left( L \right)} u_{k,l}^{M\left( L \right)} \overline{u}_{i,j}^{M\left( L \right)} } \right) + E_{ijkl}^{M\left( K \right)} u_{k,l}^{M\left( K \right)} n_{j}^{M\left( K \right)} \left( {\overline{u}_{i,q}^{M\left( K \right)} - \overline{u}_{i,q}^{M\left( L \right)} } \right)n_{q}^{M\left( K \right)} , \hfill \\ \left( {K,L} \right) = \left( {1,2} \right),\left( {2,3} \right),\left( {3,1} \right) \hfill \\ \end{gathered}$$

(17)

$$G^{\left( I \right)} = - \frac{1}{\left| Y \right|}\left( {E_{ijkl}^{{}} - E_{ijmn}^{{}} \frac{{\partial \chi_{m}^{\left( I \right)kl} }}{{\partial y_{n} }}} \right)u_{k,l}^{M\left( I \right)} \overline{u}_{i,j}^{M\left( I \right)} - \sum\limits_{k = 1}^{2} {\sum\limits_{l = 1}^{2} {\left( {E_{ijmn}^{{}} \chi_{m,n}^{\left( I \right)kl} \overline{\chi }_{i,j}^{\left( I \right)kl} - E_{ijmn}^{{}} I_{m,n}^{kl} \overline{\chi }_{i,j}^{\left( I \right)kl} } \right)} } ,\,\,\left( {I = 1,2,3} \right)$$

(18)

$G^{M\left( I \right)}$ expressed by Eq. (16) denotes the shape gradient density function for the macro outer boundary of subdomain I of the macrostructure, and $G^{{B\left( {KL} \right)}}$ expressed by Eq. (17) denotes the shape gradient density function for the interface boundary between macrostructure areas K and L (Eq. 22), and $G^{\left( I \right)}$ expressed by Eq. (18) denotes the shape gradient density function for the hole boundary of unit cell I. ${\varvec{n}}_{{}}^{\left( I \right)}$ is the outward unit normal vector on the design boundary of unit cell I. ${\varvec{G}}^{M\left( I \right)} {(} \equiv G^{M\left( I \right)} {\varvec{n}}^{M\left( I \right)} {),} \, {\varvec{G}}^{{B\left( {KL} \right)}} {(} \equiv G^{{B\left( {KL} \right)}} {\varvec{n}}^{B\left( K \right)} {)}$, and ${\varvec{G}}^{\left( I \right)} {(} \equiv G^{\left( I \right)} {\varvec{n}}^{\left( I \right)} {)}$ are vector functions called shape gradient functions.

In Eqs. (16)–(18), ${{\varvec{\chi}}}_{{}}^{\left( I \right)kl}$ and ${\overline{\varvec{\chi }}}_{{}}^{\left( I \right)kl}$ are determined by Eqs. (19) and (20), respectively. Equation (19) is the same as Eq. (6). Equation (20) is the adjoint homogenization equation for the unit cells. $\varvec{u}^{M\left( I \right)}$ and $\overline{\varvec{u}}^{M\left( I \right)}$ are determined by Eqs. (21) and (22). Equation (21) is the same as Eq. (3). Equation (22) is the adjoint equation for the macrostructure.

$$a_{\left( I \right)} ({{\varvec{\chi}}}^{\left( I \right)kl} - {\varvec{I}}^{\left( I \right)kl} ,{\overline{\varvec{\chi }}}^{\left( I \right)kl\prime } ) = 0, \, \,\,\forall {\overline{\varvec{\chi }}}^{\left( I \right)kl\prime } \in U_{Y}^{\left( I \right)} , \, (k,l = 1,2),\left( {I = 1,2,3} \right)$$

(19)

$$a_{\left( I \right)} ({{\varvec{\chi}}}^{\left( I \right)kl\prime } ,{\overline{\varvec{\chi }}}^{\left( I \right)kl} ) = \frac{1}{\left| Y \right|}\left[ {\int_{{\Omega^{\left( I \right)} }} {(E_{ijmn}^{{}} \chi_{m,n}^{\left( I \right)kl\prime } ){\text{d}}\Omega^{\left( I \right)} } } \right]u_{k,l}^{M\left( I \right)} u_{i,j}^{M\left( I \right)} , \, \forall {{\varvec{\chi}}}^{\left( I \right)kl\prime } \in U_{Y}^{\left( I \right)} , \, (k,l = 1,2),\left( {I = 1,2,3} \right)$$

(20)

$$\sum\limits_{I = 1}^{3} {l_{M\left( I \right)} \left( {{\overline{\varvec{u}}}^{M\left( I \right)\prime } } \right)} = \sum\limits_{I = 1}^{3} {a_{M\left( I \right)} \left( {\varvec{u}^{M\left( I \right)} ,\overline{\varvec{u}}^{M\left( I \right)\prime } } \right)} - \sum\limits_{I = 1}^{3} {h_{M\left( I \right)} \left( {\varvec{u}^{M\left( I \right)} ,\overline{\varvec{u}}^{M\left( I \right)\prime } } \right)} , \, \forall {\overline{\varvec{u}}}^{M\left( I \right)\prime } \in U$$

(21)

$$2\sum\limits_{I = 1}^{3} {F_{M\left( I \right)} \left( {\varvec{u}^{M\left( I \right)} - {\varvec{w}}^{M\left( I \right)} ,\varvec{u}^{M\left( I \right)\prime } } \right)} = \sum\limits_{I = 1}^{3} {a_{M\left( I \right)} \left( {\varvec{u}^{M\left( I \right)\prime } ,\overline{\varvec{u}}^{M\left( I \right)} } \right)} - \sum\limits_{I = 1}^{3} {h_{M\left( I \right)} \left( {\varvec{u}^{M\left( I \right)\prime } ,\overline{\varvec{u}}^{M\left( I \right)} } \right)} ,\forall {\varvec{u}}^{M\left( I \right)\prime } \in U$$

(22)

When calculating the macrostructure and unit cells using the finite element method, the mean shape gradient density function $\hat{G}^{\left( I \right)}$ of each domain is calculated by the weighted arithmetic mean of the element. When EN and $A_{el}^{M\left( I \right)}$ are defined as the number of elements in each domain and the element area, respectively, $\hat{G}^{\left( I \right)}$ is expressed using Eq. (23) (Fujioka et al. 2021).

$$\widehat{G}_{{}}^{\left( I \right)} = \frac{1}{{\int_{{\Omega_{{}}^{M\left( I \right)} }} {{\text{d}}\Omega_{{}}^{M\left( I \right)} } }}\int_{{\Omega_{{}}^{M\left( I \right)} }} {G_{el}^{\left( I \right)} {\text{d}}\Omega_{{}}^{M\left( I \right)} } \approx \frac{1}{{\sum\limits_{el = 1}^{EN} {A_{el}^{M\left( I \right)} } }}\sum\limits_{el = 1}^{EN} {G_{el}^{\left( I \right)} A_{el}^{M\left( I \right)} } ,\,\,(I = 1,2,3)$$

(23)

The shape gradient functions thus derived are applied to the H¹ gradient method in order to determine the optimal shapes of the macro- and microstructures.

4 Optimization system with H¹ gradient method

4.1 H¹ gradient method

The H¹ gradient method, a non-parametric shape optimization method, is a gradient method in a function space for obtaining the optimal shape variation distributed on the design boundary (Azegami and Wu 1994; Shimoda et al. 1997). In this study, we apply this method to optimize the shapes of both the macrostructure and the microstructures. Generally, shape optimization methods have issues regarding re-meshing in the shape updating process and ill-conditioning of the obtained shape (or numerical instability that causes a zigzag shape). These issues have been troublesome for designers and have required some corrective techniques. The H¹ gradient method can solve both issues simultaneously.

With the H¹ gradient method, the optimal shape variation can be obtained by applying the shape gradient function derived on the design boundaries of a fictitious linear elastic body as a Neumann or Robin boundary condition. That is, instead of directly moving the nodes of the design boundary using the sensitivity function, a distributed load proportional to the sensitivity function is applied to the design boundary to change the shape, so that not only the boundary nodes but also the internal nodes are appropriately changed. Therefore, re-meshing is practically unnecessary. Moreover, since the sensitivity function is given on the design boundary as a distributed load, a smooth boundary without zigzags is maintained without any additional smoothing process. The positive definiteness of the stiffness matrix of the fictitious linear elastic body plays an important role in reducing the objective function with this gradient method. This smoothing effect was mathematically verified by functional analysis (Azegami et al. 1997). Therefore, the resulting design can be manufactured directly by additive manufacturing.

In this study, the shape gradient functions based on Eqs. (16), (17), and (18) are applied to Eqs. (24) and (25) as external forces in the normal direction to the outer boundary of the macrostructure, the interface boundaries, and the hole boundaries of the microstructures. Equation (24) is the weak form of the governing equation of the H¹ gradient method for the optimal shape variations of the outer boundary ${\varvec{V}}^{M\left( I \right)}$ and the interface shape ${\varvec{V}}^{{B\left( {KL} \right)}}$ of the macrostructure. Equation (25) is also the weak form of the governing equation of the H¹ gradient method for the optimal shape variations of the microstructure ${\varvec{V}}^{\left( I \right)}$.

Figures 3 and 4 show schematics of Eqs. (24) and (25), respectively. The optimal shapes are updated using the obtained shape variations such as ${\varvec{x}}^{new} \varvec{ = x + V}^{M\left( I \right)} , \, {\varvec{x}}^{new} \varvec{ = x + V}^{{B\left( {KL} \right)}} , \, {\varvec{x}}^{new} \varvec{ = x + V}^{\left( I \right)}$.

$$\begin{gathered} a_{M\left( I \right)} \left( {{\varvec{V}}^{M\left( I \right)} + {\varvec{V}}^{{B\left( {KL} \right)}} ,\overline{\varvec{v}}^{M} } \right) = - \left\langle {\Delta s^{M} {(}{\varvec{G}}^{M\left( I \right)} + {\varvec{G}}^{{B\left( {KL} \right)}} {)},\overline{\varvec{v}}^{M} } \right\rangle ,\,\,\,\,\,\forall \overline{\varvec{v}}^{M} \in C_{M} \,,\left( {I = 1,2,3} \right), \, \hfill \\ \, \left( {K,L} \right) = \left( {1,2} \right),\left( {2,3} \right),\left( {3,1} \right), \hfill \\ \end{gathered}$$

(24)

$$a_{\left( I \right)} \left( {{\varvec{V}}^{\left( I \right)} ,\overline{\varvec{v}}} \right) = - \left\langle {\Delta s{\varvec{G}}^{\left( I \right)} ,\overline{\varvec{v}}} \right\rangle \,\,\,\,\,\forall \overline{\varvec{v}} \in C_{\Theta } \,,\left( {I = 1,2,3} \right)$$

(25)

Fig. 3

Schematics of shape variation analyses of macrostructures

Fig. 4

Schematics of shape variation analyses of the microstructure (or unit cell). (b) A unit cell of the microstructure

where $\Delta s^{M}$ and $\Delta s$ are small positive coefficients (called “variation coefficients”) that are multiplied by the shape gradient functions of the macro- and microstructures to adjust the size of the obtained shape variation field, respectively. $\overline{\varvec{v}}^{M}$ and $\overline{\varvec{v}}$ are the virtual displacement vectors of the macrostructure and microstructures, respectively. $C_{M}$ and $C_{\Theta }$ are kinematically admissible function spaces that satisfy the constraints of shape variations such as rigid body displacement or design constraints in the macrostructure and microstructures, respectively. When the state and adjoint equations of Eqs. (19)–(22) are all satisfied, reduction of the objective function is expressed by Eq. (26) (Azegami and Wu 1994; Shimoda et al. 1997).

$$\Delta L \simeq \sum\limits_{I = 1}^{3} {\left\langle {{\varvec{G}}^{M\left( I \right)} ,\Delta s^{M} {\varvec{V}}^{M\left( I \right)} } \right\rangle } + \sum\limits_{I,J = 1}^{3} {\left\langle {{\varvec{G}}^{{M\left( {KL} \right)}} ,\Delta s^{M} {\varvec{V}}^{M\left( I \right)} } \right\rangle } + \sum\limits_{I = 1}^{3} {\left\langle {{\varvec{G}}^{\left( I \right)} ,\Delta s{\varvec{V}}^{\left( I \right)} } \right\rangle \,} < \,0, \, {(}I \ne J{)}$$

(26)

In a concurrent multiscale shape optimization problem, if a certain microstructure distribution is defined, the corresponding macrostructure is determined, and conversely, if a certain macrostructure is defined, the corresponding microstructure distribution is determined. In order to obtain the appropriate microstructure and macrostructure concurrently from innumerable combinations, we used a method of approximately equalizing the number of convergences of both in this study. The amount of shape variations can be controlled by $\Delta s^{M}$ and $\Delta s$ in Eqs. (24) and (25). When the coefficient of the microstructure is larger, the microstructure changes faster. If the value is extremely large, it is equivalent to micro-to-macro hierarchical optimization. Although it is possible to define $\Delta s^{M}$ and $\Delta s$ empirically, in this paper, after optimizing the macrostructure and microstructures independently in advance, the coefficients of variations are adjusted based on the assumption of a linear relationship between the coefficients of variations and the number of convergences. It will be noted that although the relationship between the two is generally not linear because the shape obtained by concurrent optimization is different from those of independent optimizations, in this paper, we use this simple linear method.

4.2 Concurrent shape optimization system

Figure 5 shows a flowchart of the concurrent multiscale shape optimization system developed in this study. In the first step, the initial shapes of the macrostructure and the microstructure, the design boundary, and the target displacement of the macrostructure are defined. Next, the state equation of the microstructure (Eq. 6) is solved using a commercial FEM code to obtain the homogenization elastic tensor (Eq. 13). The state equation of the macrostructure (Eq. 3) is solved using the obtained homogenization elastic tensor in each subdomain, and the squared error between the target and the actual displacements (Eq. 2) is calculated.

Fig. 5

Flowchart of concurrent shape optimization system

The optimization process will continue until converging to the optimal design criteria. If it does not converge, the shape gradient functions of the macro- and microstructures are re-evaluated, and shape variation analyses (Eqs. 24 and 25) are performed to update the shapes of the design boundaries. Equations (24) and (25) are also solved using a commercial FEM code. Another advantage for designers is that an optimization system can be easily constructed using a commercial FEM code without differentiating the stiffness matrices.

5 Numerical calculation results

Simple numerical examples were intentionally selected based on structural mechanics and strength of materials so that the validity of the obtained shape and the appropriateness of the method could be confirmed.

5.1 Microscale optimization and interface optimization

First, the proposed method was applied separately to microscale optimization and interface optimization of a macrostructure in order to confirm the effectiveness of the proposed optimization method for each design problem.

5.1.1 Microscale optimization

This section presents only the optimization results for the microstructure. The target displacements can be arbitrarily defined and the squared error between the actual and the target displacements is minimized. The target displacements were calculated in advance to design Young’s modulus and Poisson’s ratio. It was assumed that the macrostructure consisted of one domain, and that the hole in the microstructure was optimized to obtain the desired Young’s modulus and Poisson’s ratio.

The initial shape of the microstructure is shown in Fig. 6a. The design boundary was the shape of the hole boundary in the unit cell. Figure 6b shows the initial microstructure arranged as 3 × 3 unit cells, and (c) shows the calculated homogenized elastic tensor. Equation (27) was used as the elastic matrix of the solid area in the unit cell.

$${\varvec{E}} = \left[ {\begin{array}{*{20}c} {3.0000} & {1.0000} & {0.0000} \\ {} & {3.0000} & {0.0000} \\ {sym.} & {} & {1.0000} \\ \end{array} } \right]\,\,\,{\text{MPa}}$$

(27)

Fig. 6

Initial shape of the microstructure

Figure 7a and b shows the macro- and microstructure and the boundary conditions used for designing Young’s modulus and the macrostructure for designing Poisson’s ratio, respectively. The macrostructure was a square of 500 mm × 500 mm in size with 1 mm thickness. In the Young’s modulus design, the macrostructure was fixed on the left edge and distributed loads (total 30 N) were applied on the right edge. The displacement prescribed boundary $\Gamma^{D}$ was defined along the right edge. The target displacements on the right edge $w_{1}$ were calculated using Eq. (28), where Young’ modulus in the $x_{1}$ direction was $E_{x1}$ and the total load was F.

$$w_{1} = \frac{F}{{E_{x1} }}$$

(28)

Fig. 7

Macrostructures and boundary conditions for microscale design

Figure 8 shows the optimization results for the target Young’s moduli in the x₁ direction for 1.0, 1.2, and 1.5 MPa, respectively. The target values of $w_{1}$ for 1.0, 1.2, and 1.5 MPa were calculated as 30.0, 25.0, and 20.0 mm, respectively. The final squared error ratios normalized to the initial structure were 1.18 × 10^–5, 1.54 × 10^–4, and 1.23 × 10^–4 for the target Young’s moduli of 1.0, 1.2, and 1.5 MPa, respectively. The results confirm that the optimized microstructures were obtained for the desired Young’s moduli because the squared errors between the target and actual displacements were reduced to almost zero in all three cases. When the target Young’s modulus was 1.5 MPa, the finite element analysis of the microstructure stopped because of mesh crushing. It was then re-meshed in order to continue the calculation.

Fig. 8

Optimization results for Young’s modulus design

Next, the same macro- and microstructures were used in the Poisson’s ratio design as in the Young’s modulus design. The macrostructure was fixed on the left edge and forced displacements were applied on the top and right edge as shown in Fig. 7b. The displacement prescribed boundaries $\Gamma^{D}$ were defined along the top and bottom edges. The target displacements on the right edge $w_{2}$ were calculated using Eq. (29).

$$w_{2} = \nu \frac{\Delta l}{2}$$

(29)

where Poisson’s ratio was $\nu$ and the forced displacement was $\Delta l = 1$ mm.

Figure 9 shows the optimization results for the target Poisson’s ratios of − 0.05, 0.0, and 0.5, respectively. The target values of $w_{2}$ were 0.025, 0.0, and 0.25 mm for − 0.05, 0.0, and 0.5, i.e., the squared error ratios normalized to the initial structure as 1 were 2.04 × 10^–3, 8.41 × 10^–3, and 1.48 × 10^–4 for − 0.05, 0.0, and 0.5, respectively. The results confirm that the optimized microstructures obtained the desired Poisson’s ratios because the squared errors between the target and actual displacements were reduced to almost zero in every case. It was also confirmed that different lateral holes were obtained according to the target displacements, and that the holes were clear and smooth.

Fig. 9

Optimization results for Poisson’s ratio design

5.1.2 Interface optimization

This section describes the numerical results for interface optimization. Figure 10 shows the unit cells with a center hole used for interface optimization and their calculated homogenized elastic moduli. The unit cell size of (a), (b), and (c) was 1 × 1 mm. The hole diameter was 0.2, 0.6, and 0.9 mm for (a), (b), and (c), respectively. Equation (27) was used as the elastic modulus of the solid area in all unit cells. The interface boundaries between the subdomains in the macrostructure were optimized.

Fig. 10

Unit cells with the holes used

Figure 11 shows the problem definitions and the results obtained for two cases. The macrostructure of 100 × 200 mm in size was fixed on the right and left edges, and a downward distributed load (total: 2.2 N) was applied on a part of the top and bottom edges. The macrostructure was sectioned into three subdomains with independent microstructures, as shown in Fig. 11.

Fig. 11

Problem definitions and results of interface optimization

Displacement prescribed boundaries $\Gamma^{D}$ were defined on the loaded edges on the top and bottom. The target value of the vertical displacements on $\Gamma^{D}$ was set as zero ($w_{2} = 0$ mm), corresponding to stiffness maximization. In this analysis, the interface boundaries were optimized under the area constraints for each subdomain. In Fig. 11, the same colors are used for the macrostructures and the unit cells (e.g., the unit cell in red was distributed in the red subdomain).

As case 1, when unit cell C with the biggest hole in Fig. 10c was distributed in the upper and lower subdomains and unit cell A with the smallest hole in Fig. 10a was distributed in the middle subdomain, the objective function was reduced by 10.7 % for maximum stiffness. It can be seen in Fig. 11a that the two interface boundaries obtained were symmetrical.

As case 2, when unit cells B, A, and C in Fig. 10 were, respectively, distributed in the upper, middle, and lower subdomains, the interface boundary between the middle and lower domains changed markedly and the objective function was reduced by 5.5 % for stiffness maximization as shown in Fig. 11b. It was confirmed that the interface shapes obtained were clear and smooth. These results also confirmed that the sensitivity function for the interface boundaries functioned well.

5.2 Concurrent multiscale optimization of both ends fixed beam with holes

The proposed method was applied to concurrent multiscale shape optimization of a both ends fixed beam with holes. As an initial unit cell of the microstructure, unit cell B in Fig. 10b and Eq. (27) were commonly used for all design examples in this section. As mentioned in Sect. 4.1, in all concurrent multiscale design examples in this paper, the macro- and microstructures were optimized separately in advance, and the amount of shape variation was adjusted so that the number of iterations until the convergence would become approximately equal.

5.2.1 Mono-scale optimization and concurrent multiscale optimization

This section presents the calculated results for concurrent optimization, comparing only the macroscale and microscale optimizations.

Figure 12a–c shows the macrostructure of a both ends fixed beam with holes, the half FE model of the macrostructure used, and the design boundaries of the macrostructure, respectively. A distributed load (total: 2.5 N) was applied on the upper edge. The displacement prescribed boundary $\Gamma^{D}$ was defined at a part of the upper edge as shown in Fig. 12b. The target displacements ($w_{2} = - 50.0$ mm) were defined uniformly in the direction of $x_{2}$. The shapes of the two holes and the lower edge were the design boundaries of the macrostructure as shown in Fig. 12c. Only the half domain of the macrostructure was optimized considering symmetricity. The domain was sectioned into eight subdomains, which had independent microstructures. In this optimization example, the outer boundaries, the interface boundaries between the subdomains, and the boundaries of the holes in the microstructure were optimized.

Fig. 12

Initial macrostructure

Figure 13a shows the initial and optimized structures for concurrent optimization, b shows the iteration history (vertical axis: squared error ratio normalized to the initial structure as 1; horizontal axis: number of iterations), and c shows the deformed shapes of the initial and optimized structures, respectively. The squared error ratio of the optimized structure was 1.62 × 10^–3. The objective function converged stably and decreased by 99.8% compared with the initial shape. It was confirmed that the target deformation of the boundary $\Gamma^{D}$ was achieved as shown in Fig. 13b and c as expected, that the optimized microstructures had different shapes according to the shape sensitivity distributions, and that the outer and interface boundaries moved substantially.

Fig. 13

Results of concurrent optimization of the both ends fixed beam

For comparison, Fig. 14a and b shows the results only for the microscale optimization and the macroscale optimization, respectively. In the microscale optimization, the macrostructure was sectioned into eight subdomains. The squared error ratio of the optimized structure was 1.05 × 10^–1 and 3.19 × 10^–3 in the micro- and macroscale optimizations, respectively. Both values were larger than that obtained by concurrent optimization due to the difference in the total number of degrees of design freedom. It was also confirmed that all optimal shapes obtained for the macro- and microstructures had clear and smooth boundaries.

Fig. 14

Results of mono-scale optimization

5.2.2 Concurrent optimization of microstructure and outer boundaries of macrostructure

We investigated the influence of the interface boundary optimization on the final results. Figure 15 shows the optimization results only for the outer boundary of the macrostructure and the holes of the microstructures without any interface optimization. The macrostructure was also sectioned into eight subdomains. The squared error ratio of the optimized structure was 1.95 × 10^–3. A comparison of Figs. 15 and 14 reveal that the optimized shapes of the macro- and microstructures are similar because the sensitivity function of the outer boundaries of the macrostructure was dominant. There is not much difference either in the objective function compared with Figs. 13a and 15. The interface boundaries affected the final performance, but the effect was not very large in the concurrent multiscale optimization.

Fig. 15

Concurrent optimization results for the both ends fixed beam without interface optimization

5.2.3 Concurrent optimization considering the connectivity of adjacent microstructures

As mentioned in Sect. 1, one issue of multiscale optimization concerns connectivity (or compatibility) of adjacent microstructures in additive manufacturing. The proposed shape optimization method automatically achieves unit cell connectivity between subdomains when the hole shapes within the unit cells are defined as the design boundaries. However, if the outer boundaries of the unit cell are added to the design boundaries, it is necessary to consider connectivity between subdomains.

A concurrent multiscale shape optimization was conducted considering connectivity using a simple and widely used method to investigate the influence on the final results. The same design problem as in Sect. 5.2.2 was solved considering connectivity.

Figure 16 shows the concurrent optimization results. This optimization exercise assumed that each subdomain was surrounded by a narrow solid area, which is applicable to all kinds of microstructures involving the connectivity issue. The squared error ratio of the optimized structure was 3.86 × 10^–2, and the objective function was reduced by 96.1%. The reduction was less than in Fig. 13 because the degrees of boundary design freedom were smaller. However, the optimized structure has good connectivity between the subdomains for additive manufacturing.

Fig. 16

Results of concurrent optimization without interface optimization for the both ends fixed beam considering connectivity between subdomains

5.2.4 Hierarchical optimization of microstructure and macrostructure

This section compares the proposed concurrent optimization method with hierarchical (or sequential) optimization. Figure 17a and b shows the results of optimizing the macrostructure first and then optimizing the microstructures (noted as “macro → micro”), and the results of optimizing the microstructures first and then optimizing the macrostructure (noted as “micro → macro”), respectively. In Fig. 17a, the squared error ratio after macroscale optimization was 2.18 × 10^–3 and the squared error ratio of the optimized structure was 3.55 × 10^–4. In Fig. 17b, the squared error ratio after microscale optimization was 1.05 × 10^–1 and the squared error ratio of the optimized structure was 1.98 × 10^–3. A comparison of the optimized structures confirmed that both were a little bit different depending on the order of optimization.

Fig. 17

Hierarchical optimization results for the beam with both ends fixed

The objective functions of the initial and optimized structures in all cases are compared in Fig. 18. The vertical axis is the squared error ratio normalized to the initial structure, and the horizontal axis indicates the methods used. Indicated are the initial structure, the optimized structure of macroscale optimization (Fig. 14b), the optimized structure of microscale optimization (Fig. 14a), the optimized structure of the proposed concurrent optimization (Fig. 13), the optimized structure of concurrent optimization without interface optimization (Fig. 15), the optimized structure of concurrent optimization considering connectivity (Fig. 16), the optimized structure of hierarchical optimization (macro → micro in Fig. 17a), and the optimized structure of hierarchical optimization (micro → macro in Fig. 17a).

Fig. 18

Comparison of squared errors of initial and optimized structures

In all cases except for microscale optimization, the squared error ratios converged to approximately zero. A detailed examination of the results reveals that the smaller the degrees of design freedom, the smaller the decrease in the squared error ratio as expected. The results for the proposed concurrent method are good. However, the best performance was obtained by hierarchical optimization (macro → micro). If the coefficients of variation $\Delta s^{M}$ and $\Delta s$ are optimally adjusted, it appears that both results may be reversed. Basically, changing the outer shape of the macrostructure has the largest effect, so doing this first with the hierarchical method produced better results. However, the concurrent method is advantageous in terms of calculation efficiency because the number of finite element calculations in one iteration required for sensitivity calculations was smaller in the concurrent optimizations than in the hierarchical optimizations. In addition, as there was a definite design problem dependency, the best approach may be to use the two methods selectively.

5.2.5 Stiff and compliant designs

It is possible to define the target displacements arbitrarily with the proposed method as mentioned above. This section describes the application of the proposed concurrent method for obtaining arbitrary stiffness. In Fig. 19a, the target displacement $w_{2}$ was 0 mm, so the squared error ratio of the optimized structure was 9.21 × 10^–3. In Fig. 19b, the target displacement $w_{2}$ was − 100 mm, so the squared error ratio of the optimized structure was 3.52 × 10^–2. Figure 19c shows the deformed shapes of the initial and optimized structures. The objective function decreased greatly in each optimization. The optimized structures had different shapes as expected. It was confirmed that a stiff or compliant structure could be designed with the proposed method according to the target displacement. It was also confirmed that all optimal shapes obtained for the macro- and microstructures had clear and smooth boundaries.

Fig. 19

Optimization results for the both ends fixed beam with two types of target displacement

5.3 Concurrent and mono-scale optimizations of L-shaped bracket

As another design example, the proposed method was applied to an L-shaped bracket with eight subdomains as shown in Fig. 20. The bracket was fixed at the upper edge and a distributed load (total: 0.28 N) was applied along the right edge as shown in Fig. 20a.

Fig. 20

Initial macrostructure

5.3.1 One prescribed boundary problem

The displacement prescribed boundary was defined along the right edge $\Gamma_{\text{side}}^{D}$ to which the distributed load was applied. The uniform target displacements were defined as $w_{1} = - 30.0$ mm on $\Gamma_{\text{side}}^{D}$. The design boundaries were the inner and outer boundaries of the bracket as shown in Fig. 20. The initial shape of the microstructure was unit cell B in Fig. 10b, and the elastic modulus of Eq. (27) was used for the solid area (or the unit cell material).

For comparison, the calculation results for mono-scale optimization of the micro- and macrostructures are shown in Fig. 21a and b, respectively. In the microstructure optimization, the eight independent unit cells were optimized. The normalized squared error ratios were reduced by 3.37 × 10^–1 in the microscale optimization and by 7.67 × 10^–2 in the macroscale optimization.

Fig. 21

Results of mono-scale optimization

Figure 22a–c shows the initial and optimized shapes of the L-shaped bracket for concurrent optimization, the iteration history, and the deformed shapes of the initial and optimized structures, respectively. The squared error ratio of the optimized structure was 2.90 × 10^–2. The objective function converged stably and decreased by 97.1% compared with the initial structure. It was confirmed that the target deformation was achieved and that the proposed method worked well. It was also confirmed that all optimal shapes obtained for the macro- and microstructures had clear and smooth boundaries.

Fig. 22

Results of concurrent optimization of L-shaped bracket

5.3.2 Multi-prescribed boundary problem

As another design example, the proposed method was applied to a multi-prescribed boundary problem. Both $\Gamma_{\text{bottom}}^{D}$ and $\Gamma_{\text{side}}^{D}$ were defined as the displacement prescribed boundary. $\Gamma_{\text{bottom}}^{D}$ was newly defined on a part of the bottom edge with a uniform target displacement of $w_{2} = - 10.0$ mm as shown in Fig. 23a. $\Gamma_{\text{side}}^{D}$ and the target displacement were the same as in Sect. 5.3.1 (i.e., $w_{2} = - 30.0$ on $\Gamma_{\text{side}}^{D}$). The initial shape of the microstructure and the elastic modulus of the unit cell were also the same as in Sect. 5.3.1. The design boundaries in Case (1) were the inner and outer boundaries of the bracket as shown in Fig. 23b and the hole shapes of the unit cells in the subdomains ①–⑧. In case 2, the side boundary of the macrostructure was added to Case 1 as shown in Fig. 23c.

Fig. 23

Multi-prescribed boundary problem of L-shaped bracket

Figure 24a and b shows the optimized macrostructure and unit cells for Case 1, respectively. Figure 25 shows the deformation mode obtained for Case 1. We can see that $\Gamma_{\text{side}}^{D}$ was not deformed uniformly contrary to the aim. The objective function (or squared error) decreased by only 90.8% due to the severe target displacement. Therefore, as Case 2, we added the side boundary as a design boundary to achieve the target displacement as shown in Fig. 23c. Figure 26a and b shows the optimized macrostructure and unit cells for Case 2, respectively. Figure 27 shows the deformation mode obtained for Case 2. We can see that the displacements on $\Gamma_{\text{side}}^{D}$ approached uniformity. The objective function decreased by 92.5%, but the target displacement was not completely attained. In order to achieve multiple target displacements in this design problem, it is presumably necessary to add more design boundaries and to increase the number of subdomains.

Fig. 24

Results obtained for the multi-prescribed boundary problem in Case 1

Fig. 25

Deformation mode for the multi-prescribed boundary problem in Case 1

Fig. 26

Results obtained for the multi-prescribed boundary problem in Case 2

Fig. 27

Deformation mode for the multi-prescribed boundary problem in Case 2

5.4 Initial shape dependency of final results

The proposed gradient-based method has initial shape dependence, similar to the general gradient-based optimization method. This section presents a calculation example of the initial shape dependency of the final results. Figure 28 shows a macrostructure under tension and its boundary conditions. The left edge was restrained as shown in the figure, and a distributed load was applied to the right edge. The displacement prescribed boundaries were defined along the upper and lower edges as $\Gamma_{\text{upper}}^{D}$ and $\Gamma_{\text{lower}}^{D}$. There was one subdomain. Figure 29 shows two types of initial unit cell shapes, the initial displacements, the squared errors, and target displacements on $\Gamma_{\text{upper}}^{D}$ and $\Gamma_{\text{lower}}^{D}$.

Fig. 28

A macrostructure under tension and boundary conditions

Fig. 29

Initial unit cells and target displacements

Case 1 had a circular hole, and Case 2 had a rectangular hole and filleted shape along the outer boundary. The optimized shapes of both cases were compared. In Case 1, only the shape of the hole was used as the design boundary, and in Case 2, the shape of the hole and the outer shape were defined as design boundaries. The target displacements were defined as w₂ = 0.4 on $\Gamma_{\text{upper}}^{D}$ and w₂ = − 0.4 on $\Gamma_{\text{lower}}^{D}$ for both Cases 1 and 2.

Figure 30 shows the optimized shape and the squared errors for Cases 1 and 2. It is seen that the obtained shapes are significantly different between the two cases. Since Case 1 had a small degree of design freedom the squared error was reduced by only 17.8%, and the target displacement was not achieved. In contrast, the squared error became almost zero in Case 2 and the target displacement was achieved.

Fig. 30

Calculated results for Cases 1 and 2

When the displacement squared error is used as the objective function, the initial shape affects the final shape, so the definition of the initial shape is important. To achieve the target displacement, some trial and error is required, but it is important to increase the degrees of design freedom. Specifically, it is important to increase the design boundaries, determine the initial shape while assuming the deformed shape, increase the number of subdomains, and refer to actual past calculation results.

6 Conclusions

We have proposed concurrent shape optimization of multiscale structures, using the H¹ gradient method for controlling the stiffness of the macrostructure. The macrostructures were sectioned into arbitrary subdomains having independent microstructures. The effective elastic modulus in the macrostructure was calculated using the asymptotic homogenization method in order to bridge the macro and microstructures. The squared error between the actual and the target displacements was used as an objective function for designing both stiff and compliant structures. The design boundaries were the outer and interface shapes of the macrostructure and holes in the microstructures. The constraint conditions were the state equations for the macrostructure and the homogenization equations for the microstructures. The shape gradient functions for all design boundaries were theoretically derived. In the numerical examples to confirm the effectiveness of the proposed method, the microscale and interface optimizations were initially verified on the basis of Young’s modulus and Poisson’s ratio design problems. The effectiveness of the proposed concurrent optimization method was then confirmed using a both ends fixed beam and an L-shaped bracket. Mono-scale optimization and hierarchical optimization were also performed and the results were compared. All the results showed that clear and smooth design boundaries were obtained for both macro- and microstructures as expected. The objective functions also stably converged and decreased to almost zero. This means that the stiffness of multiscale structures can be controlled to an arbitrary level or a compliant value with the proposed method.

In future work, we plan to develop a concurrent multiscale shape optimization method for vibration and strength designs based on the current proposed method, and extend its application to shape design problems for plate and shell structures with out-of-plane shape variation of macro- and/or microstructures.

Appendix

1.1 List of symbols

$\left( {\, \cdot \,} \right)^{M}$	Variables for the macrostructure
$\left( {\, \cdot \,} \right)_{M}$	Function defined for the macrostructure
${\varvec{V}}_{{}}^{\left( I \right)}$	Shape variation vector (or field) of unit cell I
${\varvec{V}}_{{}}^{M\left( I \right)}$	Shape variation vector distributed on the outer boundary of subdomain I in the macrostructure
${\varvec{V}}_{{}}^{{B\left( {KL} \right)}}$	Shape variation vector distributed on the interface boundary between subdomains K and L in the macrostructure
$\varvec{u}^{M}$	Actual displacement vector of the macrostructure
${\mathbf{w}}^{M}$	Target displacement vector of the macrostructure
$F_{M}^{(I)} (\, \cdot ,\, \cdot \,)$	Squared error of subdomain I in the macrostructure
$a_{M\left( I \right)} ( \cdot \,,\, \cdot )$	Bilinear form for internal virtual work of subdomain I in the macrostructure
$h_{M\left( I \right)} ( \cdot , \cdot )$	Bilinear form for virtual work by the Cauchy stress vector on the interface Boundary of subdomain I in the macrostructure
$l_{M\left( I \right)} ( \cdot )$	Linear form for external virtual work of subdomain I in the macrostructure
$a_{\left( I \right)} ( \cdot \,,\, \cdot )$	Bilinear form for internal virtual work of unit cell I
$\Omega^{M}$	Domain of the macrostructure
$\Gamma^{M}$	Boundary of macrostructure domain $\Omega^{M}$
$\Gamma^{D}$	Boundary for defining the target displacement in the macrostructure
${\varvec{u}}^{M\left( I \right)}$	Displacement vector in subdomain I in the macrostructure
$\Omega^{M\left( I \right)}$	Subdomain I in the macrostructure
$\Gamma^{M\left( I \right)}$	Boundary of subdomain I in the macrostructure
${\varvec{E}}_{{}}^{M\left( I \right)}$	Elastic tensor of subdomain I in the macrostructure.
$\Gamma^{{M\left( {I,J} \right)}}$	Interface boundary between subdomains I and J in the macrostructure
$\Omega^{\left( I \right)}$	Domain of unit cell I
${{\varvec{\chi}}}^{\left( I \right)kl}$	Characteristic displacement vector of microstructure I for unit initial strain component kl
${\varvec{I}}^{\left( I \right)kl}$	Unit initial strain tensor with the component kl of unit cell I
$\overline{{\left( {\, \cdot \,} \right)}}$	Virtual displacement or adjoint displacement or Lagrange variable
N	Number of domain divisions
$H_{0}^{1}$	Sobolev space of order 1
$U_{Y}^{\left( I \right)}$	Y-periodic allowable displacement space of unit cell I
$U^{M}$	Allowable displacement space of the macrostructure
${\varvec{n}}_{{}}^{M\left( K \right)}$	Outward unit normal vector of subdomain K
${\varvec{n}}_{{}}^{\left( K \right)}$	Outward unit normal vector of microstructure K.
${\varvec{P}}$	Surface force vector on the macrostructure.
$\left| Y \right|$	Periodic unit area of the microstructure.
$\left( {\, \cdot \,} \right)^{\prime }$	Shape derivative.
$\mathop {\left( {\, \cdot \,} \right)}\limits$	Material derivative.
${\varvec{G}}^{M\left( I \right)}$ ($= G^{M\left( I \right)} {\varvec{n}}^{{{(}I{)}}}$)	Shape gradient function for subdomain I in the macrostructure.
$G^{M\left( I \right)}$	Shape gradient density function for subdomain I in the macrostructure.
$G^{{B\left( {KL} \right)}}$	Shape gradient density function for the interface boundary between subdomains K and L.
$G^{\left( I \right)}$	Shape gradient density function for microstructure I
$\hat{G}^{\left( I \right)}$	Mean shape gradient density function in microstructure I
EN	Number of elements in each subdomain
$A_{el}^{M\left( I \right)}$	Area of element el in subdomain I in the macrostructure
$\Delta s^{M}$	Small positive coefficient for macrostructure
$\Delta s$	Small positive coefficient for microstructure
$\overline{\varvec{v}}^{M}$	Virtual displacement vector of the macrostructure
$\overline{\varvec{v}}$	Virtual displacement vector of the microstructure
$C_{M}$	Kinematically admissible function space for the macrostructure
$C_{\Theta }$	Kinematically admissible function space for the unit cell

1.2 Derivation of Eq. (13)

The calculation process for deriving Eq. (15) from Eq. (14) is described here.

Equation (30) shows the material derivative of the first term on the right side of Eqs. (14), and (31), (32), (33), and (34) are the second, third, fourth, and fifth terms, respectively.

$$\dot{L} = 2\sum\limits_{I = 1}^{3} {F_{M\left( I \right)} \left( {\varvec{u}^{M\left( I \right)} - {\varvec{w}}^{M\left( I \right)} ,\varvec{u}^{M\left( I \right)\prime } } \right)}$$

(30)

$$- \sum\limits_{I = 1}^{3} {\left\{ {a_{M\left( I \right)} \left( {{\varvec{u}}^{M\left( I \right)\prime } ,{\overline{\varvec{u}}}^{M\left( I \right)} } \right) + a_{M\left( I \right)} \left( {{\varvec{u}}^{M\left( I \right)} ,{\overline{\varvec{u}}}^{M\left( I \right)\prime } } \right)} \right\}} \, - \sum\limits_{I = 1}^{3} {\int_{{\Gamma^{M\left( I \right)} }} {E_{ijkl}^{M\left( I \right)} u_{k,l}^{M\left( I \right)} \overline{u}_{i,j}^{M\left( I \right)} n_{s}^{M\left( I \right)} V_{s}^{M\left( I \right)} {\text{d}}\Gamma^{M\left( I \right)} } } - \sum\limits_{I = 1}^{3} {\int_{{\Omega^{M\left( I \right)} }} {\left[ {\frac{1}{\left| Y \right|}\int_{{\Omega^{\left( I \right)} }} {\left( { - E_{ijmn}^{{}} \frac{{\partial \chi_{m}^{\left( I \right)kl\prime } }}{{\partial y_{n} }}} \right)} {\text{d}}\Omega^{\left( I \right)} } \right.} } \left. { + \frac{1}{\left| Y \right|}\int_{{\Gamma^{\left( I \right)} }} {\left( {E_{ijkl}^{{}} - E_{ijmn}^{{}} \frac{{\partial \chi_{m}^{\left( I \right)kl} }}{{\partial y_{n} }}} \right)n_{s}^{\left( I \right)} V_{s}^{\left( I \right)} {\text{d}}\Gamma^{\left( I \right)} } } \right]u_{k,l}^{M\left( I \right)} \overline{u}_{i,j}^{M\left( I \right)} {\text{d}}\Omega^{M\left( I \right)}$$

(31)

$$\begin{gathered} \,\,\,\,\,\,\,\,\, + \sum\limits_{I = 1}^{3} {\left\{ {h_{M\left( I \right)} \left( {{\varvec{u}}^{M\left( I \right)\prime } ,{\overline{\varvec{u}}}^{M\left( I \right)} } \right) + h_{M\left( I \right)} \left( {{\varvec{u}}^{M\left( I \right)} ,{\overline{\varvec{u}}}^{M\left( I \right)\prime } } \right)} \right\}} \hfill \\ \,\,\,\,\,\,\,\,\, + \int_{{\Gamma^{{M\left( {1,2} \right)}} }} {\left[ {\left( {E_{ijkl}^{M\left( 1 \right)} u_{k,l}^{M\left( 1 \right)} n_{j}^{M\left( 1 \right)} \overline{u}_{i}^{M\left( 1 \right)} } \right),_{q} n_{q}^{M} + E_{ijkl}^{M\left( 1 \right)} u_{k,l}^{M\left( 1 \right)} n_{j}^{M\left( 1 \right)} \overline{u}_{i}^{M\left( 1 \right)} \kappa^{M\left( 1 \right)} } \right]n_{s}^{M\left( 1 \right)} V_{s}^{M\left( 1 \right)} } {\text{d}}\Gamma^{{M\left( {1,2} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\, + \int_{{\Gamma^{{M\left( {1,3} \right)}} }} {\left[ {\left( {E_{ijkl}^{M\left( 1 \right)} u_{k,l}^{M\left( 1 \right)} n_{j}^{M\left( 1 \right)} \overline{u}_{i}^{M\left( 1 \right)} } \right),_{q} n_{q}^{M} + E_{ijkl}^{M\left( 1 \right)} u_{k,l}^{M\left( 1 \right)} n_{j}^{M\left( 1 \right)} \overline{u}_{i}^{M\left( 1 \right)} \kappa^{M\left( 1 \right)} } \right]n_{s}^{M\left( 1 \right)} V_{s}^{M\left( 1 \right)} } {\text{d}}\Gamma^{{M\left( {1,3} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\, + \int_{{\Gamma^{{M\left( {2,1} \right)}} }} {\left[ {\left( {E_{ijkl}^{M\left( 2 \right)} u_{k,l}^{M\left( 2 \right)} n_{j}^{M\left( 2 \right)} \overline{u}_{i}^{M\left( 2 \right)} } \right),_{q} n_{q}^{M} + E_{ijkl}^{M\left( 2 \right)} u_{k,l}^{M\left( 2 \right)} n_{j}^{M\left( 2 \right)} \overline{u}_{i}^{M\left( 2 \right)} \kappa^{M\left( 2 \right)} } \right]n_{s}^{M\left( 2 \right)} V_{s}^{M\left( 2 \right)} } {\text{d}}\Gamma^{{M\left( {2,1} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\, + \int_{{\Gamma^{{M\left( {2,3} \right)}} }} {\left[ {\left( {E_{ijkl}^{M\left( 2 \right)} u_{k,l}^{M\left( 2 \right)} n_{j}^{M\left( 2 \right)} \overline{u}_{i}^{M\left( 2 \right)} } \right),_{q} n_{q}^{M} + E_{ijkl}^{M\left( 2 \right)} u_{k,l}^{M\left( 2 \right)} n_{j}^{M\left( 2 \right)} \overline{u}_{i}^{M\left( 2 \right)} \kappa^{M\left( 2 \right)} } \right]n_{s}^{M\left( 2 \right)} V_{s}^{M\left( 2 \right)} } {\text{d}}\Gamma^{{M\left( {2,3} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\, + \int_{{\Gamma^{{M\left( {3,1} \right)}} }} {\left[ {\left( {E_{ijkl}^{M\left( 3 \right)} u_{k,l}^{M\left( 3 \right)} n_{j}^{M\left( 3 \right)} \overline{u}_{i}^{M\left( 3 \right)} } \right),_{q} n_{q}^{M} + E_{ijkl}^{M\left( 3 \right)} u_{k,l}^{M\left( 3 \right)} n_{j}^{\left( 3 \right)} \overline{u}_{i}^{M\left( 3 \right)} \kappa^{M\left( 3 \right)} } \right]n_{s}^{M\left( 3 \right)} V_{s}^{M\left( 3 \right)} } {\text{d}}\Gamma^{{M\left( {3,1} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\, + \int_{{\Gamma^{{M\left( {3,2} \right)}} }} {\left[ {\left( {E_{ijkl}^{M\left( 3 \right)} u_{k,l}^{M\left( 3 \right)} n_{j}^{M\left( 3 \right)} \overline{u}_{i}^{M\left( 3 \right)} } \right),_{q} n_{q}^{M} + E_{ijkl}^{M\left( 3 \right)} u_{k,l}^{M\left( 3 \right)} n_{j}^{\left( 3 \right)} \overline{u}_{i}^{M\left( 3 \right)} \kappa^{M\left( 3 \right)} } \right]n_{s}^{M\left( 3 \right)} V_{s}^{M\left( 3 \right)} } {\text{d}}\Gamma^{{M\left( {3,2} \right)}} \hfill \\ \end{gathered}$$

(32)

$$\,\,\,\,\,\,\,\,\, + \sum\limits_{I = 1}^{3} {\left\{ {l_{M\left( I \right)} \left( {{\overline{\varvec{u}}}^{M\left( I \right)\prime } } \right)} \right\}}$$

(33)

$$\begin{gathered} \,\,\,\,\,\,\,\,\, - \sum\limits_{I = 1}^{3} {\int_{{\Omega^{M\left( I \right)} }} {\sum\limits_{k = 1}^{2} {\sum\limits_{l = 1}^{2} {\left\{ {a_{\left( I \right)} \left( {{{\varvec{\chi}}}^{\left( I \right)kl\prime } ,{\overline{\varvec{\chi }}}^{\left( I \right)kl} } \right) + a_{\left( I \right)} \left( {{{\varvec{\chi}}}^{\left( I \right)kl} - {\varvec{I}}^{kl} ,{\overline{\varvec{\chi }}}^{\left( I \right)kl\prime } } \right)} \right\}} } {\text{d}}\Omega^{M\left( I \right)} } } \hfill \\ \,\,\,\,\,\,\,\,\, - \sum\limits_{I = 1}^{3} {\int_{{\Omega^{M\left( I \right)} }} {\int_{{\Gamma^{\left( I \right)} }} {\sum\limits_{k,l = 1,2} {\left( {E_{ijmn} \chi_{m,n}^{\left( I \right)kl} \overline{\chi }_{i,j}^{\left( I \right)kl} - E_{ijmn} I_{m,n}^{\left( I \right)kl} \overline{\chi }_{i,j}^{\left( I \right)kl} } \right)} n_{s} V_{s} {\text{d}}\Gamma^{\left( I \right)} } } {\text{d}}\Omega^{M\left( I \right)} } \hfill \\ \end{gathered}$$

(34)

where, $\kappa^{M\left( I \right)}$ is the curvature of the interface boundary on subdomain I. The relationships between the normal vectors (Eq. 35), the curvatures (Eq. 36), the displacements (Eq. 37), the domain variations (Eq. 38), and the equilibrium forces based on the Cauchy stress vector (Eq. 39) at the interface boundary $\Gamma^{M(I,J)}$ are used to derive Eq. (30)–(34) (Shi and Shimoda 2015).

$${\varvec{n}}^{M\left( I \right)} = - {\varvec{n}}^{M\left( J \right)} ,\left( {I = 1,2,3} \right),\,\left( {J = 1,2,3} \right),\,\left( {I \ne J} \right)$$

(35)

$${{\varvec{\kappa}}}^{M\left( I \right)} = - {{\varvec{\kappa}}}^{M\left( J \right)} ,\left( {I = 1,2,3} \right),\,\left( {J = 1,2,3} \right),\,\left( {I \ne J} \right)$$

(36)

$${\varvec{u}}^{M\left( I \right)} = {\varvec{u}}^{M\left( J \right)} ,\left( {I = 1,2,3} \right),\,\left( {J = 1,2,3} \right),\left( {I \ne J} \right)$$

(37)

$${\varvec{V}}_{{}}^{M\left( I \right)} = {\varvec{V}}_{{}}^{M\left( J \right)} ,\left( {I = 1,2,3} \right),\,\left( {J = 1,2,3} \right)$$

(38)

$$E_{ijkl}^{M\left( I \right)} u_{k,l}^{M\left( I \right)} n_{j}^{M\left( I \right)} = - E_{ijkl}^{M\left( J \right)} u_{k,l}^{M\left( J \right)} n_{j}^{M\left( J \right)} ,\left( {I = 1,2,3} \right),\,\left( {J = 1,2,3} \right),\,\left( {I \ne J} \right)$$

(39)

When the following Eqs. (40)–(43) are satisfied, Eq. (30)–(34) is re-expressed as Eq. (44). Here, Eq. (40) is the state equation for ${{\varvec{\chi}}}_{{}}^{\left( I \right)kl}$ in the unit cell and is the same as Eq. (6). Eq. (41) is the adjoint equation for ${\overline{\varvec{\chi }}}_{{}}^{\left( I \right)kl}$. Eq. (42) is the state equation for $\varvec{u}^{M\left( I \right)}$ in the macrostructure and is the same as Eq. (3). Equation (43) is the adjoint equation for $\overline{\varvec{u}}^{M\left( I \right)}$.

$$a_{\left( I \right)} ({{\varvec{\chi}}}^{\left( I \right)kl} - {\varvec{I}}^{\left( I \right)kl} ,{\overline{\varvec{\chi }}}^{\left( I \right)kl\prime } ) = 0, \, \,\,\forall {\overline{\varvec{\chi }}}^{\left( I \right)kl\prime } \in U_{Y}^{\left( I \right)} , \, (k,l = 1,2),\left( {I = 1,2,3} \right)$$

(40)

$$a_{\left( I \right)} ({{\varvec{\chi}}}^{\left( I \right)kl\prime } ,{\overline{\varvec{\chi }}}^{\left( I \right)kl} ) = \frac{1}{\left| Y \right|}\left[ {\int_{{\Omega^{\left( I \right)} }} {(E_{ijmn}^{{}} \chi_{m,n}^{\left( I \right)kl\prime } ){\text{d}}\Omega^{\left( I \right)} } } \right]u_{k,l}^{M\left( I \right)} u_{i,j}^{M\left( I \right)} , \, \forall {{\varvec{\chi}}}^{\left( I \right)kl\prime } \in U_{Y}^{\left( I \right)} , \, (k,l = 1,2),\left( {I = 1,2,3} \right)$$

(41)

$$\sum\limits_{I = 1}^{3} {l_{M\left( I \right)} \left( {{\overline{\varvec{u}}}^{M\left( I \right)\prime } } \right)} = \sum\limits_{I = 1}^{3} {a_{M\left( I \right)} \left( {\varvec{u}^{M\left( I \right)} ,\overline{\varvec{u}}^{M\left( I \right)\prime } } \right)} - \sum\limits_{I = 1}^{3} {h_{M\left( I \right)} \left( {\varvec{u}^{M\left( I \right)} ,\overline{\varvec{u}}^{M\left( I \right)\prime } } \right)} , \, \forall {\overline{\varvec{u}}}^{M\left( I \right)\prime } \in U$$

(42)

$$2\sum\limits_{I = 1}^{3} {F_{M\left( I \right)} \left( {\varvec{u}^{M\left( I \right)} - {\varvec{w}}^{M\left( I \right)} ,\varvec{u}^{M\left( I \right)\prime } } \right)} = \sum\limits_{I = 1}^{3} {a_{M\left( I \right)} \left( {\varvec{u}^{M\left( I \right)\prime } ,\overline{\varvec{u}}^{M\left( I \right)} } \right)} - \sum\limits_{I = 1}^{3} {h_{M\left( I \right)} \left( {\varvec{u}^{M\left( I \right)\prime } ,\overline{\varvec{u}}^{M\left( I \right)} } \right)} ,\forall {\varvec{u}}^{M\left( I \right)\prime } \in U$$

(43)

Finally, $\dot{L}$ is expressed as Eq. (15), and the shape gradient functions are derived as expressed in Eqs. (16)–(18).

$$\dot{L} = \sum\limits_{I = 1}^{3} {\left\{ { - \int_{{\Gamma^{M\left( I \right)} }} {E_{ijkl}^{M\left( I \right)} u_{k,l}^{M\left( I \right)} \overline{u}_{i,j}^{M\left( I \right)} n_{s}^{M\left( I \right)} V_{s}^{M\left( I \right)} {\text{d}}\Gamma^{M\left( I \right)} } } \right\}}$$

(44)

$$\begin{gathered} \,\,\,\,\,\,\, + \int_{{\Gamma^{{M\left( {1,2} \right)}} }} {\left\{ { - \left( {E_{ijkl}^{M\left( 1 \right)} u_{k,l}^{M\left( 1 \right)} \overline{u}_{i,j}^{M\left( 1 \right)} - E_{ijkl}^{M\left( 2 \right)} u_{k,l}^{M\left( 2 \right)} \overline{u}_{i,j}^{M\left( 2 \right)} } \right) + E_{ijkl}^{M\left( 1 \right)} u_{k,l}^{M\left( 1 \right)} n_{j}^{M\left( 1 \right)} \left( {\overline{u}_{i,q}^{M\left( 1 \right)} - \overline{u}_{i,q}^{M\left( 2 \right)} } \right)n_{q}^{M\left( 1 \right)} } \right\}n_{s}^{M\left( 1 \right)} V_{s}^{M\left( 1 \right)} {\text{d}}\Gamma^{{M\left( {1,2} \right)}} } \hfill \\ \,\,\,\,\,\,\, + \int_{{\Gamma^{{M\left( {2,3} \right)}} }} {\left\{ { - \left( {E_{ijkl}^{M\left( 2 \right)} u_{k,l}^{M\left( 2 \right)} \overline{u}_{i,j}^{M\left( 2 \right)} - E_{ijkl}^{M\left( 3 \right)} u_{k,l}^{M\left( 3 \right)} \overline{u}_{i,j}^{M\left( 3 \right)} } \right) + E_{ijkl}^{M\left( 2 \right)} u_{k,l}^{M\left( 2 \right)} n_{j}^{M\left( 2 \right)} \left( {\overline{u}_{i,q}^{M\left( 2 \right)} - \overline{u}_{i,q}^{M\left( 3 \right)} } \right)n_{q}^{M\left( 2 \right)} } \right\}n_{s}^{M\left( 2 \right)} V_{s}^{M\left( 2 \right)} {\text{d}}\Gamma^{{M\left( {2,3} \right)}} } \hfill \\ \,\,\,\,\,\,\, + \int_{{\Gamma^{{M\left( {3,1} \right)}} }} {\left\{ { - \left( {E_{ijkl}^{M\left( 3 \right)} u_{k,l}^{M\left( 3 \right)} \overline{u}_{i,j}^{M\left( 3 \right)} - E_{ijkl}^{M\left( 1 \right)} u_{k,l}^{M\left( 1 \right)} \overline{u}_{i,j}^{M\left( 1 \right)} } \right) + E_{ijkl}^{M\left( 3 \right)} u_{k,l}^{M\left( 3 \right)} n_{j}^{M\left( 3 \right)} \left( {\overline{u}_{i,q}^{M\left( 3 \right)} - \overline{u}_{i,q}^{M\left( 1 \right)} } \right)n_{q}^{M\left( 3 \right)} } \right\}n_{s}^{M\left( 3 \right)} V_{s}^{M\left( 3 \right)} {\text{d}}\Gamma^{{M\left( {3,1} \right)}} } \hfill \\ \end{gathered}$$

(45)

$$\begin{gathered} \,\,\,\,\,\,\, + \sum\limits_{I = 1}^{3} {\left\{ { - \int_{{\Omega^{M\left( I \right)} }} {\left[ {\frac{1}{\left| Y \right|}\int_{{\Gamma^{\left( I \right)} }} {\left( {E_{ijkl}^{{}} - E_{ijmn}^{{}} \frac{{\partial \chi_{m}^{\left( I \right)kl} }}{{\partial y_{n} }}} \right)u_{k,l}^{M\left( 1 \right)} \overline{u}_{i,j}^{M\left( 1 \right)} n_{s}^{\left( I \right)} V_{s}^{\left( I \right)} {\text{d}}\Gamma^{\left( I \right)} } } \right]} {\text{d}}\Omega^{M\left( I \right)} } \right\}} \hfill \\ \,\,\,\,\,\,\, - \sum\limits_{I = 1}^{3} {\int_{{\Omega^{M\left( I \right)} }} {\left( {\int_{{\Gamma^{\left( I \right)} }} {\sum\limits_{k = 1}^{2} {\sum\limits_{l = 1}^{2} {\left( {E_{ijmn}^{{}} \chi_{m,n}^{\left( I \right)kl} \overline{\chi }_{i,j}^{\left( I \right)kl} - E_{ijmn}^{{}} I_{m,n}^{kl} \overline{\chi }_{i,j}^{\left( I \right)kl} } \right)} } n_{s}^{\left( I \right)} V_{s}^{\left( I \right)} {\text{d}}\Gamma^{\left( I \right)} } } \right)} {\text{d}}\Omega^{M\left( I \right)} } \hfill \\ \end{gathered}$$

(46)

$$\begin{gathered} \, = \sum\limits_{I = 1}^{3} {\int_{{\Gamma^{M\left( I \right)} }} {G^{M\left( I \right)} {\varvec{V}}_{{}}^{M\left( I \right)} \cdot {\varvec{n}}^{{M{(}I{)}}} {\text{d}}\Gamma^{M\left( I \right)} } } + \int_{{\Gamma^{{M\left( {1,2} \right)}} }} {G^{{B\left( {12} \right)}} {\varvec{V}}_{{}}^{M\left( 1 \right)} \cdot {\varvec{n}}^{{M{(1)}}} {\text{d}}\Gamma^{{M\left( {1,2} \right)}} } \hfill \\ \, + \int_{{\Gamma^{{M\left( {2,3} \right)}} }} {G^{{B\left( {23} \right)}} {\varvec{V}}_{{}}^{M\left( 2 \right)} \cdot {\varvec{n}}^{{M{(2)}}} {\text{d}}\Gamma^{{M\left( {2,3} \right)}} } + \int_{{\Gamma^{{M\left( {3,1} \right)}} }} {G^{{B\left( {31} \right)}} {\varvec{V}}_{{}}^{M\left( 3 \right)} \cdot {\varvec{n}}^{{M{(3)}}} {\text{d}}\Gamma^{{M\left( {3,1} \right)}} } \hfill \\ \, + \sum\limits_{I = 1}^{3} {\int_{{\Omega^{M\left( I \right)} }} {\left( {\int_{{\Gamma^{\left( I \right)} }} {G_{\left( I \right)} {\varvec{V}}_{{}}^{\left( I \right)} \cdot {\varvec{n}}^{{{(}I{)}}} {\text{d}}\Gamma^{\left( I \right)} } } \right)} {\text{d}}\Omega^{M\left( I \right)} } \hfill \\ \end{gathered}$$

(15)