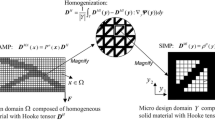
Abstract
This paper proposes a novel multiscale concurrent topology optimization for cellular structures with continuously varying microstructures in space to obtain a superior structural performance at an affordable computation cost. At microscale, multiple prototype microstructures are topologically optimized to represent all the microstructures within macrostructure by incorporating a numerical homogenization approach into a parametric level set method (PLSM), whose connectivity is guaranteed by a kinematical connective constraint approach. A shape interpolation technology is developed to map these optimized prototype microstructures and generate a series of nonuniform microstructures, which are considered as sample points and used to construct a kriging metamodel. The built kriging metamodel is then employed to predict the effective properties of all the nonuniform microstructures within macrostructure. At macroscale, the variable thickness sheet (VTS) method is employed to generate an overall free material distribution patterns using the predicted effective properties of all the nonuniform microstructures. With the help of shape interpolation technology, all the nonuniform microstructures within macrostructure are well connected with each other due to the similar topological features at their interfaces. Using the proposed method, the macrostructural topology as well as the locations and configurations of the spatially varying nonuniform microstructures can be simultaneously optimized to ensure a sufficiently large multiscale design space. Numerical examples are provided to demonstrate the validity and advantages of the proposed method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the past few decades, cellular structures containing porosity and voids have attracted considerable attention owing to their potential to provide fantastic mechanical properties in a broad range of mission-critical applications (Christensen 2000), such as high specific stiffness/strength, impact energy absorption, thermal insulation, and excellent multifunctional responses. In particular, cellular structures are commonly composed of a number of microstructures with ordinary material constituents configured in the design space (Li et al. 2016; Wang et al. 2014). Hence, by optimizing the configurations of microstructures and their layouts within cellular structures, cellular structures are flexible in tailoring specific properties. Besides, the additive manufacturing (AM) technology ensures the realization of fabricating these microstructures with complete geometric shapes (Clausen et al. 2015; Rashed et al. 2016).
Topology optimization is a design tool for a diversity of structures and materials. It has been extensively developed since the pioneer works of Bendsøe and Kikuchi (1988) and Rozvany et al. (1992). So far, several methods have been developed for topology optimization, such as the homogenization method (Allaire 2012; Bendsøe and Kikuchi 1988), solid isotropic material with penalization (SIMP) (Bendsøe and Sigmund 1999; Sigmund 2001), evolutionary structural optimization (ESO) (Huang and Xie 2009; Xie and Steven 1993), and level set method (LSM) (Allaire et al. 2004; Wang et al. 2003).
A more powerful systematic design strategy has been developed to achieve superior macrostructural performance under given sets of loads and boundary conditions by integrating a numerical homogenization method into topology optimization (Sigmund 1994). In this process, a microstructure periodically arranged in macrodesign domain actually behaves like a material, whose length scale is much smaller than that of the macroscopic structure. The effective property of the microstructure is evaluated by the numerical homogenization method, and its geometrical configuration is optimized by the topology optimization method to achieve a desired effective property, such as negative Poisson’s ratios (Andreassen et al. 2014; Wang et al. 2014), extreme shear or bulk moduli (Gao et al. 2018; Huang et al. 2011), extreme thermal expansion coefficients (Sigmund and Torquato 1996; Sigmund and Torquato 1997), multiphysics and multifunctional properties (de Kruijf et al. 2007; Guest and Prévost 2006), functionally graded properties (Li et al. 2018b; Radman et al. 2013; Zhou and Li 2008), and many others (Andreassen and Jensen 2014; Huang et al. 2015). The design strategy is further developed to optimize the microstructures for the macrostructure with the known boundary conditions (Fujii et al. 2001; Huang et al. 2013; Su and Liu 2010). It is noted that the majority of the above researches mainly focus on the design of the material microstructures itself and essentially belong to a single-scale design approach.
From the perspective of a multiscale concurrent design, the geometrical configurations of the material microstructures and the topology of the macrostructure should be optimized simultaneously. Hence, to seek the optimal distribution of the best material, the demand for an efficient multiscale concurrent computational method has become more and more intense (Xia and Breitkopf 2017). Currently, as the first attempt, several interesting studies have been investigated, where the material microstructures are assumed to be identical throughout the entire macrostructure. For example, Liu et al. (2008) presented a concurrent topology optimization method to optimize the topologies of both the macrostructure and its uniformly distributed microstructures for minimum structural compliance. Yan et al. (2014), Wang et al. (2016), and Chen et al. (2017) developed the topology optimization method for concurrent design, where both the topologies of the macrostructure and the configurations of its constituent microstructures were simultaneously optimized under the assumption that the material microstructure was assumed to be uniform over the material region of the macrostructure. With a similar design framework, the concurrent topology optimization has been extended into design problems, such as dynamic optimization (Niu et al. 2008; Vicente et al. 2016), multi-objective optimization (Deng et al. 2012; Yan et al. 2015, 2016), and uncertainly, optimization (Guo et al. 2015; Zheng et al. 2018).
As only one type of material microstructure needs to be optimized, this design approach has remarkably low computational cost. However, it may significantly restrict the design space at both scales, leading to an inferior structural performance. To address this issue, several works have been made, where the macrostructure is composed of several different kinds of microstructures. For instance, Zhang and Sun (2006) proposed a design element (DE) concept and Li et al. (2016) developed a hierarchical multiscale topology optimization method for both structure and materials, where several different microstructures of each layer were designed for a layered structure. Xu and Cheng (2018) investigated a two-scale concurrent design method with multiple microheterogeneous materials based on the criterion for principal stress orientation. Zhang et al. (2018b) proposed a novel multiscale concurrent topology optimization method for cellular structures with multiple microstructures based on ordered SIMP interpolation. Li et al. (2018a) proposed a concurrent design for cellular structures with multipatch microstructures by the discrete element density optimization method. Based on discrete element density optimization method, Deng and Chen (2017) developed a robust concurrent topology optimization approach for the multiscale structures consisting of multiple porous material under random loading uncertainty.
Actually, more general concurrent design strategy should be simultaneously to optimize the topology of the macrostructure and the geometrical configurations of the element-wise varying microstructures, in order to fully explore the design space at both scales and achieve the superior macrostructural performance. In this sense, the designed microstructures varying from point to point may display different geometrical configurations, with different effective properties and relative volume fractions. For example, Rodrigues and his co-workers (Coelho et al. 2008; Rodrigues et al. 2002) proposed a hierarchical computational method for simultaneously optimizing both the material distribution and the local material properties for each mechanical element. Based on the free material optimization concept, Schury et al. (2012) proposed a two-scale optimization method to optimize inhomogeneous macrostructure with the full elastic properties varying from point to point. Xia and Breitkopf (2014) investigated the concurrent design of structure and material under the FE2 nonlinear multiscale analysis framework with point-wise material microstructures. Sivapuram et al. (2016) proposed a new multiscale optimization approach to simultaneously optimize both structure and material, where the positions of all microstructures were predefined and fixed during the optimization. Wang et al. (2017) developed a multiscale concurrent design method to achieve the optimal structure with the spatially varying connectable graded microstructures.
However, two major concerns have to be considered when concurrently designing the macrostructure with spatially varying nonuniform microstructures. The first concern is the intensive computational cost caused by a considerable number of material microstructures to be topologically optimized. Parallel computing scheme is a straightforward method to handle this issue (Coelho et al. 2008; Li et al. 2018a; Xia and Breitkopf 2014). An alternative method is to approximate the material behavior through a reduced database model built from a set of numerical experiments of locally optimized material microstructures (Xia and Breitkopf 2015). The other more critical concern is the connectivity between two adjacent microstructures. Zhou and Li (2008) made an in-depth discussion on this issue and propose different methods to preserve the connectivity between adjacent microstructures. Cramer et al. (2015) proposed a shape interpolation technology between these optimized microstructures with maximum bulk moduli to guarantee the smooth geometrical variation within all graded microstructures. To pursue a superior macrostructural performance with spatially varying connectable nonuniform microstructures at an affordable computation cost, a novel multiscale concurrent optimization method capable of tackling these issues in a direct manner is still in demand.
The main motivation of this paper is to develop a novel multiscale concurrent optimization for cellular structures with spatially varying nonuniform microstructures to fully explore the design space at both scales with an affordable computation cost and obtain the superior macrostructural performance. Firstly, multiple prototype microstructures are topologically optimized to represent all the microstructures within macrostructure by incorporating a numerical homogenization approach into the parametric level set method (PLSM), whose connectivity is guaranteed by a kinematical connective constraint. A shape interpolation technology is developed to interpolate the level set function of these prototype microstructures and generate a series of key nonuniform microstructures as sample points. Based on these sample points, a kriging metamodel is constructed to predict the effective properties of all the nonuniform microstructures within macrostructure. The variable thickness sheet (VTS) method is employed to generate optimized material distribution patterns at macroscale using the predicted effective properties of all the nonuniform microstructures. A number of merits can be expected by using the proposed method: (1) the spatially varying nonuniform microstructures are inherently connected to each other due to the similar topological features at their interfaces; (2) a low computational cost can be expected, as the effective properties of all the nonuniform microstructures within macrostructure are predicted by the kriging metamodel; (3) a large multiscale design space can be expected, because the spatially varying nonuniform microstructures are used and multiple prototype microstructures further expand the advantages of the multiscale concurrent optimization; and (4) the macrostructural topology as well as the locations and configurations of the spatially varying nonuniform microstructures can be simultaneously optimized during the process.
2 Property evaluation for nonuniform microstructures
In this section, effective properties of each nonuniform microstructure within macrostructure are obtained to ensure a sufficiently large design space for the macroscale structural optimization. Note that these prototype microstructures actually refer to the “mother” microstructures that give birth to a series of nonuniform microstructures by shape interpolation technology. Then, they are regarded as sample points to construct kriging metamodel. Finally, the effective properties of all the nonuniform microstructures over the entire macrostructure can be predicted through the kriging metamodel.
2.1 Configuration mapping of nonuniform microstructures
Level set methods are a family of the classification technology of design domain into structural materials and void and have the inherent benefits in obtaining different connectable structural domains by setting the different values of the level set function (Hamza et al. 2014; Wang et al. 2017). In this sense, an efficient shape mapping technology is presented to yield a series of nonuniform microstructures by setting different values of the level set function of the prototype microstructure (ΦPM), which is represented as follows:
where DPM ⊂ Rd (d = 2, 3) is the fixed Eulerian reference domain containing all admissible shapes (ΩPM) of the nonuniform microstructures and ∂ΩPM denotes the structural boundary of the prototype microstructure. x denotes the point coordinates in DPM.
Then, a series of nonuniform microstructures are obtained by interpolating the level set function of the prototype microstructure as follows:
where φe ∈ [max(ΦPM), min(ΦPM)] is the shape-mapping coefficient, i.e., the level set of ΦPM, and ne is the number of nonuniform microstructures. \( {\boldsymbol{\Phi}}_e^{MM} \) is the level set function of the eth mapped nonuniform microstructure. It can be found from (2) that a unique characteristic level set function is taken for describing the shapes of all the nonuniform microstructure, and their corresponding volume fractions (effective densities at macroscale) range from 0 to 1, namely \( {\rho}_e^{MM}\in \left[0,1\right] \). The shape-mapping coefficient (φe) can be found by a bi-sectioning algorithm based on the effective density of nonuniform microstructure. The zero level set of the eth nonuniform microstructure, i.e., \( {\boldsymbol{\Phi}}_e^{MM}\left(\mathbf{x}\right)=0 \), is considered as the structural boundary (\( \partial {\varOmega}_e^{MM} \)), and the corresponding solid regions (\( {\varOmega}_e^{MM} \)) are defined by \( \left\{{\boldsymbol{\Phi}}_e^{MM}\left(\mathbf{x}\right)>0,\kern0.6em \forall \mathbf{x}\in {\mathrm{D}}^{PM}\right\} \).
As different nonuniform microstructures are represented by different layers of the level set function of prototype microstructure, all the nonuniform microstructures are characterized with the similar configuration features, especially at their edges; thus, they are connectable with each other. As shown in Fig. 1, four nonuniform microstructures with effective densities from 0.3 to 0.7 are naturally connected due to their highly similar configurations, which are extracted from different layers of the level set function of the prototype microstructure with effective density, ρPM = 0.5, by setting different level sets of the level set function, i.e., shape-mapping coefficient (φe).
Schematic example to illustrate the shape mapping technology of the level set function
However, it is hard to ensure not yielding unexpected member part breaks when the effective densities (\( {\rho}_e^{MM} \)) of the nonuniform microstructures obtained by mapping one prototype microstructure cover ranged from 0 to 1, such as the mapped microstructures with effective density values 0.1 and 0.9 as shown in Fig. 1b. When the conventional level set-based method is employed to optimize one prototype microstructure, the phenomenon can be alleviated to some extent by using the geometrical reinitialization algorithm that can preserve the gradient property of the signed-distance level set function (Wang et al. 2017). However, in conventional level set-based method, some complicated numerical processes and elaborate schemes are required, e.g., geometrical reinitialization, boundary velocity extensions, and Courant-Friedrichs-Lewy (CFL) condition. In this study, the PLSM is employed to topologically optimize the prototype microstructure, which eliminates these unfavorable numerical features. A specified interval of the mapped density of one prototype microstructure is considered to avoid yielding member part breaks. Meanwhile, to obtain the mapped nonuniform microstructures with effective densities covering from 0 to 1, multiple prototype microstructures are employed, such as \( {\rho}_{m,e}^{MM}\in \left({\rho}_m^{PM}-a,{\rho}_m^{PM}+a\right] \) and a ≤ 0.2, where \( {\rho}_m^{PM} \) is the effective density of the mth prototype microstructure, \( {\rho}_{m,e}^{MM} \) is the effective density of the eth mapped nonuniform microstructure of the mth prototype microstructure, and a is the interval coefficient to ensure all the mapped density interval of prototype microstructures to cover the range from 0 to 1. In addition, as demonstrated in Wang et al. (2017), the unexpected member part breaks would also be yielded when the mapped relative density approached to 0; thus, a relative small mapped density value (fpm) is to be set. To allow for the occurrence of void regions in optimized macrostructure, a Heaviside step function will be utilized during the macrostructure optimization (see Section 3.1).
Different from the explicit strategy by parameterizing a predefined microstructure, the presented shape mapping technology enables scaling without any prior knowledge of the prototype microstructure shape. In addition, it allows topological changes of the nonuniform microstructure. And, multiple prototype microstructures are used to expand the available property space of the nonuniform microstructures. Meanwhile, with the help of the shape interpolation technology, all the nonuniform microstructures over the entire macrostructure are well connected to each other due to the similar topological features at their interfaces.
2.2 Property estimation of mapped nonuniform microstructures
To construct the kriging metamodel, a number of nonuniform microstructures with different effective density values, which are obtained by mapping the corresponding prototype microstructure, would be regarded as sample points. For each prototype microstructure, an appropriate number of effective density values (\( {\rho}_{m,e}^{MM} \)) would be selected firstly, where \( {\rho}_{m,e}^{MM} \) is the arithmetic sequence and \( {\rho}_{m,e}^{MM}\in \left({\rho}_m^{PM}-a,{\rho}_m^{PM}+a\right],\kern0.5em {f}_{pm}\le {\rho}_m^{PM}-a\le {\rho}_m^{PM}+a\le 1 \). In order to find the level set (φe) corresponding to the graded microstructure with the effective density (\( {\rho}_{m,e}^{MM} \)) from the level set function (ΦPM), the bi-sectioning algorithm can be utilized. Specifically, it is assumed that the level set (φe) corresponding to the graded microstructure with the effective density (\( {\rho}_{m,e}^{MM} \)) is located between the level sets with φl and φu, where the initial φl = max(ΦPM) and φu = min(ΦPM), the corresponding initial \( {\rho}_l^{MM}=0 \) and \( {\rho}_u^{MM}=1 \). Then, effective densities \( {\rho}_l^{MM} \), \( {\rho}_u^{MM} \), and \( {\rho}_m^{MM} \) of the microstructures corresponding to these two level sets and their middle level set with φm = (φl + φu)/2 can be calculated through \( {\rho}_{m,e}^{MM}=\frac{1}{\mid {\varOmega}_{m,e}^{MM}\mid }{\int}_{\varOmega_{m,e}^{MM}}d{\varOmega}_{m,e}^{MM} \), where \( {\varOmega}_{m,e}^{MM} \) and \( \mid {\varOmega}_{m,e}^{MM}\mid \) are the design domain and the area or the volume of the eth mapped graded microstructure of the mth prototype microstructure, respectively. By comparing \( {\rho}_{m,e}^{MM} \), \( {\rho}_l^{MM} \), \( {\rho}_m^{MM} \), and \( {\rho}_u^{MM} \), the search interval can be narrowed through the bi-sectioning algorithm, and φl, φu, and φm can be updated. This process is repeated until the final level set (φe) corresponding to the graded microstructure with the effective density (\( {\rho}_{m,e}^{MM} \)) is found.
The effective elasticity tensor of each nonuniform microstructure is calculated via the numerical homogenization method (Andreassen and Andreasen 2014; Sigmund 1994) as follows:
where i, j, k, and l are equal to 1, 2,…, d, and d is the spatial dimension. Dpqrs corresponds to the elasticity tensor of the solid material. \( H\left({\varPhi}_{m,e}^{MM}\right) \) is the Heaviside function to indicate different parts of the design domain. \( {\boldsymbol{\upvarepsilon}}_{pq}^{0(ij)} \) is the macroscopic test unit strain field including three components in two-dimensional (2D) and six components in three-dimensional (3D) cases (Andreassen and Andreasen 2014; Sigmund 1994). The displacement (\( {\mathbf{u}}_{m,e}^{MM(ij)} \)) corresponding to locally varying strain fields (\( {\boldsymbol{\upvarepsilon}}_{pq}^{\ast}\left({\mathbf{u}}_{m,e}^{MM(ij)}\right) \)) can be calculated by solving the following equations at microscale with the given macroscopic strain \( {\boldsymbol{\upvarepsilon}}_{pq}^{0(ij)} \):
where \( {\mathbf{v}}_{m,e}^{MM(kl)} \) is the virtual displacement field and \( \overline{\mathbf{U}}\left({\varOmega}_{m,e}^{MM}\right) \) is the kinematically admissible displacement field satisfying the periodic conditions for the eth mapped nonuniform microstructure.
2.3 Property prediction of nonuniform microstructures based on the kriging metamodel
The kriging metamodel is originally developed and employed for predictions in mining engineering and geostatistics (Simpson et al. 2001). Up to now, it has been widely applied to the field of the mechanical engineering (Hamza et al. 2014; Sakata et al. 2003; Simpson et al. 2004). Recently, the approach that introduces the kriging metamodel into topology optimization is gaining acceptance and accreditation in terms of the reduced computational cost (Yoshimura et al. 2017).
The kriging metamodel of the mth prototype microstructure assumes the combination of a global model and local deviations
where ρMA denotes the prediction point and DH(ρMA) is the observed response. The first term on the right side of (5) provides the global response estimation. f(ρMA) is the ne × 1 vector of regression functions and β is the vector of regression coefficients. In this kriging metamodel, the first-order polynomial regression model is used (Zhang et al. 2018a). Z(ρMA) is the realization function of a stochastic process with mean zero, variance (\( {\sigma}_Z^2 \)), and nonzero covariance. Its covariance can be calculated by
where \( {\boldsymbol{\uprho}}_i^{MA} \) and \( {\boldsymbol{\uprho}}_j^{MA} \) are two sample points and R is the stochastic process correlation function with respect to the unknown correlation parameter vector (θ). The Gaussian correlation function is the most frequently used, which has the following expression:
where \( {\boldsymbol{\uprho}}_{i, mk}^{MA} \), \( {\boldsymbol{\uprho}}_{j, mk}^{MA} \), and θmk are the mkth components of \( {\boldsymbol{\uprho}}_i^{MA} \), \( {\boldsymbol{\uprho}}_j^{MA} \), and θ, respectively. MK represents the dimensions of training points.
The rationale of the kriging metamodel is to provide the unbiased predictor as (8). The mean squared error of the kriging metamodel at the untried point (ρMA) can be written as (9).
where u = FTR−1r(ρMA) − f(ρMA). \( \widehat{\boldsymbol{\upbeta}} \) is the generalized least square estimator of β. r(ρMA) is the correlation vector between the untried point (ρMA), and each of the ne training points (i.e., \( {\rho}_{m,1}^{MM},{\rho}_{m,2}^{MM},...,{\rho}_{m, ne}^{MM} \)). R is the ne × ne correlation matrix. Y is the column vector of true responses at the training points. F is the ne × ne matrix with each row, f(ρMA)T.
It is worth noting that all of the left terms in (7)–(11) are functions of the correlation parameter vector (θ). The maximum likelihood estimation (MLE) method in statistics is usually employed to select the value of θ, which can be obtained by solving the maximization problem as
where
Finally, the construction procedure of the kriging metamodel is transformed into solving an mk-dimensional unconstrained optimization problem. Then, according to the Gaussian process regression theory, the response of ρMA is subject to a normal distribution
At this point, for any graded microstructure with the effective density (ρMA) in the following optimizations, which satisfies the mapping density interval of the corresponding prototype microstructure, i.e., \( {\rho}^{MA}\in \left({\rho}_m^{PM}-a,{\rho}_m^{PM}+a\right] \), its effective elasticity tensor can be obtained by the corresponding kriging prediction model
Obviously, more nonuniform microstructures will lead to higher accuracy of the predicted effective properties. However, it will result in solving more equilibrium equations (4) to obtain more sample data for constructing a kriging metamodel, which will remarkably increase the computational cost. It turns out that ne = 10 key-graded microstructures for each prototype microstructure would find a balance between the accuracy and the computational cost, and the detailed description is given in Section 6.1.
2.4 Test example
A 2D test example as shown in Fig. 2 presents the effective property variation of the mapped nonuniform microstructures versus their effective densities covered from 0.05 to 1 and a series of the nonuniform microstructures generated from three different prototype microstructures, which are optimized for minimum compliance of a classical cantilever beam vertically loaded at the bottom right corner. It can be seen that the effective properties of the mapped nonuniform microstructures range from that of graded microstructure with minimum density (fpm) of 0.05 to that of the solid one, providing a sufficiently large design space for macrostructure optimization, and in the meanwhile, three prototype microstructures further expand the advantages. The connectivity of three prototype microstructures is guaranteed by a kinematical connective constraint (Cadman et al. 2013; Zhou and Li 2008), and with the help of shape interpolation, all the mapped nonuniform microstructures are well connected due to similar configuration features at their interfaces.
Test example to demonstrate the shape mapping technology and kriging metamodel
3 Multiscale concurrent topology optimization with nonuniform microstructures
Figure 3 schematically illustrates the proposed multiscale concurrent optimization for a cantilever beam composed of spatially varying nonuniform microstructures, aiming to minimum macrostructural compliance subject to the global volume constraint. Here, all the nonuniform microstructures are obtained by mapping the shape of three corresponding prototype microstructures. By using the proposed method, the macrostructural topology as well as the locations and configurations of the nonuniform microstructures can be simultaneously optimized. In the following sections, to facilitate the description and discussion, the superscripts “MA” and “MI” are applied to denote the physical quantities at macro- and microscales, respectively.
Schematic of the macrostructure with spatially varying nonuniform microstructures
3.1 Macrostructural topology optimization
To generate the overall material distribution at the macroscale under the allowable material usage constraint, the VTS method is used to solve the compliance topology optimization problem. It is stated as
where C is the structural compliance and G denotes the global volume constraint. Design variable (\( {\rho}_{Ne}^{MA} \)) denotes the relative density of the Neth macroelement, and N denotes the total number of the finite elements over the whole macrostructure. ΩMA denotes the entire macrodesign domain. ε represents the strain field. uMA is the macrodisplacement. vMA is the macrovirtual displacement field belonging to the kinematically admissible displacement field, \( \overline{\mathbf{U}}\left({\varOmega}^{MA}\right) \). \( {V}_0^{MA} \) is the volume of element, and \( {V}_{\mathrm{max}}^{MA} \) denotes the allowable maximum volume of the macrostructure. ρmin = 0.001 and ρmax = 1 are the lower and upper bounds of the macrodesign variable, respectively. The bilinear energy form and the linear load form in (16) used in macro-FE analysis are respectively stated as
where f is the body force in the macrodomain ΩMA, and τ is the traction along the boundary ΓMA. \( {\mathbf{D}}_{ijkl}^{MA}\left({\rho}_{Ne}^{MA}\right) \) is the elasticity tensor of the Neth macroelement with the density \( {\rho}_{Ne}^{MA} \), which can be interpolated by
where \( {\tilde{D}}_{Ne}^0 \) is the variable used to identify the equivalent base material property for the Neth macroelement.
During the concurrent optimization process, each macroelement is regarded as an individual microstructure with the same density. It assumes that the elasticity tensor \( {\mathbf{D}}_{ijkl}^{MA}\left({\rho}_{Ne}^{MA}\right) \) of the Neth macroelement is equivalent to the elasticity tensor \( {\mathbf{D}}_{ijkl}^H\left({\rho}_{Ne}^{MA}\right) \) of one microstructure with the same density, i.e.
where \( {\mathbf{D}}_{ijkl}^H\left({\rho}_{Ne}^{MA}\right) \) can be approximated via the above-constructed kriging metamodel.
According to (19) and (20), \( {\left({\tilde{\mathbf{D}}}_{Ne}^0\right)}_{ijkl} \) can be calculated as follows:
In this study, it is noted that \( {\left({\tilde{\mathbf{D}}}_{Ne}^0\right)}_{ijkl} \) is no longer the natural property of the solid element Ne; it practically acts as a temporal value varying in the concurrent optimization. Before macrostructure optimization at each iteration, the term \( {\left({\tilde{\mathbf{D}}}_{Ne}^0\right)}_{ijkl} \) of each microstructure needs to be calculated by (21), where the \( {\mathbf{D}}_{ijkl}^H\left({\rho}_{Ne}^{MA}\right) \) and \( {\rho}_{Ne}^{MA} \) can be obtained from the previous iteration. Then, the new \( {\left({\tilde{\mathbf{D}}}_{Ne}^0\right)}_{ijkl} \) of each microstructure will be used to update \( {\rho}_{Ne}^{MA} \).
In the optimization problem (10), it is noted that fpm determines the lower bound of the design variables, \( {\rho}_{Ne}^{MA} \). In order to allow for the occurrence of void regions during the optimization process, a Heaviside step function (Hpm) is utilized as follows:
where \( {H}_{pm}=H\left({\rho}_{Ne}^{MA}-{f}_{pm}\right) \), which is equal to 1 for the element with the density over fpm and zeros otherwise, and Dvoid = ρminDsolid is the pseudo-elasticity matrix of the void element to avoid the singularity in the numerical process. By setting fpm to a relative small value close to ρmin, only a few of nonuniform microstructures will be artificially taken as void, which guarantees the numerical convergence with little effect on the accuracy (Wang et al. 2017). In this study, an empirical value, fpm = 0.05, is used to produce reasonably for most design problems.
3.2 Microstructural topology optimization
In this study, multiple prototype microstructures are used to generate graded microstructures as sample points for constructing a kriging metamodel. Then, the kriging metamodel is used to predict the effective property of the graded microstructures from fpm = 0.05 to 1. Before the topological optimization of multiple prototype microstructures, the density clustering is implemented based on the obtained material distribution by (16), in order to efficiently construct the macrofinite element analysis by using the effective properties of multiple prototype microstructures. Namely, all the macroelements with the density \( {\rho}_{Ne}^{MA}\in \left({\rho}_m^{PM}-a,{\rho}_m^{PM}+a\right] \) would be represented by a unique prototype microstructure with the density \( {\rho}_m^{PM} \). The term \( {\tilde{\rho}}_{Ne}^{MA} \) after the density clustering operation can be defined by using the following heuristic scheme (Li et al. 2018a):
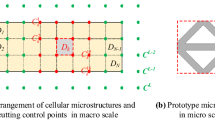
Thus, a limited number of prototype microstructures will be topologically optimized to represent all the graded microstructures with the density \( {\rho}_{Ne}^{MA}\in \left({f}_{pm},1\right] \); for example, five prototype microstructures (\( {\rho}_m^{PM}=0.1,\kern0.3em 0.3,\kern0.3em 0.5,\kern0.3em 0.7,\kern0.3em 0.9,\kern0.52em \mathrm{where}\kern0.3em a=0.1 \)) are used to map all the graded microstructures with the density intervals \( {\rho}_{Ne}^{MA}\in \left({f}_{pm},0.2\right]\kern0.2em \), \( {\rho}_{Ne}^{MA}\in \left(0.2,0.4\right]\kern0.2em \),\( {\rho}_{Ne}^{MA}\in \left(0.4,0.6\right]\kern0.3em \), \( {\rho}_{Ne}^{MA}\in \left(0.6,0.8\right]\kern0.2em \), and \( {\rho}_{Ne}^{MA}\in \left(0.8,1\right]\kern0.1em \), respectively. Here, the effective densities (\( {\rho}_m^{PM} \)) are regarded as the volume fraction constrains during the topological optimization of the prototype microstructures. Thus, the microscale topology optimization of the prototype microstructures can be stated by (19) according to the PLSM based on the compactly supported radial basis functions (CSRBFs).
where M is the types of prototype microstructures and N is the total number of the knots in the microlevel set grid for a prototype microstructure. \( {\boldsymbol{\Phi}}_m^{MI} \) is the level set function in the design domain (\( {\varOmega}_m^{MI} \)) of the mth prototype microstructure and \( {\boldsymbol{\Phi}}_m^{MI}={\boldsymbol{\upvarphi}}_m^{MI}\left(\mathbf{x}\right){\boldsymbol{\upalpha}}_m^{MI}(t) \) in PLSM, where \( {\boldsymbol{\upvarphi}}_m^{MI} \) is the vector of the CSRBF functions and \( {\boldsymbol{\upalpha}}_m^{MI}={\left[{\alpha}_{m,1}^{MI}(t),{\alpha}_{m,2}^{MI}(t),...,{\alpha}_{m,N}^{MI}(t)\right]}^{\mathrm{T}} \) is the vector of the actual design variable of the mth prototype microstructure. \( {\alpha}_{m,n}^{MI} \) indicates the expansion coefficient of the CSRBF interpolation of the nth knot in the microlevel set grid of the mth prototype microstructure. εij and εkl represent the strain field, where i, j, k, l = 1, 2, ..., d and d is the spatial dimension. uMA is the macroscale displacement field, which is calculated by substituting the effective properties \( {\mathbf{D}}_{ijkl}^H \) of all the prototype microstructures into the corresponding state equation \( a\left({\mathbf{u}}^{MA},{\mathbf{v}}^{MA},{\mathbf{D}}_{ijkl}^H\right)=l\left({\mathbf{v}}^{MA}\right) \) at the macroscale, as given in (25). vMA is the macroscale virtual displacement field belonging to the kinematically admissible displacement field \( \overline{\mathbf{U}}\left({\mathbf{u}}^{MA}\right) \). \( {\mathbf{u}}_m^{MI} \) is the microscale displacement field in the design domain \( {\varOmega}_m^{MI} \) of the mth prototype microstructure. \( {V}_0^{MA} \) denotes the volume of a macroscale finite element with solid material. \( {\rho}_m^{PM} \) indicates the relative density of the mth prototype microstructure. Gm is the local volume fraction constraint for the mth prototype microstructure, subjected to the volume fraction \( {\rho}_m^{PM}{V}_0^{MA} \). \( {\tilde{\alpha}}_{\mathrm{min}}^{MI}=0.001 \) and \( {\tilde{\alpha}}_{\mathrm{max}}^{MI}=1 \) are the lower and upper bounds of \( {\tilde{\alpha}}_{m,n}^{MI} \). And, \( {\tilde{\alpha}}_{m,n}^{MI} \) is regularized design variables, which will be used in the optimization algorithm to facilitate the numerical implementation. In this paper, multiple prototype microstructures can be simultaneously topologically optimized by using the parallel computing to improve computational efficiency.
The bilinear energy form defined in (25) is stated as
To evolve the shape and topology of the prototype microstructure at microscale, the following first-order ordinary differential equation (ODE) (Allaire et al. 2004; Wang et al. 2003) is solved:
where t is an artificial pseudo-time to enable the dynamic motion of the shape deformations, and the normal velocity field (\( {\boldsymbol{\upupsilon}}_m^{MI} \)) can be denoted as follows:
As mentioned above, the topology optimization for cellular structure with spatially varying graded microstructures has been formulated through a multiscale concurrent manner. The macroscale and microscale optimizations are actually bridged by the macroelement density (the effective density of the graded microstructure) and the effective property of the prototype microstructures, where the effective property of the macroelement with any density value can be obtained by the means of the kriging approximating model. Compared to the method of concurrently optimizing all the microstructures varying from element to element over the entire macrostructure, the proposed method can greatly reduce the computation cost, since only limited kinds of prototype microstructures are needed to be topologically optimized for cellular structure with spatially varying graded microstructures. Since the configurations of all the graded microstructures are obtained by mapping the shape of these prototype microstructures, their connectivity can be guaranteed well, as described in Section 2.4.
4 Sensitivity analysis
In this paper, the optimality criterion (OC) algorithm (Zhou and Rozvany 1991) is employed to update the design variables at both scales. Hence, it is necessary to calculate the first-order derivatives of the objective function and the constraints with respect to the design variables, where the design variables are the element densities for macrostructure optimization and the expansion coefficients of the CSRBF interpolation for prototype microstructure optimization.
4.1 Sensitivity analysis at macroscale
By the adjoint variable method (Bendsoe and Sigmund 2003; Sigmund 2001), the sensitivity of the structure compliance objective function with respect to the macroscale design variable \( {\rho}_{Ne}^{MA} \) is obtained by
where \( {\varOmega}_{Ne}^{MA} \) denotes the domain of the Neth macroelement.
Based on (21)–(23), \( {\left({\tilde{\mathbf{D}}}_{Ne}^0\right)}_{ijkl}\left({\rho}_{Ne}^{MA}\right) \) can be expressed as follows:
Similarly, the sensitivity of the volume constraint with respect to the macroscale design variable \( {\rho}_{Ne}^{MA} \) is obtained by
4.2 Sensitivity analysis at microscale
In this section, the shape derivative (Allaire et al. 2004; Wang et al. 2003) is introduced to conduct the sensitivity of boundary perturbations with respect to the microscale time variable t. The shape derivatives of C(αMI ), \( a\left({\mathbf{u}}^{MA},{\mathbf{v}}^{MA},{\mathbf{D}}_{ijkl}^H\right) \), and l(vMA) can be respectively calculated by
The following conjugate equation can be established considering the term \( \kern0.1em {\dot{\mathbf{v}}}^{MA} \) contained in (33) and (34)
Differentiating the macroscale equilibrium in (26) with respect to t yields
Substituting (33)–(35) into (36) yields
Considering that the compliance optimization is self-adjoint problem, the shape derivative of the objective function can be rewritten by substituting (37) into (32) as follows:
Based on Li et al. (2016, 2018a) and Wang et al. (2014), the derivative of the effective elasticity tensor \( {\mathbf{D}}_{ijkl}^H \) of material microstructure with respect to t can be stated as
where \( \delta \left({\varPhi}_m^{MI}\right)=\frac{1}{\pi}\cdot \frac{\xi }{{\left({\varPhi}_m^{MI}\right)}^2+{\xi}^2} \) is the derivative of the Heaviside function \( H\left({\varPhi}_m^{MI}\right) \), and ξ is chosen as two to four times the mesh size from numerical experience (Li et al. 2018a; Luo et al. 2009). \( {\boldsymbol{\upupsilon}}_m^{MI} \) denotes the normal velocity within the design domain of mth prototype microstructure.
By substituting the normal velocity \( {\boldsymbol{\upupsilon}}_m^{MI} \) defined in (29) into (39), we obtain
On the other hand, the derivative of the effective elasticity tensor \( {\mathbf{D}}_{ijkl}^H \) with respect to t can be expressed by the chain rule as
Comparing the corresponding terms in (40) and (41), the derivative of the effective elasticity tensor \( {\mathbf{D}}_{ijkl}^H \) with respect to the design variables \( {\alpha}_{m,n}^{MI} \) can be stated as
Recalling (41) and substituting (34) into (41) yields
On the other hand, the derivative of the objective function C(αMI ) with respect to t can be expressed by the chain rule as
Again, comparing the corresponding terms in (43) and (44), the derivative of the objective function C(αMI ) with respect to the design variable \( {\alpha}_{m,n}^{MI} \) can be obtained as
Similarly, the derivative of the local volume constraint Gm(αMI ) with respect to the design variable \( {\alpha}_{m,n}^{MI} \) can be given by
5 Numerical implementation
Figure 4 shows the flowchart of the proposed method for a multiscale concurrent optimization with spatially varying graded microstructures, which mainly contains three stages, i.e., the prototype microstructures optimization at microscale, effective property prediction of all the graded microstructures, and material distribution optimization at macroscale. Firstly, the effective properties (DH) of multiple prototype microstructures are calculated by the homogenization method (3), with the induced displacement field uMI obtained by the micro-FE analysis (4). Based on the macromaterial distribution (\( {\tilde{\boldsymbol{\uprho}}}^{MA} \)) after the clustering operation (24), the macrodisplacement field is obtained via (18) and (26). The sensitivity information is calculated by using (45) and (46). The microdesign variable αMI is updated by the OC algorithm, and the new shapes of prototype microstructures (\( {\boldsymbol{\Phi}}_m^{MI} \)) are outputted. Secondly, an appropriate number of graded microstructures are obtained by mapping the shape of the corresponding prototype microstructure \( {\boldsymbol{\Phi}}_m^{MI} \) (2). The effective properties (\( {\mathbf{D}}_e^H \)) of graded microstructures are calculated by the homogenization method (3) as sample points. The kriging metamodel of the corresponding density interval is constructed by using (5)–(14). Then, the effective properties of all the graded microstructures over the entire macrostructure are predicted via the constructed kriging metamodel. Finally, the macro-FE analysis is implemented to obtain the macrodisplacement fields ((17) and (18)) with the predicting \( {\widehat{\mathbf{D}}}_e^H \). The sensitivities for macroscale optimization can be calculated via (29) and (31). The macrodesign variable ρMA is updated by the OC algorithm. The concurrent optimization at microscale and macroscale is repeated until the optimal design is achieved. In this study, in order to improve computational efficiency, the topology optimizations of multiple prototype microstructures and the effective property calculations of graded microstructures can be simultaneously implemented by using the parallel computing.
Flowchart of numerical implementation of the proposed method
The connectivity of graded microstructures obtained by mapping a kind of prototype microstructure is guaranteed well. However, the connectivity of all the graded microstructures over the entire macrostructure obtained by mapping different kinds of prototype microstructures is determined by the connectivity of multiple prototype microstructures. Therefore, it is necessary to tackle the connectivity issue between the adjacent prototype microstructures to ensure the connectivity of all the graded microstructures for producing a manufacturable design. In this study, the kinematically connective constraint approach (Alexandersen and Lazarov 2015; Cadman et al. 2013; Zhou and Li 2008), as depicted in Fig. 5, is employed to guarantee the connectivity of the adjacent prototype microstructures. The predefined connectors can be achieved by setting the nondesign regions in the design domain (Fig. 5). Note that these predefined connectors will more or less limit the design space in the concurrent optimization, and thus, they may slightly compromise the performance of the optimized design. However, in engineering, it is acceptable to reasonably sacrifice structural performance in order to achieve a manufacturable design (Li et al. 2018a; Zhang et al. 2018b).
Sketch of the predefined connectors between two adjacent prototype microstructures
Predefined connectors (magenta squares or cubes) in prototype microstructures
6 Numerical examples
In this section, several 2D and 3D numerical examples are presented to demonstrate the advantages of the proposed multiscale concurrent optimization method. For all the examples, the materials are subject to plane stress conditions. Young’s modulus of the base material is E0 = 10, and Poisson’s ratio is μ = 0.3. For simplicity, each one finite element at macroscale is represented by a single graded microstructure at microscale. The microstructures are discretized into 50 × 50 four-node elements for 2D cases and 24 × 24 × 24 eight-node elements for 3D cases. Here, the orthotropic material properties are considered, which can be achieved by maintaining geometrical symmetry along X-Y (2D cases) and X-Y-Z (3D cases) directions for all the microstructures. The predefined connectors of 2D and 3D microstructures to guarantee the connectivity between two adjacent prototype microstructures are schematically showed in Fig. 6. In this study, unless otherwise specified, five prototype microstructures (i.e., \( {\rho}_m^{PM}=0.1,\kern0.3em 0.3,\kern0.3em 0.5,\kern0.3em 0.7,\kern0.3em 0.9 \)) are used to generate these corresponding nonuniform microstructures, and a total number of ne = 10 nonuniform microstructures are used to construct the kriging metamodel in the mapping density interval of each prototype microstructure. It implies that only a total number of five prototype microstructures with the intermediate densities need to be topologically optimized in the concurrent optimization. The optimization will terminate when the difference of the objective function values between two successive iterations is lower than 10−4 or the maximum 200 iteration steps of the concurrent optimization is reached.
6.1 Messerschmidt-Bölkow-Blohm beam design
The Messerschmidt-Bölkow-Blohm (MBB) beam with the length (L) of 150 and height (H) of 30 is shown in Fig. 7. It is loaded with a concentrated vertical force F = 5 at the center of the top edge and supported on rollers at the bottom right corner and on fixed supports at the bottom left corner. A mesh with 150 × 30 = 4500 four-node elements is applied to discretize the macrodesign domain. The objective function is to minimize the macrostructure compliance under a global volume constraint of 40%.
Sketch of the MBB beam
The multiscale concurrent design of the MBB beam is presented in Fig. 8, including the optimized macrostructure topology as well as the spatially varying distributed nonuniform microstructures with their optimal configuration. For a better visualization, the detailed nonuniform microstructures of some local regions are magnified. The effective property variations of the mapped nonuniform microstructures versus their effective densities, together with the effective property, configuration, and level set function of the optimized prototype microstructure with the corresponding effective density values 0.1, 0.3, 0.5, 0.7, and 0.9, are plotted in Figs. 9, 10, 11, 12, and 13, respectively. It is noted that the term \( {\mathbf{D}}_e^H\left(2,2\right) \) is eliminated due to the effective property of the graded microstructures near isotropic behavior in Figs. 9 and 10. The iterative histories of the objective function and global volume constraint, as well as the local volume constraint for the five prototype microstructures, are shown in Figs. 14 and 15, respectively. The objective function of the optimized MBB beam converges to C = 193.6650.
Multiscale concurrent design of MBB beam with compliance 193.6650
a Chart of the effective property variation of the mapped nonuniform microstructures versus their effective densities and their configurations. b The effective property, c configuration, and d level set function of the optimized prototype microstructure with the effective density of 0.1
a Chart of the effective property variation of the mapped nonuniform microstructures versus their effective densities and their configurations. b The effective property, c configuration, and d level set function of the optimized prototype microstructure with the effective density of 0.3
a Chart of the effective property variation of the mapped nonuniform microstructures versus their effective densities and their configurations. b The effective property, c configuration, and d level set function of the optimized prototype microstructure with the effective density of 0.5
a Chart of the effective property variation of the mapped nonuniform microstructures versus their effective densities and their configurations. b The effective property, c configuration, and d level set function of the optimized prototype microstructure with the effective density of 0.7
a Chart of the effective property variation of the mapped nonuniform microstructures versus their effective densities and their configurations. b The effective property, c configuration, and d level set function of the optimized prototype microstructure with the effective density of 0.9
Iterative histories of the objective function and global volume constraint
Iterative histories of the local volume constraints of five prototype microstructures
It can be seen from Fig. 8 that the multiscale concurrent design contains a number of graded microstructures with intermediate densities, and the external frame regions are occupied by a number of completely solids or high-density microstructure to effectively bear loading and resist deformation, which accords with the well-accepted design results for the MBB beam (Bendsøe and Kikuchi 1988; Bendsoe and Sigmund 2003; Sigmund 2001). By mapping the five prototype microstructures, all the obtained graded microstructures within the entire macrostructure are well connected with each other, due to their similar configuration features along the common edges, where the connectivity of the five prototype microstructures is guaranteed by the setting of predefined connectors in different prototype microstructures as shown in Fig. 6a. Figures 9, 10, 11, 12, and 13 show that the topologically optimized prototype microstructures behave in an orthotropic form to offer directional stiffness. The effective properties of all the obtained graded microstructures are accordingly bounded by that of the graded microstructure with the minimum density (fpm) of 0.05 and the solid one, and any value in between is reachable and can be obtained. Hence, the graded microstructures with effective density (fpm) from 0.05 to 1 can offer a large design space, and in addition, the topological variation of five prototype microstructures extends the available material property space to further broaden the design space, in order to achieve better structural performance. Figure 14 shows that the macrostructural topology and the graded microstructure distribution are simultaneously optimized during the design process. It takes 95 steps for the concurrent optimization to converge to a lower global compliance. This reveals the validity and efficiency of the proposed multiscale concurrent optimization method. Figure 15 shows a convergence graph of local volume constraints for five prototype microstructures with their initial designs and some snapshots during convergence, where five prototype microstructures are converged rather quick and reach the convergence configurations after about 20 iteration steps. It can be seen from Figs. 14 and 15 that the global volume constraint is conserved all the time, while the local volume constraints of all the prototype microstructures are satisfied gradually as optimization process. The violation of local volume constraints accounts for the increase of the objective function at the first few steps. When the local volume constraints of all the prototype microstructures are satisfied, the macrostructural compliance starts to reduce gradually.
To demonstrate the accuracy of the kriging metamodel, five non-key-graded microstructures with effective densities of 0.125, 0.367, 0.433, 0.678, and 0.945 are selected as illustrative examples, which can be obtained by mapping the five corresponding optimized prototype microstructures with effective densities of 0.1, 0.3, 0.5, 0.7, and 0.9. As shown in Table 1, the effective elasticity properties of five non-key-graded microstructures predicted by the kriging metamodel and those calculated strictly by using the homogenization method have very little difference, and the maximum error between these two methods among five non-key-graded microstructures is even less than 0.057%. For further explanation, the effective properties of all the mapped nonuniform microstructures within the entire macrostructure are calculated directly by the homogenization method (3). The obtained macrostructural compliance is CHM = 193.7141, which is only 0.0254% larger than that obtained by the kriging metamodel (C = 193.6650). The high consistency of the effective properties and objective functions calculated by these two methods demonstrates the high accuracy of the kriging metamodel applied to predict the effective properties of the nonuniform microstructures.
To show the advantages of the proposed multiscale concurrent optimization method, the optimized design is compared with the one-scale macrostructural design with PLSM, the one-scale homogeneous microstructural design, as well as the concurrent design with topologically optimized microstructures varied from element to element under the same global volume constraint of 40%. The optimized designs obtained by the one-scale macrostructural and microstructural design method are shown in Figs. 16 and 17, respectively. It is obvious that the proposed multiscale concurrent design has the compliance lower than that of the one-scale macrostructural and microstructural design, even with an over half lower compliance compared to that of the one-scale microstructural design. The reason is that the proposed multiscale concurrent optimization method can greatly extend the design space by simultaneously optimizing the macrostructural topology, as well as the configurations of the prototype microstructures and the spatially varying graded microstructure distributions within macrostructure. The concurrent design with topologically optimized microstructures varied from element to element is presented in Fig. 18, which ensures fully enough large design space at both scales. In this proposed multiscale concurrent design method, the obtained macrostructural performance is nearly close to that in Fig. 18. However, the proposed multiscale concurrent design method has significantly lower computational cost than the concurrent design method shown in Fig. 18, since only five kinds of prototype microstructures need to be topologically optimized for cellular structure with spatially varying graded microstructures.
Macrostructural design with compliance 201.9728
Microstructural design with compliance 497.8023
Concurrent design with spatially varying optimized microstructures with compliance 189.2433
The multiscale concurrent designs achieved with different numbers of the prototype microstructures and nonuniform microstructures are also investigated. The numbers of prototype microstructures and the corresponding optimized compliances with ten nonuniform microstructures are listed in Table 2. The numbers of nonuniform microstructures and the corresponding optimized compliances with five prototype microstructures are listed in Table 3. As the distributions of all the nonuniform microstructures within macrostructure and the optimized configurations of the prototype microstructures are almost the same to those in Figs. 8, 9, 10, 11, 12, and 13, they are not presented here. It can be seen from Table 2 that a lower compliance can be achieved, when more prototype microstructures are employed. That is because more prototype microstructures can enable to achieve a larger space of material properties. However, more prototype microstructures employed in the proposed method will result in topologically optimizing more prototype microstructures, and it will remarkably increase the computational cost. It can be seen from Table 3 that more nonuniform microstructures are used, and the closer the optimized compliance is to the value calculated by the homogenization method (CHM = 193.7141). However, more nonuniform microstructures will result in solving more equilibrium equations (4), and it will also linearly increase the computational cost. But from an overall perspective, the numbers of nonuniform microstructures have little influence on the optimized compliance. This is mainly because of the high prediction accuracy of the kriging metamodel. Therefore, five prototype microstructures and ten key-graded microstructures would be a reasonable choice to achieve trade-off between the structural performance, the computational cost, and the accuracy.
6.2 L-bracket design
As depicted in Fig. 19, the L-bracket beam is loaded with a concentrated vertical force (F) of 5 at the top position of the structural right side, and the top of the structure is fixed, where the structure size is L = 80. The design domain of macrostructure is discretized into 80 × 80 = 6400 four-node elements. The objective function is to minimize the macrostructural compliance under global volume fraction constraints. In this example, three different kinds of the global volume fraction constraints are selected, i.e., 45%, 30%, and 15%, and five prototype microstructures and ten mapped nonuniform microstructures for each prototype microstructure are used.
Sketch of L-bracket
The result of the multiscale concurrent design under the global volume constraint of 15% is presented in Fig. 20, and the optimized compliance converges to 1641.1463. Figure 20a, b shows the optimized macrostructural topology and the spatially varying distributed graded microstructures with their optimal configuration, respectively. Figure 20c shows the configurations of five optimized prototype microstructures with effective density values of 0.1, 0.3, 0.5, 0.7, and 0.9, as well as the effective property variation of the mapped graded microstructures versus their effective densities (fpm) from 0.05 to 1. The iterative histories of the objective function and global volume constraint, as well as the local volume constraint for five prototype microstructures, are plotted in Fig. 20d, e, respectively. Similar to Figs. 20, 21 and 22 present the results of the multiscale concurrent design under the corresponding global volume constraints of 30% and 45%, and the optimized compliance converges to 702.0868 and 478.8932, respectively.
Multiscale concurrent design with the volume fraction of 15%. The compliance is 1641.1463
Multiscale concurrent design with the volume fraction of 30%. The compliance is 702.0868
Multiscale concurrent design with the volume fraction of 45%. The compliance is 478.8932
It can be seen from Figs. 20c, 21c, and 22c that all the optimized prototype microstructures have orthotropic properties to offer directional stiffness, and the effective properties of all the obtained graded microstructures are accordingly bounded by that of the graded microstructure with the minimum density (fpm) of 0.05 and the solid one, which enable to supply a larger design space. Also, it is obvious that the effective properties of all the graded microstructure within macrostructure under the global volume fraction of 15% show more remarkable orthotropic properties than those under global volume fractions of 30% and 45%. This is mainly caused by the fact that when the smaller material usage is set, the more percentage of the intermediate density elements exists in the external frame regions of the L-bracket, which mainly bear deformation in the vertical direction and can provide more design freedom for the design of material microstructure with higher stiffness in the vertical direction compared with the completely solids with isotropic properties. Figures 20d, 21, and 22d show the concurrent optimization of macrostructural topology and the distribution of graded microstructures under the global volume constraints of 15%, 30%, and 45%, respectively. During the concurrent optimization process, the value of the global volume fraction keeps quite stable, and the macrostructural compliance increases at the first few steps. This is mainly because of the violation of local volume constraints, as shown in Figs. 20e, 21e, and 22e. When the local volume constraints of all the prototype microstructures are satisfied, the macrostructural compliance starts to reduce gradually. The concurrent optimization under the global volume constraints of 15%, 30%, and 45% converges to the final value after 115, 100, and 93 iteration steps, respectively. This also reveals the efficiency of the proposed multiscale concurrent optimization method.
Figure 23 shows the multiscale concurrent design of L-bracket under different global volume fractions. It is obvious that as the value of the global volume fraction increases, the optimized macrostructural compliance decreases. The optimized macrostructural topology and the distribution of spatially varying graded microstructures have no significant difference among various volume fractions. More importantly, the optimized design of the proposed method is also enable to keep stable when the global volume constraint is at a very low level, such as 7.5% and 10%, which is attractive for pursuing ultralight structure design. It can be seen that the solid materials or the higher-density microstructures with the high stiffness in vertical direction are mainly distributed at the edges of the L-bracket. The shear-resistant material microstructure with lower density is distributed in interval regions of the L-bracket. It makes sense for this kind of arrangement of the graded microstructure for the L-bracket, which can more effectively improve the bending stiffness and resist deformation caused by the external load. Hence, this demonstrates the validity and flexibility of the proposed method in fully making use of the effective properties of different graded microstructures to maximize their abilities to bear the loading.
Macrostructural compliance variation of the optimized L-bracket versus various global volume fractions and their optimized cellular structural configurations
6.3 Three-dimensional cantilever beam design
A 3D cantilever beam with the length (L) of 64, width (W) of 10, and height (H) of 16 is shown in Fig. 24. A concentrated load (F) of 5 is vertically applied at the middle of the right end, and the left end is fixed. The macrostructure is discretized by using 64 × 10 × 16 eight-node elements. The objective function is to minimize the structural compliance under the global volume fraction constraints of 20% and 40%, respectively. Five prototype microstructures and ten nonuniform microstructures for each prototype microstructure are considered. For comparison, the one-scale macrostructure designs with PLSM under the same volume fraction constraints are provided.
Sketch of the 3D cantilever beam
The result of the multiscale concurrent design for 3D cantilever beam under the global volume constraint of 20% is presented in Fig. 25, and its compliance is 185.4979. For a better visualization on the internal structures, the multiscale concurrent design presented in Fig. 25a is further displayed with several masked graded microstructures, as shown in Fig. 25b, c. Figure 25d shows the configurations of the five optimized prototype microstructures with the effective density of 0.1, 0.3, 0.5, 0.7, and 0.9, as well as the effective property variation of the mapped nonuniform microstructures versus their effective densities (fpm) from 0.05 to 1. Similar to Figs. 25 and 27 presents the results of the multiscale concurrent design for 3D cantilever beam under the global volume constraints of 40%, and the optimized compliance converges to 101.7465. As expected, for 3D structure, the designs obtained by using the proposed multiscale concurrent optimization method also keep good connectivity in geometry, due to the setting of predefined connectors as shown in Fig. 6b. As shown in Figs. 25 and 26, the solid materials or the higher-density graded microstructures are distributed at the upper and lower surfaces of the macrostructure, and the lower-density graded microstructures are located at the region between the upper and lower surfaces, which can more effectively resist the deformation caused by the external loads. The graded microstructures are reinforced and supply directional stiffness mainly in the X and Z directions, as the major deformations of the entire macrostructure under the boundary conditions shown in Fig. 24 are along these two directions.
Multiscale concurrent design with the volume fraction of 20%. The compliance is 185.4979
Multiscale concurrent design with the volume fraction of 40%. The compliance is 101.7465
Figure 27 shows the one-scale macrostructure design with PLSM under the global volume constraint of 40%, and its compliance is 121.7254. The macrostructural compliance of the proposed multiscale concurrent optimization method is 16.41% lower than that of the one-scale macrostructure design for 3D structure, and 4.11% lower for 2D structure in the first example. It is noticed the macrostructural performance achieved by the proposed multiscale concurrent optimization method for 3D structure is improved more significantly than that for the 2D structure. This is mainly caused by the fact that the design space of a 3D problem is much larger than that of a 2D problem, and the proposed multiscale concurrent optimization method can effectively explore the larger design space to obtain a better macrostructural performance. This also reveals the excellent capacity of the proposed multiscale concurrent optimization for the 3D structures.
Macrostructure designs of the 3D cantilever beam with the volume fraction of 40%. The compliance is 121.7254
7 Conclusions and future work
This paper proposes a novel multiscale concurrent topology optimization method for cellular structures with spatially varying nonuniform microstructures. In the proposed method, the macrostructural topology as well as the locations and configurations of the nonuniform microstructures within the entire macrostructure are simultaneously optimized. At microscale, multiple prototype microstructures are topologically optimized to represent all the microstructures within macrostructure by incorporating the numerical homogenization approach into PLSM. A shape interpolation technology is developed to map these optimized prototype microstructures to generate a series of nonuniform microstructures. The kriging metamodel is constructed by using the mapped nonuniform microstructures to predict the effective properties of all the nonuniform microstructures within macrostructure. At macroscale, the VTS method is employed to generate an optimized material distribution using the predicted effective properties of nonuniform microstructures. Due to their similar topological features at their edges, all the mapped nonuniform microstructures within macrostructure are inherently connected. The effective properties of all the nonuniform microstructures within macrostructure are predicted by the kriging metamodel, which can bring the considerable reduction of the computational cost. The spatially varying nonuniform microstructures fully broaden the design space, and multiple prototype microstructures further expand the capability of substantially improving the macrostructural performance. Numerical examples are presented to test the advantages of the proposed multiscale concurrent optimization in improving the macrostructural performance and pursuing ultralight structure design. The future work is to extend the proposed multiscale concurrent optimization method to other application fields, such as dynamics and functionally graded and multifunctional materials.
References
Alexandersen J, Lazarov BS (2015) Topology optimisation of manufacturable microstructural details without length scale separation using a spectral coarse basis preconditioner. Comput Methods Appl Mech Eng 290:156–182. https://doi.org/10.1016/j.cma.2015.02.028
Allaire G (2012) Shape optimization by the homogenization method vol 146. Springer Science & Business Media
Allaire G, Jouve F, Toader A-M (2004) Structural optimization using sensitivity analysis and a level-set method. J Comput Phys 194:363–393
Andreassen E, Andreasen CS (2014) How to determine composite material properties using numerical homogenization. Comput Mater Sci 83:488–495
Andreassen E, Jensen JS (2014) Topology optimization of periodic microstructures for enhanced dynamic properties of viscoelastic composite materials. Struct Multidiscip Optim 49:695–705
Andreassen E, Lazarov BS, Sigmund O (2014) Design of manufacturable 3D extremal elastic microstructure. Mech Mater 69:1–10
Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71:197–224
Bendsøe MP, Sigmund O (1999) Material interpolation schemes in topology optimization. Arch Appl Mech 69:635–654
Bendsoe MP, Sigmund O (2003) Topology optimization: theory, methods, and applications. Springer, Berlin
Cadman JE, Zhou S, Chen Y, Li Q (2013) On design of multi-functional microstructural materials. J Mater Sci 48:51–66
Chen W, Tong L, Liu S (2017) Concurrent topology design of structure and material using a two-scale topology optimization. Comput Struct 178:119–128. https://doi.org/10.1016/j.compstruc.2016.10.013
Christensen RM (2000) Mechanics of cellular and other low-density materials. Int J Solids Struct 37:93–104
Clausen A, Wang F, Jensen JS, Sigmund O, Lewis JA (2015) Topology optimized architectures with programmable Poisson’s ratio over large deformations. Adv Mater 27:5523–5527
Coelho P, Fernandes P, Guedes J, Rodrigues H (2008) A hierarchical model for concurrent material and topology optimisation of three-dimensional structures. Struct Multidiscip Optim 35:107–115
Cramer AD, Challis VJ, Roberts AP (2015) Microstructure interpolation for macroscopic design. Struct Multidiscip Optim 53:489–500. https://doi.org/10.1007/s00158-015-1344-7
de Kruijf N, Zhou S, Li Q, Mai Y-W (2007) Topological design of structures and composite materials with multiobjectives. Int J Solids Struct 44:7092–7109
Deng J, Chen W (2017) Concurrent topology optimization of multiscale structures with multiple porous materials under random field loading uncertainty. Struct Multidiscip Optim 56:1–19. https://doi.org/10.1007/s00158-017-1689-1
Deng J, Yan J, Cheng G (2012) Multi-objective concurrent topology optimization of thermoelastic structures composed of homogeneous porous material. Struct Multidiscip Optim 47:583–597. https://doi.org/10.1007/s00158-012-0849-6
Fujii D, Chen B, Kikuchi N (2001) Composite material design of two-dimensional structures using the homogenization design method. Int J Numer Methods Eng 50:2031–2051
Gao J, Li H, Gao L, Xiao M (2018) Topological shape optimization of 3D micro-structured materials using energy-based homogenization method. Adv Eng Softw 116:89–102
Guest JK, Prévost JH (2006) Optimizing multifunctional materials: design of microstructures for maximized stiffness and fluid permeability. Int J Solids Struct 43:7028–7047
Guo X, Zhao X, Zhang W, Yan J, Sun G (2015) Multi-scale robust design and optimization considering load uncertainties. Comput Methods Appl Mech Eng 283:994–1009
Hamza K, Aly M, Hegazi H (2014) A kriging-interpolated level-set approach for structural topology optimization. J Mech Des 136:011008
Huang X, Xie Y (2009) Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials. Comput Mech 43:393
Huang X, Radman A, Xie Y (2011) Topological design of microstructures of cellular materials for maximum bulk or shear modulus. Comput Mater Sci 50:1861–1870
Huang X, Zhou S, Xie Y, Li Q (2013) Topology optimization of microstructures of cellular materials and composites for macrostructures. Comput Mater Sci 67:397–407
Huang X, Zhou S, Sun G, Li G, Xie YM (2015) Topology optimization for microstructures of viscoelastic composite materials. Comput Methods Appl Mech Eng 283:503–516
Li H, Luo Z, Zhang N, Gao L, Brown T (2016) Integrated design of cellular composites using a level-set topology optimization method. Comput Methods Appl Mech Eng 309:453–475
Li H, Luo Z, Gao L, Qin Q (2018a) Topology optimization for concurrent design of structures with multi-patch microstructures by level sets. Comput Methods Appl Mech Eng 331:536–561. https://doi.org/10.1016/j.cma.2017.11.033
Li H, Luo Z, Gao L, Walker P (2018b) Topology optimization for functionally graded cellular composites with metamaterials by level sets. Comput Methods Appl Mech Eng 328:340–364
Liu L, Yan J, Cheng G (2008) Optimum structure with homogeneous optimum truss-like material. Comput Struct 86:1417–1425. https://doi.org/10.1016/j.compstruc.2007.04.030
Luo Z, Tong L, Kang Z (2009) A level set method for structural shape and topology optimization using radial basis functions. Comput Struct 87:425–434. https://doi.org/10.1016/j.compstruc.2009.01.008
Niu B, Yan J, Cheng G (2008) Optimum structure with homogeneous optimum cellular material for maximum fundamental frequency. Struct Multidiscip Optim 39:115–132. https://doi.org/10.1007/s00158-008-0334-4
Radman A, Huang X, Xie Y (2013) Topology optimization of functionally graded cellular materials. J Mater Sci 48:1503–1510
Rashed M, Ashraf M, Mines R, Hazell PJ (2016) Metallic microlattice materials: a current state of the art on manufacturing, mechanical properties and applications. Mater Des 95:518–533
Rodrigues H, Guedes JM, Bendsoe MP (2002) Hierarchical optimization of material and structure. Struct Multidiscip Optim 24:1–10. https://doi.org/10.1007/s00158-002-0209-z
Rozvany GI, Zhou M, Birker T (1992) Generalized shape optimization without homogenization. Struct Optim 4:250–252
Sakata S, Ashida F, Zako M (2003) Structural optimization using kriging approximation. Comput Methods Appl Mech Eng 192:923–939
Schury F, Stingl M, Wein F (2012) Efficient two-scale optimization of manufacturable graded structures. SIAM J Sci Comput 34:B711–B733. https://doi.org/10.1137/110850335
Sigmund O (1994) Materials with prescribed constitutive parameters: an inverse homogenization problem. Int J Solids Struct 31:2313–2329
Sigmund O (2001) A 99 line topology optimization code written in Matlab. Struct Multidiscip Optim 21:120–127
Sigmund O, Torquato S (1996) Composites with extremal thermal expansion coefficients. Appl Phys Lett 69:3203–3205
Sigmund O, Torquato S (1997) Design of materials with extreme thermal expansion using a three-phase topology optimization method. J Mech Phys Solids 45:1037–1067
Simpson TW, Mauery TM, Korte JJ, Mistree F (2001) Kriging models for global approximation in simulation-based multidisciplinary design optimization. AIAA J 39:2233–2241
Simpson TW, Booker AJ, Ghosh D, Giunta AA, Koch PN, Yang R-J (2004) Approximation methods in multidisciplinary analysis and optimization: a panel discussion. Struct Multidiscip Optim 27:302–313
Sivapuram R, Dunning PD, Kim HA (2016) Simultaneous material and structural optimization by multiscale topology optimization. Struct Multidiscip Optim 54:1267–1281. https://doi.org/10.1007/s00158-016-1519-x
Su W, Liu S (2010) Size-dependent optimal microstructure design based on couple-stress theory. Struct Multidiscip Optim 42:243–254
Vicente WM, Zuo ZH, Pavanello R, Calixto TKL, Picelli R, Xie YM (2016) Concurrent topology optimization for minimizing frequency responses of two-level hierarchical structures. Comput Methods Appl Mech Eng 301:116–136. https://doi.org/10.1016/j.cma.2015.12.012
Wang MY, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192:227–246
Wang Y, Luo Z, Zhang N, Kang Z (2014) Topological shape optimization of microstructural metamaterials using a level set method. Comput Mater Sci 87:178–186
Wang Y, Wang MY, Chen F (2016) Structure-material integrated design by level sets. Struct Multidiscip Optim 54:1145–1156. https://doi.org/10.1007/s00158-016-1430-5
Wang Y, Chen F, Wang MY (2017) Concurrent design with connectable graded microstructures. Comput Methods Appl Mech Eng 317:84–101. https://doi.org/10.1016/j.cma.2016.12.007
Xia L, Breitkopf P (2014) Concurrent topology optimization design of material and structure within FE2 nonlinear multiscale analysis framework. Comput Methods Appl Mech Eng 278:524–542
Xia L, Breitkopf P (2015) Multiscale structural topology optimization with an approximate constitutive model for local material microstructure. Comput Methods Appl Mech Eng 286:147–167. https://doi.org/10.1016/j.cma.2014.12.018
Xia L, Breitkopf P (2017) Recent advances on topology optimization of multiscale nonlinear structures. Arch Comput Methods Eng 24:227–249
Xie YM, Steven GP (1993) A simple evolutionary procedure for structural optimization. Comput Struct 49:885–896
Xu L, Cheng G (2018) Two-scale concurrent topology optimization with multiple micro materials based on principal stress orientation. Struct Multidiscip Optim 57:2093–2107. https://doi.org/10.1007/s00158-018-1916-4
Yan X, Huang X, Zha Y, Xie YM (2014) Concurrent topology optimization of structures and their composite microstructures. Comput Struct 133:103–110. https://doi.org/10.1016/j.compstruc.2013.12.001
Yan X, Huang X, Sun G, Xie YM (2015) Two-scale optimal design of structures with thermal insulation materials. Compos Struct 120:358–365. https://doi.org/10.1016/j.compstruct.2014.10.013
Yan J, Guo X, Cheng G (2016) Multi-scale concurrent material and structural design under mechanical and thermal loads. Comput Mech 57:437–446. https://doi.org/10.1007/s00466-015-1255-x
Yoshimura M, Shimoyama K, Misaka T, Obayashi S (2017) Topology optimization of fluid problems using genetic algorithm assisted by the kriging model. Int J Numer Methods Eng 109:514–532
Zhang W, Sun S (2006) Scale-related topology optimization of cellular materials and structures. Int J Numer Methods Eng 68:993–1011
Zhang J, Xiao M, Gao L, Fu J (2018a) A novel projection outline based active learning method and its combination with kriging metamodel for hybrid reliability analysis with random and interval variables. Comput Methods Appl Mech Eng 341:32–52. https://doi.org/10.1016/j.cma.2018.06.032
Zhang Y, Xiao M, Li H, Gao L, Chu S (2018b) Multiscale concurrent topology optimization for cellular structures with multiple microstructures based on ordered SIMP interpolation. Comput Mater Sci 155:74–91. https://doi.org/10.1016/j.commatsci.2018.08.030
Zheng J, Luo Z, Li H, Jiang C (2018) Robust topology optimization for cellular composites with hybrid uncertainties. Int J Numer Methods Eng 115:695–713
Zhou S, Li Q (2008) Design of graded two-phase microstructures for tailored elasticity gradients. J Mater Sci 43:5157–5167. https://doi.org/10.1007/s10853-008-2722-y
Zhou M, Rozvany G (1991) The COC algorithm, part II: topological, geometrical and generalized shape optimization. Comput Methods Appl Mech Eng 89:309–336
Funding
This research was supported by the National Basic Scientific Research Program of China (grant number JCKY2016110C012), the National Natural Science Foundation of China (grant numbers 51675196, 51705166, and 51721092), and the Program for HUST Academic Frontier Youth Team.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Helder C. Rodrigues
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhang, Y., Li, H., Xiao, M. et al. Concurrent topology optimization for cellular structures with nonuniform microstructures based on the kriging metamodel. Struct Multidisc Optim 59, 1273–1299 (2019). https://doi.org/10.1007/s00158-018-2130-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-018-2130-0