Concurrent design of hierarchical structures with three-dimensional parameterized lattice microstructures for additive manufacturing

Abstract

In this work, a novel design and modeling method is proposed to obtain hierarchical structures with non-uniform lattice microstructures based on density-based topology optimization. First of all, a parametric concept is proposed to generate a family of parameterized lattice microstructures that present similar topological features. In order to balance the structural performance and computational efficiency, we construct a Parameterized Interpolation for Lattice Material (PILM) model and the mathematical formulation incorporates two new design variables. At the macroscale, the relative density variable is applied to describe material volume fraction in the design domain, instead of using the pseudo-density in the Solid Isotropic Material with Penalization (SIMP) model. At the microscale, each macroelement is regarded as an individual microstructure controlled by an aspect ratio variable. The equivalent properties of parameterized lattice microstructures can be derived by interpolating the effective elastic matrixes of several typical microstructure unit cells, which avoid expensive iterative homogenization calculations during optimization procedure. Hence, the multiscale concurrent design method can optimize the macroscopic distribution and their spatially varying microstructural configurations simultaneously at an affordable computation cost. Several numerical examples are presented to demonstrate the effectiveness of the proposed approach. Furthermore, the obtained hierarchical structures with non-uniform lattice microstructures show good manufacturability and remarkably improved structural performance by means of the additive manufacturing and experimental testing, compared to the designs with uniform lattice microstructures.

1 Introduction

Due to the high strength-to-weight ratio, multifunctional performance, and outstanding designability characteristic, lattice materials are popularly used in a wide range of engineering applications, e.g., aerospace (Zhang et al. 2018), automotive, and bio-medical field (Khanoki and Pasini 2011; He et al. 2018). Generally, lattice materials are used to reduce the structure weight and enhance the structure performances, such as structural stiffness, shock resistance (Elnasri et al. 2007), energy absorbability (Shen et al. 2016), and heat insulation (Kim et al. 2004; Cheng et al. 2018b). Reviews about developments and applications of the lattice structures can be found in Gibson and Ashby (1990), Dong et al. (2017a), and Tamburrino et al. (2018).

The properties of such porous materials mainly depend on the topological configurations of the microstructures (Li et al. 2018). Hence, the topology design of microstructures attracts much attention. Sigmund (1994) utilized an inverse homogenization approach to construct microstructure materials with any prescribed constitutive tensor. Later, many studies focus on the design of microstructures to achieve desired or extreme properties, e.g., negative Poisson’s ratio (Evans and Alderson 2000; Wang et al. 2014; Clausen et al. 2015), bulk modulus maximization (Zhang et al. 2007; Huang et al. 2011), functionally graded properties (Zhou and Li 2008; Radman et al. 2013), and extreme thermal expansion (Sigmund and Torquato 1997; Dudek et al. 2016). It is noted that the majority of these studies mainly focus on how to obtain the desired material properties by tailoring the microstructures, ignoring the specified macrostructures and boundary conditions.

From the perspective of structural design, traditional design strategies mainly focus on macroscopic topology (Zhu et al. 2016), shape, or size optimization. Actually, in majority of engineering applications, it is highly desirable to optimize the macroscopic topology and their spatially varying microstructural configurations simultaneously to achieve the best overall performance. Nevertheless, the highly complex geometrical features of the multiscale structures bring an enormous challenge to conventional manufacturing techniques. Recently, significant advances in emerging additive manufacturing (AM) technology have made printing controlled lattice structures feasible (Tang et al. 2017). Yan et al. (2012) evaluated the manufacturability of SLM-produced periodic cellular materials and investigated the effect of unit cell size on the manufacturability and mechanical properties of the lattice structures. Choy et al. (2017) explored the deformation behaviors and compressive properties of functionally graded lattice structures fabricated by selective laser melting (SLM). Comprehensive reviews on the development and applications of additive manufacturing for lattice structures can be seen in the literatures (Hussein 2013; Dong et al. 2017). Related research has shown that it is appropriate and efficient to manufacture lattice structures with highly complex geometrical configurations. Therefore, now the challenge is focusing on how to obtain the hierarchical structures with high performance.

To deal with the second challenge, one typical hypothesis for the current multiscale design methods is that the whole macrostructure consists of identical microstructures. Regarding the history of multiscale design methodology based on this hypothesis, Liu et al. (2008) originally proposed a concurrent topology optimization method by assuming the uniformity of material microstructures in macroscale. After that, Yan et al. (2014) developed a two-scale concurrent optimization algorithm for macrostructures and their composite microstructures based on the bi-directional evolutionary structural optimization (BESO) method. Wang et al. (2016) optimized the macrostructural configuration and the material cell simultaneously in the framework of level set method (LSM). Chen et al. (2017) dealt with this issue by means of new moving iso-surface threshold (MIST) formulation and algorithm. These works give full consideration to the computational costs but reduce the design space or freedom and limit the range of possible topologies. Therefore, this hypothesis restricted the potential capacity of structures and materials, keeping the design away from the real optimum.

Recently, some researchers pointed out that a hierarchical structure with non-uniform lattice microstructures can achieve remarkably better performance compared to the uniform one. Hence, another typical hypothesis for the current multiscale design methods is to optimize the macroscopic distribution and their spatially varying microstructural configurations in an integrated manner. Recent studies related to the design of hierarchical structures with non-uniform lattice microstructures have been proposed by Rodrigues et al. (2002). Following that, Coelho et al. (2008) extended the hierarchical model for topology optimization to three-dimensional structures afterwards. Xia and Breitkopf (2014) proposed a concurrent design method of material and structure with the help of FE² non-linear multiscale analysis framework. Such hypothesis incorporates a great deal of design variables, resulting in intensive computational costs and enormous processing difficulties. Therefore, this method should be carefully considered when taking into account structural performance and computing and manufacturing costs simultaneously. In order to handle this issue, Xia and Breitkopf (2015) developed a reduced database model by viewing the local material optimization process as a generalized constitutive behavior using separated representations. Besides, Wu et al. (2018) and Fu et al. (2019) prososed a concurrent topplogy optimization method to avoid size effects with the use of substructuring. Cheng et al. (2017) presented a lattice structure topology optimization (LSTO) method for enhancing the stiffness of designed component and extended the design framework to natural frequency problem (Wang et al. 2018c) and heat conduction problem (Cheng et al. 2018c). Jin et al. (2018) proposed an optimal design and modeling method to attain lightweight non-uniform lattice structures simultaneously considering the mechanical performance and manufacturability. In the study, they just tailored the strut size in the optimized non-uniform structures without considering the configurations of the lattice cell. Further details on the multiscale design methods can be referred to the review (Xia and Breitkopf 2017). Despite the numerous studies available on multiscale structural design methods, there still remains a paucity of investigations in the existing literature, in particular related to hierarchical structures with non-uniform lattice microstructures. To deal with this problem, Wang et al. (2018a) proposed a concurrent design approach based on PAMP model for finding the optimum topologies of macrostructures and their corresponding parameterized lattice microstructures in an integrated manner. But this work only considered two-dimensional problems and single parameter lattice microstructures, which limits its application in the engineering field. Hence, a high-efficiency concurrent design method is still in demand to optimize the large-scale three-dimensional hierarchical structure for better performances.

This study presents a methodology for designing hierarchical structures with non-uniform lattice microstructures simultaneously considering structural performance and computational efficiency. In order to balance the computational cost and accuracy, the energy-based homogenization method is utilized to obtain the effective properties of lattice microstructures. Then, we construct a Parameterized Interpolation for Lattice Material (PILM) model, where a polynomial function is applied to describe the relationship of the elastic constants in terms of relative density and aspect ratio. After that, a concurrent optimization framework is put forward and the proposed mathematical formulation incorporates two design variables, relative density on the macroscale and aspect ratio on the microscale. And the conventional optimality criteria method is used to update design variables.

The remainder of this paper is organized as follows. Section 2 gives a brief introduction about the concept of parameterized lattice microstructures and the energy-based homogenization method. In Sect. 3, the method of concurrent optimization for hierarchical structures is systematically proposed and sensitivity analysis is provided. Numerical examples and mechanical testing are implemented in Sects. 4 and 5, respectively. Finally, conclusions are given in Sect. 6.

2 Mechanical properties equivalence for parameterized lattice microstructure

2.1 Parameterized lattice microstructure configuration

The lattice microstructures consist of struts with certain repeated arrangement in three-dimensional space. The unit cell is defined as illustrated in Fig. 1. Here the basic unit cell is constructed by eight cylinders (blue region) and twelve quartered cylinders (gray region). The geometric parameters are frame width, w, strut thickness with circle cross-section, d, and side length, L.

Fig. 1

Lattice material and microstructure unit cell

The theoretical formula for relative density, η, which denotes the ratio of lattice density to the solid material density, can be described as

$$ \eta =\frac{V_{\mathrm{strut}}}{V_{\mathrm{lattice}}} $$

(1)

where V_strut is the volume of the solid struts forming the lattice structure and the V_lattice is the envelope volume enclosed by the external boundaries of the lattice structure. By changing the frame width w and strut thickness d, we can get a family of lattice microstructures with varying relative density, as shown in Fig. 2.

Fig. 2

Microstructure unit cells with continuously varying relative density η

Then, on the premise that the relative density keeps consistent, the frame width and strut thickness are synchronously changed to obtained varied lattice microstructures with different ratios of w/d. For convenience, we define a variable called aspect ratio

$$ {x}_{\mathrm{inter}}=\frac{V_{\mathrm{iner}}}{V_{\mathrm{strut}}} $$

(2)

$$ {x}_{\mathrm{exter}}=\frac{V_{\mathrm{exter}}}{V_{\mathrm{strut}}} $$

(3)

where V_inter is the volume of the internal branch (blue region) and V_exter is the volume of the external frame (gray region). We can easily derive the equation

$$ {x}_{\mathrm{inter}}+{x}_{\mathrm{exter}}=1 $$

(4)

For example, Fig. 3 shows a family of lattice microstructures with the aspect ratio x_exter continuously varying from 0 to 1.

Fig. 3

Microstructure unit cells with continuously varying aspect ratio x_exter

Through the combination of the above two modes, a novel concept is herein proposed to interpolate a prototype microstructure to generate a family of parameterized lattice microstructures that present similar topological features. As shown in Fig. 4, the vertical and horizontal axes in the graph represent relative density and aspect ratio, respectively. A pair of parameters will determine the geometrical configuration of a lattice microstructure.

Fig. 4

Microstructure unit cells with different aspect ratio x_exter and relative density η

It should be mentioned that, although the lattice microstructures in Fig. 4 are used throughout the paper, the proposed concept is a common method and does not limit the application of other lattice microstructures with different controlled parameters. For example, Fig. 5 illustrates two other types of lattice microstructures controlled by 2 and 3 parameters, respectively.

Fig. 5

Two types of lattice material and microstructure unit cells. a Lattice microstructure controlled by 2 parameters. b Lattice microstructure controlled by 3 parameters

2.2 Prediction of effective elastic properties

With reference to the study of Zhong and Li (2015) on the mechanical properties of several types of lattice microstructures, we know that the edge lattice possesses superior tensile/compressive capacity and the body-centered lattice provides good performance in the bending and torsion. But it is vital to build a quantitative representation for the elastic properties of parameterized lattice microstructures, which is the basis for the proposed concurrent design method. A valid alternative is to analyze the whole lattice structures by the finite element method (FEM). Beam element and solid element are usually applied to numerical simulation of lattice structures, such as (Luxner et al. 2005; Smith et al. 2013). However, it is computationally intensive and time-consuming to generate the mesh model for the FEA analysis, due to the high complexity of lattice structures. In order to improve the computational efficiency, the numerical homogenization method (Hassani and Hinton 1998; Zhang et al. 2007) has been widely used in the prediction of effective mechanical properties for lattice structures.

In this work, the constitutive behaviors of lattice microstructures are assumed to be linear elastic and orthotropic. The equivalent properties of parameterized lattice microstructures are estimated via the energy-based homogenization method (EBHM) by imposing the periodic boundary conditions (Xia et al. 2003). Figure 6 schematically illustrates the fundamentals of the EBHM. In this method, it satisfies the following conditions: the average properties of the solid homogeneous medium should be equal to the average properties of a microstructure unit cell.

$$ \overline{\boldsymbol{\upsigma}}=\frac{1}{\left|\varOmega \right|}{\int}_{\varOmega}\boldsymbol{\upsigma} d\varOmega $$

(5)

$$ \overline{\boldsymbol{\upvarepsilon}}=\frac{1}{\left|\varOmega \right|}{\int}_{\varOmega}\boldsymbol{\upvarepsilon} d\varOmega $$

(6)

where $\overline{\boldsymbol{\upsigma}}$ and $\overline{\boldsymbol{\upvarepsilon}}$ are the average stress and averages strain, respectively. Ω is the volume of the microstructure unit cell. Follow the generalized Hooke’s law, the material constitutive relation of the microstructure unit cell can be written as

$$ \overline{\boldsymbol{\upsigma}}={\mathbf{D}}^H\overline{\boldsymbol{\upvarepsilon}} $$

(7)

where D^H is the equivalent elastic matrix of the microstructure unit cell. In a matrix notation form, (7) can be written as

$$ \left[\begin{array}{l}{\overline{\sigma}}_{11}\\ {}{\overline{\sigma}}_{22}\\ {}{\overline{\sigma}}_{33}\\ {}{\overline{\sigma}}_{12}\\ {}{\overline{\sigma}}_{23}\\ {}{\overline{\sigma}}_{31}\end{array}\right]=\left[\begin{array}{l}{D}_{11}\kern0.5em {D}_{21}\kern0.5em {D}_{31}\kern0.5em 0\kern0.5em \begin{array}{cc}\kern0.4em 0& \kern0.4em 0\end{array}\\ {}\begin{array}{cccc}{D}_{12}& {D}_{22}& {D}_{32}& \begin{array}{cc}0& \begin{array}{cc}\kern0.3em 0& \kern0.4em 0\end{array}\end{array}\end{array}\\ {}\begin{array}{cccc}{D}_{13}& {D}_{23}& {D}_{33}& \begin{array}{cc}0& \begin{array}{cc}\kern0.4em 0& \kern0.5em 0\end{array}\end{array}\end{array}\\ {}\kern0.4em \begin{array}{cccc}0& \kern1.1em 0& \kern1.2em 0& \begin{array}{cc}{D}_{44}& \begin{array}{cc}0& \kern0.5em 0\end{array}\end{array}\end{array}\\ {}\begin{array}{cccc}\kern0.3em 0& \kern1.2em 0& \kern1.2em 0& \begin{array}{cc}\kern0.6em 0& \begin{array}{cc}{D}_{55}& 0\end{array}\end{array}\end{array}\\ {}\begin{array}{cccc}\kern0.3em 0& \kern1.2em 0& \kern1.2em 0& \begin{array}{cc}\kern0.6em 0& \begin{array}{cc}\kern0.6em 0& {D}_{66}\end{array}\end{array}\end{array}\end{array}\right]\kern1em \left[\begin{array}{l}{\overline{\varepsilon}}_{11}\\ {}{\overline{\varepsilon}}_{22}\\ {}{\overline{\varepsilon}}_{33}\\ {}{\overline{\varepsilon}}_{12}\\ {}{\overline{\varepsilon}}_{23}\\ {}{\overline{\varepsilon}}_{31}\end{array}\right] $$

(8)

Fig. 6

Schematic diagram of homogenization for lattice materials

The strain energy stored in the microstructure unit cell can be calculated using the following equation

$$ U=\frac{1}{2}{\int}_{\Omega}{\sigma}_{ij}{\varepsilon}_{ij}d\Omega =\frac{1}{2}{\overline{\sigma}}_{ij}{\overline{\varepsilon}}_{ij}{\Omega}_{\mathrm{RVE}} $$

(9)

where ${\overline{\sigma}}_{ij}$ is the equivalent stress tensor, ${\overline{\varepsilon}}_{ij}$ is the equivalent strain tensor, and Ω_RVE is the volume of the solid homogeneous medium. The strain energy, U, can also be obtained directly from a finite element analysis for the microstructure unit cell. Hence, D_ij can be obtained through different strain states (see Table 1) under periodic boundary conditions (Wang et al. 2018b).

Table 1 Different strain states for acquisition of equivalent elastic indices of microstructure unit cell

Under the assumption of periodicity, the displacement field for the periodic structure (Michel et al. 1999) can be expressed as

$$ {u}_i={\overline{\varepsilon}}_{ik}{x}_k+{u}_i^{\ast } $$

(10)

where ${\overline{\varepsilon}}_{ik}$ are the average strains and ${u}_i^{\ast }$ is the periodic fluctuation field. However, (10) cannot be directly imposed on the boundaries since ${u}_i^{\ast }$ is generally unknown. For a cubic unit cell as shown in Fig. 7, the displacements on a pair of opposite boundary surfaces (Xia et al. 2003) can be transformed as

$$ {u}_i^{j+}={\overline{\varepsilon}}_{ik}{x}_k^{j+}+{u}_i^{\ast } $$

(11)

$$ {u}_i^{j-}={\overline{\varepsilon}}_{ik}{x}_k^{j-}+{u}_i^{\ast } $$

(12)

where superscripts “j+” and “j−” denote the positive and the negative directions along the jth axis. The unknown ${u}_i^{\ast }$ can be eliminated through the difference between (11) and (12)

$$ {u}_i^{j+}-{u}_i^{j-}={\overline{\varepsilon}}_{ik}\left({x}_k^{j+}-{x}_k^{j-}\right)={\overline{\varepsilon}}_{ik}\varDelta {x}_k^j $$

(13)

Fig. 7

Lattice microstructure unit cell. a Finite element mesh model. b The von Mises’ stress field corresponding to unit tensile strain. c The von Mises’ stress field corresponding to unit shear strain (scale factor = 0.2)

For any given cubic unit cell, $\varDelta {x}_k^j$ is constant. Therefore, with a specified ${\overline{\varepsilon}}_{ik}$, (13) can be written as

$$ {u}_i^{j+}\left(x,y,z\right)-{u}_i^{j-}\left(x,y,z\right)={c}_i^j\kern1.5em \left(i,j=1,2,3\right) $$

(14)

where ${c}_i^j={\overline{\varepsilon}}_{ik}\varDelta {x}_k^j$. Equation (14) can be directly applied to FE model by constraining nodal displacements on the corresponding pairs of boundary surfaces. Meanwhile, this form of boundary conditions meets not only the boundary displacement periodicity but also the boundary traction periodicity requirements (Xia et al. 2006).

Based on homogenization theory, a microstructure unit cell is analyzed under periodic boundary. It is assumed that the property constants of the parent solid material are Young’s modulus E = 100 and Poisson’s ratio μ = 0.3. Figure 7 illustrates the FE mesh model and the corresponding stress field of the microstructure unit cell. Then, the effective elastic tensor D_ij can be calculated through the finite element analysis (FEA) under different strain states (shown in Table 1).

2.3 PILM model

Table 2 lists several typical lattice microstructures and their effective elastic matrixes. Due to the geometrical symmetry, there are only three independent elastic constants for each lattice microstructure. For convenience, the independent elastic constants are denoted as D₁₁ (D₁₁ = D₂₂ = D₃₃), D₁₂ (D₁₂ = D₁₃ = D₂₃), and D₄₄ (D₄₄ = D₅₅ = D₆₆), respectively. Through a simple analysis of the results in Table 2, we can draw a conclusion as follows. At a fixed aspect ratio, all the three independent elastic constants (D₁₁, D₁₂ and D₄₄) increase with increasing the relative density as expected. At a fixed relative density, D₁₁ increases rapidly with increasing aspect ratio; however, a remarkable decrease is observed for the D₁₂ and D₄₄ with increasing the aspect ratio. Hence, aspect ratio and relative density altogether determine the effective elastic properties of the lattice microstructures.

Table 2 The effective elastic matrix of typical microstructure unit cells

Based on above analysis, it can be definitely concluded that the effective properties of lattice materials depend on the geometrical configuration as well as material usage of the microstructure unit cell. For the study in this work, the elastic constants are assumed as functions of relative density and aspect ratio. Based on this assumption, a material interpolation model, named Parameterized Interpolation for Lattice Material (PILM), is herein proposed to accurately describe the effective elastic properties of lattice microstructures in terms of relative density and aspect ratio.

Without loss of generality and considering the fitting accuracy, a fifth-order polynomial is employed to describe the relationship between the effective elastic constants and parameter variables of lattice microstructures, i.e., relative density and aspect ratio.

$$ {\displaystyle \begin{array}{l}{D}_{ij}={a}_0+{a}_1{x}_{\mathrm{exter}}+{a}_2\eta +{a}_3{x}_{\mathrm{exter}}^2+{a}_4\eta {x}_{\mathrm{exter}}+{a}_5{\eta}^2+{a}_6{x}_{\mathrm{exter}}^3+{a}_7\eta {x}_{\mathrm{exter}}^2\\ {}\kern2em +{a}_8{\eta}^2{x}_{\mathrm{exter}}+{a}_9{\eta}^3+{a}_{10}{x}_{\mathrm{exter}}^4+{a}_{11}\eta {x}_{\mathrm{exter}}^3+{a}_{12}{\eta}^2{x}_{\mathrm{exter}}^2+{a}_{13}{\eta}^3{x}_{\mathrm{exter}}\\ {}\kern2em +{a}_{14}{\eta}^4+{a}_{15}{x}_{\mathrm{exter}}^5+{a}_{16}\eta {x}_{\mathrm{exter}}^4+{a}_{17}{\eta}^2{x}_{\mathrm{exter}}^3+{a}_{18}{\eta}^3{x}_{\mathrm{exter}}^2+{a}_{19}{\eta}^4{x}_{\mathrm{exter}}\\ {}\kern2em +{a}_{20}{\eta}^5\end{array}} $$

(15)

where a_k(k = 0~20) denotes the coefficients obtained by fitting to the homogenization data. In order to accurately describe the relationship, quite a number of lattice microstructures with different relative densities and aspect ratios are used for fitting the polynomial in (15). Table 3 gives the fitting coefficients for (15). Figure 8 illustrates the fitting curved surfaces for the three independent elastic constants in terms of relative density and aspect ratio. It is observed that the fitting curved surfaces smoothly go through the interpolation data-points.

Table 3 The fitting coefficients for (15)

Fig. 8

The fitting curved surfaces for three independent elastic constants of parameterized lattice microstructures

3 Problem statement and optimization formulations

3.1 Concurrent optimization method for hierarchical structure with PILM model

Focusing on the challenge of designing lightweight hierarchical structures with superior mechanical performance, a concurrent optimization framework based on PILM model is proposed while ensuring the feasibility of modeling and manufacturing. The details about this method are given below.

Firstly, the macrostructural design domain is divided into the finite element mesh and each element consists of a kind of lattice microstructures. Figure 9 illustrates an optimized hierarchical structure composed of non-uniform lattice microstructures in the finite element framework. Here arise two basic problems: one is how to obtain the optimal topological layout at the macroscale and the other one is how to arrange the proper lattice microstructures at the microscale.

Fig. 9

An optimal cantilever beam infilled with non-uniform lattice microstructures. a Design topology and element representation by relative density variables. b Design topology and element representation by aspect ratio variables

Then, in order to deal with both problems, the relative density η and aspect ratio x_exter of lattice microstructures are introduced into each element as the design variables in the optimization process. In this paper, the aspect ratio x_exter is denoted as “x” for convenience. The relationship between the design variables and equivalent elastic properties of lattice microstructures is bridged by the PILM model, which is described in Sect. 2.3. And the design variables can be defined as

$$ \mathbf{X}={\left\{{\eta}_1,\cdots, {\eta}_i\cdots, {\eta}_n;{x}_1,\cdots, {x}_i\cdots, {x}_n\right\}}^T $$

(16)

where n is the number of finite elements within the macrostructure design domain. η_i and x_i denote the relative density value and the aspect ratio value of the underlying lattice microstructures for the ith element.

As shown in Fig. 9, the “blue domain” describes the optimal spatial material distribution and the levels of “blue” denote the variation of relative density values. In particular, the “dark blue” element (η = 1) represents solid material and the “white” element (η = 0.001) represents void material. The “gray domain” denotes non-uniform lattice microstructures and the grayscale represents the variation of aspect ratio values.

Based on the finite element method (FEM), the global stiffness matrix K of macrostructure can be obtained by assembling the element stiffness matrix k_i

$$ \mathbf{K}=\sum \limits_i^n{k}_i=\sum \limits_i^n{\int}_{\Omega_i}{\mathbf{B}}^T{\mathbf{D}}_i^H\left({\eta}_i,{x}_i\right)\mathbf{B}d{\Omega}_i $$

(17)

where B is the strain-displacement matrix and ${\mathbf{D}}_i^H\left({\eta}_i,{x}_i\right)$ is the ith element elastic matrix, which can be calculated from the fitting curved surfaces shown in Fig. 8 when the parameters η_i and x_i are applied.

Finally, the goal of the study is to minimize the overall structural compliance under the volume constraint by finding the optimal structural topology and lattice microstructure distribution. According to the information of design variables, we can construct a multiscale lattice structures automatically and rapidly in CAD. And the obtained optimized hierarchical structures consist of a cluster of non-uniformly distributed lattice microstructures. It is noticed that the density-based topology optimization results always include a number of intermediate densities, which have no obvious physical meaning, whereas the proposed concurrent optimization method effectively handles this issues. The intermediate density represents the realistic relative density of the lattice microstructures.

3.2 Formulation of optimization

The mentioned above concurrent optimization problem with the objective of compliance minimization under volume constraint can be mathematically written as

$$ {\displaystyle \begin{array}{l}\mathrm{find}:\kern1em \mathbf{X}={\left\{{\eta}_1,\cdots, {\eta}_n;{x}_1,\cdots, {x}_n\right\}}^T\\ {}\min :\kern1em C={\mathbf{F}}^T\mathbf{U}={\mathbf{U}}^T\mathbf{KU}=\sum \limits_{i=1}^n{u_i}^T{k}_i{u}_i\\ {}\mathrm{subject}\ \mathrm{to}:\kern1em \mathbf{KU}=\mathbf{F}\\ {}\kern5.25em \sum \limits_{i=1}^n{\eta}_i{v}_i=V\le \overline{V}\\ {}\kern5.25em 0<{\eta}_{\mathrm{min}}\le {\eta}_i\le {\eta}_{\mathrm{max}}\le 1,\kern0.5em i=1,\cdots, n\\ {}\kern5.25em 0\le {x}_{\mathrm{min}}\le {x}_i\le {x}_{\mathrm{max}}\le 1,\kern0.75em i=1,\cdots, n\end{array}} $$

(18)

where the objective function C denotes the overall compliance of the structure. Note that the compliance minimization problem is established on the assumption of linear elasticity and meets the static equilibrium equation KU = F. U is the nodal displacement matrix, and F is the external load vector. v_i is the volume of the ith element, and the V is the total volume of the macrodesign domain with an upper limit of $\overline{V}$. η_min and η_max are the lower and upper values of the variable η, respectively. In order to avoid the numerical singularly, η_min must be set as a positive value. Similarly, we also can set the upper and lower limits for the variable x.

3.3 Sensitivity analysis

When it comes to gradient-based optimization algorithms, it is a critical basis to obtain the sensitivities of the objective and constraint functions with respect to the design variables. Hence, the sensitivity is analytically derived by the adjoint variable method in this section.

As for the objective function, C, its first-order derivative to the relative density η_i can be written as

$$ \frac{\partial C}{\partial {\eta}_i}=2{\mathbf{U}}^T\mathbf{K}\frac{\partial \mathbf{U}}{\partial {\eta}_i}+{\mathbf{U}}^T\frac{\partial \mathbf{K}}{\partial {\eta}_i}\mathbf{U} $$

(19)

To eliminate $\frac{\partial \mathbf{U}}{\partial {\eta}_i}$, considering the equilibrium equation in (18), the differentiation with respect to the relative density variable η_i can be expressed as

$$ \frac{\partial \mathbf{K}}{\partial {\eta}_i}\mathbf{U}+\mathbf{K}\frac{\partial \mathbf{U}}{\partial {\eta}_i}=\frac{\partial \mathbf{F}}{\partial {\eta}_i} $$

(20)

For the design-independent optimization problems considered in this study, it follows $\frac{\partial \mathbf{F}}{\partial {\eta}_i}=0$. Therefore, (20) can be simplified as

$$ \frac{\partial \mathbf{U}}{\partial {\eta}_i}=-{\mathbf{K}}^{-1}\frac{\partial \mathbf{K}}{\partial {\eta}_i}\mathbf{U} $$

(21)

Substituting (21) back into (19), we yield the following equation

$$ \frac{\partial C}{\partial {\eta}_i}=-{\mathbf{U}}^T\frac{\partial \mathbf{K}}{\partial {\eta}_i}\mathbf{U} $$

(22)

Combining (17), the sensitivity of objective function with respect to the relative density variable η_i can be expressed as

$$ {\displaystyle \begin{array}{l}\frac{\partial C}{\partial {\eta}_i}=-\sum \limits_{i=1}^n{u_i}^T\frac{\partial {k}_i}{\partial {\eta}_i}{u}_i\\ {}\kern1.75em =-\sum \limits_{i=1}^n{u_i}^T\frac{\partial }{\partial {\eta}_i}\left({\int}_{\Omega_i}{\mathbf{B}}^T{\mathbf{D}}_i^H\left({\eta}_i,{x}_i\right)\mathbf{B}d{\Omega}_i\right){u}_i\\ {}\kern1.75em =-{u_i}^T\left({\int}_{\Omega_i}{\mathbf{B}}^T\frac{\partial {\mathbf{D}}_i^H\left({\eta}_i,{x}_i\right)}{\partial {\eta}_i}\mathbf{B}d{\Omega}_i\right){u}_i\end{array}} $$

(23)

It is noted that the derivative of the effective elastic matrix D^H can be easily calculated from the Parameterized Lattice Material with Interpolation (PILM) model in (15) as follows:

$$ \frac{\partial {\mathbf{D}}^H}{\partial \eta }=\left[\begin{array}{cccccc}\partial {D}_{11}/\partial \eta & \partial {D}_{12}/\partial \eta & \partial {D}_{13}/\partial \eta & 0& 0& 0\\ {}\partial {D}_{12}/\partial \eta & \partial {D}_{22}/\partial \eta & \partial {D}_{23}/\partial \eta & 0& 0& 0\\ {}\partial {D}_{13}/\partial \eta & \partial {D}_{23}/\partial \eta & \partial {D}_{33}/\partial \eta & 0& 0& 0\\ {}0& 0& 0& \partial {D}_{44}/\partial \eta & 0& 0\\ {}0& 0& 0& 0& \partial {D}_{55}/\partial \eta & 0\\ {}0& 0& 0& 0& 0& \partial {D}_{66}/\partial \eta \end{array}\right] $$

(24)

Repeat the above steps from (19) to (24) and we can obtain the sensitivity of objective function with respect to the aspect ratio variable x_i as follows

$$ {\displaystyle \begin{array}{l}\frac{\partial C}{\partial {x}_i}=-\sum \limits_{i=1}^n{u_i}^T\frac{\partial {k}_i}{\partial {x}_i}{u}_i\\ {}\kern1.75em =-\sum \limits_{i=1}^n{u_i}^T\frac{\partial }{\partial {x}_i}\left({\int}_{\Omega_i}{\mathbf{B}}^T{\mathbf{D}}_i^H\left({\eta}_i,{x}_i\right)\mathbf{B}d{\Omega}_i\right){u}_i\\ {}\kern1.75em =-{u_i}^T\left({\int}_{\Omega_i}{\mathbf{B}}^T\frac{\partial {\mathbf{D}}_i^H\left({\eta}_i,{x}_i\right)}{\partial {x}_i}\mathbf{B}d{\Omega}_i\right){u}_i\end{array}} $$

(25)

Similarly, the term $\frac{\partial {\mathbf{D}}_i^H\left({\eta}_i,{x}_i\right)}{\partial {x}_i}$ can be easily derived from the (15).

The sensitivities of the material volume V with respect to the relative density variable η_i and aspect ratio variable x_i are respectively expressed as

$$ \frac{\partial V}{\partial {\eta}_i}={v}_i $$

(26)

$$ \frac{\partial V}{\partial {x}_i}=0 $$

(27)

Based on the above sensitivity information, the mathematical programming problem in (18) can be solved by the gradient-based optimization algorithms. In this work, the well-known method of moving asymptotes (MMA) proposed by Svanberg (1987) is employed to update the design variables. Moreover, there may exist some numerical difficulties such as checkerboard pattern, mesh dependency, and local minima during the solutions. To mitigate the issues, a sensitivity filtering technique (Sigmund and Petersson 1998) is utilized in the concurrent design.

Now we have established the mathematical formulations for the concurrent optimization problem and completed the sensitivity analysis of the objective and constraint functions with respect to the design variables. The processes of the concurrent optimization method for hierarchical structures are summarized into a flowchart, as shown in Fig. 10.

Fig. 10

Flow chart of the concurrent optimization method

4 Numerical implementation

To demonstrate the capability and efficiency of the proposed approach, several numerical examples are presented in this section to illustrate the concurrent design of hierarchical structures. It is assumed that the property constants of the solid material which constructs the lattice microstructures are Young’s modulus E = 100 MPa and Poisson’s ratio μ = 0.3. The objective of the optimization problems is to minimize structural compliance under the prescribed volume constraint. And the compliance minimization problems are implemented in MATLAB referring to Liu and Tovar’s (2014) code. Besides, the MMA algorithm is used to update the design variables in the concurrent optimization procedure. The sensitivity filtering is employed for the relative density variables to eliminate mesh dependency and checkboard pattern, where the filter radius is set to two times of the element size.

4.1 A three-dimensional L-shaped beam

The first example considers a three-dimensional L-shaped beam aiming to find the optimal macrostructures and the underlying lattice microstructures simultaneously. Figure 11 illustrates the geometric dimension, boundary and load conditions of the L-shaped beam. The side length of the L-shaped beam is 60 mm with a square cross section of 20 mm × 20 mm. For simplicity, the design domain is discretized into a mesh with 5000 8-node hexahedron elements. It is loaded with a vertical line load F = 30 N, evenly distrubuted on the right top egde as shown in the figure. The left upper surface of the L-shaped beam is fixed as the boundary condition. The objective is to minimize the structural compliance under the prescribed volume fraction constraint of 40%. Note that the upper and lower relative density bounds of the lattice microstructures used in this example are set to be η_max = 0.80 and η_min = 0.10, respectively.

Fig. 11

L-shaped beam with load and boundary conditions

Figure 12 plots the convergence curves of the structural compliance and volume fraction of the L-shaped beam. As shown in the figure, it takes 83 iterations to reach the convergence. Obviously, the structural compliance decreases sharply before the first 10 iterations and then keeps declining slowly until it converges to 538.79 mJ. It is noticed that the structural compliance of the optimized L-shaped beam is almost 61.6% below the initial design. However, the volume fraction keeps almost constant during the optimization procedure.

Fig. 12

Convergence histories of global structural compliance and volume fraction for the L-shaped beam

The optimization evolution of the L-shaped beam is also given in Fig. 12, including the relative density evolution and aspect ratio evolution. As illustrated in the figure, the initial relative density and aspect ratio of the underlying lattice microstructures of the L-shaped beam are set to η_i = 0.4 and x_i = 0.5, respectively. As the iteration proceeds, the lattice microstructures with higher relative density are distributed on the vertical surface of the L-shaped beam. Meanwhile, more material tends to be distributed along the load paths, bridging the load and fixed boundaries. Besides, it is noticed that there are quite a number of lattice microstructures of intermediate relative density existing between the high-density region and the low-density region.

To further illustrate the optimization results, we reconstruct the design of the optimized L-shaped beam infilled with non-uniform lattice microstructures. As shown in Fig. 13, the non-uniform lattice microstructures of varying relative densities and aspect ratios are distributed at different positions of the L-shaped beam. From the perspective of the relative density variable, the macroscopic material layout is similar to the design obtained by LSTO method (Cheng et al. 2018a), which was proved to be reasonable. From the perspective of the aspect ratio variable, the edge lattice microstructure (with higher aspect ratio x value) possesses superior tensile/compressive capacity and the body-centered lattice microstructure (with lower aspect ratio x value) provides good performance in the bending and torsion. It can be found that the distribution of the lattice microstructures is quite reasonable from Fig. 13. For example, the lattice microstructures with higher aspect ratio are applied at the typical points A and F, which provide superior mechanical properties in horizontal and vertical directions. The shear resistant microstructures with lower aspect ratio are employed at the typical point E. Besides, quite a few lattice microstructures of intermediate aspect ratios exist in the transitional regions.

Fig. 13

Reconstruction of the optimized L-shaped beam infilled with non-uniform lattice microstructures (C = 538.79 mJ)

To further verify the effectiveness of the proposed method, we consider the following four cases as comparison. The designs in case A and case B are fully filled with uniform lattice microstructures. The distinct lattice microstructures with different aspect ratios are distributed in the design domain of the macrostructure in case C, while different lattice microstructures with varying relative densities are arranged in the design domain of the macrostructure in case D. Table 4 lists the specific information of the four cases, including lattice parameters, two-scale structure topologies, and the objective C for the four cases. It is obviously noted that the design in case D has the smallest objective value of 568.53 mJ, 59.5%, 48.7%, and 44.7% lower than the designs in cases A~C, respectively. Figure 14 shows the global compliance of the structures obtained by cases A~D. By comparing the results, it can be concluded that the stiffness of the non-uniform lattice beams is superior to the uniform lattice beam. Besides, the red dash line represents the global compliance of the concurrent design shown in Fig. 13. It is obviously noticed that the results obtained by the four cases are inferior to the concurrent design, which sufficiently verified the effectiveness of the proposed method.

Table 4 Microstructural and macrostructural topologies and their objective functions with different variables

Fig. 14

Comparison of global structural compliance for different optimized L-shaped beams

Furthermore, we also consider the traditional optimal design using solid material only by assuming with the same weight as comparison. Figure 15 shows the optimized structural topology with the traditional 0/1 solutions, and the objective C converges to 388.1 J. It can be concluded that the structural stiffness is slightly better than the optimized design with non-uniform lattice microstructures. This is mainly due to the limitations of configurations of the lattice microstructures used in this work. Even though the stiffness of the concurrent design is slightly lower than the solid material design, it can benefit from the improvement of other high performance features, e.g., good energy absorption characteristics and good heat dissipation performance, by using lattice microstructures.

Fig. 15

Optimized structural topology using solid material for the L-shaped beam

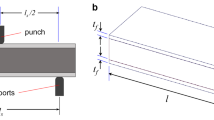
4.2 A three-dimensional three-point bending beam

A three-point bending beam is considered in this example, and Fig. 16 illustrates the geometric dimension, boundary, and load conditions. The length of the beam is 150 mm with a square cross section of 30 mm × 30 mm. Due to the symmetry of the problem, only the right half of the whole beam is considered as the design domain, which is divided with a mesh of 4320 (12 × 12 × 30) 8-node hexahedron elements. A vertical load F = 60 N is applied to the center domain of the top surface, and the length of the loading domain is set to 10 mm. It is supported on two fixed domains of the down surface with a distance of 15 mm from the two sides of the beam as shown in the figure. The objective is to minimize the structural compliance under the prescribed volume fraction constraint of 30%. Note that the upper and lower relative density bounds of the lattice microstructures used in this example are set to be η_max = 0.60 and η_min = 0.10, respectively.

Fig. 16

Three-point bending beam with load and boundary conditions

Figure 17 plots the convergence curves of the structural compliance and volume fraction of the three-point bending beam. As illustrated in the figure, it takes 53 iterations to find the optimal macrotopology and the underlying lattice microstructures. The structural compliance converges from 1311.96 mJ to 559.89 mJ with a decrease of 57.3%, while the volume fraction keeps quite stable throughout the iteration history. This result demonstrates the significant improvement in stiffness of the optimized structure over the initial structure.

Fig. 17

Convergence histories of global structural compliance and volume fraction for the three-point bending beam

The optimization results of the three-point bending beam are also given in Fig. 17, including the evolution of relative density and aspect ratio. As illustrated in the figure, the initial relative density and aspect ratio of the underlying lattice microstructures of the three-point bending beam are set to η_i = 0.3 and x_i = 0.5, respectively. As the iteration proceeds, more material tends to be distributed on the top and down surfaces, where load and boundary conditions are applied. Besides, the lattice microstructures with higher relative density are distributed along the load paths bridging those boundaries. Meanwhile, in the region of the right side of the beam, materials are removed to form a lower relative density area.

To further illustrate the optimization results, we reconstruct the design of the optimized three-point bending beam infilled with non-uniform lattice microstructures. As shown in Fig. 18, the different lattice microstructures are distributed at different positions of the beam. From the perspective of the relative density variable, the macroscopic material layout is similar to the continuum structure obtained by topology optimization (Yang et al. 2018) and this result is considered reasonable. From the perspective of the aspect ratio variable, it is noticed that the distribution of the lattice microstructures is also quite reasonable. As illustrated in Fig. 18, the microstructures with the aspect ratio x = 1 are applied at the typical points A and E, which provide superior mechanical properties in horizontal direction. The shear resistant microstructures with the aspect ratio x = 0 are employed at the typical point C. Besides, quite a few lattice microstructures of intermediate aspect ratios are distributed in the transitional regions to transfer the loads.

Fig. 18

Reconstruction of the optimized three-point bending beam infilled with non-uniform lattice microstructures

Figure 19 shows the optimized designs and their global structural compliance under different volume fraction constraints. It is noticed that the global structural compliance decreases with increasing volume fraction. Moreover, the volume fraction has significant effect on the spatial distribution of lattice microstructures. When volume fraction is relatively small, the lattice microstructures with higher relative density are mainly distributed at the positions where load and boundary conditions are applied and along the load paths which bridging those boundaries. As the volume fraction gradually increases, more material tends to be distributed at the central region of the beam.

Fig. 19

Optimized designs and their global structural compliance with different volume fractions

Similar to the previous L-shaped beam problem, the following four cases are used for comparison as shown in Fig. 16. Table 5 lists lattice parameters, two-scale structure topologies, and the objective C for the four cases. It is noted that the lattice microstructure greatly affects the topology of macrostructure and the objective C in turn. Obviously, the design in case D has the smallest objective value of 617.43 mJ, 52.9%, 47.0%, and 42.7% lower than the designs in cases A~C, respectively. But compared with the concurrent design, the structures obtained by these four cases turn out to be less optimal. Figure 20 shows the global compliance of the structures obtained by cases A~D. And the red dash line represents the global compliance of the concurrent design shown in Fig. 18, which possesses the best stiffness with the objective C = 559.89 mJ. These results clearly demonstrate the superior stiffness performance of the non-uniform lattice beam over the uniform lattice beam, especially when relative density and aspect ratio of the lattice microstructure are concurrently optimized.

Table 5 Microstructural and macrostructural topologies and their objective functions with different variables

Fig. 20

Comparison of global structural compliance for different optimized three-point bending beams

In order to validate the method with the capability of dealing with multiple variables, a design case with the new lattice type controlled by 3 parameters (as shown in Fig. 5) has been tested. The relative density and aspect ratio evolutions are given in Fig. 21. As illustrated in the figure, the initial relative density and aspect ratio of the underlying lattice microstructures of the three-point bending beam are set to η_i = 0.25, x_exter = 0.5, and x_inter = 0.5, respectively. As the iteration proceeds, more material tends to be distributed on the top and down surfaces, where load and boundary conditions are applied. Besides, the lattice microstructures with higher relative density are distributed along the load paths bridging those boundaries. Meanwhile, in the region of the right side of the beam, materials are removed to form a lower relative density area. To further illustrate the optimization results, we reconstruct the design of the optimized three-point bending beam infilled with the new lattice type controlled by 3 parameters. As shown in Fig. 22, the different lattice microstructures are distributed at different positions of the beam.

Fig. 21

Relative density and aspect ratio evolution of the three-point bending beam. a Iteration 0. b Iteration 1. c Iteration 10. d Iteration 51

Fig. 22

Reconstruction of the optimized three-point bending beam infilled with the new lattice type controlled by 3 parameters

5 Experimental validation

To further illustrate the effectiveness of the proposed method, an experimental validation is carried out for the optimized three-point bending beam via additive manufacturing and mechanical testing.

5.1 Geometric modeling and AM process

In this section, an automatic and parametric method to generate the optimal hierarchical structures is presented. The main steps are as follows: Firstly, we need to construct a single lattice unit cell parametrically according to the lattice datum. The parameterizable lattice unit cell is illustrated in Fig. 23, including three geometric parameters, i.e., frame width w, strut thickness d, and side length of the unit cell L. Based on the homogenization theory, the size dimension of lattice microstructures should be infinitesimally small compared to the macroscopic structures. However, it is worth mentioning that the obtained lattice structures must satisfy the additive manufacturing constraints, such as maximum overhanging length, minimum section thickness, and so on. Hence, the size of lattice unit cell cannot be arbitrarily small and is determined by the resolution of the 3D printing machine. In this work, the side length L is set to 5 mm considering the size dimension of the macroscopic structures and additive manufacturing constraints together. Secondly, the geometric parameters of all the lattice microstructures should be determined according to the optimization results. The frame width w and strut thickness d can be calculate from the obtained relative density and aspect ratio distribution matrixes. Then, all the lattice microstructures are created and arranged by the coordinates. Finally, the lattice components are assembled into the complete model by boolean operation.

Fig. 23

Geometry parameters of the parameterizable lattice unit cell

In this paper, the optimized three-point bending beam with non-uniform lattice microstructures under the prescribed volume fraction constraint of 30% is selected as the experimental object. In addition, other two uniform lattice beams are selected as comparison. Figure 24 shows the CAD model of the selected designs.

Fig. 24

CAD models and printed out structures of the test samples. a CAD model of beam A (infilled with uniform lattice microstructure A). b CAD model of beam B (infilled with uniform lattice microstructure B). c CAD model of the optimal beam (infilled with non-uniform lattice microstructures). d Printed out beam A. e Printed out beam B. f Printed out optimal beam

Emerging additive manufacturing technology makes possible the fabrication of hierarchical structures with non-uniform lattice microstructures. As a promising kind of additive manufacturing, stereolithography (SL) is selected to fabricate the structures due to its high printing efficiency and low cost. In this paper, the obtained hierarchical structures show good manufacturability to the additive manufacturing without extensive post-modification. The structures are printed out by a SPS350B 3D printer (Shaanxi Hengtong Intelligent Machine Co., Ltd.) under the same condition and print direction. The machine uses a UV laser with the laser power of 220 mW, the laser beam diameter of 0.12 mm, the scanning speed of 6500 mm/s, and the layer thickness of 0.1 mm. The material used in the additive manufacturing process is SPR6000B, a kind of photosensitive epoxy resin. Table 6 lists the specific information of SPR6000B. Figure 24 illustrates the printed out model of the test samples. To reduce the uncertainty of the experiments, three specimens of each design are manufactured.

Table 6 The physical characteristics of SPR6000B epoxy resin (15-min UV post-cure)

5.2 Mechanical test

All the experiments are performed on a TestResources universal testing machine with a 5-kN load cell. Figure 25 shows the test sample under the boundary and load conditions. The loading rate was set as 0.6 mm/min, which is to simulate the quasi-static compression condition. A data acquisition system was utilized to record the displacements and corresponding loads during the loading process. Besides, a digital camera was used to record the deform process of the specimens.

Fig. 25

Experimental setup for the test sample

The experimental load-displacement curves of the specimens are plotted in Fig. 26. The stiffness of the structures is usually evaluated by the slope of the linear elastic region of the load-displacement curves. The global stiffness of the three specimens is calculated via linear regression, with the resulting values of 278.4 N/mm, 366.5 N/mm, and 718.8 N/mm for two uniform lattice beams and the optimized non-uniform lattice beam, respectively. The resulting stiffness values clearly demonstrate the superior stiffness performance of the optimized non-uniform lattice beam over the uniform lattice beam, with the remarkable improved stiffness of 158.2% and 96.1%, respectively. Besides, the strength of the structures can be evaluated by the maximum bearable load, which is the force corresponding to the first local maximum in the load-displacement curve. As illustrated in the Fig. 26, the non-uniform lattice beam has the highest structural strength, with the resulting value of 3211.9 N, approximately 182.5% and 86.3% higher than the uniform lattice beam A and B. The significant improvement in the stiffness and strength for the optimized non-uniform lattice beam clearly demonstrates the validity of the proposed method.

Fig. 26

Load-displacement curves for three specimens

6 Conclusions

In this work, a novel concurrent design approach is proposed to obtain the non-uniform lattice structures with superior mechanical performance at an affordable computation cost. Realization of the proposed method begins with a parametric description of lattice microstructures. With the help of the energy-based homogenization method, the equivalent material model of parameterized lattice microstructures is established, leading to the remarkable reduction of computational cost. Then, we construct a Parameterized Interpolation for Lattice Material (PILM) model and the mathematical formulation incorporates two sets of design variables. Based on the proposed material interpolation for parameterized lattice microstructures, a concurrent optimization framework is put forward for hierarchical structures under volume fraction constraint. After that, the sensitivity analysis is carried out for the implementation of the gradient-based optimization algorithm.

Two numerical examples are presented to verify the effectiveness of the proposed method. After optimization, the results clearly demonstrate the improved performance of the obtained hierarchical structures, with a significantly decreased global compliance. Moreover, we develop the automatic and parametric modeling auxiliary application for the hierarchical structures with non-uniform lattice microstructures. In addition, three hierarchical beams were fabricated by additive manufacturing and tested under quasi-static conditions. It is found that the proposed design methodology can significantly enhance mechanical performance of the multiscale lattice structures. The improvement in performance of the optimal non-uniform lattice beam is even better with stiffness and strength approximately increasing by 158.2% and 182.5%, respectively, when compared with the uniform lattice beam A. From the perspective of the multifunctional characteristics of the lattice structures, further research work should require more thought about multidisciplinary integrated design.

7 Replication of results

The present work was performed in MATLAB R2015a referring to Liu and Tovar’s (2014) code. This section presents the main MATLAB program, which is written based on the knowledge of authors Chuang Wang and Han Zhou on Dec. 15, 2018 in Northwestern Polytechnical University (Xi’an, China). Here we show an example as illustrated in Fig. 18 of this paper.