Optimization design of metamaterial vibration isolator with honeycomb structure based on multi-fidelity surrogate model

Abstract

The hexagonal periodic structure of the honeycomb is a magic product of nature and shows great mechanical potential. In this work, a type of metamaterial vibration isolator with a honeycomb structure is proposed. The strain, deformation, and natural frequency of the vibration isolator are calculated by the two-dimensional plane finite element model and the simulation accuracies are validated by the experiments. As the design of the metamaterial vibration isolator involves time-consuming finite-element simulation, a multi-fidelity sequential optimization approach based on feasible region analysis (MF-FA) is proposed. In the proposed method, the refined and coarse mesh models are developed as the high- and low-fidelity models, and a two-phase multi-fidelity updating strategy is carried out. In the first phase, sample points are added to the constraint boundary to find the feasible solution quickly, in the second phase, the quality of the feasible optimization solution is gradually improved in the feasible region until it converges to the global optimal solution. Finally, the optimized metamaterial vibration isolator is manufactured and its superiority is validated. Results illustrate that the proposed approach can obtain a desirable optimum, whose natural frequency error between the experimental and the expected value is improved by 12.67% compared with the initial design.

1 Introduction

Vibration isolation is an important method to reduce the external transmission of mechanical equipment vibration (Snowdon 1979). Most of the elastic components used in vibration isolation are rubber and metal spring isolators. However, these two isolators have an obvious shortcoming that is excessive static deformation and instability for low-frequency vibration isolation (Rivin 2003). To address this issue, various new vibration isolation methods, such as nonlinear vibration isolation (Ibrahim 2008) and active vibration isolation (Aridogan and Basdogan 2015; Mikhailov and Bazinenkov 2017; Simonovic et al. 2016), are developed. In recent years, quasi-zero stiffness vibration isolators gain a lot of attention in nonlinear vibration isolation because they can obtain a nice effect of low-frequency vibration isolation (Fan et al. 2020; Yan et al. 2020). While these quasi-zero stiffness vibration isolators are made up of many parts, the complex system makes itself difficult to be widely used. The metamaterial is a kind of material with supernormal physical properties. The macroscopic physical properties of the material can be changed by manually adjusting the microstructure, which has a good application prospect in vibration reduction and isolation. Some scholars take advantage of the bandgap effect of metamaterials on elastic waves and build metamaterials with low-frequency local resonance band gaps in certain frequency bands by periodically attaching local resonance units to different support structures (Ma and Sheng 2016; Moscatelli et al. 2019). At present, the bandwidth of the low-frequency bandgap of the local resonant metamaterial is relatively narrow, and the vibration isolation effect at different frequencies is uneven. Therefore, the engineering application of local resonant metamaterial prototype is rare. In addition to isolating vibration by bandgap, the metamaterial can also utilize stiffness for vibration isolation, just like rubber isolators, which can not only greatly expand the frequency band of low-frequency vibration isolation, but also design the supernatural mechanical properties that rubber vibration isolators do not have by changing the microstructure parameters. There are a few kinds of research on the use of metamaterials stiffness for vibration isolation. In the snapping mechanical metamaterials literature (Plummer 2015; Rafsanjani et al. 2015; Shan et al. 2015), the experimental results show that under certain microstructural parameters, the multistable characteristics of alternating positive and negative stiffness can transform into quasi-zero stiffness characteristics, which provides a new idea for the application of metamaterials in the field of vibration isolation.

The design of vibration isolation metamaterials needs to satisfy all kinds of constraints, such as the stress constraint of base materials. When the cells of metamaterial are under external force, the distribution of stress and strain will be very different for different cell parameters. Therefore, it is necessary to optimize the microstructural parameters to reduce the stress concentration effect, so as to realize the reliable application of vibration isolation metamaterials. However, it is impractical to directly determine the optimal design parameters of vibration isolation metamaterials because the relationships between the design parameters and the performance are complicated and cannot be expressed explicitly (it can be regarded as a black box). Directly incorporated the finite-element (FE) simulation models into the optimization process will be time-consuming and even computationally prohibitive. A promising way to address this issue is to adopt surrogate models (Hu et al. 2021), which can approximate the black box models with limited FE simulation samples. To construct a surrogate model with desirable accuracy, a certain number of high-fidelity (HF) simulations are required. HF simulation models generally can reflect the majority of the physical characteristics but require expensive computation cost. However, due to the limited computational budget, it is unaffordable to use a large number of HF samples to build a high-accuracy surrogate model. Compared with the HF simulation, the low-fidelity (LF) simulation is computationally cheaper but contains fewer physical details, which may result in an inaccurate surrogate model or even a distorted one. An effective solution to address this dilemma is to construct a multi-fidelity (MF) surrogate model by incorporating both the LF and HF data into the surrogate modeling process (Park et al. 2017; Rokita and Friedmann 2018). A great number of methods have sprung up in recent years. For example, Le Gratiet et al. (Le Gratiet and Garnier 2014) proposed a multi-level multi-fidelity co-kriging model, in which a closed-form expression for the posterior distribution of the scale factor is provided; Han et al. (Han et al. 2012) put forth an alternative approach for the construction of the co-kriging covariance matrix that significantly reduced the complexity of the estimation of the hyper-parameters; Zhou et al. (Zhou et al. 2020) developed a generalized hierarchical co-kriging (GCK) surrogate model that can integrate MF data under both nested and non-nested sampling data. In addition to the development of MF surrogate modeling methodology, the application of the MF surrogate model on the industry optimization problems also attracts significant attention, e.g., the aircraft-design (Feldstein et al. 2020; Toman et al. 2019; Zhonghua et al. 2020), automobile industry (G. Sun et al. 2012; G. Sun et al. 2010), marine industry (Dong et al. 2015; Pellegrini et al. 2016; S. Sun et al. 2019), electronics engineering (Hassan et al. 2017; Koziel and Bekasiewicz 2018), and intelligent manufacturing field (Zhou et al. 2018; Zhou et al. 2017; Zhou et al. 2020).

This work investigated the application of the MF surrogate model in the design of the metamaterial vibration isolator with a honeycomb structure. MF surrogate model is constructed to incorporate two different fidelity FE simulation models, whose effectiveness of the FE simulation models is validated by the physical experiments. Then, a multi-fidelity sequential optimization approach based on feasible region analysis (MF-FA) computational to search the optimal design parameters of the metamaterial vibration isolator with honeycomb structure. Specifically, a two-phase multi-fidelity updating strategy is proposed, where in the first phase, sample points are added to the constraint boundary to find the feasible solution quickly and in the second phase, the quality of the feasible optimization solution is gradually improved in the feasible region until it converges to the global optimal solution. The metamaterial vibration isolator with the optimal design parameters is manufactured and its superiority is validated.

The rest of this paper is organized as follows. In Section 2, the details of the two different fidelity simulation models of the honeycomb structure vibration isolator are presented. In Section 3, the experimental details to validate the effectiveness of the simulation models of the honeycomb structure vibration isolator are introduced. In Section 4, a multi-fidelity sequential optimization approach based on feasible region analysis is developed for obtaining the optimal design parameters of the MI300-type honeycomb structure vibration isolator. Finally, the concluding remarks and future work are presented in Section 5.

2 Establishment of the FEM of the honeycomb structure vibration isolator

2.1 Geometric description

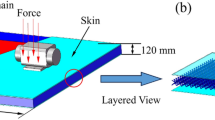
The geometry of the typical MI300-type vibration isolator is shown in Fig. 1. The MI300 vibration isolator consists of polyurethane honeycomb structure in Fig. 1a and corresponding metal packages in Fig. 1b.

Fig. 1

The geometry of the MI300 vibration isolator. a The polyurethane honeycomb structure of the MI300 vibration isolator. b The CAD drawings of the MI300 vibration isolator

The polyurethane honeycomb structure is used to isolate the vibration, and the metal packages have the effect of encapsulation and support. The polyurethane honeycomb structure is composed of hexagonal honeycomb cells with rounded corners as shown in Fig. 2.

Fig. 2

The geometry of a hexagonal honeycomb cell with rounded corner

There are mainly six geometric parameters of this hexagonal honeycomb cell, which are the length of the oblique bar of the cell $\mathit{\mathsf{L}}$, the height between the center of the oblique bar $\mathit{\mathsf{h}}$, the angle between the oblique bar and the horizontal line θ, the thickness of the oblique bar ${\mathit{\mathsf{t}}}_{\mathit{\mathsf{l}}}$, the thickness of the vertical bar ${\mathit{\mathsf{t}}}_{\mathit{\mathsf{h}}}$, the radius of the internal rounding ${\mathit{\mathsf{R}}}_{\mathit{\mathsf{f}}}$ and the depth of the cell $\mathit{\mathsf{D}}$. In addition, m and n are the numbers of the rows in the vertical and horizontal directions respectively.

2.2 Finite-element model

The finite-element simulation was performed using the finite-element software ANSYS 18. Because the hexagonal honeycomb cell is linearly stretched along the depth direction, it can be regarded as a plane strain problem when calculating the compression deformation of the honeycomb structure under the pressure load in the vertical direction. Therefore, the finite-element model can be simplified into a two-dimensional plane model as shown in Fig. 3, which was meshed with plane182 elements.

Fig. 3

The FE Model of the polyurethane honeycomb structure with hexagonal cells (m = 2, n = 4)

The upper surface of the structure is defined as the rigid displacement plane and applied with vertically downward uniformly distributed force. The degrees of the lower surface is fully constrained. The APDL language of the ANSYS software was used to establish an automated analysis process including the modeling of the parametric geometry, mesh generation, load application, constraints setting, evaluation, and post-processing. The density of the polyurethane is 1166 kg/m³, Poisson’s ratio is 0.475, the elastic modulus is 50 MPa, and the related load is 300 kgf. In the range of 1.25 times of related load, 20 load steps are settled to carry out the static analysis of the polyurethane honeycomb structure. The output values of strain, stress, stiffness, natural frequency, etc. can be obtained.

Generally speaking, the vibration isolation system composed of vibration isolators and equipment is relatively complex and needs to be simplified under certain assumptions. For example, the actual vibration isolation system can be simplified as a single-degree-of-freedom system and converted into a dynamic model of mass, spring, and damping. According to the standard GB/T 15168/2013 “Test Method for Static and Dynamic Performance of Vibration and Impact isolation Devices,” the natural frequency f (unit Hz) of the vibration isolator under rated load can be expressed as follows:

$$ f=\frac{1}{2\pi}\sqrt{\frac{k_d}{M}} $$

(1)

where $\mathit{\mathsf{M}}$ is the rated load (kgf), ${\mathit{\mathsf{k}}}_{\mathit{\mathsf{d}}}$ is the dynamic stiffness (N/m) under the related load which is usually equal to $\mathsf{1.3}{\mathit{\mathsf{k}}}_{\mathit{\mathsf{s}}}$, and ${\mathit{\mathsf{k}}}_{\mathit{\mathsf{s}}}$ can be obtained by the FE static analysis under the related load. The detailed description can be found in the standard GB/T 15168/2013.

2.3 Finite-element mesh consistency check

In order to evaluate the influence of finite-element mesh on the results, the consistency check is firstly carried out under the different mesh grid divisions. The mapping grid is used to mesh the geometry. In the thickness direction of the oblique bar, we use the number of elements to express the fine and coarse level of the mesh grid as shown in Fig. 4.

Fig. 4

The schematic diagram of mesh division for high- and low-precision finite element. a Fine mesh. b Coarse mesh

The numbers of the grid are taken from 2 to 22, respectively, and the interval is set to 2. With the change of the grid number, the calculated natural frequency of the honeycomb structure by FEM at the rated load is shown in Fig. 5.

Fig. 5

The variation of natural frequency of vibration isolator with grid components

As shown in Fig. 5, when the number of grids is greater than 12, the value of natural frequency changes very little and tends to converge. Through convergence analysis, the number of the grids in the thickness direction of the oblique bar is set to 14 and 6 for the high-fidelity and low-fidelity finite-element model respectively as shown in Fig. 4.

3 Experimental test and validation of the FE model

3.1 Numerical simulation

The initial design parameters of the MI300-type vibration isolator are $\left({\mathit{\mathsf{x}}}_{\mathsf{1}},{\mathit{\mathsf{x}}}_{\mathsf{2}},{\mathit{\mathsf{x}}}_{\mathsf{3}},{\mathit{\mathsf{x}}}_{\mathsf{4}},{\mathit{\mathsf{x}}}_{\mathsf{5}},{\mathit{\mathsf{x}}}_{\mathsf{6}}\right)=\left(\mathsf{10.3},\mathsf{0.0900},\mathsf{0.0031},\mathsf{0.0145},\mathsf{0.0075},\mathsf{0.0038}\right)$. The geometric and finite-element mesh model of the initial design is shown in Fig. 6.

Fig. 6

The geometric and finite-element model of the initial design

Through the finite-element simulation and post-processing, the load-static deformation curve, static stiffness-load curve, and related curves of the initial design are shown in Fig. 7.

Fig. 7

The simulation results of the initial design. a Load-static deformation curve. b Static stiffness-load curve. c Equivalent strain-load curve. d Nonlinear coefficient curve. e Transverse-longitudinal stiffness ratio curve. f Static deformation-deformable displacement curve. g Natural frequency of the initial design

From Fig. 7, we can get the vertical static stiffness ${\mathit{\mathsf{k}}}_{\mathit{\mathsf{s}}}=\mathsf{221.87}\mathsf{N}/\mathsf{mm}$, equivalent strain ε_max = 0.1632, nonlinear coefficientξ = 0.7363, transverse-longitudinal stiffness ratio R_k = 2.466. The ratio of static deformation under rated load to deformable displacement R_x = 0.504 and the natural frequency of the initial design can be calculated as $f=\raisebox{1ex}{$\sqrt{k_d/m}$}\!\left/ \!\raisebox{-1ex}{$2\pi $}\right.=4.935\mathrm{Hz}$. The simulation results of the initial design are shown in Table 1, which was compared with the experimental results in Section 3.3.

Table 1 Comparison of the simulation and experimental results of the initial design

3.2 Manufacturing of the polyurethane honeycomb structure

To ensure the dimensional accuracy, a four-axis milling machine DOOSAN T4050E is used for fabricating these honeycomb cells as shown in Fig. 8a. The dimensional tolerance of cells for the linear axes is less than ± 0.05 mm and the angle accuracy is less than ± 0.1°. Firstly, the whole polyurethane material is fixed with clamps. Then, different types of cutting tools are used for machining the honeycomb structure of the MI300-type vibration isolator. The experimental setup for honeycomb structure cutting and the finished product is given in Fig. 8.

Fig. 8

Manufacturing the polyurethane honeycomb structure of the initial design. a DOOSAN T4050E milling machine. b Manufacturing process. c Product of the initial design

3.3 Experimental test

In order to complete the measurement of mechanical properties such as the strain of the polyurethane honeycomb structure, the experimental static and dynamic tests are performed by using MTS universal testing machine (UTM) with a capacity of 300 kN, as shown in Fig. 9. In the experimental test, the polyurethane honeycomb structure is placed on the lower platform, and then the load is applied by moving the upper platen (pressure head) which is accurately controlled by the MTS UTM. Some kinds of tests, such as tensile, compression, and shear tests can be carried out by installing fixtures.

Fig. 9

MTS exceed microcomputer-controlled mechanical testing machine (100 kN)

The vertical and transverse static/dynamic tests were carried out according to the process specified in GB/T 15168/2013; the test process diagrams are shown in Fig. 10.

Fig. 10

Experimental test of the initial design. a Vertical test. b Transverse test

Through the mechanical property test and post-processing, the test curves of the initial design are shown in Fig. 11.

Fig. 11

The experimental results of the initial design. a Load-static deformation curve. b Static stiffness-force curve. c Nonlinear coefficient curve. d Dynamic load-deformation curve. e Transverse-longitudinal stiffness ratio curve

From Fig. 11, we can get the vertical static stiffness ${\mathit{\mathsf{k}}}_{\mathit{\mathsf{s}}}=\mathsf{225.8}\mathsf{N}/\mathsf{mm}$, nonlinear coefficientξ = 0.7232, vertical dynamic stiffness${\mathit{\mathsf{k}}}_{\mathit{\mathsf{d}}}=\mathsf{276.3}\mathsf{N}/\mathsf{mm}$, and transverse-longitudinal stiffness ratio${\mathit{\mathsf{R}}}_{\mathit{\mathsf{k}}}=\mathsf{2.450}$. The natural frequency of the initial design can be calculated $f=\raisebox{1ex}{$\sqrt{k_d/m}$}\!\left/ \!\raisebox{-1ex}{$2\pi $}\right.=4.83\mathrm{Hz}$, and the related test results are shown in Table 1 for details. It should be noted that the equivalent strain was not measured due to the lack of test equipment, such as the non-contact full-field test system VIC-3D. And whether the dimensional coordination and manufacturing constrain are met or not can be known through the machining results.

3.4 Comparison of the experimental and the simulation results

The comparison of simulation and experimental results is shown in Table 1. It can be seen that the maximum error between the finite-element simulation and the test results is only 2.17%. The finite-element simulation results are in good agreement with the measured results, which indicates that the established finite-element model for the performance analysis of the honeycomb structure is feasible and accurate.

4 Optimization design of the MI300-type honeycomb structure vibration isolator

4.1 Definition of the optimization problem

The goal of the design of the MI300-type vibration isolator is to minimize the ratio of the natural frequency difference between the design value and expected value under the constraints of the dimensional coordination of cell, the equivalent strain, the transverse-vertical stiffness ratio, and the manufacturing limitations. Therefore, the mathematical expression of the optimization design problem is defined as

$$ {\displaystyle \begin{array}{c}\mathrm{Find}\kern1em {x}_1,{x}_2,{x}_3,{x}_4,{x}_5,{x}_6\\ {}\operatorname{Min}\kern1.25em e=\mid 1-\frac{f}{f_0}\mid \\ {}s.t.{g}_1=\frac{\varepsilon_{\mathrm{max}}}{0.2}-1\le 0,{g}_2=1-\frac{\xi }{0.72}\le 0,\\ {}{g}_3=1-\frac{R_k}{2.4}\le 0,{g}_4=\frac{R_x}{0.6}-1\le 0,\\ {}{g}_5=\frac{H}{60}-1\le 0,{g}_6={T}_s\le 0,\\ {}{g}_7={K}_c\le 0\end{array}} $$

(2)

where x₁, x₂, x₃, x₄, x₅, x₆ are the design variables, g₁, g₂, g₃, g₄, g₅, g₆, g₇ are the constraints and $\mathit{\mathsf{e}}$ is the objective function. The physical meanings and the ranges of each design variable are shown in Table 2 and Table 3, respectively. Table 4 illustrates the boundary condition of the constraint functions.

Table 2 Physical meaning and ranges of design variables

Table 3 Fixed parameters and their values

Table 4 Constraint functions and their boundary conditions

As shown in Table 4, the constraints g₁, g₂, g₃, g₄ require to be evaluated by computationally expensive FE simulations, while g₅, g₆, g₇ can be calculated by mathematical formulas. The details of the FE simulations are shown in Section 2. The computationally inexpensive formulas are shown in (3) to (5).

$$ {\displaystyle \begin{array}{c}H=2m\left(h+\frac{l\cos \left({x}_1\right)}{\tan \left(\pi /2-{x}_1\right)}\right)+2\times \min \left({x}_5,{x}_6\right)+2{x}_3\\ {} where:h=2{x}_3\tan \left(\left(\frac{\pi }{2}-{x}_1\right)/2\right)+\frac{x_6}{\cos \left({x}_1\right)}-\frac{x_5}{\tan \left(\frac{\pi }{2}-{x}_1\right)}\\ {}l=\frac{\left({x}_4-{x}_5\right)}{2n\cos \left({x}_1\right)}\end{array}} $$

(3)

$$ {T}_s=2{nx}_3+\left(n+1\right){x}_5-{x}_4+1\le 0 $$

(4)

$$ {\displaystyle \begin{array}{l}{K}_c={x}_2/2-15{D}_b\le 0\\ {}\begin{array}{l} where:\\ {}\begin{array}{l}\left\{\begin{array}{l}{D}_b=2{r}_{f2}\kern0.5em if\kern0.5em {r}_{f1}<5\\ {}{D}_b=2\ \left({r}_{f2}+0.5\right)\kern0.5em if\kern0.5em {r}_{f1}\ge 5\end{array}\right.\\ {}{x}_d={x}_3-0.1\\ {}\begin{array}{l}{r}_f=\left[10{x}_d\right]\\ {}{r}_{fa}= num2 str\ \left({r}_f\right)\\ {}\begin{array}{c}{r}_{f1}= str2 double\ \left({r}_{fa}(2)\right)\\ {}{r}_{f2}= str2 double\ \left({r}_{fa}(1)\right)\end{array}\end{array}\end{array}\end{array}\end{array}} $$

(5)

In (5), the least integer function “[]” indicates the maximum integer not greater than itself, num2str() is to convert a numeric value into a string, and str2double() is to convert a string into double-precision number. The designed and expected values of natural frequency are $\mathit{\mathsf{f}}$ and ${\mathit{\mathsf{f}}}_{\mathsf{0}}$, respectively. These two values are used to calculate the objective function $\mathit{\mathsf{e}}$, as shown in Table 5.

Table 5 Details of the objective function

4.2 A multi-fidelity sequential optimization approach based on the feasible region analysis

Since relying on the high-fidelity FE simulation is computationally expensive, to relieve the computational burden, a multi-fidelity sequential optimization approach based on feasible region analysis (MF-FA) is proposed to incorporate both the high- and low-fidelity FE simulations into optimization. In the proposed MF-FA approach, a two-phase multi-fidelity sequential surrogate model optimization strategy is proposed to cope with the constraints. Specifically, in the first phase, sample points are added to the constraint boundary to find the feasible solution quickly. In the second phase, the quality of the feasible optimization solution is gradually improved in the feasible region until it converges to the global optimal solution.

The mathematical optimization model in (2) for the polyurethane honeycomb structure can be described as follows by introducing the MF surrogate model

$$ {\displaystyle \begin{array}{l}\min \kern0.8000001em \hat{f}\left(\boldsymbol{x}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern0.7em {\hat{g}}_{j1}\left(\boldsymbol{x}\right)\le 0\kern1em j=1,2\dots {J}_1\\ {}\kern1.9em {g}_{j2}\left(\boldsymbol{x}\right)\le 0\kern1em j=1,2\dots {J}_2\\ {}\kern2.5em {\boldsymbol{x}}_{lb}\le \boldsymbol{x}\le {\boldsymbol{x}}_{ub}\end{array}} $$

(6)

where $\hat{f}\left(\boldsymbol{x}\right)$ represents the surrogate of the objective function, $\kern0.1em {\hat{g}}_{j1}\left(\boldsymbol{x}\right)\kern1em j=1,2\dots {J}_1$ represents the surrogate of the computationally expensively constraints, g_j2(x) ≤ 0 j = 1, 2…J₂ represents the computationally inexpensively constraints. In this case, ${\mathit{\mathsf{J}}}_1=4,{\mathit{\mathsf{J}}}_2=3$.

The surrogate of objective function prefers to update with desirable objective function values. However, the surrogate of the constraint function pays more attention to the constraint boundary whether the accuracy is sufficient, so as to ensure that the constraint violation can be accurately judged in the optimization process.

In the sequential optimization process based on the multi-fidelity kriging model, it is necessary to make full use of the information of high- and low-fidelity sample points to search for the optimal solution. The sequential multi-fidelity kriging model can make full use of the information between the multi-fidelity analytical models obtained in the modeling process to guide the construction of the multi-fidelity model adaptively to improve the efficiency of the algorithm.

The construction of multi-fidelity kriging model generally involves the superposition of two single-fidelity kriging models. Suppose that there are low-fidelity samples ${x}_l=\left({\boldsymbol{x}}_1^l,{\boldsymbol{x}}_2^l,\dots, {\boldsymbol{x}}_{ml}^l\right)$ and corresponding responses ${f}_l=\left({\boldsymbol{f}}_1^l,{\boldsymbol{f}}_2^l,\dots, {\boldsymbol{f}}_{ml}^l\right)$, high-fidelity samples ${x}_h=\left({\boldsymbol{x}}_1^h,{\boldsymbol{x}}_2^h,\dots, {\boldsymbol{x}}_{mh}^h\right)$, and corresponding responses ${f}_h=\left({\boldsymbol{f}}_1^h,{\boldsymbol{f}}_2^h,\dots, {\boldsymbol{f}}_{nh}^h\right)$ in the current sample set. Firstly, a low-fidelity kriging model can be established through low-fidelity sample points

$$ {\hat{f}}_l(x)={\hat{\mu}}_l+{\psi_l}^{\mathbf{T}}{{\boldsymbol{\uppsi}}_l}^{-\mathbf{1}}\left({f}_l(x)-\mathbf{1}{\hat{\mu}}_h\right) $$

(7)

Then, a multi-fidelity kriging model based on the additive scaling function is constructed to achieve effective fusion between high- and low-fidelity models. The essence of the scaling function is the discrepancy function between the high-fidelity sample points and the low-fidelity kriging model, i.e., for any high-fidelity sample point, the scaling function value can be defined by

$$ c\left({x}_i^h\right)={f}_i^h-{\hat{f}}_i^l\left({x}_i^h\right) $$

(8)

where ${f}_i^h$ represents the high-fidelity response value at the point ${x}_i^h$, while ${\hat{f}}_i^l\left({x}_i^h\right)$ represents the predicted value of low-fidelity kriging at sample ${x}_i^h$.

The response set of the scaling function $C(x)=\left\{c\left({x}_1^h\right),c\left({x}_2^h\right),\dots, c\left({x}_{mh}^h\right)\right\}$ can be calculated, and the kriging model of additive scaling function can be given by

$$ \hat{\mathbf{C}}(x)={\hat{\mu}}_h+{\psi_h}^{\mathbf{T}}{\boldsymbol{\uppsi}}^{-\mathbf{1}}\left({f}_h\left(\mathrm{x}\right)-{\hat{f}}_l\left(\mathrm{x}\right)-\mathbf{1}{\hat{\mu}}_h\right) $$

(9)

According to (7) and (8), the predicted value of the multi-fidelity kriging model can be obtained by

$$ {\hat{f}}_{mf}\left(\mathrm{x}\right)={\hat{f}}_l\left(\mathrm{x}\right)+\hat{C}\left(\mathrm{x}\right) $$

(10)

Correspondingly, the predicted variance of the multi-fidelity kriging model is

$$ {\hat{s}}_{mf}\left(\mathrm{x}\right)=\sqrt{{{\hat{s}}^2}_l\left(\mathrm{x}\right)+{\hat{s}}_c^2\left(\mathrm{x}\right)} $$

(11)

where ${\hat{s}}_l(x)$and${\hat{s}}_c(x)$ are the predicted uncertainties (predicted variances) of low-fidelity kriging model and scaling function kriging model respectively.

In addition, to measure the optimization efficiency of different fidelity samples under unit computing resource, and to reflect the relative calculation cost required to obtain a sample point for different fidelity models, the simulation time of a high-fidelity response value is used as the reference to establish cost function c(t)

$$ c(t)=\frac{rc(h)}{rc(m)},m=h,l $$

(12)

where rc(h) represents the computational time of one high-fidelity simulation, rc(l) denotes that of a low-fidelity. c(t) = 1 when m = h, while c(t) > 1 when m = l.

The updating criterion of MF-FA in the first phase can be defined as (13) for searching the feasible solutions

$$ \mathrm{MF}\hbox{-} \mathrm{FA}1\left(\boldsymbol{x},t\right)={\sum}_{i=1}^{N_c}\left({\hat{g}}_{mf}^i\left(\boldsymbol{x}\right)-a{\hat{s}}_t^i\Big(\boldsymbol{x},t\Big)c(t)\right),\kern1.75em t=l, mf $$

(13)

where ${\hat{g}}_{mf}^i\left(\boldsymbol{x}\right)$ are the predicted values of the MF kriging model of the constraint functions, ${\hat{s}}_t^i\left(\boldsymbol{x},t\right)$ are the predicted variances of the different fidelity kriging models of the constraint functions, $\mathit{\mathsf{c}}\left(\mathit{\mathsf{t}}\right)$ is the cost coefficient for adjusting the global exploration and local exploitation, and the coefficient a is used to balance global and local search which is set as 1.96. To obtain the update sample, the genetic algorithm is utilized to search for the minimum value of (13).

Once a feasible solution is found, the updating criterion goes to the second phase to improve the quality of the current feasible solution. Then the sequential updating criterion needs to use the information of the MF surrogate of the objective function which can be defined as (14)

$$ \mathrm{MF}\hbox{-} \mathrm{FA}2\left(x,t\right)={w}_f{\hat{f}}_{mf}(x)+{w}_s{\hat{s}}_t\left(x,t\right)c(t)+a\max \left\{{g}_{mf}^i(x),0\right\},\kern0.5em t=l, mf $$

(14)

where ${\hat{f}}_{mf}\left(\boldsymbol{x}\right)$ is the predicted values of the MF kriging model of the objective function, w_f and w_s are the weights calculated by the entropy weight method (Qian et al. 2020a), $a\max \left\{{g}_{mf}^i(x),0\right\}$ is the penalty function to ensure the feasibility of the solutions (Qian et al. 2020b). The flowchart of the MF-FA is shown in Fig. 12.

Fig. 12

Flowchart of the MF-FA optimization framework

The MF-FA method divides the optimization process into two phases described as follows.

• Step I. Search for the feasible point

• Step I-1: To make the distribution of sampling points in the design space more uniform, the Optimal Latin Hypercube Sampling (OLHS) method is adopted to generate the initial sample points. The numbers of initial sample points of the low-fidelity model and the high-fidelity model are ${\mathit{\mathsf{n}}}_{\mathit{\mathsf{l}}}=\mathsf{6}\times \mathit{\mathsf{d}}$ and ${\mathit{\mathsf{n}}}_{\mathit{\mathsf{h}}}=\mathsf{3}\times \mathit{\mathsf{d}}$, respectively.

• Step I-2: The response values of the objective function and constraint function of initial sample points are calculated, and the MF kriging surrogate models of initial objective function and constraint functions are established.

• Step I-3: Evaluating that whether there is any point of high-fidelity solutions that satisfies the constraints in the sample points, if yes, go to Step II; otherwise, it goes to Step I-4.

• Step I-4: The MF-FA1 criterion was used to search the potential sample points that satisfy the constraints. In the search process, a genetic algorithm is used to search the design space, and the minimum point of the MF-FA1 criterion was selected to update the multi-fidelity kriging surrogate model. Then, it will go back to Step I-3.

• Step II. Search for the optimum point

• Step II-1: In the current iteration, feasible solutions already existed in the sample points. At this time, the sequential updating process should focus on improving the quality of the feasible solution. The MF-FA2 criterion is used to update the multi-fidelity kriging surrogate model. Similarly, the generation of update points is calculated by minimizing the MF-FA2 criterion.

• Step II-2: Judging whether the stopping criterion is satisfied or not, if yes, the optimization iteration is finished; otherwise, it goes to Step II-1.

4.3 Results and discussion

In the iterative process of the MF-FA algorithm, the sample space satisfying the constraints can be fully developed and explored by using the low-fidelity model in step I. The utilization efficiency of high-fidelity sample points to quickly find the global optimal solution in the feasible region is improved in step II.

In Table 6, the initial sample points of the MF-FA method are set as 18 high-fidelity sample points and 36 low-fidelity sample points respectively. The high-fidelity and low-fidelity model are calculated by using the fine mesh (14 grids) and coarse mesh (6 grids) finite-element models described in Section 2.3, respectively. The cost ratio of low/high-fidelity model is about 1:6, which means that the time of running one high-fidelity sample is six times that of the low-fidelity one. Specifically, all the initial 18 high-fidelity sample points of the polyurethane honeycomb structure are infeasible. The stopping criterion is that the total cost is 500 (equivalent) high-fidelity sample points.

Table 6 Parameter setting of the MF-FA

In order to be compared with the MF-FA algorithm, the genetic algorithm is also used to solve this engineering optimization problem. The parameters set for the GA are as follows: the population size and max iterations are 20 and 25, respectively. The crossover probability and mutation probability are 0.80 and 0.15, respectively. The generation gap is 0.95 to keep the elites in each generation.

The historical diagrams of the optimization process of GA and MF-FA are given in Fig. 13. The MF-FA algorithm firstly finds a feasible solution and has a better optimization solution within the total cost. The results shown in Fig. 13 illustrated that the MF-FA method can take full advantage of high- and low-fidelity models to obtain a better optimal solution.

Fig. 13

The optimization historical diagrams of GA and MF-FA

The optimal solutions of the two algorithms are listed in Table 7.

Table 7 The comparison of optimization results of GA and MF-FA

The optimized design calculated by MF-FA was manufactured, and the final polyurethane honeycomb structure is shown in Fig. 14.

Fig. 14

Product of the optimized design

Through the mechanical property test and post-processing, the test curves of the optimal design are shown in Fig. 15.

Fig. 15

The experimental results of the optimal design. a Load-static deformation curve. b Static stiffness-load curve. c Nonlinear coefficient curve. d Dynamic load-deformation curve. e Transverse-longitudinal stiffness ratio curve

As shown in Fig. 15, the vertical static stiffness is ${\mathit{\mathsf{k}}}_{\mathit{\mathsf{s}}}=\mathsf{310.1}\mathsf{N}/\mathsf{mm}$, the nonlinear coefficient is $\xi =\mathsf{0.7919}$, vertical dynamic stiffness is ${\mathit{\mathsf{k}}}_{\mathit{\mathsf{d}}}=\mathsf{370.2}\mathsf{N}/\mathsf{mm}$ and transversal-longitudinal stiffness ratio is ${\mathit{\mathsf{R}}}_{\mathit{\mathsf{k}}}=\mathsf{2.9579}$. The natural frequency of the optimal design can be calculated by (1) and$\mathit{\mathsf{f}}=\mathsf{5.59}\mathsf{Hz}$. The comparison of the simulation and experimental results are shown in Table 8.

Table 8 Comparison of the simulation and experimental results of the optimal design

In Table 8 and Table 9, the obtained optimal solution satisfies all the constraints. The natural frequency error between the experimental and the expected value (6 Hz) is just 6.83%, which is improved by 12.67% compared with the initial design. And the experimental error mainly comes from the changes in mechanical properties caused by non-uniformity and different batches of the polyurethane material.

Table 9 Comparison of the initial and optimal designs

According to the requirements of CB 1359–2002 “Rubber Vibration Isolators for Ships”, the natural frequency variation of vibration isolation in the main bearing direction should not exceed 15%. Therefore, the optimized design meets the standard requirements. The proposed MF-FA algorithm can effectively handle the computationally expensive optimization problems in practical engineering cases. The product of the MI300-type vibration isolator is made by assembling the polyurethane honeycomb structure with metal fittings as shown in Fig. 16.

Fig. 16

The product of MI300-type vibration isolator

5 Conclusions

In this work, a type of metamaterial vibration isolator with a honeycomb structure is proposed. The mechanical performances of which are computed by the finite-element method and are validated by the physical experiments. A multi-fidelity sequential optimization approach based on feasible region analysis is proposed for the design optimization of the metamaterial vibration isolator with a honeycomb structure. A two-phase multi-fidelity updating strategy is introduced to reduce the computational burden and to improve optimization accuracy. The final obtained optimal solution is manufactured and tested. Based on the testing results, some conclusions can be drawn as follows: (1) The two-dimensional plane finite-element model can be employed to accurately simulate the static mechanical performances of the metamaterial vibration isolator with a honeycomb structure; (2) MF-FA method can take full advantage of high- and low-fidelity models to obtain a better optimal solution compared with that only relying on high-fidelity simulations with the less computational costs; (3) The natural frequency from the simulation results at the optimum is 5.98 Hz, which is in good agreement with the physical experiments that is with 5.59 Hz. Compared with the initial design, the natural frequency error between the experimental and the expected value of the obtained optimum is improved by 12.67%.

There are also some limitations of the proposed optimization method. When there are a huge number of constraints, the feasible area is very small and disconnected. The proposed optimization method only searches within the whole feasible area during Phase II, which may lead to very low searching efficiency in these cases. What’s more, the effectiveness of the penalty function method is highly dependent on the accuracy of each individual MF model, which is hard to ensure if the computational cost is limited. Extending the proposed method to multiple constraint problems will be investigated in our future work. It is also noted that the geometry uncertainty is not considered in the design optimization of the metamaterial vibration isolator. As a part of future work, extending the proposed approach to robust optimization/reliability optimization will be investigated to consider the effects of the geometry uncertainty.