Introduction

Laser welding (LW), as a promising advanced manufacturing technology, has been widely used in the aerospace, shipbuilding, energy, and automotive industries (Liu et al. 2016; Zhou et al. 2016b, 2017b). It is prominent over other joining technologies due to its significant advantages such as a high degree of automation, enhanced joint strength, high energy density, and a narrow heat-affected zone (Huang and Kovacevic 2009; Chaki et al. 2015; Jiang et al. 2016; Saravanan et al. 2017; Zhou et al. 2018). However, one of the major issues of laser welding is welding-induced distortion during the LW process, which significantly decreases the quality of the welding joints, especially in strength and dimensional accuracy. Therefore, additional post-weld treatments are usually required to correct the welding-induced distortions for a satisfactory level of joint strength and dimensional accuracy of the welded structures (Islam et al. 2015). Post-weld treatments are always time-consuming, costly, and practical only in the most critical applications. For industrial applications where the cost budget is critical, the best practice is to minimize or control the welding-induced distortions by selecting the appropriate laser welding process parameters. The challenge is how to predict the welding-induced angular distortions in the process parameter space accurately and efficiently. A promising way is to adopt approximation model, which are also termed as metamodel since they provide “model of model”, fitting the relationships between the output responses and input process parameters (Benyounis and Olabi 2008; Shan and Wang 2010; Zhou et al. 2017c).

In a broad sense, these methods can be divided into two types: physical experiments based approximation modeling and finite element simulation based approximation modeling. In the first approach (Murugan and Gunaraj 2005; Pal et al. 2010; Sudhakaran et al. 2012; Narwadkar and Bhosle 2016; Adamczuk et al. 2017), laser welding experiments conducted at the sample points generated by some design of experiment methods. Next, approximation models are constructed to fit the relationship between the input process parameters and the welding-induced angular distortion. Finally, the accuracy of the developed approximation model is verified. If the accuracy level of the approximation model can meet the predefined requirement, it will be used for predicting the angular distortion at any given laser welding process parameters. For example, Murugan et al. (Murugan and Gunaraj 2005) conducted a five-factor five-level central composite rotatable design for gas metal arc (GMA) welding on structural steel plates (IS:2062). Based on the obtained experimental data, a second-order polynomial surface regression (PSR) model was developed to correlate angular distortion with multipass GMA process parameters. Sudhakaran et al. (Sudhakaran et al. 2012) conducted five-factor five-level central composite rotatable design for gas tungsten arc (GTA) welding on 202-grade stainless plates and predicted the angular distortion at different process parameters by adopting a PSR model. Narwadkar et al. (Narwadkar and Bhosle 2016) applied Taguchi method to generate three levels and three factors sample plan for metal inert gas (MIG) welding on Fe410WA steel, then a simple mathematical model is developed for predicting the angular distortion. The main shortcoming of these methods is that the required laser welding experiments for approximation modeling are time-consuming and costly due to the highly nonlinear and non-smooth relationships between process parameters and angular distortion.

On the other hand, in the finite element simulation based approximation modeling approach, the welding-induced angular distortions at the generated sample points, which are used to construct the approximation model, are obtained by running computational simulation model (Islam et al. 2014; Tian et al. 2014; Islam et al. 2015; Lostado et al. 2015; Rong et al. 2016). For example, Islam et al. (Islam et al. 2015) developed an inexpensive deformation prediction framework for lap joint fillet weld by integrating FEM and quadratic PSR. Then this framework was successfully combined with genetic algorithms for identifying promising process parameters with minimum weld deformation. Tian et al. (2014) applied back-propagation neural network (BPNN) for the prediction of angular distortion generated in GTA bead-on-plate welding process, where the angular distortion for S304L stainless steel was simulated using FEM. Rong et al. (2016) built BPNN based on FEM data to predict the angular distortion of the welded structures in no gap butt joint and then used it to decrease the weld distortion. To some extent, these methods make it possible to predict the distortion at process parameters with considerably less computationally and cost demands. However, due to the differences between the results from simulations and experiments, constructing the approximation model based on the data from computational simulation model may result in an impractical relationship between process parameter and angular distortion. For example, Rong et al. (2015) built an approximation model based on the finite element model for predicting the angular distortion of tungsten inert gas arc welding, demonstrating that there exist large differences between the predicted values and the actual results.

To make a trade-off between high accuracy and low expense, this paper proposes a variable-fidelity approximation modeling approach for predicting the welding-induced angular distortion in the laser welding process. In the variable-fidelity approximation modeling approach, a three-dimensional thermo-mechanical finite element model is developed as a low-fidelity model, in which a large number of samples are evaluated to provide a general trend of the relationship between process parameters and angular distortion. Whereas, the physical welding experiment is taken as a high-fidelity model, in which a small number of samples are conducted to enhance the prediction accuracy of the approximation model. Specifically, a low-fidelity radial basis function (RBF) model is firstly constructed based on the sample data from the finite element model. Then, a linear tuning strategy is introduced to bring the low-fidelity RBF model as close as possible to the data from the physical welding experiments. Finally, the variable-fidelity approximation model (VFAM) is obtained by adopting a scaling function to calibrate the differences between the tuning low-fidelity approximation model and the high-fidelity data. The variable-fidelity approximation model can be used to predict the angular distortion if its prediction accuracy is achieved.

The rest of the paper is organized as follows. In Sect. 2, a detailed description of the proposed approach is presented. In Sect. 3, the details of the high-fidelity laser welding experiments are provided. The low-fidelity three-dimensional FEM and simulation, including geometry modeling, thermo-mechanical analysis, and simulation results are presented in Sect. 4. In Sect. 5, the implementation of the proposed approach and a comparison between the single-fidelity approximation modeling approach and the proposed approach are discussed in details. Finally, the concluding remarks and future work are given in Sect. 6.

The proposed approach

Problem definition

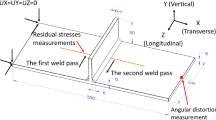
Figure 1 demonstrates the schematic diagram of the fiber laser keyhole welding process. Generally, the weld distortions are mainly caused by the changes of the temperature field of the welding pool during the welding process. The illustration of the angular distortion is plotted in Fig. 2. According to numerous actual tests and surveys (Park and An 2016; Rong et al. 2017), the angular distortion of the fiber laser keyhole welding is mainly influenced by three welding process parameters including the laser power (LP), the welding speed (WS), and the laser focal position (LFP). Considering these circumstances (Sathiya et al. 2009; Ghosal and Chaki 2010; Sathiya et al. 2012; Rossini et al. 2015; Gao et al. 2016; Zhou et al. 2016): (a) Low laser power and high welding speed go against the flowing of molten metal, which can result in incomplete fusion, imperfections of filled groove or even spatter; (b) excessive large focal position will reduce the laser absorptivity and cause the root concavity and incompletely filled groove (Singh et al. 2014), the following boundaries are used for welding process parameters

$$\begin{aligned} 2\hbox {(kW)}\le & {} LP\le 3\hbox {(kW)}, \hbox {2.5 (m/min)}\le WS\le \hbox {3 (m/min)}, \nonumber \\&-2\hbox {(mm)}\le \hbox {LFP}\le 0\hbox {(mm)} \end{aligned}$$
(1)
Fig. 1
figure 1

Schematic plot of laser welding process

Full size image
Fig. 2
figure 2

The illustration of angular distortion

Full size image
Fig. 3
figure 3

The framework of the proposed approach

Full size image

The proposed variable-fidelity approximation modeling approach

The goal of the proposed variable-fidelity approximation modeling approach is to predict the angular distortion by integrating the data from both low-fidelity finite element simulation and high-fidelity physical experiment. The low-fidelity finite element simulation and the high-fidelity physical experiment are regarded as white box models (Li et al. 2009). They are just used for obtaining the angular distortion under some process parameters. That is to say, they are not directly used to find the relationships between the laser welding process parameters and angular distortion. Figure 3 demonstrates the framework of the proposed variable-fidelity approximation modeling approach. As a start, two sampling sets, \(X^{h}=\left\{ {x_1^h ,x_2^h ,\ldots ,x_M^h } \right\} \) with a small number of samples, \(X^{l}=\left\{ {x_1^l ,x_2^l ,\ldots ,x_N^l } \right\} \) with a large number of samples, for high-fidelity and low-fidelity models are generated using the design of experiment (DOE) approach. It should be noticed that the term “a large number of samples” and “a small number of samples” imply the relative meaning of sample amount by comparing with each other. Then high-fidelity laser welding experiments will be conducted at the sample set \(X^{h}\) to obtain the angular distortions. The details of the implementation of the laser welding experiment are presented in Sect. 3. At the same time, the low-fidelity finite element simulation will be performed at the sample set \(X^{l}\) for obtaining the angular distortions. The detailed descriptions of the three-dimensional FEM and simulation, including geometry modeling and thermo-mechanical analysis are presented in Sect. 4.

In view of modeling the relationships between the laser welding process parameters and angular distortion, they are regarded as black-box functions because we just use the obtained data to approximate the relationships. Based on the two different levels fidelity data, a low-fidelity RBF model is constructed. Then, a linear tuning strategy is introduced to make the low-fidelity RBF model close to the high-fidelity data. The obtained tuning approximation model is taken as a base approximation model and is mapped to the high-fidelity data by using a scaling function. Finally, the variable-fidelity approximation model can be expressed by the tuning approximation model and the scaling function. The variable-fidelity approximation model is defined as

$$\begin{aligned} y_{vf} (x)=\hat{{y}}_{l, \mathrm{tuned}} (x)+d(x)=c_0 +c_1 \hat{{y}}_l (x)+d(x) \end{aligned}$$
(2)

where \(\hat{{y}}_l \) is the constructed low-fidelity RBF model, \(\hat{{y}}_{l, \mathrm{tuned}} (x)=c_0 +c_1 \hat{{y}}_l (x)\) is the tuning low-fidelity approximation model, \(c_0 \) and \(c_1 \) are the introduced tuning parameters, and d(x) denotes the scaling function which is used to map the difference between the high-fidelity data and the tuning low-fidelity approximation model \(\hat{{y}}_{l, \mathrm{tuned}} (x)\).

The remainder of this section will describe the proposed variable-fidelity approximation modeling approach in more details.

Construct the low-fidelity RBF model

The low-fidelity RBF model is constructed based on the data from the finite element simulation. Suppose \(f^{l}=\left\{ {f_1^l ,f_2^l ,\ldots ,f_N^l } \right\} \) is the angular distortions vector obtained by running the finite element simulations at the low-fidelity sample set \(X^{l}=\left\{ {x_1^l ,x_2^l ,\ldots ,x_N^l } \right\} \), a low-fidelity RBF model for weld distortion prediction can be expressedas,

$$\begin{aligned} \hat{{y}}_l (x)=\sum _{p=1}^N {w_p^l } \phi _l \left( \left\| {x-x_p^l } \right\| \right) \end{aligned}$$
(3)

where x is the process parameter, N is the number of sample points in \(X^{l}\), \(x_p^l \) is the \(p^{\text {th}}\) sample point in \(X^{l}\), and \(\left\| {x-x_p^l } \right\| \) denotes the Euclidean distance between the process parameter x and the \(p^{\text {th}}\) low-fidelity sample points, which is defined as,

$$\begin{aligned} \left\| {x-x_p^l } \right\| =\sqrt{(x-x_p^l )^{T}(x-x_p^l )} \end{aligned}$$
(4)

\(\phi _l ({\bullet })\) represents the radial basis functions. Commonly used radial basis functions are (Wang et al. 2014; Chen and Kuo 2017; Zhou et al. 2015, 2017a)

(1) Bi-harmonic \(\phi _l \left( r \right) =r\); (2) Thin-plate spline \(\phi _l \left( r \right) =r^{2}\log (r)\);

(3) Multiquadric \(\phi _l \left( r \right) =\sqrt{r^{2}+\upsilon ^{2}}\) (4) Cubic \(\phi _l \left( r \right) =\left( {r+\upsilon } \right) ^{3}\)

(5) Gaussian \(\phi _l \left( r \right) =e^-\left( {\upsilon r^{2}} \right) \) (6) Inverse-multiquadric \(\phi _l \left( r \right) =\frac{1}{\sqrt{r^{2}+\upsilon ^{2}}}\)

where \(\upsilon \) is a constant value and \(0<\upsilon \le 1\)

The unknown interpolation vector \(w^{l}\) is obtained by minimizing the sum of the squares of deviations, which is expressed as,

$$\begin{aligned} J_1 =\sum _{s=1}^N {\left[ {f(x_s^l )-\sum _{p=1}^N {w_p^l \phi _l \left( \left\| {x_s^l -x_p^l )} \right\| \right) } } \right] } ^{2} \end{aligned}$$
(5)

Once the above optimization is solved, the interpolation vector \(w^{l}\) can be obtained as,

$$\begin{aligned} w^{l}=\left( {\Phi _l^T \Phi _l +\Lambda _l } \right) ^{-1}\Phi _l^T f^{l} \end{aligned}$$
(6)

where \(\Lambda _l \) are zero except for the regularization parameters on the diagonal. \(\Phi _l \) is a design matrix. Due to the advantages of less parameter setting and excellent overall performance, the Gaussian radial basis function is used as the radial basis. Then the design matrixes \(\Phi _l \) can be expressed as,

$$\begin{aligned} \Phi _l =\left( {\begin{array}{cccc} e^{-\left( \upsilon \cdot \left\| {x_1^l -x_1^l } \right\| \right) ^{2}}&{} e^{-\left( \upsilon \cdot \left\| {x_1^l -x_2^l } \right\| \right) ^{2}}&{}\cdots &{} {e^{-\left( \upsilon \cdot \left\| {x_1^l -x_N^l } \right\| \right) ^{2}}} \\ e^{-\left( \upsilon \cdot \left\| {x_2^l -x_1^l } \right\| \right) ^{2}}&{} e^{-\left( \upsilon \cdot \left\| {x_2^l -x_2^l } \right\| \right) ^{2}}&{}\cdots &{}e^{-\left( \upsilon \cdot \left\| {x_2^l -x_N^l } \right\| \right) ^{2}} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {e^{-\left( \upsilon \cdot \left\| {x_N^l -x_1^l } \right\| \right) ^{2}}}&{} e^{-\left( \upsilon \cdot \left\| {x_N^l -x_2^l } \right\| \right) ^{2}}&{}\cdots &{} {e^{-\left( \upsilon \cdot \left\| {x_N^l -x_N^l } \right\| \right) ^{2}}} \\ \end{array}} \right) \nonumber \\ \end{aligned}$$
(7)

Tuning the low-fidelity RBF model

In this work, a linear tuning strategy is introduced to bring the low-fidelity RBF model close to the high-fidelity data. Suppose \(f^{h}=\left\{ {f_1^h ,f_2^h ,\ldots ,f_M^h } \right\} \) is the weld distortions vector obtained by conducting laser welding experiments at the high-fidelity sample set \(X^{h}=\left\{ {x_1^h ,x_2^h ,\ldots ,x_M^h } \right\} \), in the linear tuning strategy two tuning parameters \(c_0 \) and \(c_1 \) are introduced and the minimization optimization problem is formulated as,

$$\begin{aligned} \begin{array}{l} \min :L(c_0 ,c_1 )=\sum _{i=1}^M {\left[ {f^{h}(x_i^h )-(c_0 +c_1 \hat{{y}}_l (x_i^h ))} \right] ^{2}} \\ s.t.\,l_0 \le c_0 \le u_0 ,l_1 \le c_1 \le u_1 \\ \end{array} \end{aligned}$$
(8)

where \(L(c_0 ,c_1 )\) represents the loss function in a square sense, \(x_i^h \) is the \(i^{\text {th}}\) sample points in \(X^{h}\), \(f^{h}(x_i^h )\) is the weld distortion from high-fidelity model at \(x_i^h \), M is the number of high-fidelity sample points in \(X^{h}\), and \(l_0 \), \(u_0 \), \(l_1 \), and \(u_1 \) are the boundary constraints for tuning parameters, which represent the prior knowledge of the global constant bias and multiplicative scaling between low-fidelity and high-fidelity data. This is very helpful to avoid the over-fitting problem in conventional linearity when there is no enough data. Different types of tuning parameters \(c_0 \) and \(c_1 \) can be selected, such as the constant term, the linear term, and the quadratic term. In this work, the tuning parameters \(c_0 \) and \(c_1 \) are assumed to be unknown but fixed as a constant to simplify the modeling procedure.

Several approaches are available for determining these two tuning parameters, e.g., the cross-validation, the least square method, and the maximum likelihood estimation. Owning to its convenience and easy application ability, the least square method is used in this work.

Once the optimal tuning parameters \(c_0^*\) and \(c_1^*\) are obtained by solving the optimization problem in Eq. (8), the tuning low-fidelity approximation model \(\hat{{y}}_{l, \mathrm{tuned}} (x)\) can be expressed as,

$$\begin{aligned} \hat{{y}}_{l, \mathrm{tuned}} (x)=c_0^*+c_1^*\hat{{y}}_l (x) \end{aligned}$$
(9)

Difference calibrated using a scaling function

The obtained tuning low-fidelity approximation model in Eq. (9) will not be enough to fit the high-fidelity laser welding experiment when the data are far from sufficient to explore the behavior of the weld distortion on the space of the process parameters. Therefore, it is quite necessary to account for the remaining discrepancy between the tuning low-fidelity approximation model and the high-fidelity data. The remaining discrepancy \(d=\left\{ {d_1 ,d_2 ,\ldots ,d_m } \right\} \) between the high-fidelity responses and the obtained tuning low-fidelity approximation model can be calculated as,

$$\begin{aligned} d_i (x_i^h )=f^{h}(x_i^h )-(c_0^*+c_1^*\hat{{y}}_l (x_i^h )),i=1,2,\ldots M \end{aligned}$$
(10)

Since the relationship between the high-fidelity sample set \(X^{h}\) and the remaining discrepancy vector \({{\varvec{d}}}\) is not a priori, a scaling function, which is specified as a line combination of some radial basis functions with weight factors, is formulated as,

$$\begin{aligned} \hat{{d}}(x)=\sum _{q=1}^M {w_q^s } \phi _s \left( \left\| {x-x_q^h } \right\| \right) \end{aligned}$$
(11)

where \(\phi _s ({\bullet })\) is the selected Gaussian radial basis function and \(\left\| {x-x_q^h } \right\| \) denotes the Euclidean distance between the process parameter x and the \(q^{\text {th}}\) high-fidelity sample points, which is defined as,

$$\begin{aligned} \left\| {x-x_q^h } \right\| =\sqrt{(x-x_q^h )^{T}(x-x_q^h )} \end{aligned}$$
(12)

In Eq. (11), \(w^{s}\) are unknown weight factors, which can be obtained by minimizing the sum of the squares of deviations

$$\begin{aligned} J_2= & {} \sum _{i=1}^M \left[ f^{h}(x_i^h )-(c_0^*+c_1^*\hat{{y}}_l (x_i^h )) \right. \nonumber \\&\left. -\sum _{q=1}^M {w_q^s } \phi _s \left( \left\| {x_i^h -x_q^h } \right\| \right) \right] ^{2} \end{aligned}$$
(13)

To avoid repeating two very similar analyses, a weight penalty term is added to the sum of the squares of deviations. Then, the cost function is minimized as,

$$\begin{aligned} \Gamma= & {} \sum _{i=1}^M \left[ f^{h}(x_i^h )-(c_0^*+c_1^*\hat{{y}}_l (x_i^h )) \right. \nonumber \\&\left. -\sum _{q=1}^M {w_q^s } \phi _s \left( \left\| {x_i^h -x_q^h } \right\| \right) \right] ^{2}{+}\sum _{q=1}^M {\ell _q } (w_q^s )^{2} \end{aligned}$$
(14)

where \(\ell \) is the non-negative regularization vector, which is used to control the additional weight penalty term.

To solve Eq. (14) for obtaining the values of unknown weight factors, the partial derivatives of the cost function related to each \(w_q^s \) are calculated. The partial derivative at \(q^{\text {th}}\) coefficient can be expressed as,

$$\begin{aligned} \frac{\partial \Gamma }{\partial w_q^s }= & {} 2\sum _{i=1}^M \Bigg (f^{h}(x_i^h )-(c_0^*+c_1^*\hat{{y}}_l (x_i^h ))\nonumber \\&-\sum _{q=1}^M {w_q^s } \phi _s \left( \left\| {x_i^h -x_q^h } \right\| \right) \Bigg )\frac{\partial \sum _{q=1}^M {w_q^s } \phi _s \left( \left\| {x_i^h -x_q^h } \right\| \right) }{\partial w_q^s }\nonumber \\&{+2}\ell _q w_q^s \end{aligned}$$
(15)

Equating the above expression to zero leads to the equation

$$\begin{aligned}&\sum _{i=1}^M {(f^{h}(x_i^h )-(c_0^*+c_1^*\hat{{y}}_l (x_i^h )))\phi _s \left( \left\| {x_i^h -x_q^h } \right\| \right) } {+}\ell _q w_q^s \nonumber \\&\quad =\sum _{i=1}^m {\left( \sum _{q=1}^M {w_q^s } \phi _s \left( \left\| {x_i^h -x_q^h } \right\| \right) \phi _s \left( \left\| {x_i^h -x_q^h } \right\| \right) \right) } \end{aligned}$$
(16)

There are M such equations, for \(1\le i\le M\), each representing one constraint on the solution. When matrices and vectors are adopted, the problem to obtain the unknown weight factors \(w^{s}\) can be rewritten as,

$$\begin{aligned} \Phi _s^T \Phi _s w^{s}{+}\Lambda _s w^{s}\hbox {=}\Phi _s^T d \end{aligned}$$
(17)

where \(\Phi _s \) is the design matrix is

$$\begin{aligned} \Phi _s =\left( {{\begin{array}{cccc} {\phi _s \left( \left\| {x_1^h -x_1^h } \right\| \right) }&{} {\phi _s \left( \left\| {x_1^h -x_2^h } \right\| \right) }&{}{\cdots }&{} {\phi _s \left( \left\| {x_1^h -x_M^h } \right\| \right) } \\ \phi _s \left( \left\| {x_2^h -x_1^h } \right\| \right) &{} \phi _s \left( \left\| {x_2^h -x_2^h } \right\| \right) &{}\cdots &{} \phi _s \left( \left\| {x_2^h -x_M^h } \right\| \right) \\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ {\phi _s \left( \left\| {x_M^h -x_1^o } \right\| \right) }&{} {\phi _s \left( \left\| {x_M^h -x_2^h } \right\| \right) }&{}{\cdots }&{} {\phi _s \left( \left\| {x_M^h -x_M^h } \right\| \right) } \\ \end{array} }} \right) \end{aligned}$$
(18)

\(\Lambda _s \) are all zero except for the regularization parameters along its diagonal.

$$\begin{aligned} \Lambda _s =\left( {{\begin{array}{cccc} \ell _{1}&{} {0}&{}{\cdots }&{} 0 \\ 0 &{}\ell _{2}&{}\cdots &{} 0 \\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ 0&{} {0}&{}{\cdots }&{} {\ell _{M}} \\ \end{array} }} \right) \end{aligned}$$
(19)

Solving Eq. (17), the unknown weight factors \(w^{s}\) can be obtained as,

$$\begin{aligned} w^{s}=\left( {\Phi _s^T \Phi _s +\Lambda _s } \right) ^{-1}\Phi _s^T d^{T} \end{aligned}$$
(20)

Finally, substituting Eq. (20) to Eq. (11), the scaling function can be obtained.

Table 1 The chemical composition of stainless steel 316L (in weight)
Full size table

Build the variable-fidelity approximation model

After the scaling function is constructed, the variable-fidelity approximation model can be expressed as,

$$\begin{aligned} y_{vf} (x)= & {} c_0^*+c_1^*\left( \sum _{p=1}^N {w_p^l } \phi _l \left( \left\| {x-x_p^l } \right\| \right) \right) \nonumber \\&+\sum _{q=1}^M {w_q^s } \phi _s \left( \left\| {x-x_q^h } \right\| \right) \end{aligned}$$
(21)

The prediction accuracy of the variable-fidelity approximation model should be checked before applying it to predict the weld distortion at un-sampled laser welding process parameters. Generally, two types of validation approaches are available, one of which requires additional test points and the other is not required (e.g., leave-one-out (LOO) cross-validation approach and bootstrap approach). In this work, validation approach via additional test points and the LOO cross-validation error metric are adopted to demonstrate the effectiveness of the proposed variable-fidelity approximation modeling approach. If the desired level of accuracy of the constructed variable-fidelity approximation model is not achieved, sample points from high-fidelity laser welding experiments can be added because additional high-fidelity samples can make a greater contribution to the prediction accuracy of the constructed variable-fidelity approximation model. The more high-fidelity samples, the more accurate the variable-fidelity approximation model will be. While the cost of the experiment will also increase.

Laser welding experiment

Material

The laser welding was conducted on a 3 mm-thick stainless steel 316L plate. Table 1 shows the chemical composition in weight percent of the base metal. The size of each specimen is \({100}\times {8}0\times {3}\mathrm{mm}^{3}\). To eliminate the interference from oxidation film and prevent the welding bead being polluted by oil, the specimen had been pretreated and degreased with acetone before welding.

Laser welding system

Figure 4 demonstrates the setup of laser welding used in this work. The laser welder utilized here was a ytterbium-doped fiber laser device (IPG YLR-4000) with the maximum average power of the laser was 4000 W. The continuous laser travels through the optical fiber to the laser welder head. The laser header is installed on the robot ABB IRB4400. A focusing lens with the focal length of 250 mm was placed in the laser welder head. The focused laser irradiated on the specimen. The radius of the light spot on the surface of the specimen was about 0.3 mm. The angle between the vertical direction of the weldment and laser beam was set to be 8\(^{0}\). Argon was utilized as shielding gas during the welding with a flow rate of 1.0 m\(^{3}\)/h.

Fig. 4
figure 4

Laser welding equipment

Full size image

The height vernier caliper shown in Fig. 5 was used to measure the maximum welding angle distortion of welded specimen with the off-line mode. To obtain the angle distortion of welded specimen, the following procedures were performed. Firstly, the surfaces of the welded specimen and measuring paw were cleaned with anhydrous alcohol. Secondly, the front, middle and rear positions of the welded specimen were marked. Thirdly, the measuring pawl of the height vernier caliper was placed on the surface of the three marked points to read the angle distortions. Finally, the maximum angle distortion among these three points will be selected as the angle distortion of welded specimen.

Fig. 5
figure 5

Angular distortion measurement platform

Full size image

Finite element simulation

In this study, a three-dimensional thermo-mechanical finite element model is developed as a low-fidelity model to simulate the angular distortion of the fiber laser keyhole welding (Zhou et al. 2018). Due to complex changes in the actual welding process, simplifying assumptions are made as follows,

  1. 1.

    The properties of material obey the Mises yield criterion.

  2. 2.

    The yielding behavior of the plastic zone is subject to the plastic flow criterion and strengthening criterion.

  3. 3.

    Elastic strain, plastic strain, and temperature strain are inseparable.

  4. 4.

    The impacts of sticky and creep are not considered during stress changing procedure.

  5. 5.

    The physical and mechanical properties of the material vary with the temperature. The material properties are isotropic.

Geometry modeling

Figure 6 shows the mesh employed for finite element simulation. Considering the symmetry of the model, the size of the finite element model takes half of the true welding workpiece to improve the computational efficiency in welding simulation. The computational domain has a dimension of \({100}\times {40}\times 3\hbox {mm}^{3}\). The welding heat source is applied on the symmetrical surface to simulate the fiber laser keyhole welding process. Since the changes of temperature and stress fields are complex at the weld-forming region, the grids in this region are refined. While as the increase of the distance from the weld-forming region, the changes of the temperature field and the stress field will weaken. A proper coarser mesh is adopted to effectively improve the computational efficiency. The model contains 44,646 four-node hexagonal elements and 36,308 nodes.

In the actual welding process, the workpiece is welded under the free state without any fixture. While in the simulation process the model may be deformed due to the expansion and contraction of the material. Therefore, it is necessary to limit the degrees of freedom for some key nodes to prevent rigid displacement of the model. As illustrated in Fig. 6, the degrees of freedom in the z and y directions at point A are limited. At point B, a constraint on the degrees of freedom in the z direction is applied. The constraint on the degrees of freedom in the x direction is applied to the line \(\hbox {L}_{1}\). A symmetry constraint is also applied to the symmetric plane.

Fig. 6
figure 6

Illustration of the 3D finite element model

Full size image

Thermo-mechanical analysis

Computational modeling laser welding is a coupled thermo-mechanical problem. It contains several coupling phenomena, such as nonlinear heat flow, weld pool physics, non-linear material behavior at high temperatures, thermal deformation, and mechanical distortion (Islam et al. 2015). However, in the computational modeling of laser welding, the general idea is to adopt a weakly coupled model, in which a simplified heat input model is used to replace the physics in the weld and the mechanical analysis is performed independently of the thermal analysis. This method is computationally effective and useful when the main purpose is to study transient temperature, distortion, and stress fields other than the complex physical properties of the metal. Since the goal of this study is to investigate welding-induced distortion, a sequential coupling method is adopted. Only the influence of the welding temperature field on the stress field is considered and the influence of the welding stress field on the temperature field is ignored.

Thermal analysis

In the process of laser heat transfer, obtaining the welding temperature field is a nonlinear transient heat transfer problem. The law of conservation of energy is the most basic criterion in thermal analysis of laser welding. Therefore, during the thermal analysis of weld pool, the force and displacement are ignored and only the energy is considered. In this step, the value of the temperature at each node is obtained by the instantaneous heat conduction equation given below

$$\begin{aligned} \rho C_P \left( {\frac{\partial T}{\partial \hbox {t}}-v\frac{\partial T}{\partial x}} \right)= & {} \frac{\partial }{\partial x}\left( {k_x \frac{\partial T}{\partial x}} \right) +\frac{\partial }{\partial y}\left( {k_y \frac{\partial T}{\partial y}} \right) \nonumber \\&+\frac{\partial }{\partial z}\left( {k_z \frac{\partial T}{\partial z}} \right) +Q \end{aligned}$$
(22)

where \(\rho \) is the density of the material, \(C_P \) is the specific heat capacity and T is the instantaneous temperature, \(k_x \), \(k_y \), and \(k_z \) are thermal conductivities in the directions of x, y, and z, Q is the rate of heat production within each unit volume, and v denotes the welding speed.

The initial condition can be expressed as,

$$\begin{aligned} T\left( {x,y,z,0} \right) =T_0 \end{aligned}$$
(23)

where \(T_0 \) is the initial temperature (\(T_0 =300\,\hbox {K})\).

The boundary condition can be expressed by

$$\begin{aligned}&k_n \frac{\partial T}{\partial n}-q+h\left( {T-T_0 } \right) +\sigma \varepsilon \left( {T^{4}-T_0^4 } \right) \nonumber \\&\quad =0\left( {x,y,z} \right) \in S\quad t>0 \end{aligned}$$
(24)

where S is the boundary to be calculated, \(k_n \) is the thermal conductivity on the boundary surface S, h is the convection coefficient, \(\varepsilon \) is the radiation heat transfer coefficient, and q is the heat flux on the boundary surface S.

Typically, the complex physics of heat generation or weld pool is simplified considerably and replaced by a heat input model. In this work, the previously developed body heat source model, made by combining double-ellipsoids, rotating-Gaussian, and a cone (Jiang et al. 2016), is adopted for FEM simulation. The illustration of the heat source model is plotted in Fig. 7.

Fig. 7
figure 7

Heat source model

Full size image
Table 2 Temperature dependent thermal properties of stainless steel 316L
Full size table

Thermo-physical properties of the material will change as the temperature increases during the welding process, especially when the temperature between liquidus and solidus (Islam et al. 2014). Therefore, thermo-physical properties of stainless steel need to be set in the finite element simulation. The specific heat capacity and thermal conductivity change with temperature are listed in Table 2.

Mechanical analysis

After calculating the temperature field of fiber laser keyhole welding, the thermal analysis units of the model are transformed into the corresponding structural units. Then the temperatures of the nodes are put into the structural model as thermal loading to calculate the stress-strain field.

The stress-strain relationship of the material in the case of elasticity and plasticity is

$$\begin{aligned} \left\{ {d\sigma } \right\} =\left[ D \right] \left\{ {d\varepsilon } \right\} -\left\{ C \right\} dT \end{aligned}$$
(25)

where \(\left[ D \right] \) is an elastic or plastic matrix, \(\left\{ C \right\} \) is a temperature-related matrix, and \(\left\{ {d\varepsilon } \right\} \) is the total strain including elastic strain, plastic strain, and thermal strain.

In the thermo-elastic finite element analysis of fiber laser keyhole welding, the welding transient temperature field analysis serves as the basis for the calculation of stress field. The temperature increment is loaded on each element of the finite element model to obtain the displacement increment of each node on the unit. The strain increment can be expressed as (Rong et al. 2017)

$$\begin{aligned} \left\{ {d\varepsilon } \right\} ^{e}=\left[ D \right] \left\{ {d\delta } \right\} ^{e} \end{aligned}$$
(26)

where \(\left\{ {d\varepsilon } \right\} ^{e}\) is the strain increment of each unit and \(\left\{ {d\delta } \right\} ^{e}\) is the displacement increment of the unit node.

Discussion of simulation results

The temperature field of fiber laser keyhole welding is divided into two processes, the heat source loading process and the cooling process. The heat source loading process contains 160 time steps with there are 5 sub-steps involved in each. The cooling process contains 840 steps. The time integral method is used to calculate the heat balance equation. Figure 8 demonstrates the cloud plot of the transient temperature field at a typical process parameter \((LP=3\,\hbox {kW}, WS=3\hbox {m}/\min ,LFP=-1\hbox {mm})\). Because the welding speed of fiber laser keyhole welding is faster than those of the traditional welding techniques, the smaller heat affected zone can result in a faster coolingprocess.

Fig. 8
figure 8

Temperature field distributions during heating and cooling processes

Full size image

Once the analysis results of temperature field of each step are obtained, these results will be placed into the calculation model of the stress field. Then, the angular distortion can be obtained by adopting the time integral method. Figure 9 shows the cloud plot of the distortion after cooling. As illustrated in Fig. 9, bending distortions occur along both sides of the welding bead. The distortions at the edge of the sheet are significantly larger than those of the welding region. This is because during the loading process of the heat source, the extremely high heat input makes the temperature of the fusion zone significantly higher than the temperatures of the other areas of the workpiece. The thermal expansion of the material is hindered in producing plastic distortion. In the subsequent cooling process, shrinkages with varying degrees occur. Uneven transverse shrinkage finally results in angular distortion, whose direction is perpendicular to the welding bead.

Results and discussion

Design of experiments

The aim of the design of experiment (DOE) is to decrease the effect of errors in simulation or experiments on the responses, while allowing engineers to build an approximation model more efficiently. A lot of DOE approaches, such as the Hammersley sequence sampling design (HSSD), uniform design (UD), faces centered design (FCD), and optimal Latin hypercube sampling (OLHS), are available to generate sample points that can provide a good coverage of the design space. In this study, the OLHS is adopted to spread the points throughout the design space. The OLHS is a modified LHS where the combination of factor levels for each factor is optimized, rather than randomly combined. The OLHS allows the designer total freedom in selecting the number of designs to run on an available computational budget (Zhou et al. 2016). Specifically, the OLHS developed by Jin et al. [36] is used, where an enhanced stochastic evolutionary algorithm to evaluate the maximin distance criterion of points in the searching space to obtain space filling sample points. For the low-fidelity finite element model, 32 sample points are generated, while the total number of sample points available for the high-fidelity laser welding experiment is limited to 12. The generated sampling plan is illustrated in Fig. 10. Table 3 summarizes the generated sample points and corresponding low-fidelity and high-fidelity angular distortions.

Fig. 9
figure 9

Displacement distribution after cooling

Full size image
Fig. 10
figure 10

The sampling plan generated by optimal Latin hypercube sampling

Full size image

The construction of the variable-fidelity approximation model

Based on the sample data listed in Table. 3, the low-fidelity RBF model \(\hat{{y}}_l (x)\) is constructed firstly. Figure 11a–c plot the three-dimensional (3D) surfaces of the low-fidelity RBF model for the angular distortion. To obtain the tuning parameters \(c_0 \) and \(c_1 \), the following minimization optimization problem is solved,

$$\begin{aligned} \min :L(c_0 ,c_1 )= & {} \sum _{i=1}^M {\left[ {f^{h}(x_i^h )-(c_0 +c_1 \hat{{y}}_l (x_i^h ))} \right] ^{2}} \nonumber \\&s.t.-50\le c_0 \le 50,-5\le c_1 \le 5 \end{aligned}$$
(27)

The obtained optimal tuning parameters are \(c_0^*=50\) and \(c_1^*=0.9553\). Then the tuning low-fidelity approximation model \(\hat{{y}}_{l, \mathrm{tuned}} (x)\) can be expressed as,

$$\begin{aligned} \hat{{y}}_{l, \mathrm{tuned}} (x)=50+0.9553\hat{{y}}_l (x) \end{aligned}$$
(28)

The three-dimensional surfaces of the tuning low-fidelity approximation model for the angular distortion are also illustrated in Fig. 11d–f. As can be observed from Fig. 11, the responses from the tuning low-fidelity approximation model are a litter larger than the low-fidelity RBF model in some process parameter region.

Table 3 The angular distortions from two different fidelity models
Full size table
Fig. 11
figure 11

The 3D surfaces of the low-fidelity RBF model and the tuning low-fidelity approximation model

Full size image

As mentioned in Sect. 2.2.3, it is necessary to account for the remaining discrepancy between the tuning low-fidelity approximation model and the high-fidelity data when the high-fidelity data are far from sufficient to explore the behavior of the weld distortion on the space of the process parameters. The differences between the tuning low-fidelity approximation model and high-fidelity data are calculated by Eq. (10) and are summarized in Table 4. The scaling function can be constructed by taking the high-fidelity sample set and the remaining differences as inputs and output, which is demonstrated in Fig. 12. As illustrated from Fig. 12, there exist large remaining differences in the boundary area of the process parameter domain. By using this scaling function to take the remaining differences into consideration, the finally variable-fidelity approximation model can be obtained as shown in Fig. 13. In the next subsection, two validation approaches will be adopted to compare the prediction accuracy of the obtained variable-fidelity approximation model with those of approximation models, which are constructed with single-fidelity data.

Table 4 The remaining differences between the tuning low-fidelity approximation model and the high-fidelity data
Full size table
Fig. 12
figure 12

The 3D surfaces of the scaling function for angular distortion

Full size image
Fig. 13
figure 13

The variable-fidelity approximation model for angular distortion

Full size image

Discussion of prediction accuracy of the variable-fidelity approximation model

To measure the prediction ability of the variable-fidelity approximation model, two validation approaches are introduced. The first one is the leave-one-out cross-validation approach, which does not require additional test points. The basic processes of obtaining the relative LOO error for each sample point can be divided into four steps.

Step 1: :

For the high-fidelity sample set \(X^{h}=\left\{ {x_1^h ,x_2^h ,\ldots ,}\right. \left. {x_M^h } \right\} \), remove one of the sample points.

Step 2: :

Construct the approximation model based on the remaining sample points \(X_{-i}^h =\left\{ {x_1^h ,x_2^h ,\ldots ,x_{i-1}^h ,}\right. \left. {x_{i+1}^h ,\ldots ,x_M^h } \right\} \) and use it to predict the response value for the omitted sample.

Step 3: :

Calculate the absolute values of the relative difference between the actual and predicted values for the omitted sample.

$$\begin{aligned} RE_{LOO} =\left( {\hat{{f}}^{-i}(x_i^h )-f^{h}(x_i^h )} \right) /f^{h}(x_i^h ) \end{aligned}$$
(29)

where \(f^{h}(x_i^h )\) is the actual high-fidelity response value at \(x_i^h \), \(\hat{{f}}^{-i}(x_i^h )\) is the predicted value of \(x_i^h \) using the approximation model constructed based on the sample set \(X_{-i}^h =\left\{ {x_1^h ,x_2^h ,\ldots ,x_{i-1}^h ,x_{i+1}^h ,\ldots ,x_M^h } \right\} \).

Step 4: :

Repeat Step 1 to Step 3 until all sample points in the high-fidelity sample set are considered.

Figure 14 summarizes the comparison results among variable-fidelity approximation model (VFAM), single-fidelity RBF approximation model based on high-fidelity data (HFRBFAM), and single-fidelity BPNN approximation model based on high-fidelity data (HFBPAM). Since the single-fidelity RBF approximation model based on low-fidelity data (LFRBFAM) and the single-fidelity BPNN approximation model based on low-fidelity data (LFBPAM) do not use the high-fidelity data, it is meaningless to valid them by using the leave-one-out cross-validation approach. As can be seen from Fig. 14, the relative LOO errors from the proposed VFAM are smaller than ones from HFRBFAM at the most high-fidelity sample points (9/12), which indicates that the prediction accuracy of VFAM outperforms that of HFRBFAM. Compared with HFBPAM, the proposed VFAM outperforms it at all high-fidelity sample points, except for the relative LOO errors at NO.3 and NO.7.

Fig. 14
figure 14

The comparison results among HFRBFAM, HFBPAM, and VFAM considering LOO error metrics

Full size image

To further illustrate the merits of the proposed approach, a comparison of the prediction accuracy among VFAM, LFRBFAM, HFRBFAM, LFBPAM, and HFBPAM is made by conducting additional laser welding experiments. Additional 5 test points within the design domain are generated and summarized in Table 5. Taking the absolute values of relative errors between test values and the predicted values from LFRBFAM, HFRBFAM, LFBPAM, and HFBPAM as the baseline, the bar-charts plotted in Fig. 15 shows the relative improvement percentages of the VFAM. As illustrated in Fig. 15, the absolute values of relative errors are reduced by a maximum of 96% and a minimum of 58% using the VFAM compared to the LFRBFAM. Compared with LFBPAM, the absolute values of relative errors are reduced by a maximum of 93% and a minimum of 44% using the VFAM. This is what we expected as the low-fidelity finite element simulation results can only reflect the trend of angular distortion changing of the process parameters. Notice that although the HFRBFAM and HFBPAM are constructed using the high-fidelity experimental data, their mean absolute value of the relative error are still larger than the VFAM by about 15% and 40%, respectively. The reason is that the VFAM can make full use of the data from low-fidelity finite element model and obtains desired accuracy of an approximation model with a small amount of high-fidelity sample points.

Table 5 The additional test points
Full size table
Fig. 15
figure 15

The comparison results among VFAM, LFRBFAM, HFRBFAM, LFBPAM, and HFBPAM on additional test points

Full size image

Discussion of the contributes rates of process parameters on angular distortion

Based on the constructed variable-fidelity approximation model, the contribution rates of the process parameters and their interactions contribution rates to angular distortion are analyzed and summarized in Fig 16. In Fig 16, the positive contribution rates indicate that their corresponding output response will increase with an increase in the discussed process parameters; otherwise, decreases. The magnitude of the bars demonstrated its degree of importance to the bead geometrical characteristics. The symbol \(\cap \) indicates the interaction contribution rate to the output performance for different combination types of process parameters. As observed in Fig. 16, LP has the most significant positive contribution rate to angular distortion, which accounts for nearly 70% of the total part. LFP has the most significant negative contribution rate to angular distortion (about 22%), indicating that it will be very helpful to decrease the magnitude of angular distortion by selecting a larger LFP. In terms of the interactions between process parameters, the interactions contribution rates of LP and LFP exhibits the strongest interactions (about 3.2%), which is about 2 times more than that of LFP\(\cap \)WS. WS has positive contribution rates to angular distortion, while its contribution is not obvious.

Fig. 16
figure 16

Contribute rates of process parameters on angular distortion

Full size image

Conclusion

In this work, a variable-fidelity approximation modeling approach is developed to predict the welding-induced angular distortion in the whole process parameter space. The proposed variable-fidelity approximation modeling approach has been applied to predict the angular distortion of fiber laser keyhole welding on 316L stainless steel. Two different types of validation approaches are used to measure the prediction accuracy of the variable-fidelity approximation model. Following conclusions can be drawn: 1) the variable-fidelity approximation model, which can make full use of the data from both the low-fidelity finite element model and high-fidelity laser welding experiment, significantly outperforms the single-fidelity approximation models solely based on low-fidelity or high-fidelity models. 2) by analyzing the contribution rates of the process parameters and their interactions contribution rates to angular distortion, it is found that LP has the most significant positive contribution rates to the angular distortion, LFP has the most negative contribution rate to the angular distortion, while the effect of WS on angular distortion is relatively weaker.

Overall, the proposed variable-fidelity approximation modeling approach provides a promising way to predict welding-induced angular distortion in laser welding. It is noted that this study does not assess the uncertainty, such as variations of the process parameters and imprecise measurements, associated with the prediction of welding-induced angular distortion. Since the uncertainty may cause angular distortion variation, adopting some uncertainty information quantification approaches, e.g., an efficient probability distribution function aggregation approach proposed by Cai et al. (Cai et al. 2017), to consider the uncertainty during the prediction of the angular distortion will be investigated in our future work.